Daily Runoff Prediction Method Based on Secondary Decomposition and the GTO-Informer-GRU Model
Abstract
1. Introduction
- (1)
- Develop a high-precision daily runoff prediction methodology specifically tailored for water resource management in the Liyuan Basin, Yunnan Province;
- (2)
- Investigate the effectiveness of STL-CEEMDAN secondary decomposition in processing complex hydrological time series with multi-scale variability;
- (3)
- Validate the superiority of the GTO-optimized Informer-GRU hybrid architecture in capturing both global and local temporal patterns in runoff dynamics;
- (4)
- Provide a comprehensive technical framework and practical insights for water resource management and flood control in similar plateau mountainous watersheds.
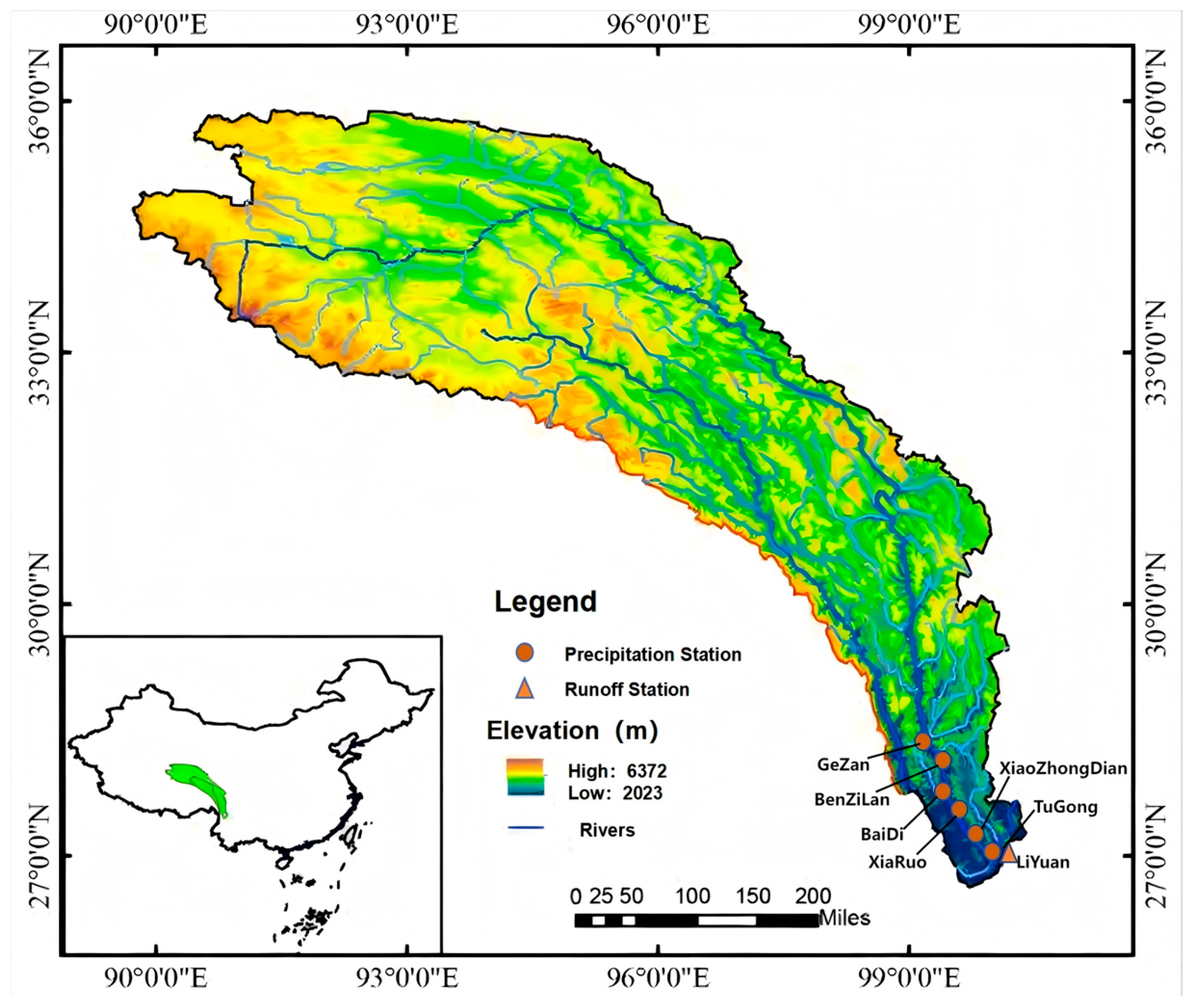
2. Study Area and Data Sources
3. Research Methods
3.1. Time Series Secondary Decomposition
3.1.1. STL Decomposition Method
3.1.2. CEEMDAN Decomposition Method
3.1.3. STL-CEEMDAN Joint Decomposition
3.2. Deep Informer-GRU Network Architecture Construction and Optimization
3.2.1. Informer
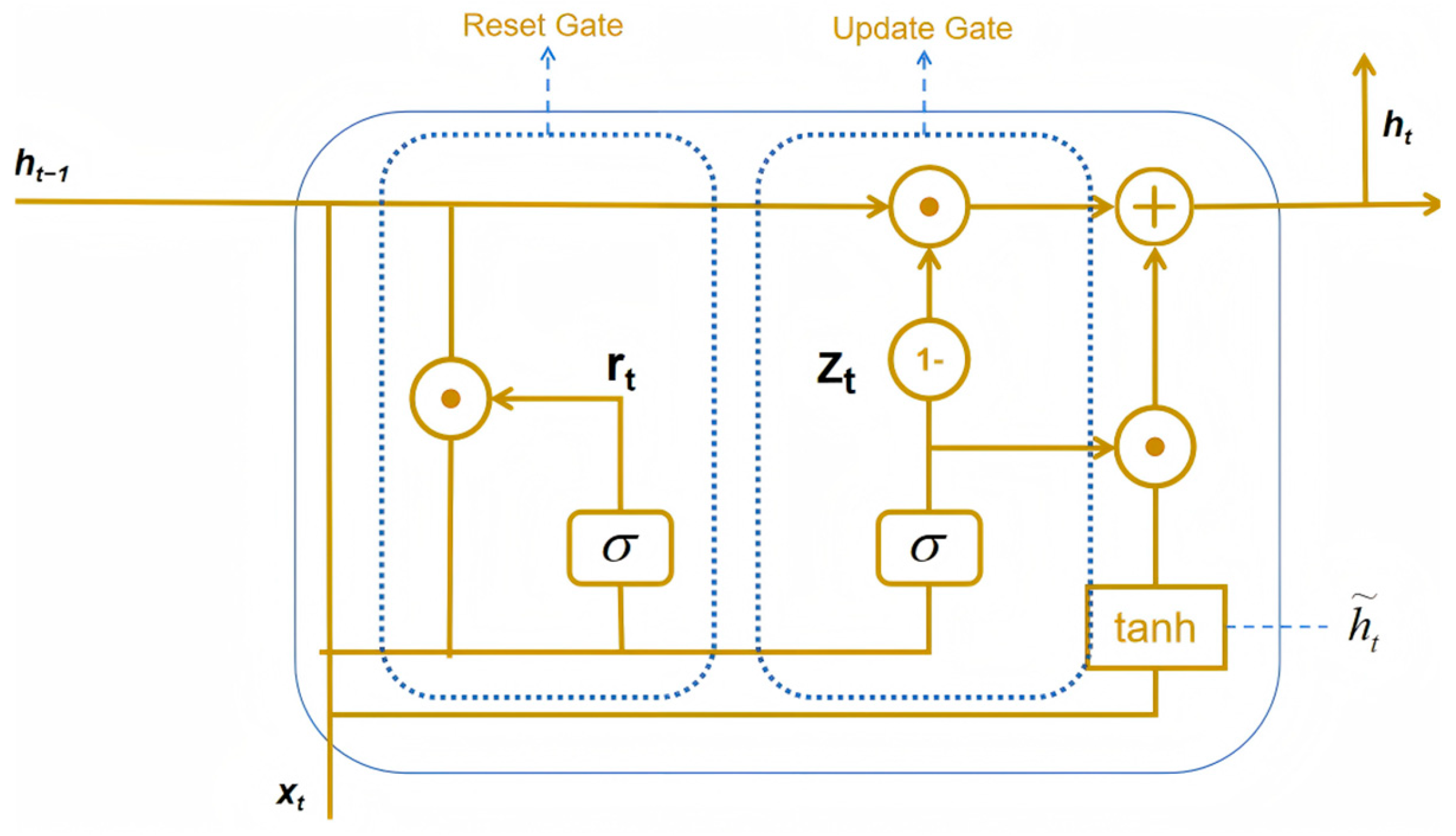
3.2.2. GRU
3.2.3. Informer-GRU Network Construction
3.2.4. Forecasting Process
3.3. Model Training and Optimization Methods
3.3.1. GTO Optimization Algorithm
3.3.2. Multi-Objective Loss Function Design
3.3.3. Interpretability Methods
3.4. Model Evaluation Metrics
4. Results Analysis
4.1. Data Preprocessing
4.2. STL-CEEMDAN Secondary Decomposition
4.2.1. STL Decomposition
- (1)
- Original Runoff Series: The series exhibits approximately nine complete cycles, indicating distinct inter-annual periodicity. Peak values show non-uniform distribution with inter-annual variations in intensity, where some years display significantly higher peaks than others. This pattern likely reflects differences in precipitation intensity and climate variability impacts across different years.
- (2)
- Trend Component: The trend component reveals long-term evolution patterns of the runoff series, manifesting as a nonlinear variation process. The first half primarily shows an ascending trend, potentially associated with factors such as reduced watershed vegetation and long-term precipitation increases. The latter half exhibits smooth curves with gradual long-term changes, possibly related to stable underlying surface conditions and consistent precipitation patterns. The final segment shows a declining trend, potentially linked to increased watershed water consumption and ecological restoration activities.
- (3)
- Seasonal Component: Displays regular oscillations with annual periodicity (365 days), with peaks concentrated during the rainy season (e.g., summer) and troughs during the dry season (e.g., winter). The amplitude variations of the seasonal component closely resemble those of the original series, indicating that seasonal variations are the dominant factor in runoff changes. This characteristic aligns with hydrological systems being significantly influenced by seasonal precipitation patterns.
- (4)
- Residual Component: Exhibits periodic fluctuation characteristics, indicating that the residual contains information from short-term meteorological events causing runoff fluctuations, irregular hydrological processes, extreme event information, measurement noise, and other random disturbances. This provides an information foundation for CEEMDAN decomposition.

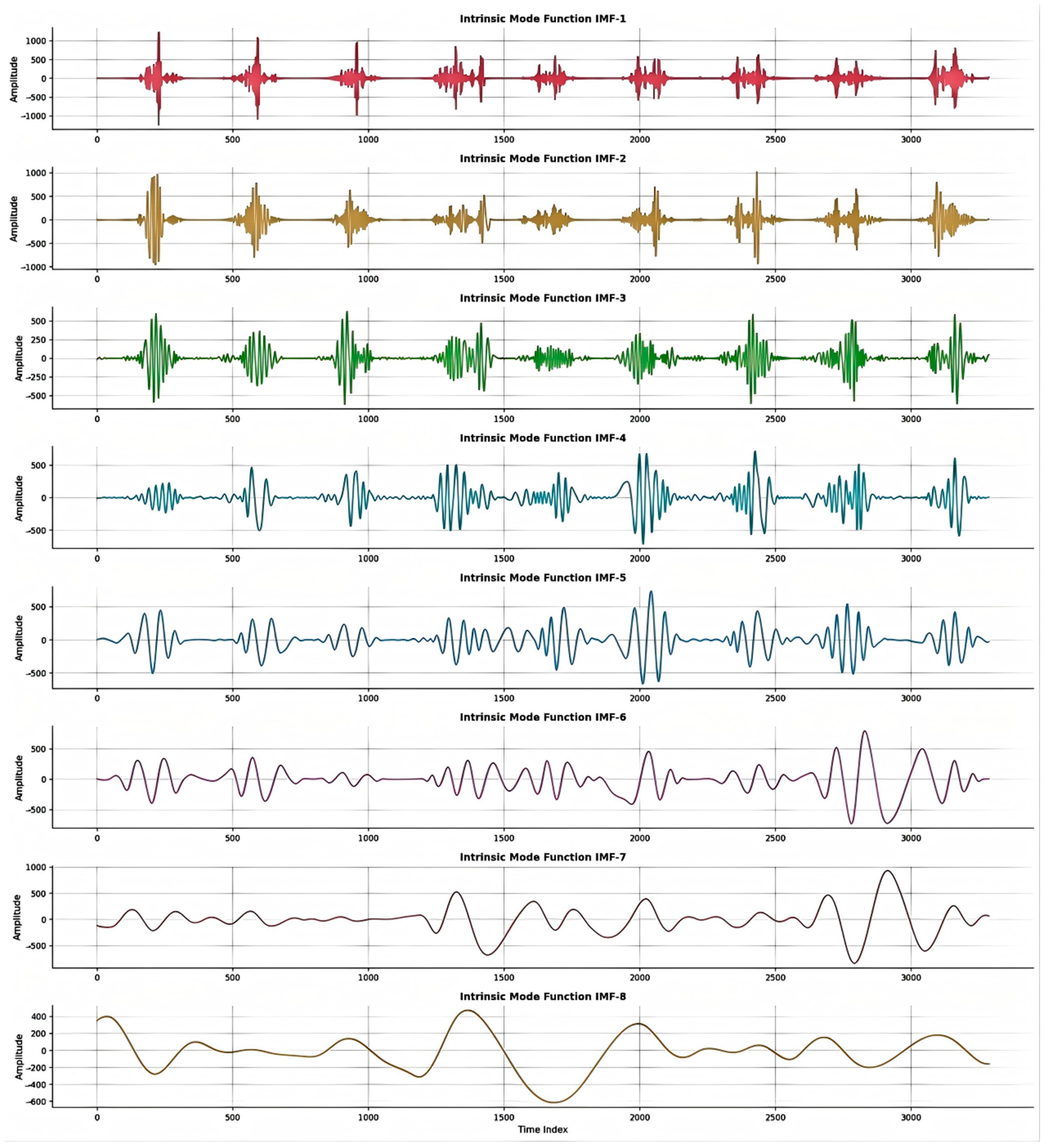
4.2.2. CEEMDAN Decomposition
4.3. Dataset Preparation and Splitting
4.4. GTO Optimization Results
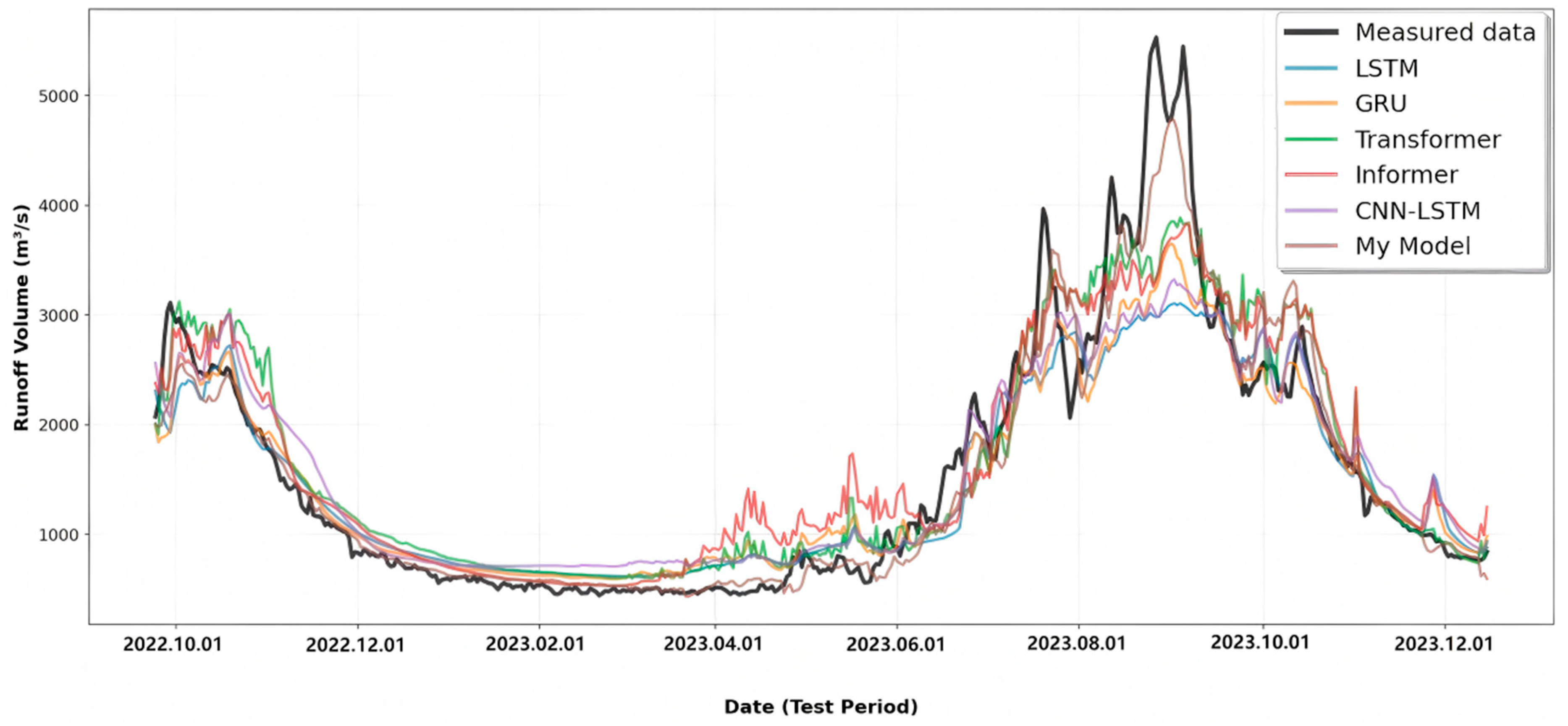
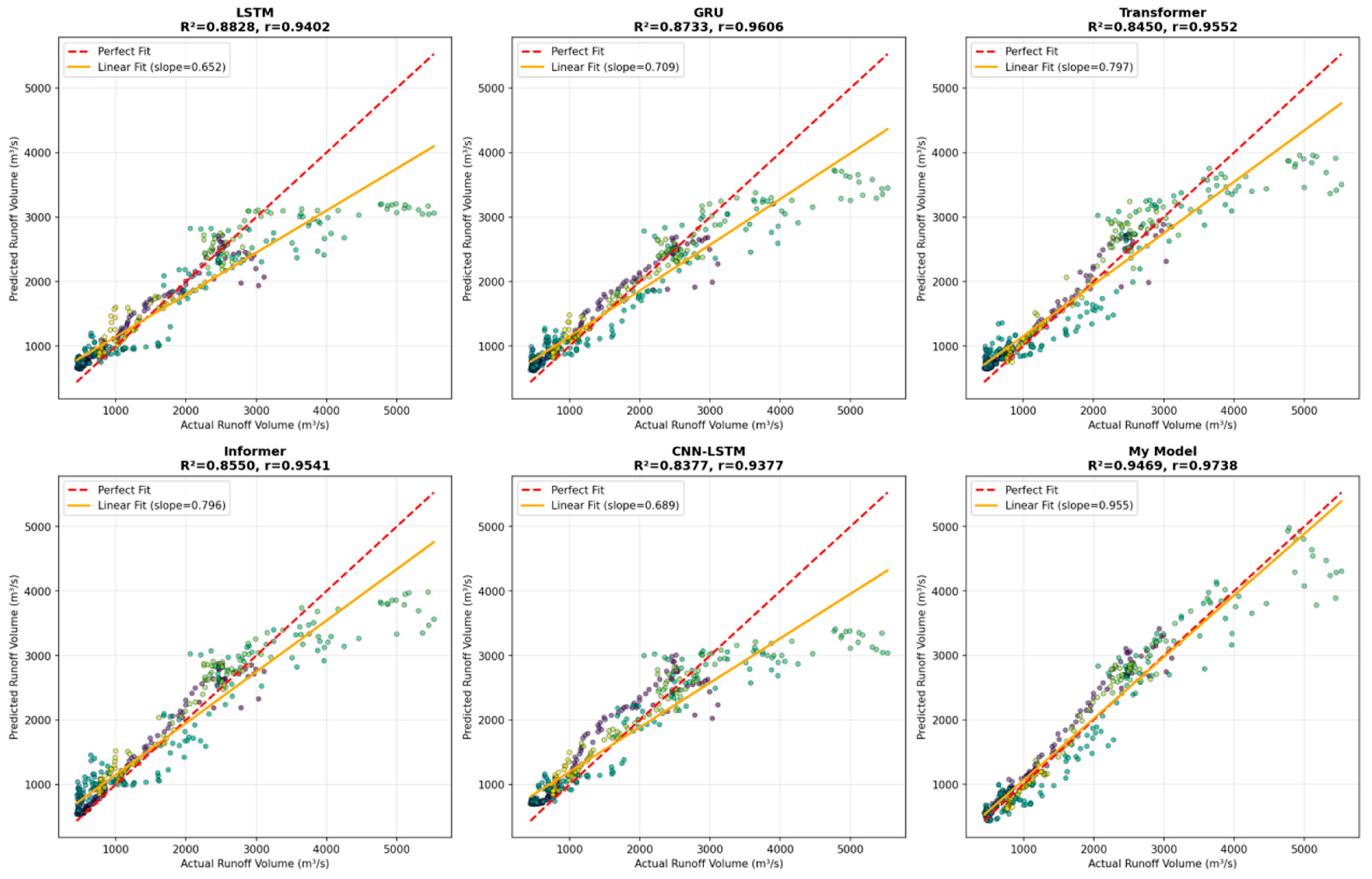
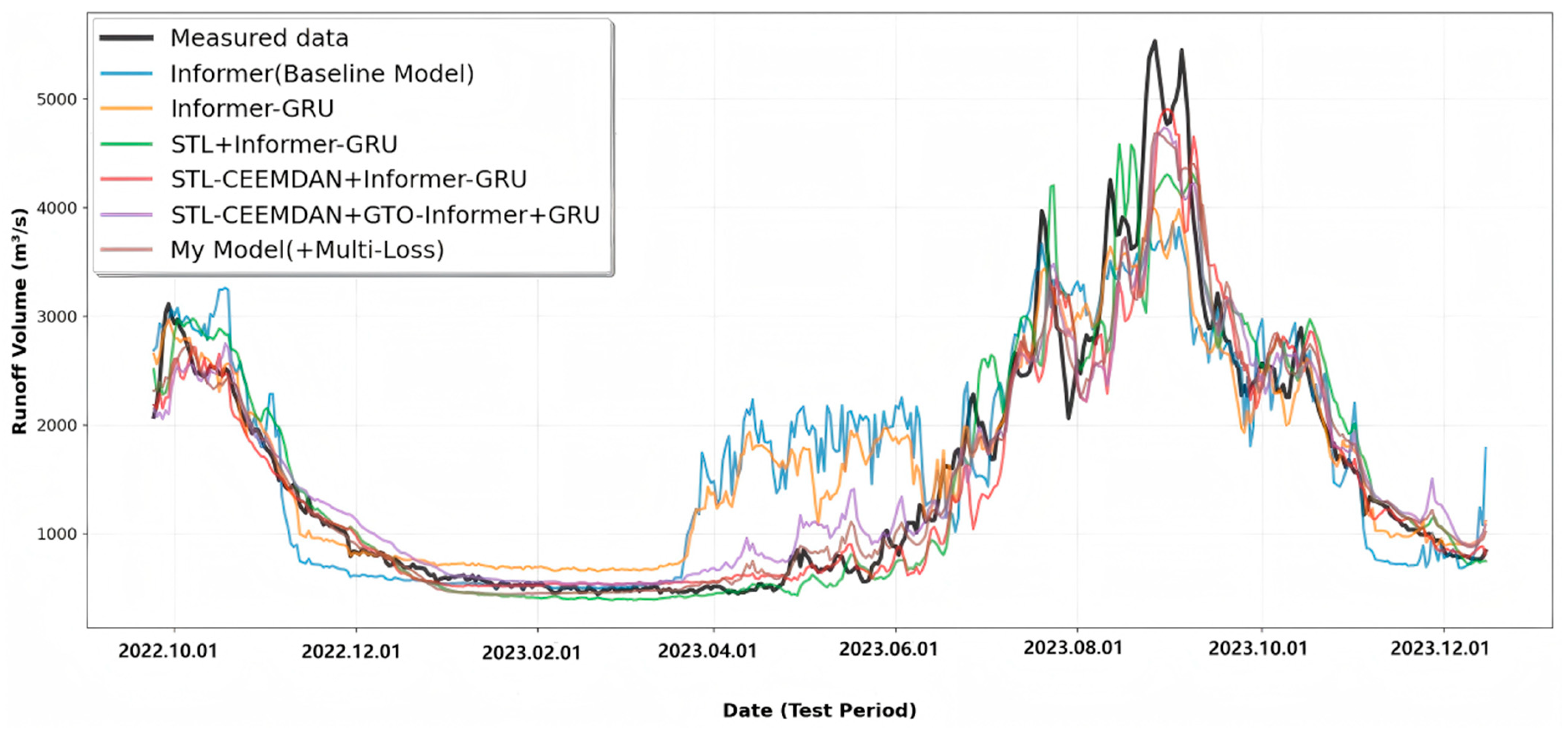
4.5. Prediction Results Analysis
4.6. Comparative Experiment Results Analysis
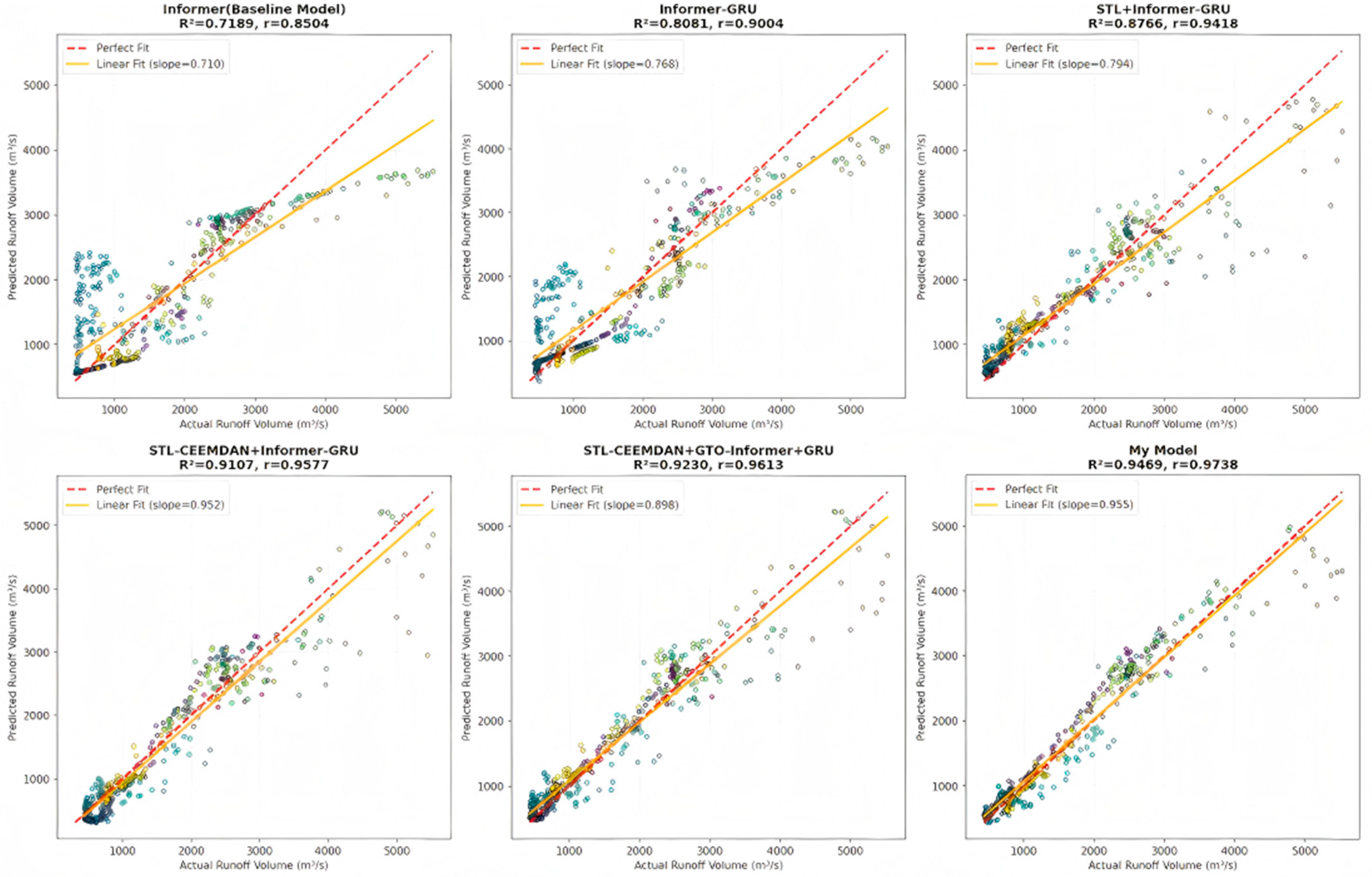
4.7. Ablation Experiment Results Analysis
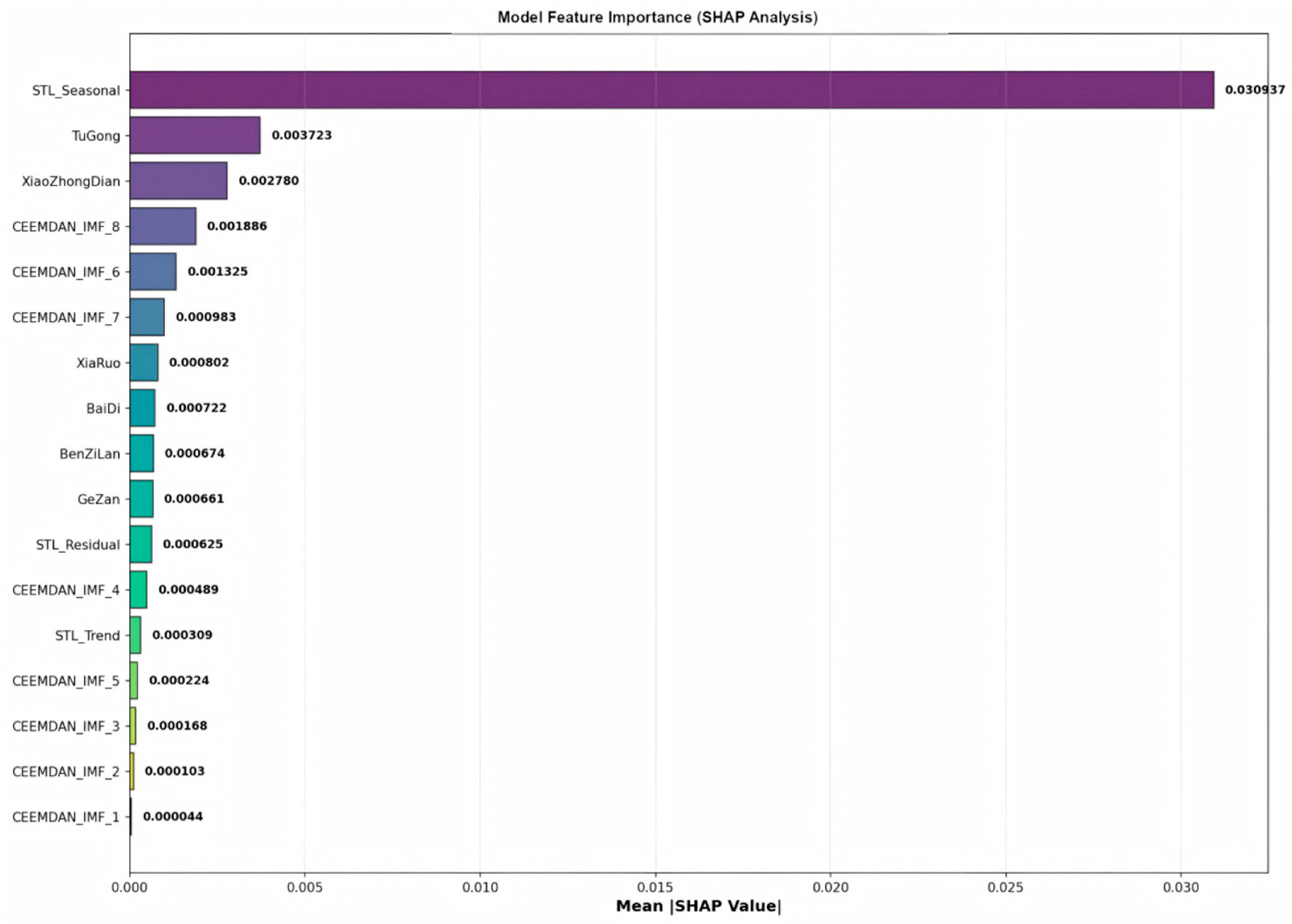
4.8. Model Interpretability Analysis
5. Discussion
5.1. Model Performance Comparison with Existing Studies
5.2. Applicability Analysis and Generalization Potential
5.3. Implications for Water Resource Management in Yunnan Region
5.4. Methodological Limitations and Future Research Directions
6. Conclusions
- (1)
- Dual decomposition strategy significantly enhances feature extraction capability: The STL-CEEMDAN hierarchical decomposition framework achieves precise separation of multi-scale features in runoff data. STL effectively extracts deterministic components such as trend and seasonality, while CEEMDAN further decomposes residuals into IMF components of different frequencies, filtering high-frequency noise while preserving critical information such as extreme events and short-term fluctuations. Compared to single decomposition methods, dual decomposition enhances the physical interpretability of input features, providing more targeted inputs for subsequent model learning.
- (2)
- Informer-GRU hybrid architecture enables synergistic modeling of global and local features: By integrating Informer’s ProbSparse attention mechanism with GRU’s gating memory mechanism, the model simultaneously captures long-range dependencies in runoff sequences (such as inter-annual trends) and local temporal features (such as short-term flood fluctuations). This synergy enhances the model’s capability to fit complex hydrological processes.
- (3)
- GTO optimization and multi-objective loss function improve model performance and robustness: The GTO algorithm achieves global optimization of model architectural parameters (such as hidden layer numbers and attention heads) and training hyperparameters (such as learning rate and batch size), avoiding the problem of traditional parameter tuning falling into local optima. The multi-objective loss function comprehensively considers metrics such as MSE, MAE, and NSE, balancing numerical accuracy with the physical rationality of hydrological processes, making the model more robust in runoff prediction.
- (4)
- Case validation demonstrates excellent prediction accuracy and generalization capability: In daily runoff prediction for the Liyuan watershed from 2015–2023, the model achieved R2 and NSE values of 0.9469 and KGE of 0.9582 on the test set, significantly outperforming comparative models such as LSTM, GRU, and Transformer. Time-series curve and scatter plot analyses show that the model can accurately track runoff peaks, valleys, and seasonal variations, with particularly smaller prediction deviations during extreme flood periods. Ablation experiments confirm that the cumulative contribution of key components such as dual decomposition and GTO optimization improves model performance by 31.72% compared to the baseline Informer.
- (5)
- Feature importance analysis reveals prediction decision mechanisms: SHAP analysis indicates that seasonal components extracted by STL are the core features affecting prediction (average SHAP value of 0.0394), reflecting the essential nature of watershed runoff being driven by seasonal precipitation. Local precipitation stations (such as TuGong station) and medium-low frequency IMF components contribute significantly to short-term fluctuation prediction, validating the model’s effective identification of hydrological process driving factors.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Solaimani, K. Rainfall-runoff prediction based on artificial neural network (a case study: Jarahi watershed). Am.-Eurasian J. Agric. Environ. Sci. 2009, 5, 856–865. [Google Scholar]
- Li, F.F.; Cao, H.; Hao, C.F.; Qiu, J. Daily Streamflow Forecasting Based on Flow Pattern Recognition. Water Resour. Manag. 2021, 35, 4601–4620. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z.; Dong, J.; Cui, X.; Tao, S.; Chen, X. Robust runoff prediction with explainable artificial intelligence and meteorological variables from deep learning ensemble model. Water Resour. Res. 2023, 59, e2023WR035676. [Google Scholar] [CrossRef]
- Mao, G.; Wang, M.; Liu, J.; Wang, Z.; Wang, K.; Meng, Y.; Zhong, R.; Wang, H.; Li, Y. Comprehensive comparison of artificial neural networks and long short-term memory networks for rainfall-runoff simulation. Phys. Chem. Earth Parts a/b/c 2021, 123, 103026. [Google Scholar] [CrossRef]
- Han, H.; Morrison, R.R. Improved runoff forecasting performance through error predictions using a deep-learning approach. J. Hydrol. 2022, 608, 127653. [Google Scholar] [CrossRef]
- Lei, X.H.; Wang, H.; Yang, M.X.; Gui, Z.L. Research Progress on Meteorological Hydrological Forecasting under Changing Environments. J. Hydraul. Eng. 2018, 49, 9–18. (In Chinese) [Google Scholar]
- Zhu, S.; Zhou, J.; Ye, L.; Meng, C. Streamflow estimation by support vector machine coupled with different methods of time series decomposition in the upper reaches of Yangtze River, China. Environ. Earth Sci. 2016, 75, 531. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, C.; Wu, Q.; Li, Z.; Jian, S.; Chen, Y. Application of temporal convolutional network for flood forecasting. Hydrol. Res. 2021, 52, 1455–1468. [Google Scholar] [CrossRef]
- Yin, H.; Zhu, W.; Zhang, X.; Xing, Y.; Xia, R.; Liu, J.; Zhang, Y. Runoff predictions in new-gauged basins using two transformer-based models. J. Hydrol. 2023, 622, 129684. [Google Scholar] [CrossRef]
- Zhou, J.; Peng, T.; Zhang, C.; Sun, N. Data pre-analysis and ensemble of various artificial neural networks for monthly streamflow for ecasting. Water 2018, 10, 628. [Google Scholar] [CrossRef]
- Wilbrand, K.; Taormina, R.; ten Veldhuis, M.-C.; Visser, M.; Hrachowitz, M.; Nuttall, J.; Dahm, R. Predicting streamflow with LSTM networks using global datasets. Front. Water 2023, 5, 1166124. [Google Scholar] [CrossRef]
- Clark, S.R.; Lerat, J.; Perraud, J.-M.; Fitch, P. Deep learning for monthly rainfall–runoff modelling: A large-sample comparison with conceptual models across Australia. Hydrol. Earth Syst. Sci. 2024, 28, 1191–1213. [Google Scholar] [CrossRef]
- Wang, F.; Mu, J.; Zhang, C.; Wang, W.; Bi, W.; Lin, W.; Zhang, D. Deep Learning Model for Real-Time Flood Forecasting in Fast-Flowing Watershed. J. Flood Risk Manag. 2025, 18, e70036. [Google Scholar] [CrossRef]
- Xu, D.M.; Li, Z.; Wang, W.C.; Hong, Y.H.; Gu, M.; Hu, X.X.; Wang, J. WaveTransTimesNet: An enhanced deep learning monthly runoff prediction model based on wavelet transform and transformer architecture. Stoch. Environ. Res. Risk Assess. 2025, 39, 883–910. [Google Scholar] [CrossRef]
- Jia, S.; Wang, X.; Xu, Y.J.; Liu, Z.; Mao, B. A New Data-Driven Model to Predict Monthly Runoff at Watershed Scale: Insights from Deep Learning Method Applied in Data-Driven Model. Water Resour. Manag. 2024, 38, 5179–5194. [Google Scholar] [CrossRef]
- Wang, S.; Wang, W.; Zhao, G. A novel deep learning rainfall–runoff model based on Transformer combined with base flow separation. Hydrol. Res. 2024, 55, 576–594. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, R.; Wang, W.; Zheng, Q.; Ma, R.; Tang, R.; Wang, Y. Runoff prediction using combined machine learning models and signal decomposition. J. Water Clim. Change 2025, 16, 230–247. [Google Scholar] [CrossRef]
- He, F.; Wan, Q.; Wang, Y.; Wu, J.; Zhang, X.; Feng, Y. Daily Runoff Prediction with a Seasonal Decomposition-Based Deep GRU Method. Water 2024, 16, 618. [Google Scholar] [CrossRef]
- Wang, S.; Yang, K.; Peng, H. Using a seasonal and trend decomposition algorithm to improve machine learning prediction of inflow from the Yellow River, China, into the sea. Front. Mar. Sci. 2025, 12, 1540912. [Google Scholar] [CrossRef]
- Aerts, J.C.J.H. A Review of Cost Estimates for Flood Adaptation. Water 2018, 10, 1646. [Google Scholar] [CrossRef]
- Yu, L.; Wang, X.; Wang, J. An Adaptive Rolling Runoff Forecasting Framework Based on Decomposition Methods. Water Resour. Manag. 2025, 1–24. [Google Scholar] [CrossRef]
- Shiri, F.M.; Perumal, T.; Mustapha, N.; Mohamed, R. A Comprehensive Overview and Comparative Analysis on Deep Learning Models. J. Artif. Intell. 2024, 6, 301–360. [Google Scholar] [CrossRef]
- Roy, S.; Mehera, R.; Pal, R.K.; Bandyopadhyay, S.K. Hyperparameter optimization for deep neural network models: A comprehensive study on methods and techniques. Innov. Syst. Softw. Eng. 2025, 21, 789–800. [Google Scholar] [CrossRef]
- Chen, H.; Kang, L.; Zhou, L.; Zhang, W.; Wen, Y.; Ye, J.; Qin, R. Hybrid multi-module for short-term forecasting of river runoff considering spatio-temporal features. Hydrol. Res. 2025, 56, 60–73. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 4144–4147. [Google Scholar] [CrossRef]
- Ma, X.; Wang, R.; Zhang, Y.; Jiang, C.; Abbas, H. A name disambiguation module for intelligent robotic consultant in industrial internet of things. Mech. Syst. Signal Process. 2020, 136, 106413. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, Z.; Zhang, W.; Yang, J. Application of the ResNet-Transformer Model for Runoff Prediction Based on Multi-source Data Fusion. Water Resour. Manag. 2025. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Hussien, A.G.; Bouaouda, A.; Alzaqebah, A.; Kumar, S.; Hu, G.; Jia, H. An in-depth survey of the artificial gorilla troops optimizer: Outcomes, variations, and applications. Artif. Intell. Rev. 2024, 57, 246. [Google Scholar] [CrossRef]
- Li, Q.; Ishidaira, H.; Bastola, S.; Magome, J. Intercomparison of Hydrological Modeling Performance with Multi-Objective Optimization Algorithm in Different Climates. Annu. J. Hydraul. Eng. JSCE 2009, 53, 19–24. [Google Scholar]
- Huo, J.; Liu, L. Evaluation method of multiobjective functions’ combination and its application in hydrological model evaluation. Comput. Intell. Neurosci. 2020, 2020, 8594727. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. Available online: https://proceedings.neurips.cc/paper/2017/hash/8a20a8621978632d76c43dfd28b67767-Abstract.html (accessed on 30 August 2025).
- Bhargava, D.; Gupta, L.K. Explainable AI in Neural Networks Using Shapley Values. In Biomedical Data Analysis and Processing Using Explainable (XAI) and Responsive Artificial Intelligence (RAI); Khamparia, A., Gupta, D., Khanna, A., Balas, V.E., Eds.; Intelligent Systems Reference Library; Springer: Singapore, 2022; Volume 222. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, R.; Sun, W.; Sun, Y. Advances in Chemical Conditioning of Residual Activated Sludge in China. Water 2023, 15, 345. [Google Scholar] [CrossRef]



| Optimization Category | Parameter Type | Before Optimization | After Optimization |
|---|---|---|---|
| Dataset Parameters | window size | 24 | 26 |
| Label length | 12 | 13 | |
| Forecast step | 1 | 1 | |
| Model Architecture | GRU hidden layers | [110, 353, 499, 223] | [502, 303, 184, 393, 458, 169] |
| Transformer model dimension | 185 | 350 | |
| Number of attention heads | 11 | 12 | |
| Dropout rate | 0.0615 | 0.0735 | |
| Encoder layers | 2 | 3 | |
| Decoder layers | 2 | 1 | |
| Training Hyperparameters | Learning rate | 0.000063 | 0.000095 |
| Batch size | 43 | 39 | |
| Maximum epochs | 38 | 33 | |
| Multi-objective Loss Weights | MSE () | 0.3399 | 0.3418 |
| MAE () | 0.2413 | 0.3624 | |
| Huber () | 0.2880 | 0.2089 | |
| NSE () | 0.1417 | 0.2404 | |
| Correlation () | 0.1117 | 0.1475 |
| Index | Validation Set | Test Set |
|---|---|---|
| R2 | 0.956412 | 0.946936 |
| NSE | 0.956412 | 0.946936 |
| KGE | 0.825308 | 0.958182 |
| RMSE | 268.26 | 271.51 |
| MAE | 181.49 | 186.78 |
| Model | R2 | NSE | RMSE | MAE | KGE |
|---|---|---|---|---|---|
| LSTM | 0.882800 | 0.882800 | 492.98 | 322.47 | 0.838660 |
| GRU | 0.873301 | 0.873301 | 419.54 | 266.01 | 0.735504 |
| Transformer | 0.845000 | 0.845000 | 383.46 | 255.98 | 0.802750 |
| Informer | 0.855000 | 0.855000 | 385.49 | 246.83 | 0.812250 |
| CNN-LSTM | 0.837734 | 0.837734 | 474.79 | 308.23 | 0.727351 |
| My Model | 0.946936 | 0.946936 | 271.51 | 186.78 | 0.958182 |
| Model | R2 | NSE | MAE | KGE | R2 Improvement |
|---|---|---|---|---|---|
| Informer (Baseline) | 0.718869 | 0.718869 | 422.57 | 0.772414 | 0 |
| +GRU | 0.808096 | 0.808096 | 371.68 | 0.821542 | 12.41% |
| +STL | 0.876647 | 0.876647 | 263.40 | 0.831677 | 8.48% |
| +CEEMDAN | 0.910695 | 0.910695 | 243.94 | 0.930806 | 3.88% |
| +GTO | 0.922986 | 0.922986 | 206.68 | 0.921828 | 1.34% |
| +Multi-Loss (MyModel) | 0.946936 | 0.946936 | 186.78 | 0.958182 | 2.59% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Ma, Y.; Hu, A.; Wang, Y.; Tian, H.; Dong, L.; Zhu, W. Daily Runoff Prediction Method Based on Secondary Decomposition and the GTO-Informer-GRU Model. Water 2025, 17, 2775. https://doi.org/10.3390/w17182775
Yu H, Ma Y, Hu A, Wang Y, Tian H, Dong L, Zhu W. Daily Runoff Prediction Method Based on Secondary Decomposition and the GTO-Informer-GRU Model. Water. 2025; 17(18):2775. https://doi.org/10.3390/w17182775
Chicago/Turabian StyleYu, Haixin, Yi Ma, Aijun Hu, Yifan Wang, Hai Tian, Luping Dong, and Wenjie Zhu. 2025. "Daily Runoff Prediction Method Based on Secondary Decomposition and the GTO-Informer-GRU Model" Water 17, no. 18: 2775. https://doi.org/10.3390/w17182775
APA StyleYu, H., Ma, Y., Hu, A., Wang, Y., Tian, H., Dong, L., & Zhu, W. (2025). Daily Runoff Prediction Method Based on Secondary Decomposition and the GTO-Informer-GRU Model. Water, 17(18), 2775. https://doi.org/10.3390/w17182775






