Evaluating Infiltration Methods for the Assessment of Flooding in Urban Areas
Abstract
1. Introduction
2. Materials and Methods
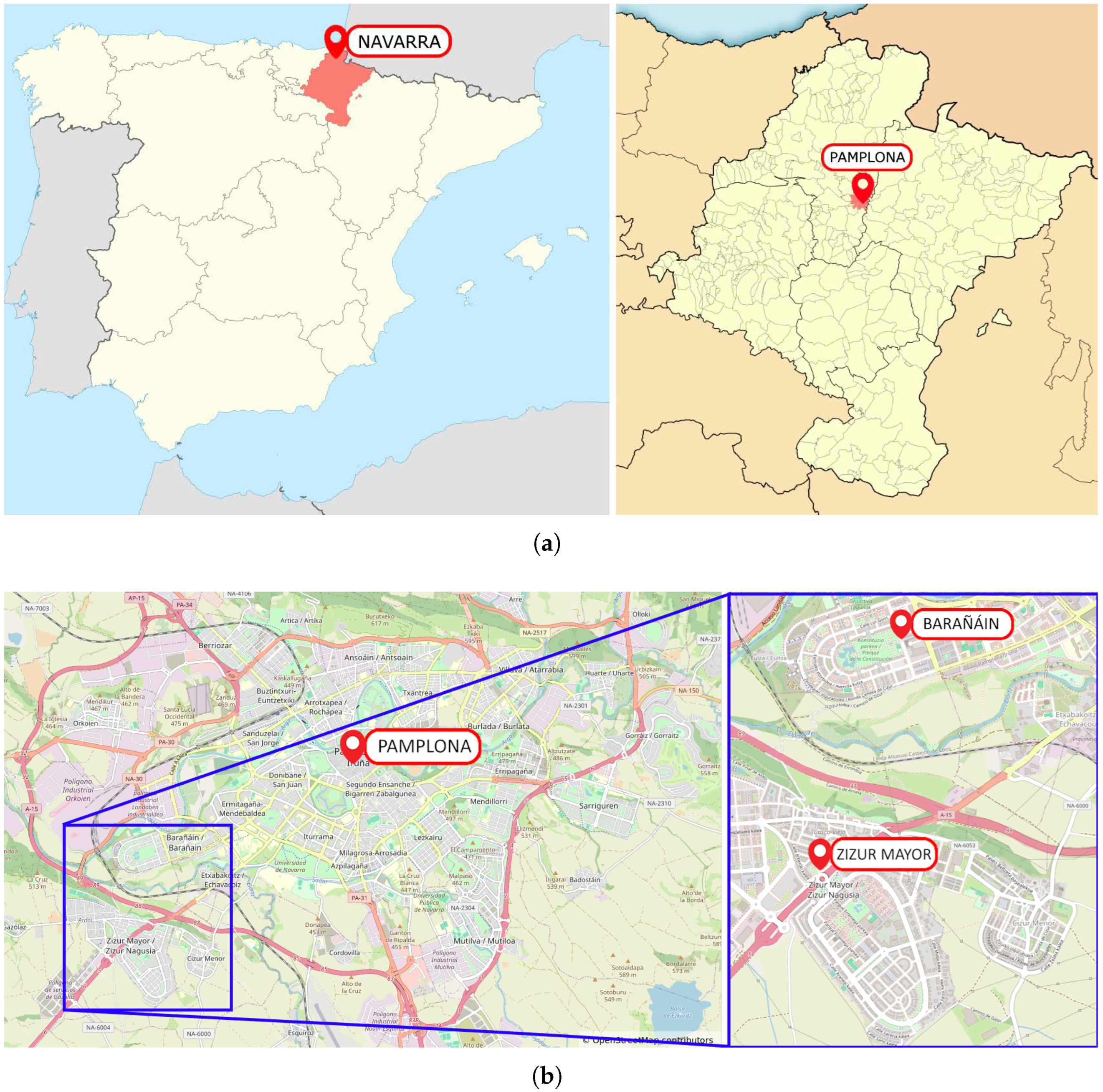
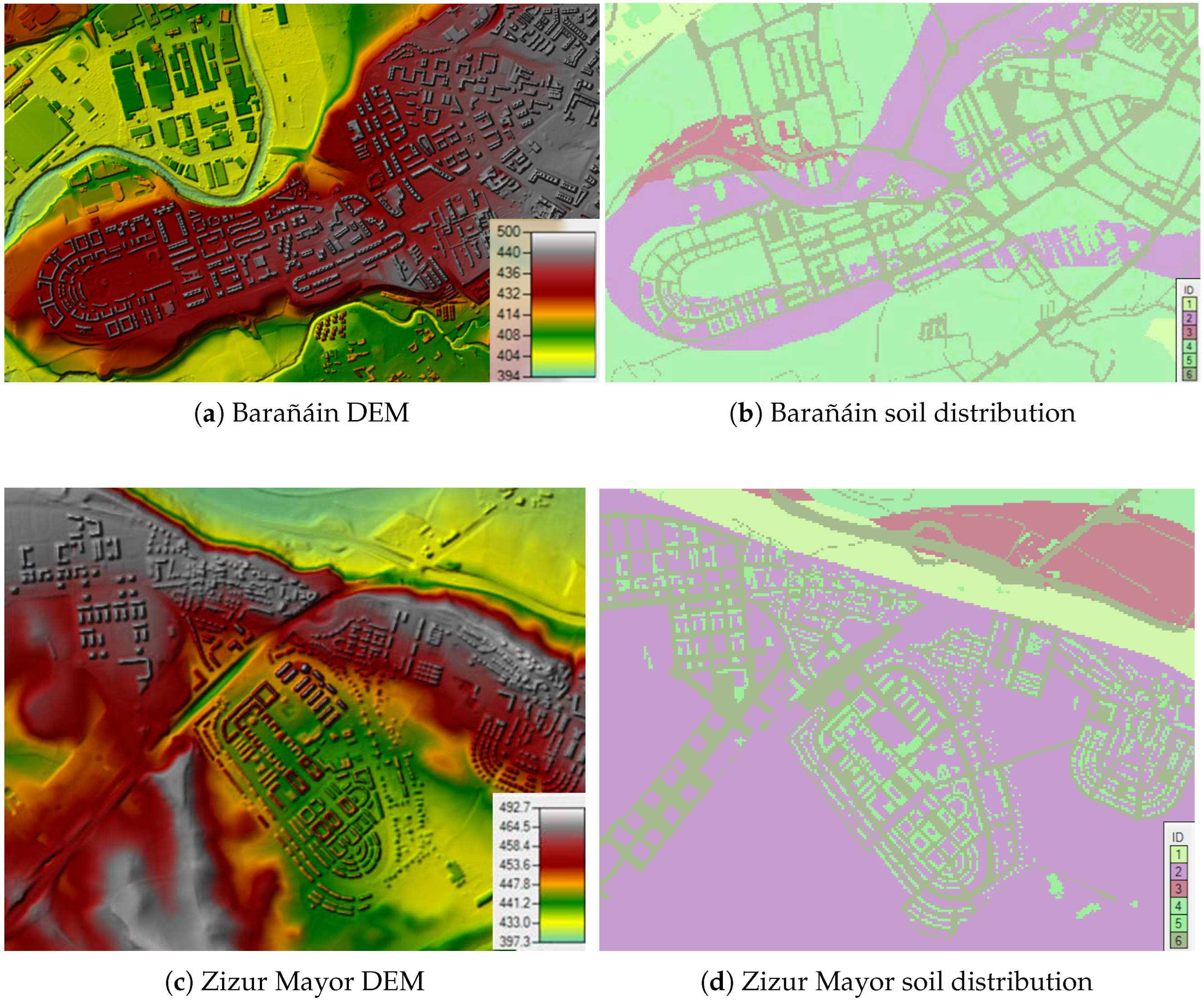
2.1. Case Study
- Digital elevation (terrain and surface) models (DEMs).
- Land cover (CORINE Land Cover project).
- Soil cover.
- 20 July 2010—6:30 p.m. to 7:20 p.m.
- 20 July 2010—9:10 p.m. to 10:40 p.m.
- 18 September 2019—6:30 a.m. to 7:20 a.m.
- 18 September 2019—4:00 p.m. to 4:50 p.m.
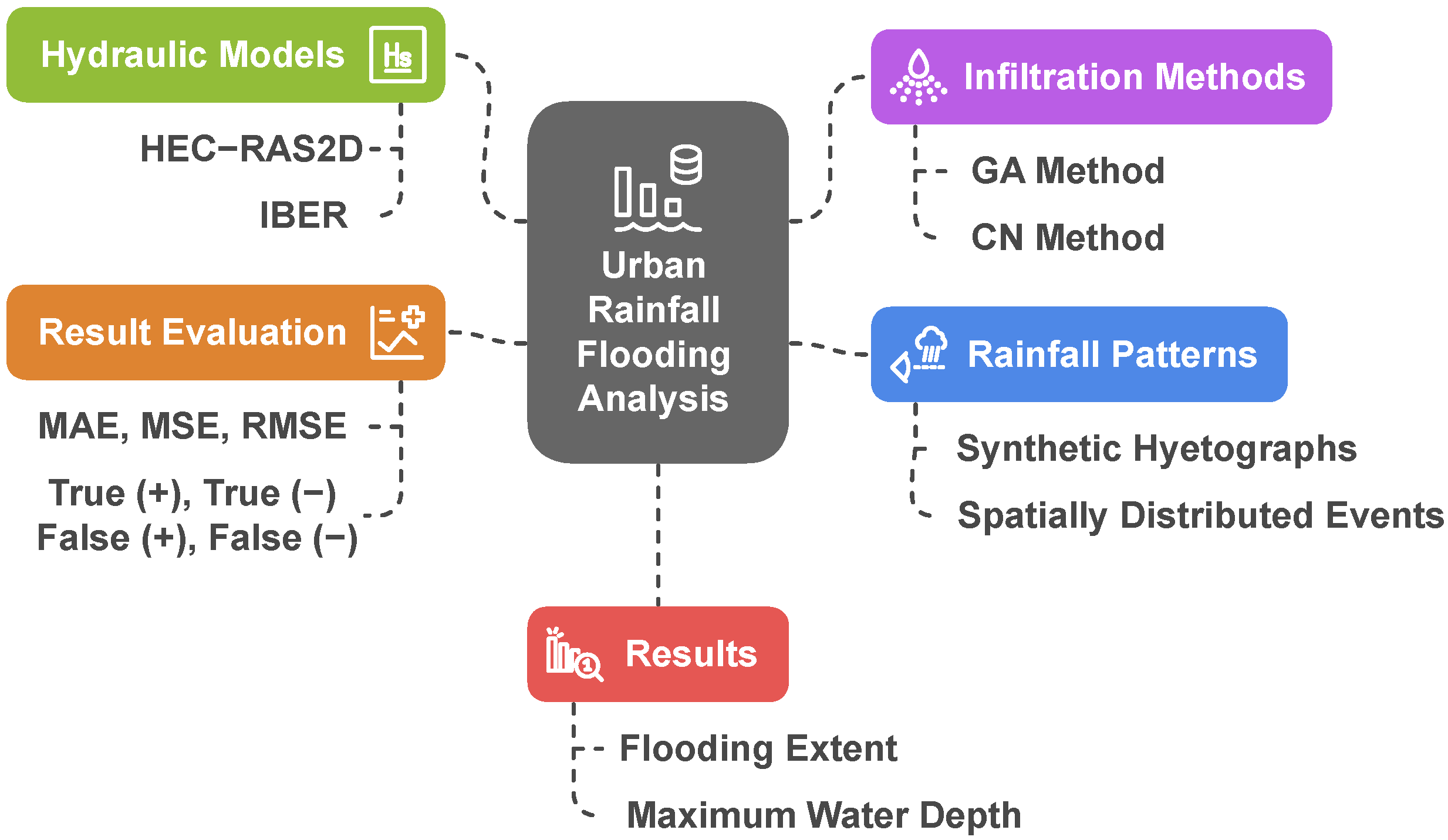
2.2. Methodological Framework
- The two rasters related to a given hydraulic model and rainfall storm, but with infiltration computed with the two different methods.
- The two rasters derived from the two hydraulic models fed with the same rainfall storm and applying the same infiltration method.
3. Results
3.1. Simulation Results
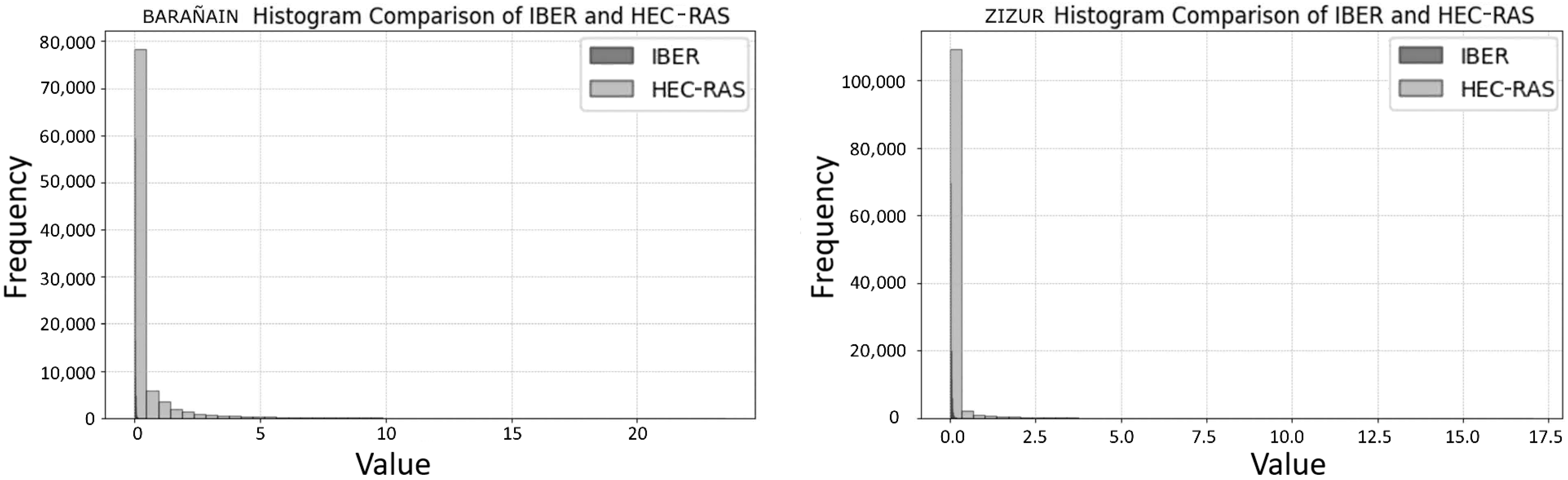
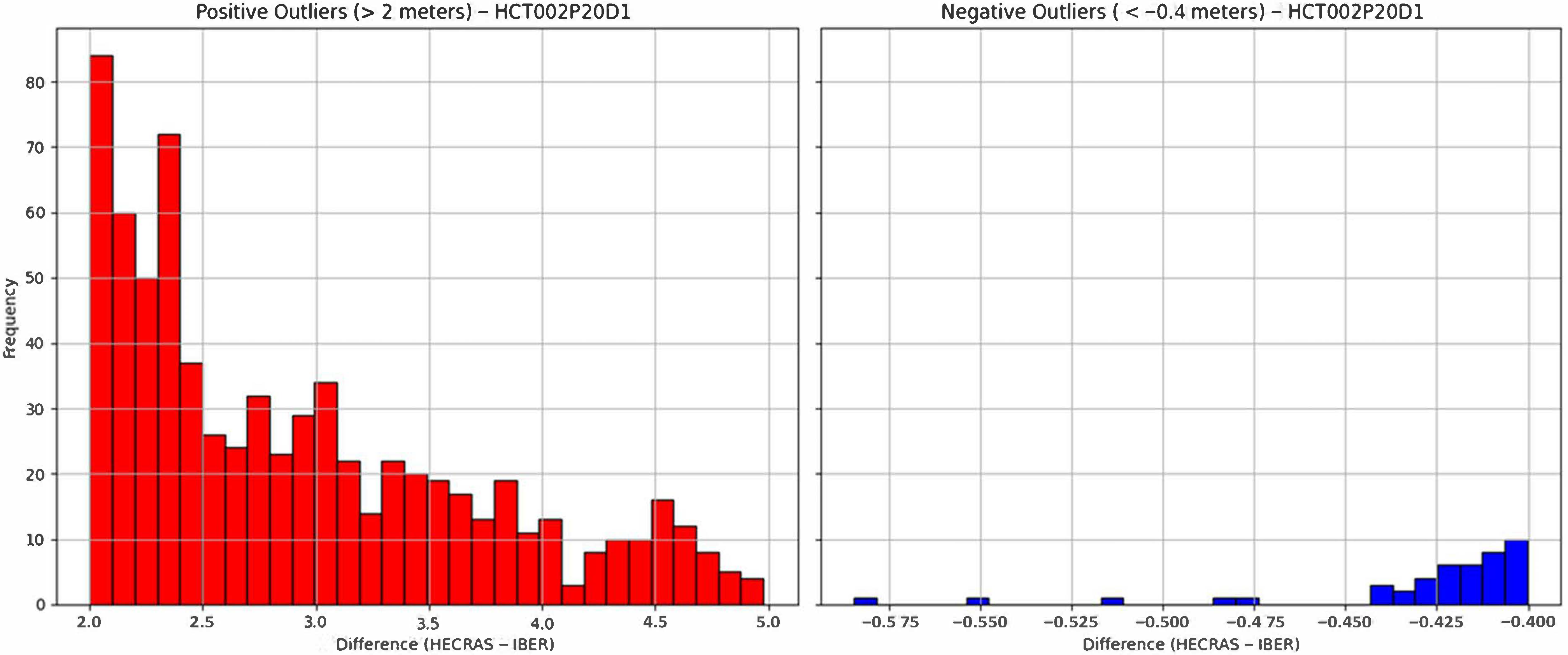
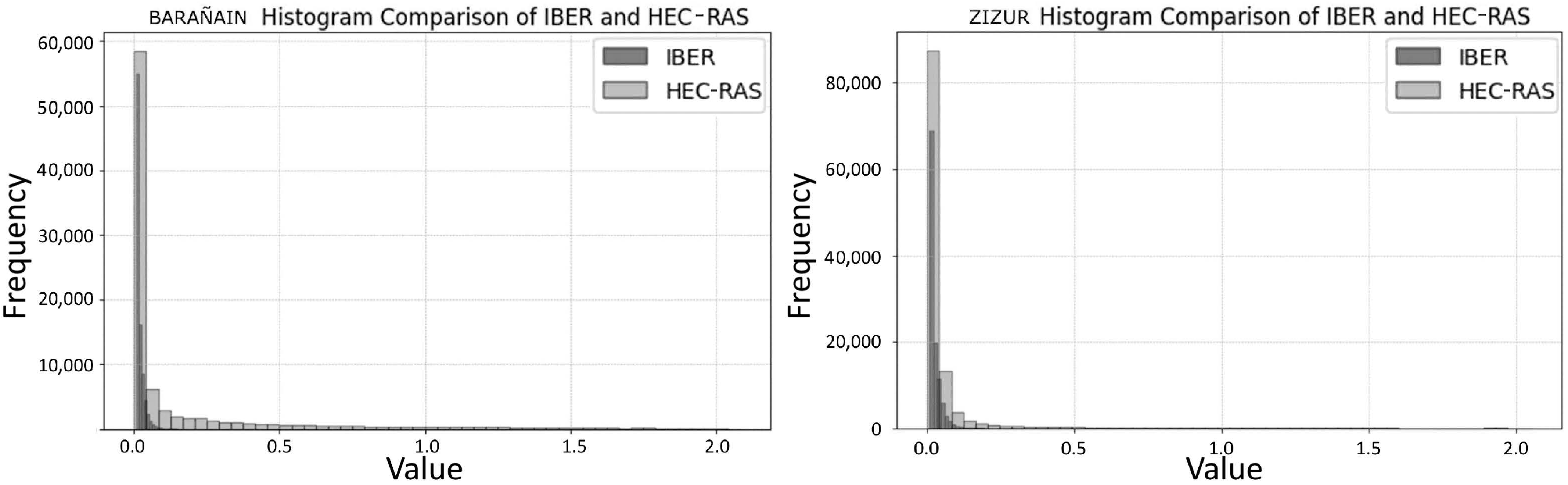
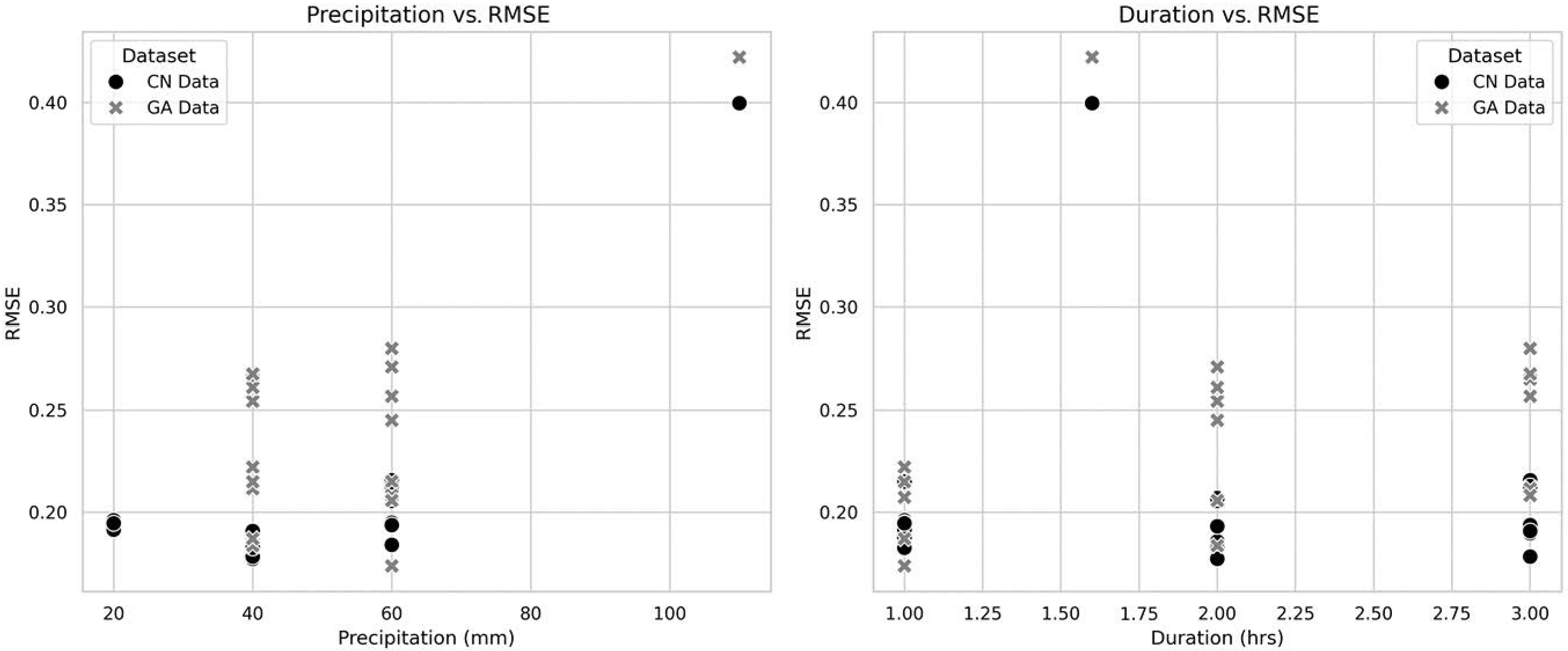
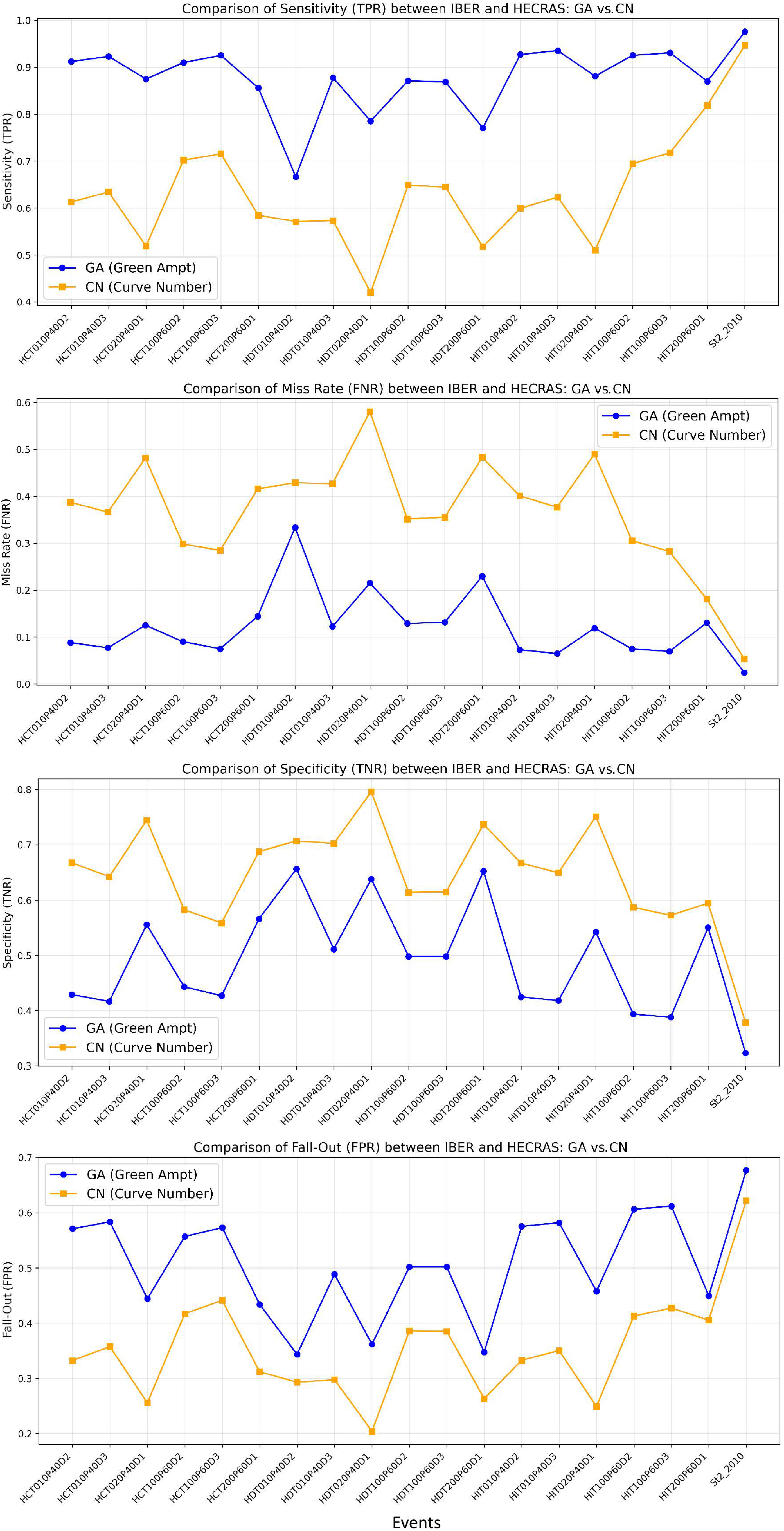
3.2. Model Comparisons and Performance Assessment
3.2.1. Effect of Infiltration Method
3.2.2. Effect of Hydraulic Model
3.3. Considerations Regarding Study Limitations
4. Conclusions
- The choice of an infiltration method fairly influences both water depths and flood extents: Green-Ampt produces more conservative water depth estimates, whereas Curve Number tends to underestimate localized inundation areas.
- Of the two hydraulic models, IBER delivers broader flood extents and lower water depth errors compared to HEC-RAS, suggesting its suitability for studies where spatial coverage accuracy is critical.
- The hyetograph peak position modulates model sensitivity. In this sense, left-skewed storms improve inundation detection, while right-skewed peaks reduce sensitivity by approximately 10%.
- For urban flood risk assessment and planning, the IBER model with the Green-Ampt infiltration method offers the most conservative and reliable predictions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barbosa, S.A.; Wang, Y.; Goodall, J.L. Exploring infiltration effects on coastal urban flooding: Insights from nuisance to extreme events using 2D/1D hydrodynamic modeling and crowdsourced flood reports. Sci. Total. Environ. 2025, 968, 178908. [Google Scholar] [CrossRef] [PubMed]
- Green, H.W.; Ampt, G.A. Studies on Soil Phyics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef]
- Philip, J.R. An infiltration equation with physical significance. Soil Sci. 1954, 77, 153–158. [Google Scholar] [CrossRef]
- Mein, R.G.; Larson, C.L. Modeling infiltration during a steady rain. Water Resour. Res. 1973, 9, 384–394. [Google Scholar] [CrossRef]
- Smith, R.E. The infiltration envelope: Results from a theoretical infiltrometer. J. Hydrol. 1972, 17, 1–22. [Google Scholar] [CrossRef]
- Smith, R.E.; Parlange, J. A parameter-efficient hydrologic infiltration model. Water Resour. Res. 1978, 14, 533–538. [Google Scholar] [CrossRef]
- Horton, R.E. The role of infiltration in the hydrologic cycle. EOS Trans. Am. Geophys. Union 1933, 14, 446–460. [Google Scholar] [CrossRef]
- Holtan, H.N. A Concept for Infiltration Estimates in Watershed Engineering; Agricultural Research Service, United States Department of Agriculture: Washington, DC, USA, 1961. [Google Scholar]
- Overton, D.E. Mathematical Refinement of an Infiltration Equation for Watershed Engineering; U.S. Department ofAgricultural Service: Washington, DC, USA, 1964. [Google Scholar]
- Singh, V.P.; Yu, F.X. Derivation of Infiltration Equation Using Systems Approach. J. Irrig. Drain. Eng. 1990, 116, 837–858. [Google Scholar] [CrossRef]
- Grigorjev, V.Y.; Iritz, L. Dynamic simulation model of vertical infiltration of water in soil. Hydrol. Sci. J. 1991, 36, 171–179. [Google Scholar] [CrossRef]
- Mishra, S.K.; Singh, V.P. SCS-CN Method. In Soil Conservation Service Curve Number (SCS-CN) Methodology; Springer: Dordrecht, The Netherlands, 2003; pp. 84–146. [Google Scholar] [CrossRef]
- Kostiakov, A. On the Dynamics of the Coefficients of Water Percolation in Soils and on the Necessity of Studying It from a Dynamic Point of View for Purpose of Amelioration. In Transactions of the Sixth Commission of the International Society of Soil Science; Fauser, O., Ed.; Sixth Commission; International Society of Soil Science: Rome, Italy, 1932; pp. 17–21. [Google Scholar]
- Furman, A.; Warrick, A.W.; Zerihun, D.; Sanchez, C.A. Modified Kostiakov Infiltration Function: Accounting for Initial and Boundary Conditions. J. Irrig. Drain. Eng. 2006, 132, 587–596. [Google Scholar] [CrossRef]
- Huggins, L.F.; Monke, E.J. A Mathematical Model for Simulating the Hydrologic Response of a Watershed. Water Resour. Res. 1968, 4, 529–539. [Google Scholar] [CrossRef]
- Collis-George, N. Infiltration equations for simple soil systems. Water Resour. Res. 1977, 13, 395–403. [Google Scholar] [CrossRef]
- Loveridge, M.; Rahman, A.; Hill, P.; Babister, M. Investigation into Probabilistic Losses for Design Flood Estimation: A Case Study for The Orara River Catchment, Nsw. Australas. J. Water Resour. 2013, 17, 13–24. [Google Scholar] [CrossRef]
- Imteaz, M.; Mahbub, I. Improved Continuing Losses Estimation Using Initial Loss-Continuing Loss Model for Medium Sized Rural Catchments. Am. J. Eng. Appl. Sci. 2009, 2, 796–803. [Google Scholar] [CrossRef][Green Version]
- Siriwardena, L.; Hill, P.; Mein, R. Investigation of a Variable Proportional Loss Model for Use in Flood Estimation; Monash University: Melbourne, Australia, 1997. [Google Scholar][Green Version]
- Ilahee, M. Modelling Losses in Flood Estimation. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, 2005. [Google Scholar][Green Version]
- Joshi, J. Effect of Surface Characteristics and Rainfall in Infiltration Rate: A Case Study of Kaligandaki River Basin. J. Eng. Technol. Plan. 2023, 4, 96–111. [Google Scholar] [CrossRef]
- Pristianto, H. Improving Infiltration Modeling for Papua’s Small Watershed by Using Rstudio Software Analysis. Int. J. GEOMATE 2024, 26, 44–52. [Google Scholar] [CrossRef]
- Kencanawati, M.; Anwar, N.; Maulana, M.A. Modification of basic hydrology formulation based on an approach of the rational method at field measurement. IOP Conf. Ser. Earth Environ. Sci. 2021, 930, 012051. [Google Scholar] [CrossRef]
- Potdar, D.; Patil, A.; Nale, V. Comparative evaluation of different infiltration models under different soils. Ecol. Environ. Conserv. 2024, 30, 296–302. [Google Scholar] [CrossRef]
- Mesele, H.; Grum, B.; Aregay, G.; Berhe, G.T. Evaluation and comparison of infiltration models for estimating infiltration capacity of different textures of irrigated soils. Environ. Syst. Res. 2024, 13, 26. [Google Scholar] [CrossRef]
- Mirzaee, S.; Zolfaghari, A.A.; Gorji, M.; Dyck, M.; Ghorbani Dashtaki, S. Evaluation of infiltration models with different numbers of fitting parameters in different soil texture classes. Arch. Agron. Soil Sci. 2013, 60, 681–693. [Google Scholar] [CrossRef]
- Mishra, S.K.; Tyagi, J.V.; Singh, V.P. Comparison of infiltration models. Hydrol. Process. 2003, 17, 2629–2652. [Google Scholar] [CrossRef]
- Ramaswamy, M.V.; Yashas Kumar, H.K.; Reddy, V.J.; Nyamathi, S.J. Enhancing infiltration rate predictions with hybrid machine learning and empirical models: Addressing challenges in southern India. Acta Geophys. 2025, 73, 3453–3475. [Google Scholar] [CrossRef]
- Wang, X.; Sample, D.J.; Pedram, S.; Zhao, X. Performance of two prevalent infiltration models for disturbed urban soils. Hydrol. Res. 2017, 48, 1520–1536. [Google Scholar] [CrossRef]
- Hossain Anni, A.; Cohen, S.; Praskievicz, S. Sensitivity of urban flood simulations to stormwater infrastructure and soil infiltration. J. Hydrol. 2020, 588, 125028. [Google Scholar] [CrossRef]
- Guo, K.; Guan, M.; Yu, D. Urban surface water flood modelling—A comprehensive review of current models and future challenges. Hydrol. Earth Syst. Sci. 2021, 25, 2843–2860. [Google Scholar] [CrossRef]
- Alkaddour, A.; Shadoud, M.; Hashemi, M.; Mahmoud, F.; Hammad, M.; Youssef, Y.; Mucsi, L. Urban flood susceptibility mapping using the AHP model and geospatial tools in Quwaiq River Basin, Aleppo Governorate, Syria. DYSONA—Appl. Sci. 2026, 7, 1–19. [Google Scholar] [CrossRef]
- Abdo, H.; Zeng, T.; Alshayeb, M.; Prasad, P.; Ahmed, M.; Albanai, J.; Alharbi, M.; Mallick, J. Multi-criteria analysis and geospatial applications-based mapping flood vulnerable areas: A case study from the eastern Mediterranean. Nat. Hazards 2024, 121, 1003–1031. [Google Scholar] [CrossRef]
- Wahba, M.; Sharaan, M.; Elsadek, W.; Kanae, S.; Hassan, H. Examination of the efficacy of machine learning approaches in the generation of flood susceptibility maps. Environ. Earth Sci. 2024, 83, 429. [Google Scholar] [CrossRef]
- Adelana, A.O. Urban soil infiltration rates on different land use types in southwest Nigeria: Actual versus model estimates. LAUTECH J. Eng. Technol. 2024, 18, 7–21. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Roy, M. Rural-urban spatial inequality in water and sanitation facilities in India: A cross-sectional study from household to national level. Appl. Geogr. 2017, 85, 27–38. [Google Scholar] [CrossRef]
- Sage, J.; Berthier, E.; Gromaire, M.C. Modeling Soil Moisture Redistribution and Infiltration Dynamics in Urban Drainage Systems. J. Hydrol. Eng. 2020, 25, 04020041. [Google Scholar] [CrossRef]
- Strohbach, M.W.; Döring, A.O.; Möck, M.; Sedrez, M.; Mumm, O.; Schneider, A.K.; Weber, S.; Schröder, B. The “Hidden Urbanization”: Trends of Impervious Surface in Low-Density Housing Developments and Resulting Impacts on the Water Balance. Front. Environ. Sci. 2019, 7, 29. [Google Scholar] [CrossRef]
- Instituto Geográfico Nacional. Available online: https://centrodedescargas.cnig.es/CentroDescargas/home (accessed on 25 March 2025).
- Chow, V.T. Applied Hydrology; McGraw Hill: Columbus, OH, USA, 1994. [Google Scholar]
- Mediero, L.; Soriano, E.; Oria, P.; Bagli, S.; Castellarin, A.; Garrote, L.; Mazzoli, P.; Mysiak, J.; Pasetti, S.; Persiano, S.; et al. Pluvial flooding: High-resolution stochastic hazard mapping in urban areas by using fast-processing DEM-based algorithms. J. Hydrol. 2022, 608, 127649. [Google Scholar] [CrossRef]
- SAIH Ebro River Basin. Available online: https://www.saihebro.com/ (accessed on 25 March 2025).
- Scientific Software Group. HEC-RAS; Scientific Software Group: Salt Lake City, UT, USA, 2006. [Google Scholar] [CrossRef]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. Rev. Int. Métod. Numér. Cálc. Diseño Ing. 2014, 30, 1–10. [Google Scholar] [CrossRef]
- United States Department of Agriculture, Soil Conservation Service. Urban Hydrology for Small Watersheds; Technical Release 55 (TR-55); United States Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 1986.
- Samela, C.; Persiano, S.; Bagli, S.; Luzzi, V.; Mazzoli, P.; Humer, G.; Reithofer, A.; Essenfelder, A.; Amadio, M.; Mysiak, J.; et al. Safer_RAIN: A DEM-Based Hierarchical Filling-&-Spilling Algorithm for Pluvial Flood Hazard Assessment and Mapping Across Large Urban Areas. Water 2020, 12, 1514. [Google Scholar] [CrossRef]
- Sathyanarayanan, S. Confusion Matrix-Based Performance Evaluation Metrics. Afr. J. Biomed. Res. 2024, 27, 4023–4031. [Google Scholar] [CrossRef]
- Viji, R.; Prasanna, P.R.; Ilangovan, R. Modified SCS-CN and Green-Ampt Methods in Surface Runoff Modelling for the Kundahpallam Watershed, Nilgiris, Western Ghats, India. Aquat. Procedia 2015, 4, 677–684. [Google Scholar] [CrossRef]
- Wang, W.; Chen, W.; Huang, G. Urban Stormwater Modeling with Local Inertial Approximation Form of Shallow Water Equations: A Comparative Study. Int. J. Disaster Risk Sci. 2021, 12, 745–763. [Google Scholar] [CrossRef]
- Van Mullem, J. Runoff and peak discharges using Green-Ampt infiltration model. J. Hydraul. Eng. 1991, 117, 354–370. [Google Scholar] [CrossRef]
- Ficklin, D.; Zhang, M. A comparison of the curve number and Green-Ampt models in an agricultural watershed. Trans. ASABE 2013, 56, 61–69. [Google Scholar] [CrossRef]
- Su, B.; Huang, H.; Zhu, W. An urban pluvial flood simulation model based on diffusive wave approximation of shallow water equations. Hydrol. Res. 2017, 50, 138–154. [Google Scholar] [CrossRef]
- Martins, R.; Leandro, J.; Chen, A.S.; Djordjević, S. A comparison of three dual drainage models: Shallow water vs local inertial vs. diffusive wave. J. Hydroinform. 2017, 19, 331–348. [Google Scholar] [CrossRef]
- Bergeson, C.B.; Martin, K.L.; Doll, B.; Cutts, B.B. Soil infiltration rates are underestimated by models in an urban watershed in central North Carolina, USA. J. Environ. Manag. 2022, 313, 115004. [Google Scholar] [CrossRef]
- Balacumaresan, H.; Imteaz, M.A.; Hossain, I.; Aziz, M.A.; Choudhury, T. Superiority of artificial neural networks over conventional hydrological models in simulating urban catchment runoff. J. Hydroinform. 2024, 26, 2162–2186. [Google Scholar] [CrossRef]
- Khastagir, A.; Hossain, I.; Anwar, A.H.M.F. Efficacy of linear multiple regression and artificial neural network for long-term rainfall forecasting in Western Australia. Meteorol. Atmos. Phys. 2022, 134, 69. [Google Scholar] [CrossRef]
- Balacumaresan, H.; Imteaz, M.A.; Aziz, M.A.; Choudhury, T. Use of Artificial Intelligence Modelling for the Dynamic Simulation of Urban Catchment Runoff. Water Resour. Manag. 2024, 38, 3657–3683. [Google Scholar] [CrossRef]








| Data | Source | Resolution | Application |
|---|---|---|---|
| Digital elevation model (DEM) | [39] | 2 m | Terrain, model geometry |
| CORINE Land Cover (CLC 2018) | [39] | 10 m | Infiltration model parameters (Green-Ampt, Curve Number) |
| Rainfall events (observed, distributed) | [41] | 15 m and 10 min (1 raster/step) | Rainfall events, boundary conditions for hydraulic model |
| Rainfall events (observed, point rainfall) | [42] | 10 min | Rainfall events, boundary conditions for hydraulic model |
| IDF curves for Pamplona city | [42] | 15 min | Synthetic hyetographs, boundary conditions for hydraulic model |
| Settings | HEC–RAS | IBER |
|---|---|---|
| Terrain and topography | DEM (2 m) | DEM (2 m) |
| Geometry and mesh | Quadrilateral min. area 0.5 m2 avg. area 10 m2 | Triangular side length 2 m |
| Infiltration parameters | Values proposed in [40], based on soil cover and land use | |
| Roughness coefficients | Manning coefficient based on soil cover and land use | |
| Boundary conditions | Rainfall events (see Table 1) | |
| Equations | Diffusion wave | Shallow Water Equations (SWEs) |
| Event | RMSE | MAE | Pre | NPV | Sens | Miss Rate | Spec | Fall-Out | Acc |
|---|---|---|---|---|---|---|---|---|---|
| 20JUL2010_2110 | 0.270 | 0.052 | 0.974 | 0.924 | 0.823 | 0.177 | 0.990 | 0.010 | 0.937 |
| HCP20D1 | 0.116 | 0.010 | 0.998 | 0.973 | 0.554 | 0.447 | 1.000 | 0.000 | 0.974 |
| HCP40D1 | 0.151 | 0.018 | 0.994 | 0.949 | 0.490 | 0.510 | 1.000 | 0.000 | 0.951 |
| HCP60D1 | 0.178 | 0.026 | 0.989 | 0.935 | 0.508 | 0.493 | 0.999 | 0.001 | 0.938 |
| HCP40D2 | 0.148 | 0.018 | 0.995 | 0.952 | 0.507 | 0.493 | 1.000 | 0.000 | 0.955 |
| HCP60D2 | 0.179 | 0.026 | 0.991 | 0.937 | 0.526 | 0.475 | 0.999 | 0.001 | 0.940 |
| HCP40D3 | 0.150 | 0.018 | 0.995 | 0.952 | 0.509 | 0.491 | 1.000 | 0.000 | 0.954 |
| HCP60D3 | 0.181 | 0.026 | 0.991 | 0.936 | 0.531 | 0.469 | 0.999 | 0.001 | 0.940 |
| HDP20D1 | 0.123 | 0.010 | 0.997 | 0.977 | 0.575 | 0.426 | 1.000 | 0.000 | 0.978 |
| HDP40D1 | 0.150 | 0.017 | 0.991 | 0.957 | 0.510 | 0.490 | 1.000 | 0.000 | 0.958 |
| HDP60D1 | 0.176 | 0.024 | 0.986 | 0.938 | 0.494 | 0.506 | 0.999 | 0.001 | 0.941 |
| HDP40D2 | 0.162 | 0.025 | 0.994 | 0.918 | 0.374 | 0.626 | 1.000 | 0.000 | 0.922 |
| HDP60D2 | 0.180 | 0.025 | 0.987 | 0.938 | 0.531 | 0.469 | 0.999 | 0.001 | 0.941 |
| HDP40D3 | 0.151 | 0.018 | 0.993 | 0.955 | 0.519 | 0.481 | 1.000 | 0.000 | 0.956 |
| HDP60D3 | 0.182 | 0.026 | 0.987 | 0.937 | 0.528 | 0.472 | 0.999 | 0.001 | 0.940 |
| HIP20D1 | 0.114 | 0.010 | 0.998 | 0.973 | 0.550 | 0.450 | 1.000 | 0.000 | 0.974 |
| HIP40D1 | 0.150 | 0.018 | 0.995 | 0.949 | 0.488 | 0.512 | 1.000 | 0.000 | 0.952 |
| HIP60D1 | 0.213 | 0.026 | 0.819 | 0.973 | 0.810 | 0.190 | 0.975 | 0.025 | 0.954 |
| HIP40D2 | 0.146 | 0.017 | 0.997 | 0.954 | 0.508 | 0.492 | 1.000 | 0.000 | 0.956 |
| HIP60D2 | 0.177 | 0.025 | 0.990 | 0.938 | 0.520 | 0.480 | 0.999 | 0.001 | 0.942 |
| HIP40D3 | 0.150 | 0.018 | 0.995 | 0.954 | 0.523 | 0.477 | 1.000 | 0.000 | 0.956 |
| HIP60D3 | 0.179 | 0.026 | 0.993 | 0.938 | 0.528 | 0.472 | 1.000 | 0.000 | 0.942 |
| Event | RMSE | MAE | Pre | NPV | Sens | Miss Rate | Spec | Fall-Out | Acc |
|---|---|---|---|---|---|---|---|---|---|
| 20JUL2010_2110 | 0.104 | 0.041 | 0.998 | 0.785 | 0.102 | 0.898 | 1.000 | 0.000 | 0.790 |
| HCP40D1 | 0.020 | 0.006 | 0.813 | 0.984 | 0.837 | 0.163 | 0.981 | 0.019 | 0.968 |
| HCP60D1 | 0.026 | 0.009 | 0.952 | 0.965 | 0.844 | 0.156 | 0.990 | 0.010 | 0.963 |
| HCP40D2 | 0.022 | 0.007 | 0.717 | 0.989 | 0.855 | 0.145 | 0.974 | 0.026 | 0.965 |
| HCP60D2 | 0.023 | 0.009 | 0.923 | 0.973 | 0.873 | 0.127 | 0.985 | 0.016 | 0.965 |
| HCP40D3 | 0.024 | 0.007 | 0.713 | 0.989 | 0.871 | 0.129 | 0.972 | 0.028 | 0.964 |
| HCP60D3 | 0.023 | 0.009 | 0.912 | 0.975 | 0.882 | 0.118 | 0.982 | 0.018 | 0.964 |
| HDP20D1 | 0.043 | 0.010 | 0.380 | 0.951 | 0.044 | 0.957 | 0.996 | 0.004 | 0.948 |
| HDP40D1 | 0.017 | 0.006 | 0.844 | 0.978 | 0.798 | 0.202 | 0.984 | 0.016 | 0.966 |
| HDP60D1 | 0.027 | 0.010 | 0.961 | 0.950 | 0.797 | 0.203 | 0.992 | 0.008 | 0.952 |
| HDP40D2 | 0.018 | 0.006 | 0.768 | 0.983 | 0.815 | 0.185 | 0.977 | 0.023 | 0.963 |
| HDP60D2 | 0.026 | 0.010 | 0.948 | 0.962 | 0.840 | 0.160 | 0.989 | 0.011 | 0.959 |
| HDP40D3 | 0.018 | 0.006 | 0.771 | 0.983 | 0.818 | 0.182 | 0.977 | 0.023 | 0.963 |
| HDP60D3 | 0.025 | 0.010 | 0.948 | 0.962 | 0.842 | 0.158 | 0.989 | 0.011 | 0.960 |
| HIP40D1 | 0.021 | 0.006 | 0.762 | 0.988 | 0.854 | 0.146 | 0.977 | 0.023 | 0.968 |
| HIP60D1 | 0.024 | 0.009 | 0.923 | 0.976 | 0.877 | 0.123 | 0.986 | 0.015 | 0.968 |
| HIP40D2 | 0.024 | 0.007 | 0.641 | 0.993 | 0.880 | 0.120 | 0.971 | 0.029 | 0.966 |
| HIP60D2 | 0.026 | 0.007 | 0.864 | 0.985 | 0.907 | 0.093 | 0.976 | 0.024 | 0.966 |
| HIP40D3 | 0.029 | 0.008 | 0.626 | 0.994 | 0.904 | 0.096 | 0.968 | 0.032 | 0.965 |
| HIP60D3 | 0.033 | 0.008 | 0.845 | 0.986 | 0.916 | 0.084 | 0.972 | 0.028 | 0.964 |
| Event | RMSE | MAE | Pre | NPV | Sens | Miss Rate | Spec | Fall-Out | Acc |
|---|---|---|---|---|---|---|---|---|---|
| St2_2019 | 0.072 | 0.143 | 0.724 | 0.973 | 0.973 | 0.027 | 0.721 | 0.279 | 0.829 |
| St2_2010 | 0.096 | 0.207 | 0.894 | 0.958 | 0.980 | 0.020 | 0.798 | 0.202 | 0.913 |
| St1_2019 | 0.056 | 0.118 | 0.602 | 0.992 | 0.984 | 0.016 | 0.753 | 0.247 | 0.816 |
| St1_2010 | 0.049 | 0.119 | 0.459 | 0.999 | 0.996 | 0.004 | 0.798 | 0.202 | 0.827 |
| HIT200P60D1 | 0.064 | 0.117 | 0.836 | 0.847 | 0.841 | 0.159 | 0.843 | 0.157 | 0.842 |
| HIT100P60D3 | 0.101 | 0.171 | 0.662 | 0.969 | 0.977 | 0.023 | 0.588 | 0.412 | 0.764 |
| HIT100P60D2 | 0.099 | 0.167 | 0.649 | 0.965 | 0.973 | 0.027 | 0.592 | 0.408 | 0.758 |
| HIT020P40D1 | 0.071 | 0.136 | 0.524 | 0.996 | 0.993 | 0.007 | 0.689 | 0.311 | 0.767 |
| HIT010P40D3 | 0.092 | 0.155 | 0.563 | 0.986 | 0.985 | 0.015 | 0.593 | 0.407 | 0.729 |
| HIT010P40D2 | 0.088 | 0.154 | 0.543 | 0.986 | 0.983 | 0.017 | 0.601 | 0.399 | 0.725 |
| HIT002P20D1 | 0.025 | 0.065 | 0.814 | 0.941 | 0.844 | 0.156 | 0.928 | 0.072 | 0.905 |
| HDT200P60D1 | 0.055 | 0.111 | 0.625 | 0.986 | 0.976 | 0.024 | 0.743 | 0.257 | 0.814 |
| HDT100P60D3 | 0.078 | 0.142 | 0.663 | 0.938 | 0.940 | 0.060 | 0.656 | 0.344 | 0.775 |
| HDT100P60D2 | 0.077 | 0.137 | 0.666 | 0.933 | 0.935 | 0.065 | 0.658 | 0.342 | 0.775 |
| HDT020P40D1 | 0.049 | 0.107 | 0.533 | 0.994 | 0.984 | 0.016 | 0.762 | 0.238 | 0.810 |
| HDT010P40D3 | 0.064 | 0.120 | 0.574 | 0.965 | 0.945 | 0.055 | 0.687 | 0.313 | 0.767 |
| HDT010P40D2 | 0.068 | 0.129 | 0.937 | 0.665 | 0.937 | 0.063 | 0.665 | 0.335 | 0.703 |
| HDT002P20D1 | 0.045 | 0.116 | 0.383 | 0.999 | 0.996 | 0.004 | 0.813 | 0.187 | 0.832 |
| HCT200P60D1 | 0.074 | 0.137 | 0.629 | 0.991 | 0.988 | 0.012 | 0.682 | 0.318 | 0.790 |
| HCT100P60D3 | 0.103 | 0.174 | 0.674 | 0.953 | 0.967 | 0.033 | 0.584 | 0.416 | 0.764 |
| HCT100P60D2 | 0.097 | 0.167 | 0.668 | 0.959 | 0.968 | 0.032 | 0.609 | 0.391 | 0.770 |
| HCT020P40D1 | 0.070 | 0.136 | 0.543 | 0.995 | 0.990 | 0.010 | 0.695 | 0.305 | 0.774 |
| HCT010P40D3 | 0.090 | 0.156 | 0.584 | 0.98 | 0.978 | 0.022 | 0.610 | 0.390 | 0.742 |
| HCT010P40D2 | 0.085 | 0.150 | 0.558 | 0.981 | 0.976 | 0.024 | 0.614 | 0.386 | 0.735 |
| HCT002P20D1 | 0.061 | 0.133 | 0.357 | 0.999 | 0.997 | 0.003 | 0.739 | 0.261 | 0.772 |
| Event | RMSE | MAE | Pre | NPV | Sens | Miss Rate | Spec | Fall-Out | Acc |
|---|---|---|---|---|---|---|---|---|---|
| St2_2010 | 0.101 | 0.033 | 0.343 | 0.999 | 0.996 | 0.004 | 0.892 | 0.108 | 0.898 |
| HIT200P60D1 | 0.072 | 0.018 | 0.417 | 0.997 | 0.920 | 0.080 | 0.950 | 0.050 | 0.949 |
| HIT100P60D3 | 0.110 | 0.028 | 0.446 | 0.995 | 0.926 | 0.074 | 0.930 | 0.070 | 0.929 |
| HIT100P60D2 | 0.102 | 0.027 | 0.431 | 0.995 | 0.921 | 0.079 | 0.929 | 0.071 | 0.929 |
| HIT020P40D1 | 0.073 | 0.020 | 0.313 | 0.998 | 0.935 | 0.065 | 0.943 | 0.057 | 0.942 |
| HIT010P40D3 | 0.079 | 0.020 | 0.260 | 0.999 | 0.961 | 0.039 | 0.948 | 0.052 | 0.948 |
| HIT010P40D2 | 0.075 | 0.019 | 0.262 | 0.999 | 0.957 | 0.043 | 0.949 | 0.051 | 0.949 |
| HDT200P60D1 | 0.041 | 0.011 | 0.658 | 0.991 | 0.879 | 0.121 | 0.968 | 0.032 | 0.963 |
| HDT100P60D3 | 0.051 | 0.012 | 0.647 | 0.995 | 0.929 | 0.071 | 0.965 | 0.035 | 0.963 |
| HDT100P60D2 | 0.050 | 0.012 | 0.645 | 0.995 | 0.927 | 0.073 | 0.965 | 0.035 | 0.963 |
| HDT020P40D1 | 0.045 | 0.015 | 0.299 | 0.995 | 0.858 | 0.142 | 0.938 | 0.062 | 0.936 |
| HDT010P40D3 | 0.055 | 0.017 | 0.297 | 0.996 | 0.886 | 0.114 | 0.937 | 0.063 | 0.936 |
| HDT010P40D2 | 0.054 | 0.017 | 0.290 | 0.996 | 0.884 | 0.116 | 0.937 | 0.063 | 0.936 |
| HCT200P60D1 | 0.061 | 0.015 | 0.578 | 0.994 | 0.903 | 0.097 | 0.960 | 0.040 | 0.957 |
| HCT100P60D3 | 0.083 | 0.019 | 0.523 | 0.995 | 0.920 | 0.080 | 0.954 | 0.046 | 0.952 |
| HCT100P60D2 | 0.074 | 0.018 | 0.520 | 0.995 | 0.917 | 0.083 | 0.955 | 0.045 | 0.953 |
| HCT020P40D1 | 0.069 | 0.020 | 0.333 | 0.997 | 0.919 | 0.081 | 0.939 | 0.061 | 0.939 |
| HCT010P40D3 | 0.076 | 0.021 | 0.305 | 0.998 | 0.928 | 0.072 | 0.940 | 0.060 | 0.940 |
| HCT010P40D2 | 0.073 | 0.020 | 0.298 | 0.998 | 0.926 | 0.074 | 0.941 | 0.059 | 0.941 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianucci, P.; Fernández-Fidalgo, J.; Kyaw, K.K.; Soriano, E.; Mediero, L. Evaluating Infiltration Methods for the Assessment of Flooding in Urban Areas. Water 2025, 17, 2773. https://doi.org/10.3390/w17182773
Bianucci P, Fernández-Fidalgo J, Kyaw KK, Soriano E, Mediero L. Evaluating Infiltration Methods for the Assessment of Flooding in Urban Areas. Water. 2025; 17(18):2773. https://doi.org/10.3390/w17182773
Chicago/Turabian StyleBianucci, Paola, Javier Fernández-Fidalgo, Kay Khaing Kyaw, Enrique Soriano, and Luis Mediero. 2025. "Evaluating Infiltration Methods for the Assessment of Flooding in Urban Areas" Water 17, no. 18: 2773. https://doi.org/10.3390/w17182773
APA StyleBianucci, P., Fernández-Fidalgo, J., Kyaw, K. K., Soriano, E., & Mediero, L. (2025). Evaluating Infiltration Methods for the Assessment of Flooding in Urban Areas. Water, 17(18), 2773. https://doi.org/10.3390/w17182773





