Numerical Simulation of Sloshing Tanks with Shallow Water Model Using Low Numerical Diffusion Schemes and Its Application to Tuned Liquid Dampers
Abstract
1. Introduction
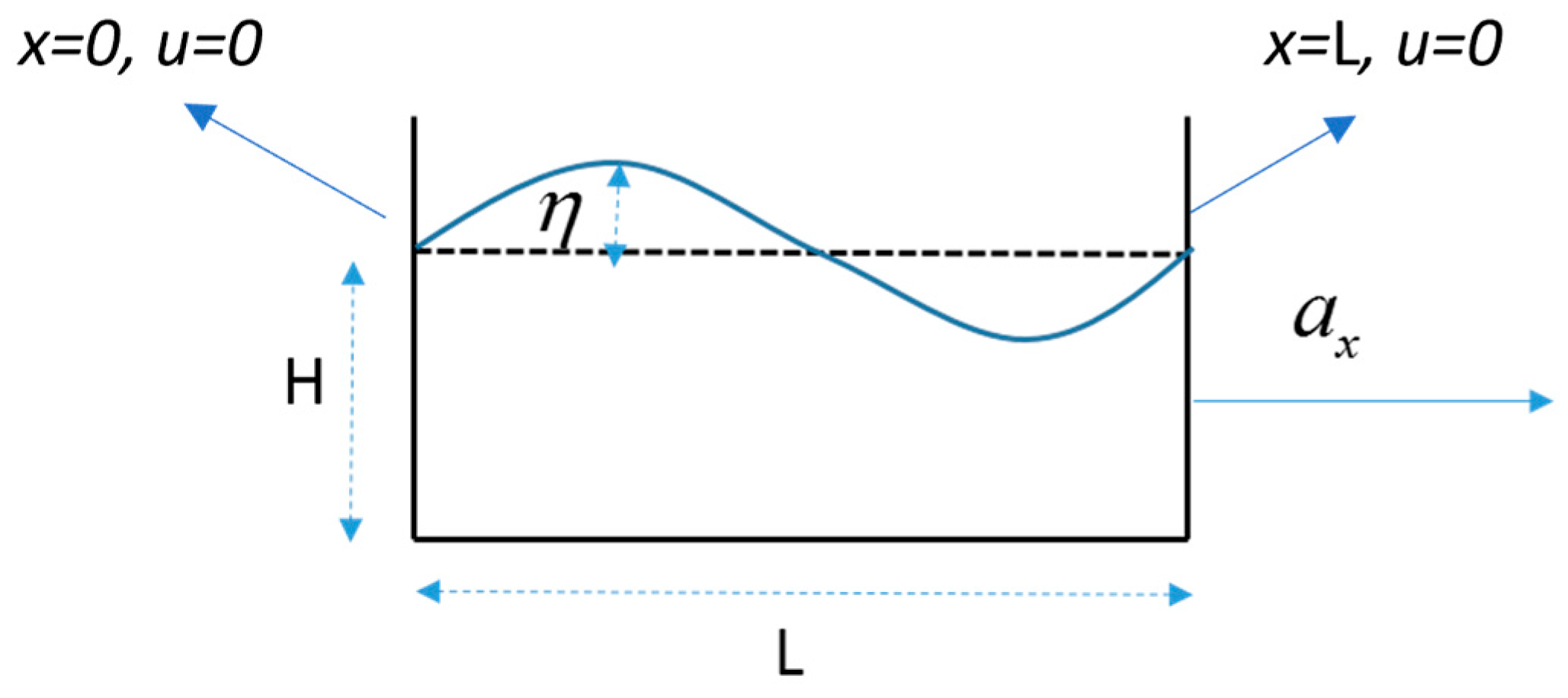
2. Methodology
3. Numerical Methods
3.1. Upwind Schemes
3.1.1. Temporal Discretization
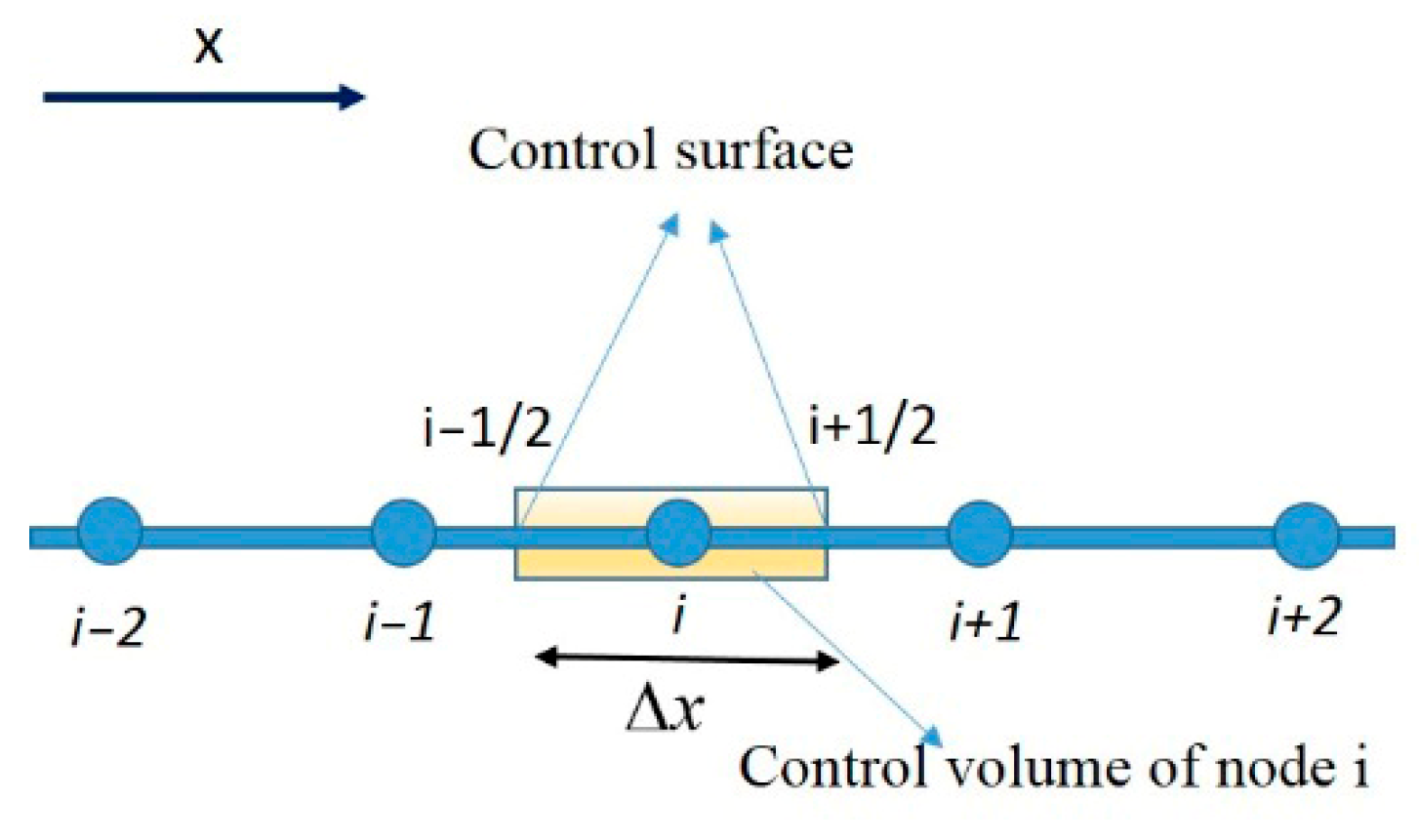
3.1.2. Spatial Discretization
First-Order Upwind
Higher-Order Upwind
3.2. MacCormack Method
3.3. Central Difference in Time and Space
3.4. Implicit and Semi-Implicit Method
3.4.1. Preissmann Method
3.4.2. Staggered Method
3.5. Separation of Variables Scheme
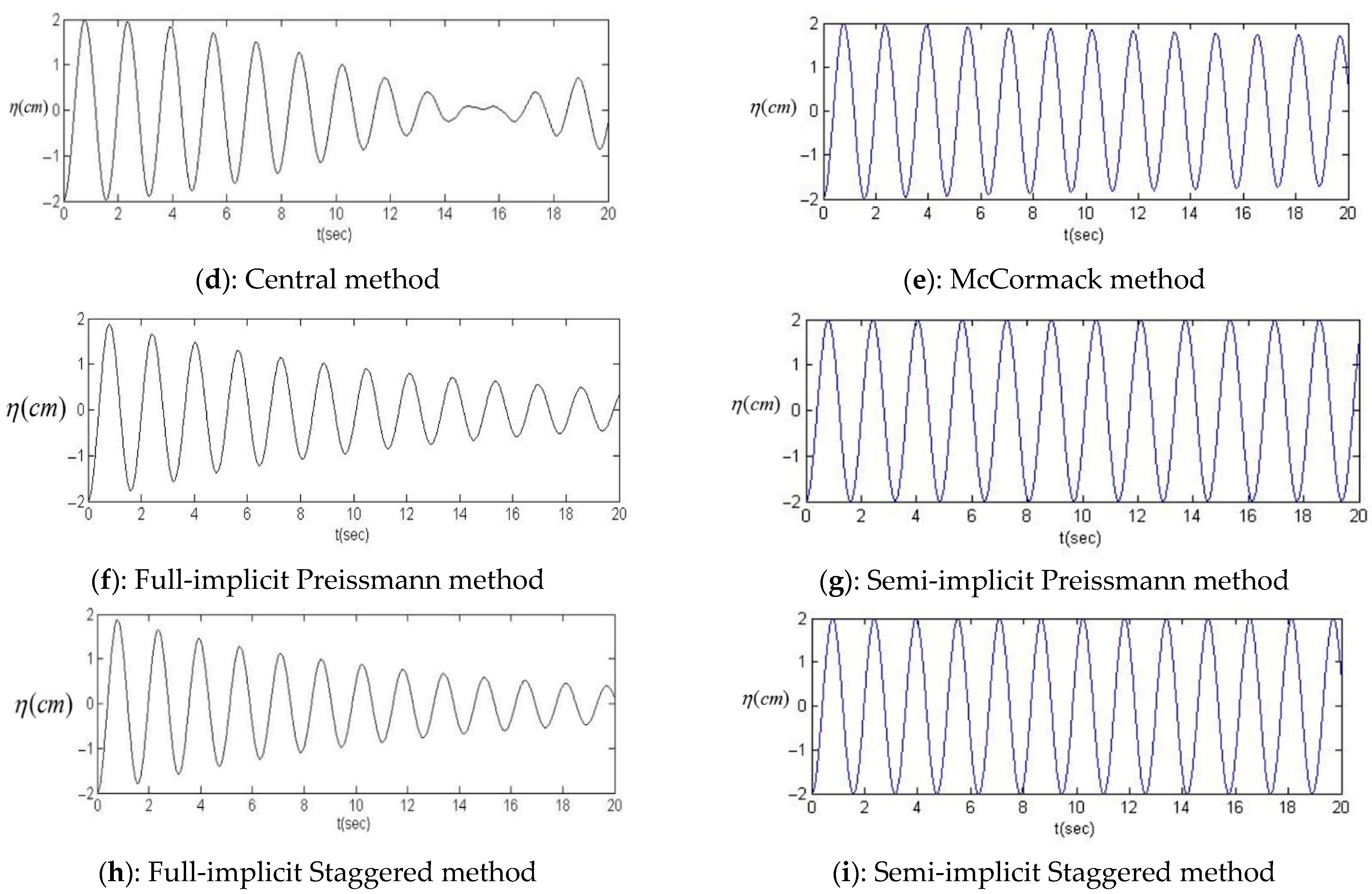
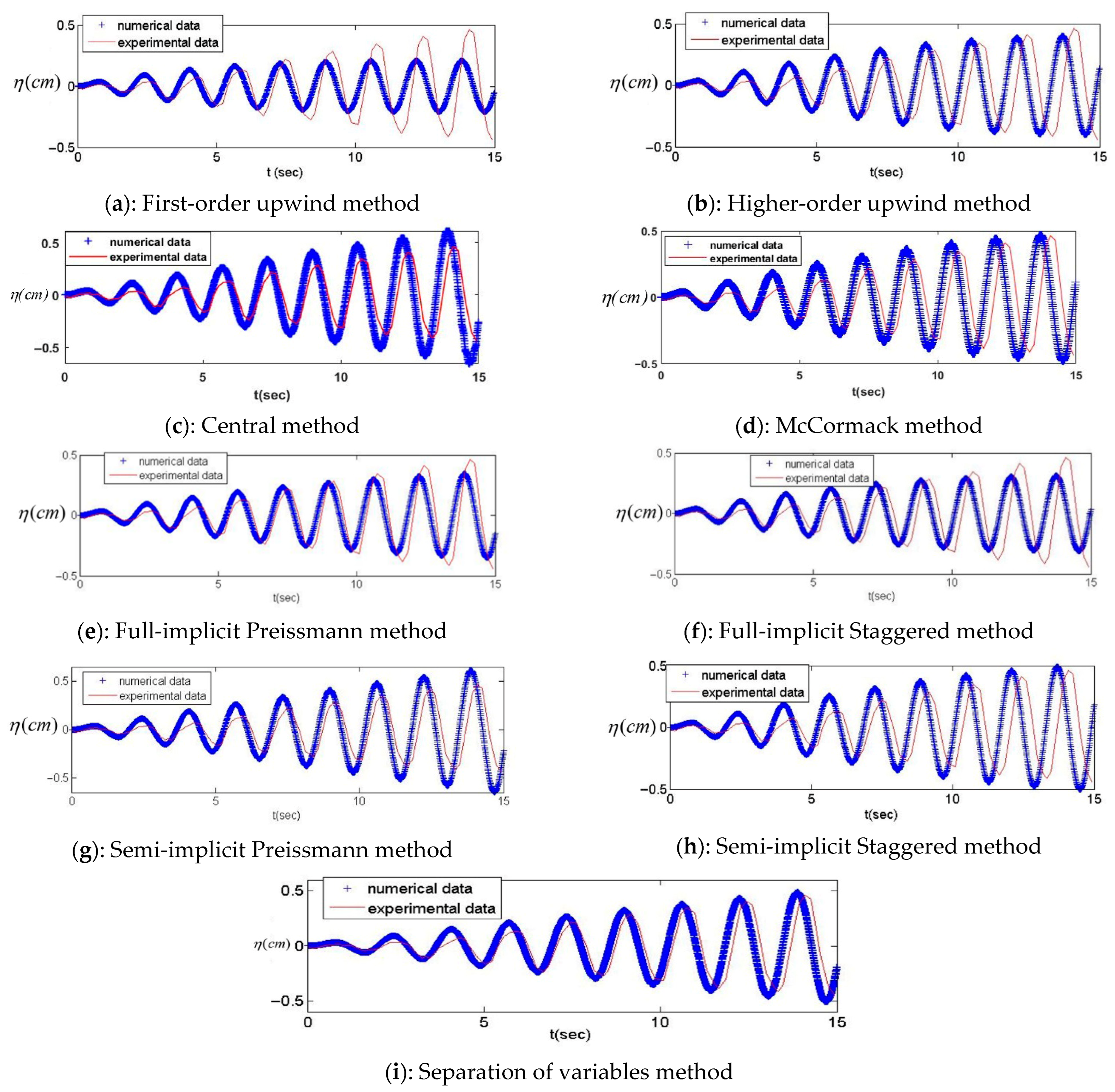
4. Test Cases and Results
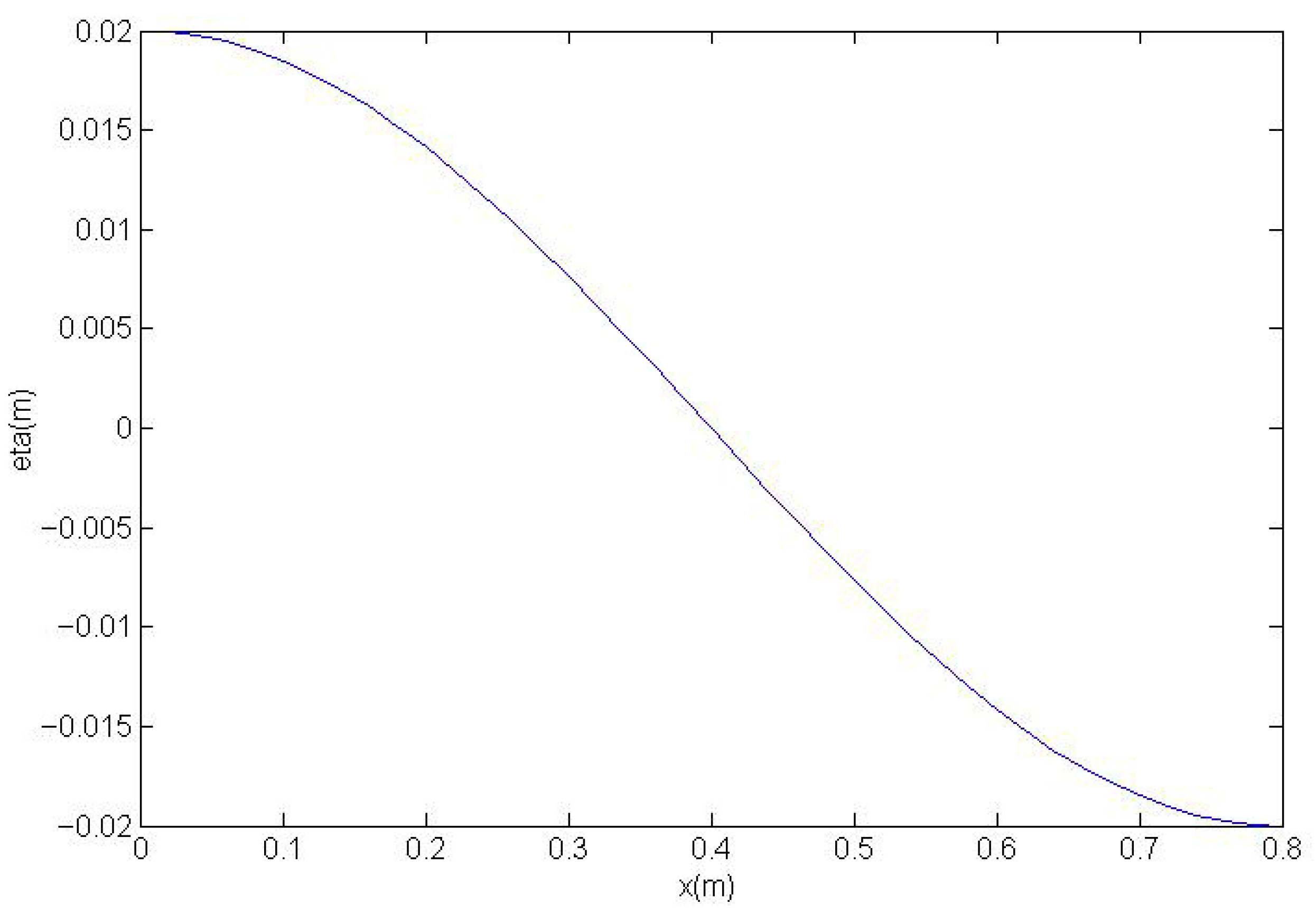
4.1. Perturbation Test
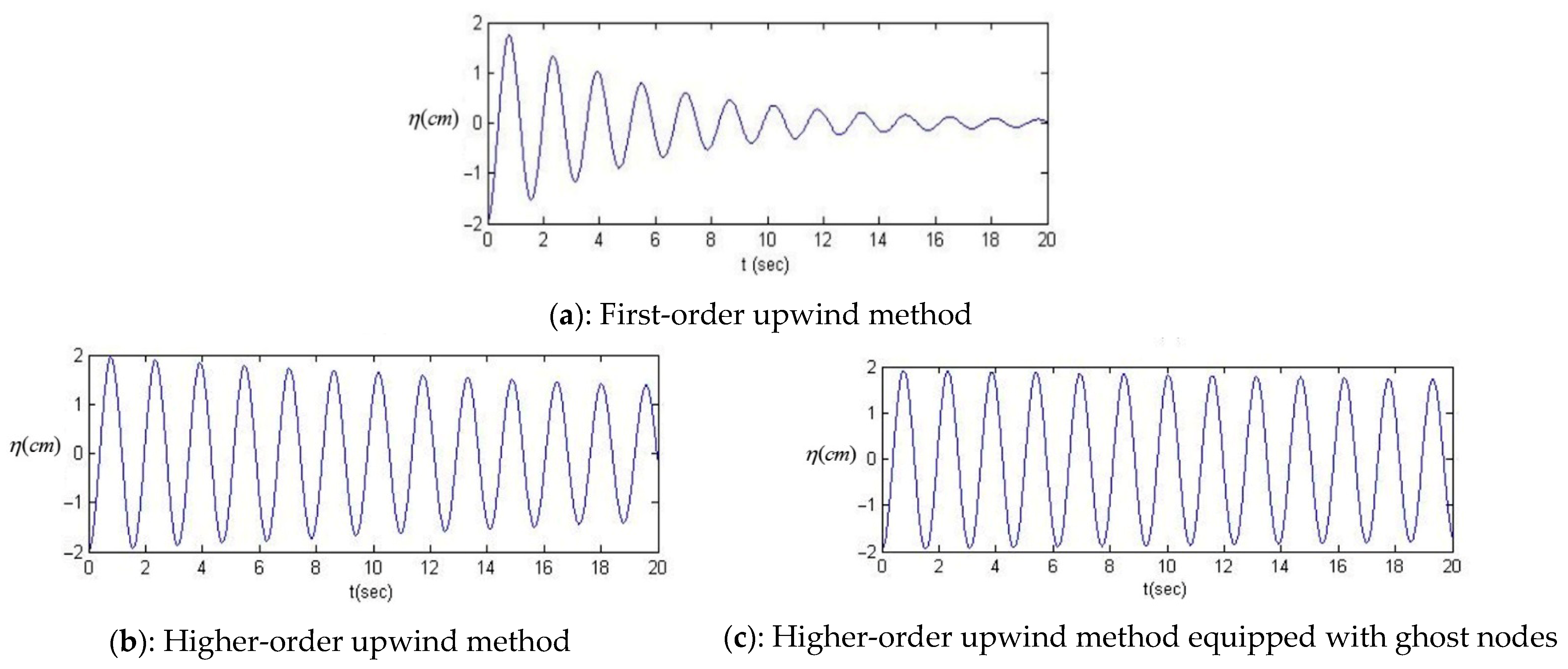
4.2. Sloshing Test
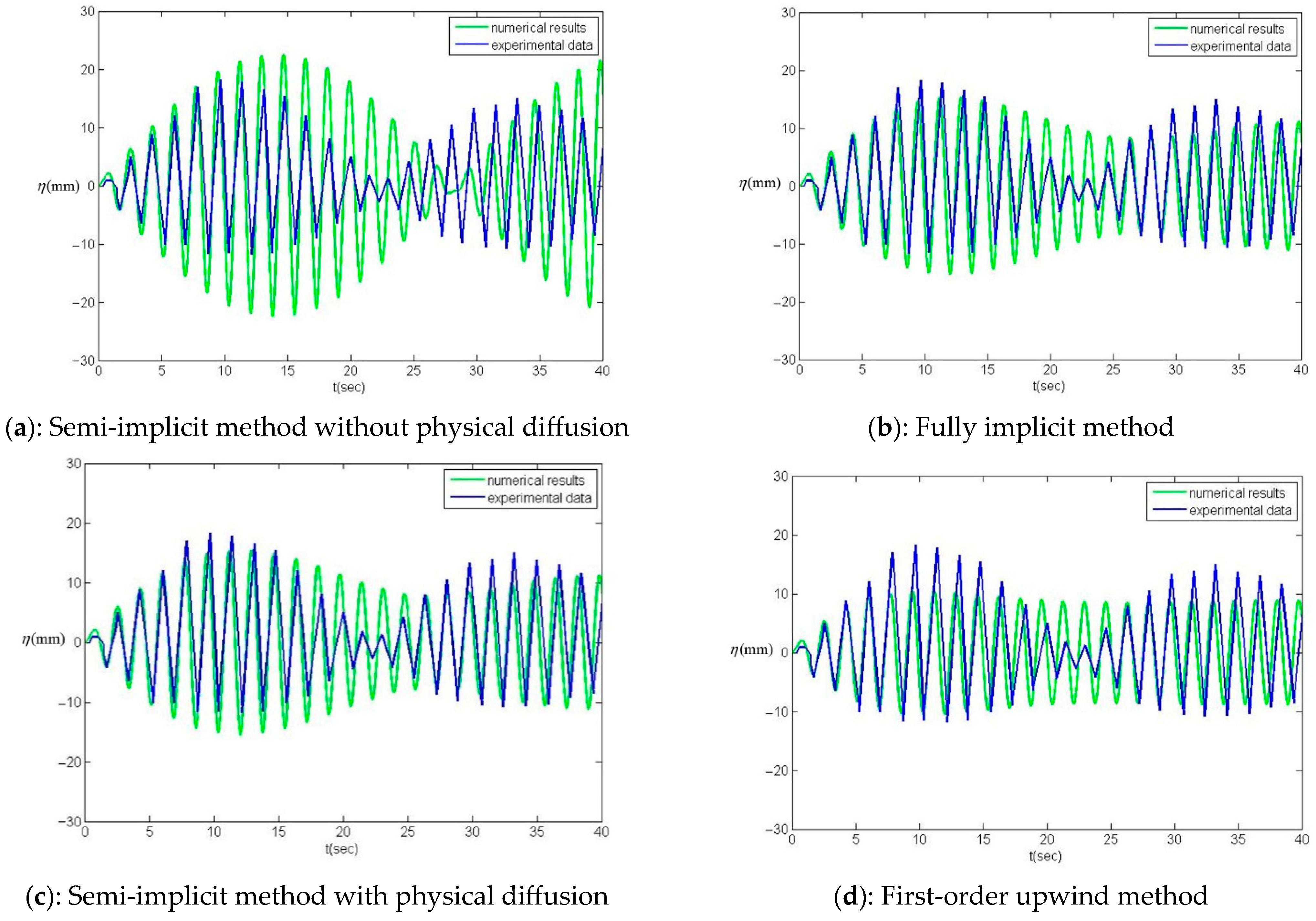
4.3. Physical Diffusion
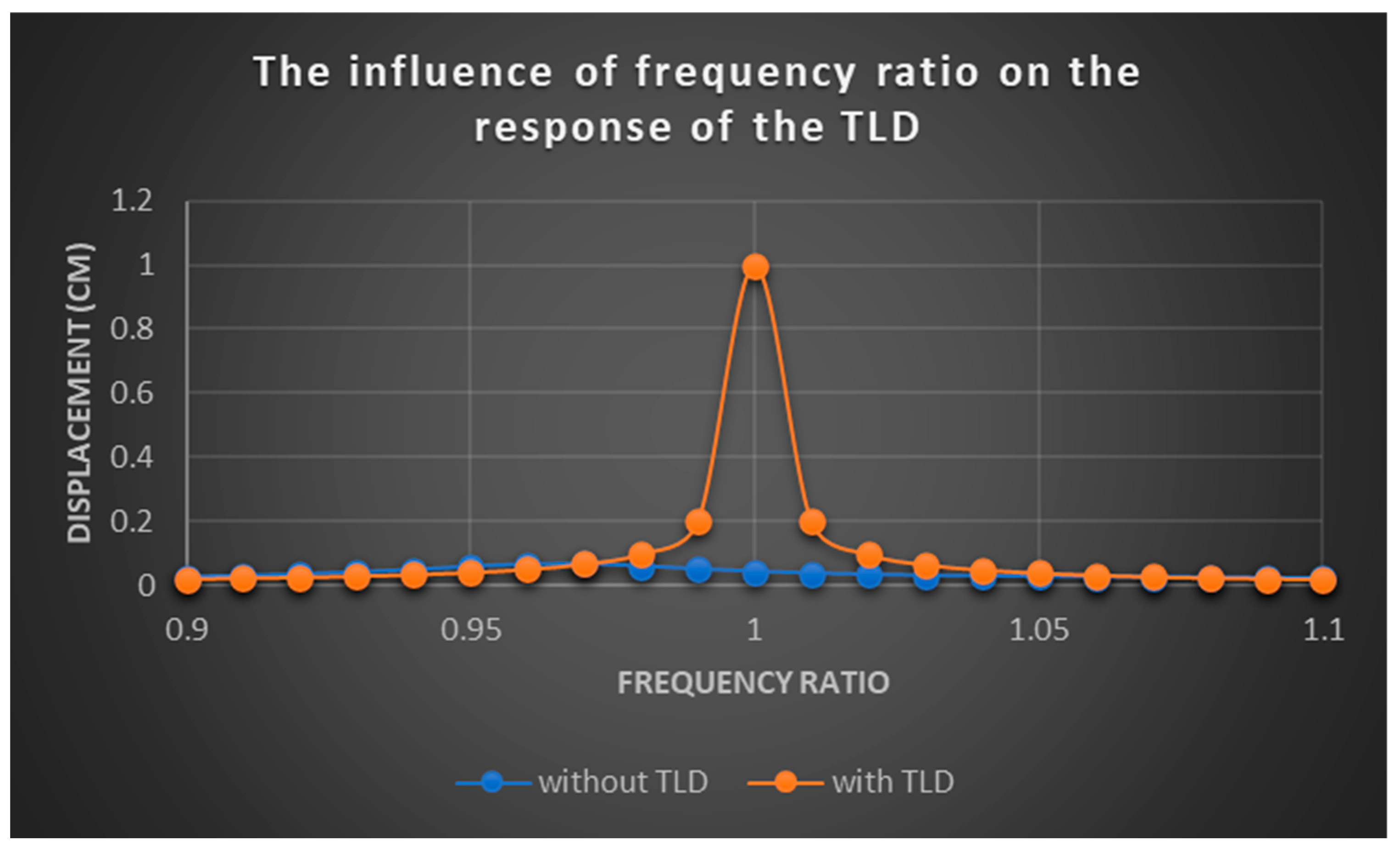
4.4. Tuned Liquid Damper Test
4.4.1. The Influence of Frequency Ratio on the Response of the TLD
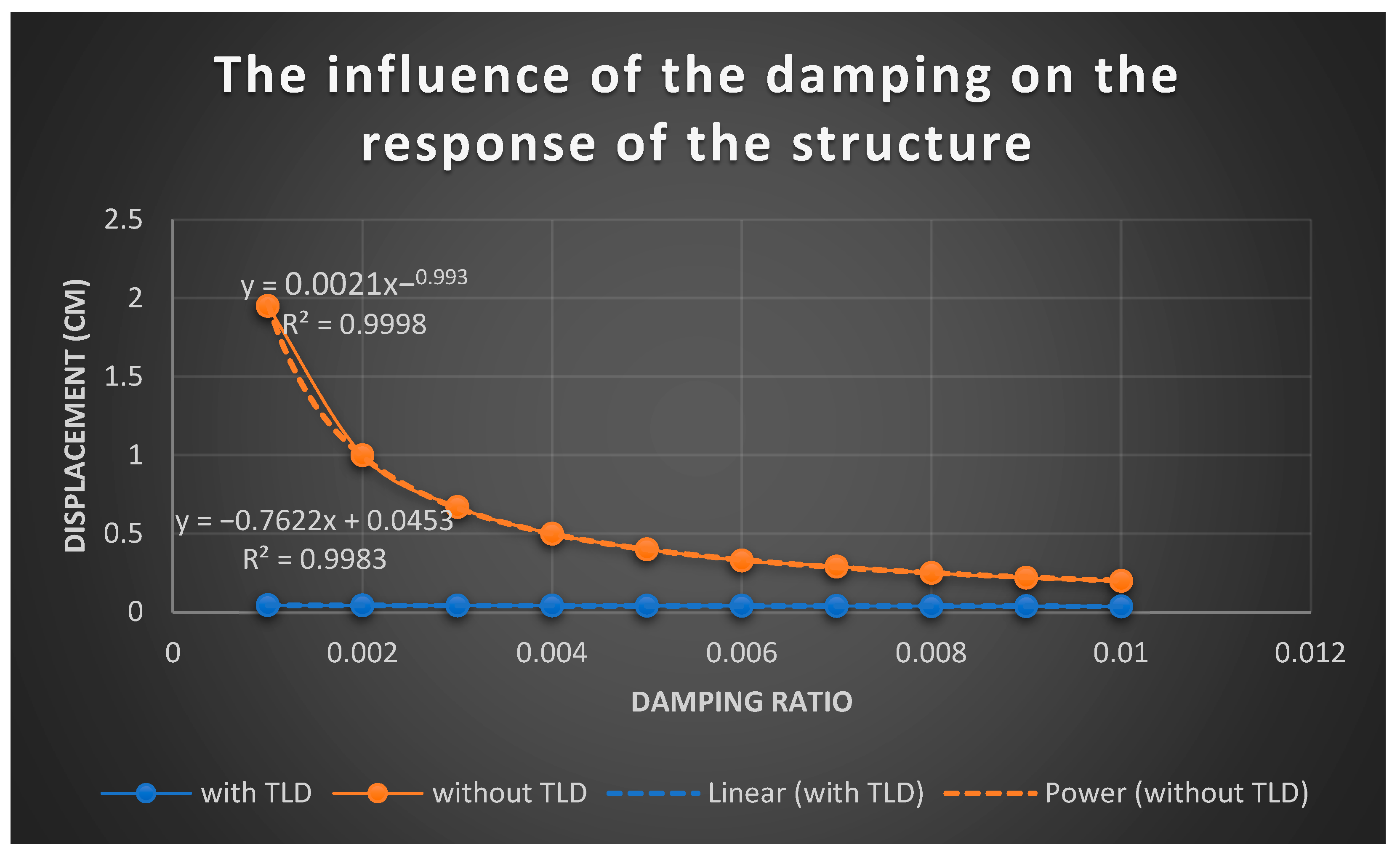
4.4.2. The Influence of Damping on the Response of TLD
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Evaluation of Matrix
Appendix A.2. First-Order Upwind
Appendix A.3. Higher-Order Upwind
Appendix A.4. MacCormack Method
Appendix A.5. Central Method
Appendix A.6. Preissmann Method
| 1/(2Δt) | −αH/Δx | 1/(2Δt) | αH/Δx | 0 | 0 | 0 | 0 | |
| 0 | LL | 0 | 0 | 0 | 0 | 0 | 0 | |
| −αg/Δx | 1/(2Δt) | αg/Δx | 1/(2Δt) | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1/(2Δt) | −αH/Δx | 1/(2Δt) | αH/Δx | 0 | 0 | |
| 0 | 0 | −αg/Δx | 1/(2Δt) | αg/Δx | 1/(2Δt) | 0 | 0 | |
| 0 | 0 | 0 | 0 | 1/(2Δt) | −αH/Δx | 1/(2Δt) | αH/Δx | |
| 0 | 0 | 0 | 0 | −αg/Δx | 1/(2Δt) | αg/Δx | 1/(2Δt) | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | LL |
| η1 | |
| u1 | |
| η2 | |
| u2 | |
| η3 | |
| u3 | |
| η4 | |
| u4 |
| 1/(2Δt)(η1ⁿ) + H(1 − α)/Δx (u1ⁿ) + 1/(2Δt)(η2ⁿ) − H(1 − α)/Δx (u2ⁿ) | |
| 0 | |
| g(1 − α)/Δx(η1ⁿ) + 1/(2Δt)(u1ⁿ) − g(1 − α)/Δx(η2ⁿ) + 1/(2Δt)(u2ⁿ) + a | |
| 1/(2Δt)(η2ⁿ) + H(1 − α)/Δx (u2ⁿ) + 1/(2Δt)(η3ⁿ) − H(1 − α)/Δx (u3ⁿ) | |
| g(1 − α)/Δx (η2ⁿ) + 1/(2Δt)(u2ⁿ) − g(1 − α)/Δx (η3ⁿ) + 1/(2Δt)(u3ⁿ) + a | |
| 1/(2Δt)(η3ⁿ) + H(1 − α)/Δx (u3ⁿ) + 1/(2Δt)(η4ⁿ) − H(1 − α)/Δx (u4ⁿ) | |
| g(1 − α)/Δx (η3ⁿ) + 1/(2Δt)(u3ⁿ) − g(1 − α)/Δx (η4ⁿ) + 1/(2Δt)(u4ⁿ) + a | |
| 0 |
Appendix A.7. Staggered Method
| LL | 0 | 0 | 0 | 0 | 0 | 0 | |
| −αH/(2Δx) | 1/Δt | αH/(2Δx) | 0 | 0 | 0 | 0 | |
| 0 | −αg/(2Δx) | 1/Δt | αg/(2Δx) | 0 | 0 | 0 | |
| 0 | 0 | −αH/(2Δx) | 1/Δt | αH/(2Δx) | 0 | 0 | |
| 0 | 0 | 0 | −αg/(2Δx) | 1/Δt | αg/(2Δx) | 0 | |
| 0 | 0 | 0 | 0 | −αH/(2Δx) | 1/Δt | αH/(2Δx) | |
| 0 | 0 | 0 | 0 | 0 | 0 | LL |
| = | u1 |
| η1 | |
| u2 | |
| η2 | |
| u3 | |
| η3 | |
| u4 |
| = | 0 |
| 1/Δt (η1ⁿ) + H(1 − α)/(2Δx) (u1ⁿ) − H(1 − α)/(2Δx) (u2ⁿ) | |
| g(1 − α)/(2Δx) (η1ⁿ) + 1/Δt (u2ⁿ) − g(1 − α)/(2Δx) (η2ⁿ) + a | |
| 1/Δt (η2ⁿ) + H(1 − α)/(2Δx) (u2ⁿ) − H(1 − α)/(2Δx) (u3ⁿ) | |
| g(1 − α)/(2Δx) (η2ⁿ) + 1/Δt (u3ⁿ) − g(1 − α)/(2Δx) (η3ⁿ) + a | |
| 1/Δt (η3ⁿ) + H(1 − α)/(2Δx) (u3ⁿ) − H(1 − α)/(2Δx) (u4ⁿ) | |
| 0 |
References
- Khanpour, M.; Mohammadian, A.; Shirkhani, H.; Kianoush, R. Analytical solution to a coupled system including tuned liquid damper and single degree of freedom under free vibration with modal decomposition method. Phys. Fluids 2024, 36, 057128. [Google Scholar] [CrossRef]
- Sun, L.M.; Fujino, Y.; Pacheco, B.M.; Chaiseri, P. Modelling of tuned liquid damper (TLD). J. Wind Eng. Ind. Aerodyn. 1992, 43, 1883–1894. [Google Scholar] [CrossRef]
- Tait, M.; El Damatty, A.; Isyumov, N.; Siddique, M.R. Numerical flow models to simulate tuned liquid dampers (TLD) with slat screens. J. Fluids Struct. 2005, 20, 1007–1023. [Google Scholar] [CrossRef]
- Bhattacharjee, E.; Halder, L.; Sharma, R.P. An experimental study on tuned liquid damper for mitigation of structural response. Int. J. Adv. Struct. Eng. 2013, 5, 3. [Google Scholar] [CrossRef]
- Malekghasemi, H.; Ashasi-Sorkhabi, A.; Ghaemmaghami, A.R.; Mercan, O. Experimental and numerical investigations of the dynamic interaction of tuned liquid damper–structure systems. J. Vib. Control. 2015, 21, 2707–2720. [Google Scholar] [CrossRef]
- Sun, L.; Fujino, Y. A semi-analytical model for tuned liquid damper (TLD) with wave breaking. J. Fluids Struct. 1994, 8, 471–488. [Google Scholar] [CrossRef]
- Marivani, M.; Hamed, M. Evaluate pressure drop of slat screen in an oscillating fluid in a tuned liquid damper. Comput. Fluids 2017, 156, 384–401. [Google Scholar] [CrossRef]
- Love, J.; Tait, M. Parametric depth ratio study on tuned liquid dampers: Fluid modelling and experimental work. Comput. Fluids 2013, 79, 13–26. [Google Scholar] [CrossRef]
- Khanpour, M.; Mohammadian, A.; Shirkhani, H.; Kianoush, R. Simulation of Sloped-Bed Tuned Liquid Dampers Using a Nonlinear Shallow Water Model. Water 2024, 16, 1394. [Google Scholar] [CrossRef]
- Pandit, A.; Biswal, K. Seismic control of multi degree of freedom structure outfitted with sloped bottom tuned liquid damper. Structures 2020, 25, 229–240. [Google Scholar] [CrossRef]
- Housner, G.W. The dynamic behavior of water tanks. Bull. Seism. Soc. Am. 1963, 53, 381–387. [Google Scholar] [CrossRef]
- Faltinsen, O.M. A Nonlinear Theory of Sloshing in Rectangular Tanks. J. Ship Res. 1974, 18, 224–241. [Google Scholar] [CrossRef]
- Solaas, F.; Faltinsen, O.M. Combined Numerical and Analytical Solution for Sloshing in Two-dimensional Tanks of General Shape. J. Ship Res. 1997, 41, 118–129. [Google Scholar] [CrossRef]
- Wu, G.X.; Ma, Q.W.; Taylor, R.E. Numerical simulation of sloshing waves in a 3D tank based on a finite element method. Appl. Ocean Res. 1998, 20, 337–355. [Google Scholar] [CrossRef]
- Bahreini Toussi, I.; Kianoush, R.; Mohammadian, A. Numerical and experimental investigation of rectangular liq-uid-containing structures under seismic excitation. Infrastructures 2020, 6, 1. [Google Scholar] [CrossRef]
- Marivani, M.; Hamed, M. Numerical simulation of structure response outfitted with a tuned liquid damper. Comput. Struct. 2009, 87, 1154–1165. [Google Scholar] [CrossRef]
- Liu, D.; Lin, P. A Numerical Study of Three-Dimensional Liquid Sloshing in Tanks. J. Comput. Phys. 2008, 227, 3921–3939. [Google Scholar] [CrossRef]
- Cao, X.; Ming, F.; Zhang, A. Sloshing in a rectangular tank based on SPH simulation. Appl. Ocean Res. 2014, 47, 241–254. [Google Scholar] [CrossRef]
- Moslemi, M.; Farzin, A.; Kianoush, M. Nonlinear sloshing response of liquid-filled rectangular concrete tanks under seismic excitation. Eng. Struct. 2019, 188, 564–577. [Google Scholar] [CrossRef]
- Sun, P.-N.; Le Touzé, D.; Oger, G.; Zhang, A.-M. An accurate FSI-SPH modeling of challenging fluid-structure interaction problems in two and three dimensions. Ocean Eng. 2021, 221, 10855. [Google Scholar] [CrossRef]
- Abbott, M.; Minns, A. Computational Hydraulics, 2nd ed.; Taylor and Francis: London, UK, 2017. [Google Scholar]
- Saburin, D.S. Tank sloshing simulations in shallow-water approximation. In Proceedings of the VI International Conference on Computational Methods in Marine Engineering, Rome, Italy, 15–17 June 2015; pp. 1039–1050. [Google Scholar]
- Banerji, P.; Murudi, M.; Shah, A.H.; Popplewell, N. Tuned liquid dampers for controlling earthquake response of structures. Earthq. Eng. Struct. Dyn. 2000, 29, 587–602. [Google Scholar] [CrossRef]
- Mohammadian, A.M.; Le Roux, D.Y. Fourier analysis of a class of upwind schemes in shallow water systems for gravity and Rossby waves. Int. J. Numer. Methods Fluids 2008, 57, 389–416. [Google Scholar] [CrossRef]
- Kurganov, A. Finite-volume schemes for shallow-water equations. Acta Numer. 2018, 27, 289–351. [Google Scholar] [CrossRef]
- MacCormack, R.W. Numerical Solution of the Interaction of a Shock Wave with a Laminar Boundary Layer; Lectures Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1971; Volume 8, pp. 151–163. [Google Scholar]
- Chaudhry, M.H.; Hussaini, M.Y. Second-Order Accurate Explicit Finite-Difference Schemes for Water Hammer Analysis. ASME J. Fluids Eng. 1985, 107, 523–529. [Google Scholar] [CrossRef]
- AMARA, L.; Berreksi, A.; Achour, B. Adapted MacCormack Finite-Differences Scheme for Water Hammer Simulation. J. Civ. Eng. Sci. 2013, 2, 226–233. [Google Scholar]
- Fennema, R.J.; Chaudhry, M.H. Explicit Numerical Schemes for Unsteady Free-Surface Flows with Shocks. Water Resour. Res. 1986, 22, 1923–1930. [Google Scholar] [CrossRef]
- Garcia, R.; Khahawita, R.A. Numerical solution of the St Venant equations with the MacCormack finite-differences scheme. Int. J. Numer. Methods Fluids 1986, 6, 259–274. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Li, Z.; Sun, B.; Zhou, H. Applicability of Preissmann box scheme for calculation of transcritical flow in pipes. Water Supply 2019, 19, 1429–1437. [Google Scholar] [CrossRef]
- Preissmann, A. Propagation des intumescences dans les canaux et Les Rivieres. In Proceedings of the 1 Congres de l’Association Francaise de Calcule, Grenoble, France, 1961. (In French). [Google Scholar]
- Wu, W. Computational River Dynamics; Taylor & Francis: London, UK, 2008. [Google Scholar]
- Popescu, I. Computational Hydraulics: Numerical Methods and Modelling; IWA Publishing: London, UK, 2014. [Google Scholar]
- Abbott, M.B.; Basco, D.R. Computational Fluid Dynamics; Longman Scientific and Technical: New York, NY, USA, 1989. [Google Scholar]
- Liu, F.; Feyen, J.; Berlamont, J. Computation method for regulating unsteady flow in open channels. J. Irrig. Drain. Eng. 1992, 118, 674–689. [Google Scholar] [CrossRef]
- Venutelli, M. Stability and accuracy of weighted four-point implicit finite difference schemes for open channel flow. J. Hydraul. Eng. 2002, 128, 281–288. [Google Scholar] [CrossRef]
- Guo, D.; Yu, B. Implementation of the Preissmann scheme to solve the Hairsine-Rose erosion equations: Verification and evaluation. J. Hydrol. 2016, 541, 988–1002. [Google Scholar] [CrossRef]
- Gallouët, T.; Gastaldo, L.; Herbin, R.; Latché, J.-C. An unconditionally stable pressure correction scheme for compressible barotropic Navier-Stokes equations. ESAIM Math. Model. Numer. Anal. 2007, 42, 303–331. [Google Scholar] [CrossRef]
- Herbin, R.; Kheriji, W.; Latché, J.-C. On some implicit and semi-implicit staggered schemes for the shallow water and Euler equations. ESAIM Math. Model. Numer. Anal. 2014, 48, 1807–1857. [Google Scholar] [CrossRef]
- Humar, J. Dynamics of Structures, 3rd ed.; CRC Press: Cleveland, OH, USA, 2012. [Google Scholar]
- Wazwaz, A.M. Partial Differential Equations and Solitary Waves Theory; Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Chopra, A.K. Dynamic of Structures, Theory and Applications to Earthquake Engineering, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Gottlieb, S.; Shu, C.-W. Total variation diminishing Runge-Kutta schemes. Math. Comput. 1996, 67, 73–85. [Google Scholar] [CrossRef]
- Liu, X.; Mohammadian, A.; Sedano, J. Three-dimensional modeling of non-hydrostatic free-surface flows on un-structured grids. Int. J. Numer. Methods Fluids 2016, 82, 130–147. [Google Scholar] [CrossRef]
- Chen, Y.; Hwang, W.; Ko, C. Sloshing behaviors of rectangular and cylindrical liquid tanks subjected to harmonic and seismic excitations. Earthq. Eng. Struct. Dyn. 2007, 36, 1701–1717. [Google Scholar] [CrossRef]
- Ashasi-Sorkhabi, A.; Malekghasemi, H.; Ghaemmaghami, A.; Mercan, O. Experimental investigations of tuned liquid damper-structure interactions in resonance considering multiple parameters. J. Sound Vib. 2017, 388, 141–153. [Google Scholar] [CrossRef]








| Structure | Water Tank | |||
|---|---|---|---|---|
| Mass (kg) | Stiffness (KN/m) | Daming Coefficient (KN. s/m) | Length (m) | Water depth (m) |
| 282 | 4997.5 | 4.75 | 0.46 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khanpour, M.; Mohammadian, A.; Shirkhani, H.; Kianoush, R. Numerical Simulation of Sloshing Tanks with Shallow Water Model Using Low Numerical Diffusion Schemes and Its Application to Tuned Liquid Dampers. Water 2025, 17, 2703. https://doi.org/10.3390/w17182703
Khanpour M, Mohammadian A, Shirkhani H, Kianoush R. Numerical Simulation of Sloshing Tanks with Shallow Water Model Using Low Numerical Diffusion Schemes and Its Application to Tuned Liquid Dampers. Water. 2025; 17(18):2703. https://doi.org/10.3390/w17182703
Chicago/Turabian StyleKhanpour, Mahdiyar, Abdolmajid Mohammadian, Hamidreza Shirkhani, and Reza Kianoush. 2025. "Numerical Simulation of Sloshing Tanks with Shallow Water Model Using Low Numerical Diffusion Schemes and Its Application to Tuned Liquid Dampers" Water 17, no. 18: 2703. https://doi.org/10.3390/w17182703
APA StyleKhanpour, M., Mohammadian, A., Shirkhani, H., & Kianoush, R. (2025). Numerical Simulation of Sloshing Tanks with Shallow Water Model Using Low Numerical Diffusion Schemes and Its Application to Tuned Liquid Dampers. Water, 17(18), 2703. https://doi.org/10.3390/w17182703







