Abstract
Water resource carrying capacity is a key measure of sustainability, commonly employed to evaluate how well water resources can sustain economic and social growth. With China’s rapid economic growth and modernization, water resources in certain regions are now being used at or beyond their sustainable threshold. This study evaluates the present state of water resource carrying capacity in Taizhou City, located in southeastern China. Using relevant data from 2012 to 2022 on society, economy, water resources, and ecology, the weights of the evaluation indicators were determined using both the entropy weight method and principal component analysis. Subsequently, a comprehensive evaluation model for water resource carrying capacity was developed by applying the TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution) method. The comprehensive proximity index for water resource carrying capacity in Taizhou City averaged 0.4864 between 2012 and 2022, indicating a moderate level overall but exhibiting a declining trend, suggesting an approaching threshold of utilization limits. The range was between 0.3461 and 0.7143. In 2017, the comprehensive proximity index was 0.3461 (low water resource carrying capacity level, with water resources already suffering damage and various subsystems developing uncoordinatedly). However, the comprehensive proximity index for water resource carrying capacity improved significantly from 2018 to 2022. A combination of rising industrial water demand and a decrease in both the absolute volume and proportional allocation of water for ecological purposes drove the overall decline in the progress rate in 2017. Taizhou City has formulated strict water resource management policies and measures, resulting in a decrease in indicators such as industrial water consumption, residential water consumption, and industrial wastewater discharge, as well as an increase in indicators such as ecological water consumption and ecological water utilization rate. As a result, the comprehensive water resource carrying capacity saw a notable rise during 2018–2019. The study results provide a reference for the rational use of water resources in Taizhou City and are of certain significance for promoting the coordinated economic and social development of Taizhou City.
1. Introduction
Water resource carrying capacity serves as a key measure to evaluate how well regional water resources can sustain balanced socioeconomic and ecological development [1,2,3]. The concept of water resource carrying capacity is commonly understood in three ways: the maximum feasible level of water resource development, the largest population sustainable, and the greatest extent of economic and social development that can be supported [4]. Despite varying definitions, water resource carrying capacity is fundamentally a complex, integrated system encompassing both natural and social aspects. This inherent complexity enables it to effectively represent the interactions between water resources, environmental conditions, and human activities.
Assessing water resource carrying capacity requires comprehensive consideration of multiple factors, including total water resources and distribution, development and utilization, socioeconomic activities and water demand levels, and ecological and environmental constraints. Multi-criteria assessment models are frequently employed in holistic water resource carrying capacity studies, as they consolidate diverse indicators into a single scalar value or rating. They enable the assessment and comparison of water resource carrying capacity in terms of time and space. Existing studies have adopted various methods such as fuzzy theory [5,6,7], gray correlation analysis [8,9,10], the TOPSIS model [11,12,13], and machine learning technology [14,15,16]. Nevertheless, a major limitation in current studies is the absence of systematic attribution analysis to determine the underlying causes of deficiencies in water resource carrying capacity. The lack of such analysis diminishes the practical utility of these evaluations, often turning them from a potential starting point for targeted solutions into merely a terminal assessment of existing conditions.
The choice of weighting method in multi-criteria assessment directly affects the scientific validity and credibility of the results. Among the current mainstream methods, objective weighting methods based on data characteristics are more popular due to their repeatability advantages, such as entropy weighting [17,18,19] and principal component analysis [20,21,22]. Subjective empowerment rules that rely on expert experience are susceptible to cognitive biases. It is worth noting that existing research lacks an in-depth discussion of the applicability and combined application of the two methods, especially regarding the complex characteristics of water resource systems. The construction of a subjective–objective integrated weighting system still needs to be explored. The lag in methodological research has constrained the practical application value of water resource carrying capacity evaluation results in differentiated watershed management.
This study focuses on Taizhou City in southeastern China, aiming to systematically assess its water resource carrying capacity and reveal the fundamental contradictions between water supply and demand in the region under rapid modernization, coastal industrial agglomeration, and unique geographical conditions (hilly terrain with “seven mountains, one water, and two fields” and a climate prone to frequent typhoons). The study addresses core issues such as seasonal water shortages, low industrial water use efficiency, and the risk of seawater intrusion, and constructs a multi-dimensional evaluation framework tailored to coastal cities. Building on the current assessment of Taizhou City’s water resource carrying capacity and the broader spatiotemporal patterns observed across Zhejiang Province, this study innovatively incorporates a comprehensive evaluation dimension of “water resources-society-economy-ecology,” breaking through the traditional single evaluation model centered on water volume. The significance of this research lies in both theoretical and practical dimensions: on the one hand, by employing principal component analysis and entropy weighting methods, this study explores a dynamic evaluation model for the integration of multidisciplinary technologies, thereby filling a regional research gap in the study of water resource carrying capacity in coastal hilly cities. On the other hand, the research findings can provide a scientific basis for Taizhou City to optimize the South Taizhou-Wenzhou Water Resource Allocation Project, develop resilient urban planning strategies, and advance the transition toward water-saving industries. Additionally, the findings contribute to establishing a cross-regional water resource coordination management mechanism under the Yangtze River Delta Integration Strategy.
2. Materials and Methods
2.1. Study Area
Taizhou City is located on the central coast of Zhejiang Province, China, between 28°01′ and 29°20′ north latitude and 120°17′ and 121°56′ east longitude. It has a land area of 10,072 square kilometers and an inland water and sea area of 6910 square kilometers. Rolling hills, crisscrossing waterways, intersecting capes, and scattered islands characterize the city. It has a total coastline of 651 km, with three bays (Taizhou Bay, Sanmen Bay, and Yueqing Bay) and 12 island groups comprising 691 islands, making it one of the prefecture-level cities with the most islands in China (Figure 1).
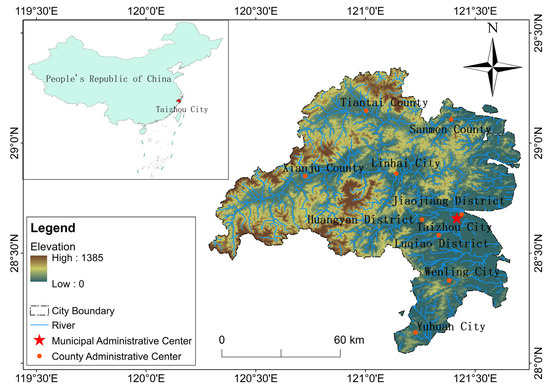
Figure 1.
Overview of the Taizhou River Basin.
From 2012 to 2022, the trend in total water resources in Taizhou City was consistent with precipitation, with significant fluctuations in total volume. The average total water resources volume was 10.108 billion m3, with the lowest total water resources volume recorded in 2020 at 6.032 billion m3 and the highest total water resources volume recorded in 2019 at 14.967 billion m3. The annual average rainfall is 1790.25 mm, with the lowest annual rainfall recorded in 2017 at 1376.1 mm and the highest in 2019 at 2256.9 mm. Annual precipitation exhibits significant interannual variability and a spatial distribution characterized by higher levels in the west and lower levels in the east. High values occur in western Taizhou, with the highest values in the Yong’an River’s upper reaches and the Yongning River’s upper reaches in Huangyan. Low values occur in southern Taizhou, eastern Linhai, and the coastal areas of Sanmen.
2.2. Data Sources and Processing
The Taizhou Municipal Water Resources Bureau Water Resources Bulletin, which provides basic data such as total water resources and water use structure, was accessed on 12 March 2024 (https://slj.zjtz.gov.cn/col/col1229024947). The Taizhou Municipal Bureau of Statistics Statistical Yearbook provides data on population density, population growth rate, and other relevant metrics, which we accessed on 12 March 2024 (https://tjj.zjtz.gov.cn/col/col1229020469/index.html). The Zhejiang Provincial Bureau of Statistics Public Data provides data on water environment quality, pollutant discharge, and other relevant information, which we accessed on 12 March 2024 (https://tjj.zj.gov.cn/col/col1525563/index.html). The data processing includes the following: (1) data preprocessing; (2) data cleansing: remove outliers and missing values to ensure data quality; and (3) standardized processing: standardize water resources, population, and economic data to eliminate dimensional effects.
2.3. Methods
This study establishes an assessment framework for evaluating water resource carrying capacity in Taizhou City. Based on the entropy-weighted TOPSIS model to quantify the carrying capacity level [23,24,25], it proposes strategies and implementation paths for the optimal allocation of water resources in Taizhou City, including measures such as water conservation, industrial structure adjustment, and ecological restoration. Combining the situation in Taizhou City, it proposes a phased and regional water resource allocation plan (Figure 2).
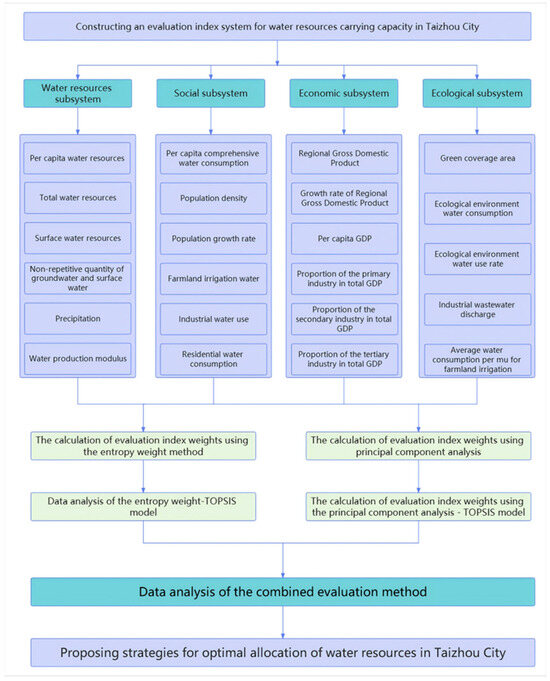
Figure 2.
Study Framework Diagram. entropy weight–TOPSIS model.
2.3.1. Construction of a Water Resource Carrying Capacity Evaluation System
Selection of Evaluation Subsystems
The concept of ecological civilization sets higher standards for socioeconomic development models. It aims to foster harmony between human society and nature by prioritizing respect for, adaptation to, and preservation of the natural world, moving beyond a narrow focus on resource conservation and environmental protection. Therefore, the water resource carrying capacity indicator system, grounded in an ecological civilization perspective, seeks to reconcile the fundamental conflict between socioeconomic development and resource–environmental conservation, ultimately fostering harmony between humanity and nature. The developed evaluation index system for water resource carrying capacity reflects both the regional water conditions and ecological status while also assessing whether human activities remain within the area’s resource and environmental limits [26,27,28]. Within the context of ecological civilization, this study identified four primary objective dimensions for the water resource carrying capacity evaluation system: water resources, social, economic, and ecological subsystems.
- (1)
- Water resources subsystem
The water resources subsystem forms the core of carrying capacity studies. As a fundamental natural resource vital to human survival and socioeconomic production, water resources play a crucial role in regional development and ecological conservation. This subsystem reflects the capacity of regional water resources to sustain human activities, with their utilization efficiency and sustainability heavily influenced by water quality.
- (2)
- Social subsystem
The social subsystem serves as a key focus in water resource carrying capacity studies, with its developmental level being closely linked to the water resource system. Population dynamics are a primary driver of social impacts on water resource systems, given the indispensable role water plays in sustaining human life. As the core component of the social subsystem, population size, demographic attributes, and residents’ lifestyles and living standards are key determinants of water resource sustainability.
- (3)
- Economic subsystem
The economic subsystem constitutes a key component in assessing water resource carrying capacity. Regional economic development relies on water resources, and its scale and industrial structure directly affect water demand. Improvements in economic development levels help to increase water resource reuse rates, strengthen water resource protection, and improve water pollution control. This subsystem must account for both the scale of economic growth and the water use efficiency of economic activities.
- (4)
- Ecological subsystem
Ecological subsystems form the basis for human survival and development and are intrinsically linked to regional socioeconomic advancement, water resource availability, and aquatic environmental conditions. Regional ecological and environmental systems and water resource systems are interdependent and mutually restrictive. On the one hand, ecological systems significantly contribute to soil and water conservation, thereby enhancing the regional carrying capacity of water resources. In contrast, socioeconomic activities such as urban expansion, farmland encroachment, and the discharge of industrial and agricultural effluents exert substantial environmental pressure, which constrains the development of carrying capacity.
Principles for Designing Evaluation Indicators
A scientifically robust and well-structured evaluation framework is essential for accurately assessing water resource carrying capacity. Establishing such a system depends on a solid theoretical foundation and the careful selection of representative indicators. To ensure objectivity, effectiveness, and comprehensiveness in the evaluation process, the choice of indicators should adhere to the following principles:
- (1)
- The principle of scientific
The evaluation indicator system is constructed based on scientific theory and empirical research to ensure that the indicators are clear in meaning, the data sources are reliable, and the period is complete. The selected indicators should be typical and explainable, objectively reflecting the core elements of regional water resources’ essential characteristics and carrying capacity, avoiding subjectivity and arbitrariness, and ensuring that the assessment results support decision-making.
- (2)
- Systemic principles
The evaluation indicator system should reflect the water resource system’s multi-dimensional interrelationships and overall nature. It should cover subsystems such as natural hydrology, socioeconomics, and the ecological environment, and consider key elements such as water quantity, water quality, and spatiotemporal distribution. Through the synergistic and restrictive relationships between indicators, an organic network should be constructed that highlights the system’s overall function while revealing internal coupling mechanisms.
- (3)
- Hierarchy principle
The logical relationships between each layer are clearly defined based on a hierarchical structure comprising the target, system, and indicator layers. The target layer focuses on the comprehensive state of carrying capacity, while the system layer is broken down into dimensions such as resource supply, utilization efficiency, and ecological constraints. The indicator layer uses concrete parameters to ensure clear information transmission paths between layers, coordination, and consistency between local and overall evaluations.
- (4)
- Principles of sustainable development
The evaluation indicator system should consider the dialectical relationship between water resource development and protection. It should introduce long-term indicators such as resource regeneration capacity, ecological service value, and intergenerational equity. It should reflect the current carrying capacity status and quantify future development resilience through potential assessment indicators, promoting sustainable coordination between human activity and water resources.
- (5)
- Operational principle
When selecting evaluation indicators, priority should be given to data availability, calculation standardization, and statistical consistency. Data sources should primarily be based on statistical information or standardized monitoring data released regularly by authoritative departments, avoiding subjective estimates.
Establishment of an Evaluation Indicator System
Wang et al. [29] evaluated the water resource carrying capacity of Guangzhou using a comprehensive framework of 16 indicators, which included per capita Gross Domestic Product (GDP), per capita water resources, and industrial water consumption. Similarly, Zhou et al. [30] utilized 19 indicators, including per capita water availability and the water production coefficient, to evaluate conditions in the Pearl River Delta. Liu et al. [31] selected 15 indicators, including soil erosion rate, surface water utilization rate, agricultural water quota, and water consumption per unit of GDP, to study water resource carrying capacity in Henan Province. Deng et al. [32] selected 12 indicators, including population density, urbanization rate, and per capita daily domestic water consumption, to comprehensively evaluate water resources in the Hanjiang River Basin. This study analyzes the natural geography, climate characteristics, water resources overview, and water resources development and utilization status of Taizhou City, screening out 4 subsystems and 23 evaluation indicators, as shown in Table 1 below.

Table 1.
Taizhou City Water Resource Carrying Capacity Evaluation Index System.
Based on this framework, the study utilizes two objective weighting approaches, namely the entropy method and principal component analysis, to ascertain the weights associated with the 23 indicators. The TOPSIS model is then employed to assess the water resource carrying capacity across multiple weighting schemes. Ultimately, a more scientific and precise method for evaluating water resource carrying capacity is identified through a comprehensive comparison. This study aims to support the sustainable development, utilization, and protection of water resources in Taizhou City while also providing a reference for other Chinese cities in water resource management and carrying capacity assessment.
2.3.2. Water Resource Carrying Capacity Evaluation
Calculation of Evaluation Indicator Weights Based on the Entropy Weight Method
Rooted in information entropy theory, the entropy weight method assesses indicator dispersion by computing their entropy values: a lower entropy value indicates greater dispersion and a higher weight in the comprehensive evaluation [33]. When the numerical values of an indicator are completely equal, the indicator loses its evaluative efficacy. Therefore, by calculating information entropy, the weights of each indicator can be determined, establishing a quantitative foundation for multi-indicator comprehensive evaluation. Entropy, as a core concept in information theory, represents the degree of uncertainty in a system. Information quantity is positively correlated with uncertainty, and entropy values increase accordingly. Conversely, the entropy value then decreases. Specifically, a lower entropy value indicates a more concentrated distribution of the indicator’s data, warranting a higher weight in the comprehensive evaluation. Conversely, a higher entropy value corresponds to a lower weight.
Before performing the entropy method, indicators with inconsistent directions must be preprocessed. This includes two types of standardization methods: normalization and inversion. The specific steps are as follows:
- (1)
- Use the extreme value method to make the indicators dimensionless
Indicators require normalization to a common scale to remove dimensional discrepancies. Positive indicators represent factors that enhance water resource carrying capacity, and their values are positively correlated with carrying capacity scores. Negative indicators reflect limiting factors, and increases in their values will decrease carrying capacity scores.
For positive indicators:
For negative indicators:
where represents the standardized indicator value. represents the actual value of the jth indicator in the ith year. is the maximum value of , and is the minimum value of .
- (2)
- Non-negative translation
The principle of entropy-based weight calculation requires that data values cannot be less than or equal to 0. This is because the entropy-based weight calculation process involves applying a logarithmic function transformation to the data, and the logarithmic function requires the data to be positive. If negative numbers or 0 appear in the original data, a “non-negative shift” operation should be performed. “Non-negative shift” involves adding a constant value to all observed data of an indicator to ensure non-negativity. The shift value is specified as 0.001.
After completing data preprocessing and eliminating the effects of different units of measurement, perform entropy weight analysis. The specific steps are as follows:
- (1)
- Information entropy value
Calculate the proportion of the jth indicator in the ith year:
Calculate the information entropy for each indicator:
where n represents the number of years.
- (2)
- Information utility value
- (3)
- Indicator weight coefficient
Calculation of Evaluation Indicator Weights Based on Principal Component Analysis
Principal component analysis combines multiple correlated indicators to a certain extent into a linear combination to reduce the number of dimensions while retaining as much information as possible from the original dataset. Following dimensionality reduction, the resulting variables are mutually linearly independent. These new variables represent linear combinations of the original ones. The importance of each principal component decreases progressively, with later components accounting for less variance and possessing a diminished capacity to synthesize the original information. Principal component analysis reduces dimensions by intensively processing data information. For example, 23 original indicator values are extracted into four comprehensive principal components. In addition, principal component analysis can be used for weight calculation and comprehensive competitiveness research. That is, principal components have three practical application scenarios: information condensation, which condenses multiple analysis items into several key summary indicators; weight calculation, which uses variance explanation rate values to calculate the weights of each summary indicator; and comprehensive competitiveness, which involves using component scores and variance explanation rates to calculate a comprehensive score for comparative analysis of comprehensive competitiveness.
Principal component analysis uses load factor information to calculate weights. The calculation consists of three steps, as follows:
- (1)
- Calculate the linear combination coefficient matrix
- (2)
- Calculate the comprehensive score coefficient
- (3)
- Calculate the weight and normalize the comprehensive score coefficient to obtain the weight values of each indicator
Assessment of Water Resource Carrying Capacity Based on the TOPSIS Model
The TOPSIS method is a widely used comprehensive evaluation technique that leverages the full range of information in the original dataset, producing results that effectively differentiate among evaluation options [34,35]. The procedure begins by normalizing the raw data matrix and identifying the ideal best and worst solutions via a cosine-based approach. It then calculates the distances from each evaluated object to these reference solutions, ultimately determining their relative closeness to the ideal outcome as a measure of performance. This approach is advantageous due to its minimal requirements for data distribution and sample size, as well as its computational simplicity.
The TOPSIS approach ranks alternatives by their relative similarity to an ideal solution. These findings indicate a positive association between dataset scale and quality, where larger volumes of data are generally associated with superior outcomes, while conversely, smaller datasets often yield inferior results. Therefore, the positive and negative ideal solutions, as well as the distances to them, are determined based on the scale of the data. Finally, the relative proximity value S is obtained. The order of preference is determined by combining the S value with the ranking. The procedure is detailed below:
- (1)
- Dimensionless data. Equations (1) and (2) are used to calculate the positive and negative indicators to obtain a dimensionless normalized matrix.
The completed dimensionless matrix Y is
where is the dimensionless value corresponding to item j in year i.
- (2)
- Calculate the weighted matrix. Based on the normalized matrix, multiply each indicator by its corresponding weight to obtain the weighted matrix :
- (3)
- Identify the positive and negative ideal solutions. Positive ideal solution:
The negative ideal solution:
where and are the maximum and minimum values of the jth indicator in the weighted matrix, respectively.
- (4)
- Compute the Euclidean distance from each evaluation object to both the positive and negative ideal solutions. Distance from the positive ideal solution:
Distance from the negative ideal solution:
- (5)
- Calculate the relative proximity of each evaluation object to the optimal solution using the distance to the negative ideal solution. The resulting score ranges from 0 to 1, with higher values indicating better performance:
Relative proximity can comprehensively reflect the level of water resource carrying capacity. To ensure a scientifically sound evaluation of Taizhou City’s water resource carrying capacity and maintain relatively objective grading criteria, based on the actual water resource conditions of Taizhou City and drawing on the classification criteria established by Cheng et al. [36], this study adopts an equidistant classification method. The relative proximity values are categorized into five levels, each corresponding to a distinct water resource carrying capacity condition in Taizhou City. The detailed grade classifications are shown in Table 2.

Table 2.
TOPSIS evaluation result classification standards.
3. Results
3.1. Weight Calculation Using the Entropy Weight Method
Using dimensionless data from 23 indicators—such as per capita water resources, per capita water use, regional GDP, and green coverage rate—between 2012 and 2022, the entropy weight method was applied to determine each indicator’s weight. The results are shown in Figure 3 and Figure 4. As indicated in Figure 3 and Figure 4, the water resources subsystem carries the greatest weight, accounting for 28.77%. Among these, X5 has the highest weighting at 5.2650%, while X4 has the lowest at 3.6889%. The ecological subsystem has the lowest weighting at 19.12%. Among these, X22 has the highest weighting at 6.4784%, while X20 has the lowest at 2.7544%. The social subsystem has a weighting of 28.19%. Among these, X9 has the highest weighting at 5.7795%, while X12 has the lowest at 1.7947%. The economic subsystem has a weighting of 23.91%. Among these, X18 has the highest weighting at 5.8901%, while X14 has the lowest at 2.8163%.
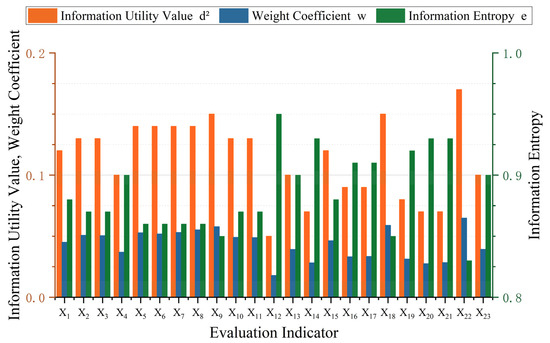
Figure 3.
Evaluation indicators: information entropy value, information utility value, and weight coefficient.
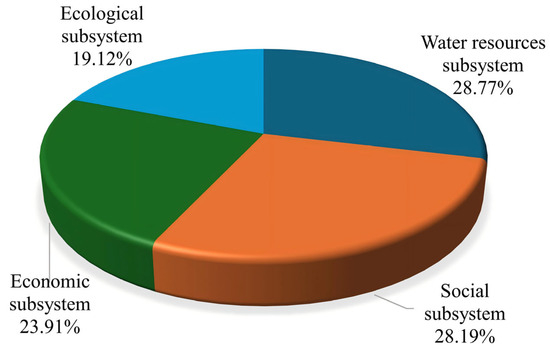
Figure 4.
Weight distribution of criteria layers based on the entropy weight method.
3.2. Weight Calculation in Principal Component Analysis
Principal component analysis (PCA) was performed on the 23 original indicators for Taizhou City (2012–2022) using IBM SPSS Statistics 28.0 statistical software. The data were processed using the PCA method to obtain the eigenvalues and variance explained by the principal components influencing water resource carrying capacity in Taizhou City from 2012 to 2022, as shown in Figure 5. As shown in Figure 5, the cumulative contribution rate of the first four principal components reached 92.543% > 85%, and their eigenvalues were all greater than 1. These principal components capture the influence of the selected indicators on Taizhou City’s water resource carrying capacity and reflect its interannual variations. Consequently, the first four principal components were chosen for further analysis.
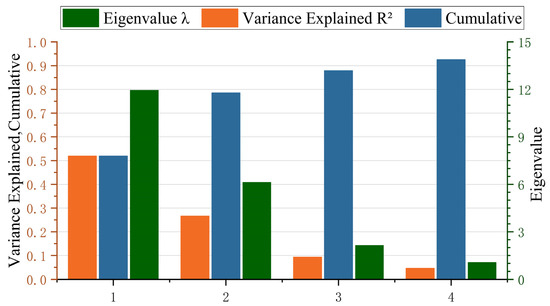
Figure 5.
Principal component eigenvalues and variance explained.
Principal component loadings were derived from the first four components, with the results displayed in Figure 6. Figure 6 displays the loading factors of X7, X8, X9, X10, X11, X16, X17, and X22 on principal component 1 are close to 1, indicating a strong positive correlation with principal component 1. The absolute values of the load factors of X13, X15, X18, X19, and X21 on principal component 1 are close to 1, indicating a strong negative correlation with principal component 1. The loadings of X1, X2, X3, X4, X5, and X6 on principal component 2 are close to 1, indicating a strong positive correlation with principal component 2. The loadings of X17, X18, X19, X20, X21, and X22 on principal component 2 are close to 0, indicating a weak correlation with principal component 2. The loadings of X20 and X21 on principal component 3 are close to 1, indicating a strong positive correlation with principal component 3. The absolute value of the loading of X12 on principal component 3 is close to 1, indicating a strong negative correlation with principal component 3. The loading of X14 on principal component 4 is close to 1, indicating a strong positive correlation with principal component 4.
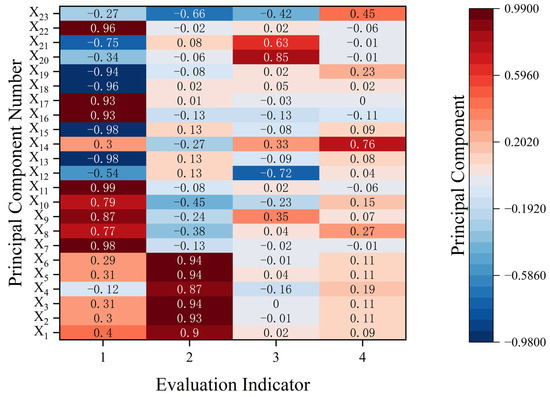
Figure 6.
Principal component load coefficients.
Using principal component eigenvalues, variance explanation rates, and load factors, the weights were calculated based on principal component analysis to obtain the comprehensive score coefficients and weights of the principal components of the factors influencing water resource carrying capacity in Taizhou City from 2012 to 2022. Figure 7 and Figure 8 show that the social subsystem has the highest weight ratio of 28.13%. Among these, X10 has the highest proportion at 5.25%, while X12 has the lowest at 3.97%. The ecological subsystem has the lowest weight ratio at 20.73%. Among these, X21 has the highest proportion at 4.50%, while X20 has the lowest at 3.08%. The economic subsystem accounts for 25.92% of the weight. Among these, X13 has the highest proportion at 4.75%, while X14 has the lowest at 3.62%. The water resources subsystem accounts for 25.21% of the weight. Among these, X1 has the highest proportion at 4.54%, while X4 has the lowest at 3.65%.
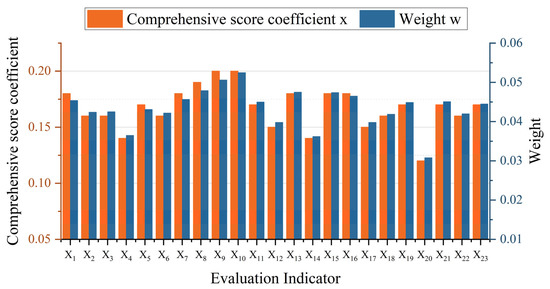
Figure 7.
Comprehensive score coefficient and weighting of evaluation indicators.
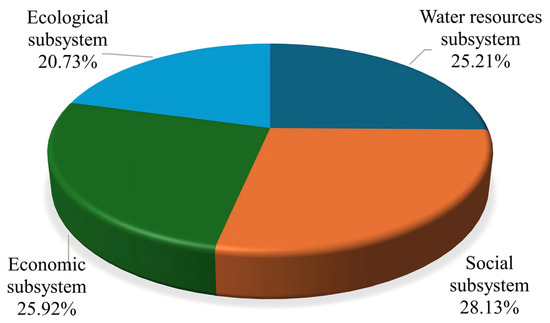
Figure 8.
Weight distribution of criteria layers based on principal component analysis.
3.3. Data Analysis of the Entropy Weight–TOPSIS Model
The water resource carrying capacity of Taizhou City from 2012 to 2022 was evaluated using the entropy weight–TOPSIS model, which included the calculation of distances to both positive and negative ideal solutions along with the corresponding relative closeness indices. Referring to the evaluation grading criteria, the water resource carrying capacity assessment results for Taizhou City were obtained, as shown in Table 3 and Figure 9. As shown in Table 3, Taizhou City’s water resource carrying capacity from 2012 to 2022 was generally between Level II and Level IV, between good and relatively poor. No year showed a great or poor water resource carrying capacity, and proximity showed an overall fluctuating upward trend over the year interval. The positive ideal solution distance decreased from 0.1528 in 2012 to 0.1371 in 2022, showing a fluctuating downward trend. The negative ideal solution distance increased from 0.1232 in 2012 to 0.1500 in 2022, generally consistent with the overall trend. From 2012 to 2017, the proximity decreased from 0.4462 to 0.3226, a year-on-year decrease of 27.70%. From 2018 to 2022, the proximity data fluctuated, increasing from 0.4854 to 0.5225, showing a trend of first increasing, then decreasing, followed by a sharp rise and a sharp decline.

Table 3.
Results of Taizhou City’s water resource carrying capacity evaluation based on entropy weight–TOPSIS.
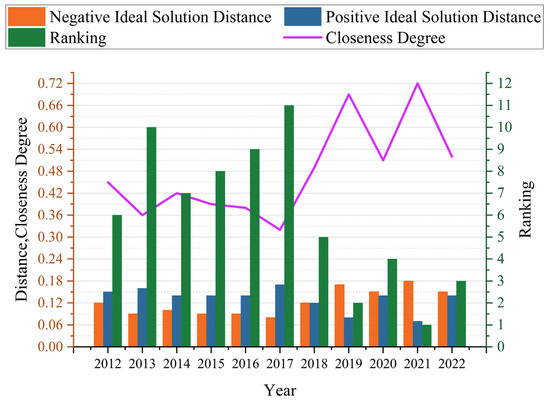
Figure 9.
Results of Taizhou City water resource carrying capacity evaluation based on entropy weight–TOPSIS.
3.4. Data Analysis Using Principal Component Analysis and the TOPSIS Model
A comprehensive evaluation model based on principal component analysis (PCA) and the TOPSIS method was used to assess the water resource carrying capacity of Taizhou City. The distances to the positive and negative ideal solutions, as well as the relative proximity, were calculated for Taizhou City’s water resource carrying capacity from 2012 to 2022. Based on the grading criteria, the evaluation results are summarized in Table 4. Table 4 shows that Taizhou City’s water resource carrying capacity from 2012 to 2022 was generally between Grade II and Grade IV, between good and relatively poor. No year showed a great or poor water resource carrying capacity, and the proximity degree showed a fluctuating upward trend within the year range. The positive ideal solution distance D decreased from 0.1171 in 2012 to 0.1330 in 2022, showing a fluctuating downward trend. The negative ideal solution distance D1 increased from 0.1232 in 2012 to 0.1443 in 2022, generally aligning with the overall trend. From 2012 to 2017, the proximity decreased from 0.4340 to 0.3696, showing a fluctuating trend of first decreasing, then increasing, and then decreasing again. During the period from 2018 to 2022, the proximity data fluctuated, but the variation was not significant, increasing from 0.5157 to 0.5205, representing a year-on-year increase of 0.93%.

Table 4.
Taizhou City’s water resource carrying capacity evaluation results are based on principal component analysis, called TOPSIS.
3.5. Data Analysis Using the Combined Evaluation Method
Two objective weighting approaches, namely the entropy method and principal component analysis, were utilized to determine the weights of the indicators. The entropy weighting method identified industrial wastewater discharge, the proportion of GDP contributed by the tertiary industry, and the population growth rate as the most influential factors. In contrast, principal component analysis highlighted agricultural irrigation water use, population growth rate, and population density as key determinants. As shown in Figure 10, the evaluation results of water resource carrying capacity levels under different weights using the TOPSIS model are generally consistent, but there are some differences between individual years. Therefore, a combined evaluation method was used for analysis, taking the average of the proximity values calculated by the entropy weight–TOPSIS model and the principal component analysis–TOPSIS model as the comprehensive proximity value. The results of the combined evaluation method are presented in Table 5. Analysis using the entropy-weighted TOPSIS, PCA–TOPSIS, and combined evaluation models reveals an overall upward trend in Taizhou City’s water resource carrying capacity over the past 11 years. Among the 11 years, 2021, 2019, and 2020 had the highest comprehensive scores, at 0.7143, 0.6962, and 0.5340, respectively. Results from the entropy-weighted TOPSIS evaluation, principal component analysis–TOPSIS model, and combined evaluation method all indicate that the comprehensive proximity was highest in 2021. Additionally, in 2021, Taizhou City’s per capita water resources and water production moduli were 2164 m3 and 151,000 m3/km2, respectively, significantly higher than the national average of 2099 m3 and 30.87 million m3/km2. This suggests that Taizhou City’s overall water resource carrying capacity exceeds the national average, aligning with the 2021 assessment results from the combined evaluation method.
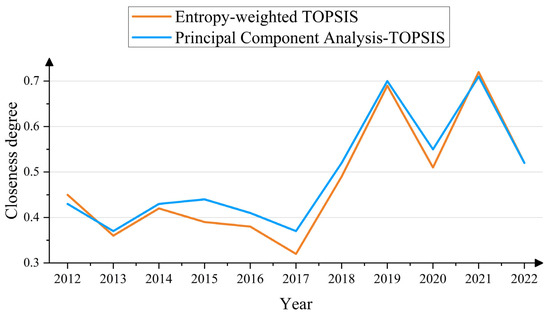
Figure 10.
Comparison of the closeness calculated by the entropy weight–TOPSIS model and the principal component analysis–TOPSIS model.

Table 5.
Evaluation results of the water resources carrying capacity of Taizhou City by the combined evaluation method.
4. Discussion
4.1. Water Resource Carrying Capacity Assessment Methods
Previous studies have primarily focused on constructing indicator systems and optimizing single models [37,38]. This study innovatively incorporates a comprehensive evaluation dimension encompassing “water resources-society-economy-ecology”, breaking away from the traditional single evaluation model centered on water quantity. By combining the entropy weight method with principal component analysis (PCA), this study overcomes the limitations of traditional single-weighting models [39]. Combining the entropy weight method with principal component analysis essentially integrates information from two dimensions: “the amount of information provided by the data” and “the inherent data structure of the indicators”. This integration effectively offsets the limitations of either method alone, particularly addressing the critical weakness of the entropy weight method when handling correlated indicators. Consequently, it significantly enhances the scientific rigor of determining indicator weights and improves the accuracy of evaluation outcomes [40,41]. Through PCA and the entropy weight method, this study explores a dynamic evaluation model integrating multidisciplinary technologies, filling a regional gap in research on water resource carrying capacity in coastal hilly cities [42].
4.2. Analysis of Taizhou City’s Water Resource Carrying Capacity Based on the Combination Evaluation Method
From 2012 to 2022, Taizhou’s water resource carrying capacity showed an overall fluctuating upward trend. Although it remained at Level IV (relatively poor condition) in 2013, 2016, and 2017, the overall trend was still improving. Since Zhejiang Province launched the “Five-Water Co-governance” strategy in 2013 [43], initial results were seen as early as 2014 [44]. However, from 2015 to 2016, numerous issues in water resource development and management led to insufficient water supply to meet economic and social production demands, resulting in a decline in the comprehensive adequacy index. Starting in 2017, Zhejiang Province continued advancing the “Five-Water Co-governance” initiative, incorporating the “complete elimination of water quality sections below Class V” into its key livelihood projects. This sustained improvement in the province’s water environment led to a steady increase in water resource carrying capacity. Between 2019 and 2022, the carrying capacity fluctuated upward to Grade II–III, indicating a state ranging from good to fair, reflecting a marked improvement.
Notably, in 2020, total water resources decreased by approximately 60% year-on-year, with precipitation and water production moduli also experiencing significant declines. Meanwhile, negative indicators such as industrial wastewater discharge and annual water supply volume remained largely unchanged, leading to a marked reduction in water resource carrying capacity for the year. Similarly, 2022 saw a year-on-year decrease of approximately 50% in the water production modulus and a decline of about 32% in the ecological and environmental water utilization rate. Negative indicators such as industrial water consumption and wastewater discharge showed no improvement, further highlighting the consumption and pollution pressures on water resources from social production, resulting in a substantial decline in carrying capacity.
4.3. Taizhou City Water Resource Carrying Capacity Protection Strategy
In response to issues such as insufficient water supply and prominent water pollution in Taizhou City, this study proposes four strategies. (1) Enhance water supply capacity: Enhance the storage capacity of existing reservoirs in Taizhou City [45,46]. Optimize the layout of inter-regional water diversion projects [47,48]. Strengthen the development of non-conventional water resources [49,50] and improve the groundwater dynamic monitoring system [51,52,53]. The aforementioned measures can enhance indicators such as per capita water resources, total water resources, and ecological and environmental water usage. (2) Improve water resource utilization efficiency: In the agricultural sector, promote efficient water-saving irrigation technologies [54]. Additionally, promote water-saving household appliances and use fiscal subsidies to encourage residents to install water-saving equipment. The aforementioned measures can reduce indicators such as agricultural irrigation water consumption, residential water consumption, and average water consumption per mu of farmland. (3) Promote ecological and environmental protection for water resources: Implement comprehensive basin management [55]. Strengthen water source protection [56] and ensure ecological base flow [57]. The aforementioned measures can increase indicators such as the water production modulus, green coverage area, and ecological environment water utilization rate. (4) Public education and raising water conservation awareness: Incorporate water conservation education into local regulations. Produce a series of science popularization videos and disseminate them through platforms like Douyin and WeChat Video Accounts. The aforementioned measures can reduce indicators such as residential water consumption. All measures increase or decrease corresponding indicators, thereby enhancing Taizhou’s water resource carrying capacity.
5. Conclusions
This study focuses on Taizhou City, analyzing its water resource carrying capacity over the past 11 years and the influence of socioeconomic factors. It comprehensively used the entropy weight method, principal component analysis, and TOPSIS model to reveal the water resource carrying capacity level of Taizhou City in detail. Based on the water resource carrying capacity issues identified through the calculations, a series of measures for optimizing water resource carrying capacity were proposed to further enhance the water resource carrying capacity of Taizhou City.
Water resource carrying capacity exhibits phased fluctuations. During the study period, the average comprehensive proximity index was 0.4864, ranging from 0.3461 to 0.7143, showing an overall “U-shaped” trend. From 2012 to 2017, the carrying capacity continued to decline due to the surge in industrial water use and insufficient ecological base flow. Following 2018, carrying capacity markedly improved, driven by advances in recycled water projects and the enforcement of water-saving policies, peaking in 2021. The factors influencing water resource carrying capacity exhibit multi-dimensional coupling characteristics. The entropy weight method weight calculation results indicate that industrial wastewater discharge volume, the proportion of the tertiary industry, and the population growth rate serve as key indicators. According to the principal component analysis weighting results, agricultural irrigation water use and population density are identified as critical indicators. Both models indicate that industrial pollution loads, inefficient agricultural water use, and population concentration pressures are the core contradictions constraining carrying capacity. This is closely related to Taizhou City’s topographical characteristics of “seven mountains, one water, and two fields” and the high water consumption attributes of its dominant industries, such as manufacturing. The study validated the applicability of the “water resources-society-economy-ecology” comprehensive evaluation framework in Taizhou City. This study addresses the vulnerability of Taizhou City’s water resources system and the need to enhance its carrying capacity, providing strategies from four different levels to provide scientific support for the development and security of Taizhou City’s water resources.
Author Contributions
Conceptualization, C.X. and H.C.; methodology, J.Y.; software, Y.C.; validation, Y.W.; formal analysis, H.Q.; investigation, H.C.; resources, J.T.; data curation, W.W.; writing—original draft preparation, C.X.; writing—review and editing, H.C.; visualization, Z.L.; supervision, T.Y.; project administration, H.C.; funding acquisition, H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Zhejiang Provincial Natural Science Foundation, grant number ZCLQ24E0901; the Scientific Research Fund of the Zhejiang Provincial Education Department, grant number Y202352492; the Zhejiang Provincial Water Resources Department Science and Technology Program, grant number RC2213; and the Huzhou Science and Technology Plan Project, grant number 2023GZ64.
Data Availability Statement
The Taizhou Municipal Water Resources Bureau Water Resources Bulletin provides basic data such as total water resources and water use structure (https://slj.zjtz.gov.cn/col/col1229024947). The Taizhou Municipal Bureau of Statistics Statistical Yearbook provides data on population density, population growth rate, and other relevant metrics (https://tjj.zjtz.gov.cn/col/col1229020469/index.html). The Zhejiang Provincial Bureau of Statistics Public Data provides data on water environmental quality, pollutant discharge, and other relevant information (https://tjj.zj.gov.cn/col/col1525563/index.html).
Acknowledgments
We thank the Zhejiang Hydrological Management Center for providing hydrological and meteorological data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, Q.; Zhu, M.; Zhang, C.; Zhou, Q. The Driving Effect of Spatial-Temporal Difference of Water Resources Carrying Capacity in the Yellow River Basin. J. Clean. Prod. 2023, 388, 135709. [Google Scholar] [CrossRef]
- Chen, H.; Huang, S.; Qiu, H.; Xu, Y.P.; Teegavarapu, R.S.V.; Guo, Y.; Nie, H.; Xie, H.; Xie, J.; Shao, Y.; et al. Assessment of Ecological Flow in River Basins at a Global Scale: Insights on Baseflow Dynamics and Hydrological Health. Ecol. Indic. 2025, 178, 113868. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, S.; Gao, C.; Tang, X. Coupling Coordination and Driving Mechanisms of Water Resources Carrying Capacity under the Dynamic Interaction of the Water-Social-Economic-Ecological Environment System. Sci. Total Environ. 2024, 920, 171011. [Google Scholar] [CrossRef] [PubMed]
- Naimi Ait-Aoudia, M.; Berezowska-Azzag, E. Water Resources Carrying Capacity Assessment: The Case of Algeria’s Capital City. Habitat Int. 2016, 58, 51–58. [Google Scholar] [CrossRef]
- Yu, D.; Xu, Z.; Wang, W. Bibliometric Analysis of Fuzzy Theory Research in China: A 30-Year Perspective. Knowl.-Based Syst. 2018, 141, 188–199. [Google Scholar] [CrossRef]
- Liang, H.; Zou, J.; Li, Z.; Khan, M.J.; Lu, Y. Dynamic Evaluation of Drilling Leakage Risk Based on Fuzzy Theory and PSO-SVR Algorithm. Future Gener. Comput. Syst. 2019, 95, 454–466. [Google Scholar] [CrossRef]
- Yang, H.; Zhu, Z.; Li, C.; Li, R. A Novel Combined Forecasting System for Air Pollutants Concentration Based on Fuzzy Theory and Optimization of Aggregation Weight. Appl. Soft Comput. 2020, 87, 105972. [Google Scholar] [CrossRef]
- Hu, A.; Xie, N. Construction and Application of a Novel Grey Relational Analysis Model Considering Factor Coupling Relationship. Grey Syst. Theory Appl. 2025, 15, 1–20. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, X.; Yang, J. Teaching Evaluation Algorithm Based on Grey Relational Analysis. Complexity 2021, 2021, 5596518. [Google Scholar] [CrossRef]
- Hamzaçebi, C.; Pekkaya, M. Determining of Stock Investments with Grey Relational Analysis. Expert Syst. Appl. 2011, 38, 9186–9195. [Google Scholar] [CrossRef]
- Çelikbilek, Y.; Tüysüz, F. An In-Depth Review of Theory of the TOPSIS Method: An Experimental Analysis. J. Manag. Anal. 2020, 7, 281–300. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, P.; Yao, Y. BMW-TOPSIS: A Generalized TOPSIS Model Based on Three-Way Decision. Inf. Sci. 2022, 607, 799–818. [Google Scholar] [CrossRef]
- Ramakrishnan, K.R.; Chakraborty, S. A Cloud TOPSIS Model for Green Supplier Selection. Facta Univ. Ser. Mech. Eng. 2020, 18, 375–397. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Peng, W.; Tabatabaei, M.; Kalogirou, S.A.; Soltanian, S.; Hosseinzadeh-Bandbafha, H.; Mahian, O.; Lam, S.S. Machine Learning Technology in Biodiesel Research: A Review. Prog. Energy Combust. Sci. 2021, 85, 100904. [Google Scholar] [CrossRef]
- Sarkar, C.; Das, B.; Rawat, V.S.; Wahlang, J.B.; Nongpiur, A.; Tiewsoh, I.; Lyngdoh, N.M.; Das, D.; Bidarolli, M.; Sony, H.T. Artificial Intelligence and Machine Learning Technology Driven Modern Drug Discovery and Development. Int. J. Mol. Sci. 2023, 24, 2026. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Lim, M.K.; Qu, Y.; Ni, D.; Xiao, Z. Supply Chain Risk Management with Machine Learning Technology: A Literature Review and Future Research Directions. Comput. Ind. Eng. 2023, 175, 108859. [Google Scholar] [CrossRef] [PubMed]
- Chen, P. Effects of the Entropy Weight on TOPSIS. Expert Syst. Appl. 2021, 168, 114186. [Google Scholar] [CrossRef]
- Li, Z.; Luo, Z.; Wang, Y.; Fan, G.; Zhang, J. Suitability Evaluation System for the Shallow Geothermal Energy Implementation in Region by Entropy Weight Method and TOPSIS Method. Renew. Energy 2022, 184, 564–576. [Google Scholar] [CrossRef]
- Zhe, W.; Xigang, X.; Feng, Y. An Abnormal Phenomenon in Entropy Weight Method in the Dynamic Evaluation of Water Quality Index. Ecol. Indic. 2021, 131, 108137. [Google Scholar] [CrossRef]
- Greenacre, M.; Groenen, P.J.F.; Hastie, T.; D’Enza, A.I.; Markos, A.; Tuzhilina, E. Principal Component Analysis. Nat. Rev. Methods Prim. 2022, 2, 100. [Google Scholar] [CrossRef]
- Odhiambo Omuya, E.; Onyango Okeyo, G.; Waema Kimwele, M. Feature Selection for Classification Using Principal Component Analysis and Information Gain. Expert Syst. Appl. 2021, 174, 114765. [Google Scholar] [CrossRef]
- Lamichhane, S.; Eğilmez, G.; Gedik, R.; Bhutta, M.K.S.; Erenay, B. Benchmarking OECD Countries’ Sustainable Development Performance: A Goal-Specific Principal Component Analysis Approach. J. Clean. Prod. 2021, 287, 125040. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Bao, J.; Wei, T.; Xu, S. A Research on the Evaluation of China’s Food Security under the Perspective of Sustainable Development-Based on an Entropy Weight TOPSIS Model. Agriculture 2022, 12, 1926. [Google Scholar] [CrossRef]
- Jing, X.; Tao, S.; Hu, H.; Sun, M.; Wang, M. Spatio-Temporal Evaluation of Ecological Security of Cultivated Land in China Based on DPSIR-Entropy Weight TOPSIS Model and Analysis of Obstacle Factors. Ecol. Indic. 2024, 166, 112579. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, Z.; Xu, C.; Cai, G.; Zhan, J. Assessment of Provincial Waterlogging Risk Based on Entropy Weight TOPSIS-PCA Method. Nat. Hazards 2021, 108, 1545–1567. [Google Scholar] [CrossRef]
- Lv, B.; Liu, C.; Li, T.; Meng, F.; Fu, Q.; Ji, Y.; Hou, R. Evaluation of the Water Resource Carrying Capacity in Heilongjiang, Eastern China, Based on the Improved TOPSIS Model. Ecol. Indic. 2023, 150, 110208. [Google Scholar] [CrossRef]
- Li, J.; Meng, Z.; Zhang, J.; Chen, Y.; Yao, J.; Li, X.; Qin, P.; Liu, X.; Cheng, C. Prediction of Seawater Intrusion Run-Up Distance Based on K-Means Clustering and ANN Model. J. Mar. Sci. Eng. 2025, 13, 377. [Google Scholar] [CrossRef]
- Wang, G.; Xiao, C.; Qi, Z.; Meng, F.; Liang, X. Development Tendency Analysis for the Water Resource Carrying Capacity Based on System Dynamics Model and the Improved Fuzzy Comprehensive Evaluation Method in the Changchun City, China. Ecol. Indic. 2021, 122, 107232. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L.; Zhang, S.; Gao, C. Dynamic Simulation and Comprehensive Evaluation of the Water Resources Carrying Capacity in Guangzhou City, China. Ecol. Indic. 2022, 135, 108528. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Z.; Zhang, B.; Yang, Q. Evaluating Water Resources Carrying Capacity of Pearl River Delta by Entropy Weight-TOPSIS Model. Front. Environ. Sci. 2022, 10, 967775. [Google Scholar] [CrossRef]
- Liu, P.; Lü, S.; Han, Y.; Wang, F.; Tang, L. Comprehensive Evaluation on Water Resources Carrying Capacity Based on Water-Economy-Ecology Concept Framework and EFAST-Cloud Model: A Case Study of Henan Province, China. Ecol. Indic. 2022, 143, 109392. [Google Scholar] [CrossRef]
- Deng, L.; Yin, J.; Tian, J.; Li, Q.; Guo, S. Comprehensive Evaluation of Water Resources Carrying Capacity in the Han River Basin. Water 2021, 13, 249. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Yoon, K.P.; Kim, W.K. The Behavioral TOPSIS. Expert Syst. Appl. 2017, 89, 266–272. [Google Scholar] [CrossRef]
- Pandey, V.; Komal; Dincer, H. A Review on TOPSIS Method and Its Extensions for Different Applications with Recent Development. Soft Comput. 2023, 27, 18011–18039. [Google Scholar] [CrossRef]
- Cheng, K.; Fu, Q.; Meng, J.; Li, T.X.; Pei, W. Analysis of the Spatial Variation and Identification of Factors Affecting the Water Resources Carrying Capacity Based on the Cloud Model. Water Resour. Manag. 2018, 32, 2767–2781. [Google Scholar] [CrossRef]
- Song, X.; Kong, F.; Zhan, C. Assessment of Water Resources Carrying Capacity in Tianjin City of China. Water Resour. Manag. 2011, 25, 857–873. [Google Scholar] [CrossRef]
- Mei, H.; Liu, Y.; Du, H.; Yang, X. Advances in Study on Water Resources Carrying Capacity in China. Procedia Environ. Sci. 2010, 2, 1894–1903. [Google Scholar] [CrossRef]
- Pliego-Martínez, O.; Martínez-Rebollar, A.; Estrada-Esquivel, H.; de la Cruz-Nicolás, E. An Integrated Attribute-Weighting Method Based on PCA and Entropy: Case of Study Marginalized Areas in a City. Appl. Sci. 2024, 14, 2016. [Google Scholar] [CrossRef]
- Wu, R.M.X.; Zhang, Z.; Yan, W.; Fan, J.; Gou, J.; Liu, B.; Gide, E.; Soar, J.; Shen, B.; Fazal-e-Hasan, S.; et al. A Comparative Analysis of the Principal Component Analysis and Entropy Weight Methods to Establish the Indexing Measurement. PLoS ONE 2022, 17, e0262261. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, X.; Li, B.; Wu, P.; Cai, X.; Luo, Y.; Deng, X.; Jiang, M. A Groundwater Quality Assessment Model for Water Quality Index: Combining Principal Component Analysis, Entropy Weight Method, and Coefficient of Variation Method for Dimensionality Reduction and Weight Optimization, and Its Application. Water Environ. Res. 2024, 96, e11155. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Lei, Y.; Wu, T.; Chen, K. Evaluating Water Resources Carrying Capacity: The Empirical Analysis of Hubei Province, China 2008–2020. Ecol. Indic. 2022, 144, 109454. [Google Scholar] [CrossRef]
- Tian, J.; Han, Y.; Shen, J.; Zhu, Y. Leveraging Sustainable Development of Agriculture with Sustainable Water Management: The Empirical Investigation of “Five Water Cohabitation” of Zhejiang Province in China. Environ. Monit. Assess. 2022, 194, 124. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Zhang, Q.; You, H.; Liu, Y. Multi-Dimensional Assessment, Regional Differences, and Influencing Factors of Agricultural Water Pollution from the Perspective of Grey Water Footprint in Zhejiang Province, China. Agriculture 2024, 14, 2031. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, W.; Li, M.; Wang, Q.; Zhou, H. Flood Control Storage Substitution from Multiple to Single-Reservoir and Storage Reservation Strategy for Hydropower Optimization in Cascade Reservoir Systems. J. Hydrol. 2025, 662, 133926. [Google Scholar] [CrossRef]
- Tang, Z.; Deng, X.; Guo, A.; Wang, Y.; Chang, J.; Liang, Y.; Li, Z.; Zhai, D.; Zheng, R. Dynamic Compensation Operating Rule of Parallel Reservoirs to Enhance Sufficient Hydrological and Reservoir Capacity Compensation. J. Hydrol. 2025, 657, 133149. [Google Scholar] [CrossRef]
- Zhao, R.; Gan, T.; Wang, X.; Wang, H. Research on Parameter Optimization of the Optimal Schedule Model of Water Resources for the Jiaodong Water Transfer Project Based on the ICCP Model. Water 2023, 15, 2731. [Google Scholar] [CrossRef]
- Chen, H.; Xu, B.; Qiu, H.; Huang, S.; Teegavarapu, R.S.V.; Xu, Y.P.; Guo, Y.; Nie, H.; Xie, H. Adaptive Assessment of Reservoir Scheduling to Hydrometeorological Comprehensive Dry and Wet Condition Evolution in a Multi-Reservoir Region of Southeastern China. J. Hydrol. 2025, 648, 132392. [Google Scholar] [CrossRef]
- Xu, Z.; Ding, Y.; Han, S.C.; Zhang, C. Predicting the Performance of Lithium Adsorption and Recovery from Unconventional Water Sources with Machine Learning. Water Res. 2024, 266, 122374. [Google Scholar] [CrossRef]
- Zhang, D.; Xie, X.; Wang, T.; Wang, B.; Pei, S. Research on Water Resources Allocation System Based on Rational Utilization of Brackish Water. Water 2022, 14, 948. [Google Scholar] [CrossRef]
- Barati, A.A.; Azadi, H.; Scheffran, J. A System Dynamics Model of Smart Groundwater Governance. Agric. Water Manag. 2019, 221, 502–518. [Google Scholar] [CrossRef]
- Chen, H.; Huang, S.; Xu, Y.-P.; Teegavarapu, R.S.V.; Guo, Y.; Nie, H.; Xie, H. Using Baseflow Ensembles for Hydrologic Hysteresis Characterization in Humid Basins of Southeastern China. Water Resour. Res. 2024, 60, e2023WR036195. [Google Scholar] [CrossRef]
- Thakur, J.K. Hydrogeological Modeling for Improving Groundwater Monitoring Network and Strategies. Appl. Water Sci. 2017, 7, 3223–3240. [Google Scholar] [CrossRef]
- Xiuling, D.; Qian, L.; Lipeng, L.; Sarkar, A. The Impact of Technical Training on Farmers Adopting Water-Saving Irrigation Technology: An Empirical Evidence from China. Agriculture 2023, 13, 956. [Google Scholar] [CrossRef]
- Moore, S. Toward Effective River Basin Management (RBM): The Politics of Cooperation, Sustainability, and Collaboration in the Delaware River Basin. J. Environ. Manag. 2021, 298, 113421. [Google Scholar] [CrossRef]
- Nel, J.L.; Le Maitre, D.C.; Roux, D.J.; Colvin, C.; Smith, J.S.; Smith-Adao, L.B.; Maherry, A.; Sitas, N. Strategic Water Source Areas for Urban Water Security: Making the Connection between Protecting Ecosystems and Benefiting from Their Services. Ecosyst. Serv. 2017, 28, 251–259. [Google Scholar] [CrossRef]
- Cheng, B.; Li, H. Improving Water Saving Measures Is the Necessary Way to Protect the Ecological Base Flow of Rivers in Water Shortage Areas of Northwest China. Ecol. Indic. 2021, 123, 107347. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).