Combining Machine Learning Models and Satellite Data of an Extreme Flood Event for Flood Susceptibility Mapping
Abstract
1. Introduction
1.1. General and Literature Review
| Area of Interest | Algorithms | Evaluation | Data Split Train/Test (%) | Total Points | Resolution (m) | Ref. |
|---|---|---|---|---|---|---|
| Ibaraki, Japan | ANN-MLP SVR GBR Lasso | MAE MSE RMSE R2 AUC/ROC | 70/30 | 224 | 30 × 30 | [11] |
| Berlin, Germany | CNN ANN RF SVM | AUC/Kappa | 80/20 | 3934 | 30 × 30 10 × 10 5 × 5 2 × 2 | [12] |
| Idukki, Kerala India | AdaBoost Gradient Boosting XGBoost CatBoost SGB | AUC Precision Recall NP | 70/30 | 1500 | 30 × 30 | [13] |
| Periyar River, India | LR SVM Naive Bayes RF Ada Boosting Gradient Boosting XGBoost | AUC/ROC | 30/70 | 188 | 30 × 30 | [19] |
| Fujairah, UAE | xDeepFM DNN SVM RF | recall precision accuracy | 75/25 | 2400 | 30 × 30 | [20] |
| Salzburg, Austria | MCDA (AHP, ANP) ML (RF, SVM) | AUC/ROC | 70/30 | 30 × 30 | [21] | |
| Metlili, Morocco | RF CART SVM XGBoost | AUC | 70/30 | 204 | 30 × 30 | [22] |
| Karun, Iran Gorganrud, Iran | Deep Forest CFM Multi-gained scanning | AUC/ROC OA KC | 27/73 | 4160 1278 | 30 × 30 | [23] |
| Wilayat As-Suwayq, Oman | XGBoost RF CatBoost | AUC | 70/30 | 446 | 5 × 5 | [24] |
| Haraz, Iran | ANN CART FDA GLM GAM BRT MARS MaxEnt | AUC/ROC | – | 201 | 20 × 20 | [25] |
| Ref. | Flood Conditioning Factors |
|---|---|
| [11] | Elevation, Slope, Aspect, Plane Curvature, Profile Curvature, TWI, SPI, DTStreams, DTRiver, DTRoads, Land Cover |
| [12] | Elevation, Slope, Aspect, Curvature, TWI, DTRiver, DTRoads, DTDrainage, CN, AP, FP |
| [13] | Elevation, Slope, Aspect, Curvature, STI, TRI, TWI, SPI, DTRoads, DTStreams, Soil, Geology, Geomorphology, LULC, NDVI, Rainfall |
| [19] | Elevation, Slope, Aspect, Flow Direction, Drainage Density, SPI, STI, TPI, NDWI, Rainfall |
| [20] | Elevation, Slope, Curvature, Drainage Density, SPI, TWI, STI, TRI, NDVI, DTDrainage, Rainfall, Land Use, Geology |
| [21] | Elevation, Slope, Aspect, TWI, SPI, DTRoads, DTDrainage, NDVI, Geology, Rainfall, Land Cover |
| [22] | Elevation, Slope, Aspect, Plan Curvature, TWI, SPI, DTStreams, DTRoads, Lithology, Rainfall, LULC, NDVI |
| [23] | Elevation, Slope, Aspect, Curvature, Plan Curvature, Profile Curvature, TPI, TRI, TWI, SPI, Convergence Index, LULC, NDVI, Valley Depth, LS Factor, Flow Accumulation, MCA, HOFD, VOFD, CN, MFI |
| [24] | Elevation, Slope, Curvature, TRI, TWI, SPI, DTDrainage, Drainage Density, DTRoads, NDVI, Geology, Soil Type, Rainfall |
| [25] | Elevation, Slope, Curvature, SPI, TWI, River Density, DTRiver, NDVI, Land Cover, Lithology, Rainfall |
1.2. Objectives and Structure of the Study
- Supporting the development of an early warning system for flood susceptibility through the exploitation of satellite-derived rainfall data.
- Application and comparative analysis of machine learning models (LR, SVM, RF, XGBoost) to produce accurate flood susceptibility maps.
- Calculation of feature importance scores to evaluate the influence of each input variable on model predictions.
- Investigation of the impact of different initial training conditions on model performance.
- Development of an FSM based on a 1000-year return period rainfall scenario at the 24 h scale.
- Provision of recommendations for flood risk management and planning in the case study, based on the results obtained.
2. Study Area and Data
2.1. Study Area
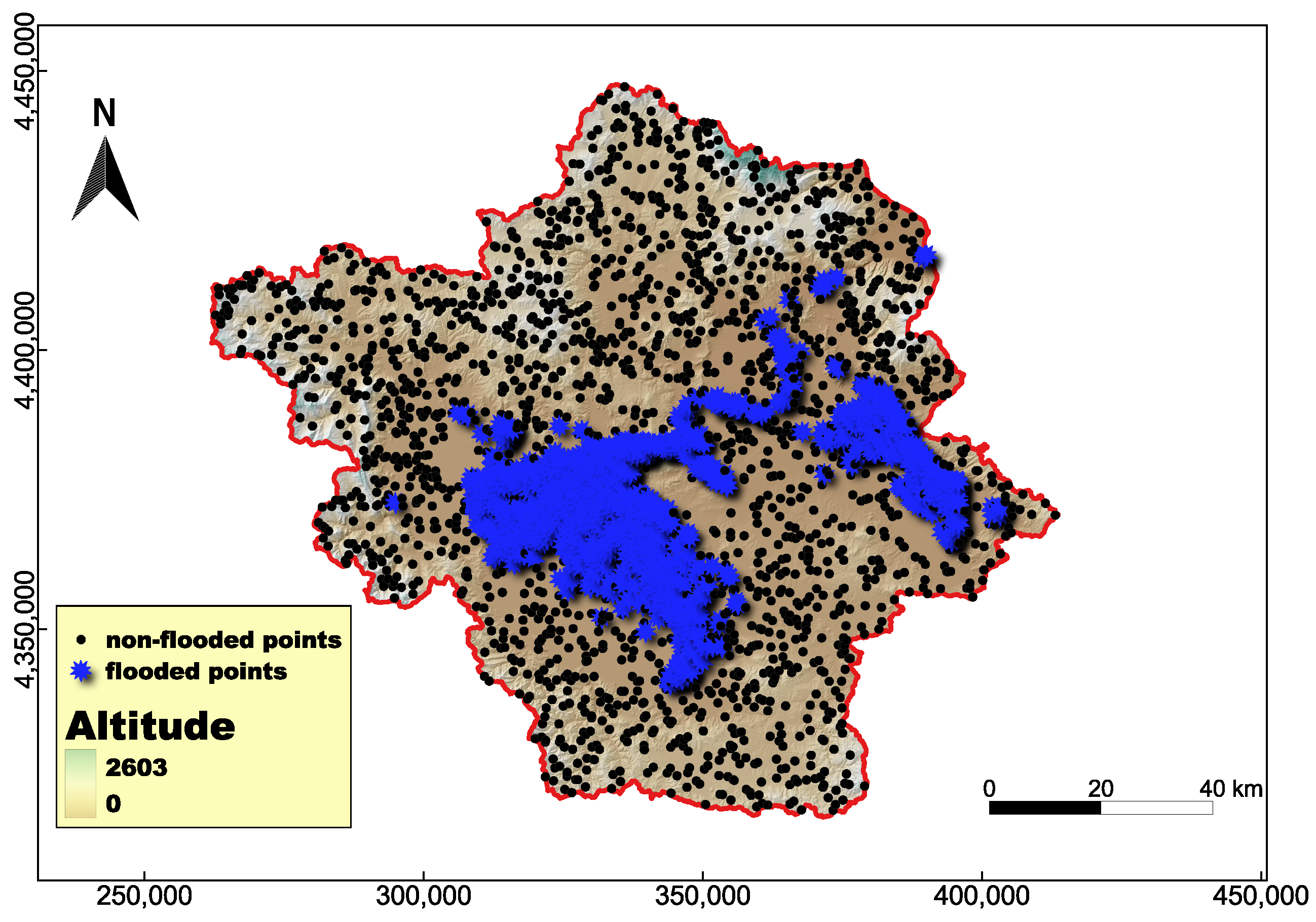
2.2. Flood Inventory Map
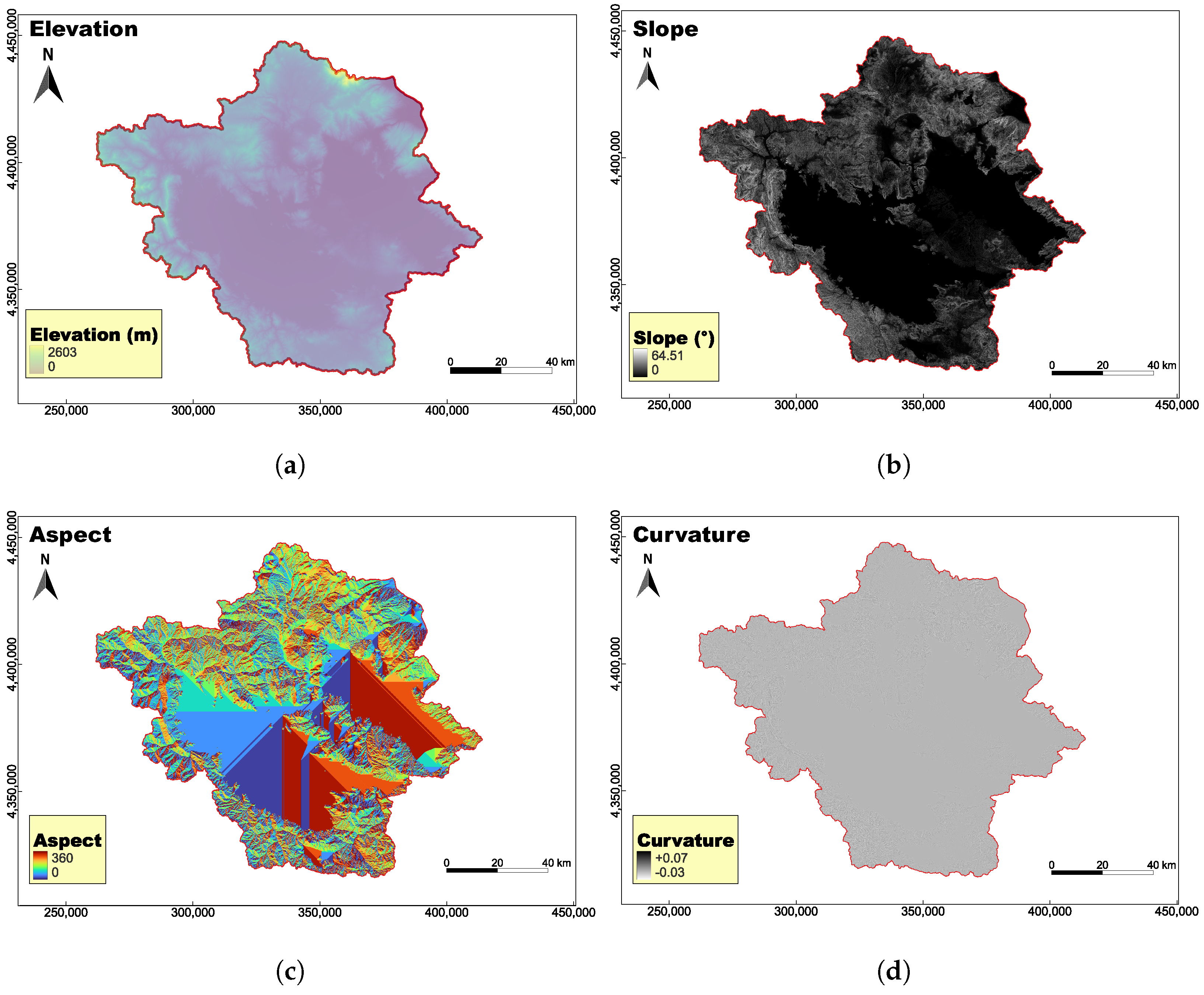
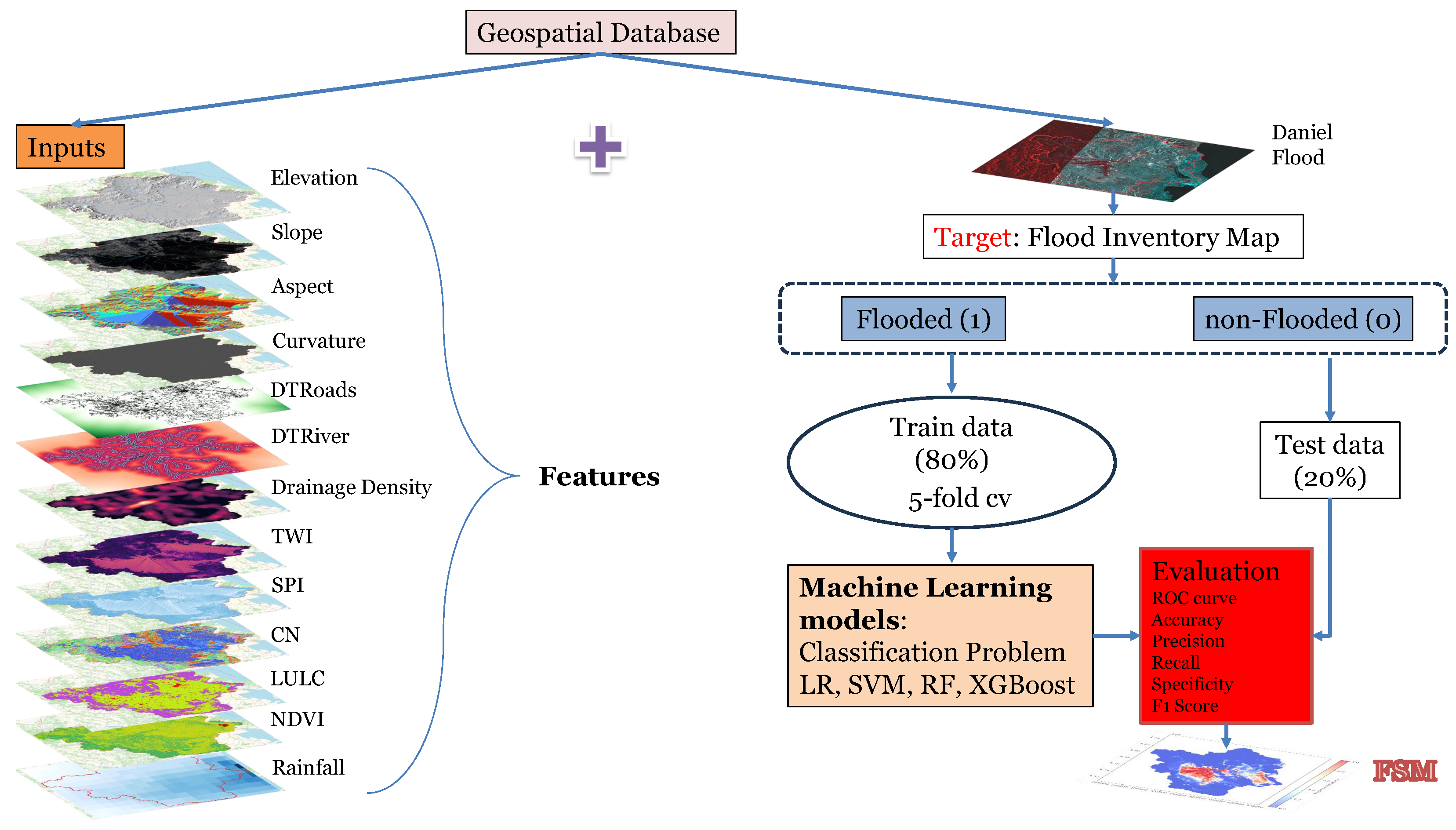
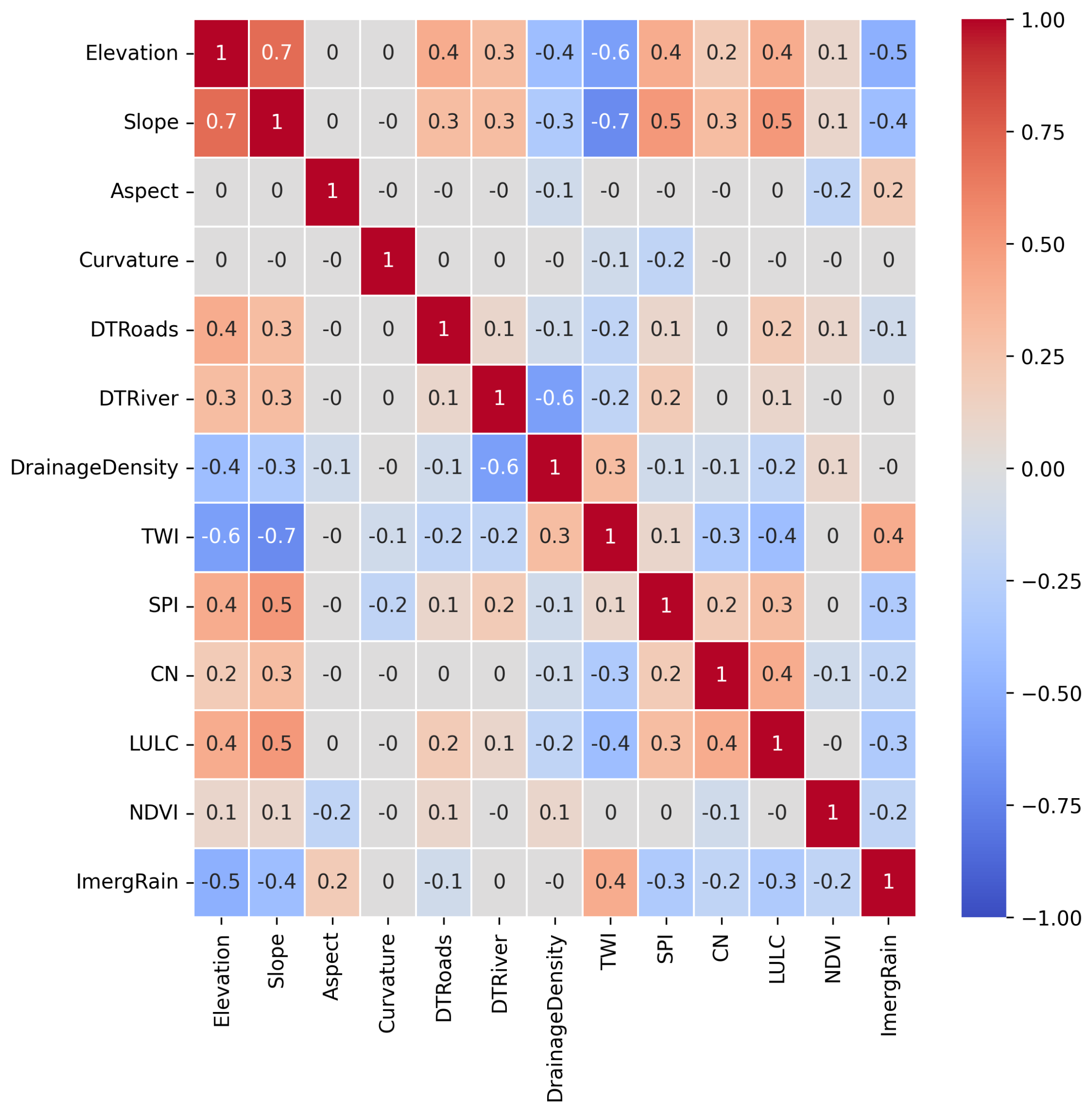
2.3. Flood Conditioning Factors
- −1–0: dead plant;
- 0–0.33: diseased plant;
- 0.33–0.66: moderate healthy plant;
- 0.66–1: very healthy plant.
| Data | Source |
|---|---|
| DEM | From Copernicus GLO 30 https://dataspace.copernicus.eu/ (accessed on 15 December 2024) [31] |
| Slope | Calculated from DEM |
| Aspect | Calculated from DEM |
| Curvature | Calculated from DEM |
| DTRoads | From OSM https://www.openstreetmap.org/ (accessed on 10 December 2024) |
| DTRiver | From GeoData http://geodata.gov.gr/ (accessed on 8 January 2025) |
| Drainage Density | From hydrographic network—GeoData http://geodata.gov.gr/ (accessed on 8 January 2025) |
| TWI | Calculated from DEM |
| SPI | Calculated from DEM |
| CN | Calculated from slope, soil, land use [33] |
| LULC | From National Cadastre CORINE 2018 https://ktimatologio.gr/ (accessed on 5 January 2025) |
| NDVI | From Copernicus Sentinel 2 https://browser.dataspace.copernicus.eu/ (accessed on 5 February 2025) |
| Rainfall | From Giovanni https://giovanni.gsfc.nasa.gov/giovanni/ (accessed on 7 March 2025) |
| Flooded Area | From Copernicus Sentinel 1 https://browser.dataspace.copernicus.eu/ (accessed 10 February 2025) |
3. Materials and Methods
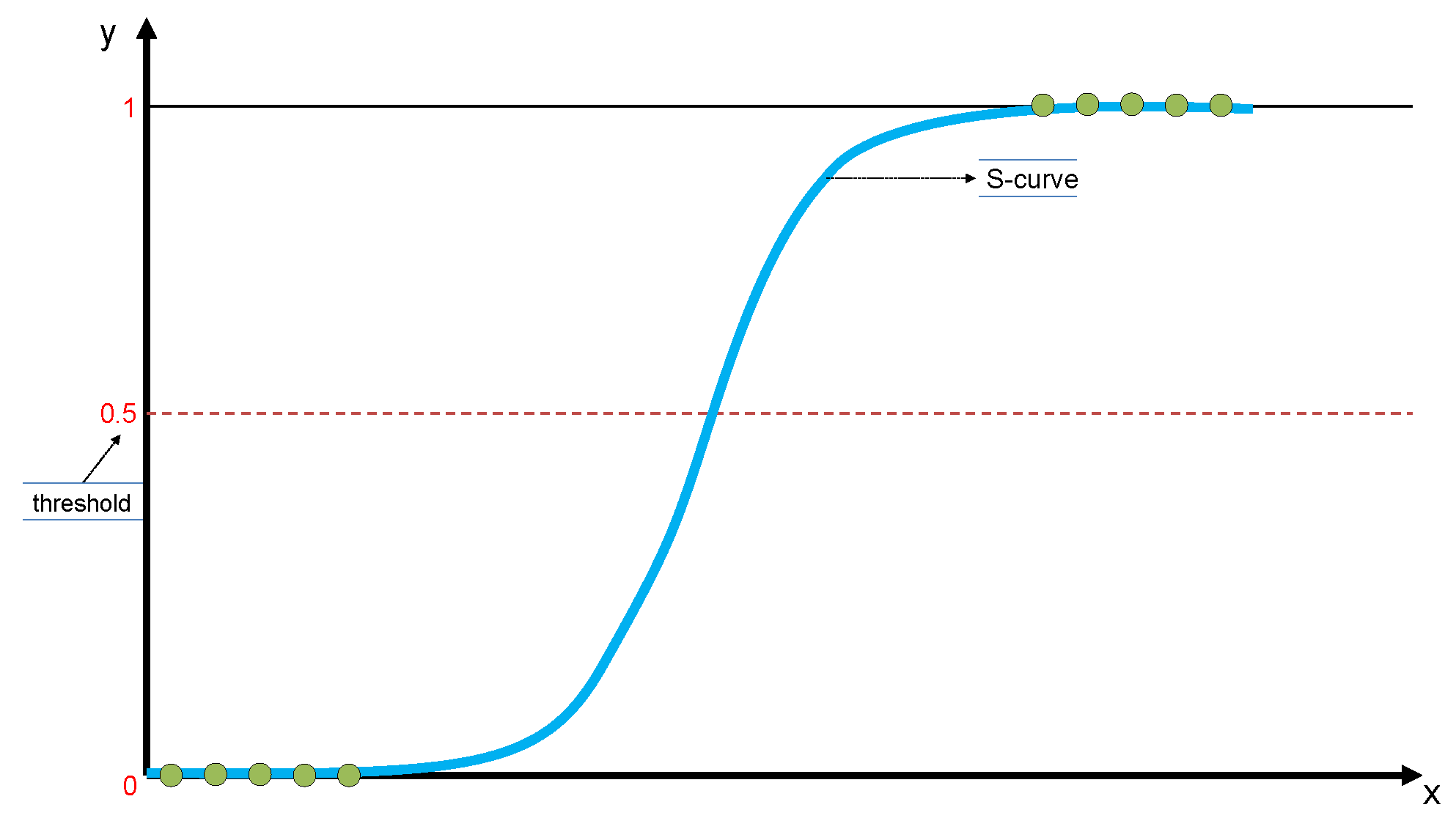
3.1. Logistic Regression (LR)
3.2. Support Vector Machine (SVM)
3.3. Random Forest (RF)
3.4. Extreme Gradient Boosting (XGBoost)
3.5. Feature Importance
- Coefficient-based feature importance;
- Permutation-based feature importance;
- Tree-based feature importance;
- SHapley Additive exPlanations (SHAP).
3.6. Evaluation Metrics
- True Positives: The number of instances where the model correctly predicted the positive class;
- True Negatives: The number of instances where the model correctly predicted the negative class;
- False Positives: The number of instances where the model incorrectly predicted the negative class for a positive case;
- False Negatives: The number of instances where the model incorrectly predicted the positive class for a negative case.
4. Analysis and Results
4.1. Problem and Model Setup
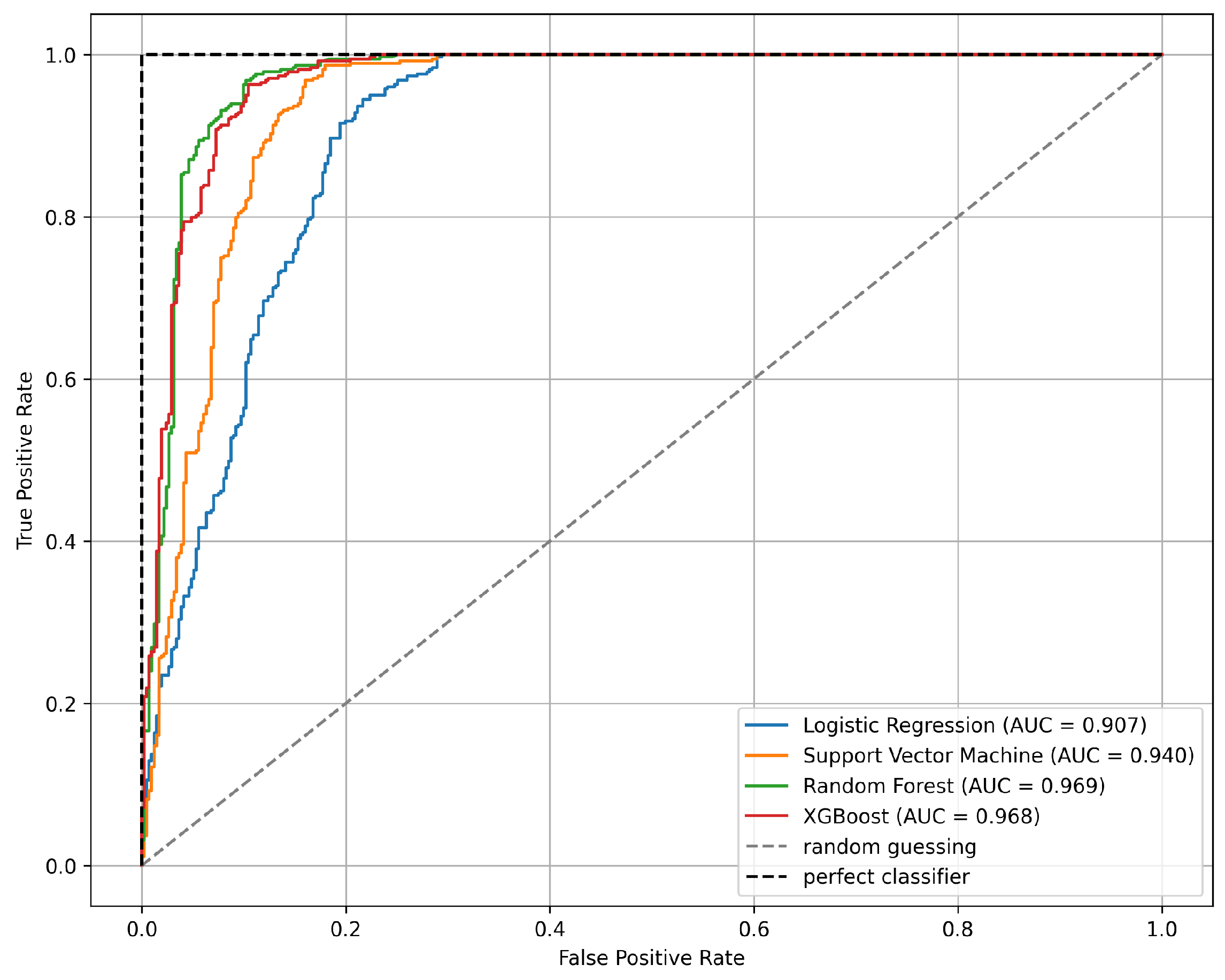
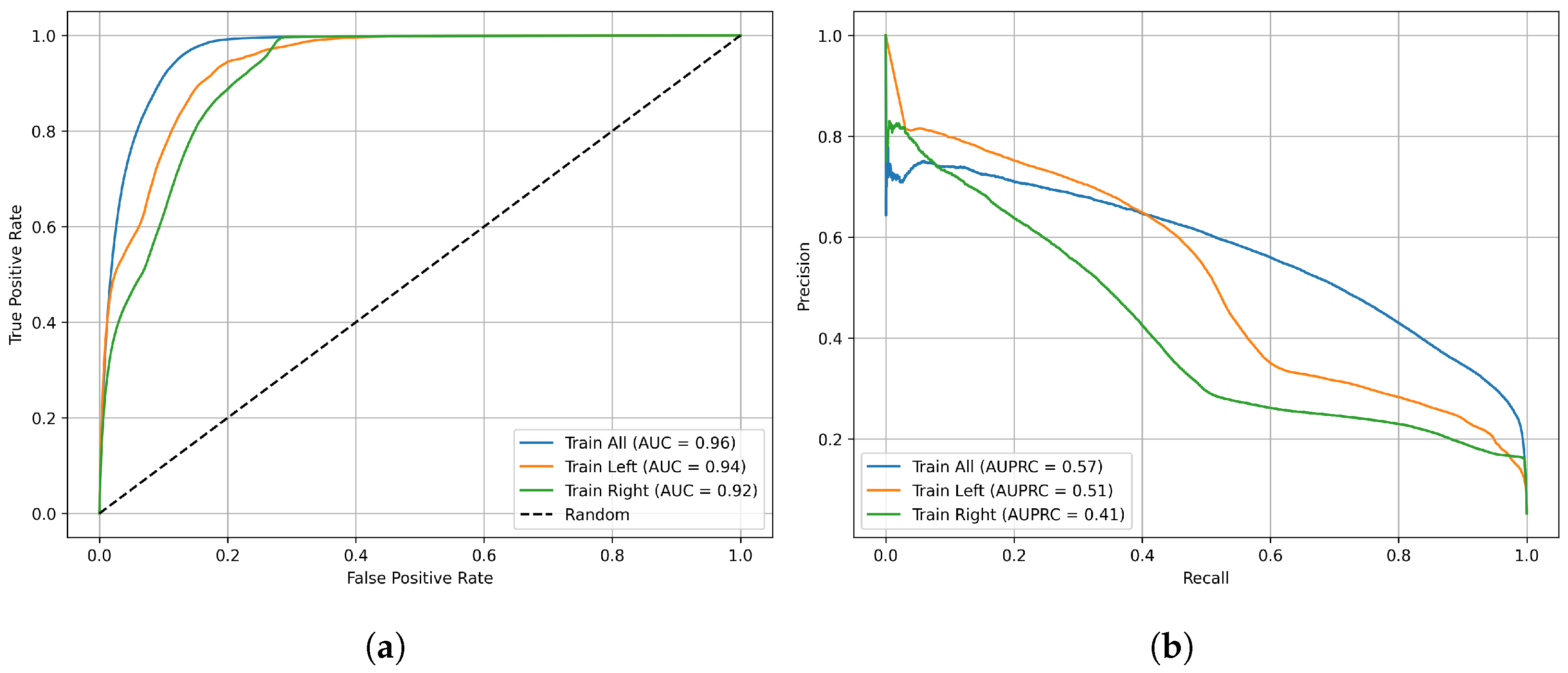
4.2. Results and Comparison
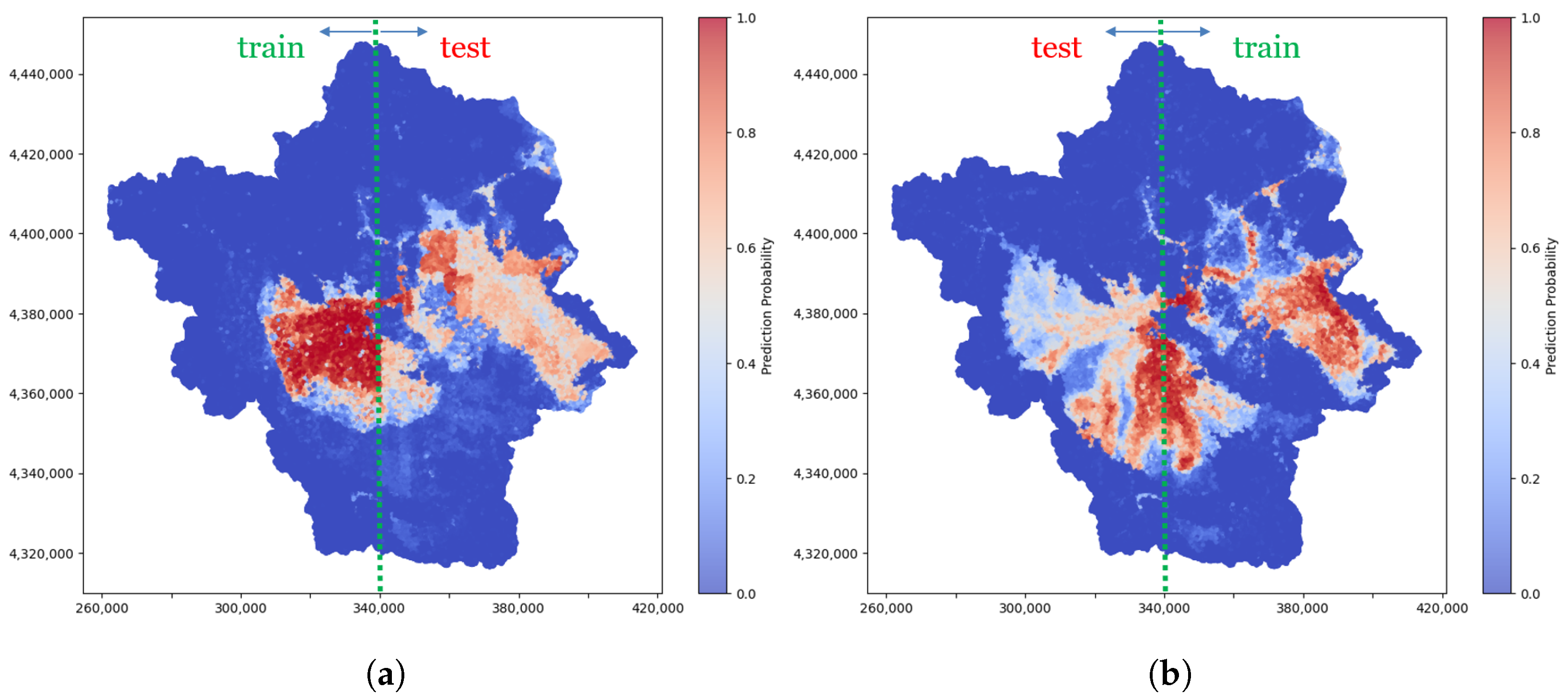
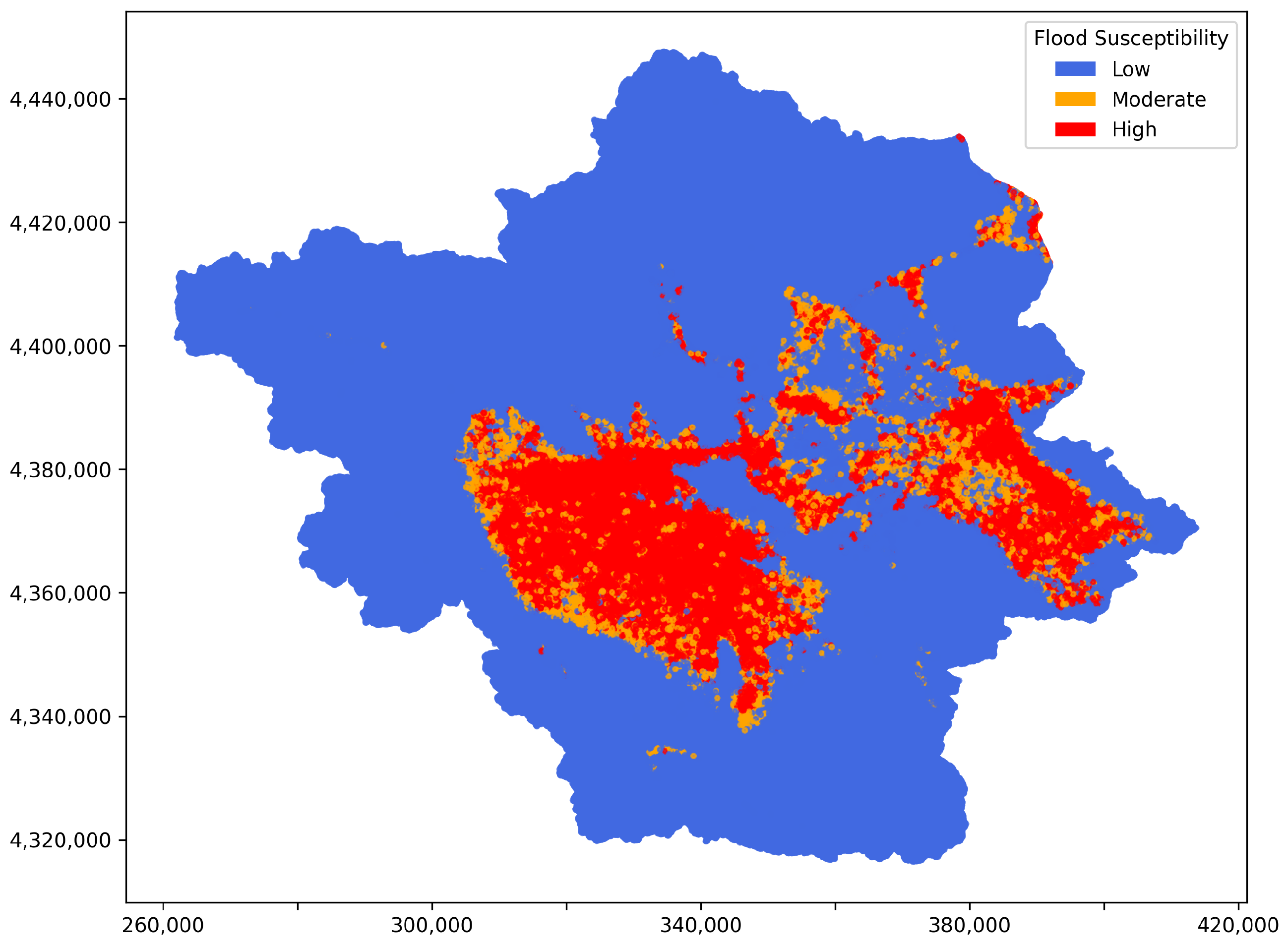
4.3. FSM Maps
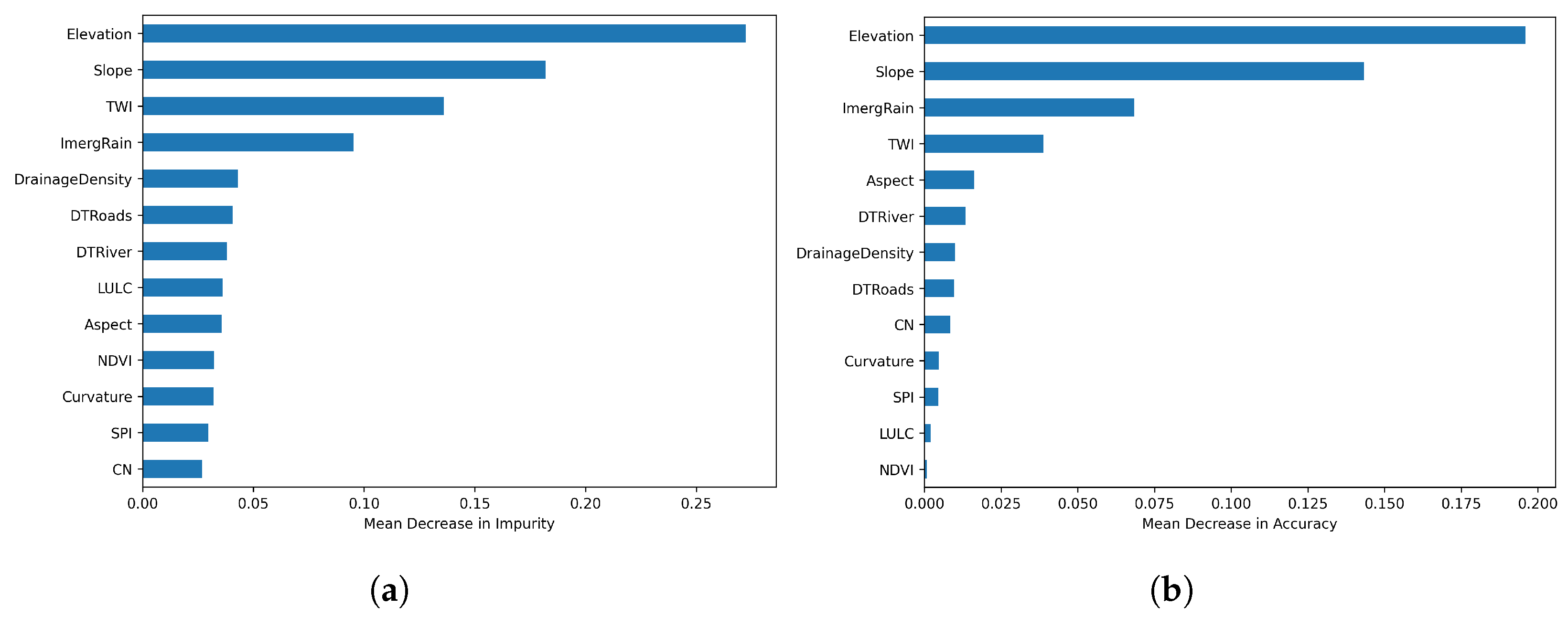
4.4. Feature Importance
4.5. Initial Data Experimentation
4.6. FSM for T = 1000-Year Rainfall Scenario
5. Discussion and Future Research Directions
6. Summary and Conclusions
- Tree-based models, particularly RF and XGBoost, outperformed the other algorithms, achieving the highest Area Under the Curve AUC scores—RF: 0.969; XGBoost: 0.968; SVM: 0.940; LR: 0.907.
- Feature importance analysis revealed that the most influential factors contributing to flood susceptibility, in decreasing order, are elevation, slope, rainfall and TWI, providing valuable insights for model interpretation and decision making.
- The choice of initial training data impacts model performance and generalizability, highlighting the need for careful dataset selection in spatial prediction tasks.
- The identified areas with high flood susceptibility are the eastern and the central-to-southern regions, offering useful information for targeted risk mitigation and planning efforts.
- Machine learning algorithms offer a promising approach for flood susceptibility mapping and can be extended as an early warning system, requiring significantly less time compared to traditional models.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jonkman, S.N. Global Perspectives on Loss of Human Life Caused by Floods. Nat. Hazards 2005, 34, 151–175. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, Y.; Li, N. Extreme Flood Disasters: Comprehensive Impact and Assessment. Water 2022, 14, 1211. [Google Scholar] [CrossRef]
- European Commission. Directive 2007/60/EC of the European Parliament and of the Council of 23 October 2007 on the Assessment and Management of Flood Risks; L 288, 6.11.2007; Official Journal of the European Communities: Aberdeen, UK, 2007; p. 27. [Google Scholar]
- Bentivoglio, R.; Isufi, E.; Jonkman, S.N.; Taormina, R. Deep learning methods for flood mapping: A review of existing applications and future research directions. Hydrol. Earth Syst. Sci. 2022, 26, 4345–4378. [Google Scholar] [CrossRef]
- Avila-Aceves, E.; Plata-Rocha, W.; Monjardin-Armenta, S.A.; Rangel-Peraza, J.G. Geospatial modelling of floods: A literature review. Stoch. Environ. Res. Risk Assess. 2023, 37, 4109–4128. [Google Scholar] [CrossRef]
- Abdullah, M.F.; Siraj, S.; Hodgett, R.E. An Overview of Multi-Criteria Decision Analysis (MCDA) Application in Managing Water-Related Disaster Events: Analyzing 20 Years of Literature for Flood and Drought Events. Water 2021, 13, 1358. [Google Scholar] [CrossRef]
- Liuzzo, L.; Sammartano, V.; Freni, G. Comparison between Different Distributed Methods for Flood Susceptibility Mapping. Water Resour. Manag. 2019, 33, 3155–3173. [Google Scholar] [CrossRef]
- Chen, H.; Yang, D.; Hong, Y.; Gourley, J.J.; Zhang, Y. Hydrological data assimilation with the Ensemble Square-Root-Filter: Use of streamflow observations to update model states for real-time flash flood forecasting. Adv. Water Resour. 2013, 59, 209–220. [Google Scholar] [CrossRef]
- Soomro, S.E.H.; Hu, C.; Boota, M.W.; Ahmed, Z.; Chengshuai, L.; Zhenyue, H.; Xiang, L.; Soomro, M.H.A.A. River Flood Susceptibility and Basin Maturity Analyzed Using a Coupled Approach of Geo-morphometric Parameters and SWAT Model. Water Resour. Manag. 2022, 36, 2131–2160. [Google Scholar] [CrossRef]
- Stoleriu, C.C.; Urzica, A.; Mihu-Pintilie, A. Improving flood risk map accuracy using high-density LiDAR data and the HEC-RAS river analysis system: A case study from north-eastern Romania. J. Flood Risk Manag. 2020, 13, e12572. [Google Scholar] [CrossRef]
- Wahba, M.; Sharaan, M.; Elsadek, W.M.; Kanae, S.; Hassan, H.S. Examination of the efficacy of machine learning approaches in the generation of flood susceptibility maps. Environ. Earth Sci. 2024, 83, 429. [Google Scholar] [CrossRef]
- Seleem, O.; Ayzel, G.; de Souza, A.C.T.; Bronstert, A.; Heistermann, M. Towards urban flood susceptibility mapping using data-driven models in Berlin, Germany. Geomat. Nat. Hazards Risk 2022, 13, 1640–1662. [Google Scholar] [CrossRef]
- Saravanan, S.; Abijith, D.; Reddy, N.M.; Kss, P.; Janardhanam, N.; Sathiyamurthi, S.; Sivakumar, V. Flood susceptibility mapping using machine learning boosting algorithms techniques in Idukki district of Kerala India. Urban Clim. 2023, 49, 101503. [Google Scholar] [CrossRef]
- Seydi, S.T.; Sadegh, M. Novel Kolmogorov-Arnold network architectures for accurate flood susceptibility mapping: A comparative study. J. Hydrol. 2025, 661, 133553. [Google Scholar] [CrossRef]
- Wedajo, G.K.; Lemma, T.D.; Fufa, T.; Gamba, P. Integrating Satellite Images and Machine Learning for Flood Prediction and Susceptibility Mapping for the Case of Amibara, Awash Basin, Ethiopia. Remote Sens. 2024, 16, 2163. [Google Scholar] [CrossRef]
- Kourgialis, N.N.; Karatzas, G.P. A national scale flood hazard mapping methodology: The case of Greece—Protection and adaptation policy approaches. Sci. Total Environ. 2017, 601–602, 441–452. [Google Scholar] [CrossRef]
- Tsinidis, G.; Koutas, L. Geotechnical and Structural Damage to the Built Environment of Thessaly Region, Greece, Caused by the 2023 Storm Daniel. Geotechnics 2025, 5, 16. [Google Scholar] [CrossRef]
- Dimitriou, E.; Efstratiadis, A.; Zotou, I.; Papadopoulos, A.; Iliopoulou, T.; Sakki, G.-K.; Mazi, K.; Rozos, E.; Koukouvinos, A.; Koussis, A.D.; et al. Post-Analysis of Daniel Extreme Flood Event in Thessaly, Central Greece: Practical Lessons and the Value of State-of-the-Art Water-Monitoring Networks. Water 2024, 16, 980. [Google Scholar] [CrossRef]
- Sreekala, S.; Geetha, P.; Madhu, D. Flood Susceptibility Map of Periyar River Basin Using Geo-Spatial Technology and Machine Learning Approach. Remote. Sens. Earth Syst. Sci. 2024, 8, 1–21. [Google Scholar] [CrossRef]
- Al-Ruzouq, R.; Shanableh, A.; Jena, R.; Gibril, M.B.A.; Hammouri, N.A.; Lamghari, F. Flood susceptibility mapping using a novel integration of multi-temporal sentinel-1 data and eXtreme deep learning model. Geosci. Front. 2024, 15, 101780. [Google Scholar] [CrossRef]
- Nachappa, T.G.; Piralilou, S.T.; Gholamnia, K.; Ghorbanzadeh, O.; Rahmati, O.; Blaschke, T. Flood susceptibility mapping with machine learning, multi-criteria decision analysis and ensemble using Dempster Shafer Theory. J. Hydrol. 2020, 590, 125275. [Google Scholar] [CrossRef]
- Hitouri, S.; Mohajane, M.; Lahsaini, M.; Ali, S.A.; Setargie, T.A.; Tripathi, G.; D’antonio, P.; Singh, S.K.; Varasano, A. Flood Susceptibility Mapping Using SAR Data and Machine Learning Algorithms in a Small Watershed in Northwestern Morocco. Remote Sens. 2024, 16, 858. [Google Scholar] [CrossRef]
- Seydi, S.T.; Kanani-Sadat, Y.; Hasanlou, M.; Sahraei, R.; Chanussot, J.; Amani, M. Comparison of Machine Learning Algorithms for Flood Susceptibility Mapping. Remote Sens. 2023, 15, 192. [Google Scholar] [CrossRef]
- Al-Kindi, K.M.; Alabri, Z. Investigating the Role of the Key Conditioning Factors in Flood Susceptibility Mapping through Machine Learning Approaches. Earth Syst. Environ. 2024, 8, 63–81. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Valavi, R.; Shahabi, H.; Chapi, K.; Shirzadi, A. Novel forecasting approaches using combination of machine learning and statistical models for flood susceptibility mapping. J. Environ. Manag. 2018, 217, 1–11. [Google Scholar] [CrossRef]
- Iliopoulou, T.; Malamos, N.; Koutsoyiannis, D. Regional Ombrian Curves: Design Rainfall Estimation for a Spatially Diverse Rainfall Regime. Hydrology 2022, 9, 67. [Google Scholar] [CrossRef]
- Mimikou, M.; Koutsoyiannis, D. Extreme floods in Greece: The case of 1994. In Proceedings of the US-ITALY Research Workshop on the Hydrometeorology, Impacts, and Management of Extreme Floods, Perugia, Italy, 13–17 November 1995. [Google Scholar]
- Bathrellos, G.D.; Skilodimou, H.D.; Soukis, K.; Koskeridou, E. Temporal and Spatial Analysis of Flood Occurrences in the Drainage Basin of Pinios River (Thessaly, Central Greece). Land 2018, 7, 106. [Google Scholar] [CrossRef]
- Valkaniotis, S.; Papathanassiou, G.; Marinos, V.; Saroglou, C.; Zekkos, D.; Kallimogiannis, V.; Karantanellis, E.; Farmakis, I.; Zalachoris, G.; Manousakis, J.; et al. Landslides Triggered by Medicane Ianos in Greece, September 2020: Rapid Satellite Mapping and Field Survey. Appl. Sci. 2022, 12, 12443. [Google Scholar] [CrossRef]
- Kumar, P.; Bhatnagar, R.; Gaur, K.; Bhatnagar, A. Classification of Imbalanced Data:Review of Methods and Applications. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1099, 012077. [Google Scholar] [CrossRef]
- Copernicus DEM. 2022. Available online: https://doi.org/10.5270/esa-c5d3d65 (accessed on 15 December 2024).
- USDA. Hydrology. In National Engineering Handbook; United States Department of Agriculture, Soil Conservation Service, US Government Printing Office: Washington, DC, USA, 1972. [Google Scholar]
- Efstratiadis, A.; Koukouvinos, A.; Michaelidi, E.; Galiouna, E.; Tzouka, K.; Koussis, A.D.; Mamassis, N.; Koutsoyiannis, D. Description of Regional Approaches for the Estimation of Characteristic Hydrological Quantities, DEUCALION—Assessment of Flood Flows in Greece under Conditions of Hydroclimatic Variability: Development of Physically-Established Conceptual-Probabilistic; Department of Water Resources and Environmental Engineering—National Technical University of Athens, National Observatory of Athens: Athens, Greece, 2014. [Google Scholar]
- Cox, D.R. The Regression Analysis of Binary Sequences. J. R. Stat. Soc. Ser. (Methodol.) 1958, 20, 215–232. [Google Scholar] [CrossRef]
- Myung, I.J. Tutorial on Maximum Likelihood Estimation. J. Math. Psychol. 2003, 47, 90–100. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A Training Algorithm for Optimal Margin Classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992. [Google Scholar] [CrossRef]
- Schölkopf, B. The Kernel Trick for Distances. In Proceedings of the 13th International Conference on Neural Information Processing Systems (NIPS’00), Hong Kong, China, 3–6 October 2006; MIT Press: Cambridge, MA, USA, 2000; pp. 283–289. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco, CA, USA, 13–17 August 2016; pp. 784–794. [Google Scholar]
- Kaggle Competitions. Available online: https://www.kaggle.com/competitions (accessed on 24 September 2024).
- Amjad, M.; Ahmad, I.; Ahmad, M.; Wróblewski, P.; Kamiński, P.; Amjad, U. Prediction of Pile Bearing Capacity Using XGBoost Algorithm: Modeling and Performance Evaluation. Appl. Sci. 2022, 12, 2126. [Google Scholar] [CrossRef]
- Rengasamy, D.; Mase, J.M.; Kumar, A.; Rothwell, B.; Torres, M.T.; Alexander, M.R.; Winkler, D.A.; Figueredo, G.P. Feature importance in machine learning models: A fuzzy information fusion approach. Neurocomputing 2022, 511, 163–174. [Google Scholar] [CrossRef]
- Vatsal. Feature Importance in Machine Learning, Explained. Towards Data Science. Available online: https://towardsdatascience.com/feature-importance-in-machine-learning-explained-443e35b1b284/ (accessed on 20 April 2025).
- Tangirala, S. Evaluating the Impact of GINI Index and Information Gain on Classification Using Decision Tree Classifier Algorithm. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 612–619. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- D’Agostino, A. The Explanation You Need on Binary Classification Metrics. Medium. Available online: https://medium.com/data-science/the-explanation-you-need-on-binary-classification-metrics-321d280b590f (accessed on 25 April 2025).
- Grewal, R.; Cote, J.A.; Baumgartner, H. Multicollinearity and measurement error in structural equation models: Implications for theory testing. Mark. Sci. 2004, 23, 519–529. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Iliopoulou, T.; Koukouvinos, A.; Malamos, N. A stochastic framework for rainfall intensity-time scale-return period relationships. Part I: Theory and estimation strategies. Hydrol. Sci. J. 2024, 69, 1082–1091. [Google Scholar] [CrossRef]
- Iliopoulou, T.; Koutsoyiannis, D.; Malamos, N.; Koukouvinos, A.; Dimitriadis, P.; Mamassis, N.; Tepetidis, N.; Markantonis, D. A stochastic framework for rainfall intensity-time scale-return period relationships. Part II: Point modelling and regionalization over Greece. Hydrol. Sci. J. 2024, 69, 1092–1112. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Iliopoulou, T.; Koukouvinos, A.; Malamos, N.; Mamassis, N.; Dimitriadis, P.; Tepetidis, N.; Markantonis, D. Production of Maps with Updated Parameters of the Ombrian Curves at Country Level (Implementation of the EU Directive 2007/60/EC in Greece); Technical Report; Department of Water Resources and Environmental Engineering—National Technical University of Athens: Athens, Greece, 2023; Available online: https://www.itia.ntua.gr/2273/ (accessed on 20 April 2025). (In Greek)
- Perera, D.; Seidou, O.; Agnihotri, J.; Rasmy, M.; Smakhtin, V.; Coulibaly, P.; Mehmood, H. Flood Early Warning Systems: A Review of Benefits, Challenges and Prospects; UNU-INWEH Report Series; Issue 08; United Nations University-Institute for Water, Environment and Health: Hamilton, ON, Canada, 2019; Available online: https://inweh.unu.edu/flood-early-warning-systems-a-review-of-benefits-challenges-and-prospects/ (accessed on 15 April 2025)ISBN 978-92-808-6096-2.
- Ioannidis, R.; Sargentis, G.-F.; Koutsoyiannis, D. Landscape design in infrastructure projects - is it an extravagance? A cost-benefit investigation of practices in dams. Landsc. Res. 2022, 47, 370–387. [Google Scholar] [CrossRef]
- Singh, P.; Diwakar, M.; Shankar, A.; Shree, R.; Kumar, M. A review on SAR image and its despeckling. Arch. Comput. Methods Eng. 2021, 28, 4633–4653. [Google Scholar] [CrossRef]
- Yan, J.; Gebremichael, M. Estimating actual rainfall from satellite rainfall products. Atmos. Res. 2009, 92, 481–488. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Bluecat: A Local Uncertainty Estimator for Deterministic Simulations and Predictions. Water Resour. Res. 2022, 58, e2021WR031215. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning through Physics-Informed Neural Networks: Where We Are and What’s Next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier Neural Operator for Parametric Partial Differential Equations. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual Event, 3–7 May 2021. [Google Scholar]
- Dikshit, A.; Pradhan, B. Interpretable and explainable AI (XAI) model for spatial drought prediction. Sci. Total Environ. 2021, 801, 149797. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A Review of Machine Learning Interpretability Methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef]
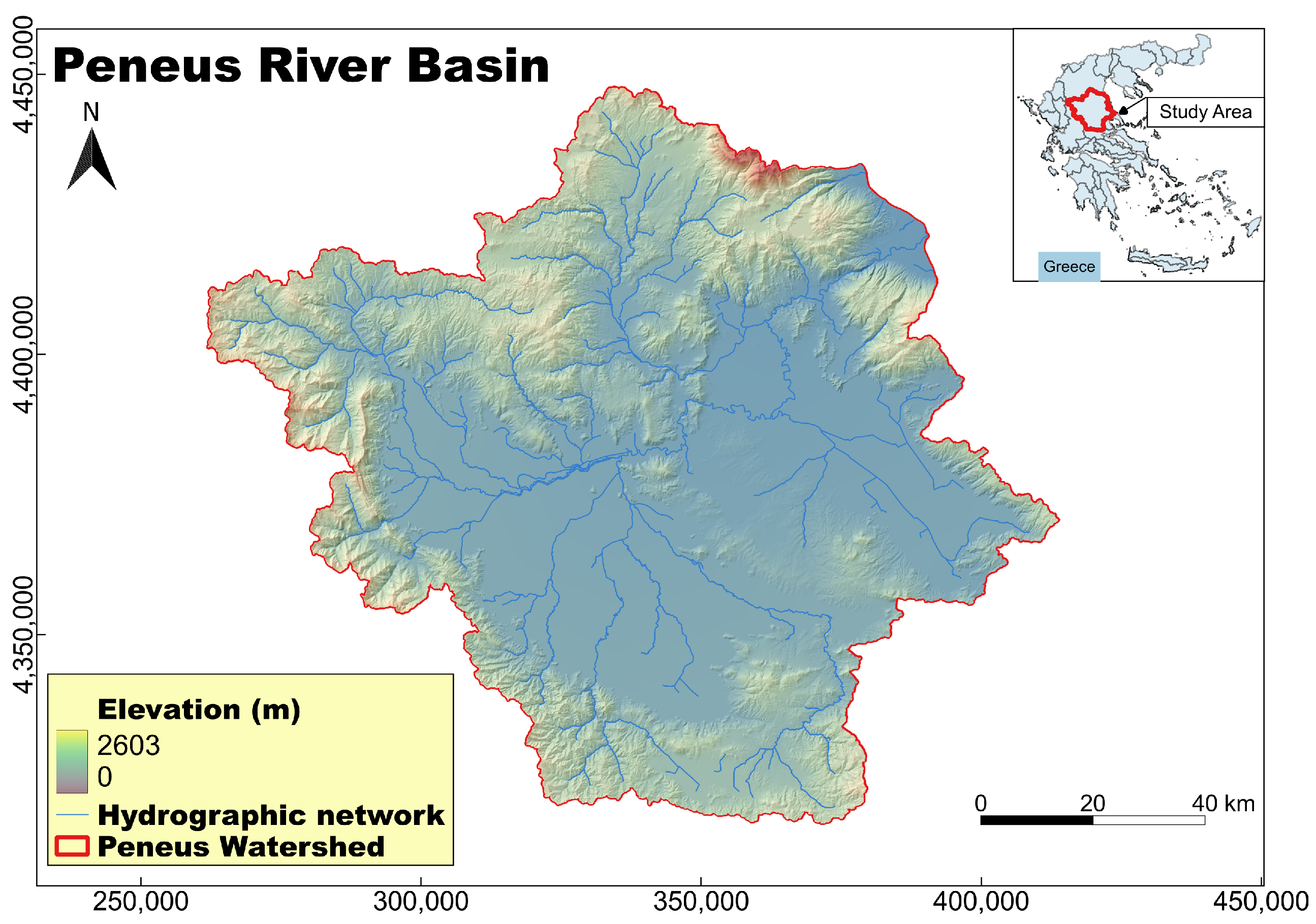
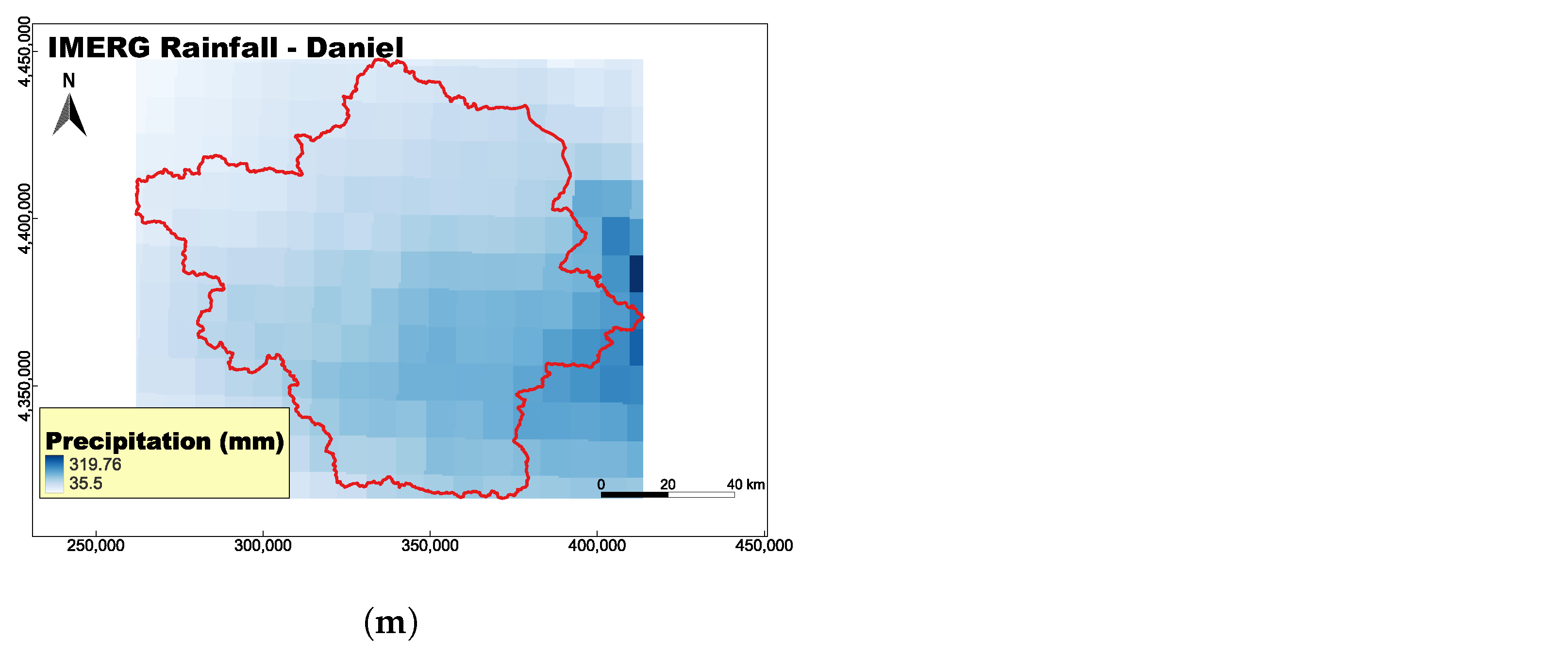






| GGRS87 (m) | WGS84 (°) | ||
|---|---|---|---|
| X | 262,000 | Long. | 38.95 N |
| 414,000 | 40.18 N | ||
| Y | 4,315,000 | Lat. | 21.25 E |
| 4,448,000 | 22.99 E | ||
| Description | Split Percentage (%) | Number of Samples | Flooded | Non-Flooded |
|---|---|---|---|---|
| Training | 80 | 3160 | 1595 | 1565 |
| Testing | 20 | 790 | 379 | 411 |
| Total | 100 | 3950 | 1974 | 1976 |
| Model | Hyperparameter Values |
|---|---|
| LR | max iter = 1000; scoring = ‘accuracy’; multi class = ‘auto’; solver = ‘lbfgs’ |
| SVM | C = 2; gamma = ‘scale’; kernel = ‘radial basis function (rbf)’; scaler = ‘StandardScaler’ |
| RF | no. estimators = 200; max depth = 20; min samples split = 2; min samples leaf = 1; max features = ‘sqrt’ |
| XGBoost | no. estimators = 100; max depth = 7; learning rate = 0.1; subsample = 1.0; colsample by tree = 0.8 |
| Model | Accuracy | Precision | Recall/Sensitivity | Specificity | F1 Score |
|---|---|---|---|---|---|
| LR | 0.85 | 0.76 | 1.00 | 0.71 | 0.86 |
| SVM | 0.86 | 0.78 | 0.99 | 0.75 | 0.88 |
| RF | 0.93 | 0.89 | 0.97 | 0.89 | 0.93 |
| XGBoost | 0.93 | 0.89 | 0.96 | 0.90 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tepetidis, N.; Benekos, I.; Iliopoulou, T.; Dimitriadis, P.; Koutsoyiannis, D. Combining Machine Learning Models and Satellite Data of an Extreme Flood Event for Flood Susceptibility Mapping. Water 2025, 17, 2678. https://doi.org/10.3390/w17182678
Tepetidis N, Benekos I, Iliopoulou T, Dimitriadis P, Koutsoyiannis D. Combining Machine Learning Models and Satellite Data of an Extreme Flood Event for Flood Susceptibility Mapping. Water. 2025; 17(18):2678. https://doi.org/10.3390/w17182678
Chicago/Turabian StyleTepetidis, Nikos, Ioannis Benekos, Theano Iliopoulou, Panayiotis Dimitriadis, and Demetris Koutsoyiannis. 2025. "Combining Machine Learning Models and Satellite Data of an Extreme Flood Event for Flood Susceptibility Mapping" Water 17, no. 18: 2678. https://doi.org/10.3390/w17182678
APA StyleTepetidis, N., Benekos, I., Iliopoulou, T., Dimitriadis, P., & Koutsoyiannis, D. (2025). Combining Machine Learning Models and Satellite Data of an Extreme Flood Event for Flood Susceptibility Mapping. Water, 17(18), 2678. https://doi.org/10.3390/w17182678








