A Deterministic Combinatorial Approach to Investigate Interactions of Soil Hydraulic Parameters on River Flow Modelling

Abstract

Hydrological modeling is essential for the sustainable management of watershed systems. Physically based models like MOHID-Land simulate soil water dynamics using Richards’ equation, parameterized through the van Genuchten–Mualem (VGM) model. Although the sensitivity of individual VGM parameters—residual water content (${\theta }_r$), saturated water content (${\theta }_s$), pore size distribution ($n$), inverse of air entry pressure ($\alpha$), and saturated hydraulic conductivity ($K_{sat}$)—is well documented, their combined effects remain underexplored. This study assessed both isolated and joint impacts of these parameters through a deterministic ±10% perturbation scheme, resulting in 31 unique parameter combinations. Model performance was evaluated using the Nash–Sutcliffe Efficiency (NSE) and Percent Bias (PBIAS). Full-parameter interaction achieved the best results (NSE = 0.50, PBIAS = 25.32), compared to the uncalibrated baseline (NSE = 0.01, PBIAS = 34.06). The pair ${\theta }_s$ and $n$ emerged as the most influential. Adding secondary parameters to this core pair yielded only marginal performance gains, while removing them from the full set caused similarly marginal declines. These findings reveal a hierarchical sensitivity structure, emphasizing ${\theta }_s$ and $n$ as key targets for calibration. Prioritizing this pair enables a more efficient soil calibration process, preserving model accuracy while reducing computational cost by limiting parameter space exploration.

1. Introduction

Hydrological modeling of watershed systems is a fundamental tool for understanding the movement and storage of water in soils, playing a pivotal role in the sustainable planning and management of water resources [1,2]. These models differ significantly in their approaches, ranging from simplified conceptual frameworks to highly detailed physically based systems.

Among these, physically based models, such as MOHID-Land, distinguish themselves by providing a mechanistic representation of hydrological processes through the direct numerical solution of partial differential equations [3]. This capability is essential for simulating complex watershed responses under dynamic environmental conditions, offering a distinct advantage over models that rely on more simplified conceptual or empirical formulations [4]. For instance, widely used and extensively validated hydrological models like the Soil and Water Assessment Tool (SWAT) are particularly effective for large-scale applications but often approximate soil infiltration and moisture dynamics using empirical methods, such as the Curve Number (CN) approach for surface runoff generation and layered water balance schemes for soil water movement [5].

Crucially, an accurate representation of soil water dynamics is one of the most important components of physically based models. This process is typically governed by Richards’ equation [6], whose performance strongly depends on accurately defined soil hydraulic parameters. The van Genuchten–Mualem (VGM) model remains the most widely adopted framework for describing these parameters. It requires five key variables: residual water content (${\theta }_r$), saturated water content (${\theta }_s$), a shape parameter related to pore size distribution ($n$), an air entry pressure parameter ($\alpha$), and saturated hydraulic conductivity ($K_{sat}$) [7,8]. Numerous studies have calibrated one or more of these parameters, demonstrating that such variations can substantially alter model predictions in the MOHID-Land system, where the redistribution of soil moisture is central to the hydrological balance [9,10,11].

Within this context, sensitivity analysis is essential for identifying the most influential parameters and informing calibration strategies. Oliveira et al. [12] pioneered sensitivity assessments in MOHID-Land by analyzing the impact of individual parameter perturbations on streamflow duration curves. Their approach applied one-at-a-time, positive-only variations—focused primarily on $K_{sat}$ among the VGM parameters—and employed a sensitivity index based on the effect of these variations on flow class along the flow duration curve. However, the analysis did not incorporate negative variations, symmetric perturbations, or explore interactions between parameters. More recently, Sales et al. [11] expanded this investigation by perturbing all five VGM parameters using a centered-difference scheme. Their method estimated local sensitivities from the derivative of residuals, based on symmetric ±10% perturbations around baseline values for each parameter. While more comprehensive, this approach combined individually optimized values under the implicit assumption of linear system behavior—an assumption often violated in nonlinear hydrological models [13]. Consequently, potential interactive effects among parameters remained unaddressed. This limitation is intrinsic to local sensitivity approaches, which, while computationally convenient, do not capture the complexity of nonlinear interactions—particularly in models that integrate Richards equation with time-varying boundary conditions or that simulate surface flows through Saint-Venant equations [14]. Considering this gap, the present study explicitly addresses how parameter interactions influence model performance, thereby extending the line of research line initiated in Sales et al. [11].

Ideally, capturing these interactions would require variance-based global sensitivity methods; however, their application in MOHID-Land is constrained by the high computational demand of executing thousands of simulations [15]. Dai et al. [16] recommend variance-based global sensitivity methods, such as Sobol indices and the Absolute Moment Approximation (AMA), which decompose model output variance to assess both main and higher-order parameter effects. Although such techniques are methodologically rigorous, their practical implementation remains challenging in this context [16]. This gap between the limitations of local analyses and the computational challenges of global approaches motivates the search for alternative frameworks tailored to complex hydrological models.

As a feasible alternative, this study adopts a deterministic and exhaustive combinatorial approach, explicitly designed to quantify both individual and combined effects of the five VGM parameters. By maintaining the same ±10% perturbation range established in Sales et al. [11], we constructed and evaluated all 31 non-empty combinations of the five VGM parameters, performing one simulation per scenario. This deterministic strategy enabled a systematic assessment of parameter interactions and their influence on model performance, using streamflow as the response variable. Unlike stochastic algorithms or high-dimensional sampling techniques, this approach offers a computationally viable alternative for complex models. The fixed perturbation range allowed for a standardized comparison of parameter effects, reducing potential biases associated with scale-dependent variances. Notably, the method revealed how specific combinations of parameters influence simulation accuracy—insights that would likely be overlooked by traditional local sensitivity methods.

Ultimately, this work aims not only to improve calibration protocols for MOHID-Land but also to contribute methodologically to the ongoing discourse on practical sensitivity assessment in distributed hydrological modeling. Systematic approaches of this nature have shown promise in other domains [17], albeit primarily through automated techniques. Here, we present a fully deterministic and interpretable alternative, expanding the toolkit available for the physically based calibration of soil hydraulic properties in complex watershed systems.

2. Materials and Methods

2.1. Study Area

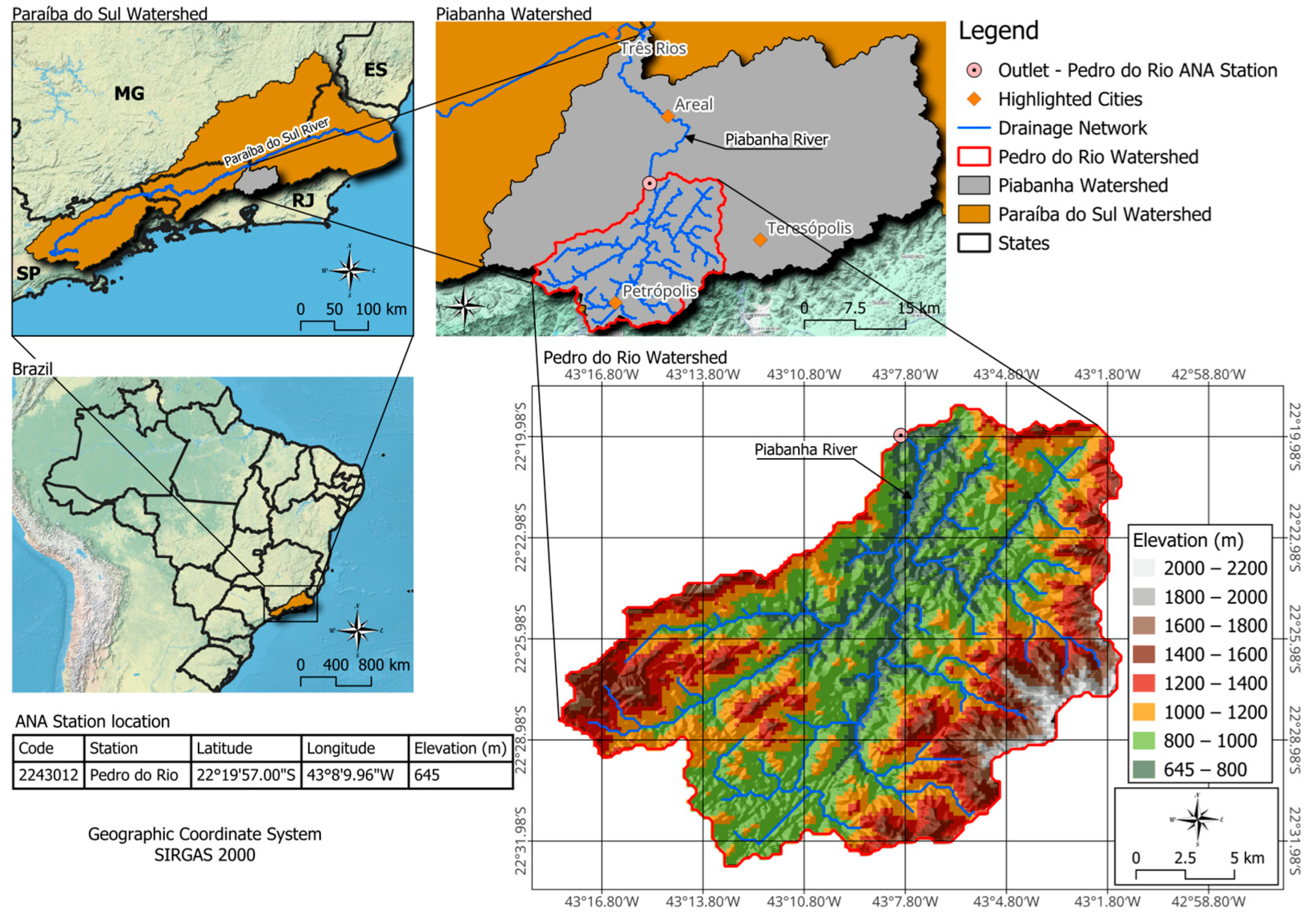
The Pedro do Rio watershed, encompassing approximately 420 km², accounts for roughly 55% of the municipality of Petrópolis, located in the mountainous area of Rio de Janeiro State. It lies within the Atlantic Forest biome, globally recognized as a biodiversity hotspot, and supports diverse ecosystems rich in endemic species. Hydrologically, the watershed belongs to the Piabanha River basin, itself a significant tributary of the Paraíba do Sul basin—a critical freshwater source for domestic, agricultural, and industrial demands across the states of São Paulo, Minas Gerais, and Rio de Janeiro (Figure 1).

Owing to its ecological and hydrological significance, the Pedro do Rio watershed was designated as one of three pilot study areas under the Integrated Studies in Experimental and Representative Basins (ISERB, or EIBEX in Portuguese) Project, a national program coordinated by the Brazilian Geological Survey (BGS, or SGB in Portuguese). EIBEX aims to implement long-term monitoring of hydrological and environmental variables in basins that typify the complex physical, environmental, socioeconomic, and water-resource dynamics prevalent throughout Brazil [18]. This watershed is extensively monitored, hosting multiple hydrometeorological stations that provide high-resolution data essential for diverse scientific studies in hydrology, ecology, and environmental management. The watershed’s outlet contains a streamflow gauging station operated by the National Water and Sanitation Agency (NWSA, or ANA in Portuguese), providing crucial observational data for model calibration and validation.

As of 2022, Petrópolis had approximately 278,881 inhabitants, with a population density of 352.5 residents per km² [19]. This demographic concentration places substantial pressure on local water resources, intensifying both demand and the potential for environmental degradation. The watershed’s economy is strongly influenced by agriculture, particularly the cultivation of cereal, legume, and oilseed cultivation, which, while economically vital, exacerbate water withdrawal and contribute to soil erosion and sediment transport through agrochemical runoff [20].

Topographically, the basin is characterized by pronounced relief, with elevations ranging from 645 m at the outlet to 2200 m in the headwaters, resulting in a vertical drop of approximately 1450 m. Steep slopes dominate the landscape, with 44.6% classified as strongly undulating (20–35%) and an additional 36.4% categorized as mountainous terrain (45–75%). The region is subject to severe landslide risks, partly due to irregular settlement in high-slope areas, which comprise a large portion of the watershed.

Climatic gradients closely follow elevation changes: upland areas in the watershed experience higher precipitation, exceeding 2000 mm annually, while lower-elevation areas receive around 1300 mm per year. This pattern reflects a clear spatial distribution of rainfall, strongly influenced by the mountainous topography, with precipitation decreasing progressively from the headwaters to the watershed outlet. Seasonal variability is also pronounced, with heavy rainfall concentrated in the summer months, which can lead to flash floods and erosion, particularly in areas with sparse vegetation cover [21]. The spatial distribution of precipitation and isohyets is illustrated in Costa et al. [22].

Land use within the watershed is markedly heterogeneous, reflecting a complex mosaic of urban expansion, agricultural activity, and relatively well-preserved Atlantic Forest fragments. Approximately 62% of the basin remains under dense forest cover, including sections of the Serra dos Órgãos National Park, highlighting the region’s ecological significance. Agricultural and pastoral lands, primarily situated along riparian corridors and slopes, occupy around 26% of the area, while urban development comprises roughly 7%, with ongoing expansion linked to the proximity of the metropolitan Rio de Janeiro area. This urban growth exacerbates risks associated with flooding and landslides. The remaining land cover consists of rocky outcrops on steep gradients, further complicating hydrological responses and increasing erosion potential [18,21].

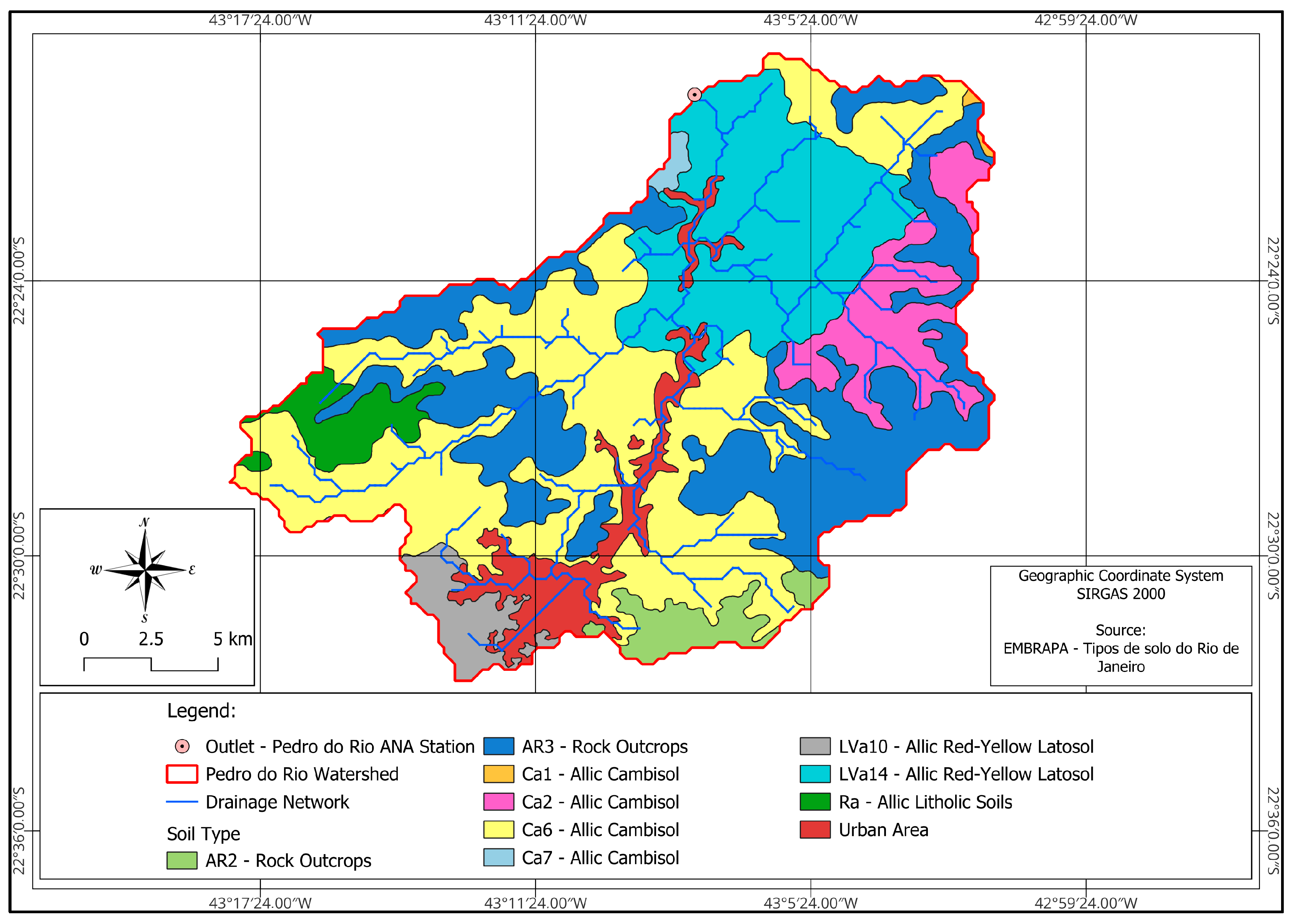
The soil map used in this study was produced under the Rio de Janeiro Project, a series of multidisciplinary studies of the physical environment conducted by the SGB, in partnership with other institutions, at a scale of 1:250,000 for the entire state of Rio de Janeiro [23]. Soil classification follows the Brazilian Soil Classification System (BSCS, or SiBCS in Portuguese) proposed by EMBRAPA [24], in which soils are grouped according to pedogenetic development, mineralogical composition, and their chemical and physical properties.

In the representative watershed, the predominant soil class is the Allic Cambisol, covering 66.74% of the basin area (Figure 2). Cambisols are soils at an intermediate stage of weathering, retaining several characteristics of their parent material. They typically exhibit low permeability and variable depth, ranging from shallow to moderately deep profiles. The qualifier Allic indicates high aluminum saturation, conferring natural acidity and potential aluminum toxicity, which limits agricultural use without proper soil amendment [24]. Within this soil class, multiple mapped units exist, represented by specific codes such as Ca1, Ca2, Ca6, and Ca7. These units differentiate the same soil class based on criteria such as depth, texture, drainage, and topographic position, enabling more precise mapping of soil variability across the landscape.

The second most representative soil class is the Allic Red-Yellow Latosol, which accounts for 22.83% of the basin area. Latosols are highly weathered soils, generally very deep and uniform, with high porosity and good drainage. These characteristics provide favorable conditions for root development and water percolation. Like Cambisols, this soil class also comprises multiple mapped units (e.g., LVa10, LVa14), which distinguish variations in depth, texture, and landscape position.

Additional minor soil units include Allic Litholic Soils (Ra), which are very shallow soils strongly influenced by the underlying bedrock, commonly occurring on steep slopes, and Rock Outcrops (e.g., AR2, AR3), where vegetation is limited due to the absence of soil cover. Urbanized areas were also mapped within the basin, reflecting anthropogenic land use rather than natural soil classes. In total, ten different soil classes are recognized within the watershed, each represented by mapped units in accordance with the classification system.

Taken together, these demographic, physiographic, climatic, and land use characteristics establish the Pedro do Rio watershed as a hydrologically complex and environmentally sensitive system, necessitating comprehensive monitoring and modeling efforts.

2.2. MOHID-Land Model Overview

The MOHID-Land model is a physically based hydrological model designed for the multifaceted simulation of hydrological processes intrinsic to watershed systems. Its computational architecture is inherently capable of assimilating and faithfully representing with fidelity the spatial heterogeneities associated with land cover, soil typology diversity, and complex subsurface hydrodynamics. This capability grants MOHID-Land remarkable versatility, enabling its broad applicability across diverse hydrological research contexts, ranging from detailed analyses of small micro-basins to modeling at the scale of large macro-basins of considerable geographic extent. The code can be accessed from an online repository (https://github.com/Mohid-Water-Modelling-System/Mohid, accessed on 1 December 2024). It employs the Finite Volume Method (FVM) to solve conservation equations for mass and momentum over a structured grid, combining horizontal and vertical discretization. The horizontal grid follows a user-defined resolution, while vertical discretization defines soil layer thicknesses down to a user-specified depth, beyond which no flow is simulated. This configuration allows for high-resolution representation of terrain, land cover, and soil properties, enabling the model to capture spatial heterogeneity across various hydrological domains [25].

Surface flow is routed through a drainage network derived from digital elevation data, in which cells are linked downslope to form channel segments. Overland and channel flows are computed using the Saint-Venant equation (Equation (1)), allowing for 2D simulation of surface runoff and 1D simulation of channel flow. Exchange fluxes between soil layers, the surface, and river networks are determined based on pressure gradients, accurately capturing interactions between compartments such as infiltration, percolation, exfiltration, and baseflow [12].

$${\displaystyle \frac{\partial Q_i}{\partial t}}+v_j{\displaystyle \frac{\partial Q_i}{\partial x_j}}=-g A\left({\displaystyle \frac{\partial H}{\partial x_i}}+S_{fi}\right)$$

(1)

where $Q_i$ is discharge [m³/s], $t$ is time [s], $A$ is flow area [m²], v is velocity [m/s], $x_i$ is the flow direction, $x_j$ are spatial directions, $g$ is gravitational acceleration [m/s²], $H$ is hydraulic head [m], and $S_{fi}$ is the friction slope [m/m], which is computed using the empirical Manning’s equation.

Vegetation dynamics are simulated using a modified version of the Environmental Policy Integrated Climate (EPIC) model [26], which drives crop development through the accumulation of heat units (degree-days). This approach quantifies thermal time required for plant growth, enabling stage-specific simulation of phenology. The model also represents root growth, leaf area index (LAI), canopy height, and total biomass production. Water uptake from the root zone is modeled as a function of soil matric potential, following the approach proposed by Feddes et al. [27], which identifies four critical suction thresholds governing plant water stress. Under optimal soil moisture (h₂ < h < h₃), stress is minimal, and water uptake is maximized. Stress increases linearly when conditions deviate from this optimal range, reaching maximum inhibition at h < h₄ or h > h₁.

Evapotranspiration is simulated using the dual crop coefficient method proposed by Allen et al. [28], which distinguishes between basal crop water use and evaporation from exposed soil. Crop coefficients are assigned dynamically according to phenological stages, ensuring consistency between water demand and plant development. While MOHID-Land does not simulate atmospheric processes internally, it relies on externally supplied meteorological data (precipitation, temperature, solar radiation, cloud cover, relative humidity, wind speed, and wind velocity) as boundary inputs, enabling flexible coupling with observational data or climate model outputs.

2.2.1. MOHID-Land Soil Water Dynamics

MOHID-Land employs a fully three-dimensional representation of unsaturated flow processes, enabling detailed simulation of vertical and lateral water redistribution within the soil profile in response to pressure and moisture gradients. The transient movement of water within the soil in MOHID-Land is governed by the Richards equation (Equation (2)), a highly nonlinear partial differential equation due to the strong dependence of unsaturated hydraulic conductivity $K\left(\theta \right)$ on soil water content [6].

$${\displaystyle \frac{\partial \theta }{\partial t}}=-{\displaystyle \frac{\partial Q_i}{x_d}}-S\left(h\right)={\displaystyle \frac{\partial }{x_d}}\left(K\left(\theta \right){\displaystyle \frac{\partial H}{\partial x_d}}\right)A-S\left(h\right)$$

(2)

where $K\left(\theta \right)$ is the unsaturated hydraulic conductivity [m/s], $Q$ is the flux [m³/s], $A$ is the area [m²], $\theta$ is the water content [m³/m³], $H$ is the hydraulic gradient (topography + hydrostatic pressure + suction pressure) [m], $x_d$ is the flow direction, and $S\left(h\right)$ is the term for water uptake from the soil by plant roots [m³/s].

It is formulated under the continuum assumption with a representative elementary volume, meaning that water content and hydraulic properties are considered continuous over a defined length scale [29]. The classical Richards equation combines mass conservation and Darcy–Buckingham flux relationships [30] and assumes that air in the pores remains at atmospheric pressure, so that air does not impede water movement. These assumptions introduce important limitations. In soils with very low air permeability or highly compacted layers, air can become trapped, generating positive pore pressures that locally restrict water movement. This creates preferential flow paths that the classical Richards equation cannot represent, often leading to an underestimation of localized infiltration [31]. Additionally, the parabolic nature of the Richards equation imposes monotonic fluxes—meaning that water content changes smoothly and continuously without overshooting or oscillating—which prevents the standard formulation from capturing saturation overshoot, where water content temporarily exceeds equilibrium saturation at the wetting front [32,33].

Despite these limitations, the Richards equation remains the most widely used model for unsaturated flow due to its general applicability and computational efficiency. Extensions have been proposed specifically to address the inability of the classical formulation to capture saturation overshoot and preferential flow caused by air entrapment in compacted soils [31,32,33]. While these modifications improve the representation of such phenomena, the classical Richards equation still forms the backbone of most soil water modeling frameworks [30].

In MOHID-Land, the soil domain is bounded by two primary interfaces: the lower boundary, corresponding to impermeable bedrock, redirects infiltrated water as lateral subsurface flow along the terrain slope, while the upper boundary, the soil–atmosphere interface, applies precipitation, evapotranspiration, and other climatic fluxes. Constant air pressure is assumed at this interface, consistent with the classical Richards assumptions. Soil water retention is represented through VGM functional relationships (Equations (3) and (4)) [11,12], while vertical and lateral hydraulic anisotropy is accounted for through a $KF$ multiplier (Equation (5)), where a value of 1 indicates isotropy and other values reflect degrees of directional variation [34]. These boundary conditions and hydraulic parameterizations allow MOHID-Land to simulate realistic water redistribution, with anisotropy playing a critical role in sloped or stratified soils by enhancing lateral flow and influencing streamflow and groundwater recharge.

$$\theta \left(h\right)={\theta }_r+{\displaystyle \frac{{\theta }_s-{\theta }_r}{{\left[{1+\left(\alpha \left|h\right|\right)}^n\right]}^m}}$$

(3)

$$K\left(\theta \right)=K_{sat} S_e^L{(1-{(1-S_e^{1/m})}^m)}^2$$

(4)

$$KF={\displaystyle \raisebox{1ex}{$K_{sat,hor}$}\!\left/ \!\raisebox{-1ex}{$K_{sat}$}\right.}$$

(5)

where ${\theta }_s$ is the saturated water content [m³/m³], ${\theta }_r$ is the residual water content [m³/m³], $h$ is the suction pressure [m], $K_{sat}$ is the saturated hydraulic conductivity [m/s], $\alpha$ is the curve adjustment parameter, related to the inverse of the air entry [m⁻¹], $n$ is the curve adjustment parameter, related to the pore size distribution [dimensionless], $m$ is obtained from the relation $1-1/n$, $L$ is the empirical pore connectivity [m], equal to 0.5 [8], $KF$ is the hydraulic conductive multiplying factor [dimensionless], and $K_{sat,hor}$ is the horizontal saturated conductivity [m/s].

2.2.2. Model Set-Up (Baseline Simulation—S1)

The model domain was discretized using a regular grid with a spatial resolution of 200 m, encompassing 160 rows by 200 columns. The lower-left coordinate of the grid is anchored at 43.36° W and 22.59° S. Elevation data were obtained from the 30 m resolution Topodata digital elevation model [35] and subsequently interpolated to match the model’s spatial resolution.

River channel geometry was represented by trapezoidal cross-sections, parameterized based on upstream drainage areas and derived from field surveys conducted between 2019 and 2021 under the direction of the Piabanha Watershed Committee (

Table 1. Dimensions of cross-sections based on field measurements.

Drainage Area (km2)	Heights (m)	Top Width (m)	Bottom Width (m)
2.00	1.50	3.00	1.00
6.32	2.00	4.60	1.00
12.60	2.00	5.10	2.00
34.40	2.00	8.70	2.00
49.18	5.00	11.20	6.00
103.45	5.00	14.00	6.00
419.33	5.00	19.00	6.00

Note: Adapted from Sales et al. [11].

). Each row in Table 1 represents the geometric parameters (heights, top width, and bottom width) of the trapezoidal cross-sections associated with a specific upstream drainage area. The smallest drainage area corresponds to the most upstream node of the drainage network, while the largest area represents the watershed outlet. Intermediate drainage areas are control points, and cross-sections for all other nodes are interpolated between these values to ensure that each node in the network is assigned a representative channel geometry.

Land use and land cover data were sourced from the 30 m resolution MapBiomas project [36] and used to assign vegetation classes and Manning’s roughness coefficients, which ranged from 0.03 to 0.16 s·m^(−1/3). Three predominant land cover types—forest, pasture, and agriculture—guided the assignment of crop coefficients ($Kc$), varying from 0.6 to 1.0, in accordance with Food and Agriculture Organization (FAO) guidelines [28], as detailed in

Table 2. Surface and vegetation coefficients.

Land Use Classes	Manning Coefficient	${\mathit{K}}_{\mathit{c}}$			Feddes Coefficients
		Initial	Mid-Season	End Season	${\mathit{h}}_1$	${\mathit{h}}_2$	${\mathit{h}}_3$	${\mathit{h}}_4$
Dense Forest	0.160	0.95	1.00	1.00	0	−1	−3.3	−150
Pasture	0.038	0.40	1.05	0.85	−0.1	−0.25	−8	−80
Agriculture	0.045	0.60	1.15	0.90	−0.1	−0.25	−15	−80
Urban	0.040	-	-	-	-	-	-	-
Rocky Outcrop	0.030	-	-	-	-	-	-	-

Note: Manning coefficients estimated according to Chow [37]; pasture and agriculture Feddes coefficients obtained from HYDRUS 1D model [38]; and forest Feddes coefficients defined according to Grinevskii [39]. Adapted from Sales et al. [11].

.

Soil texture [40] and bulk density [41] data from the Brazilian Agricultural Research Corporation (EMBRAPA), headquartered in Brasília, Brazil, were used as input. These datasets are provided as raster layers (90 m resolution), derived from national soil surveys and interpolations. The data were processed using the MOHID Soil Tool (https://github.com/dhiegosales/MOHID-SOIL-TOOL, accessed on 12 December 2024), which extracts soil texture fractions (sand, silt, and clay) and bulk density for each soil type polygon and depth layer. In the study area, 10 distinct soil types were identified. The EMBRAPA dataset contains six vertical layers, which were used to discretize the soil profile into seven computational layers in MOHID-Land. Since the last two layers share the same parameters, the model preserves six unique layers as shown in

Table 3. Vertical discretization of the 3D soil domain.

Model Layers		EMBRAPA Layers
ID	Thickness
1	5 cm	0–5 cm
2	10 cm	5–15 cm
3	15 cm	15–30 cm
4	30 cm	30–60 cm
5	40 cm	60–100 cm
6	300 cm	100–200 cm
7	300 cm

Note: Adapted from Sales et al. [11].

.

The soil texture and density values for each soil type and layer were then used as input for the Rosetta pedo-transfer model, generating the hydraulic parameters of the van Genuchten–Mualem formulation (${\theta }_r$, ${\theta }_s$, $\alpha$, $n$, $K_{sat}$). In total, 60 parameter sets (10 soil types × 6 layers) were produced and implemented in MOHID-Land. Therefore, the soil profile is not uniform across layers: each depth interval is characterized by distinct hydraulic properties derived from texture and bulk density, ensuring a realistic vertical heterogeneity consistent with the EMBRAPA dataset. The full set of hydraulic parameters is presented in Appendix A (

Table A1. Soil properties (EMBRAPA) and corresponding hydraulic parameters generated by the Rosetta pedotransfer model for each soil type and layer—Generated in MOHID Soil Tool.

Layer	Soil Type (Polygons)	EMBRAPA Input				Rosetta Output
		Sand (%)	Silt (%)	Clay (%)	Density (g/cm3)	${\mathit{\theta }}_{\mathit{r}}$ (m3/m3)	${\mathit{\theta }}_{\mathit{s}}$ (m3/m3)	$\mathit{n}$ (-)	$\mathit{\alpha }$(m−1)	${\mathit{K}}_{\mathit{s}\mathit{a}\mathit{t}}$ (m/s)
0–5 cm	AR2—Rock outcrops	51.82	19.34	28.84	1.08	0.106	0.512	1.364	1.033	8.407 × 10−6
0–5 cm	AR3—Rock outcrops	51.02	18.47	30.5	1.06	0.109	0.521	1.356	1.042	8.805 × 10−6
0–5 cm	Ca1—Allic Cambisol	53.1	17.19	29.71	1.07	0.108	0.518	1.357	1.088	8.930 × 10−6
0–5 cm	Ca2—Allic Cambisol	50.18	16.9	32.92	1.11	0.111	0.514	1.344	1.094	7.218 × 10−6
0–5 cm	Ca6—Allic Cambisol	48.37	17.2	34.43	1.15	0.112	0.506	1.338	1.092	5.989 × 10−6
0–5 cm	Ca7—Allic Cambisol	46.27	16.9	36.83	1.13	0.116	0.516	1.330	1.086	6.199 × 10−6
0–5 cm	LVa10—Allic Red-Yellow Latosol	46.37	18.12	35.52	1.18	0.113	0.500	1.334	1.072	5.102 × 10−6
0–5 cm	LVa14—Allic Red-Yellow Latosol	46.9	16.36	36.74	1.18	0.115	0.503	1.328	1.116	5.209 × 10−6
0–5 cm	Ra—Allic Litholic Soils	52.79	18.22	29	1.07	0.107	0.516	1.362	1.061	8.894 × 10−6
0–5 cm	Urban area	45.89	18.8	35.31	1.19	0.113	0.496	1.335	1.057	4.841 × 10−6
5–15 cm	AR2—Rock outcrops	50.58	20.44	28.98	1.04	0.107	0.522	1.365	0.985	9.429 × 10−6
5–15 cm	AR3—Rock outcrops	49.53	19.61	30.86	1.04	0.110	0.526	1.356	1.001	9.163 × 10−6
5–15 cm	Ca1—Allic Cambisol	51.96	19.3	28.74	1.05	0.107	0.520	1.364	1.023	9.372 × 10−6
5–15 cm	Ca2—Allic Cambisol	49.08	17.86	33.06	1.08	0.112	0.521	1.345	1.055	7.841 × 10−6
5–15 cm	Ca6—Allic Cambisol	47.49	18.07	34.43	1.12	0.113	0.513	1.340	1.058	6.563 × 10−6
5–15 cm	Ca7—Allic Cambisol	48.37	17.17	34.46	1.12	0.113	0.514	1.339	1.083	6.690 × 10−6
5–15 cm	LVa10—Allic Red-Yellow Latosol	45.12	19.11	35.77	1.16	0.114	0.505	1.336	1.039	5.365 × 10−6
5–15 cm	LVa14—Allic Red-Yellow Latosol	48.01	16.12	35.87	1.17	0.114	0.504	1.331	1.123	5.539 × 10−6
5–15 cm	Ra—Allic Litholic Soils	50.96	19.39	29.66	1.04	0.108	0.524	1.360	1.012	9.458 × 10−6
5–15 cm	Urban area	45.34	19.03	35.63	1.17	0.113	0.502	1.336	1.044	5.180 × 10−6
15–30 cm	AR2—Rock outcrops	49.56	17.8	32.64	1.09	0.111	0.518	1.347	1.062	7.644 × 10−6
15–30 cm	AR3—Rock outcrops	48.57	16.71	34.72	1.09	0.114	0.522	1.338	1.085	7.487 × 10−6
15–30 cm	Ca1—Allic Cambisol	52.48	15.66	31.86	1.07	0.111	0.523	1.347	1.121	8.736 × 10−6
15–30 cm	Ca2—Allic Cambisol	49.25	15.04	35.71	1.12	0.115	0.517	1.332	1.138	6.840 × 10−6
15–30 cm	Ca6—Allic Cambisol	47.33	15.81	36.86	1.16	0.115	0.509	1.328	1.124	5.679 × 10−6
15–30 cm	Ca7—Allic Cambisol	46.09	15.24	38.67	1.17	0.117	0.509	1.320	1.136	5.360 × 10−6
15–30 cm	LVa10—Allic Red-Yellow Latosol	44.28	17.04	38.68	1.19	0.117	0.503	1.322	1.094	4.756 × 10−6
15–30 cm	LVa14—Allic Red-Yellow Latosol	47.62	14.66	37.72	1.2	0.116	0.501	1.322	1.165	4.949 × 10−6
15–30 cm	Ra—Allic Litholic Soils	50.52	16.43	33.06	1.08	0.112	0.522	1.343	1.096	8.075 × 10−6
15–30 cm	Urban area	45.53	17.1	37.37	1.2	0.115	0.498	1.326	1.099	4.674 × 10−6
30–60 cm	AR2—Rock outcrops	46.36	19.1	34.54	1.15	0.113	0.505	1.340	1.040	5.708 × 10−6
30–60 cm	AR3—Rock outcrops	46.36	17.9	35.74	1.16	0.114	0.505	1.334	1.071	5.520 × 10−6
30–60 cm	Ca1—Allic Cambisol	51.05	17.73	31.23	1.15	0.108	0.500	1.351	1.093	6.378 × 10−6
30–60 cm	Ca2—Allic Cambisol	45.8	16.59	37.61	1.18	0.116	0.504	1.325	1.106	5.094 × 10−6
30–60 cm	Ca6—Allic Cambisol	43.76	15.85	40.39	1.21	0.118	0.502	1.314	1.125	4.395 × 10−6
30–60 cm	Ca7—Allic Cambisol	43.52	15.35	41.13	1.22	0.119	0.501	1.310	1.138	4.224 × 10−6
30–60 cm	LVa10—Allic Red-Yellow Latosol	40.53	16.02	43.45	1.21	0.122	0.507	1.305	1.112	4.170 × 10−6
30–60 cm	LVa14—Allic Red-Yellow Latosol	43	14.09	42.91	1.25	0.121	0.497	1.301	1.171	3.756 × 10−6
30–60 cm	Ra—Allic Litholic Soils	47.52	17.76	34.72	1.15	0.113	0.506	1.338	1.075	5.871 × 10−6
30–60 cm	Urban area	40.26	15.9	43.84	1.23	0.122	0.502	1.302	1.118	3.836 × 10−6
60–100 cm	AR2—Rock outcrops	55.45	16.01	28.53	1.25	0.102	0.472	1.359	1.211	5.097 × 10−6
60–100 cm	AR3—Rock outcrops	55.25	15.24	29.51	1.26	0.104	0.471	1.353	1.230	4.877 × 10−6
60–100 cm	Ca1—Allic Cambisol	59.44	15.43	25.13	1.25	0.097	0.466	1.379	1.272	5.973 × 10−6
60–100 cm	Ca2—Allic Cambisol	55.29	13.92	30.79	1.26	0.105	0.475	1.346	1.259	4.898 × 10−6
60–100 cm	Ca6—Allic Cambisol	51.07	13.16	35.77	1.26	0.112	0.483	1.324	1.240	4.328 × 10−6
60–100 cm	Ca7—Allic Cambisol	50.91	11.99	37.1	1.25	0.114	0.489	1.319	1.262	4.511 × 10−6
60–100 cm	LVa10—Allic Red-Yellow Latosol	44.7	13.56	41.74	1.23	0.120	0.500	1.306	1.185	4.205 × 10−6
60–100 cm	LVa14—Allic Red-Yellow Latosol	48.77	12.54	38.69	1.27	0.116	0.486	1.312	1.241	3.953 × 10−6
60–100 cm	Ra—Allic Litholic Soils	56.81	15.55	27.64	1.25	0.101	0.470	1.364	1.237	5.363 × 10−6
60–100 cm	Urban area	45.44	14.08	40.48	1.25	0.118	0.493	1.309	1.182	3.927 × 10−6
100–200 cm	AR2—Rock outcrops	48.54	13.81	37.65	1.25	0.115	0.488	1.318	1.204	4.201 × 10−6
100–200 cm	AR3—Rock outcrops	49.81	12.53	37.66	1.25	0.115	0.489	1.317	1.242	4.372 × 10−6
100–200 cm	Ca1—Allic Cambisol	52.47	12.71	34.82	1.24	0.111	0.487	1.329	1.254	4.858 × 10−6
100–200 cm	Ca2—Allic Cambisol	52.38	11.66	35.97	1.25	0.113	0.487	1.323	1.281	4.698 × 10−6
100–200 cm	Ca6—Allic Cambisol	48.93	12.36	38.72	1.25	0.116	0.491	1.313	1.240	4.287 × 10−6
100–200 cm	Ca7—Allic Cambisol	49.45	10.98	39.57	1.25	0.117	0.493	1.309	1.275	4.385 × 10−6
100–200 cm	LVa10—Allic Red-Yellow Latosol	45.55	13.22	41.23	1.24	0.119	0.497	1.306	1.199	4.122 × 10−6
100–200 cm	LVa14—Allic Red-Yellow Latosol	50.4	11.49	38.11	1.27	0.115	0.486	1.313	1.276	4.149 × 10−6
100–200 cm	Ra—Allic Litholic Soils	50.51	12.57	36.92	1.24	0.114	0.491	1.320	1.243	4.616 × 10−6
100–200 cm	Urban area	47.28	12.84	39.88	1.26	0.117	0.490	1.309	1.222	3.964 × 10−6

).

In the model, hydraulic conductivity anisotropy is represented by the $KF$ multiplier, which was set to 10—the default value in MOHID-Land—indicating that horizontal conductivity is ten times higher than vertical conductivity.

The meteorological data required for the calculation of reference evapotranspiration were obtained from the ERA5 global reanalysis model [42]. This model, which provides hourly data on a 0.25° × 0.25° grid, was selected for its ability to provide long and continuous time series. The reliability and accuracy of ERA5 data for hydrological and climatological studies have been extensively documented in the scientific literature, with numerous studies validating its suitability for different regions, including Brazil [43,44,45,46]. Given this extensive use by the scientific community, we considered the ERA5 dataset to be an appropriate source for the meteorological parameters used in this study.

Precipitation inputs were compiled from 39 local rain gauges and consolidated into 15 representative stations using a clustering based on median rainfall characteristics [22]. Missing rainfall data were interpolated using UNESCO-IHE’s HyKit toolbox [47], which integrates station proximity and elevation to account for spatial heterogeneity—particularly important given the region’s pronounced orographic variability.

2.3. Van Genuchten Parameters Interactions and Scenarios

To rigorously evaluate the individual and combined influences of soil hydraulic parameters within the VGM framework—namely ${\theta }_s$, ${\theta }_r$, $\alpha$, $n$, and $K_{sat}$, hereafter referred to as $P_1$ through $P_5$—a deterministic combinatorial strategy was adopted. Each parameter was perturbed by a fixed ±10% multiplicative factor, as specified by Sales et al. [11], relative to its baseline value. Specifically, the factors applied were 1.1 for ${\theta }_s$ and $n$, and 0.9 for ${\theta }_r$, $\alpha$, and $K_{sat}$.

The methodological foundation rests on the mathematical construction of the power set of the parameter space. Let $P=\{P_1,P_2,\dots ,P_j\}$ denote the set of VGM parameters under analysis, where $j=5$. The power set $\mathcal{P}\left(P\right)$ includes all $2^j$ subsets of $P$. Excluding the null set (which corresponds to the unperturbed baseline simulation), the total number of unique simulations required to evaluate all non-empty parameter combinations is denoted by $C$ and given by:

$$\mathrm{C}=2^j-1=2^5-1=31$$

(6)

The use of base 2 in this formulation is justified by the binary nature of each perturbation decision—a parameter is either included in each simulation (perturbed) or not (kept at its default value). Such inclusion/exclusion logic naturally follows a binary combinatorial structure, which is classically modeled using powers of two. Each subset $S_k\subseteq P$ corresponds to a distinct simulation scenario in which exactly $k$ parameters are perturbed ($1\le k\le 5)$. For example, all subsets of cardinality $k=2$ correspond to pairwise interactions, such as $\{P1,P2\}$, $\left\{P1,P3\right\}$, …. For $k=5$, there is only one subset, containing all parameters: $\{P1,P2,P3,P4,P5\}$.

Simulation scenarios were generated using MOHID Soil Tool (MST), a dedicated Python-based software (version 4.0.3) with a graphical interface optimized for Windows 10/11 × 64 systems. MST was specifically developed to transform soil texture and bulk density data into hydraulic parameters through the following computational pipeline: (i) data ingestion, (ii) soil texture preprocessing, (iii) compaction analysis, (iv) derivation of VGM parameters via the Rosetta API, (v) application of multiplicative perturbation factors, and (vi) export of formatted input files for MOHID-Land. The executable version of the software along with its user manual is available at: https://github.com/dhiegosales/MOHID-SOIL-TOOL (accessed on 12 December 2024). Additionally, the complete set of input files can be accessed at: https://zenodo.org/records/14914611 (accessed on 23 February 2025). These resources enable replication of the results and verification of the methodology. Comprehensive technical documentation is provided in Sales et al. [11] to support correct application and interpretation of the tool.

Table 4. Simulation scenarios for evaluating interactions among VGM parameters.

SIM	MST Multiplying Factor					Parameter Perturbated
	${\mathit{\theta }}_{\mathit{s}}$	${\mathit{\theta }}_{\mathit{r}}$	$\mathit{\alpha }$	$\mathit{n}$	${\mathit{K}}_{\mathit{s}\mathit{a}\mathit{t}}$
S1	1	1	1	1	1	-
S2	1.1	1	1	1	1	${\theta }_s$
S3	1	0.9	1	1	1	${\theta }_r$
S4	1	1	0.9	1	1	$\alpha$
S5	1	1	1	1.1	1	$n$
S6	1	1	1	1	1.1	$K_{sat}$
S7	1.1	0.9	1	1	1	${\theta }_s$, ${\theta }_r$
S8	1.1	1	0.9	1	1	${\theta }_s$, $\alpha$
S9	1.1	1	1	1.1	1	${\theta }_s$, $n$
S10	1.1	1	1	1	1.1	${\theta }_s$, $K_{sat}$
S11	1	0.9	0.9	1	1	${\theta }_r,\alpha$
S12	1	0.9	1	1.1	1	${\theta }_r,n$
S13	1	0.9	1	1	1.1	${\theta }_r,K_{sat}$
S14	1	1	0.9	1.1	1	$\alpha ,n$
S15	1	1	0.9	1	1.1	$\alpha ,K_{sat}$
S16	1	1	1	1.1	1.1	$n,K_{sat}$
S17	1.1	0.9	0.9	1	1	${\theta }_s$, ${\theta }_r,\alpha$
S18	1.1	0.9	1	1.1	1	${\theta }_s$, ${\theta }_r,n$
S19	1.1	0.9	1	1	1.1	${\theta }_s$, ${\theta }_r,K_{sat}$
S20	1.1	1	0.9	1.1	1	${\theta }_s,\alpha ,n$
S21	1.1	1	0.9	1	1.1	${\theta }_s,\alpha ,K_{sat}$
S22	1.1	1	1	1.1	1.1	${\theta }_s,n,K_{sat}$
S23	1	0.9	0.9	1.1	1	${\theta }_r,\alpha ,n$
S24	1	0.9	0.9	1	1.1	${\theta }_r,\alpha ,K_{sat}$
S25	1	0.9	1	1.1	1.1	${\theta }_r,n,K_{sat}$
S26	1	1	0.9	1.1	1.1	$\alpha ,n,K_{sat}$
S27	1.1	0.9	0.9	1.1	1	${\theta }_s$, ${\theta }_r,\alpha ,n$
S28	1.1	0.9	0.9	1	1.1	${\theta }_s$, ${\theta }_r,\alpha ,K_{sat}$
S29	1.1	0.9	1	1.1	1.1	${\theta }_s$, ${\theta }_r,n,K_{sat}$
S30	1.1	1	0.9	1.1	1.1	${\theta }_s$,$\alpha ,n,K_{sat}$
S31	1	0.9	0.9	1.1	1.1	${\theta }_r$,$\alpha ,n,K_{sat}$
S32	1.1	0.9	0.9	1.1	1.1	${{\theta }_s,\theta }_r$,$\alpha ,n,K_{sat}$

summarizes the baseline scenario (S1) and the 31 combinatorial simulations (S2–S32), detailing the specific VGM parameters perturbed in each scenario. A value of 1.0 in this table indicates that the parameter’s baseline value, which corresponds to the specific soil type and depth, remains unchanged; these values are detailed in the appendix (Table A1). Factors of 1.1 and 0.9 correspond to +10% and −10% perturbations, respectively. For instance, S2 tests $K_{sat}$ in isolation; S7 evaluates the joint influence of $K_{sat}$ and ${\theta }_s$; and S32 includes all five parameters simultaneously.

Simulations were independently executed on the High-Performance Computing (HPC) cluster of the Escola de Sagres, affiliated with the Instituto Politécnico da Universidade do Estado do Rio de Janeiro (UERJ). This infrastructure enabled efficient and reproducible parallel execution computationally intensive model runs.

By maintaining the same ±10% perturbation range established in Sales et al. [11], we constructed and evaluated all 31 non-empty combinations of the five VGM parameters, performing one simulation for each scenario. This deterministic strategy enabled a systematic assessment of parameter interactions and their influence on model performance, using streamflow as the response variable. Unlike stochastic algorithms or high-dimensional sampling techniques, this approach offers a computationally efficient alternative for complex models. The fixed perturbation range allowed for a standardized comparison of parameter effects, reducing potential biases from scale-dependent variances. Notably, the method revealed how specific combinations of parameters affect simulation accuracy—insights that would likely be missed by traditional local sensitivity methods.

2.4. Model Evaluation

The combinatorial simulation experiments were conducted over the 2006–2008 period, with 2006 designated as a model warm-up year and therefore excluded from the performance evaluation. The observed streamflow dataset was provided at a daily time step, yielding a total of 731 observations from 1 January 2007 to 31 December 2008. This specific period was selected because it coincides with the calibration window adopted by Sales et al. [11], providing a solid comparative basis and methodological consistency between studies. Aligning the time frame with that calibration benchmark allows for direct assessment of model performance under equivalent boundary and input conditions. Additionally, limiting the simulation to this shorter period reduced the computational demands inherent to the MOHID-Land model, thereby enabling a computationally efficient yet scientifically robust sensitivity analysis. It is important to note that observational errors were not explicitly quantified in this deterministic setup, as the primary objective was to isolate parameter-driven variability in model performance.

Model performance was quantitatively assessed using two widely recognized hydrological metrics: the Nash–Sutcliffe Efficiency (NSE) and the Percentage Bias (PBIAS), defined, respectively, by Equations (7) and (8). Both indices were computed using the open-access application ErrUncSeriesAnalyzer: Error and Uncertainty Analysis Tool, version 2.0.0, available at https://github.com/dhiegosales/ErrUncSeriesAnalyzer (accessed on 28 August 2024). This approach is standard practice in the field and provides a robust framework for evaluating both the model’s predictive skill and its long-term water balance:

$$NSE=1-\left[{\displaystyle \frac{\sum _{i=1}^p{(Q_i^{obs}-Q_i^{sim})}^2}{\sum _{i=1}^p{(Q_i^{obs}-Q_{mean}^{obs})}^2}}\right]$$

(7)

$$PBIAS={\displaystyle \frac{\sum _{i=1}^p(Q_i^{sim}-Q_i^{obs})}{\sum _{i=1}^p{Q}_i^{obs}}} 100$$

(8)

where $Q_i^{sim}$ is the simulated flow for day $i$ [m³/s]; $Q_i^{obs}$ is the observed flow on day $i$ [m³/s]; $Q_{mean}^{obs}$ is the observed mean flow for the period [m³/s]; $Q_{mean}^{sim}$ is the simulated mean flow for the period under consideration [m³/s]; and $p$ is the total number of days in that same period.

The NSE measures the model’s predictive skill by comparing variance of residuals to the variance in the observed data. NSE values range from −∞ to 1, where values closer to 1 indicate higher model accuracy. According to Moriasi et al. [48], NSE > 0.80 is classified as “Very Good,” 0.70–0.80 as “Good,” 0.50–0.70 as “Satisfactory,” and values below 0.50 as “Unsatisfactory.” PBIAS quantifies the average deviation between simulated and observed volumes, with an ideal value of 0. Positive values reflect overestimation, while negative values indicate underestimation. Performance thresholds for PBIAS are as follows: within ±5% is “Very Good,” ±5–10% is “Good,” ±10–15% is “Satisfactory,” and greater than ±15% is “Unsatisfactory.”

To identify patterns and groupings among the simulation outcomes, a hierarchical cluster analysis was applied to the NSE and PBIAS scores. Prior to clustering, the performance metrics were normalized using the StandardScaler class from the Python scikit-learn library to ensure comparability in the distance computations. The clustering procedure employed Ward’s linkage method [49,50], which minimizes the total within-cluster variance during agglomeration. The resulting dendrogram visually represented the hierarchical structure of simulation performance, allowing the identification of groups with similar behavior in terms of model accuracy and bias.

2.5. Computational Infrastructure

The exhaustive interaction experiment, necessitated by the physically based and spatially distributed complexity of the MOHID-Land model, required substantial computational resources. A total of 32 simulations were executed on the HPC Escola de Sagres. Its infrastructure operates under a Linux environment and is accessed remotely via SSH protocol, requiring prior compilation of the MOHID-Land source code for Unix-based systems.

Each simulation was configured to utilize ten computational threads. Up to six independent model instances were executed concurrently, effectively leveraging the cluster’s parallel processing capabilities. Despite the high computational demand of the model, the simulations were successfully completed with a relatively modest memory allocation of only 1 GB per process, underscoring the computational efficiency achieved through optimized thread management and parallel scheduling. Further details regarding runtime and overall computational cost are provided in Section Computational Cost.

3. Results

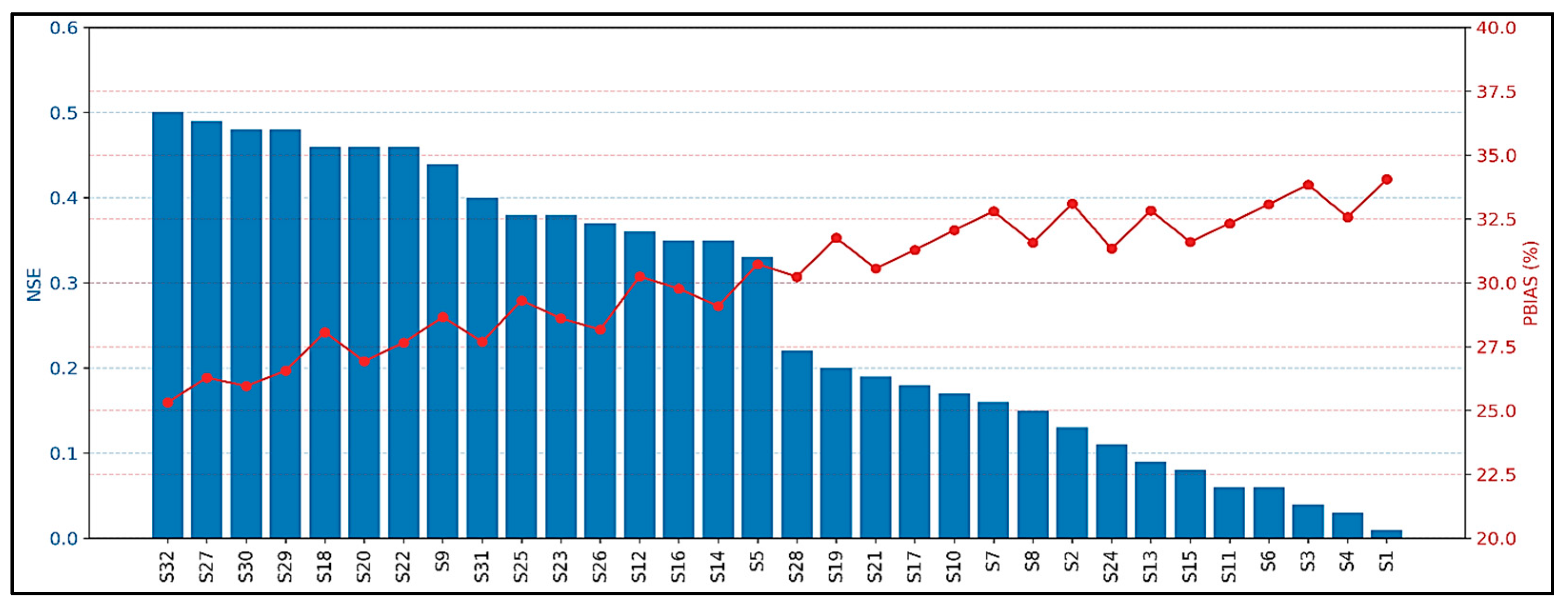
The simultaneous perturbation of all five VGM parameters—in simulation S32 resulted in the highest performance among all evaluated scenarios. This configuration yielded an NSE of 0.50 and the lowest PBIAS of 25.32 (

Table 5. Performance metrics for combinatorial simulation scenarios (ranked by NSE).

SIM	PBIAS	NSE	SIM	PBIAS	NSE
S32	25.32	0.50	S28	30.24	0.22
S27	26.30	0.49	S19	31.76	0.20
S30	25.96	0.48	S21	30.56	0.19
S29	26.56	0.48	S17	31.29	0.18
S18	28.07	0.46	S10	32.07	0.17
S20	27.93	0.46	S7	32.80	0.16
S22	27.66	0.46	S8	31.58	0.15
S9	28.66	0.44	S2	33.10	0.13
S31	27.69	0.40	S24	31.34	0.11
S25	29.31	0.38	S13	32.83	0.09
S23	28.62	0.38	S15	31.60	0.08
S26	28.17	0.37	S11	32.33	0.06
S12	30.26	0.36	S6	33.08	0.06
S16	29.78	0.35	S3	33.84	0.04
S14	29.09	0.35	S4	32.57	0.03
S5	30.73	0.33	S1	34.06	0.01

), thereby establishing S32 as the most effective configuration identified within the proposed experimental framework. This result empirically reinforces the assumption advanced by Sales et al. [11], namely that the simultaneous perturbation of all VGM parameters—even with uniform, fixed-magnitude adjustments—is more effective in capturing the coupled, nonlinear interactions that govern unsaturated flow and soil–water retention processes than isolated or partial combinations of parameter modifications. In contrast, the baseline simulation S1, which employed default parameter values without any perturbation, resulted in substantially lower model performance, with an NSE of 0.01 and a PBIAS of 34.06.

Beyond the assessment of absolute performance for individual simulations (S2–S6), this analysis also aimed to elucidate the nature of interactions among VGM parameters—specifically, to identify potential synergistic, complementary, or antagonistic behaviors. In this context, complementarity is defined as a scenario in which the joint perturbation of two or more parameters yields a performance gain that results from interdependence, even if not strictly amplifying in nature.

A notable complementary interaction emerged between ${\theta }_s$ and $n$. When perturbed individually, ${\theta }_s$ (S2: NSE = 0.13; PBIAS = 33.10) and $n$ (S5: NSE = 0.33; PBIAS = 30.73) yielded modest improvements in model performance. However, their combined perturbation in simulation S9 resulted in a substantially higher NSE of 0.44 and a reduced PBIAS of 28.66. Although this joint effect exceeded the performance of each parameter individually, it remained slightly below the theoretical sum of their separate contributions (0.13 + 0.33 = 0.46), suggesting a complementary yet sub-additive interaction. This finding underscores a functional coupling between ${\theta }_s$ and $n$, likely reflecting their joint control over the unsaturated flow regime, particularly through their influence on the soil moisture retention curve and hydraulic conductivity.

Expanding upon the ${\theta }_s$–$n$ complementarity, the inclusion of a third parameter in selected simulations offered further insights into higher-order interactions. Specifically, configurations involving three-parameter combinations—S20 (${\theta }_s$, $\alpha$, $n$), S22 (${\theta }_s$, $n$, $K_{sat}$), and S18 (${\theta }_s$, ${\theta }_r$, $n$)—exhibited a marginal increase in performance, with NSE values rising to 0.46 and PBIAS narrowing to the range of 27.66–28.07. Though these gains over S9 (NSE = 0.44) are incremental, they suggest that $\alpha$, $K_{sat}$, and ${\theta }_r$ provide supportive secondary effects when integrated with the dominant ${\theta }_s$–$n$ configuration.

Importantly, these parameters—when tested in isolation (e.g., S3 for ${\theta }_r$, S4 for $\alpha$, and S6 for $K_{sat}$)—produced only limited improvements in performance. Their enhanced effectiveness in multi-parameter contexts highlights the nonlinear and interactive nature of soil hydraulic processes. These findings reinforce the notion that hydrological model calibration benefits not only from optimizing dominant parameters, but also from considering emergent interactions that arise in combinatorial configurations.

To further elucidate the relative sensitivity and potential redundancy among the VGM parameters, exclusion tests were performed by systematically omitting one parameter from the full five-parameter high-performing configuration. These four-parameter configurations—S27 (excluding $K_{sat}$; NSE = 0.49), S30 (excluding ${\theta }_r$; NSE = 0.48), and S29 (excluding $\alpha$; NSE = 0.48)—exhibited only marginal reductions in model performance (≤0.02 decrease in NSE) alongside negligible changes in PBIAS relative to the full five-parameter best-performing scenario (S32). Such results indicate that while $K_{sat}$, ${\theta }_r$, and $\alpha$ contribute modest incremental gains when individually added to the remaining four-parameter set, their marginal utility diminishes within a near-optimal multi-parameter framework. Hence, the removal of any one of these parameters from the comprehensive high-performing combination exerts a minimal detrimental effect on model fidelity.

Complementing this insight is the pronounced and pivotal influence of the parameter $n$. This is clearly demonstrated by comparing the isolated perturbation of $n$ in simulation S5 (NSE = 0.33) with the four-parameter scenario excluding $n$ in S28 (NSE = 0.22). The substantial decline in model performance upon removing $n$ from the parameter set (S28) underscores its critical role in driving calibration success. Moreover, the fact that $n$ alone (S5) outperforms both the four-parameter combination without it (S28) and each of the other parameters individually highlights its uniquely strong and amplifying contribution to the model’s predictive capability. The significant performance gap between S28 and the full five-parameter high-performing scenario S32 further confirms that accurate representation and perturbation of $n$ are essential to capturing the complex hydrological processes simulated by MOHID-Land. Collectively, these results emphasize that $n$ is a cornerstone parameter, whose inclusion substantially enhances model fidelity and robustness.

Hence, while the full parameter set in simulation S32 delivers the best overall performance, highly effective results can be attained with reduced parameter combinations, especially those including the core parameters ${\theta }_s$ and $n$. The exclusion of ${\theta }_s$, $\alpha$, or $K_{sat}$ results in only marginal performance losses, reinforcing a clear sensitivity hierarchy among the VGM parameters. These findings provide valuable guidance for the development of efficient and computationally cost-effective calibration strategies within distributed hydrological modeling frameworks.

Figure 3 visually reinforces these conclusions by illustrating the distribution of NSE values across simulation scenarios. The height of the NSE bars show a clear pattern of declining model efficiency as parameter combinations become sparser or less optimal. Scenarios approaching the completeness of S32 consistently demonstrate higher NSE values. Notably, the exclusion scenarios S27, S29, and S30 feature NSE bars nearly indistinguishable from that of S32, corroborating the inference that omitting any of these parameters results in minimal impact on model performance.

The behavior of the PBIAS line is notably more erratic, indicating that improvements in NSE are not always accompanied by proportional reductions in volumetric bias. This decoupling underscores the multidimensional nature of model evaluation: whereas NSE captures fidelity in temporal dynamics, PBIAS reflects systematic over or underestimation of flow volumes. Consequently, performance assessments based on a single metric may obscure critical aspects of model behavior. The joint interpretation of NSE and PBIAS—especially when visualized through clustering and graphical diagnostics—therefore provides a more robust and comprehensive framework for evaluating the sensitivity and interactions of hydrological parameters.

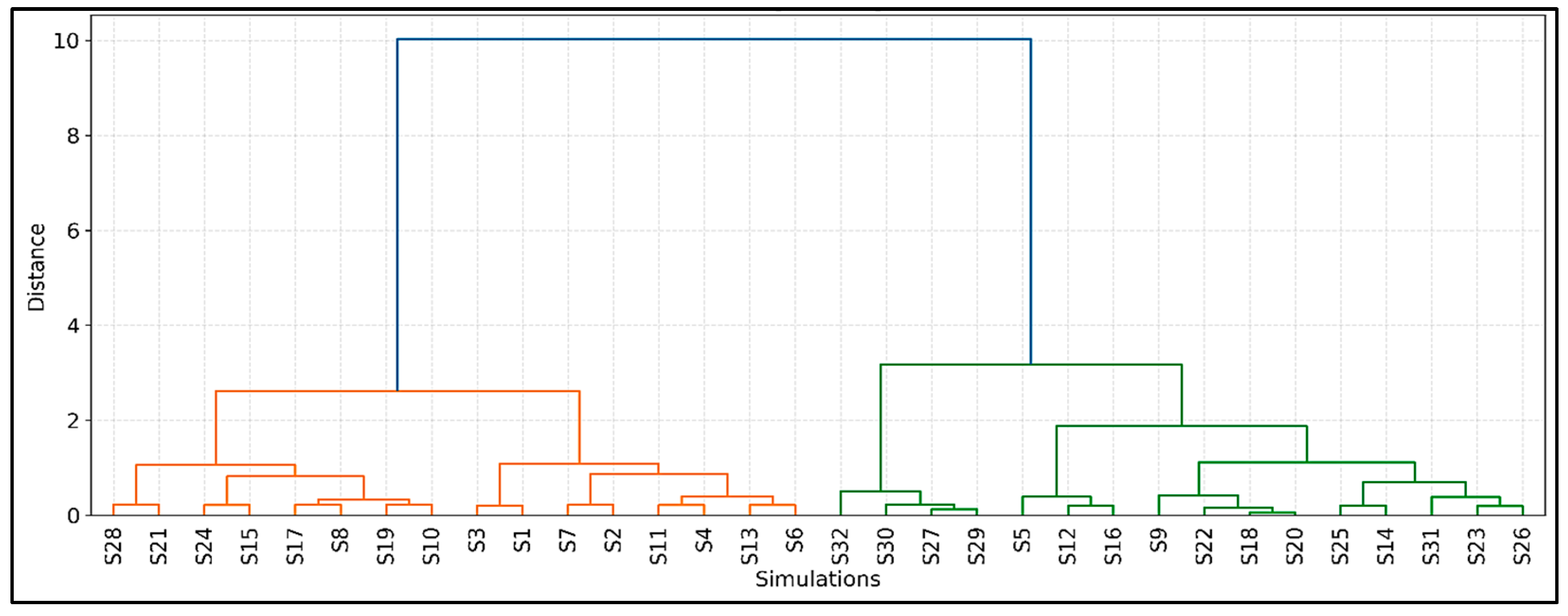
In addition to the individual evaluation of NSE and PBIAS metrics, the visual representation provided by the dendrogram (Figure 4) introduces a complementary analytical layer by clustering simulation scenarios based on their joint performance profiles. Constructed from standardized NSE and PBIAS values, this hierarchical clustering simultaneously integrates both metrics, offering a multidimensional assessment of model behavior. The dendrogram distinguishes clusters using colors (orange, green, and blue), highlighting groups of simulations with similar efficiency–bias characteristics. By grouping simulations with comparable efficiency–bias characteristics, the dendrogram uncovers performance patterns that are not always apparent through univariate analysis. As such, it reinforces—and in some instances refines—the insights derived from the direct metric evaluation, providing a more integrative diagnostic perspective on parameter configuration effectiveness.

A clear separation is evident in the dendrogram between the simulations with lower performance (located further to the left, with low NSE values, such as S28, S21, S24) and those that achieved higher efficiency (towards the right, including S32 and associated simulations). This initial clustering structure reflects the model’s sensitivity to the calibration of key parameters, with the baseline simulation (S1) distinctly separated distant from the best-performing group, reinforcing the significance of parameter optimization.

Within the cluster of relatively high-performing simulations, the proximity of S32 (full calibration) to S27 (excluding $K_{sat}$), S30 (excluding ${\theta }_r$), and S29 (excluding $\alpha$) in the dendrogram indicates that, in terms of the combined profile of NSE and PBIAS, the individual exclusion of these parameters results in a comparable overall outcome. This is consistent with marginal performance losses quantified in Table 5 and visualized by the similar NSE bars in Figure 3.

Interestingly, the position of S9 (calibration of ${\theta }_s$ and $n$) in a distinct yet relatively proximate subgroup to the high-performing configurations may indicate that while this synergistic combination is crucial for good performance, its specific trade-off profile between efficiency and bias (PBIAS of 28.66%) slightly differentiates it from the full calibration profile (PBIAS of 25.32%). The dendrogram suggests that other combinations of three or four parameters may display alternative balances between these metrics, resulting in an overall performance similarity that clusters them closer to S32.

The dispersion of simulations with isolated parameter calibration (S2, S3, S4, S5, S6) along the dendrogram, and their tendency to cluster in branches further from the high-performing group, reinforces the notion that individual parameter calibration, with the notable exception of $n$ (S5), is insufficient to attain high model efficiency. The relatively closer position of S5 to the best-performing group in the dendrogram underscores the pronounced influence of the $n$ parameter, as previously highlighted in the analysis of Table 5 and Figure 3.

4. Discussion

The results of this study underscore the critical importance of soil parameter calibration in enhancing the performance of the MOHID-Land model. This is clearly evidenced by the stark contrast between the poorly performing baseline simulation (S1), which yielded an NSE of 0.01 and a PBIAS of 34.06, and the significantly improved high-performing configuration (S32). The achievement of an NSE of 0.50 and a PBIAS of 25.32% through the simultaneous perturbation of all five VGM parameters highlights the model’s potential for delivering robust hydrological simulations when appropriately parameterized. These findings reinforce the broader consensus in the literature, highlighting that site-specific parameter optimization is essential for minimizing predictive uncertainty and improving model realism [51,52].

A distinctive contribution of this study lies in its methodological approach: a fully structured, deterministic framework that allowed for the systematic analysis of all five VGM parameters. By exhaustively evaluating every non-empty subset of parameter combinations (31 in total), this design provided a clear, objective, and reproducible assessment of both individual parameter effects and their complex interactions. Such a strategy is especially valuable for computationally demanding models like MOHID-Land, where simulation budgets are constrained and interpretability is critical. Unlike stochastic approaches, such as Monte Carlo or Latin Hypercube Sampling, which often obfuscate interpretation due to their inherent sampling variability, the deterministic, fixed-magnitude perturbation approach (±10%) employed here ensures consistent, scenario-by-scenario comparability, minimizing potential biases from extreme values and enhancing the interpretability of results.

At this stage it is important to acknowledge that alternative approaches—such as ensemble-based data assimilation methods (e.g., Ensemble Kalman Filter or Ensemble Smoother)—could in principle provide additional robustness by explicitly incorporating observational uncertainties into the calibration process [53]. However, due to the high computational cost of MOHID-Land (each simulation requiring more than one day), such methods were unfeasible for this study, highlighting a practical limitation that restricts the exploration of ensemble-based uncertainty analyses. Therefore, the deterministic perturbation framework adopted here represents a pragmatic balance between scientific rigor and computational feasibility, while still enabling a structured and interpretable assessment of parameter interactions.

One of the central insights from this comprehensive analysis is the dominant and functionally complementary role of the parameters ${\theta }_s$ and $n$, which govern key aspects of soil water dynamics. This finding aligns well with established hydrological theory and previous empirical studies emphasizing the critical influence of these parameters in governing unsaturated flow processes. Specifically, ${\theta }_s$ primarily increases the total soil water storage capacity by regulating gravitational water retention and baseflow contributions [54,55], effectively determining how much water the soil can hold. In contrast, $n$ influences the steepness of the soil water retention curve, modulating the rate of infiltration and accelerating drainage efficiency [56,57]. The functional complementarity observed between ${\theta }_s$ and $n$ thus reflects a crucial balance between enhancing soil water storage and ensuring its timely release, a dynamic essential for accurate representation of unsaturated flow and reliable hydrological simulations.

These findings not only corroborate but also extend the conclusions of Sales et al. [11], who previously identified $n$ as the most sensitive parameter in the MOHID framework. Moreover, they complement the results of Verbist et al. [58], whose global sensitivity analysis using Sobol indices highlighted the importance of $n$ through total-order effects, particularly in runoff generation. Although Verbist et al. [58] found limited first-order sensitivity for $n$, the present study—applying a deterministic perturbation scheme—demonstrates that $n$ exerts substantial influence even when perturbed individually (S5, NSE = 0.33) and, notably, exhibits amplified effects when combined with other functionally synergistic parameters such as ${\theta }_s$.

This interpretation provides a nuanced counterpoint to the findings of Pan et al. [59], who reported that the sensitivity of $n$ is amplified when its correlation with $\alpha$ is considered. However, their analysis employed large and asymmetric parameter ranges, which may have inflated interaction effects. In contrast, the present study’s use of symmetric ±10%, minimizing bias and ensuring that observed interactions reflect intrinsic parameter dynamics rather than sampling artifacts. Nevertheless, this fixed perturbation range may constrain the exploration of extreme sensitivity scenarios, representing a methodological limitation of the chosen approach. This methodological refinement not only corroborates the isolated sensitivity of $n$ noted by Sales et al. [11] but also reinforces the practical relevance of $n$ in controlled calibration schemes. For instance, in simulation S14, where both $n$ and α were perturbed, an NSE of 0.35 was achieved—exceeding the isolated performance of either parameter ($n$: 0.33; $\alpha$: 0.03), but still below the core ${\theta }_s$–$n$ configuration (S9: NSE = 0.44). This indicates that while $\alpha$ has marginal influence on its own (S4: NSE = 0.03), it can offer incremental gains when combined with more dominant parameters. This context-dependent interaction further highlights the utility of structured perturbation frameworks in isolating parameter effects with clarity, something often obscured in stochastic methodologies.

Combinatorial design also allowed for a structured assessment of the relative influence of each VGM parameter under controlled calibration settings. While the omission of ${\theta }_r$, $\alpha$, or $K_{sat}$ from the high-performance configuration led to only marginal losses in model performance, this result should not be interpreted as evidence of functional irrelevance.

The hydrological functions of ${\theta }_r$, $\alpha$, and $K_{sat}$ are well established in the literature. ${\theta }_r$ governs residual water content and contributes to water availability under dry conditions [60,61]. $\alpha$ regulates the inverse of the air-entry pressure and is particularly relevant during post-dry infiltration events where steep wetting fronts interact with the capillary fringe [11]. $K_{sat}$ controls the infiltration–runoff partitioning during high-intensity rainfall [60,61].

Their relatively subdued influence on isolation, as observed here, may be attributed to two plausible, non-exclusive factors. First, the ±10% perturbation range—while ensuring physical plausibility and cross-scenario comparability—may not be sufficient to fully activate the dynamic effects of these parameters, especially in the hydrological regime studied. Second, the baseline parameter estimates, derived from pedotransfer functions (e.g., Rosetta) and soil datasets (e.g., EMBRAPA), may carry non-negligible uncertainty. If the initial values are not well aligned with local soil characteristics, small symmetric perturbations around such biased estimates may fail to explore regions of greater sensitivity—not because the parameters are functionally inert, but because the reference point is suboptimal.

In addition, it is important to recognize that observational streamflow data also carry non-negligible measurement uncertainty, which was not explicitly accounted for in this deterministic framework. While the purpose here was to isolate parameter-driven variability, unmodeled observational errors may partly influence performance scores such as NSE and PBIAS. This highlights a limitation regarding the potential impact of data uncertainty on quantitative evaluation of model performance.

This interpretation aligns with foundational insights from sensitivity theory, which emphasizes the role of parameter interaction, identifiability, and structural uncertainty in complex hydrological models [62,63]. Rather than undermining the findings, these considerations underscore their methodological transparency and practical relevance. The deterministic framework adopted here provides a conservative yet robust baseline, and future investigations may benefit from expanding perturbation ranges within physically realistic bounds, or from incorporating site-specific measurements to refine initial parameterization.

Importantly, while the inclusion of ${\theta }_r$, α, and $K_{sat}$ in specific triadic combinations with the dominant pair ${\theta }_s$–$n$ (e.g., ${\theta }_s$–α–$n$, ${\theta }_s$–$n$–$K_{sat}$, and ${\theta }_s$–${\theta }_r$–$n$) yielded slight improvements in model performance, these gains were marginal—typically increasing NSE from 0.44 to 0.46. Such incremental enhancement suggests that these secondary parameters exert a limited additive influence under the hydrological and structural conditions assessed. Their contribution appears to fine-tune, rather than transform, the model’s behavior, indicating that their calibration may be most impactful when core hydrophysical processes—primarily governed by ${\theta }_s$ and $n$—have already been well resolved.

This restrained response further reinforces the centrality of ${\theta }_s$ and $n$ as the primary levers of model fidelity in the MOHID-Land framework, at least under the parameter ranges and boundary conditions tested. Rather than undermining the importance of ${\theta }_r$, $\alpha$, and $K_{sat}$, these findings indicate that their influence operates primarily through hydrological accommodation—refining model behavior under transitional or boundary conditions rather than driving core flow dynamics. Their calibration priority, therefore, should be context sensitive.

These quantitative results are further corroborated by the general hydrological behavior associated with VGM parameter perturbations, as synthesized by Sales et al. [11] and summarized in

Table 6. Functional response of VGM parameters to ±10% perturbation: Implications for streamflow under wet and dry conditions.

Parameter	Sensitivity	Parameter Perturbation	Streamflow Effect (Wet)	Streamflow Effect (Dry)
$n$	High	Increase	Decrease	Increase
${\theta }_s$	Middle-high	Increase	Decrease	Increase
$K_{sat}$	Middle	Increase	Decrease	Increase
${\theta }_r$	Middle-low	Decrease	Decrease	Increase
$\alpha$	Low	Decrease	Decrease	Increase

Note: Adapted from Sales et al. [11].

. This framework classifies parameter sensitivity and elucidates how specific perturbations propagate to streamflow variations under contrasting wet and dry hydrological conditions, where we consider the wet period as corresponding to October–March and the dry period as April–September, which is typical of the tropical regime [11,21].

A key pattern that emerges is that the effect of perturbation is consistently inverse between wet and dry periods. Increases in $n$, ${\theta }_s$, and $K_{sat}$ reduce streamflow under wet conditions (attenuating peak flows) while enhancing streamflow under dry conditions (supporting baseflow). Conversely, decreases in ${\theta }_r$ and $\alpha$ produce the same dual outcome: lower streamflow under wet conditions and higher streamflow under dry conditions.

This consistency across parameters is particularly relevant for calibration. It means that, despite their differing sensitivities, the parameters converge toward the same management implication: increasing $n$, ${\theta }_s$, and $K_{sat}$ while reducing ${\theta }_r$ and $\alpha$ simultaneously contributes to dampening wet-season peaks and strengthening dry-season baseflows. Such adjustments reflect the mechanistic roles of these parameters in governing soil water storage, retention, and release dynamics.

It is worth noting that, if the calibration goal were the opposite—namely, to reduce baseflow during dry periods while increasing streamflow in wet periods—the direction of parameter adjustments identified in Table 6 could simply be inverted. In this case, decreasing $n$, ${\theta }_s$, and $K_{sat}$ while increasing ${\theta }_r$ and $\alpha$ would achieve the desired hydrological effect.

By linking quantitative sensitivity results to the hydrological logic summarized in Table 6, this study not only reinforces the validity of the findings but also provides a clear guideline for prioritizing parameter adjustments in calibration efforts aimed at reconciling peak and baseflow dynamics.

Taking these findings together, these findings substantially advance prior research by integrating a computationally efficient and methodologically transparent approach to sensitivity analysis in hydrological modeling. The adoption of uniform, controlled perturbation magnitudes proved instrumental in minimizing distortions from extreme values while enhancing comparability of results. It is, however, important to acknowledge that the ±10% perturbation range, although physically plausible, may underrepresent the full behavioral spectrum of parameters such as ${\theta }_s$ and $n$—particularly given their persistent dominance in both this and previous studies [11], and that initial parameter uncertainties and observational errors could influence the quantified sensitivities. Consequently, expanding the perturbation range in future studies—within physically defensible bounds—could provide additional insights into model behavior and sensitivity gradients. Nevertheless, the present findings provide a practical and actionable framework for prioritizing parameter calibration under constrained computational resources. In particular, the consistent and substantial influence of ${\theta }_s$ and $n$ across all interaction levels underscores their status as core calibration targets. By isolating and quantifying these effects with methodological rigor, this study contributes not only to improved simulation performance but also to a deeper mechanistic understanding of unsaturated flow processes in complex hydrological systems like MOHID-Land.

Computational Cost

The average runtime per simulation was approximately 49.65 h, resulting in a cumulative execution time of 1588.83 h across the 32 model runs. Conducted over approximately 13 consecutive days, this timeline demonstrates the practical viability of exhaustive combinatorial calibration when supported by high-performance computing (HPC) infrastructure.

A clear benchmark for evaluating this computational strategy is provided by Sales et al. [11], who performed a similar simulation-based experiment using four conventional personal computers with heterogeneous hardware configurations. Despite conducting only 11 simulations over the same hydrological period, their experiment required a total of 1998 h of processing time—averaging 182 h per machine—and spanned approximately 45 uninterrupted days.

This stark contrast underscores the strategic advantage of centralized HPC environments, which significantly reduces runtime, improves throughput, and enables deeper model exploration. Notably, the accelerated computation afforded by parallel processing was crucial for executing the full combinatorial design—an approach that would likely be impractical under standard multi-PC configurations.

Beyond efficiency gains, the HPC-based methodology enhances transparency, reproducibility, and scientific rigor. It enables other researchers to replicate or extend the experimental design with minimal variation, thereby aligning with emerging standards in robust and open hydrological modeling. This underscores the relevance of dedicated computational infrastructure as a catalyst for advancing methodological innovation in hydrological calibration.

5. Conclusions

The findings of this study underscore the critical importance of proper parameterization in the MOHID-Land model for achieving robust and reliable hydrological simulations. “Among the five VGM parameters evaluated, ${\theta }_s$ and $n$ consistently emerged as the most influential. They exert dominant control across all tested scenarios, highlighting them as foundational targets for calibration. This allows a favorable balance between predictive accuracy and computational cost, which is particularly relevant for large-scale or operational applications of distributed hydrological models.

The inclusion of ${\theta }_r$, $\alpha$, or $K_{sat}$ into the core ${\theta }_s$–$n$ combination produced only marginal improvements, indicating additive rather than synergistic effects, and even in four-parameter configurations, the incremental gains remained limited, suggesting that targeted three-parameter combinations may provide a practical compromise between model fidelity and computational efficiency. While the full five-parameter calibration yielded the highest overall performance, the incremental gain over the best triadic configurations was relatively small, reinforcing the central role of ${\theta }_s$ and $n$.

Importantly, some limitations should be acknowledged: the ±10% perturbation range may underrepresent the full sensitivity of ${\theta }_s$ and $n$, initial parameter estimates derived from pedotransfer functions or soil datasets may carry biases, observational uncertainties in streamflow were not explicitly modeled, and computational constraints restricted the use of ensemble-based or stochastic calibration approaches. Future studies could expand perturbation ranges, incorporate site-specific measurements, and account for observational uncertainties to refine sensitivity analyses and improve model robustness.

Based on these findings, we recommend a two-step soil calibration strategy: first, an initial multi-parameter exploration within physically plausible perturbation ranges to broadly sample the response surface; second, a focused refinement stage targeting ${\theta }_s$ and $n$ to optimize model performance efficiently. This structured approach balances hydrological realism with operational feasibility while providing a transparent and replicable framework.

In summary, this study delivers empirical evidence and methodological guidance for deterministic soil calibration in distributed hydrological models, highlights calibration priorities, clarifies parameter interactions, and acknowledges methodological limitations, providing actionable insights for improving predictive accuracy in complex watershed systems. We also encourage future work to integrate recent advancements in sensitivity analysis and data assimilation methods to further enhance calibration practices.