Quantifying the Comprehensive Water Resources and Environment Carrying Capacity in Wuhan City Based on the “Human-Water-City” Framework
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources and Processing
2.3. Research Method
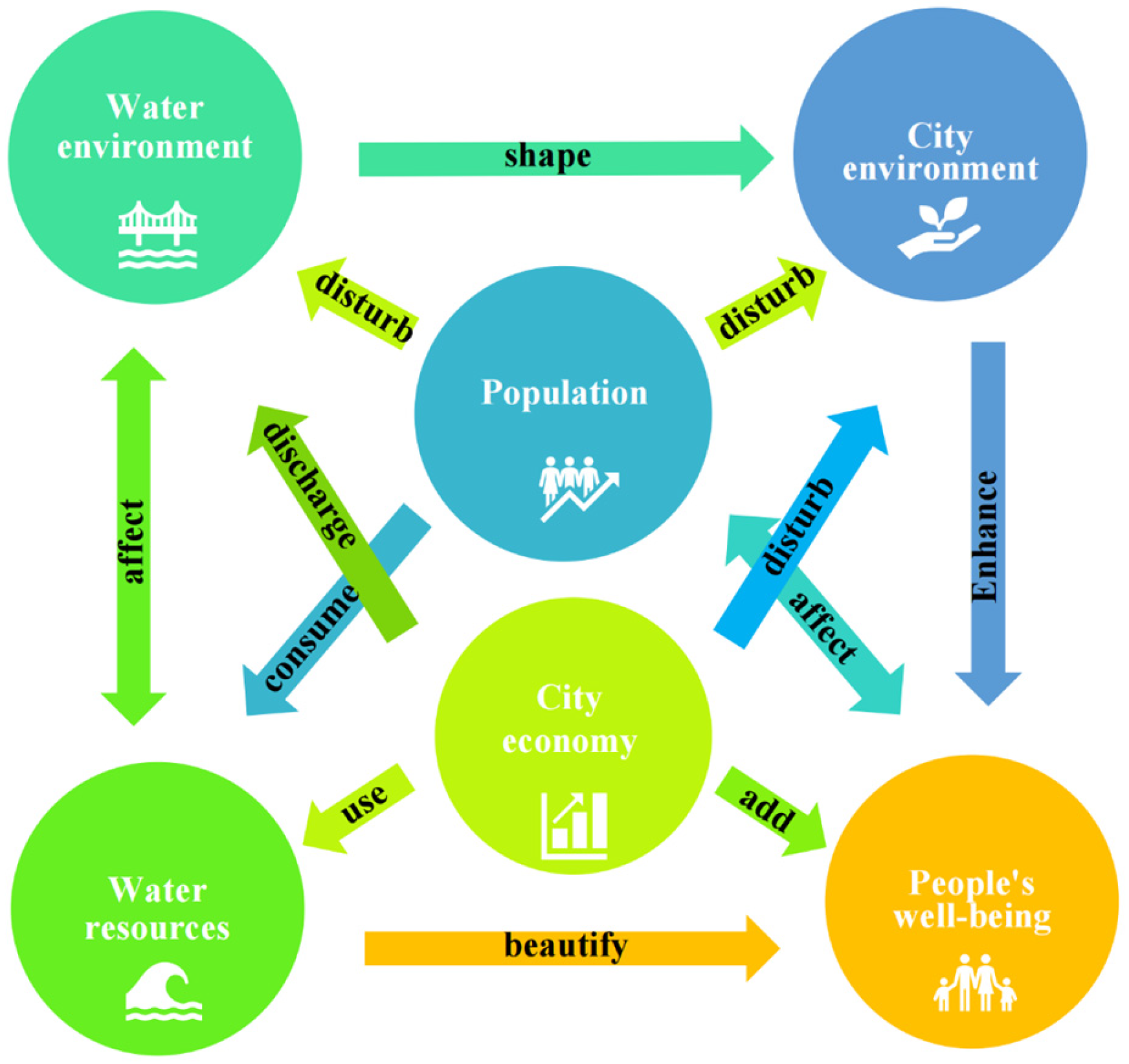
2.3.1. “Human-Water-City” Feedback Framework
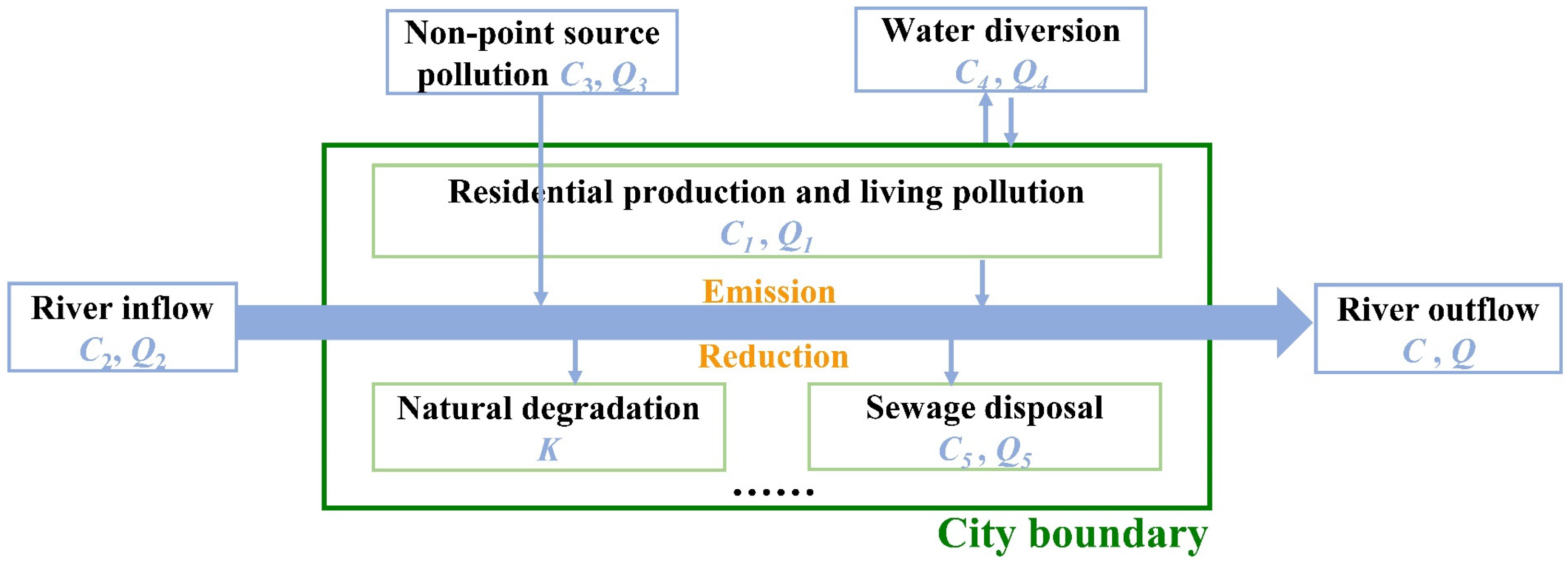
2.3.2. CWRECC Based on the HWC Framework
- (1)
- Analysis of Water Resources Carrying Capacity
- (2)
- Analysis of Water Environment Carrying Capacity
- (3)
- Comprehensive Assessment of the CWRECC
- (4)
- Quantitative Measurement Model of the CWRECC
- (5)
- Equations related to water resources.
- (6)
- Equations related to the aquatic environment.
3. Results
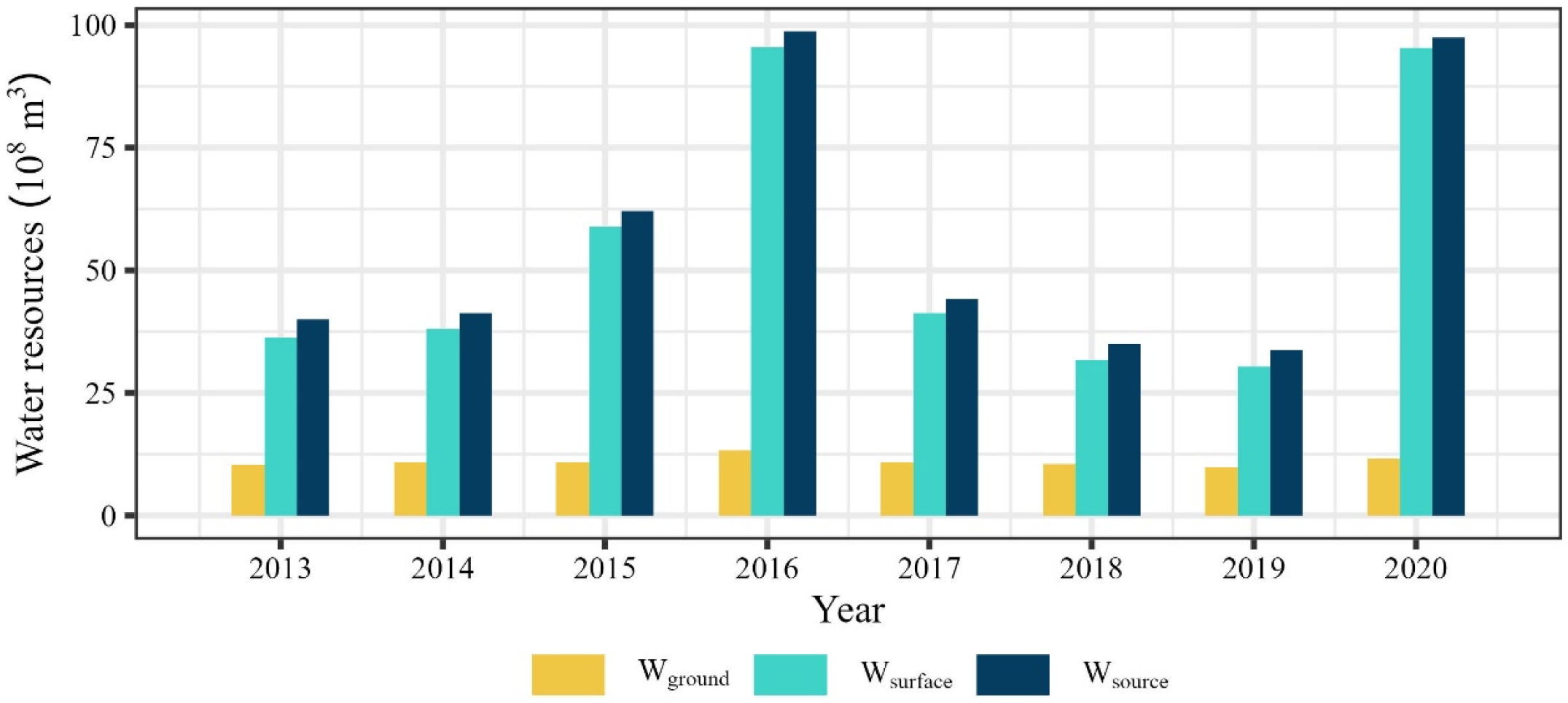
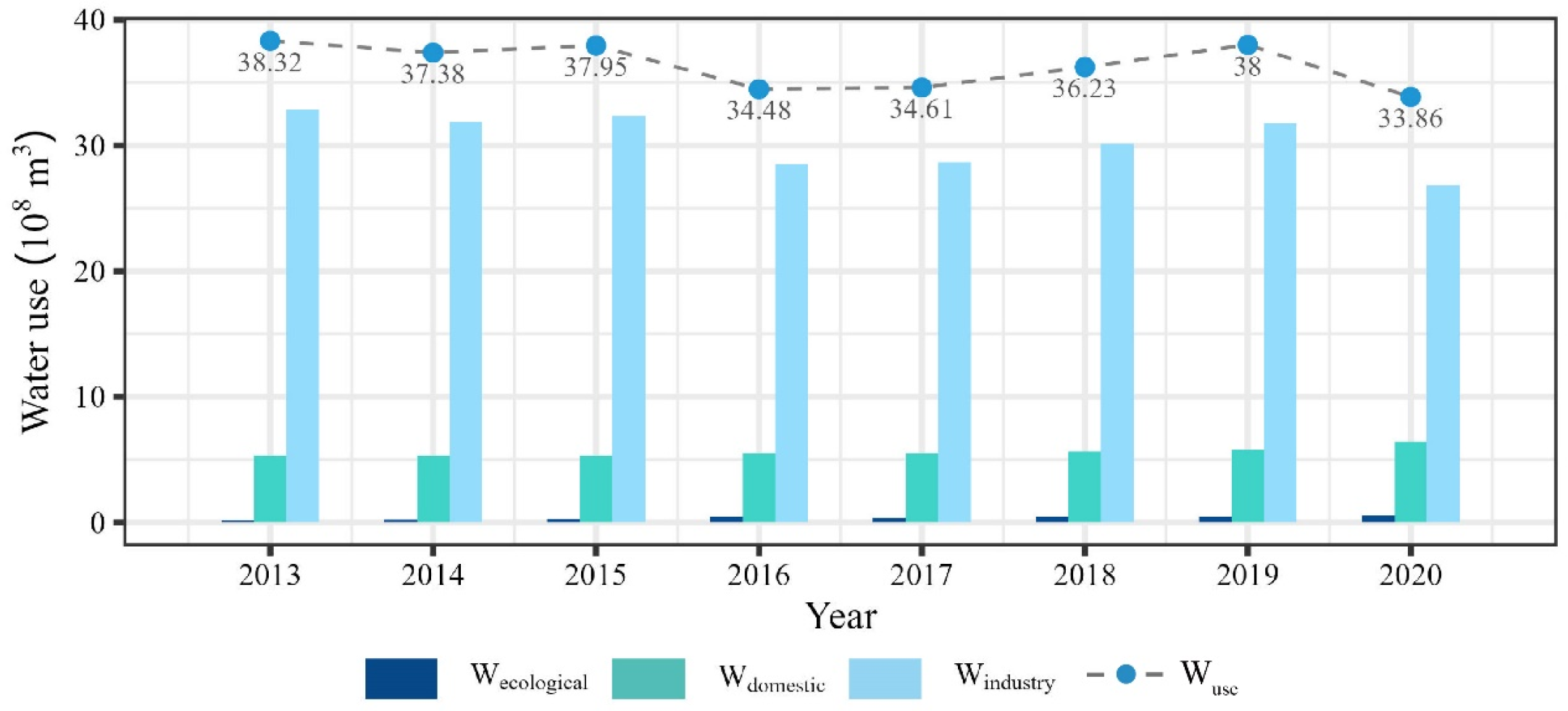
3.1. Analysis of Water Resources Carrying Capacity in Wuhan
3.2. Analysis of Water Environment Carrying Capacity in Wuhan
3.3. Comprehensive Assessment of CWRECC in Wuhan
3.4. Quantitative Measurement of the CWRECC in Wuhan
3.4.1. The Maximum Population That the CWRECC Could Sustain in Wuhan
3.4.2. The Maximum GDP That the CWRECC Could Sustain in Wuhan
4. Conclusions
- (1)
- The water resources carrying capacity analysis reveals that Wuhan maintained a substantial water surplus throughout the study period, with annual Wcapacity exceeding Wuse by 4.271 × 109 to 1.224 × 1010 m3. This surplus indicates sufficient water resources to support sustainable urban development in Wuhan. Notably, the Wcapacity/Wuse ratio peaked at 4.61 in 2020, while maintaining a minimum ratio of 2.11 in 2013, demonstrating consistent water resource adequacy.
- (2)
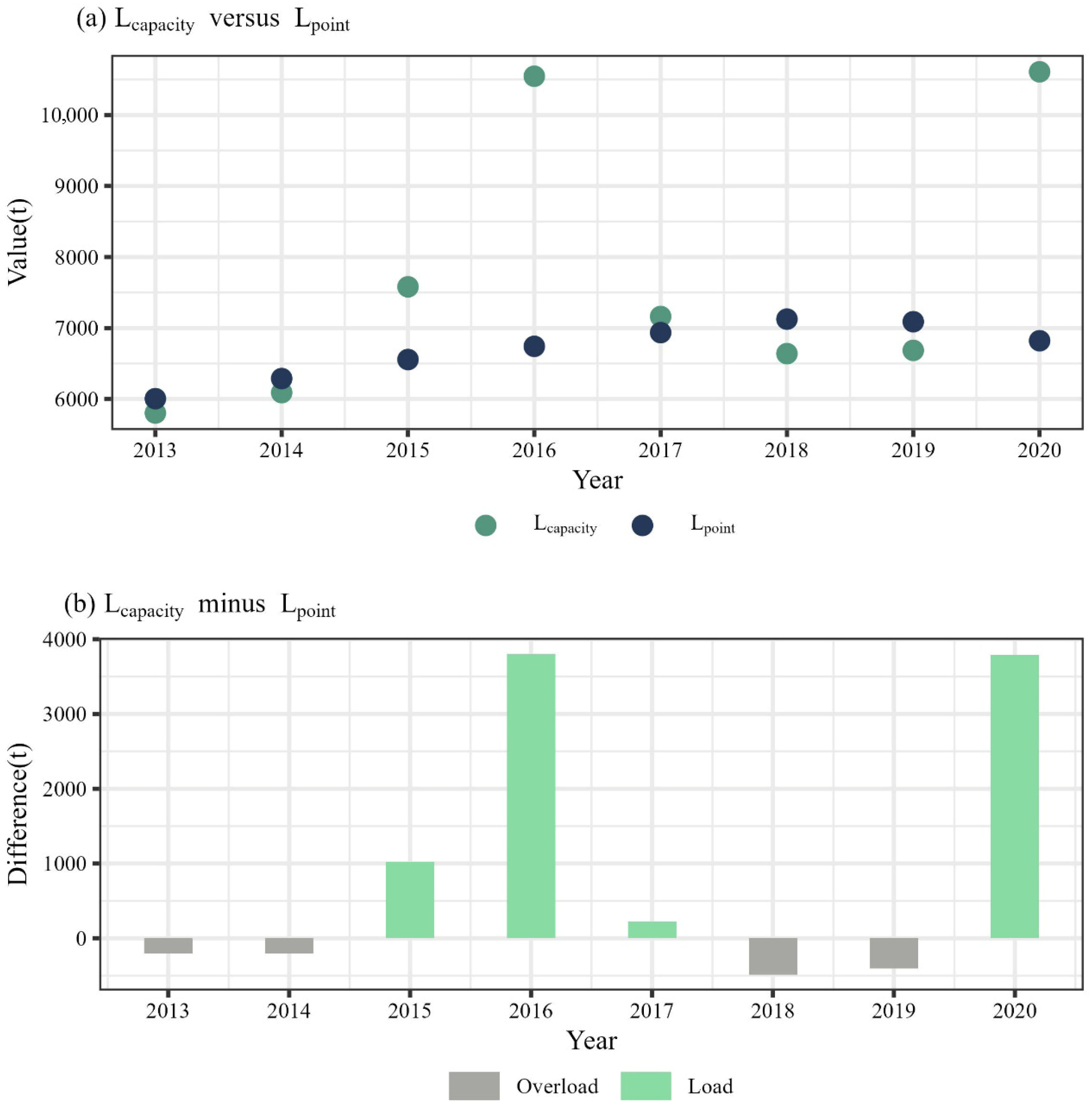
- The water environment carrying capacity analysis reveals that Wuhan maintained sustainable water quality in 2015–2017, effectively accommodating pollutants from production and the daily activities of residents. However, Lpoint exceeded Lcapacity in 2013, 2014, 2018, and 2019 by 202, 198, 486, and 404 tons, respectively, representing 3.48–7.32% of Lcapacity. These findings highlight limitations in Wuhan’s current capabilities for natural degradation and artificial wastewater treatment in addressing water pollution.
- (3)
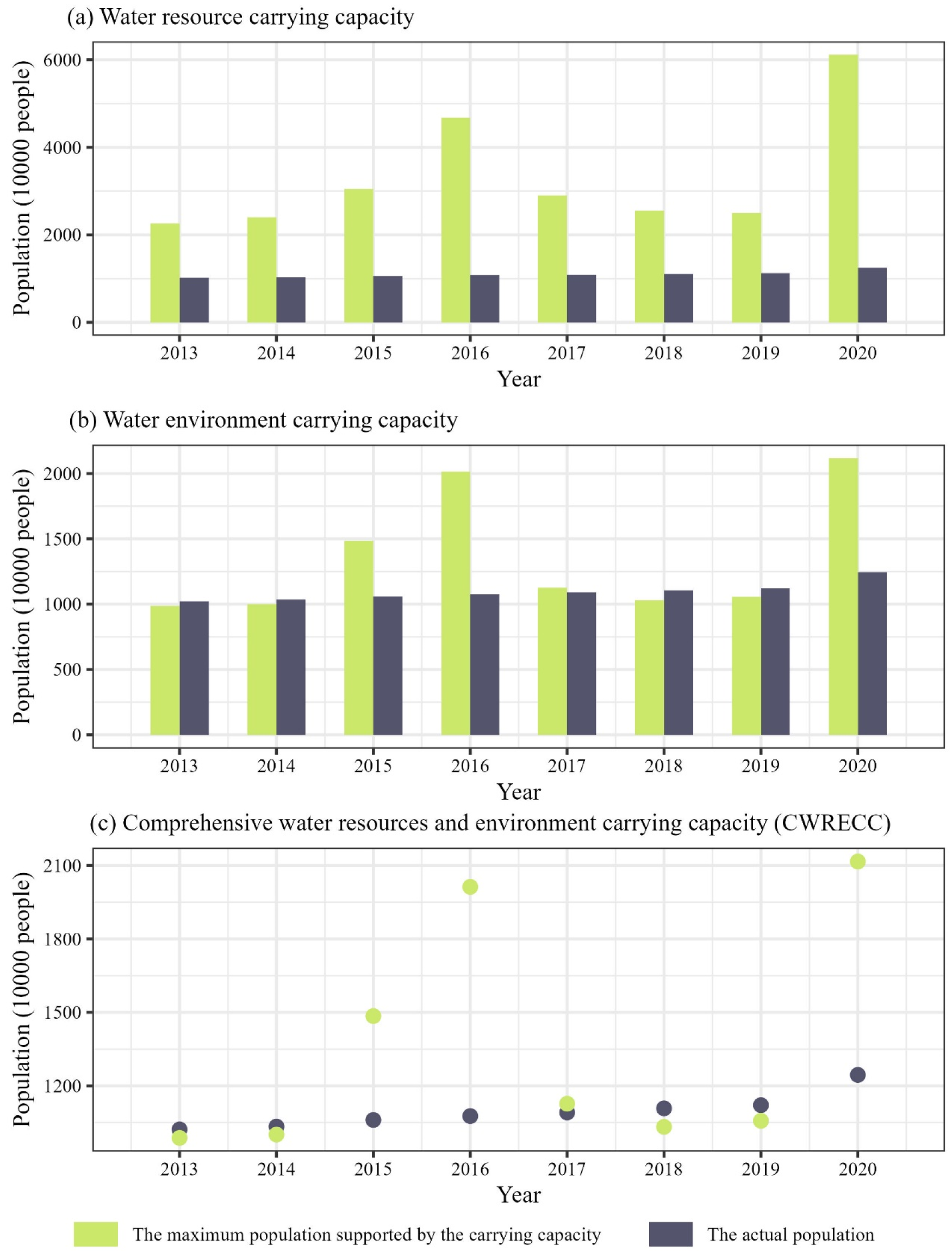
- The CWRECC assessment reveals that Wuhan’s integrated index I peaked at 0.56 and 0.57 in 2016 and 2020, respectively, indicating more sustainable carrying capacity conditions. Conversely, the index reached its lowest values of 0.24 in both 2018 and 2019, primarily due to reduced precipitation that negatively impacted local water resources. This hydrological deficit impaired the urban water cycle, resulting in inadequate dilution and reduction of pollutants.
- (4)
- The quantitative CWRECC assessment demonstrates that the water environment carrying capacity frequently serves as the limiting factor due to persistent pollution challenges. From an integrated water quantity-quality perspective, Wuhan maintained sustainable development in 2015, 2016, 2017, and 2020, with CWRECC-supported population and GDP exceeding actual values. However, overload conditions occurred in 2013, 2014, and 2018–2019, when actual population (10.22, 10.34, 11.08, and 11.21 million) and GDP (874.8, 1002.6, 1492.9, and 1622.3 billion yuan) surpassed CWRECC thresholds (population: 9.88, 10.01, 10.33, and 10.57 million; GDP: 849.5, 976.5, 1402.9, and 1538.9 billion yuan). These findings indicate periodic CWRECC overload during 2013–2014 and 2018–2019.
- (5)
- In urban areas, the interplay among “Human”, “Water”, and “City” involves multiple elements that influence each other. The relationships involved are mostly not unidirectional feedback but rather complex, interrelated, and interactive feedback loops. The study of water resources carrying capacity pursues the sustainable development of “Human”, “Water”, and “City”, and it is a complex, interdisciplinary, and highly practical research field. Previous research generally relied on indicator system methods or simple mathematical equations to evaluate the water resources carrying capacity. For instance, Wang et al. [60] used the entropy method and a synergistic theoretical model to assess water resources carrying capacity using multiple indicators. The results show that the comprehensive evaluation indicator (CEI) of Wuhan exceeded 2.0 in 2016. Yang et al. [61] employed the variable fuzzy evaluation method with seven relative evaluation indices to assess water resource carrying capacity. For Wuhan in 2020, the result was graded as level 3 as level 3. Wei et al. [62] applied 22 indicators to establish the vigor-pressure-organization-state-resilience-management (VPOSRM) evaluation index system and utilized a projection pursuit model optimized by a quantum genetic algorithm to calculate comprehensive evaluation indicators. The results demonstrated that Wuhan’s water environmental carrying capacity improved from grade IV (unhealthy) to grade III (healthy). Through the above methods, only relative scores or rankings are generated to assess the water resources carrying capacity. On the one hand, the objectivity of the indicator selection and evaluation criteria needs to be enhanced. On the other hand, the mutual feedback relationships between influencing factors are not considered, so the quantitative value of the carrying capacity (such as sustainable population or economic scale) cannot be accurately obtained. Departing from this, our study investigates the precise threshold in the city by considering the complex interplay among “Human”, “Water”, and “City”. Moreover, unlike the traditional single-perspective analysis, this study integrates both water quantity and quality aspects based on the “Cannikin Law” principle to develop a comprehensive CWRECC measurement model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Year | Wsurface (108 m3) | Wground (108 m3) | Wsource (108 m3) |
|---|---|---|---|
| 2013 | 36.25 | 10.31 | 39.93 |
| 2014 | 38.07 | 10.84 | 41.23 |
| 2015 | 58.85 | 10.86 | 62.03 |
| 2016 | 95.55 | 13.31 | 98.73 |
| 2017 | 41.22 | 10.97 | 44.18 |
| 2018 | 31.75 | 10.54 | 34.96 |
| 2019 | 30.34 | 9.73 | 33.75 |
| 2020 | 95.37 | 11.67 | 97.48 |
| Year | Wlocal (108 m3) | Wtransit (108 m3) | Wreuse (108 m3) | Wcapacity (108 m3) |
|---|---|---|---|---|
| 2013 | 38.15 | 35.90 | 6.97 | 81.03 |
| 2014 | 40.07 | 35.90 | 7.31 | 83.28 |
| 2015 | 59.82 | 35.90 | 7.79 | 103.51 |
| 2016 | 95.56 | 35.90 | 8.04 | 139.51 |
| 2017 | 43.11 | 35.90 | 8.32 | 87.33 |
| 2018 | 33.96 | 37.32 | 8.59 | 79.87 |
| 2019 | 32.33 | 40.26 | 8.42 | 81.00 |
| 2020 | 94.80 | 53.17 | 8.27 | 156.24 |
| Year | Windustry (108 m3) | Wdomestic (108 m3) | Wecological (108 m3) | Wuse (108 m3) |
|---|---|---|---|---|
| 2013 | 32.82 | 5.33 | 0.18 | 38.32 |
| 2014 | 31.86 | 5.31 | 0.21 | 37.38 |
| 2015 | 32.35 | 5.34 | 0.25 | 37.95 |
| 2016 | 28.56 | 5.51 | 0.41 | 34.48 |
| 2017 | 28.66 | 5.56 | 0.39 | 34.61 |
| 2018 | 30.12 | 5.67 | 0.44 | 36.23 |
| 2019 | 31.75 | 5.74 | 0.51 | 38.00 |
| 2020 | 26.89 | 6.41 | 0.56 | 33.86 |
References
- Bao, C.; Fang, C. Water Resources Flows Related to Urbanization in China: Challenges and Perspectives for Water Management and Urban Development. Water Resour. Manag. 2012, 26, 531–552. [Google Scholar] [CrossRef]
- Yu, H.; Song, Y.; Chang, X.; Gao, H.; Peng, J. A Scheme for a Sustainable Urban Water Environmental System During the Urbanization Process in China. Engineering 2018, 4, 190–193. [Google Scholar] [CrossRef]
- Chen, M.; Liu, W.; Tao, X. Evolution and Assessment on China’s Urbanization 1960–2010: Under-Urbanization or over-Urbanization? Habitat Int. 2013, 38, 25–33. [Google Scholar] [CrossRef]
- Liang, L.; Chen, M.; Lu, D. Revisiting the Relationship Between Urbanization and Economic Development in China Since the Reform and Opening-Up. Chin. Geogr. Sci. 2022, 32, 1–15. [Google Scholar] [CrossRef]
- National Bureau of Statistics of China. China Statistical Yearbook 2021; China Statistics Press: Beijing, China, 2021. (In Chinese) [Google Scholar]
- Hale, R.L.; Armstrong, A.; Baker, M.A.; Bedingfield, S.; Betts, D.; Buahin, C.; Buchert, M.; Crowl, T.; Dupont, R.R.; Ehleringer, J.R.; et al. iSAW: Integrating Structure, Actors, and Water to Study Socio-Hydro-Ecological Systems. Earth’s Future 2015, 3, 110–132. [Google Scholar] [CrossRef]
- Liu, J.; Dietz, T.; Carpenter, S.R.; Alberti, M.; Folke, C.; Moran, E.; Pell, A.N.; Deadman, P.; Kratz, T.; Lubchenco, J.; et al. Complexity of Coupled Human and Natural Systems. Science 2007, 317, 1513–1516. [Google Scholar] [CrossRef]
- Chen, X.; Li, F.; Li, X.; Hu, Y.; Hu, P. Evaluating and Mapping Water Supply and Demand for Sustainable Urban Ecosystem Management in Shenzhen, China. J. Clean. Prod. 2020, 251, 119754. [Google Scholar] [CrossRef]
- Wang, Y. Urban Land and Sustainable Resource Use: Unpacking the Countervailing Effects of Urbanization on Water Use in China, 1990–2014. Land Use Policy 2020, 90, 104307. [Google Scholar] [CrossRef]
- Miller, J.D.; Hutchins, M. The Impacts of Urbanisation and Climate Change on Urban Flooding and Urban Water Quality: A Review of the Evidence Concerning the United Kingdom. J. Hydrol. Reg. Stud. 2017, 12, 345–362. [Google Scholar] [CrossRef]
- Han, D.; Currell, M.J.; Cao, G. Deep Challenges for China’s War on Water Pollution. Environ. Pollut. 2016, 218, 1222–1233. [Google Scholar] [CrossRef]
- Bu, J.; Li, C.; Wang, X.; Zhang, Y.; Yang, Z. Assessment and Prediction of the Water Ecological Carrying Capacity in Changzhou City, China. J. Clean. Prod. 2020, 277, 123988. [Google Scholar] [CrossRef]
- Zhou, X.-Y.; Zheng, B.; Khu, S.-T. Simulation Platform of Human-Environment Systems for Water Environment Carrying Capacity Research. J. Clean. Prod. 2020, 250, 119577. [Google Scholar] [CrossRef]
- Liao, X.; Ren, Y.; Shen, L.; Shu, T.; He, H.; Wang, J. A “Carrier-Load” Perspective Method for Investigating Regional Water Resource Carrying Capacity. J. Clean. Prod. 2020, 269, 122043. [Google Scholar] [CrossRef]
- Wei, Y.; Huang, C.; Lam, P.T.I.; Yuan, Z. Sustainable Urban Development: A Review on Urban Carrying Capacity Assessment. Habitat Int. 2015, 46, 64–71. [Google Scholar] [CrossRef]
- Zhu, M.; Shen, L.; Tam, V.W.Y.; Liu, Z.; Shu, T.; Luo, W. A Load-Carrier Perspective Examination on the Change of Ecological Environment Carrying Capacity during Urbanization Process in China. Sci. Total Environ. 2020, 714, 136843. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Wang, Y.; Ma, X.; Wang, Y.; Yang, G.; Zhu, L. Evaluation of Resources and Environmental Carrying Capacity of 36 Large Cities in China Based on a Support-Pressure Coupling Mechanism. Sci. Total Environ. 2019, 688, 838–854. [Google Scholar] [CrossRef]
- UNESCO; FAO. Carrying Capacity Assessment: A Resource Accounting Methodology for Assessing the Sustainability of National Economies in the Context of Population, Resources, Environment and Development; UNESCO; FAO: Rome, Italy, 1985. [Google Scholar]
- Shi, Y.; Qu, Y. The Carrying Capacity of Water Resources and Its Reasonable Use of Urumqi River; Science Press: Beijing, China, 1992. (In Chinese) [Google Scholar]
- Liu, H.; Xia, J.; Zou, L.; Huo, R. Comprehensive Quantitative Evaluation of the Water Resource Carrying Capacity in Wuhan City Based on the “Human–Water–City” Framework: Past, Present and Future. J. Clean. Prod. 2022, 366, 132847. [Google Scholar] [CrossRef]
- Gong, L.; Jin, C. Fuzzy Comprehensive Evaluation for Carrying Capacity of Regional Water Resources. Water Resour. Manag. 2009, 23, 2505–2513. [Google Scholar] [CrossRef]
- Cui, Y.; Feng, P.; Jin, J.; Liu, L. Water Resources Carrying Capacity Evaluation and Diagnosis Based on Set Pair Analysis and Improved the Entropy Weight Method. Entropy 2018, 20, 359. [Google Scholar] [CrossRef]
- Ren, L.; Gao, J.; Song, S.; Li, Z.; Ni, J. Evaluation of Water Resources Carrying Capacity in Guiyang City. Water 2021, 13, 2155. [Google Scholar] [CrossRef]
- Wu, L.; Su, X.; Ma, X.; Kang, Y.; Jiang, Y. Integrated Modeling Framework for Evaluating and Predicting the Water Resources Carrying Capacity in a Continental River Basin of Northwest China. J. Clean. Prod. 2018, 204, 366–379. [Google Scholar] [CrossRef]
- Hu, A.; Li, Q. A Pressure-State-Response-Support Framework for Assessing Regional Water Environmental Carrying Status. Front. Environ. Sci. 2022, 10, 1023180. [Google Scholar] [CrossRef]
- Wang, G.; Xiao, C.; Qi, Z.; Meng, F.; Liang, X. Development Tendency Analysis for the Water Resource Carrying Capacity Based on System Dynamics Model and the Improved Fuzzy Comprehensive Evaluation Method in the Changchun City, China. Ecol. Indic. 2021, 122, 107232. [Google Scholar] [CrossRef]
- Yang, J.; Lei, K.; Khu, S.; Meng, W. Assessment of Water Resources Carrying Capacity for Sustainable Development Based on a System Dynamics Model: A Case Study of Tieling City, China. Water Resour. Manag. 2015, 29, 885–899. [Google Scholar] [CrossRef]
- Sun, S.; Fang, C.; Lv, J. Spatial Inequality of Water Footprint in China: A Detailed Decomposition of Inequality from Water Use Types and Drivers. J. Hydrol. 2017, 553, 398–407. [Google Scholar] [CrossRef]
- Jia, Z.; Cai, Y.; Chen, Y.; Zeng, W. Regionalization of Water Environmental Carrying Capacity for Supporting the Sustainable Water Resources Management and Development in China. Resour. Conserv. Recycl. 2018, 134, 282–293. [Google Scholar] [CrossRef]
- Hu, G.; Zeng, W.; Yao, R.; Xie, Y.; Liang, S. An Integrated Assessment System for the Carrying Capacity of the Water Environment Based on System Dynamics. J. Environ. Manag. 2021, 295, 113045. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Engel, B. Water Environment Carrying Capacity in Bosten Lake Basin. J. Clean. Prod. 2018, 199, 574–583. [Google Scholar] [CrossRef]
- Wei, S.; Yang, H.; Song, J.; Abbaspour, K.C.; Xu, Z. System Dynamics Simulation Model for Assessing Socio-Economic Impacts of Different Levels of Environmental Flow Allocation in the Weihe River Basin, China. Eur. J. Oper. Res. 2012, 221, 248–262. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, H.; Mu, H.; Luo, J.; Bao, X.; Bian, J.; Delgado Martín, J. Risk Assessment of Water Resources and Environmental Carrying Capacity in Yinchuan City. Hum. Ecol. Risk Assess. An. Int. J. 2019, 25, 120–131. [Google Scholar] [CrossRef]
- Zhou, F.; Zhang, W.; Jiang, A.; Peng, H.; Li, L.; Deng, L.; Sun, Y.; Wang, H. Spatial-Temporal Variation Characteristics and Coupling Coordination of the “Water Resources—Water Environment—Water Ecology” Carrying Capacity in the Three Gorges Reservoir Area. Ecol. Indic. 2023, 154, 110874. [Google Scholar] [CrossRef]
- Zhou, X.-Y.; Zheng, B.; Khu, S.-T. Validation of the Hypothesis on Carrying Capacity Limits Using the Water Environment Carrying Capacity. Sci. Total Environ. 2019, 665, 774–784. [Google Scholar] [CrossRef]
- Deng, R.; Chu, Z. Path of Wuhan City Implementing Strategy of City of Strong Talent Pool in 14th Five-Year Plan Period from Perspective of Push and Pull Theory. J. Jianghan Univ. (Soc. Sci. Ed.) 2023, 40, 93. (In Chinese) [Google Scholar] [CrossRef]
- Li, J.; Wen, Y. Study on coordinate development between population urbanization and land urbanization in Wuhan. J. Cent. China Norm. Univ. 2018, 52, 108–114. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Zhang, F.; Wang, W.; Xiao, R. Effects of Rapid Urbanization on Ecological Functional Vulnerability of the Land System in Wuhan, China: A Flow and Stock Perspective. J. Clean. Prod. 2020, 248, 119284. [Google Scholar] [CrossRef]
- Wuhan Municipal Bureau of Statistics. Wuhan Statistical Yearbook; Wuhan Municipal Bureau of Statistics: Wuhan, China, 2022. (In Chinese) [Google Scholar]
- Song, F.; Yang, X.; Wu, F. Catastrophe Progression Method Based on M-K Test and Correlation Analysis for Assessing Water Resources Carrying Capacity in Hubei Province. J. Water Clim. Chang. 2018, 11, 556–567. [Google Scholar] [CrossRef]
- Wen, C.; Zhan, Q.; Zhan, D.; Zhao, H.; Yang, C. Spatiotemporal Evolution of Lakes under Rapid Urbanization: A Case Study in Wuhan, China. Water 2021, 13, 1171. [Google Scholar] [CrossRef]
- Dey, J.; Vijay, R. Geospatial Assessment of Seasonal Water Quality of Malad Creek, Mumbai, India: An Impact of Sewage Discharge. Ind. J. GEO-Mar. Sci. 2022, 51, 811–821. [Google Scholar] [CrossRef]
- Ociepa, E.; Kisiel, A.; Lach, J. Protection of Surface Waters from the Discharge of Rain-Water Sewage from Sewage System. Soc. Ecol. Chem. Engn. 2009, 3, 115–120. [Google Scholar]
- Tian, J.; Ji, J.; Liu, Z.; Huang, J.; Xue, W. Effect Evaluation of Decentralized Domestic Sewage Treatment Facilities in Rural Areas—A Case Study of Nantong City, China. Water Sci. Technol. 2023, 88, 711–722. [Google Scholar] [CrossRef]
- Dams, J.; Dujardin, J.; Reggers, R.; Bashir, I.; Canters, F.; Batelaan, O. Mapping Impervious Surface Change from Remote Sensing for Hydrological Modeling. J. Hydrol. 2013, 485, 84–95. [Google Scholar] [CrossRef]
- Wuhan Municipal Bureau of Statistics. Wuhan Statistical Yearbook 2013–2020; Wuhan Municipal Bureau of Statistics: Wuhan, China, 2021. (In Chinese) [Google Scholar]
- Wuhan Municipal Water Authority. Water Resources Bulletin of Wuhan City 2013–2020; Wuhan Municipal Water Authority: Wuhan, China, 2021. (In Chinese) [Google Scholar]
- Hubei Provincial Department of Water Resources. Water Resources Bulletin of Hubei Province 2013–2020; Hubei Provincial Department of Water Resources: Wuhan, China, 2021. (In Chinese) [Google Scholar]
- Wuhan Municipal Ecology and Environment Bureau. Environmental Quality Bulletin of Wuhan City 2013–2020; Wuhan Municipal Ecology and Environment Bureau: Wuhan, China, 2021. (In Chinese) [Google Scholar]
- Johnes, P.J. Evaluation and Management of the Impact of Land Use Change on the Nitrogen and Phosphorus Load Delivered to Surface Waters: The Export Coefficient Modelling Approach. J. Hydrol. 1996, 183, 323–349. [Google Scholar] [CrossRef]
- Xia, B.; Li, S.; Mei, Z.; Shen, W.; Mi, M.; Qiang, Z.; Zhang, L. Identifying Critical Riparian Zones for Eco-Environmental Management of the Yangtze River through Pollution Mapping. J. Environ. Manag. 2025, 376, 124555. [Google Scholar] [CrossRef]
- Xue, Y.; Kong, X.; Mao, Z.; Zhang, C.; Xue, B.; Shi, X.; Gu, X. Hydrological Variation Drives Changes in Food Web Structure and Ecosystem Function with Potential Hysteresis in a Large Temperate Shallow Lake. J. Hydrol. 2025, 650, 132463. [Google Scholar] [CrossRef]
- Breyer, B.; Zipper, S.; Qiu, J. Sociohydrological Impacts of Water Conservation Under Anthropogenic Drought in Austin, TX (USA). Water Resour. Res. 2018, 54, 3062–3080. [Google Scholar] [CrossRef]
- Xia, J.; Zhang, Y.; She, D.; Zhang, S.; Yang, J.; Lv, M.; Zhang, X.; Luo, A.; Wu, S.; Liu, Y. Urban Water System Theory and Its Model Development and Application. Sci. China Earth Sci. 2024, 67, 704–724. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, H. Interpretation of cannikin law in human resource management. J. Nanning Teach. Coll. 2009, 67, 11. [Google Scholar]
- Wei, F.; Zhang, X.; Xu, J.; Bing, J.; Pan, G. Simulation of Water Resource Allocation for Sustainable Urban Development: An Integrated Optimization Approach. J. Clean. Prod. 2020, 273, 122537. [Google Scholar] [CrossRef]
- GB3838-2002; Surface Water Environmental Quality Standards. Ministry of Ecology and Environment of the People’s Republic of China: Beijing, China, 2002. (In Chinese)
- GB_T 31962-2015; Water Quality Standards for Urban Sewage Discharge. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2015. (In Chinese)
- GB 18918-2002; Pollutant Discharge Standards for Urban Sewage Treatment Plants. Ministry of Ecology and Environment of the People’s Republic of China: Beijing, China, 2002. (In Chinese)
- Wang, Y.; Cheng, H.; Huang, L. Water Resources Carrying Capacity Evaluation of a Dense City Group: A Comprehensive Water Resources Carrying Capacity Evaluation Model of Wuhan Urban Agglomeration. Urban Water J. 2018, 15, 615–625. [Google Scholar] [CrossRef]
- Yang, J.; Yang, P.; Zhang, S.; Wang, W.; Cai, W.; Hu, S. Evaluation of Water Resource Carrying Capacity in the Middle Reaches of the Yangtze River Basin Using the Variable Fuzzy-Based Method. Environ. Sci. Pollut. Res. 2023, 30, 30572–30587. [Google Scholar] [CrossRef]
- Wei, X.; Wang, J.; Wu, S.; Xin, X.; Wang, Z.; Liu, W. Comprehensive Evaluation Model for Water Environment Carrying Capacity Based on VPOSRM Framework: A Case Study in Wuhan, China. Sustain. Cities Soc. 2019, 50, 101640. [Google Scholar] [CrossRef]





| No. | Expression | Explanation | Unit |
|---|---|---|---|
| 1 | Wcapacity | Total available water resources | 106 m3 |
| 2 | Wlocal | Local available water resources | 106 m3 |
| 3 | Wsurface | Surface water resources | 106 m3 |
| 4 | Wground | Groundwater resources | 106 m3 |
| 5 | Wsource | Total water resources | 106 m3 |
| 6 | Wtransit | Transit water resources | 106 m3 |
| 7 | Wreuse | Reclaimed wastewater | 106 m3 |
| 8 | Wuse | Total water use | 106 m3 |
| 9 | rw | Reuse rate | % |
| 10 | Windustry | Industrial water use | 106 m3 |
| 11 | Wdomestic | Domestic water use | 106 m3 |
| 12 | Wecological | Ecological water use | 106 m3 |
| 13 | Wprimary | Primary industrial water use | 106 m3 |
| 14 | Wsecondary | Secondary industrial water use | 106 m3 |
| 15 | Wtertiary | Tertiary industrial water use | 106 m3 |
| 16 | WCdomestic | Domestic water use for urban residents | 106 m3 |
| 17 | WRdomestic | Domestic water use for rural residents | 106 m3 |
| 18 | Q | Outflow rate from the city | m3/a |
| 19 | C | Concentration of pollutants in the outflow from the city | kg/m3 |
| 20 | t | Time | a |
| 21 | V | Total water resources of the city | m3 |
| 22 | Qi (i = 1, 2, …, n) | Flow rate of pollutants from various sources | m3/a |
| 23 | Ci (i = 1, 2, …, n) | Concentration of pollutants from various sources | kg/m3 |
| 24 | Qj (j = n + 1, n + 2, …, m) | Flow rate of pollutants from various pollution reduction measures | m3/a |
| 25 | Cj (j = n + 1, n + 2, …, m) | Concentration of pollutants from various pollution reduction measures | kg/m3 |
| 26 | K | Natural degradation coefficient | - |
| 27 | E | Water circulation period index | a |
| 28 | Lout | Total pollutant load | kg |
| 29 | Cs | Local water quality standard limit value for the river outlet section | kg/m3 |
| 30 | Lmax | Maximum limit of pollutant load in the outflow | kg |
| 31 | Lpoint | Pollutant load from residents | kg |
| 32 | Lsum | Pollutant load from all other sources and reduction measures excluding Lpoint | kg |
| 33 | Lcapacity | Allowable pollutant load from residents | kg |
| 34 | IW | Index of water resources carrying capacity | - |
| 35 | IL | Index of water environment carrying capacity | - |
| 36 | I | Integrated index of CWRECC | - |
| 37 | α | Weight | - |
| 38 | Pre | Precipitation | mm |
| 39 | T | Technological level | 108 yuan |
| 40 | GDPprimary | GDP of the primary industries | 108 yuan |
| 41 | GDPsecondary | GDP of the secondary, industries | 108 yuan |
| 42 | GDPtertiary | GDP of the tertiary industries | 108 yuan |
| 43 | WCper | Domestic water consumption per capita in urban areas | L/d |
| 44 | WRper | Domestic water consumption per capita in rural areas | L/d |
| 45 | PCt | Urban resident population | 104 people |
| 46 | PR | Rural resident population | 10,000 people |
| 47 | p | Total population | 10,000 people |
| 48 | c | Urbanization rate | % |
| 49 | Dpoint | Sewage discharge from residents | 104 t |
| 50 | DCdomestic | Domestic sewage discharge of urban residents | 104 t |
| 51 | pc | Coefficient of domestic sewage discharge for urban residents | - |
| 52 | Dsecondary | Industrial sewage discharge of the secondary industries | 104 t |
| 53 | Dtertiary | Industrial sewage discharge of the tertiary industries | 104 t |
| 54 | pi | Coefficient of industrial sewage discharge for the secondary and tertiary industries | - |
| 55 | sw | Sewage treatment rate | % |
| 56 | Cnsw | Pollutant concentration of the sewage discharge | mg/L |
| 57 | Lsw | Reduction load of sewage treatment | kg |
| 58 | Csw | Pollutant concentration after sewage treatment | mg/L |
| 59 | AB | Built-up area at the end of the year | km2 |
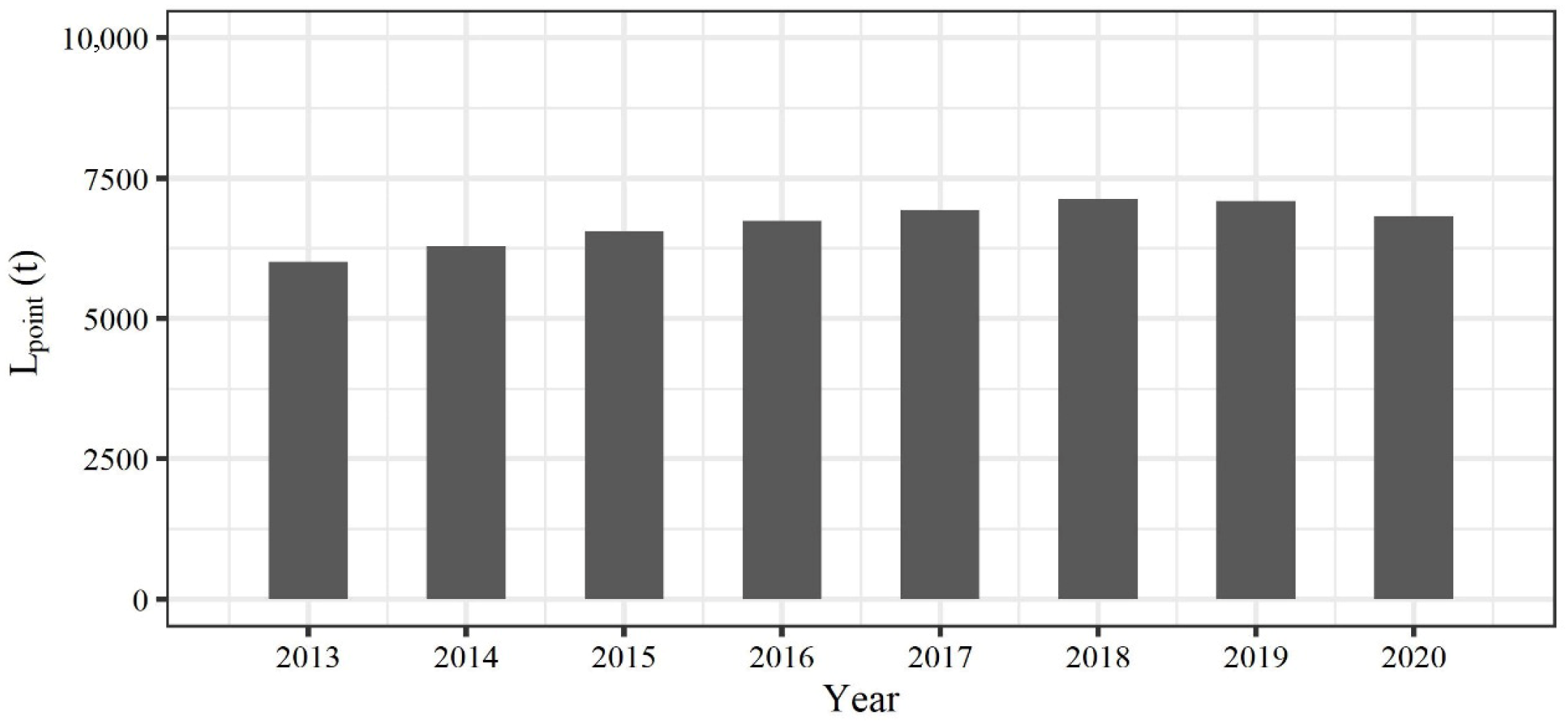
| Year | Lsum (t) | Lmax (t) | Lcapacity (t) |
|---|---|---|---|
| 2013 | 124,657 | 128,127 | 5802 |
| 2014 | 141,642 | 145,324 | 6090 |
| 2015 | 133,248 | 137,205 | 7580 |
| 2016 | 148,942 | 153,723 | 10,546 |
| 2017 | 144,809 | 149,391 | 7162 |
| 2018 | 130,482 | 135,079 | 6639 |
| 2019 | 138,733 | 143,446 | 6685 |
| 2020 | 174,942 | 179,858 | 10,609 |
| Year | IW | IL | I |
|---|---|---|---|
| 2013 | 0.53 | −0.03 | 0.25 |
| 2014 | 0.55 | −0.03 | 0.26 |
| 2015 | 0.63 | 0.14 | 0.38 |
| 2016 | 0.75 | 0.36 | 0.56 |
| 2017 | 0.60 | 0.03 | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Dong, Y.; Xia, J.; Wang, G.; Ma, J. Quantifying the Comprehensive Water Resources and Environment Carrying Capacity in Wuhan City Based on the “Human-Water-City” Framework. Water 2025, 17, 2489. https://doi.org/10.3390/w17162489
Liu H, Dong Y, Xia J, Wang G, Ma J. Quantifying the Comprehensive Water Resources and Environment Carrying Capacity in Wuhan City Based on the “Human-Water-City” Framework. Water. 2025; 17(16):2489. https://doi.org/10.3390/w17162489
Chicago/Turabian StyleLiu, Huiyuan, Yi Dong, Jun Xia, Guoqing Wang, and Jun Ma. 2025. "Quantifying the Comprehensive Water Resources and Environment Carrying Capacity in Wuhan City Based on the “Human-Water-City” Framework" Water 17, no. 16: 2489. https://doi.org/10.3390/w17162489
APA StyleLiu, H., Dong, Y., Xia, J., Wang, G., & Ma, J. (2025). Quantifying the Comprehensive Water Resources and Environment Carrying Capacity in Wuhan City Based on the “Human-Water-City” Framework. Water, 17(16), 2489. https://doi.org/10.3390/w17162489







