Abstract
Reliable estimates of aquifer properties are needed for groundwater resources management and for engineering applications. Pumping tests conducted in fractured aquifers using an open borehole may not produce a proper characterization of the aquifer properties leading to the failure of engineering solutions. In this work, we apply a radial flow model to reproduce the time drawdown curves recorded at an observation borehole instrumented with multi-level piezometers drilled in the Permo-Triassic sandstone, which is a complex fractured hydraulic unit. The radial flow model and the optimization code PEST are used to estimate the aquifer hydraulic parameter values. The model is then used to investigate the implications of replacing the multi-level piezometers with an open borehole. The results show that the open borehole does not only significantly alter the groundwater head and flow patterns around the borehole, but the analysis of the time drawdown curve obtained would produce estimates of aquifer properties that bear no relationship with the actual hydraulic properties of the aquifer. For engineering control studies, the pumping test must be carefully designed to account for the presence of fractures, and these must be represented in the analysis tools to ensure the correct characterization of the hydraulic system.
1. Introduction
Reliable estimates of aquifer properties are needed to inform a range of groundwater activities, including sustainable groundwater abstraction, management of aquifers, engineering applications and others. Urban construction activities, which can be affected by shallow groundwater, is an example where groundwater control may need to be put in place to allow the engineering activities in the short term and to prevent the long-term problem of groundwater flooding. For example, dewatering schemes, involving pumping water out of the aquifer are used to minimize the groundwater effects on structures and to create dry excavation pits at construction sites [1,2]. The design of these schemes is informed by detailed conceptual models of the groundwater system, which provide estimates of groundwater levels and flows, the hydraulic characteristics of the aquifer, especially spatial heterogeneity of transmissivity and storage, and recharge and discharge to and from the aquifer [3,4].
One method to acquire values of porosity and permeability to inform a conceptual groundwater model is by the laboratory analysis of core plugs taken from cored boreholes. However, these small-scale experiments yield results that are representative of the sample location only. Down-hole geophysical techniques, on the other hand, provide indications of the flow mechanism but do not yield precise quantitative data [5]. Other experiments, for example, the use of saline tracer tests allow the determination of the location of in-flowing and out-flowing fractures inside a borehole [6]. Pumping tests, when undertaken in conjunction with suitable measurements, can test the response of the aquifer over larger rock volumes. However, interpretation and analysis of pumping test data in complex, fractured aquifers is not straightforward and simple analytical solutions that assume aquifer homogeneity are not applicable [7,8,9,10]. Furthermore, understanding how pumped and observation boreholes interact with the hydrological system is key as open boreholes may act as a large fissure and disturb the groundwater regime [11]. The instrumentation of observation boreholes, therefore, with isolated piezometers installed along the depth of the borehole can provide key information that allow the construction of an accurate representation of the flow pattern across the hydrogeological system [12]. The challenge, however, is to interpret the test results while capitalizing on the large amount of field data collected at these piezometers.
Several methods are used to interpret pumping test data and can be divided into two methods to solve the radial flow equations: analytical or exact solutions and numerical methods or numerical approximations [13,14]. While several analytical methods have been developed to deal with complex pumped borehole and aquifer hydrogeological settings, e.g., the methods incorporated in the AQTESOLV software [15], these methods rely on a simplified conceptualization of the hydraulic system. These simplifications include the representation of the internal and external boundary conditions and the assumption of homogeneous hydraulic properties. Ref. [16] discusses state-of-the-art methods used for the interpretation of pumping test data obtained from fractured aquifers and based on analytical solutions and type curves. Numerical methods, even though they do not provide a continuous solution across the hydrogeological domain like analytical solutions, they account for more complex boundary conditions and vertical and horizontal heterogeneity [17]. Most importantly they allow the calculation of fluxes across the domain, which can inform the conceptual model.
In the United Kingdom, the Permo-Triassic sandstone aquifer is a major aquifer that provides important groundwater resources for large-scale public and industrial water supply, with the Sherwood Sandstone Group forming the most important aquifer [18]. Although often considered a largely homogeneous aquifer, the complex hydrogeological nature of the Permo-Triassic sandstone was recently highlighted by the work of [19] through the analysis of groundwater hydrographs recorded at boreholes drilled in the Penrith Sandstone and the St. Bees sandstone. Their analysis of aquifer property data showed extensive variation in porosity and permeability with depth. The Penrith Sandstone, for example, shows a complex layering of interbedded hard silicified materials comprising friable beds and coarse beds of sandstone. The impact of geological heterogeneity on the groundwater system within the sandstone aquifers had been previously underestimated, for example, the aeolian facies of the Penrith Sandstone have been hypothesized as homogeneous [19]. Averaging the permeability and groundwater flows vertically across the aquifer, therefore, is not always a valid assumption.
In 1978, a five-year program of investigation was initiated by the North West Water Authority in England to address the management options to protect the Permo-Triassic aquifer against saline intrusion and connate saline groundwater problems [20]. A range of techniques, including pumping tests, laboratory tests, packer testing, and piezometer tests, were employed to understand the groundwater dynamics of the system and to assess aquifer properties. A pumping test was carried out at Kenyon Junction, situated on the Sherwood Sandstone aquifer in north-west England, with an observation borehole instrumented with multi-level piezometers. The Kenyon Junction pumping test results demonstrate the complexity of the hydraulic system in the Sherwood Sandstone Group and how results obtained from open observation boreholes can be misleading.
Ref. [20] provide a permeability profile of the aquifer at the Kenyon Junction borehole using differential temperature, with distinct horizons representing fissured zones contributing to the flow in the borehole. Ref. [12] analyze the results of the Kenyon Junction pumping test using a numerical model consisting of two layers. The upper layer represents the water table, and the lower layer represents the average drawdown in the aquifer. The model is based on the approach detailed by [14], where they use an exponential mathematical equation to represent the delayed yield of water from the phreatic surface [21,22]. However, the use of the delayed yield approach is superseded by the work of [23] who demonstrates that the process of delayed response in a pumped homogeneous anisotropic unconfined aquifer can be reproduced by using constant values of specific storage and specific yield [24]. In addition, the model used by [14] falls short from using all the piezometer data and relies on averaging the permeability over the depth of the aquifer, yielding limited information on the vertical permeability profile.
Studies that use boreholes equipped with multi-level piezometers to explore groundwater flow movement and estimate aquifer characteristics include [25] who presented a methodology based on the use of a multi-level sampling well in conjunction with a series of short pumping test to create a hydraulic tomography of the aquifer. Ref. [26] developed a numerical model based on the Galerkin finite-element approach to solve axisymmetric flow problems involving pumping from multi-layered aquifers. Ref. [27] employ a hybrid genetic/Levenberg-Markardt algorithms alongside Neuman and Witherspoon model to estimate the hydraulic parameters of multiple alternating aquifers and aquitards in Tianjin, China. Ref. [28] analyzed pumping test results at multi-level piezometers for groundwater flow control using a cutoff wall in a large-scale excavation site in Tokyo, Japan. They applied an axisymmetric finite-element groundwater model to evaluate the hydraulic parameter values and develop an understanding of the correlation among the cutoff wall length, discharge and drawdown and highlight the effectiveness of using multi-aquifer pumping test to produce the aquifer hydraulic parameter values across the aquifer layers to allow groundwater flow control. Ref. [29] used the numerical model MODFLOW and multilayer analytical approaches (see [30]) to highlight how multi-depth pumping tests have the capability to estimate aquifer characteristics and resolve uncertainties for groundwater management and exploration, a practice that is not being used regularly by hydrogeologists.
The aim of this work is to explore the behavior of the sandstone aquifers by revisiting the pumping test conducted at Kenyon Junction site using techniques that exploit recent advances in numerical modeling. We illustrate how detailed piezometric data can be analyzed using complex numerical models to characterize the hydraulic properties of the aquifer at different depths. We use optimization tools to estimate the hydraulic parameter values, a task that is difficult to achieve considering the number of parameters involved [31]. This methodology may prove essential for the analysis of the hydrogeological results obtained from complex field experiments such as those produced by the new NERC/UKRI research facility on the Sherwood sandstone in Cheshire, called the Cheshire Observatory [32,33]. Finally, we apply the developed numerical model to demonstrate the importance of using multilevel piezometer boreholes to characterize complex hydrogeological systems. A theoretical scenario is considered where the observation borehole is assumed to be an open borehole and in connection with the different layers within the aquifer. We contrast the differences between data obtained from the open borehole and those obtained from the borehole with multi-piezometers to illustrate the errors resulting from this simplification when determining the aquifer properties and the consequent adverse impact this may have on conceptual understanding of the aquifer, for example, for construction dewatering in urban development projects.
2. Study Area and Conceptual Model
The pumping test was conducted at the Kenyon Junction in the Permo-Triassic Sandstone aquifer of the Lower Mersey Basin in northwest England (Figure 1). The Sherwood Sandstone Group, which reaches a thickness of 500 m locally, is a fine to medium-grained sandstone and forms the major aquifer in the area [20]. The intergranular permeability and fissure development make the potential of groundwater flow within the aquifer [12].
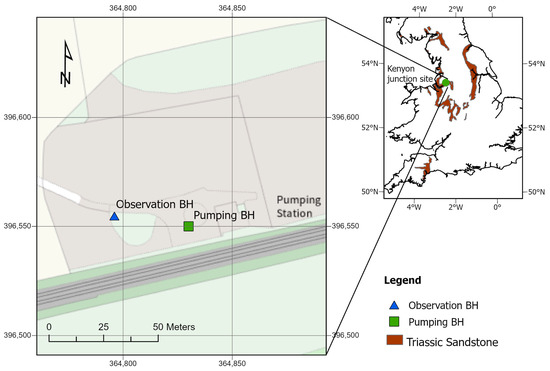
Figure 1.
Abstraction and observation boreholes at Kenyon Junction site in northwest England. ‘Contains OS data © Crown copyright and database rights 2025’.
The pumped and observation boreholes are 34.5 m apart [12]. The pumped borehole is drilled to a depth of approximately 91.5 m and has multiple sections with different diameters. The upper section is cased and just meets the rest water table as illustrated in Figure 2. The average diameter of the remaining sections of the pumped borehole is approximately 60 cm. The observation borehole, which is equipped with seven piezometers as shown in Figure 2 is 100 m deep. The piezometers are 25 mm in diameter and have short, screened sections of 1 m in contact with the aquifer [12]. The positions of these piezometers are shown in Figure 2. The upper piezometer is very close to the position of the rest water table and groundwater heads recorded at this piezometer are assumed to represent the water table elevation with time.
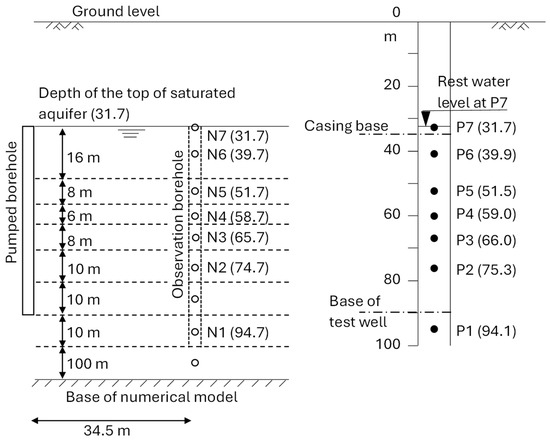
Figure 2.
Conceptual representation of the hydrogeological layered system and the corresponding numerical discretization.
The pumping test consists of a pumping phase lasting one day with an abstraction rate of 1619 m3/day followed by a recovery phase. The test results from the pumping phase are used in the analysis presented in this work.
The right illustration in Figure 2 shows the observation borehole drilled from ground surface down to 100 m together with the pumped well, the seven piezometers, and the rest water depths from the ground surface. The piezometers in this figure are labeled from P1, the deepest piezometer to P7, the shallowest one. The conceptual model of the hydrogeological system consists, therefore, of seven saturated horizons, the depths of which are determined in such a way that the piezometers occupy the middle of these horizons. One extra layer is added at the base to represent the part of the aquifer that is not in contact with either the pumped or the observation boreholes. The pumped borehole occupies the center of the aquifer in the model and is in contact with the upper six geological layers as shown in Figure 2.
The physical information available indicates that the pumped borehole partially penetrates the aquifer, and the solid casing is just below the rest water level. The pumped borehole can be assumed open to the full saturated thickness and the solid casing impact can be ignored. No internal boundaries restricting the movement of the groundwater are believed to exist, and the aquifer system is not receiving water from any adjacent aquifer. The outer boundary is set as a no flow boundary 10 km away from the center of the pumped borehole to minimize its impact on the simulated drawdown response. The aquifer is assumed to receive no recharge during the test duration and that there are no adjacent pumping affecting the test results. Initial runs include the radial symmetry assumption as no hydraulic property variations are recorded across the horizontal dimension of the aquifer. The model is first used, therefore, in a two-dimension vertical slice setting. The third dimension is included when the open borehole impact on groundwater flows is studied. Piezometers P1 to P7 are represented by Nodes N1 to N7 as shown in Figure 2 (Left illustration).
3. Materials and Methods
The pumping test results were previously published in the work of [12] and in the work of [11] and revisited here for analysis with more sophisticated numerical tools. However, we use the time drawdown data of the pumped phase of the pumping test only in our analysis. These field data show different starting piezometric levels of the curves recorded at the piezometers. The starting elevation of the curve at the uppermost piezometer is higher than the starting elevation of the curve at the lowermost piezometer indicating a downward pre-test regional groundwater flow. The impact of regional groundwater flow is removed from the time-groundwater level curves by subtracting the groundwater level values at time zero of each curve from the corresponding subsequent groundwater levels. This is deemed acceptable as the impact of pumping on groundwater flows and heads can be superimposed on the regional flows in the aquifer. The field data used in this work, which are converted into time drawdown data, are a modified version of those published originally by [11,12] due to this adjustment.
The numerical model employed to simulate the groundwater heads, and referred to as COOMPuTe (Cylindrical Object-Oriented Model for Pumping Test), is a radial flow model that solves the finite difference equation (Equation (1)) using a cylindrical grid [34]. In this model, the pumped borehole occupies the center of the numerical grid. Horizontally, the grid nodes are distributed along the radial directions with a resolution that decreases away from the center of the grid. Multiple layers of numerical nodes can be created to represent vertical heterogeneity. This produces a two-dimensional vertical slice model that is often used when hydrogeological radial symmetry is assumed within the aquifer. A three-dimensional representation of the hydrogeological system can be created by dividing the domain horizontally using multiple vertical slices at equal angular spacing. The grid nodes in this case are connected in the radial, circumferential, and vertical dimensions as per Equation (1):
where
is the hydraulic head [L] at a point at grid with coordinates
is the specific storage [L−1]
is a sink-source per unit volume term [T−1]
, , and are the hydraulic conductivity values [L T−1] along the coordinates, respectively.
In this application, the numerical model is built as a vertical slice with eight hydrogeological layers representing the saturated part of the aquifer as shown in the left-hand schematic of Figure 2. The numerical grids occupy the center of these hydrogeological layers; however, there is an additional numerical grid at the top of the uppermost layer that simulates the movement of the water table. The conductance values between the nodes representing the water table are calculated using the hydraulic parameter values of the layers they are located in. In total, nine numerical grids are used but piezometer locations coincide with seven of them only. The uppermost numerical grid represents the water table and sits initially at the top of the top hydrogeological layer (Layer 1). All other numerical layers occupy the center of the hydrogeological layer at the onset of pumping. The lowest hydrogeological layer (Layer 8) is added at the base of the model to represent the remaining part of the aquifer that may contribute to the pumped water.
The time drawdown data recorded at the seven piezometers within the observation borehole are used to calibrate the model and estimate the hydraulic parameter values of the eight hydrogeological layers. The calibration involves the adjustment of the values of 25 parameters. These are the horizontal and vertical hydraulic conductivity values as well as the specific storage values of the layers, plus the value of the specific yield used to set the storage coefficient value at the nodes representing the water to table. Due to this large number of parameters that need to be estimated, the parameter estimation code PEST [35], is used to optimize the solution. The objective function used for this optimization is the root mean square error between the observed and simulated drawdown values at the seven piezometers.
4. Results and Discussion
Given the likelihood of vertical variation in hydraulic parameters in the aquifer, while the model consists of eight layers, it is highly likely that some layers have the same hydraulic characteristics if they are not affected by processes leading to different hydraulic parameters, e.g., fracturing. To address this, the PEST software is applied repeatedly with increasing complexity of model setup. The first model setup (model M1) assumes that all the layers have the same hydraulic characteristics, which required the optimization of four hydraulic parameter values by PEST. The match between the observed and simulated drawdown curves highlights the layers with hydraulic parameter values that do not conform with the values of other layers. In the second and third PEST runs, the hydraulic parameter values of the upper layer (Model M2) and the fourth and eighth layers from top (Model M3) are included as separate variables and optimized. The sum of the squared residuals () used by PEST as the objective function improved with the increased model setup complexity. Table 1 shows the values of φ decreasing from a value of 102.4 in Model 1 to 10.46 in Model 3. While the match between the observed and simulated time drawdown curves was satisfactory using the optimized hydraulic parameter values for Model 3, it was decided to undertake a fourth run (Model 4) where the hydraulic parameter values of all layers are optimized by PEST. This run yielded a value of 2.59 with an almost perfect match between the observed and simulated time drawdown curves as shown in Figure 3.

Table 1.
Model setups and corresponding sum of squared residuals (φ) calculated by PEST.
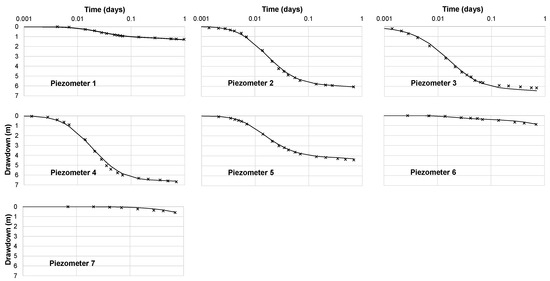
Figure 3.
Observed (dotted) versus simulated (continuous) time drawdown curves at the piezometers (Observed data after [11,12]).
Table 2 shows the hydraulic parameter values of all layers as optimized in Model 4. The specific yield value of the upper layer is only reported as the water table remains within this layer during the pumping duration. The low specific yield value estimated by PEST is of concern here as it does not represent the specific yield values usually used in sandstone aquifers. Ref. [12] indicate, however, that the regional aquifer response over a long time period indicated a specific yield of 10% to 15%, but pumping test analysis estimate much smaller storage coefficient values in the range of 0.0004 to 0.01.

Table 2.
Hydraulic parameter values of all layers optimized by PEST in Model 4.
Comparing the results in Table 1 to those reported in the literature (Table 7.5.2 in [18]) for the area shows that medium to coarse (2049 mD or 1.3 m/d) comparable with the more permeable layers 3, 4 and 6–8. The lower permeability layers (1, 2 and 5) are comparable with medium grain materials (629 mD or 0.4 m/d). This shows that the model does produce realistic values for the area. Ref. [12] reports the values of 1.2 m/d for horizontal hydraulic conductivity and 0.4 m/d for vertical hydraulic conductivity for the lower layer representing responses in P2–5. This is using a two-layer model and ensuring that the results from the lower layer fit between the drawdown plots for P4 and P5. Whilst not a direct comparison, the average from the work reported here is close to these values when averaging the same interval analyzed by [12] ( average of 1.3 m/d and average of 0.4 m/d; layers 2 to 6; equivalent to P2–P5). However, the approach reported in [12] does not allow the vertical variation in hydraulic conductivity to be determined.
Figure 3 shows the simulated time drawdown curves compared to the observed ones at the seven piezometers plotted on a horizontal logarithmic time scale and a vertical arithmetic scale. The observed time drawdown curves follow the S-shape curves typically observed in unconfined aquifers and related to whether the pumped water is released from borehole storage, the part of the aquifer between the pumped borehole and observation borehole, the elastic (specific) storage, or the specific yield of the aquifer [36]. The simulated time drawdown curves reproduce this behavior and match the observed curves almost perfectly. The only main discrepancy that can be identified is the match at piezometers P3 and P4. The observed drawdown values recorded at piezometer P4 are higher than those recorded at the lower P3 piezometer, a behavior that could not be reproduced by the model even with the manual tuning of the hydraulic parameter values. The simulated drawdown values at P3 are always greater or very close to those simulated at P4.
Figure 4 illustrates the differences in the groundwater flow pattern within each of the eight layers in the model by plotting the contour lines of the drawdown values and the flow vectors calculated at the end of the pumping phase (one day). To produce the plots in Figure 4, the model is run in three-dimensional mode by introducing vertical grids that divide the circumferential dimension into eight equal portions. While the drawdown values at the nodes inside the pumped borehole are the same, the volumes of water released from the layers into the pumped borehole are different due to the heterogeneity of the hydraulic system. The flows withdrawn from the layers and calculated at the end of the pumping duration () are also shown in Figure 4 next to the central grid node representing the abstraction borehole. Comparing the amount of water withdrawn from Layers 4, 5 and 6 for example, shows the contrast between the contribution of these layers to the pumped groundwater where Layers 4 and 6 contribute 592 and 633 m3/day, Layer 5 contributes 67.4 m3/day only. This shows that altering the hydraulic gradient in a complex hydrogeological system through pumping or creating other artificial discharge features such as earth excavations, needs to be studied carefully and the over-simplification of the hydraulic system can lead to erroneous conclusions.
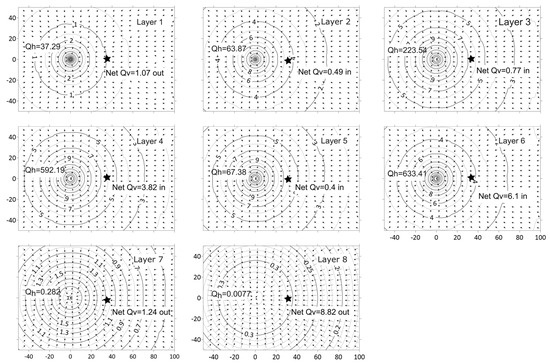
Figure 4.
Drawdown contours and flow vectors calculated at the end of the pumping duration. Values in boxes show the volume of groundwater entering the pumped borehole or entering/leaving the observation borehole in m3/day. Asterisk represents the location of the observation borehole.
The instrumentation of the borehole at Kenyon Junction with multiple piezometers to record groundwater head response to pumping at an adjacent borehole offers the opportunity to demonstrate the complexity of Permo-Triassic sandstone as an aquifer and which is usually over-simplified as a homogeneous porous medium. Using an open observation borehole is a common practice used when conducting pumping tests. However, data collected at an open observation borehole drilled in a complex layered hydraulic system like the one discussed in this work can yield misleading results. To illustrate this, we use the three-dimensional model parametrized with the hydraulic parameter values optimized for model M4 (Table 2). To represent the observed borehole as an open borehole, we connect the nodes N1 to N7 in Figure 2 with a high vertical hydraulic conductivity value, which forces the hydraulic heads simulated at these nodes to be the same during the simulation.
Figure 5 shows the time drawdown curve simulated at Nodes N1 to N7, assuming that the borehole is open and that water can move vertically freely between nodes N1 to N7, compared to those recorded on site at Piezometers P1 to P7. The time drawdown curves simulated at the open borehole are almost identical at each model layer and if these were used to estimate the hydraulic conductivity and the storage coefficient values of the aquifer, we would have characterized the aquifer incorrectly. Figure 5 also shows the time drawdown curves calculated at two sets of grid nodes equivalent to Nodes N1 to N7. Both sets are located at the same distance from the pumped borehole, but the first set is opposite to the open borehole across the pumped borehole and referred to as Set A. The second set is perpendicular to the line connecting Set A to the open borehole and is referred to as Set B. Noting that the nodes of these two sets are not connected vertically as Nodes N1 to N7, the time drawdown curves simulated at these sets do not show a perfect match with the observed curves indicating that the drilling of an open borehole in this heterogeneous layered system affects the circumferential groundwater flow pattern.
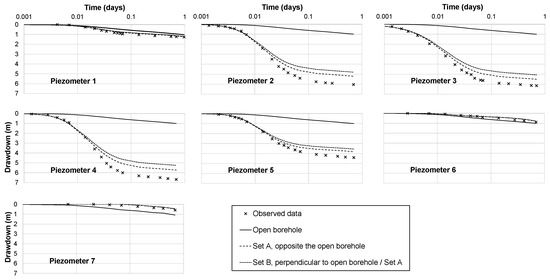
Figure 5.
Observed versus simulated time drawdown curves. Solid line (Open borehole), dashed line (Set A), and dotted lines (Set B) (Observed data after [11,12]).
Figure 6 illustrates the impact of the open observation borehole on the contour lines of the drawdown values and the flow vectors simulated at the end of the pumping duration. The open observation borehole acts as a conduit that allows the movement of groundwater flow across the layers. The net vertical inflows to or outflows from the layers () are shown next to the open observation borehole (shown as an asterisk) in Figure 6. For this case study, the drilling of an open borehole through the layers makes the groundwater discharge from the borehole at Layer 1 (the upper most layer) and Layer 8 (the layer at the base) and enter all other layers under the influence of pumping at the abstraction borehole. This is also illustrated with the flow vectors converging to the open borehole at Layers 1 and 8 and diverging out the open borehole at all other layers.
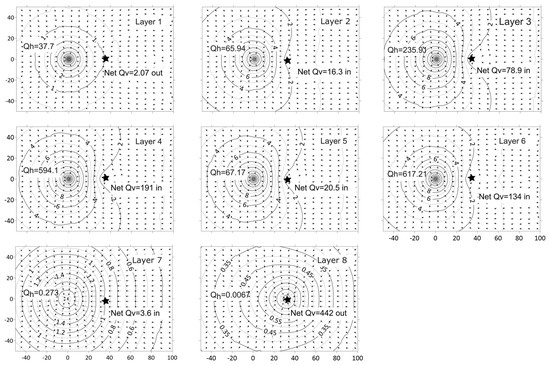
Figure 6.
Drawdown contours and flow vectors calculated at the end of the pumping duration with the observation borehole assumed to be open and connecting the layers in contact with. Values in boxes show the volume of groundwater entering the pumped borehole or entering/leaving the observation borehole in m3/day. Asterisk represents the location of the observation borehole.
5. Conclusions
In this paper we use a radial flow numerical model to simulate the time drawdown curves recorded at a borehole instrumented with seven piezometers. The numerical model has successfully produced the observed time drawdown curves aided with a mathematical tool PEST that is used to optimize the values of the hydraulic parameter values of the hydrological layers. The pumping test results demonstrate that the Permo-Triassic Sherwood Sandstone is a complex heterogeneous layered system with vertical hydraulic gradient observed across the aquifer and groundwater flow through higher permeability horizons, where flow is likely concentrated in fissures.
The availability of an observation borehole equipped with multi-piezometers at the Kenyon Junction site not only provided the opportunity to employ sophisticated numerical tools to explore the heterogeneity of the Permo-Triassic sandstone but also highlighted the importance of designing the pumping test and instrumenting the observation boreholes correctly to reveal the complexity of the hydrogeological system. Here we demonstrate how an open borehole drilled in a complex fractured system produces field results that may not bear any relationship to the hydraulics of the aquifer and may produce misleading information required in engineering applications. We show that the time drawdown curve obtained from an open borehole is not representative of any of the piezometer observed data and that the open borehole acts as a groundwater conduit and impact the groundwater heads in its adjacent area of the aquifer.
In this work, the aquifer is represented as multiple layers of certain thickness and with different transmissivity values. This is still far from reality where a single fissure may allow the passage of high volumes of groundwater while the rest materials of the layer may not be as transmissive. This approach adequately highlights the need to account for the complexity of the Permo-Triassic sandstone aquifer and not over-simplifying it as a homogeneous aquifer. However, more sophisticated approaches, for example, using stochastic means to represent the fractures in a simulation, may be required to fully cover the uncertainties related to fracture presence in a hydraulic system.
Finally, aquifer storage can be obtained from the pumping test analysis through the evaluation of the specific storage parameter, representing the elastic storage of the aquifer, and the specific yield parameter, representing the amount of water released by pore drainage. Water resources studies are highly dependent on the estimated storage coefficient value of the aquifer, and which combines these two parameters. However, for groundwater controls, it must be noted that significant amount of water can be released from the aquifer elastic storage into construction works even before the water table has started to move down. The conceptual understanding of the hydrological system carried out with a correctly designed field experiment to estimate the hydraulic parameters controlling the movement of groundwater are of paramount importance for the success of construction works specifically in urban environments.
This study of the Kenyon junction hydraulic test data highlights the potential complexity of the flow field in the vicinity of pumping wells, and the need for high-resolution monitoring data to resolve the influence of aquifer heterogeneity. Opportunities for further research are afforded by a new NERC/UKRI research facility on the Sherwood sandstone in Cheshire, called the Cheshire Observatory. This combines abstraction and reinjection boreholes with high-resolution multilevel groundwater monitoring and 3D thermal and chemical tracer study capabilities. The Observatory, which is operated by the British Geological Survey is available to the UK science community and provides opportunities for further research in the characterization of the Sherwood sandstone and the development and improvement of tools such as the radial flow model applied here for the analysis of the field results.
Author Contributions
Conceptualization, S.W., A.H. and M.M.; methodology, S.W., A.H. and M.M.; software, M.M.; validation, M.M., A.H. and S.W.; formal analysis, M.M., A.H. and S.W.; investigation, M.M., A.H. and S.W.; writing—original draft preparation, M.M.; writing—review and editing, M.M., A.H. and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the UKRI NERC-funded Hydro-JULES research program (grant NE/X019063/1).
Data Availability Statement
Model results available on request from the authors.
Acknowledgments
Mansour and Hughes publish with the permission of the Executive Director of the British Geological Survey. The comments from two anonymous reviewers are gratefully acknowledged for improving the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pujades-Garnes, E.; Badiella, G.; Jurado, A.; Carrera, J.; Vazquez-Suñe, E. An approach for the design of dewatering systems: The case of an excavation for the construction of the assembly shaft of a tunnel boring machine. Bull. Eng. Geol. Environ. 2024, 83, 296. [Google Scholar] [CrossRef]
- Kohsaka, N.; Miyake, N. Application of Multi-layer Dewatering and Vertical Recharge System in Dewatering for Underground Works. In Groundwater Updates; Sato, K., Iwasa, Y., Eds.; Springer: Tokyo, Japan, 2000. [Google Scholar] [CrossRef]
- Preene, M.; Roberts, T. Groundwater Control. In Geological Society, London, Engineering Geology Special Publications; Geological Society of London: London, UK, 2025; Volume 31. [Google Scholar] [CrossRef]
- Banks, V.J.; Mansour, M.M.; Bricker, S.H.; Lawrence, U.; Lelliott, M.R.; Nedumpallile Vasu, N. Conceptual models. In Geological Society, London, Engineering Geology Special Publications; Geological Society of London: London, UK, 2025; Volume 31. [Google Scholar] [CrossRef]
- Bliss, C.J.; Rushton, K.R. The reliability of packer tests for estimating the hydraulic conductivity of aquifers. Q. J. Eng. Geol. 1984, 17, 81–91. [Google Scholar] [CrossRef]
- Maurice, L.; Barker, J.A.; Atkinson, T.C.; Williams, A.T.; Smart, P.L. A tracer methodology for identifying ambient flows in boreholes. Groundwater 2011, 49, 227–238. [Google Scholar] [CrossRef] [PubMed]
- Edwards, M.G.; Lloyd, J.W. Pumping test data interpretation and drift inflow assessment by finite-difference radial modelling. Int. J. Mine Water 1992, 11, 15–34. [Google Scholar] [CrossRef]
- Tamayo-Mas, E.; Bianchi, M.; Mansour, M. Impact of model complexity and multi-scale data integration on the estimation of hydrogeological parameters in a dual-porosity aquifer. Hydrogeol. J. 2018, 26, 1917–1933. [Google Scholar] [CrossRef]
- Upton, K.A.; Butler, A.P.; Jackson, C.R.; Mansour, M. Modelling boreholes in complex heterogeneous aquifers. Environ. Model. Softw. 2019, 118, 48–60. [Google Scholar] [CrossRef]
- Hemker, C.J.; Maas, C. Unsteady flow to wells in layered and fissured aquifer systems. J. Hydrol. 1987, 90, 231–249. [Google Scholar] [CrossRef]
- Walthall, S.; Ingram, J.A. The investigation of aquifer parameters using multiple piezometers. Groundwater 1984, 22, 25–30. [Google Scholar] [CrossRef]
- Rushton, K.R.; Howard, K.W.F. The unreliability of open observation boreholes in unconfined aquifer pumping tests. Groundwater 1982, 20, 546–550. [Google Scholar] [CrossRef]
- Kruseman, G.P.; de Ridder, N.A. Analysis and Evaluation of Pumping Test Data; The 521 International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1990; Publication 47. [Google Scholar]
- Rushton, K.R.; Redshaw, S.C. Seepage and Groundwater Flow; John Wiley and Sons: Chichester, UK, 1979. [Google Scholar]
- Duffield, G.M. AQTESOLV for Windows User’s Guide, Version 4.5; HydroSOLVE, Inc.: Reston, VA, USA, 2007. [Google Scholar]
- Neilsen, K.A. Fractured Aquifers: Formation Evaluation by Well Testing; Trafford Publishing: Victoria, BC, Canada, 2007. [Google Scholar]
- Anderson, M.P.; Woessner, W.W.; Hunt, R.J. Applied Groundwater Modeling Simulation of Flow and Advective Transport, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Allen, D.J.; Brewerton, L.J.; Coleby, L.M.; Gibbs, B.R.; Lewis, M.A.; MacDonald, A.M.; Wagstaff, S.J.; Williams, A.T. The Physical Properties of Major Aquifers in England and Wales; British Geological Survey: Nottingham, UK, 1997; 333p, WD/97/034. (Unpublished). [Google Scholar]
- Colyer, A.; Butler, A.; Peach, D.; Hughes, A.G. How groundwater time series and aquifer property data explain heterogeneity in the Permo-Triassic sandstone aquifers of the Eden Valley, Cumbria, UK. Hydrogeol. J. 2021, 30, 445–462. [Google Scholar] [CrossRef]
- Ireland, R.J.; Brassington, F.C. An investigation of complex saline groundwater problems in the Permo Triassic sandstones of North West England. Sci. Total Environ. 1981, 21, 261–266. [Google Scholar] [CrossRef]
- Boulton, N.S. The drawdown of the water-table under non-steady conditions near a pumped well in an unconfined formation. Proc. Inst. Civil. Eng. 1954, 3, 564. [Google Scholar] [CrossRef]
- Boulton, N.S. Unsteady radial flow to a pumped well allowing for delayed yield from storage. Int. Assoc. Sci. Hydrol. Rome 1954, 2, 472–477. [Google Scholar]
- Neuman, S.P. Theory of flow in unconfined aquifers considering delayed response of the water table. Water Resour. Res. 1972, 8, 1031–1045. [Google Scholar] [CrossRef]
- Li, Y.; Neuman, S.P. Flow to a well in a five-layer system with application to the Oxnard Basin. Groundwater 2007, 45, 672–682. [Google Scholar] [CrossRef] [PubMed]
- Butler, J.J.; McElwee, C.D.; Bohling, G.C. Pumping tests in networks of multilevel sampling wells: Motivation and methodology. Water Resour. Res. 1999, 35, 3553–3560. [Google Scholar] [CrossRef]
- Pandit, A.; Abi Aoun, J.M. Numerical Modeling of Axisymmetric Flow. Groundwater 1994, 32, 458–464. [Google Scholar] [CrossRef]
- Ha, D.; Zheng, G.; Zhou, H.; Zeng, C.; Zhang, H. Estimation of hydraulic parameters from pumping tests in a multiaquifer system. Undergr. Space 2020, 5, 210–222. [Google Scholar] [CrossRef]
- Miyake, N.; Kohsaka, N.; Ishikawa, A. Multi-aquifer pumping test to determine cutoff wall length for groundwater flow control during site excavation in Tokyo, Japan. Hydrogeol. J. 2008, 16, 995–1001. [Google Scholar] [CrossRef]
- Alam, N.; Olsthoorn, T.N. Multidepth Pumping Tests in Deep Aquifers. Groundwater 2014, 52, 148–160. [Google Scholar] [CrossRef]
- Hemker, C.J. Transient well flow in layered aquifer systems: The uniform well-face drawdown solution. J. Hydrol. 1999, 225, 19–44. [Google Scholar] [CrossRef]
- Hvilshøj, S.; Jensen, K.H.; Barlebo, H.C.; Madsen, B. Analysis of pumping tests of partially penetrating wells in an unconfined aquifer using inverse numerical optimization. Hydrogeol. J. 1999, 7, 365–379. [Google Scholar] [CrossRef]
- Bowes, M.; Crewdson, E.; Elsome, J.; Spence, M. UK Geoenergy Observatories Cheshire: Hydraulic Testing of TH0424 Technical Summary; British Geological Survey: Nottingham, UK, 2023; 59p, OR/23/037. (Unpublished). [Google Scholar]
- Available online: https://www.ukgeos.ac.uk/cheshire-observatory (accessed on 31 July 2025).
- Mansour, M.M.; Hughes, A.G.; Spink, A.E.F. User Manual for the Layered R-Theta Numerical Model (COOMPuTe); British Geological Survey: Nottingham, UK, 2007; 71p, OR/07/029. (Unpublished). [Google Scholar]
- Doherty, J. PEST-Model-Independent Parameter Estimation. User Manual, 7th ed.; Watermark Numerical Computing: Brisbane, Australia, 2018. [Google Scholar]
- Mansour, M.; Christelis, V.; Upton, K.; Hughes, A. Simulation of complex groundwater flow processes in low-fidelity radial flow model using a mathematical representation of the variation of vertical hydraulic conductivity with depth. Hydrol. Process. 2024, 38, e70039. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).