Next Article in Journal
A Practical Method for Ecological Flow Calculation to Support Integrated Ecological Functions of the Lower Yellow River, China
Previous Article in Journal
A Deep Reinforcement Learning Framework for Cascade Reservoir Operations Under Runoff Uncertainty
Previous Article in Special Issue
Ecosystem Services in Urban Blue-Green Infrastructure: A Bibliometric Review
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 17
Issue 15
10.3390/w17152325
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Decentralized Coupled Grey–Green Infrastructure for Resilient and Cost-Effective Stormwater Management in a Historic Chinese District

by
Yongqi Liu
1,
Ziheng Xiong
2,
Mo Wang
2,*,
Menghan Zhang
2,
Rana Muhammad Adnan
3,4,
Weicong Fu
5,
Chuanhao Sun
6,* and
Soon Keat Tan
7
1
Art School, Hunan University of Information Technology, Changsha 410151, China
2
College of Architecture and Urban Planning, Guangzhou University, Guangzhou 510006, China
3
Water Science and Environmental Research Centre, College of Chemistry and Environmental Engineering, Shenzhen University, Shenzhen 518060, China
4
Center for Global Health Research, Saveetha Institute of Medical and Technical Sciences, Chennai 600001, India
5
College of Landscape and Art, Fujian Agriculture and Forestry University, Fuzhou 350028, China
6
Shanghai Research Institute for Intelligent Autonomous Systems, Tongji University, Shanghai 201210, China
7
School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore
*
Authors to whom correspondence should be addressed.
Water 2025, 17(15), 2325; https://doi.org/10.3390/w17152325
Submission received: 19 June 2025 / Revised: 26 July 2025 / Accepted: 1 August 2025 / Published: 5 August 2025
(This article belongs to the Special Issue Sustainable Water Treatment Systems: Green Infrastructure and Bioremediation)
Browse Figures
Versions Notes

Abstract

Coupled grey and green infrastructure (CGGI) offers a promising pathway toward sustainable stormwater management in historic urban environments. This study compares CGGI and conventional grey infrastructure (GREI)-only strategies across four degrees of layout centralization (0%, 33.3%, 66.7%, and 100%) in the Quanzhou West Street Historic Reserve, China. Using a multi-objective optimization framework integrating SWMM simulations, life-cycle cost (LCC) modeling, and resilience metrics, we found that the decentralized CGGI layouts reduced the total LCC by up to 29.6% and required 60.7% less green infrastructure (GI) area than centralized schemes. Under nine extreme rainfall scenarios, the GREI-only systems showed slightly higher technical resilience (Tech-R: max 99.6%) than CGGI (Tech-R: max 99.1%). However, the CGGI systems outperformed GREI in operational resilience (Oper-R), reducing overflow volume by up to 22.6% under 50% network failure. These findings demonstrate that decentralized CGGI provides a more resilient and cost-effective drainage solution, well-suited for heritage districts with spatial and cultural constraints.

1. Introduction

Historical and cultural districts serve as repositories of collective memory and urban heritage, frequently designated as Urban Historic Conservation Areas. These zones are characterized by unique architectural and cultural attributes that underpin a city’s sustainable urban identity [1]. However, intensified urbanization and climate variability have exacerbated the vulnerability of these environments [2,3]. In particular, the proliferation of impervious surfaces and constrained spatial configurations have increased flood susceptibility, especially under pluvial conditions [4,5].
The Quanzhou West Street Historic Reserve exemplifies such urban challenges. As a dense, coastal heritage corridor in southeastern China, the district has undergone extensive transformation due to commercial revitalization and tourism-driven redevelopment [6]. This transformation has led to the loss of permeable surfaces, significantly diminishing the district’s natural capacity to absorb stormwater [7]. Concurrently, intensifying precipitation patterns—linked to a shifting global hydrological cycle—have increased the incidence of short-duration, high-intensity storms [8,9]. These trends collectively jeopardize the structural integrity and cultural sustainability of heritage precincts [10,11,12,13].
Traditionally, stormwater has been managed through grey infrastructure (GREI), which includes subsurface pipes, culverts, and storm drains designed to convey runoff efficiently [14]. While GREI systems are effective under routine conditions, they are inflexible and prone to failures during extreme events, often contributing to downstream flooding and water quality degradation [15,16,17]. In heritage districts, the expansion or retrofitting of GREI is often constrained by spatial, cultural, and economic limitations [17].
As a complementary or alternative approach, green infrastructure (GI) offers a nature-based solution to manage stormwater at its source. Practices such as bioretention, permeable pavement, and green roofs enhance infiltration, delay peak flows, and improve water quality [18,19]. However, the limited capacity of GI during severe rainfall events restricts its standalone utility in dense urban contexts. An integrated approach—coupled grey–green infrastructure (CGGI)—has emerged to leverage the reliability of GREI with the adaptability and environmental benefits of GI [20]. Recent comparative studies (e.g., Zhang et al. [21], Zhou et al. [22], and Liu et al. [23]) have demonstrated that hybrid systems often outperform conventional GREI in terms of urban flooding mitigation and adaptability. However, most of these studies have focused on modern urban contexts with flexible spatial layouts, neglecting historic and culturally constrained districts.
Decentralized CGGI layouts, which distribute hydraulic loads across multiple outlets and infiltration points, offer enhanced redundancy and reduced systemic vulnerability during extreme events [24,25]. However, implementing such systems in compact, heritage-constrained districts introduces challenges, such as identifying optimal drainage routes, balancing hydraulic reliability with land availability, and mitigating disturbances to the built environment [26]. These challenges necessitate a robust multi-objective optimization framework that integrates hydraulic modeling, cost minimization, and resilience metrics [27,28]. Prior studies have successfully employed such methods to determine optimal configurations for low-impact development [29,30], yet their applicability to heritage districts remains limited. In these districts, design decisions are constrained not only by engineering and spatial limitations but by socio-political, regulatory, and cultural preservation concerns.
In addition, the existing literature often neglects equity-oriented dimensions of urban transformation, particularly within regenerated historic cores. For instance, Zhao et al. [31] demonstrated that the rural-to-urban mobility of marginal residents varies markedly across spatial gradients in China, underscoring the need to consider inclusivity and accessibility in infrastructure planning. Similarly, Xu et al. [32] emphasized the importance of intermediary policy mechanisms—such as green finance incentives and stakeholder engagement—in promoting sustainable and socially responsive urban development. These insights are particularly relevant for heritage infrastructure projects, where fiscal constraints, community sensitivities, and long-term viability must be harmonized.
Technological innovation further broadens the scope of infrastructure planning in such areas. The emerging integration of photovoltaic systems and energy storage systems has shown promise in enhancing infrastructure resilience and sustainability, particularly when embedded in multifunctional urban systems [33]. While the present study focuses on stormwater management, its underlying optimization framework and modular layout logic are technologically compatible, potentially supporting the integration of smart infrastructure elements—such as sensor-based control, energy-harvesting pavement, or photovoltaic-enabled drainage covers—in future heritage district upgrades.
The evaluation of CGGI effectiveness requires appropriate performance indicators. Resilience—defined as the capacity of drainage systems to withstand and recover from shocks—has gained prominence in this regard [34,35,36]. Distinctions between technical resilience (Tech-R), which reflects system performance under extreme rainfall, and operational resilience (Oper-R), which considers structural failure scenarios, are particularly relevant in contexts where system fragility and cultural sensitivity co-exist. Despite advances in resilience modeling, standardized metrics remain underdeveloped [14,37,38]. Recent approaches propose quantifying resilience through overflow load ratios and temporal performance curves [39,40], providing a basis for comparative assessments across drainage strategies.
To address these challenges, this study applies a comprehensive hydrological-optimization framework to the Quanzhou West Street Historic Reserve. The specific aims of this study are as follows: (1) to develop a resilience-focused optimization model tailored to heritage district constraints; (2) to identify cost-effective and hydraulically reliable layout alternatives; (3) to assess system performance under extreme rainfall and infrastructure failure using Tech-R and Oper-R indices. This approach offers critical insights for the sustainable integration of drainage infrastructure within culturally significant urban landscapes.

2. Materials and Methods

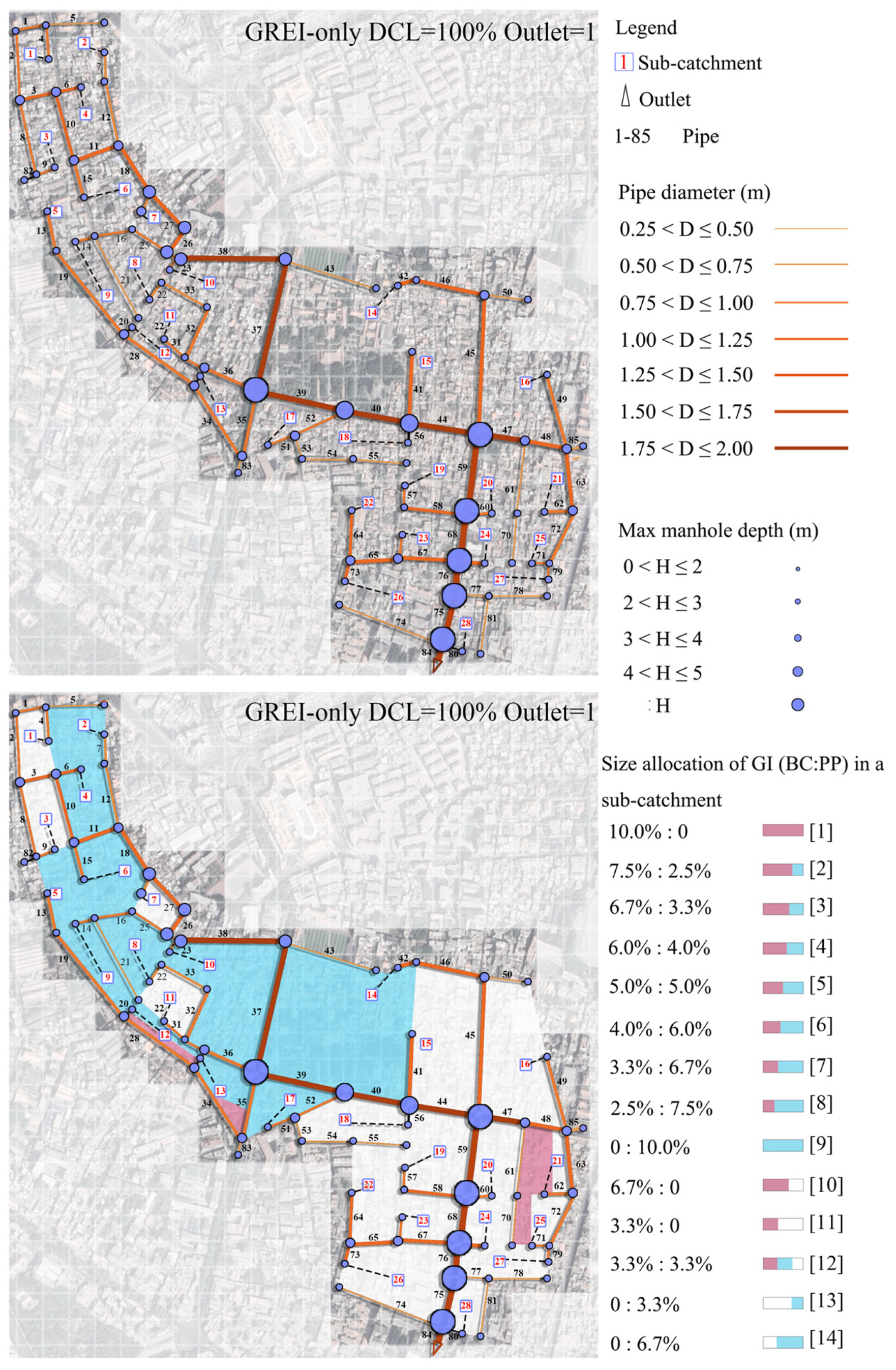
2.1. Study Area and Data Sources

The Quanzhou West Street Historic Reserve, located in Quanzhou, Fujian Province, China, is a nationally recognized cultural preservation zone characterized by dense Ming- and Qing-era architecture, narrow stone-paved streets, and minimal open space (Figure 1). The area spans approximately 45.85 ha, with over 91.6% classified as impervious surface, including residential blocks, commercial alleys, and pedestrian corridors. The land use is dominated by historic buildings, with limited vegetation confined to internal courtyards and temple grounds [41]. The study area features a gentle west-to-east slope with an average gradient of 0.1–0.3%.
The city experiences a humid subtropical monsoon climate with an average annual rainfall of 1000 mm, predominantly concentrated in the flood-prone months of April to September [42]. High-intensity short-duration rainfall events have become more frequent in recent decades, making pluvial flood risk a significant concern for this heritage district [43].

2.2. Stormwater Modeling Framework

The Storm Water Management Model (SWMM) v5.1, developed by the U.S. EPA, was used to simulate runoff dynamics and to assess drainage performance [44]. Parameter values were derived from analogous urban catchments and literature references [45,46]. The model was set up as follows: 28 sub-catchments, delineated using ArcGIS 10.8 based on road networks and elevation; 54 nodes; 85 pipes; 4 candidate outlets (see Table A1 and Figure 2); land surface parameters typical of imperviousness and hydrological soil groups; design storms of 5-year. A 6-h timeline was used for baseline compliance, and 25-, 50-, and 100-year storms (6-, 12-, and 24-h durations) were used for stress testing [47].

2.3. Green Infrastructure Practices

Two GI types were employed, namely bioretention cells (BCs) and porous pavement (PP), selected for their modularity, low-intrusion nature, and suitability for narrow alleys and historic courtyards [48,49]. This selection is particularly relevant to the Quanzhou West Street Historic Conservation Area, which features high-density buildings, narrow street networks, and strict heritage protection regulations. In such a context, larger or deep-rooted GI installations (e.g., rain gardens) risk damaging underground relics, while green roofs are often infeasible due to the limitations of traditional architectural forms. By contrast, BCs and PP can be flexibly integrated into existing paved surfaces or open courtyard spaces, aligning with cultural preservation constraints. The design parameters were adapted from Sun et al. [50] and Wang et al. [51], and are summarized in Table A2. The GI placement was restricted to non-building space using spatial zoning masks derived from conservation overlay maps.

2.4. Optimization Strategy

The optimization framework integrates hydraulic reliability constraints with life-cycle cost (LCC) minimization. Two infrastructure strategies—GREI-only and CGGI—were evaluated across four degrees of centralization (DCL) (i.e., 100%, 66.7%, 33.3%, and 0%). The DCL was defined as the ratio of the total drainage load handled by centralized pipes to the system-wide load. Layouts were generated using a graph-theoretic topology generator, following Bakhshipour et al. [52].

2.4.1. Objective Function and Cost Components

The objective function minimizes the total LCC, comprising capital construction costs (CapEx) and the operation–maintenance costs (OpEx) over a 30-year period. The total LCC for each scheme was calculated using the following equation:
L C C = ∑ i = 1 n ( C a p E x i + ∑ y = 1 30 O p E x i , y ( 1 + r ) y )
where i denotes each component (e.g., pipes, porous pavement, bioretention cell), CapExi is the capital cost of component i, OpExi,y is the annual O&M cost in year y, r is the discount rate, and n is the total number of infrastructure components. The annual O&M rates were set at 10%, 4%, and 8% of capital costs for GREI, PP, and BCs, respectively [53]. Cost present values were computed using a 2% discount rate [54]. Equations and full cost functions follow those outlined by Yao et al. [55].
The LCC assessment was conducted based on the GI allocation outcomes from SWMM simulations under different layout scenarios. For the CGGI configurations, both GI and conventional pipe costs were included; for the GREI-only schemes, only pipe systems were considered.

2.4.2. Decision Variables and Constraints

Decision variables include the number and location of outlets, pipe diameters and slopes, and the GI type and placement. Hydraulic reliability was ensured through compliance with a design storm having a return period of 5 years and a duration of 6 h, based on local intensity–duration–frequency (IDF) curves. The GI installation was restricted to available non-building spaces within each sub-catchment, excluding areas designated as culturally sensitive through spatial zoning masks [56].

2.4.3. Optimization Algorithms

The GREI network was optimized using an adaptive genetic algorithm embedded within a graph-theoretic layout generator, previously demonstrated to perform efficiently in urban drainage studies [52,57]. The CGGI layouts were generated by superimposing GI elements onto GREI configurations, with binary-encoded chromosomes representing layout variables (pipe attributes, GI area, and location). Optimization was performed using the NSGA-II algorithm, selected for its demonstrated efficiency in handling multi-objective drainage network problems. The NSGA-II (Non-dominated Sorting Genetic Algorithm II) was used to solve the multi-objective layout problem, implemented in MATLAB R2022a. The chromosome was binary-encoded, representing pipe diameters, outlet location, and GI type and area. The key settings are as follows: population size, 200; generations, 500; crossover probability, 0.9; mutation probability, 0.05; tournament size, 2 [24,58]. The layout generator and optimizer were integrated into a MATLAB-SWMM interface using a customized batch file controller.

2.5. Resilience Assessment Framework

Resilience was evaluated under two distinct dimensions, including Tech-R and Oper-R, following Butler et al. [59] and Mugume et al. [60].
Tech-R quantifies the system’s capacity to manage extreme rainfall events without flooding, defined as the proportion of rainfall volume managed without overflow [61,62]. Nine rainfall scenarios were simulated using 6-h, 12-h, and 24-h design storms with return periods of 25, 50, and 100 years, reflecting regional flood risks under current and projected climate conditions.
Oper-R, by contrast, measures the system’s robustness under infrastructure failure conditions, such as pipe blockages or deterioration of the GI. Pipe failure was modeled by increasing the Manning’s roughness coefficient to 100 (simulating complete blockage), and the GI failure was modeled as total functional loss within affected sub-catchments. A total of 136,000 pipe failure combinations were simulated using MATLAB R2022a, with overflow volumes benchmarked against a baseline 5-year, 6-h design storm [63,64,65].

3. Results and Discussion

3.1. Trade-Offs Between Layout Centralization and Life-Cycle Cost

The DCL significantly influences both the economic efficiency and physical configuration of stormwater systems. In the case of the Quanzhou West Street Historic Reserve, where underground space is constrained and heritage preservation is critical, decentralized drainage strategies offer notable advantages (Figure 2, Figure A1, Figure A2 and Figure A3).
Lower DCL led to a reduction in pipe diameters and manhole depths in both the GREI-only and the CGGI systems (Table 1; see also detailed specifications in Table A3 and Table A4). For instance, in the GREI-only layouts, shifting from a fully centralized (DCL = 100%) to a fully decentralized configuration (DCL = 0%) reduced the mean pipe diameter by 0.18 m and the average manhole depth by 0.21 m. Similar reductions were observed in the CGGI layouts. This outcome can be explained by the shorter hydraulic flow paths and diminished head losses associated with decentralized systems, consistent with the findings in Bakhshipour et al. [52] and Hesarkazzazi et al. [66].
Decentralized configurations substantially reduced the total GI installation area, reflecting the improved hydraulic efficiency achieved through the distributed runoff management. As shown in Table 2, the total GI area required in the most decentralized CGGI scheme (DCL = 0%) was 1450 m2, compared to 3650 m2 in the fully centralized layout (DCL = 100%). This reduction of more than 60% indicates that decentralized layouts manage stormwater more effectively with fewer GI installations, thanks to shorter flow paths and localized infiltration. Among the GI types, PP accounted for the vast majority of the implemented GI across all DCL scenarios. Its dominance is attributed to its compatibility with the narrow pedestrian alleys and existing stone pavement typical of the Quanzhou West Street Historic Reserve. The flexibility of PP also makes it easier to retrofit without damaging heritage features. BCs, on the other hand, were applied sparingly—mostly in temple courtyards and internal open spaces—due to stricter spatial and cultural limitations. As the layout shifted from centralized to decentralized, the spatial distribution of the GI became more even across sub-catchments, allowing for greater use of the available non-building areas and reducing the concentration of infrastructure in specific zones. This spatial dispersion also enhanced system resilience by distributing infiltration capacity and minimizing the risk of overflow at critical nodes. These findings suggest that the decentralized CGGI strategies not only reduce infrastructure footprints but improve spatial integration and cultural sensitivity in heritage districts.
Importantly, PP comprised the majority of the GI across all scenarios, due to its compatibility with the narrow alleys and pedestrian zones characteristic of the Quanzhou West Street Historic Reserve. Its flexible deployment allowed for integration without disturbing historic surfaces. As a result, the decentralized CGGI schemes minimized both structural intrusiveness and potential cultural impacts.

3.2. Life-Cycle Cost Efficiency of Optimized Strategies

The LCC analysis indicated that decentralized drainage layouts offer substantial economic advantages compared to centralized configurations. For the GREI-only layouts, the LCC declined from USD 30,897,000 to USD 19,455,000 between the most centralized and most decentralized designs. Similarly, the CGGI layouts demonstrated a cost reduction from USD 29,298,000 to USD 18,251,000 (Table 3). These savings stemmed primarily from reduced GREI construction and maintenance costs.
Although the GI components increased the capital expenditures slightly, they represented a minimal proportion of the total LCCs—ranging from 11.5% in centralized layouts to just 2.9% in decentralized configurations. Moreover, the O&M costs for the GI were consistently lower than for the GREI systems, in agreement with cost-performance benchmarks reported by Houle et al. [53]. For heritage districts, like the Quanzhou West Street Historic Reserve, where large-scale infrastructure interventions may be socially or politically constrained, the use of decentralized CGGI provides a cost-effective and culturally sensitive alternative. The modular nature of GI practices, such as PP, enables incremental implementation and easier public acceptance, enhancing both feasibility and flexibility.

3.3. Performance Under Extreme Rainfall Events

Tech-R, evaluated from overflow volumes across nine extreme rainfall scenarios, demonstrates that decentralized configurations significantly enhance system performance under stress conditions. Across all the rainfall durations and return periods, lower DCL consistently achieved higher Tech-R scores in both the GREI-only and the CGGI systems (Table 4).
For example, under a 100-year, 6-h storm, the GREI-only layout with DCL = 0% attained a Tech-R of 99.5%, compared to 97.5% at DCL = 100%. The CGGI systems showed a similar trend, albeit with slightly lower resilience in high-intensity rainfall events. This marginal underperformance stems from the reduced hydraulic capacity of the downsized GREI pipes in the CGGI configurations, a design compromise necessitated by spatial and heritage constraints, a limitation also observed by Sun et al. [37].
Despite this, the CGGI layouts still achieved Tech-R values above 98% in most scenarios, indicating acceptable performance given the additional ecological and aesthetic benefits provided by the GI. These findings align with recommendations in Butler et al. [59] and He et al. [61], which advocate for hybrid approaches in flood-prone urban environments.

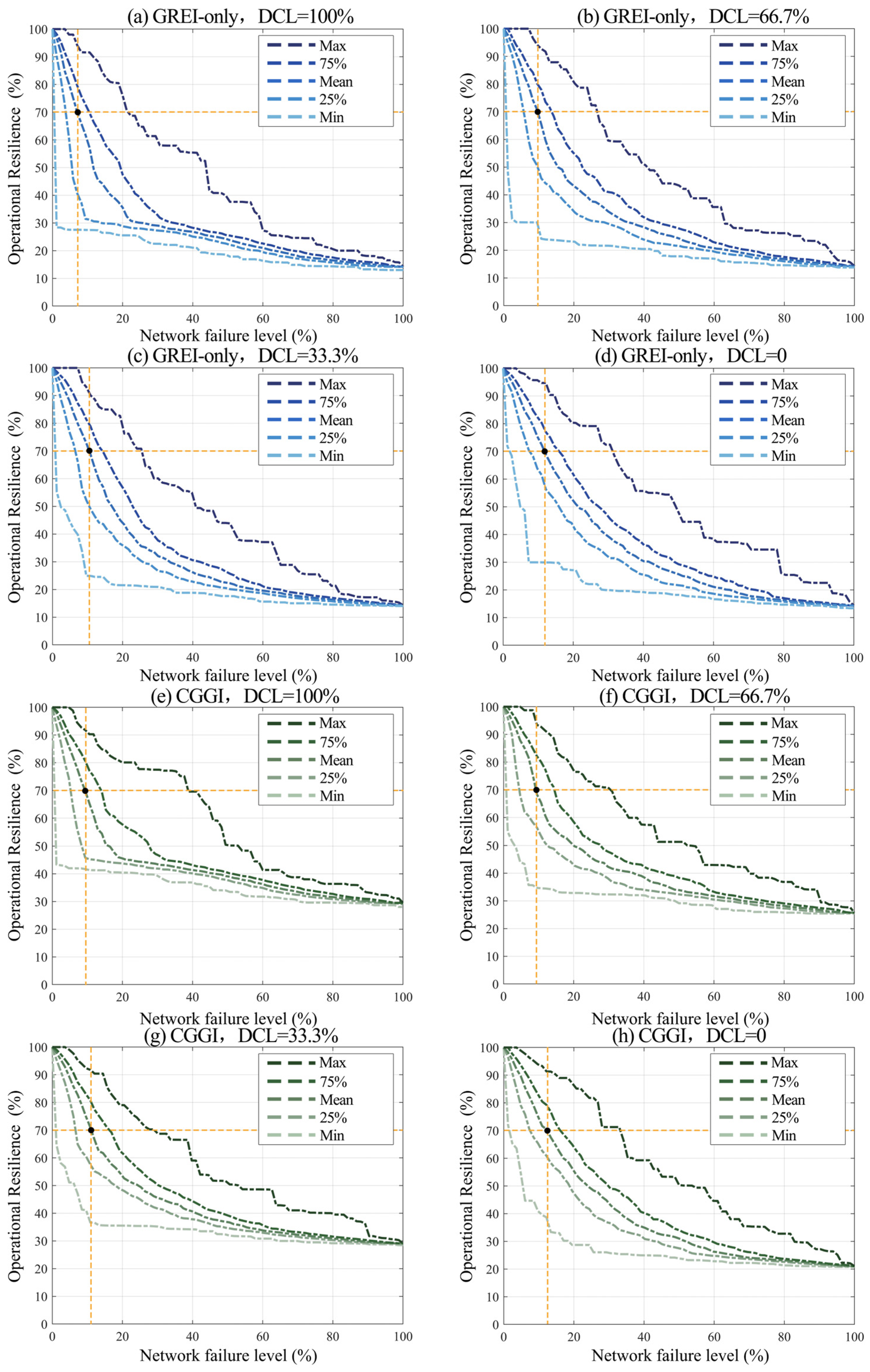
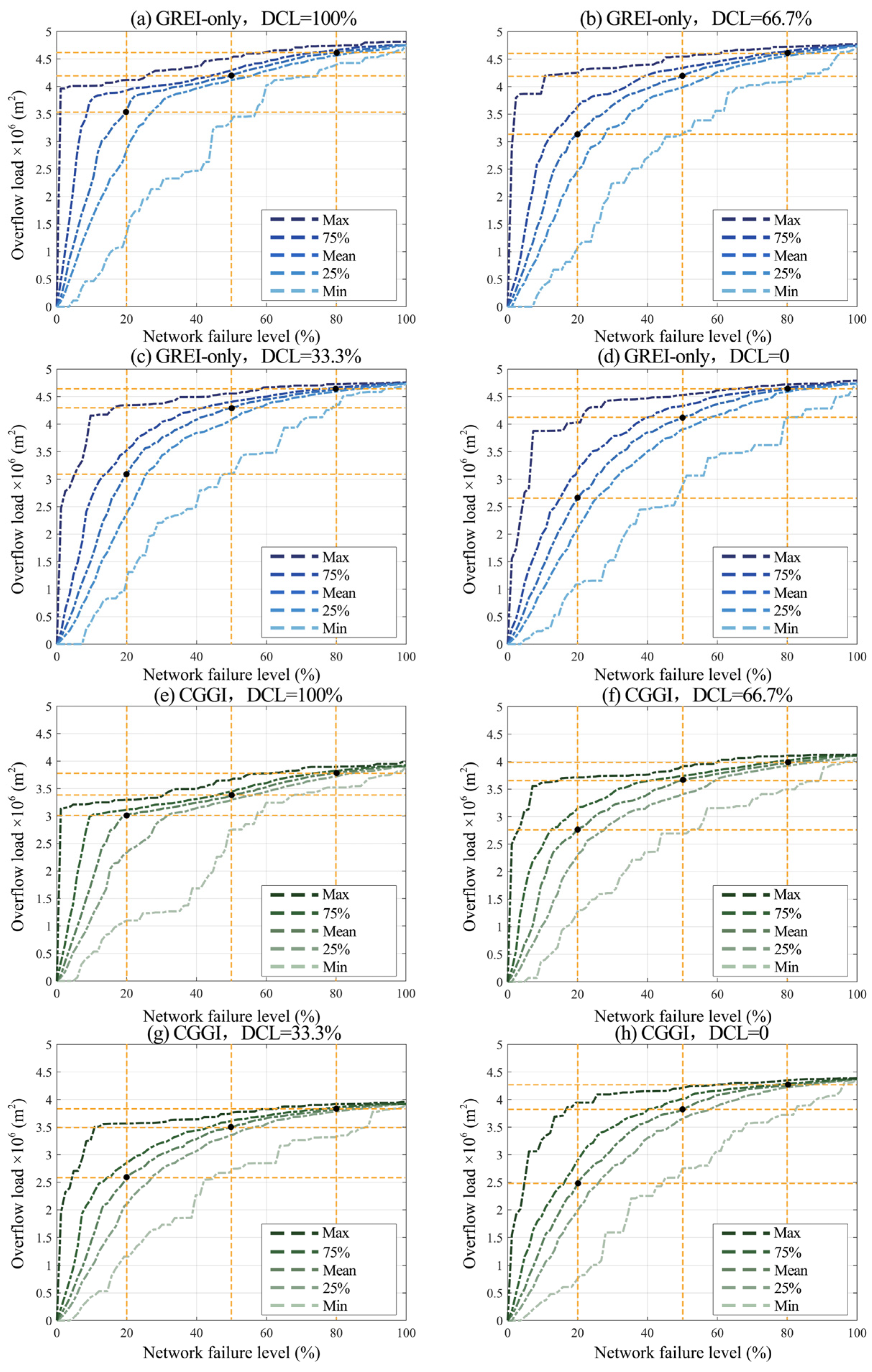
3.4. Performance Under Structural Failure Scenarios

Figure 3 presents the Oper-R curves across various network failure levels for both the GREI-only and the CGGI systems. Figure 3a–d illustrate the GREI-only configurations, showing a general decline in Oper-R as failure intensity increases. Notably, in Figure 3d (DCL = 0%), the decentralized GREI-only system performs better under moderate failure (e.g., 20–50%) than the more centralized layout (Figure 3a), but its performance degrades sharply under higher failure rates due to reduced backup interconnectivity. By contrast, Figure 3e–h depict the CGGI layouts, which consistently show higher resilience across all failure levels. Particularly in Figure 3h (DCL = 0%), the decentralized CGGI configuration sustains operational resilience even beyond 60% network failure—reaching an average Oper-R of 34.8%, significantly outperforming the corresponding GREI-only case (Figure 3d, 21.5%). This improvement stems from the distributed GI elements, which continue functioning independently despite partial network disruptions. Figure 3e,f (DCL = 100% and 66.7%, respectively) indicate that, even in the centralized CGGI layouts, resilience remains higher than their GREI-only counterparts, although the benefit narrows under more intense failures. Figure 3g (DCL = 33.3%) shows a balanced performance, confirming that even partial decentralization in the CGGI layouts enhances reliability. Collectively, these subfigures demonstrate how each combination of layout centralization and infrastructure type affects resilience under failure. The results support this study’s core objective by validating the decentralized CGGI as the most reliable configuration in heritage-constrained, failure-prone environments.
Simulated pipe failures (up to 80%) resulted in less overflow volume in the CGGI systems compared to the GREI-only systems across all the DCL (Figure 4). For instance, at 50% failure, the CGGI layouts showed an average overflow reduction of 19.0% relative to the GREI-only configurations. This improvement stems from the decentralized infiltration function of the GI elements, which remain operational even when the GREI components are partially disabled. Porous pavement and bioretention features provide decentralized redundancy, enhancing system robustness under stress. These results mirror the resilience profiles described in Johansson et al. [67] and Lim [64], where decentralized stormwater systems exhibit better fault tolerance.
In fully decentralized layouts (DCL = 0%), overflow volumes remained the lowest under all failure levels. However, at 80% failure, overflow slightly increased in decentralized layouts compared to centralized ones—likely due to loss of interconnectivity and fewer backup flow paths. This indicates that decentralized designs must still be carefully configured to prevent isolated system breakdowns in extreme cases.
On average, the CGGI systems exhibited higher operational resilience, with Oper-R values ranging from 26.5% to 65.1%, compared to 9.9% to 54.5% for the GREI-only schemes, underscoring the reliability benefits of hybrid infrastructure. These differences highlight the reliability advantages of hybrid infrastructure, especially in heritage districts where maintenance and access for emergency repairs are restricted.

3.5. Implications for Heritage Urban Drainage Planning

The integration of CGGI into heritage urban districts demands a careful balance between hydraulic performance, long-term cost-efficiency, and the preservation of cultural assets. In the case of the Quanzhou West Street Historic Reserve, the simulation results demonstrated that the decentralized CGGI configurations not only enhanced technical and operational resilience under extreme rainfall and failure scenarios but significantly reduced the required infrastructure footprint—minimizing excavation and disturbance to historical features.
The flexibility of GI elements, such as porous pavement and bioretention cells, allows for context-sensitive placement within courtyards, temple grounds, and pedestrian alleys, supporting retrofitting without compromising built heritage. Additionally, these elements contribute ecological co-benefits—such as microclimatic regulation and habitat enrichment—while improving the aesthetic quality of dense, stone-dominated urban streetscapes [68]. This multifunctionality aligns with findings by Elmqvist et al. [69], Kim and Song [70], and more recent studies (e.g., Zhang and MacKenzie, [71]; Fang et al. [72]), emphasizing the growing role of GI in adaptive heritage management. From a planning perspective, CGGI offers a modular, socially acceptable alternative for infrastructure upgrades in areas with restricted access or political sensitivity. Future design guidelines should prioritize low-intrusion GI options along existing corridors, and leverage community engagement to integrate nature-based solutions into cultural landscapes. This study provides empirical support for such strategies by demonstrating their resilience, cost-effectiveness, and spatial compatibility with historic urban morphology.
Future studies should explore real-time monitoring and adaptive control strategies for CGGI in heritage districts, incorporating sensor networks and IoT-based feedback systems. Additionally, further research could focus on integrating water quality modeling, ecological co-benefit quantification, and participatory stakeholder engagement to guide CGGI placement. Finally, multi-scenario modeling under climate uncertainty and urban redevelopment pressures would strengthen long-term planning resilience.

3.6. Limitations

Several limitations of this study should be acknowledged, particularly in relation to the specificity of the modeling assumptions and the contextual constraints of the case site. First, while the SWMM-based hydrological modeling and optimization framework was calibrated to reflect the local conditions of the Quanzhou West Street Historic Reserve, the absence of detailed real-time monitoring data—such as measured runoff volumes, infiltration rates, and flow velocities—may introduce deviations between simulated and actual system behavior [73]. Such discrepancies could be more pronounced under complex mixed runoff scenarios typical of historic districts [26,74]. Second, the spatial allocation of the GI components was based on generalized assumptions regarding available non-building space. In practice, the feasibility of GI deployment in heritage precincts is subject to strict architectural protection policies, land-use negotiations, and stakeholder approvals, which may limit the applicability of some proposed configurations [75]. Third, the resilience assessment framework focused on overflow load and structural performance metrics. While these indices capture hydraulic behavior under extreme rainfall and failure scenarios, other important aspects—such as water quality performance, ecological benefits, and long-term maintenance adaptability—were not quantified in this study [76]. These dimensions are particularly relevant in multifunctional heritage environments where ecological services and aesthetic integration are key considerations. Finally, the optimization process was limited to predefined design storms and static network configurations [77]. In reality, climate variability, urban redevelopment, and aging infrastructure may alter hydrological responses and system vulnerability over time. Incorporating dynamic system evolution, probabilistic risk assessment, and stakeholder-driven scenario testing would provide a more comprehensive basis for resilient infrastructure planning.

4. Conclusions

This study evaluated the performance of CGGI versus GREI for stormwater management in the Quanzhou West Street Historic Reserve. A hydrological-optimization framework was applied to assess layout strategies under varying degrees of centralization. The results showed that the decentralized CGGI layouts reduced life-cycle costs by up to 29.6%, required 60.7% less green infrastructure area, and improved operational resilience by reducing overflow volumes up to 22.6% under 50% failure conditions. Although the GREI-only systems showed marginally higher technical resilience during extreme rainfall (max 99.6% vs. 99.1%), CGGI offered superior adaptability and spatial compatibility with heritage constraints. These findings suggest that decentralized CGGI is a cost-effective, resilient, and heritage-sensitive approach for historic urban districts. Future research should incorporate dynamic climate scenarios, multi-hazard assessments, and stakeholder-driven design preferences to further refine infrastructure strategies.

Author Contributions

Conceptualization, Y.L., M.W., and C.S.; methodology, M.W. and C.S.; software, Y.L., Z.X., and C.S.; validation, M.Z. and W.F.; formal analysis, Z.X.; investigation, Z.X., R.M.A., and W.F.; resources, M.W. and S.K.T.; data curation, C.S.; writing—original draft preparation, Y.L., M.W. and C.S.; writing—review and editing, M.W., R.M.A., and S.K.T.; visualization, Z.X., M.Z., and C.S.; supervision, M.W., R.M.A., and S.K.T.; project administration, M.W.; funding acquisition, Y.L. and M.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Guangdong Basic and Applied Basic Research Foundation, China [grant number 2023A1515030158, 2025A1515012916], Guangdong Provincial Philosophy and Social Sciences Planning Project [grant number GD25YSH07], Guangzhou City School (Institute) Enterprise Joint Funding Project, China [grant number 2024A03J0317], and the Major Program of the National Natural Science Foundation of China [grant number 62394334].

Data Availability Statement

This study did not report any publicly archived datasets.

Acknowledgments

The authors have reviewed and edited the output and take full responsibility for the content of this publication.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
BCsBioretention cells
CGGICoupled grey and green infrastructure
DCLDegrees of layout centralization
GIGreen infrastructure
GREIGrey infrastructure
IDFIntensity–duration–frequency
LCCLife-cycle cost
O&MOperation–maintenance
Oper-ROperational resilience
PPPorous pavement
SWMMStorm Water Management Model
Tech-RTechnical resilience

Appendix A

Water 17 02325 g0a1
Figure A1. Optimized spatial configurations of the GREI-only and CGGI drainage schemes under DCL = 100%, Outlet = 1.
Figure A1. Optimized spatial configurations of the GREI-only and CGGI drainage schemes under DCL = 100%, Outlet = 1.
Water 17 02325 g0a1
Water 17 02325 g0a2
Figure A2. Optimized spatial configurations of the GREI-only and CGGI drainage schemes under DCL = 66.7%, Outlet = 2.
Figure A2. Optimized spatial configurations of the GREI-only and CGGI drainage schemes under DCL = 66.7%, Outlet = 2.
Water 17 02325 g0a2
Water 17 02325 g0a3
Figure A3. Optimized spatial configurations of the GREI-only and CGGI drainage schemes under DCL = 33.3%, Outlet = 3.
Figure A3. Optimized spatial configurations of the GREI-only and CGGI drainage schemes under DCL = 33.3%, Outlet = 3.
Water 17 02325 g0a3
Table A1. Characteristics of sub-catchments used in the SWMM modeling for the case study.
Table A1. Characteristics of sub-catchments used in the SWMM modeling for the case study.
No. Sub-CatchmentA (ha)I (%)W (m)S (%)N-IN-PD-i (mm)D-p (mm) Max-R
(mm/h)		Min-R
(mm/h)		D-c (h)D-t (day)
10.848583.60.10.0240.152.16.51103.8111.442.757
21.27 85127.30.10.0240.152.16.51103.8111.442.757
30.919091.40.10.0240.152.16.51103.8111.442.757
41.2090119.50.10.0240.152.16.51103.8111.442.757
51.3088130.50.10.0240.152.16.51103.8111.442.757
61.5495153.60.10.0240.152.16.51103.8111.442.757
70.709570.50.10.0240.152.16.51103.8111.442.757
81.4290142.10.10.0240.152.16.51103.8111.442.757
90.979097.10.10.0240.152.16.51103.8111.442.757
103.4285341.50.10.0240.152.16.51103.8111.442.757
111.0995108.90.10.0240.152.16.51103.8111.442.757
120.779576.60.10.0240.152.16.51103.8111.442.757
131.0290102.20.10.0240.152.16.51103.8111.442.757
147.1560715.40.10.0240.152.16.51103.8111.442.757
153.4190340.70.10.0240.152.16.51103.8111.442.757
162.0590205.20.10.0240.152.16.51103.8111.442.757
171.1695116.50.10.0240.152.16.51103.8111.442.757
181.5795156.60.10.0240.152.16.51103.8111.442.757
192.0095199.70.10.0240.152.16.51103.8111.442.757
201.1795117.30.10.0240.152.16.51103.8111.442.757
211.7497173.90.10.0240.152.16.51103.8111.442.757
221.5594155.00.10.0240.152.16.51103.8111.442.757
231.1498114.20.10.0240.152.16.51103.8111.442.757
240.609560.40.10.0240.152.16.51103.8111.442.757
251.3498133.80.10.0240.152.16.51103.8111.442.757
262.7995278.50.10.0240.152.16.51103.8111.442.757
271.0196101.40.10.0240.152.16.51103.8111.442.757
280.729872.20.10.0240.152.16.51103.8111.442.757
Note: A: area; I: impervious area; W: width; S: slope; N-I: n-impervious area; N-P: n-perv; D-i: dstore-impervious area; D-p: dstore-pervious; Max-R: maxrate; Min-R: minrate; D-c: decay constant; and D-t: drying time.
Table A2. Design parameters of permeable pavement (PP) and bioretention cells (BCs) applied in the SWMM simulation.
Table A2. Design parameters of permeable pavement (PP) and bioretention cells (BCs) applied in the SWMM simulation.
LayerParameterPPBCsLayerParameterPPBCs
Surface layerBerm height (mm)-450PavementThickness (mm)100-
Vegetation volume fraction (m3/m3)-0.05Void ration (voids/solids) (m3/m3)0.15-
Surface roughness (Manning’s n)0.0120.1Impervious surface fraction0-
Surface slope (percent)0.50.5Permeability (mm/h)500-
Soil layerThickness (mm)-900Clogging factor0-
Porosity (m3/m3)-0.5Storage layerThickness (mm)300300
Field capacity (volume fraction) (m3/m3)-0.15Void ration (voids/solids) (m3/m3)0.40.67
Wilting point (volume fraction) (m3/m3)-0.08Seepage rate to native soil (mm/h)500500
Conductivity (mm/h)-50Clogging factor00
Conductivity slope-10Underdrain layerFlow coefficient2.52.5
Suction head (mm)-80Flow exponent0.50.5
Offset height (mm)100150
Table A3. Pipe diameters for each conduit in the optimized GREI-only and CGGI schemes under the varying DCL.
Table A3. Pipe diameters for each conduit in the optimized GREI-only and CGGI schemes under the varying DCL.
No. PipeDiameter (m)
GREI-OnlyCGGI
DCL = 100%DCL = 66.7%DCL = 33.3%DCL = 0%DCL = 100%DCL = 66.7%DCL = 33.3%DCL = 0%
10.600.25 0.25 0.25 0.53 0.25 0.25 0.40
20.600.25 0.53 0.600.600.25 0.53 0.53
30.800.53 0.600.600.800.53 0.53 0.53
40.53 0.53 0.25 0.25 0.53 0.53 0.25 0.25
50.25 0.25 0.25 0.25 0.25 0.25 0.25 0.60
60.800.600.600.800.800.600.600.25
70.600.25 0.25 0.600.35 0.25 0.25 0.60
80.53 0.53 0.53 0.800.53 0.53 0.53 0.80
90.53 1.000.801.20 0.53 1.000.8 00.80
101.000.800.600.25 1.000.800.600.60
111.000.800.601.001.000.600.53 0.60
120.600.600.25 0.8 00.35 0.600.25 0.60
130.801.20 1.20 0.25 0.601.20 1.20 1.00
140.601.20 1.20 0.53 0.401.20 1.20 1.00
151.000.800.801.000.800.600.600.60
160.600.800.800.400.53 0.800.800.60
170.800.800.800.25 0.800.800.800.53
181.20 0.600.800.53 1.200.600.800.53
190.800.600.800.25 0.600.53 0.600.60
200.800.25 0.800.600.800.25 0.600.80
210.25 1.000.800.800.25 1.000.800.80
220.601.000.800.800.53 0.800.800.53
230.800.800.800.53 0.800.800.53 0.53
241.20 0.400.600.401.20 0.400.53 0.53
250.600.800.600.400.53 0.800.600.25
261.20 0.600.600.25 1.20 0.400.400.25
271.20 0.25 0.25 0.25 1.20 0.25 0.25 0.25
280.800.400.25 0.25 0.800.400.25 0.53
290.400.800.25 0.800.400.800.25 0.40
300.800.53 0.53 0.25 0.800.53 0.53 0.80
310.600.600.600.600.600.600.600.60
320.800.600.53 0.600.800.600.53 0.80
330.800.25 0.53 0.800.800.25 0.53 0.25
340.800.25 0.800.800.800.25 0.600.25
350.800.800.801.000.800.800.601.50
360.800.801.000.25 0.800.801.001.00
371.50 0.25 0.25 1.20 1.50 0.25 0.25 1.20
381.50 1.001.001.20 1.50 1.001.000.25
391.501.201.50 1.50 1.50 1.20 1.5 0.80
401.50 1.20 1.20 1.20 1.50 1.001.000.25
411.000.800.25 0.25 0.800.800.25 0.25
421.20 0.800.25 2.001.20 0.800.25 0.80
430.25 2.001.50 0.800.25 1.5 1.50 1.00
442.001.001.20 1.001.50 1.001.20 1.00
451.20 0.801.002.001.20 0.801.001.20
461.20 0.801.002.001.20 0.800.801.20
471.20 0.25 0.800.25 1.20 0.25 0.800.80
481.20 0.25 0.25 0.25 1.20 0.25 0.25 0.25
490.800.800.800.600.400.800.800.60
500.25 0.602.001.000.25 0.53 1.50 0.80
510.600.801.50 0.600.53 0.801.500.25
520.600.53 0.800.25 0.53 0.53 0.600.25
530.25 0.25 0.800.800.25 0.25 0.600.25
540.25 0.25 0.801.000.25 0.25 0.600.25
550.25 0.800.25 1.000.25 0.800.25 0.25
560.800.25 0.800.600.800.25 0.800.80
570.800.800.800.800.800.600.801.00
580.802.001.000.800.802.001.000.53
592.000.53 0.400.802.000.53 0.35 0.80
600.600.800.600.600.600.8 00.600.60
610.25 0.25 0.800.600.25 0.25 0.800.60
620.800.25 0.800.800.400.25 0.800.25
631.000.25 0.800.25 1.000.25 0.800.25
640.800.25 0.600.25 0.400.25 0.600.80
651.000.800.600.25 1.000.600.600.60
660.600.601.000.800.53 0.600.800.80
671.20 2.000.800.401.20 2.000.800.35
682.000.800.25 0.25 2.000.800.25 0.25
690.400.400.600.25 0.400.400.600.25
700.25 0.800.25 0.25 0.25 0.800.25 0.25
710.600.800.800.25 0.600.800.800.25
720.800.25 0.800.800.800.25 0.800.80
730.801.001.000.53 0.801.001.000.60
740.25 2.000.800.53 0.25 2.000.800.60
752.002.000.53 0.53 2.002.000.53 0.60
762.000.600.25 0.25 2.000.53 0.25 0.25
770.25 0.600.25 0.53 0.25 0.53 0.25 0.40
780.25 0.250.600.53 0.25 0.25 0.53 0.25
790.53 0.600.601.2 0.53 0.53 0.53 1.00
800.6 00.251.20 0.25 0.53 0.25 1.20 1.5
810.25 1.202.000.800.25 1.20 1.50 0.80
820.25 0.251.002.000.25 0.25 1.001.20
830.25 2.000.25 0.25 2.000.25
842.000.25 2.000.25
850.25 0.25
Table A4. Manhole depths for each node in the optimized GREI-only and CGGI schemes under the varying DCL.
Table A4. Manhole depths for each node in the optimized GREI-only and CGGI schemes under the varying DCL.
No. ManholeDepth (m)
GREI-onlyCGGI
DCL = 100%DCL = 66.7%DCL = 33.3%DCL = 0%DCL = 100%DCL = 66.7%DCL = 33.3%DCL = 0%
11.861.991.05 1.05 1.871.971.05 1.44
21.781.802.171.421.701.802.171.05
31.05 1.421.791.05 1.05 1.421.791.57
42.242.651.541.782.252.651.531.92
52.511.872.931.832.511.812.921.45
61.601.051.421.771.481.05 1.412.10
71.433.533.814.331.433.533.783.87
82.642.263.343.902.652.153.312.80
92.941.601.05 2.092.941.571.05 2.47
101.922.713.182.701.712.643.103.64
111.932.643.103.551.862.573.033.57
122.002.172.132.111.942.122.121.05
133.042.022.021.643.052.012.012.23
143.181.051.05 1.223.191.05 1.05 1.53
153.241.681.491.05 3.251.711.441.36
162.361.052.401.752.361.05 2.192.04
171.05 1.952.453.171.05 1.932.453.19
181.741.872.033.051.731.641.982.78
193.561.051.722.71 3.571.05 1.482.71
201.891.551.531.551.841.551.531.05
212.041.911.361.05 1.951.901.361.78
222.061.931.05 1.661.971.921.05 2.00
232.591.051.141.05 2.591.05 1.141.05
243.842.452.091.583.852.442.091.58
251.05 1.981.561.05 1.05 1.981.561.05
262.171.811.05 2.472.171.811.05 1.05
272.311.672.141.05 2.311.662.142.00
281.05 1.051.05 1.251.05 1.05 1.05 1.05
294.102.903.602.254.102.903.602.61
304.263.274.262.414.273.264.261.69
314.914.223.713.364.423.713.672.02
325.024.323.613.795.024.313.573.83
332.712.983.033.872.83 2.972.803.91
342.522.162.714.112.742.162.714.00
352.811.694.971.05 2.801.684.472.93
362.111.764.861.952.041.774.361.05
371.631.051.831.05 1.631.05 1.671.18
381.352.081.691.881.342.081.532.08
391.05 2.381.05 2.181.05 2.381.05 2.38
401.693.171.711.05 1.672.961.673.16
415.164.532.272.385.174.532.253.48
421.351.051.05 1.05 1.351.05 1.05 1.05
432.091.472.512.422.081.472.512.42
442.051.321.821.05 2.301.321.821.32
452.341.051.731.342.591.05 1.731.05
465.264.632.182.255.274.621.962.12
471.05 1.941.901.351.05 1.891.901.35
481.751.791.551.671.741.781.561.67
495.324.691.891.665.334.691.891.84
501.411.761.05 1.551.411.691.05 1.76
511.05 1.051.371.05 1.05 1.05 1.371.05
521.05 1.051.921.05 1.05 1.05 1.921.05
535.424.792.42.265.434.792.331.73
541.05 1.051.561.571.05 1.05 1.521.05
551.05 1.051.05 1.40 1.05 1.05 1.05 1.20
561.05 1.051.33 1.40 1.05 1.05 1.33 1.40
571.05 1.331.401.40 1.05 1.33 1.4 1.33
581.331.401.40 1.60 1.33 1.40 1.33 1.40
591.40 1.331.40 1.33 1.15 1.33 1.33 1.40
601.331.401.60 1.33 1.33 1.40 1.40 1.40
611.60 1.601.60 1.20 1.60 1.40 1.60 1.33
621.60 1.601.40 1.20 1.401.40 1.20 1.33
631.80 1.401.40 1.401.60 1.20 1.40 1.40
641.60 1.201.601.80 1.60 1.20 1.40 1.60
651.40 1.401.80 1.40 1.33 1.33 1.80 1.40
661.40 1.601.40 1.60 1.20 1.60 1.40 1.33
671.60 1.401.33 1.60 1.60 1.40 1.33 1.20
681.40 1.331.60 2.001.40 1.33 1.40 2.00
691.60 1.202.001.80 1.60 1.20 1.80 1.80
701.20 2.001.80 1.60 1.20 1.80 1.80 1.60
712.001.801.60 1.40 2.001.80 1.60 1.40
721.80 1.601.60 1.40 1.60 1.60 1.40 1.60
731.60 1.401.60 1.80 1.20 1.33 1.40 1.60
741.40 1.331.60 1.60 1.33 1.33 1.60 1.33
751.60 1.601.40 1.60 1.60 1.60 1.40 1.60
761.60 1.331.60 1.60 1.60 1.33 1.60 1.60
771.40 1.601.40 1.40 1.40 1.60 1.40 1.40
781.60 1.601.40 1.20 1.20 1.40 1.40 1.15
791.60 1.401.20 1.40 1.20 1.40 1.15 1.40
801.40 1.201.401.60 1.33 1.201.40 1.60
811.20 1.601.601.33 1.20 1.60 1.60 1.40
821.40 1.801.33 1.33 1.40 1.80 1.33 1.20
831.60 1.401.40 1.60 1.33 1.33
841.331.40 1.33 1.33
851.40 1.33

References

  1. Fu, L.; Zhang, Q.; Tang, Y.; Pan, J.; Li, Q. Assessment of urbanization impact on cultural heritage based on a risk-based cumulative impact assessment method. Herit. Sci. 2023, 11, 177. [Google Scholar] [CrossRef]
  2. Piontek, F.; Müller, C.; Pugh, T.A.M.; Clark, D.B.; Deryng, D.; Elliott, J.; Colón González, F.d.J.; Flörke, M.; Folberth, C.; Franssen, W.; et al. Multisectoral climate impact hotspots in a warming world. Proc. Natl. Acad. Sci. USA 2014, 111, 3233–3238. [Google Scholar] [CrossRef]
  3. Wu, J.; Lu, Y.; Gao, H.; Wang, M. Cultivating historical heritage area vitality using urban morphology approach based on big data and machine learning. Comput. Environ. Urban Syst. 2022, 91, 101716. [Google Scholar] [CrossRef]
  4. Sesana, E.; Gagnon, A.S.; Ciantelli, C.; Cassar, J.; Hughes, J.J. Climate change impacts on cultural heritage: A literature review. WIREs Clim. Chang. 2021, 12, e710. [Google Scholar] [CrossRef]
  5. Zhou, S.; Zhang, D.; Wang, M.; Liu, Z.; Gan, W.; Zhao, Z.; Xue, S.; Müller, B.; Zhou, M.; Ni, X.; et al. Risk-driven composition decoupling analysis for urban flooding prediction in high-density urban areas using Bayesian-Optimized LightGBM. J. Clean. Prod. 2024, 457, 142286. [Google Scholar] [CrossRef]
  6. Song, W. Retain the common ground: Implications of research on fringe belt and urban green infrastructure for urban landscape revitalisation, a case of Quanzhou. Landsc. Res. 2022, 48, 64–87. [Google Scholar] [CrossRef]
  7. Adnan, R.M.; Mostafa, R.R.; Wang, M.; Parmar, K.S.; Kisi, O.; Zounemat-Kermani, M. Improved random vector functional link network with an enhanced remora optimization algorithm for predicting monthly streamflow. J. Hydrol. 2025, 650, 132496. [Google Scholar] [CrossRef]
  8. Liu, H.; Zou, L.; Xia, J.; Chen, T.; Wang, F. Impact assessment of climate change and urbanization on the nonstationarity of extreme precipitation: A case study in an urban agglomeration in the middle reaches of the Yangtze river. Sustain. Cities Soc. 2022, 85, 104038. [Google Scholar] [CrossRef]
  9. Borah, A.; Bardhan, R.; Bhatia, U. Protecting heritage: Insights into effective flood management using green infrastructure in a highly urbanized environment. Int. J. Disaster Risk Reduct. 2023, 98, 104075. [Google Scholar] [CrossRef]
  10. Crowley, K.; Jackson, R.; O’Connell, S.; Karunarthna, D.; Anantasari, E.; Retnowati, A.; Niemand, D. Cultural heritage and risk assessments: Gaps, challenges, and future research directions for the inclusion of heritage within climate change adaptation and disaster management. Clim. Resil. Sustain. 2022, 1, e45. [Google Scholar] [CrossRef]
  11. Dai, T.; Zheng, X.; Yang, J. A systematic review of studies at the intersection of urban climate and historical urban landscape. Environ. Impact Assess. Rev. 2022, 97, 106894. [Google Scholar] [CrossRef]
  12. Su, J.; Wang, M.; Zhang, D.; Yuan, H.; Zhou, S.; Wang, Y.; Adib Mohammad Razi, M. Integrating technical and societal strategies in Nature-based Solutions for urban flood mitigation in Guangzhou, a heritage city. Ecol. Indic. 2024, 162, 112030. [Google Scholar] [CrossRef]
  13. Lafrenz Samuels, K.; Platts, E.J. Global Climate Change and UNESCO World Heritage. Int. J. Cult. Prop. 2022, 29, 409–432. [Google Scholar] [CrossRef]
  14. Kourtis, I.M.; Tsihrintzis, V.A. Adaptation of urban drainage networks to climate change: A review. Sci. Total Environ. 2021, 771, 145431. [Google Scholar] [CrossRef] [PubMed]
  15. Chen, W.; Wang, W.; Huang, G.; Wang, Z.; Lai, C.; Yang, Z. The capacity of grey infrastructure in urban flood management: A comprehensive analysis of grey infrastructure and the green-grey approach. Int. J. Disaster Risk Reduct. 2021, 54, 102045. [Google Scholar] [CrossRef]
  16. Roozbahani, A.; Behzadi, P.; Massah Bavani, A. Analysis of performance criteria and sustainability index in urban stormwater systems under the impacts of climate change. J. Clean. Prod. 2020, 271, 122727. [Google Scholar] [CrossRef]
  17. Zhang, K.; Manuelpillai, D.; Raut, B.; Deletic, A.; Bach, P.M. Evaluating the reliability of stormwater treatment systems under various future climate conditions. J. Hydrol. 2019, 568, 57–66. [Google Scholar] [CrossRef]
  18. Li, L.; Collins, A.M.; Cheshmehzangi, A.; Chan, F.K.S. Identifying enablers and barriers to the implementation of the Green Infrastructure for urban flood management: A comparative analysis of the UK and China. Urban For. Urban Green. 2020, 54, 126770. [Google Scholar] [CrossRef]
  19. Staddon, C.; Ward, S.; De Vito, L.; Zuniga-Teran, A.; Gerlak, A.K.; Schoeman, Y.; Hart, A.; Booth, G. Contributions of green infrastructure to enhancing urban resilience. Environ. Syst. Decis. 2018, 38, 330–338. [Google Scholar] [CrossRef]
  20. Tansar, H.; Duan, H.-F.; Mark, O. A multi-objective decision-making framework for implementing green-grey infrastructures to enhance urban drainage system resilience. J. Hydrol. 2023, 620, 129381. [Google Scholar] [CrossRef]
  21. Zhang, Y.; Yin, H.; Zhang, D.; Kong, F.; Xu, J.; Wang, M.; Yuan, H. Enhancing resilience of green-grey infrastructure by integrating two redundancy strategies into a multi-objective optimization and service period assessment framework. Sustain. Cities Soc. 2025, 128, 106474. [Google Scholar] [CrossRef]
  22. Zhou, S.; Diao, H.; Wang, J.; Jia, W.; Xu, H.; Xu, X.; Wang, M.; Sun, C.; Qiao, R.; Wu, Z. Multi-stage optimization framework for synergetic grey-green infrastructure in response to long-term climate variability based on shared socio-economic pathways. Water Res. 2025, 274, 123091. [Google Scholar] [CrossRef] [PubMed]
  23. Liu, M.; Wang, Z.; Wang, M.; Li, X.; Zhang, Y.; Yang, B.; Lai, C. A framework for optimization and assessment of long-term urban stormwater management scenarios under climate change and performance challenges. J. Environ. Manag. 2025, 390, 126298. [Google Scholar] [CrossRef] [PubMed]
  24. Wang, M.; Liu, M.; Zhang, D.; Qi, J.; Fu, W.; Zhang, Y.; Rao, Q.; Bakhshipour, A.E.; Tan, S.K. Assessing and optimizing the hydrological performance of Grey-Green infrastructure systems in response to climate change and non-stationary time series. Water Res. 2023, 232, 119720. [Google Scholar] [CrossRef] [PubMed]
  25. Park, S.; Kim, J.; Yun, H.; Kang, J. Exploring the network structure of coupled green-grey infrastructure to enhance urban pluvial flood resilience: A scenario-based approach focusing on ‘centralized’ and ‘decentralized’ structures. J. Environ. Manag. 2024, 370, 122344. [Google Scholar] [CrossRef]
  26. Zhou, H.; Gao, C.; Luan, Q.; Shi, L.; Lu, Z.; Liu, J. Multi-objective optimization of distributed green infrastructure for effective stormwater management in space-constrained highly urbanized areas. J. Hydrol. 2024, 644, 132065. [Google Scholar] [CrossRef]
  27. Wang, L.; Zhao, J.; Xiong, Z.; Zhuang, J.a.; Wang, M. Integrating Grey–Green Infrastructure in Urban Stormwater Management: A Multi–Objective Optimization Framework for Enhanced Resilience and Cost Efficiency. Appl. Sci. 2025, 15, 3852. [Google Scholar] [CrossRef]
  28. Zhang, X.; Jia, H. Low impact development planning through a comprehensive optimization framework: Current gaps and future perspectives. Resour. Conserv. Recycl. 2023, 190, 106861. [Google Scholar] [CrossRef]
  29. Ghodsi, S.H.; Zahmatkesh, Z.; Goharian, E.; Kerachian, R.; Zhu, Z. Optimal design of low impact development practices in response to climate change. J. Hydrol. 2020, 580, 124266. [Google Scholar] [CrossRef]
  30. Zhao, Y.; Yingrui, G.; Moru, L.; Zhifeng, Z.; Pengjun, Z. Mobility constraints of residents in marginal rural areas of megacities: Evidence from Beijing, China. J. Transp. Geogr. 2025, 127, 104259. [Google Scholar] [CrossRef]
  31. Xu, A.; Dai, Y.; Hu, Z.; Qiu, K. Can green finance policy promote inclusive green growth?-Based on the quasi-natural experiment of China’s green finance reform and innovation pilot zone. Int. Rev. Econ. Financ. 2025, 100, 104090. [Google Scholar] [CrossRef]
  32. Li, Y.; Li, H.; Miao, R.; Qi, H.; Zhang, Y. Energy–Environment–Economy (3E) Analysis of the Performance of Introducing Photovoltaic and Energy Storage Systems into Residential Buildings: A Case Study in Shenzhen, China. Sustainability 2023, 15, 9007. [Google Scholar] [CrossRef]
  33. Aghaloo, K.; Sharifi, A.; Habibzadeh, N.; Ali, T.; Chiu, Y.-R. How nature-based solutions can enhance urban resilience to flooding and climate change and provide other co-benefits: A systematic review and taxonomy. Urban For. Urban Green. 2024, 95, 128320. [Google Scholar] [CrossRef]
  34. Zheng, J.; Li, J.; Zeng, J.; Huang, G.; Chen, W. Application of a time-dependent performance-based resilience metric to establish the potential of coupled green-grey infrastructure in urban flood management. Sustain. Cities Soc. 2024, 112, 105608. [Google Scholar] [CrossRef]
  35. Zhou, S.; Xu, X.; Xu, H.; Zhao, Z.; Yuan, H.; Wang, Y.; Qiao, R.; Wu, T.; Jia, W.; Wang, M.; et al. From heat resilience to sustainable co-benefits: Adaptive urban morphology generation based on multimodal data fusion and a novel generative framework. Sustain. Cities Soc. 2025, 127, 106452. [Google Scholar] [CrossRef]
  36. Sun, C.; Rao, Q.; Xiong, Z.; Liu, M.; Liu, Y.; Fan, C.; Li, J.; Keat Tan, S.; Wang, M.; Zhang, D. Optimized resilience coupled with cost-effectiveness for grey and green infrastructure: A case study in a historical and cultural area, Guangzhou, China. Ecol. Indic. 2024, 167, 112684. [Google Scholar] [CrossRef]
  37. Rodina, L. Defining “water resilience”: Debates, concepts, approaches, and gaps. WIREs Water 2019, 6, e1334. [Google Scholar] [CrossRef]
  38. Mattos Tiago, S.; Oliveira Paulo Tarso, S.; de Souza Bruno, L.; de Oliveira Nilo, D.; Vasconcelos Jose, G.; Lucas Murilo, C. Improving Urban Flood Resilience under Climate Change Scenarios in a Tropical Watershed Using Low-Impact Development Practices. J. Hydrol. Eng. 2021, 26, 05021031. [Google Scholar] [CrossRef]
  39. Zhang, Y.; Yin, H.; Liu, M.; Kong, F.; Xu, J. Evaluating the effectiveness of environmental sustainability indicators in optimizing green-grey infrastructure for sustainable stormwater management. Water Res. 2025, 272, 122932. [Google Scholar] [CrossRef]
  40. Huang, K.; Kang, P.; Zhao, Y. Quantitative research of street interface morphology in urban historic districts: A case study of west street historic district, Quanzhou. Herit. Sci. 2024, 12, 226. [Google Scholar] [CrossRef]
  41. Wang, M.; Zhao, J.; Su, J.; Adnan, R.; Yang, M. Navigating Flooding Challenges in Historical Urban Contexts: Integrating Nature-Based Solutions with Spatial Multi-Criteria Assessments in Quanzhou. Land 2025, 14, 452. [Google Scholar] [CrossRef]
  42. Wang, X.; Li, H.; Wang, Y.; Zhao, X. Assessing climate risk related to precipitation on cultural heritage at the provincial level in China. Sci. Total Environ. 2022, 835, 155489. [Google Scholar] [CrossRef] [PubMed]
  43. Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.0; National Risk Management Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Cincinnati, OH, USA, 2010; p. 276. [Google Scholar]
  44. Sun, C.; Rao, Q.; Wang, M.; Liu, Y.; Xiong, Z.; Zhao, J.; Fan, C.; Rana, M.A.I.; Li, J.; Zhang, M. Multi-stage optimization of drainage systems for integrated grey–green infrastructure under backward planning. Water 2024, 16, 1825. [Google Scholar] [CrossRef]
  45. Farina, A.; Di Nardo, A.; Gargano, R.; van der Werf, J.A.; Greco, R. A simplified approach for the hydrological simulation of urban drainage systems with SWMM. J. Hydrol. 2023, 623, 129757. [Google Scholar] [CrossRef]
  46. Sharma, S.; Kumar, S.; Singh, A. Assessment of Green Infrastructure for sustainable urban water management. Environ. Dev. Sustain. 2023, 1–10. [Google Scholar] [CrossRef]
  47. Liu, Y.; Engel, B.A.; Flanagan, D.C.; Gitau, M.W.; McMillan, S.K.; Chaubey, I.; Singh, S. Modeling framework for representing long-term effectiveness of best management practices in addressing hydrology and water quality problems: Framework development and demonstration using a Bayesian method. J. Hydrol. 2018, 560, 530–545. [Google Scholar] [CrossRef]
  48. Sun, Y.-w.; Li, Q.-y.; Liu, L.; Xu, C.-d.; Liu, Z.-p. Hydrological simulation approaches for BMPs and LID practices in highly urbanized area and development of hydrological performance indicator system. Water Sci. Eng. 2014, 7, 143–154. [Google Scholar] [CrossRef]
  49. Wang, M.; Zhang, D.; Cheng, Y.; Tan, S.K. Assessing performance of porous pavements and bioretention cells for stormwater management in response to probable climatic changes. J. Environ. Manag. 2019, 243, 157–167. [Google Scholar] [CrossRef]
  50. Bakhshipour, A.E.; Bakhshizadeh, M.; Dittmer, U.; Haghighi, A.; Nowak, W. Hanging Gardens Algorithm to Generate Decentralized Layouts for the Optimization of Urban Drainage Systems. J. Water Resour. Plan. Manag. 2019, 145, 04019034. [Google Scholar] [CrossRef]
  51. Houle James, J.; Roseen Robert, M.; Ballestero Thomas, P.; Puls Timothy, A.; Sherrard, J. Comparison of Maintenance Cost, Labor Demands, and System Performance for LID and Conventional Stormwater Management. J. Environ. Eng. 2013, 139, 932–938. [Google Scholar] [CrossRef]
  52. Dong, Y. Performance assessment and design of ultra-high performance concrete (UHPC) structures incorporating life-cycle cost and environmental impacts. Constr. Build. Mater. 2018, 167, 414–425. [Google Scholar] [CrossRef]
  53. Yao, Y.; Hu, C.; Liu, C.; Yang, F.; Ma, B.; Wu, Q.; Li, X.; Soomro, S.-E.-H. Comprehensive performance evaluation of stormwater management measures for sponge city construction: A case study in Gui’an New District, China. J. Flood Risk Manag. 2022, 15, e12834. [Google Scholar] [CrossRef]
  54. Meerow, S.; Newell, J.P. Spatial planning for multifunctional green infrastructure: Growing resilience in Detroit. Landsc. Urban Plan. 2017, 159, 62–75. [Google Scholar] [CrossRef]
  55. Haghighi, A.; Bakhshipour, A.E. Optimization of Sewer Networks Using an Adaptive Genetic Algorithm. Water Resour. Manag. 2012, 26, 3441–3456. [Google Scholar] [CrossRef]
  56. Yang, B.; Zhang, T.; Li, J.; Feng, P.; Miao, Y. Optimal designs of LID based on LID experiments and SWMM for a small-scale community in Tianjin, north China. J. Environ. Manag. 2023, 334, 117442. [Google Scholar] [CrossRef] [PubMed]
  57. Butler, D.; Farmani, R.; Fu, G.; Ward, S.; Diao, K.; Astaraie-Imani, M. A New Approach to Urban Water Management: Safe and Sure. Procedia Eng. 2014, 89, 347–354. [Google Scholar] [CrossRef]
  58. Mugume, S.N.; Gomez, D.E.; Fu, G.; Farmani, R.; Butler, D. A global analysis approach for investigating structural resilience in urban drainage systems. Water Res. 2015, 81, 15–26. [Google Scholar] [CrossRef] [PubMed]
  59. He, L.; Li, S.; Cui, C.-H.; Yang, S.-S.; Ding, J.; Wang, G.-Y.; Bai, S.-W.; Zhao, L.; Cao, G.-L.; Ren, N.-Q. Runoff control simulation and comprehensive benefit evaluation of low-impact development strategies in a typical cold climate area. Environ. Res. 2022, 206, 112630. [Google Scholar] [CrossRef]
  60. Yu, L.; Yan, Y.; Pan, X.; Yang, S.; Liu, J.; Yang, M.; Meng, Q. Research on the Comprehensive Regulation Method of Combined Sewer Overflow Based on Synchronous Monitoring—A Case Study. Water 2022, 14, 3067. [Google Scholar] [CrossRef]
  61. Mulligan, J.; Bukachi, V.; Clause, J.C.; Jewell, R.; Kirimi, F.; Odbert, C. Hybrid infrastructures, hybrid governance: New evidence from Nairobi (Kenya) on green-blue-grey infrastructure in informal settlements. Anthropocene 2020, 29, 100227. [Google Scholar] [CrossRef]
  62. Lim, T. Land, Water, Infrastructure and People: Considerations of Planning for Distributed Stormwater Management Systems; University of Pennsylvania: Philadelphia, PA, USA, 2017. [Google Scholar]
  63. Wang, J.; Liu, G.-h.; Wang, J.; Xu, X.; Shao, Y.; Zhang, Q.; Liu, Y.; Qi, L.; Wang, H. Current status, existent problems, and coping strategy of urban drainage pipeline network in China. Environ. Sci. Pollut. Res. 2021, 28, 43035–43049. [Google Scholar] [CrossRef] [PubMed]
  64. Hesarkazzazi, S.; Bakhshipour, A.E.; Hajibabaei, M.; Dittmer, U.; Haghighi, A.; Sitzenfrei, R. Battle of centralized and decentralized urban stormwater networks: From redundancy perspective. Water Res. 2022, 222, 118910. [Google Scholar] [CrossRef] [PubMed]
  65. Johansson, J.; Hassel, H. Modelling, Simulation and Vulnerability Analysis of Interdependent Technical Infrastructures. In Risk and Interdependencies in Critical Infrastructures: A Guideline for Analysis; Hokstad, P., Utne, I.B., Vatn, J., Eds.; Springer: London, UK, 2012; pp. 49–65. [Google Scholar]
  66. Wang, M.; Fu, X.; Zhang, D.; Chen, F.; Liu, M.; Zhou, S.; Su, J.; Tan, S.K. Assessing urban flooding risk in response to climate change and urbanization based on shared socio-economic pathways. Sci. Total Environ. 2023, 880, 163470. [Google Scholar] [CrossRef] [PubMed]
  67. Elmqvist, T.; Andersson, E.; Frantzeskaki, N.; McPhearson, T.; Olsson, P.; Gaffney, O.; Takeuchi, K.; Folke, C. Sustainability and resilience for transformation in the urban century. Nat. Sustain. 2019, 2, 267–273. [Google Scholar] [CrossRef]
  68. Kim, D.; Song, S.-K. The Multifunctional Benefits of Green Infrastructure in Community Development: An Analytical Review Based on 447 Cases. Sustainability 2019, 11, 3917. [Google Scholar] [CrossRef]
  69. Zhang, B.; MacKenzie, A. Trade-offs and synergies in urban green infrastructure: A systematic review. Urban For. Urban Green. 2024, 94, 128262. [Google Scholar] [CrossRef]
  70. Fang, X.; Li, J.; Ma, Q. Integrating green infrastructure, ecosystem services and nature-based solutions for urban sustainability: A comprehensive literature review. Sustain. Cities Soc. 2023, 98, 104843. [Google Scholar] [CrossRef]
  71. Dotto, C.B.; Mannina, G.; Kleidorfer, M.; Vezzaro, L.; Henrichs, M.; McCarthy, D.T.; Freni, G.; Rauch, W.; Deletic, A. Comparison of different uncertainty techniques in urban stormwater quantity and quality modelling. Water Res. 2012, 46, 2545–2558. [Google Scholar] [CrossRef]
  72. Moura Rezende, O.; Ribeiro da Cruz de Franco, A.B.; Beleño de Oliveira, A.K.; Pitzer Jacob, A.C.; Gomes Miguez, M. A framework to introduce urban flood resilience into the design of flood control alternatives. J. Hydrol. 2019, 576, 478–493. [Google Scholar] [CrossRef]
  73. Ronchi, S.; Arcidiacono, A.; Pogliani, L. Integrating green infrastructure into spatial planning regulations to improve the performance of urban ecosystems. Insights from an Italian case study. Sustain. Cities Soc. 2020, 53, 101907. [Google Scholar] [CrossRef]
  74. Rezvani, S.M.H.S.; de Almeida, N.M.; Falcão, M.J.; Duarte, M. Enhancing urban resilience evaluation systems through automated rational and consistent decision-making simulations. Sustain. Cities Soc. 2022, 78, 103612. [Google Scholar] [CrossRef]
  75. Wang, M.; Li, Y.; Yuan, H.; Zhou, S.; Wang, Y.; Adnan Ikram, R.M.; Li, J. An XGBoost-SHAP approach to quantifying morphological impact on urban flooding susceptibility. Ecol. Indic. 2023, 156, 111137. [Google Scholar] [CrossRef]
  76. Liu, X.; Liang, X.; Li, X.; Xu, X.; Ou, J.; Chen, Y.; Li, S.; Wang, S.; Pei, F. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. Urban Plann. 2017, 168, 94–116. [Google Scholar] [CrossRef]
  77. Pradhan, S.; Al-Ghamdi, S.G.; Mackey, H.R. Greywater recycling in buildings using living walls and green roofs: A review of the applicability and challenges. Sci. Total Environ. 2019, 652, 330–344. [Google Scholar] [CrossRef]
Water 17 02325 g001
Figure 1. Base layout plan of the Quanzhou West Street Historic Reserve used in the case study.
Figure 1. Base layout plan of the Quanzhou West Street Historic Reserve used in the case study.
Water 17 02325 g001
Water 17 02325 g002
Figure 2. Optimized spatial configurations of the GREI-only and CGGI drainage schemes under DCL = 0, Outlet = 4.
Figure 2. Optimized spatial configurations of the GREI-only and CGGI drainage schemes under DCL = 0, Outlet = 4.
Water 17 02325 g002
Water 17 02325 g003
Figure 3. Operational resilience (Oper-R) of the optimized GREI-only and CGGI schemes under simulated pipeline failure scenarios: (a–d) GREI-only schemes at DCL = 100%, 66.7%, 33.3%, and 0%, respectively; (e–h) CGGI schemes at DCL = 100%, 66.7%, 33.3%, and 0%, respectively. Each curve represents different quantiles (max, 75%, mean, 25%, and min) of Oper-R as network failure levels increase from 0% to 100%.
Figure 3. Operational resilience (Oper-R) of the optimized GREI-only and CGGI schemes under simulated pipeline failure scenarios: (a–d) GREI-only schemes at DCL = 100%, 66.7%, 33.3%, and 0%, respectively; (e–h) CGGI schemes at DCL = 100%, 66.7%, 33.3%, and 0%, respectively. Each curve represents different quantiles (max, 75%, mean, 25%, and min) of Oper-R as network failure levels increase from 0% to 100%.
Water 17 02325 g003
Water 17 02325 g004
Figure 4. Overflow volumes (m3) of the optimized GREI-only and CGGI schemes under varying pipeline failure scenarios.
Figure 4. Overflow volumes (m3) of the optimized GREI-only and CGGI schemes under varying pipeline failure scenarios.
Water 17 02325 g004
Table 1. Maximum and mean pipe diameters and manhole depths for the optimized GREI-only and CGGI schemes under varying DCL levels.
Table 1. Maximum and mean pipe diameters and manhole depths for the optimized GREI-only and CGGI schemes under varying DCL levels.
ParameterUnitGREI-OnlyCGGI
DCL = 100%DCL = 66.7%DCL = 33.3%DCL = 0%DCL = 100%DCL = 66.7%DCL = 33.3%DCL = 0%
Max pipe
diameter		m2.002.002.001.502.002.001.501.50
Mean pipe
diameter		m0.820.710.720.640.770.680.670.60
Max manhole depthm5.424.794.984.355.424.794.484.00
Mean manhole depthm2.081.901.921.872.031.861.871.83
Table 2. Green infrastructure (GI) allocation in the optimized CGGI schemes across different DCL. PP: porous pavement; BCs: bioretention cells. All areas are in m2.
Table 2. Green infrastructure (GI) allocation in the optimized CGGI schemes across different DCL. PP: porous pavement; BCs: bioretention cells. All areas are in m2.
Sub-Catchment No.DCL (%)
10066.733.30
PPBCsPPBCsPPBCsPPBCs
100000000
220000000750
3005000000
42000750750750
52250150022502250
6250075075000
70000125000
822507507502250
9100015050500500
1057502000003750
110000175000
127525500125255025
131250125000500
1412000120001200000
150000375000
160000125000
172000200075000
180000250000
190000100000
20000075000
211000000000
22001750750750
2300000000
24007500000
251500002250750
260000001500
27005000000
2800000000
Total362525265050342525142525
Table 3. Life-cycle cost (LCC) of the optimized GREI-only and CGGI schemes under different DCL. All values are in thousands of U.S. dollars (×103 USD).
Table 3. Life-cycle cost (LCC) of the optimized GREI-only and CGGI schemes under different DCL. All values are in thousands of U.S. dollars (×103 USD).
SchemeDCL (%)Capital GREIO&M GREICapital PPO&M PPCapital BCsO&M BCsTotal LCC
GREI-only1009537.0221,359.54----30,896.56
66.77184.4316,090.59----23,275.02
33.36947.8715,560.77----22,508.64
06005.2913,449.71----19,455.00
CGGI1008966.8420,082.55128.41115.041.973.5229,298.33
66.76790.0815,207.3794.2184.393.896.9622,186.9
33.36390.8414,313.23121.74109.061.973.5220,940.36
05602.0512,546.6051.0745.751.973.5218,250.96
Table 4. Technical resilience (Tech-R, %) of the optimized GREI-only and CGGI schemes under extreme rainfall events.
Table 4. Technical resilience (Tech-R, %) of the optimized GREI-only and CGGI schemes under extreme rainfall events.
Scheme DCL (%)6-h Storm12-h Storm24-h Storm
Return Period = 25 yr Return
Period =
50 yr 		Return
Period = 100 yr 		Return Period = 25 yr Return
Period =
50 yr 		Return
Period = 100 yr 		Return Period = 25 yr Return
Period =
50 yr 		Return
Period = 100 yr
GREI-only10099.698.797.599.698.998.099.799.298.4
66.799.999.599.199.999.799.399.999.799.5
33.310099.498.799.999.598.910099.699.2
010099.899.410099.899.510099.999.6
CGGI10099.698.396.799.698.697.499.799.098.0
66.710099.698.910099.799.110099.899.3
33.399.798.997.799.899.198.199.899.398.6
010099.799.110099.799.110099.899.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Liu, Y.; Xiong, Z.; Wang, M.; Zhang, M.; Adnan, R.M.; Fu, W.; Sun, C.; Tan, S.K. Decentralized Coupled Grey–Green Infrastructure for Resilient and Cost-Effective Stormwater Management in a Historic Chinese District. Water 2025, 17, 2325. https://doi.org/10.3390/w17152325

AMA Style

Liu Y, Xiong Z, Wang M, Zhang M, Adnan RM, Fu W, Sun C, Tan SK. Decentralized Coupled Grey–Green Infrastructure for Resilient and Cost-Effective Stormwater Management in a Historic Chinese District. Water. 2025; 17(15):2325. https://doi.org/10.3390/w17152325

Chicago/Turabian Style

Liu, Yongqi, Ziheng Xiong, Mo Wang, Menghan Zhang, Rana Muhammad Adnan, Weicong Fu, Chuanhao Sun, and Soon Keat Tan. 2025. "Decentralized Coupled Grey–Green Infrastructure for Resilient and Cost-Effective Stormwater Management in a Historic Chinese District" Water 17, no. 15: 2325. https://doi.org/10.3390/w17152325

APA Style

Liu, Y., Xiong, Z., Wang, M., Zhang, M., Adnan, R. M., Fu, W., Sun, C., & Tan, S. K. (2025). Decentralized Coupled Grey–Green Infrastructure for Resilient and Cost-Effective Stormwater Management in a Historic Chinese District. Water, 17(15), 2325. https://doi.org/10.3390/w17152325

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop