A Deep Reinforcement Learning Framework for Cascade Reservoir Operations Under Runoff Uncertainty

Abstract

Effective management of cascade reservoir systems is essential for balancing hydropower generation, flood control, and ecological sustainability, especially under increasingly uncertain runoff conditions driven by climate change. Traditional optimization methods, while widely used, often struggle with high dimensionality and fail to adequately address inflow variability. This study introduces a novel deep reinforcement learning (DRL) framework that tightly couples probabilistic runoff forecasting with adaptive reservoir scheduling. We integrate a Long Short-Term Memory (LSTM) neural network to model runoff uncertainty and generate probabilistic inflow forecasts, which are then embedded into a Proximal Policy Optimization (PPO) algorithm via Monte Carlo sampling. This unified forecast–optimize architecture allows for dynamic policy adjustment in response to stochastic hydrological conditions. A case study on China’s Xiluodu–Xiangjiaba cascade system demonstrates that the proposed LSTM-PPO framework achieves superior performance compared to traditional baselines, notably improving power output, storage utilization, and spillage reduction. The results highlight the method’s robustness and scalability, suggesting strong potential for supporting resilient water–energy nexus management under complex environmental uncertainty.

1. Introduction

Amidst the global transition toward sustainable energy systems and the pursuit of carbon neutrality, hydropower has reaffirmed its pivotal role as a large-scale renewable energy source [1]. Beyond its capability to deliver stable and dispatchable electricity, hydropower contributes significantly to mitigating climate change and ensuring energy security. In regions such as the United Kingdom, facilities like the Dinorwig pumped-storage station exemplify hydropower’s capacity to stabilize grids that increasingly rely on intermittent renewable sources [2]. Similarly, countries such as India are experiencing rapid growth in clean energy adoption, underscoring hydropower’s essential position in diversified energy portfolios [3]. With the continued development of large cascade reservoir systems in major river basins, the demand for integrated operation has intensified—necessitating a balance between flood control, hydropower production, and ecological objectives. Among the various operational strategies, mid- to long-term scheduling remains a cornerstone for enhancing water resource efficiency and system resilience [4].

Most existing studies frame reservoir operation problems under deterministic inflow scenarios or simplified stochastic inputs, primarily focusing on single- or multi-objective optimization such as maximizing hydropower output or minimizing spillage [5]. Classical optimization approaches such as Dynamic Programming (DP) and its improved variants [6,7] like Successive Approximation (DPSA) have been widely applied. However, DP suffers severely from the “curse of dimensionality,” which becomes prohibitive in large-scale, multi-reservoir systems with complex interdependencies [8]. Variants such as DPSA attempt to alleviate this by decomposing the system into single-reservoir subproblems, yet this decomposition-coordination trade-off often sacrifices global optimality [9]. Additionally, methods like linear programming (LP) [10] are efficient for convex formulations such as flood mitigation [11], but fail to capture nonlinearities inherent in hydropower production curves [12]. To address these limitations, heuristic algorithms such as Genetic Algorithms (GA) [13] and Particle Swarm Optimization (PSO) [14] have been introduced, offering enhanced computational efficiency and solution flexibility [15]. Nonetheless, their reliance on parameter tuning and initial population quality can lead to convergence toward local optima, and their robustness under dynamic or extreme hydrological scenarios remains limited.

A pervasive shortcoming of these methodologies is their reliance on fixed or statistically expected inflow inputs, which poorly capture the increasing uncertainty and non-stationarity of runoff processes. This oversight may result in suboptimal operation strategies, especially under extreme hydrological or climate scenarios. As a consequence, the robustness and adaptability of long-term planning could be significantly compromised. The increasing variability in hydrological patterns, driven by climate change [16] and frequent extreme events [17], exacerbates these challenges, underscoring the necessity for optimization frameworks that explicitly incorporate runoff uncertainty [18]. Stochastic approaches [19], such as Stochastic Dynamic Programming (SDP) and Implicit Stochastic Optimization (ISO), have been developed to incorporate inflow variability. SDP models inflow uncertainty through transition probability matrices but suffers from accuracy loss due to discretization, especially in high-variability regimes [20]. ISO, by contrast, employs massive deterministic sampling to extract operational heuristics, which can be effective in data-rich basins like the upper Yellow River [21], yet its adaptability to changing climate conditions is limited.

Reinforcement Learning (RL) offers a promising alternative by enabling agents to learn adaptive scheduling strategies through interaction with a dynamic environment [22]. Algorithms like Q-learning [23] and its deep learning-based successors have shown potential in water resource systems with uncertain inflows. Recent advancements in Deep Reinforcement Learning (DRL) have expanded the capabilities of RL in handling high-dimensional state-action spaces [24], especially when integrated with multi-objective optimization frameworks. Deep Reinforcement Learning have demonstrated superior adaptability compared to traditional techniques, enabling real-time policy adjustment in response to runoff variability and structural system changes [25]. Despite these developments, a critical challenge remains: the disjoint treatment of inflow prediction and operational optimization. Current RL-based approaches typically respond to sampled or expected inflow scenarios, but fail to incorporate uncertain runoff directly into the learning process.

To bridge this gap, we propose a novel forecast–optimize framework that integrates data-driven runoff prediction with adaptive operation optimization. This unified architecture couples a Long Short-Term Memory (LSTM) [26] neural network for probabilistic runoff forecasting with a Proximal Policy Optimization (PPO) [27] reinforcement learning agent for multi-reservoir scheduling. The LSTM model captures nonlinear temporal dynamics and seasonal trends in runoff data, producing probabilistic distributions rather than deterministic point forecasts. These distributions are embedded into the PPO algorithm’s state space through Monte Carlo sampling, allowing the learning of policies that are sensitive to hydrological uncertainty and variability. This integration not only enables more robust and adaptive control but also resolves the long-standing decoupling between prediction and optimization. A real-world case study on the lower Jinsha River cascade reservoir system demonstrates that our method significantly outperforms both DPSA and deterministic PPO baselines, achieving higher power output and lower water spillage. These findings validate the effectiveness and robustness of our proposed framework and underscore its potential for enhancing long-term water-energy system resilience in the face of increasing uncertainty.

The remainder of this paper is organized as follows. Section 2 describes the formulation model, and the implementation of our proposed deep reinforcement learning framework with different components. Section 3 introduces a case study of the cascade reservoir system in the Jinsha River, China and Section 4 presents the detailed results and further discussion. Finally, the conclusions of this study are drawn in Section 5.

2. Methods

2.1. Cascade Reservoir Mid- to Long-Term Optimization Model

The mid- to long-term optimization of cascade reservoir operations leverages the regulatory capacity of reservoirs to redistribute natural runoff, thereby maximizing the comprehensive benefits of the cascade system. Based on the engineering background and actual scheduling requirements from dispatch operators, the proposed model selects three key objectives: power generation, water spillage, and remaining storage capacity.

Power generation is the most direct measure of operational efficiency and is a critical metric in every scheduling period. Water spillage reflects the effective utilization of available inflows—lower spillage indicates more efficient water use—especially relevant during high inflow periods in the flood season. Remaining storage capacity, defined as the difference between total and current reservoir volume, indicates the flood mitigation potential and is crucial during both flood and drawdown periods.

A weighted-sum approach is used to construct a multi-objective joint optimization model aimed at maximizing the comprehensive benefits of the cascade system. This method allows flexible emphasis on different objectives without requiring normalization. As a result, the objective function is define as follows:

$$E=max\sum _{t=1}^T\sum _{i=1}^M\left(\alpha G_{i,t}-\beta D_{i,t}+\gamma W_{i,t}\right)$$

(1)

where:

• E is the total comprehensive benefit of the cascade system.
• $G_{i,t}$ is the power generation of reservoir i at time t (in ${10}^8$ kWh), with weight $\alpha$.
• $D_{i,t}$ is the water spillage (in ${10}^8$ m³ ), with weight $\beta$.
• $W_{i,t}$ is the remaining storage capacity (in ${10}^8$ m³ ), with weight $\gamma$.
• T is the total number of time periods; M is the number of reservoirs.

To ensure the feasibility and operational realism of the optimization model, the objective function must be subject to a series of physical, hydraulic, and policy-driven constraints. These constraints reflect the fundamental principles of water balance, engineering safety limits, and system operation requirements, and are essential for maintaining the integrity of the cascade system across all reservoirs and time periods. The following words define the key constraints applied to the model, including water balance, reservoir water levels, discharge capacity, power output, and boundary conditions.

(1)

Water Balance:

$$V_{i,t+1}=V_{i,t}+(I_{i,t}-O_{i,t})·\Delta T$$

(2)

where $V_{i,t}$ and $V_{i,t+1}$ denote the storage of reservoir i at time t and $t+1$ respectively. $I_{i,t}$ is the inflow to reservoir i, which follows a probability distribution $\mathcal{N}({\mu }_t,{\sigma }_t)$ for the headwater reservoir ($i=1$), and is equal to the outflow of the upstream reservoir for downstream ones. $O_{i,t}$ is the outflow; $\Delta T$ is the time interval length.

(2)

Water Level Constraints:

$$Z_{i,t}^{min}\le Z_{i,t}\le Z_{i,t}^{max}$$

(3)

$$|Z_{i,t}-Z_{i,t+1}|\le \Delta Z_i$$

(4)

where $Z_{i,t}^{min}$ and $Z_{i,t}^{max}$ are the minimum and maximum allowable water levels, and $\Delta Z_i$ is the maximum permissible fluctuation for reservoir i during one period.

(3)

Discharge Constraints:

$$O_{i,t}^{min}\le O_{i,t}\le O_{i,t}^{max}$$

(5)

where $O_{i,t}^{min}$ and $O_{i,t}^{max}$ are the minimum and maximum allowable discharges for reservoir i, determined by dam safety, navigation, ecological, and water supply requirements.

(4)

Power Output Constraints:

$$N_{i,t}^{min}\le N_{i,t}\le N_{i,t}^{max}\left(H_{i,t}\right)$$

(6)

where $N_{i,t}^{min}$ is the minimum allowable output, and $N_{i,t}^{max}\left(H_{i,t}\right)$ is the maximum output derived from the water head $H_{i,t}$ based on the reservoir’s head-output curve.

(5)

Boundary Conditions:

$$Z_{i,1}=Z_i^{\mathrm{begin}},Z_{i,T}=Z_i^{\mathrm{end}}$$

(7)

where $Z_i^{\mathrm{begin}}$ and $Z_i^{\mathrm{end}}$ are the initial and final water levels for reservoir i over the scheduling horizon.

The goal is to determine the optimal operation trajectory or dispatching policy for each reservoir in the cascade system, such that the overall comprehensive benefit E is maximized, subject to all physical and operational constraints outlined above.

2.2. Problem Reformulation

The mid- to long-term optimization of cascade reservoir operations is a high-dimensional, nonlinear, and constraint-rich problem. Due to the complex hydraulic coupling, stochastic inflows, and multiple conflicting objectives, this problem is considered NP-hard, indicating that it is computationally intractable to solve optimally using conventional optimization methods in polynomial time. Classical techniques such as dynamic programming or mixed-integer programming face severe limitations in scalability and solution tractability, especially when applied to long scheduling horizons and large-scale reservoir systems.

To address these challenges, we reformulate the original optimization problem into a Markov Decision Process (MDP) framework, which is well-suited for modeling sequential decision-making under uncertainty. In the MDP setting, the reservoir system is viewed as a dynamic environment where an agent interacts with the system by taking actions based on observed states and receives feedback in the form of rewards. The goal is to learn a policy that maximizes the cumulative expected reward over time.

The MDP is defined by the following components:

The action at time step t is defined as the set of target end-of-period water levels for all reservoirs:

$$A_t=\{Z_{1,t+1},Z_{2,t+1},\dots ,Z_{M,t+1}\}$$

(8)

where M denotes the number of reservoirs, and $Z_{i,t+1}$ is the end-of-period water level for reservoir i at time t.

The state at time $t+1$ consists of the current water levels of all reservoirs, the inflow to the headwater reservoir, and the time index:

$$S_{t+1}=\{Z_{1,t+1},Z_{2,t+1},\dots ,Z_{M,t+1},I_{1,t+1},t+1\}$$

(9)

Here, $I_{1,t+1}$ represents the inflow to the headwater reservoir at time $t+1$. This inflow is modeled as a random variable drawn from a normal distribution $\mathcal{N}({\mu }_t,{\sigma }_t)$. To efficiently sample from this distribution and ensure consistent uncertainty representation across decision episodes, we apply stratified sampling by dividing the distribution into N equal-probability intervals and selecting the expected value within each interval as the representative inflow.

The reward at each time step is defined based on the original objective function, capturing the trade-offs among power generation, water spillage, and flood control capacity:

$$R_t=\sum _{i=1}^M\left(\alpha G_{i,t}-\beta D_{i,t}+\gamma W_{i,t}\right)$$

(10)

where $G_{i,t}$ is the hydropower output, $D_{i,t}$ is the spilled water volume, and $W_{i,t}$ is the remaining storage capacity for reservoir i at time t. The coefficients $\alpha$, $\beta$, and $\gamma$ are user-defined weights reflecting the relative importance of each objective.

The MDP formulation naturally accommodates the stochasticity of inflows and the dynamic interdependence among reservoirs, making it a robust foundation for intelligent, adaptive water resources management. This reformulation into an MDP allows the use of reinforcement learning algorithms to derive optimal or near-optimal dispatch policies.

2.3. Deep Reinforcement Learning Framework

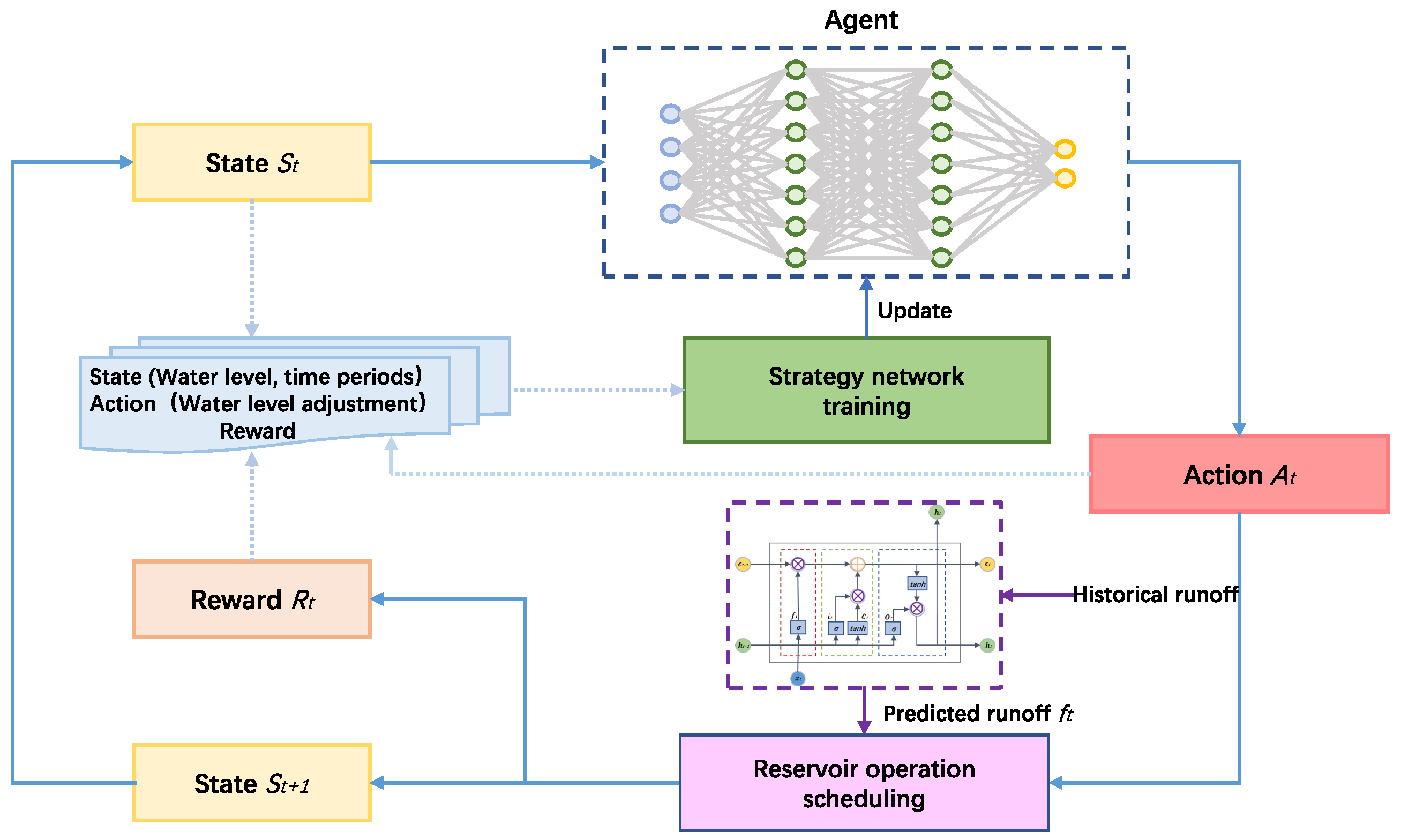
As shown in Figure 1, this study proposes a novel mid- to long-term optimization framework for cascade reservoir operations that integrates Long Short-Term Memory (LSTM) networks with Proximal Policy Optimization (PPO). The proposed framework links probabilistic runoff forecasting with uncertainty-aware decision-making by first using LSTM to extract temporal features from historical runoff data and generate probabilistic forecasts (e.g., mean and standard deviation). These forecasts are then incorporated into a PPO-based multi-objective scheduling model via Monte Carlo sampling. The agent learns adaptive strategies through interaction with the environment, balancing hydropower generation, flood control, and ecological objectives. By embedding runoff uncertainty directly into the optimization process, the proposed approach enhances the robustness and responsiveness of scheduling decisions under complex hydrological conditions.

2.3.1. LSTM-Based Probabilistic Runoff Forecasting

The Long Short-Term Memory (LSTM) network, a specialized form of recurrent neural network (RNN), is employed in this study to model the temporal dynamics of runoff processes and generate probabilistic inflow forecasts. Unlike traditional RNNs, which often suffer from vanishing or exploding gradient problems when modeling long sequences, LSTMs incorporate a sophisticated internal gating mechanism that enables the retention and selective forgetting of information across extended time steps. This structure enhances the network’s capacity to learn long-range dependencies in time series data, making it particularly suitable for hydrological applications characterized by seasonal and inter-annual variability. The architecture of the LSTM model is illustrated in Figure 2.

The LSTM architecture consists of memory cells regulated by three primary gates: the forget gate, the input gate, and the output gate. These gates collectively control the flow of information into, through, and out of each memory cell.

(1)

Forget Gate

The forget gate determines which parts of the previous cell state should be retained or discarded. It takes as input the current external input vector $x_t$ and the previous hidden state $h_{t-1}$, and produces a forget vector $f_t$ via a sigmoid activation function. Mathematically, this is expressed as:

$$f_t=\sigma (W_f·[h_{t-1},x_t]+b_f)$$

(11)

Here, $\sigma$ and $W_f$ represent the weight matrix and bias for the forget gate, respectively.

(2)

Input Gate

The input gate regulates the incorporation of new information into the current cell state. It first generates a candidate cell state ${\tilde{C}}_t$ using a hyperbolic tangent activation function:

$${\tilde{C}}_t=tanh(W_c·[h_{t-1},x_t]+b_c)$$

(12)

Simultaneously, an input activation vector $i_t$ is calculated using a sigmoid function:

$$i_t=\sigma (W_i·[h_{t-1},x_t]+b_i)$$

(13)

The new cell state $C_t$ is then updated by combining the contributions from the forget and input gates:

$$C_t=f_t\times C_{t-1}+i_t\times {\tilde{C}}_t$$

(14)

(3)

Output Gate

The output gate governs the generation of the new hidden state $h_t$, which also serves as the output of the LSTM unit. The gate output $o_t$ is calculated as:

$$o_t=\sigma (W_o·[h_{t-1},x_t]+b_o)$$

(15)

Then, the hidden state $h_t$ is updated as:

$$h_t=o_t\times tanh\left(C_t\right)$$

(16)

where $W_o$ and $b_o$ are the weight and bias parameters for the output gate.

(4)

Probabilistic Output Layer

To explicitly account for inflow uncertainty, we extend the conventional LSTM by incorporating a probabilistic output layer. Rather than producing deterministic point estimates, the model outputs the parameters of a probability distribution, thereby capturing both the expected value and the associated uncertainty.

For continuous-valued prediction tasks, we assume that the output follows a Gaussian (normal) distribution. The mean ${\mu }_t$ and the log-variance $log\left({\theta }_t^2\right)$ of the distribution are derived from the hidden state $h_t$ through fully connected layers:

$${\mu }_t=W_{\mu }{h}_t+b_{\mu }$$

(17)

$$log\left({\sigma }_t^2\right)=W_{\sigma }{h}_t+b_{\sigma }$$

(18)

To ensure that the variance ${\theta }_t^2$ remains strictly positive, it is obtained by exponentiating the log-variance:

$${\sigma }_t^2=exp(W_{\sigma }{h}_t+b_{\sigma })$$

(19)

This probabilistic formulation enables the generation of full runoff distributions, rather than single deterministic predictions. These distributions are subsequently sampled via Monte Carlo techniques and incorporated into the state space of the reinforcement learning agent. As a result, the learned policies are inherently sensitive to inflow variability and are thus more robust under stochastic hydrological conditions.

2.3.2. Cascade Reservoir Scheduling Based on PPO

The Proximal Policy Optimization (PPO) algorithm, an advanced reinforcement learning algorithm, is developed based on the policy gradient method. It integrates the advantages of value function methods (QL) to enhance the efficiency and stability of policy gradient approaches, addressing the challenge of insufficient utilization of experimental data in traditional policy gradient algorithms.

The interaction between the Agent and the environment over T time steps forms a sequence $\tau =\{s_1,a_1,s_2,a_2,\dots ,s_T,a_T\}$, where $s_t$ represents the state at time t and $a_t$ denotes the action taken at time t. The probability of sequence $\tau$ occurring under policy $\theta$ is:

$$p_{\theta }\left(\tau \right)=p\left(s_1\right)\prod _{t=1}^T{p}_{\theta }(a_t\mid s_t)p(s_{t+1}\mid s_t,a_t)$$

(20)

The expected feedback value of the Agent under policy $\tau$ is:

$${\overline{R}}_{\theta }=\sum _{\tau }R\left(\tau \right)p_{\theta }\left(\tau \right)$$

(21)

To maximize $R_{\theta }$, the gradient ascent method is employed to update the neural network parameters $\theta$ of the Agent. Using the derivative formula of the log function, the gradient of the expected feedback value is derived as:

$$\nabla {\overline{R}}_{\theta }=\sum _{\tau }R\left(\tau \right)\nabla p_{\theta }\left(\tau \right)=\sum _{\tau }R\left(\tau \right)p_{\theta }\left(\tau \right){\displaystyle \frac{\nabla p_{\theta }\left(\tau \right)}{p_{\theta }\left(\tau \right)}}=\sum _{\tau }R\left(\tau \right)p_{\theta }\left(\tau \right)\nabla log{p}_{\theta }\left(\tau \right)$$

(22)

An approximate expectation is obtained using the average of N samples:

$$\nabla {\overline{R}}_{\theta }={\displaystyle \frac{1}{N}}\sum _{n=1}^{N}R\left({\tau }^n\right)\nabla log{p}_{\theta }\left({\tau }^n\right)={\displaystyle \frac{1}{N}}\sum _{n=1}^N\sum _{t=1}^{T_n}R\left({\tau }^n\right)\nabla log{p}_{\theta }(a_t^n\mid s_t^n)$$

(23)

The parameters $\theta$ of the Agent’s neural network are updated using $\nabla {\overline{R}}_{\theta }$. This process iteratively refines the policy through continuous interaction between the Agent and the environment until convergence.

In policy gradient methods, after the neural network parameters $\theta$ of the agent’s policy are updated, the data sampled under the previous parameters becomes invalid for subsequent updates because it is inherently associated with the policy that generated it. However, policy improvement methods demand a substantial number of samples, and generating new samples for each parameter update incurs significant computational costs. The Proximal Policy Optimization (PPO) algorithm addresses this issue by leveraging the sampled data multiple times across parameter updates. We denote $\nabla {\overline{R}}_{\theta }={\mathbb{E}}_{\tau \sim p_{\theta }}\left[R\left(\tau \right)\nabla log{p}_{\theta }\left(\tau \right)\right]$. If we aim to compute the gradient using the data sampled under the parameters ${\theta }^{\prime }$, then:

$$\nabla {\overline{R}}_{\theta }={\mathbb{E}}_{\tau \sim p_{{\theta }^{\prime }}}\left[{\displaystyle \frac{p_{\theta }\left(\tau \right)}{p_{{\theta }^{\prime }}\left(\tau \right)}}R\left(\tau \right)\nabla log{p}_{\theta }\left(\tau \right)\right]$$

(24)

To express $R\left(\tau \right)$ in a form related to $A^{\theta }(s_t,a_t)$, the above equation can be rewritten as:

$$\nabla {\overline{R}}_{\theta }={\mathbb{E}}_{(s_t,a_t)\sim {\tau }_{{\theta }^{\prime }}}\left[{\displaystyle \frac{p_{\theta }(a_t\mid s_t)}{p_{{\theta }^{\prime }}(a_t\mid s_t)}}{A}^{\theta }(s_t,a_t)\nabla log{p}_{\theta }(a_t^n\mid s_t^n)\right]$$

(25)

Defining the objective function:

$$J^{{\theta }^{\prime }}\left(\theta \right)={\mathbb{E}}_{(s_t,a_t)\sim {\tau }_{{\theta }^{\prime }}}\left[{\displaystyle \frac{p_{\theta }(a_t\mid s_t)}{p_{{\theta }^{\prime }}(a_t\mid s_t)}}{A}^{{\theta }^{\prime }}(s_t,a_t)\right]$$

(26)

To ensure that the distribution of $\theta$ does not deviate significantly from ${\theta }^{\prime }$, a KL divergence penalty term is added:

$$J_{\mathrm{PPO}}^{{\theta }^{\prime }}\left(\theta \right)=J^{{\theta }^{\prime }}\left(\theta \right)-\beta \mathrm{KL}(\theta ,{\theta }^{\prime })$$

(27)

where $\beta$ is a penalty coefficient. If the KL divergence is large, $\beta$ increases to strengthen the penalty; if small, $\beta$ decreases to reduce the penalty. The PPO algorithm updates the Agent’s neural network parameters using $J_{\mathrm{PPO}}^{{\theta }^{\prime }}\left(\theta \right)$, balancing exploration and exploitation to achieve stable policy improvement.

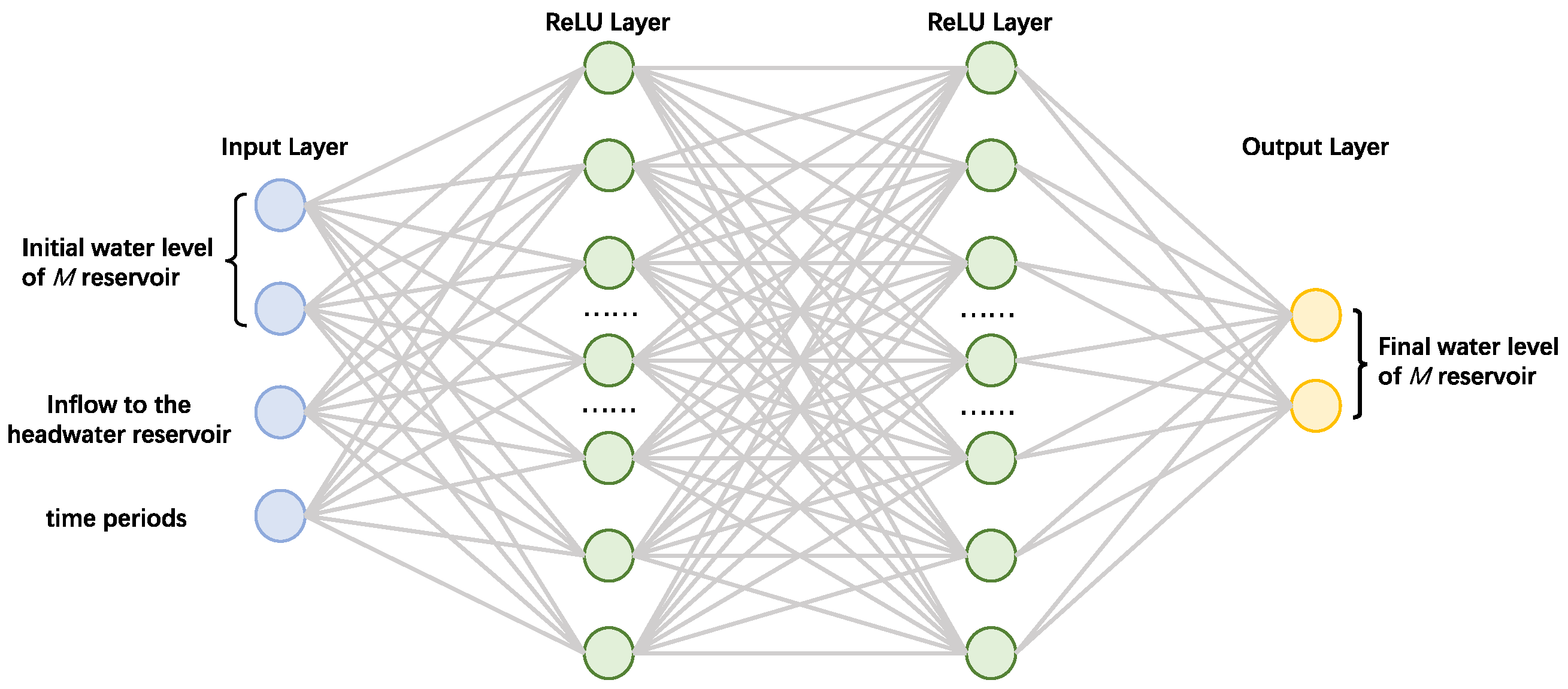
To construct a reinforcement learning algorithm Agent, it is also necessary to incorporate relevant data from cascade reservoir scheduling, which determines the number of input and output nodes in the Agent’s policy neural network. The structure of the policy neural network designed in this study is illustrated in Figure 3. The input layer nodes of the policy network include the initial water levels of each reservoir in the cascade during the current scheduling period, the inflow to the headwater reservoir during that period, and the index of the current time period within the entire scheduling horizon. These input nodes correspond to the state variables of the scheduling environment. The hidden layers of the network are not subject to specific structural constraints; based on the model’s complexity and commonly used PPO architectures, this study adopts two fully connected layers with ReLU activation functions as the hidden layers. The output layer represents the final water levels of each reservoir at the end of the current scheduling period, corresponding to the Agent’s actions in the scheduling environment.

After constructing the policy neural network, it is trained using sample datasets collected from interactions with the scheduling environment. In the dataset, states serve as the inputs and actions serve as the outputs of the network. The policy network is optimized by minimizing a loss function derived from the feedback (reward) values.

3. Case Study

3.1. Study Area and Reservoir Characteristics

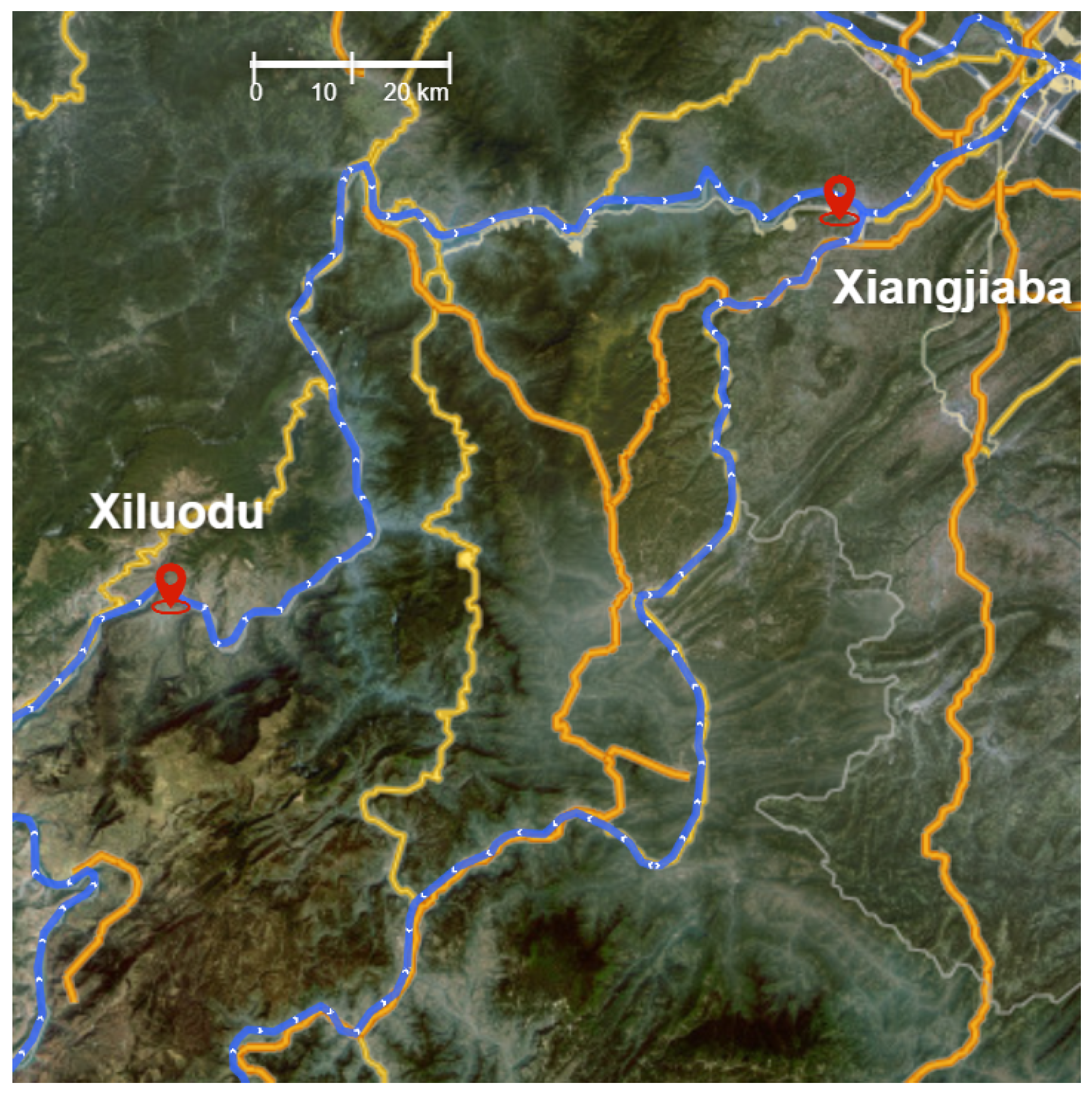
To evaluate the effectiveness of the proposed LSTM-PPO framework, we conduct a case study on the Xiluodu–Xiangjiaba cascade reservoir system located in the lower reaches of the Jinsha River, a major tributary of the Yangtze River in southwestern China. A GIS map of the reservoir system is provided in Figure 4 to illustrate its geographic context. These two hydropower stations are among the largest in China, both in terms of installed capacity and reservoir volume.

The basic parameters of Xiluodu and Xiangjiaba hydropower stations is shown in

Table 1. Basic Parameters of Xiluodu and Xiangjiaba Hydropower Stations.

Power Station	Rated Output (10,000 kW)	Total Reservoir Capacity (100 million m3)	Output Coefficient	Head Loss (m)	Daily Water Level Fluctuation (m/d)
Xiluodu	1260	129.1	8.8	3	3
Xiangjiaba	600	51.63	8.8	0.8	4

. The upstream Xiluodu Reservoir has a rated capacity of 12.6 GW and a total storage volume of 12.91 billion cubic meters. The downstream Xiangjiaba Reservoir, situated in close proximity, has an installed capacity of 6.0 GW and a total volume of 5.163 billion cubic meters. Both reservoirs share a power generation coefficient of 8.8 and exhibit operational flexibility, with daily allowable water level fluctuations of up to 3 m for Xiluodu and 4 m for Xiangjiaba. Given the short travel time of outflows between the two reservoirs—typically within a single day—the hydraulic delay is negligible in the context of mid- to long-term scheduling.

In this study, the inflow between the two reservoirs is ignored due to its minor magnitude relative to the outflow of Xiluodu. Thus, the outflow from Xiluodu is directly used as the inflow to Xiangjiaba in the simulation model, which simplifies the cascade coupling mechanism without compromising realism.

3.2. Experimental Scenarios

The evaluation is performed under multiple temporal resolutions—monthly, weekly, and daily—to examine the model’s adaptability across different planning horizons and hydrological regimes. Historical data from the year 2020 are used for all scenarios.

At the monthly scale, the model simulates a one-year scheduling period. The monthly regulation period constraints of Xiluodu hydropower station and Xiangjiaba hydropower station are shown in

Table 2. Monthly Regulation Period Constraints of Xiluodu Hydropower Station.

Period	Water Level Limit		Outflow Limit		Output Limit
	Upper (m)	Lower (m)	Upper (m3/s)	Lower (m3/s)	Upper (10,000 kW)	Lower (10,000 kW)
2020/1	600	540	50,513	1200	1260	200
2020/2	600	540	50,513	1200	1260	200
2020/3	600	540	50,513	1200	1260	200
2020/4	600	540	50,513	1200	1260	200
2020/5	560	540	50,513	1200	1260	200
2020/6	560	540	50,513	1200	1260	200
2020/7	560	540	50,513	1200	1260	200
2020/8	600	540	50,513	1200	1260	200
2020/9	600	540	50,513	1200	1260	200
2020/10	600	540	50,513	1200	1260	200
2020/11	600	540	50,513	1200	1260	200
2020/12	600	540	50,513	1200	1260	200

and

Table 3. Monthly Regulation Period Constraints of Xiangjiaba Hydropower Station.

Period	Water Level Limit		Outflow Limit		Output Limit
	Upper (m)	Lower (m)	Upper (m3/s)	Lower (m3/s)	Upper (10,000 kW)	Lower (10,000 kW)
2020/1	380	370	50,513	1700	600	100
2020/2	380	370	50,513	1700	600	100
2020/3	380	370	50,513	1700	600	100
2020/4	380	370	50,513	1700	600	100
2020/5	372.5	370	50,513	1700	600	100
2020/6	372.5	370	50,513	1700	600	100
2020/7	372.5	370	50,513	1700	600	100
2020/8	380	370	50,513	1700	600	100
2020/9	380	370	50,513	1700	600	100
2020/10	380	370	50,513	1700	600	100
2020/11	380	370	50,513	1700	600	100
2020/12	380	370	50,513	1700	600	100

. Initial and terminal water levels are set at 590 m for Xiluodu and 377 m for Xiangjiaba. Both reservoirs are subject to standard operational constraints, including reservoir elevation, outflow discharge, and power output limits. During the flood season (May to August), the upper elevation limits are reduced to accommodate flood control requirements. The monthly Regulation Period Constraints of Xiluodu Hydropower Station.

At the weekly scale, the simulation focuses on the dry season from January to March 2020. During this period, the water level at Xiluodu decreases from 590 m to 577 m, while Xiangjiaba’s level rises modestly from 376 m to 377 m. All operational constraints follow the same formulation as in the monthly scenario. The detailed weekly regulation period constraints for cascade reservoirs are shown in

Table 4. Weekly Regulation Period Constraints for Cascade Reservoirs.

Reservoir	Water Level Limit		Outflow Limit		Output Limit
	Upper (m)	Lower (m)	Upper (m3/s)	Lower (m3/s)	Upper (10,000 kW)	Lower (10,000 kW)
Xiluodu	600	540	50,513	1200	1260	200
Xiangjiaba	380	370	50,513	1700	600	100

.

At the daily scale, the model simulates operations during a flood-prone period spanning 18 July to 30 July 2020. This short-term, high-inflow scenario is particularly relevant for assessing the model’s ability to balance energy production with flood mitigation. The initial and final reservoir levels are 565 m and 578 m for Xiluodu, and 372 m and 374 m for Xiangjiaba, respectively. All other constraints are consistent with those used in the weekly model.

3.3. Evaluation Strategy and Baseline Algorithms

To benchmark the proposed LSTM-PPO framework, two well-established optimization methods are used as baselines:

• Successive Approximation Dynamic Programming (DPSA): DPSA is a classical iterative approach for solving multistage decision problems in large-scale water resources systems. It builds upon traditional dynamic programming (DP), addressing the “curse of dimensionality” by decomposing the multi-reservoir system into a sequence of single-reservoir subproblems. The core idea is to optimize one reservoir at a time while keeping the operation policies of the remaining reservoirs fixed, and then iteratively update the policies in a coordinated manner until convergence. In each iteration, DPSA evaluates the expected return of the current policy for a given reservoir, assuming that the policies of all other reservoirs remain unchanged. The reservoir is then re-optimized using dynamic programming techniques (e.g., value iteration), and its policy is updated accordingly. This procedure continues in a cyclic fashion across all reservoirs, progressively improving the overall system performance.
  In our implementation, the water level of each reservoir is discretized using a step size of 0.1 m, and the release decision (action) is also discretized into uniform intervals. Deterministic inflow values (i.e., expected inflows) are used as inputs, ignoring inflow uncertainty. The optimization horizon is consistent with the LSTM-PPO setup (e.g., daily time steps over multiple years). We initialize the reservoir policies using a static rule-based policy derived from traditional reservoir operation curves. A total of 10 successive approximation iterations are performed. Each iteration includes a policy evaluation step and a policy improvement step. If the average absolute deviation of release decisions across all states between two iterations is below ${10}^{-3}$, the algorithm is considered to have converged.
• Deterministic PPO (D-PPO): This baseline employs the Proximal Policy Optimization (PPO) algorithm, omitting any modeling of inflow uncertainty. Like DPSA, D-PPO operates under the assumption of deterministic inflows, which are set as the expected values. The network architecture remains identical to that of the proposed LSTM-PPO framework, including the LSTM-based actor and critic networks, allowing the model to capture temporal dependencies.
  The main difference lies in the lack of an uncertainty representation in the input. D-PPO directly uses historical inflow time series as input to the LSTM layers without any stochastic augmentation. All hyperparameters—such as learning rate ($3\times {10}^{-4}$), batch size (64), discount factor ($\gamma =0.99$), clipping ratio (0.2), and entropy coefficient (0.01)—are kept consistent with LSTM-PPO to ensure fair comparison. This baseline allows us to isolate and assess the added value of uncertainty-aware modeling in the proposed framework.

The performance evaluation strategies vary across temporal scales as follows: For weekly and monthly scales, the maximum power generation is adopted as the exclusive metric to compare the three methods. In contrast, the daily scale employs a multi-metric assessment for the LSTM-PPO algorithm, including total power generation, water spillage, and remaining storage volume.

This experimental design enables a comprehensive evaluation of the proposed framework’s robustness, scalability, and operational effectiveness across varying temporal and hydrological conditions.

4. Results

This section presents a comprehensive analysis of the performance of the proposed LSTM-PPO framework in comparison with two benchmark approaches: Successive Approximation Dynamic Programming (DPSA) and Deterministic Proximal Policy Optimization (D-PPO). The evaluation is conducted across monthly, weekly, and daily scheduling scales to assess convergence behavior, operational effectiveness, and adaptability under different hydrological conditions and objective configurations.

4.1. Programming Frameworks and Environment

All algorithms, including LSTM-PPO, DPSA, and D-PPO, are implemented using Python 3.9 with PyTorch 1.13 for neural network modeling. Simulations were run on a workstation equipped with an Intel Xeon CPU @ 2.4 GHz, 32 GB RAM, and an NVIDIA RTX 3090 GPU.

4.2. Effectiveness of the Proposed Algorithm

In the training process of the PPO algorithm within the LSTM-PPO framework, the agent was trained over 500 episodes to ensure stable convergence of the policy. The learning rate for the policy network was set to $1\times {10}^{-4}$, while the learning rate for the value network is set to $1\times {10}^{-3}$. The Adam optimizer was employed to update the network parameters efficiently. The policy neural network consisted of two hidden layers with 256 units each, both using ReLU activation functions, which effectively captured the complex nonlinear relationships between the state variables and the action variables. This configuration of training parameters and network architecture provided a solid foundation for the agent to learn adaptive scheduling strategies under stochastic hydrological conditions

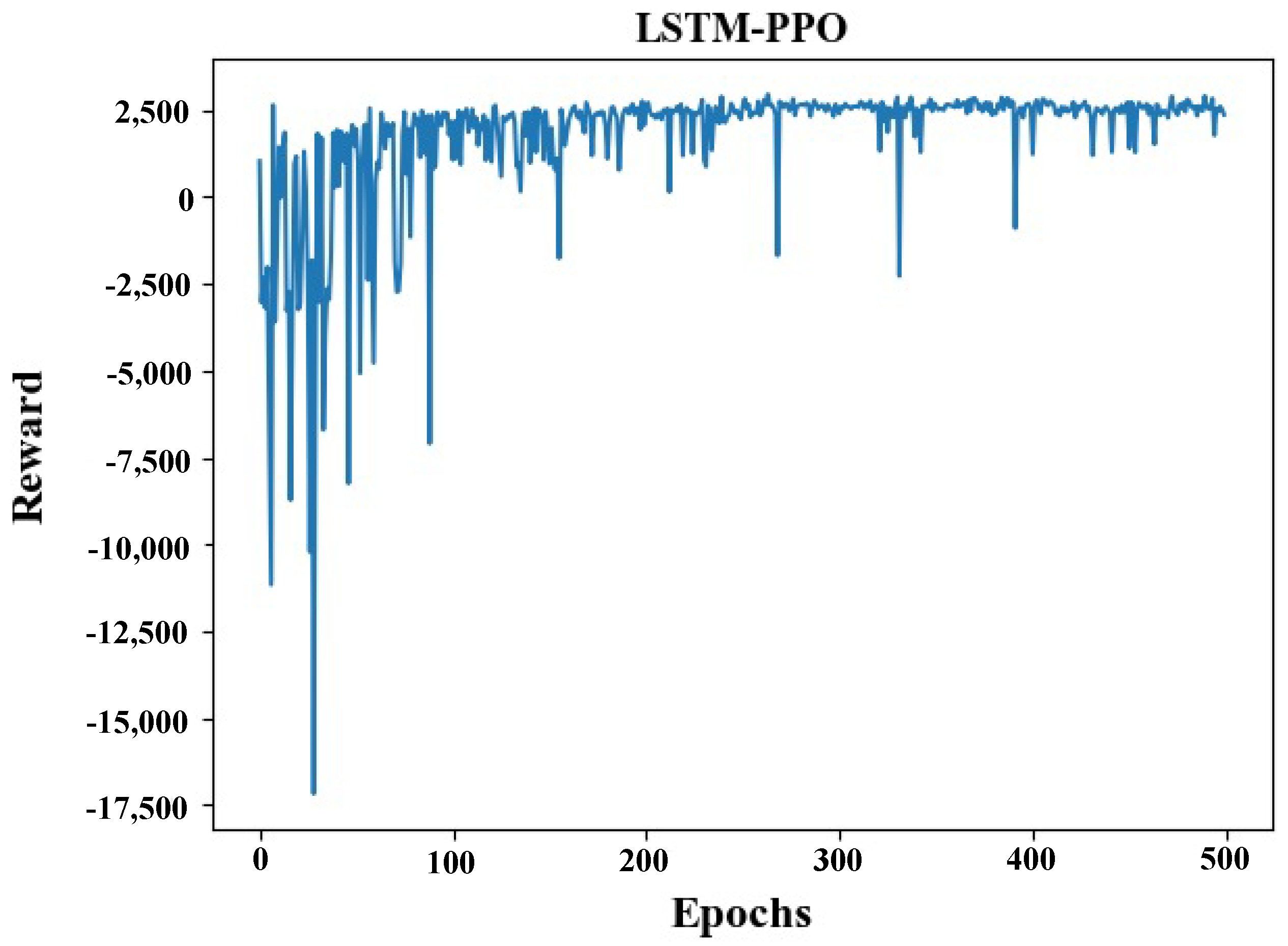
To assess the convergence and learning stability of the LSTM-PPO algorithm, we monitor the cumulative reward and individual objective components over multiple training episodes, as shown in Figure 5. The learning curves show that the LSTM-PPO agent consistently converges to a stable policy within a reasonable number of iterations. This indicates that the integration of probabilistic runoff information does not hinder, and may in fact facilitate, efficient policy learning. Furthermore, the policy demonstrates consistent behavior under repeated sampling of stochastic inflows, reflecting its robustness under uncertainty.

As shown in

Table 5. Runtime performance comparison across algorithms.

Algorithm	Average Training Time per Episode (s)	Power Generation (s)
DPSA	1.2	244.8
D-PPO	1.8	315
LSTM-PPO	2.0	358

, We report the average training time per episode and total convergence time for each algorithm across 10 independent experiments. The LSTM-PPO framework incurs higher computational costs compared to the baseline methods, primarily attributable to the recurrent architecture of the LSTM network and the Monte Carlo sampling required for uncertainty modeling. Specifically, the average training time per episode for LSTM-PPO is 2.0 s, compared to 1.8 s for D-PPO and 1.2 s for DPSA. The total convergence time for LSTM-PPO is also longer than that of D-PPO and DPSA. Nevertheless, the added computational burden is justified by its superior performance in power generation efficiency, spillage reduction, and convergence stability, particularly under conditions of high inflow uncertainty. These results underscore the trade-off between computational cost and operational performance, highlighting the practical value of the proposed framework for real-world reservoir management where robustness under uncertainty is of paramount importance.

4.3. The Performance Comparison of Different Algorithms

To assess the effectiveness of the proposed LSTM-PPO algorithm, a series of comparative experiments were conducted under monthly and weekly scheduling resolutions. The goal of these experiments was to evaluate the performance of LSTM-PPO in contrast with two baseline methods.

4.3.1. Monthly-Scale Scheduling

At the monthly time scale, the scheduling horizon covers a full year (January to December 2020), focusing on maximizing hydropower power output.

Table 6. Month-scale optimization results under different algorithms.

Algorithm	Reservoir	Power Generation (108 kWh)
DPSA	Xiluodu	645.4333
	Xiangjiaba	319.7764
	Total	965.2097
D-PPO	Xiluodu	643.6201
	Xiangjiaba	322.0318
	Total	965.6519
LSTM-PPO	Xiluodu	643.9738
	Xiangjiaba	322.2645
	Total	966.2383

summarizes the aggregated performance metrics. The DPSA algorithm achieved a total energy output of 965.2097 × ${10}^8$ kWh and the D-PPO method slightly improved the energy output to 965.6519 × ${10}^8$ kWh. In contrast, the LSTM-PPO framework maintained a higher level of power generation (966.2383 × ${10}^8$ kWh). These results suggest that, under relatively stable monthly inflow conditions, the incorporation of probabilistic forecasting provides modest gains in resource utilization efficiency.

To further verify the statistical significance of performance disparities between the proposed LSTM-PPO algorithm and baseline methods, we executed 10 independent experimental runs for each algorithm. A two-tailed t-test with a significance level set at $\alpha$ = 0.05 was subsequently employed to analyze key performance metrics, including power generation, spillage, and remaining storage. This statistical procedure aimed to rigorously assess whether the observed performance improvements of the LSTM-PPO algorithm possess robust statistical validity.

In terms of total power generation, the mean difference between LSTM-PPO and DPSA reaches $1.0286$ × ${10}^8$ kWh, with a corresponding p-value of 0.032 (p < 0.05). Similarly, the mean difference between LSTM-PPO and D-PPO is $0.5864$ × ${10}^8$ kWh, accompanied by a p-value of 0.047 (p < 0.05). These results collectively indicate that the total power generation of LSTM-PPO is statistically significantly higher than that of both DPSA and D-PPO.

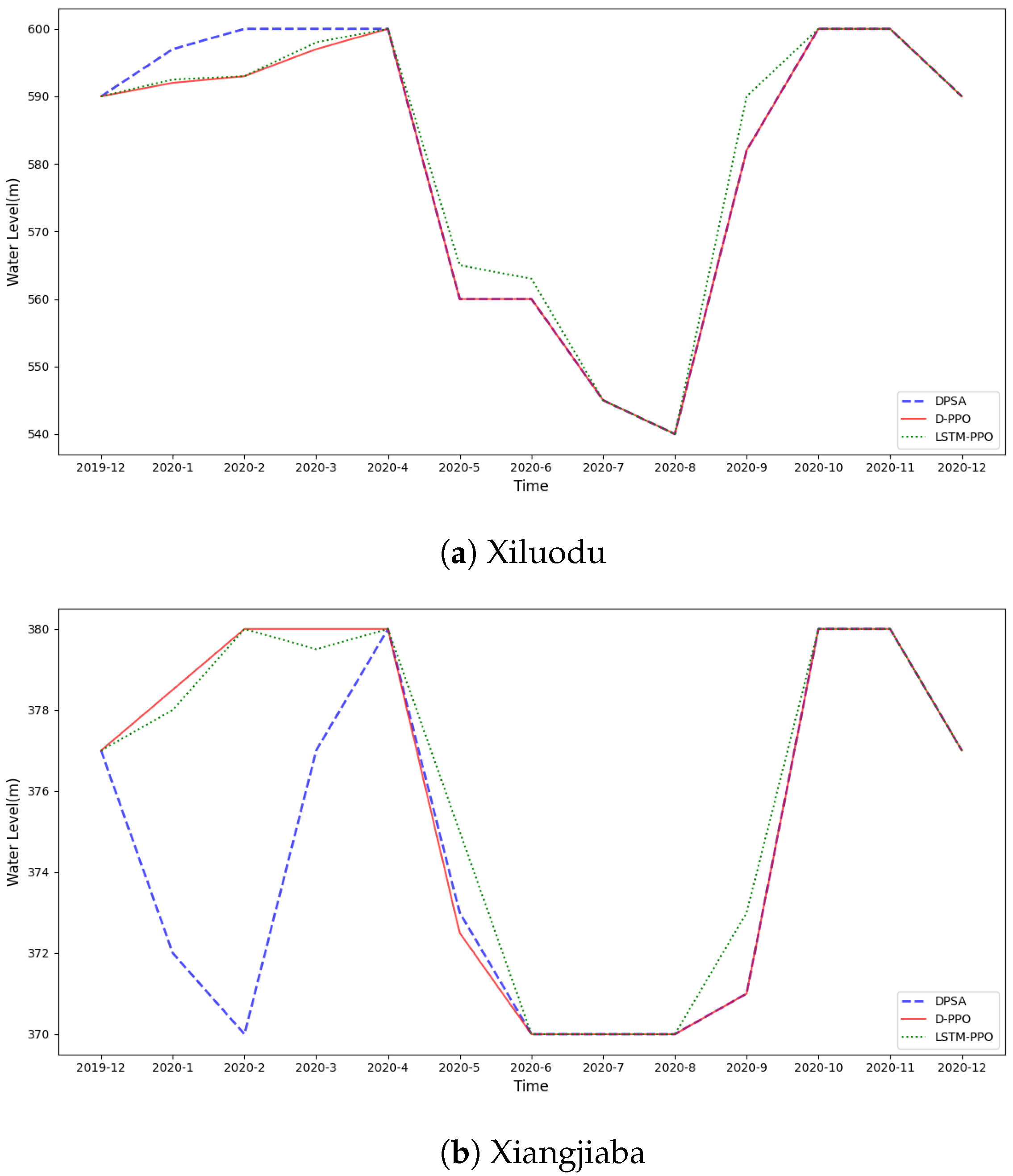
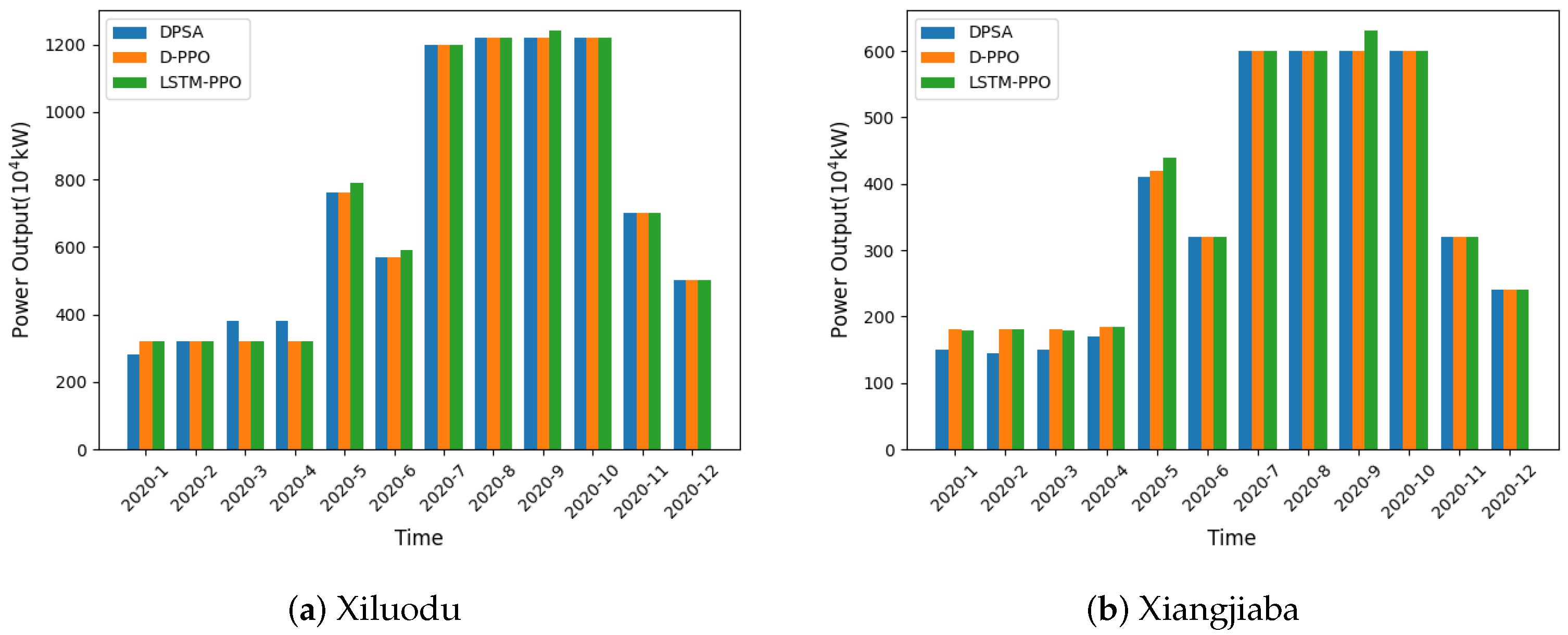
Water level and power output trajectories, shown in Figure 6 and Figure 7, indicate that all three algorithms follow similar seasonal operation patterns. However, the LSTM-PPO model tends to preserve higher water levels before and after the flood season, providing greater flexibility for handling unforeseen runoff extremes.

4.3.2. Weekly-Scale Scheduling

In the weekly-scale scenario, the models simulate operations for the first quarter of 2020—representing the dry season with relatively low and stable inflows. This scenario is particularly useful for examining how the algorithms perform under limited water availability and tighter operational margins.

As presented in

Table 7. Weekly-scale optimization results under different algorithms.

Algorithm	Reservoir	Power Generation (108 kWh)
DPSA	Xiluodu	84.2652
	Xiangjiaba	41.0535
	Total	125.3187
D-PPO	Xiluodu	83.0531
	Xiangjiaba	42.6153
	Total	125.6684
LSTM-PPO	Xiluodu	83.0545
	Xiangjiaba	42.6144
	Total	125.6689

, the DPSA approach yielded a total energy output of 125.3187 × ${10}^8$ kWh and the D-PPO method improved slightly on these metrics, generating 125.6684 × ${10}^8$ kWh. The LSTM-PPO framework achieved nearly identical results, indicating that in low-variability hydrological conditions, uncertainty-aware scheduling does not significantly outperform deterministic baselines. Nevertheless, it maintains robust performance, showing no degradation under dry-season constraints.

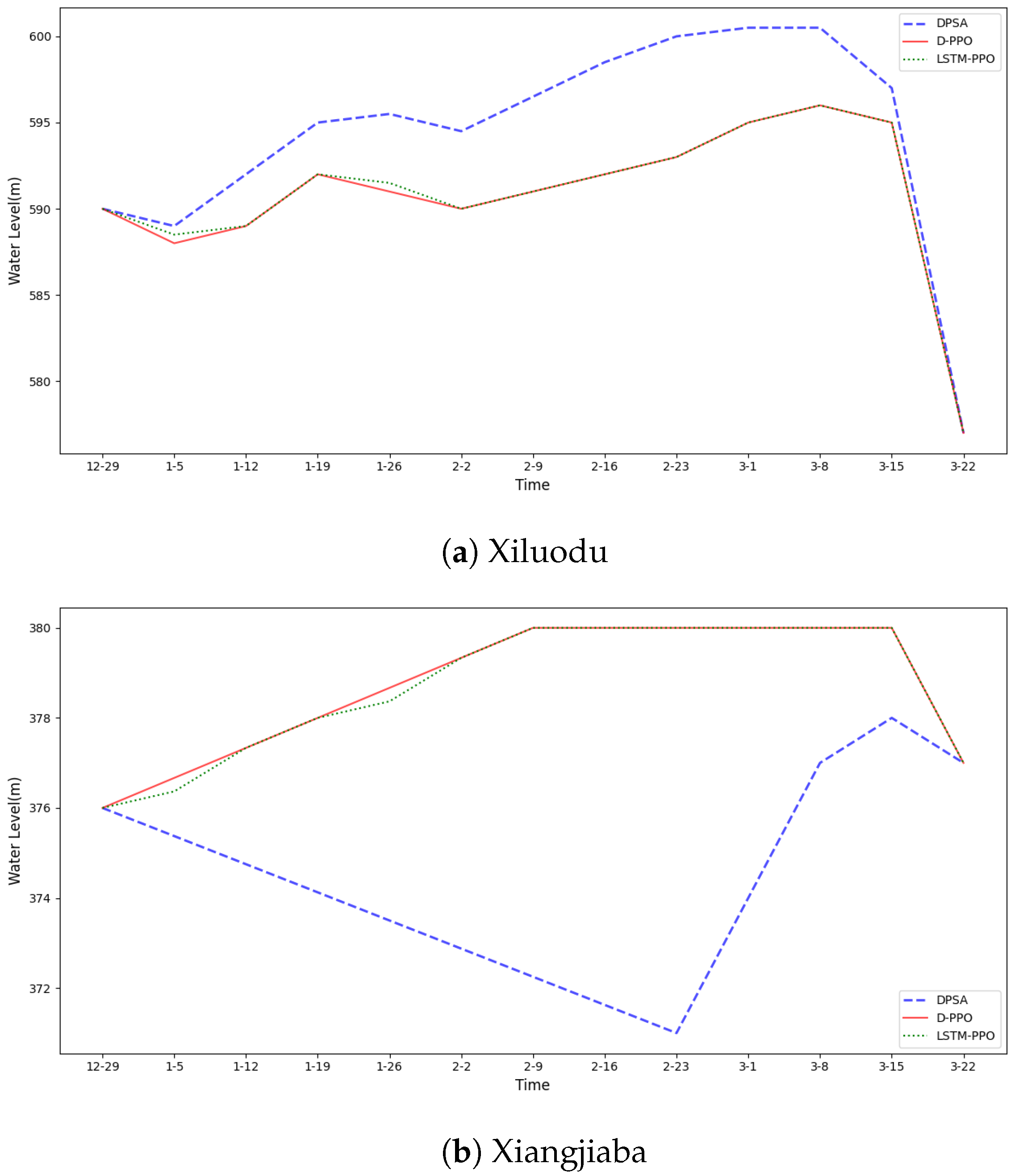
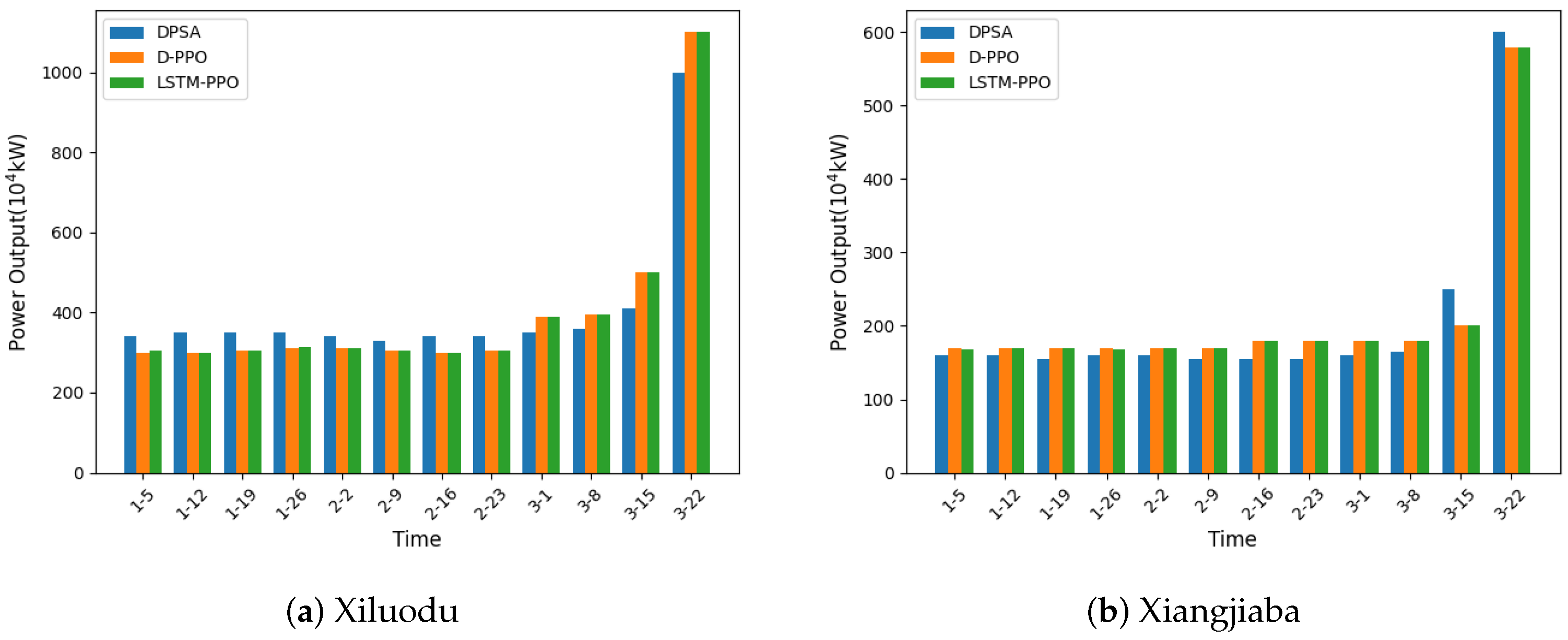
As shown in Figure 8 and Figure 9, the weekly water level and output profiles further confirm that the LSTM-PPO model is capable of reproducing optimal operational patterns under minimal inflow variation, while offering the added benefit of being better prepared for stochastic scenarios.

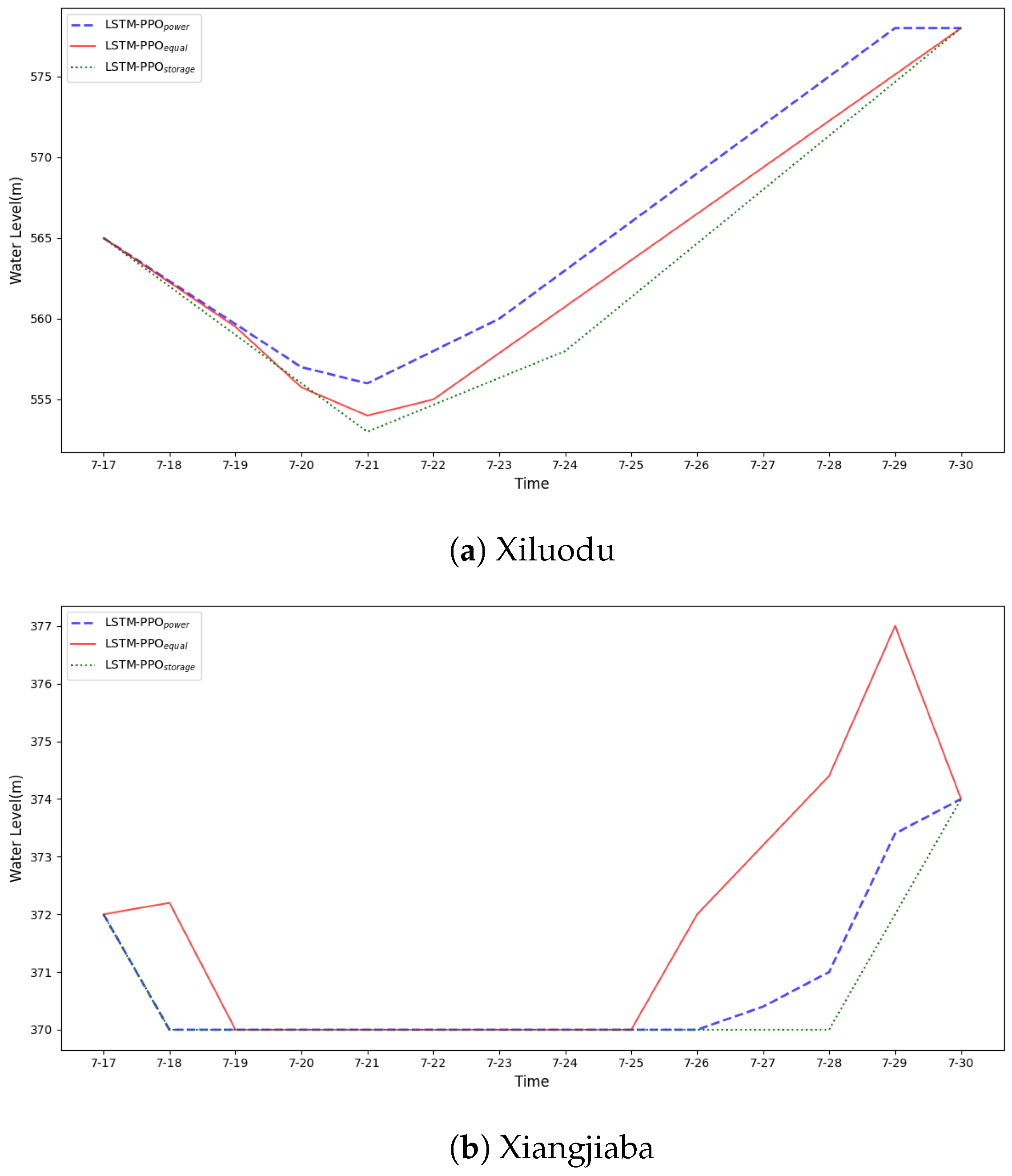
4.4. Daily-Scale Scheduling with Multi-Objective Trade-Offs

To evaluate the flexibility of the LSTM-PPO framework under short-term, high-resolution conditions, a daily-scale scenario was simulated over a 13-day period (18–30 July 2020) during the flood season. The high inflows during this period necessitate a delicate balance between maximizing generation, minimizing spillage, and increasing storage for flood mitigation.

Three optimization configurations were tested:

• Power-Maximization (LSTM-PPO_power): Emphasizes energy production exclusively.
• Equal-Weighting (LSTM-PPO_equal): Assigns equal weights to energy generation and residual storage.
• Storage-Prioritization (LSTM-PPO_storage): Prioritizes residual storage with a 100:1 weight ratio over power generation.

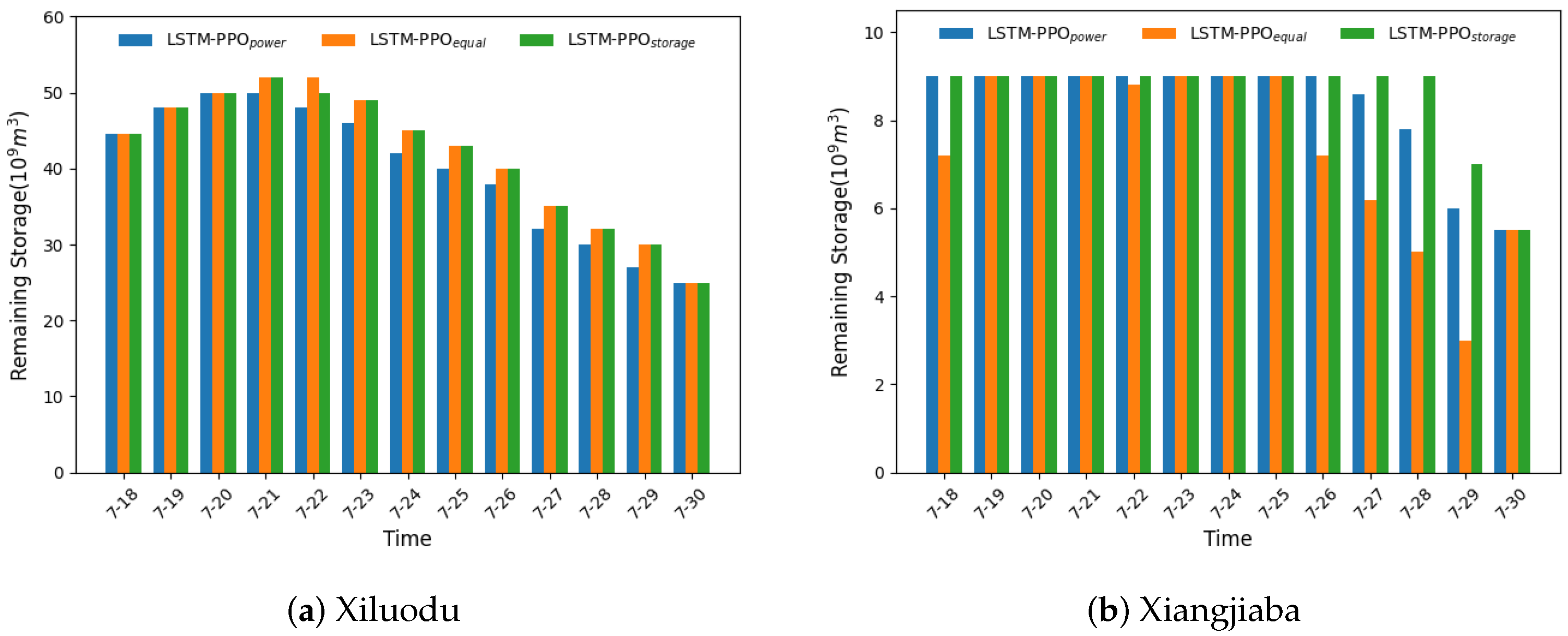
As shown in

Table 8. Daily-scale optimization results under different multi-objective weightings.

Objective	Reservoir	Remaining Storage (108 m3)	Spillage (108 m3)	Power Generation (108 kWh)
LSTM-PPOpower	Xiluodu	529.03	13.53	39.31
	Xiangjiaba	109.60	22.71	18.72
	Total	638.63	36.24	58.03
LSTM-PPOequal	Xiluodu	557.15	17.01	37.21
	Xiangjiaba	97.58	23.41	18.72
	Total	654.73	40.42	55.93
LSTM-PPOstorage	Xiluodu	555.92	15.88	37.70
	Xiangjiaba	112.02	26.54	17.71
	Total	667.94	42.42	55.40

, prioritizing storage (LSTM-PPO_storage) results in significantly higher remaining reservoir volume (6.68 billion m³) and increased spillage (42.42 million m³), but a reduced energy output of 55.40 million kWh. In contrast, the LSTM-PPO_power configuration maximizes generation (58.03 million kWh) but at the cost of lower residual storage and increased risk during peak inflows.

As shown in Figure 10 and Figure 11, the corresponding water level and output trajectories illustrate how the LSTM-PPO framework dynamically adjusts scheduling strategies according to the specified objectives. For example, under LSTM-PPO_storage, water levels are elevated more cautiously during peak inflow periods to enhance buffer capacity, whereas LSTM-PPO_power favors aggressive discharge and generation early in the horizon.

These results highlight the flexibility and adaptability of the LSTM-PPO framework in handling multi-objective trade-offs under daily-scale, high-flow conditions. By adjusting objective weightings, decision-makers can tailor dispatch strategies to emphasize either energy production or flood resilience, enabling the development of context-specific policies that align with broader water resource management goals.

4.5. Discussion

The results of this study offer compelling evidence that integrating probabilistic runoff forecasting with deep reinforcement learning (DRL) significantly enhances the operational performance of cascade reservoirs under conditions of hydrological uncertainty. This improvement is particularly notable when compared to traditional optimization techniques such as Dynamic Programming with Successive Approximation (DPSA) and even deterministic DRL approaches that disregard inflow variability. These findings affirm the initial hypothesis that a unified forecast–optimize framework can better accommodate the nonlinear, stochastic, and multi-objective nature of reservoir scheduling, especially in the face of increasing climate-induced runoff uncertainty.

From a comparative perspective, the performance advantages of the LSTM-PPO framework align with and extend insights from recent literature. Prior studies have shown that DRL methods are effective in large-scale water resource systems due to their ability to handle high-dimensional state-action spaces and learn adaptive strategies over long horizons. However, most existing approaches either assume deterministic inflow inputs or rely on static stochastic representations, thereby decoupling inflow prediction from policy learning. This study addresses that gap by integrating a Long Short-Term Memory (LSTM) network to generate probabilistic forecasts and embedding this uncertainty information directly into the RL agent’s state representation via Monte Carlo sampling. In doing so, the framework allows the policy to adapt to a wider range of hydrological scenarios, including extreme events and shifting seasonal patterns.

The empirical evaluation across monthly, weekly, and daily scheduling horizons demonstrates the robustness and flexibility of the proposed framework. On the monthly scale, where inflow variability is less pronounced, the LSTM-PPO model achieved comparable generation to baseline methods but exhibited improved water storage efficiency and lower spillage. These outcomes suggest that even under relatively stable conditions, incorporating probabilistic forecasting into the decision-making loop enhances operational resilience. On the weekly and daily scales—particularly during flood-prone periods—the advantages of uncertainty-aware scheduling become more pronounced. The LSTM-PPO agent was able to proactively adjust reservoir levels and outflows in anticipation of uncertain high inflows, thereby achieving a better balance between power generation and flood control. Notably, experiments involving multi-objective trade-offs showed that the framework could dynamically shift its operational emphasis in response to changing weightings, highlighting its adaptability and practical utility for real-world reservoir management.

The broader implications of these findings extend to the management of water-energy nexus systems under climate change. As runoff regimes become more variable and less predictable, static or deterministic scheduling strategies are increasingly inadequate. The proposed framework demonstrates how integrating machine learning-based forecasting and adaptive control can support more intelligent, resilient infrastructure management. This is especially relevant for regions facing seasonal extremes, shifting precipitation patterns, and conflicting water use priorities. Moreover, the unified architecture proposed here offers a generalizable methodology that can be adapted to other environmental systems involving uncertainty, sequential decision-making, and competing objectives.

Nonetheless, several limitations and areas for future research remain. First, while the LSTM network effectively captures temporal dependencies in historical runoff data, it does not account for exogenous climatic factors such as temperature, precipitation forecasts, or El Niño–Southern Oscillation indices, which may further enhance prediction accuracy. Future models could integrate multi-modal inputs to better capture complex climatic drivers. Second, although the PPO algorithm performed robustly in our setting, alternative DRL architectures—such as Soft Actor-Critic (SAC) [28] or Transformer-based agents [29]—may offer improved sample efficiency and stability, particularly in more complex basin systems. Third, while this study focuses on two large-scale reservoirs, extending the framework to full river basins with multiple water uses (e.g., irrigation, urban supply, ecological flow requirements) could provide a more comprehensive decision-support tool. Finally, incorporating stakeholder preferences, regulatory constraints, and economic valuation into the reward design could further align the learning framework with real-world decision-making contexts.

5. Conclusions

This study presents a unified deep reinforcement learning framework aimed at optimizing cascade reservoir operations under runoff uncertainty. By integrating a probabilistic runoff forecasting model based on Long Short-Term Memory (LSTM) networks with a Proximal Policy Optimization (PPO) scheduling algorithm, the proposed LSTM-PPO architecture establishes a coherent forecast–optimize paradigm. This coupling enables the direct incorporation of inflow uncertainty into policy learning, thereby enhancing the adaptability and resilience of reservoir operation strategies. Comprehensive experiments on the Xiluodu–Xiangjiaba cascade system demonstrate that the LSTM-PPO framework outperforms both traditional deterministic optimization approaches and baseline DRL models that neglect hydrological uncertainty. Specifically, the proposed method achieves improved power generation efficiency, reduced water spillage, and more robust storage regulation across multiple temporal resolutions and objective configurations. These findings underscore the importance of embedding uncertainty modeling directly into the optimization process, especially in the context of non-stationary climatic and hydrological regimes. Looking forward, this framework provides a promising foundation for further exploration of intelligent water resource management under uncertainty. Future research may extend this work by incorporating additional objectives such as ecological flow maintenance, integrating climate projection data, or scaling the approach to larger, more complex basin-wide systems.