Numerical Simulation Study of Rainfall-Induced Saturated–Unsaturated Landslide Instability and Failure

Abstract

Rainfall infiltration is a key factor affecting the stability of the slope. To study the impact of rainfall on the instability mechanism and stability of slopes, this paper employs numerical simulation to establish a rainfall infiltration slope model and conducts a saturated–unsaturated slope flow and solid coupling numerical analysis. By combining the strength reduction method with the calculation of slope stability under rainfall infiltration, the safety factor of the slope is obtained. A comprehensive analysis is conducted from the perspectives of the seepage field, displacement field and other factors to examine the impact of heavy rainfall patterns and rainfall intensities on the instability mechanism and stability of the slope. The results indicate that heavy rainfall causes the transient saturation zone within the landslide body to continuously move upward, forming a continuous sliding surface inside the slope, which may lead to instability and sliding of the soil in the upper part of the slope toe. The heavy rainfall patterns significantly affect the temporal and spatial evolution of pore water pressure, displacement and safety factors of the slope. Pore water pressure and displacement show a positive correlation with the rainfall intensity at various times during heavy rainfall events. The pre-peak rainfall pattern causes the largest decrease in the safety factor of the slope, and the slope failure occurs earlier, which is the most detrimental to the stability of the slope. The rainfall intensity is inversely proportional to the safety factor. As the rainfall intensity increases, the decrease in the slope’s safety factor becomes more significant, and the time required for slope instability is also shortened. The results of this study provide a scientific basis for analyzing rainfall-induced slope instability and failure.

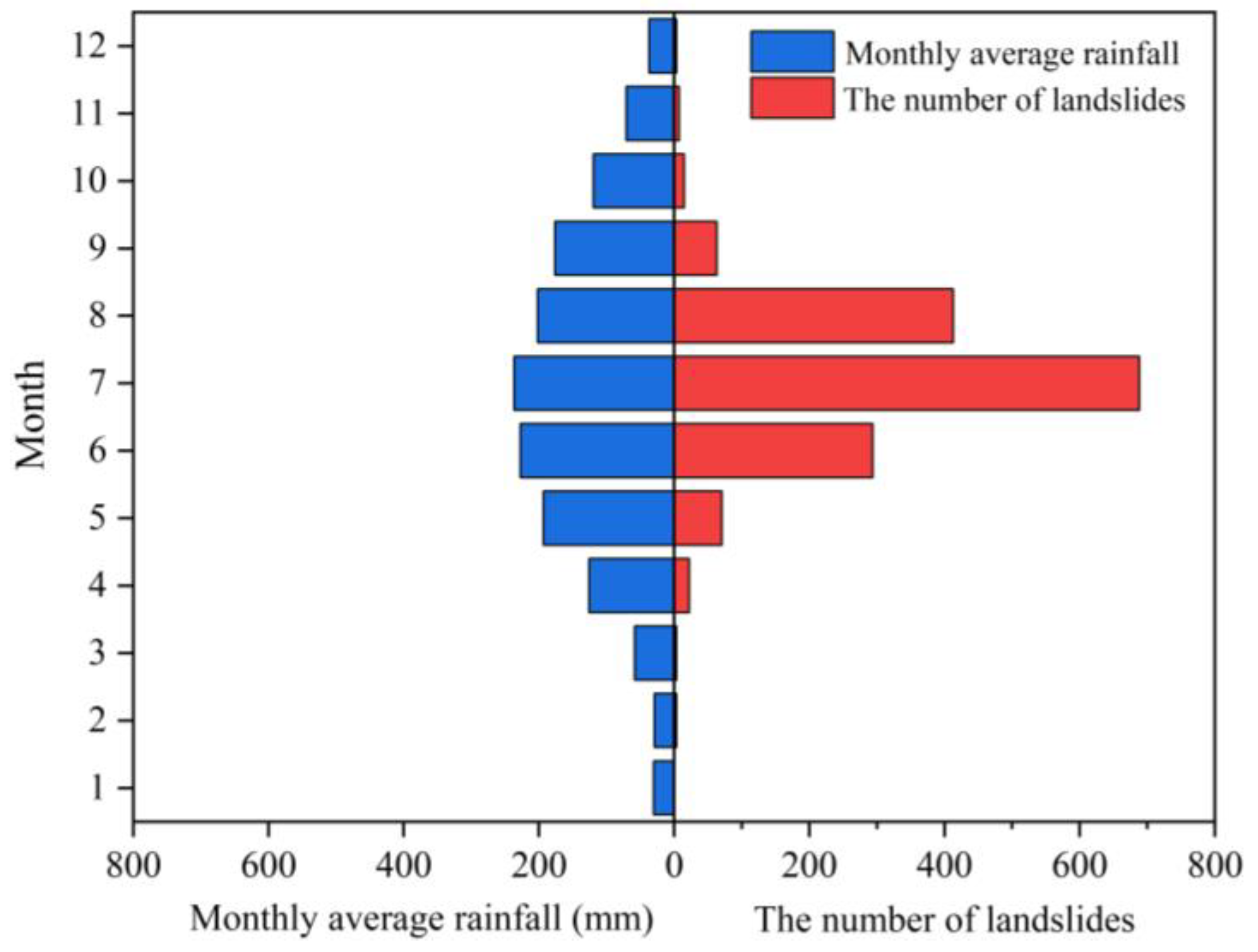
1. Introduction

Landslides are the second most significant natural disaster after earthquakes, causing hundreds of billions of dollars in economic losses and serious casualties worldwide each year [1,2]. The occurrence of landslides is closely related to natural factors and human activities, with rainfall being one of the major influencing factors [3,4]. Rainfall, especially heavy rainfall, can cause the slope materials to (1) increase in moisture content and decrease in matric suction [5,6]; (2) experience a reduction in negative pore water pressure (PWP) and effective stress; (3) present an increase in self-weight and a decrease in shear strength [7,8]. Furthermore, continuous intense rainfall can cause rapid increases in water head within fractures, leading to greater driving forces for slope failure and thereby triggering slope instability [9,10]. Figure 1 shows the relationship between the monthly occurrence frequency of landslides and the average monthly rainfall in the Chongqing region of China. The monthly landslide occurrence frequency is positively correlated with the average monthly rainfall, indicating that the rainwater infiltration effect is a significant trigger for landslides in this area. Therefore, studying the stability of saturated–unsaturated slopes under intense rainfall infiltration has significant practical importance.

Considering the significant impact of rainfall infiltration on landslide stability, researchers both domestically and internationally have conducted extensive studies on this issue. These studies primarily focus on the relationships between rainfall and the strength of landslide materials, pore water pressure and landslide failure mechanisms. Sun et al. [11] conducted a simulated analysis of landslide stability changes under rainfall using Geo-studio 2018 in conjunction with indoor model experiments. They discovered that landslide stability is closely related to the depth of rainfall infiltration. Kafle et al. [12] conducted a transient hydrological analysis to examine the effects of rainfall and reservoir water level fluctuations on the characteristics of slope masses. They found that rainfall increases pore water pressure and reduces shear strength, making it the primary cause of ongoing deformation in slopes, while reservoir water level fluctuations are the main cause of sudden displacements in slopes. Sun et al. [13] conducted numerical simulations based on field monitoring results, concluding that changes in pore water pressure at the sliding surface caused by rainfall infiltration are key factors in landslide initiation. By monitoring relevant data on rainfall-induced instability of fill slopes, they identified that the reduction in matrix suction, which leads to decreased shear strength at the sliding surface, is a critical factor for landslide triggering. Reid et al. [14] investigated the relationship between rainfall amounts and the probability of slope instability. They found that when monthly rainfall reaches or exceeds 300 mm and heavy rainfall exceeds 250 mm, the probability of landslide instability is significantly higher. Rahardjo et al. [15] found that slope stability and pore water pressure are highly sensitive to prior rainfall, with prolonged effects. Regmi et al. [16] conducted model tests on the failure characteristics of gently inclined slopes, revealing a certain pattern between rainfall intensity, the initiation time of sliding and the location of the slip at the base of the slope. Collins and Znidarcic [17], through numerous rainfall-induced landslide cases and theoretical analysis, identified two types of failure modes for rainfall-induced landslides. One mode occurs when the infiltration rate of the slope’s soil and rock is high, leading to rapid development of pore water pressure and quick advancement of the wetting front. In this case, the soil and rock are more likely to reach saturation quickly. Under rainfall conditions, this type of slope experiences shallow instability, as permeability typically plays a dominant role at this time. The other mode occurs when the infiltration rate of the slope’s soil and rock is low, resulting in a slow development of pore water pressure and a gradual advancement of the wetting front. In this case, the soil and rock are less likely to reach saturation. Under rainfall conditions, this type of landslide experiences deeper instability and failure, as the reduction in matrix suction leads to a decrease in the shear strength of the slip surface. Tohari et al. [18] confirmed this through laboratory tests, demonstrating that during the rainfall infiltration process, the unstable area of the slope gradually expands, and instability can be induced without the soil and rock reaching saturation. Xie et al. [19,20,21] found that the slope deformation in active rotating landslides is mainly attributed to the sliding or rotation of the landslide mass along the sliding surface via experiments and field tests. The pre-failure tilt behavior in rain-induced rotating landslides can be predicted through slope tilt measurement. In recent years, deep learning has been widely applied in the field of slope seepage [22,23]. By using intelligent algorithms to analyze and process rainfall-induced landslide monitoring data, effective predictions of instability and failure have been achieved. This also provides new insights for the stability analysis of rainfall-induced slopes.

As mentioned above, it is clear that previous scholars have recognized the importance of rainfall infiltration for slope stability. Rainfall not only raises the groundwater level, creating a transient saturation zone in the soil and rock above the groundwater table, but it also increases the pore water pressure in the corresponding areas. Due to the influence of factors such as the initial moisture content of the soil and rock, infiltration capacity, type of rainfall, duration of rainfall and rainfall intensity, the process of rainfall infiltration in saturated–unsaturated slopes is highly complex and uncertain. Therefore, revealing the comprehensive and accurate impact of rainfall infiltration on slope instability and failure is a topic worthy of in-depth research. This study takes a typical landslide in the Three Gorges Reservoir area of southwest China as an example to establish a numerical simulation model. It considers the interaction between unstable rainfall infiltration and non-linear deformation to conduct a fluid–solid coupling analysis of saturated–unsaturated slopes. By analyzing the effects of different types and intensities of rainfall on slope instability and failure from multiple perspectives, including the seepage field, displacement field and safety factor (SF), this study aims to reveal the intrinsic patterns of slope instability and failure under rainfall infiltration.

2. Numerical Methodology

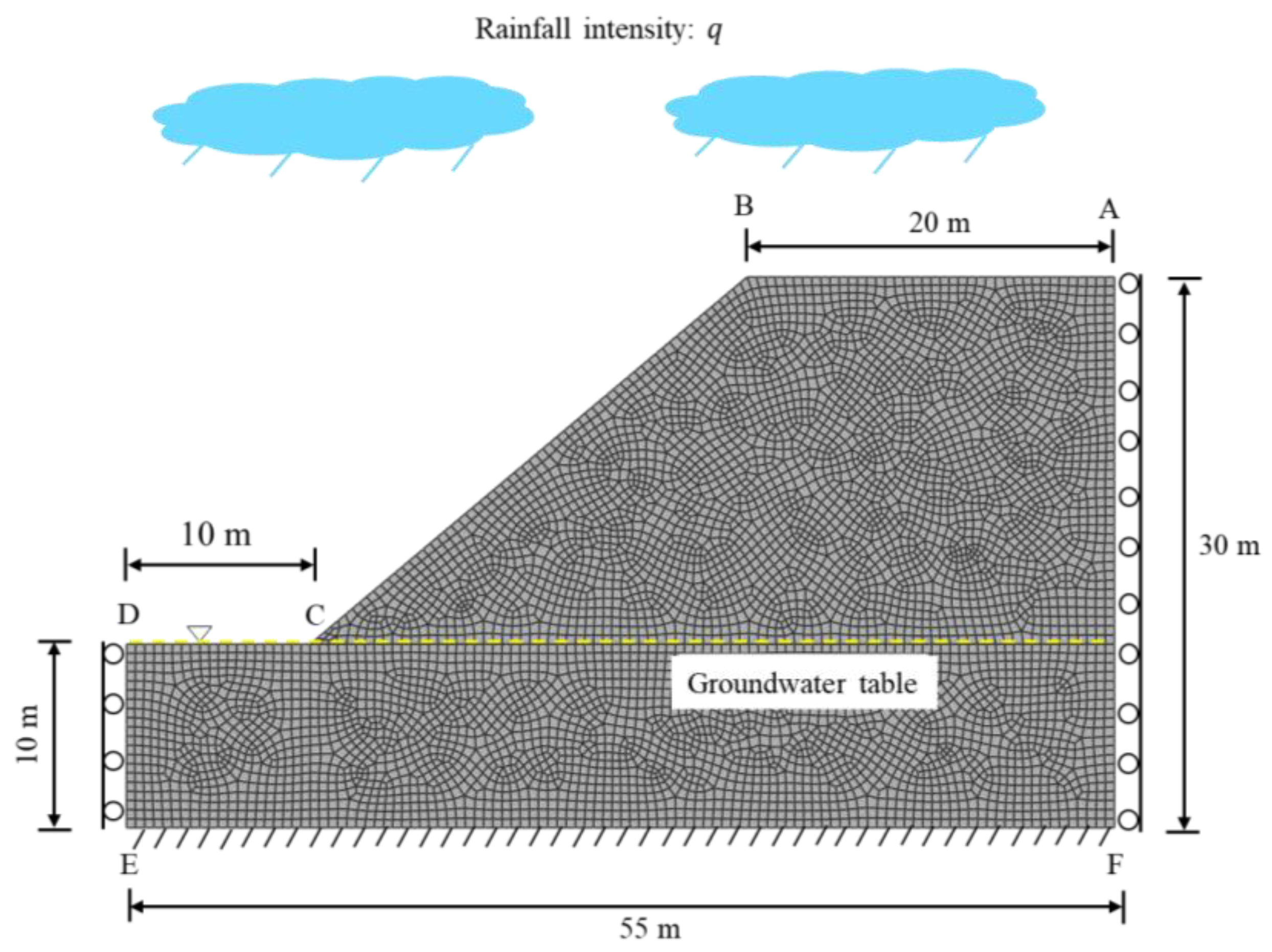
2.1. Geometry and Boundary Conditions

The established slope model is shown in Figure 2, where the length of the slope crest (BA) is 20 m; the slope angle $\theta$ is 40°; the height of the right slope (FA) is 30 m; the height of the left slope (ED) is 10 m; and the length of the slope base (EF) is 55 m. The landslide model is discretized into 4-node Lagrangian elements with degrees of freedom for displacement and PWP (C3D8P) for coupled flow analysis. The slope is meshed with an element size of 0.5 m, resulting in a total of 25,124 quadrilateral elements in the model area. The constitutive model for the soil is based on ideal elastoplasticity, and the yield criterion follows the Mohr–Coulomb strength criterion. The calculations determine the stress, displacement and plastic strain for all nodes within the model. Rainwater infiltration occurs perpendicular to the slope crest surface (i.e., the BA surface) by applying surface pore fluid in ABAQUS, with an infiltration rate equal to the rainfall intensity $q$. For the slope surface (i.e., the BC surface), the corresponding infiltration rate is equal to $q\mathit{cos}\theta$. It should be noted that no other external loads are applied to the slope. It should be noted that a landslide with multiple-material domains or complex geometries may be more realistic, but this would also increase the complexity of finite element simulations. Herein, a simplified finite element model is used for the interpretation of results. Similar simplifications of the numerical model can also be found in Gu et al. [24], Cho et al. [25] and Cheng et al. [26].

2.2. Analysis Step

The current fluid–solid coupling numerical analysis of rainfall-induced slope stability is conducted. This analysis consists of three stages: the steady-state analysis step, the transient analysis step and the static analysis step. In the steady-state analysis step, the fluid velocity and volume do not change over time, allowing for the balance of self-weight stresses in the slope before rainfall, which establishes the initial state of the slope. In the transient analysis step, the variations in PWP, displacement and saturation concerning rainfall duration can be obtained, providing the slope conditions at different rainfall times. Subsequently, a general static analysis step is used to conduct a stability analysis of the slope after rainfall, during which the strength reduction method (SRM) is applied to calculate the SF of the slope.

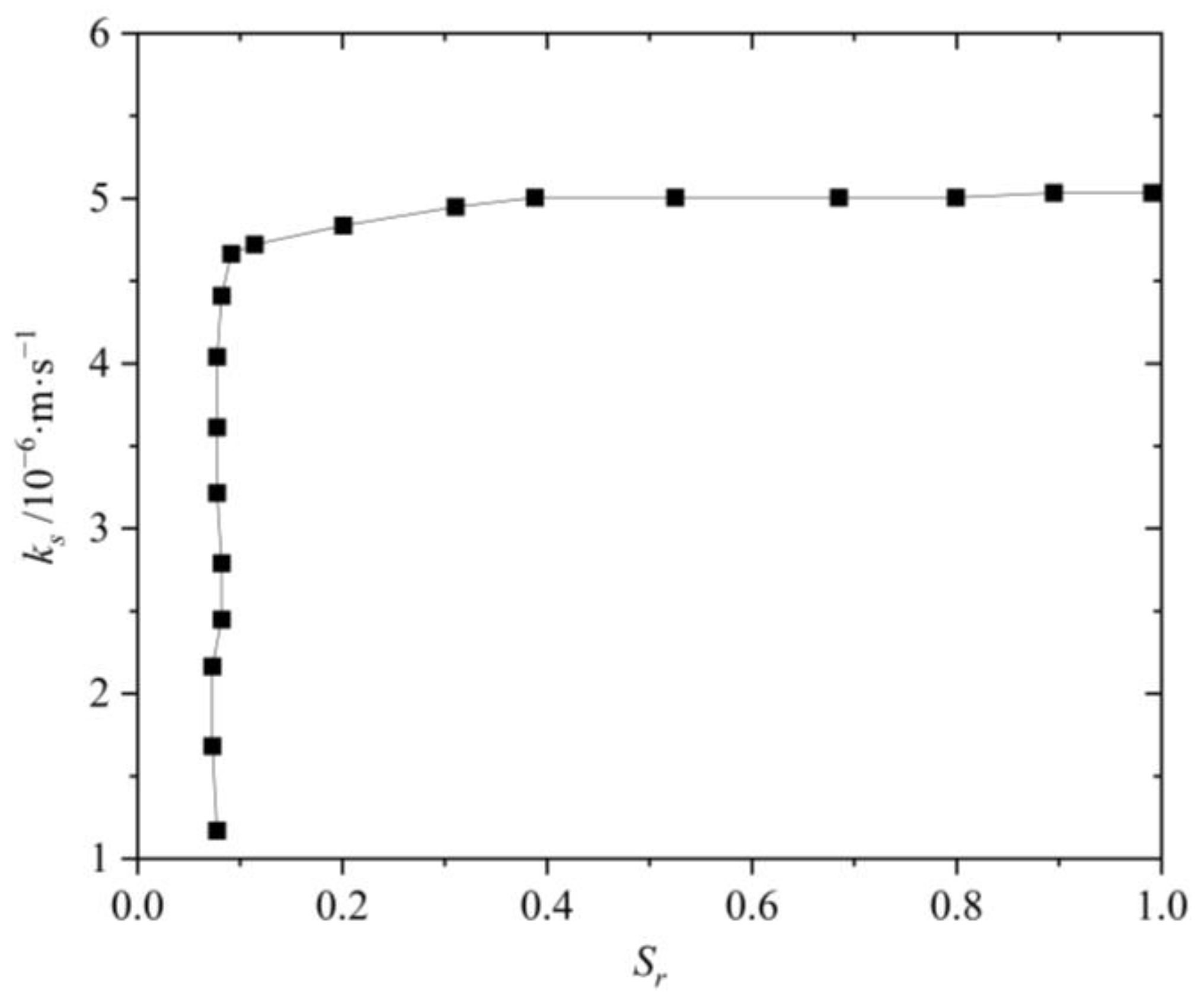
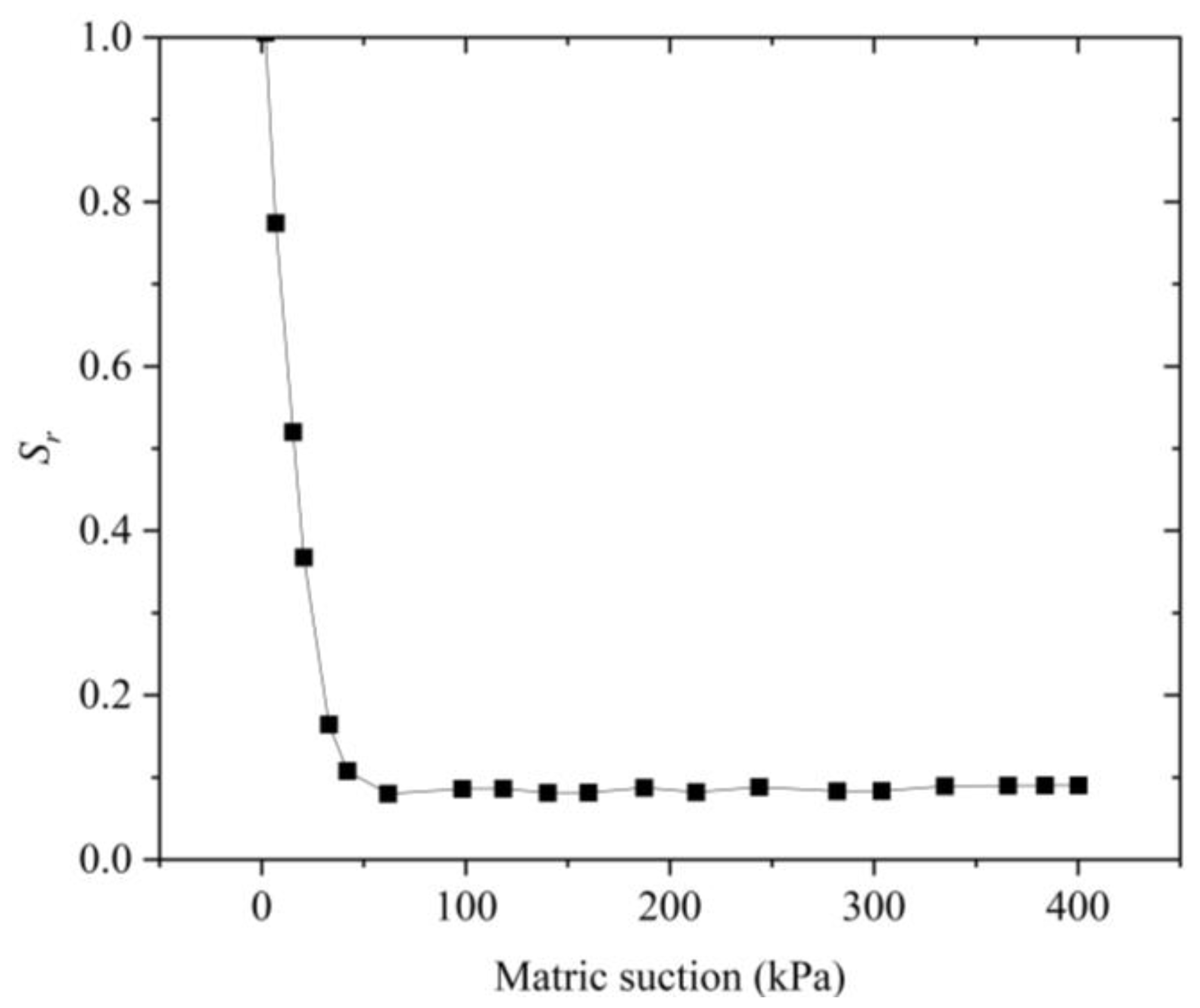
2.3. Model Parameters

The slope is assumed to be homogeneous with identical properties throughout the entire numerical domain. The parameters are summarized in

Table 1. Soil parameters of the unsaturated slope.

Soil Parameters	Values
Effective cohesion $c^{\prime }$ (kPa)	15
Effective friction angle ${\theta }^{\prime }$ (°)	30
Young’s modulus E (MPa)	100
Unit weight $\gamma$ (kN/m3)	19.5
Poisson’s ratio $v$	0.3
Saturated hydraulic conductivity ks (m/s)	2.8 × 10−6

. It is important to note that, there has been no experimental research on the properties of unsaturated soil in landslides within the Three Gorges Reservoir area. In this context, the soil properties of the unsaturated slope are based on the studies conducted by Cho et al. [24] and Gu et al. [25].

To reflect the influence of the stress in the slope soil on the infiltration process, material properties are assigned to the numerical model. The seepage parameters of the slope soil under intermittent rainfall are calculated to assess the impact of the infiltration process on the principal stresses over time in the elements. The pore pressure function is given by Equation (1):

$$k_w={\displaystyle \frac{a_w{k}_{ws}}{a_w+{\left[b_w\left(u_a-u_w\right)\right]}^{c_w}}}$$

(1)

where $k_w$ is the permeability coefficient of the soil; $k_{ws}$ is the permeability coefficient of the soil when it is saturated, with a value of 5.0 $\times$ 10⁻⁶ m/s; $u_a$ and $u_w$ represent the air pressure and water pressure in the soil, respectively. Since the slope surface is in contact with the atmosphere, $u_a$ is set to 0. $a_w$, $b_w$ and $c_w$ are the soil coefficients, with values of 1000, 0.01 and 1.70, respectively.

The relationship between the saturation of the soil material and the matric suction is given by Equation (2):

$$s_r=s_i+{\displaystyle \frac{(s_n-s_i)a_s}{{a_s+\left[b_s\right(u_a-u_w\left)\right]}^{c_s}}}$$

(2)

where $s_r$ is the saturation; $s_i$ is the residual saturation, with a value of 0.08; $s_n$ is the maximum saturation, and its value is 1; $a_s$, $b_s$ and $c_s$ are material coefficients, with values of 1, 5.0 × 10⁻⁵ and 3.5, respectively.

By using Equations (1) and (2), the change in the permeability coefficient with saturation and the moisture retention curve can be calculated, as shown in Figure 3 and Figure 4. It is clear that soil saturation increases with the increase in the permeability coefficient, while the matric suction of the soil increases as the saturation decreases.

2.4. Simulation Scheme

This study primarily investigates the effects of rainfall patterns, rainfall intensity and other parameters on the seepage and stability of landslides. The specific numerical analysis scheme is presented in

Table 2. Numerical analysis scheme.

Scheme	Rainfall Intensity q (mm/h)	Rainfall Duration t (h)	Rainfall Patterns	Influencing Factors
Scheme 1	10	90	Uniform	Rainfall
Scheme 2	10	90	Uniform, triangular, pre-peak, post-peak	Rainfall patterns
Scheme 3	10, 5, 2	90	Uniform	Rainfall intensity

. Four different rainfall patterns are selected: uniform, triangular, pre-peak and post-peak, as shown in Figure 5. The uniform pattern maintains a constant intensity throughout the rainfall duration (see Figure 5a). The triangular pattern features an intensity that initially increases over time, reaching a maximum during the mid-rainfall period, after which the intensity gradually decreases (see Figure 5b). The pre-peak rainfall pattern has an intensity that gradually decreases over time (see Figure 5c), while the post-peak pattern exhibits an intensity that gradually increases (see Figure 5d). To better reveal the impact of rainfall patterns on the mechanisms of slope instability and stability, the cumulative rainfall for the four patterns is equal for rainfall.

According to local rainfall data and meteorological rainfall classification standards [27,28], the average annual number of rainy days in the region over the past 10 years is 288 days, with an average annual precipitation of 914.6 mm. Most of the rainfall occurs between June and September. In the past 5 years, several instances of intense short-duration rainfall in the area have exceeded 40 mm/h, with 24 h rainfall reaching up to 250 mm. The longest duration of intermittent rainfall can last up to 10 days. Therefore, to study the effects of rainfall intensity on slope seepage and stability, three common rainfall levels are selected: moderate rain, heavy rain and torrential rain, with the corresponding q being 2 mm/h, 5 mm/h and 10 mm/h, respectively. The rainfall pattern is uniform, and the rainfall duration time t is 90 h.

3. Results and Discussion

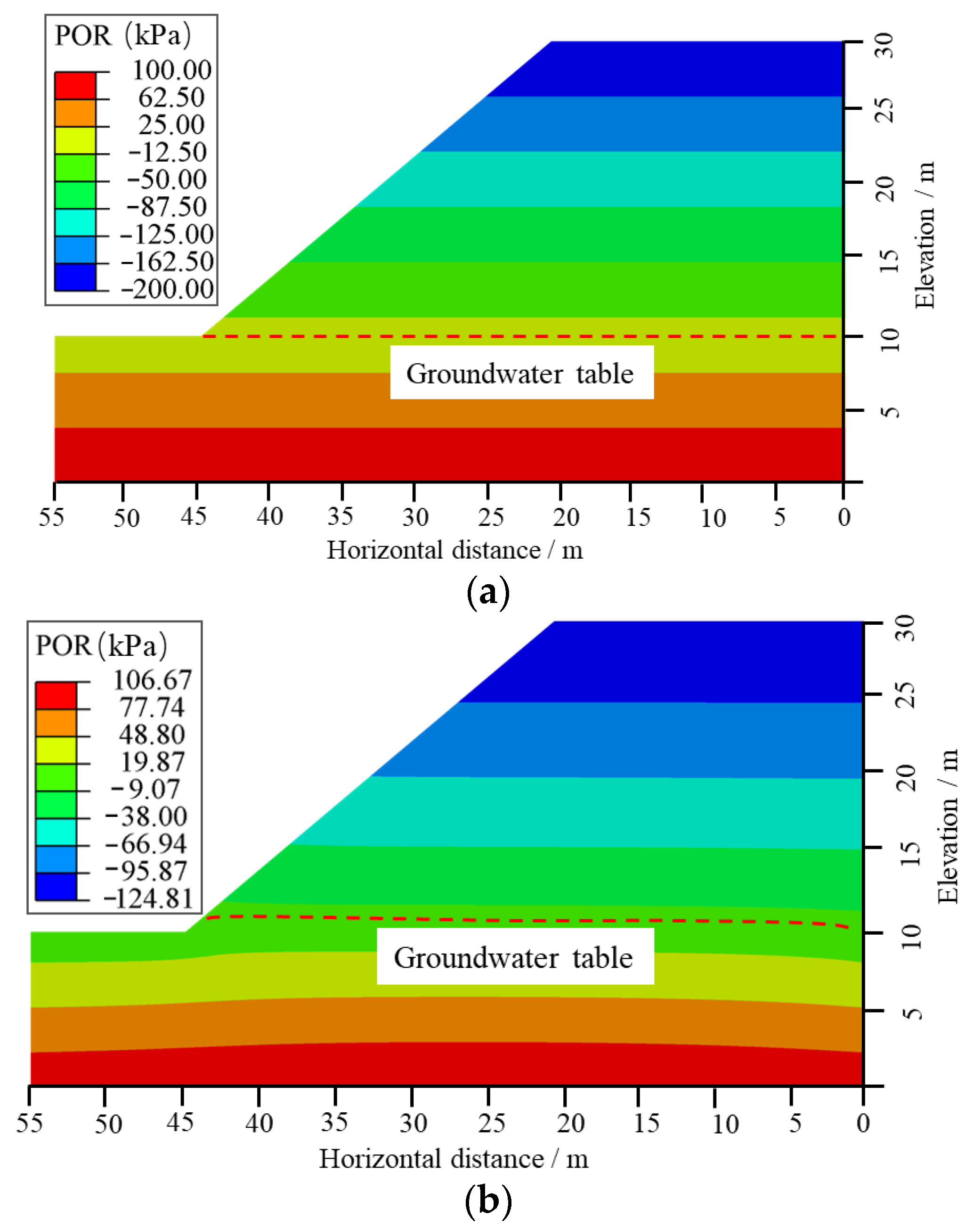
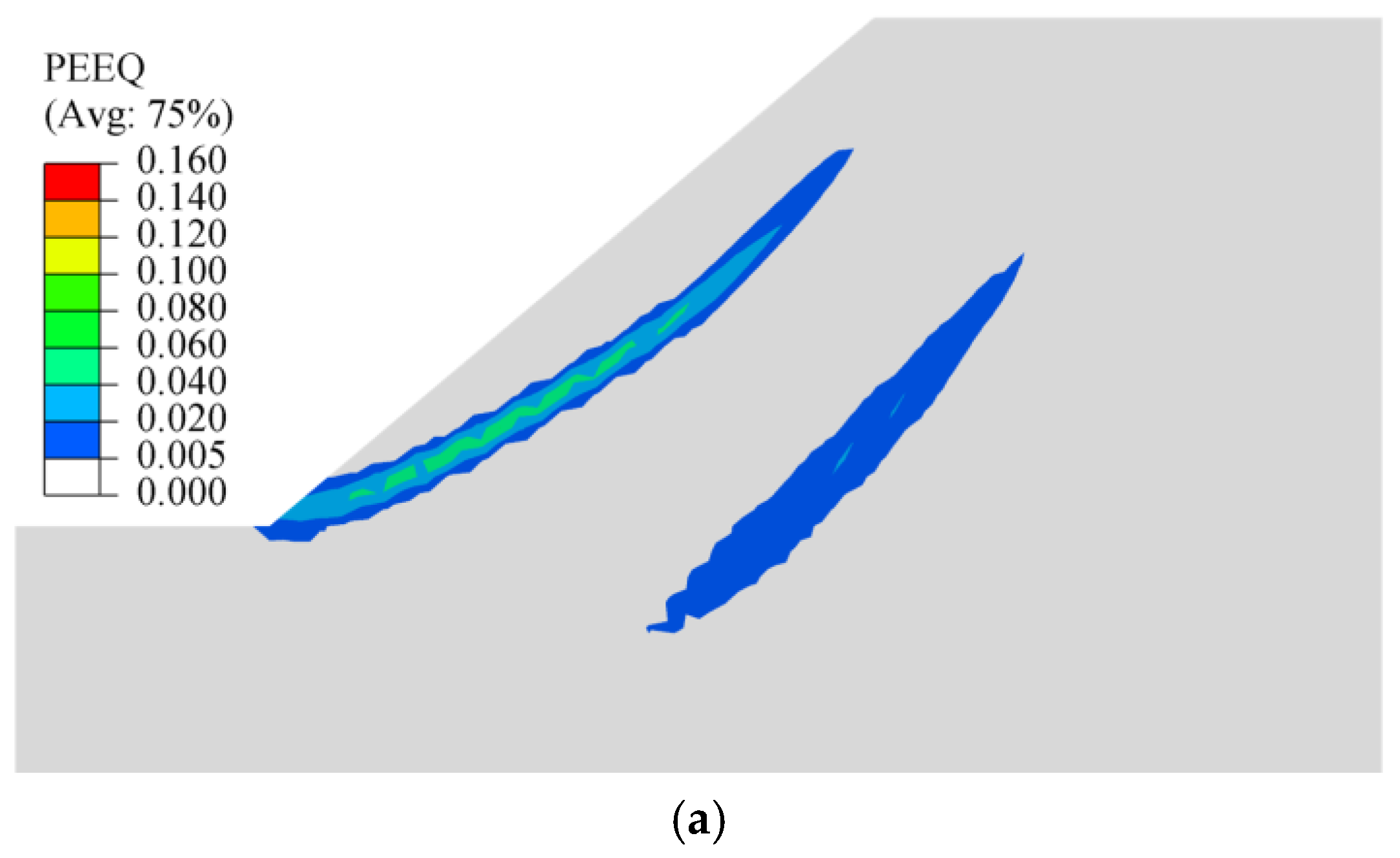
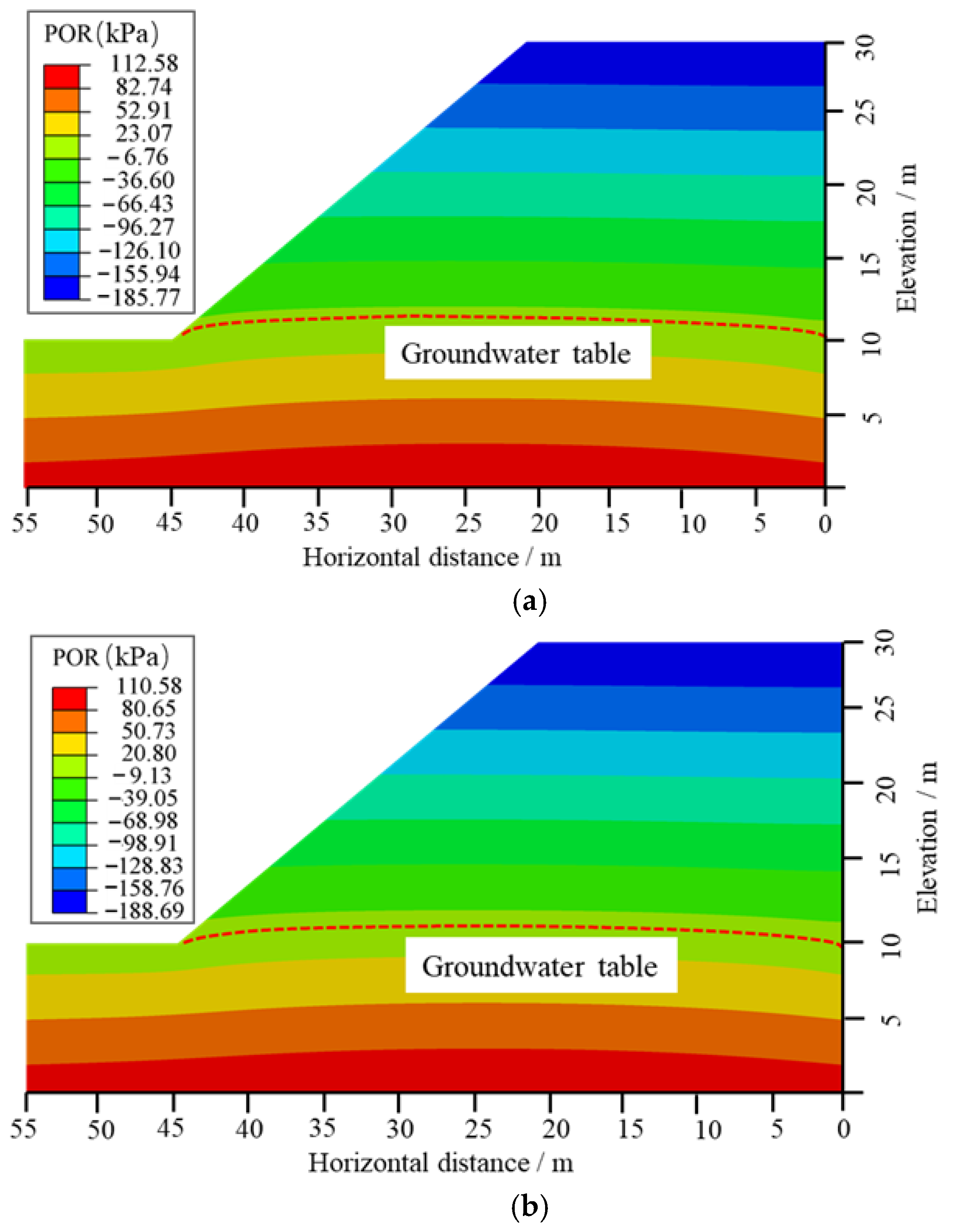
3.1. Analysis of Slope Stability Under Rainfall

To investigate the extent and degree of the impact of heavy rainfall on slope instability and failure, a fluid–solid coupling analysis of the entire process of rainfall infiltration in the slope is conducted. The rainfall pattern is uniform, with the $q$ considered under extreme conditions set at 10 mm/h, lasting for 90 h, resulting in a total precipitation of 900 mm by the end of the rainfall.

Figure 6a shows the distribution of pore water pressure (PWP) in the slope before rainfall (i.e., $t$ = 0 h). The dashed line represents the wetting front, which is the groundwater level under steady-state conditions and serves as the boundary between the saturated and unsaturated zones of the slope soil. The PWP values above the dashed line are negative, indicating the presence of an unsaturated zone, which is beneficial for slope stability. As the height of the slope decreases, the magnitude of PWP increases linearly.

Figure 6b shows the PWP distribution map of the landslide after 90 h of rainfall. It can be seen in this figure that the difference in PWP in the unsaturated zone above the groundwater level before and after rainfall is significant. The variation in PWP is greatest in the soil at the top of the slope, followed by the slope face, while the variation is smallest in the soil at the bottom of the slope. Rainfall can cause a temporary increase in negative PWP in the originally unsaturated zone of the slope, leading to a closed phenomenon where the pressure head contour lines from the top of the slope move inward from high (zero) to low and back to high. This occurs because the shallow soil in the landslide responds first to the rainfall, while the deeper soil responds more slowly. Additionally, after 90 h of rainfall, the wetting front within the landslide body continuously rises toward the surface, with the wetting front at the toe of the slope being the first to rise slowly. This indicates that the transient saturated zone will continuously move upward, initially affecting the toe of the slope. Therefore, when the slope becomes unstable, the toe is the first to experience failure.

Figure 7 shows the distribution of accumulated equivalent plastic strain (PEEQ) before and after rainfall. The location and magnitude of PEEQ serve as important criteria for assessing slope instability and failure. In the figure, it can be seen that after rainfall infiltration, the areas of increased shear strain in the slope shift compared to before the rainfall. At this point, a continuous slip surface has formed, with the lower part of the slip surface connecting to the toe of the slope and the upper part reaching the crest. The PEEQ occurs on the upper surface of the slope toe, indicating that the soil in the upper part of the slope toe may experience instability and sliding under the influence of rainfall infiltration. As rainfall fully infiltrates, the surface layer of the soil gradually approaches saturation, and the values of PEEQ increase sharply, indicating that local failure may have occurred under these conditions.

In practical engineering, the SF is commonly used to evaluate slope stability [20,21]. This paper employs the SRM using Abaqus finite element analysis to calculate the SF of the slope. The procedure for determining the SF via SRM can be outlined in the following steps:

(1)

Define the field variable, typically the strength reduction factor (SRF).

(2)

Specify the material properties that change with the field variables.

(3)

Establish the boundary conditions, and achieve numerical equilibrium.

(4)

Adjust and increase the field variable (i.e., SRF) until the numerical calculation fails to converge.

The SRM for calculating the SF of the ABAQUS has been utilized by many scholars and experts for landslide stability analysis.

Figure 8 shows the variation in the slope safety factor with rainfall duration. It can be observed in the figure that during prolonged continuous rainfall, the slope safety factor gradually decreases with the duration of rainfall. The SF of the slope before rainfall is 1.23, indicating a stable condition. Under heavy rainfall intensity ($q$ = 10 mm/h), the SF of the slope gradually decreases with the duration of rainfall. The variation in the SF is more significant during the early phase of rainfall, while the changes are smaller in the later phase. This is because during the early phase of rainfall, the water content in the soil is low. As rainfall infiltrates, there is a significant change in the water content of the slope, leading to a substantial increase in PWP. This greatly reduces the soil’s matric suction, resulting in a significant decrease in the soil’s shear strength, which causes the SF to decrease rapidly. After a period of continuous rainfall, once the water content in the upper soil layer of the slope increases to a certain level, it can no longer accommodate additional rainfall infiltration. The permeability coefficient of the slope soil also decreases accordingly, and at this point, the SF no longer decreases significantly.

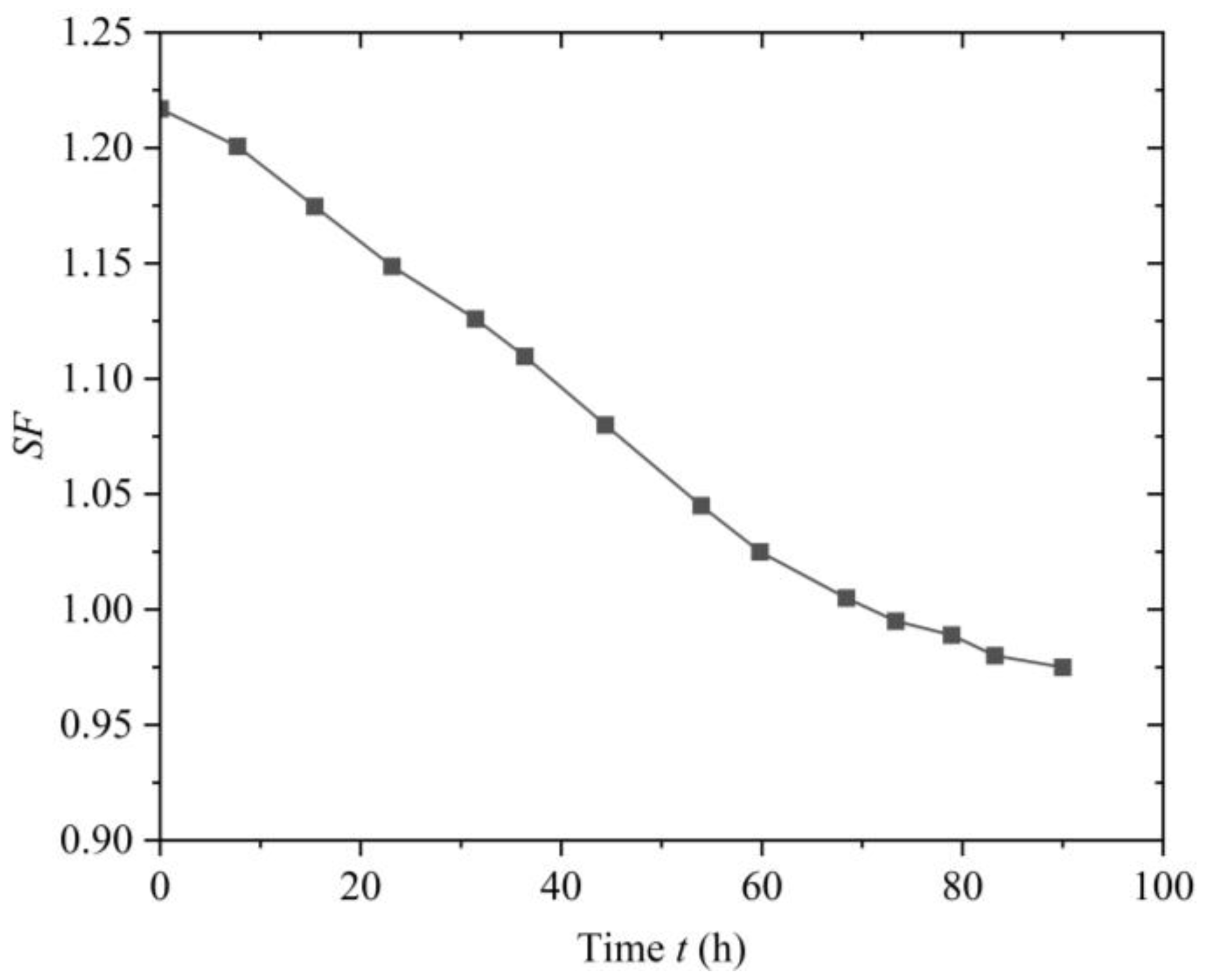
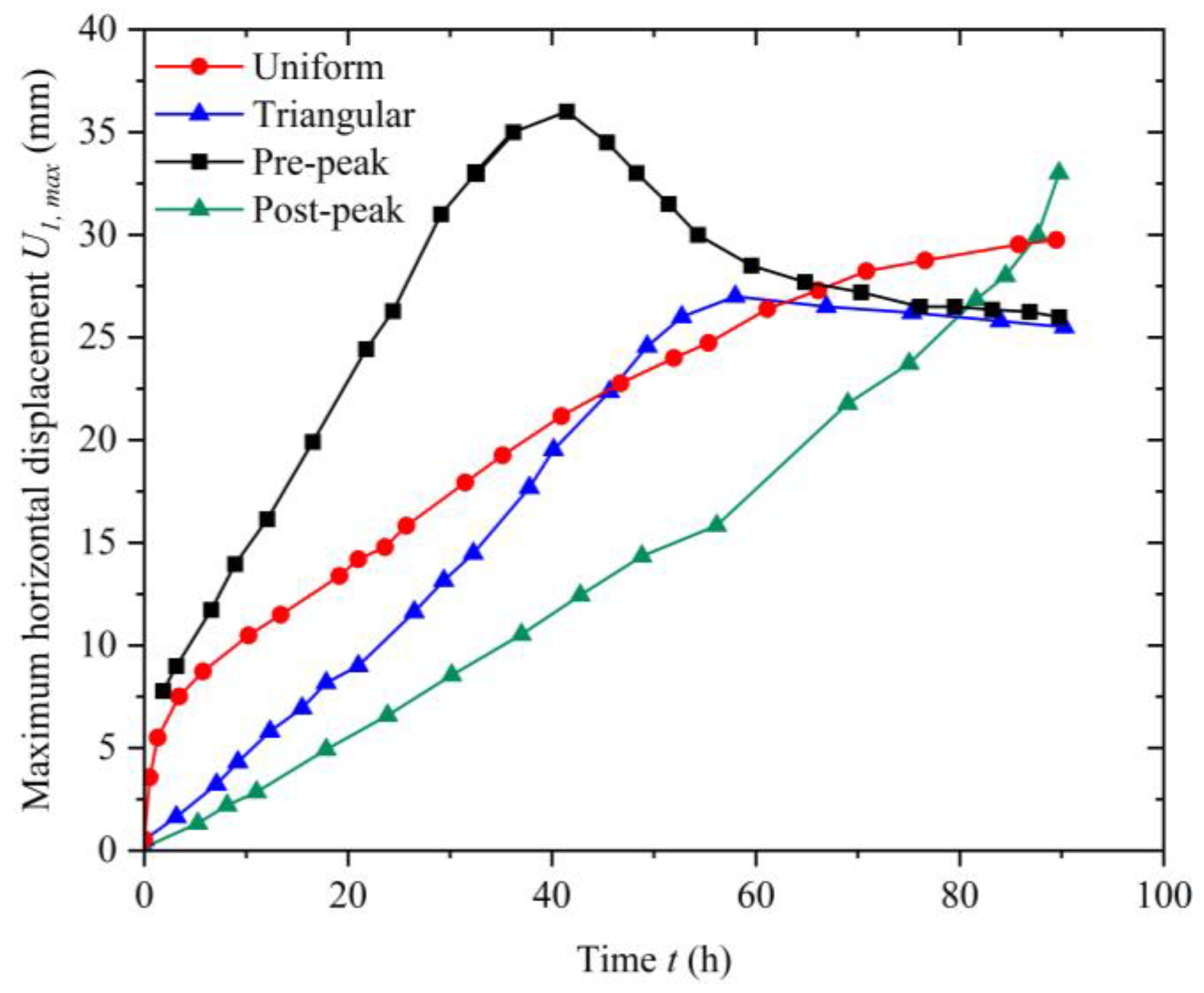
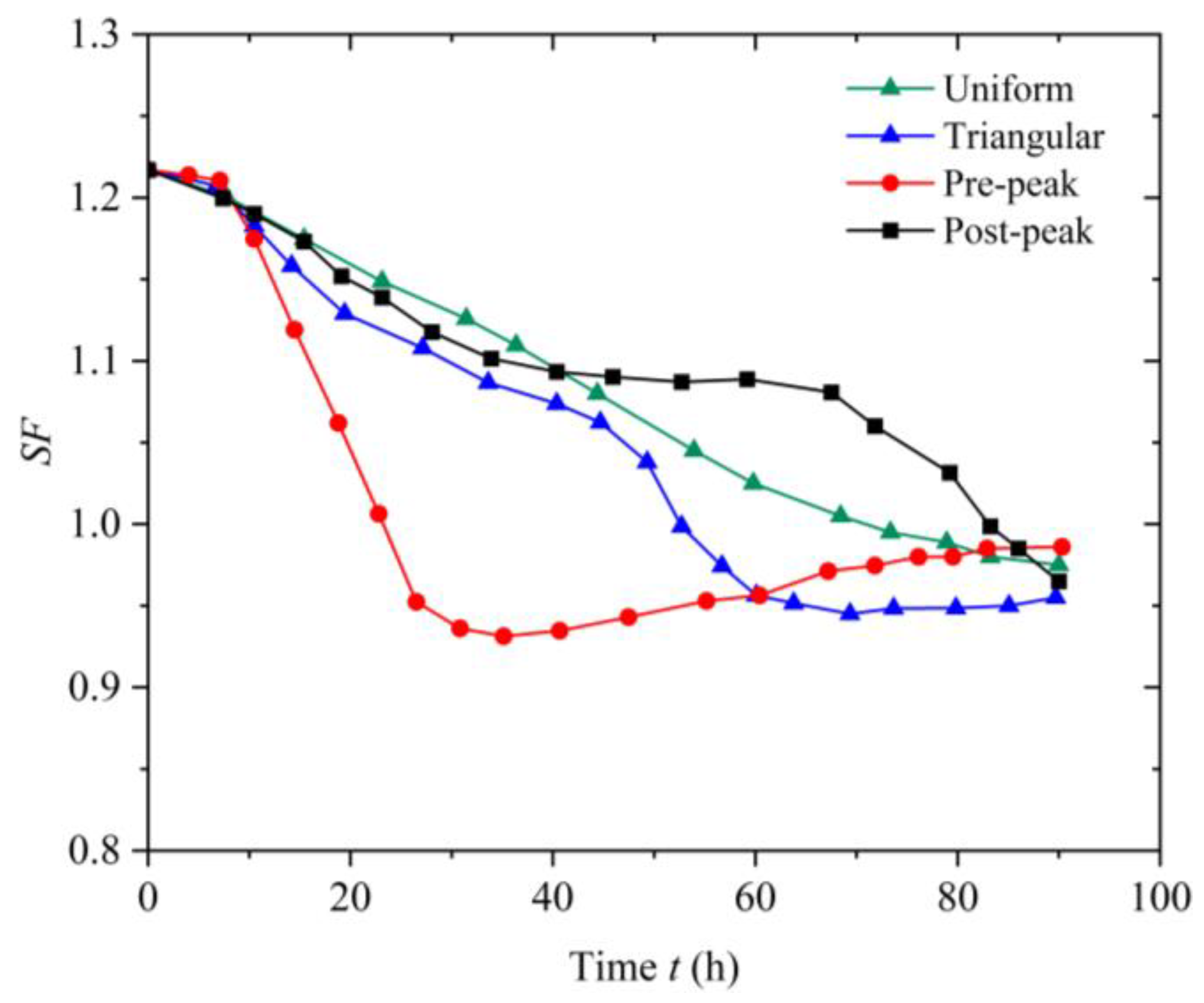
3.2. The Impact of Rainfall Patterns on Slope Instability and Failure

Figure 9 illustrates the distribution of PWP within the slope after 90 h of rainfall under different rainfall patterns. It can be observed that, with the same total rainfall amount and duration, the distribution of PWP within the slope varies with different rainfall patterns, showing differences in PWP changes. Based on the variations in the contour lines of PWP, it is evident that the pre-peak rainfall has a relatively small impact on the PWP within the slope, while the post-peak rainfall has a significantly larger effect on the PWP of the slope soil.

To further investigate the influence of rainfall patterns on PWP distribution in the slope, Figure 10 presents the temporal and spatial evolution of PWP at the slope-free face (i.e., the BC face) above the groundwater level under four different rainfall patterns. In Figure 10, it is evident that rainfall patterns have a significant impact on the distribution of PWP at the slope-free face. After 24 h of rainfall, the order of influence of the four rainfall patterns is as follows: pre-peak > uniform > triangular > post-peak. This is primarily because pre-peak represents a sudden heavy rainfall, which increases the PWP at the slope-free face due to its rapid intensity, while post-peak has a lower initial rainfall intensity, resulting in the smallest impact on the PWP at the slope-free face. After 60 h of rainfall, the influence changes to triangular > uniform > post-peak > pre-peak. This is mainly because the rainfall intensity of triangular sharply increases during this period, becoming significantly greater than the other three types of rainfall. As a result, the PWP at the slope-free face is higher than that corresponding to the other rainfall types at the same time. After the rainfall ends (i.e., after 90 h), the order of influence is post-peak > uniform > triangular > pre-peak. This is primarily because the rainfall intensity of post-peak continues to increase over time, leading to a rise in PWP at the slope-free face. In contrast, pre-peak experiences a decrease in rainfall intensity, allowing PWP to dissipate over time, making it the lowest among all rainfall patterns. Overall, under all rainfall conditions, the variation in PWP at the slope-free face aligns closely with elevation, with higher PWP corresponding to rainfall patterns with greater intensity at the same time.

Figure 11 shows the time-series curves of maximum horizontal deformation $U_{1, max}$ for the landslide under different rainfall patterns. It is important to note that the $U_{1, max}$ refers to the highest deformation value at various locations within the landslide at a specific moment of rainfall. In this figure, it can be seen that, for the uniform and post-peak rainfall patterns, the $U_{1, max}$ increases with the duration of rainfall. In contrast, for the triangular and pre-peak rainfall patterns, the $U_{1, max}$ initially increases and then decreases as rainfall time progresses. Due to the differing concentrated rainfall periods of the four rainfall patterns, the timing of the maximum values of their respective $U_{1, max}$ also varies. For the uniform intensity and post-peak rainfall patterns, since their rainfall intensity does not decrease over time, the $U_{1, max}$ for both occurs at the end of the rainfall, reaching 25 mm and 36 mm, respectively. The $U_{1, max}$ for the triangular rainfall pattern is 27 mm, occurring at 58 h of rainfall. The $U_{1, max}$ for the pre-peak rainfall pattern is 36 mm, occurring at 38 h of rainfall. Subsequently, due to the decrease in rainfall for these two patterns, the amount of infiltrated water within the slope decreases, combined with drainage from the slope, resulting in a slight rebound in horizontal displacement.

Figure 12 presents the slope displacement cloud map at the time of maximum horizontal displacements under four rainfall patterns. In the figure, it can be observed that when the maximum horizontal displacements are reached for all four patterns, the horizontal displacements are concentrated at the bottom of the slope. It can be inferred that during the slope failure process, deformation will first occur at the bottom of the slope, leading to a loss of support in the upper and middle sections. Under the effects of rainfall and self-weight, sliding will occur downward, resulting in overall instability and failure of the slope, which exhibits distinct characteristics of traction failure. Additionally, the pre-peak rainfall reaches the maximum horizontal displacement earlier than the other three rainfall patterns, and its maximum horizontal displacement is also the highest among the four. Therefore, under the same total rainfall and duration, the pre-peak rainfall is the most unfavorable for slope stability.

Figure 13 shows the variation in the SF of the slope over time under different rainfall patterns. In this figure, it can be seen that, with the same total rainfall and duration, different rainfall patterns significantly affect the timing of slope failure. Both the uniform and post-peak rainfall patterns exhibit a trend where the SF decreases over time. The SF of the slope under uniform rainfall shows a relatively stable decreasing trend overall. At 73 h into the rainfall, the safety factor drops from 1.23 to 0.995 and then continues to decline as the rainfall persists. Under trailing peak rainfall, the SF of the slope drops from 1.23 to 1.07 at 67 h into the rainfall. At this point, the slope remains stable, but the safety margin is low. Following this, as the rainfall intensity gradually increases, the SF decreases rapidly. By 83 h into the rainfall, the SF falls to 0.995, and the slope begins to destabilize and fail. The SF continues to decrease with the ongoing rainfall, reaching a minimum value of 0.965 by the end of rainfall.

Both triangular and pre-peak rainfall patterns show a trend where the SF initially decreases and then increases over time. However, due to differences in the concentration of rainfall, the times at which the slopes begin to destabilize and fail vary between the two. For the triangular rainfall, the SF falls below 1 at 52 h, indicating that the slope begins to destabilize. By 70 h, the SF reaches a minimum value of 0.95. For the pre-peak rainfall, most of the rainfall is concentrated in the first 30 h, causing the SF to significantly decrease by the 5th hour. It drops to 0.998 by 22 h, indicating that the slope begins to destabilize and fail. After this point, the SF continues to decline, reaching a minimum value of 0.930 at 30 h into the rainfall. Subsequently, as the rainfall intensity decreases, the SF starts to rise slowly. Therefore, under conditions of the same total rainfall and duration, the pre-peak rainfall results in the earliest occurrence of slope failure, and the minimum SF is the lowest among the four rainfall types. This indicates that pre-peak rainfall is the least favorable for slope stability.

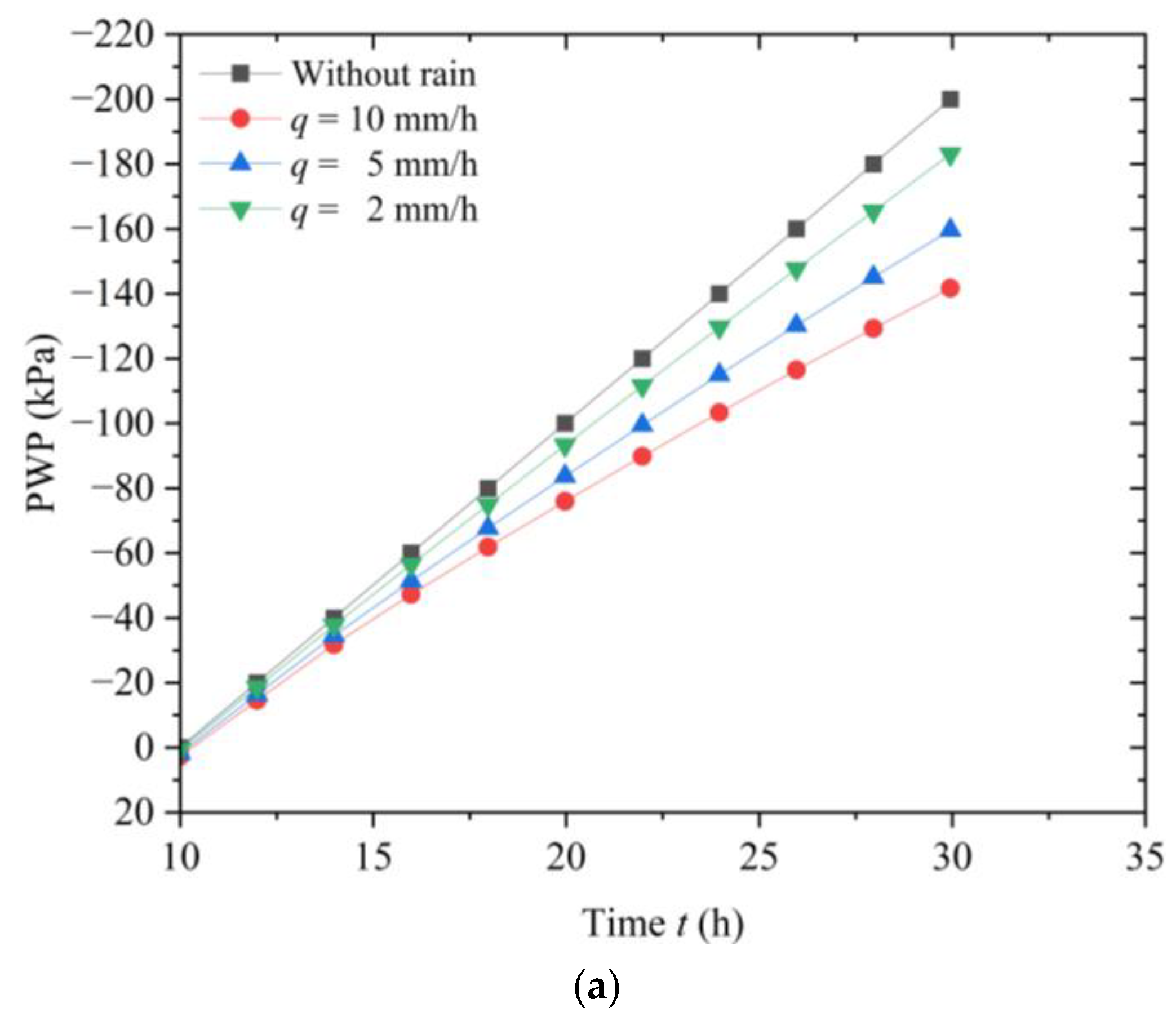
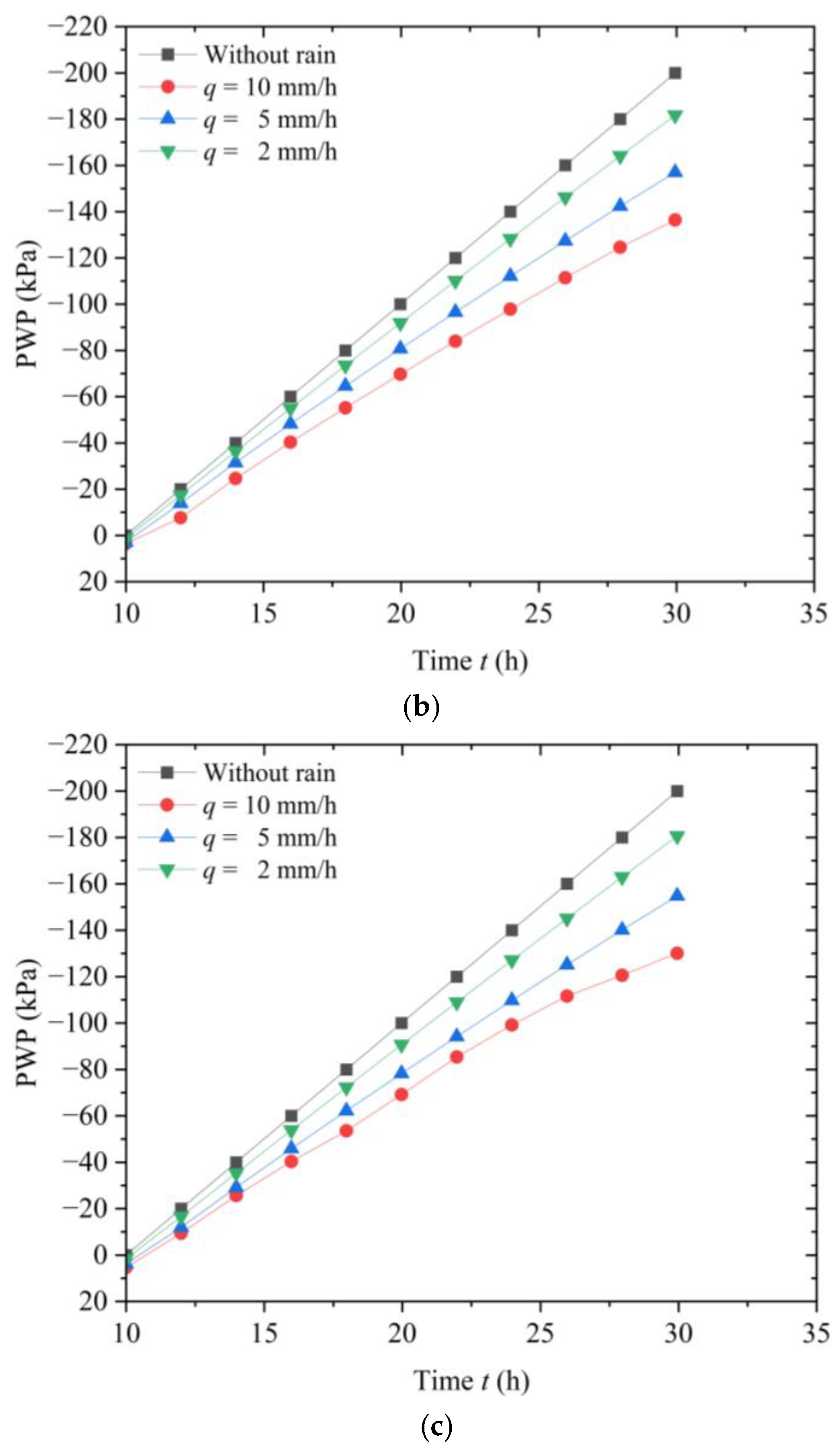
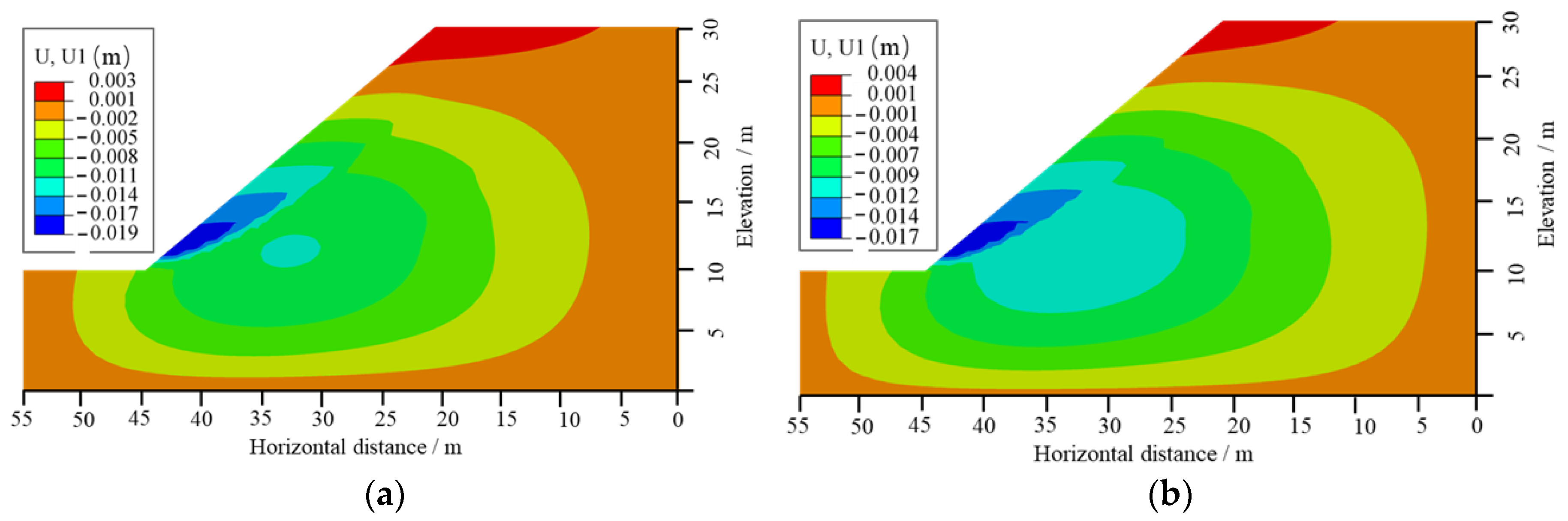
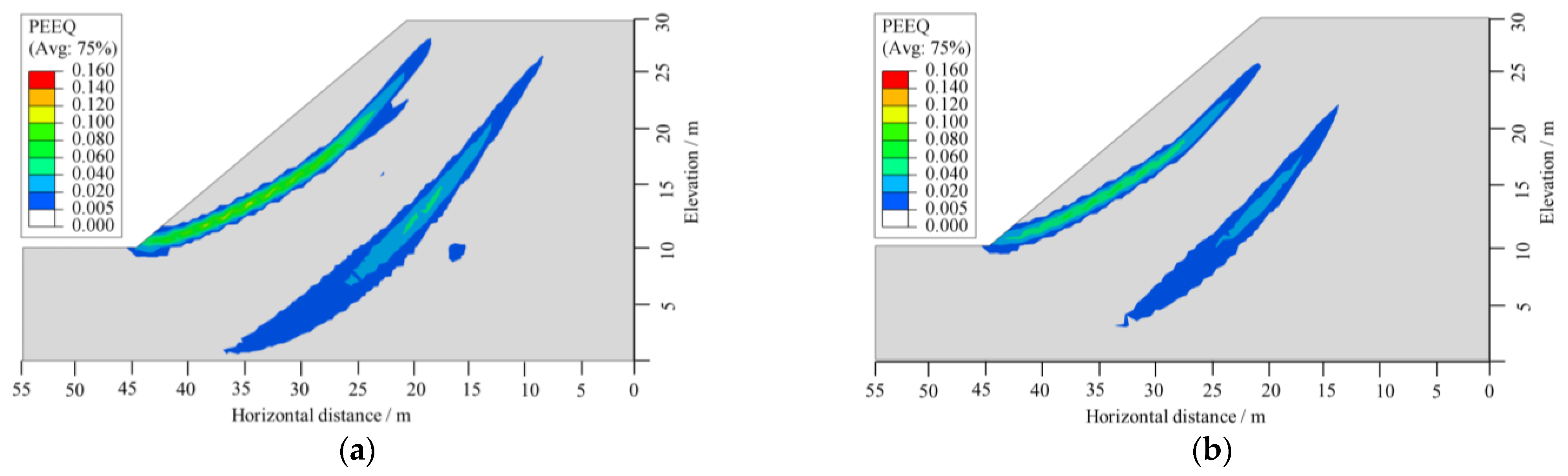
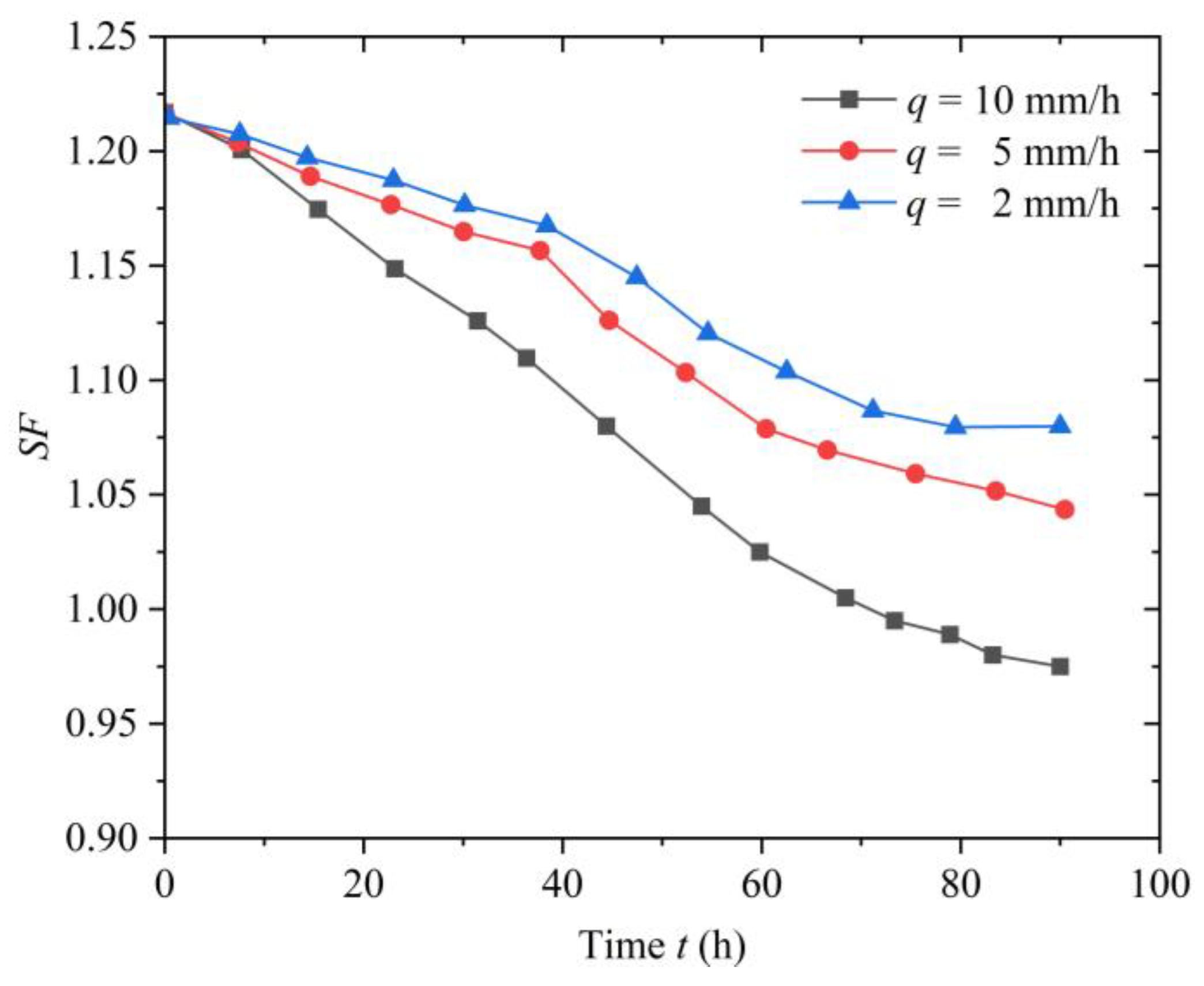
3.3. The Impact of Rainfall Intensity on Slope Instability and Failure

Figure 14 shows the distribution of PWP in the landslide during a 90 h rainfall event for both heavy and moderate rainfall. In Figure 6 and Figure 14, it can be seen that, under the same rainfall duration, different levels of rainfall have varying effects on the PWP of slope soil. As the rainfall intensity changes, the PWP in the slope body continuously varies. At the top of the slope, in the initial state, the PWP value of the surface soil is between −198 kPa and −00 kPa. After 90 h of rainfall, when the rainfall intensity reaches a heavy downpour, the PWP value of the surface soil at the top of the slope is between −123 kPa and −124 kPa. When the rainfall intensity is heavy rain, the PWP value of the surface soil at the top of the slope is between −154 kPa and −155 kPa. When the rainfall intensity is moderate rain, the PWP value is between −180 kPa and −181 kPa. It can be concluded that, within the same rainfall duration, the higher the rainfall intensity, the greater the impact on the PWP of the surface soil at the top of the slope. As the rainfall intensity increases, the PWP of the surface soil also rises, indicating a corresponding decrease in matric suction. This trend is also observed in the PWP of the soil on the slope surface and at the base. Additionally, with the increase in rainfall intensity, the wetting front continuously rises from its initial position toward the surface of the slope, indicating that the transient saturated zone is moving upward progressively.

Figure 15 illustrates the temporal and spatial evolution of PWP above the groundwater level at the slope face under three different rainfall intensities. In the figure, it is evident that as the rainfall intensity increases, the changes in PWP on the slope face soil are more significant, with more rainwater infiltrating these areas, thereby increasing the likelihood of slope instability. Additionally, Figure 15 also shows that, with greater rainfall intensity, the depth of influence on the slope face soil becomes deeper.

Figure 16 illustrates the trend of $U_{1, max}$ of the slope over time under different rainfall intensities. In the figure, it can be observed that the $U_{1, max}$ of the slope increases with the duration of rainfall for all three rainfall intensities. In the initial phase of rainfall, the differences in $U_{1, max}$ among the three intensities are minimal. However, after 40 h of rainfall, the $U_{1, max}$ significantly increases with higher rainfall intensity. As the rainfall intensity increases, the amount of water infiltration also rises, resulting in a larger saturated zone at the sliding surface and toe of the slope by the end of rainfall. This leads to the soil absorbing water, softening and losing shear strength, making it more susceptible to failure. At the end of rainfall, the $U_{1, max}$ of the slope under rainfall intensities of $q$ = 10 mm/h, 5 mm/h and 2 mm/h is 25 mm, 19 mm and 17 mm, respectively. It is evident that the $U_{1, max}$ at a rainfall intensity of $q$ = 10 mm/h is significantly greater than that at $q$ = 5 mm/h and $q$ = 2 mm/h, indicating a correspondingly more severe degree of slope damage.

Figure 17 presents the displacement contour maps for the $U_{1, max}$ timings under rainfall intensities $q$ = 10 mm/d, 5 mm/d and 2 mm/d. In Figure 12a and Figure 17, it is observed that when the $U_{1, max}$ is reached for all three intensities, the displacements are concentrated at the base of the slope. The slope exhibits distinct characteristics of tensile failure. During the infiltration process, a significant amount of moisture transfers to the toe of the slope, increasing pore water pressure and decreasing shear strength at this location. This makes the toe more susceptible to failure compared to other parts of the slope, subsequently affecting the overall stability of the slope. As rainfall intensity increases, the horizontal displacement at the toe of the slope also increases, further elevating the risk of instability and failure.

Figure 18 shows the PEEQ contour maps at 90 h under different rainfall intensities. In Figure 6a and Figure 18, it can be observed that, while maintaining the same rainfall duration of 90 h, the infiltration effects of different rainfall intensities lead to varying phenomena in the PEEQ zones. At a rainfall intensity of 2 mm/h, the plastic strain zone of the slope is primarily concentrated in a smaller area. At 5 mm/h, the PEEQ zone extends to a certain degree compared to the previous intensity. In contrast, at a higher rainfall intensity of 10 mm/h, the PEEQ zone further extends and presents two distinct areas that are approaching connection.

Figure 19 shows the variation in the SF with rainfall duration under different rainfall intensities. It can be observed that, for all three rainfall intensities, the SF of the slope decreases as the rainfall duration increases, and the higher the rainfall intensity, the lower the SF. With rainfall intensities $q$ = 5 mm/h and 2 mm/h, the SF of the slope reaches minimum values of 1.07 and 1.04, respectively, indicating that while the slope does not fail, the safety margin is not high. At a rainfall intensity of $q$ = 10 mm/d, instability begins to occur after 73 h of rainfall. Additionally, the stability of the slope is worse at the end of rainfall, with the safety factor being the lowest among the three intensities at 0.97. Therefore, the greater the rainfall intensity, the poorer the stability of the slope at the end of rainfall.

4. Conclusions

In this paper, numerical simulations were performed to examine the instability and failure of saturated–unsaturated landslides triggered by rainfall. The impacts of rainfall, rainfall patterns and rainfall intensity on pore water pressure, displacement and the safety factor of the slope were thoroughly analyzed. The main findings are summarized as follows:

(1)

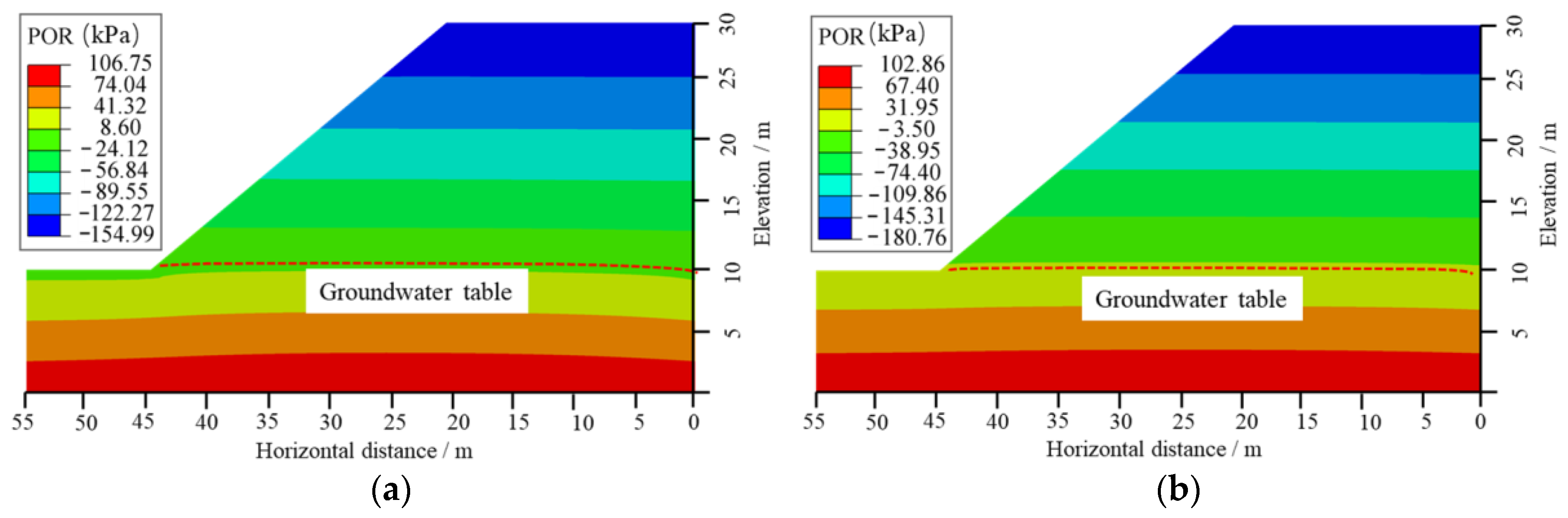
Heavy rainfall can cause a temporary increase in negative PWP in the original unsaturated zone of the slope, leading to a closed phenomenon where the PWP isohyets extend from the slope crest to the interior. This process also elevates the free water surface. Meanwhile, under the infiltration of heavy rainfall, a through-going slip surface forming from the slope toe to the crest may develop within the slope, which is likely to trigger slope instability and sliding.

(2)

The influence of heavy rainfall patterns on the spatio-temporal evolution of slope PWP, displacement and SF is remarkably significant. The dynamic evolution of PWP is closely related to the rainfall intensity at various times, showing a direct proportional relationship. Moreover, for the same time point, rainfall patterns with higher intensities exhibit more pronounced deformation responses, particularly at the toe of the slope, where the horizontal deformation response of the soil and rock is most evident. With a constant total rainfall amount, the pre-peak rainfall pattern resulted in the greatest decrease in the SF of the slope and the earliest occurrence of failure. This indicates that the pre-peak rainfall pattern is most detrimental to slope stability. Therefore, monitoring and preventive measures should be enhanced for slopes under pre-peak rainfall pattern conditions.

(3)

For a uniform rainfall pattern, when the rainfall duration is the same, a higher rainfall intensity results in more water infiltrating into the slope. This leads to greater changes in PWP and maximum displacement, making the slope more susceptible to instability and failure. As the rainfall intensity increases, the reduction in the SF of the slope becomes more significant, and the time required for slope failure decreases. Therefore, in practical engineering, it is essential to enhance the forecasting of heavy rainfall and strengthen the monitoring and reinforcement of at-risk slopes.