Abstract
Phosphorus (P) is a problematic waterborne pollutant, and considerable efforts have been taken to monitor its presence and transport in locales struggling with eutrophication. Most historical P datasets consist of intermittent grab samples, necessitating the construction of surrogacy models to explore P at high resolutions. In Iowa, models using historical data to relate turbidity to particulate P (PartP) have successfully been created. However, it is unknown how comprehensively historical datasets reflect Iowa’s hydrologic conditions and how well these models perform during flows not well represented within the existing data. In this study, we analyzed historical P datasets from 16 major Iowa rivers to determine how well they captured the rivers’ full range of streamflow conditions. While these datasets contained sufficient samples during low and average flows, they typically under-sampled high flows—containing few values above the 85–95th percentiles. Therefore, we collected new data in each river during wet conditions, with ~300 samples taken from 2021 to 2024. These new sampling results largely aligned with the existing surrogacy models and slightly improved model performance, suggesting that utilizing turbidity to predict PartP is appropriate in nearly all streamflow conditions. These findings may prove consequential for robustly modeling PartP due to its dynamic nature and disproportionately high transport during wet weather events.
1. Introduction
The nutrient phosphorus (P) is a major pollutant of concern in the United States (US) Midwest [1] and throughout the world [2]. Widespread alterations to the P biogeochemical cycle have been made to improve human well-being, most notably through the utilization of P to boost agricultural outputs [3,4,5], the incorporation of P within industrial activities [6], and the management of municipal wastewater containing P [7]. However, these actions have driven P concentrations far above their natural levels in numerous waterbodies [8], resulting in eutrophication [9]. Eutrophic waters can suffer from harmful algal blooms [10], which present a myriad of human [11] and ecological health concerns [12]. P has traditionally been viewed as the limiting factor for harmful algal blooms in inland freshwater rivers and lakes [13]. Additionally, P is a scarce resource, with only limited quantities readily available for agricultural or industrial uses [14]. Therefore, the inadvertent transport of P to rivers and streams results in wasted economic potential, along with environmental consequences.
Because of its importance, monitoring P concentrations and loads in river systems has long been a priority for many researchers and stakeholders [15]. However, measuring waterborne P includes several challenges. Quantification often requires that water be transported to a laboratory to undergo analytical procedures [16], and most historical P datasets thus consist of intermittent grab samples [17]. Datasets containing high-resolution (i.e., daily or sub-daily observations) P records are exceedingly rare, and determining real-time P concentrations via direct measurement remains infeasible at large spatial or temporal scales [18]. Intermittent or episodic P measurements often fail to capture key aspects of P transport [19]. P concentrations are often dynamic in rivers and streams [20], as they can change quickly due to an influx of P stemming from point source discharges [21], fertilizer and manure application [22], or wet weather events triggering increased erosion [23]. The subtleties of nutrient transport and the occurrence of elevated P conditions can be difficult to detect with sampling schedules following fixed monthly or weekly schedules [24].
Furthermore, several molecular forms of waterborne P are often present in eutrophic waterbodies, with each typically requiring its own measurement techniques. Total P (TP), which measures all P forms in a water column, can be divided into particulate P (PartP) and dissolved P. PartP consists of suspended P particles typically bound to sediment or organic materials (e.g., plant detritus). Dissolved P consists of water-soluble P particles, with orthophosphate (OP) being the simplest and most abundant form in midwestern surface water. These P forms often have different sources [25] and follow different transport pathways [24]. Consequently, many watersheds suffering from eutrophication may struggle with either PartP or OP disproportionately [26]. The presence of multiple P forms influences nutrient dynamics within a river system [27] and further complicates nutrient monitoring efforts [28].
These challenges have necessitated the development of modeling techniques to better estimate and quantify P in riverine systems. Streamflow-based models, such as the Load Estimator (LOADEST) [29] and Weighted Regression on Time, Discharge, and Season (WRTDS) [30] methods, have proven valuable for modeling long-term P behavior in several rivers [31,32,33,34]. While effective at describing temporal trends spanning multiple decades, these methods can struggle with modeling episodic events involving the increased delivery of nutrients to streams [31,35]. Surrogacy models have proven more effective at capturing short-term P dynamics [36,37]. In such models, historical water quality data are used to form a statistical relationship between parameters that are “easy to measure” and P. “Easy to measure” parameters are generally those that can be repeatedly monitored in situ with minimal cost and effort. Once a surrogacy model has been constructed, continuous observations of an “easy to measure” parameter can be collected onsite. The model can then use these observations to continuously predict P concentrations at high temporal resolutions and in real-time. Numerous P surrogacy models have been constructed and deployed throughout the world [38,39,40].
In the midwestern State of Iowa, surrogacy models relating turbidity to PartP have successfully been created in several of the State’s major rivers [41]. Turbidity, a quantitative measurement of water clarity, has proven closely linked to sediment and suspended P transport in Iowa’s rivers [42,43] and has been used in several agricultural watersheds to predict P [37,44,45]. In this setup, turbidity is viewed as the “easy to measure” parameter, as in situ turbidimeters can repeatedly and robustly record turbidity in a waterbody. Iowa surface waters have long been plagued by P [46], and these surrogacy models were developed to better study P transport mechanisms [47], improve P modeling at the watershed scale [48], and assist tracking Iowa’s progress in meeting statewide P reduction goals [49,50]. While historical measurements of turbidity and PartP were used to create these models, the degree to which these data capture the hydrologic conditions contained in these river systems has largely remained unknown. P transport varies considerably across streamflow regimes [51,52,53], so understanding the historical flow conditions when samples were collected is key to identifying potential limitations within surrogacy models. In other words, deploying such models for streamflow conditions not well-represented in the data may not be appropriate. The scarcity of historical data under high-flow conditions is considered a challenge in water quality modeling efforts [54], so exploring this issue in Iowa’s surrogacy models is essential before they can be deployed for their desired applications.
In this study, we explored the properties of existing riverine P data within Iowa’s major rivers and assessed how well these data reflected the various flow values observed within these rivers. We then sought to collect new data during conditions with limited historical monitoring to enhance surrogacy models. More specifically, our objectives were to (1) provide a statistical overview of existing P data within Iowa’s major rivers, (2) quantify the degree to which these data captured Iowa’s hydrologic conditions, (3) collect new P data under flow conditions where existing data has been sparse, and (4) validate previously constructed P surrogacy models with these new data.
2. Materials and Methods
2.1. Sites and Regional Setting
This study focused on 16 sites located along major rivers within the US State of Iowa (Figure 1). These sites have often been used in analyses concerning water quality and quantity in Iowa because of their location near the State’s border [44,48,55,56]. Indeed, these 16 sites are the most downstream locations within these river systems where streamflow is measured and water quality data have consistently been collected. Their combined tributary area encompasses over 90% of Iowa’s total land area. Descriptions about processes at these 16 sites are thus generally viewed as indicative of statewide hydrologic and water quality behavior in Iowa. Out of these sixteen rivers, eight (Des Moines, Iowa, Maquoketa, Skunk, Turkey, Wapsipinicon, Upper Iowa, and Yellow) outfall to the Mississippi River on Iowa’s eastern border, five (Boyer, Floyd, Little Sioux, Rock, and Soldier) discharge to Missouri River on Iowa’s western border, and three (Nishnabotna, Nodaway, and Thompson) flow south into the State of Missouri.
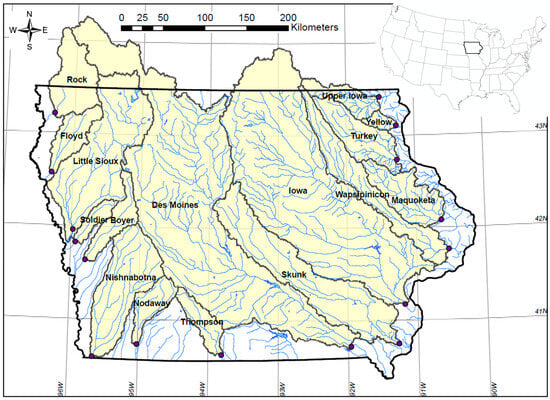
Figure 1.
Location map of the US State of Iowa (map inset), the 16 sites analyzed in this study (purple dots), and their corresponding watersheds (yellow areas).
Table 1 lists metadata items for these 16 sites, including the Site IDs denoting the locations used for water quality sampling and streamflow monitoring. Historical water quality data have been collected at each site for over 20 years by the Iowa Department of Natural Resources (IDNR). These rivers are part of the IDNR’s ambient stream monitoring program that collects monthly grab samples at each site, which are then analyzed for various water quality constituents—including P and turbidity. Streamflow has also been measured at these locations by the US Geological Survey (USGS), which operates stream gauges co-located with the IDNR’s sampling points. These gauges follow the standard USGS flow measurement protocols that utilize stage-discharge relationships to report streamflow every 15 min [57]. Daily streamflow values are produced by taking the arithmetic mean of each day’s 15 min measurements [58]. All gauges have been operational over the past several decades, resulting in robust, uninterrupted daily streamflow records throughout water quality sampling efforts. From time to time, the USGS has also collected water quality grab samples at most of these sites. However, their sampling has not been conducted with the same regularity as the IDNR, and P data collected by the USGS typically involves monthly or bimonthly observations spanning a few years.

Table 1.
Metadata for the 16 sites analyzed in this study.
Like many midwestern states in the US Cornbelt, Iowa is dominated by agricultural land use (~80%). Row crop production, mainly corn and soybean rotations, comprises most agricultural lands, although ~10% are used primarily as livestock pastures. Iowa supports a leading livestock industry where hogs, cattle, chickens, and turkeys are the major commodities. These intensive agricultural activities are reflected in this study’s watersheds, as even the basins that house Iowa’s largest metropolitan areas (e.g., Des Moines and Iowa, which contain the cities of Des Moines and Cedar Rapids, respectively) have only <5% urban land use. Fertilizer and manure are the primary sources (~70%) of P found in Iowa’s rivers, whereas P originating from municipal sources (e.g., urban runoff and wastewater effluent) is relatively minor (~10%) [59]. However, many important differences exist among these rivers, and P fate and transport are not uniform across Iowa [48].
Most importantly, these watersheds span a variety of landform regions [60], which influence sediment [61] and nutrient loss [26,62,63]. The surficial geology of these watersheds largely consists of glacial deposits consisting of fine-textured glacial till and silty loess of varying ages overlying flat-lying sedimentary bedrock. Soils in the watersheds are dominated by thick, organic-rich material that formed in grasslands (~67% of Iowa) and more clay-rich Alfisols (~20% of Iowa) that formed under hardwood forest. Like most Iowa, these soils have textures of silt loam, loam or clayey loam in both surface and subsurface horizons. While agricultural activities dominate each watershed, the extent of specific activities (e.g., livestock feeding operations or pastureland coverages) varies throughout the State [64]. Several larger watersheds contain impoundments, such as reservoirs or low-head dams, that greatly influence nutrient transport [65,66], while other smaller watersheds are entirely free-flowing. These variations in Iowa’s geology, land use, and hydraulic controls result in differing P yields and ratios between dissolved P and PartP across the 16 sites [26].
2.2. Assembly and Analysis of Existing P Data
2.2.1. Assembly of Historical P Data
Historical P and turbidity data spanning 1998–2021 from the 16 sites were retrieved from the IDNR and USGS databases. This timeframe was chosen because 1998 coincided with the beginning of the IDNR’s ambient monitoring program, and 2021 was the last complete calendar of sample collection at the time of our initial analysis. IDNR data were obtained from the AQuIA database (https://programs.iowadnr.gov/aquia/) (accessed on 15 April 2025), while USGS data were obtained from the National Water Information System (https://waterdata.usgs.gov/nwis/) (accessed on 1 May 2025). Both databases are publicly accessible, and all datasets have also been included in the Supplementary Materials. Daily streamflow values were retrieved from the National Water Information System and paired with coincident water quality samples.
Historically, two forms of P have been measured in Iowa: (1) TP and (2) OP. The procedure for measuring OP consists of filtering grab samples onsite using a 0.45-micron filter followed by analytical quantification in a laboratory setting. Because PartP was not measured directly, we estimated PartP concentrations by subtracting a sample’s OP concentrations from its TP concentration. While this definition of PartP is not entirely accurate, it was necessitated by OP being the only dissolved form of P available in the historical records. In Iowa surface waters, OP has been found to consistently comprise 90–95% of all dissolved P in the samples when all forms have been measured, regardless of streamflow rate and overall TP levels. Because of this consistent ratio, surrogacy models utilizing this formulation of PartP have performed comparably to those using a more strict PartP definition [67]. Several other studies have also successfully employed this PartP assumption when modeling P transport in Midwestern rivers [26,68,69]. In a few rare instances (~1% of samples), OP levels were greater than TP. Since this is physically impossible (i.e., it occurs as an artifact of analytical procedures under very low P concentrations), we assigned these data as non-detects with a detection limit equivalent to that of TP.
Overall, approximately 10% of P samples were below their detection limits. For the past 20 years, the IDNR has used a detection limit of 0.01 mg/L for its P measurements. Earlier detection limits were higher (usually 0.05 or 0.1 mg/L). All PartP and OP non-detects were set to half their detection limit in the statistical procedures described herein. This provided a simple method of incorporating these data points into our analysis, and numerous studies exploring P in surface waters have taken a similar approach [15,70,71]. All references to P concentrations in this study use units of mg/L as P, and all turbidity values use nephelometric turbidity units (NTU). Streamflow values are reported using cubic meters per second (cms). The analytical procedures used by the IDNR and USGS to quantify these parameters have been included in the Supplementary Materials.
2.2.2. Statistical Analysis of P Data
The assembly of these historical data resulted in P datasets spanning multiple decades at each of the 16 sites, with sample counts ranging from 237 to 565 among the sites. We calculated several descriptive statistics of PartP and OP at the 16 sites using these historical data. Along with calculating the mean, standard deviation (std), median, and maximum concentrations, we also determined the skewness (i.e., the third statistical moment) and the correlations between P concentrations and streamflow. Boxplots were created to visualize historical P levels across Iowa. Additionally, several figures were constructed to visually summarize each PartP and OP dataset’s timeseries, correlation with streamflow, seasonal behavior, and streamflow distribution (Supplementary Materials), as is standard practice when examining coincident water quality and flow data [72].
We also created histograms of each site’s PartP and OP concentrations to visualize their probability distributions (Supplementary Materials). To determine which parametric distributions may be appropriate for describing P behavior in Iowa rivers, we fit several potential distributions to each dataset. This procedure involved selecting a handful of probability distributions (e.g., normal, lognormal, gamma, etc.) commonly associated with water quality data [73,74,75] and estimating these distributions’ parameters using maximum likelihood estimation. Once a distribution’s parameters were estimated, the Bayesian Information Criteria (BIC) was used to assess goodness of fit—with a lower BIC corresponding to a better-fitting distribution. A Kolmogorov–Smirnov test was also performed on each fitted distribution [76], where it was compared to the original dataset to quantity the likelihood that these historical P concentrations could be drawn for the distribution in question. The full list of parametric distributions analyzed, along with the results of the fitting procedures, have been included in the Supplementary Materials. All distribution fitting was conducted using the python fitter package (version 1.7.1), which expands upon the widely used SciPy package (version 1.16.0) [77].
2.2.3. Assessment of Streamflow Conditions Captured by Existing Data
To determine the extent to which existing P data had captured the full range of streamflow conditions, we compared streamflow values on days where PartP samples had been collected to the overall population of daily streamflow. Figure 2 represents this conceptually using two example sites. This figure displays the standard hydrograph containing daily flow values from the beginning of sampling through 2021. The superimposed dark blue dots represent the flows on days when PartP samples were collected. Comparing these two datasets (i.e., all flows and sampled flows) helps reveal how well existing P data represents the full range of flow conditions. Similar plots for each of the 16 sites have been included in the Supplementary Materials.
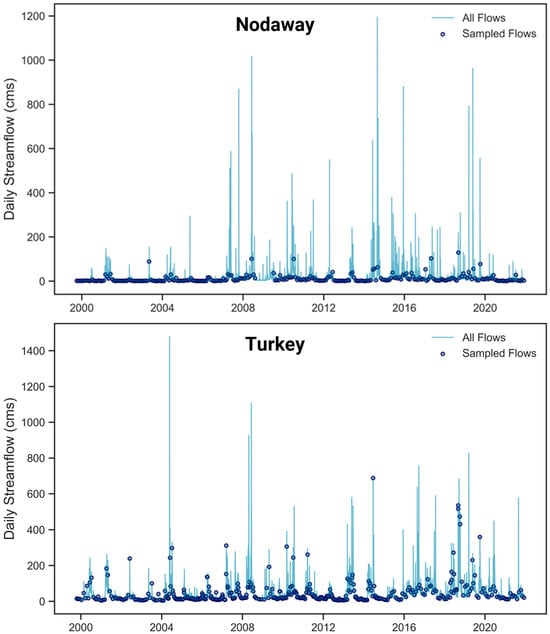
Figure 2.
Hydrographs of daily streamflow values in the Nodaway (top) and Turkey (bottom) rivers. Blue dots represent the days on which P data have historically been collected.
We investigated this concept more formally by creating two-sample quantile–quantile (Q-Q) plots, which placed the quantiles for the sampled flows against the quantiles for all flows (Figure 3). Perfect alignment between these datasets would result in the plots’ points lying along the 1:1 reference line. Instead, we noted a consistent pattern on each Q-Q plot where points deviated from the 1:1 line during higher streamflow conditions. These divergences always occurred beneath the 1:1 line, suggesting that streamflow values were no longer well represented within the existing P data above a certain flow threshold. Conceptually, this aligns with the hydrographs plotting sampled flows alongside all daily streamflow values (Figure 2, Supplementary Materials). In all rivers, low and medium flow conditions appeared well-captured by existing datasets, yet high-flow values were not readily present. Therefore, we determined that additional P samples needed to be gathered during high streamflow periods to comprehensively describe P transport Iowa—specifically aiming to validate PartP surrogacy models under these conditions.
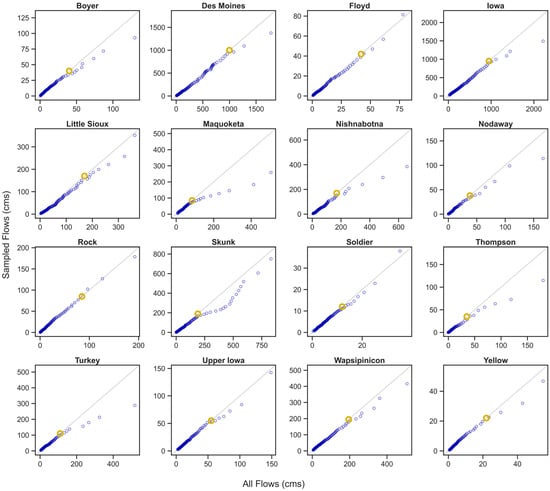
Figure 3.
Two-sample quantile–quantile plots comparing all daily flow values at a site (x-axis) to flow values on days on which P data has historically been collected (y-axis). The gold dots present the flow threshold where the quantiles diverge from the 1:1 line.
2.3. Collection of New P Data
A sampling procedure was developed to systematically collect new PartP and turbidity data during high flows at the 16 sites. Thresholds for high flow conditions were determined by noting the flow value where points in the Q-Q plot diverged from the 1:1 line (Figure 3, gold dots). Table 2 summarizes these thresholds for each site; we aimed to collect new PartP and turbidity data when flow values exceeded these thresholds. Each threshold’s corresponding empirical streamflow percentile was also included for reference. Given the highly skewed nature of PartP transport in Iowa [78], we questioned what portion of PartP loads have historically been delivered at flow values above these thresholds. We thus gathered recent multidecade estimates of PartP loads exported for these rivers [26] and calculated the percentage of the total load that occurred on days where flow values exceeded each site’s corresponding threshold.

Table 2.
Flow sampling thresholds. The “Threshold Percentile” column refers to the thresholds’ corresponding empirical percentiles. The “% of PartP Load Above Threshold” column refers to the estimated percentage of historical PartP loads (2005–2024) that occurred when streamflow values were above the flow sampling threshold.
Our procedure for collecting new data involved a mixture of grab sampling and the deployment of automated sampling equipment. Beginning in 2021, we worked with local volunteers to collect grab samples at sites upon their exceedance of the flow thresholds. At a handful of rivers that were especially remote and prone to flashy conditions, we deployed automated ISCO samplers (6712 Full-size Portable Sampler; Teledyne Labs, Lincoln, NE, USA), which were triggered remotely during high flows. Real-time flow levels were tracked to determine when grab samples should be collected and when the automated sampling equipment should be initiated.
Our sampling objective was to collect data during at least two wet weather events at each site. We especially wanted to monitor events during the spring and summer, when P concentrations tend to be largest in Iowa rivers. Sampling efforts in eastern Iowa rivers took place from 2021 to 2022, while data collection in western Iowa spanned 2022–2024. Due to resource constraints, it was infeasible to sample both regions of the State simultaneously. Widespread drought conditions persisted throughout Iowa from 2022 to 2023, resulting in limited sampling opportunities during these years.
Following collection, subsamples were taken and filtered on-site, and were used to quantify OP. The collected water was stored in coolers and transported to a local laboratory for analysis within 48 h of collection—corresponding to the maximum holding time for OP. TP, OP, and turbidity were measured using analytical procedures and techniques identical to those utilized in the historical datasets. The full list of analytical procedures used in this study has been included in the Supplementary Materials. PartP was calculated for each sample by subtracting its OP concentration from its TP concentration—a manner identical to that used to quantify PartP for the existing data. Streamflow was likewise determined for each sample using the stream gauge measurement coincident with sample retrieval. No censored values were present among any of the newly collected data.
2.4. Surrogacy Model Validation
With these new samples, we investigated how well these data points aligned with the P surrogacy models that had previously been assembled. We recreated these surrogacy models using the existing data and followed the procedures outlined by previous studies [41,79], where a statistical relationship between turbidity and PartP is inferred. This formulation consisted of site-specific simple linear regression models fit to log-transformed turbidity and PartP values. The regression equations took the following form:
where PartP is the predicted Part P concentration, Turbidity is the measured turbidity, and β0 and β1 are regression coefficients found using ordinary least squares. Models were created for all 16 sites, and all estimation was conducted using the python statsmodel package (version 0.14.4). Several metrics, including the coefficient of determination (R2) and root mean square error (RMSE), were calculated for each model. We then retransformed using exponentiation to convert model coefficients to their original units and improve interpretation. The retransformed models were formulated as follows:
ln[PartP] = β0 + β1 × ln[Turbidity]
PartP = exp(β0) × Turbidityβ1
The newly collected data points—consisting of turbidity and PartP measurements at each site—were overlayed on the existing data points and models to visually gauge their compatibility. These points were combined with the original datasets, and the surrogacy modeling process was repeated. The new models were compared to their original counterparts by exploring discrepancies between R2 and RMSE metrics. We also examined whether the new model coefficients fell within the confidence intervals specified by the original equations.
3. Results
3.1. Statistical Summary of P in Iowa Rivers
Table 3 contains a statistical summary of PartP and OP concentrations in the 16 rivers. Mean PartP concentrations ranged from 0.10 ± 0.25 (Upper Iowa) to 0.53 ± 1.25 (Boyer) mg/L, with an overall average of 0.27 mg/L. For OP, mean concentrations spanned 0.05 ± 0.06 (Thompson) to 0.43 ± 0.33 (Boyer), with an average of 0.13 mg/L. At all 16 sites, mean PartP concentrations were higher than the mean OP. The highest historical PartP concentration measured during the study period was 9.31 mg/L (Nishnabotna), and this value was much larger than the maximum OP value (2.93 mg/L, Boyer). The largest PartP observations typically occurred during May, June, and July, whereas the greatest OP values were primarily found in February, March, and April (Supplementary Materials).

Table 3.
Statistical summary of historical P sampling data in Iowa. The “Flow R” column refers to the correlation with daily streamflow values. The “Best dist” column refers to the best fitting parametric probability distribution (i.e., the distribution with the lowest BIC), and the “KS p-val” contains the p-value from the corresponding Kolmogorov–Smirnov test.
Figure 4 contains boxplots of the historical PartP and OP concentrations within each river. All datasets contained positive skewness (2.2–9.8 for PartP and 0.4–8.9 for OP), with many instances of the highest concentrations exceeding median values by an order of magnitude. Indeed, all mean concentrations exceeded the median. Median PartP concentrations ranged from 0.04 (Yellow) to 0.24 (Nishnabotna) mg/L, and median OP values spanned 0.04 (Wapsipinicon)–0.31 (Boyer) mg/L. Median OP concentrations were larger than their PartP counterparts at 4 of the sites.
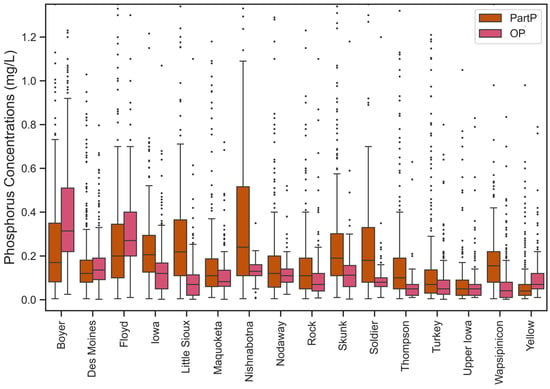
Figure 4.
Boxplots of the historical P data in Iowa. The y-axis limit was set to 1.3 mg/L to improve readability.
A general pattern was observed where PartP concentrations demonstrated higher variance and stronger correlations with streamflow than OP. In all cases, std and maximum PartP values were greater than that of OP. This difference was notable in several rivers (e.g., the Nodaway contained a PartP std of 0.56 and a maximum value of 4.50, compared to 0.06 and 0.52 for OP). Likewise, PartP’s correlation with streamflow was almost always stronger than OP’s. These correlations varied substantially between sites, ranging from 0.02 to 0.76 (PartP) and −0.22–0.36 (OP), but were almost always larger for PartP, with the Iowa being the lone exception. The difference was again quite large in the Nodaway, as its correlations were 0.76 (PartP) and −0.03 (OP).
The distribution fitting procedure yielded mixed results (Table 3, Supplementary Materials). Generally, lognormal and Pareto distributions were found to be preferable for describing PartP concentrations, as their BIC values were lowest in 14 of the 16 sites. A wide range of best-fitting distributions was obtained for OP, including lognormal, Pareto, Weibull, logistic, and exponential. The results of the Kolmogorov–Smirnov tests suggested that most of the best-fitting distributions were unsuitable for describing the historical data. In this setup, the null hypothesis of the Kolmogorov–Smirnov test was that the historical P data originated from the best-fitting estimated probability distribution, where p-value above 0.05 indicated that we fail to reject this null hypothesis. Five sites had distributions with p-values > 0.05 for PartP—four were lognormal, and one was Pareto. For OP, four sites had p-values > 0.05 (three lognormal and one logistic).
3.2. Data Collection Results
Our data collection efforts during high flows yielded a total of 292 new samples across the 16 sites (Table 4), which came from 66 distinct wet weather events. The number of events sampled at each site varied (ranging from two to eight events) and was heavily dependent upon how many times flows exceeded their thresholds throughout our sampling period. Additionally, the nature of events (i.e., how long streamflow levels persisted about the sampling thresholds) influenced the number of samples that could be collected. Generally, efforts were made to space out sample collection throughout the course of an event—gathering samples on the rising, peak, and falling components of the hydrograph if possible, so long as flows were above the threshold. This typically resulted in two to six samples being captured per event.

Table 4.
Summary of water quality sampling data collected for this study.
The PartP and turbidity data collected under these high flow conditions were much larger than the median values observed in the historical datasets. Turbidity in the newly collected samples routinely exceeded 1000 NTU, with an average of 917 NTU compared to 103 NTU in the historical data. PartP concentrations in our sampled data were also considerably larger (mean of 1.83 mg/L compared to 0.27 mg/L in the historical data). At a handful of sites (Des Moines, Floyd, and Skunk), our largest PartP measurements exceeded the maximum concentrations found within the historical data. For example, the maximum PartP concentration previously measured in the Des Moines was 1.03 mg/L, but our sampling efforts produced several data points with even greater concentrations (maximum of 1.76 mg/L).
3.3. Construction of Final Models
The newly collected samples were superimposed over the surrogacy models that related turbidity to PartP based on historical data (Figure 5). There was largely good agreement between the newly collected data and the existing models, and the curvilinear nature of the relationship noted between PartP and turbidity [80,81] was also evident in these new samples. A few sites demonstrated a slight bias in this comparison, where most of the newly collected data points resided above the existing models. However, most (~90%) of these data aligned within the 95% confidence intervals predicted by the original models (Supplementary Materials).
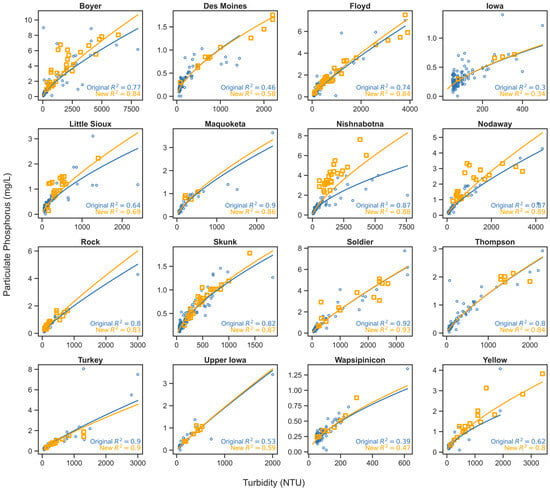
Figure 5.
PartP surrogacy models. The original models, which were constructed using historical data (blue dots), are represented with the blue lines, while the new models, which were constructed using new data (orange squares) alongside historical data are represented with the orange lines.
Furthermore, when these models incorporated the new data alongside the historical datasets, they remained largely unchanged (Figure 5). The coefficients (i.e., the slope and intercept) produced by these new models fell within the 95% confidence intervals of the original estimates. In all cases, model performance metrics were improved (Table 4, R2 Scores column), with increased R2 values. The agreement between the newly collected data and the existing models, along with improved model performance, suggested that these new data collected under wet conditions validated and enhanced the PartP surrogacy models.
4. Discussion
4.1. P Transport Behavior in Iowa
The statistical summary compiled in this study is consistent with previous work describing P transport in midwestern agricultural watersheds. While eutrophic conditions were present in all rivers, the magnitude and frequency of elevated P events varied across the State. Indeed, the mean P levels in all sites were above the limit (TP concentration of 0.08 mg/L) recommended by the US Environmental Protection Agency for optimal ecological health in the Cornbelt ecoregion [82]. Numerous samples exceeded this threshold by several orders of magnitude, but the severity of exceedances ranged considerably—consistent with previous studies noting the effects of differing geologic and agricultural practices on P transport in Iowa [26,46,83].
While mean PartP concentrations were generally higher than OP, both P species contribute to eutrophication and exhibited substantial positive skewness. However, several important distinctions between PartP and OP behavior were noted. Most importantly, PartP was more closely linked with streamflow than OP, which aligns with its well-known behavior as a runoff-driven pollutant exacerbated during periods of intense erosion [84,85]. Although OP transport can have a runoff component [86], it is also delivered in baseflow [87] or during snowmelt events [88], where high OP mobilization can occur despite only moderate increases in streamflow. This distinction was reflected in the statistical results demonstrating higher std and maximum values for PartP than OP. Because of the ubiquitous P content in Iowa soils, PartP is rarely source-limited [89]. Rather, its presence is related to fluctuations in rainfall and runoff, and PartP delivery to streams is effectively determined by the amount of erosion occurring during a wet weather event [90]. Because individual events can vastly exceed median streamflow conditions, PartP concentrations can spike significantly and to a greater extent than OP, even under its largest releases. Therefore, PartP is the dominant P species in the situations resulting in the highest TP concentrations and loads in Iowa.
The attempts to fit parametric distributions to PartP and OP concentration data were somewhat unsuccessful. The results of the Kolmogorov–Smirnov tests implied that P concentrations could only be described using these distributions in a handful of sites, as there were only four instances of p-values exceeding 0.05 for PartP and OP. Among the viable distributions, the lognormal was the most ubiquitous. While this distribution has shown an ability to describe nutrient levels [91,92,93], its application is not universal [94]. The lognormal distribution has also been found to effectively represent daily streamflow values in the Midwest [95], so strong relationships between streamflow and nutrient transport may result in its suitability for modeling P. Further work is needed to comprehensively determine optimal distributions for P concentrations in Iowa. The influence of non-detects has been observed to confound distribution fitting efforts for environmental data [71], so transforming these data points more robustly may improve the distribution goodness of fit.
4.2. Validation of Existing Surrogacy Models
The under-sampling of high flows found throughout the historical P data has been noted in numerous other datasets where sampling was conducted using fixed schedules and intervals [96,97,98]. Disruptions caused by severe weather and flood conditions concomitant with high flows were also factors in the limitations observed within Iowa’s existing data. However, it is often the case that sampling schedules are simply unlikely to coincide with wet weather events, given the flashiness and skewness exhibited by many agricultural river networks [55,97,99]. High-flow data is, therefore, inordinately valuable in most riverine water quality modeling applications [30], and the utility of many existing datasets in describing nutrient transport often depends upon their fortuitousness in sampling during high flows.
Despite the limitations in Iowa’s existing P data, the new samples collected by our monitoring efforts largely validated the surrogacy models built using these historical datasets. While the relationship between P and streamflow has been shown to be variable [100] and influenced by hysteresis [53], the relationship between PartP and turbidity appears more stable. Since turbidity in Iowa rivers is indicative of waterborne sediment content [101], it has stronger correlations with PartP than streamflow [41]. The curvilinear relationship between turbidity and PartP used to construct these surrogacy models can likely be inferred using samples that do not necessarily coincide with peak flows as long as sediment content is sufficiently above concentrations associated with conditions dominated by baseflow [102]. The fact that these models remained mostly unchanged suggests that they can be deployed for nearly all streamflow levels, thus enhancing their ability to model P throughout Iowa. However, uncertainty still surrounds these models’ application during peak flows, which can result in catastrophic flooding in Iowa [103]. As these extreme events are rare and evade advanced forecasting, sample collection during these events is exceptionally difficult, and uncertainty associated with transport during peak flows is a limitation felt by many nutrient modeling efforts [104].
Even with the validation of these models, it may be advantageous for the IDNR and USGS to incorporate event sampling into their fixed-schedule programs. While such efforts would require additional costs and manpower, they may prove beneficial in enhancing the understanding of the fate and transport of nutrients and other pollutants of concern. Furthermore, the minimal difference between the existing and high-flow datasets should be considered specific to this surrogacy modeling exercise. It does not suggest that the existing datasets effectively capture all water quality parameters or runoff-related pollutants. Further study is needed to determine how appropriate these datasets are for other water quality modeling applications in Iowa.
4.3. The Importance of High Flows in P Transport
Finally, these results highlight that the accurate quantification of PartP during high flows is essential for both understanding temporal dynamics and estimating long-term loads. Because of PartP’s skewed nature and its strong correlation with streamflow, a disproportionate amount of it is exported from Iowa during high-flow conditions (Table 2). Knowledge about the loads on such days is essential to determine how much PartP has been exported by a given river. This, in turn, is essential in determining historical PartP trends—a key metric in determining overall watershed health and assessing progress toward nutrient reduction goals. Whereas PartP concentrations can often remain consistent during low flows, wet weather events typically result in the most abrupt and immediate shifts in PartP [37]. This behavior is such that it cannot realistically be captured at a statewide scale with grab sampling and can only be described using high-resolution modeling [39]. The surrogacy models validated in this study present an avenue for continuously modeling PartP, which may reduce the uncertainty associated with P loads during high flows and help better identify specific factors triggering PartP loss across Iowa.
5. Conclusions
This study explored historical P datasets (collected by the IDNR and USGS) from 16 of Iowa’s major rivers. It also evaluated how well these data captured streamflow conditions observed in these rivers throughout the sampling timeframe. Analysis of these data demonstrated considerable spatiotemporal variations in PartP and OP concentrations across Iowa. PartP tended to be more closely correlated with streamflow than OP while containing a greater degree of variance, and PartP’s maximum concentrations were also higher than those of OP. This suggested that the events producing the largest TP loads in Iowa are predominantly driven by PartP transport.
Two-sample Q-Q plots were used to compare all measured daily streamflow values to those on which P had been sampled. This analysis revealed that while the historical datasets had adequately captured low- and medium-flow conditions, high-flow values (exceeding the 90th percentile) were sparse. A sampling effort was undertaken between 2021 and 2024, with new P and turbidity measurements taken in the 16 rivers when flows exceeded predefined thresholds. These new data were evaluated against existing surrogacy models that used turbidity to predict PartP concentrations in each river. There was largely good agreement between the previous models and new data, suggesting that these surrogacy models could be deployed along the 16 rivers under nearly all flow conditions. Ultimately, this study validated the existing surrogacy models and emphasized their utility in accurately quantifying PartP transport in eutrophic rivers and streams.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/w17152194/s1: All data used in this study (i.e., datasets containing historical P and turbidity measurements in Iowa rivers, newly collected P and turbidity measurements, and historical streamflow data); Tables and Figures providing a full statistical summary of P concentrations in Iowa rivers (i.e., descriptive statistics, historical timeseries, histograms, and potential distributions); Figures comparing streamflow on days where P has historically been monitored to the full streamflow and the corresponding quantile–quantile plots; Figures superimposing the newly collected data over existing PartP surrogacy models.
Author Contributions
Conceptualization, E.S.A., K.E.S. and L.J.W.; methodology, E.S.A., K.E.S. and L.J.W.; validation, E.S.A. and K.E.S.; formal analysis, E.S.A.; investigation, E.S.A.; resources, K.E.S. and L.J.W.; data curation, E.S.A.; writing—original draft preparation, E.S.A.; writing—review and editing, K.E.S. and L.J.W.; visualization, E.S.A. and K.E.S.; supervision, K.E.S. and L.J.W.; project administration, K.E.S. and L.J.W.; funding acquisition, E.S.A., K.E.S. and L.J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Iowa Nutrient Research Center, grant numbers 2020-05 and 2022-03.
Data Availability Statement
The newly collected data utilized for this study have been included in the Supplementary Materials. All historical datasets have also been included in the Supplementary Materials. Additionally, these datasets are publicly available and can be retrieved online. USGS streamflow and water quality data can be found on the National Water Information System (https://waterdata.usgs.gov/nwis/) (accessed on 1 May 2025), and IDNR water quality data can be found on the AQuIA database (https://programs.iowadnr.gov/aquia/) (accessed on 15 April 2025).
Acknowledgments
The authors would like to acknowledge the invaluable assistance provided by local volunteers, including individuals associated with Iowa Lakeside Laboratory, Golden Hills RC&D, and the Izaak Walton League, in helping collect the water quality samples needed for this study’s completion. The authors also wish to thank the USGS and IDNR for their past and present efforts in monitoring water quality and quantity in Iowa.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BIC | Bayesian Information Criteria |
| cms | Cubic meters per second |
| IDNR | Iowa Department of Natural Resources |
| mg/L | Milligrams per liter |
| N | Nitrogen |
| NTU | Nephelometric turbidity units |
| ON | Organic nitrogen |
| OP | Orthophosphate |
| PartP | Particulate phosphorus |
| P | Phosphorus |
| Q-Q | Two-sample quantile–quantile |
| R | Pearson correlation coefficient |
| R2 | Coefficient of determination |
| RMSE | Root mean squared error |
| std | Sample standard deviation |
| TP | Total phosphorus |
| US | United States of America |
| USGS | United States Geological Survey |
References
- Carpenter, S.R. Phosphorus control is critical to mitigating eutrophication. Proc. Natl. Acad. Sci. USA 2008, 105, 11039–11040. [Google Scholar] [CrossRef] [PubMed]
- Correll, D.L. The role of phosphorus in the eutrophication of receiving waters: A review. J. Environ. Qual. 1998, 27, 261–266. [Google Scholar] [CrossRef]
- Tunney, H.; Breeuwsma, A.; Withers, P.; Ehlert, P. Phosphorus Fertilizer Strategies: Present and Future; CAB International: Wallingford, UK, 1997. [Google Scholar]
- Griffin, T.; Honeycutt, C.; He, Z. Changes in soil phosphorus from manure application. Soil. Sci. Soc. Am. J. 2003, 67, 645–653. [Google Scholar] [CrossRef]
- Eghball, B.; Power, J.F. Phosphorus-and nitrogen-based manure and compost applications corn production and soil phosphorus. Soil. Sci. Soc. Am. J. 1999, 63, 895–901. [Google Scholar] [CrossRef]
- Villalba, G.; Liu, Y.; Schroder, H.; Ayres, R.U. Global phosphorus flows in the industrial economy from a production perspective. J. Ind. Ecol. 2008, 12, 557–569. [Google Scholar] [CrossRef]
- Donnert, D.; Salecker, M. Elimination of phosphorus from municipal and industrial waste water. Water Sci. Technol. 1999, 40, 195–202. [Google Scholar] [CrossRef]
- Jones, R.; Lee, G.F. Recent advances in assessing impact of phosphorus loads on eutrophication-related water quality. Water Res. 1982, 16, 503–515. [Google Scholar] [CrossRef]
- Conley, D.J.; Paerl, H.W.; Howarth, R.W.; Boesch, D.F.; Seitzinger, S.P.; Havens, K.E.; Lancelot, C.; Likens, G.E. Controlling eutrophication: Nitrogen and phosphorus. Science 2009, 323, 1014–1015. [Google Scholar] [CrossRef] [PubMed]
- Sellner, K.G.; Doucette, G.J.; Kirkpatrick, G.J. Harmful algal blooms: Causes, impacts and detection. J. Ind. Microbiol. Biotechnol. 2003, 30, 383–406. [Google Scholar] [CrossRef] [PubMed]
- Grattan, L.M.; Holobaugh, S.; Morris, J.G., Jr. Harmful algal blooms and public health. Harmful Algae 2016, 57, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Hallegraeff, G.M. Harmful algal blooms: A global overview. Man. Harmful Mar. Microalgae 2003, 33, 1–22. [Google Scholar]
- Wurtsbaugh, W.A.; Paerl, H.W.; Dodds, W.K. Nutrients, eutrophication and harmful algal blooms along the freshwater to marine continuum. Wiley Interdiscip. Rev. Water 2019, 6, e1373. [Google Scholar] [CrossRef]
- Cordell, D.; White, S. Peak phosphorus: Clarifying the key issues of a vigorous debate about long-term phosphorus security. Sustainability 2011, 3, 2027–2049. [Google Scholar] [CrossRef]
- Worsfold, P.; McKelvie, I.; Monbet, P. Determination of phosphorus in natural waters: A historical review. Anal. Chim. Acta 2016, 918, 8–20. [Google Scholar] [CrossRef] [PubMed]
- Estela, J.M.; Cerdà, V. Flow analysis techniques for phosphorus: An overview. Talanta 2005, 66, 307–331. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhao, L.; Yu, F.; Du, Q. Detection of phosphorus species in water: Technology and strategies. Analyst 2019, 144, 7130–7148. [Google Scholar] [CrossRef] [PubMed]
- Islam, S.; Reza, M.N.; Jeong, J.-T.; Lee, K.-H. Sensing technology for rapid detection of phosphorus in water: A review. J. Biosyst. Eng. 2016, 41, 138–144. [Google Scholar] [CrossRef]
- Jarvie, H.P.; Withers, J.; Neal, C. Review of robust measurement of phosphorus in river water: Sampling, storage, fractionation and sensitivity. Hydrol. Earth Syst. Sci. 2002, 6, 113–131. [Google Scholar] [CrossRef]
- Anderson, E.S.; Schilling, K.E. Intensive short-term sampling with long-term consequences: Characterizing pollutant transport with implications for developing monitoring. Environ. Monit. Assess. 2024, 196, 1130. [Google Scholar] [CrossRef] [PubMed]
- Bowes, M.J.; Smith, J.T.; Jarvie, H.P.; Neal, C. Modelling of phosphorus inputs to rivers from diffuse and point sources. Sci. Total Environ. 2008, 395, 125–138. [Google Scholar] [CrossRef] [PubMed]
- Tabbara, H. Phosphorus loss to runoff water twenty-four hours after application of liquid swine manure or fertilizer. J. Environ. Qual. 2003, 32, 1044–1052. [Google Scholar] [CrossRef] [PubMed]
- Kronvang, B.; Vagstad, N.; Behrendt, H.; Bøgestrand, J.; Larsen, S. Phosphorus losses at the catchment scale within Europe: An overview. Soil Use Manag. 2007, 23, 104–116. [Google Scholar] [CrossRef]
- Jones, A.S.; Horsburgh, J.S.; Mesner, N.O.; Ryel, R.J.; Stevens, D.K. Influence of sampling frequency on estimation of annual total phosphorus and total suspended solids loads. JAWRA J. Am. Water Resour. Assoc. 2012, 48, 1258–1275. [Google Scholar] [CrossRef]
- Yang, Y.-Y.; Toor, G.S. Sources and mechanisms of nitrate and orthophosphate transport in urban stormwater runoff from residential catchments. Water Res. 2017, 112, 176–184. [Google Scholar] [CrossRef] [PubMed]
- Anderson, E.S.; Schilling, K.E. The speciation of Iowa’s nutrient loads and the implications for midwestern nutrient reduction strategies. J. Soil Water Conserv. 2024, 79, 233–246. [Google Scholar] [CrossRef]
- Drewry, J.; Newham, L.; Greene, R.; Jakeman, A.; Croke, B. A review of nitrogen and phosphorus export to waterways: Context for catchment modelling. Mar. Freshw. Res. 2006, 57, 757–774. [Google Scholar] [CrossRef]
- Jackson-Blake, L.A.; Dunn, S.M.; Helliwell, R.; Skeffington, R.; Stutter, M.; Wade, A.J. How well can we model stream phosphorus concentrations in agricultural catchments? Environ. Model. Softw. 2015, 64, 31–46. [Google Scholar] [CrossRef]
- Runkel, R.L.; Crawford, C.G.; Cohn, T.A. Load Estimator (LOADEST): A FORTRAN Program for Estimating Constituent Loads in Streams and Rivers; US Geological Survey: Reston, VA, USA, 2004. [Google Scholar]
- Hirsch, R.M.; Moyer, D.L.; Archfield, S.A. Weighted regressions on time, discharge, and season (WRTDS), with an application to Chesapeake Bay river inputs. JAWRA J. Am. Water Resour. Assoc. 2010, 46, 857–880. [Google Scholar] [CrossRef] [PubMed]
- Isles, P.D. A random forest approach to improve estimates of tributary nutrient loading. Water Res. 2024, 248, 120876. [Google Scholar] [CrossRef] [PubMed]
- Medalie, L. Concentration and Flux of Total and Dissolved Phosphorus, Total Nitrogen, Chloride, and Total Suspended Solids for Monitored Tributaries of Lake Champlain, 1990–2012; US Geological Survey: Reston, VA, USA, 2014. [Google Scholar]
- Lee, C.J.; Hirsch, R.M.; Crawford, C.G. An Evaluation of Methods for Computing Annual Water-Quality Loads; US Geological Survey: Reston, VA, USA, 2019. [Google Scholar]
- Zhang, Q.; Hirsch, R.M. River water-quality concentration and flux estimation can be improved by accounting for serial correlation through an autoregressive model. Water Resour. Res. 2019, 55, 9705–9723. [Google Scholar] [CrossRef]
- Defew, L.; May, L.; Heal, K. Uncertainties in estimated phosphorus loads as a function of different sampling frequencies and common calculation methods. Mar. Freshw. Res. 2013, 64, 373–386. [Google Scholar] [CrossRef]
- Viviano, G.; Salerno, F.; Manfredi, E.C.; Polesello, S.; Valsecchi, S.; Tartari, G. Surrogate measures for providing high frequency estimates of total phosphorus concentrations in urban watersheds. Water Res. 2014, 64, 265–277. [Google Scholar] [CrossRef] [PubMed]
- Jones, A.S.; Stevens, D.K.; Horsburgh, J.S.; Mesner, N.O. Surrogate measures for providing high frequency estimates of total suspended solids and total phosphorus concentrations 1. JAWRA J. Am. Water Resour. Assoc. 2011, 47, 239–253. [Google Scholar] [CrossRef]
- Settle, S.; Goonetilleke, A.; Ayoko, G.A. Determination of surrogate indicators for phosphorus and solids in urban stormwater: Application of multivariate data analysis techniques. Water Air Soil Pollut. 2007, 182, 149–161. [Google Scholar] [CrossRef]
- Kämäri, M.; Tarvainen, M.; Kotamäki, N.; Tattari, S. High-frequency measured turbidity as a surrogate for phosphorus in boreal zone rivers: Appropriate options and critical situations. Environ. Monit. Assess. 2020, 192, 1–20. [Google Scholar] [PubMed]
- Robertson, D.M.; Hubbard, L.E.; Lorenz, D.L.; Sullivan, D.J. A surrogate regression approach for computing continuous loads for the tributary nutrient and sediment monitoring program on the Great Lakes. J. Great Lakes Res. 2018, 44, 26–42. [Google Scholar] [CrossRef]
- Anderson, E.S.; Schilling, K.E.; Jones, C.S.; Weber, L.J. Estimating Iowa’s riverine phosphorus concentrations via water quality surrogacy. Heliyon 2024, 10, e37377. [Google Scholar] [CrossRef] [PubMed]
- Schilling, K.E.; Kim, S.-W.; Jones, C.S. Use of water quality surrogates to estimate total phosphorus concentrations in Iowa rivers. J. Hydrol. Reg. Stud. 2017, 12, 111–121. [Google Scholar] [CrossRef]
- Loperfido, J.; Just, C.L.; Papanicolaou, A.N.; Schnoor, J.L. In situ sensing to understand diel turbidity cycles, suspended solids, and nutrient transport in Clear Creek, Iowa. Water Resour. Res. 2010, 46, W06525. [Google Scholar] [CrossRef]
- Garrett, J.D. Concentrations, Loads, and Yields of Select Constituents from Major Tributaries of the Mississippi and Missouri Rivers in Iowa, Water Years 2004-2008; US Geological Survey: Reston, VA, USA, 2012. [Google Scholar]
- Stutter, M.; Dawson, J.J.; Glendell, M.; Napier, F.; Potts, J.M.; Sample, J.; Vinten, A.; Watson, H. Evaluating the use of in-situ turbidity measurements to quantify fluvial sediment and phosphorus concentrations and fluxes in agricultural streams. Sci. Total Environ. 2017, 607, 391–402. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Chan, K.S.; Schilling, K.E. Total phosphorus concentration trends in 40 Iowa rivers, 1999 to 2013. J. Environ. Qual. 2016, 45, 1351–1358. [Google Scholar] [CrossRef] [PubMed]
- Wise, D.R.; Anning, D.W.; Miller, O. Spatially Referenced Models of Streamflow and Nitrogen, Phosphorus, and Suspended-Sediment Transport in Streams of the Southwestern United States; US Geological Survey: Reston, VA, USA, 2019. [Google Scholar]
- Schilling, K.E.; Streeter, M.T.; Seeman, A.; Jones, C.S.; Wolter, C.F. Total phosphorus export from Iowa agricultural watersheds: Quantifying the scope and scale of a regional condition. J. Hydrol. 2020, 581, 124397. [Google Scholar] [CrossRef]
- Christianson, R.; Christianson, L.; Wong, C.; Helmers, M.; McIsaac, G.; Mulla, D.; McDonald, M. Beyond the nutrient strategies: Common ground to accelerate agricultural water quality improvement in the upper Midwest. J. Environ. Manag. 2018, 206, 1072–1080. [Google Scholar] [CrossRef] [PubMed]
- Nowatzke, L.; Arbuckle, J.G., Jr. Iowa Farmers and the Iowa Nutrient Reduction Strategy: Survey Results from the Missouri-Little Sioux Watershed. Iowa State University: Ames, IA, USA, 2018. [Google Scholar]
- Williamson, T.N.; Dobrowolski, E.G.; Kreiling, R.M. Phosphorus sources, forms, and abundance as a function of streamflow and field conditions in a Maumee River tributary, 2016–2019. J. Environ. Qual. 2023, 52, 492–507. [Google Scholar] [CrossRef] [PubMed]
- Mellander, P.E.; Jordan, P.; Shore, M.; Melland, A.R.; Shortle, G. Flow paths and phosphorus transfer pathways in two agricultural streams with contrasting flow controls. Hydrol. Process. 2015, 29, 3504–3518. [Google Scholar] [CrossRef]
- Bowes, M.J.; House, W.A.; Hodgkinson, R.A.; Leach, D.V. Phosphorus–discharge hysteresis during storm events along a river catchment: The River Swale, UK. Water Res. 2005, 39, 751–762. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, R.M.; Archfield, S.A.; De Cicco, L.A. A bootstrap method for estimating uncertainty of water quality trends. Environ. Model. Softw. 2015, 73, 148–166. [Google Scholar] [CrossRef]
- Anderson, E.S.; Schilling, K.E. Baseflow Index Trends in Iowa Rivers and the Relationships to Other Hydrologic Metrics. Hydrology 2025, 12, 116. [Google Scholar] [CrossRef]
- Jones, C.S.; Davis, C.A.; Drake, C.W.; Schilling, K.E.; Debionne, S.H.; Gilles, D.W.; Demir, I.; Weber, L.J. Iowa statewide stream nitrate load calculated using in situ sensor network. JAWRA J. Am. Water Resour. Assoc. 2018, 54, 471–486. [Google Scholar] [CrossRef]
- Eberts, S.M.; Woodside, M.D.; Landers, M.N.; Wagner, C.R. Monitoring the Pulse of Our Nation’s Rivers and Streams—The US Geological Survey Streamgaging Network; US Geological Survey: Reston, VA, USA, 2019. [Google Scholar]
- Granato, G.E.; Ries, K.G., III; Steeves, P.A. Compilation of Streamflow Statistics Calculated from Daily Mean Streamflow Data Collected During Water Years 1901–2015 for Selected US Geological Survey Streamgages; US Geological Survey: Reston, VA, USA, 2017. [Google Scholar]
- Robertson, D.M.; Saad, D.A. Spatially Referenced Models of Streamflow and Nitrogen, Phosphorus, and Suspended-Sediment Loads in Streams of the Midwestern United States; US Geological Survey: Reston, VA, USA, 2019. [Google Scholar]
- Prior, J.C. Landforms of Iowa; University of Iowa Press: Iowa City, IA, USA, 1991. [Google Scholar]
- Cruse, R.; Flanagan, D.; Frankenberger, J.; Gelder, B.; Herzmann, D.; James, D.; Krajewski, W.; Kraszewski, M.; Laflen, J.; Opsomer, J. Daily estimates of rainfall, water runoff, and soil erosion in Iowa. J. Soil Water Conserv. 2006, 61, 191–199. [Google Scholar] [CrossRef]
- Mallarino, A.; Stewart, B.; Baker, J.; Downing, J.; Sawyer, J. Phosphorus indexing for cropland: Overview and basic concepts of the Iowa phosphorus index. J. Soil Water Conserv. 2002, 57, 440–447. [Google Scholar] [CrossRef]
- Zaimes, G.N.; Schultz, R.C.; Isenhart, T.M. Streambank Soil and Phosphorus Losses Under Different Riparian Land-Uses in Iowa 1. JAWRA J. Am. Water Resour. Assoc. 2008, 44, 935–947. [Google Scholar] [CrossRef]
- Andersen, D.S.; Pepple, L.M. A county-level assessment of manure nutrient availability relative to crop nutrient capacity in Iowa: Spatial and temporal trends. Trans. ASABE 2017, 60, 1669–1680. [Google Scholar] [CrossRef]
- Powers, S.M.; Tank, J.L.; Robertson, D.M. Control of nitrogen and phosphorus transport by reservoirs in agricultural landscapes. Biogeochemistry 2015, 124, 417–439. [Google Scholar] [CrossRef]
- Schilling, K.E.; Anderson, E.; Streeter, M.T.; Theiling, C. Long-term nitrate-nitrogen reductions in a large flood control reservoir. J. Hydrol. 2023, 620, 129533. [Google Scholar] [CrossRef]
- Anderson, E.S. An Investigation of Iowa’s Riverine Phosphorus Loads and Statewide Phosphorus Budget; The University of Iowa: Iowa City, IA, USA, 2022. [Google Scholar]
- Dolph, C.L.; Boardman, E.; Danesh-Yazdi, M.; Finlay, J.C.; Hansen, A.T.; Baker, A.C.; Dalzell, B. Phosphorus transport in intensively managed watersheds. Water Resour. Res. 2019, 55, 9148–9172. [Google Scholar] [CrossRef]
- Shinohara, R.; Ouellette, L.; Nowell, P.; Parsons, C.T.; Matsuzaki, S.-i.S.; Voroney, R.P. The composition of particulate phosphorus: A case study of the Grand River, Canada. J. Great Lakes Res. 2018, 44, 527–534. [Google Scholar] [CrossRef]
- Kayhanian, M.; Singh, A.; Meyer, S. Impact of non-detects in water quality data on estimation of constituent mass loading. Water Sci. Technol. 2002, 45, 219–225. [Google Scholar] [CrossRef] [PubMed]
- Helsel, D.R. More than obvious: Better methods for interpreting nondetect data. Environ. Sci. Technol. 2005, 39, 419A–423A. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, R.M.; De Cicco, L.A. User Guide to Exploration and Graphics for RivEr Trends (EGRET) and Dataretrieval: R Packages for Hydrologic Data; US Geological Survey: Reston, VA, USA, 2015. [Google Scholar]
- McBride, G.B. Using Statistical Methods for Water Quality Management: Issues, Problems and Solutions; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Beck, M.B. Water quality modeling: A review of the analysis of uncertainty. Water Resour. Res. 1987, 23, 1393–1442. [Google Scholar] [CrossRef]
- Nwaiwu, E.N.; Bitrus, A. Fitting probability distributions to component water quality data from a treatment plant. Glob. J. Environ. Sci. 2005, 4, 151–154. [Google Scholar] [CrossRef]
- Berger, V.W.; Zhou, Y. Kolmogorov–smirnov test: Overview. In Wiley Statsref: Statistics Reference Online; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Schilling, K.E.; Isenhart, T.; Wolter, C.F.; Streeter, M.T.; Kovar, J.L. Contribution of streambanks to phosphorus export from Iowa. J. Soil Water Conserv. 2022, 77, 103–112. [Google Scholar] [CrossRef]
- Garrett, J.D. Total Phosphorus Loadings for the Cedar River at Palo, Iowa, 2009–2020; US Geological Survey: Reston, VA, USA, 2021. [Google Scholar]
- Garrett, J.D. The Use of Continuous Water-Quality Time-Series Data to Compute Nutrient Loadings for Selected Iowa Streams, 2008–2017; US Geological Survey: Reston, VA, USA, 2019. [Google Scholar]
- Lannergård, E.E.; Ledesma, J.L.; Fölster, J.; Futter, M.N. An evaluation of high frequency turbidity as a proxy for riverine total phosphorus concentrations. Sci. Total Environ. 2019, 651, 103–113. [Google Scholar] [CrossRef] [PubMed]
- USEPA. Ambient Water Quality Criteria Recommendations: Rivers and Streams in Nutrient Ecoregion VII. EPA/822/B/00/018; Office of Water, US Environmental Protection Agency: Washington, DC, USA, 2000. [Google Scholar]
- Klatt, J.; Mallarino, A.; Downing, J.; Kopaska, J.; Wittry, D. Soil phosphorus, management practices, and their relationship to phosphorus delivery in the Iowa Clear Lake agricultural watershed. J. Environ. Qual. 2003, 32, 2140–2149. [Google Scholar] [CrossRef] [PubMed]
- Fox, G.A.; Purvis, R.A.; Penn, C.J. Streambanks: A net source of sediment and phosphorus to streams and rivers. J. Environ. Manag. 2016, 181, 602–614. [Google Scholar] [CrossRef] [PubMed]
- Krasa, J.; Dostal, T.; Jachymova, B.; Bauer, M.; Devaty, J. Soil erosion as a source of sediment and phosphorus in rivers and reservoirs–Watershed analyses using WaTEM/SEDEM. Environ. Res. 2019, 171, 470–483. [Google Scholar] [CrossRef] [PubMed]
- Shore, M.; Murphy, S.; Mellander, P.-E.; Shortle, G.; Melland, A.R.; Crockford, L.; O’Flaherty, V.; Williams, L.; Morgan, G.; Jordan, P. Influence of stormflow and baseflow phosphorus pressures on stream ecology in agricultural catchments. Sci. Total Environ. 2017, 590, 469–483. [Google Scholar] [CrossRef] [PubMed]
- Schilling, K.E.; Streeter, M.T.; Isenhart, T.M.; Beck, W.J.; Tomer, M.D.; Cole, K.J.; Kovar, J.L. Distribution and mass of groundwater orthophosphorus in an agricultural watershed. Sci. Total Environ. 2018, 625, 1330–1340. [Google Scholar] [CrossRef] [PubMed]
- Wilson, H.; Elliott, J.; Macrae, M.; Glenn, A. Near-surface soils as a source of phosphorus in snowmelt runoff from cropland. J. Environ. Qual. 2019, 48, 921–930. [Google Scholar] [CrossRef] [PubMed]
- Anderson, E.S.; Schilling, K.E.; Jones, C.; Weber, L.; Wolter, C. Iowa’s Annual Phosphorus Budget: Quantifying the Inputs and Outputs of Phosphorus Transport Processes. Land 2024, 13, 1483. [Google Scholar] [CrossRef]
- Eghball, B.; Gilley, J.E. Phosphorus risk assessment index evaluation using runoff measurements. J. Soil Water Conserv. 2001, 56, 202–206. [Google Scholar] [CrossRef]
- Andersson, A. Mechanisms for log normal concentration distributions in the environment. Sci. Rep. 2021, 11, 16418. [Google Scholar] [CrossRef] [PubMed]
- Shumway, R.H.; Azari, R.S.; Kayhanian, M. Statistical approaches to estimating mean water quality concentrations with detection limits. Environ. Sci. Technol. 2002, 36, 3345–3353. [Google Scholar] [CrossRef] [PubMed]
- Maestre, A.; Pitt, R.; Durrans, S.R.; Chakraborti, S. Stormwater quality descriptions using the three parameter lognormal distribution. J. Water Manag. Modeling. 2005, 13, 247–274. [Google Scholar] [CrossRef]
- Reimann, C.; Filzmoser, P. Normal and lognormal data distribution in geochemistry: Death of a myth. Consequences for the statistical treatment of geochemical and environmental data. Environ. Geol. 2000, 39, 1001–1014. [Google Scholar] [CrossRef]
- Blum, A.G.; Archfield, S.A.; Vogel, R.M. On the probability distribution of daily streamflow in the United States. Hydrol. Earth Syst. Sci. 2017, 21, 3093–3103. [Google Scholar] [CrossRef]
- Skeffington, R.; Halliday, S.; Wade, A.; Bowes, M.; Loewenthal, M. Using high-frequency water quality data to assess sampling strategies for the EU Water Framework Directive. Hydrol. Earth Syst. Sci. 2015, 19, 2491–2504. [Google Scholar] [CrossRef]
- Mackay, A.; Taylor, M. Event-based water quality sampling method for application in remote rivers. River Res. Appl. 2012, 28, 1105–1112. [Google Scholar] [CrossRef]
- Lessels, J.; Bishop, T. A post-event stratified random sampling scheme for monitoring event-based water quality using an automatic sampler. J. Hydrol. 2020, 580, 123393. [Google Scholar] [CrossRef]
- Chien, H.; Yeh, P.J.-F.; Knouft, J.H. Modeling the potential impacts of climate change on streamflow in agricultural watersheds of the Midwestern United States. J. Hydrol. 2013, 491, 73–88. [Google Scholar] [CrossRef]
- Bieroza, M.; Heathwaite, A. Seasonal variation in phosphorus concentration–discharge hysteresis inferred from high-frequency in situ monitoring. J. Hydrol. 2015, 524, 333–347. [Google Scholar] [CrossRef]
- Jones, C.S.; Schilling, K.E. From agricultural intensification to conservation: Sediment transport in the Raccoon River, Iowa, 1916–2009. J. Environ. Qual. 2011, 40, 1911–1923. [Google Scholar] [CrossRef] [PubMed]
- Deasy, C.; Brazier, R.; Heathwaite, A.; Hodgkinson, R. Pathways of runoff and sediment transfer in small agricultural catchments. Hydrol. Process. Int. J. 2009, 23, 1349–1358. [Google Scholar] [CrossRef]
- Gilles, D.; Young, N.; Schroeder, H.; Piotrowski, J.; Chang, Y.-J. Inundation mapping initiatives of the Iowa Flood Center: Statewide coverage and detailed urban flooding analysis. Water 2012, 4, 85–106. [Google Scholar] [CrossRef]
- McMillan, H.; Krueger, T.; Freer, J. Benchmarking observational uncertainties for hydrology: Rainfall, river discharge and water quality. Hydrol. Process. 2012, 26, 4078–4111. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).