Cascade Reservoir Outflow Simulation Based on Physics-Constrained Random Forest
Abstract
1. Introduction
2. Materials and Methods
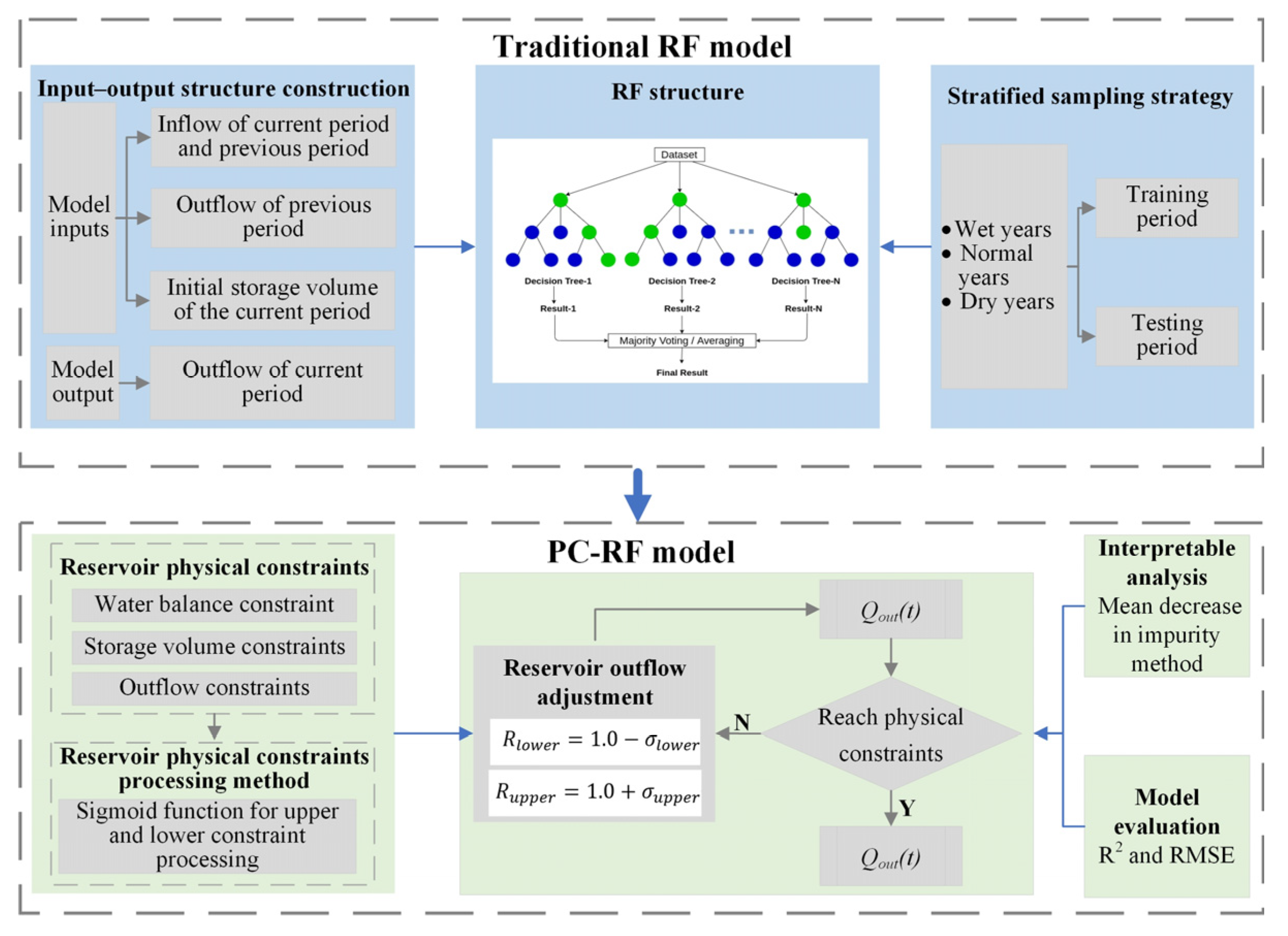
2.1. Physics-Constrained Random Forest Model (PC-RF)
2.1.1. Input–Output Structure Construction
2.1.2. Standsrd RF
2.1.3. Stratified Sampling Strategy
2.1.4. Physical Constraints and Processing Method
- (1)
- Water balance constraint
- (2)
- Storage volume constraints
- (3)
- Outflow constraints
2.2. Reference Model
2.3. Model Evaluation
2.4. Mean Decrease in Impurity Method
3. Case Description
3.1. Study Area
3.2. Data
4. Results
4.1. Dataset Sampling
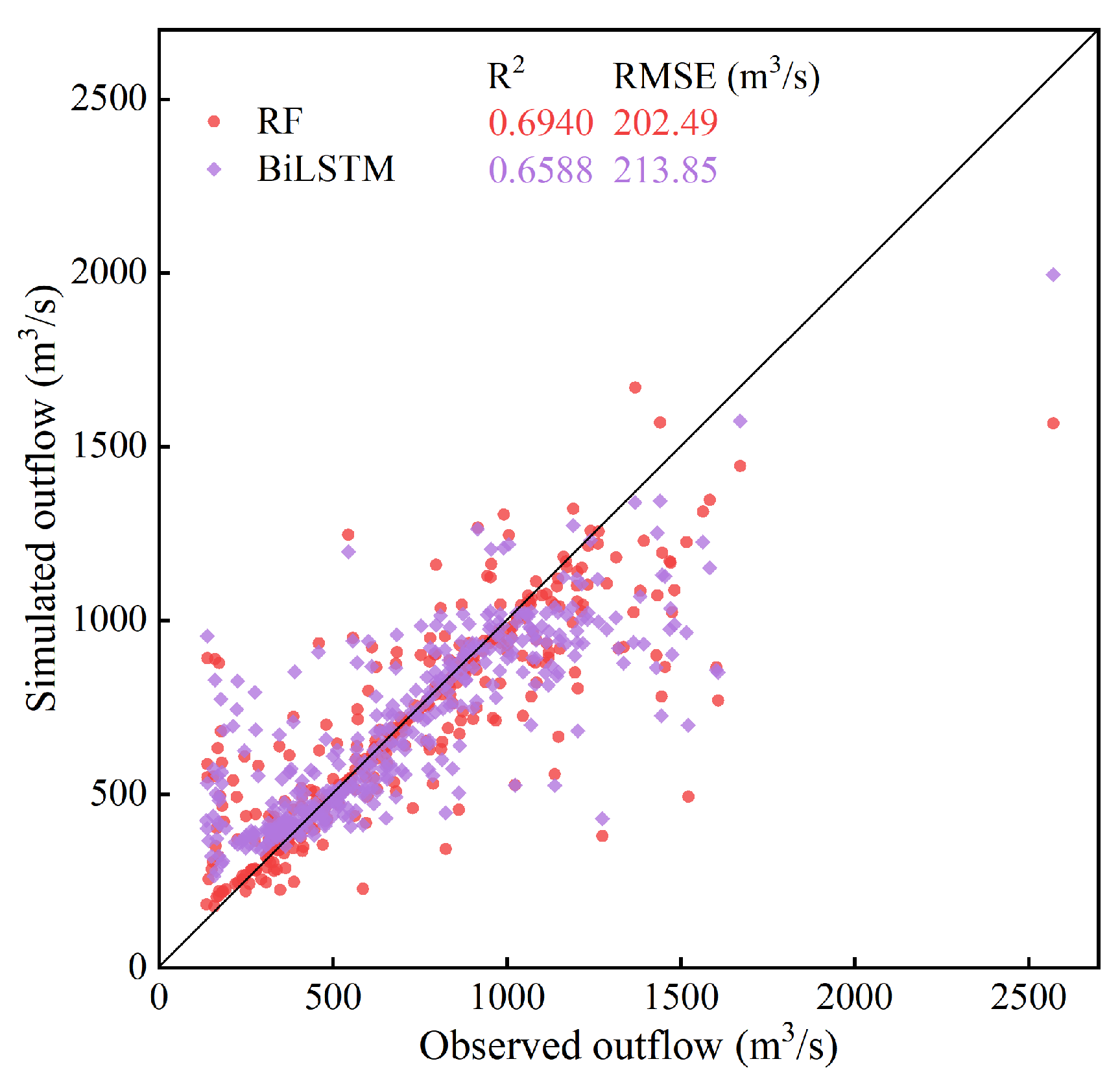
4.2. Assessment of RF and BiLSTM Models Without Physical Constraints
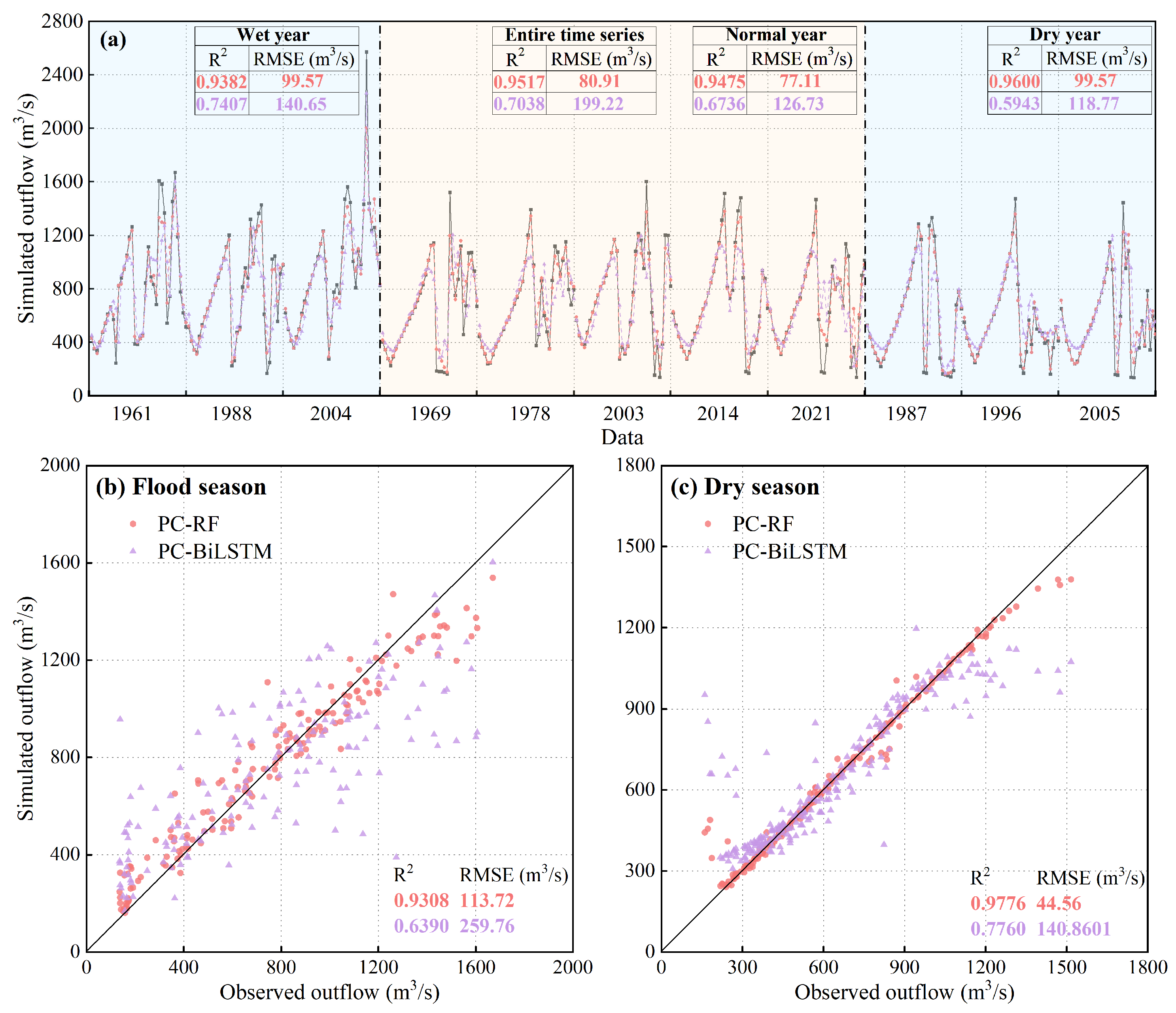
4.3. Assessment of PC-RF and PC-BiLSTM Models
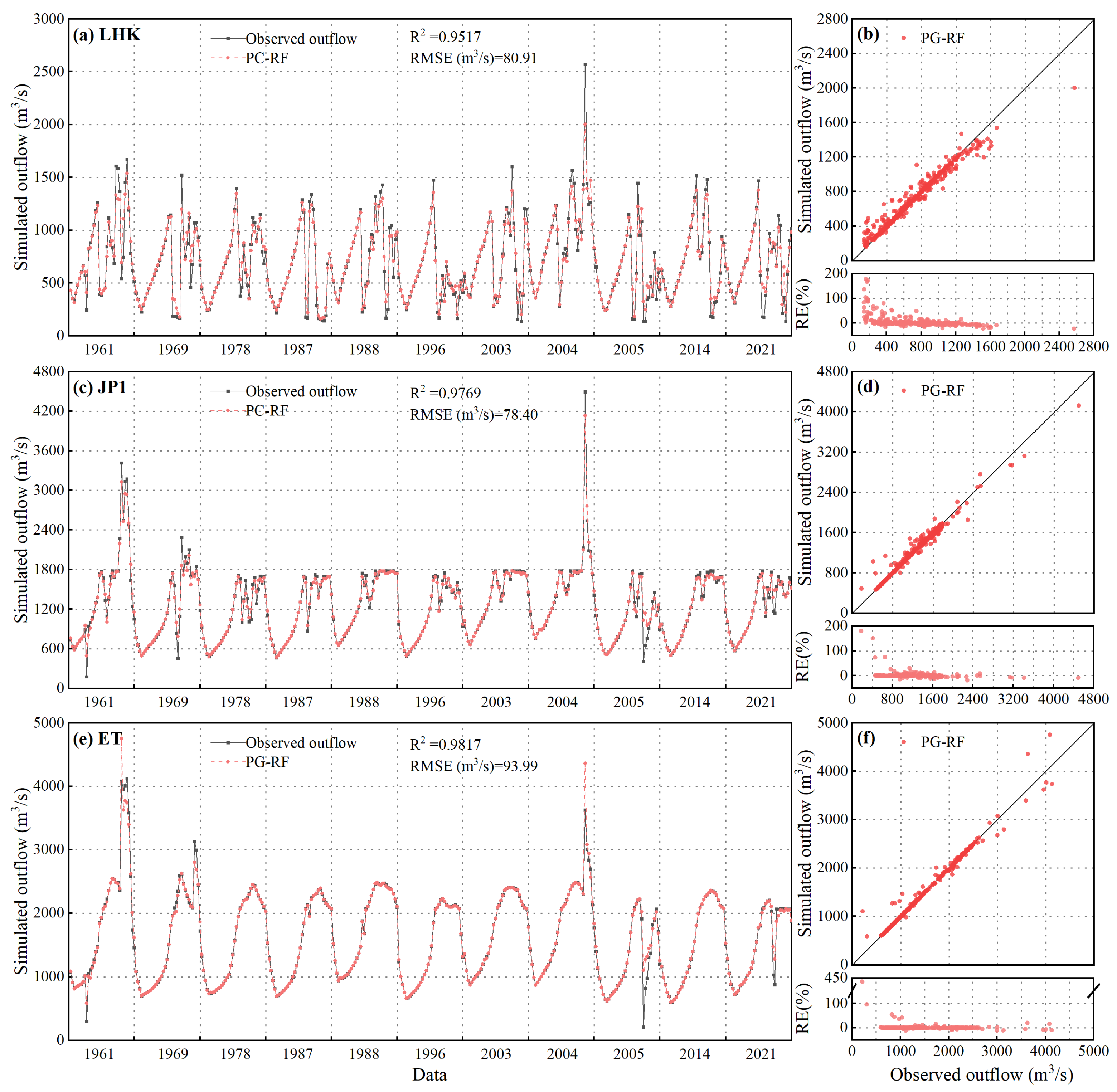
4.4. Assessment of PC-RF Model in Simulating Outflow for Cascade Reservoirs
5. Discussion
5.1. The Enhanced Effect of PC-RF Model
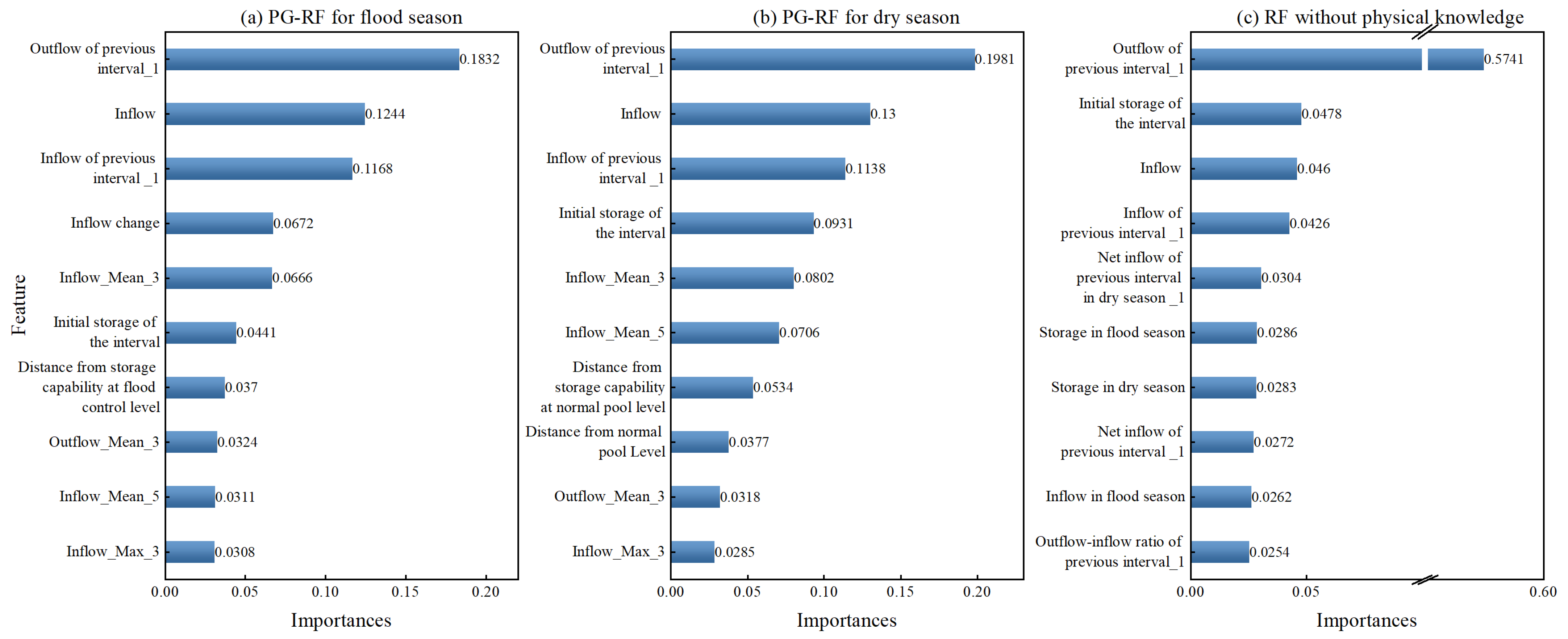
5.2. An Interpretable Analysis of the PC-RF Model
5.3. Limitations
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine learning |
| RF | Random forest |
| PC-RF | Physics-constrained RF |
| RNN | Recurrent neural network |
| LSTM | Long short-term memory |
| BiLSTM | Bidirectional LSTM |
| PC-BiLSTM | Physics-constrained BiLSTM |
| R2 | Coefficient of determination |
| RMSE | Root mean square error |
| MDI | Mean decrease in impurity |
| LHK | Lianghekou |
| JP1 | Jinping I |
| ET | Ertan |
References
- Li, Y.; Zhao, G.; Allen, G.H.; Gao, H.L. Diminishing storage returns of reservoir construction. Nat. Commun. 2023, 14, 3203. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C.Y.; Liu, C.H.; Fan, C.Y.; Liu, K.; Chen, T.; Zeng, F.X.; Zhan, P.F.; Song, C.Q. Estimation of water storage capacity of Chinese reservoirs by statistical and machine learning models. J. Hydrol. 2024, 630, 130674. [Google Scholar] [CrossRef]
- Zajac, Z.; Revilla-Romero, B.; Salamon, P.; Burek, P.; Hirpa, F.A.; Beck, H. The impact of lake and reservoir parameterization on global streamflow simulation. J. Hydrol. 2017, 548, 552–568. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Pokhrel, Y.; Miguez-Macho, G. High-Resolution Modeling of Reservoir Release and Storage Dynamics at the Continental Scale. Water Resour. Res. 2019, 55, 787–810. [Google Scholar] [CrossRef]
- Bai, B.X.; Mu, L.X.; Tan, Y.M. A Global Lakes/Reservoirs Surface Extent Dataset (GLRSED): An Integration of Multi-Source Data. Geosci. Data J. 2025, 12, e285. [Google Scholar] [CrossRef]
- Wu, W.Y.; Eamen, L.; Dandy, G.; Razavi, S.; Kuczera, G.; Maier, H.R. Beyond engineering: A review of reservoir management through the lens of wickedness, competing objectives and uncertainty. Environ. Model. Softw. 2023, 167, 105777. [Google Scholar] [CrossRef]
- Giuliani, M.; Lamontagne, J.R.; Reed, P.M.; Castelletti, A. A State-of-the-Art Review of Optimal Reservoir Control for Managing Conflicting Demands in a Changing World. Water Resour. Res. 2021, 57, e2021WR029927. [Google Scholar] [CrossRef]
- Qie, G.P.; Zhang, Z.X.; Getahun, E.; Mamer, E.A. Comparison of Machine Learning Models Performance on Simulating Reservoir Outflow: A Case Study of Two Reservoirs in Illinois, USA. J. Am. Water Resour. Assoc. 2023, 59, 554–570. [Google Scholar] [CrossRef]
- Ahmad, A.; El-Shafie, A.; Razali, S.F.M.; Mohamad, Z.S. Reservoir Optimization in Water Resources: A Review. Water Resour. Manag. 2014, 28, 3391–3405. [Google Scholar] [CrossRef]
- Ren, K.; Huang, Q.; Huang, S.Z.; Ming, B.; Leng, G.Y. Identifying complex networks and operating scenarios for cascade water reservoirs for mitigating drought and flood impacts. J. Hydrol. 2021, 594, 125946. [Google Scholar] [CrossRef]
- Zhu, B.R.; Liu, J.; Lin, J.Q.; Liu, Y.; Zhang, D.; Ren, Y.F.; Peng, Q.D.; Yang, J.; He, H.J.; Feng, Q. Cascade reservoirs adaptive refined simulation model based on the mechanism-AI coupling modeling paradigm. J. Hydrol. 2022, 612, 128229. [Google Scholar] [CrossRef]
- Wannasin, C.; Brauer, C.C.; Uijlenhoet, R.; Torfs, P.; Weerts, A.H. Machine learning for real-time reservoir operation simulation: Comparing input variables and algorithms for the Sirikit Reservoir, Thailand. J. Hydroinformatics 2024, 26, 3151–3171. [Google Scholar] [CrossRef]
- Chen, Y.A.; Li, D.H.; Zhao, Q.K.; Cai, X.M. Developing a generic data-driven reservoir operation model. Adv. Water Resour. 2022, 167, 104274. [Google Scholar] [CrossRef]
- Chen, L.H.; Yu, J.; Teng, J.; Chen, H.; Teng, X.; Li, X.F. Optimizing Joint Flood Control Operating Charts for Multi-reservoir System Based on Multi-group Piecewise Linear Function. Water Resour. Manag. 2022, 36, 3305–3325. [Google Scholar] [CrossRef]
- Mahmoud, A.; Hu, T.S.; Jing, P.R.; Liu, Y.; Li, X.; Wang, X. Enhancing interpretability of AI models in reservoir operation simulation: Exploring and mitigating principal inconsistencies through theory-guided multi-objective artificial neural networks. J. Hydrol. 2024, 639, 131618. [Google Scholar] [CrossRef]
- Yang, S.Y.; Yang, D.W.; Chen, J.S.; Zhao, B.X. Real-time reservoir operation using recurrent neural networks and inflow forecast from a distributed hydrological model. J. Hydrol. 2019, 579, 124229. [Google Scholar] [CrossRef]
- Longyang, Q.; Zeng, R.J. A Hierarchical Temporal Scale Framework for Data-Driven Reservoir Release Modeling. Water Resour. Res. 2023, 59, e2022WR033922. [Google Scholar] [CrossRef]
- Lang, L.C.; Gao, X.; Li, Y.K.; Li, Z.H.; Wu, F. Incorporating multi-timescale data into a single long short-term memory network to enhance reservoir-regulated streamflow simulation. J. Hydrol. 2025, 654, 132806. [Google Scholar] [CrossRef]
- Zhang, D.; Peng, Q.; Lin, J.; Wang, D.; Liu, X.; Zhuang, J. Simulating Reservoir Operation Using a Recurrent Neural Network Algorithm. Water 2019, 11, 865. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, J.Q.; Peng, Q.D.; Wang, D.S.; Yang, T.T.; Sorooshian, S.; Liu, X.F.; Zhuang, J.B. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef]
- Zheng, Y.L.; Liu, P.; Cheng, L.; Xie, K.; Lou, W.; Li, X.; Luo, X.R.; Cheng, Q.; Han, D.Y.; Zhang, W. Extracting operation behaviors of cascade reservoirs using physics-guided long-short term memory networks. J. Hydrol.-Reg. Stud. 2022, 40, 101034. [Google Scholar] [CrossRef]
- Chen, R.T.; Wang, D.G.; Mei, Y.W.; Lin, Y.E.; Lin, Z.Q.; Zhang, Z.; Zhuang, S.J.; Zhu, J.X.; Kam, J.; Wu, Y.P.; et al. A knowledge-guided LSTM reservoir outflow model and its application to streamflow simulation in reservoir-regulated basins. J. Hydrol. 2025, 658, 133164. [Google Scholar] [CrossRef]
- Yu, B.; Zheng, Y.; He, S.K.; Xiong, R.; Wang, C. Physics-encoded deep learning for integrated modeling of watershed hydrology and reservoir operations. J. Hydrol. 2025, 657, 133052. [Google Scholar] [CrossRef]
- Zheng, Y.L.; Liu, P.; Cheng, Q.; Xu, H.; Luo, X.R.; Liu, W.B.; Li, X.; Ye, H.; Lei, H.X.; Zhang, W. Operational Interval Extraction Based on Long-Short Term Memory Networks for Building More Feasible Reservoir Operation Models. Water Resour. Res. 2025, 61, e2024WR038147. [Google Scholar] [CrossRef]
- Snee, R.D. Validation of Regression Models: Methods and Examples. Technometrics 1977, 19, 415–428. [Google Scholar] [CrossRef]
- May, R.J.; Maier, H.R.; Dandy, G.C. Data splitting for artificial neural networks using SOM-based stratified sampling. Neural Netw. 2010, 23, 283–294. [Google Scholar] [CrossRef] [PubMed]
- Zheng, F.; Chen, J.; Maier, H.R.; Gupta, H. Achieving Robust and Transferable Performance for Conservation-Based Models of Dynamical Physical Systems. Water Resour. Res. 2022, 58, e2021WR031818. [Google Scholar] [CrossRef]
- Shen, C.; Laloy, E.; Elshorbagy, A.; Albert, A.; Bales, J.; Chang, F.J.; Ganguly, S.; Hsu, K.L.; Kifer, D.; Fang, Z.; et al. HESS Opinions: Incubating deep-learning-powered hydrologic science advances as a community. Hydrol. Earth Syst. Sci. 2018, 22, 5639–5656. [Google Scholar] [CrossRef]
- Tripathy, K.P.; Mishra, A.K. Deep learning in hydrology and water resources disciplines: Concepts, methods, applications, and research directions. J. Hydrol. 2024, 628, 130458. [Google Scholar] [CrossRef]
- Scornet, E. Trees, forests, and impurity-based variable importance in regression. Ann. Inst. Henri Poincare-Probab. Stat. 2023, 59, 21–52. [Google Scholar] [CrossRef]



| Reservoir | Normal Pool Level (m) | Flood Control Level (m) | Dead Water Level (m) | Storage Capability at Normal Pool Level (108 m3) | Storage Capability at Flood Control Level (108 m3) | Dead Storage (108 m3) | Reservoir Capability | Installed Capacity (MW) |
|---|---|---|---|---|---|---|---|---|
| LHK | 2865 | 2845.9 | 2785 | 101.5 | 81.5 | 35.9 | multi-year | 3000 |
| JP1 | 1880 | 1859.0 | 1800 | 77.6 | 61.6 | 28.4 | yearly | 3600 |
| ET | 1200 | 1190.0 | 1155 | 57.9 | 48.5 | 24.0 | seasonal | 3300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Yu, L.; Zhang, Y.; Jia, B.; Zhang, L.; Luo, S. Cascade Reservoir Outflow Simulation Based on Physics-Constrained Random Forest. Water 2025, 17, 2154. https://doi.org/10.3390/w17142154
Zhou Z, Yu L, Zhang Y, Jia B, Zhang L, Luo S. Cascade Reservoir Outflow Simulation Based on Physics-Constrained Random Forest. Water. 2025; 17(14):2154. https://doi.org/10.3390/w17142154
Chicago/Turabian StyleZhou, Zehui, Lei Yu, Yu Zhang, Benyou Jia, Luchen Zhang, and Shaoze Luo. 2025. "Cascade Reservoir Outflow Simulation Based on Physics-Constrained Random Forest" Water 17, no. 14: 2154. https://doi.org/10.3390/w17142154
APA StyleZhou, Z., Yu, L., Zhang, Y., Jia, B., Zhang, L., & Luo, S. (2025). Cascade Reservoir Outflow Simulation Based on Physics-Constrained Random Forest. Water, 17(14), 2154. https://doi.org/10.3390/w17142154






