Morphodynamic Interactions Between Sandbar, Beach Profile, and Dune Under Variable Hydrodynamic and Morphological Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. CS-Model Description
2.2. Experimental Setup and Flume Characteristics
2.3. Reference Scenario
2.4. Scenarios Definition
3. Results
3.1. CS-Model
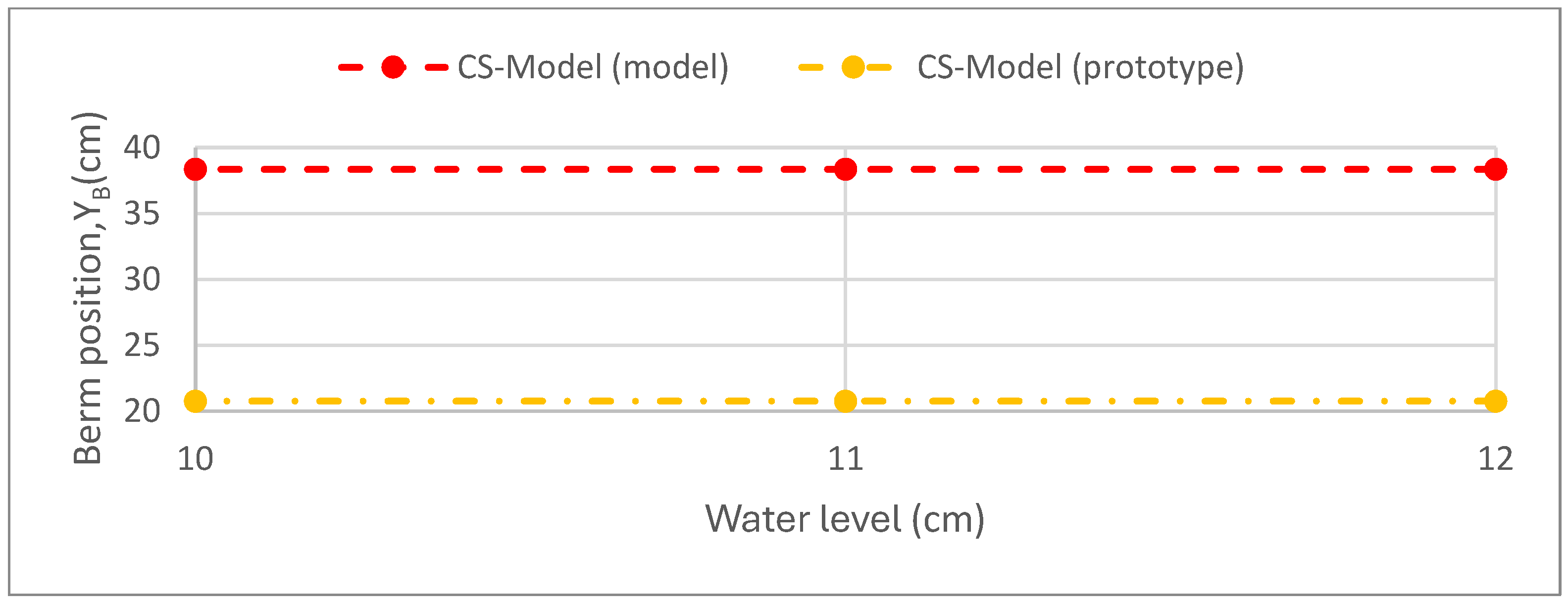
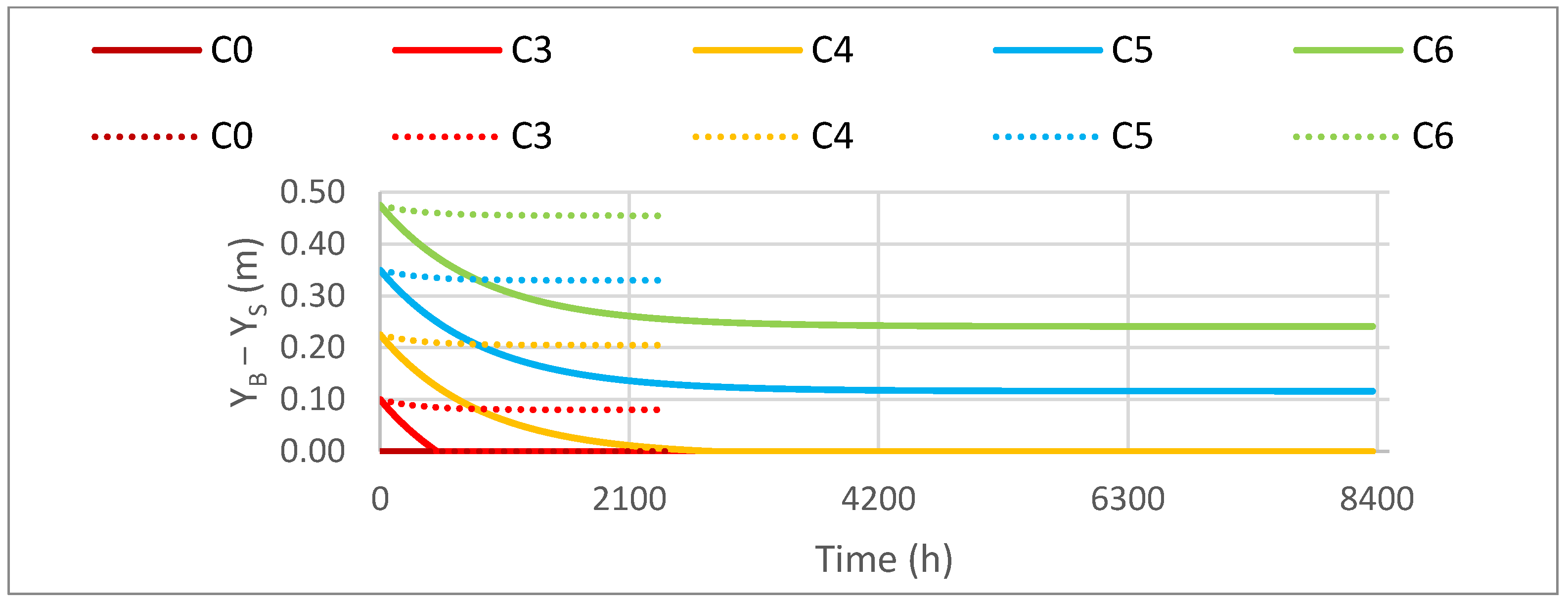
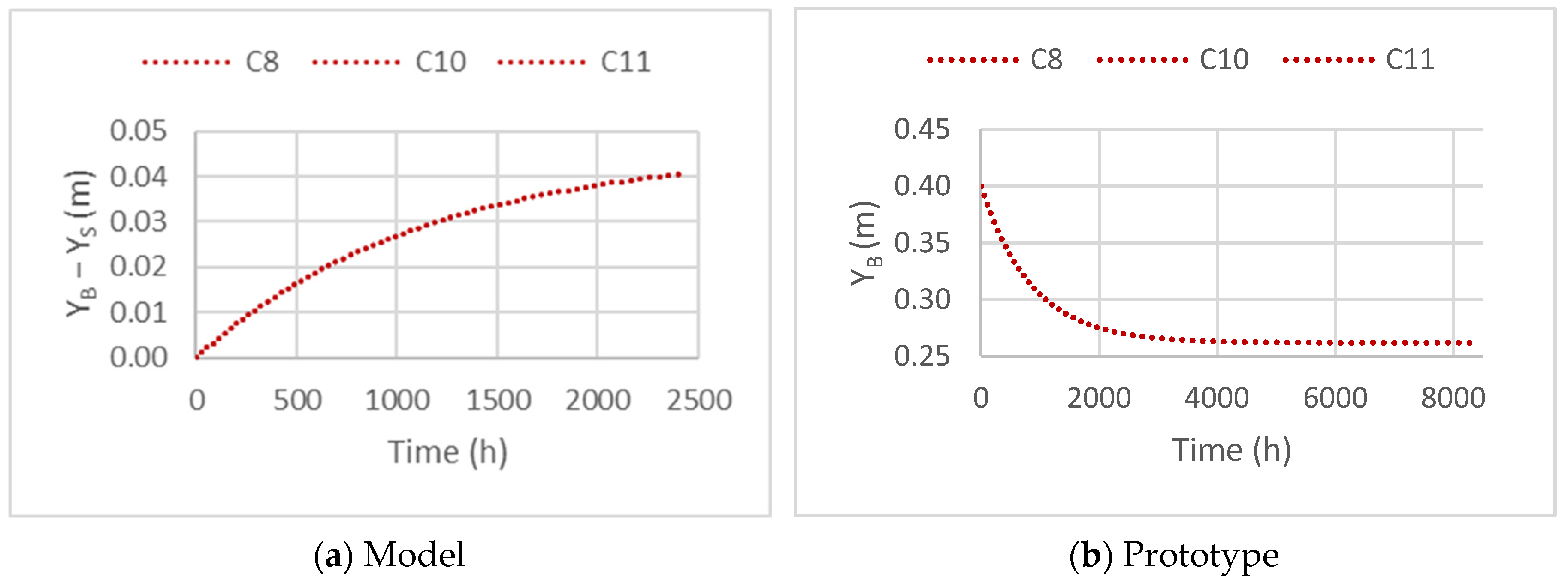
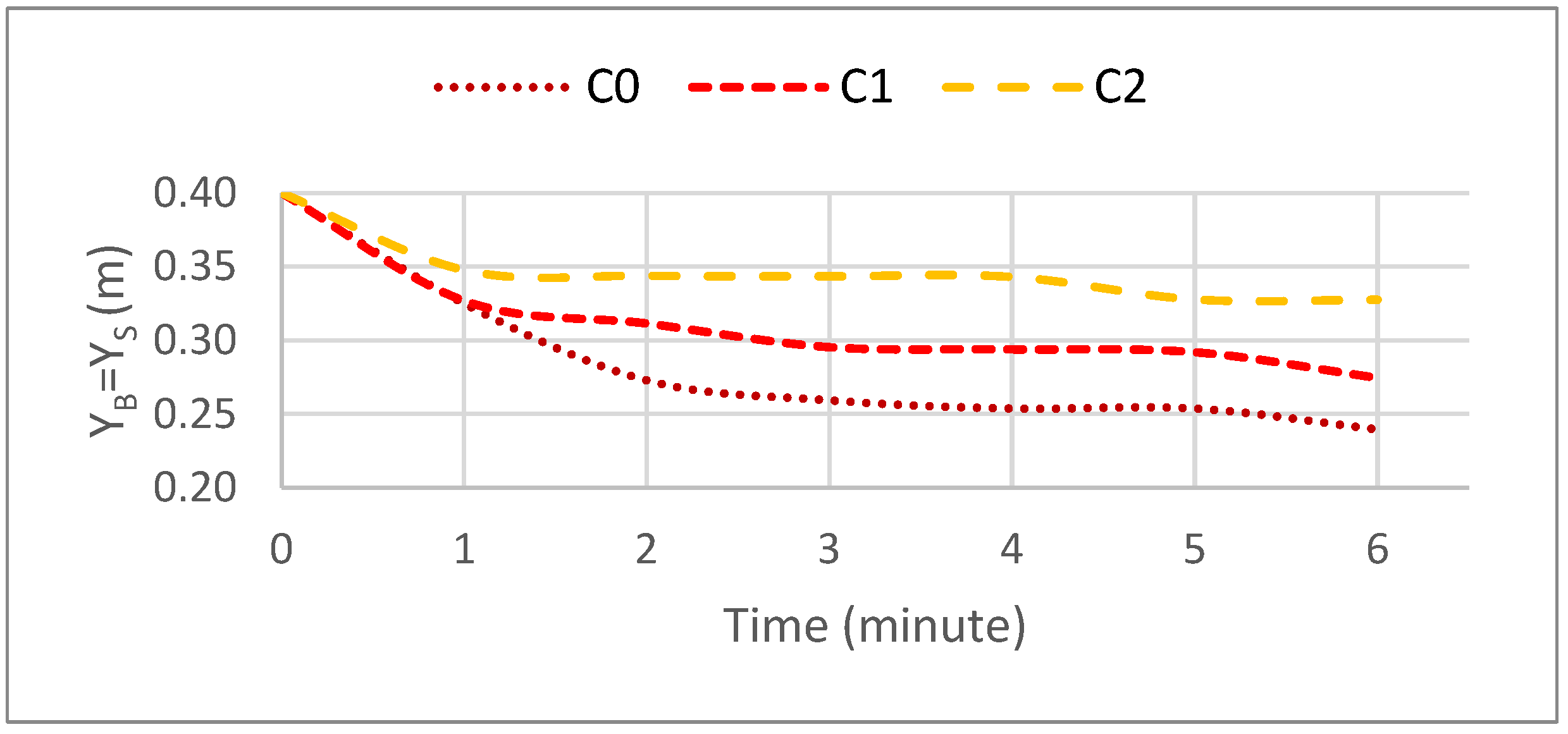
3.1.1. Water Level
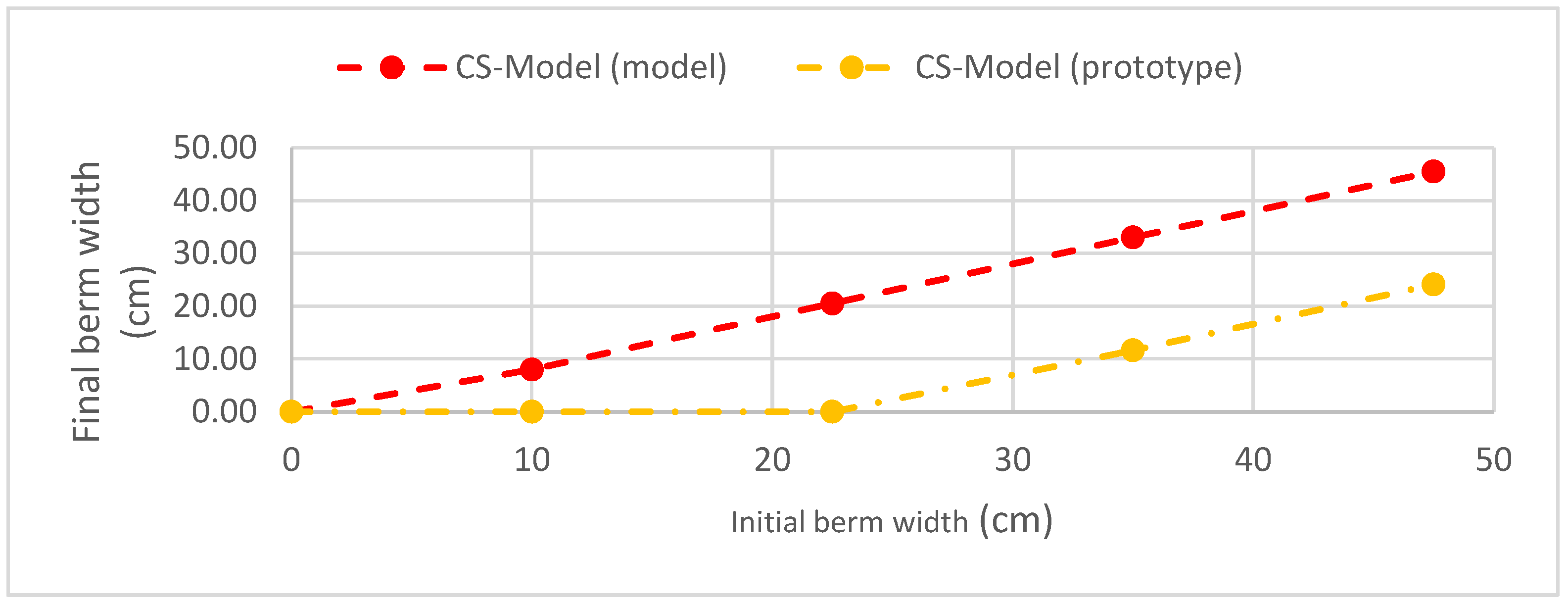
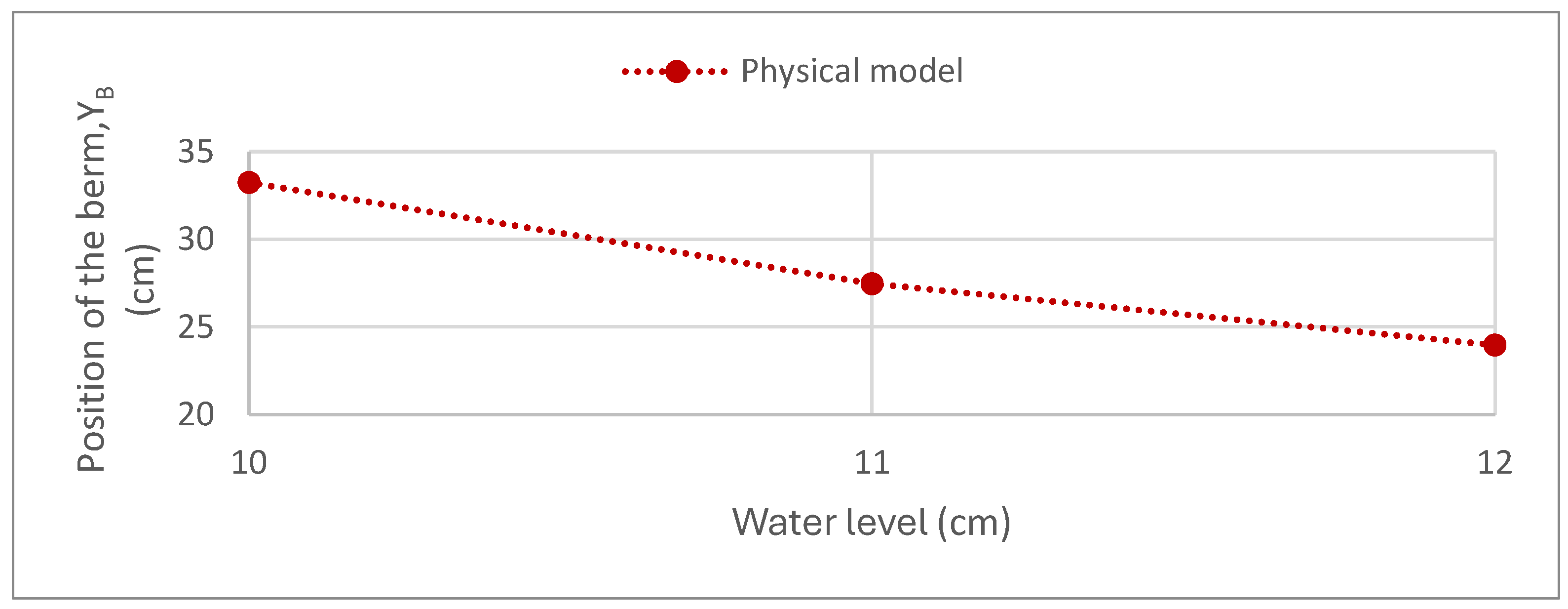
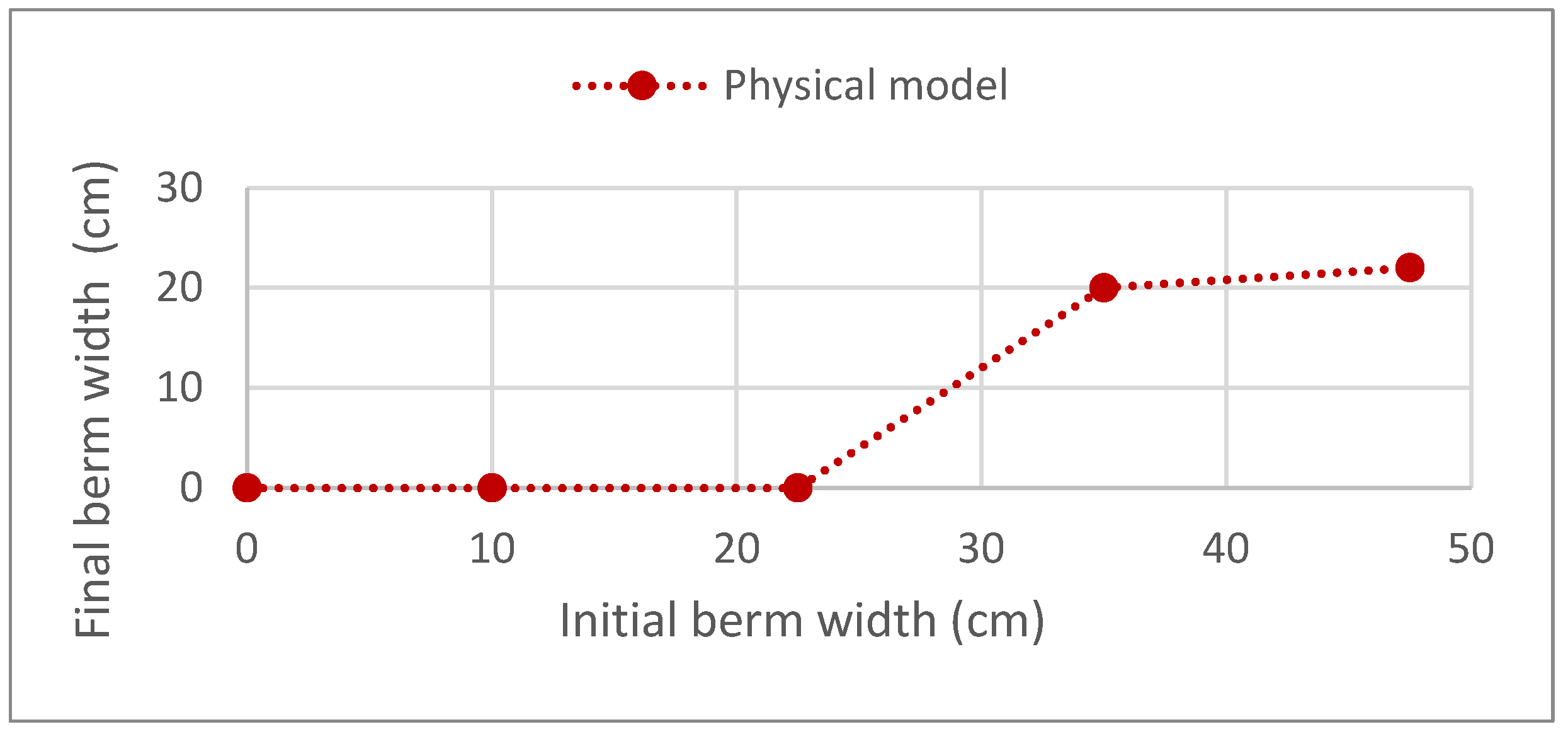
3.1.2. Berm Width
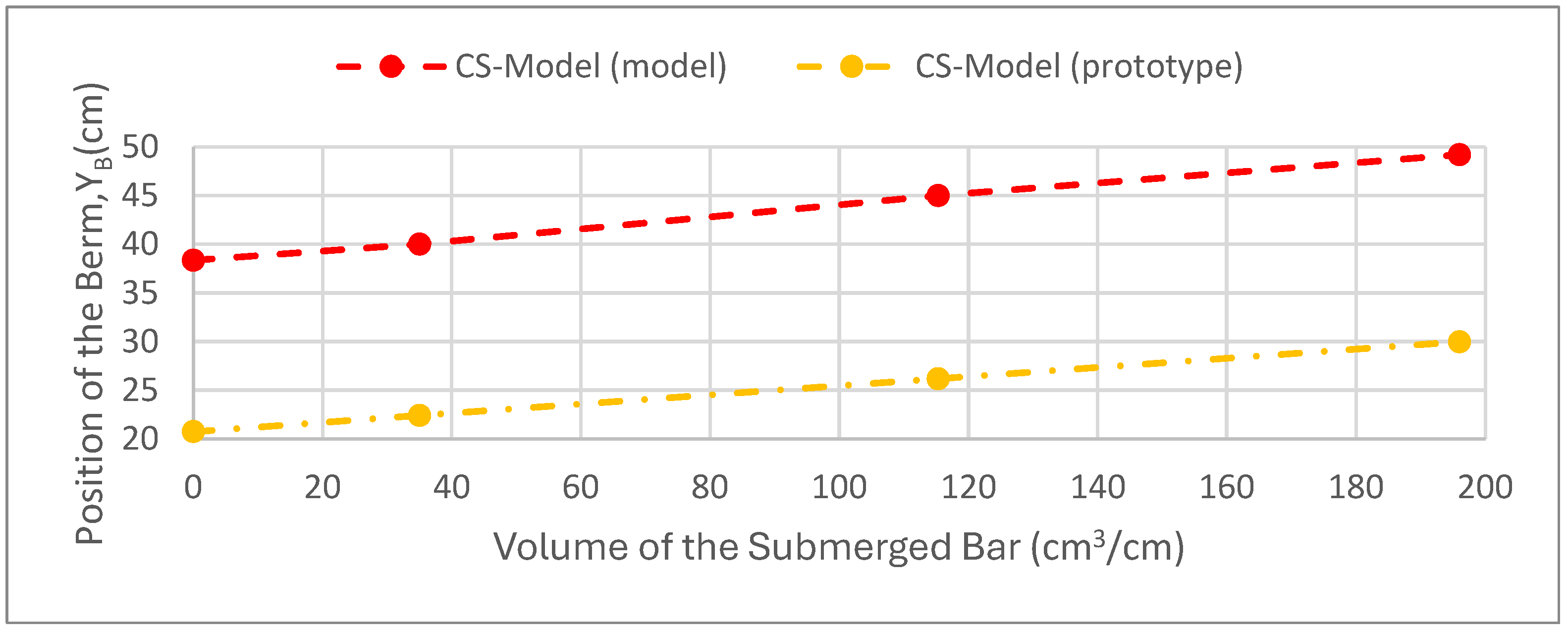
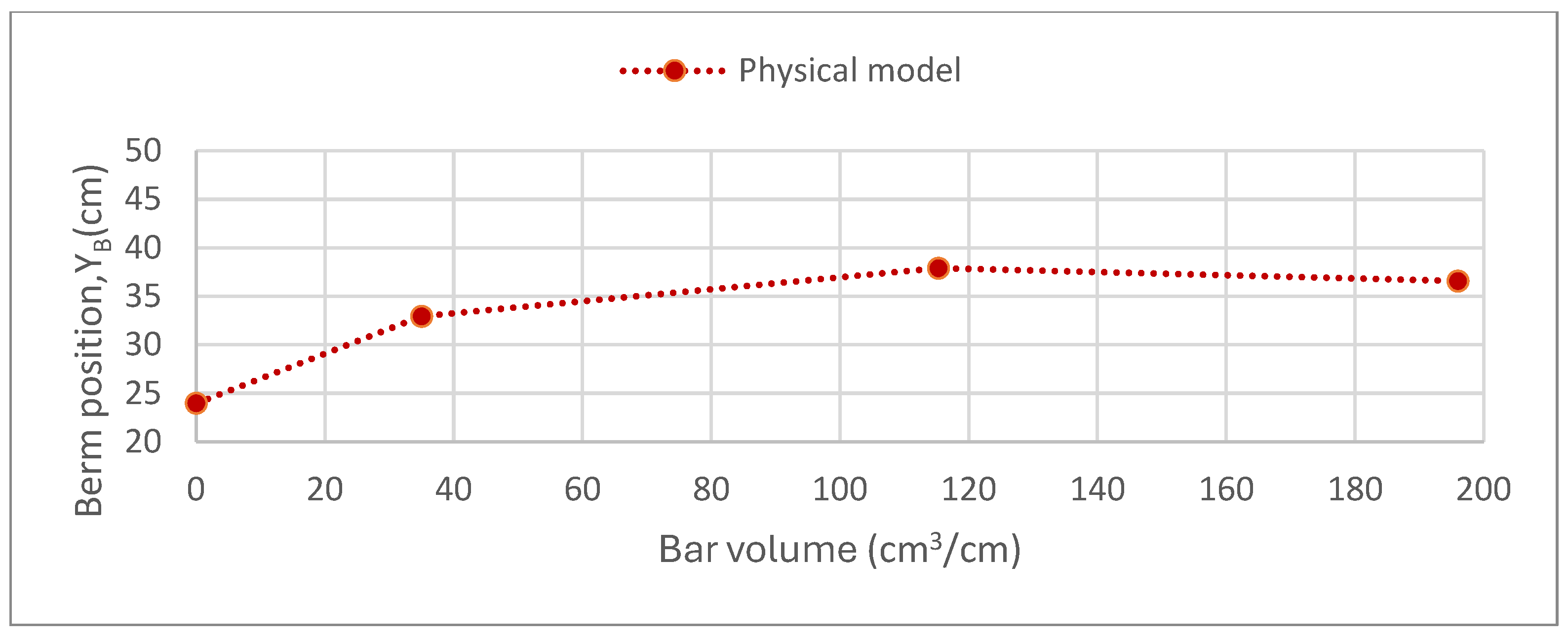
3.1.3. Volume of the Bar
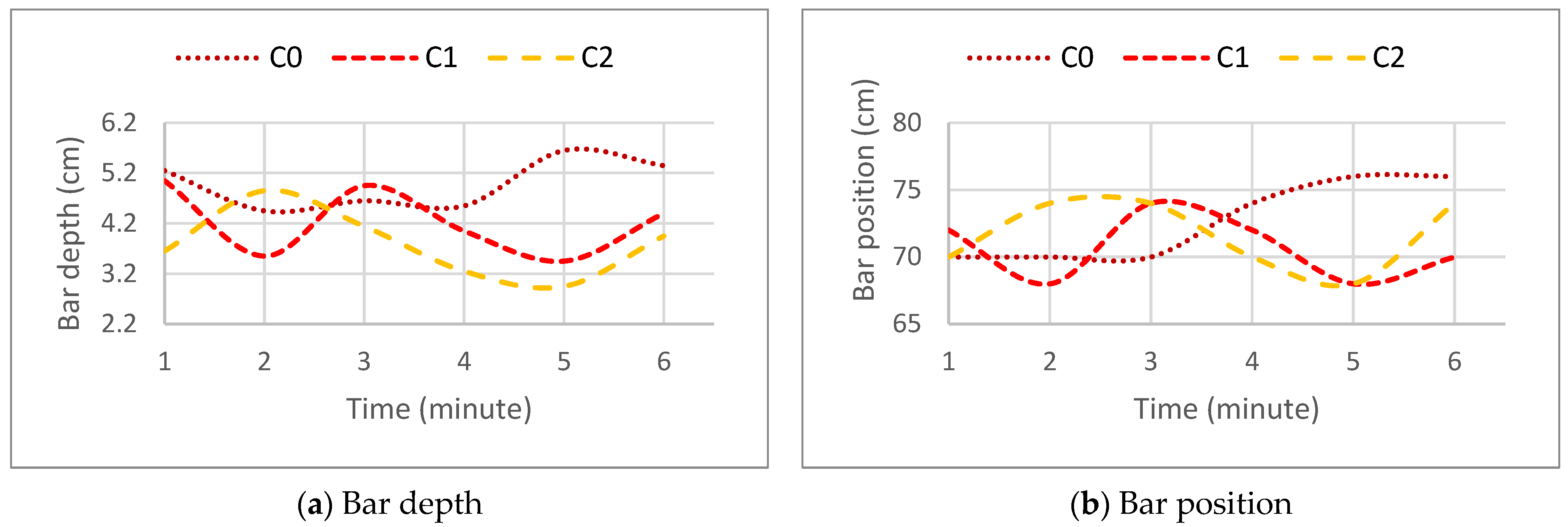
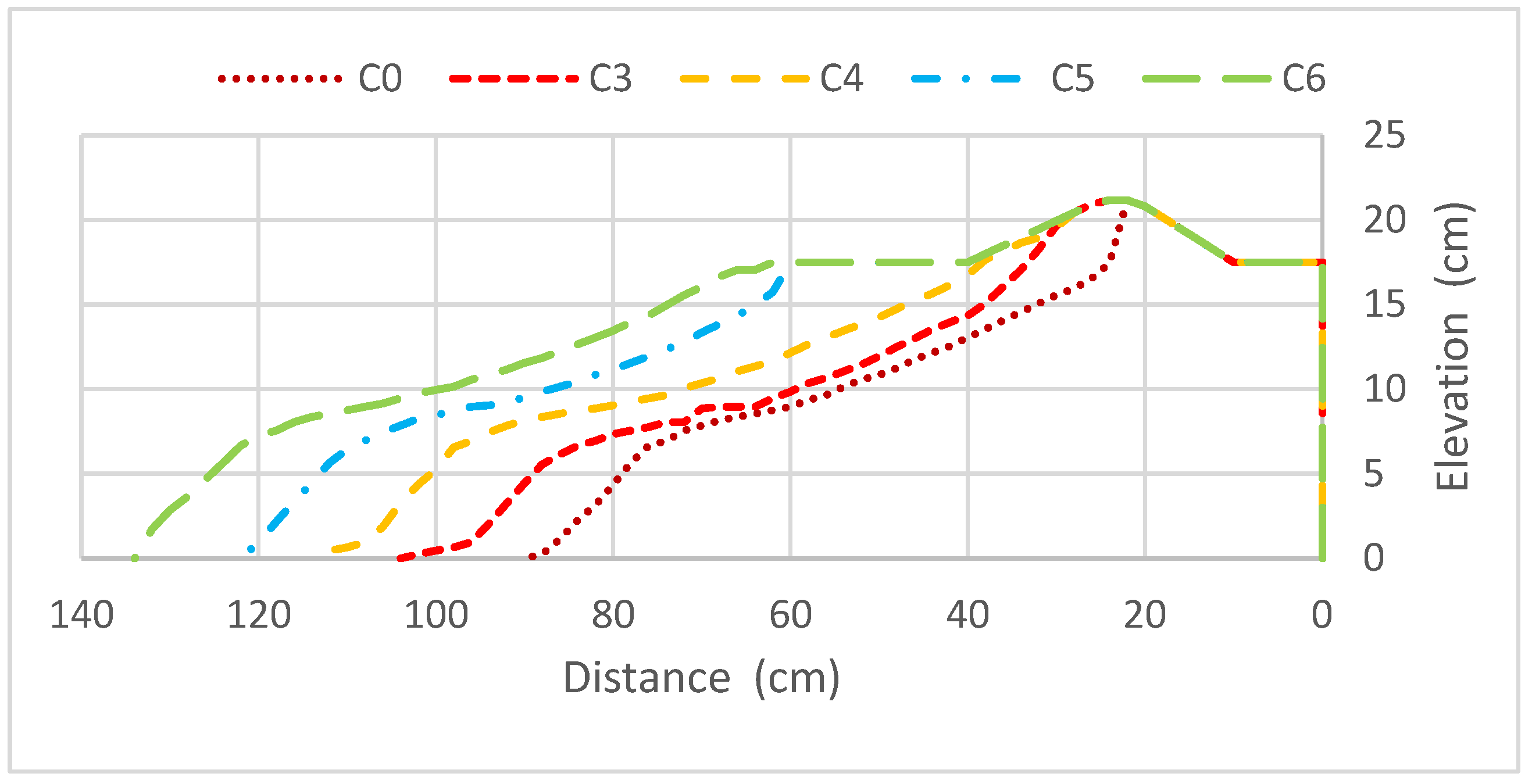
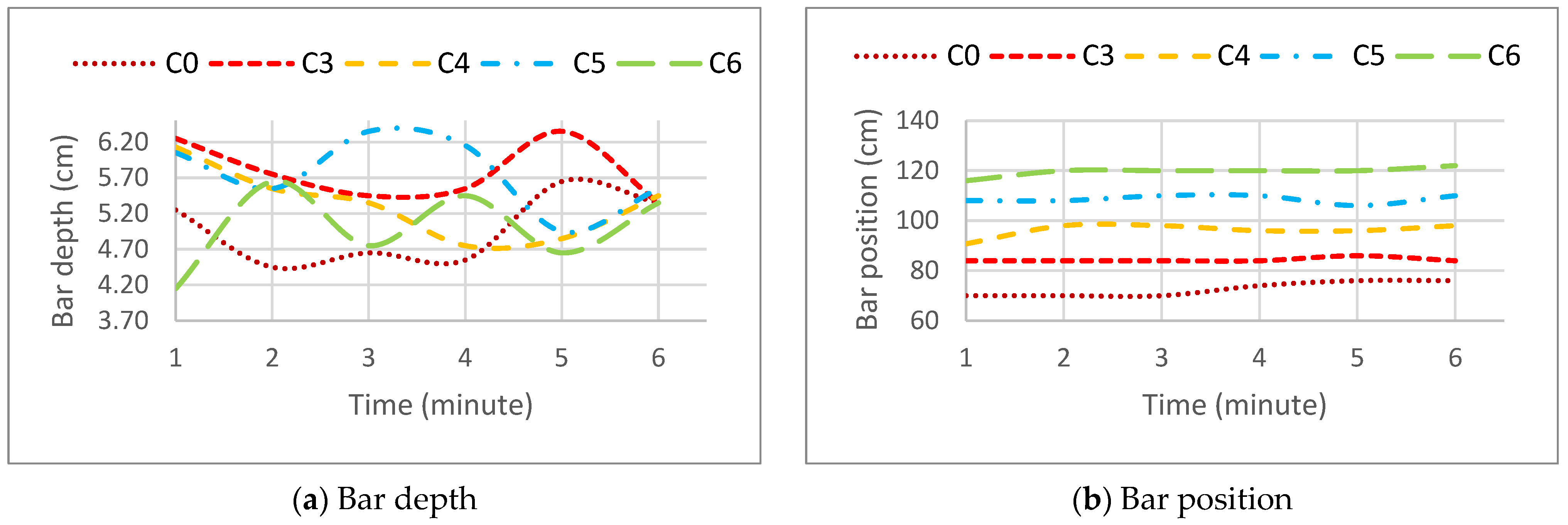
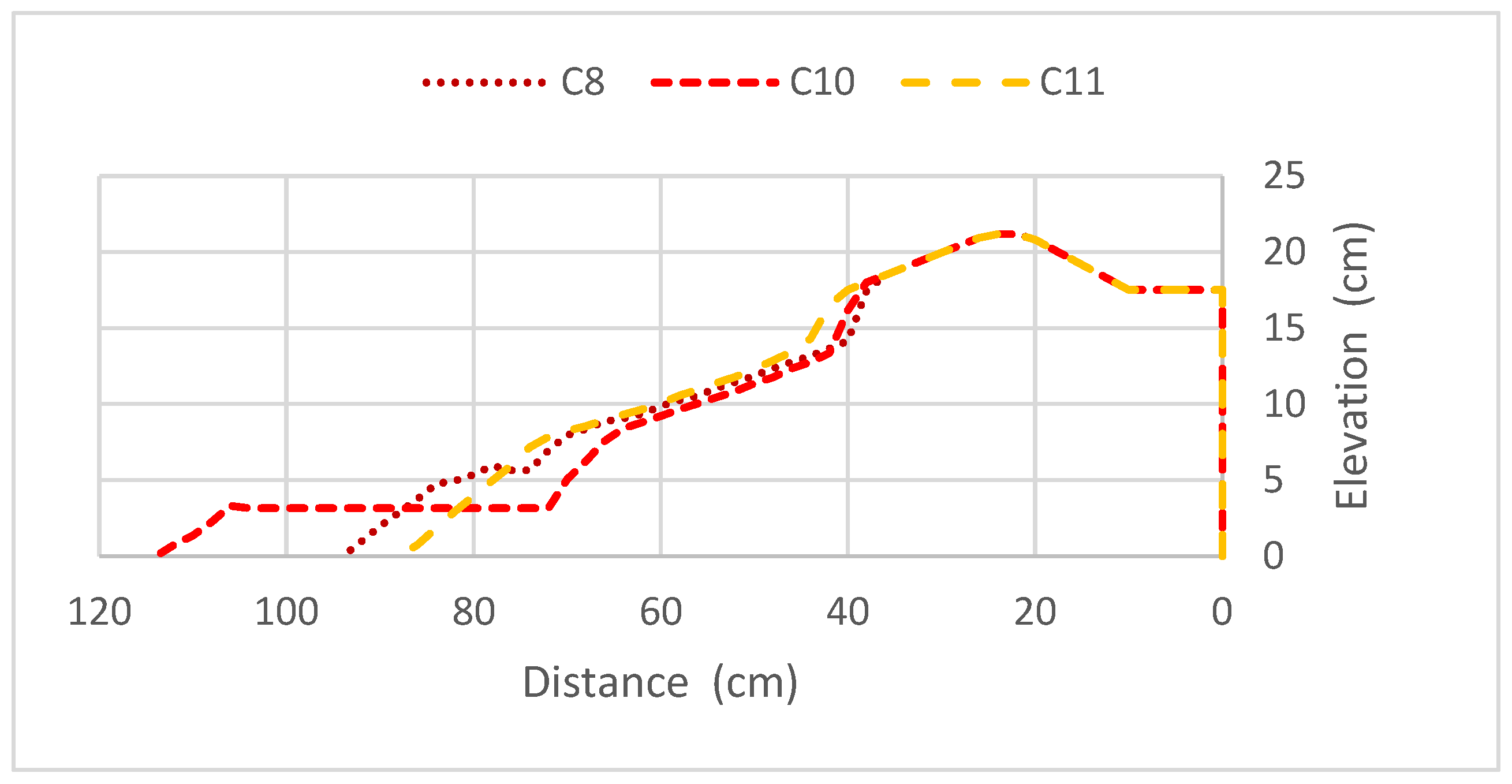
3.1.4. Bar Shape
3.2. Flume Tests Results Assessment
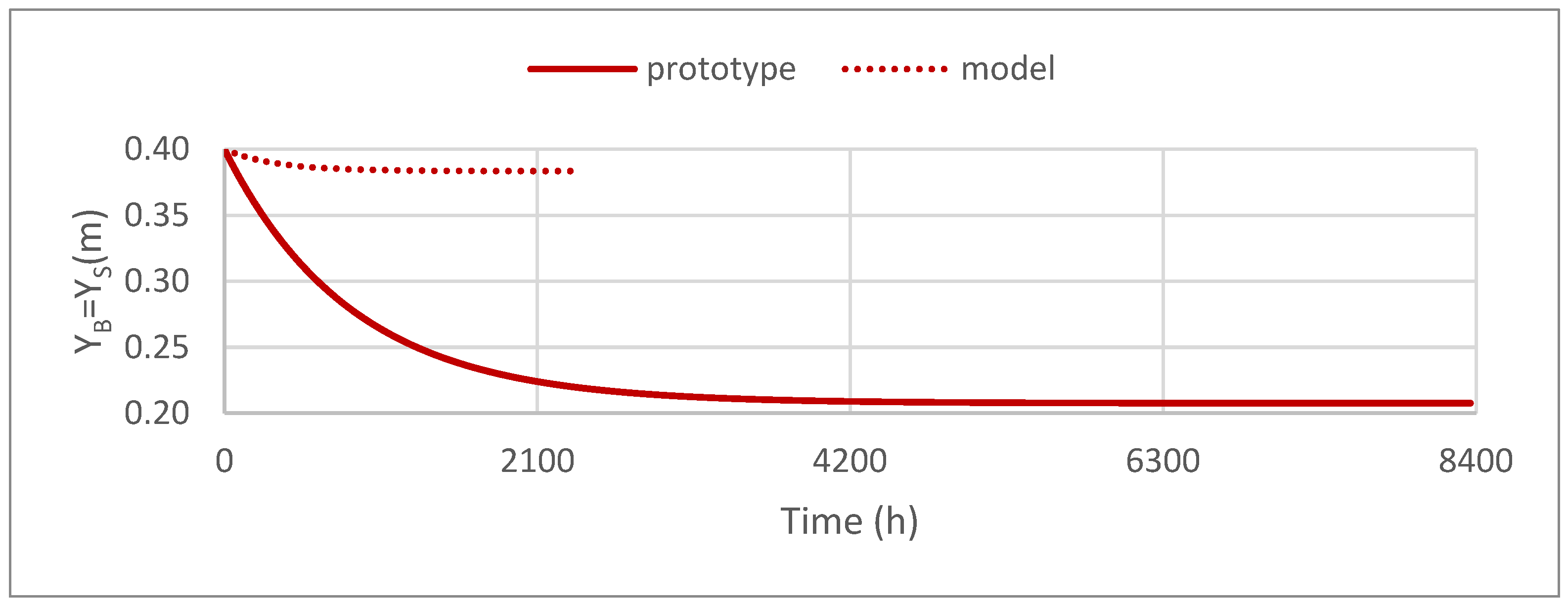
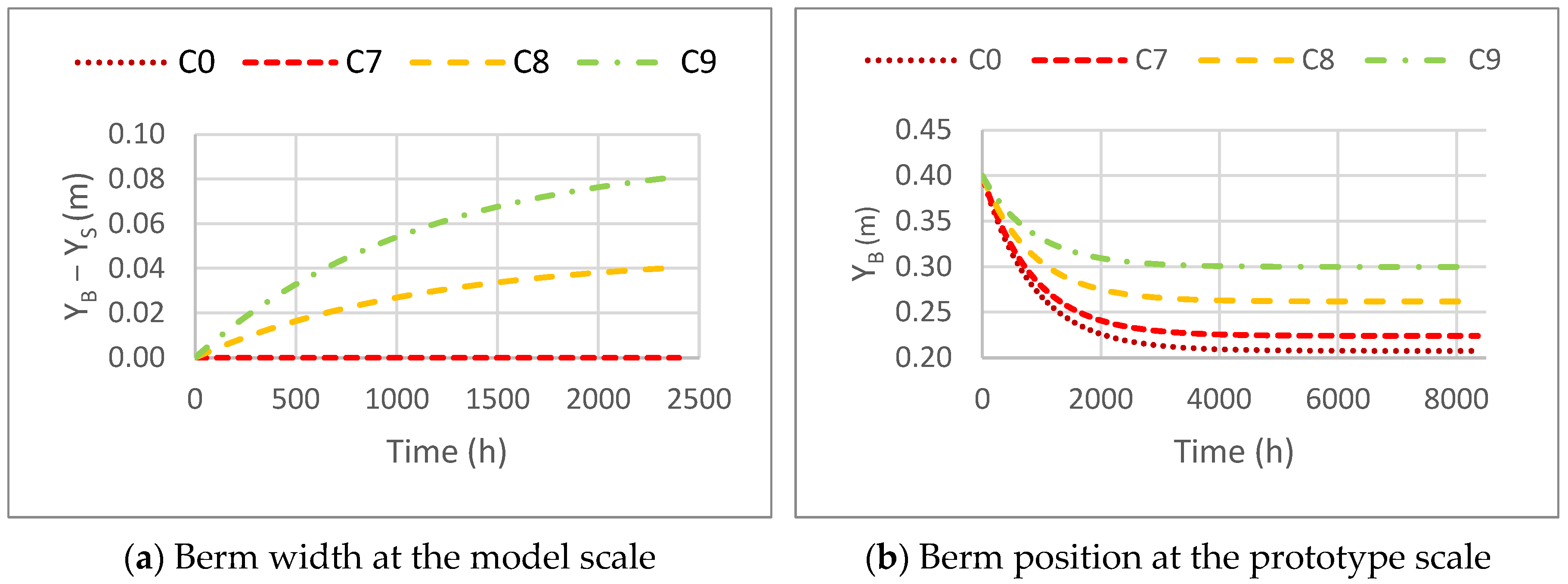
3.2.1. Water Level
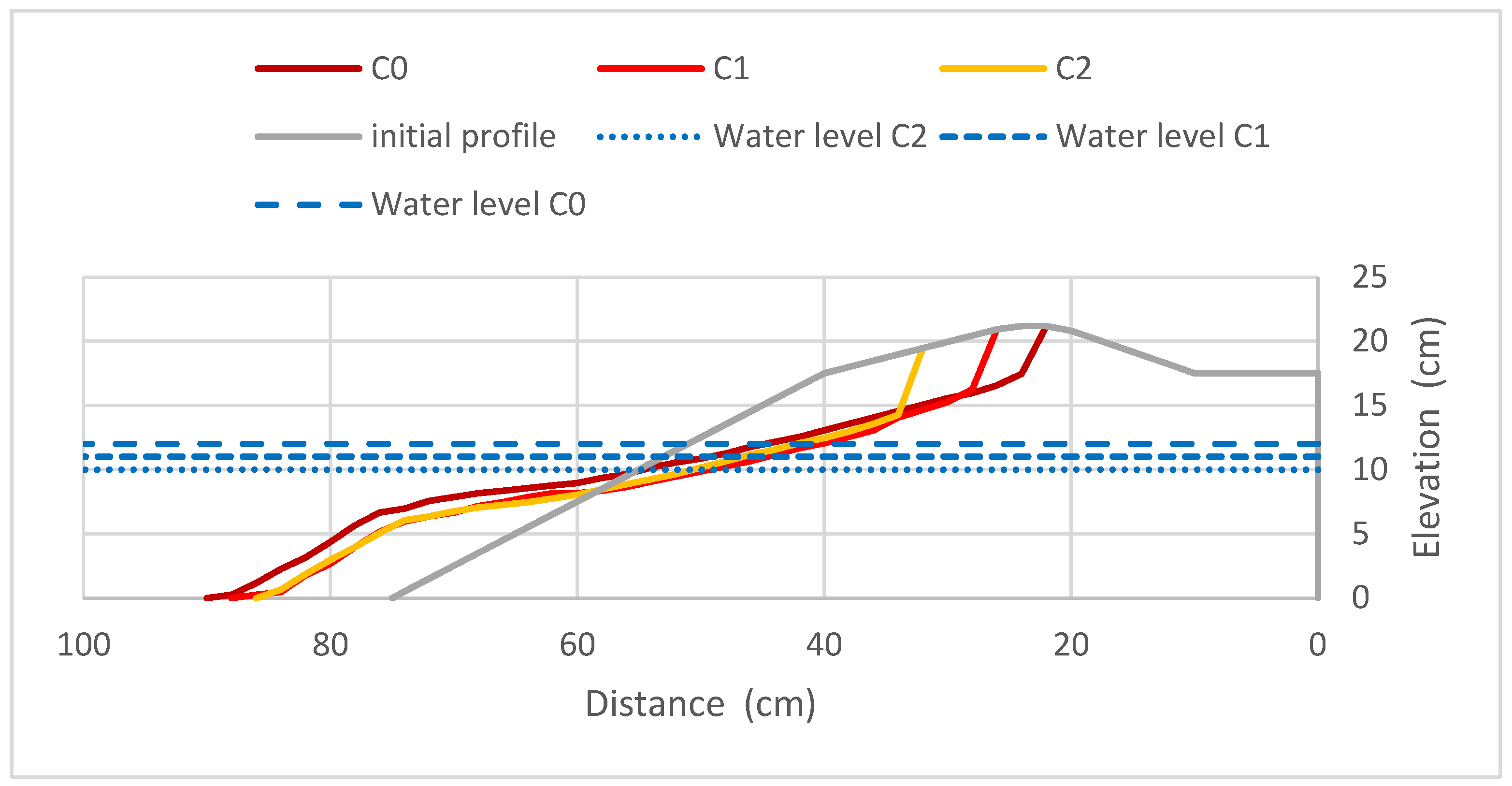
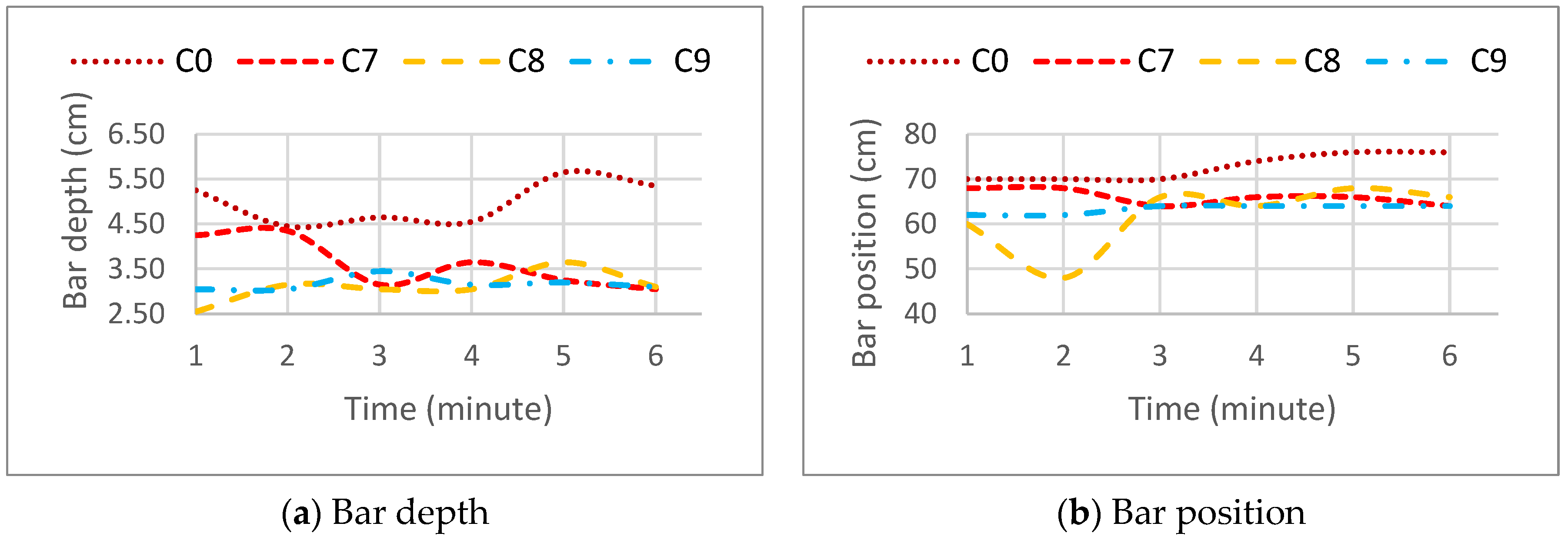
3.2.2. Berm Width
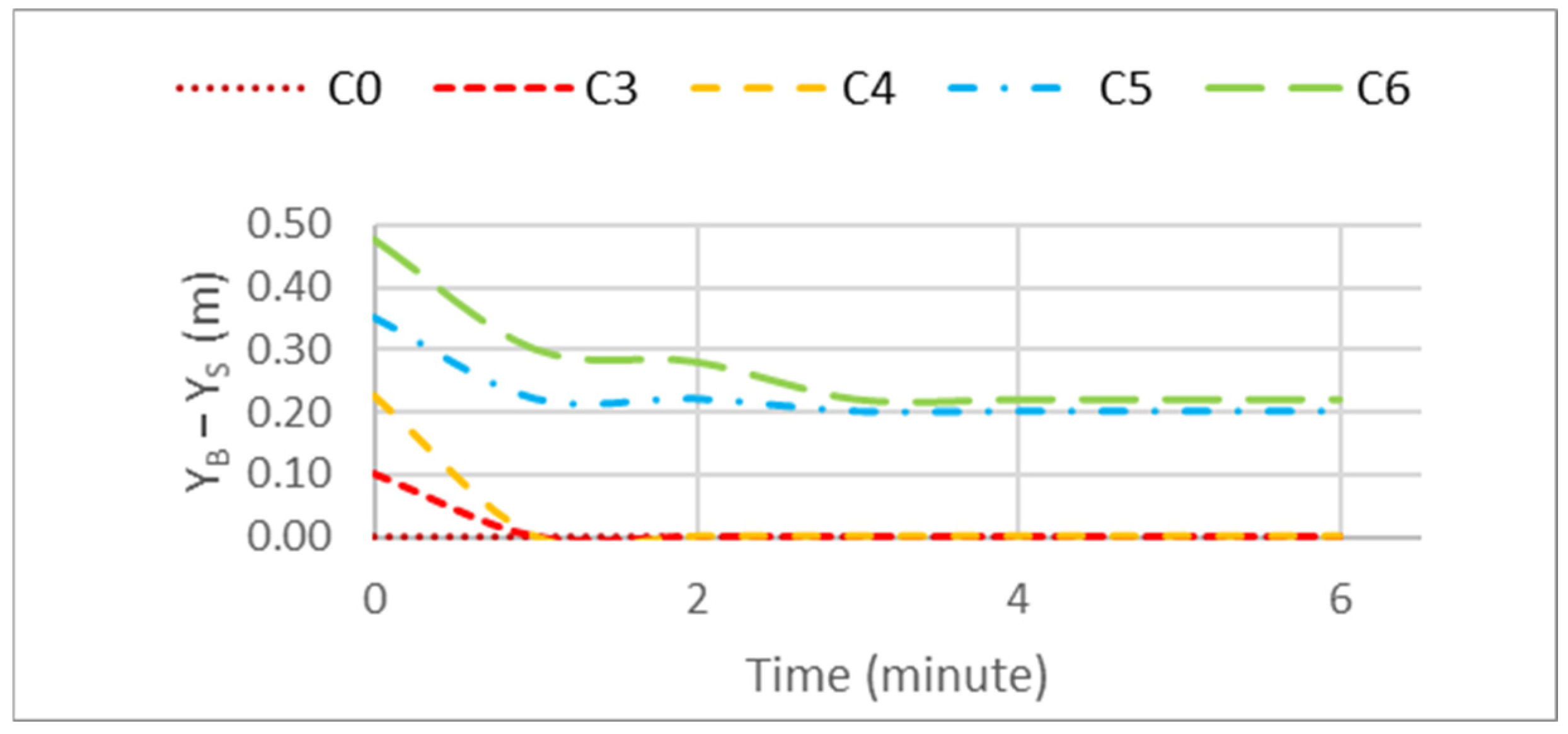
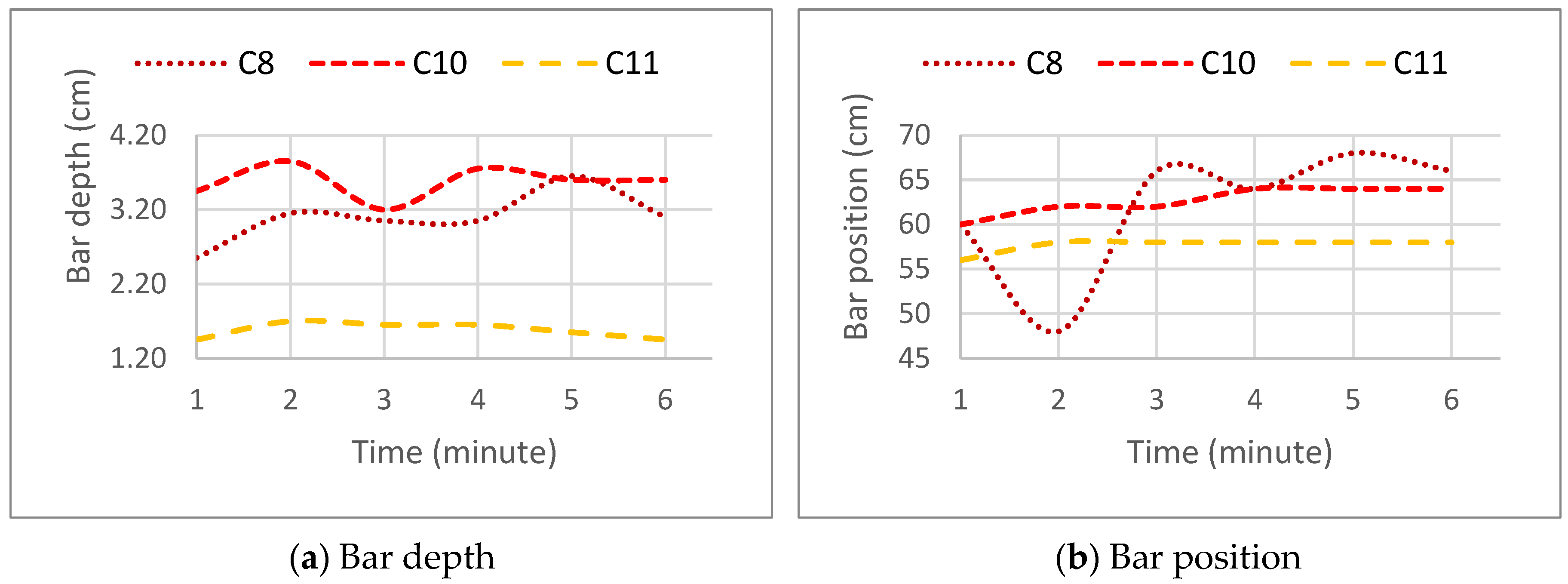
3.2.3. Volume of the Bar
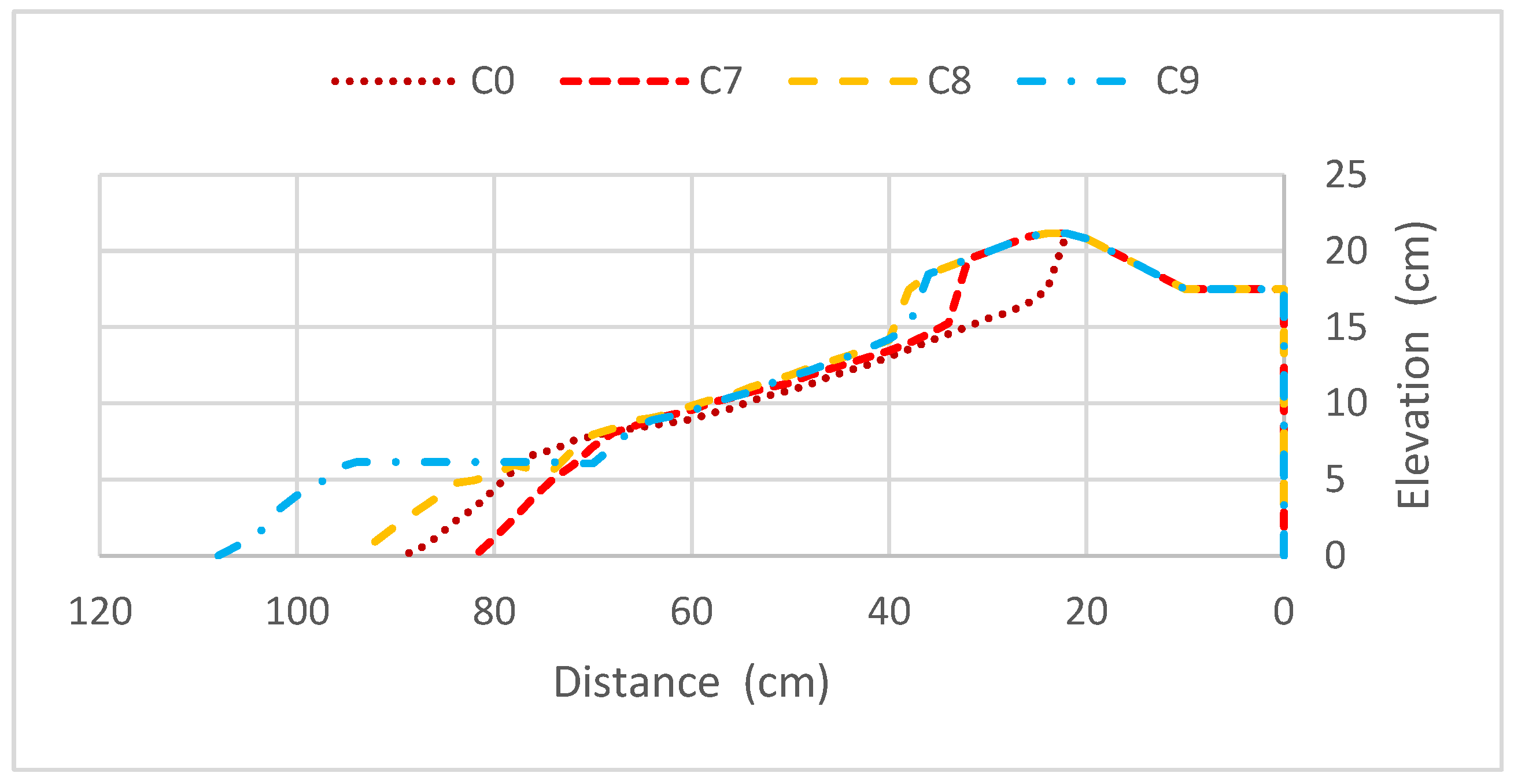
3.2.4. Bar Shape
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- D’Alessandro, F.; Tomasicchio, G.R.; Frega, F.; Leone, E.; Francone, A.; Pantusa, D.; Barbaro, G.; Foti, G. Beach–Dune System Morphodynamics. J. Mar. Sci. Eng. 2022, 10, 627. [Google Scholar] [CrossRef]
- Larson, M.; Palalane, J.; Fredriksson, C.; Hanson, H. Simulating cross-shore material exchange at decadal scale. Theory and model component validation. Coast. Eng. 2016, 116, 57–66. [Google Scholar] [CrossRef]
- Marinho, B.; Coelho, C.; Larson, M.; Hanson, H. Simulating cross-shore evolution towards equilibrium of different beach nourishment schemes. Proc. Coast. Dyn. 2017, 2017, 15. [Google Scholar]
- Masselink, G.; Hughes, M.; Knight, J. Introduction to Coastal Processes and Geomorphology; Routledge: London, UK, 2014. [Google Scholar]
- Roelvink, D.; Reniers, A.; van Dongeren, A.; van Thiel de Vries, J.; McCall, R.; Lescinski, J. Modelling storm impacts on beaches, dunes and barrier islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- DHI MIKE 21. User Manual; DHI Water & Environment: Singapore, 2012. [Google Scholar]
- Guimarães, A.; Coelho, C.; Veloso-Gomes, F.; Silva, P.A. 3D Physical Modeling of an Artificial Beach Nourishment: Laboratory Procedures and Nourishment Performance. J. Mar. Sci. Eng. 2021, 9, 613. [Google Scholar] [CrossRef]
- Marinho, B. Artificial Nourishments as a Coastal Defense Solution: Monitoring and Modelling Approaches. Ph.D. Thesis, Universidade de Aveiro, Aveiro, Portugal, 2018. [Google Scholar]
- D’Alessandro, F.; Tomasicchio, G.R. Wave–dune interaction and beach resilience in large-scale physical model tests. Coast. Eng. 2016, 116, 15–25. [Google Scholar] [CrossRef]
- Larson, M.; Erikson, L.; Hanson, H. An analytical model to predict dune erosion due to wave impact. Coast. Eng. 2004, 51, 675–696. [Google Scholar] [CrossRef]
- Vitousek, S.; Barnard, P.L.; Limber, P.; Erikson, L.; Cole, B. A model integrating longshore and cross-shore processes for predicting long-term shoreline response to climate change. J. Geophys. Res. Earth Surf. 2017, 122, 782–806. [Google Scholar] [CrossRef]
- Fisher, J.S.; Overton, M.F.; Chisholm, T. Field Measurements of Dune Erosion. In Coastal Engineering 1986; American Society of Civil Engineers: Reston, VA, USA, 1987; pp. 1107–1115. [Google Scholar]
- Nishi, R.; Kraus, N. Mechanism and calculation of sand dune erosion by storms. In Proceedings of the 25th Coastal Engineering Conference, American Society of Civil Engineers (ASCE), Orlando, FL, USA, 2–6 September 1996; pp. 3034–3047. [Google Scholar]
- Larson, M.; Donnelly, C.; Jiménez, J.A.; Hanson, H. Analytical model of beach erosion and overwash during storms. Proc. Inst. Civil. Eng.-Marit. Eng. 2009, 162, 115–125. [Google Scholar] [CrossRef]
- Vale, D.; Pires, R. Avaliação do Espraiamento e Galgamento em Estruturas Costeiras. Projeto de Licenciatura em Engenharia Civil. Não Publicado. Universidade de Aveiro, Aveiro, Portugal, 2022. (In Portuguese). [Google Scholar]
- Coelho, C. Riscos de Exposição de Frentes Urbanas para Diferentes Intervenções de Defesa Costeira. Ph.D. Thesis, Universidade de Aveiro, Aveiro, Portugal, 2005. (In Portuguese). [Google Scholar]
- van Rijn, L.C.; Tonnon, P.K.; Walstra, D.J.R. Numerical modelling of erosion and accretion of plane sloping beaches at different scales. Coast. Eng. 2011, 58, 637–655. [Google Scholar] [CrossRef]
- Puleo, J.A.; Lanckriet, T.; Conley, D.; Foster, D. Sediment transport partitioning in the swash zone of a large-scale laboratory beach. Coast. Eng. 2016, 113, 73–87. [Google Scholar] [CrossRef]
- Ferreira, A.M.; Coelho, C.; Silva, P.A. Medium-Term Effects of Dune Erosion and Longshore Sediment Transport on Beach–Dune Systems Evolution. J. Mar. Sci. Eng. 2024, 12, 1083. [Google Scholar] [CrossRef]
- Van Rijn, L.C.; Tonnon, P.K.; Sánchez-Arcilla, A.; Cáceres, I.; Grüne, J. Scaling laws for beach and dune erosion processes. Coast. Eng. 2011, 58, 623–636. [Google Scholar] [CrossRef]
- Borsje, B.W.; van Wesenbeeck, B.K.; Dekker, F.; Paalvast, P.; Bouma, T.J.; van Katwijk, M.M.; de Vries, M.B. How ecological engineering can serve in coastal protection. Ecol. Eng. 2011, 37, 113–122. [Google Scholar] [CrossRef]
- Raquel, S. Avaliação Experimental e Numérica de Parâmetros Associados a Modelos de Evolução da Linha de Costa. Ph.D. Thesis, Universidade do Porto, Porto, Portugal, 2010. (In Portuguese). [Google Scholar]
- Chun, I.; Lim, H.S.; Shim, J.S.; Park, K.S. Numerical Analysis of the Performance of Perforated Coastal Structures under Irregular Wave Conditions. J. Coast. Res. 2015, 315, 1159–1169. [Google Scholar] [CrossRef]
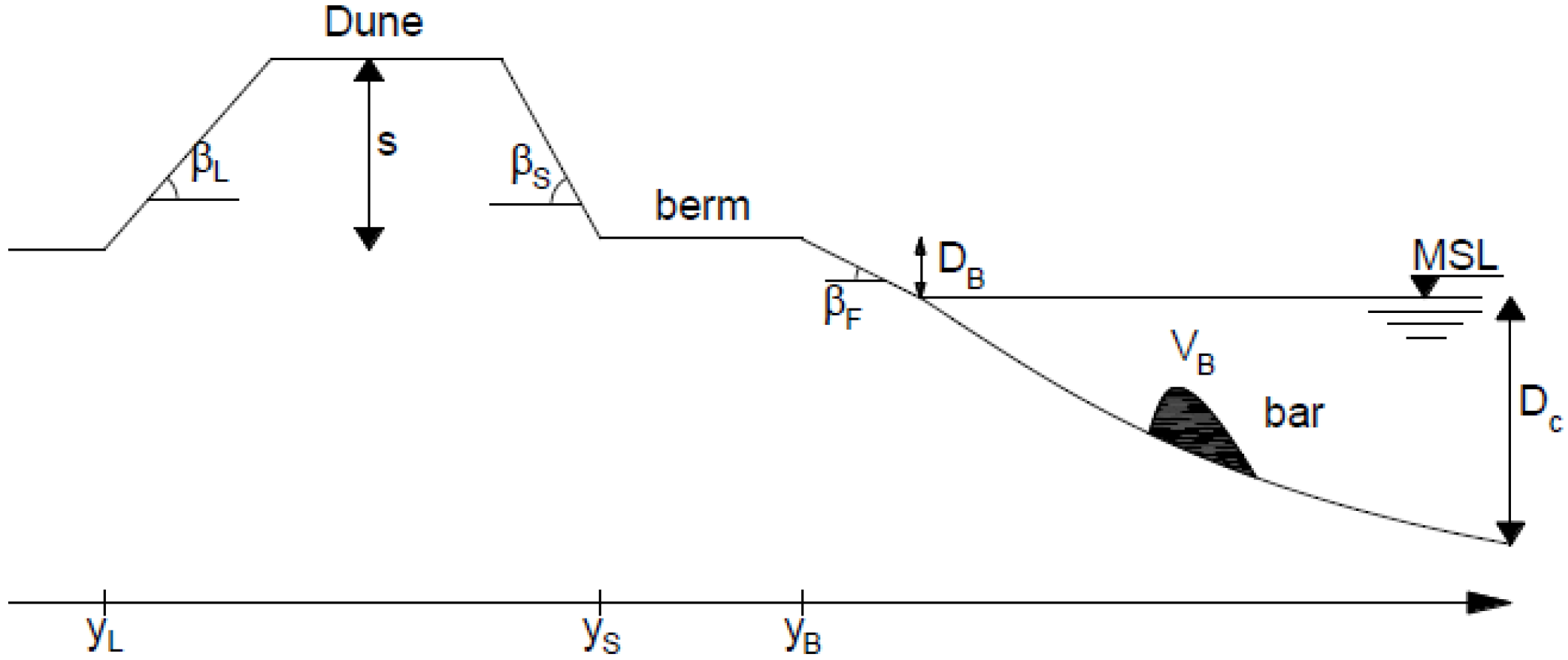
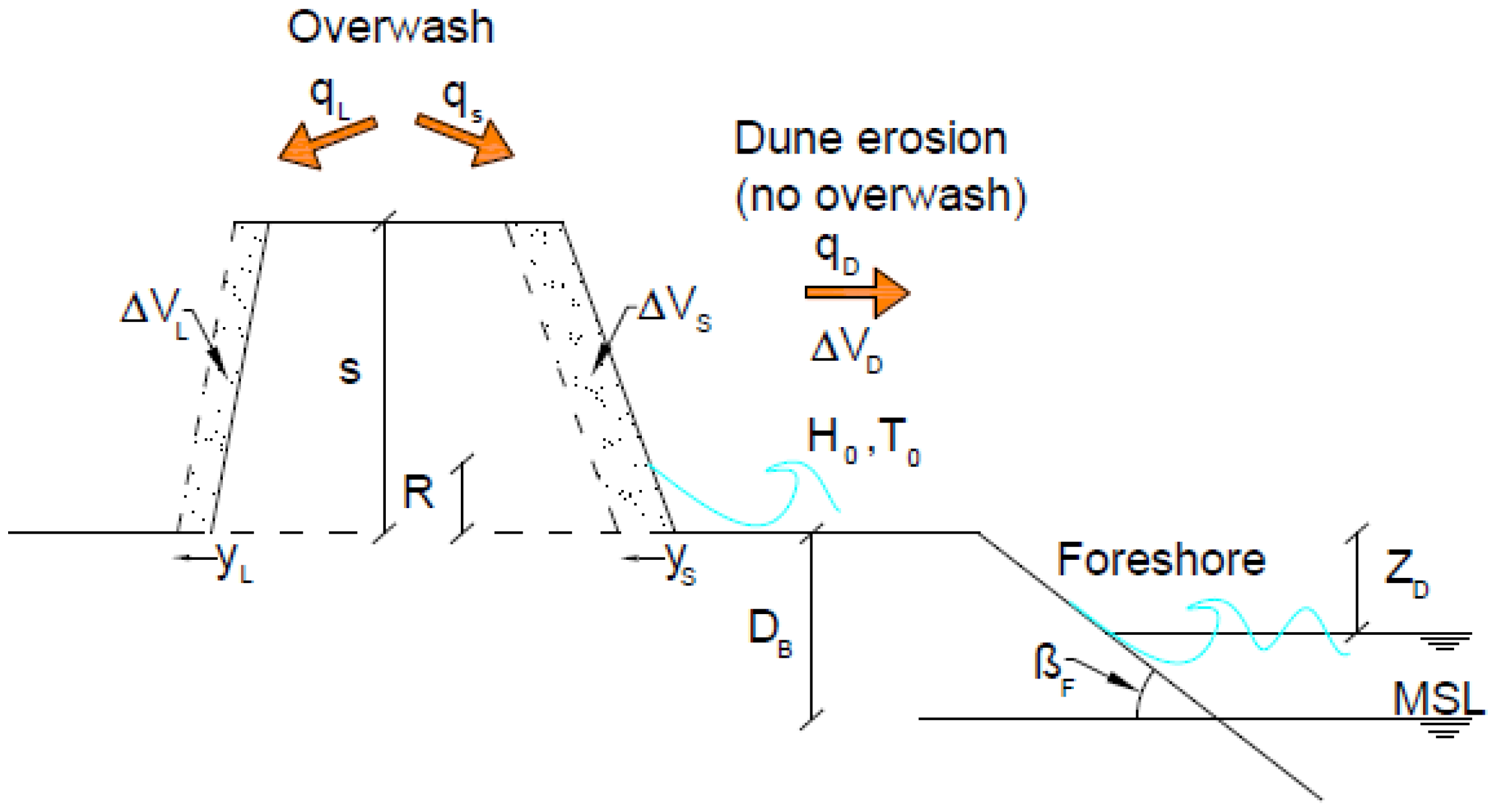
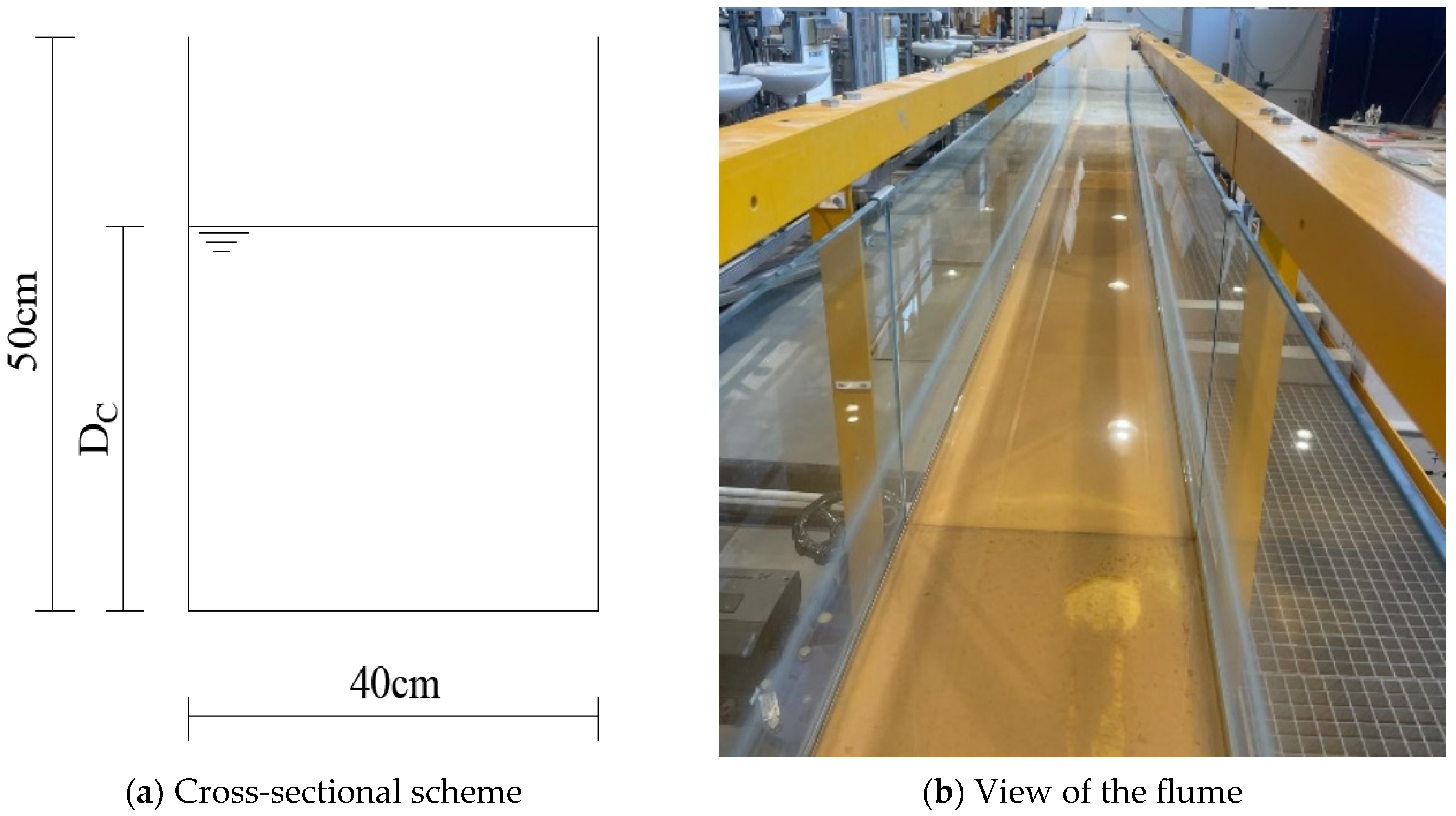
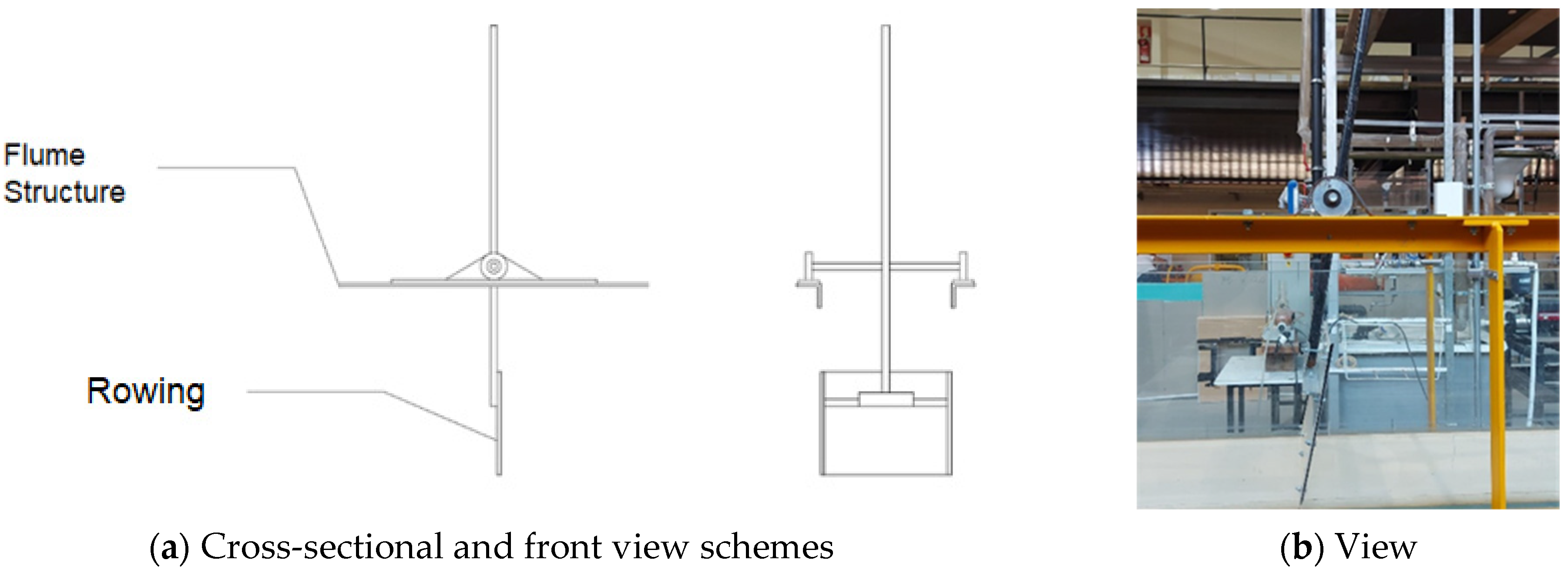

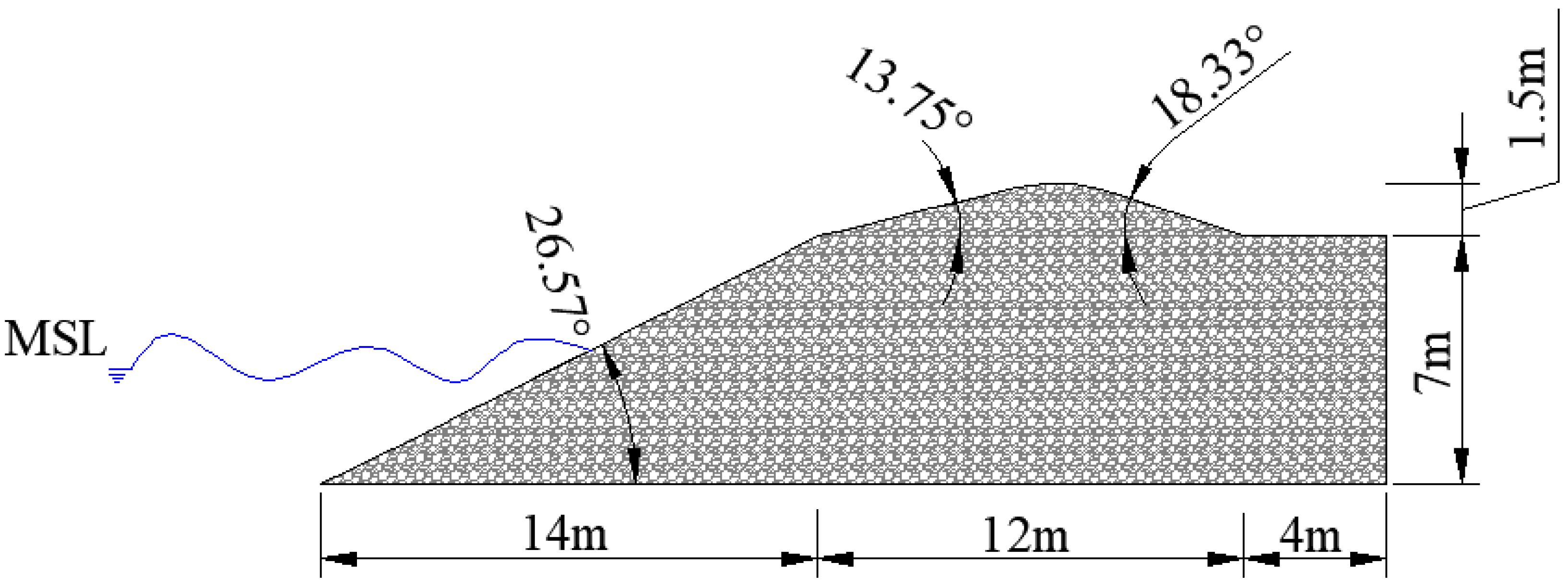
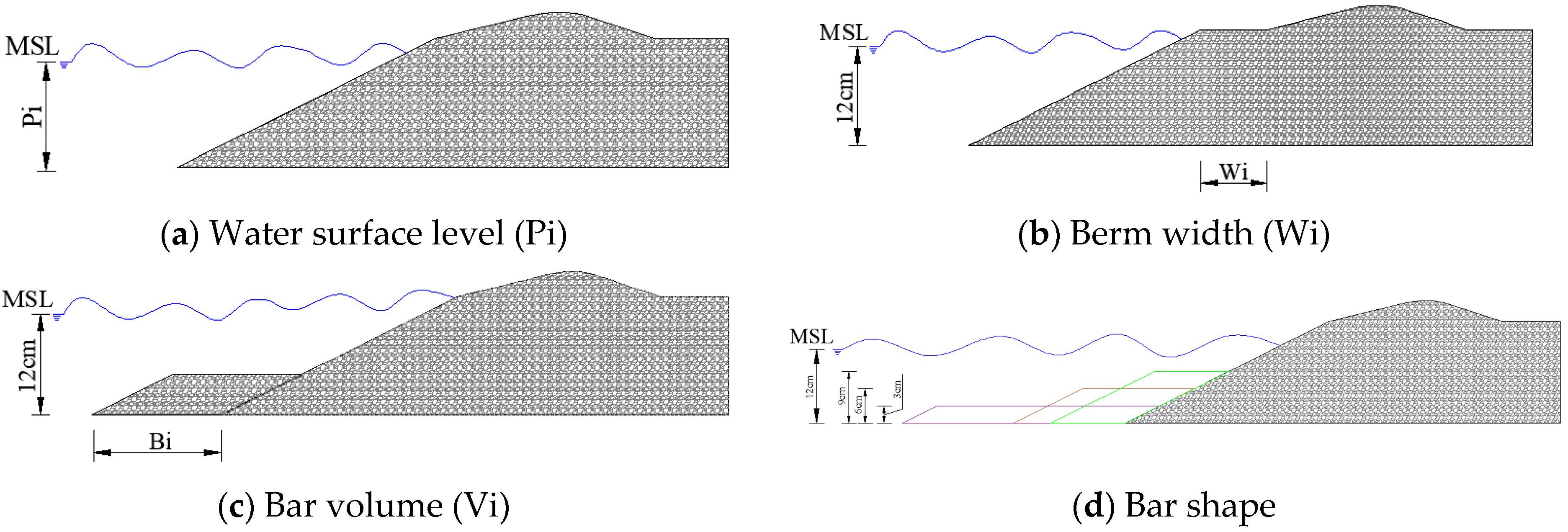
| H0 (cm) | T (s) | YL (cm) | YS (cm) | βL (°) | βS (°) | βF (°) | S (cm) |
|---|---|---|---|---|---|---|---|
| 5 | 1.48 | 10 | 40 | 18.33 | 13.75 | 26.56 | 3.75 |
| Scenarios | YB (cm) | DB (cm) | DC (cm) | VB0 (cm3/cm) |
|---|---|---|---|---|
| C0 | 40.00 | 5.50 | 12.00 | 0.00 |
| C1 | 40.00 | 6.50 | 11.00 | 0.00 |
| C2 | 7.50 | 10.00 | ||
| C3 | 50.00 | 5.50 | 12.00 | 0.00 |
| C4 | 62.50 | |||
| C5 | 75.00 | |||
| C6 | 87.50 | |||
| C7 | 40.00 | 5.50 | 12.00 | 35.00 |
| C8 | 115.30 | |||
| C9 | 196.00 | |||
| C10 | 40.00 | 5.50 | 12.00 | 115.30 |
| * C11 |
| Test | Time (Minutes) | Volume | Differences | ||
|---|---|---|---|---|---|
| Erosion (×10−3 m3/m) | Deposition (×10−3 m3/m) | Absolute 1 (×10−3 m3/m) | Relative 2 (%) | ||
| C0 | 1 | 5.09 | 6.35 | 1.27 | 24.88 |
| 2 | 8.56 | 9.36 | 0.80 | 9.35 | |
| 3 | 9.56 | 10.67 | 1.11 | 11.61 | |
| 4 | 9.71 | 11.32 | 1.61 | 16.58 | |
| 5 | 10.12 | 11.31 | 1.19 | 11.76 | |
| 6 | 10.86 | 11.53 | 0.66 | 6.08 | |
| C1 | 1 | 6.59 | 6.33 | 0.26 | 4.00 |
| 2 | 7.54 | 7.41 | 0.13 | 1.77 | |
| 3 | 8.61 | 7.93 | 0.68 | 7.93 | |
| 4 | 9.12 | 8.81 | 0.30 | 3.33 | |
| 5 | 9.61 | 9.00 | 0.61 | 6.36 | |
| 6 | 11.66 | 7.99 | 3.67 | 31.47 | |
| C2 | 1 | 5.63 | 5.41 | 0.22 | 3.95 |
| 2 | 6.52 | 6.05 | 0.47 | 7.24 | |
| 3 | 6.93 | 6.97 | 0.04 | 0.54 | |
| 4 | 7.31 | 7.16 | 0.14 | 1.95 | |
| 5 | 8.15 | 7.40 | 0.74 | 9.11 | |
| 6 | 8.09 | 7.85 | 0.24 | 2.99 | |
| Test | Time (Minutes) | Volume | Differences | ||
|---|---|---|---|---|---|
| Erosion (×10−3 m3/m) | Deposition (×10−3 m3/m) | Absolute 1 (×10−3 m3/m) | Relative 2 (%) | ||
| C3 | 1 | 7.35 | 8.13 | 0.79 | 10.69 |
| 2 | 9.03 | 9.26 | 0.23 | 2.56 | |
| 3 | 9.73 | 9.59 | 0.13 | 1.38 | |
| 4 | 10.25 | 10.09 | 0.15 | 1.50 | |
| 5 | 11.19 | 10.31 | 0.87 | 7.81 | |
| 6 | 11.53 | 10.68 | 0.85 | 7.40 | |
| C4 | 1 | 11.66 | 9.72 | 1.94 | 16.63 |
| 2 | 12.40 | 10.40 | 2.00 | 16.12 | |
| 3 | 12.66 | 10.94 | 1.72 | 13.58 | |
| 4 | 12.68 | 11.08 | 1.60 | 12.60 | |
| 5 | 13.25 | 11.09 | 2.16 | 16.29 | |
| 6 | 13.30 | 10.90 | 2.40 | 18.03 | |
| C5 | 1 | 6.63 | 7.64 | 1.01 | 15.15 |
| 2 | 7.63 | 8.80 | 1.17 | 15.27 | |
| 3 | 8.37 | 9.15 | 0.79 | 9.38 | |
| 4 | 8.50 | 9.31 | 0.82 | 9.59 | |
| 5 | 9.02 | 10.07 | 1.06 | 11.70 | |
| 6 | 9.54 | 10.56 | 1.02 | 10.64 | |
| C6 | 1 | 7.27 | 7.12 | 0.15 | 2.06 |
| 2 | 9.25 | 8.42 | 0.83 | 8.97 | |
| 3 | 9.89 | 10.13 | 0.24 | 2.43 | |
| 4 | 10.74 | 10.33 | 0.41 | 3.82 | |
| 5 | 11.41 | 10.54 | 0.87 | 7.62 | |
| 6 | 11.44 | 10.75 | 0.69 | 6.03 | |
| Test | Time (Minutes) | Volume | Differences | ||
|---|---|---|---|---|---|
| Erosion (×10−3 m3/m) | Deposition (×10−3 m3/m) | Absolute 1 (×10−3 m3/m) | Relative 2 (%) | ||
| C7 | 1 | 4.02 | 3.22 | 0.80 | 19.89 |
| 2 | 4.68 | 3.56 | 1.12 | 23.92 | |
| 3 | 5.18 | 4.02 | 1.16 | 22.39 | |
| 4 | 5.22 | 3.88 | 1.34 | 25.66 | |
| 5 | 5.50 | 4.42 | 1.08 | 19.63 | |
| 6 | 5.49 | 4.61 | 0.88 | 16.03 | |
| C8 | 1 | 1.90 | 2.03 | 0.13 | 7.00 |
| 2 | 2.53 | 2.74 | 0.20 | 8.01 | |
| 3 | 2.83 | 3.46 | 0.62 | 22.00 | |
| 4 | 2.81 | 3.39 | 0.58 | 20.46 | |
| 5 | 2.94 | 3.85 | 0.91 | 30.78 | |
| 6 | 3.28 | 3.93 | 0.66 | 19.97 | |
| C9 | 1 | 2.55 | 2.23 | 0.32 | 12.72 |
| 2 | 2.68 | 2.28 | 0.39 | 14.76 | |
| 3 | 2.99 | 2.58 | 0.41 | 13.87 | |
| 4 | 3.18 | 2.91 | 0.27 | 8.64 | |
| 5 | 3.32 | 3.03 | 0.29 | 8.87 | |
| 6 | 3.30 | 3.13 | 0.17 | 5.29 | |
| Test | Time (Minutes) | Volume | Differences | ||
|---|---|---|---|---|---|
| Erosion (×10−3 m3/m) | Deposition (×10−3 m3/m) | Absolute 1 (×10−3 m3/m) | Relative 2 (%) | ||
| C10 | 1 | 1.12 | 1.59 | 0.47 | 41.56 |
| 2 | 1.67 | 2.31 | 0.65 | 38.75 | |
| 3 | 2.43 | 3.19 | 0.77 | 31.54 | |
| 4 | 2.49 | 3.54 | 1.05 | 41.95 | |
| 5 | 2.47 | 3.70 | 1.22 | 49.52 | |
| 6 | 2.76 | 3.88 | 1.13 | 40.84 | |
| C11 | 1 | 0.65 | 0.95 | 0.30 | 45.69 |
| 2 | 1.06 | 1.15 | 0.09 | 8.93 | |
| 3 | 1.06 | 1.25 | 0.19 | 17.63 | |
| 4 | 1.03 | 1.29 | 0.27 | 26.00 | |
| 5 | 0.97 | 1.28 | 0.31 | 31.64 | |
| 6 | 0.89 | 1.32 | 0.44 | 49.27 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sequeira, A.; Coelho, C.; Lima, M. Morphodynamic Interactions Between Sandbar, Beach Profile, and Dune Under Variable Hydrodynamic and Morphological Conditions. Water 2025, 17, 2112. https://doi.org/10.3390/w17142112
Sequeira A, Coelho C, Lima M. Morphodynamic Interactions Between Sandbar, Beach Profile, and Dune Under Variable Hydrodynamic and Morphological Conditions. Water. 2025; 17(14):2112. https://doi.org/10.3390/w17142112
Chicago/Turabian StyleSequeira, Alirio, Carlos Coelho, and Márcia Lima. 2025. "Morphodynamic Interactions Between Sandbar, Beach Profile, and Dune Under Variable Hydrodynamic and Morphological Conditions" Water 17, no. 14: 2112. https://doi.org/10.3390/w17142112
APA StyleSequeira, A., Coelho, C., & Lima, M. (2025). Morphodynamic Interactions Between Sandbar, Beach Profile, and Dune Under Variable Hydrodynamic and Morphological Conditions. Water, 17(14), 2112. https://doi.org/10.3390/w17142112








