Experimental Investigation of Flow Characteristics Inside a Venturi Tube Under Gas-Containing Conditions
Abstract
1. Introduction
2. Experiments
2.1. Experimental Setup
2.2. Experimental Conditions
2.3. Experimental Validation
3. Experimental Results and Discussions
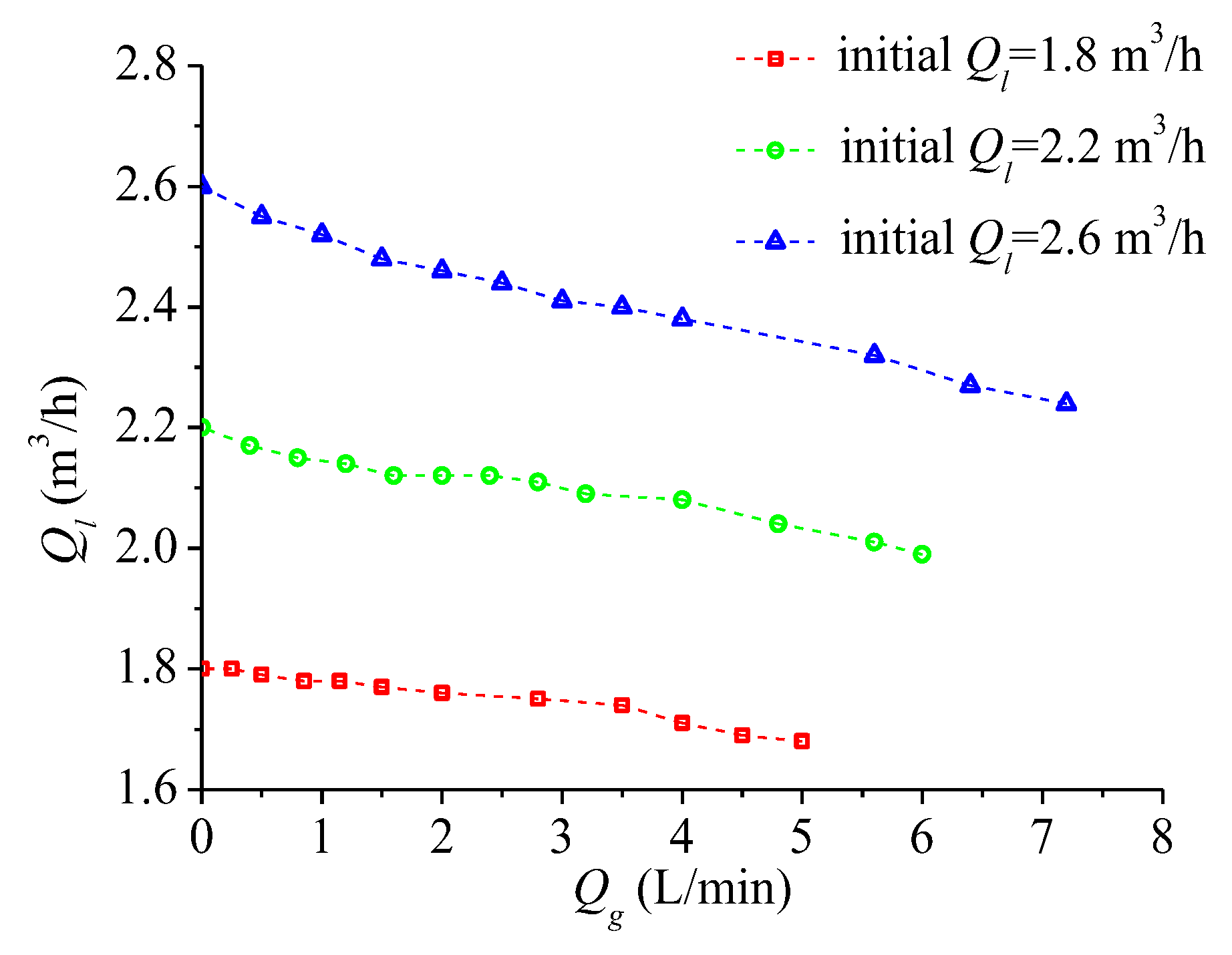
3.1. Variation of Ql Under Gas Containing Conditions
3.2. Variation in Flow Structure Under Gas-Containing Conditions
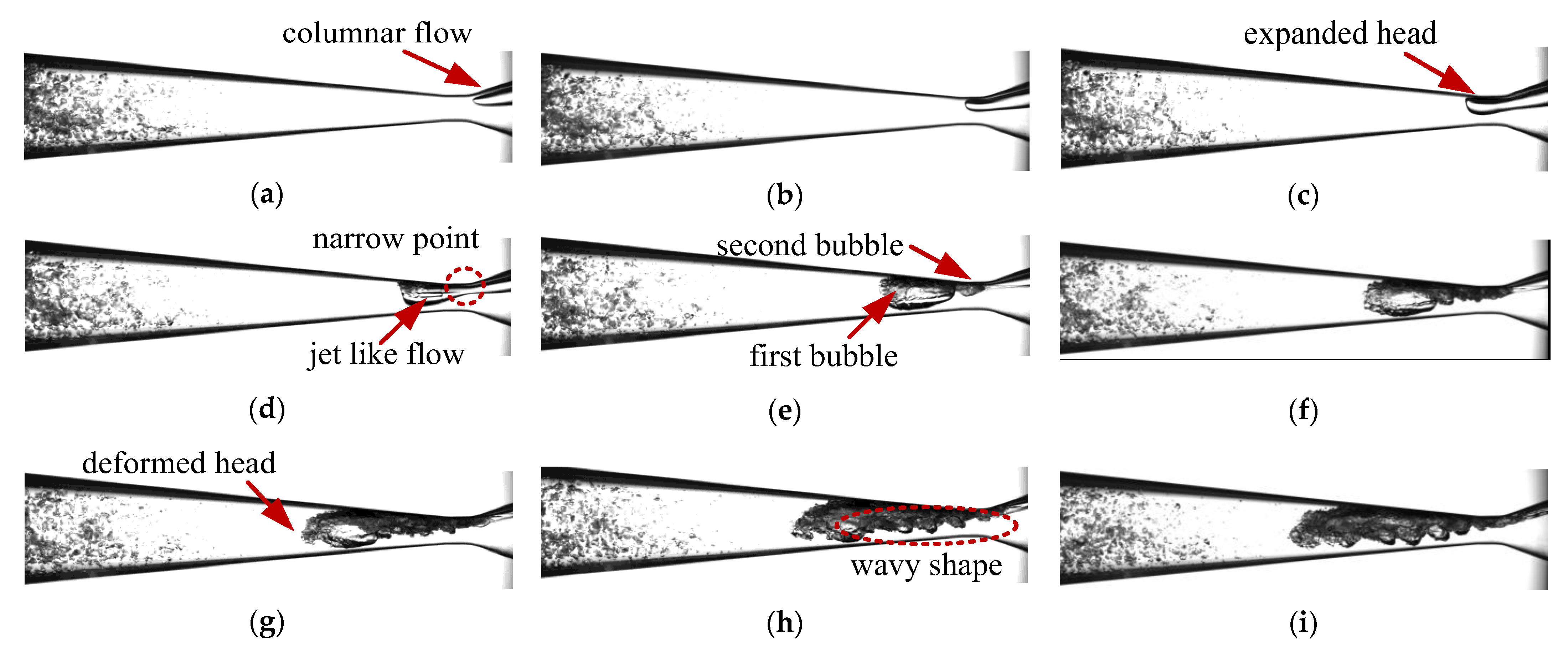
3.2.1. Evolution of the Two-Phase Flow
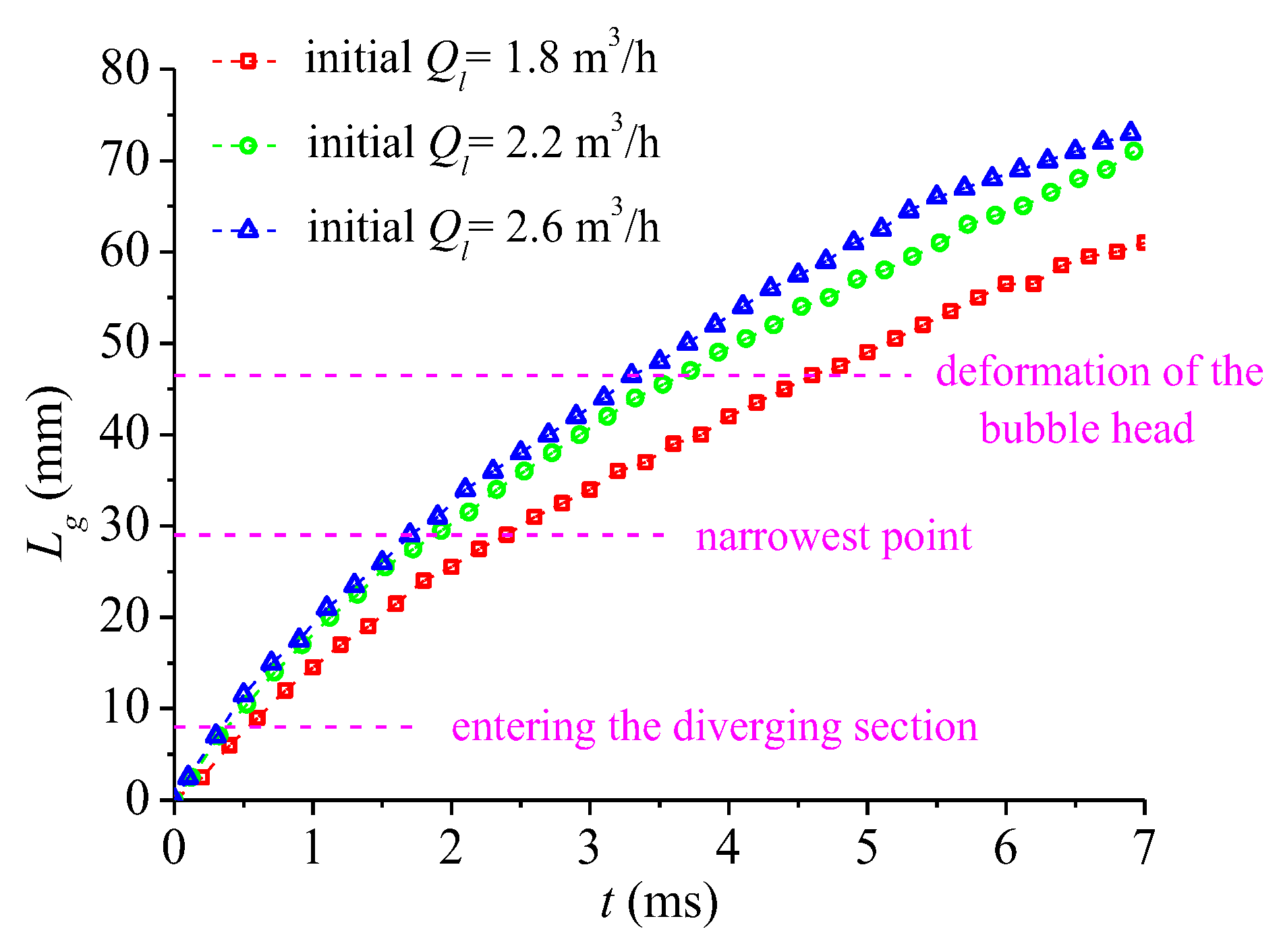
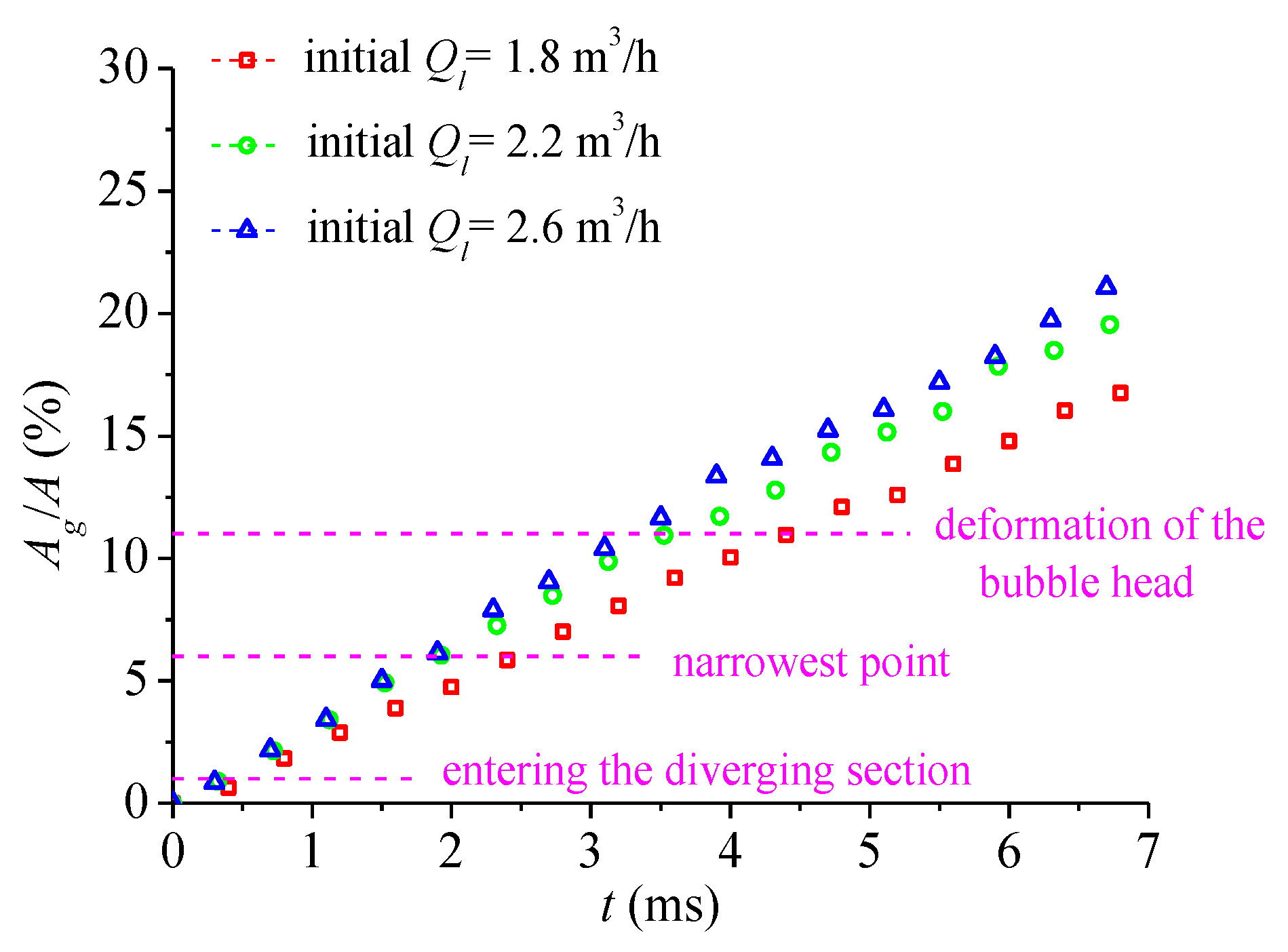
3.2.2. Variation in Two-Phase Flow Under Different Liquid Flow Rates
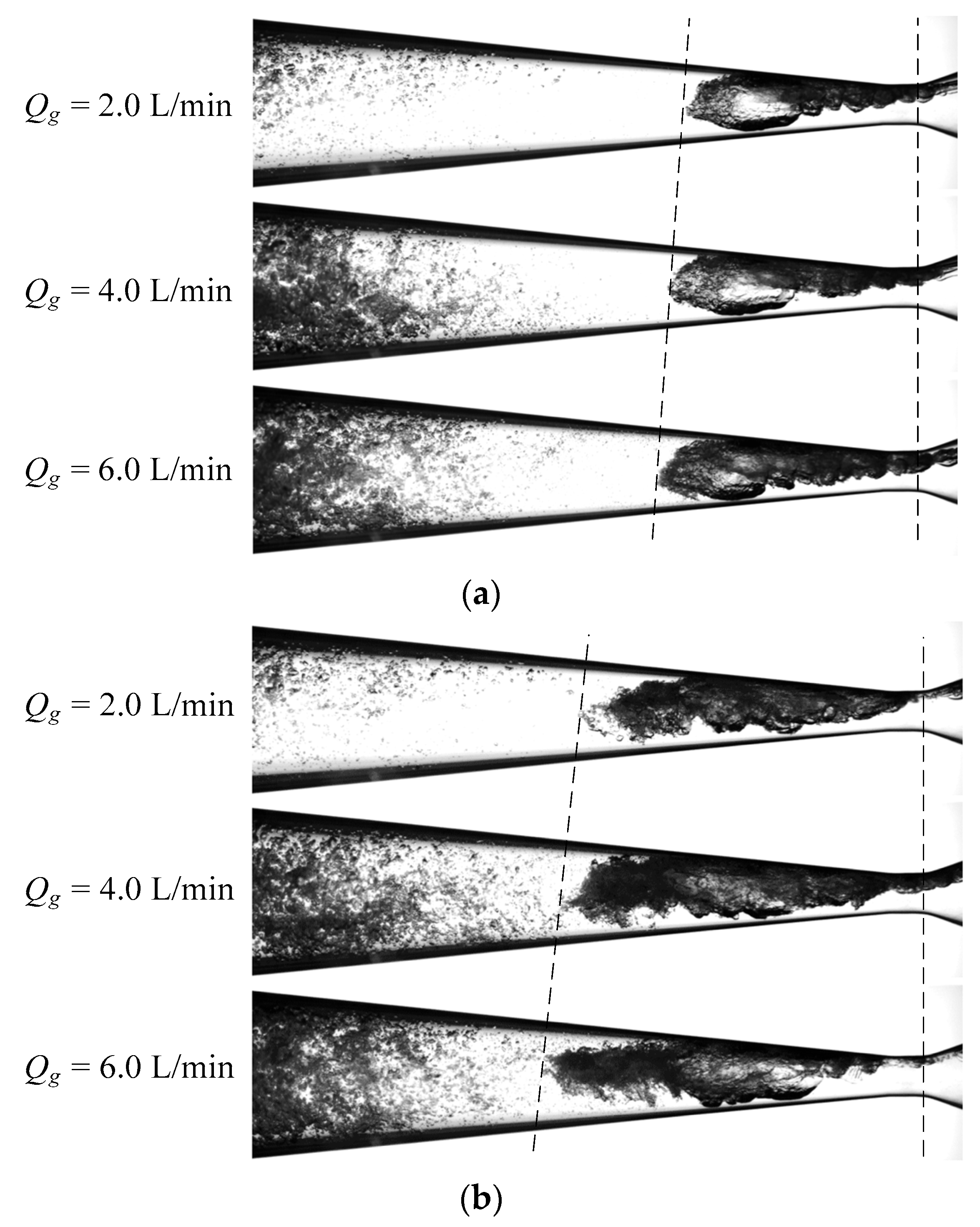
3.2.3. Variation in Two-Phase Flow Under Different Gas Flow Rates
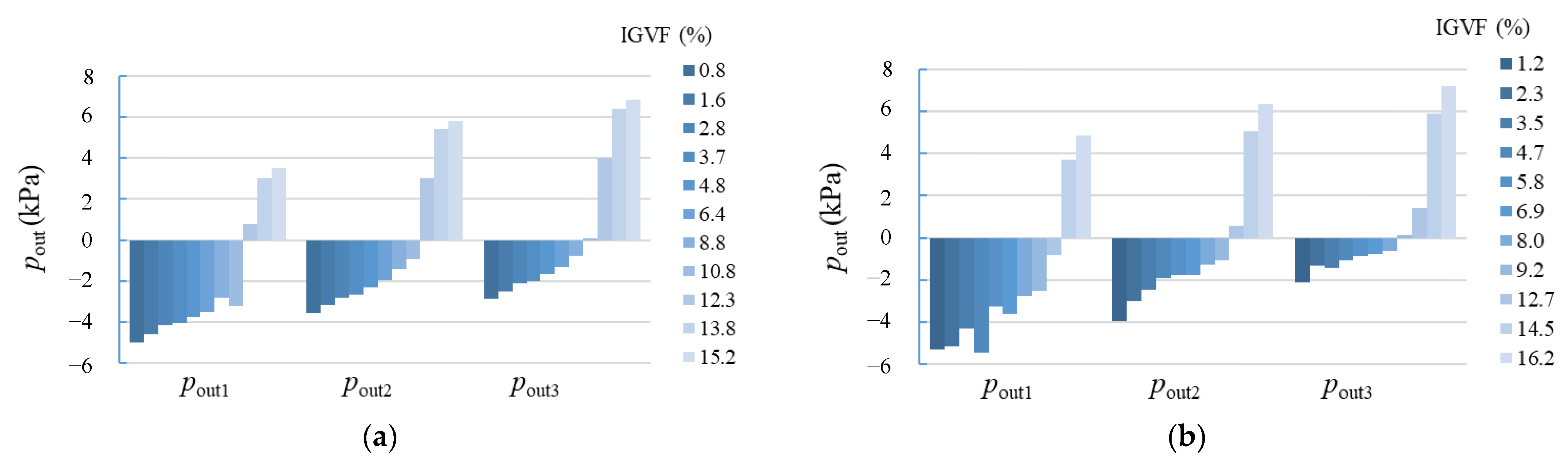
3.3. Variation in Pressure Characteristics Under Gas Containing Conditions
4. Conclusions
- 1.
- High-speed photography was used to record the development of an air–water two-phase flow inside a horizontal venturi tube. The variation in inlet gas volume fraction (IGVF) was from 0 to 16% due to the regulation of the upstream gas flow rate. When the gas flow entered the converging section of the venturi tube, the gas-phase region was in the form of a columnar bubble. When the bubble was moving into the throat section, there was an expansion on the bubble head. After the bubble entered the diverging section, the head of the bubble underwent further expansion and fragmentation, while smaller bubbles were generated.
- 2.
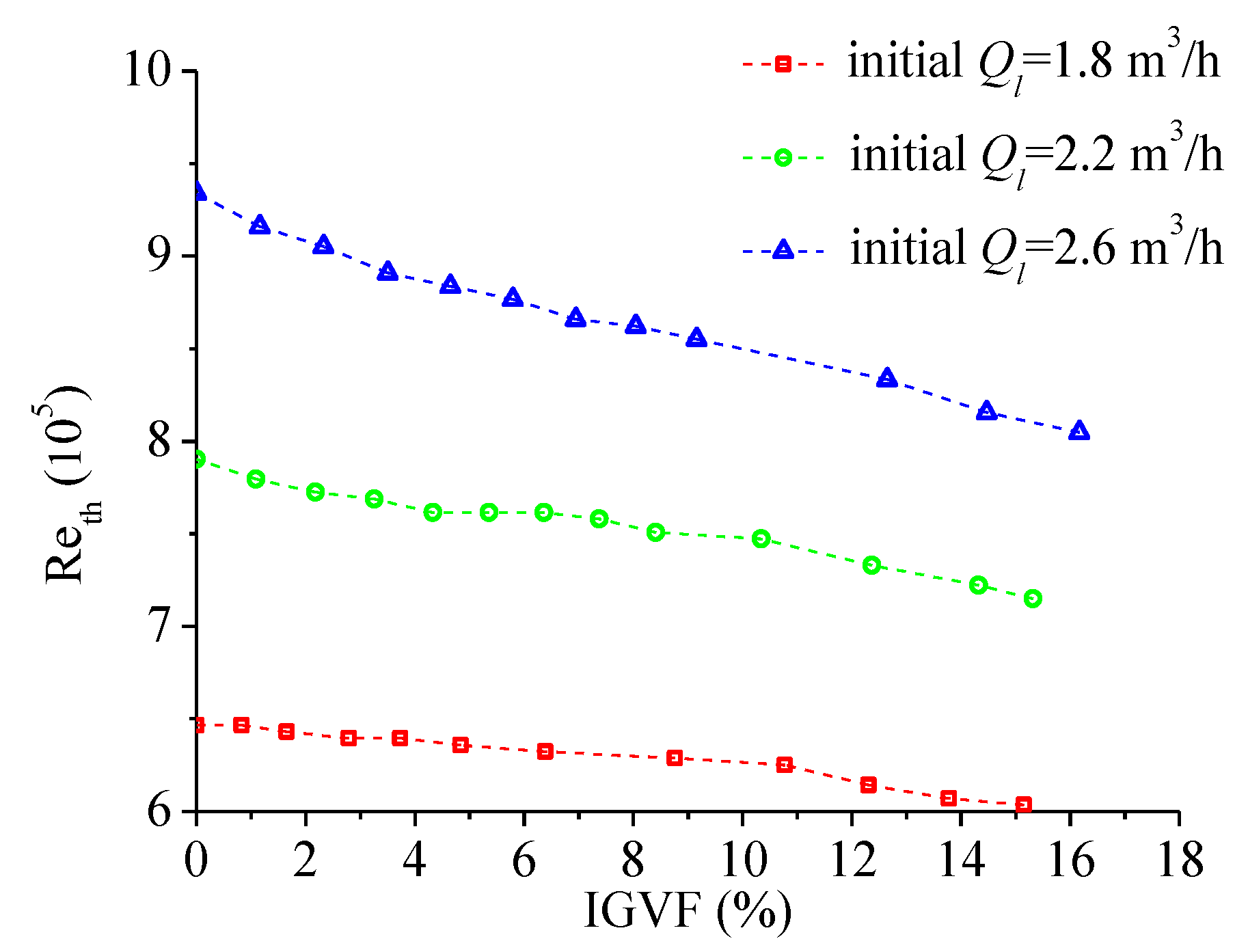
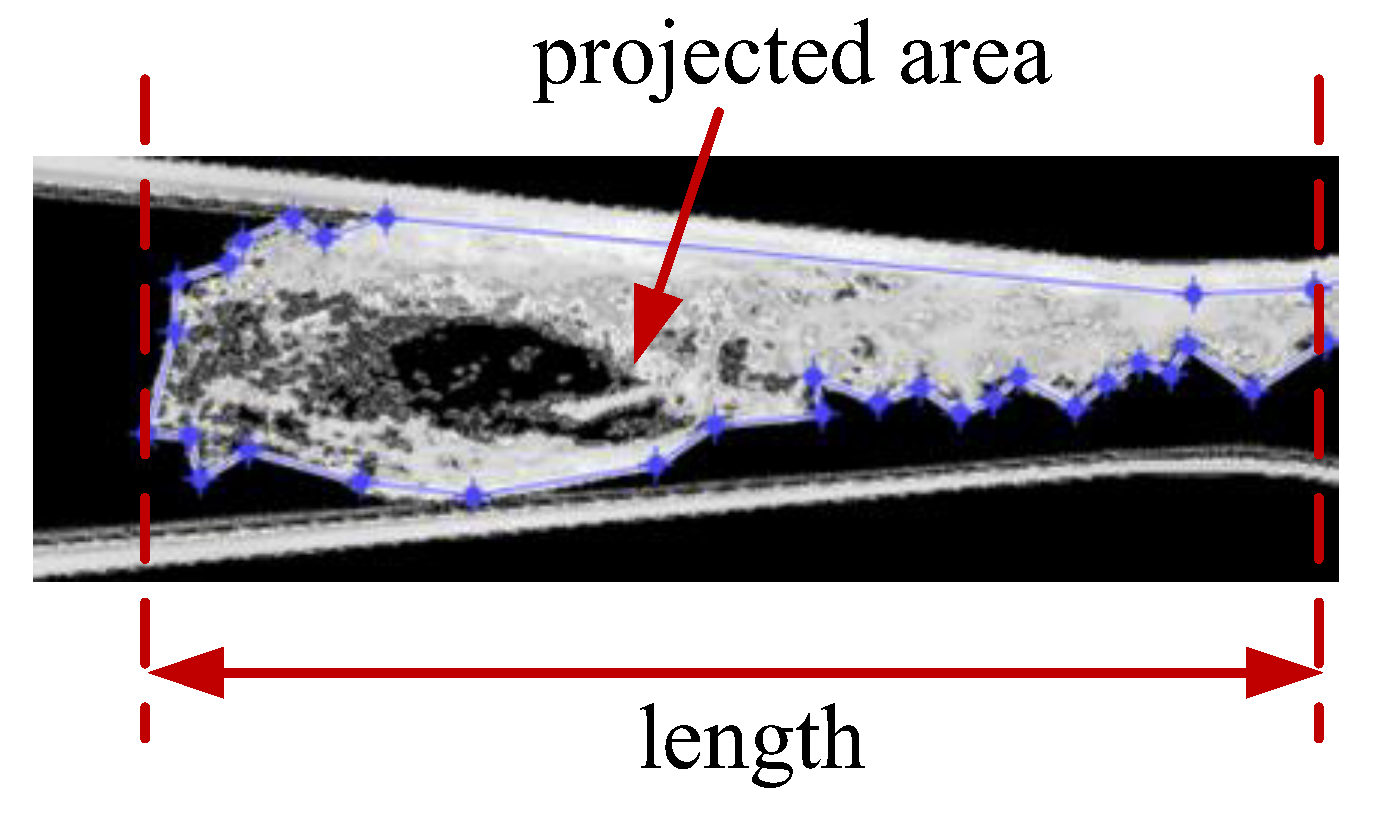
- Under conditions with different gas contents, the evolution of the two-phase flow was similar, but the main difference was the rate of evolution. Two parameters, defined as characteristic length (Lg) and projected area (Ag), were used to quantitatively describe the bubble development process. With the increase in the IGVF, Lg of the gas-phase region increased but the growth rate was slowing down, which is due to the effects from downstream smaller bubbles. Based on the processing of experimental images, the projected area of the main bubble increased linearly with the increase in IGVF.
- 3.
- By measuring the flow rate in the experiment system under different conditions, it could be seen that the liquid flow rate decreased with increasing gas content. When the value of IGVF exceeded 10%, the liquid flow rate decreased faster due to the blockage caused by high gas content. Time-averaged pressures upstream and downstream of the venturi tube were recorded, revealing that an IGVF of approximately 10% was also a critical point for significant changes in pressure characteristics. With the increase in gas content, the pressure drop indicated an increase in losses.
- 4.
- This study has some limitations. As the flow of the experimental system was powered by a centrifugal pump, the instantaneous pressure would be affected by the operation of the pump. Further research could explore the pressure pulsation characteristics of the gas–liquid two-phase flow.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, H.; Xu, Y.; Xiong, X.; Mamat, E.; Wang, J.; Zhang, T. Prediction of pressure drop in Venturi based on drift-flux model and boundary layer theory. Flow Meas. Instrum. 2020, 71, 101673. [Google Scholar] [CrossRef]
- Fang, L.; Zhang, T. Performance of a horizontally mounted venturi in low-pressure wet gas flow. Chin. J. Chem. Eng. 2008, 16, 320–324. [Google Scholar] [CrossRef]
- Nugraha, K.W.; Yuliati, L.; Winarto. The effect of venturi tube divergence angle geometry on wastewater treatment. J. Adv. Res. Fluid Mech. Therm. Sci. 2025, 128, 48–58. [Google Scholar] [CrossRef]
- Liu, Y. Utilization of the venturi effect to introduce micro-particles for epidermal vaccination. Med. Eng. Phys. 2007, 29, 390–397. [Google Scholar] [CrossRef] [PubMed]
- Tseng, T.M.; Chen, P.Y.; Tseng, H.; Lin, H.C.; Chang, C.Y.; Hung, S.H. An unexpected route for otolaryngology bacterial contamination with a venturi atomizer. Rhinology 2014, 52, 156–161. [Google Scholar] [PubMed]
- Li, X.; Huang, Z.; Meng, Z.; Wang, B.; Li, H. Oil-water two-phase flow measurement using a venturi meter and an oval gear flow meter. Chem. Eng. Commun. 2010, 197, 223–231. [Google Scholar] [CrossRef]
- Elperin, T.; Fominykh, A.; Klochko, M. Performance of a venturi meter in gas-liquid flow in the presence of dissolved gases. Flow Meas. Instrum. 2002, 13, 13–16. [Google Scholar] [CrossRef]
- Long, X.; Zhang, J.; Wang, J.; Xu, M.; Lyu, Q.; Ji, B. Experimental investigation of the global cavitation dynamic behavior in a venturi tube with special emphasis on the cavity length variation. Int. J. Multiph. Flow. 2017, 89, 290–298. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Q.; Yang, Z.; Liang, R.; Li, Z. High-speed photography and particle image velocimetry of cavitation in a venturi tube. Phys. Fluids 2024, 36, 045147. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Gao, J.; Tang, P.; Huang, F. Structural optimization of the venturi fertilizer applicator using head loss calculation methods. Fluids 2025, 10, 87. [Google Scholar] [CrossRef]
- Tang, P.; Zhang, Z. Structural optimization based on response surface methodology for the venturi injector used in fertigation system. Horticulturae 2025, 11, 223. [Google Scholar] [CrossRef]
- Steven, R.N. Wet gas metering with a horizontally mounted venturi meter. Flow Meas. Instrum. 2002, 12, 361–372. [Google Scholar] [CrossRef]
- Yasuda, K.; Ako, D. Effect of venturi tube shape on reaction performance by hydrodynamic cavitation. J. Chem. Eng. Jpn. 2019, 52, 280–282. [Google Scholar] [CrossRef]
- Li, M.; Bussonnière, A.; Bronson, M.; Xu, Z.; Liu, Q. Study of venturi tube geometry on the hydrodynamic cavitation for the generation of microbubbles. Miner. Eng. 2019, 132, 268–274. [Google Scholar] [CrossRef]
- Wu, Y.; Zu, Y.; Xu, E.; Miao, Z.; Wu, D.; Hu, Y. The effect of swirling shear blade on gas-liquid flow pattern and mass transfer performance in venturi injector. Chem. Eng. Sci. 2024, 299, 120549. [Google Scholar] [CrossRef]
- Song, Y.; Wang, D.; Yin, J.; Li, J.; Cai, K. Experimental studies on bubble breakup mechanism in a venturi bubble generator. Ann. Nucl. Energy 2019, 130, 259–270. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, X.; Li, C.; Zou, Y.; Li, G.; Chen, Y.; Chen, G.; Duan, J. Bubble behavior, flow characteristics, and mass transfer enhancement in self-priming Venturi tubes. Chem. Eng. Sci. 2023, 270, 118536. [Google Scholar] [CrossRef]
- Ozkan, F.; Ozturk, M.; Baylar, A. Experimental investigations of air and liquid injection by venturi tubes. Water Environ. J. 2006, 20, 114–122. [Google Scholar] [CrossRef]
- Fujiwara, A.; Okamoto, K.; Hashiguchi, K.; Peixinho, J.; Takagi, S.; Matsumoto, Y. Bubble breakup phenomena in a venturi tube. In Proceedings of the FEDSM2007, San Diego, CA, USA, 30 July–2 August 2007. [Google Scholar]
- Ding, G.; Li, Z.; Chen, J.; Cai, X. An investigation on the bubble transportation of a two-stage series venturi bubble generator. Chem. Eng. Res. Des. 2021, 174, 345–356. [Google Scholar] [CrossRef]
- Chai, B.; Yang, J.; Wang, X. Force Characteristics of centrifugal pump as turbine during start-up process under gas–liquid two-phase conditions. Actuators 2022, 11, 370. [Google Scholar] [CrossRef]
- Zhu, G.; Tang, Z.; Feng, J.; Yan, S.; Li, Y.; Cui, W. Effect of inlet gas volume fraction on shafting vibration of multiphase pumps under low discharge conditions. Ocean. Eng. 2024, 294, 116803. [Google Scholar] [CrossRef]
- Verde, W.M.; Biazussi, J.; Porcel, C.E.; Estevam, V.; Tavares, A.; Neto, S.J.A.; Rocha, P.S.D.M.V.; Bannwart, A.C. Experimental investigation of pressure drop in failed Electrical Submersible Pump (ESP) under liquid single-phase and gas-liquid two-phase flow. J. Petrol. Sci. Eng. 2021, 198, 108127. [Google Scholar] [CrossRef]
- He, D.; Zhao, L.; Chang, Z.; Zhang, Z.; Guo, P.; Bai, B. On the performance of a centrifugal pump under bubble inflow: Effect of gas-liquid distribution in the impeller. J. Petrol. Sci. Eng. 2021, 203, 108587. [Google Scholar] [CrossRef]
- Ahn, S.H.; Xiao, Y.; Wang, Z.; Zhou, X.; Luo, Y. Numerical prediction on the effect of free surface vortex on intake flow characteristics for tidal power station. Renew. Energ. 2017, 101, 617–628. [Google Scholar] [CrossRef]
- Huang, X.; Fang, T.; Pang, K.; Guo, Q.; Qiu, B.; Lu, J. Air-entrained vortex in open intake: Time–frequency analysis and the interaction with subsurface vortices. Phys. Fluids 2022, 34, 113313. [Google Scholar] [CrossRef]
- Song, Y.; Shentu, Y.; Qian, Y.; Yin, J.; Wang, D. Experiment and modeling of liquid-phase flow in a venturi tube using stereoscopic piv. Nucl. Eng. Technol. 2021, 53, 79–92. [Google Scholar] [CrossRef]








| Variable | Device | Measurement Range | Uncertainty |
|---|---|---|---|
| Liquid flow rate | electromagnetic flowmeter | 0–10 m3/h | ±0.5% |
| Gas flow rate | gas flowmeter | 0–100 L/min | ±0.5% |
| Pressure | pressure sensor | −100–100 kPa | ±0.25% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Lu, C.; Huang, X.; Jiang, A.; Liu, X. Experimental Investigation of Flow Characteristics Inside a Venturi Tube Under Gas-Containing Conditions. Water 2025, 17, 2080. https://doi.org/10.3390/w17142080
Guo Q, Lu C, Huang X, Jiang A, Liu X. Experimental Investigation of Flow Characteristics Inside a Venturi Tube Under Gas-Containing Conditions. Water. 2025; 17(14):2080. https://doi.org/10.3390/w17142080
Chicago/Turabian StyleGuo, Qiang, Chaoshan Lu, Xianbei Huang, Aibo Jiang, and Xiaodong Liu. 2025. "Experimental Investigation of Flow Characteristics Inside a Venturi Tube Under Gas-Containing Conditions" Water 17, no. 14: 2080. https://doi.org/10.3390/w17142080
APA StyleGuo, Q., Lu, C., Huang, X., Jiang, A., & Liu, X. (2025). Experimental Investigation of Flow Characteristics Inside a Venturi Tube Under Gas-Containing Conditions. Water, 17(14), 2080. https://doi.org/10.3390/w17142080





