What Are the Key Factors Influencing the Water Price in Interbasin Water Transfer Projects? An Integrated Fuzzy Decision-Making Trial and Evaluation Laboratory (DEMATEL)–Interpretive Structural Model (ISM)–Grey Relational Analysis (GRA) Method
Abstract
1. Introduction
2. Methodology
2.1. Establishment of the Influencing Factor System
2.1.1. Socio-Economic Factors
2.1.2. Political System Factors
2.1.3. Natural Environment Factors
2.1.4. Engineering Factors
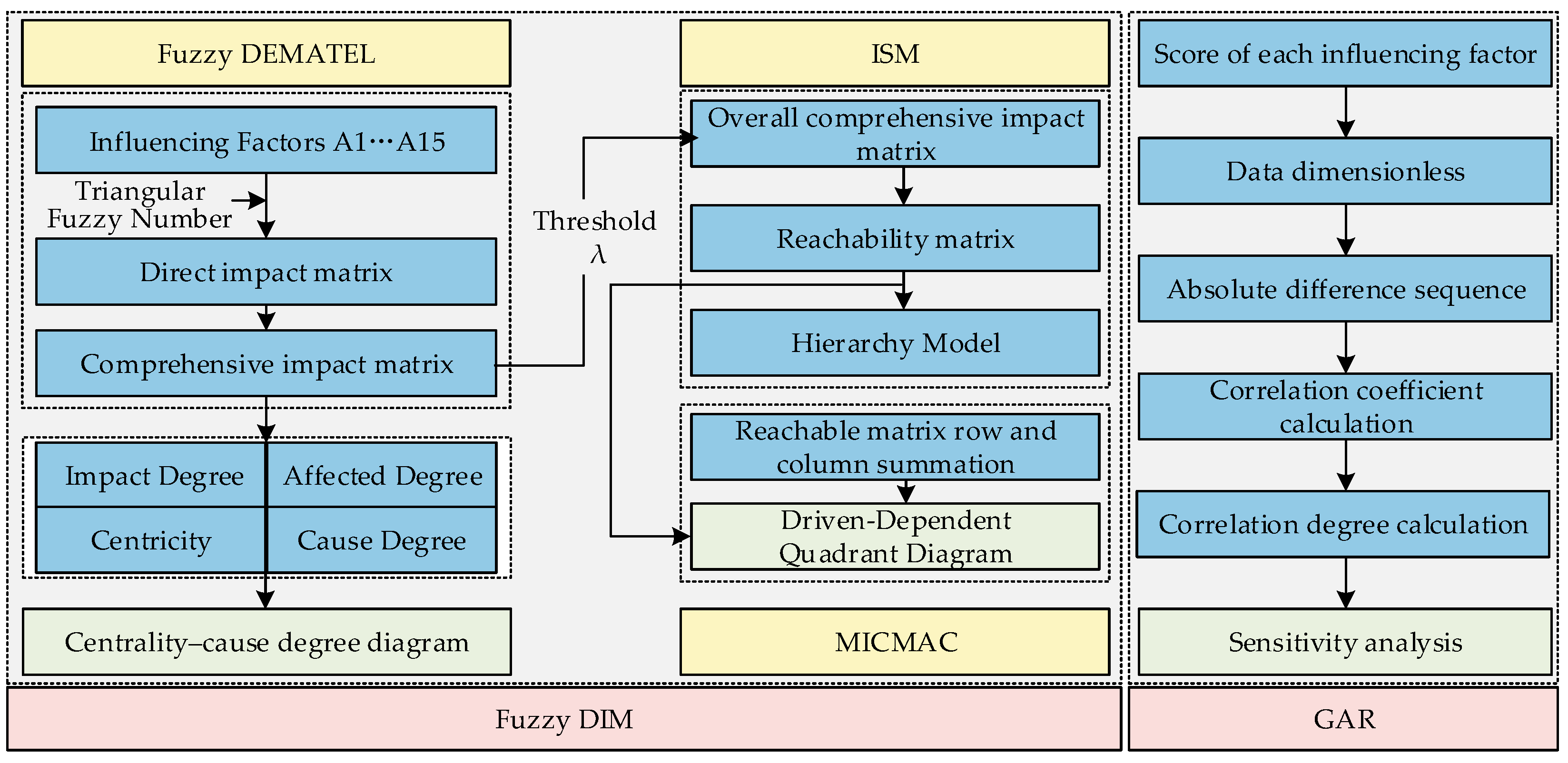
2.2. Research Framework
2.3. Research Methods
2.3.1. Fuzzy DIM Model
2.3.2. GRA Method
3. Results
3.1. Fuzzy DIM Analysis
3.2. GRA
4. Discussion
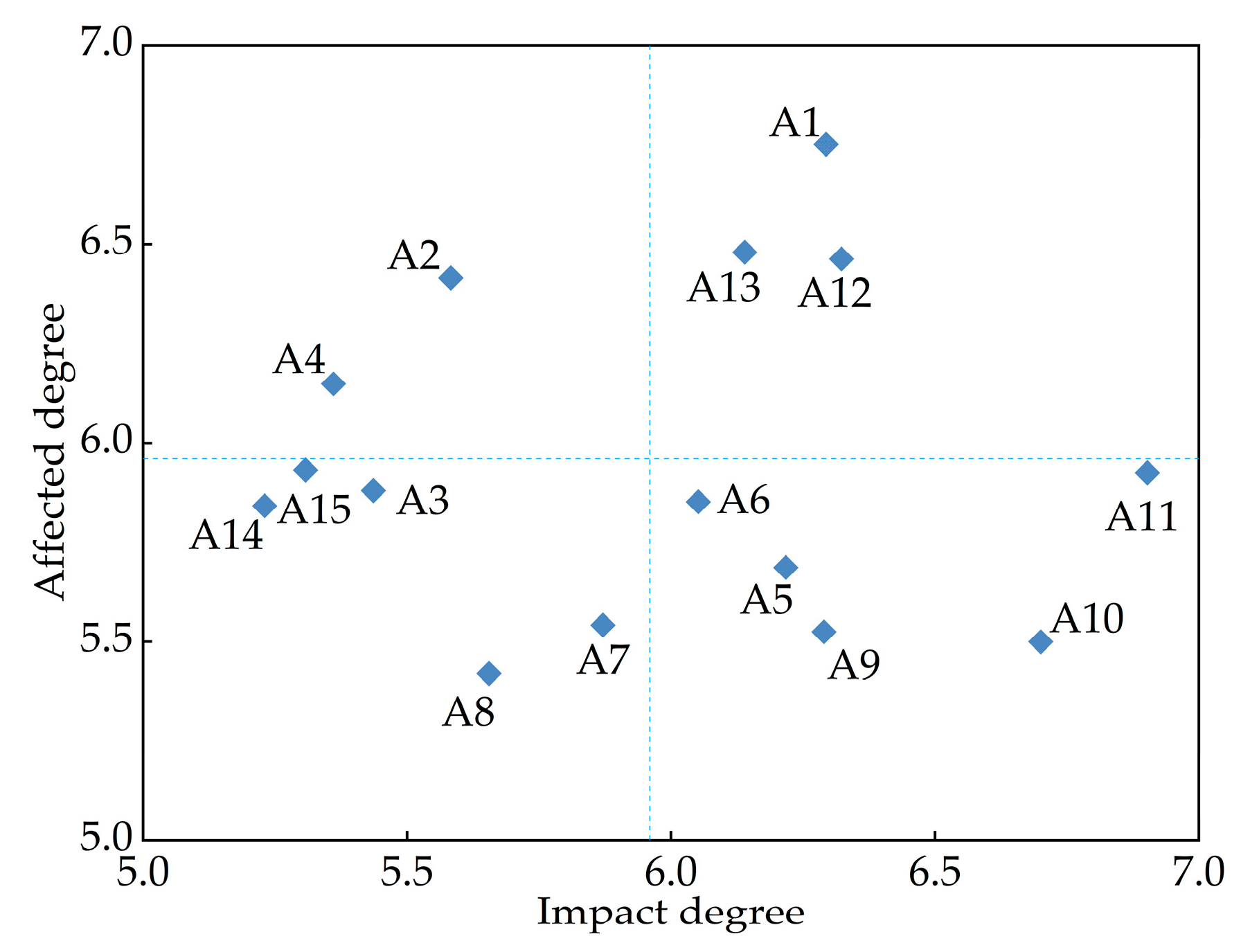
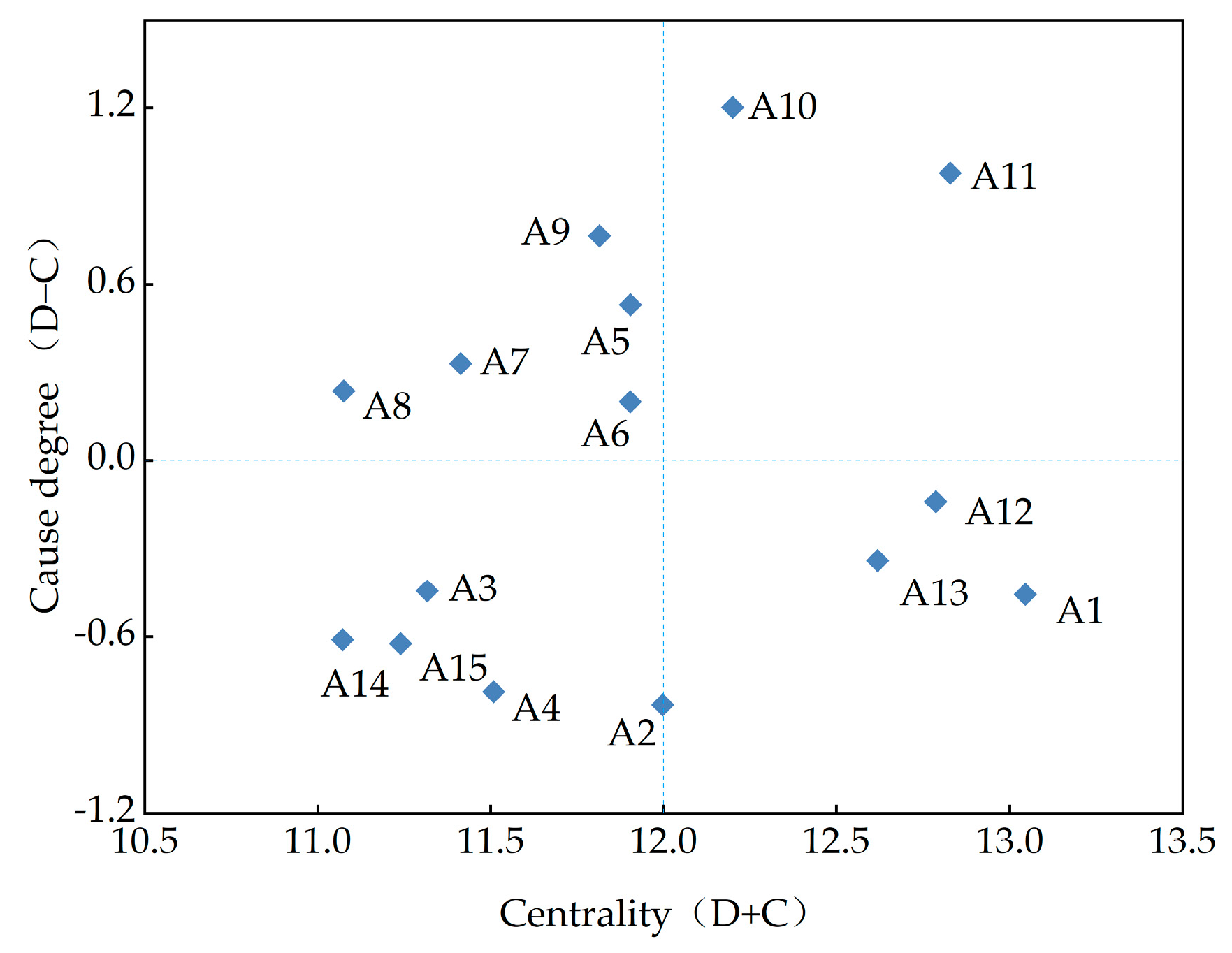
- The socioeconomic development level (A1) is a strong result factor, with the highest centrality and affected degree. It is also an intermediate-level factor that influences the water price of IWTPs and significantly affects other factors. The impact of the socioeconomic development level on the water price of IWTPs is mainly reflected in aspects such as the water supply cost, water demand, and payment capacity. Governments and enterprises in developed areas may be more willing to invest funds in constructing efficient water treatment facilities, water pipelines, and monitoring systems to improve water supply efficiency and quality. These inputs are reflected in the water price, resulting in relatively higher water prices. In areas with high water demand and widespread awareness of water-saving technologies among water users, water pricing focuses more on promoting water conservation through price leverage, such as by implementing tiered water pricing to encourage efficient water use. Water users have a strong ability to pay for water resources and can afford higher prices.
- The diversification of water resources (A9) is strongly influenced by natural environmental factors and ranks second in its degree of correlation. It is also an intermediate-level factor with a weak driving force and degree of dependence that influences the water prices of IWTPs. The impact of the diversification of water resources on the water prices of IWTPs is mainly reflected in multiple aspects. For example, the diversification of water resources provides more options for IWTPs but also increases the complexity of water pricing. The supply and demand relationships must be balanced through a water pricing mechanism. If there are local water sources or other water diversion projects in the area, IWTPs need to be reasonably priced and compete with alternative water sources to avoid water resource waste caused by oversupply. Diversified water resources can alleviate seasonal water shortages to some extent; however, measures should be taken to reduce prices during the wet season and increase prices during the dry season to ensure the basic benefits of the project. Therefore, the water price should be formulated based on the water source cost, supply–demand relationship of water resources, and policy objectives to ensure scientific and reasonable cost allocation and differentiated pricing.
- The demand of water users (A3) is one of the key influencing factors for the pricing of IWTPs and is a result of socioeconomic factors, which are surface-level factors affecting water prices. Water demand can be divided into rigid and elastic demands. Rigid demand is less sensitive to water prices and is the bottom line of the water price formulation. As a basic livelihood requirement, water prices must cover the water supply cost and ensure affordability for low-income groups. Elastic demand is highly sensitive to water prices, such as major water-consuming industries that are sensitive to water prices. Reasonable pricing can force enterprises to upgrade their water-saving technologies. Agriculture is a major water user; however, farmers have a poor ability to afford water. Water conservation must be incentivized through seasonal floating water prices or water-saving incentives. When formulating water prices for IWTPs, user classification should be refined, the composition of water prices should be made public, and water users’ recognition of pricing rationality should be enhanced.
- The cost of the project’s water supply (A12) is a result of political system factors and ranks third in impact, degree of being affected, and centrality, being an intermediate-level factor affecting the water price for engineering. The cost of a project’s water supply is the core basis for the water price of IWTPs, directly affecting the rationality, sustainability, and social acceptance of water prices. The water price should cover the cost of the water supply to ensure sustainable operation of the project. Interbasin water transfer involves multiple stakeholders, and cost allocation must be determined through negotiation. An unreasonable allocation may lead to excessively high or low water prices in certain areas. For example, the water source area may demand an increase in water prices owing to excessive ecological restoration costs, whereas water-receiving areas may wish to lower the water price owing to high water consumption. By optimizing the cost structure, establishing dynamic water price-adjustment mechanisms, and diversifying cost-sharing mechanisms, it is possible to ensure that water prices can cover costs while considering social equity.
- National policies and regulations (A5), a causal factor belonging to political system and natural environment factors, ranks fourth in causal degree. IWTPs usually serve major national strategic needs, such as ensuring food security, ecological security, and regional coordinated development. Water prices are usually formulated by the government and must be coordinated with national strategic goals to ensure the sustainable operation of the project. Simultaneously balancing public welfare and marketization can ensure that the project can meet both social public interests and achieve “self-hematopoietic” functions. For water-transfer projects with strong public welfare, the government may lower water prices through financial subsidies to alleviate the burden on water users.
5. Conclusions and Prospects
- A literature review and expert consultations were conducted to identify the factors influencing water prices in IWTPs. Fifteen factors were identified and divided into four categories: socioeconomic, political system, natural environment, and engineering.
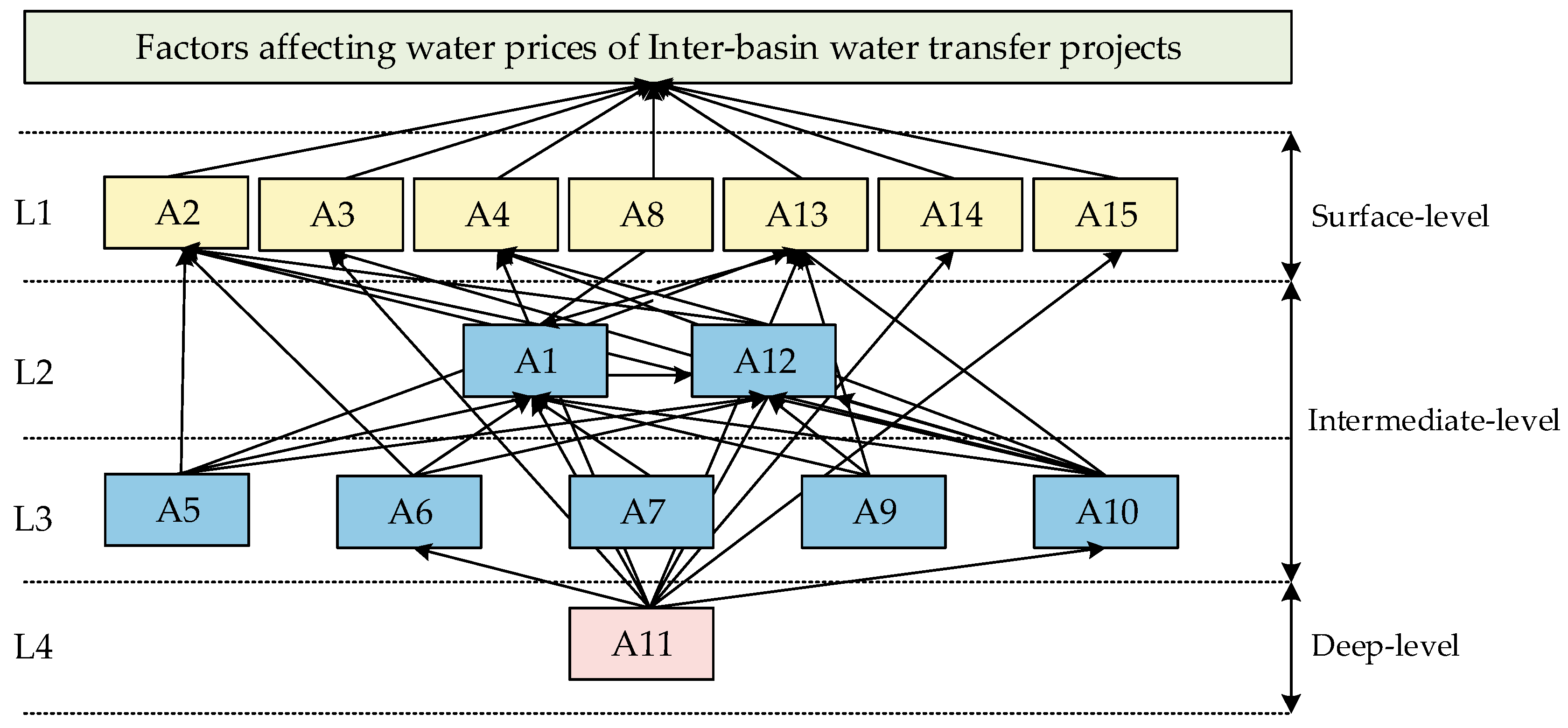
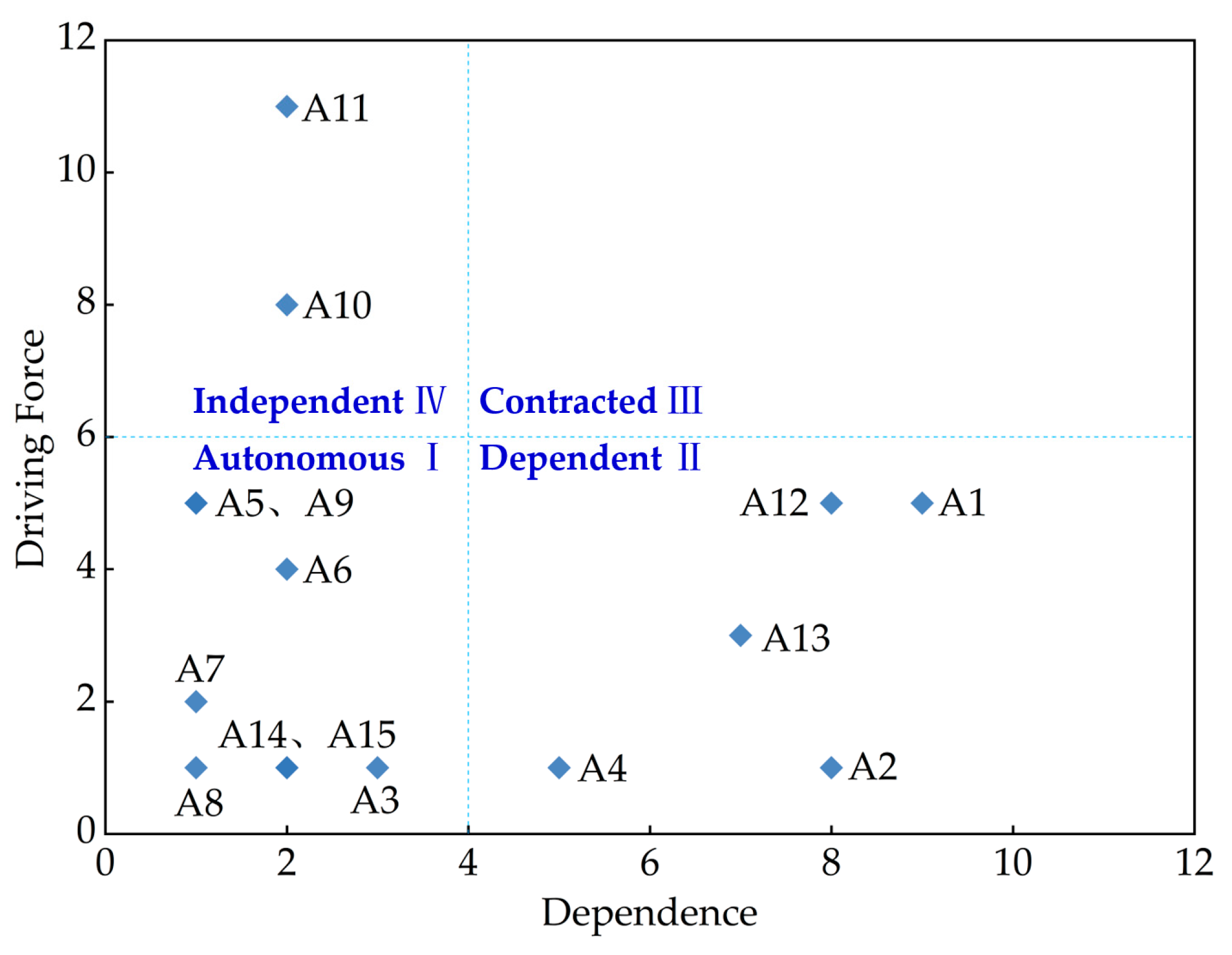
- Water resource abundance and scarcity (A10) and water availability (A11) are key factors with strong driving forces and low dependency that influence other factors. However, the dependent factors, namely socioeconomic development level (A1), regional industrial structure (A2), affordability to water users (A4), cost of the project’s water supply (A12), and guaranteed water supply rate (A13), are also key factors that require attention because of their strong influence on the results.
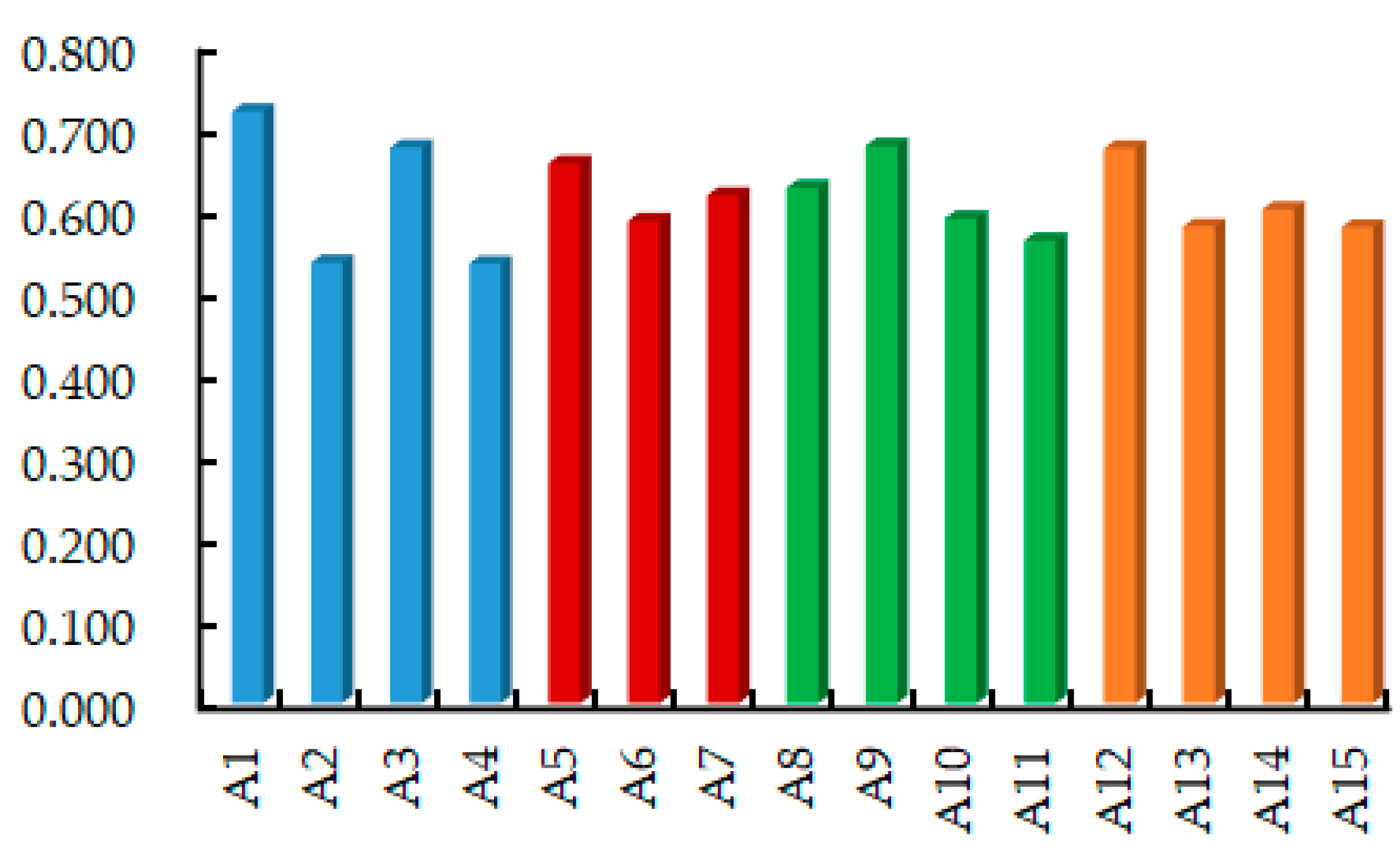
- Based on the GRA method, the top five factors influencing the water price for IWTPs were determined as follows: socioeconomic development level (A1), diversification of water resources (A9), water demand of water users (A3), cost of project’s water supply (A12), and national policies and regulations (A5).
- By investigating the factors influencing the water price for IWTPs, the effectiveness of the fuzzy DIM and GRA methods in studying the degree of influencing factors and the method of determining key factors were verified. Furthermore, determining the adjacency matrix of the ISM by setting a threshold is more objective than the previously used expert determination methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tu, Y.; Wang, H.Y.; Zhou, X.Y.; Shen, W.J.; Lev, B. Comprehensive evaluation of security, equity, and efficiency on regional water resources coordination using a hybrid multi-criteria decision-making method with different hesitant fuzzy linguistic term sets. J. Clean. Prod. 2021, 310, 127447. [Google Scholar] [CrossRef]
- Schlamovitz, J.L.; Becker, P. Differentiated vulnerabilities and capacities for adaptation to water shortage in Gaborone, Botswana. Int. J. Water Resour. Dev. 2021, 37, 278–299. [Google Scholar] [CrossRef]
- Rehman, R.; Aslam, M.S.; Jasińska, E.; Javed, M.F.; Goňo, M. Guidelines for the Technical Sustainability Evaluation of the Urban Drinking Water Systems Based on Analytic Hierarchy Process. Resources 2023, 12, 8. [Google Scholar] [CrossRef]
- Siddik, M.A.; Dickson, K.E.; Rising, J.; Ruddell, B.L.; Marston, L.T. Interbasin water transfers in the United States and Canada. Sci. Data 2023, 10, 27. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.W.; Chen, L. Coincidence probability of precipitation for the middle route of South-to-North water transfer project in China. J. Hydrol. 2013, 499, 19–26. [Google Scholar] [CrossRef]
- Pasi, N.; Smardon, R. Inter-mmlinking of rivers: A solution for water crisis in india or a decision in doubt. J. Sci. Policy Gov. 2012, 2, 1. [Google Scholar]
- Liu, J.G.; Zang, C.F.; Tian, S.Y.; Liu, J.G.; Yang, H.; Jia, S.F.; You, L.Z.; Liu, B.; Zhang, M. Water conservancy projects in China: Achievements, challenges and way forward. Glob. Environ. Change-Hum. Policy Dimens. 2013, 23, 633–643. [Google Scholar] [CrossRef]
- Su, Q.M.; Chen, X. Efficiency analysis of metacoupling of water transfer based on the parallel data envelopment analysis model: A case of the South-North Water Transfer Project-Middle Route in China. J. Clean. Prod. 2021, 313, 127952. [Google Scholar] [CrossRef]
- Sun, S.; Tang, Q.H.; Konar, M.; Fang, C.L.; Liu, H.X.; Liu, X.C.; Fu, G.T. Water transfer infrastructure buffers water scarcity risks to supply chains. Water Res. 2023, 229, 119442. [Google Scholar] [CrossRef]
- Bui, D.T.; Talebpour Asl, D.; Ghanavati, E.; Al-Ansari, N.; Khezri, S.; Chapi, K.; Amini, A.; Pham, B.T. Effects of Inter-Basin Water Transfer on Water Flow Condition of Destination Basin. Sustainability 2020, 12, 338. [Google Scholar] [CrossRef]
- Rogers, S.; Chen, D.; Jiang, H.; Rutherfurd, I.; Wang, M.; Webber, M.; Crow-Miller, B.; Barnett, J.; Finlayson, B.; Jiang, M.; et al. An integrated assessment of China’s South–North Water Transfer Project. Geogr. Res. 2019, 58, 49–63. [Google Scholar] [CrossRef]
- Naghani, S.S.; Moghaddam, M.A.; Monfared, S.A.H. Inter-basin water transfer: A sustainable solution or an ephemeral painkiller to water shortage? Environ. Dev. Sustain. 2024, 26, 23025–23058. [Google Scholar] [CrossRef]
- Wang, X.D.; Hu, C.M.; Liang, J.; Wang, J.; Dong, S.Y. A Study of the factors influencing the construction risk of steel truss bridges based on the improved DEMATEL-ISM. Buildings 2023, 13, 41. [Google Scholar] [CrossRef]
- Liu, W.; Huang, Q.C. Research on Carbon Footprint Accounting in the Materialization Stage of Prefabricated Housing Based on DEMATEL-ISM-MICMAC. Appl. Sci. 2023, 13, 13148. [Google Scholar] [CrossRef]
- He, L. Study on risk factors of substation construction project based on DEMATEL. Proj. Manag. Technol. 2024, 22, 18–21. [Google Scholar]
- Chen, Z.; Huang, P.; Huang, W. Group intelligence fusion emergency decision-making method with dual-driven DEMATEL in a social network environment. J. Saf. Environ. 2024, 24, 2336–2347. [Google Scholar]
- Zhang, J.; Li, J.; You, J.W. Research on Influencing Factors of Cost Control of Centralized Photovoltaic Power Generation Project Based on DEMATEL-ISM. Sustainability 2024, 16, 5289. [Google Scholar] [CrossRef]
- Liu, W.; Hu, Y.H.; Huang, Q.C. Research on Critical Factors Influencing Organizational Resilience of Major Transportation Infrastructure Projects: A Hybrid Fuzzy DEMATEL-ISM-MICMAC Approach. Buildings 2024, 14, 1598. [Google Scholar] [CrossRef]
- Xie, J.H.; Tian, F.J.; Li, X.Y.; Chen, Y.Q.; Li, S.Y. A study on the influencing factors and related paths of farmer’s participation in food safety governance-based on DEMATEL-ISM-MICMAC model. Sci. Rep. 2023, 13, 11372. [Google Scholar] [CrossRef]
- Li, H.B.; Xiang, Y.R.; Xia, Y.H.; Yang, W.J.; Tang, X.T.; Lin, T. What Are the Obstacles to Promoting Photovoltaic Green Roofs in Existing Buildings? The Integrated Fuzzy DEMATEL-ISM-ANP Method. Sustainability 2023, 15, 16862. [Google Scholar] [CrossRef]
- Liu, T.; Wang, P.; Cao, J.; He, Y.; Weng, Z. Internet-based recycling by urban residents in China: Evaluation of influencing factors using DEMATEL and ISM. Int. J. Environ. Sci. Technol. 2025, 22, 2517–2530. [Google Scholar] [CrossRef]
- Luo, X.; Huang, X. Research on Cost Control of Prefabricated Building Based on Interpretative Structural Modeling Method. Constr. Econ. 2021, 42, 73–77. [Google Scholar]
- Li, L.; Bai, F.; Mao, B.; Lei, Y. Research on the High-quality Developmentof Green Building Based on ISM-MICMAC: A Case Study of Shenyang. Constr. Econ. 2022, 43, 98–104. [Google Scholar]
- Zheng, Y.; Shi, H. Research on Hierarchical Relationship of Influencing Factors of Green Building Development Based on ISM. J. Anhui Inst. Archit. Ind. 2022, 30, 83–89. [Google Scholar]
- Tan, T.; Chen, K.; Xue, F.; Lu, W.S. Barriers to Building Information Modeling (BIM) implementation in China’s prefabricated construction: An interpretive structural modeling (ISM) approach. J. Clean. Prod. 2019, 219, 949–959. [Google Scholar] [CrossRef]
- Deng, J.X.; Li, X.X.; Rao, J.T. Research on Influencing Factors and Driving Path of BIM Application in Construction Projects Based on the SD Model in China. Buildings 2023, 13, 2794. [Google Scholar] [CrossRef]
- Yuan, H.P.; Yang, Y. BIM Adoption under Government Subsidy: Technology Diffusion Perspective. J. Constr. Eng. Manag. 2020, 146, 04019089. [Google Scholar] [CrossRef]
- Xu, H.Y.; Chang, R.D.; Dong, N.; Zuo, J.; Webber, R.J. Interaction mechanism of BIM application barriers in prefabricated construction and driving strategies from stakeholders’ perspectives. Ain Shams Eng. J. 2023, 14, 101821. [Google Scholar] [CrossRef]
- Jang, S.; Lee, G. Process, productivity, and economic analyses of BIM based multi-trade prefabrication—A case study. Autom. Constr. 2018, 89, 86–98. [Google Scholar] [CrossRef]
- Lin, M.C.; Ren, Y.F.; Feng, C.; Li, X.J. Analyzing resilience influencing factors in the prefabricated building supply chain based on SEM-SD methodology. Sci. Rep. 2024, 14, 17393. [Google Scholar] [CrossRef]
- Belay, S.; Goedert, J.; Woldesenbet, A.; Rokooei, S.; Matos, J.; Sousa, H. Key BIM Adoption Drivers to Improve Performance of Infrastructure Projects in the Ethiopian Construction Sector: A Structural Equation Modeling Approach. Adv. Civ. Eng. 2021, 2021, 7473176. [Google Scholar] [CrossRef]
- Chang, C.Y.; Pan, W.J.; Howard, R. Impact of Building Information Modeling Implementation on the Acceptance of Integrated Delivery Systems: Structural Equation Modeling Analysis. J. Constr. Eng. Manag. 2017, 143, 04017044. [Google Scholar] [CrossRef]
- Wang, P.; Yu, Y. Research on Influencing Factors of Resilience of High-tech Ship Industry Chain Based on Fuzzy DEMATEL-ISM. Sci. Technol. Manag. Res. 2023, 43, 196–204. [Google Scholar]
- Zhu, W.X.; Zhang, J.; Wang, D.; Ma, C.S.; Zhang, J.F.; Chen, P. Study on the Critical Factors Influencing High-Quality Development of Green Buildings for Carbon Peaking and Carbon Neutrality Goals of China. Sustainability 2023, 15, 5035. [Google Scholar] [CrossRef]
- Mustafa, M.; Malik, M.O.F. Factors Hindering Solar Photovoltaic System Implementation in Buildings and Infrastructure Projects: Analysis through a Multiple Linear Regression Model and Rule-Based Decision Support System. Buildings 2023, 13, 1786. [Google Scholar] [CrossRef]
- Hu, W.; Kong, D.; He, X. Analysis on Influencing Factors of Green Building Development Based on BP-WINGS. Soft Sci. 2020, 34, 75–81. [Google Scholar]
- Peng, Z.Y.; Yin, J.X.; Zhang, L.L.; Zhao, J.; Liang, Y.; Wang, H. Assessment of the Socio-Economic Impact of a Water Diversion Project for a Water-Receiving Area. Pol. J. Environ. Stud. 2020, 29, 1771–1784. [Google Scholar] [CrossRef]
- Schnuelle, C.; Wassermann, T.; Stuehrmann, T. Mind the Gap-A Socio-Economic Analysis on Price Developments of Green Hydrogen, Synthetic Fuels, and Conventional Energy Carriers in Germany. Energies 2022, 15, 3541. [Google Scholar] [CrossRef]
- Chen, M.; Wang, K. The combining and cooperative effects of carbon price and technological innovation on carbon emission reduction: Evidence from China’s industrial enterprises. J. Environ. Manag. 2023, 343, 118188. [Google Scholar] [CrossRef]
- Vidal-Lamolla, P.; Molinos-Senante, M.; Poch, M. Understanding the Residential Water Demand Response to Price Changes: Measuring Price Elasticity with Social Simulations. Water 2024, 16, 2501. [Google Scholar] [CrossRef]
- Marlim, M.S.; Kang, D.S. Improving operational efficiency in water distribution network with hourly water pricing to benefit consumers and providers. J. Water Process Eng. 2025, 72, 107457. [Google Scholar] [CrossRef]
- Marques, G.; Possantti, I.; Dalcin, A.P.; Daiello, J.; Gonzalez, I.; Todeschini, F.; Goldenfum, J. An integrated hydro-finance approach towards sustainable urban stormwater and flood control management. J. Clean. Prod. 2024, 470, 143364. [Google Scholar] [CrossRef]
- Jia, J.J.; Liang, Q.; Jiang, M.R.; Wu, H.Q. Household water price and income elasticities under increasing-block pricing policy in China: An estimation using nationwide large-scale survey data. Environ. Res. Commun. 2024, 6, 061002. [Google Scholar] [CrossRef]
- Zhang, G.J.; Wu, H.Q.; Liu, Y.Z.; Chen, X.; Song, P.F. Does Residents’ Perception of Information Influence the Implementation Effect of Increasing-Block Water Pricing Policy? Water Econ. Policy 2024, 10. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, C.; Wu, L.; Liu, J.; Li, D.; Wang, G. Demand analysis of urban reclaimed water considering water quality and water price. J. Water Resour. Water Eng. 2024, 35, 60–70. [Google Scholar]
- Hughes, N.; Gupta, M.; Whittle, L.; Westwood, T. An Economic Model of Spatial and Temporal Water Trade in the Australian Southern Murray-Darling Basin. Water Resour. Res. 2023, 59, e2022WR032559. [Google Scholar] [CrossRef]
- Ribeiro, F.W.; da Silva, S.M.O.; de Souza, F.D.; Carvalho, T.M.N.; Lopes, T. Diversification of urban water supply: An assessment of social costs and water production costs. Water Policy 2022, 24, 980–997. [Google Scholar] [CrossRef]
- Yu, H.; Ge, J.J. Recent advances in Ru-based electrocatalysts toward acid electrochemical water oxidation. Curr. Opin. Electrochem. 2023, 39, 101296. [Google Scholar] [CrossRef]
- Cooper, B.; Burton, M.; Crase, L. Exploring customer heterogeneity with a scale-extended latent class choice model: Experimental evidence drawn from urban water users. Aust. J. Agric. Resour. Econ. 2023, 67, 176–197. [Google Scholar] [CrossRef]
- Liu, Y.; Chong, F.T.; Jia, J.J.; Cao, S.L.; Wang, J. Proper Pricing Approach to the Water Supply Cost Sharing: A Case Study of the Eastern Route of the South to North Water Diversion Project in China. Water 2022, 14, 2842. [Google Scholar] [CrossRef]
- Qin, C.H.; Jiang, S.; Zhao, Y.; Zhu, Y.N.; Wang, Q.M.; Wang, L.Z.; Qu, J.L.; Wang, M. Research on Water Rights Trading and Pricing Model between Agriculture and Energy Development in Ningxia, China. Sustainability 2022, 14, 15748. [Google Scholar] [CrossRef]
- Wang, S.W.; Liu, S.B.; Yao, S.P.; Guo, X.; Soomro, S.E.H.; Niu, C.J.; Quan, L.Y.; Hu, C.H. Game Theory Applications in Equilibrium Water Pricing of Multiple Regional Sources and Users. Water 2024, 16, 1845. [Google Scholar] [CrossRef]
- Hur, A.Y.; Page, M.A.; Guest, J.S.; Ploschke, C.M. Financial analysis of decentralized water reuse systems in mission critical facilities at US Army installations. Environ. Sci. Water Res. Technol. 2024, 10, 603–613. [Google Scholar] [CrossRef]
- Nawar, B.; Scardigno, A.; Sagardoy, J.A. Treatment and reuse of water: Economic feasibility and assessment of water pricing policies in Ouardanine irrigation district (Tunisia). NEW MEDIT 2024, 23, 73–93. [Google Scholar] [CrossRef]
- Berbel, J.; Gutierrez-Marín, C.; Expósito, A. Impacts of irrigation efficiency improvement on water use, water consumption and response to water price at field level. Agric. Water Manag. 2018, 203, 423–429. [Google Scholar] [CrossRef]
- Ma, L.; Wang, Q. Do Water Transfer Projects Promote Water Use Efficiency? Case Study of South-to-North Water Transfer Project in Yellow River Basin of China. Water 2024, 16, 1367. [Google Scholar] [CrossRef]
- Peng, X.; Li, N.N. Water Pricing Mechanism for China’s South-to-North Water Diversion Project: Design, Evaluation, and Suggestions. J. Am. Water Resour. Assoc. 2022, 58, 1230–1239. [Google Scholar] [CrossRef]
- Chen, L.; Xiao, H.; Liu, X.; Liu, W. Sensitivity analysis of influencing factors of open-pit mine slope stability based on grey correlation. Bull. Surv. Mapp. 2024, 1, 145–149. [Google Scholar] [CrossRef]
- Marlin, D.; Lamont, B.T.; Hoffman, J.J. Choice situation, strategy, and performance: A reexamination. Strateg. Manag. J. 1994, 15, 229–239. [Google Scholar] [CrossRef]
- Gunasekaran, J.; Sevvel, P.; John Solomon, I.; Vasanthe Roy, J. Multi objective optimization of parameters during FSW of AZ80A-AZ31B Mg alloys using grey relational analysis. J. Mech. Sci. Technol. 2024, 38, 4971–4982. [Google Scholar] [CrossRef]
- Zhu, R.; Bhutta, Z.M.; Zhu, Y.; Ubaidullah, F.; Saleem, M.; Khalid, S. Grey relational analysis of country-level entrepreneurial environment: A study of selected forty-eight countries. Front. Environ. Sci. 2022, 10, 985426. [Google Scholar] [CrossRef]
- Luo, M.; Wang, D.; Wang, X.; Lu, Z. Analysis of Surface Settlement Induced by Shield Tunnelling: Grey Relational Analysis and Numerical Simulation Study on Critical Construction Parameters. Sustainability 2023, 15, 14315. [Google Scholar] [CrossRef]
| Method | Characteristics | Application |
|---|---|---|
| DEMATEL [13,14,15,16,17] | Assessment of causality and degree of influence between factors | Project construction risk, emergency decision-making, cost control, carbon footprint |
| MICMAC [18,19,20] | Categorizes the attributes and determines the role and status of influencing factors | Photovoltaic green roofs, organizational resilience of projects |
| ISM [21,22,23,24,25] | Delineates the system hierarchy and qualitatively analyzes the influencing relationship between each factor | Internet-based recycling by urban residents, cost control, high-quality development of green building, barriers to BIM implementation |
| ANP [20] | Determines the overall weighting of the factors | Photovoltaic green roofs |
| SD [26,27,28,29,30,31] | Explores the intrinsic connection between the influencing factors through quantitative methods | BIM application barriers, BIM adoption under government subsidy |
| SEM–SD [32] | Probes the mechanisms underpinning influencing factors, assesses the gradation of influence on objects, and executes a sensitivity simulation analysis | Prefabricated building supply chain |
| Structural Equation [31,32] | Allows for the analysis of the direct and indirect impacts of latent constructs between exogenous and endogenous variables | Performance of infrastructure projects |
| Fuzzy DEMATEL–ISM [18,33] | Allows for the analysis of the interrelationships, hierarchical structure, and mechanisms of factors, and addresses the shortcomings in semantic ambiguity | Organizational resilience of projects, photovoltaic green roofs |
| Dual-Drive DEMATEL [16] | Avoids the disadvantages of DEMATEL method relying on subjective experience calculation | Emergency decision-making |
| DEMATEL–ISM–MICMAC [14] | Determines the role of factors and clarifies their position in complex systems by calculating the driving force and dependence | Carbon footprint, high-quality development of green buildings |
| MLRM, RBDSS [34] | — | Implementation of photovoltaic power generation projects |
| BP-WINGS [35] | — | Green building development |
| Dimension | Number | Critical Factors | Related Literature |
|---|---|---|---|
| Socio-economic factors | A1 | Socio-economic development level | [36,37] |
| A2 | Regional industrial structure | [38] | |
| A3 | Water demand of water users | [39,40] | |
| A4 | Affordability to water users | [41] | |
| Political system factors | A5 | National policies and regulations | [42,43] |
| A6 | Government subsidies and incentives | [44] | |
| A7 | Institutional and market factors | [45] | |
| Natural environment factors | A8 | Water resources’ quality | [44] |
| A9 | Diversification of water resources | [46] | |
| A10 | Water resource abundance and scarcity | [47] | |
| A11 | Water availability | [48] | |
| Engineering factors | A12 | Cost of project’s water supply | [49,50] |
| A13 | Guaranteed water supply rate | [51] | |
| A14 | Project investment structure | [52] | |
| A15 | Project profitability | [53] |
| Semantic Variables | TFN |
|---|---|
| No impact | (0, 0, 0.25) |
| Low impact | (0, 0.25, 0.5) |
| Has a certain impact | (0.25, 0.5, 0.7) |
| Has a high impact | (0.5, 0.75, 1) |
| Has a very significant impact | (0.75, 1, 1) |
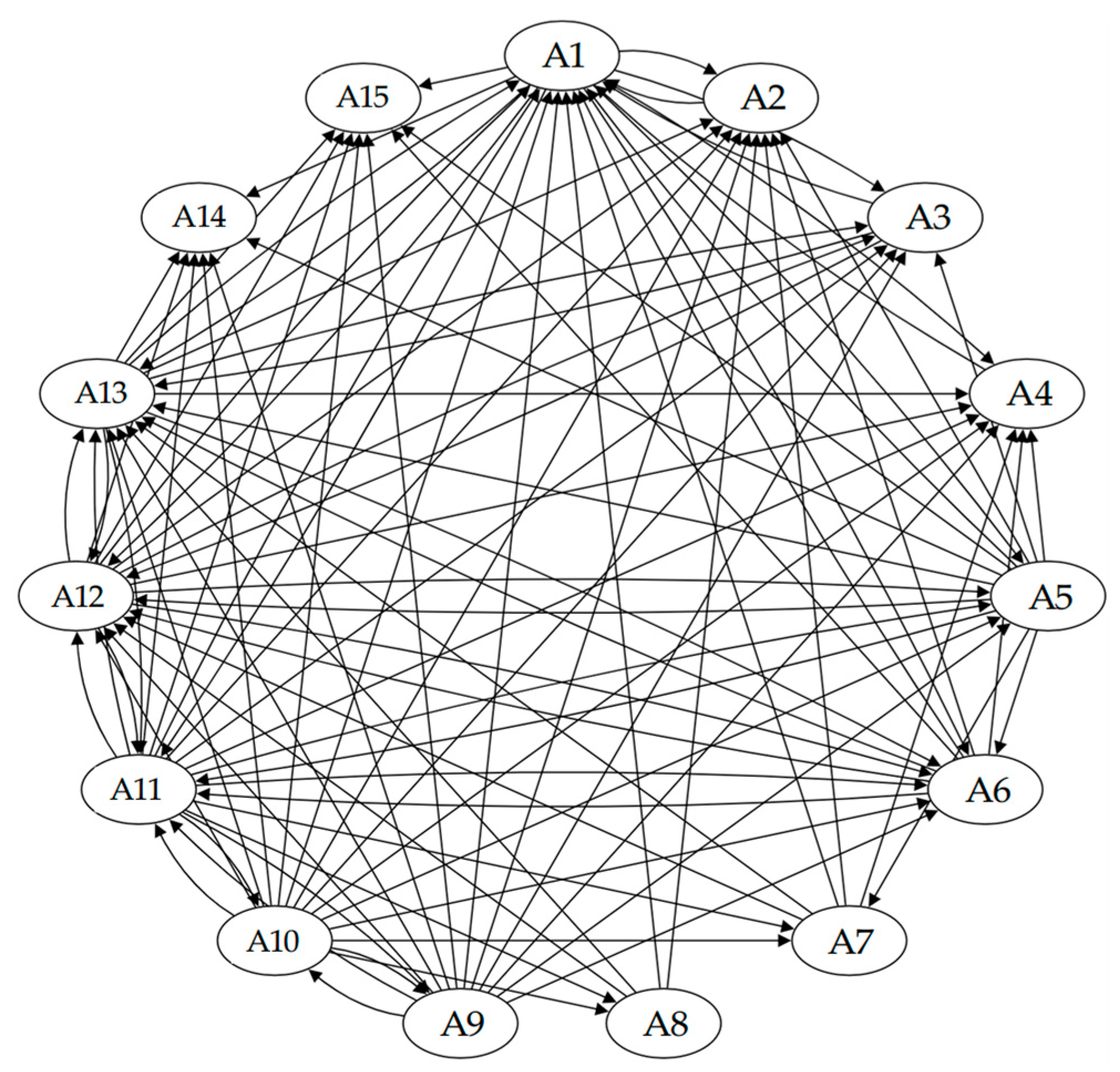
| Factor | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.411 | 0.462 | 0.417 | 0.443 | 0.406 | 0.418 | 0.395 | 0.392 | 0.388 | 0.384 | 0.417 | 0.453 | 0.461 | 0.425 | 0.423 |
| A2 | 0.437 | 0.347 | 0.370 | 0.384 | 0.369 | 0.369 | 0.359 | 0.353 | 0.355 | 0.349 | 0.372 | 0.394 | 0.395 | 0.365 | 0.365 |
| A3 | 0.410 | 0.392 | 0.310 | 0.386 | 0.351 | 0.355 | 0.331 | 0.337 | 0.341 | 0.342 | 0.366 | 0.402 | 0.401 | 0.350 | 0.364 |
| A4 | 0.412 | 0.380 | 0.372 | 0.320 | 0.345 | 0.361 | 0.335 | 0.316 | 0.324 | 0.332 | 0.361 | 0.394 | 0.398 | 0.350 | 0.360 |
| A5 | 0.480 | 0.453 | 0.405 | 0.422 | 0.343 | 0.424 | 0.406 | 0.376 | 0.389 | 0.378 | 0.413 | 0.446 | 0.454 | 0.414 | 0.416 |
| A6 | 0.455 | 0.447 | 0.396 | 0.427 | 0.395 | 0.343 | 0.394 | 0.364 | 0.371 | 0.374 | 0.404 | 0.445 | 0.434 | 0.397 | 0.407 |
| A7 | 0.463 | 0.441 | 0.379 | 0.402 | 0.385 | 0.395 | 0.316 | 0.353 | 0.361 | 0.357 | 0.391 | 0.431 | 0.422 | 0.392 | 0.385 |
| A8 | 0.434 | 0.408 | 0.377 | 0.394 | 0.361 | 0.365 | 0.341 | 0.297 | 0.352 | 0.349 | 0.388 | 0.420 | 0.419 | 0.372 | 0.379 |
| A9 | 0.480 | 0.448 | 0.411 | 0.432 | 0.408 | 0.414 | 0.387 | 0.395 | 0.337 | 0.407 | 0.433 | 0.465 | 0.459 | 0.406 | 0.409 |
| A10 | 0.502 | 0.483 | 0.454 | 0.471 | 0.421 | 0.437 | 0.416 | 0.404 | 0.423 | 0.357 | 0.463 | 0.493 | 0.499 | 0.438 | 0.442 |
| A11 | 0.525 | 0.502 | 0.472 | 0.483 | 0.437 | 0.448 | 0.429 | 0.419 | 0.431 | 0.446 | 0.396 | 0.501 | 0.509 | 0.447 | 0.458 |
| A12 | 0.479 | 0.451 | 0.424 | 0.448 | 0.402 | 0.420 | 0.384 | 0.389 | 0.400 | 0.396 | 0.415 | 0.395 | 0.465 | 0.422 | 0.435 |
| A13 | 0.470 | 0.443 | 0.418 | 0.429 | 0.392 | 0.407 | 0.384 | 0.372 | 0.387 | 0.376 | 0.404 | 0.446 | 0.385 | 0.409 | 0.419 |
| A14 | 0.396 | 0.379 | 0.337 | 0.344 | 0.335 | 0.348 | 0.330 | 0.322 | 0.330 | 0.321 | 0.347 | 0.391 | 0.387 | 0.296 | 0.367 |
| A15 | 0.399 | 0.379 | 0.337 | 0.365 | 0.337 | 0.350 | 0.337 | 0.333 | 0.336 | 0.332 | 0.356 | 0.389 | 0.392 | 0.360 | 0.305 |
| Factor | Impact Degree | Affected Degree | Causal Degree | Centrality | Factor Attribute | ||||
|---|---|---|---|---|---|---|---|---|---|
| fi | Rank | ei | Rank | fi − ei | Rank | fi + ei | Rank | ||
| A1 | 6.3 | 4 | 6.8 | 1 | −0.5 | 11 | 13.0 | 1 | R |
| A2 | 5.6 | 11 | 6.4 | 4 | −0.8 | 15 | 12.0 | 6 | R |
| A3 | 5.4 | 12 | 5.9 | 8 | −0.4 | 10 | 11.3 | 12 | R |
| A4 | 5.4 | 13 | 6.1 | 5 | −0.8 | 14 | 11.5 | 10 | R |
| A5 | 6.2 | 6 | 5.7 | 11 | 0.5 | 4 | 11.9 | 7 | C |
| A6 | 6.1 | 8 | 5.9 | 9 | 0.2 | 7 | 11.9 | 8 | C |
| A7 | 5.9 | 9 | 5.5 | 12 | 0.3 | 5 | 11.4 | 11 | C |
| A8 | 5.7 | 10 | 5.4 | 15 | 0.2 | 6 | 11.1 | 14 | C |
| A9 | 6.3 | 5 | 5.5 | 13 | 0.8 | 3 | 11.8 | 9 | C |
| A10 | 6.7 | 2 | 5.5 | 14 | 1.2 | 1 | 12.2 | 5 | C |
| A11 | 6.9 | 1 | 5.9 | 7 | 1.0 | 2 | 12.8 | 2 | C |
| A12 | 6.3 | 3 | 6.5 | 3 | −0.1 | 8 | 12.8 | 3 | R |
| A13 | 6.1 | 7 | 6.5 | 2 | −0.3 | 9 | 12.6 | 4 | R |
| A14 | 5.2 | 15 | 5.8 | 10 | −0.6 | 12 | 11.1 | 15 | R |
| A15 | 5.3 | 14 | 5.9 | 6 | −0.6 | 13 | 11.2 | 13 | R |
| Factor | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| A2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A5 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| A6 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| A7 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A9 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| A10 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| A11 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| A12 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| A13 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| A14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| A15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Factor | Reachable Set | Antecedent Set | Intersection |
|---|---|---|---|
| A1 | 1, 2, 4, 12, 13 | 1, 5, 6, 7, 9, 10, 11, 12, 13 | 1, 12, 13 |
| A2 | 2 | 1, 2, 5, 6, 9, 10, 11, 12 | 2 |
| A3 | 3 | 3, 10, 11 | 3 |
| A4 | 4 | 1, 4, 10, 11, 12 | 4 |
| A5 | 1, 2, 5, 12, 13 | 5 | 5 |
| A6 | 1, 2, 6, 12 | 6, 11 | 6 |
| A7 | 1, 7 | 7 | 7 |
| A8 | 8 | 8 | 8 |
| A9 | 1, 2, 9, 12, 13 | 9 | 9 |
| A10 | 1, 2, 3, 4, 10, 11, 12, 13 | 10, 11 | 10, 11 |
| A11 | 1, 2, 3, 4, 6, 10, 11, 12, 13, 14, 15 | 10, 11 | 10, 11 |
| A12 | 1, 2, 4, 12, 13 | 1, 5, 6, 9, 10, 11, 12, 13 | 1, 12, 13 |
| A13 | 1, 12, 13 | 1, 5, 9, 10, 11, 12, 13 | 1, 12, 13 |
| A14 | 14 | 11, 14 | 14 |
| A15 | 15 | 11, 15 | 15 |
| Level | Element Set | Impact Degree |
|---|---|---|
| L1 | 2, 3, 4, 8, 13, 14, 15 | Surface level |
| L2 | 1, 12 | Intermediate level |
| L3 | 5, 6, 7, 9, 10 | Intermediate level |
| L4 | 11 | Deep level |
| Factor | Dependence | Driving Force | Factors | Dependence | Driving Force | Factors | Dependence | Driving Force |
|---|---|---|---|---|---|---|---|---|
| A1 | 9 | 5 | A6 | 2 | 4 | A11 | 2 | 11 |
| A2 | 8 | 1 | A7 | 1 | 2 | A12 | 8 | 5 |
| A3 | 3 | 1 | A8 | 1 | 1 | A13 | 7 | 3 |
| A4 | 5 | 1 | A9 | 1 | 5 | A14 | 2 | 1 |
| A5 | 1 | 5 | A10 | 2 | 8 | A15 | 2 | 1 |
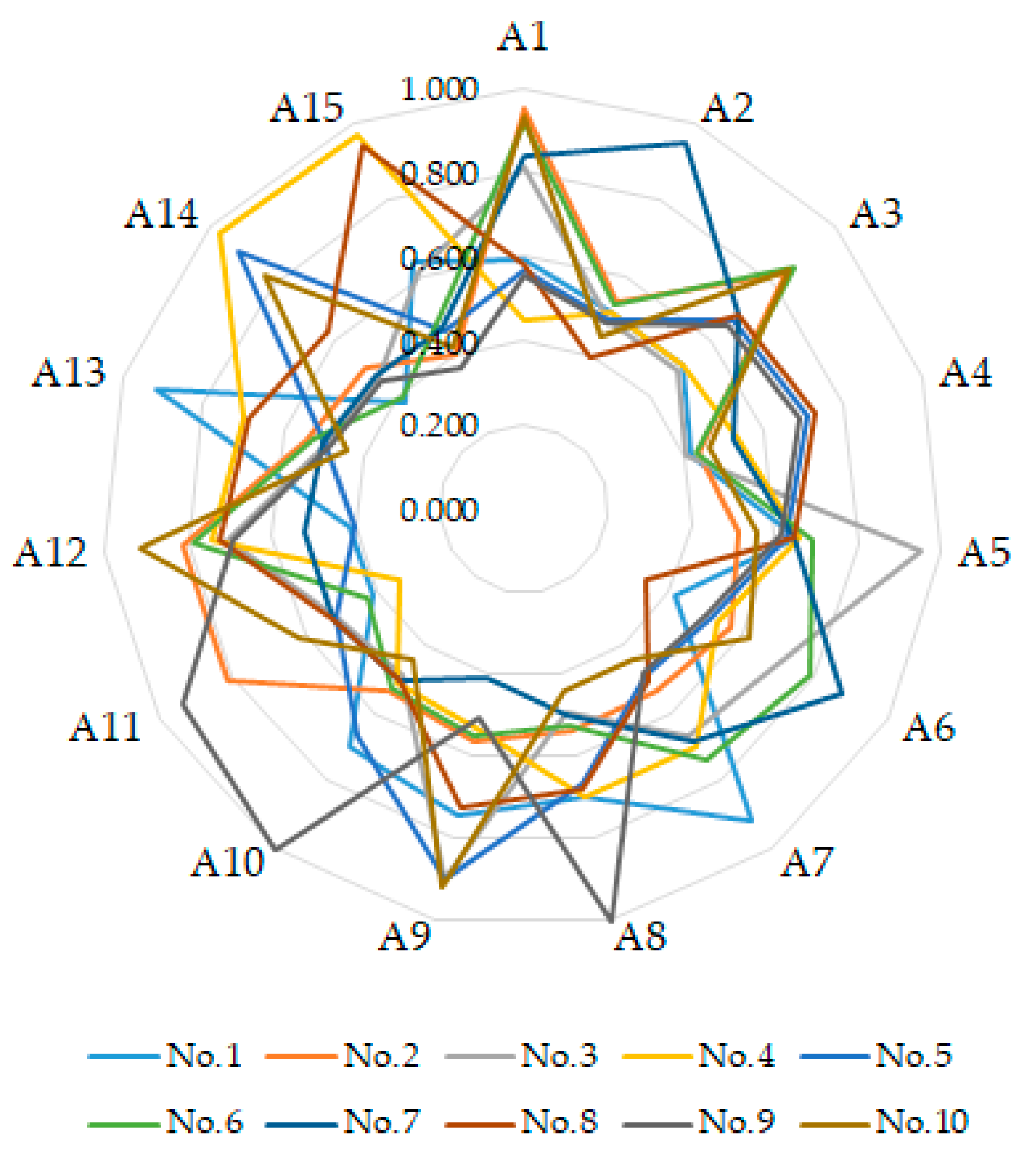
| No. | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.590 | 0.510 | 0.510 | 0.416 | 0.652 | 0.416 | 0.918 | 0.701 | 0.747 | 0.701 | 0.416 | 0.416 | 0.918 | 0.381 | 0.641 |
| 2 | 0.949 | 0.539 | 0.836 | 0.435 | 0.515 | 0.567 | 0.539 | 0.539 | 0.567 | 0.539 | 0.812 | 0.812 | 0.539 | 0.503 | 0.397 |
| 3 | 0.812 | 0.492 | 0.492 | 0.404 | 0.949 | 0.710 | 0.668 | 0.492 | 0.903 | 0.492 | 0.515 | 0.710 | 0.492 | 0.462 | 0.613 |
| 4 | 0.449 | 0.510 | 0.510 | 0.534 | 0.660 | 0.534 | 0.701 | 0.701 | 0.534 | 0.510 | 0.340 | 0.747 | 0.701 | 0.974 | 0.974 |
| 5 | 0.567 | 0.492 | 0.668 | 0.710 | 0.630 | 0.515 | 0.492 | 0.668 | 0.903 | 0.668 | 0.515 | 0.404 | 0.492 | 0.911 | 0.462 |
| 6 | 0.918 | 0.529 | 0.861 | 0.428 | 0.692 | 0.789 | 0.738 | 0.529 | 0.555 | 0.529 | 0.428 | 0.789 | 0.529 | 0.391 | 0.494 |
| 7 | 0.836 | 0.948 | 0.684 | 0.524 | 0.645 | 0.875 | 0.684 | 0.501 | 0.410 | 0.501 | 0.524 | 0.524 | 0.501 | 0.470 | 0.470 |
| 8 | 0.578 | 0.395 | 0.684 | 0.728 | 0.645 | 0.336 | 0.501 | 0.684 | 0.728 | 0.501 | 0.524 | 0.728 | 0.684 | 0.627 | 0.941 |
| 9 | 0.555 | 0.484 | 0.652 | 0.692 | 0.616 | 0.505 | 0.484 | 1.000 | 0.505 | 1.000 | 0.933 | 0.692 | 0.484 | 0.454 | 0.366 |
| 10 | 0.933 | 0.445 | 0.849 | 0.464 | 0.555 | 0.616 | 0.445 | 0.445 | 0.918 | 0.445 | 0.616 | 0.918 | 0.445 | 0.830 | 0.420 |
| Factor | Correlation Degree | Rank | Factor | Correlation Degree | Rank | Factor | Correlation Degree | Rank |
|---|---|---|---|---|---|---|---|---|
| A1 | 0.719 | 1 | A6 | 0.586 | 10 | A11 | 0.562 | 13 |
| A2 | 0.535 | 14 | A7 | 0.617 | 7 | A12 | 0.674 | 4 |
| A3 | 0.675 | 3 | A8 | 0.626 | 6 | A13 | 0.579 | 11 |
| A4 | 0.534 | 15 | A9 | 0.677 | 2 | A14 | 0.600 | 8 |
| A5 | 0.656 | 5 | A10 | 0.589 | 9 | A15 | 0.578 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhu, J.; Shi, J.; Wang, S. What Are the Key Factors Influencing the Water Price in Interbasin Water Transfer Projects? An Integrated Fuzzy Decision-Making Trial and Evaluation Laboratory (DEMATEL)–Interpretive Structural Model (ISM)–Grey Relational Analysis (GRA) Method. Water 2025, 17, 2022. https://doi.org/10.3390/w17132022
Wang J, Zhu J, Shi J, Wang S. What Are the Key Factors Influencing the Water Price in Interbasin Water Transfer Projects? An Integrated Fuzzy Decision-Making Trial and Evaluation Laboratory (DEMATEL)–Interpretive Structural Model (ISM)–Grey Relational Analysis (GRA) Method. Water. 2025; 17(13):2022. https://doi.org/10.3390/w17132022
Chicago/Turabian StyleWang, Jiangrui, Jiwei Zhu, Jiawei Shi, and Siqi Wang. 2025. "What Are the Key Factors Influencing the Water Price in Interbasin Water Transfer Projects? An Integrated Fuzzy Decision-Making Trial and Evaluation Laboratory (DEMATEL)–Interpretive Structural Model (ISM)–Grey Relational Analysis (GRA) Method" Water 17, no. 13: 2022. https://doi.org/10.3390/w17132022
APA StyleWang, J., Zhu, J., Shi, J., & Wang, S. (2025). What Are the Key Factors Influencing the Water Price in Interbasin Water Transfer Projects? An Integrated Fuzzy Decision-Making Trial and Evaluation Laboratory (DEMATEL)–Interpretive Structural Model (ISM)–Grey Relational Analysis (GRA) Method. Water, 17(13), 2022. https://doi.org/10.3390/w17132022








