Analysis of the Energy Loss Characteristics of a Francis Turbine Under Off-Design Conditions with Sand-Laden Flow Based on Entropy Generation Theory
Abstract
1. Introduction
2. Numerical Methodology
2.1. Solid–Liquid Two-Phase Flow Equations
2.2. Turbulence Model
2.3. Entropy Generation Theory
3. Geometric and Physical Models and Boundary Conditions
3.1. Three-Dimensional Water Model
3.2. Mesh Generation and Grid Independence Verification
3.3. Boundary Conditions
3.4. Comparison Validation
4. Results of Sediment-Laden Flow Simulations
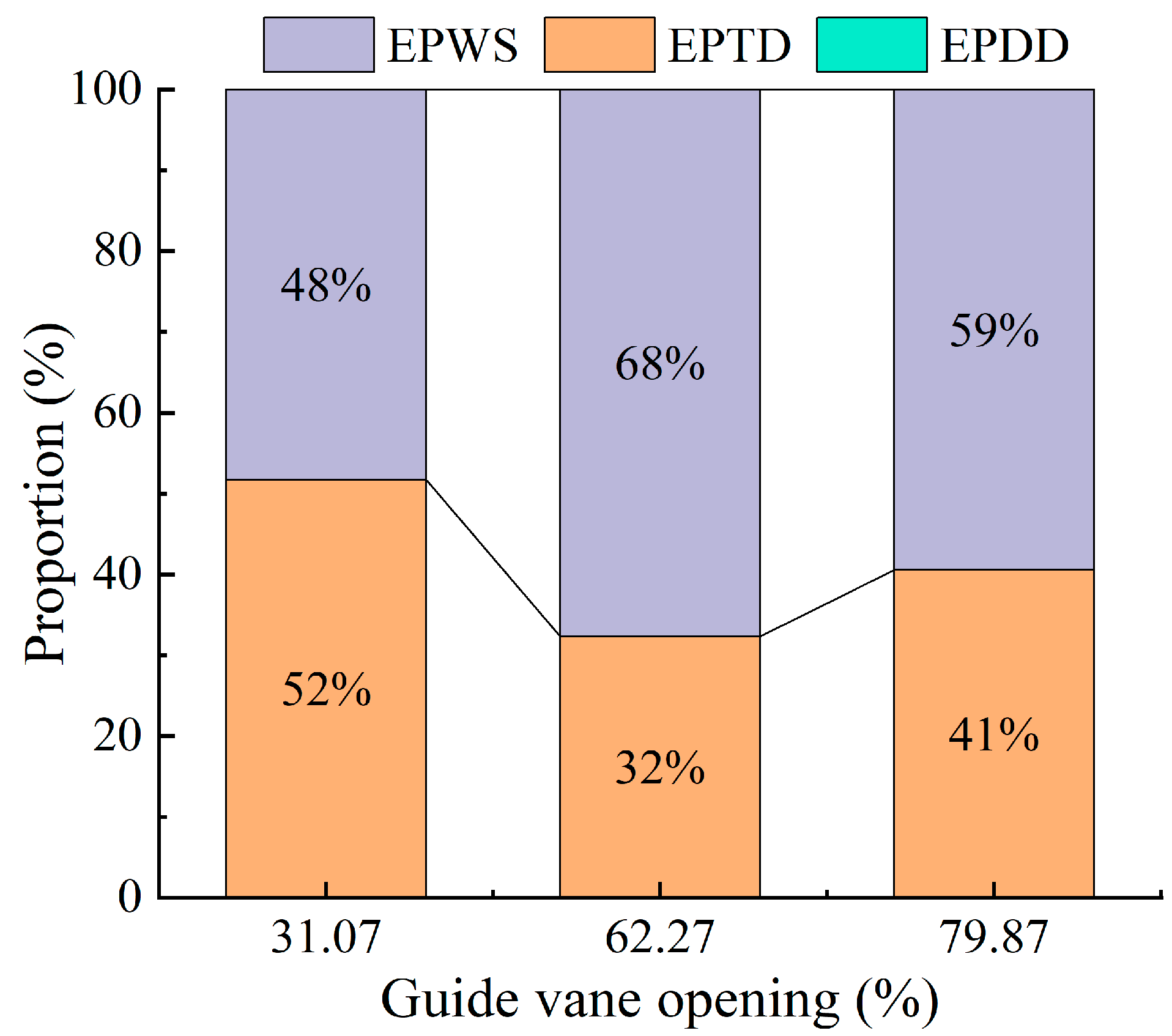
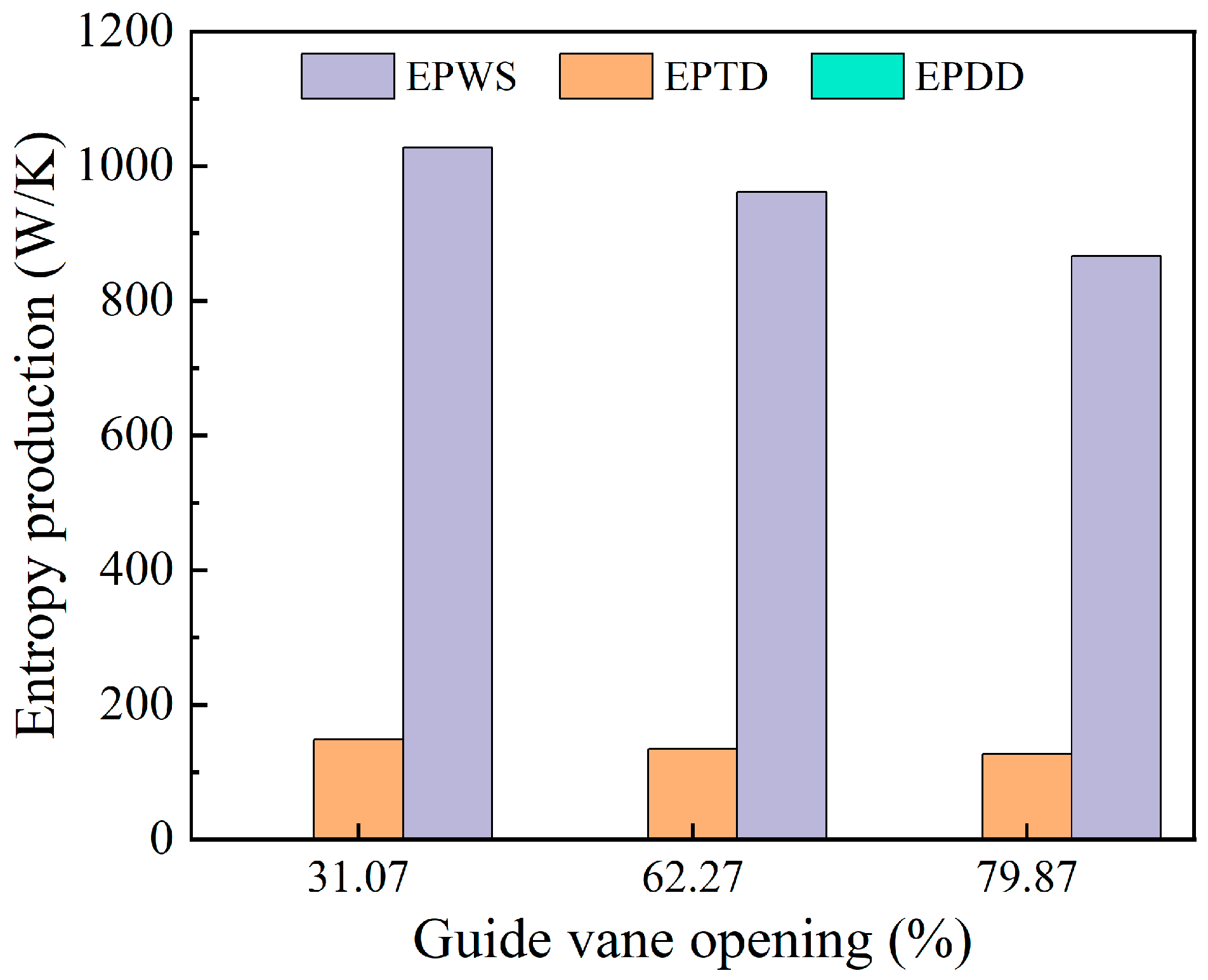
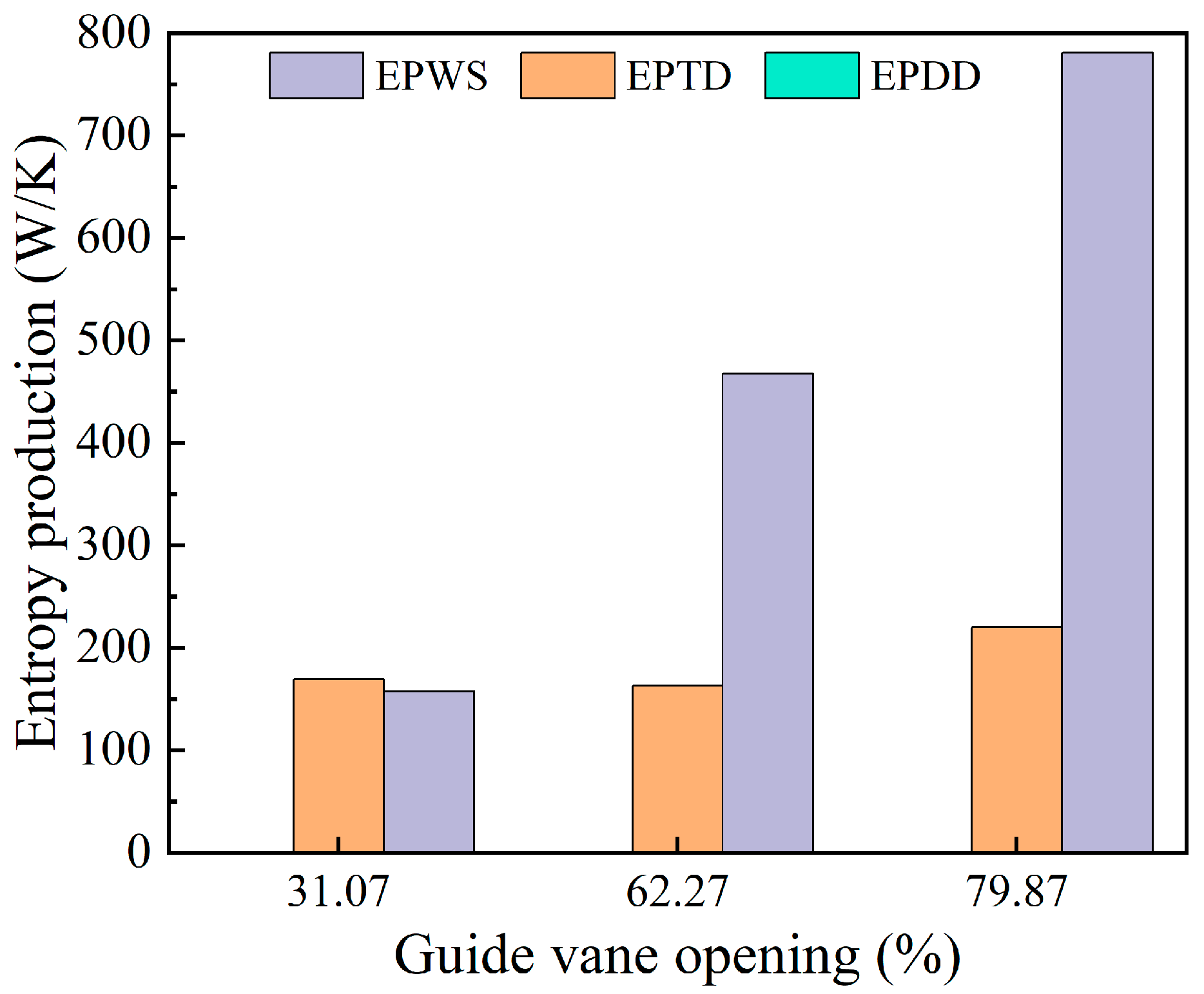
4.1. Entropy Generation Characteristics
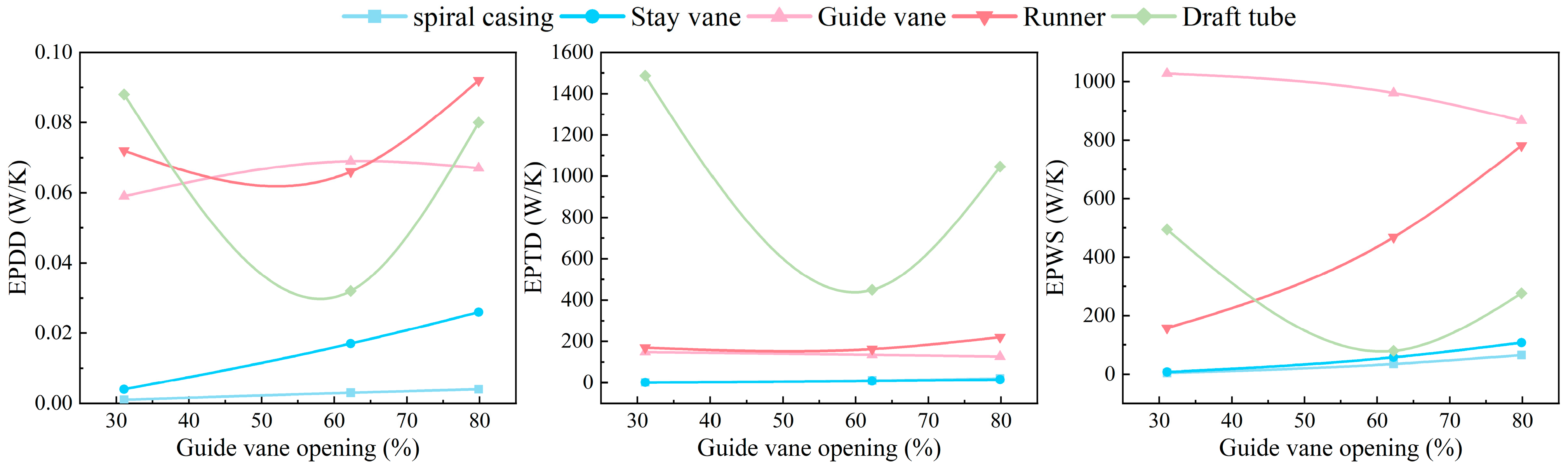
4.2. Energy Loss Analysis of the Key Flow-Passing Components
4.2.1. Energy Loss in the Spiral Casing and Stay Vanes
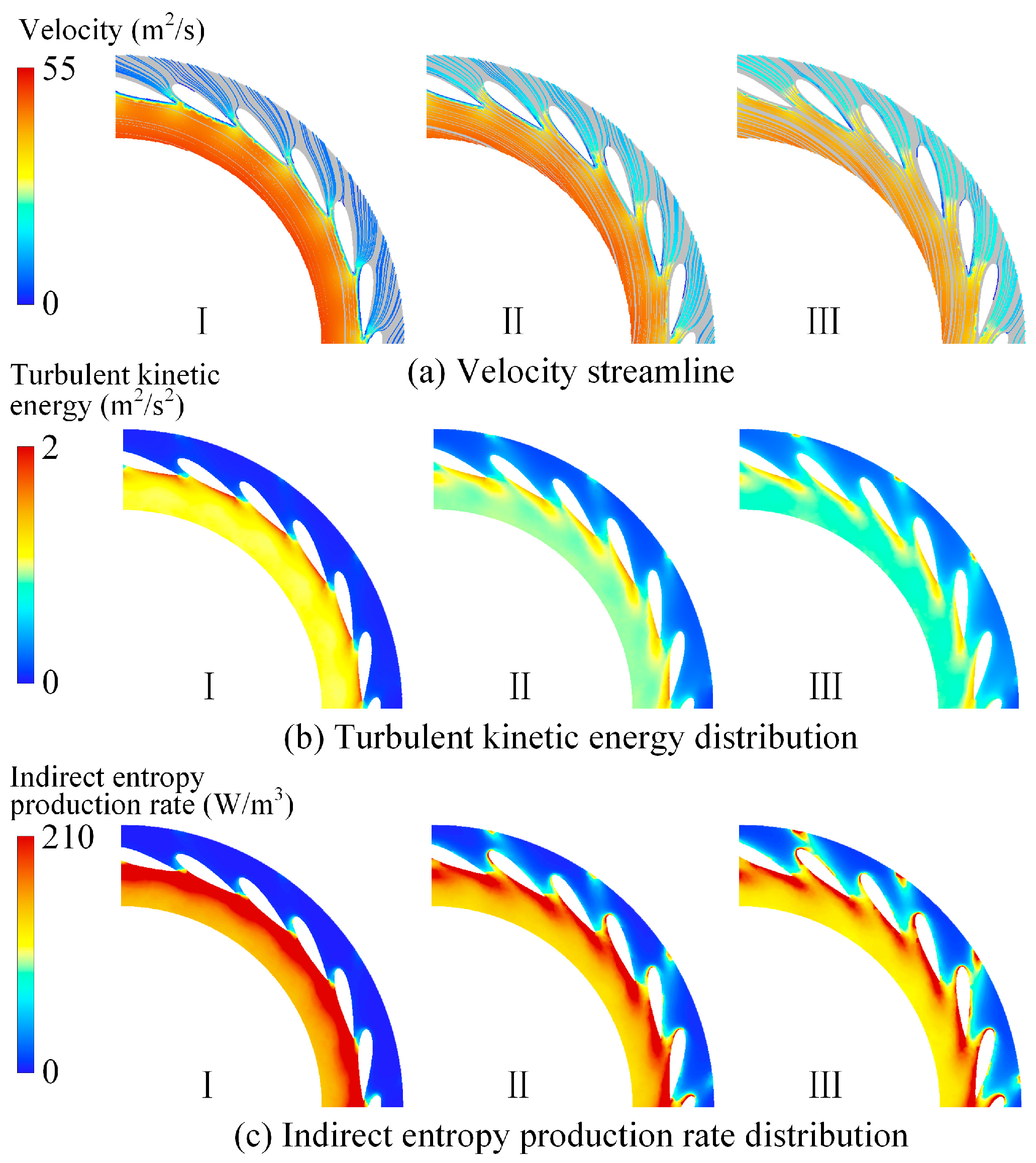
4.2.2. Energy Loss in Guide Vanes
4.2.3. Energy Loss in the Runner
4.2.4. Energy Loss in the Draft Tube
5. Conclusions
- (1)
- Under varying guide vane openings, indirect entropy generation and wall-related entropy generation are the dominant contributors to the total energy loss, whereas direct entropy generation accounts for less than 1% of the total energy loss. Indirect entropy generation is primarily concentrated in the draft tube, whereas wall-related entropy generation is mainly distributed in the near-wall regions of the guide vanes, runner, and draft tube.
- (2)
- The total indirect entropy generation exhibits a non-monotonic trend, initially decreasing and then increasing with an increasing guide vane opening. This variation is mainly governed by the flow regime in the draft tube: at small openings, reduced vortices near the walls of the conical diffuser result in lower entropy generation, while at large openings, intensified secondary vortices in the elbow section cause entropy to rise again. The total wall entropy generation also exhibits a non-monotonic trend, first increasing and then decreasing, which is attributed to the rising shear stress from the velocity gradients on the runner blade surfaces and the nonlinear variation in the shear stress along the draft tube walls. In contrast, wall entropy generation in the guide vanes is relatively less affected by the change in the opening.
- (3)
- With an increasing guide vane opening, the entropy generation in the spiral casing and stay vane region tends to increase, that in the adjustable guide vane region tends to decrease, that in the runner region tends to increase, and that in the draft tube region tends to first decrease and then increase.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, X. Studies of Solid-liquid Two-phase Turbulent Flows and Wear in Hydraulic Turbomachinery. J. Hydrodyn. 1996, 6, 606–609. [Google Scholar]
- Liu, X.; Zeng, Y.; Hua, H.; Yu, Z.; Pang, J.; Tian, C.A. Study on sediment abrasion of turbine runner blades in Yuzixi hydropower station. J. Xihua Univ. (Nat. Sci. Ed.) 2020, 39, 67–73. [Google Scholar]
- Wei, X.-Y.; Pei, J.; Wang, W.-Q.; Yu, Z.-F. Numerical study on sediment erosion characteristics of Francis turbine runner. Eng. Fail. Anal. 2024, 161, 108270. [Google Scholar] [CrossRef]
- Shrestha, R.; Gurung, P.; Chitrakar, S.; Thapa, B.; Neopane, H.P.; Guo, Z.; Qian, Z. Review on experimental investigation of sediment erosion in hydraulic turbines. Front. Mech. Eng. 2024, 10, 1526120. [Google Scholar] [CrossRef]
- Pang, J.; Liu, H.; Liu, X.; Yang, H.; Peng, Y.; Zeng, Y.; Yu, Z. Study on sediment erosion of high head Francis turbine runner in Minjiang River basin. Renew. Energy 2022, 192, 849–858. [Google Scholar] [CrossRef]
- Thapa, B.S.; Dahlhaug, O.G.; Thapa, B. Sediment erosion in hydro turbines and its effect on the flow around guide vanes of Francis turbine. Renew. Sustain. Energy Rev. 2015, 49, 1100–1113. [Google Scholar] [CrossRef]
- Yang, J.; Peng, C.; Li, C.; Liu, X.; Liu, J.; Wang, Z. Design and verification of Francis turbine working in sand laden hydro-power plant. Renew. Energy 2023, 207, 40–46. [Google Scholar] [CrossRef]
- Wang, H.; Pang, J.; Liu, X.; Zhou, Z.; Gang, Y.; Lai, Z.; Wang, J.; Qin, B. Analysis on cause of erosion of guide vane of high-head Francis turbine in sandy river. Energy Sci. Eng. 2024, 12, 3704–3717. [Google Scholar] [CrossRef]
- Wang, H.; Pang, J.; Lai, Z.; Li, S.; Jiang, D.; Wang, X.; Xiang, P.; Yao, B.; Zeng, Y.; Liu, X. Influence of guide vane skirt structure on sediment erosion of high-head turbine in high hardness and sandy river. Phys. Fluids 2024, 36, 103317. [Google Scholar] [CrossRef]
- Zhou, Z.; Xu, K.; Gang, Y.; Xiang, W.; Zhang, Z.; Li, Y.; Pang, J.; Liu, X. Design of a single-channel wear test device for the Francis-99 turbine guide mechanism and sediment wear testing. Phys. Fluids 2025, 37, 033346. [Google Scholar] [CrossRef]
- Cruzatty, C.; Jimenez, D.; Valencia, E.; Zambrano, I.; Mora, C.; Luo, X.; Cando, E. A Case Study: Sediment Erosion in Francis Turbines Operated at the San Francisco Hydropower Plant in Ecuador. Energies 2021, 15, 8. [Google Scholar] [CrossRef]
- Gautam, S.; Acharya, N.; Lama, R.; Chitrakar, S.; Neopane, H.P.; Zhu, B.; Dahlhaug, O.G. Numerical and experimental investigation of erosive wear in Francis runner blade optimized for sediment laden hydropower projects in Nepal. Sustain. Energy Technol. Assess. 2022, 51, 101954. [Google Scholar] [CrossRef]
- Zhou, Z.; Xiang, P.; Xu, K.; Liu, J.; Gang, Y.; Wang, H.; Pang, J.; Liu, X. Effect of Sand Particle Size on Sand-Water Flow in a Francis-99 Distributor. Energy Sci. Eng. 2025. [Google Scholar] [CrossRef]
- Gong, R.; Wang, H.; Chen, L.; Li, D.; Zhang, H.; Wei, X. Application of entropy production theory to hydro-turbine hydraulic analysis. Sci. China Technol. Sci. 2013, 56, 1636–1643. [Google Scholar] [CrossRef]
- Zhou, L.; Hang, J.; Bai, L.; Krzemianowski, Z.; El-Emam, M.A.; Yasser, E.; Agarwal, R. Application of entropy production theory for energy losses and other investigation in pumps and turbines: A review. Appl. Energy 2022, 318, 119211. [Google Scholar] [CrossRef]
- Liu, K.; Liu, H.; Qu, L.; Liu, D.; Chi, F.; Kan, K.; Zhou, D. Analysis of Hydraulic Loss Characteristics of Francis Turbine Based on Entropy Production Theory. Water Resour. Power 2024, 42, 157–161. [Google Scholar]
- Yu, A.; Tang, Y.; Tang, Q.; Cai, J.; Zhao, L.; Ge, X. Energy analysis of Francis turbine for various mass flow rate conditions based on entropy production theory. Renew. Energy 2022, 183, 447–458. [Google Scholar] [CrossRef]
- Yu, Z.F.; Wang, W.Q.; Yan, Y.; Liu, X.S. Energy loss evaluation in a Francis turbine under overall operating conditions using entropy production method. Renew. Energy 2021, 169, 982–999. [Google Scholar] [CrossRef]
- Ahn, S.H.; Tian, H.; Cao, J.; Duo, W.; Wang, Z.; Cui, J.; Li, Y.; Huang, G.; Yu, Y. Hydraulic performances of a bulb turbine with full field reservoir model based on entropy production analysis. Renew. Energy 2023, 211, 347–360. [Google Scholar] [CrossRef]
- Wang, X.; Yan, Y.; Wang, W.Q.; Hu, Z.P. Evaluating energy loss with the entropy production theory: A case study of a micro horizontal axis river ducted turbine. Energy Convers. Manag. 2023, 276, 116553. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, H.; Xia, X.; Li, X.; Zuo, Q.; Xie, B.; Chen, W. Optimization of a radial inflow turbine rotor with splitter blades based on entropy production theory and artificial neural network. Appl. Therm. Eng. 2024, 252, 123759. [Google Scholar] [CrossRef]
- Liang, A.; Li, H.; Zhang, W.; Yao, Z.; Zhu, B.; Wang, F. Study on pressure fluctuation and rotating stall characteristics in the vaneless space of a pump-turbine in pump mode. J. Energy Storage 2024, 94, 112385. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2003, 47, 2205–2215. [Google Scholar] [CrossRef]
- Mathieu, J.; Scott, J. An Introduction to Turbulent Flow; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 2012, 32, 1598–1605. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Hou, H.C.; Xu, C.; He, W.; Li, Z. Application of entropy production method to centrifugal pump energy loss evaluation. J. Drain. Irrig. Mach. Eng. 2017, 35, 277–282, 288. [Google Scholar]
- Lu, J.L.; Wang, L.K.; Liao, W.L.; Zhao, Y.P.; Ji, Q.F. Entropy production analysis for vortex rope of a turbine model. J. Hydraul. Eng. 2019, 50, 233–241. [Google Scholar]
- Kan, K.; Zhang, Q.; Xu, Z.; Chen, H.; Zheng, Y.; Zhou, D.; Binama, M. Runaway characteristics of bidirectional horizontal axial flow pump withsuper low head based on entropy production theory. Trans. Chin. Soc. Agric. Eng. 2021, 37, 49–57. [Google Scholar]
- Duan, L.; Wu, X.; Ji, Z.; Xiong, Z.; Zhuang, J. The flow pattern and entropy generation in an axial inlet cyclone with reflux cone and gaps in the vortex finder. Powder Technol. 2016, 303, 192–202. [Google Scholar] [CrossRef]
- Stern, F.; Wilson, R.V.; Coleman, H.W.; Paterson, E.G. Comprehensive Approach to Verification and Validation of CFD Simulations—Part 1: Methodology and Procedures. J. Fluids Eng. 2001, 123, 793–802. [Google Scholar] [CrossRef]
- Roy, C.J. Grid Convergence Error Analysis for Mixed-Order Numerical Schemes. AIAA J. 2012, 41, 595–604. [Google Scholar] [CrossRef]
- Daniels, S.; Rahat, A.; Tabor, G.; Fieldsend, J.; Everson, R. Shape optimisation of the sharp-heeled Kaplan draft tube: Performance evaluation using Computational Fluid Dynamics. Renew. Energy 2020, 160, 112–126. [Google Scholar] [CrossRef]
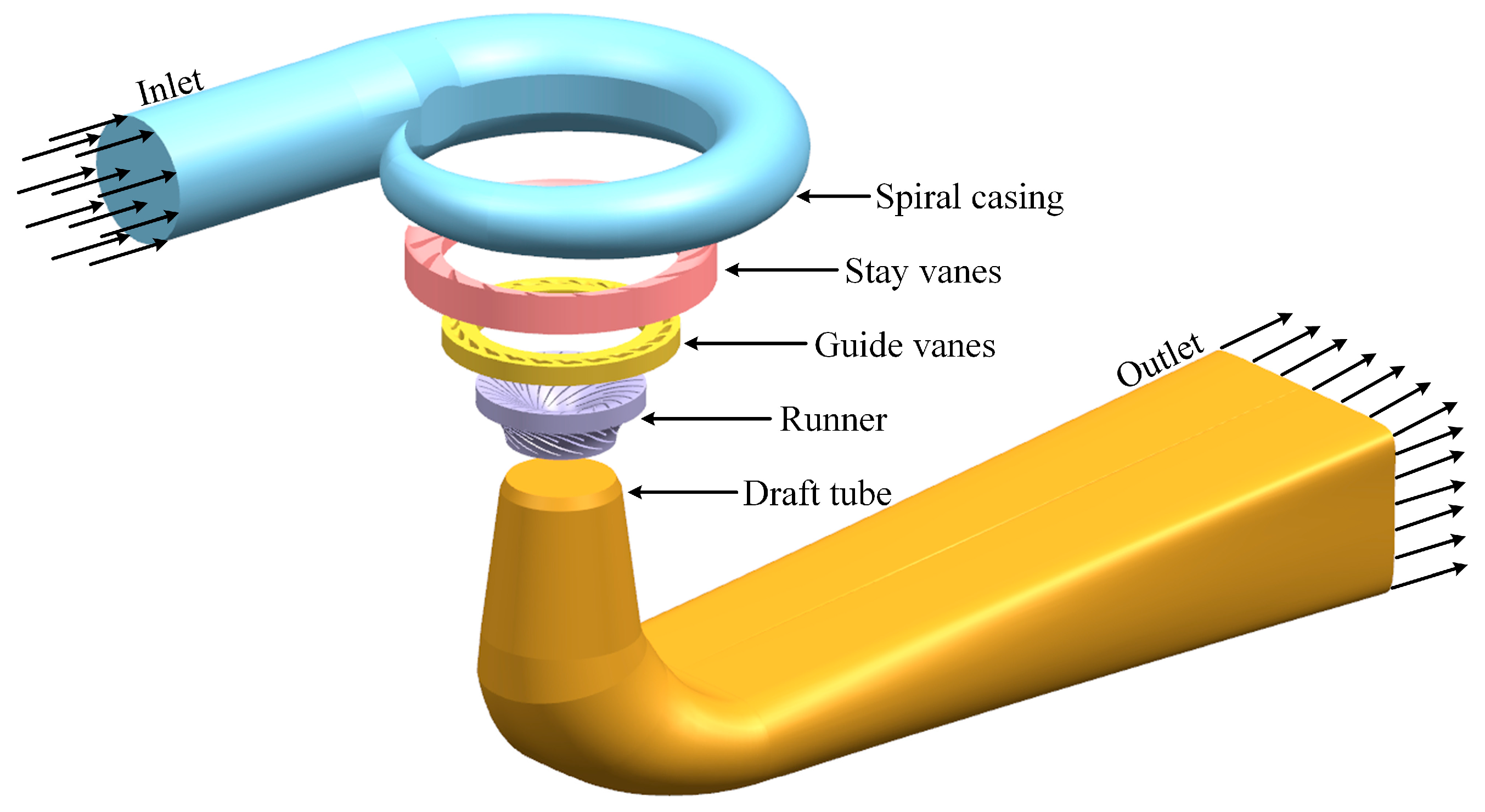






| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Design head (m) | 283 | Design flow (m3/s) | 16 |
| Runner diameter (m) | 0.630 | Rated speed (rpm) | 500 |
| Stay vane | 16 | Guide vane | 24 |
| Runner’s long blade | 15 | Runner’s short blade | 15 |
| Opening I | Opening II | Opening III | ||||
|---|---|---|---|---|---|---|
| Grid Number (×104) | Efficiency (%) | Grid Number (×104) | Efficiency (%) | Grid Number (×104) | Efficiency (%) | |
| G1 | 1739 | 86.6 | 2049 | 95.6 | 1941 | 94.3 |
| G2 | 920 | 86.2 | 925 | 95.3 | 926 | 94.0 |
| G3 | 590 | 82.1 | 572 | 92.7 | 563 | 90.9 |
| Opening | r21 | pr | Fs | GCI | |
|---|---|---|---|---|---|
| I | 0.471 | 1.237 | 15.310 | 1.25 | 0.0237 |
| II | 0.549 | 1.304 | 12.961 | 1.25 | 0.0228 |
| III | 0.523 | 1.280 | 13.691 | 1.25 | 0.0231 |
| Spiral Casing | Stay Vane | Guide Vane | Runner | Draft Tube | |||
|---|---|---|---|---|---|---|---|
| I | II | III | |||||
| Grid number (×104) | 81 | 58 | 252 | 257 | 258 | 206 | 323 |
| Opening | Guide Vane Opening (%) | Power (MW) | Total Pressure Inlet (kPa) | Pressure Outlet (kPa) |
|---|---|---|---|---|
| I | 31.07 | 10 | 2596 | 67.477 |
| II | 62.27 | 30 | 2582 | 67.477 |
| III | 79.87 | 40 | 2571 | 67.477 |
| Opening | I | II | III |
|---|---|---|---|
| Actual | 84.5% | 92.6% | 91.5% |
| Numerical | 86.2% | 95.3% | 94.0% |
| Difference | 2.01% | 2.92% | 2.73% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Xu, K.; Wang, Z.; Xiao, Y.; Xu, Y.; Huang, C.; Pang, J.; Liu, X. Analysis of the Energy Loss Characteristics of a Francis Turbine Under Off-Design Conditions with Sand-Laden Flow Based on Entropy Generation Theory. Water 2025, 17, 2002. https://doi.org/10.3390/w17132002
Lu X, Xu K, Wang Z, Xiao Y, Xu Y, Huang C, Pang J, Liu X. Analysis of the Energy Loss Characteristics of a Francis Turbine Under Off-Design Conditions with Sand-Laden Flow Based on Entropy Generation Theory. Water. 2025; 17(13):2002. https://doi.org/10.3390/w17132002
Chicago/Turabian StyleLu, Xudong, Kang Xu, Zhongquan Wang, Yu Xiao, Yaogang Xu, Changjiu Huang, Jiayang Pang, and Xiaobing Liu. 2025. "Analysis of the Energy Loss Characteristics of a Francis Turbine Under Off-Design Conditions with Sand-Laden Flow Based on Entropy Generation Theory" Water 17, no. 13: 2002. https://doi.org/10.3390/w17132002
APA StyleLu, X., Xu, K., Wang, Z., Xiao, Y., Xu, Y., Huang, C., Pang, J., & Liu, X. (2025). Analysis of the Energy Loss Characteristics of a Francis Turbine Under Off-Design Conditions with Sand-Laden Flow Based on Entropy Generation Theory. Water, 17(13), 2002. https://doi.org/10.3390/w17132002






