Abstract
Detection and analysis of hydroclimatic trends are crucial for quantifying climate change, global warming, and their potential impacts. This study investigates hydroclimatic trends over the South African Sugar Belt (SASB) under a changing climate using nonparametric and innovative trend detection techniques for the periods 1980–2022, 2025–2050, and 2050–2080. Statistical tests, including the original and modified Mann–Kendall test, sequential Mann–Kendall test, and Innovative Trend Analysis were performed to detect trends and changes in hydroclimatic variables over the SASB’s dryland and irrigated regions. An 18-month low-pass filter was applied to 19 GCMs of the CMIP6, which were downscaled to a local setting. The results indicate contrasting rainfall trends: a positive trend in the dryland region and a negative trend in the irrigated region from 1980 to 2022. Under low- (SSP2–4.5) and high-emission (SSP5–8.5) scenarios, both regions exhibited a significant drying trend from 1980 to 2080, with the irrigated region drying and warming faster than the dryland region. Mann–Kendall tests and Innovative Trend Analysis revealed robust positive trends in surface air temperatures across the SASB, with even stronger trends projected for the future, potentially promoting water loss in the area. Compound dry–hot events were also projected to cause significant socioeconomic impacts in the near and distant future. Future studies can explore nonparametric and monotonic trend detection and analysis for water quality parameters in the SASB under a changing climate.
1. Introduction
Trend analysis is fundamental for investigating the temporal behaviour of a variable, allowing researchers to identify increasing, decreasing, or stationary patterns. Climate analysis, meanwhile, is critical for determining the adaptation strategies and understanding the dynamics of crop production, such as sugarcane [1], to establish climate change resilience. While some studies have focused on analysing climate trends over historical periods [2,3], few studies have explored future climate projections [4,5]. Although observed climate trends are vital for revealing patterns, projecting and monitoring future climate trends are equally crucial for weather- and climate-sensitive sectors such as water resources management, crop production, and public health.
Indeed, global warming is affecting several social, environmental, and economic sectors worldwide [6,7,8,9,10]. Evidence of global warming and climate change, and their impacts on these sectors, underscores the significance of climate monitoring and projections. Global warming and climate change can arise from both natural and anthropogenic forcings worldwide. Global warming and climate change are normally used interchangeably, while global warming only relates to a single aspect of climate change [6]. Global warming is defined according to increased mean global surface temperature compared to that during the 1850–1900 pre-industrial era [11]. While the rise in global temperature is largely attributed to Greenhouse Gas (GHG) emissions, climate change is more expansive, encompassing shifts in climate patterns and associated earth system responses. The Intergovernmental Panel on Climate Change [12] defines climate change as “a change in the state of the climate that can be identified by changes in the means and variations in its properties, that occurs for longer period of time”. Specifically, these changes specifically manifest as shifts in temperature, precipitation, wind patterns, sea level rise, and the frequency and intensity of extreme weather and climate events [6]. Such extreme events include heatwaves, tropical cyclones, wildfires, droughts, and floods. Most of these events are mainly induced by extreme precipitation, extreme temperatures, or a combination of both.
Marengo et al. [13] indicate an upward trend in annual rainfall in Brazil, which is mainly attributed to the frequent occurrence of extreme rainfall events. Also, dos Santos et al. [14] observed positive trends for minimum and maximum temperatures, which concurred with statistically insignificant rainfall trends over Nebraska.
Surface air temperature increases of 0.02 and 0.03 °C/yr were observed in South Africa [2,4]. These trends corresponded with weak rainfall and vegetation fraction trends over the country, except for the east coast plains [2,4]. Moisture distribution indicates a steep gradient from west to east in South Africa, but strong drying trends are noticeable around the winter rainfall region [4]. Furthermore, Kruger and Nxumalo [2] projected disparate rainfall trends over the west and east of South Africa, e.g., an increase in the west and a decrease in the east. In contrast, projected rainfall characteristics are different from the observed characteristics. Hence, accurate climate projections are important for decision-making, preparedness, and climate change resilience, especially for local water management, health hazards, and crop production.
The uptake of technological advancements in the South African highlands has led to increased maize yields [15], while declining sugarcane yields are also evident in the lowland regions [16,17,18]. It can be noted that climate change is likely to accelerate water loss through enhanced potential evapotranspiration, which will consequently contribute to low streamflow and river run-off [19,20]. Water stress and drought conditions also suppress annual sugarcane yield in the southeast lowland regions [16]. Furthermore, rainfall and surface air temperatures are key determinants of economic crop production, such as sugarcane in South Africa [16] and other developing countries. It can be noted that some nations can afford sustainable crop production through artificial rainfall enhancement methods like cloud seeding [21], while others cannot afford the cost. Sufficient rainfall is required for optimal harvests in the growing season. Different studies have argued about the different amounts of annual rainfall (e.g., 800 mm/yr) required for sugarcane production per growing season [22,23]. Yet rainfall trends, patterns, and general characteristics are chiefly affected by climate variability and change. Therefore, the downscaling of Global Climate Models (GCMs) into more local regions where the manifest impacts of climate variability and change are imperative for informed planning, management, and decision-making within climate-dependent sectors is key. In this study, 19 GCMs of the Sixth Coupled Model Intercomparison Project (CMIP6) were examined and downscaled into a local context to uncover hydroclimatic trends in the SASB.
This study aims to detect and analyse observed and simulated hydroclimatic trends using nonparametric and innovative trend detection techniques under a changing climate over the SASB. The periods considered are 1980–2022 (historical), 2025–2050 (near-future projections), and 2050–2080 (far-future projections).
2. Study Area and Methodology
2.1. Description of Study Area
The SASB, extending approximately from 23 to 31° S and 28 to 32.5° E, is characterised by diverse land use types and livelihoods, including vegetation, water bodies, and crop and livestock production. Within this region, large-scale and small-scale sugarcane farmers primarily grow sugarcane for sugar production. This critical agricultural region is highly vulnerable to climate variability and change, which reduces water availability and consequently impacts annual sugarcane yields [16]. The southern African vegetation fraction drops from east–west following rainfall characteristics [24]. In the study area, the Normalised Difference Vegetation Index (NDVI) spectrum ranges between 0.2 and 0.8, but vegetation fraction equal to or greater than 0.6 is predominant [16]. As shown in Figure 1a, monthly mean precipitation over the SASB can reach up to 100 mm/month. A notable spatial difference can be observed, with the irrigated region (e.g., 26.8° S and 31.5° E) appearing wetter than the dryland region (e.g., 30.5° S and 30.9° E) from December to May. This may be partially attributed to rainfall-bearing mechanisms such as tropical cyclogenesis, active over the Mozambique Channel. Despite these heterogeneous seasonal rainfall characteristics between the dryland and irrigated regions of the SASB, the cloud cover fraction (CCF) remains uniform (50%) across the area (Figure 1a,b). A high CCF (50%) was observed over the east coast of South Africa, while a steady decrease was observed from east–west in South Africa (Figure 1b). These meteorological conditions favour sugarcane cultivation, especially in the lowland regions of the country. The top sugarcane-producing provinces in South Africa are KwaZulu-Natal (KZN) and Mpumalanga. However, parts of other provinces (e.g., Limpopo and Eastern Cape) with CCFs of 50% also have minimal contributions towards annual sugarcane yield in the country.
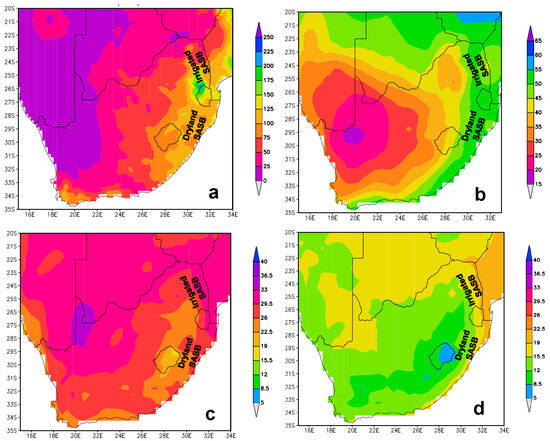
Figure 1.
Characteristics of December to May climate over SASB where data was area-averaged for this study. (a) CHIRPS rainfall (mm/month), (b) Climatic Research Unit Time Series version 4.08 (CRU TS4.08) cloud fraction (%), (c) CRU TS4.08 Tmax (°C), and (d) CRU TS4.08 Tmin (°C).
The SASB is also characterised by strong temperature gradients of maximum (Tmax) and minimum (Tmin) temperatures from the coast moving inland (Figure 1c,d). During December to May the irrigated region of the SASB records high Tmax and Tmin values, averaging 30 °C and 18 °C, respectively. For the broader study area, the mean Tmax is 25 °C while the mean Tmin is 15°C in the study area from December to May (Figure 1c,d). Although the irrigated region receives sufficient monthly rainfall (100 mm/month; Figure 1a), scorching surface temperatures could accelerate potential evapotranspiration. In contrast, the inland advancement of the sea-breeze and onshore flow bring cool weather conditions in parts of the dryland region, especially Mount Edgecombe, Greater Durban, KZN.
2.2. Data and Methods
Climate Hazards group InfraRed Precipitation with Stations (CHIRPS) is a recent high-resolution (0.05°) rainfall dataset that is almost globally available since it covers 50° N to 50° S and across all longitudes [25]. The CHIRPS dataset is particularly suitable for monitoring global climate change and agricultural drought over land [25]. In this study, the CHIRPS rainfall dataset was employed to characterise the mean climate of the study area and for the detection of observed rainfall trends. The Climatic Research Unit gridded Time Series (CRU TS4.08) [26], was used for CCF (%) and temperature analyses (e.g., mean temperatures, Tmax, and Tmin). Surface water levels (SWLs) for the Klipfontein and Nooigedacht Dams were obtained from South African National Department of Water and Sanitation. In this study, 19 GCMs of CMIP6 were locally downscaled to project future climate change and its socioeconomic consequences through innovative and nonparametric trend detection techniques over the SASB. Table 1 below provides details of the GCMs of CMIP6 used in this study. Some of these models were previously used in Africa and elsewhere [5,27,28]. We employed statistical downscaling, which is a robust technique used to assess the relationship between large- and local-scale climate parameters [28]. This technique also allows for the downscaling of GCM projections to local or regional scales, e.g., the SASB in this case. Both the observed and simulated data for rainfall and temperature were derived from the Royal Netherlands Meteorological Institute (KNMI) Climate Explorer.

Table 1.
Description of CMIP6 GCMs used in this study. More details at https://wcrp-cmip.org/cmip-model-and-experiment-documentation/#models (accessed on 12 March 2025).
Future climate change was projected using representative low and high Shared Socioeconomic Pathways (SSPs; SSP2–4.5 and SSP5–8.5). This was imperative in the quest for Climate Action (Sustainable Development Goal [SDG] 13) in the SASB. Like other hydroclimatic fields, SSP2–4.5 and SSP5–8.5 were accessed through the KNMI Climate Explorer for the periods 1980–2022, 2025–2050, and 2050–2080. An 18-month low-pass filter was applied to the mean ensemble of these 19 GCMs of CMIP6 in order to remove seasonal cycles [29]. Specific details about the GCMs used in this study are available on the CMIP6 webpage (https://wcrp-cmip.org/cmip-model-and-experiment-documentation/#models (accessed on 12 March 2025)). We evaluated the relationship between the observed and projected rainfall, while both surface air temperature and rainfall were considered for trend detection, which was a focus of this study. Our study area (dryland and irrigated regions of the SASB) is partially gauged with hydrological stations, which do not measure meteorological components. For model performance evaluation, we used rainfall measurements from station-based (Global Precipitation Climatology Centre version 8 [GPCC8]), CRU TS4, and satellite products (CHIRPS). Due to sparse meteorological observations in our study area, we used PGCC8, CRU TS4, and CHIRPS data as “targets” for prediction. However, the model outputs from PGCC8 and CRU TS4 were statistically insignificant and not reported in this study. Additionally, since observed and projected rainfall had different units of measurement, both were expressed as novel standardised MAP values (see Figure A1). In addition, Multivariate Linear Regression (MLR) was employed to predict rainfall, and the equation for this is shown below
where is the dependent variable (observed rainfall) and the values are the independent variables, projected rainfall from SSP2-4.5 and SSP5-8.5. is the intercept from the model summary output, while , … are coefficients of the terms and denotes the standard error. MLR described the relationship between the dependent variable (“target”) and one or more independent variables. We also showed the comparison between observed and projected rainfall through correlation (), mean absolute error (), mean square error (), and root mean square error (), based on the following equations:
Note that represents the simulation time in years, is the total number of simulation years, is the calibration point , is the observed MAP at location at year , denotes the long-term mean of the observed MAP at location for the simulation period, and is the simulated MAP at location at year . values equal to 1 indicate an accurate model, while and must be low, e.g., close to 0, to indicate an accurate model. In some instances, values of 0.2 and 0.5 also demonstrate relatively accurate models. The validation period was between 1981 and 2022 because CHIRPS data is available from 1981 [25]. Whilst we intended to test CHIRPS data (which is recent and quasi-global) in our study area, it was also imperative to use well-documented datasets such as PGCC8 and CRU TS4. It can be noted that GCMs, PGCC8, and CRU TS4 data have a coarse scale (180° W–180° E and 60° N–60° S), while CHIRPS data is quasi-global (50° N–50° S) across all longitudes. Hence, we downscaled them into a fine scale of 1 × 1 grid points over dryland (30.5° S and 30.9° E) and irrigated (26.8° S and 31.5° E) regions of the SASB.
It is important to note that GCMs and Regional Climate Models (RCMs) inherently contain uncertainties and biases [30]. To address these challenges and analyse trends, the modified Mann–Kendall (mmky1lag) test and Innovative Trend Analysis (ITA) were employed in this study. The Mann–Kendall Trend Test (MKTT) is a nonparametric rank-based technique that is used to detect monotonic trends in geophysical time series. This technique is resistant to outliers in a dataset [31,32,33]. Statistics () were calculated as shown below:
and
Note that the average value of statistic is given by and that the variance () can be calculated as shown below:
In Equation (8), above, denotes the number of data points in a tied group and represents the number of tied groups in a time series. Considering the random and independent time series, statistic can be assumed to be normally distributed [34], and the statistic is given by the following equation:
To relate the Kendall tau () and statistic , the following equation is used:
Note that is expressed as
Rainfall, temperature, Palmer Drought Severity Index (PDSI), and SWL trends were tested at a 95% confidence level, and the null hypothesis (e.g., no trend) was rejected if threshold. The modified MKTT was performed in R software version 4.4.2, following the relevant codes. Innovative Trend Analysis (ITA) was used in conjunction with the Modified MKTT in order to increase confidence in the results obtained in this study.
Here, the mmky1lag function for the modified MKTT, version 1.6, was used in this study. This version considers serially correlated data that involves a variance correction approach through using the lag-1 correlation coefficient only [33]. Through this approach, statistics and p-value are recalculated based on corrected and old variances; hence, such robust techniques were desired for this type of research. It can be noted that the modified MKTT and ITA provided useful characteristics of hydroclimatic trends. Those characteristics are magnitude, strength, and direction, but both the modified MKTT and ITA do not indicate when trend changes start and/or end. Therefore, a sequential MKTT was applied to locate potential trend turning points (PTTPs; trend changes). The sequential MKTT uses forward/prograde ) time series and backward/retrograde time series on the same plot to quantify trend characteristics [34]. A PTTP is identified if the intersection between the prograde and retrograde trends is TRUE [34], but the significance of the PTTP is only declared if they diverge beyond threshold. On the other hand, to compare cases of , these are normally counted and represented by so that statistic can be calculated from Equation (12), below:
The variance and mean of are calculated using Equations (13) and (14) below.
Notably, standardised magnitudes of ) are calculated with Equation (15).
3. Results and Discussion
3.1. MKTT and ITA Statistics
Table 2 reveals statistically insignificant rainfall trends over both dryland and irrigated regions of the SASB from 1980 to 2022. These are indicated by statistics of and with at the 95% confidence level over the dryland and irrigated regions, respectively. Further, these weak drying trends over the irrigated region of the SASB (Table 2) concur with the findings of previous studies [35]. Surface air temperatures have a robust positive/upward trend (e.g., ) in both the dryland and irrigated regions of the SASB. These results coincide with dipping SWLs at Klipfontein Dam and diminishing soil moisture across the SASB (Table 2). Although the characteristics of rainfall trends are statistically insignificant, abrupt surface air temperature increases serve as empirical evidence for global warming and its locally manifested consequences.

Table 2.
MKTT and ITA statistics of historical hydroclimate variables over SASB from 1980 to 2022.
It is surprising to note that the SWL at Nooigedacht Dam exhibits a statistically significant positive trend, which was charaterised by with and at the 95% confidence level. These findings could support the northward expansion of the SASB under a well-monitored irrigation system (Table 2). However, the influences of non-climatic forcings that affect water availability over the irrigated region of the SASB should also be considered for the adequate planning of local water management and crop production. Non-climatic forcings include water transfer schemes (e.g., that increase or reduce SWLs) and water abstraction for domestic and other agricultural use in this area [36]. Table 2 provides the characteristics of the observed hydroclimatic trends from 1980 to 2022. Table 3 below details the characteristics of projected climate change for the periods 1980–2022, 2025–2050, and 2050–2080. The mmky1lag of the modified MKTT employed in this study was superior to the traditional MKTT because it calculated statistics for the variables before and after bias correction. Here, all the projected trends were statistically significant () at the 95% confidence level. Table 3 shows that under the low-emission scenario (e.g., SSP2–4.5), the irrigated region was projected to dry faster (e.g., ) than the dryland region (e.g., ), while under a high-emission scenario (e.g., SSP5–8.5), the dryland region was expected to dry faster (e.g., ) than the irrigated region (e.g., ). These results are consistent before and after bias correction, but the bias correction step was useful for adjusting the overestimation of statistics under improved p-values and corrected variance.

Table 3.
MKTT and ITA statistics for projected climate change from GCMs of CMIP6 for 1980–2080, with 1980–2022 as baseline record.
Both SSP2–4.5 and SSP5–8.5 showed that surface air temperatures are projected to increase at an alarming rate across the SASB (Table 3). These robust positive trends of surface air temperatures are indicated by scores of 14 under both SSP2–4.5 and SSP5–8.5 in both dryland and irrigated regions before bias correction (Table 3). Under both SSP2–4.5 and SSP5–8.5, the dryland region was projected to warm faster than the irrigated region (Table 3). All statistical measures (, slope, and ) are indicative of strong positive temperature trends across the SASB, which also strengthens the empirical evidence of future climate change in this study. Therefore, the observed evidence of climate change necessitates immediate Climate Action, enabling farmers and water managers to make informed decisions effectively. Enhanced surface temperatures, for instance, could accelerate surface and subsurface water loss while potentially lowering groundwater recharge rates, thereby increasing the risk of dry spells and water shortages in the area. To prepare for these impacts, end-users of weather and climate information, such as farmers and water managers, can leverage these bias-corrected and locally downscaled GCM projections. Preparedness includes technological advancements [15], financial considerations, and best management practices that could help farmers and water managers to best cope with climate change. These are crucial for sustainable crop production and water resource management and allocation over the SASB. Sustainable crop production (e.g., sugarcane) and water security are socioeconomic imperatives in South Africa, especially in relation to their proposed downstream sectors such as bioethanol production.
3.2. Observed Hydroclimatic Trends
Six PTTPs were identified, in 1981, 2003, 2006, 2009, 2011, and 2012. However, these PTTPs are statistically insignificant, as they do not diverge beyond threshold of . However, this number of PTTPs signals a strong multiyear rainfall variability over the SASB (Figure 2a,b). Strong year-to-year rainfall fluctuation was more pronounced further inland as compared to in the dryland region, which is located towards the coast (Figure 2a,b). Even when the sequential MKTT was used, rainfall still showed unappreciable trends in the study area, except for in the late 1980s (e.g., 1987, 1988, and 1989). In these years (1987, 1988, and 1989), rainfall maxima up to 2005 were observed, and a weak drying trend became more pronounced across the SASB. The recent drying trend corresponds to a sudden surface air temperature increase in the area (Figure 2a–d). We note that minimal rainfall also coincides with drought years and enhanced surface air temperatures (Figure 2a–d and Figure 3a–d). These climate changes could potentially cause adverse effects on annual sugarcane yield [16] and water availability (Figure 3a–d). As expected, the characteristics of PDSI (Figure 3a,b) closely resemble those of rainfall (Figure 2a,b). This contrasts with SWL trends (Figure 3c,d), which exhibit behaviour largely independent of natural rainfall variability. These observed differences can be attributed to non-climatic forcings that also affect surface water availability.
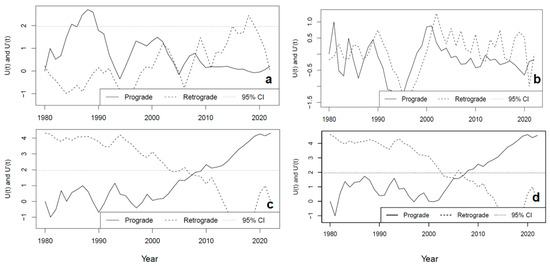
Figure 2.
Observed rainfall and surface air temperature trends over SASB from 1980 to 2022: (a) rainfall over dryland region, (b) rainfall over irrigated region, (c) surface air temperatures over dryland region, (d) surface air temperatures over irrigated region.
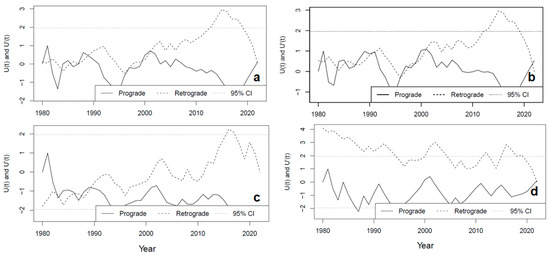
Figure 3.
Observed trends of sampled PDSI and SWL over SASB from 1980 to 2022: (a) PDSI over dryland region, (b) PDSI over irrigated region, (c) SWL at Klipfontein Dam, (d) SWL at Nooigedacht Dam. Klipfontein Dam in dryland region, Nooigedacht Dam located in irrigated region of SASB.
McCarthy and Humphries [36] highlighted these non-climatic forcings of surface water variability in the study area. So, planning and decision-making with respect to local water resource management and allocation in a changing climate can also consider non-climatic forcings. Five PTTPs were identified, in 1983, 1984, 1987, 1988, and 1990, for the SWL of Klipfontein Dam from 1982 to 2022 (Figure 3c), whilst no PTTPs occurred for SWL at Nooigedacht Dam from 1981 to 2022 (Figure 3d). A statistically significant negative trend () was observed in the SWL of Klipfontein Dam (Figure 3c). These results relate to previous studies [34], which reported prolonged drought between 2014 and 2016 in parts of KZN. On the other hand, dropping SWLs in the study area indicate water shortages and consequent adverse effects on agriculture and the public, because water is a social and economic imperative. Local authorities and interested parties can rely on this empirical evidence of climate change and global warming in their quest for Climate Action—SDG13. It can be noted that a weak positive trend was observed in SWL at Nooigedacht Dam, especially when considering more recent observations (Figure 3c).
However, a positive SWL trend may not always be indicate genuine water security. In some instances, extreme rainfall can cause anomalous SWLs, thereby altering the structure of the time series and the resultant trend. To overcome this shortcoming, a stepwise trend analysis is normally used. However, this technique is more suitable for water quality studies, where trends are tested before and after a specific scenario or the introduction of best management practices.
3.3. Projected Climate Change
Strong multiyear rainfall variability was detected in most statistical analyses performed in this study (e.g., Figure 2a,b and Figure 4a,b). Rainfall reduction was observed over the SASB, but most important were the contrasting climate patterns found between the irrigated and dryland regions (Figure 4a,b). It was found that the irrigated region was more susceptible and sensitive to climate variability and change than the dryland region. Rainfall is largely influenced by rainfall-bearing mechanisms, such as the shifting of the Intertropical Convergence Zone (ITCZ), tropical cyclones, and cut-off lows [37,38,39]. Rainfall extremes manifest differently between dryland and irrigated regions. In some instances, extreme rainfall events adversely affect the irrigated areas without significant impacts on the dryland region of the SASB, and vice versa. Extreme mean monthly and annual rainfall occurred in February 2000 over the irrigated region, largely resulting from the landfall of tropical cyclone (TC) Eline from the Mozambique Channel.
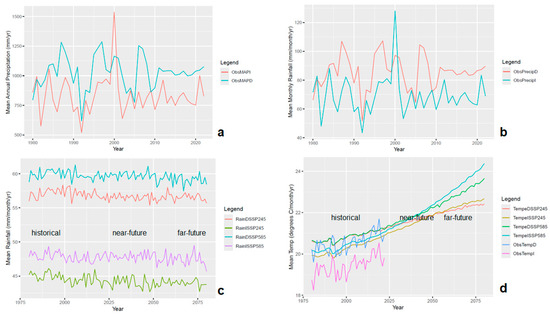
Figure 4.
Observed and projected climate changes over SASB: (a) Mean Annual Precipitation (MAP) over dryland and irrigated regions from 1980 to 2022; (b) mean monthly precipitation over dryland and irrigated regions from 1980 to 2022 (c) projected precipitation under low-GHG-emission scenario (SSP2–4.5) and high-GHG-emission scenario (SSP5–8.5) from 1980 to 2080; (d) projected surface air temperatures under low-GHG-emission scenario (SSP2–4.5) and high-GHG-emission scenario (SSP5–8.5) from 1980 to 2080 with observed mean monthly surface air temperatures over dryland and irrigated regions.
TC Eline not only deposited a substantial amount of rainfall over northeastern South Africa but also tracked approximately 2000 km across southern Africa, eventually approaching the cool Atlantic Ocean [39]. However, its impacts, including floods and loss of life, varied significantly across affected countries such as South Africa, Mozambique, and Zimbabwe [39]. Diverse hydroclimate patterns over the regions of the SASB were also recognised during April 2022, when the dryland region was adversely affected by severe flooding because of a cut-off low-pressure system [37]. In this case, extreme rainfall was more pronounced over the dryland region than the irrigated region of the SASB (Figure 4a,b).
The SASB is characterised by diverse land use and land cover changes. Some land uses, such as sugarcane plantations, require substantial rainfall (e.g., 800 mm/yr) for optimal harvest within a season. However, extreme rainfall is equally detrimental to sugarcane cultivation. For instance, the extreme rainfall event of April 2022 in KwaZulu-Natal, which reached 400 mm/month, led to an increase in the estimated return period values, exceeding both the 1-in-10 years and 1-in-50 years thresholds [40]. Extreme rainfall events further cause severe damage to sugarcane agriculture, which manifests as soil erosion, flooding, and the submerging of sugarcane crops and fields. Additionally, periods of extremely low rainfall (i.e., drought conditions) also diminish available water, consequently leading to reduced annual crop yields in this area. Such environmental changes could exert short- and long-term detrimental effects on the sustainability of crop production (e.g., sugarcane) across the SASB. Moreover, the remotely sensed and projected rainfall used in this study do not bear significant resemblance (Figure 4a–d), but this information could be useful in a quest to best cope with climate variability and change. It was startling that both the dryland and irrigated regions of the SASB were projected to receive low/high rainfall under low/high-GHG-emission scenarios (Figure 4c). This indicates that under a high-GHG-emission scenario (SSP5–8.5), extreme rainfall events could become more prevalent in these regions.
These findings further suggest that mitigation and adaptation strategies (e.g., Climate Action—SDG13) are immediately needed for sustainable crop production and water security. This can also be beneficial to the prospects of downstream sectors, like the proposed bioethanol strategy in the area. Based on climate observations, strong temperature variability averaging around 20°C/month/yr is more pronounced inland. Conversely, the highest surface air temperatures, also averaging approximately 20°C, are more noticeable towards the coast (Figure 4d).
Observations indicate that surface air temperatures increase with rising GHG emissions and levels of development in the area (Figure 4d). In this study, the dryland region was found to be 1°C/month/yr warmer than the irrigated region (Figure 4d). However, surface air temperatures over the irrigated region are characterised by strong annual variability (Figure 4d). This also corresponds with observed rainfall trends in the irrigated region during 2004. The trend changes over the dryland region occurred 17 years later (in 2020) under SSP2–4.5 (Figure 5a,b). Other PTTPs for rainfall were located in 2005, 2006, 2008, 2011, 2012, 2013, 2014, and 2018.
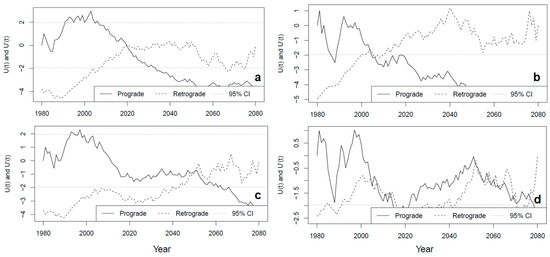
Figure 5.
Projected rainfall trends under low and high GHG emissions over SASB for periods 1980–2022, 2025–2050, and 2050–2080: (a) SSP2–4.5 projections over dryland region, (b) SSP2–4.5 projections over irrigated region, (c) SSP5–8.5 projections over dryland region, (d) SSP5–8.5 projections over irrigated region.
Additionally, strong rainfall variability, indicated by numerous re-occurring PTTPs between 2050 and 2080 under SSP5–8.5 projections, is evident over the irrigated region (Figure 5d). Under SSP5–8.5 projections, only one PTTP was detected, in 2051 (far-future), over the dryland region of the SASB from 1980 to 2080. These drying trends are statistically significant () under both SSP2–4.5 and SSP5–8.5 scenarios. Projections under SSP5-8.5 indicated the potential strengthening of rainfall and water security over the irrigated region between 2030 and 2050 (Figure 5d). It is important to note that extreme rainfall events present both opportunities, such as increased SWLs, and significant challenges, including disasters and the loss of lives and livelihoods due to flooding. Year-to-year temperature variations were detected between 1980 and 2000, and temperature projections suggest an abrupt increase until 2080 (Figure 6a–d). It can be emphasised that the drastic and sudden temperature increases detected in this study are signals of global warming and its local consequences. These temperature change projections (Figure 6a–d) could depend on efforts devoted towards Climate Action, especially reductions in GHG emissions.
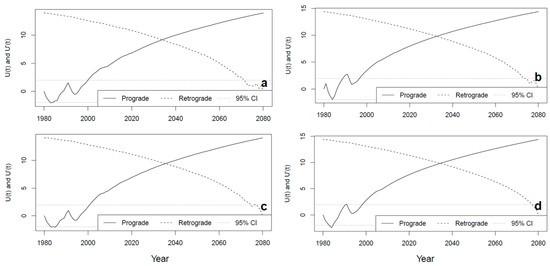
Figure 6.
Projected temperature trends under low and high GHG emissions over SASB for historical, near-future, and far-future periods: (a) SSP2–4.5 projections over dryland region, (b) SSP2–4.5 projections over irrigated region, (c) SSP5–8.5 projections over dryland region, (d) SSP5–8.5 projections over irrigated region.
Unlike rainfall, which exhibited strong multiyear variability and statistically insignificant observed trends, surface air temperatures depicted robust positive observed and projected trends from the late 1990s and early 2000s to 2080 (Figure 6a–d). Only one PTTP was identified in each scenario (e.g., SSP2–4.5 and SSP5–8.5) for projected surface air temperature trends in both regions of the SASB. These PTTPs were located in 2034 and 2033 over the dryland and irrigated regions under the SSP2–4.5 scenario, respectively (Figure 6a,b), while PTTPs were identified in 2036 for the dryland region and 2035 for the irrigated region under the SSP5–8.5 scenario (Figure 6c,d). These PTTPs suggest that the irrigated region is projected to become drier earlier then the dryland region. It is also evident that the irrigated region is projected to warm faster than the dryland region during both the 2025–2050 and 2050–2080 periods (Figure 6a–d). These warming trends align with the faster projected drying trends over the irrigated region of the SASB for similar periods (2025–2050 and 2050–2080; Figure 5c,d). Notably, all surface air temperature trends mentioned are statistically significant at the 95% confidence level. Under SSP2–4.5 projections, statistics of 1.993 and 2.159 were obtained for the dryland and irrigated regions, respectively, whilst statistics of 2.115 and 2.336 were obtained under SSP5–8.5 projections for the dryland and irrigated regions, respectively. These results signify a need for different approaches in terms of climate vulnerability and change and the required adaptive capacity for climate resilience in these two agroclimatic regions of the SASB.
4. Conclusions
The observed rainfall depicted disparate trends over the dryland and irrigated regions of the SASB. This discrepancy was indicated by statistics and Sen’s slopes, which both showed a positive observed rainfall trend over the dryland region. A negative statistically insignificant trend of observed rainfall was noticeable over the irrigated region of the SASB from 1980 to 2022. Under both low- (SSP2–4.5) and high-emission (SSP5–8.5) scenarios, a significant drying trend () was observable in both the dryland and irrigated regions of the SASB for the periods 1980–2022, 2025–2050, and 2050–2080. Notably, the irrigated region of the SASB was projected to dry faster than the dryland region, as indicated by the early start of the PTTP over the irrigated region. Surface air temperatures showed robust positive trends () across the SASB under both observations and projections. The statistics for the projected trend of surface air temperatures over the dryland and irrigated regions under low- and high-emission scenarios are as follows: 6.931, 4.557, 3.650, and 2.832, respectively.
These statistics are indicative of potential abrupt temperature increase in the area. Similarly, the irrigated region was also projected to warm faster than the dryland region. These findings suggest that differentiated and localised adaptation and mitigation strategies for water and viable agriculture (e.g., crop cultivation) are immediately required in the SASB. These strategies could potentially benefit the prospects of downstream sectors such as sugarcane-based bioethanol production in this area.
Effective Climate Action should integrate climate modelling to establish robust decision-support tools for farmers and water managers across the SASB. Our findings revealed a decline in both surface and subsurface water availability throughout the area, with the notable exception of Nooigedacht Dam. While this anomaly could suggest a northward extension of the SASB, the positive trends of SWL at Nooigedacht Dam may also be attributed to other non-climatic forcings influencing local surface water variations. Moving forward, beyond the quest for building climate change resilience in this region, future studies could benefit from employing nonparametric and monotonic trend detection and analysis for water quality parameters in the changing climate over the SASB.
Author Contributions
Conceptualization: T.W.M., H.C.; Methodology: T.W.M., H.C.; Formal Analysis: T.W.M., H.C.; Resources: T.W.M.; Data Curation: T.W.M., H.C.; Software: T.W.M.; Writing—Original Draft: T.W.M., H.C.; Writing—Review and Editing: T.W.M., H.C.; Supervision: H.C. All authors have read and agreed to the published version of the manuscript.
Funding
Support from the M&D Bursary at the University of South Africa is recognised.
Data Availability Statement
The datasets used in this study are available upon request. SWLs can be requested from the National Department of Water and Sanitation.
Acknowledgments
The authors appreciate KNMI Climate Explorer for allowing the interactive plotting and archiving of the datasets used in this study. The authors are thankful to the National Department of Water and Sanitation for providing the SWL data used in this study. The R software developers are also appreciated.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A

Table A1.
Most used phrases and acronyms for R programming for this study.
Table A1.
Most used phrases and acronyms for R programming for this study.
| Phrase | Description | |
|---|---|---|
| ObsPrecipI | Observed precipitation in irrigated region | |
| ObsMAPI | Observed mean annual precipitation in irrigated region | |
| ObsPrecipD | Observed precipitation in dryland region | |
| ObsMAPD | Observed mean annual precipitation in dryland region | |
| MAP | Mean annual precipitation | |
| SSP | Shared socioeconomic pathway | |
| RainDSSP245 | Rainfall projection for dryland region under SSP2–4.5 | |
| RainISSP245 | Rainfall projection for irrigated region under SSP2–4.5 | |
| RainDSSP585 | Rainfall projection for dryland region under SSP5–8.5 | |
| RainISSP585 | Rainfall projection for irrigated region under SSP5–8.5 | |
| TempeDSSP245 | Temperature projection for dryland region under SSP2–4.5 | |
| TempeISSP245 | Temperature projection for irrigated region under SSP2–4.5 | |
| TempeDSSP585 | Temperature projection for dryland region under SSP5–8.5 | |
| TempeISSP585 | Temperature projection for irrigated region under SSP5–8.5 | |
| ObsTempD | Observed temperature in dryland region | |
| ObsTempI | Observed temperature in irrigated region | |
Appendix B
Appendix B presents comparisons between observed and simulated rainfall. It was found that the GCMs explained less variation in rainfall in the long term (Table A2), while in the short term, the GCMs could explain more than 50% of the rainfall variability. A strong relationship () between observed and simulated rainfall was observed from 2013 to 2022 (Table A4).

Table A2.
Model summary output: 1981–2022.
Table A2.
Model summary output: 1981–2022.
| Regression Statistics | |||||
|---|---|---|---|---|---|
| Multiple R | 0.473731 | ||||
| R2 | 0.224421 | ||||
| Adjusted R2 | 0.184648 | ||||
| Standard Error | 0.902968 | ||||
| Observations | 42 | ||||
| ANOVA | |||||
| df | SS | MS | F | Significance F | |
| Regression | 2 | 9.201277 | 4.600638 | 5.642519 | 0.007042 |
| Residual | 39 | 31.79872 | 0.815352 | ||
| Total | 41 | 41 | |||
| Coefficients | Standard Error | t Stat | p-Value | ||
| Intercept | 1.1 × 10−14 | 0.139331 | 7.8 × 10−14 | 1 | |
| SSP2–4.5 | −0.5098 | 0.188687 | −2.70183 | 0.010155 | |
| SSP5–8.5 | 0.620228 | 0.188687 | 3.287075 | 0.002148 | |

Table A3.
Model summary output: 2013–2022.
Table A3.
Model summary output: 2013–2022.
| Regression Statistics | |||||
|---|---|---|---|---|---|
| Multiple R | 0.792119 | ||||
| R2 | 0.627453 | ||||
| Adjusted R2 | 0.521011 | ||||
| Standard Error | 0.636928 | ||||
| Observations | 10 | ||||
| ANOVA | |||||
| df | SS | MS | F | Significance F | |
| Regression | 2 | 4.782755619 | 2.391378 | 5.894782 | 0.03156 |
| Residual | 7 | 2.839739498 | 0.405677 | ||
| Total | 9 | 7.622495117 | |||
| Coefficients | Standard Error | t Stat | p-Value | ||
| Intercept | −0.11202 | 0.213551564 | −0.52457 | 0.61608 | |
| SSP2–4.5 | −0.38926 | 0.194579353 | −2.00053 | 0.085553 | |
| SSP5–8.5 | 0.679096 | 0.215057432 | 3.157743 | 0.015979 | |
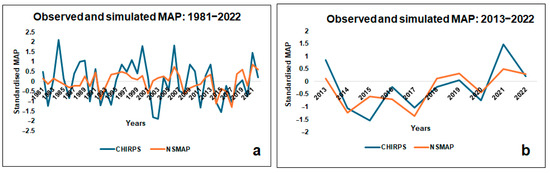
Figure A1.
Comparison of observed and simulated rainfall: (a) 1981–2022 period, (b) 2013–2022 period.
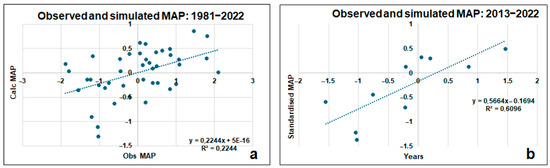
Figure A2.
Scatter of observed and simulated rainfall: (a) 1981–2022 period, (b) 2013–2022 period.

Table A4.
Metrics for model evaluation.
Table A4.
Metrics for model evaluation.
| Evaluation Period | ||
|---|---|---|
| Metrics | 2013–2022 | 1981–2022 |
| MAE | 0.47 | 0.68 |
| MSE | 0.31 | 0.76 |
| RMSE | 0.55 | 0.87 |
| r | 0.78 | 0.47 |
References
- Silva, W.K.D.M.; Medeiros, S.E.L.; Da Silva, L.P.; Coelho Junior, L.M.; Abrahão, R. Sugarcane production and climate trends in Paraíba state (Brazil). Environ. Monit. Assess. 2020, 192, 392. [Google Scholar] [CrossRef]
- Kruger, A.C.; Nxumalo, M.P. Historical rainfall trends in South Africa: 1921–2015. Water SA 2017, 43, 285–297. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Pradhan, R.K.; Petropoulos, G.P.; Pandey, V.; Gupta, M.; Yaduvanshi, A.; Wan Jaafar, W.Z.; Mall, R.K.; Sahai, A.K. Long-Term Trend Analysis of Precipitation and Extreme Events over Kosi River Basin in India. Water 2021, 13, 1695. [Google Scholar] [CrossRef]
- Jury, M.R. Historical and projected climatic trends in KwaZulu-Natal: 1950–2100. Water SA 2022, 48, 369–379. [Google Scholar]
- Sun, J.; Yan, H.; Bao, Z.; Wang, G. Investigating Impacts of Climate Change on Runoff from the Qinhuai River by Using the SWAT Model and CMIP6 Scenarios. Water 2022, 14, 1778. [Google Scholar] [CrossRef]
- Adepoju, O.A.; Afinowi, O.A.; Tauheed, A.M.; Danazumi, A.U.; Dibba, L.B.; Balogun, J.B.; Flore, G.; Saidu, U.; Ibrahim, B.; Balogun, O.O.; et al. Multisectoral Perspectives on Global Warming and Vector-borne Diseases: A Focus on Southern Europe. Curr. Trop. Med. Rep. 2023, 10, 47–70. [Google Scholar] [CrossRef]
- Labrousse, C.; Ludwig, W.; Pinel, S.; Sadaoui, M.; Toreti, A.; Lacquement, G. Declining water resources in response to global warming and changes in atmospheric circulation patterns over southern Mediterranean France. Hydrol. Earth Syst. Sci. 2022, 26, 6055–6071. [Google Scholar] [CrossRef]
- Lobell, D.B.; Schlenker, W.; Costa-Roberts, J. Climate trends and global crop production since 1980. Science 2011, 333, 616–620. [Google Scholar] [CrossRef]
- Srivastav, A.L.; Dhyani, R.; Ranjan, M.; Madhav, S.; Sillanpää, M. Climate-resilient strategies for sustainable management of water resources and agriculture. Environ. Sci. Pollut. Res. 2021, 28, 41576–41595. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, Z.; Singh, V.P.; Zhang, Y.; Feng, S.; Xu, Y.; Hao, F. Drought propagation under global warming: Characteristics, approaches, processes, and controlling factors. Sci. Total Environ. 2022, 838, 156021. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration (NASA). Vital Signs of the Planet. 2018. Available online: https://climate.nasa.gov/vital-signs/global-temperature/ (accessed on 31 March 2025).
- Legg, S. IPCC, 2021: Climate change 2021-the physical science basis. Interaction 2021, 49, 44–45. [Google Scholar]
- Marengo, J.A.; Ambrizzi, T.; Alves, L.M.; Barreto, N.J.; Simões Reboita, M.; Ramos, A.M. Changing Trends in Rainfall Extremes in the Metropolitan Area of São Paulo: Causes and Impacts. Front. Clim. 2020, 2, 3. [Google Scholar] [CrossRef]
- dos Santos, C.A.; Neale, C.M.; Mekonnen, M.M.; Gonçalves, I.Z.; de Oliveira, G.; Ruiz-Alvarez, O.; Safa, B.; Rowe, C.M. Trends of extreme air temperature and precipitation and their impact on corn and soybean yields in Nebraska, USA. Theor. Appl. Clim. 2022, 147, 1379–1399. [Google Scholar] [CrossRef]
- Jury, M.R. Climate Modulation of Crop Yield over the South African Highlands. Earth Interact. 2025, 29, 240007. [Google Scholar] [CrossRef]
- Mbhamali, T.W.; Jury, M.R. Climate-sensitivity of sugarcane yield in the southeastern Africa lowlands. Int. J. Clim. 2021, 41, 4187–4200. [Google Scholar] [CrossRef]
- Dubb, A. Dynamics of decline in small-scale sugarcane production in South Africa: Evidence from two ‘rural’ wards in the Umfolozi region. Land Use Policy 2015, 48, 362–376. [Google Scholar] [CrossRef]
- Dubb, A. The Rise and Decline of Small-Scale Sugarcane Production in South Africa: A Historical Perspective; Institute for Poverty Land and Agrarian Studies, UWC: Bellville, South Africa, 2013. [Google Scholar]
- Collins, M.R.; Knutti, J.; Arblaster, J.L.; Dufresne, T.; Fichefet, P.; Friedlingstein, X.; Gao, W.J.; Gutowski, T.; Johns, G.; Krinner, M.; et al. Long-Term Climate Change: Projections, Commitments and Irreversibility. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Jury, M.R. South Africa’s Future Climate: Trends and Projections. In The Geography of South Africa; Knight, J., Rogerson, C., Eds.; World Regional Geography Book Series; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Korneev, V.P.; Koloskov, B.P.; Bychkov, A.A.; Petrunin, A.M.; Chastukhin, A.V. Cloud Seeding for Improving Weather in Megacities. Russ. Meteorol. Hydrol. 2022, 47, 523–529. [Google Scholar] [CrossRef]
- Doorenbos, J.; Kassam, A.H.; Bentvelsen, C.I.M. Yield Response to Water, FAO Irrigation and Drainage Paper; Food and Agriculture Organization of the United Nations: Rome, Italy, 1979. [Google Scholar]
- Verheye, W.H. Soils, Plant Growth and Crop Production; EOLSS Publications: Abu Dhabi, United Arab Emirates, 2010; Volume 3, ISBN 978-1-84826-369-7. [Google Scholar]
- Chikoore, H.; Jury, M.R. Intraseasonal Variability of Satellite-Derived Rainfall and Vegetation over Southern Africa. Earth Interact. 2010, 14, 1–26. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Afsari, R.; Nazari-Sharabian, M.; Hosseini, A.; Karakouzian, M. A CMIP6 Multi-Model Analysis of the Impact of Climate Change on Severe Meteorological Droughts through Multiple Drought Indices—Case Study of Iran’s Metropolises. Water 2024, 16, 711. [Google Scholar] [CrossRef]
- Bergant, K.; Kajfež-Bogataj, L.; Črepinšek, Z. Statistical downscaling of general-circulation-model-simulated average monthly air temperature to the beginning of flowering of the dandelion (Taraxacum officinale) in Slovenia. Int. J. Biometeorol. 2002, 46, 22–32. [Google Scholar] [CrossRef]
- Jury, M.R. Climate trends in the Cape Town area, South Africa. Water SA 2020, 46, 438–447. [Google Scholar]
- Chokkavarapu, N.; Mandla, V.R. Comparative study of GCMs, RCMs, downscaling and hydrological models: A review toward future climate change impact estimation. SN Appl. Sci. 2019, 1, 1698. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Mbatha, N.; Xulu, S. Time Series Analysis of MODIS-Derived NDVI for the Hluhluwe-Imfolozi Park, South Africa: Impact of Recent Intense Drought. Climate 2018, 6, 95. [Google Scholar] [CrossRef]
- Jury, M.R. Climate trends across South Africa since 1980. Water SA 2018, 44, 297–307. [Google Scholar] [CrossRef]
- McCarthy, T.S.; Humphries, M.S. Contamination of the water supply to the town of Carolina, Mpumalanga, January 2012. S. Afr. J. Sci. 2013, 109, 1–10. [Google Scholar] [CrossRef]
- Mashao, F.M.; Mothapo, M.C.; Munyai, R.B.; Letsoalo, J.M.; Mbokodo, I.L.; Muofhe, T.P.; Matsane, W.; Chikoore, H. Extreme Rainfall and Flood Risk Prediction over the East Coast of South Africa. Water 2023, 15, 50. [Google Scholar] [CrossRef]
- Ramotubei, T.S.; Landman, W.A.; Mateyisi, M.J.; Nangombe, S.; Beraki, A.F. Response of the global ITCZ to different ENSO phases and how the ITCZ determined from the maximum precipitation compares with the surface tropical wind convergence. Environ. Dev. 2025, 55, 101210. [Google Scholar] [CrossRef]
- Reason, C.J.C.; Keibel, A. Tropical cyclone Eline and its usual penetration and impacts over the South African mainland. Am. Meteorol. Soc. 2004, 19, 789–805. [Google Scholar]
- Kruger, A.; Letsatsi, N. Scientific Meteorological and Climatological News from the South African Weather Service NEWS. Available online: https://www.researchgate.net/publication/386352236_Scientific_meteorological_and_climatological_news_from_the_South_African_Weather_Service_NEWS#fullTextFileContent (accessed on 15 April 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).