Abstract
Fishing boats anchored away from the wharf or revetment are typically in side-by-side configurations due to their small size. Expanding on previous physical model tests investigating regular wave interactions with multi-boat and bow-and-stern-anchored fishing arrays, this study examines the hydrodynamic effects of irregular wave conditions. The Hilbert–Huang transform (HHT), an adaptive time–frequency processing technique, was applied to investigate multi-order nonlinear oscillatory elements in dynamic systems. It is found that the roll and heave motions of each boat are dominated by the wave-frequency components, whereas the sway motion is dominated by the low-frequency components. When multi-boats are anchored side by side, the roll and heave motion of the lee-side boat has a greater wave-frequency response compared with other boats, while for sway motion, the middle boat seems a little higher than others. The nonlinear dynamics of the roll and sway motion for a single boat is very large. An increase in the number of parallel boats has significant effect on reducing these responses. The variation trends of the three motion responses of the boat on the weather and lee sides are obviously different in each form.
1. Introduction
As extreme weather events have grown in frequency and intensity in recent years, ensuring the operational safety of fishing vessels—a cornerstone of marine livelihoods and coastal economic stability—has emerged as a critical priority demanding urgent attention. Characterized by compact dimensions and reduced structural robustness relative to commercial counterparts, these vessels face amplified risks during typhoon seasons or fishing suspensions. To mitigate hazards, multi-boats anchored side by side are widely adopted in ports or sheltered waters. Despite this practice, hydrodynamic investigations targeting small-scale fishing fleets remain notably scarce. Early foundational work by Li [1] and Zhou [2] established theoretical frameworks for evaluating anchor–chain dynamics and mooring tensions under combined environmental loads, informing subsequent engineering standards. Concurrently, Wang [3] and Zhang [4] pioneered comprehensive assessments of port sheltering efficacy, integrating geospatial factors, hydrological conditions, and anchorage patterns to propose optimal strategies—particularly advocating bow–stern multi-vessel anchoring for small to medium fleets. Recent advancements include Duan [5], who experimentally quantified mooring force variations on paired 450 HP vessels under diverse wind–wave–current scenarios, and Zhao [6], whose SAM-RSM model simulations contrasted hydrodynamic behaviors of vessels anchored over sloped versus flat seabed. While these studies advance single-vessel analyses, critical gaps persist in understanding interactive dynamics of clustered fleets—a configuration offering both computational efficiency and ecological validity for real-world risk assessments.
Current hydrodynamic inquiries into multi-vessel proximity predominantly address large commercial ships or floating docks, yet their methodologies hold transferable insights. For instance, McTaggart [7] and Kashiwagi [8] respectively elucidated motion interference between dissimilar ships and wave drift forces in adjacent floating systems. Luo [9] experimentally quantified cable forces and hull impacts between docked bulk carriers and cruise ships under onshore/offshore winds, revealing heightened mechanical stresses during lateral wind exposure. Transdisciplinary studies by Gao [10] on multi-floating logistics platforms and Qu et al. [11,12,13], employing hydrodynamic analysis software (AQWA-LINE and AQWA-DRIFT software module), further demonstrated how wave-exposed outer vessels exhibit amplified motions compared to sheltered counterparts, with mooring loads being directionally sensitive to wind/current vectors. Parallel insights emerge from aquaculture research: Bi and Ma et al. [14,15,16,17,18] systematically analyzed wave interactions with modular platforms—comprising up to nine interconnected units—through hybrid experimental–numerical approaches, while Pessoa [19] decoupled linear and nonlinear wave responses in LNG carrier–platform systems. Notably, emerging investigations into “gap resonance” phenomena (Xu [20], Zhou [21], Ding [22], Cheng et al. [23,24,25], Gao et al. [26,27,28,29,30]) between tightly spaced floating bodies underscore the criticality of frequency-dependent hydrodynamic coupling—a consideration equally pertinent to clustered fishing fleets. These scholars employed numerical simulation methods to investigate gap fluid resonance and wave–structure interactions in multi-floating-body structures. The most significant distinction from the present study’s subject lies in the fact that their examined floating bodies remained physically independent without interconnections.
Compared with large merchant vessels, fishing boats are relatively small in scale and more susceptible to the effects of wind and waves. Currently, there is a significant lack of research on the anchoring stability of small-scale fishing boats within harbors, making the investigation of mooring stability conditions for fishing boats in port environments critically important for their operational safety. To qualitatively study the hydrodynamic characteristics of fishing boats during side-by-side anchoring operations within harbors, the motivation and novelty of this research lie in two key aspects: firstly, to investigate the anchoring method for multi-fishing boats that are flexibly connected and anchored at both the bow and stern of each boat; secondly, to analyze the dynamic responses of multi-fishing boats anchored together, especially the effect of the number of anchored boats. Additionally, utilizing the Hilbert–Huang transform (HHT), the study uncovered the inherent characteristics of the nonlinear responses. This paper is organized as follows. Section 2 provides a brief description of the experimental setup, wave parameters, and time–frequency analysis methodology. Section 3 presents the application of this method to analyzing the dynamic response of a single boat in irregular waves. It further compares the dynamic responses of each boat in four forms and examines the motion characteristics of multi-boat systems. Finally, Section 4 summarizes the study’s conclusions.
2. Brief Introduction of Physical Model Test
The physical model experiment was performed in a wave tank with dimensions of 50 m (length) × 26 m (width) × 1.2 m (depth). To minimize wave reflection, energy-dissipating porous media were installed on three lateral boundaries and behind the segmented wavemaker. A schematic of the experimental setup is depicted in Figure 1, including the arrangement of 48 individually controlled wave paddles.

Figure 1.
Photograph of experimental setup.
Following a comprehensive evaluation of geometric constraints imposed by the experimental tank dimensions, coupled with hydrodynamic considerations including wave generation capabilities and instrumental precision limits of the measurement systems, the model scale was selected as 1:12. This selection ensures adherence to Froude similarity requirements while maintaining acceptable levels of experimental uncertainty. Four identical boat models were fabricated using polyvinyl chloride (PVC) material, representing a benchmark hull form corresponding to a nominal propulsion power of 100 horsepower (HP). The primary operational specifications of both the prototype and model boats are summarized in Table 1.

Table 1.
Key parameters of the fishing boats.
The fishing boat under investigation in this study employs a bow and stern anchoring system within port confines, as opposed to conventional alongside-wharf mooring. Figure 2 illustrates the layout of the stern mooring system. The bow mooring system mirrors this configuration identically, comprising an anchor, chain cable, and anchor rope assembly. The properties of the mooring system are detailed in Table 2. It should be noted that the scaled-down dimensions of the prototype anchor rope, derived from Froude-scaling (gravitational similarity) and geometric similarity (length scaling), are impractically small for experimental manipulation. To enhance operational feasibility, the anchor rope’s submerged weight was concentrated in the touchdown zone steel chain segment, and its elasticity was simulated via calibrated springs [31]. Similarly, for the steel chain, full compliance with diameter similarity requirements was precluded while satisfying Froude scaling (gravitational similarity) and geometric similarity (length scaling). Consequently, diameter constraints were intentionally relaxed in this study. The physical model chain implemented in the experiments is showcased in Figure 3.

Figure 2.
Experimental photograph of the anchoring system.

Table 2.
Key parameters of the mooring system.

Figure 3.
Steel chain for text.
In harbor anchoring operations, fishing boats commonly adopt side-by-side tandem anchoring configurations, where adjacent boats are secured using nylon mooring cables. To restrict the relative motion between them, operational practice dictates minimizing inter-boat spacing through close-proximity coupling. This configuration, while standard in maritime operations, creates significant experimental challenges in physical model testing: the constrained interstitial space between boat models precludes the deployment of measurement instrumentation, thereby limiting quantitative investigation into gap resonance phenomena within the inter-vessel channel. Figure 4 illustrates the operational mooring configurations between boats in real-world anchoring scenarios and their corresponding experimental simulation counterparts. These models were anchored side by side to simulate single-, double-, triple-, and quadruple-boat anchoring scenarios (Figure 5). Boats were labeled sequentially from the weather side (Boat A) to the lee side (Boat D), with intermediate positions designated as B and C.

Figure 4.
Layout of ropes between boats.
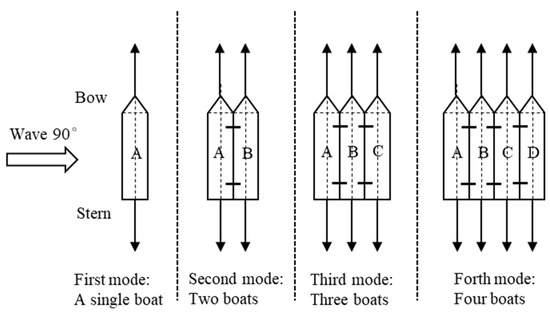
Figure 5.
The wave incidence direction and rules for naming fishing boats in four forms.
The present experimental study primarily employed irregular waves to simulate wave environmental loads, utilizing the Goda-modified Jonswap spectrum for wave energy characterization. Considering the wave period characteristics in China’s nearshore fishing ports, the prototype-scale wave parameters are specified in Table 3. Prior to positioning the boat model in the basin, wave gauges were deployed at the intended model location. The wave maker generated waves based on the Jonswap spectrum with selected parameters. Time-series wave elevation data acquired by the gauges underwent spectral analysis and were compared against the target Jonswap spectrum. Iterative adjustment of constituent wave parameters was performed until statistical properties achieved convergence, thereby validating the generated wave field as compliant with requirements.

Table 3.
Irregular wave parameters.
Wave elevation data were acquired using LYL-III wave gauges with an accuracy of <±2% F.S. (Full Scale) and a resolution of 0.3 mm. Six-degree-of-freedom (6DOF) motions of the boat were measured via a non-contact motion capture system, capable of simultaneously tracking multi-boat displacements in surge, sway, heave, roll, pitch, and yaw. The system achieves angular resolution under ±0.05° and linear displacement resolution below ±0.05 cm. During the physical model experiment, the wave gauge had a sampling interval of 0.02 s and collected 32,768 data points, resulting in a total sampling duration of approximately 650 s. The six-component force gauge operated with a sampling interval of 0.01 s and acquired 46,000 data points. Data spanning 460 s from the stationary phase of the wave generation process was collected for analysis. The full experimental protocols, including instrumentation calibration, are documented in Sun [31] and An [32].
In this study, the nonlinear dynamic of the multi-fishing boats anchored together were analyzed using the Hilbert–Huang transform (HHT). The time series of the motion responses of each boat are processed using empirical mode decomposition (EMD) and mixing mode separation technique; then, the method of Hibert spectral analysis (HSA) is adopted to deal with the decomposition results (Huang [33]; Huang and Wu [34]; Kim and Park [35]). In the study, through temporal integration of the Hilbert spectrum across the entire time domain, the marginal Hilbert spectrum (MHS) is generated in this analysis. This spectral representation enables quantitative characterization of signal amplitude distribution patterns as they evolve with frequency variations throughout the complete frequency spectrum. Within the marginal Hilbert spectrum framework, the detection of energy components at specific frequencies suggests that transient oscillations corresponding to those frequencies may manifest in localized temporal intervals across the full signal duration. This interpretation aligns with a probabilistic analysis of spectral energy distribution. Consequently, the MHS methodology demonstrates particular advantage in analyzing nonstationary signals characterized by time-varying frequency content.
3. Results
3.1. Motion Responses for a Single Boat
By accounting for both the incident wave directionality and the aligned configuration of the boat array, this study investigates the dynamic responses of individual hulls across three principal degrees of freedom: rolling, heaving, and swaying motions. The subsequent analysis focuses on quantifying the single-boat response characteristics within these critical motion modes. All derived dynamic response parameters are normalized to full-scale prototype values following established dimensional scaling principles, ensuring accurate representation of real-world hydrodynamic behavior.
Figure 6 shows the time history of the roll motion of a single boat. After being decomposed into a finite number of intrinsic mode functions (IMFs), the initial five empirical mode components and their corresponding MHS for the roll motion of the single boat are presented in Figure 7. These visualizations are systematically arranged in descending order of the modal frequency components, ranging from the highest to the lowest frequency bands. Analysis reveals that the dominant modal frequency associated with the boat’s roll motion is primarily localized in the 0.2 to 0.3 Hz range. Notably, the spectral peak frequency corresponds closely to the designated incident wave frequency (fs = 0.25 Hz), indicating a resonant coupling between the vessel dynamics and wave excitation. Simultaneously, the wave-frequency motion response exhibits an amplitude exceeding that of all other combined modes by a factor of more than 200. In addition, the fifth empirical mode, which is concentrated in the low frequency (f = 0.011 Hz), was a little larger than other modes except Mode 1. The low-frequency components of roll motion are small but do exist, and there are no high-frequency components.
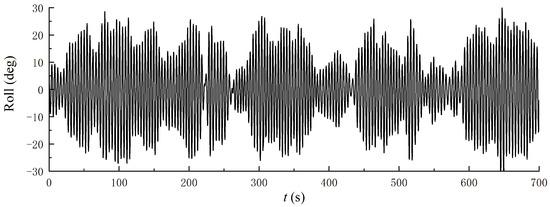
Figure 6.
Recorded roll motion time series of a single boat.
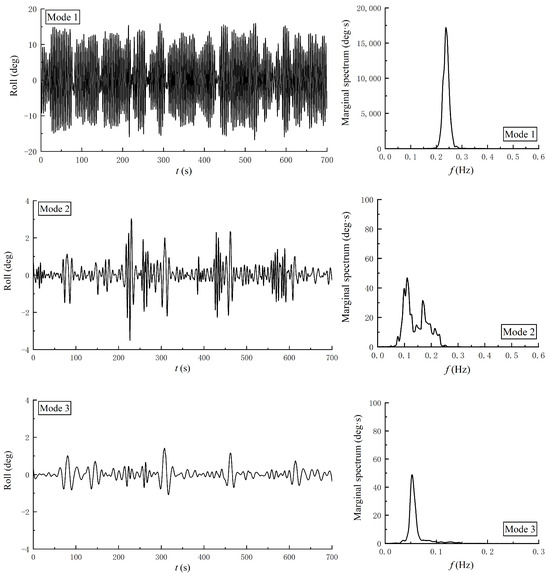
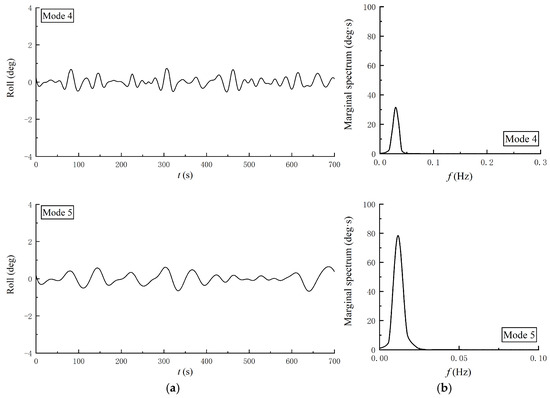
Figure 7.
The empirical modes and the associated MHS of roll motion for a single boat. (a) Time history of Mode 1 to Mode 5; (b) MHS of Mode 1 to Mode 5.
Figure 8 displays the time history of the heave motion. Figure 9 shows the first six empirical modes and the corresponding MHS. Among all the empirical modes, the amplitudes of the response in Mode 1 and Mode 2 are higher than others. Their energies are concentrated in the region of 0.1~0.4 Hz, and they also have energy concentration near the peak frequency of the incident wave. The heave motion also is dominated by the wave-frequency component. It is worth noting that there is also a significant motion response in the low-frequency shown in Mode 6. Notably absent are high-frequency oscillations within the spectral composition of heave motion dynamics.
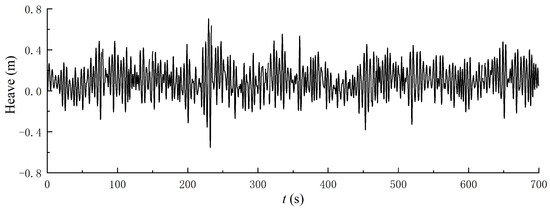
Figure 8.
Recorded heavy motion time series of a single boat.
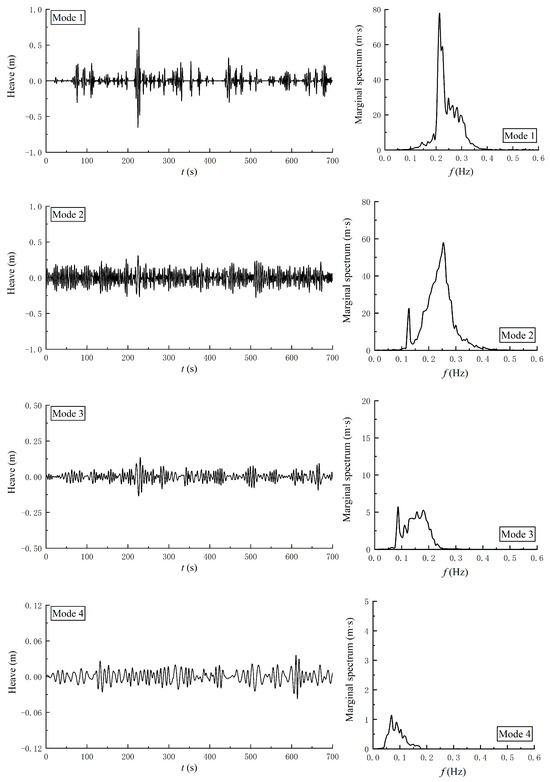
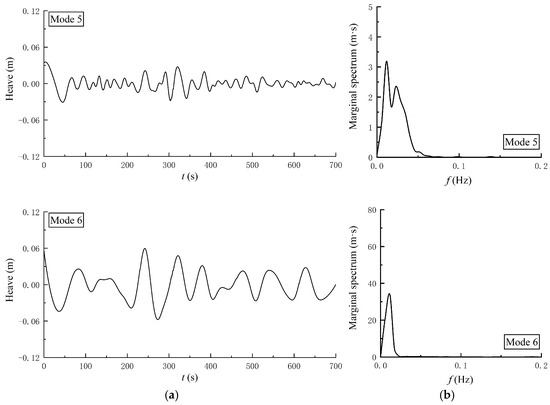
Figure 9.
The empirical modes and the associated MHS of heave motion for a single boat. (a) Time history of Mode 1 to Mode 6; (b) MHS of Mode 1 to Mode 6.
In this experiment, the fishing boat was fixed by two anchoring systems at the bow and the stern, and there were no restrictions in the other two directions. So, when the direction of wave incidence is perpendicular to the boat’s hull, the sway motion has no restoring force to return the boat to the original position, as shown in Figure 10. Figure 11 shows the first five empirical modes and the corresponding MHS. It can be seen that the larger energy amplitudes are distributed in modes 4, 5, and 3, whose energies concentrated in the region of 0~0.5 Hz. It means there are many low-frequency components in sway motion. Among them, the largest response amplitude in Mode 4 surpasses that of the wave-frequency components (mode 1) by a factor of approximately 400.
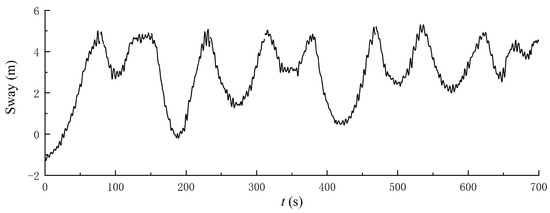
Figure 10.
Recorded sway motion time series of a single boat.
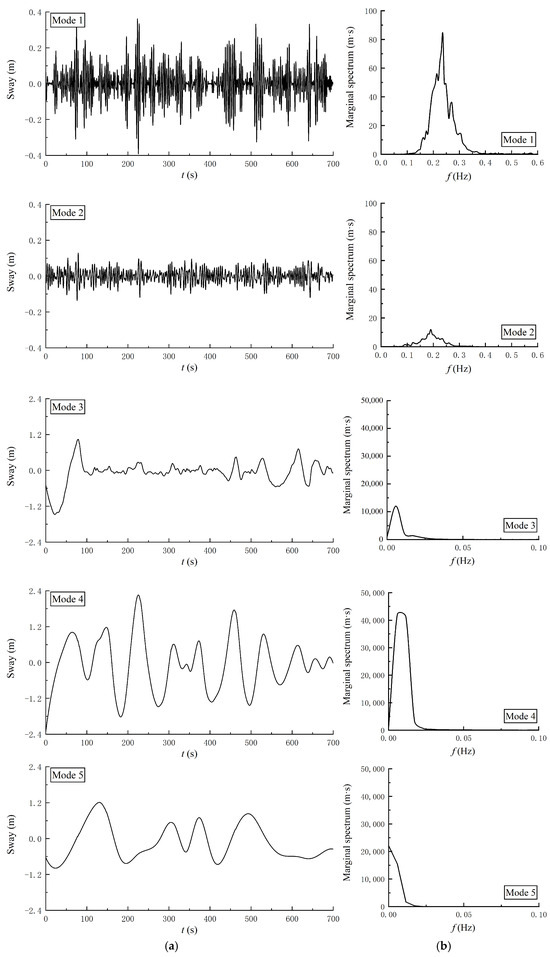
Figure 11.
The empirical modes and the associated MHS of sway motion for a single boat. (a) Time history of Mode 1 to Mode 5; (b) MHS of Mode 1 to Mode 5.
Based on the above analysis, the dominant empirical modes identified are Mode 1 of the roll motion, Modes 1 and 2 of the heave motion, and Mode 4 of the sway motion. The dominant empirical modes of these three motion components align broadly with those reported for corresponding motions in Ma et al.’s study of multi-body floating aquaculture platforms [18]. This alignment demonstrates the applicability of the present computational methodology to side-by-side anchored fishing boats. Subsequent research will focus on the MHS associated with these dominant modes, which is the dominant marginal Hilbert spectrum (DMHS).
3.2. Motion Responses for Multi-Boats Anchored Together
In this section, the comparisons of the DMHS of each boat, when multi-boats are anchored side by side, are analyzed. Figure 12 depicts the DMHS of roll motion for each boat. For two anchored boats, the peak value of the roll marginal spectrum of the boat on the lee side (Boat B) is about 4 times larger than that of the boat on the weather side (Boat A). Their frequency ranges are all in the range of 0.15~0.4 Hz, which is a little wider than the range of a single boat. The frequency of the energy peak is close to that of the incident wave (fs = 0.25 Hz). Similarly, for three or four anchored boats, the leeside boat consistently exhibits the highest peak in its roll marginal spectrum. Furthermore, the spectral energy of all boats is predominantly distributed within the wave-frequency band. It is obvious that, when multi-boats anchored together, the roll issue of the boat on the lee side is more sensitive to waves and deserves attention. The three-boat side-by-side anchoring configuration can be analogized to the three-square-net-cage aquaculture platform studied by Ma et al. [18]. In their research, the DMHS peaks of the leeside and central net-cage exhibited comparable magnitudes, both exceeding those of the weatherside unit. Dimensional discrepancies between the aquaculture platform and the present fishing boats, compounded by the differences in inter-structure connectivity, account for the observed response variations of each unit in the DMHS characteristics of the roll motion.
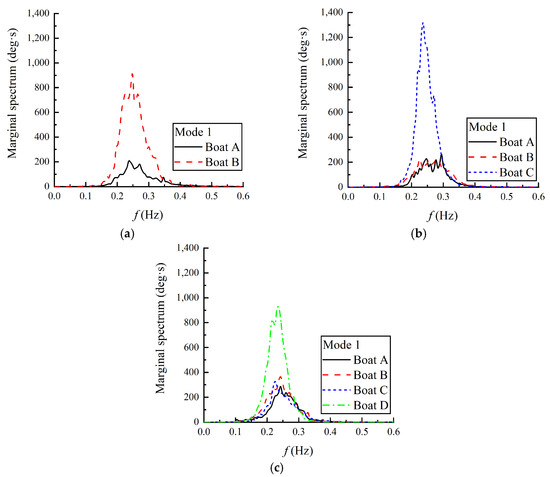
Figure 12.
Comparison of the DMHS of roll motion. (a) Two boats anchored together; (b) three boats anchored together; (c) four boats anchored together.
Figure 13 shows the DMHS of heave motion for each boat. In Mode 1, when two boats are anchored, the peak value of the boat on the lee side (Boat B) is slightly lower than the other boat. Similarly, when three or four boats are anchored, the peak value of the lee-side boat remains the lowest. Conversely, in Mode 2, the peak value of the lee-side boat is obviously higher than that of the other boats, especially when three boats are anchored. In addition, the frequencies of the energy peak in both Modes 1 and 2 are all close to that of the incident wave. The heave responses of the three boats exhibit comparable patterns to those observed in the three net cages of the aquaculture platform [18].
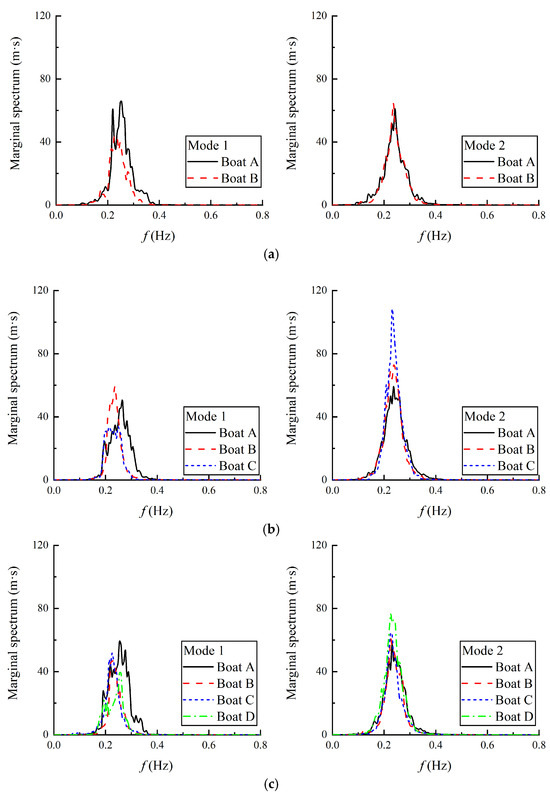
Figure 13.
Comparison of the DMHS of heave motion. (a) Two boats anchored together; (b) three boats anchored together; (c) four boats anchored together.
Figure 14 displays the DMHS of sway motion for each boat. Overall, the sway energy peak of each boat has the same order of magnitude. When two boats are anchored, it seems that Boat B exhibits a slightly higher energy peak, whereas the frequency corresponding to this peak is a little lower than Boat A. This indicates a more noticeable low-frequency characteristic in Boat B. While when three or four boats are anchored, the peak value of Boat B is also a little higher than other boats, but the frequency ranges of four boats are all in the same low-frequency range. A little different from Ma [18], the marginal spectra of sway motions for the three side-by-side anchored boats exhibited no substantial disparities, with only a marginally higher peak observed in the center boat. Notably, the aquaculture net cages in Ma’s configuration demonstrated significantly elevated spectral peaks at the central cage compared to the other units—a phenomenon that remains causally unexplained in the referenced paper.
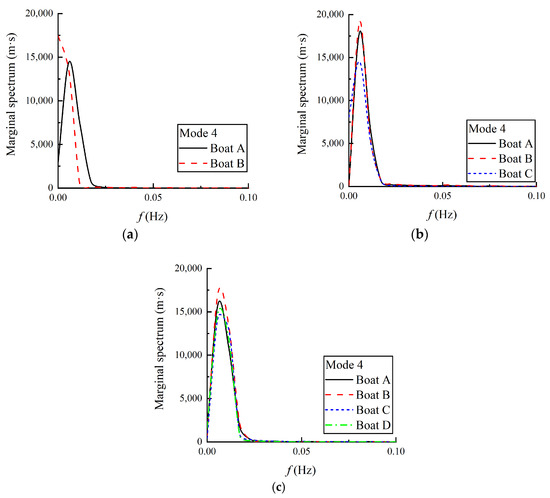
Figure 14.
Comparison of the DMHS of sway motion. (a) Two boats anchored together; (b) three boats anchored together; (c) four boats anchored together.
It can be observed from the above figures that, when multi-boats are anchored together, the DMHS of the roll and heave motion of the lee-side boat is higher than that of other boats, while the DMHS of the sway motion of the middle boat (Boat B) is a little higher. Figure 15 presents a comparison among these boats with higher peak values. For the roll motion shown in Figure 15a, the peak value of the single boat is also the largest. When three boats were anchored, the peak value of DMHS of the lee-side boat seems to be higher than those observed when either two or four boats were anchored. This conclusion can also be observed in the heave motion controlled by Mode 2 (Figure 15c). In Mode 1, the peak value of the single boat seems a little higher (Figure 15b). For sway motion, the peak value of the single boat is also the largest. When there are more than two parallel boats anchored together, the response of the sway motion will be significantly reduced, but an increase in the number of parallel boats has no significant effect on the sway response. Two primary mechanisms underlie this phenomenon. Firstly, the wave shadowing effect significantly reduces the wave energy and, consequently, the motion energy, for the lee-side boat when two boats are anchored side-by-side, compared to a single boat. However, as the number of boats increases to three or more, the wave shadowing effect saturates (reaches its maximum reduction potential). This saturation occurs because the effective boat-beam-to-wavelength ratio exceeds a critical threshold (0.35). Beyond this point, increasing the number of boats yields diminishing returns and does not substantially further reduce the motion energy per boat. Secondly, the flexible connections provided by the nylon lines between each boat constrain the hydrodynamic interactions between adjacent boats, limiting the potential for motion amplification or complex coupled responses. The complex interplay of contributing factors introduces significant uncertainty in the dynamic response of individual boats during multi-boat side-by-side anchoring operations.
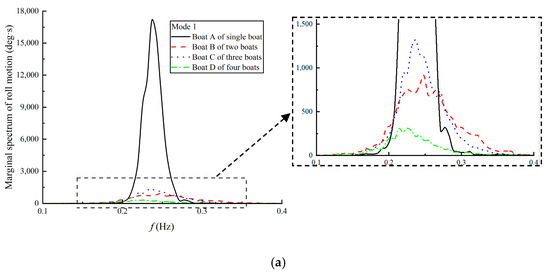
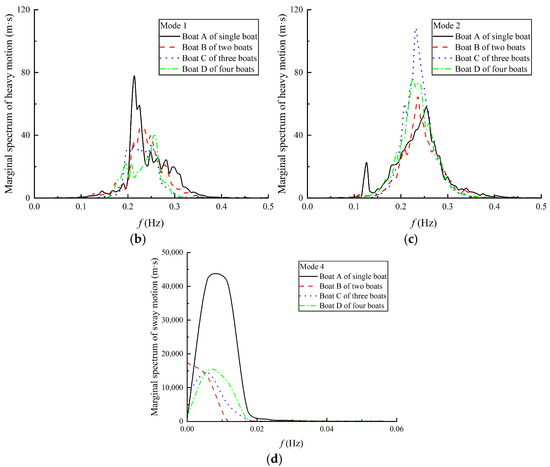
Figure 15.
Comparison of the DMHS of three motions between the boat on the lee side of waves and a single boat. (a) Mode 1 of roll motion; (b) Mode 1 of heave motion; (c) Mode 2 of heave motion; (d) Mode 4 of sway motion.
4. Discussion and Conclusions
In this study, the hydrodynamic performance of multi-fishing boats anchored side by side is investigated by physical experiments. Different configurations are considered, i.e., a single boat anchored and two, three, and four boats anchored together. Employing the Hilbert–Huang transform (HHT) as a time–frequency analysis tool, this study investigated the multi-order nonlinear motion components of each boat. The conclusions gained from the analysis are summarized as follows.
- (1)
- The motion of roll, heave, and sway all can be regarded as the superposition of the wave frequency and low-frequency responses, and they have no high-frequency components. For roll and heave motion, the amplitudes of the wave-frequency components are larger than those of the low-frequency components, while the sway motion is the opposite.
- (2)
- When multi-boats are anchored side by side, there exist obvious differences in the motion response for each boat. For roll motion, the response of the boat on the lee side is the highest among all boats. For heave motion, there is little difference in the wave-frequency component dominated by Mode 1, whereas for Mode 2, the response of the boat on the lee side is a little higher than that of other boats. As for sway motion, it seems the response of the middle boat is a little higher than others. So, special attention should be paid to the roll and heave motion response of the boat on the lee side and the sway motion response of the middle boat.
- (3)
- When a single boat was anchored, the wave-frequency response of its roll motion and the low-frequency response of its sway motion were very large. In order to decrease these responses, one or two more boats can be tied to the lee side of this boat, although this did not significantly impact the wave-frequency heave response of the boat.
The primary limitations of this study are twofold. First, the investigation focused exclusively on a specific vessel hull form under corresponding wave conditions, resulting in a limited sample size. Only wave periods approaching the vessel’s natural roll period (i.e., inducing resonance conditions) were examined, while other wave periods remain unaddressed. Second, due to the constraints of article length and the lack of time, wave incidence directions beyond those tested were not explored. Future research will expand upon these aspects to provide a more comprehensive understanding. This experimental study on the multi-boats anchored side by side can be used as a guide for the layout optimization of such designs.
Author Contributions
Conceptualization, Y.-Y.S. and D.-S.Y.; methodology, Y.-Y.S. and D.-S.Y.; software, D.-S.Y.; validation, Y.-Y.S., D.-S.Y. and Y.-Z.X.; formal analysis, D.-S.Y. and Y.-Z.X.; investigation, Y.-Y.S. and D.-S.Y.; resources, G.W.; data curation, Y.-Z.X., D.C. and X.L.; writing—original draft preparation, Y.-Y.S. and D.-S.Y.; writing—review and editing, G.W., Y.-Z.X., and X.L.; visualization, Y.-Z.X. and D.C.; supervision, G.W. and X.L.; project administration, Y.-Y.S.; funding acquisition, Y.-Y.S. and G.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the National Key R&D Program of China (No. 2024YFD2400800) and the Central Public-interest Scientific Institution Basal Research Fund, CAFS (No. 2023TD88; No. 2024XT0801).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HHT | Hilbert–Huang transform |
| DOF | Degrees of freedom |
| MHS | Marginal Hilbert spectrum |
| DMHS | Dominant marginal Hilbert spectrum |
| EMD | Empirical mode decomposition |
| HSA | Hibert spectral analysis |
| IMFs | Intrinsic mode functions |
References
- Li, T.Y.; Zhou, C.Q.; Liu, T.G.; Liu, L. The dynamic force acted on the chain cable of mooring fishing ships in the wind and the waves. J. Huazhong Univ. Sci. Technol. 1998, 26, 98–100. [Google Scholar]
- Zhou, C.Q.; Liu, T.G.; Li, T.Y. Analysis of chain tension for fishing vessel anchoring in rough water. J. Fish. Sci. China 1999, 6, 79–81. [Google Scholar]
- Wang, C.C.; Luan, S.G.; Hao, X.Y.; Gui, J.S.; Zheng, Y.N. Factors analysis on fishing ports sheltered from the typhoon. Fish. Mod. 2009, 36, 65–66+70. [Google Scholar]
- Zhang, C.; Luan, S.G.; Xia, L.Y. On the influencing factors of the shelter capacity of fishing ports. Value Eng. 2014, 33, 287–288. [Google Scholar]
- Duan, R.H.; Li, M.Y.; Du, J.Y. Reliability Test Analysis of 42m Double Fishing Boat Parallel Mooring. Fish. Mod. 2023, 50, 85–93. [Google Scholar]
- Zhao, X.Y.; Zhang, B.; Liu, H.W.; Liu, X.L.; Tang, J.C. Hydrodynamic Response of a Fishing Vessel Moored over Sloping Bottom. Shipbuild. China 2022, 63, 61–72. [Google Scholar]
- McTaggart, K.; Cumming, D.; Hsiung, C.; Li, L. Seakeeping of Two Ships in Close Proximity. Ocean Eng. 2003, 30, 1051–1063. [Google Scholar] [CrossRef]
- Kashiwagi, M.; Endo, K.; Yamaguchi, H. Wave Drift Forces and Moments on Two Ships Arranged Side-by-Side in Waves. Ocean Eng. 2005, 32, 529–555. [Google Scholar] [CrossRef]
- Luo, W.; He, Y.P.; Yu, L. Study on a Model Experiment of Two Ships Anchoring. Ship Eng. 2007, 29, 1–4. [Google Scholar]
- Gao, F.; Yan, L.; Shen, W.J.; Geng, B.L.; Meng, X.W. Test Study on Mooring Characteristics for Multi-Body Floating System under the Action of Wind, Wave, and Current. J. Waterw. Harb. 2017, 38, 555–560. [Google Scholar]
- Qu, Z.Y. Hydrodynamic Analysis and Mooring Scheme Design for Double Ship Mooring in Large Ship Terminals. Master’s Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 2018. [Google Scholar]
- Qu, Z.Y.; Dou, P.L.; Han, X.C. Hydrodynamic Characteristics of Side-by-Side Mooring of Large Ship Wharf. Mar. Technol. 2019, 1, 14–20. [Google Scholar]
- Kong, L.H.; Sun, Y.B.; Qu, Z.Y. Double ship mooring of large ship in dock. Ship Sci. Technol. 2020, 42, 55–59. [Google Scholar]
- Bi, C.W.; Ma, C.; Zhao, Y.P.; Xin, L.X. Physical Model Experimental Study on the Motion Responses of a Multi-Module Aquaculture Platform. Ocean Eng. 2021, 239, 109862. [Google Scholar] [CrossRef]
- Ma, C.; Bi, C.W.; Xu, Z.; Zhao, Y.P. Dynamic Behaviors of a Hinged Multi-Body Floating Aquaculture Platform under Regular Waves. Ocean Eng. 2022, 243, 110278. [Google Scholar] [CrossRef]
- Ma, C.; Zhao, Y.P.; Bi, C.W. Numerical Study on Hydrodynamic Responses of a Single-Point Moored Vessel-Shaped Floating Aquaculture Platform in Waves. Aquac. Eng. 2022, 96, 102216. [Google Scholar] [CrossRef]
- Ma, C.; Zhao, Y.P.; Xu, Z.; Bi, C.W. Experimental Investigation on the Wave Performance with the Interference of Floating Aquaculture Cages in Single and Tandem Arrangements. Ocean Eng. 2022, 262, 112255. [Google Scholar] [CrossRef]
- Ma, C.; Xie, S.; Bi, C.W.; Zhao, Y.P. Nonlinear Dynamic Analysis of Aquaculture Platforms in Irregular Waves Based on Hilbert–Huang Transform. J. Fluid Struct. 2023, 117, 103831. [Google Scholar] [CrossRef]
- Pessoa, J.; Fonseca, N.; Soares, C.G. Side-by-Side FLNG and Shuttle Tanker Linear and Second Order Low Frequency Wave Induced Dynamics. Ocean Eng. 2016, 111, 234–253. [Google Scholar] [CrossRef]
- Xu, L.Y. Investigation on Hydrodynamic Interaction between Multiple Floating Bodies. Master’s Thesis, Shang Hai Jiao Tong University, Shanghai, China, 2014. [Google Scholar]
- Zhou, G.L.; Xiao, W.B.; Ou, Y.P. Recent Progress in Hydrodynamic Model Test for Two Floating Bodies at Close Proximity in Waves. J. Ship Mech. 2016, 20, 1201–1210. [Google Scholar]
- Ding, Y.F.; Walther, H.J.; Shao, Y.L. Effect of Wave-Current Interaction on Gap Resonance between Side-by-Side Barges. Appl. Ocean Res. 2024, 150, 104073. [Google Scholar] [CrossRef]
- Cheng, Y.; Fu, L.; Dai, S.S.; Collu, M.; Ji, C.Y.; Yuan, Z.M.; Incecik, A. Experimental and Numerical Investigation of WEC-Type Floating Breakwaters: A Single-Pontoon Oscillating Buoy and a Dual-Pontoon Oscillating Water Column. Coast. Eng. 2022, 177, 104188. [Google Scholar] [CrossRef]
- Cheng, Y.; Fu, L.; Dai, S.S.; Collu, M.; Cui, L.; Yuan, Z.M.; Incecik, A. Experimental and Numerical Analysis of a Hybrid WEC-Breakwater System Combining an Oscillating Water Column and an Oscillating Buoy. Renew. Sustain. Energy Rev. 2022, 169, 112909. [Google Scholar] [CrossRef]
- Cheng, Y.; Gong, J.L.; Zhang, J. Hydrodynamic Investigation on a Single-Point Moored Offshore Cage-Wave Energy Converter Hybrid System. Ocean Eng. 2024, 299, 116848. [Google Scholar] [CrossRef]
- Gao, J.L.; Mi, C.L.; Song, Z.W.; Liu, Y.Y. Transient gap resonance between two closely-spaced boxes triggered by nonlinear focused wave groups. Ocean Eng. 2024, 305, 117938. [Google Scholar] [CrossRef]
- Mi, C.L.; Gao, J.L.; Song, Z.W.; Liu, Y.Y. Hydrodynamic wave forces on two side-by-side barges subjected to nonlinear focused wave groups. Ocean Eng. 2025, 317, 120056. [Google Scholar] [CrossRef]
- Song, Z.W.; Jiao, Z.H.; Gao, J.L.; Mi, C.L.; Liu, Y.Y. Numerical investigation on the hydrodynamic wave forces on the three barges in proximity. Ocean Eng. 2025, 316, 119941. [Google Scholar] [CrossRef]
- Mi, C.L.; Gao, J.L.; Song, Z.W.; Yan, M.Y. Gap Resonance Between a Stationary Box and a Vertical Wall Induced by Transient Focused Wave Groups. China Ocean Eng. 2025. [Google Scholar] [CrossRef]
- Gong, S.K.; Gao, J.L.; Yan, M.Y.; Song, Z.W.; Shi, H.B. Effects of floater motion on wave loads during steady-state gap resonance occurring between two non-identical boxes. Ocean Eng. 2025, 323, 120649. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Xiong, Y.Z.; An, X.T.; Yu, D.S.; Wang, G. Experimental Study on the Roll Motion of Small-Scale Multi-Boat Anchored Side by Side under Wave Action. Ocean Eng. 2024, 42, 130–140. [Google Scholar]
- An, X.T. Experimental Study on Hydrodynamic Characteristics of Fishing Vessels Anchored Side by Side in the Harbor. Master’s Thesis, Dalian Ocean University, Dalian, China, 2024. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A Review on Hilbert-Huang Transform: Method and Its Applications to Geophysical Studies. Rev. Geophys. 2008, 46, RG2006. [Google Scholar] [CrossRef]
- Kim, Y.; Park, M.J. Identification of the Nonlinear Roll Damping and Restoring Moment of a FPSO Using Hilbert Transform. Ocean Eng. 2015, 109, 381–388. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).