Prediction of Sluice Seepage Based on Impact Factor Screening and the IKOA-BiGRU Model
Abstract
1. Introduction
2. Impact Factor Screening Method of Sluice Seepage
2.1. Principle of the MIC
2.2. Impact Factor Screening Method Based on the MIC–CFS
3. Sluice Seepage Prediction Model Based on the IKOA–BiGRU
3.1. The Statistical Model of Sluice Seepage
3.2. LSTM Model
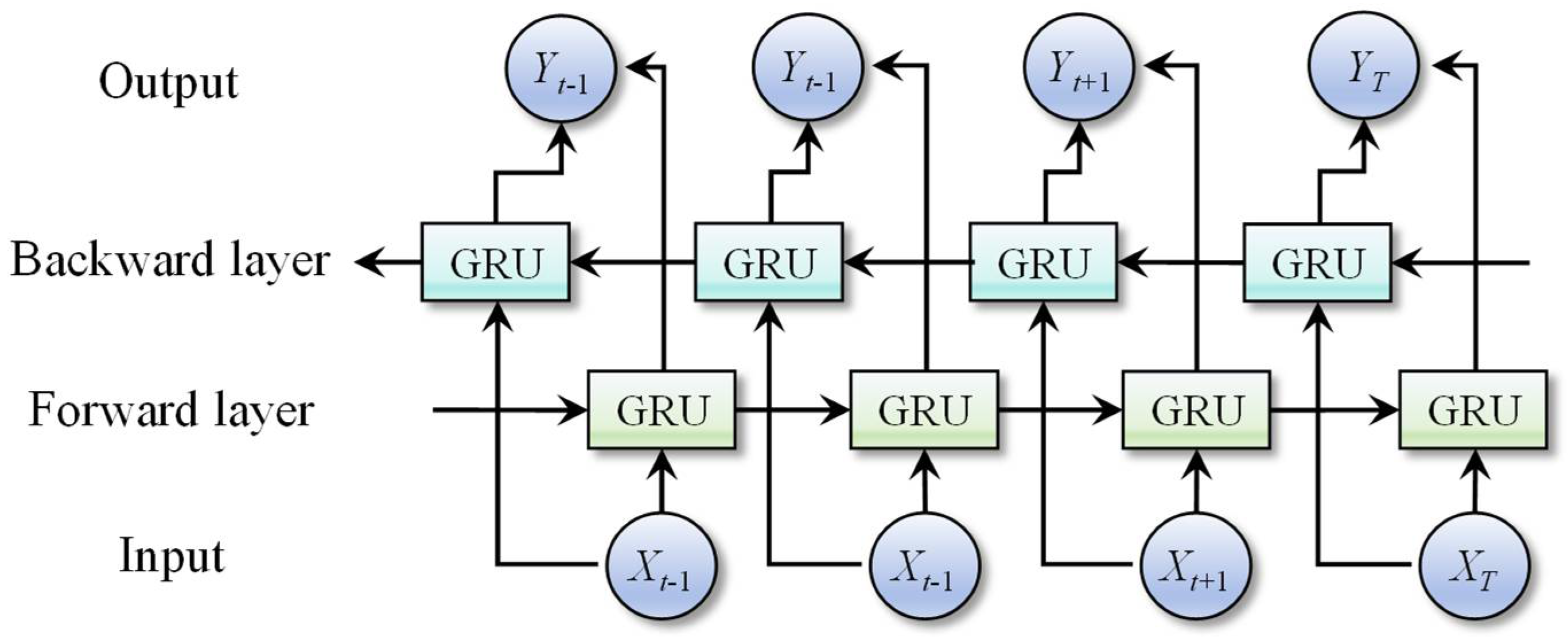
3.3. Bidirectional Gated Recurrent Unit
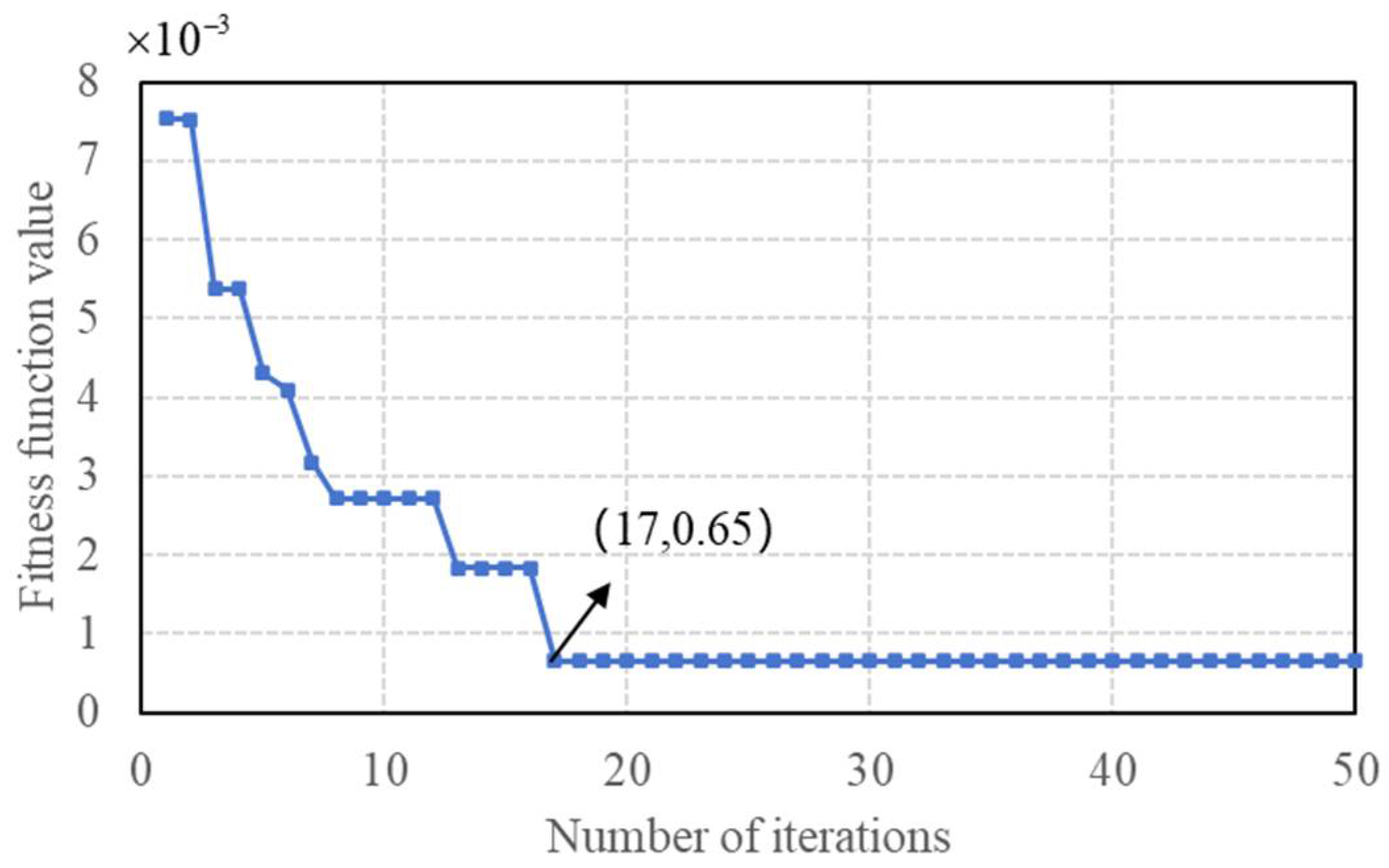
3.4. Improved Kepler Optimization Algorithm
- (1)
- Bernoulli chaotic mapping
- (2)
- Runge–Kutta-inspired position update
- (3)
- ESQ exploration enhancement
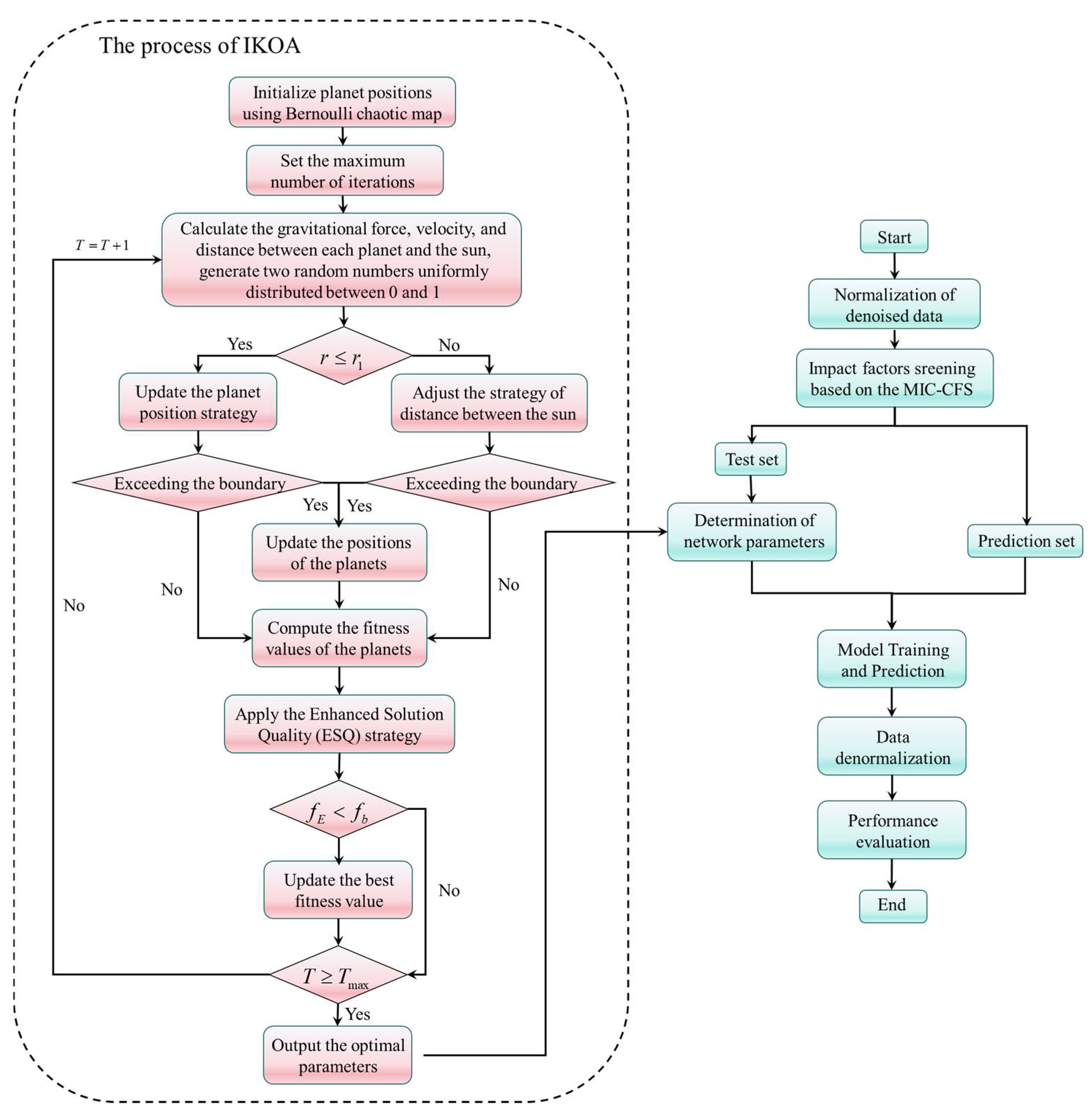
3.5. Establishment Steps of the Proposed Prediction Model
4. Case Study
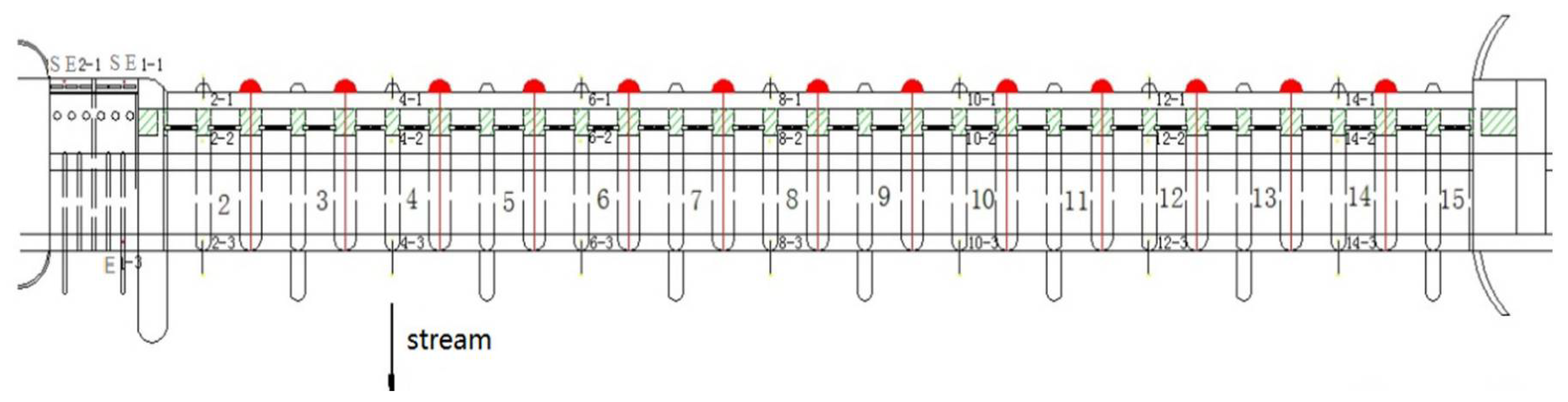
4.1. Project Overview
4.2. Results and Discussion
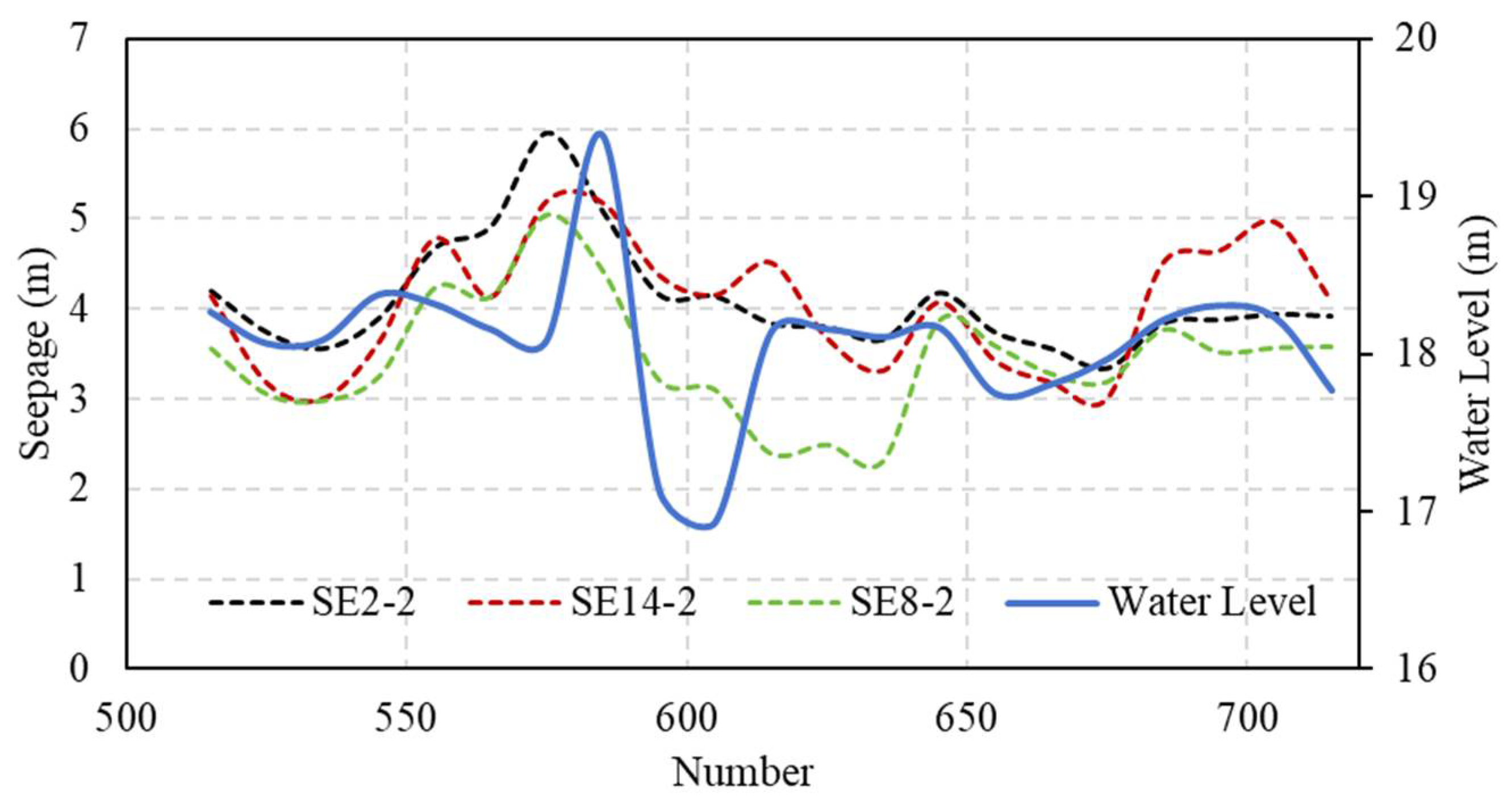
4.2.1. Impact Factor Screening Results
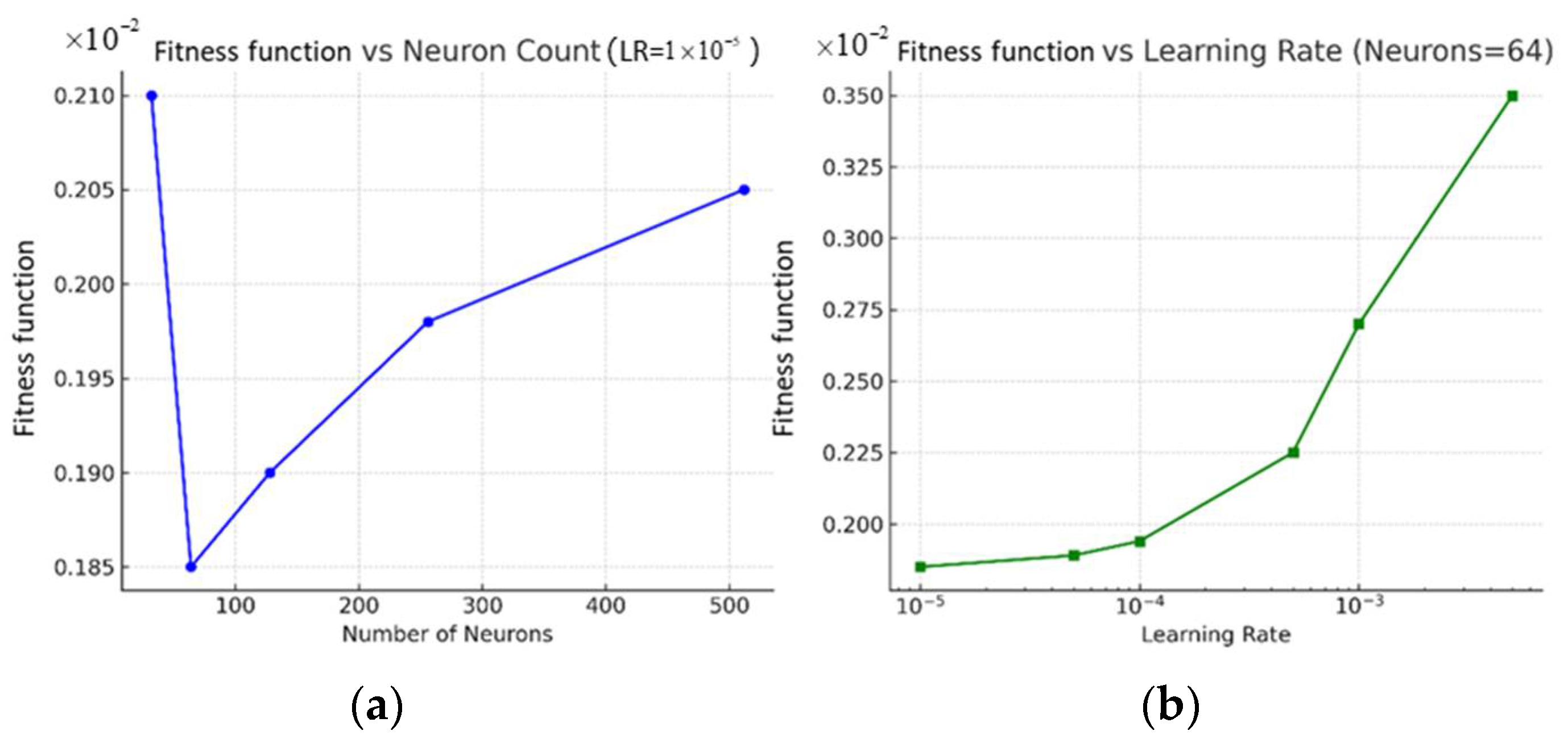
4.2.2. Results of the IKOA–BIGRU Model
4.2.3. Model Interpretability Analysis Through SHAP
4.2.4. Fitting and Prediction Results Comparison
5. Conclusions
- (1)
- The main impact factor screening method based on the MIC–CFS effectively identifies a set of features with high relevance to sluice seepage and low redundancy. The process of the selection reduces the complexity of the prediction model significantly, mitigates the risk of overfitting, and enhances the overall generalization and prediction accuracy.
- (2)
- By optimizing the Kepler optimization algorithm (KOA) based on chaotic mapping, Runge–Kutta position updating, and ESQ strategies, the efficiency of the optimization algorithm is significantly improved. The integration of the improved Kepler optimization algorithm (IKOA) for hyperparameter tuning effectively reduces the uncertainty associated with manual parameter selection, improving the efficiency of model development as a result.
- (3)
- The case study demonstrates that, compared to other predictive models, the IKOA–BiGRU model exhibits obvious advantages in sluice seepage prediction. Incorporating the BiGRU model into the prediction framework effectively compensates for the limitations of the GRU in capturing deep temporal features of sluice seepage data, enabling a more accurate representation of seepage patterns. The proposed model demonstrates superior prediction performance, with R2 values ranging from 0.974 to 0.988 and MAE values between 0.074 and 0.064. Comparative analyses further vali-date the effectiveness and feasibility of the proposed model, highlighting its potential as a valuable reference for practical sluice seepage forecasting.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, X.; Wu, Z.; Liu, L.; Wen, Y.; Yu, S.; Zhao, Z.; Li, Z. Analysis of Sluice Foundation Seepage Using Monitoring Data and Numerical Simulation. Adv. Civ. Eng. 2019, 2019, 2850916. [Google Scholar]
- Zhang, T.; Li, C.; Du, X.; Yu, Y. Anti-seepage Technology for a Sluice Foundation on Soft Soil. Appl. Mech. Mater. 2014, 638, 384–388. [Google Scholar]
- Ma, F.; Hu, J.; Ye, W. Study on key technical elements of technical specification for sluice safety monitoring. Water Resour. Hydropower Eng. 2019, 50, 90–94. (In Chinese) [Google Scholar]
- Chen, S. Sluices and barrages. In Hydraulic Structures; Springer: Berlin/Heidelberg, Germany, 2015; pp. 643–713. [Google Scholar]
- Huang, Z.; Gu, C.; Peng, J.; Wu, Y.; Gu, H.; Shao, C.; Zheng, S.; Zhu, M. A Statistical Prediction Model for Sluice Seepage Based on MHHO-BiLSTM. Water 2024, 16, 191. [Google Scholar] [CrossRef]
- Cai, X.; Cui, Z.; Guo, X.; Li, F.; Zhang, Y. Seismic Safety Design and Analysis of Hydraulic Sluice Chamber Structure Based on Finite Element Method. Comput. Intell. Neurosci. 2022, 2022, 6183588. [Google Scholar] [CrossRef]
- Chen, L. Safety Monitoring of Sluice Gate of Xinglong Water Control Project on Hanjiang River. Rural. Water Conserv. Hydropower China 2015, 8, 165–167. [Google Scholar]
- Liu, Y.; Luo, L.; Wu, G. Analysis and Study on Seepage Safety Monitoring of Zhaoshandu Diversion Project. In Proceedings of the 2022 8th ICHCE, Xi’an, China, 25–27 November 2022; pp. 1027–1031. [Google Scholar]
- Yu, G.; Wang, Z.; Zhang, B.; Xie, Z. The grey relational analysis of sluice monitoring data. Procedia Eng. 2011, 15, 5192–5196. [Google Scholar]
- Liu, B.; Cen, W.; Zheng, C.; Li, D.; Wang, L. A combined optimization prediction model for earth-rock dam seepage pressure using multi-machine learning fusion with decomposition data-driven. Expert Syst. Appl. 2024, 242, 122798. [Google Scholar] [CrossRef]
- Fatehi-Nobarian, B.; Fard Moradinia, S. Wavelet–ANN hybrid model evaluation in seepage prediction in nonhomogeneous earthen dams. Water Pract. Technol. 2024, 19, 2492–2511. [Google Scholar] [CrossRef]
- Rehamnia, I.; Al-Janabi, A.M.S.; Sammen, S.S.; Pham, B.T.; Prakash, I. Prediction of seepage flow through earthfill dams using machine learning models. HydroResearch 2024, 7, 131–139. [Google Scholar] [CrossRef]
- Cao, W.; Wen, Z.; Feng, Y.; Zhang, S.; Su, H. A multi-point joint prediction model for high-arch dam deformation considering spatial and temporal correlation. Water 2024, 16, 1388. [Google Scholar] [CrossRef]
- Shao, C.; Gu, C.; Yang, M.; Xu, Y.; Su, H. A novel model of dam displacement based on panel data. Struct. Control. Health Monit. 2018, 25, e2037. [Google Scholar] [CrossRef]
- Cai, S.; Gao, H.; Zhang, J.; Peng, M. A self-attention-LSTM method for dam deformation prediction based on CEEMDAN optimization. Appl. Soft Comput. 2024, 159, 111615. [Google Scholar] [CrossRef]
- Lei, W.; Wang, J. Dynamic Stacking ensemble monitoring model of dam displacement based on the feature selection with PCA-RF. J. Civ. Struct. Health Monit. 2022, 12, 557–578. [Google Scholar] [CrossRef]
- Kang, X.; Li, Y.; Zhang, Y.; Wen, L.; Sun, X.; Wang, J. PCA-IEM-DARNN: An enhanced dual-stage deep learning prediction model for concrete dam deformation based on feature decomposition. Measurement 2025, 242, 115664. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, D.; Cao, Z.; Liu, Y. Spatio-temporal water height prediction for dam break flows using deep learning. Ocean Eng. 2024, 302, 117567. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, D.; Wu, X.; Chen, X.; Georgakis, C.; Qiu, J. Research on prediction of dam seepage and dual analysis of lag-sensitivity of influencing factors based on MIC optimizing random forest algorithm. KSCE J. Civ. Eng. 2023, 27, 508–520. [Google Scholar] [CrossRef]
- Shi, Z.; Li, J.; Wang, Y.; Gu, C.; Jia, H.; Xu, N.; Pan, W. Characterization Model Research on Deformation of Arch Dam Based on Correlation Analysis Using Monitoring Data. Mathematics 2024, 12, 3110. [Google Scholar] [CrossRef]
- Peng, J.; Xie, W.; Wu, Y.; Sun, X.; Zhang, C.; Gu, H.; Zhu, M.; Zheng, S. Prediction for the Sluice Deformation Based on SOA-LSTM-Weighted Markov Model. Water 2023, 15, 3724. [Google Scholar] [CrossRef]
- Ma, Z.; Lou, B.; Shen, Z.; Ma, F.; Luo, X.; Ye, W.; Li, D. A Deformation Analysis Method for Sluice Structure Based on Panel Data. Water 2024, 16, 1287. [Google Scholar] [CrossRef]
- Xing, Y.; Chen, Y.; Huang, S.; Wang, P.; Xiang, Y. Research on dam deformation prediction model based on optimized SVM. Processes 2022, 10, 1842. [Google Scholar] [CrossRef]
- Xu, Y.; Bao, T.; Yuan, M.; Zhang, S. A Reservoir Dam Monitoring Technology Integrating Improved ABC Algorithm and SVM Algorithm. Water 2025, 17, 302. [Google Scholar] [CrossRef]
- Jiang, Z. Monitoring model group of seepage behavior of earth-rock dam based on the mutual information and support vector machine algorithms. Struct. Health Monit. 2024, 24, 466–480. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Li, Y.; Wen, L.; Sun, X. AF-OS-ELM-MVE: A new online sequential extreme learning machine of dam safety monitoring model for structure deformation estimation. Adv. Eng. Inform. 2024, 60, 102345. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, Z.; Huang, J. Intelligent Prediction on Cement Take of Dam Foundation Grouting Based on GOA-ELM Model. Hydraul. Struct. Hydrodyn. 2024, 608, 121–131. [Google Scholar]
- Ou, B.; Zhang, C.; Xu, B.; Fu, S.; Liu, Z.; Wang, K. Innovative Approach to Dam Deformation Analysis: Integration of VMD, Fractal Theory, and WOA-DELM. Struct. Control Health Monit. 2024, 2024, 1710019. [Google Scholar] [CrossRef]
- Al-Hardanee, O.F.; Demirel, H. Hydropower Station Status Prediction Using RNN and LSTM Algorithms for Fault Detection. Energies 2024, 17, 5599. [Google Scholar] [CrossRef]
- Yang, X.; Xiang, Y.; Wang, Y.; Shen, G. A Dam Safety State Prediction and Analysis Method Based on EMD-SSA-LSTM. Water 2024, 16, 395. [Google Scholar] [CrossRef]
- Hu, Y.; Gu, C.; Meng, Z.; Shao, C.; Min, Z. Prediction for the Settlement of Concrete Face Rockfill Dams Using Optimized LSTM Model via Correlated Monitoring Data. Water 2022, 14, 2157. [Google Scholar] [CrossRef]
- Abdi, E.; Taghi Sattari, M.; Milewski, A.; Ibrahim, O.R. Advancements in Hydrological Modeling: The Role of bRNN-CNN-GRU in Predicting Dam Reservoir Inflow Patterns. Water 2025, 17, 1660. [Google Scholar] [CrossRef]
- Hua, G.; Wang, S.; Xiao, M.; Hu, S. Research on the Uplift Pressure Prediction of Concrete Dams Based on the CNN-GRU Model. Water 2023, 15, 319. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, H.; Xia, H.; Song, D.; Zhu, Z.; Chen, Z.; Lu, J. A multi-level prediction model of concrete dam displacement considering time hysteresis and residual correction. Meas. Sci. Technol. 2024, 36, 015107. [Google Scholar] [CrossRef]
- Ma, N.; Niu, X.; Chen, X.; Wei, W.; Zhang, Y.; Kang, X.; Wu, J. Analysis of Concrete Dam Deformation Prediction Based on the ResNet-GRU-SGWO Model. Adv. Civ. Eng. 2024, 2024, 4791788. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J.; Li, Z.; Lu, Q. ISSA optimized spatiotemporal prediction model of dissolved oxygen for marine ranching integrating DAM and Bi-GRU. Front. Mar. Sci. 2024, 11, 1473551. [Google Scholar] [CrossRef]
- Reshef, D.; Reshef, Y.; Finucane, H.; Grossman, S.; McVean, G.; Turnbaugh, P.; Sabeti, P. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef]
- Wu, T.; Wang, M.; Xi, Y.; Zhao, Z. Malicious URL Detection Model Based on Bidirectional Gated Recurrent Unit and Attention Mechanism. Appl. Sci. 2022, 12, 12367. [Google Scholar] [CrossRef]
- Saito, A.; Yamaguchi, A. Pseudorandom number generation using chaotic true orbits of the Bernoulli map. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 063122. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.; Gandomi, A.; Chu, X.; Chen, H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]










| Input: - BIGRU hyperparameter search space H = {h₁, h₂,…, h_D} e.g., h = [learning rate, number of neurons] - f(h): Objective function - N: Number of planets (population size) - Tmax: Max number of iterations - Bound: lower & upper bounds for each hyperparameter Output: - h_best: Optimal hyperparameter set - f(h_best): Best validation performance |
| 1. Initialization with Bernoulli Chaotic Mapping: for i in 1 to N: for each dimension d in H: β = rand() in [0, 1] if 0 <= z [i][d] <= 1−β: z[i][d] = z[i][d]/(1-β) else: z[i][d] = (z[i][d]-(1-β)/) 2. Evaluate fitness F[i] = f(P[i]) Set global_best = best P[i] with minimum F[i] 3. For T in 1 to Tmax: a. For each planet i: i. Runge-Kutta Inspired Position Update Compute k1 =0.5*(rand() *f(P[i])) k2 = 0.5*(rand()*(f(P[i])+q2*k1*Δx/2 – (C* f(P[i])+q1*k1*Δx/2) k3 = 0.5*(rand()*(f(P[i])+q2*k2*Δx/2 – (C* f(P[i])+q1*k2*Δx/2) k4 =0.5*(rand()*(f(P[i])+q2*k3*Δx/2 – (C* f(P[i])+q1*k3*Δx/2) SM = (1/6) * (k1 + 2*k2 + 2*k3 + k4) f = a * exp(-b*rand()*T/Tmax) SF=2*(0.5-rand())*f New_P[i] = (f(P[i])-rand()*f(P[i])) + SF *(SM+2*rand()*f(P[i])- f(P[i])) If New_P[i] violates bounds: Relocate with stochastic repositioning: New_P[i][d] = Lower[d] + rand() * (Upper[d] - Lower[d]) ii. Apply ESQ strategy: r ∈ {−1, 0, 1}, u ∈ [0, 2], β ∈ [0, 1] ReferencePosition = (P[r1] + P[r2] + P[r3])/3 ω = rand(0,2)*exp(-c*T/Tmax) ESQ_Position_temp=β* ReferencePosition+(1-β)* f(P[i]) If ω < 1: ESQ_Position = ESQ_Position_temp+r*ω*|(ESQ_Position_temp- Ref erencePosition) + rand()| else: ESQ_Position = ESQ_Position_temp+ | r*ω* (u* ESQ_Position_temp- Ref erencePosition) + rand()| Evaluate f(ESQ_Position) If f(ESQ_Position) < f(P[i]): P[i] = ESQ_Position iii. Evaluate New fitness F[i] = f(P[i]) b. Update global_best if new best found 4. Return global_best, f(global_best) |
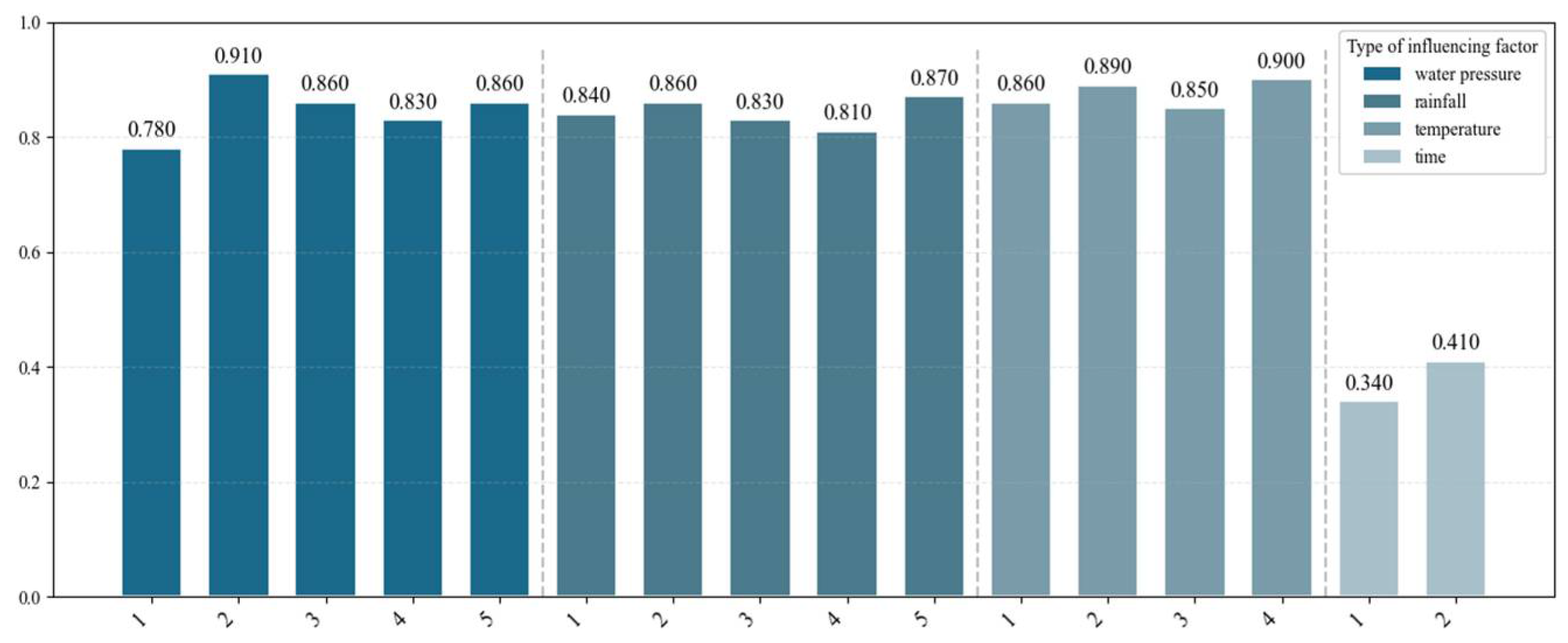
| Coefficient | MIC | Pearson | |
|---|---|---|---|
| Impact factors about water pressure | 0.84 | 0.95 | |
| 0.98 | 0.89 | ||
| 0.94 | 0.92 | ||
| 0.85 | 0.87 | ||
| 0.81 | 0.84 | ||
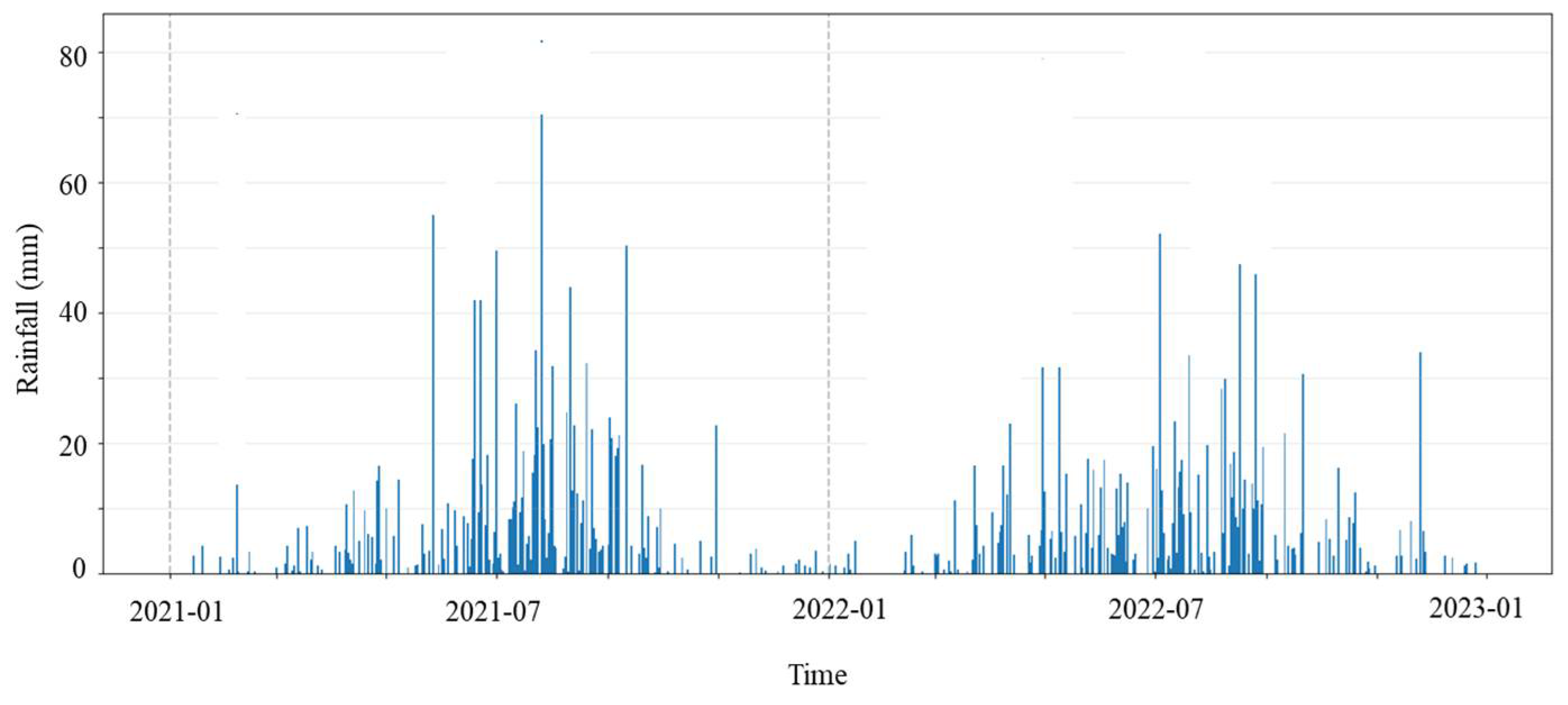
| Impact factors about rainfall | 0.83 | 0.81 | |
| 0.73 | 0.44 | ||
| 0.74 | 0.43 | ||
| 0.77 | 0.58 | ||
| 0.75 | 0.69 | ||
| Impact factors about temperature | 0.68 | −0.23 | |
| 0.63 | 0.27 | ||
| 0.72 | 0.33 | ||
| 0.63 | −0.43 | ||
| Impact factors about time | 0.44 | 0.06 | |
| 0.44 | 0.21 | ||
| Evaluation Metric | IKOA–BiGRU Model | Stepwise Regression Model | IKOA–LSTM Model | IKOA–GRU Model | |
|---|---|---|---|---|---|
| SE2-2 | MAE | 0.0567 | 0.3005 | 0.1348 | 0.1319 |
| MSE | 0.0051 | 0.1123 | 0.0254 | 0.0239 | |
| RMSE | 0.0709 | 0.3282 | 0.1579 | 0.1531 | |
| R2 | 0.9853 | 0.5896 | 0.9183 | 0.9321 | |
| WI | 0.9595 | 0.7473 | 0.8984 | 0.9058 | |
| KGE | 0.9659 | 0.7941 | 0.9245 | 0.9117 | |
| SE8-2 | MAE | 0.0638 | 0.09 | 0.0643 | 0.0795 |
| MSE | 0.0054 | 0.0124 | 0.0063 | 0.0082 | |
| RMSE | 0.0729 | 0.1112 | 0.0776 | 0.0882 | |
| R2 | 0.9879 | 0.9721 | 0.9844 | 0.9805 | |
| WI | 0.9636 | 0.9481 | 0.9612 | 0.9532 | |
| KGE | 0.9749 | 0.9544 | 0.9645 | 0.9665 | |
| SE14-2 | MAE | 0.0743 | 0.1138 | 0.1014 | 0.0986 |
| MSE | 0.0124 | 0.0186 | 0.0214 | 0.0181 | |
| RMSE | 0.1112 | 0.1317 | 0.1335 | 0.1346 | |
| R2 | 0.9736 | 0.9587 | 0.9514 | 0.9597 | |
| WI | 0.9601 | 0.9379 | 0.9438 | 0.9461 | |
| KGE | 0.9655 | 0.9476 | 0.9546 | 0.9498 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Peng, J.; Zhang, C.; Zheng, S. Prediction of Sluice Seepage Based on Impact Factor Screening and the IKOA-BiGRU Model. Water 2025, 17, 1850. https://doi.org/10.3390/w17131850
Sun X, Peng J, Zhang C, Zheng S. Prediction of Sluice Seepage Based on Impact Factor Screening and the IKOA-BiGRU Model. Water. 2025; 17(13):1850. https://doi.org/10.3390/w17131850
Chicago/Turabian StyleSun, Xiaoran, Jianhe Peng, Chunlin Zhang, and Sen Zheng. 2025. "Prediction of Sluice Seepage Based on Impact Factor Screening and the IKOA-BiGRU Model" Water 17, no. 13: 1850. https://doi.org/10.3390/w17131850
APA StyleSun, X., Peng, J., Zhang, C., & Zheng, S. (2025). Prediction of Sluice Seepage Based on Impact Factor Screening and the IKOA-BiGRU Model. Water, 17(13), 1850. https://doi.org/10.3390/w17131850






