Improved Reinforcement Learning for Multi-Objective Optimization Operation of Cascade Reservoir System Based on Monotonic Property
Abstract
1. Introduction
2. Optimality Condition for Multi-Objective Operation of Cascade Reservoir System
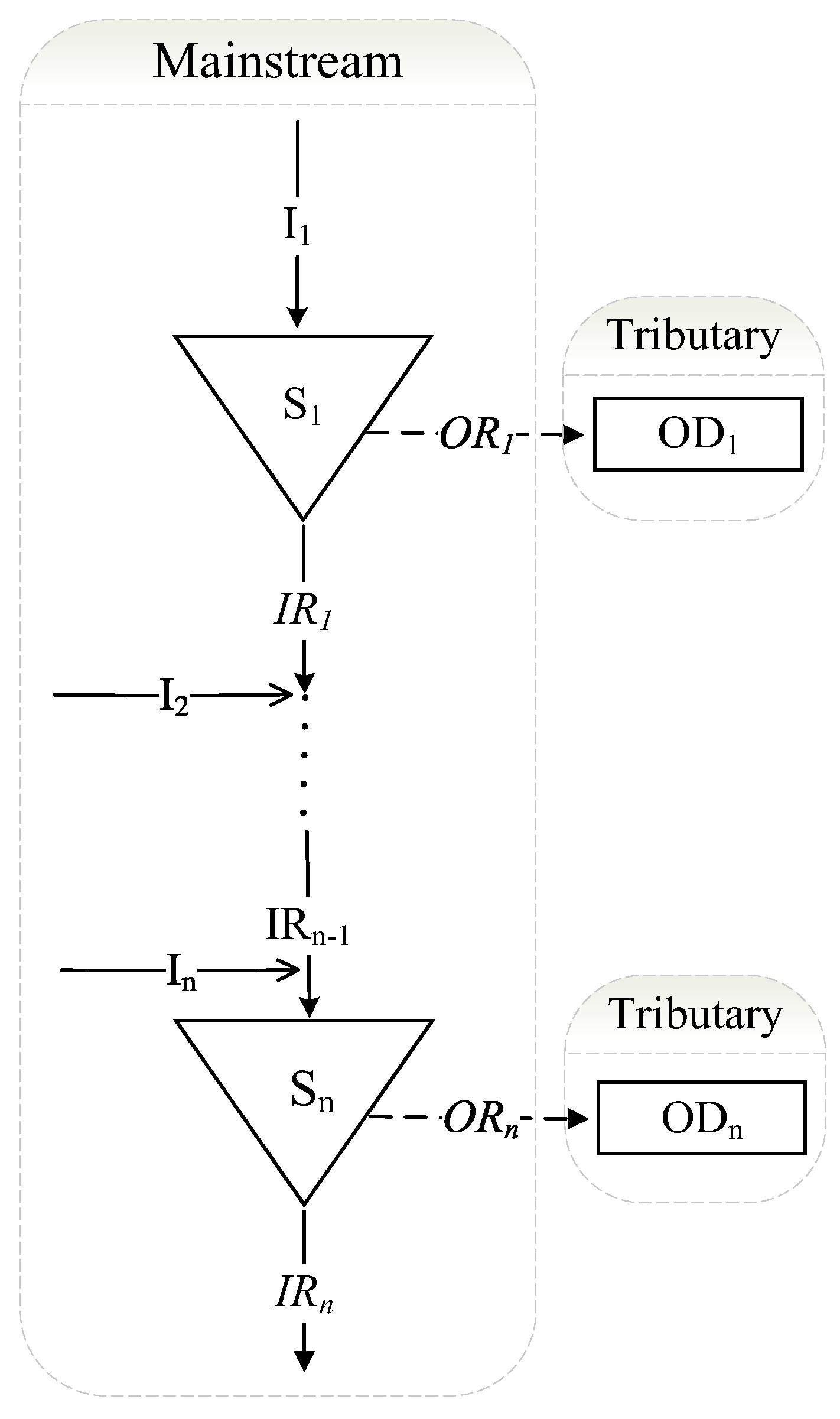
2.1. Stochastic Optimization Operation Model for Cascade Reservoir System
2.2. Stochastic Dynamic Programming for System Optimization Operation
2.3. Reinforcement Learning for System Optimization Operation
2.4. The Optimality Principle of Equal Marginal Utility
3. Monotonic Property for Multi-Objective Optimization Operation of Cascade Reservoir Systems
3.1. Monotonic Property of Water Release for the Tributary Use
3.2. Monotonic Property of Water Release for the Mainstream Use
3.3. Quantitative Analysis Based on the Monotonic Property
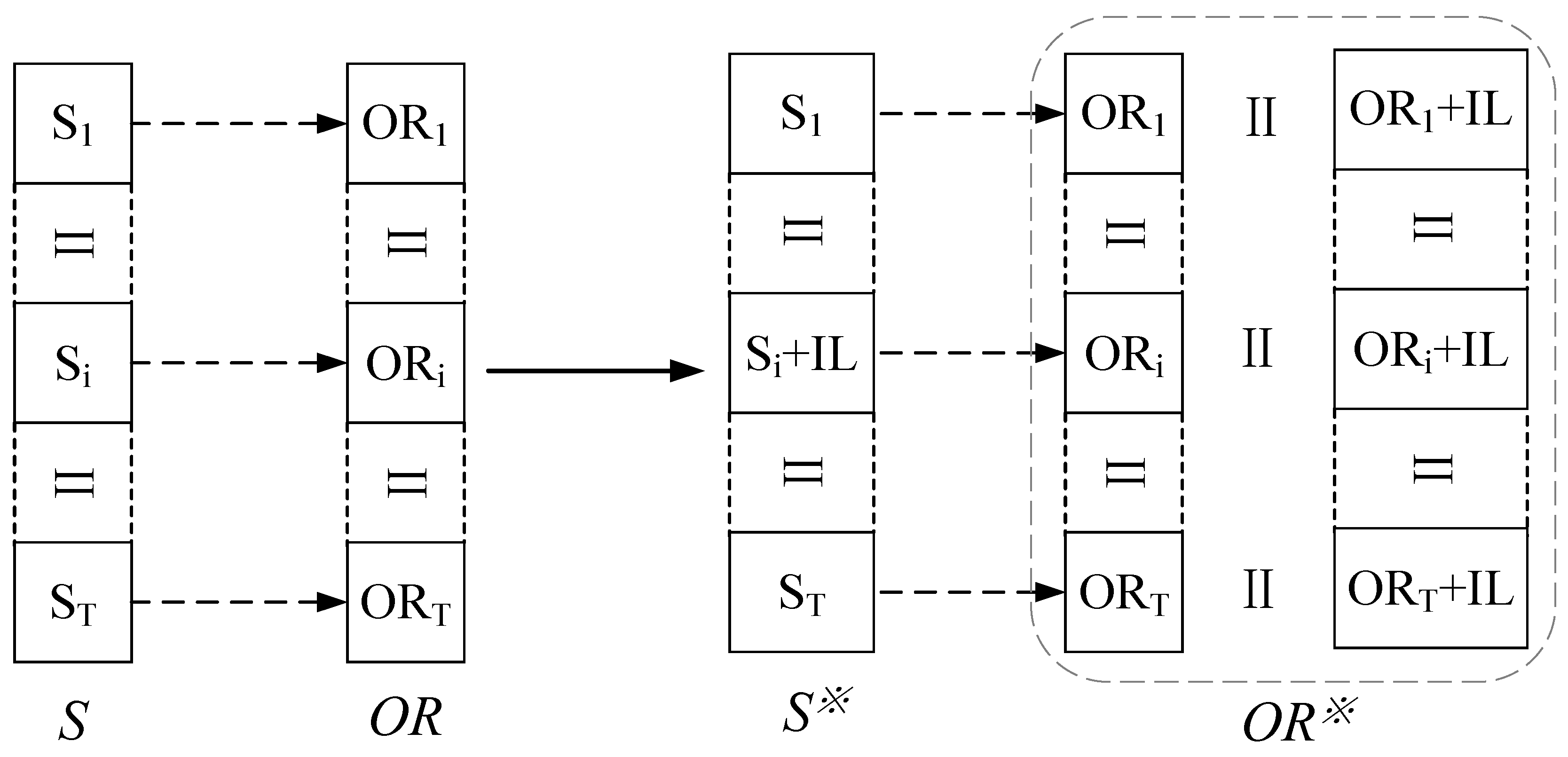
4. Improved Reinforcement Learning Method for Optimization Operation of Cascade Reservoir System
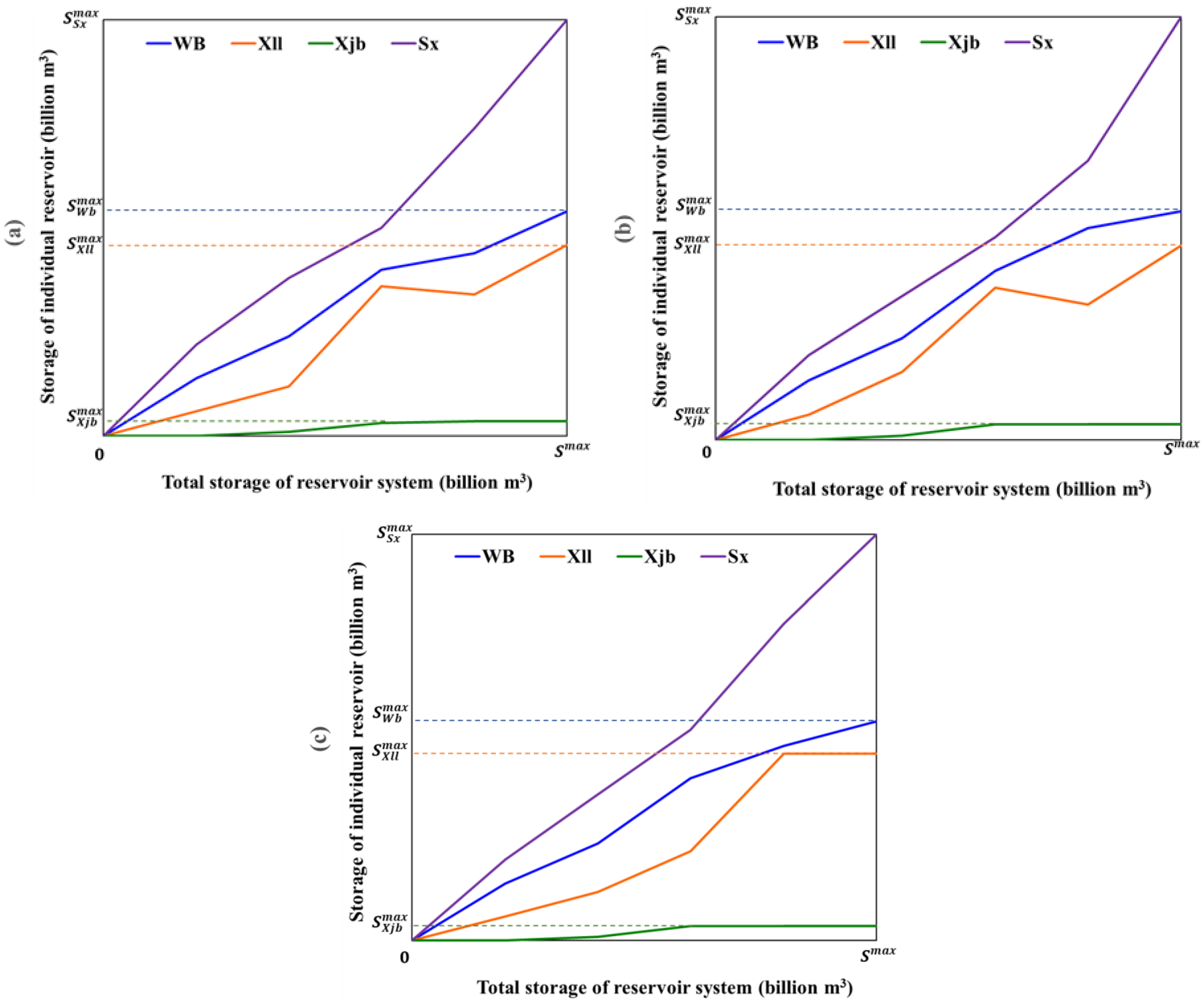
5. Case Study
5.1. System Description
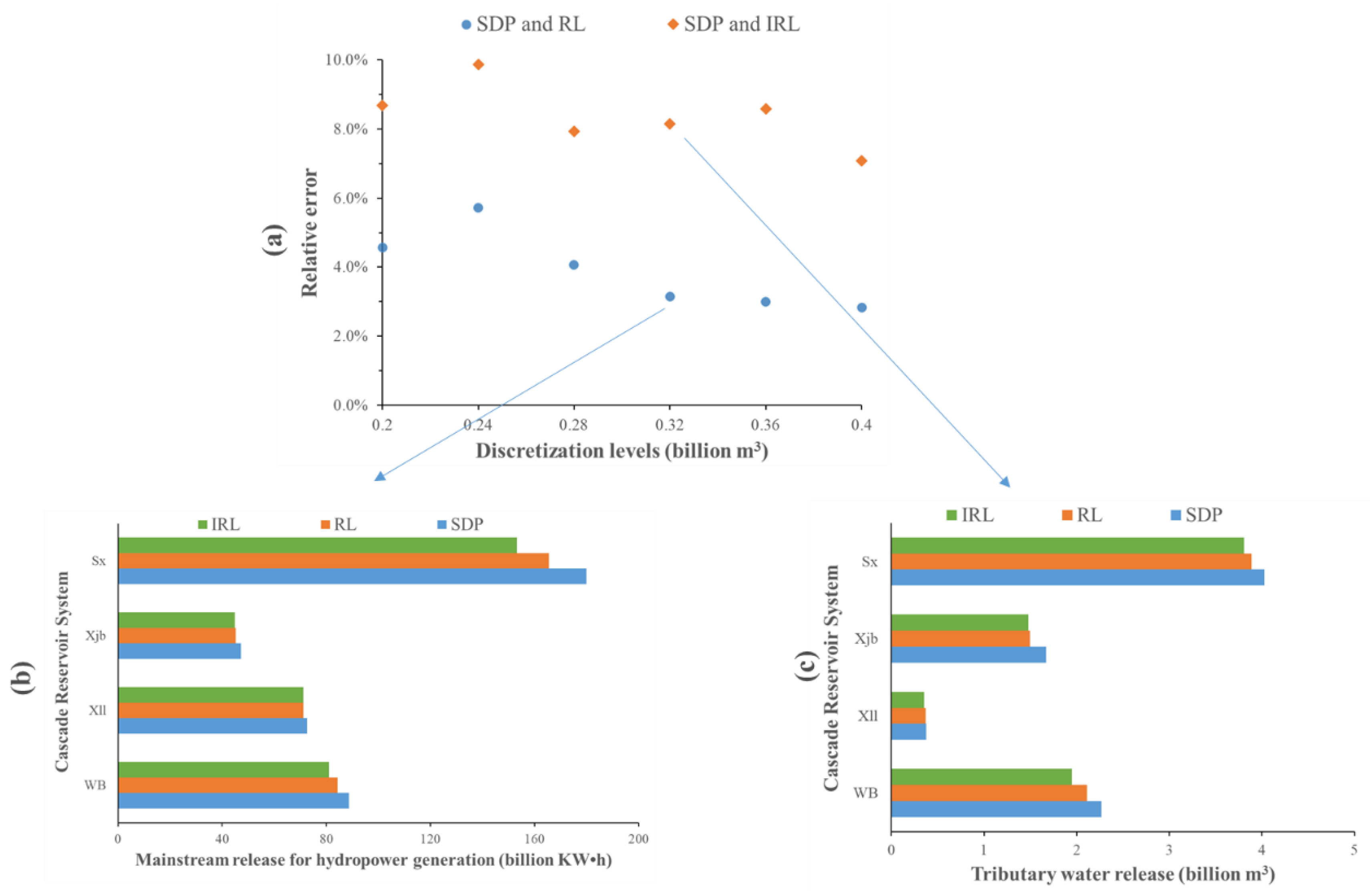
5.2. Comparison Analysis of Optimization Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yeh, W.W.G. Reservoir Management and Operations Models: A State-of-the-Art Review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Oliverira, R.; Loucks, D.P. Operating Rules for Multireservoir Systems. Water Resour. Res. 1997, 33, 839–852. [Google Scholar] [CrossRef]
- Ahmad, A.; El-Shafie, A.; Razali, S.F.M.; Mohamad, Z.S. Reservoir Optimization in Water Resources: A Review. Water Resour. Manag. 2014, 28, 3391–3405. [Google Scholar] [CrossRef]
- Wurbs, R.A. Reservoir System Simulation and Optimization Models. J. Water Resour. Plan. Manag. 1993, 119, 455–472. [Google Scholar] [CrossRef]
- Labadie, J. Optimal Operation of Multi-Reservoir Systems: State-of-the-Art Review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Rani, D.; Moreira, M.M. Simulation-Optimization Modeling: A Survey and Potential Application in Reservoir Systems Operation. Water Resour. Manag. 2010, 24, 1107–1138. [Google Scholar] [CrossRef]
- Dobson, B.; Wagener, T.; Pianosi, F. An Argument-Driven Classification and Comparison of Reservoir Operation Optimization Methods. Adv. Water Resour. 2019, 128, 74–86. [Google Scholar] [CrossRef]
- Giuliani, M.; Lamontagne, J.R.; Reed, P.M.; Castelletti, A. A State-of-the-Art Review of Optimal Reservoir Control for Managing Conflicting Demands in a Changing World. Water Resour. Res. 2021, 57, e2021WR029927. [Google Scholar] [CrossRef]
- Mendoza-Ramírez, R.; Silva, R.; Domínguez-Mora, R.; Juan-Diego, E.; Carrizosa-Elizondo, E. Comparison of Two Convergence Criterion in the Optimization Process Using a Recursive Method in a Multi-Reservoir System. Water 2022, 14, 2952. [Google Scholar] [CrossRef]
- Powell, W. Approximate Dynamic Programming: Solving the Curses of Dimensionality, 2nd ed.; Wiley: Hoboken, NJ, USA, 2011; ISBN 9780470604458. [Google Scholar]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018; ISBN 9780262039246. [Google Scholar]
- Tilmant, A.; Kelman, R. A Stochastic Approach to Analyze Trade-Offs and Risks Associated with Large-Scale Water Resources Systems. Water Resour. Res. 2007, 43, W06425. [Google Scholar] [CrossRef]
- Howson, H.R.; Sancho, N.G.F. A New Algorithm for the Solution of Multistate Dynamic Programming Problems. Math. Program. 1975, 8, 104–116. [Google Scholar] [CrossRef]
- Turgeon, A. Optimal Operation of Multireservoir Power Systems with Stochastic Inflows. Water Resour. Res. 1980, 16, 275–283. [Google Scholar] [CrossRef]
- Turgeon, A.; Charbonneau, R. An Aggregation-Disaggregation Approach to Long-Term Reservoir Management. Water Resour. Res. 1998, 34, 3585–3594. [Google Scholar] [CrossRef]
- Zeng, X.; Hu, T.S.; Xiong, L.H.; Cao, Z.X.; Xu, C.Y. Derivation of Operation Rules for Reservoirs in Parallel with Joint Water Demand. Water Resour. Res. 2015, 51, 9539–9563. [Google Scholar] [CrossRef]
- Zeng, X.; Hu, T.S.; Cai, X.M.; Zhou, Y.L.; Wang, X. Improved Dynamic Programming for Parallel Reservoir System Operation Optimization. Adv. Water Resour. 2019, 131, 103373. [Google Scholar] [CrossRef]
- Beiranvand, B.; Ashofteh, P.S. A Systematic Review of Optimization of Dams Reservoir Operation Using the Meta-heuristic Algorithms. Water Resour. Manag. 2023, 37, 3457–3526. [Google Scholar] [CrossRef]
- Emami, M.; Nazif, S.; Mousavi, S.F.; Karami, H.; Daccache, A. A hybrid constrained coral reefs optimization algorithm with machine learning for optimizing multi-reservoir systems operation. J. Environ. Manag. 2021, 286, 112250. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.S. Learning to Predict by the Methods of Temporal Differences. Mach. Learn. 1988, 3, 9–44. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H.; Dayan, P. Technical Note: Q-Learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Castro Freibott, R.; García Sánchez, Á.; Espiga-Fernández, F.; González-Santander de la Cruz, G. Intraday Multireservoir Hydropower Optimization with Alternative Deep Reinforcement Learning Configurations. In Decision Sciences (DSA ISC 2024); Lecture Notes in Computer Science; Juan, A.A., Faulin, J., Lopez-Lopez, D., Eds.; Springer: Cham, Switzerland, 2025; Volume 14778. [Google Scholar]
- Luo, W.; Wang, C.; Zhang, Y.; Zhao, J.; Huang, Z.; Wang, J.; Zhang, C. A Deep Reinforcement Learning Approach for Joint Scheduling of Cascade Reservoir System. J. Hydrol. 2025, 651, 132515. [Google Scholar] [CrossRef]
- Lee, J.H.; Labadie, J.W. Stochastic Optimization of Multireservoir Systems via Reinforcement Learning. Water Resour. Res. 2007, 43, W11408. [Google Scholar] [CrossRef]
- Castelletti, A. A Reinforcement Learning Approach for the Operational Management of a Water System. In Proceedings of IFAC Workshop Modelling and Control in Environmental Issues; Elsevier: Yokohama, Japan, 2001; pp. 22–23. [Google Scholar]
- Xu, W.; Zhang, X.; Peng, A.B.; Liang, Y. Deep Reinforcement Learning for Cascaded Hydropower Reservoirs Considering Inflow Forecasts. Water Resour. Manag. 2020, 34, 3003–3018. [Google Scholar] [CrossRef]
- Wu, R.; Wang, R.; Hao, J.; Wu, Q.; Wang, P. Multiobjective Hydropower Reservoir Operation Optimization with Transformer-Based Deep Reinforcement Learning. arXiv 2023, arXiv:230705643. [Google Scholar]
- Mitjana, F.; Denault, M.; Demeester, K. Managing Chance-Constrained Hydropower with Reinforcement Learning and Backoffs. Adv. Water Resour. 2022, 169, 104308. [Google Scholar] [CrossRef]
- Zhao, T.T.G.; Cai, X.M.; Lei, X.H.; Wang, H. Improved Dynamic Programming for Reservoir Operation Optimization with a Concave Objective Function. J. Water Resour. Plan. Manag. 2012, 138, 590–596. [Google Scholar] [CrossRef]
- Zhao, T.T.G.; Zhao, J.S.; Yang, D.W. Improved Dynamic Programming for Hydropower Reservoir Operation. J. Water Resour. Plan. Manag. 2014, 140, 365–374. [Google Scholar] [CrossRef]
- Zhao, T.T.G.; Zhao, J.S.; Lei, X.H.; Wang, X.; Wu, B.S. Improved Dynamic Programming for Reservoir Flood Control Operation. Water Resour. Manag. 2017, 31, 2047–2063. [Google Scholar] [CrossRef]
- You, J.Y.; Cai, X.M. Hedging Rule for Reservoir Operations: 1. A Theoretical Analysis. Water Resour. Res. 2008, 44, W01415. [Google Scholar] [CrossRef]
- Shiau, J.T. Analytical Optimal Hedging with Explicit Incorporation of Reservoir Release and Carryover Storage Targets. Water Resour. Res. 2011, 47, W01515. [Google Scholar] [CrossRef]
- Zeng, X.; Lund, J.R.; Cai, X.M. Linear versus Nonlinear (Convex and Concave) Hedging Rules for Reservoir Optimization Operation. Water Resour. Res. 2021, 57, e2020WR029160. [Google Scholar] [CrossRef]
- Fama, E.F. Multiperiod Consumption-Investment Decisions. Am. Econ. Rev. 1970, 60, 163–174. [Google Scholar]
- Draper, A.J.; Lund, J.R. Optimal Hedging and Carryover Storage Value. J. Water Resour. Plan. Manag. 2004, 130, 83–87. [Google Scholar] [CrossRef]
- Carroll, C.D.; Kimball, M.S. On the Concavity of the Consumption Function. Econometrica 1996, 64, 981–992. [Google Scholar] [CrossRef]
- Johnson, S.A.; Stedinger, J.R.; Staschus, K. Heuristic Operating Policies for Reservoir System Simulation. Water Resour. Res. 1991, 27, 673–685. [Google Scholar] [CrossRef]
- Sand, G.M. An Analytical Investigation of Operating Policies for Water-Supply Reservoirs in Parallel. Ph.D. Dissertation, Cornell University, Ithaca, NY, USA, 1984. [Google Scholar]
- Lund, J.R.; Ferreira, I. Operating Rule Optimization for Missouri River Reservoir System. J. Water Resour. Plan. Manag. 1996, 122, 287–295. [Google Scholar] [CrossRef]
- Perera, B.J.C.; Codner, P.G. Reservoir Targets for Urban Water Supply Systems. J. Water Resour. Plan. Manag. 1996, 122, 270–279. [Google Scholar] [CrossRef]
- Nalbantis, I.; Koutsoyiannis, D. A Parametric Rule for Planning and Management of Multiple Reservoir Systems. Water Resour. Res. 1997, 33, 2165–2177. [Google Scholar] [CrossRef]
- Zhao, J.S.; Cai, X.M.; Wang, Z.J. Optimality conditions for a two-stage reservoir operation problem. Water Resour. Res. 2011, 47, W08503. [Google Scholar] [CrossRef]
- You, J.Y.; Cai, X.M. Hedging Rule for Reservoir Operations: 2. A Numerical Model. Water Resour. Res. 2008, 44, W01416. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, Z.; Xu, Y.; Wang, S.; Wang, P. Discussion on the monotonicity principle of the two-stage problem in joint optimal operation of cascade hydropower stations. J. Hydrol. 2023, 623, 129803. [Google Scholar] [CrossRef]
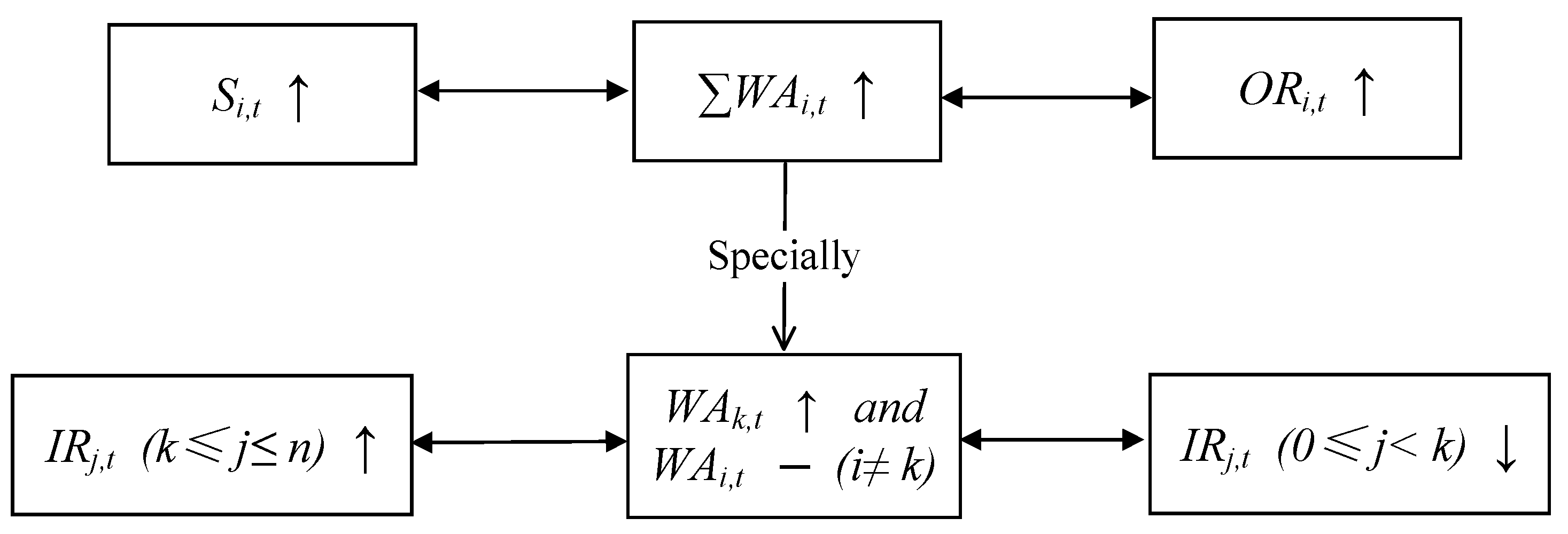


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Ma, H.; Chen, S.; Xu, Y.; Zeng, X. Improved Reinforcement Learning for Multi-Objective Optimization Operation of Cascade Reservoir System Based on Monotonic Property. Water 2025, 17, 1681. https://doi.org/10.3390/w17111681
Li X, Ma H, Chen S, Xu Y, Zeng X. Improved Reinforcement Learning for Multi-Objective Optimization Operation of Cascade Reservoir System Based on Monotonic Property. Water. 2025; 17(11):1681. https://doi.org/10.3390/w17111681
Chicago/Turabian StyleLi, Xiang, Haoyu Ma, Sitong Chen, Yang Xu, and Xiang Zeng. 2025. "Improved Reinforcement Learning for Multi-Objective Optimization Operation of Cascade Reservoir System Based on Monotonic Property" Water 17, no. 11: 1681. https://doi.org/10.3390/w17111681
APA StyleLi, X., Ma, H., Chen, S., Xu, Y., & Zeng, X. (2025). Improved Reinforcement Learning for Multi-Objective Optimization Operation of Cascade Reservoir System Based on Monotonic Property. Water, 17(11), 1681. https://doi.org/10.3390/w17111681




