Hydraulic Disconnection Between Aquifers: Assessing the Hydrogeologic Controls on Inter-Aquifer Exchange and Induced Recharge in Pumped, Multi-Aquifer Systems
Abstract
1. Introduction
2. Materials and Methods
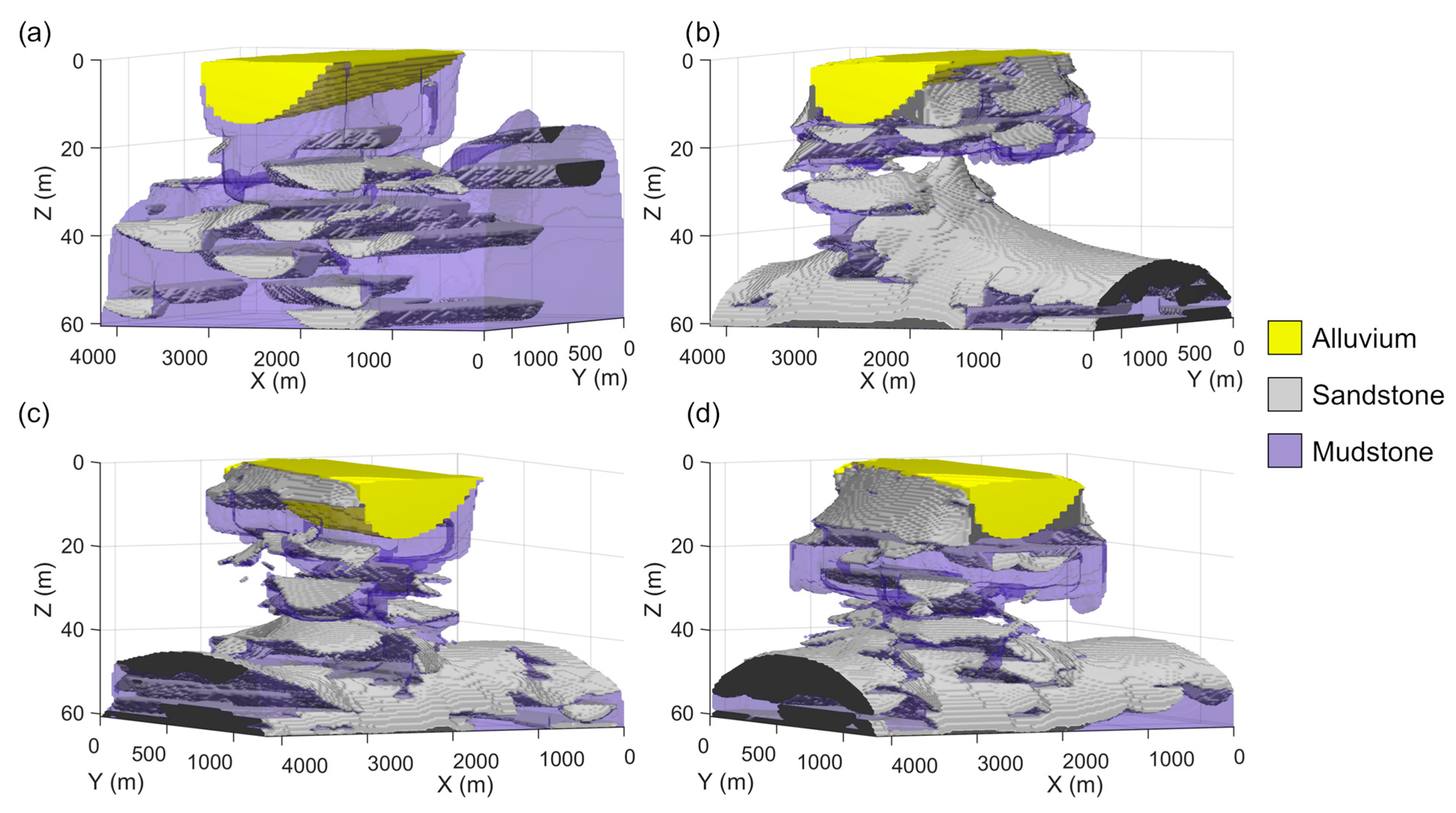
2.1. Geostatistical Simulation of Aquifer Heterogeneity
2.2. Variably Saturated Flow Modeling
2.3. Connectivity Metrics
3. Results
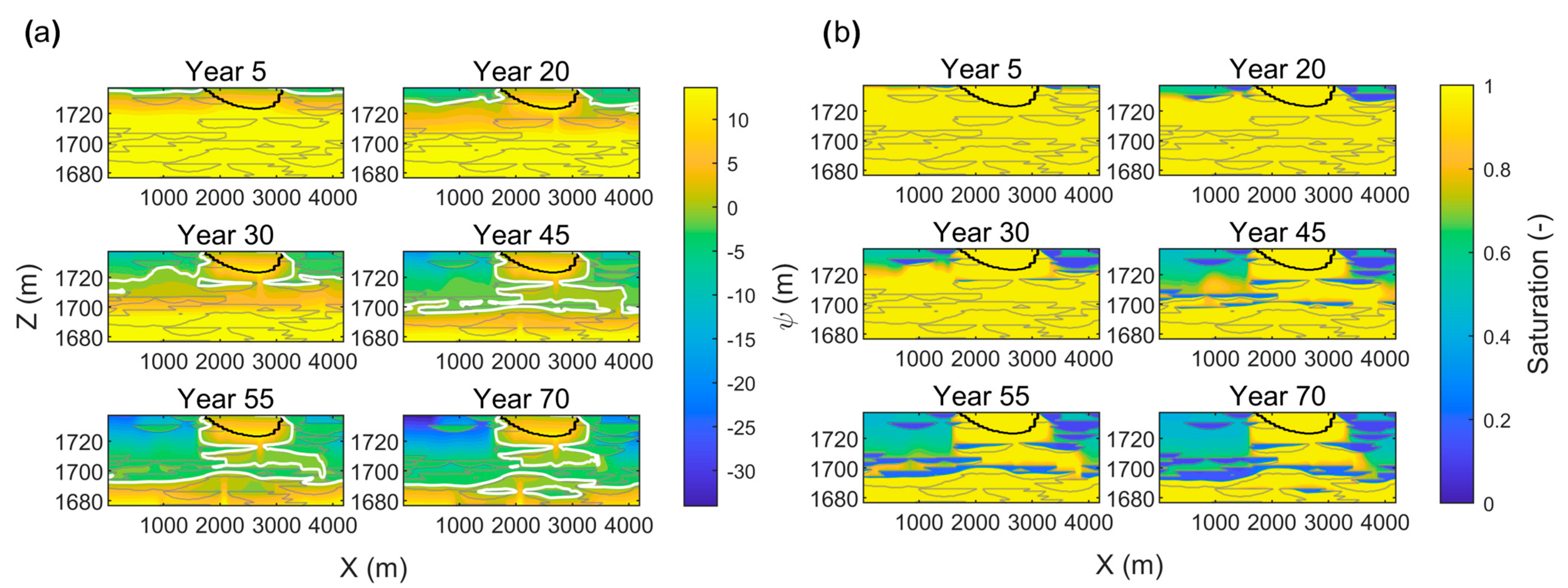
3.1. Pressure, Saturation, and Flux Dynamics
3.2. Inter-Aquifer Flow and Seepage
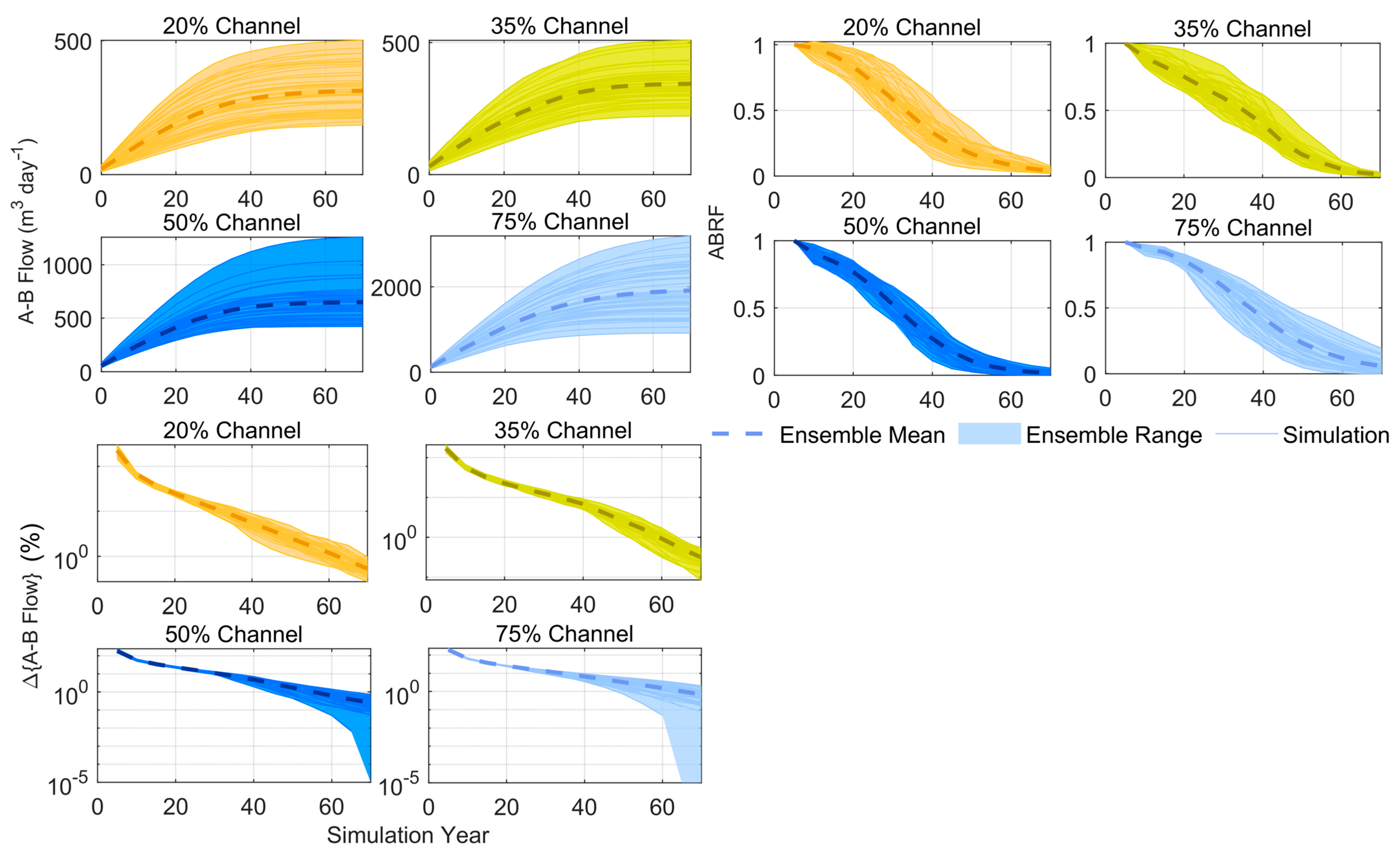
3.3. Sensitivity to Sandstone Channel Architecture
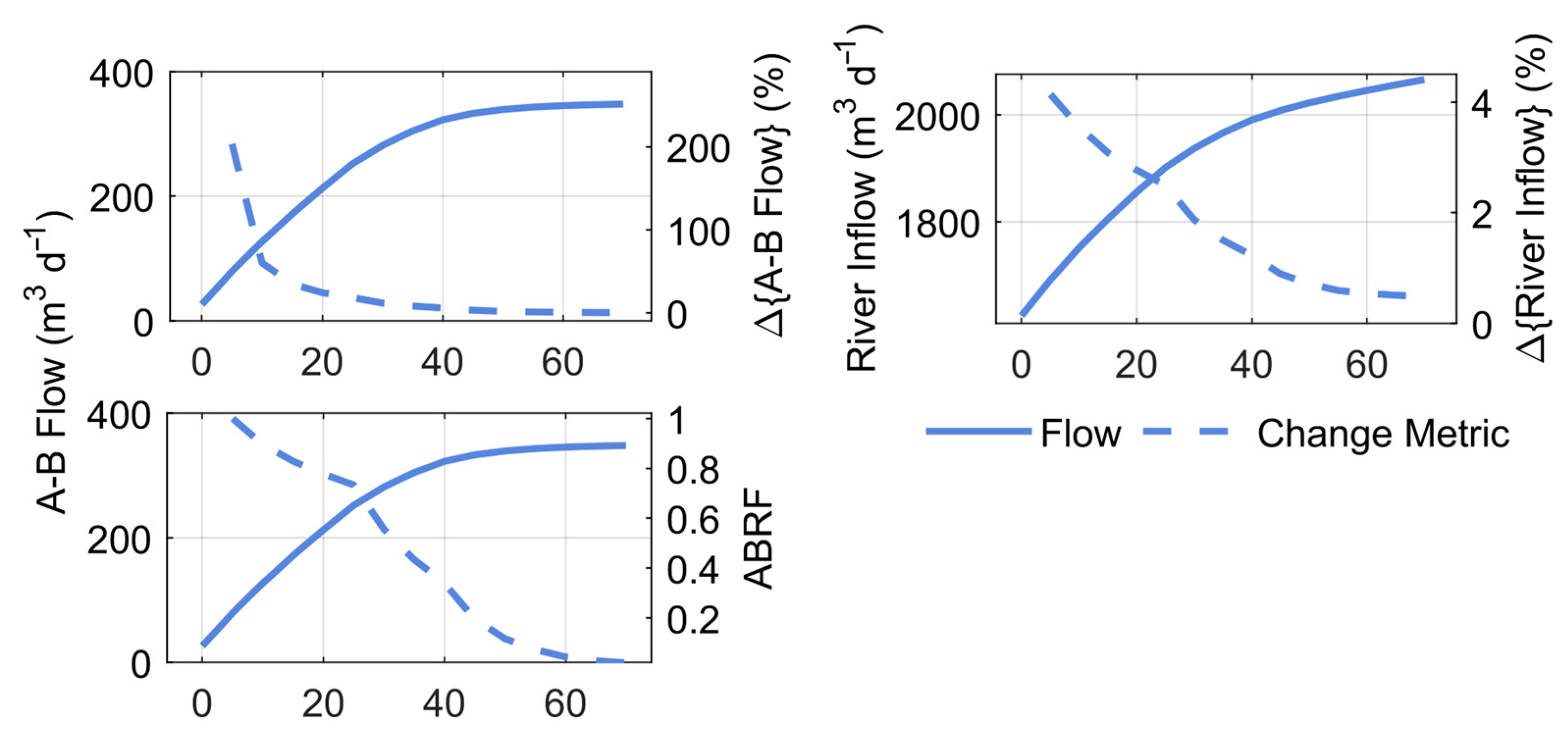
3.3.1. A-B Flow
3.3.2. A-B Flow Percentage Change
3.3.3. Alluvial-to-Bedrock Flow Response Function
3.4. Connectivity Structure of Heterogeneity
4. Discussion
4.1. Disconnection Dynamics
4.2. Heterogeneity Controls for Inter-Aquifer Flow
4.3. Definition of Disconnection
4.4. Management Implications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| K | Hydraulic conductivity |
| c | (subscript) Clogging layer |
| a | (subscript) Aquifer |
| b | Thickness |
| d | Depth |
| m | Meters |
| h | Hydraulic head |
| x, y, z | Principal axes |
| Krw | Relative permeability |
| W | Volumetric source or sink |
| ∅ | Drainable porosity |
| Sy | Specific yield |
| Se | Effective saturation |
| Sw | Total water saturation |
| α | van Genuchten alpha |
| n | van Genuchten n |
| m | van Genuchten m |
| sp | Stress period |
| t | Time |
| Q | Volumetric flow rate |
| A-B | Alluvial–Bedrock |
| ABRF | Alluvial bedrock response function |
| CV | Coefficient of variation |
| σ | Standard deviation |
| MLR | Multiple linear regression |
| VSF | Variably saturated flow |
| MFUSG | MODFLOW-USG |
| A-BSS_% | Alluvial bedrock sandstone fraction |
| MCC | Maximum connected components |
| NCC | Number connected components |
| ZCC | Z-span connected components |
| DY | Dynamic |
| 3D | Three-dimensional |
| 2D | Two-dimensional |
References
- Fox, G.A.; Durnford, D.S. Unsaturated hyporheic zone flow in stream/aquifer conjunctive systems. Adv. Water Resour. 2003, 26, 989–1000. [Google Scholar] [CrossRef]
- Brunner, P.; Cook, P.G.; Simmons, C.T. Disconnected surface water and groundwater: From theory to practice. Groundwater 2011, 49, 460–467. [Google Scholar] [CrossRef] [PubMed]
- Hunt, R.J.; Prudic, D.E.; Walker, J.F.; Anderson, M.P. Importance of unsaturated zone flow for simulating recharge in a humid climate. Groundwater 2008, 46, 551–560. [Google Scholar] [CrossRef]
- Desilets, S.L.E.; Ferre, T.P.A.; Troch, P.A. Effects of stream-aquifer disconnection on local flow patterns. Water Resour. Res. 2008, 44, W09501. [Google Scholar] [CrossRef]
- Shanafield, M.; Cook, P.G.; Brunner, P.; McCallum, J.; Simmons, C.T. Aquifer response to surface water transience in disconnected streams. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Theis, C.V. The effect of a well on the flow of a nearby stream. Eos Trans. Am. Geophys. Union 1941, 22, 734–738. [Google Scholar] [CrossRef]
- Su, G.W.; Jasperse, J.; Seymour, D.; Constantz, J.; Zhou, Q. Analysis of pumping-induced unsaturated regions beneath a perennial river. Water Resour. Res. 2007, 43, W08421. [Google Scholar] [CrossRef]
- Frei, S.; Fleckenstein, J.H.; Kollet, S.J.; Maxwell, R.M. Patterns and dynamics of river–aquifer exchange with variably-saturated flow using a fully-coupled model. J. Hydrol. 2009, 375, 383–393. [Google Scholar] [CrossRef]
- Swanson, S.K.; Bahr, J.M.; Bradbury, K.R.; Anderson, K.M. Evidence for preferential flow through sandstone aquifers in Southern Wisconsin. Sediment. Geol. 2006, 184, 331–342. [Google Scholar] [CrossRef]
- Maples, S.R.; Foglia, L.; Fogg, G.E.; Maxwell, R.M. Sensitivity of hydrologic and geologic parameters on recharge processes in a highly heterogeneous, semi-confined aquifer system. Hydrol. Earth Syst. Sci. 2020, 24, 2437–2456. [Google Scholar] [CrossRef]
- Fleckenstein, J.H.; Niswonger, R.G.; Fogg, G.E. River-aquifer interactions, geologic heterogeneity, and low-flow management. Groundwater 2006, 44, 837–852. [Google Scholar] [CrossRef]
- Meier, P.M.; Carrera, J.; Sánchez-Vila, X. An evaluation of Jacob’s method for the interpretation of pumping tests in heterogeneous formations. Water Resour. Res. 1998, 34, 1011–1025. [Google Scholar] [CrossRef]
- Knudby, C.; Carrera, J. On the use of apparent hydraulic diffusivity as an indicator of connectivity. J. Hydrol. 2006, 329, 377–389. [Google Scholar] [CrossRef]
- Dann, R.L.; Close, M.E.; Pang, L.; Flintoft, M.J.; Hector, R.P. Complementary use of tracer and pumping tests to characterize a heterogeneous channelized aquifer system in New Zealand. Hydrogeol. J. 2008, 16, 1177–1191. [Google Scholar] [CrossRef]
- Ronayne, M.J.; Gorelick, S.M.; Caers, J. Identifying discrete geologic structures that produce anomalous hydraulic response: An inverse modeling approach. Water Resour. Res. 2008, 44, W08426. [Google Scholar] [CrossRef]
- DesRoches, A.J.; Butler, K.E.; Pelkey, S. Influence of fracture anisotropy and lithological heterogeneity on wellfield response in a fluvial sandstone aquifer of the Carboniferous Moncton Subbasin, Canada. Hydrogeol. J. 2013, 21, 559. [Google Scholar] [CrossRef]
- Tang, Q.; Kurtz, W.; Schilling, O.S.; Brunner, P.; Vereecken, H.; Franssen, H.J.H. The influence of riverbed heterogeneity patterns on river-aquifer exchange fluxes under different connection regimes. J. Hydrol. 2017, 554, 383–396. [Google Scholar] [CrossRef]
- Bruen, M.P.; Osman, Y.Z. Sensitivity of stream–aquifer seepage to spatial variability of the saturated hydraulic conductivity of the aquifer. J. Hydrol. 2004, 293, 289–302. [Google Scholar] [CrossRef]
- Renard, P.; Allard, D. Connectivity metrics for subsurface flow and transport. Adv. Water Resour. 2013, 51, 168–196. [Google Scholar] [CrossRef]
- Rosenberry, D.O. Unsaturated-zone wedge beneath a large, natural lake. Water Resour. Res. 2000, 36, 3401–3409. [Google Scholar] [CrossRef]
- Brunner, P.; Cook, P.G.; Simmons, C.T. Hydrogeologic controls on disconnection between surface water and groundwater. Water Resour. Res. 2009, 45, W01422. [Google Scholar] [CrossRef]
- Brunner, P.; Simmons, C.T.; Cook, P.G. Spatial and temporal aspects of the transition from connection to disconnection between rivers, lakes and groundwater. J. Hydrol. 2009, 376, 159–169. [Google Scholar] [CrossRef]
- Schilling, O.S.; Irvine, D.J.; Hendricks Franssen, H.J.; Brunner, P. Estimating the spatial extent of unsaturated zones in heterogeneous river-aquifer systems. Water Resour. Res. 2017, 53, 10583–10602. [Google Scholar] [CrossRef]
- Wada, Y.; Van Beek, L.P.; Van Kempen, C.M.; Reckman, J.W.; Vasak, S.; Bierkens, M.F. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37, L20402. [Google Scholar] [CrossRef]
- Werner, A.D.; Zhang, Q.; Xue, L.; Smerdon, B.D.; Li, X.; Zhu, X.; Yu, L.; Li, L. An initial inventory and indexation of groundwater mega-depletion cases. Water Resour. Manag. 2013, 27, 507–533. [Google Scholar] [CrossRef]
- Paschke, S.S. (Ed.) Groundwater Availability of the Denver Basin Aquifer System; U.S. Geological Survey Professional Paper 1770; U.S. Geological Survey: Reston, VA, USA, 2011; 274p. [CrossRef]
- Ruybal, C.J.; Hogue, T.S.; McCray, J.E. Assessment of groundwater depletion and implications for management in the Denver basin aquifer system. J. Am. Water Resour. Assoc. 2019, 55, 1130–1148. [Google Scholar] [CrossRef]
- Cognac, K.E.; Ronayne, M.J. Changes to inter-aquifer exchange resulting from long-term pumping: Implications for bedrock groundwater recharge. Hydrogeol. J. 2020, 28, 1359–1370. [Google Scholar] [CrossRef]
- Ronayne, M.J.; Gorelick, S.M.; Zheng, C. Geological modeling of submeter scale heterogeneity and its influence on tracer transport in a fluvial aquifer. Water Resour. Res. 2010, 46, W10519. [Google Scholar] [CrossRef]
- Irvine, D.J.; Brunner, P.; Franssen, H.J.H.; Simmons, C.T. Heterogeneous or homogeneous? Implications of simplifying heterogeneous streambeds in models of losing streams. J. Hydrol. 2012, 424, 16–23. [Google Scholar] [CrossRef]
- Deutsch, C.A.; Tran, T.T. FLUVSIM: A program for object-based stochastic modeling of fluvial depositional systems. Comput. Geosci. 2002, 28, 525–535. [Google Scholar] [CrossRef]
- Raynolds, R.G. Upper Cretaceous and Tertiary stratigraphy of the Denver basin, Colorado. Rocky Mt. Geol. 2002, 37, 111–134. [Google Scholar] [CrossRef]
- Panday, S.; Langevin, C.D.; Niswonger, R.G.; Ibaraki, M.; Hughes, J.D. MODFLOW-USG: An Unstructured Grid Version of MODFLOW for Simulating Groundwater Flow and Tightly Coupled Processes Using a Control Volume Finite-Difference Formulation; Version 1; U.S. Geological Survey Techniques and Methods: Reston, VA, USA, 2013. [CrossRef]
- Panday, S. USG-Transport: The Block-Centered Transport Process for MODFLOW-USG; Version 1.4.0; GSI Environmental: Houston, TX, USA, 2019; Available online: https://www.gsi-net.com/en/software/free-software/USG-Transport.html (accessed on 1 May 2023).
- Hort, H.M.; Stockwell, E.B.; Newell, C.J.; Scalia, J., IV; Panday, S. Modeling and evaluation of PFOS retention in the unsaturated zone above the water table. Groundw. Monit. Remediat. 2024, 44, 38–48. [Google Scholar] [CrossRef]
- Vonk, M.A.; Collenteur, R.A.; Panday, S.; Schaars, F.; Bakker, M. Time Series Analysis of Nonlinear Head Dynamics Using Synthetic Data Generated with a Variably Saturated Model. Groundwater 2024, 62, 748–760. [Google Scholar] [CrossRef]
- Huyakorn, P.S.; Springer, E.P.; Guvanasen, V.; Wadsorth, T.D. A three dimensional finite element model for simulating water flow in variably saturated porous media. Water Resour. Res. 1986, 22, 1790–1808. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil. Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Properties of porous media affecting fluid flow. J. Irrig. Drain. Div. 1966, 92, 61–88. [Google Scholar] [CrossRef]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. Geological Survey Modular Ground-Water Model—User Guide to Modularization Concepts and the Ground-Water Flow Process; US Geological Survey Open-File Report; U.S. Geological Survey: Reston, VA, USA, 2000. [CrossRef]
- Colorado Division of Water Resources (CDWR). State Water Level Database, Colorado Government. 2022. Available online: https://dwr.state.co.us/Tools/GroundWater/WaterLevels (accessed on 17 November 2022).
- Lapey, L.A. Hydrogeologic Parameters of the Kiowa Research Core, Kiowa, Colorado. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 2001. [Google Scholar]
- Woodard, L.; Sanford, W.; Raynolds, R.G. Stratigraphic variability of specific yield within bedrock aquifers of the Denver Basin, Colorado. Rocky Mt. Geol. 2002, 37, 229–236. [Google Scholar] [CrossRef]
- Brown and Caldwell. South Platte Decision Support System Alluvial Groundwater Model Update Documentation; Colorado Water Conservation Board and Division of Water Resources: Denver, CO, USA, 2017.
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Parajuli, K.; Sadeghi, M.; Jones, S.B. A binary mixing model for characterizing stony-soil water retention. Agric. For. Meteorol. 2017, 244, 1–8. [Google Scholar] [CrossRef]
- Morel-Seytoux, H.J.; Meyer, P.D.; Nachabe, M.; Tourna, J.; Van Genuchten, M.T.; Lenhard, R.J. Parameter equivalence for the Brooks-Corey and van Genuchten soil characteristics: Preserving the effective capillary drive. Water Resour. Res. 1996, 32, 1251–1258. [Google Scholar] [CrossRef]
- Harbaugh, A.W. A Computer Program for Calculating Subregional Water Budgets Using Results from the U.S. Geological Survey Modular Three-Dimensional Ground-Water Flow Model; U.S. Geological Survey: Reston, VA, USA, 1990; 46p. [CrossRef]
- King, P.R. The connectivity and conductivity of overlapping sand bodies. In North Sea Oil and Gas Reservoirs—II, Proceedings of the 2nd North Sea Oil and Gas Reservoirs Conference organized and hosted by the Norwegian Institute of Technology (NTH), Trondheim, Norway, 8–11 May 1989; Springer: Dordrecht, The Netherlands, 1990; pp. 353–362. [Google Scholar] [CrossRef]
- Pardo-Iguzquiza, E.; Dowd, P. CONNEC3D: A computer program for connectivity analysis of 3D random set models. Comput. Geosci. 2003, 29, 775–785. [Google Scholar] [CrossRef]
- Rains, M.C.; Fogg, G.E.; Harter, T.; Dahlgren, R.A.; Williamson, R.J. The role of perched aquifers in hydrological connectivity and biogeochemical processes in vernal pool landscapes, Central Valley, California. Hydrol. Process. 2006, 20, 1157–1175. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Vázquez-Suñé, E.; Capino, B.; Abarca, E.; Carrera, J. Estimation of recharge from floods in disconnected stream-aquifer systems. Groundwater 2007, 45, 579–589. [Google Scholar] [CrossRef]
- Ringleb, J.; Sallwey, J.; Stefan, C. Assessment of managed aquifer recharge through modeling: A review. Water 2017, 8, 579. [Google Scholar] [CrossRef]
- Dillon, P.; Stuyfzand, P.; Grischek, T.; Lluria, M.; Pyne, R.D.G.; Jain, R.C.; Schwarz, J.; Wang, W.; Fernandez, C.; Pettenati, M.; et al. Sixty years of global progress in managed aquifer recharge. Hydrogeol. J. 2019, 27, 1–30. [Google Scholar] [CrossRef]
- Szabo, Z.; Szijarto, M.; Toth, A.; Madl-Szonyi, J. The significance of groundwater table inclination for nature-based replenishment of groundwater-dependent ecosystems by managed aquifer recharge. Water 2023, 15, 1077. [Google Scholar] [CrossRef]
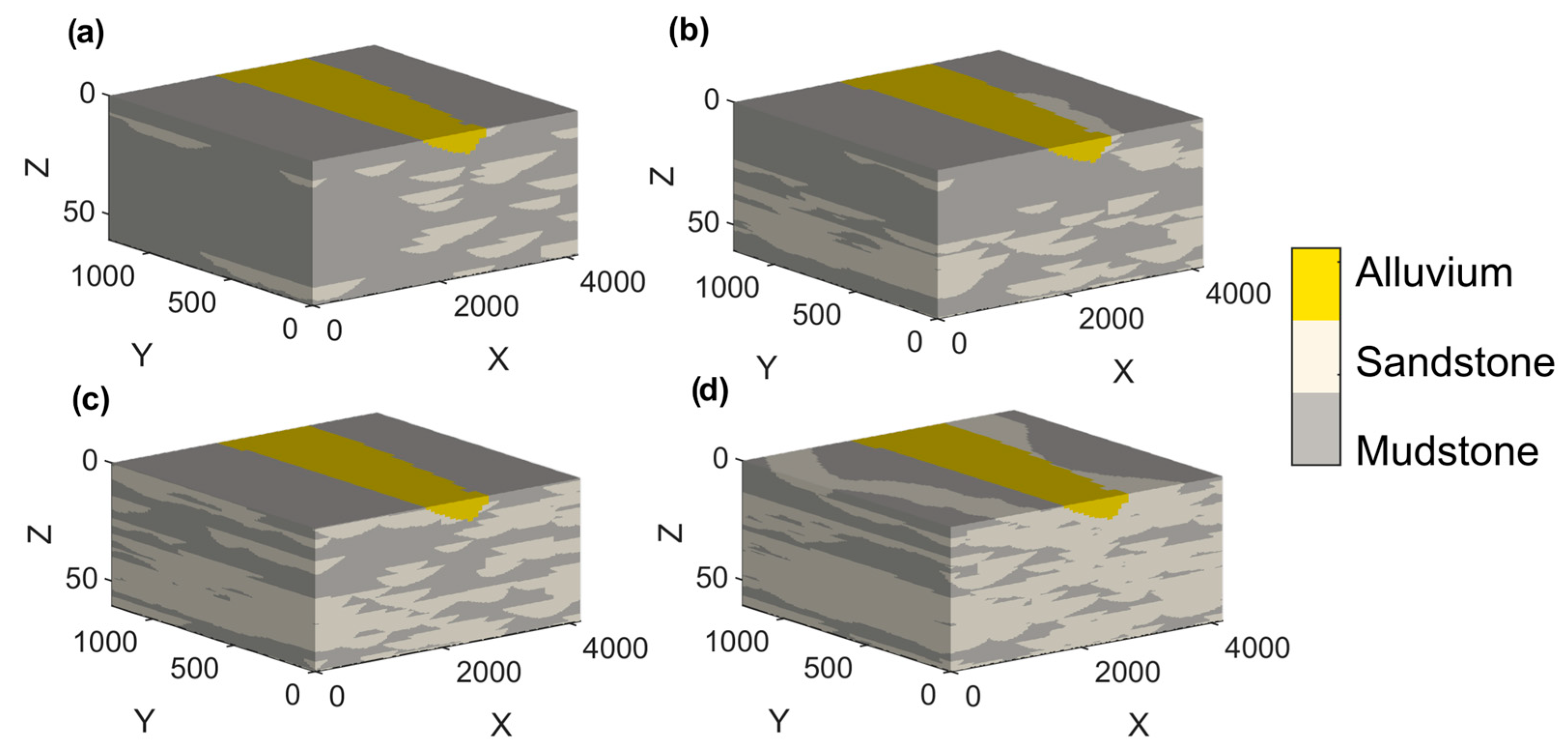
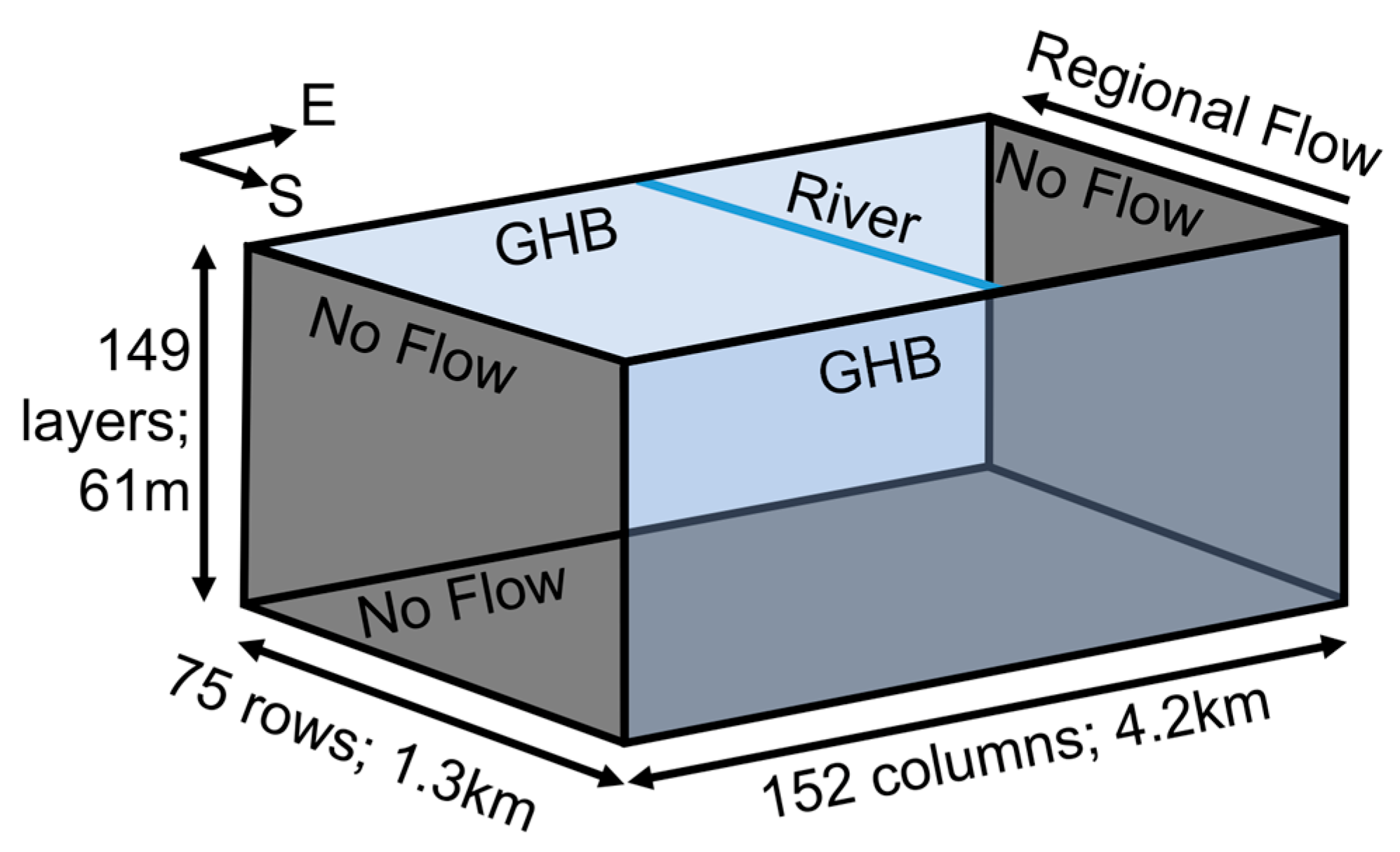
| FLUVSIM Parameters | Values | ||
| # rows, columns, layers | 75, 152, 149 | ||
| Δx, Δy, Δz | 27.7 m, 16.9 m, 0.41 m | ||
| channel | |||
| proportions | 20%, 35%, 50%, 70% | ||
| orientation | 0° (North/South) | ||
| sinuosity (departure, length scale) | Departure 350 m; Length scale: 900 m | ||
| thickness | 4 m ± 1 m | ||
| width-to-thickness ratio | 200 | ||
| MODFLOW-USG Parameters | Sandstone | Mudstone | Alluvium |
| Saturated Hydraulic Conductivity (m day−1) | 0.3 | 0.001 | 65 |
| Specific Storage (m−1) | 0.000017 | 0.000056 | 0.0001 |
| Specific Yield (-) | 0.18 | 0.15 | 0.36 |
| Specific Retention (-) | 0.12 | 0.23 | 0.1 |
| van Genuchten α (m−1) | 0.79 | 1.9 | 14.5 |
| van Genuchten n (-) | 10.4 | 1.31 | 2.68 |
| Brooks-Corey P (-) | 3.21 | 9.45 | 4.19 |
| Ensemble Mean | Minimum | Maximum | σ | CV | ||
|---|---|---|---|---|---|---|
| A-B Flow (m3 day−1) | 20% | 313 | 184 | 501 | 81 | 0.26 |
| 35% | 344 | 222 | 508 | 60 | 0.17 | |
| 50% | 650 | 423 | 1258 | 154 | 0.24 | |
| 75% | 1913 | 919 | 3187 | 554 | 0.29 | |
| Δ{A-B Flow} | 20% | 0.53 | 0.27 | 0.97 | 0.15 | 0.28 |
| 35% | 0.32 | 0.085 | 0.55 | 0.10 | 0.31 | |
| 50% | 0.25 | −0.010 | 0.74 | 0.16 | 0.64 | |
| 75% | 0.68 | −0.040 | 2.1 | 0.45 | 0.66 | |
| ABRF | 20% | 0.037 | 0.018 | 0.075 | 0.012 | 0.34 |
| 35% | 0.022 | 0.0058 | 0.040 | 0.0074 | 0.34 | |
| 50% | 0.016 | −0.00080 | 0.054 | 0.011 | 0.69 | |
| 75% | 0.055 | −0.0027 | 0.19 | 0.040 | 0.74 |
| Channel Fraction | Predictor | Model | |||||
|---|---|---|---|---|---|---|---|
| Estimate | 1 SE | p-Value | 2 RMSE | 3 R-Squared | p-Value | ||
| 20% | Intercept | 153 | 48 | 4 2.67 × 10–3 | 56.7 | 0.52 | 4.0 × 10–7 |
| A-BSS_% | 3 | 0.7 | 2.78 × 10–4 | ||||
| MCCDY | 0.0010 | 0.0005 | 5.27 × 10–2 | ||||
| NCCDY | −1.1 | 1.03 | 2.80 × 10–1 | ||||
| ZCCDY | −2 | 1.8 | 2.14 × 10–1 | ||||
| ABZCCDY | 3 | 1.6 | 8.26 × 10–2 | ||||
| 35% | Intercept | 3 | 62 | 9.63 × 10–1 | 39.8 | 0.57 | 4.3 × 10–8 |
| A-BSS_% | 2.7 | 0.5 | 4.71 × 10–6 | ||||
| MCCDY | 3.2 × 10−5 | 1.7E-04 | 8.49 × 10–1 | ||||
| NCCDY | −0.028 | 0.4 | 9.47 × 10–1 | ||||
| ZCCDY | 0.5 | 0.8 | 5.32 × 10–1 | ||||
| ABZCCDY | 5 | 0.8 | 6.88 × 10–8 | ||||
| 50% | Intercept | 100 | 124 | 4.24 × 10–1 | 104 | 0.56 | 6.0 × 10–8 |
| A-BSS_% | 6 | 1.2 | 2.55 × 10–5 | ||||
| MCCDY | 0.0019 | 0.0005 | 4.78 × 10–4 | ||||
| NCCDY | −2.6 | 1.0 | 1.04 × 10–2 | ||||
| ZCCDY | −5 | 1.3 | 8.53 × 10–4 | ||||
| ABZCCDY | 1.06 | 0.6 | 7.04 × 10–2 | ||||
| 75% | Intercept | 403 | 408 | 3.29 × 10–1 | 193 | 0.88 | 3.1 × 10–20 |
| A-BSS_% | −5 | 4 | 1.95 × 10–1 | ||||
| MCCDY | 0.010 | 0.00079 | 3.76 × 10–6 | ||||
| NCCDY | −2.5 | 2.2 | 2.73 × 10–1 | ||||
| ZCCDY | −34 | 4 | 6.26 × 10–11 | ||||
| ABZCCDY | 3 | 2.1 | 1.56 × 10–1 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cognac, K.E.; Ronayne, M.J. Hydraulic Disconnection Between Aquifers: Assessing the Hydrogeologic Controls on Inter-Aquifer Exchange and Induced Recharge in Pumped, Multi-Aquifer Systems. Water 2025, 17, 1635. https://doi.org/10.3390/w17111635
Cognac KE, Ronayne MJ. Hydraulic Disconnection Between Aquifers: Assessing the Hydrogeologic Controls on Inter-Aquifer Exchange and Induced Recharge in Pumped, Multi-Aquifer Systems. Water. 2025; 17(11):1635. https://doi.org/10.3390/w17111635
Chicago/Turabian StyleCognac, Kristen E., and Michael J. Ronayne. 2025. "Hydraulic Disconnection Between Aquifers: Assessing the Hydrogeologic Controls on Inter-Aquifer Exchange and Induced Recharge in Pumped, Multi-Aquifer Systems" Water 17, no. 11: 1635. https://doi.org/10.3390/w17111635
APA StyleCognac, K. E., & Ronayne, M. J. (2025). Hydraulic Disconnection Between Aquifers: Assessing the Hydrogeologic Controls on Inter-Aquifer Exchange and Induced Recharge in Pumped, Multi-Aquifer Systems. Water, 17(11), 1635. https://doi.org/10.3390/w17111635






