LSTM-Based Forecasting of Coastal Hypoxia in South Korea: Evaluating the Roles of Tide Level and Model Architecture
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
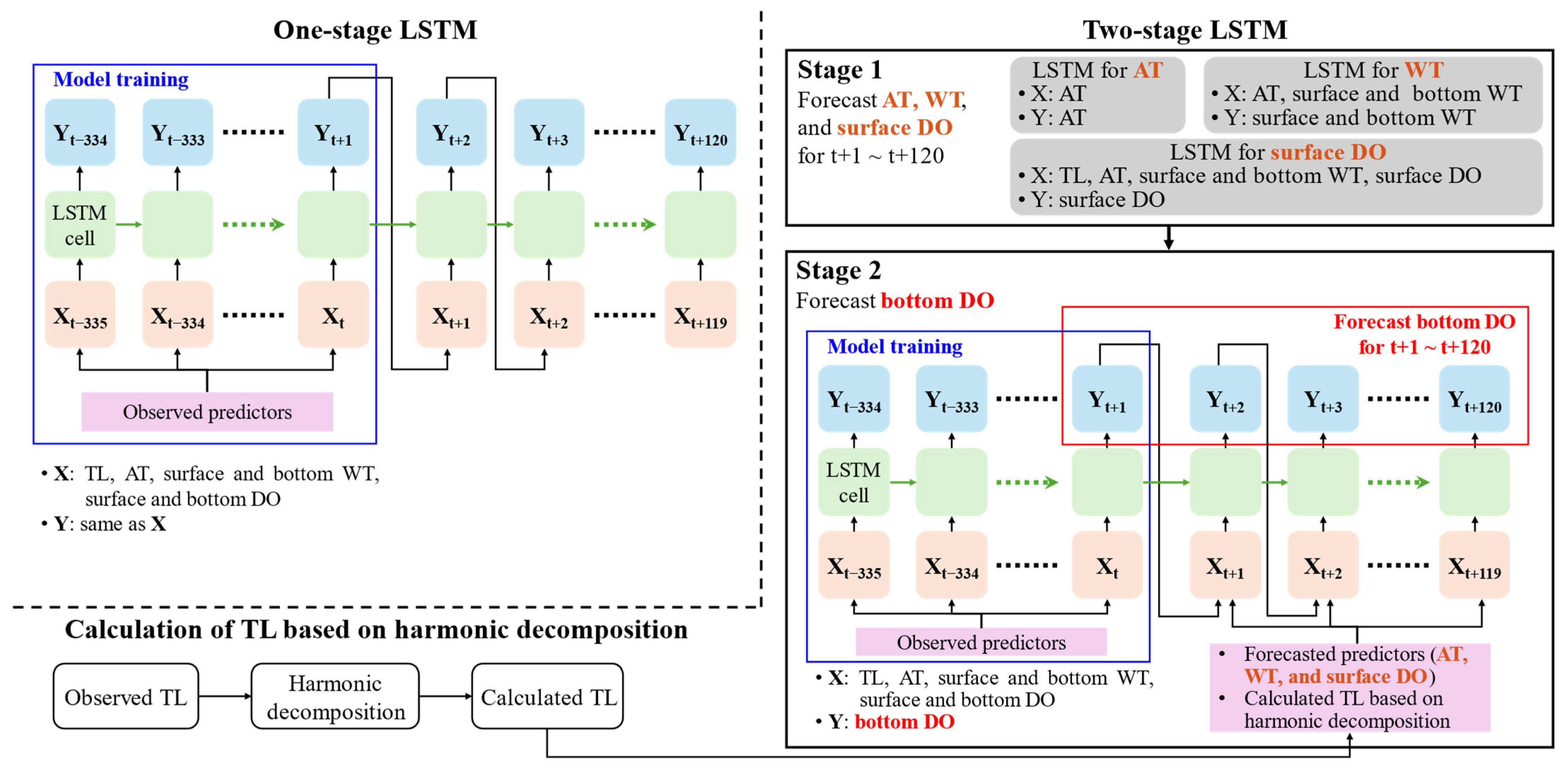
2.2. LSTM Architectures
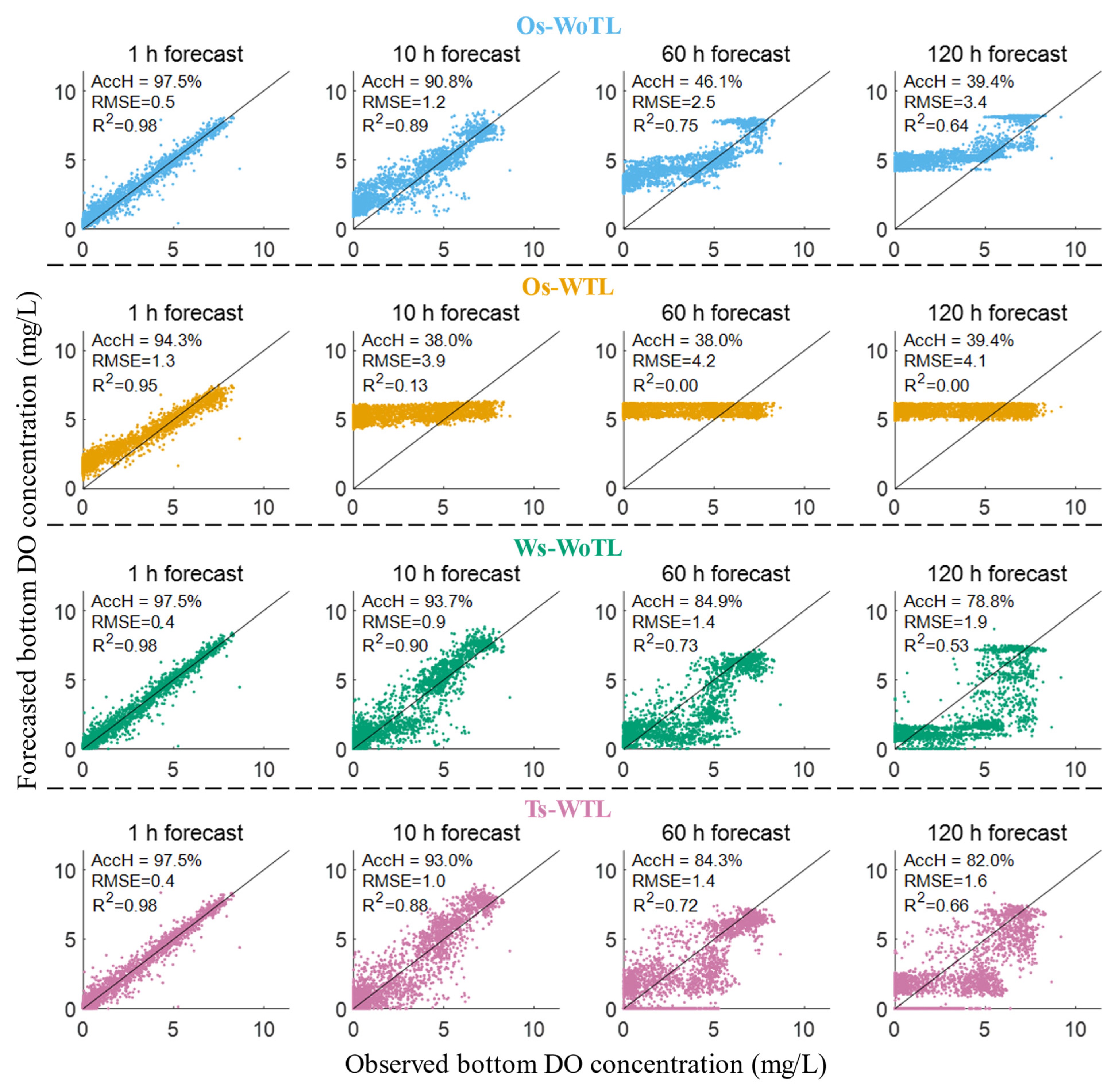
- One-stage without TL (Os-WoTL): A single LSTM model is trained to forecast all variables simultaneously. The predictor excludes TL.
- One-stage with TL (Os-WTL): Same as Os-WoTL, but with tide level included as an additional predictor.
- Two-stage without TL (Ts-WoTL): Stage 1 forecasts AT, WT, and surface DO; these predicted variables are then used as inputs in Stage 2 to forecast bottom DO.
- Two-stage with TL (Ts-WTL): Same as Ts-WoTL, except that the predictor set includes tide level calculated by harmonic decomposition.
2.3. LSTM Hyperparameters
2.4. Model Evaluation
2.5. Tide Level Calculation Based on Harmonic Decomposition
2.6. Wavelet Coherence Analysis
3. Results
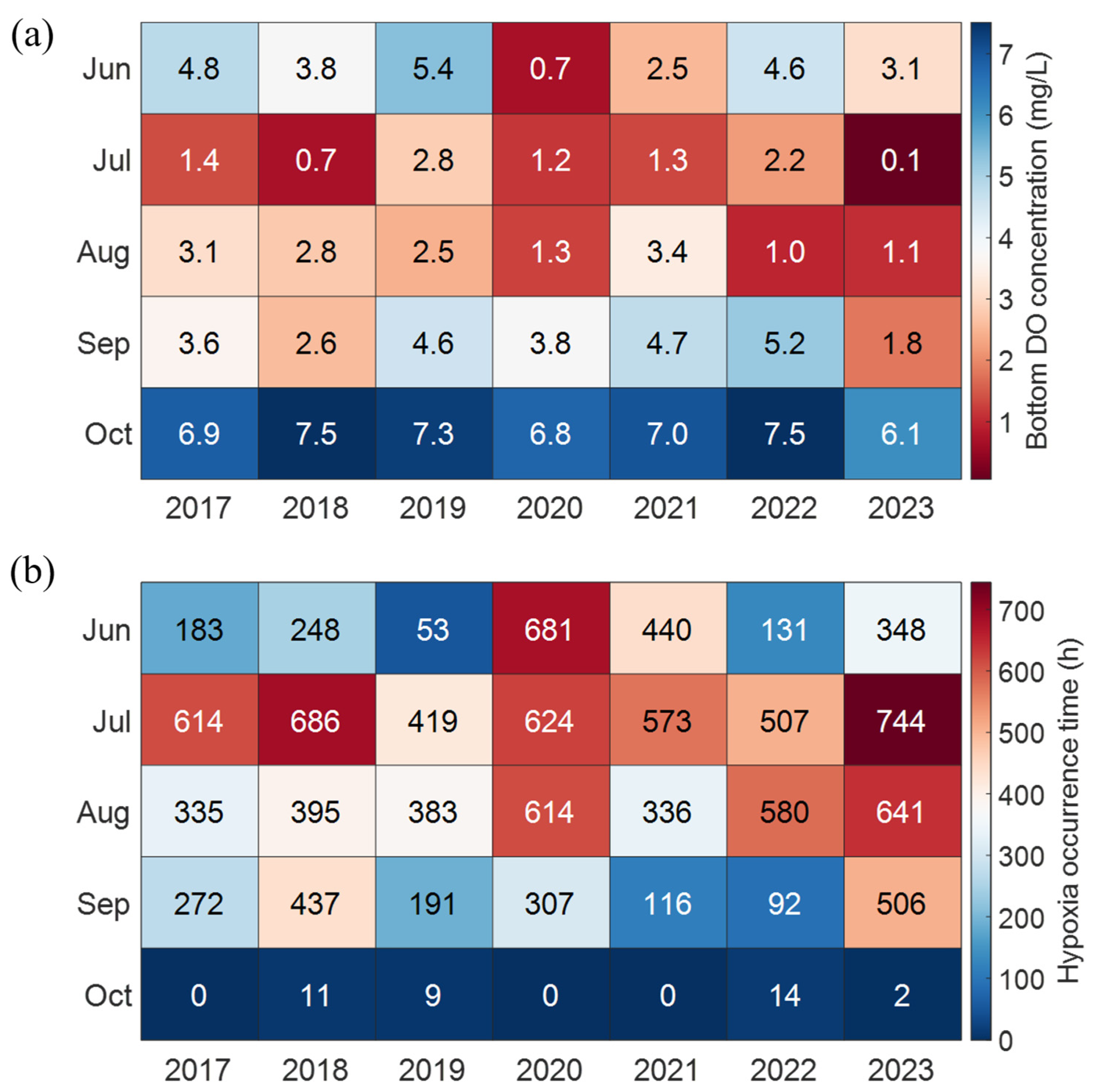
3.1. Occurrence of Hypoxia in Gamak Bay
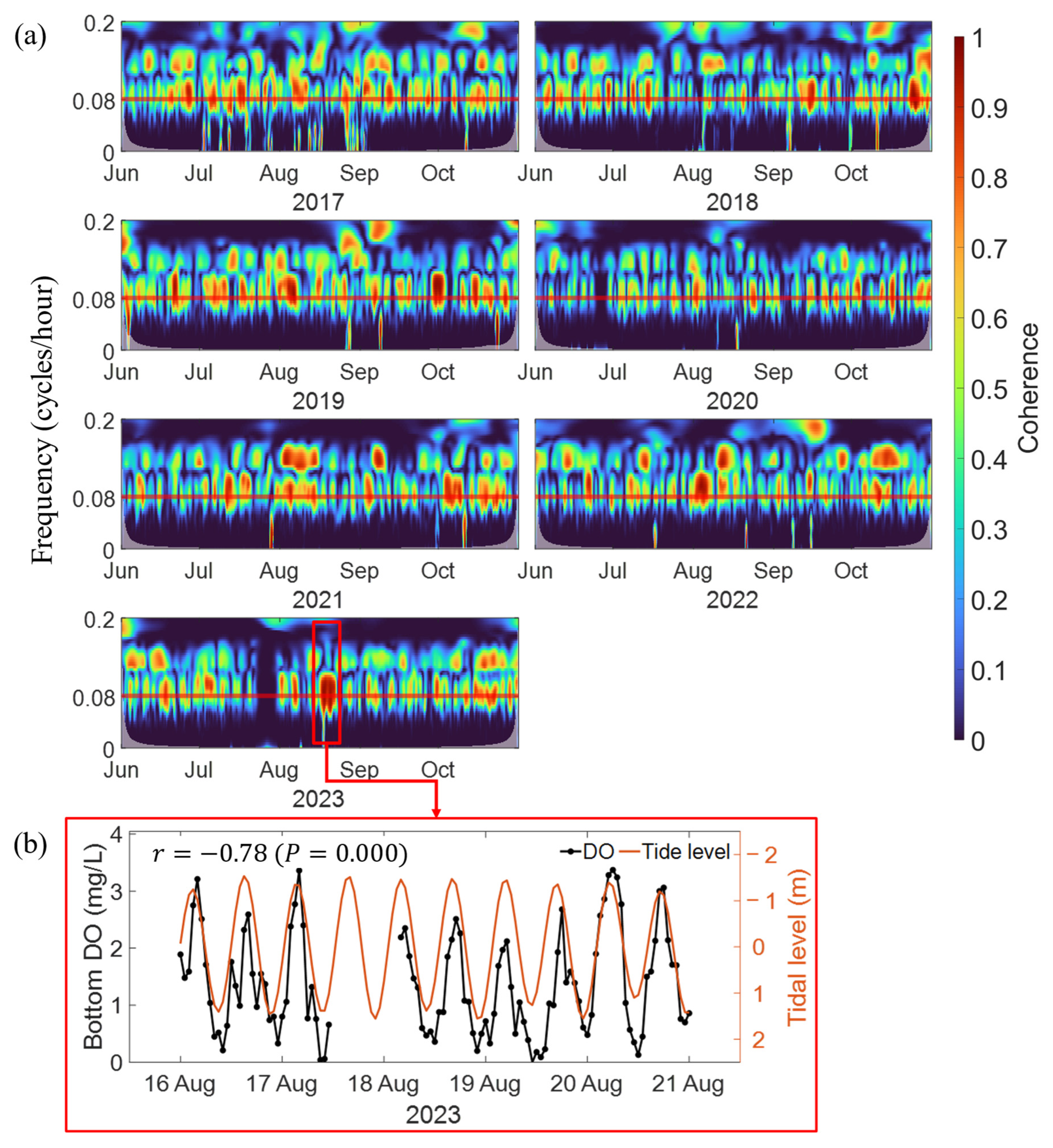
3.2. Correlation Between Bottom DO Concentration and Tide Level
3.3. Comparison of Model Accuracy
3.3.1. One- vs. Two-Stage LSTM Models with and Without Tide Level
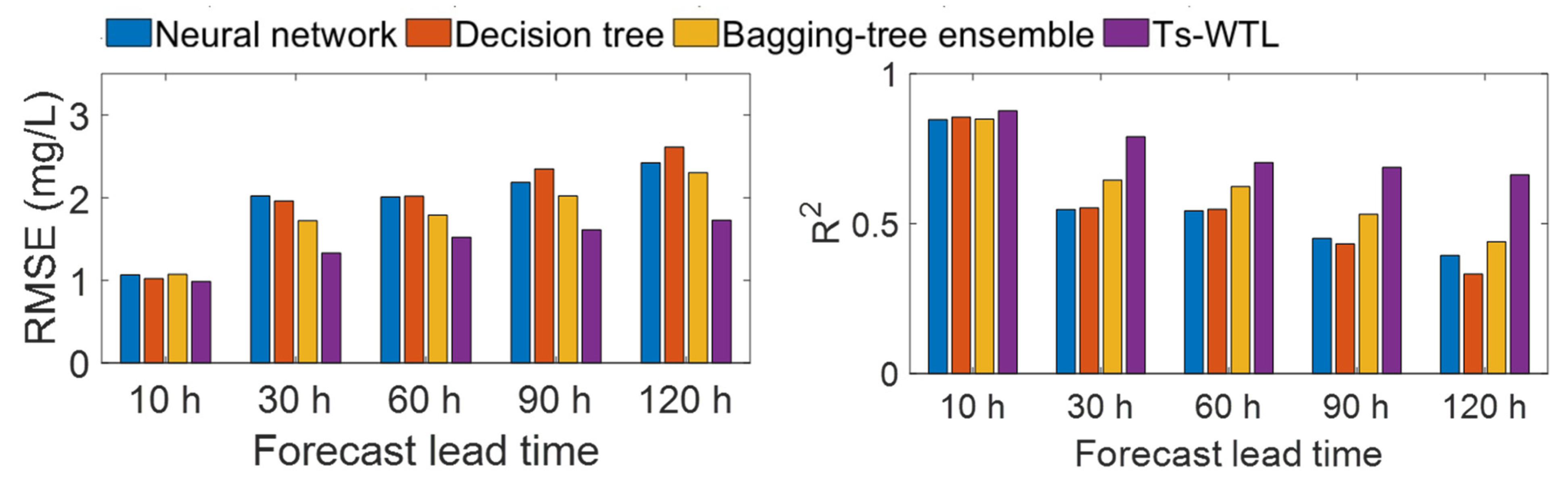
3.3.2. Benchmarking Ts-WTL Against Other Machine-Learning Models
4. Discussion
4.1. Causal Relationship Between Bottom DO Concentration and Environmental Variables
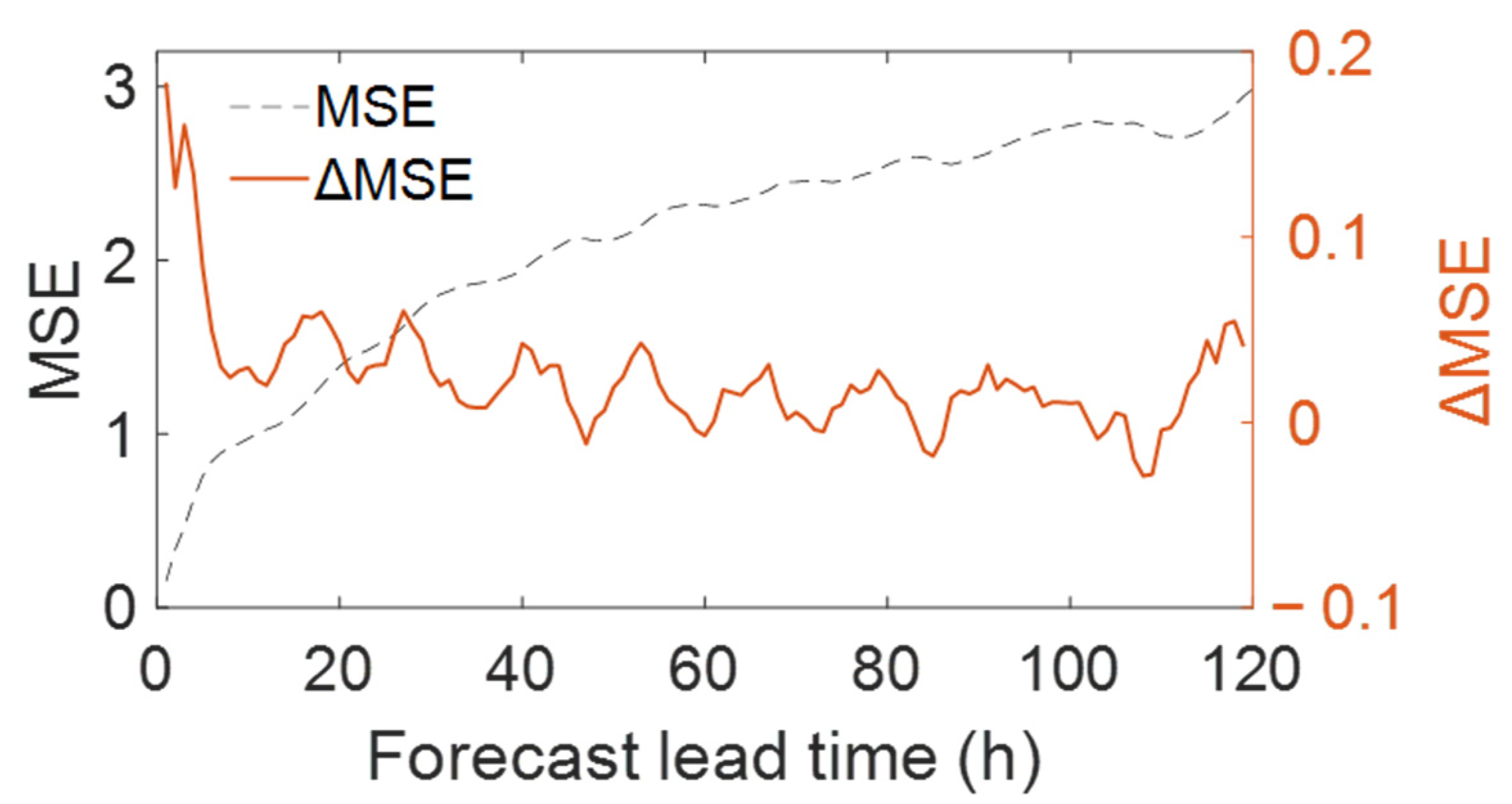
4.2. Considerations for Determining the Forecasting Horizon for Hypoxia
4.3. Future Considerations for Improving Model Accuracy
4.3.1. Hypoxia Characteristics in Gamak Bay
4.3.2. Phase Classification of Bottom DO Concentration
4.3.3. Hyperparameter Optimization
4.4. Real-World Management Implication
5. Conclusions
- Tide level, calculated using harmonic decomposition, significantly improved the long-term prediction of bottom DO concentration.
- The two-stage LSTM approach, which separates the prediction of intermediate environmental variables from the final DO forecast, outperformed conventional one-stage models in accuracy and hypoxia detection capability.
- The Ts-WTL model, which integrates tidal information into the two-stage framework, yielded the best overall performance, with a 120 h forecast RMSE of 1.6 mg/L and AccH (hypoxia prediction accuracy) of 82.0%.
- In benchmark comparisons with neural networks, decision trees, and bagging-tree ensemble, the proposed Ts-WTL approach consistently outperformed all alternatives.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Diaz, R.J.; Rosenberg, R. Spreading dead zones and consequences for marine ecosystems. Science 2008, 321, 926–929. [Google Scholar] [CrossRef]
- Conley, D.J.; Carstensen, J.; Ærtebjerg, G.; Christensen, P.B.; Dalsgaard, T.; Hansen, J.L.; Josefson, A.B. Long-term changes and impacts of hypoxia in Danish coastal waters. Ecol. Appl. 2007, 17, S165–S184. [Google Scholar] [CrossRef]
- Rabalais, N.N.; Turner, R.E.; Wiseman, W.J., Jr. Gulf of Mexico hypoxia, aka “The dead zone”. Annu. Rev. Ecol. Syst. 2002, 33, 235–263. [Google Scholar] [CrossRef]
- Kim, H.; Franco, A.C.; Sumaila, U.R. A selected review of impacts of ocean deoxygenation on fish and fisheries. Fishes 2023, 8, 316. [Google Scholar] [CrossRef]
- Wang, Z.; Pu, D.; Zheng, J.; Li, P.; Lü, H.; Wei, X.; Li, M.; Li, D.; Gao, L. Hypoxia-induced physiological responses in fish: From organism to tissue to molecular levels. Ecotoxicol. Environ. Saf. 2023, 267, 115609. [Google Scholar] [CrossRef]
- Jeong, H.; Choi, S.; Cho, H. Characteristics of Hypoxic Water Mass Occurrence in the Northwestern Gamak Bay, Korea, 2017. J. Korean Soc. Mar. Environ. Saf. 2021, 27, 708–720. [Google Scholar] [CrossRef]
- Seo, J.; Park, S.; Lee, J.; Choi, J. Structural changes in macrozoobenthic communities due to summer hypoxia in Gamak Bay, Korea. Ocean. Sci. J. 2012, 47, 27–40. [Google Scholar] [CrossRef]
- Kim, J.; Park, J.; Jung, C.; Choi, W.; Lee, W.; Lee, Y. Physicochemical characteristics of seawater in Gamak Bay for a period of hypoxic water mass disappearance. J. Korean Soc. Mar. Environ. Saf. 2010, 16, 241–248. [Google Scholar]
- Oh, H.; Lee, S.; Lee, W.; Jung, R.; Hong, S.; Kim, N.; Tilburg, C. Sustainability evaluation for shellfish production in Gamak Bay based on the systems ecology 1. EMERGY evaluation for shellfish production in Gamak Bay. J. Environ. Sci. Int. 2008, 17, 841–856. [Google Scholar] [CrossRef]
- Ock, L.M.; Jin, P.S.; Soon, K.T. Influence of reclamation works on the marine environment in a semi-enclosed bay. J. Ocean Univ. China 2006, 5, 219–227. [Google Scholar] [CrossRef]
- Regier, P.J.; Ward, N.D.; Myers-Pigg, A.N.; Grate, J.; Freeman, M.J.; Ghosh, R.N. Seasonal drivers of dissolved oxygen across a tidal creek–marsh interface revealed by machine learning. Limnol. Oceanogr. 2023, 68, 2359–2374. [Google Scholar] [CrossRef]
- Long, J.; Lu, C.; Lei, Y.; Chen, Z.Y.; Wang, Y. Application of an improved LSTM model based on FECA and CEEMDAN VMD decomposition in water quality prediction. Sci. Rep. 2025, 15, 12847. [Google Scholar] [CrossRef] [PubMed]
- Fang, P.; Wang, Y.; Zhao, Y.; Kang, J. Analysis of Prediction Confidence in Water Quality Forecasting Employing LSTM. Water 2025, 17, 1050. [Google Scholar] [CrossRef]
- De Rango, A.; Furnari, L.; Cortale, F.; Senatore, A.; Mendicino, G. Wildfire Early Warning System Based on a Smart CO2 Sensors Network. Sensors 2025, 25, 2012. [Google Scholar] [CrossRef]
- Guo, Q.; He, Z.; Wang, Z. Assessing the effectiveness of long short-term memory and artificial neural network in predicting daily ozone concentrations in Liaocheng City. Sci. Rep. 2025, 15, 6798. [Google Scholar] [CrossRef]
- Li, J.; Meng, Z.; Zhang, J.; Chen, Y.; Yao, J.; Li, X.; Peng, Q.; Liu, X.; Cheng, C. Prediction of Seawater Intrusion Run-Up Distance Based on K-Means Clustering and ANN Model. J. Mar. Sci. Eng. 2025, 13, 377. [Google Scholar] [CrossRef]
- Chen, X.; Shen, Z.; Li, Y.; Yang, Y. Tidal modulation of the hypoxia adjacent to the Yangtze Estuary in summer. Mar. Pollut. Bull. 2015, 100, 453–463. [Google Scholar] [CrossRef]
- Tyler, R.M.; Brady, D.C.; Targett, T.E. Temporal and spatial dynamics of diel-cycling hypoxia in estuarine tributaries. Estuaries Coasts 2009, 32, 123–145. [Google Scholar] [CrossRef]
- Lanoux, A.; Etcheber, H.; Schmidt, S.; Sottolichio, A.; Chabaud, G.; Richard, M.; Abril, G. Factors contributing to hypoxia in a highly turbid, macrotidal estuary (the Gironde, France). Environ. Sci. Process. Impacts 2013, 15, 585–595. [Google Scholar] [CrossRef]
- Automated Synoptic Observing System. Available online: https://data.kma.go.kr/cmmn/main.do (accessed on 10 February 2023).
- Lee, M.; Kim, B.; Kwon, Y.; Kim, J. Characteristics of the marine environment and algal blooms in Gamak Bay. Fish. Sci. 2009, 75, 401–411. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Doodson, A.T. The harmonic development of the tide-generating potential. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1921, 100, 305–329. [Google Scholar]
- Ocean Data in Grid Framework. Available online: http://www.khoa.go.kr/oceangrid/khoa/intro.do (accessed on 12 February 2023).
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave propagation and sampling theory—Part I: Complex signal and scattering in multilayered media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef]
- Maraun, D.; Kurths, J. Cross wavelet analysis: Significance testing and pitfalls. Nonlinear Process. Geophys. 2004, 11, 505–514. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Wilson, P.C. Water quality notes: Dissolved oxygen: Sl313/ss525, 1/2010. EDIS 2010, 2010, 1–8. [Google Scholar] [CrossRef]
- Robinson, C. Microbial respiration, the engine of ocean deoxygenation. Front. Mar. Sci. 2019, 5, 533. [Google Scholar] [CrossRef]
- Park, S.; Kim, K.; Hibino, T.; Kim, K. Machine learning-based prediction of seasonal hypoxia in eutrophic estuary using capacitive potentiometric sensor. Mar. Environ. Res. 2024, 196, 106445. [Google Scholar] [CrossRef]
- Vaquer-Sunyer, R.; Duarte, C.M. Thresholds of hypoxia for marine biodiversity. Proc. Natl. Acad. Sci. USA 2008, 105, 15452–15457. [Google Scholar] [CrossRef]
- National Institute of Fisheries Science. 2024 Climate Change Impact and Research Report in the Fisheries Sector; National Institute of Fisheries Science: Busan, Republic of Korea, 2024. [Google Scholar]
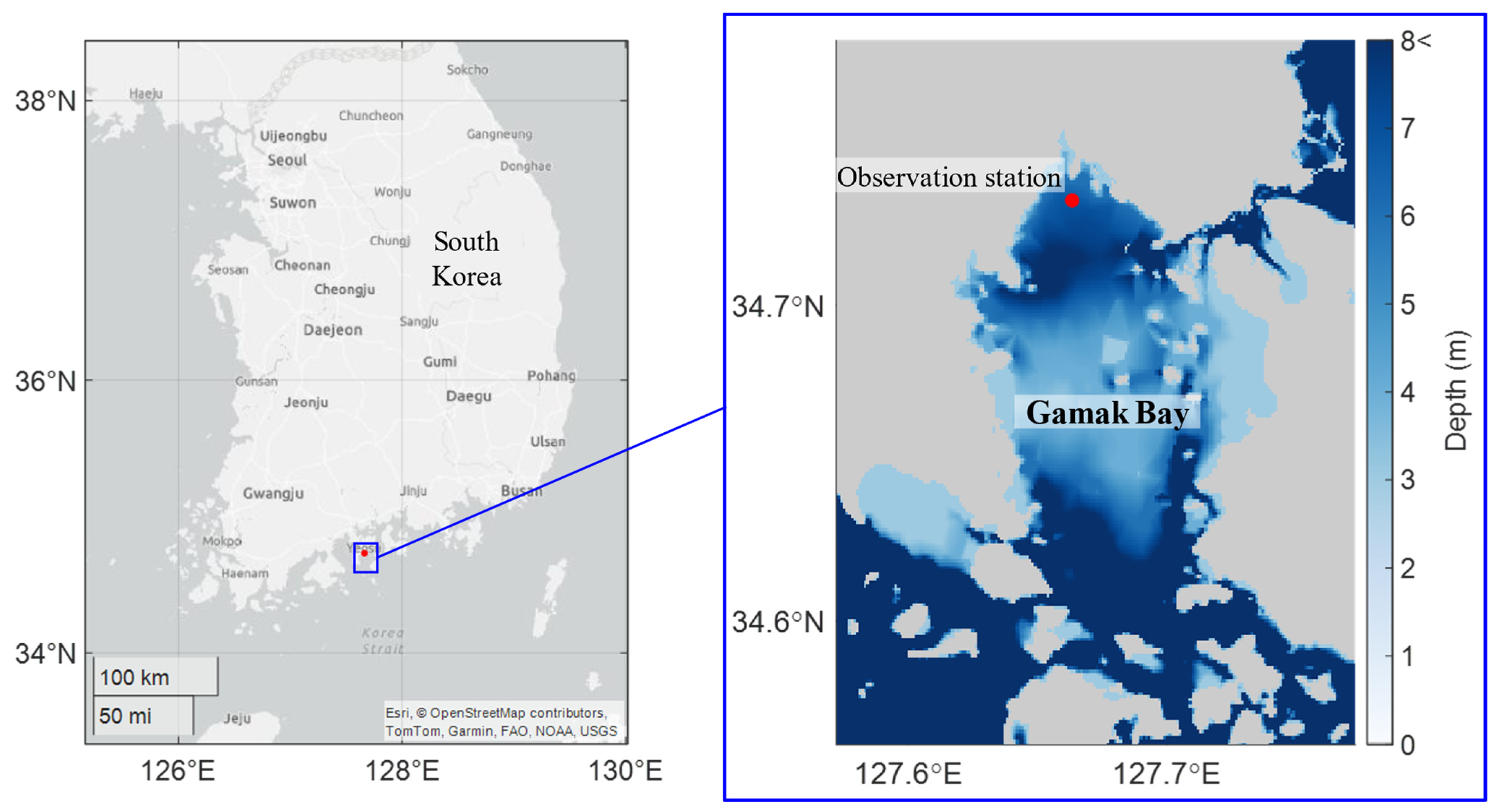



| Min | Max | Mean | Median | Standard Deviation | Missing Rate (%) | |
|---|---|---|---|---|---|---|
| TL 1 (m) | −1.7 | 1.7 | −0.1 | 0.0 | 0.8 | 0.0 |
| AT 2 (°C) | 3.1 | 36.2 | 21.5 | 22.0 | 5.1 | 0.0 |
| Surface WT 3 (°C) | 13.7 | 32.5 | 23.8 | 24.3 | 4.1 | 5.7 |
| Bottom WT 3 (°C) | 13.7 | 30.4 | 22.4 | 22.8 | 3.4 | 4.6 |
| Surface DO 4 (mg/L) | 0.0 | 19.8 | 8.3 | 8.3 | 2.0 | 9.0 |
| Bottom DO 4 (mg/L) | 0.0 | 12.9 | 4.1 | 4.3 | 3.0 | 5.7 |
| Major Tidal Constituents | Amplitude (cm) | Phase Lag (°) | Period (h) |
|---|---|---|---|
| M2 | 101.2 | 253.9 | 12.4 |
| S2 | 47.4 | 282.7 | 12.0 |
| K1 | 20.2 | 190.7 | 23.9 |
| O1 | 12.2 | 152.6 | 25.8 |
| Surface DO | Tide Level | Surface WT | Bottom WT | AT | |
|---|---|---|---|---|---|
| Correlation coefficient | 0.09 | −0.07 | −0.71 | −0.55 | −0.67 |
| Feature importance | 19.90 | 8.79 | 17.55 | 18.85 | 6.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Park, S.-E.; Kim, K. LSTM-Based Forecasting of Coastal Hypoxia in South Korea: Evaluating the Roles of Tide Level and Model Architecture. Water 2025, 17, 1622. https://doi.org/10.3390/w17111622
Park S, Park S-E, Kim K. LSTM-Based Forecasting of Coastal Hypoxia in South Korea: Evaluating the Roles of Tide Level and Model Architecture. Water. 2025; 17(11):1622. https://doi.org/10.3390/w17111622
Chicago/Turabian StylePark, Seongsik, Sung-Eun Park, and Kyunghoi Kim. 2025. "LSTM-Based Forecasting of Coastal Hypoxia in South Korea: Evaluating the Roles of Tide Level and Model Architecture" Water 17, no. 11: 1622. https://doi.org/10.3390/w17111622
APA StylePark, S., Park, S.-E., & Kim, K. (2025). LSTM-Based Forecasting of Coastal Hypoxia in South Korea: Evaluating the Roles of Tide Level and Model Architecture. Water, 17(11), 1622. https://doi.org/10.3390/w17111622






