Intelligent Prediction of Water-CO2 Relative Permeability in Heterogeneous Porous Media Towards Carbon Sequestration in Saline Aquifers
Abstract
1. Introduction
2. Materials and Methods
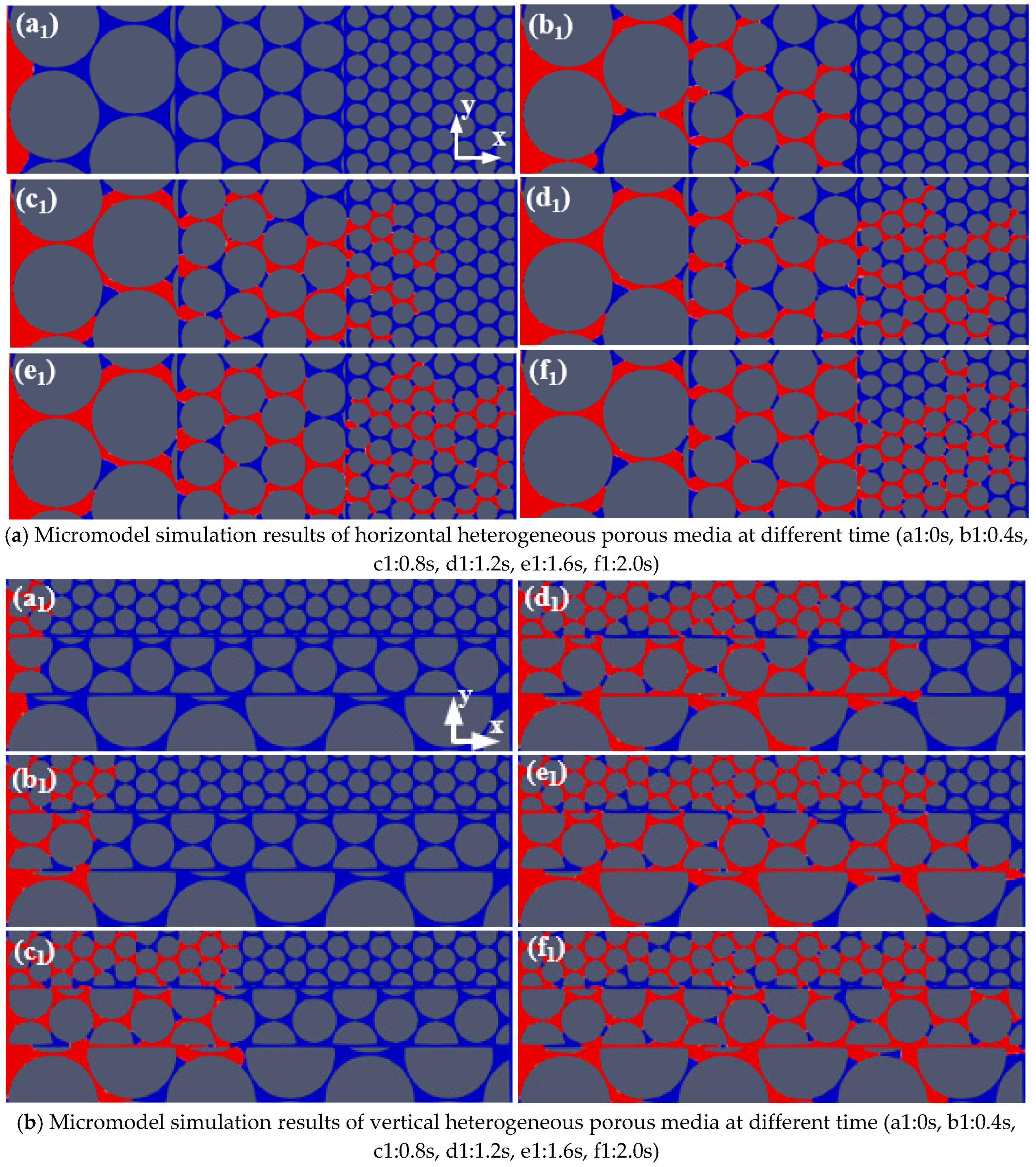
2.1. Micromodel Simulations
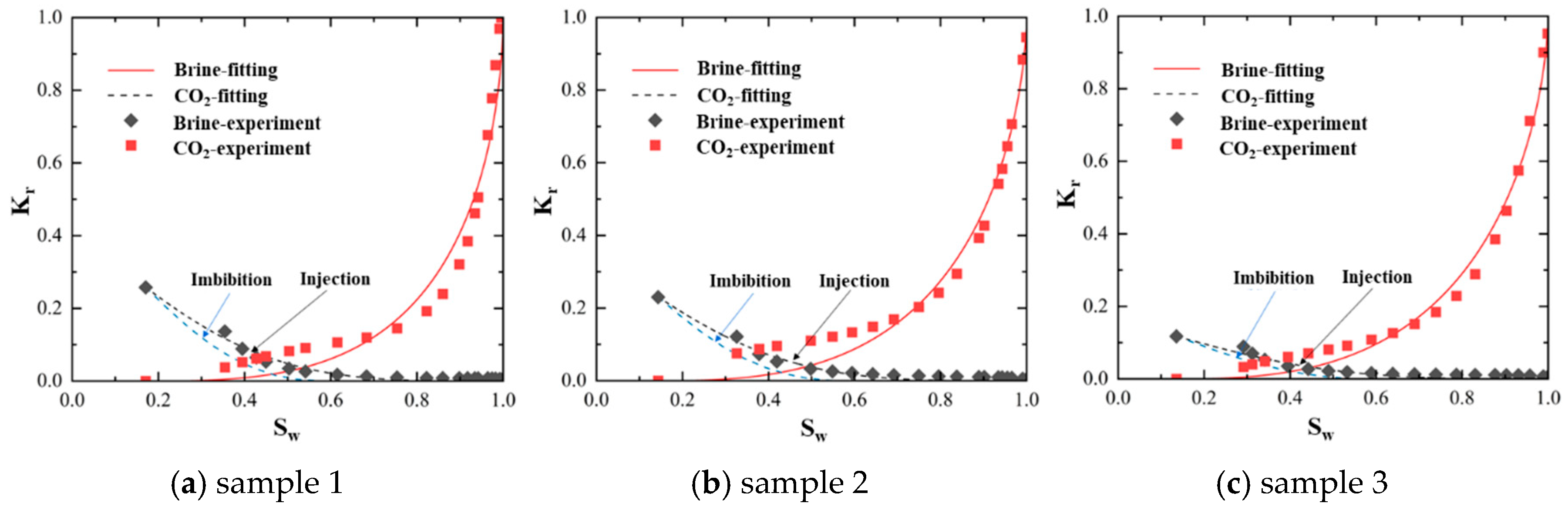
2.2. Core Experiments
- (1)
- High heterogeneity zone—cores displayed prominent layering and significant variations in grain size distribution;
- (2)
- Medium heterogeneity zone—cores showed moderate variations in composition with some visible bedding planes;
- (3)
- Low heterogeneity zone—cores appeared more uniform but still contained subtle heterogeneous features.
2.3. Relative Permeability Acquisition
2.4. Artificial Neural Network (ANN) Model Set up
- (1)
- Building a dataset for model training through micromodel simulation and core experiments. Determining the input and output data, and the ratio of training and testing.
- (2)
- Training models separately for CO2 and brine to construct a prediction model for two-phase relative permeability.
- (3)
- Prediction of the relative permeability and validation of model accuracy.
3. Results
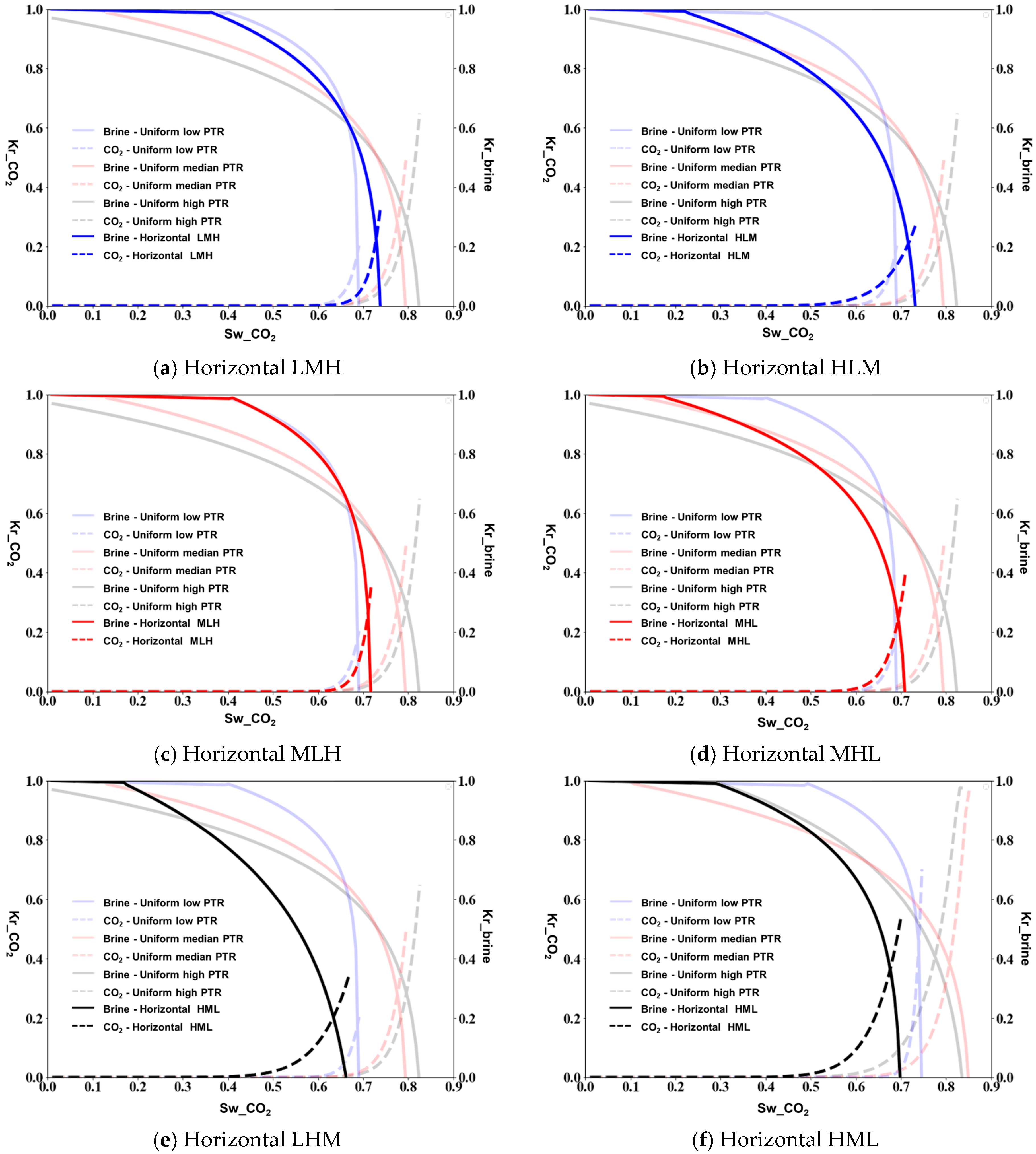
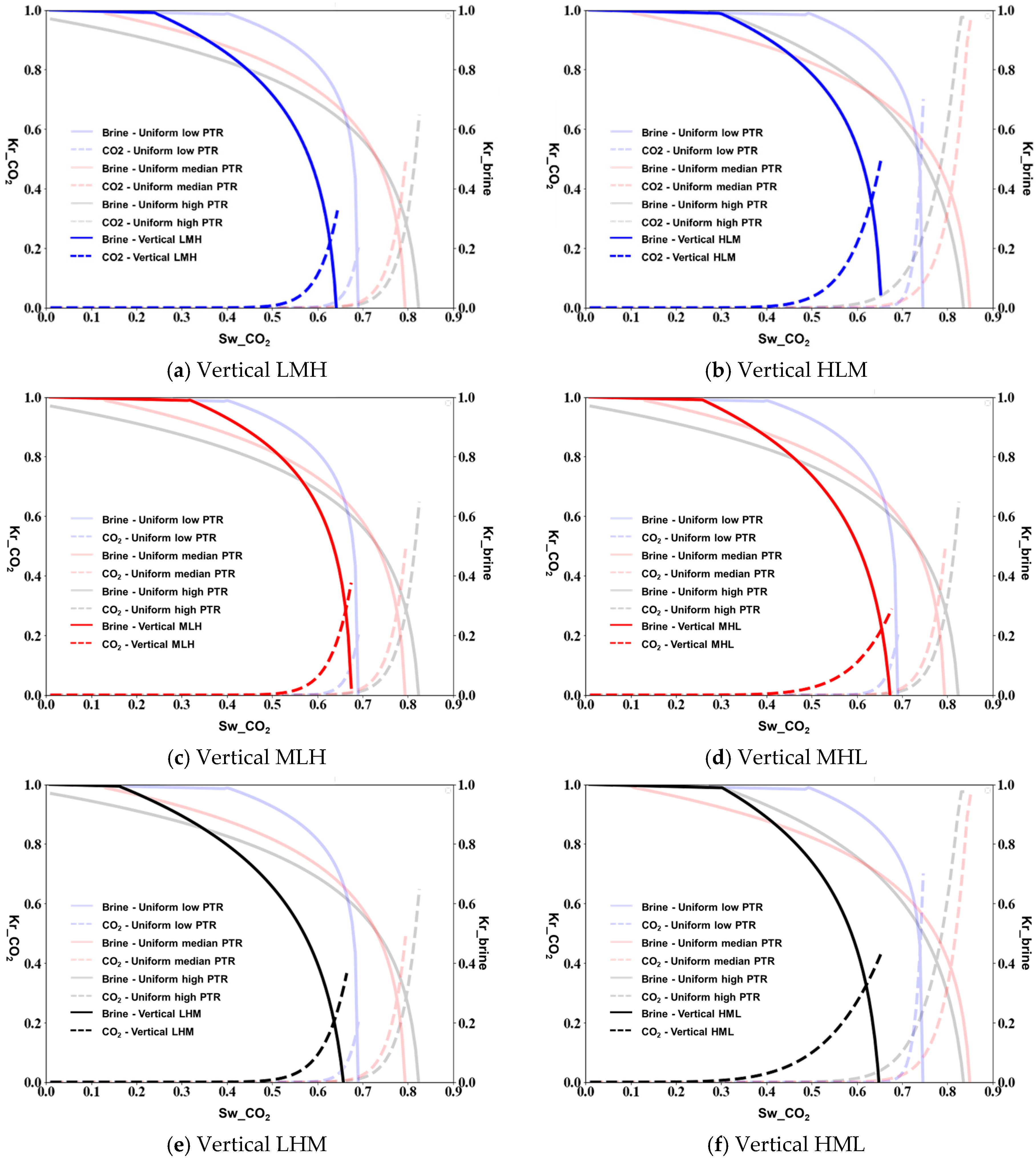
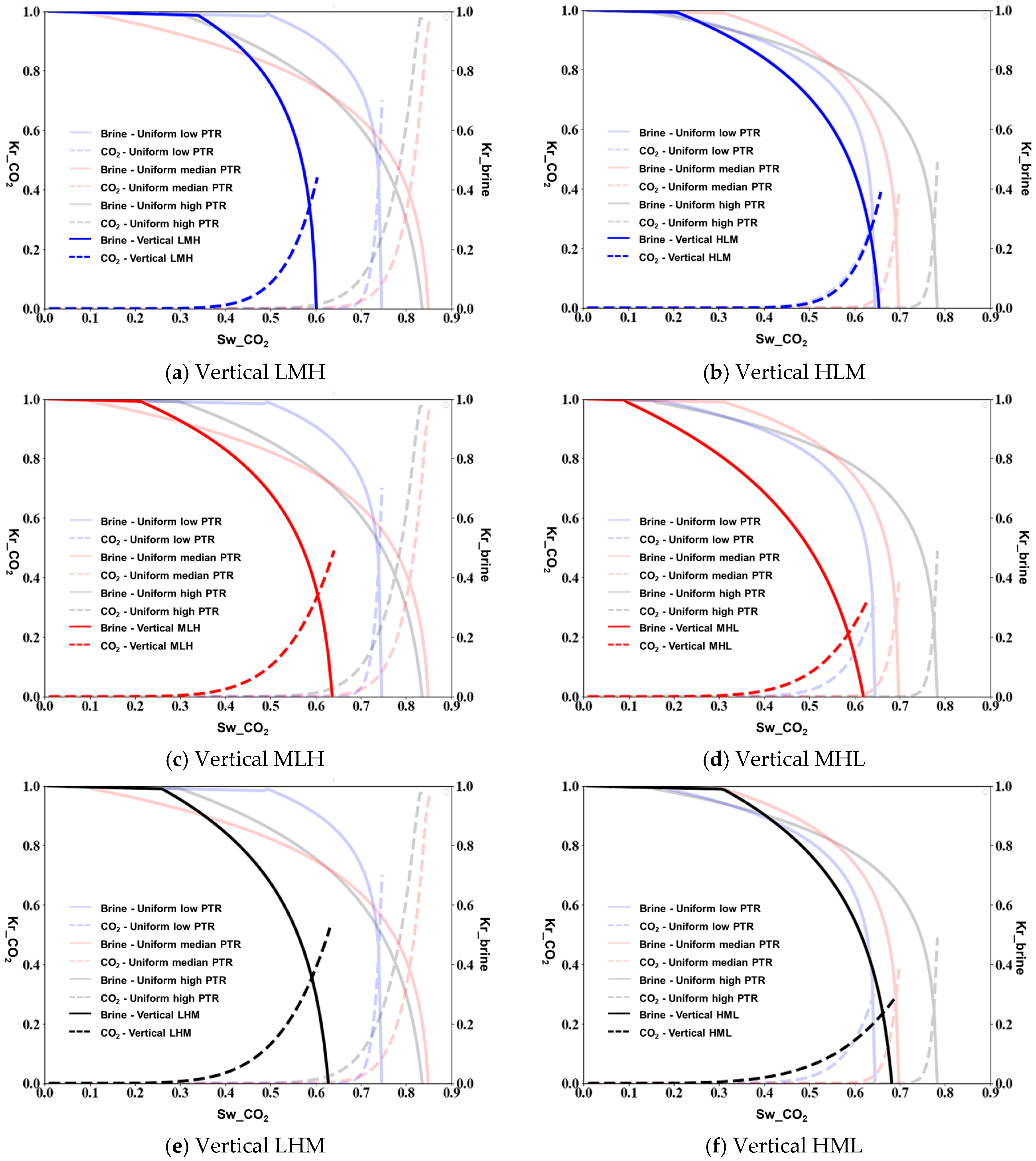
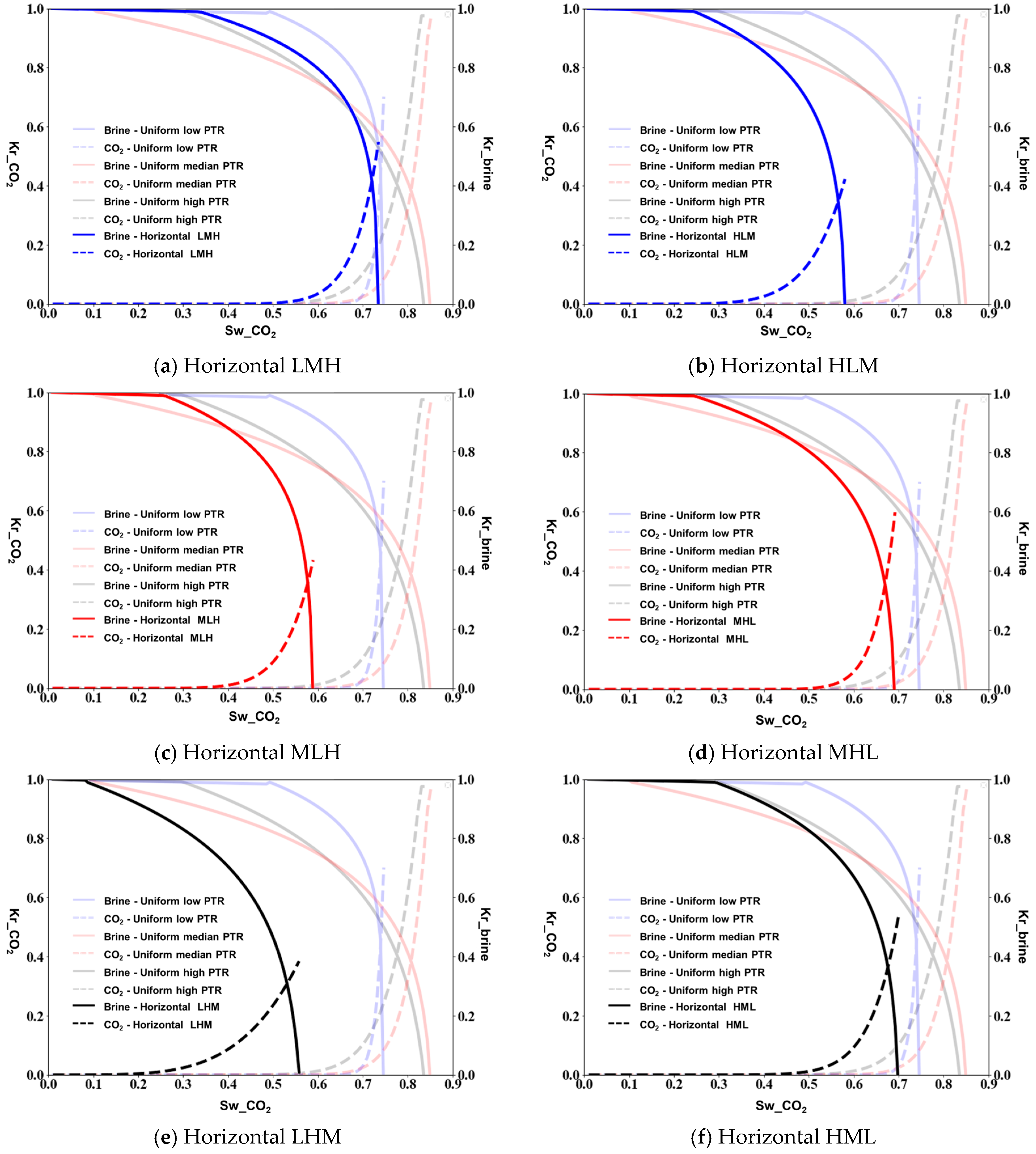
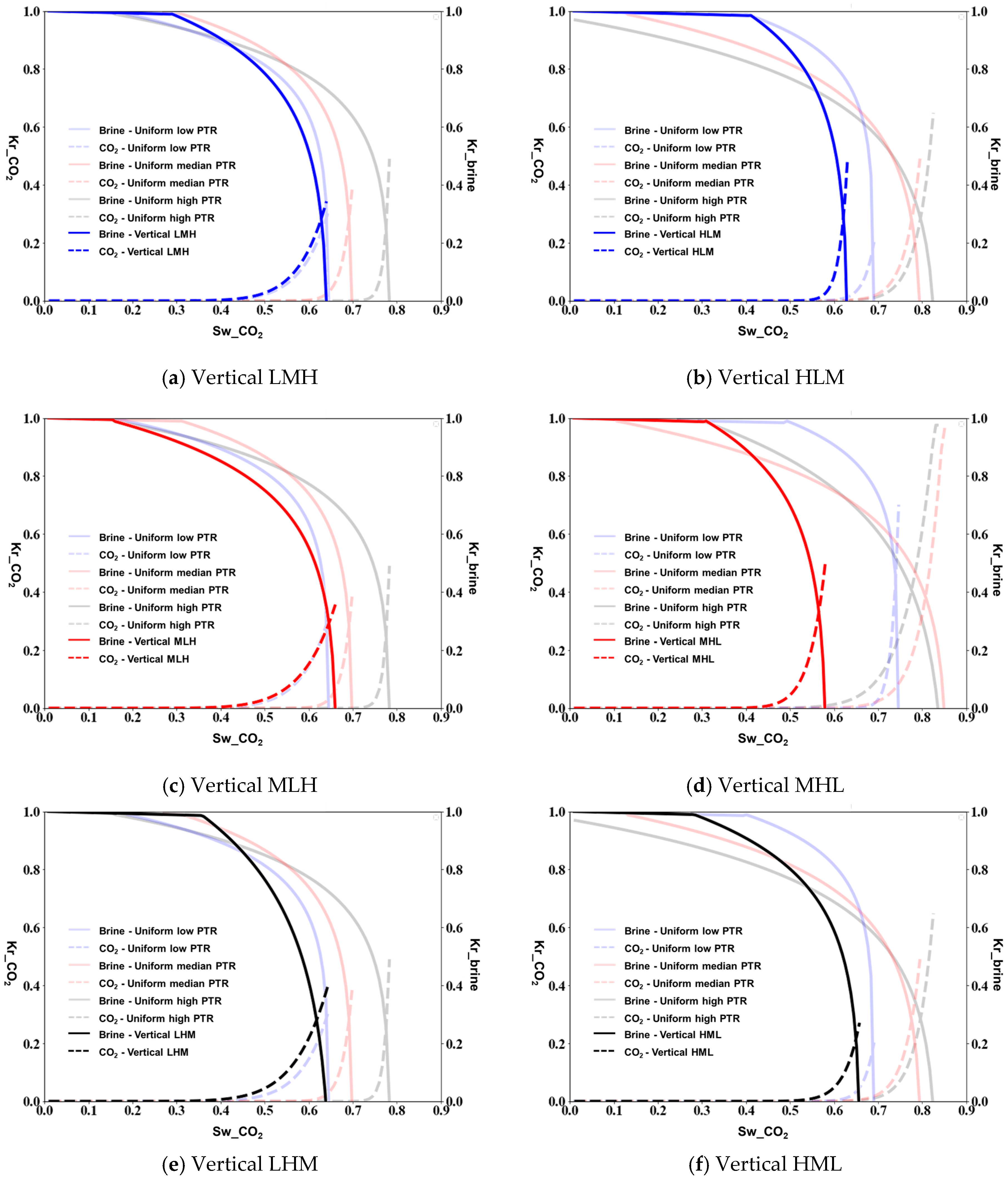
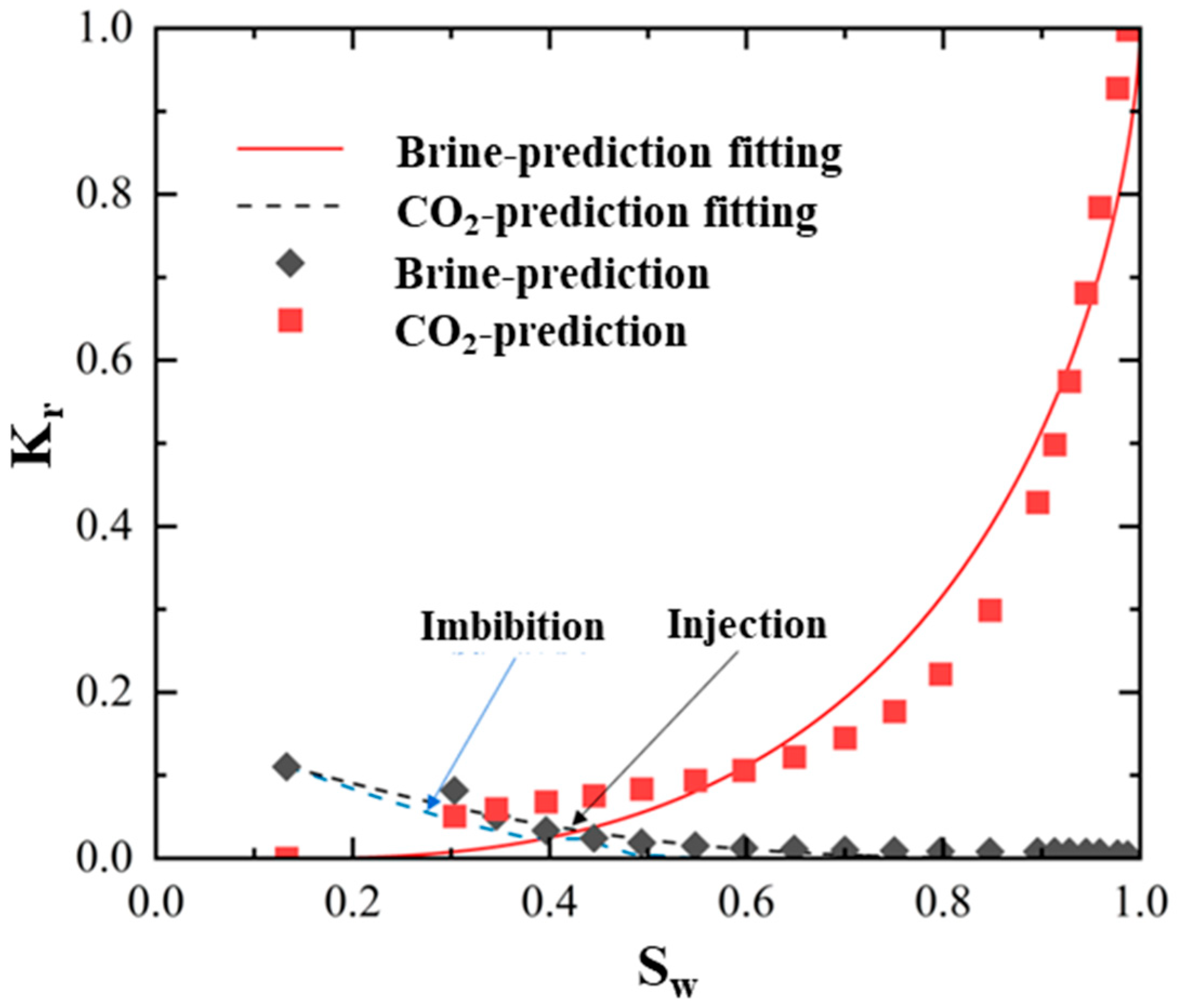
3.1. Relative Permeability of Micromodels
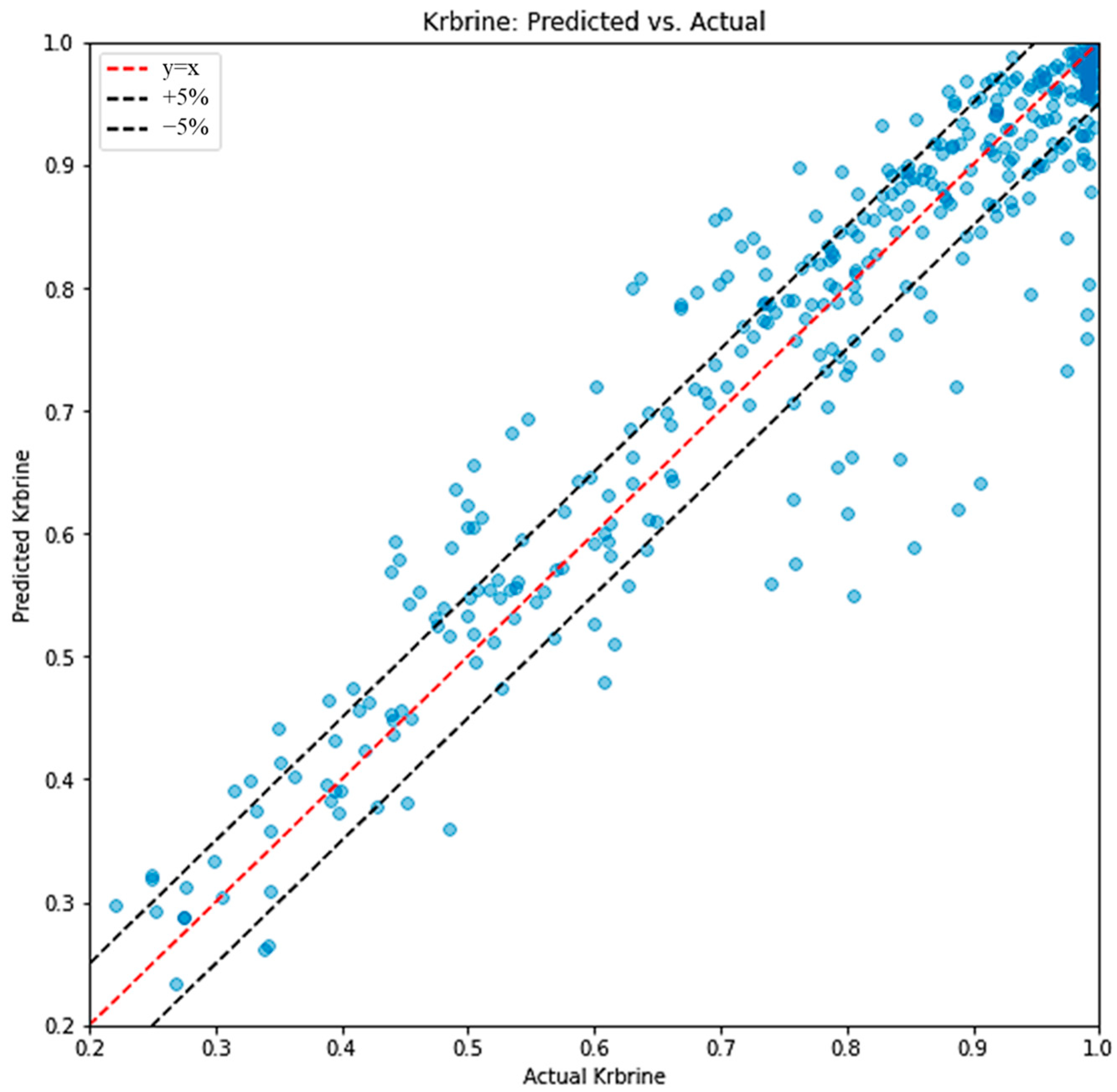
3.2. The Accuracy of the Present Intelligence Model and Validation
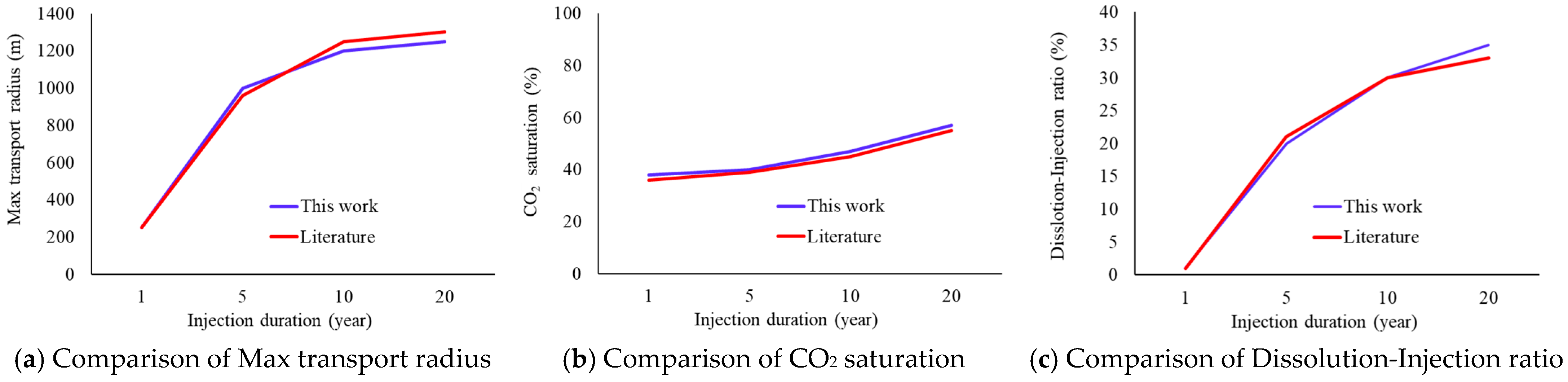
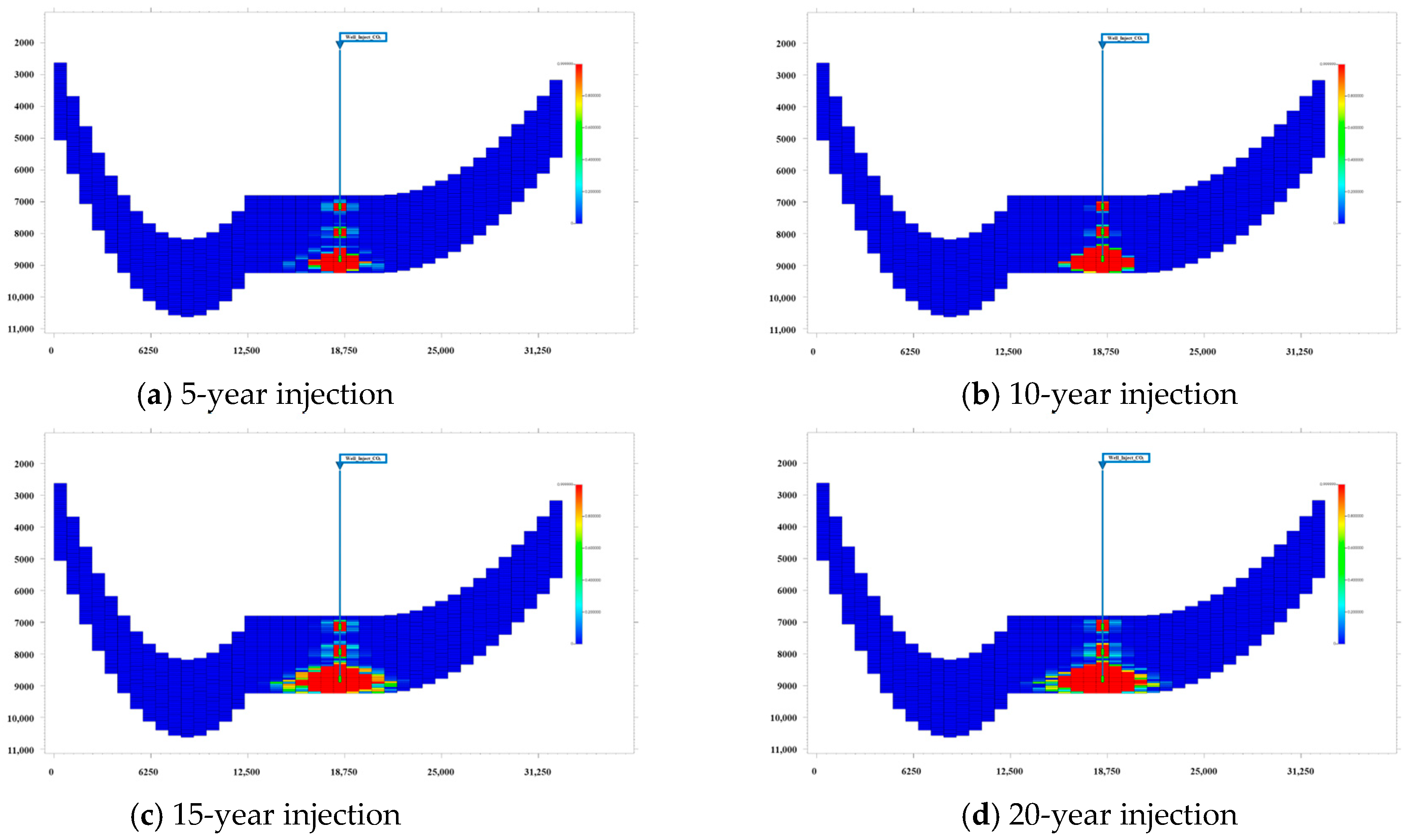
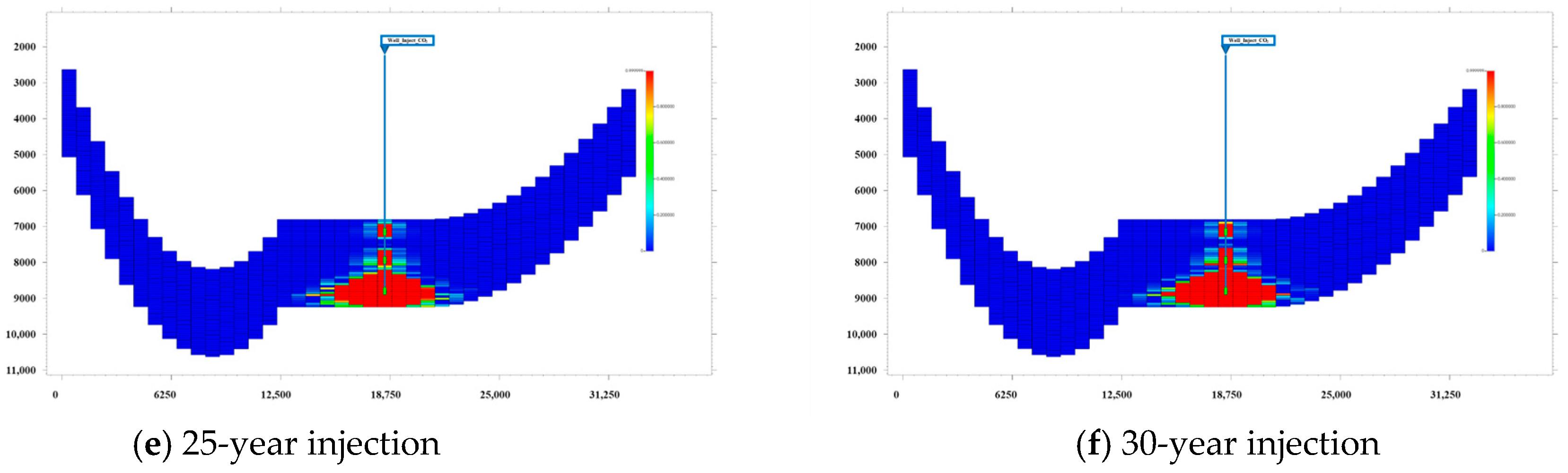
3.3. Actual Field Application
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PTR | Pore-throat ratio |
| PV | Pore volume |
| LMH | The heterogeneous porous structure hierarchically assembled by uniform pore blocks with low, median and high pore-throat ratio |
| LHM | The heterogeneous porous structure hierarchically assembled by uniform pore blocks with low, high and median pore-throat ratio |
| MLH | The heterogeneous porous structure hierarchically assembled by uniform pore blocks with median, low and high pore-throat ratio |
| MHL | The heterogeneous porous structure hierarchically assembled by uniform pore blocks with median, high and low pore-throat ratio |
| HLM | The heterogeneous porous structure hierarchically assembled by uniform pore blocks with high, low and median pore-throat ratio |
| HML | The heterogeneous porous structure hierarchically assembled by uniform pore blocks with high, median and low pore-throat ratio |
| He | The heterogeneity order, which quantitatively indicates the heterogeneity of the hierarchical heterogeneous porous structure |
References
- Bachu, S. Review of CO2 storage efficiency in deep saline aquifers. Int. J. Greenh. Gas. Control. 2015, 40, 188–202. [Google Scholar] [CrossRef]
- Benson, S.M.; Cole, D.R. CO2 Sequestration in Deep Sedimentary Formations. Elements 2008, 4, 325–331. [Google Scholar] [CrossRef]
- Song, H.; Lao, J.; Zhou, Y.; Xie, Z.; Wang, Y.; Yue, M. Microscopic regulation mechanisms of pore heterogeneity and flow conditions on CO2 residual trapping and sequestration capacity. Phys. Fluids 2025, 37, 013108. [Google Scholar] [CrossRef]
- Lao, J.; Xie, Z.; Du, S.; Zhou, Y.; Song, H. Reducing energy consumption and enhancing trapping and capacity of CO2 sequestration: The effects of pore heterogeneity and fluid properties. Energy 2024, 304, 132088. [Google Scholar] [CrossRef]
- Krevor, S.; Blunt, M.J.; Benson, S.M.; Pentland, C.H.; Reynolds, C.; Al-Menhali, A.; Niu, B. Capillary trapping for geologic carbon dioxide storage—From pore scale physics to field scale implications. Int. J. Greenh. Gas. Control. 2015, 40, 221–237. [Google Scholar] [CrossRef]
- Brooks, R.H. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1965. [Google Scholar]
- Honarpour, M.; Koederitz, L.; Harvey, A.H. Relative Permeability of Petroleum Reservoirs; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Akbarabadi, M.; Piri, M. Relative permeability hysteresis and capillary trapping characteristics of supercritical CO2/brine systems: An experimental study at reservoir conditions. Adv. Water Resour. 2013, 52, 190–206. [Google Scholar] [CrossRef]
- Bennion, D.B.; Bachu, S. Drainage and Imbibition Relative Permeability Relationships for Supercritical CO2/Brine and H2S/Brine Systems in Intergranular Sandstone, Carbonate, Shale, and Anhydrite Rocks. SPE Reserv. Eval. Eng. 2008, 11, 487–496. [Google Scholar] [CrossRef]
- Koltermann, C.E.; Gorelick, S.M. Heterogeneity in sedimentary deposits: A review of structure-imitating, process-imitating, and descriptive approaches. Water Resour. Res. 1996, 32, 2617–2658. [Google Scholar] [CrossRef]
- Al-Menhali, A.; Niu, B.; Krevor, S. Capillarity and wetting of carbon dioxide and brine during drainage in Berea sandstone at reservoir conditions. Water Resour. Res. 2015, 51, 7895–7914. [Google Scholar] [CrossRef]
- Espinoza, D.N.; Santamarina, J.C. Water-CO2-mineral systems: Interfacial tension, contact angle, and diffusion-Implications to CO2 geological storage. Water Resour. Res. 2010, 46, 15355–15365. [Google Scholar] [CrossRef]
- Dai, Z.; Samper, J.; Wolfsberg, A.; Levitt, D. Identification of relative conductivity models for water flow and solute transport in unsaturated bentonite. Phys. Chem. Earth Parts A/B/C 2008, 33, S177–S185. [Google Scholar] [CrossRef]
- Jia, W.; McPherson, B.; Pan, F.; Dai, Z.; Moodie, N.; Xiao, T. Impact of three-phase relative permeability and hysteresis models on forecasts of storage associated with CO2-EOR. Water Resour. Res. 2018, 54, 1109–1126. [Google Scholar] [CrossRef]
- Johnson, E.; Bossler, D.; Bossler, V.N. Calculation of Relative Permeability from Displacement Experiments. Trans. AIME 1959, 216, 370–372. [Google Scholar] [CrossRef]
- Toth, J.; Bodi, T.; Szucs, P.; Civan, F. Convenient formulae for determination of relative permeability from unsteady-state fluid displacements in core plugs. J. Pet. Sci. Eng. 2002, 36, 33–44. [Google Scholar] [CrossRef]
- Mijic, A.; LaForce, T.C.; Muggeridge, A.H. CO2 injectivity in saline aquifers: The impact of non-Darcy flow, phase miscibility, and gas compressibility. Water Resour. Res. 2014, 50, 4163–4185. [Google Scholar] [CrossRef]
- Berg, S.; Oedai, S.; Ott, H. Displacement and mass transfer between saturated and unsaturated CO2–brine systems in sandstone. Int. J. Greenh. Gas. Control. 2013, 12, 478–492. [Google Scholar] [CrossRef]
- Reynolds, C.A.; Blunt, M.J.; Krevor, S. Multiphase Flow Characteristics of Heterogeneous Rocks From CO2 Storage Reservoirs in the United Kingdom. Water Resour. Res. 2018, 54, 729–745. [Google Scholar] [CrossRef]
- Krevor, S.C.M.; Pini, R.; Zuo, L.; Benson, S.M. Relative permeability and trapping of CO2 and water in sandstone rocks at reservoir conditions. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Amirian, E.; Dejam, M.; Chen, Z. Performance forecasting for polymer flooding in heavy oil reservoirs. Fuel 2018, 216, 83–100. [Google Scholar] [CrossRef]
- Zhang, T.; Li, D.; Lu, D.; Yang, J. Research on the reconstruction method of porous media using multiple-point geostatistics. Sci. China-Phys. Mech. Astron. 2010, 53, 122–134. [Google Scholar] [CrossRef]
- Gupta, I.; Rai, C.S.; Sondergeld, C.H.; Devegowda, D. Rock Typing in Eagle Ford, Barnett, and Woodford Formations. SPE Reserv. Eval. Eng. 2018, 21, 654–670. [Google Scholar] [CrossRef]
- Zeinedini, E.; Dabir, B.; Dadvar, M. Integrating computational fluid dynamic, artificial intelligence techniques, and pore network modeling to predict relative permeability of gas condensate. Sci. Rep. 2022, 12, 21457. [Google Scholar] [CrossRef]
- Khosravi, R.; Simjoo, M.; Chahardowli, M. Low salinity water flooding: Estimating relative permeability and capillary pressure using coupling of particle swarm optimization and machine learning technique. Sci. Rep. 2024, 14, 13213. [Google Scholar] [CrossRef] [PubMed]
- Yoga, H.F.; Russell, T.J.; Purswani, P. Predictive Model for Relative Permeability Using Physically-Constrained Artificial Neural Networks. SPE J. 2024, 29, 928–942. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Kazemifar, F.; Blois, G.; Kyritsis, D.C.; Christensen, K.T. Quantifying the flow dynamics of supercritical CO2–water displacement in a 2D porous micromodel using fluorescent microscopy and microscopic PIV. Adv. Water Resour. 2016, 95, 352–368. [Google Scholar] [CrossRef]
- Song, H.; Lao, J.; Zhang, L.; Xie, C.; Wang, Y. Underground hydrogen storage in reservoirs: Pore-scale mechanisms and optimization of storage capacity and efficiency. Appl. Energy 2023, 337, 120901. [Google Scholar] [CrossRef]
- Pini, R.; Benson, S.M. Capillary pressure heterogeneity and hysteresis for the supercritical CO2/water system in a sandstone. Adv. Water Resour. 2017, 108, 277–292. [Google Scholar] [CrossRef]
- Jasak, H. OpenFOAM: Open source CFD in research and industry. Int. J. Nav. Arch. Ocean. 2009, 1, 89–94. [Google Scholar]
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J. Comput. Phys. 2012, 231, 5653–5668. [Google Scholar] [CrossRef]
- Zhou, Y.; Tang, L.; Song, Z.; Pan, B.; Ming, Y.; Liu, J.; Song, H. Research on CO2 sequestration in saline aquifers with different relative permeability considering CO2 phase conditions. Energy 2024, 313, 133739. [Google Scholar] [CrossRef]
- Tao, T.M.; Watson, A.T. Accuracy of JBN Estimates of Relative Permeability: Part 2—Algorithms. Soc. Pet. Eng. J. 1984, 24, 215–223. [Google Scholar] [CrossRef]
- Tao, T.M.; Watson, A.T. Accuracy of JBN Estimates of Relative Permeability: Part 1—Error Analysis. Soc. Pet. Eng. J. 1984, 24, 209–214. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Diao, Y.; Zhu, G.; Li, X.; Bai, B.; Li, J.; Wang, Y.; Zhao, X.; Zhang, B. Characterizing CO2 plume migration in multi-layer reservoirs with strong heterogeneity and low permeability using time-lapse 2D VSP technology and numerical simulation. Int. J. Greenh. Gas. Control. 2020, 92, 102880. [Google Scholar] [CrossRef]
- Diao, Y.; Liu, T.; Wei, N.; Ma, X.; Jin, X.; Fu, L. Classification and assessment methodology of carbon dioxide geological storage in deep saline aquifers. China Geol. 2023, 50, 943–951. [Google Scholar]





| Parameter | Interpretation | |
|---|---|---|
| Input | RP_h_b | Relative permeability of brine with high pore-throat ratio |
| RP_m_b | Relative permeability of brine with median pore-throat ratio | |
| RP_l_b | Relative permeability of brine with low pore-throat ratio | |
| RP_h_c | Relative permeability of CO2 with high pore-throat ratio | |
| RP_m_c | Relative permeability of CO2 with median pore-throat ratio | |
| RP_l_c | Relative permeability of CO2 with low pore-throat ratio | |
| Density_c | Density of CO2 | |
| Density_b | Density of brine | |
| Viscosity_c | Viscosity of CO2 | |
| Viscosity_b | Viscosity of brine | |
| Gamma | Interfacial tension | |
| CA | Contact angle | |
| He | Heterogeneity order | |
| SCO₂ | CO2 saturation | |
| Output | Krb | Relative permeability of brine for the reservoir |
| KrCO2 | Relative permeability of CO2 for the reservoir |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Lao, J.; Luo, X.; Zhou, Y.; Song, H. Intelligent Prediction of Water-CO2 Relative Permeability in Heterogeneous Porous Media Towards Carbon Sequestration in Saline Aquifers. Water 2025, 17, 1598. https://doi.org/10.3390/w17111598
Wang J, Lao J, Luo X, Zhou Y, Song H. Intelligent Prediction of Water-CO2 Relative Permeability in Heterogeneous Porous Media Towards Carbon Sequestration in Saline Aquifers. Water. 2025; 17(11):1598. https://doi.org/10.3390/w17111598
Chicago/Turabian StyleWang, Jiulong, Junming Lao, Xiaotian Luo, Yiyang Zhou, and Hongqing Song. 2025. "Intelligent Prediction of Water-CO2 Relative Permeability in Heterogeneous Porous Media Towards Carbon Sequestration in Saline Aquifers" Water 17, no. 11: 1598. https://doi.org/10.3390/w17111598
APA StyleWang, J., Lao, J., Luo, X., Zhou, Y., & Song, H. (2025). Intelligent Prediction of Water-CO2 Relative Permeability in Heterogeneous Porous Media Towards Carbon Sequestration in Saline Aquifers. Water, 17(11), 1598. https://doi.org/10.3390/w17111598