Microscopic Air–Water Properties in Non-Uniform Self-Aerated Flows
Abstract
1. Introduction
2. Experimental Apparatus
3. Results
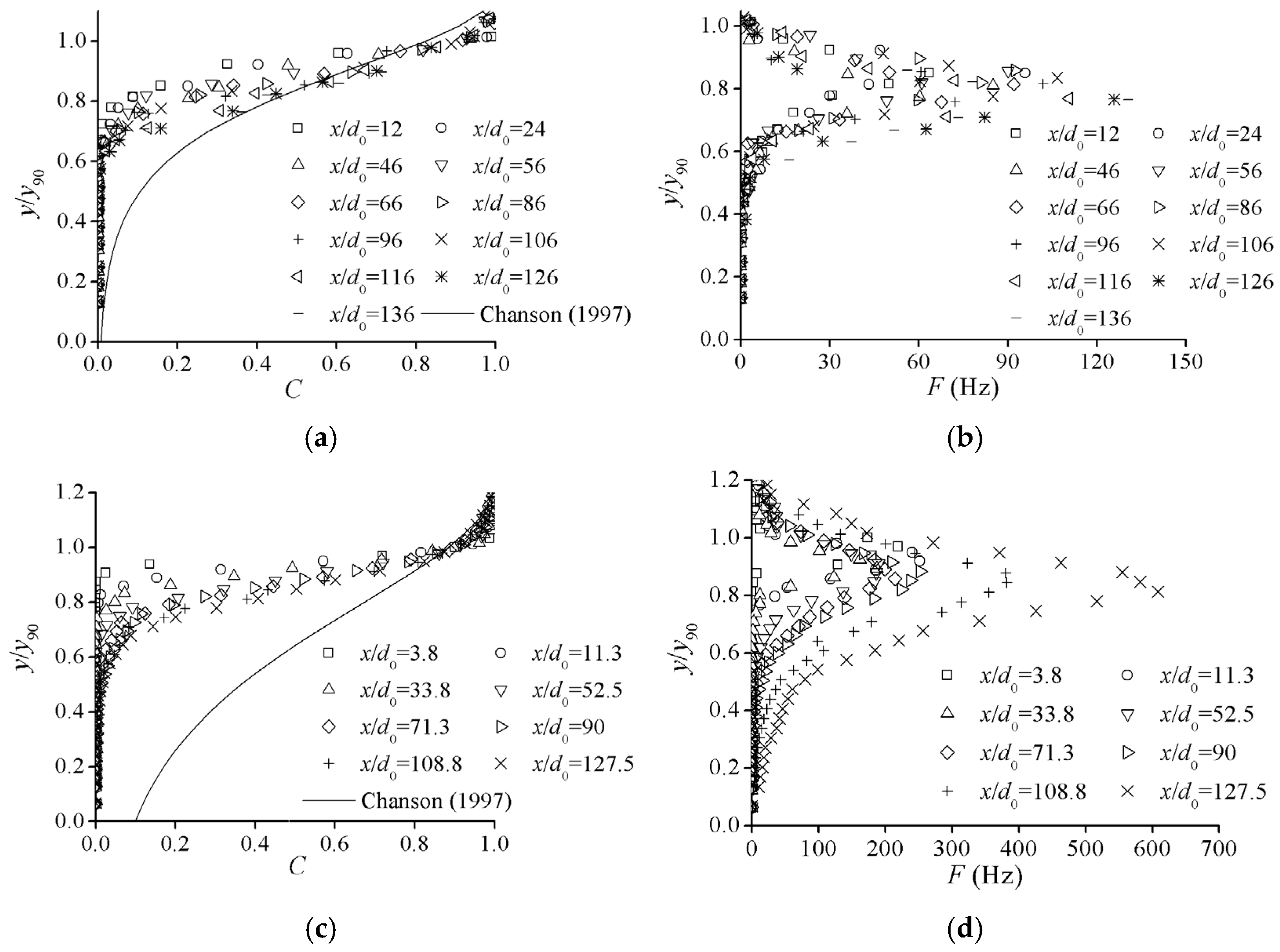
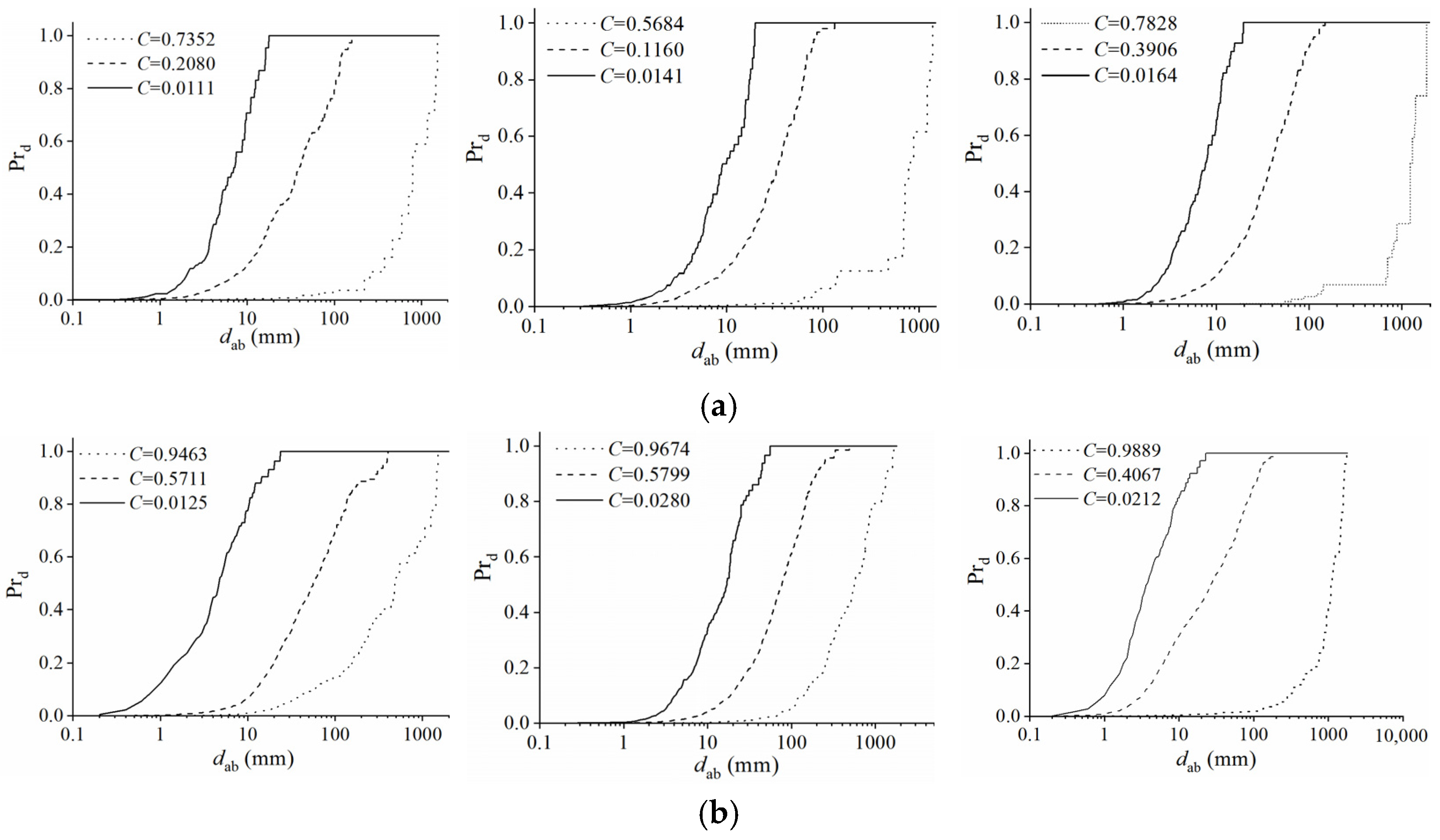
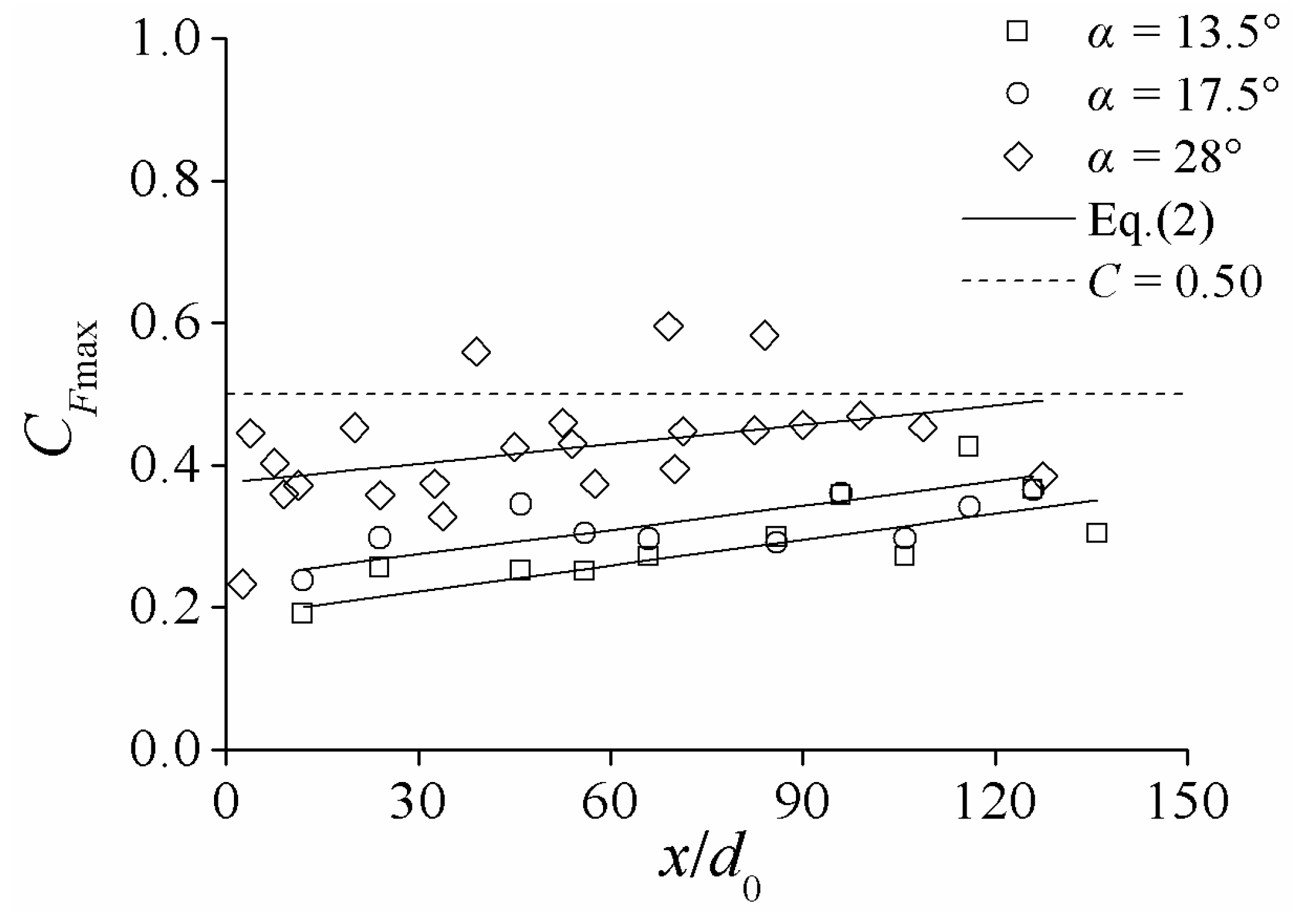
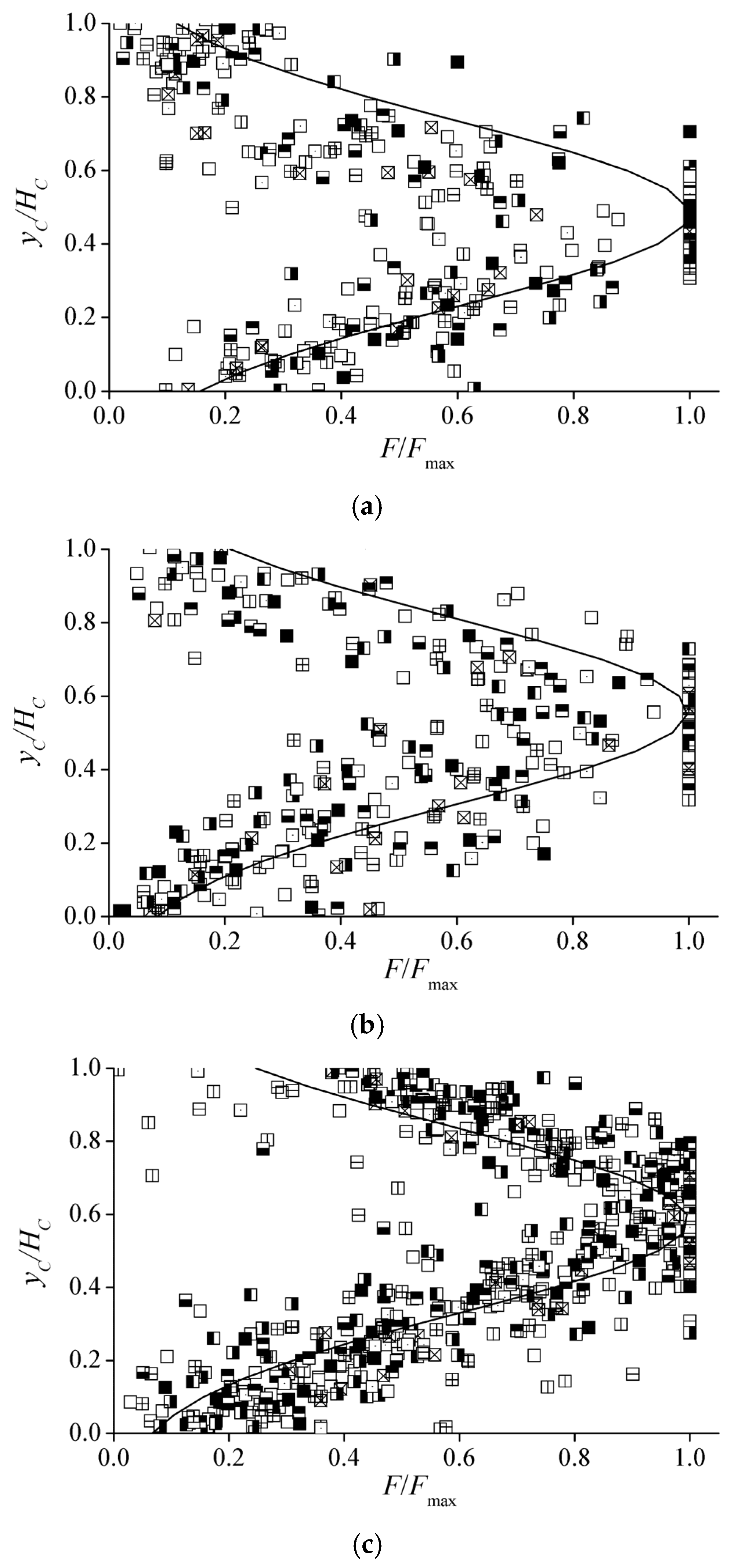
3.1. Bubble Size and Air Concentration Distributions
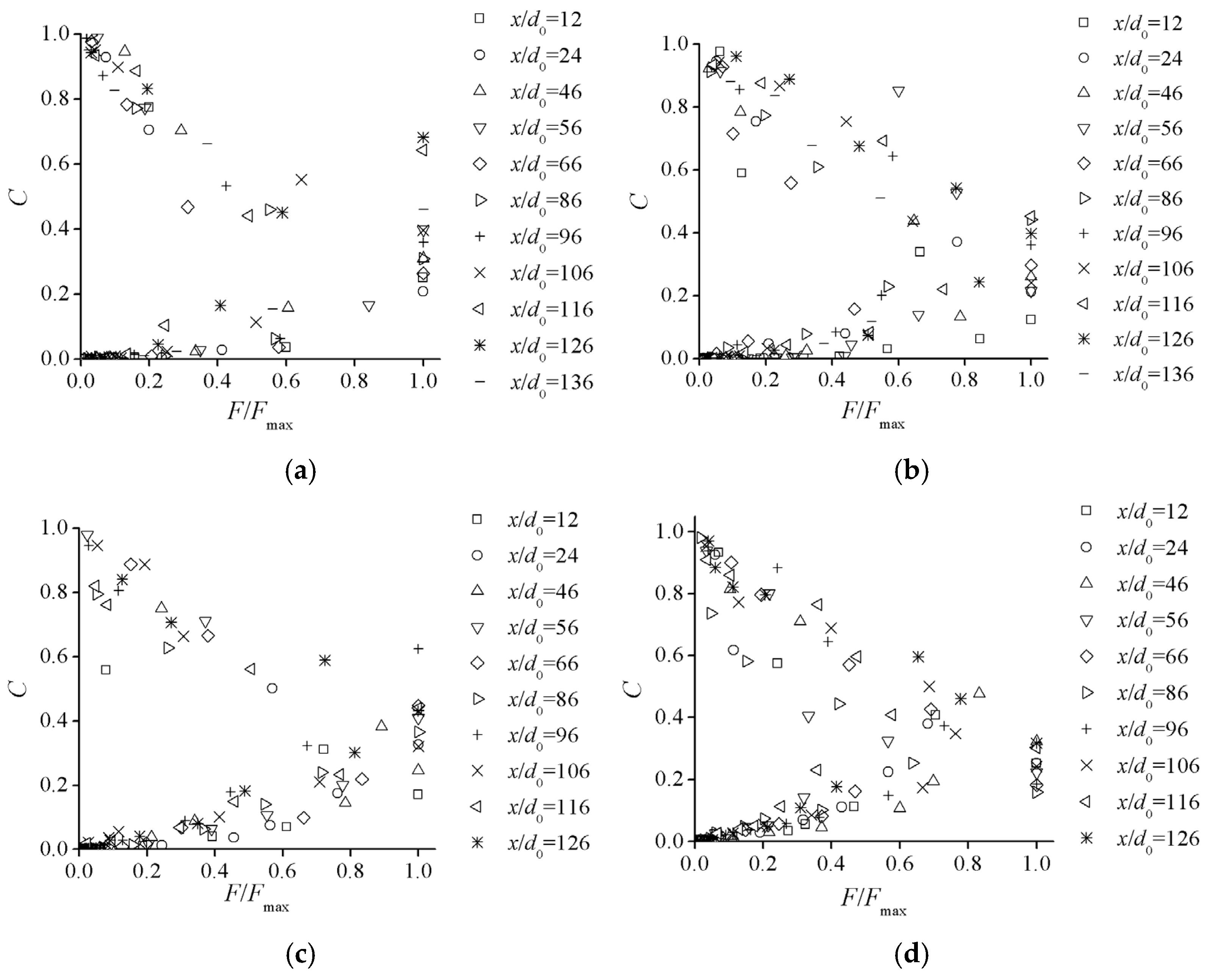
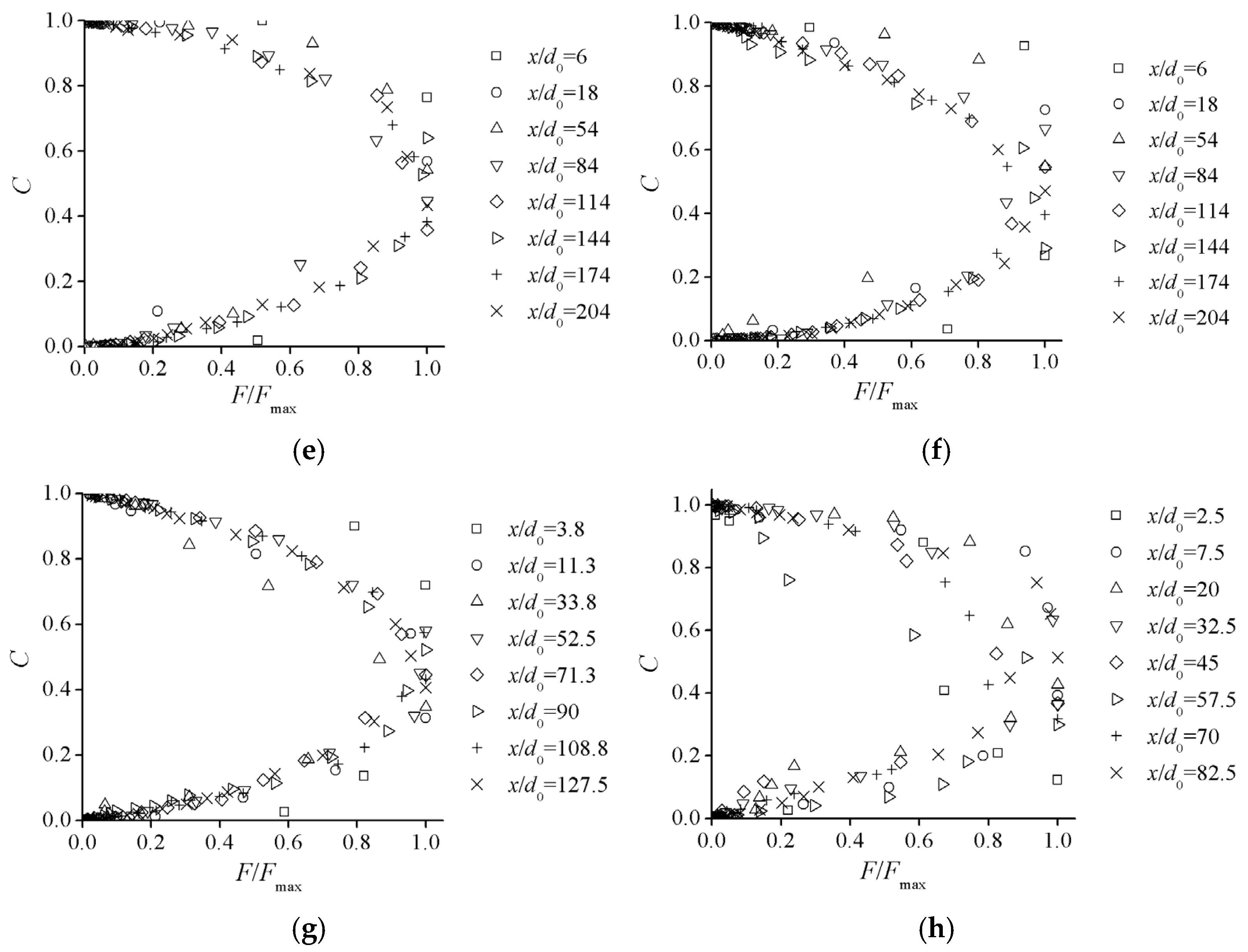
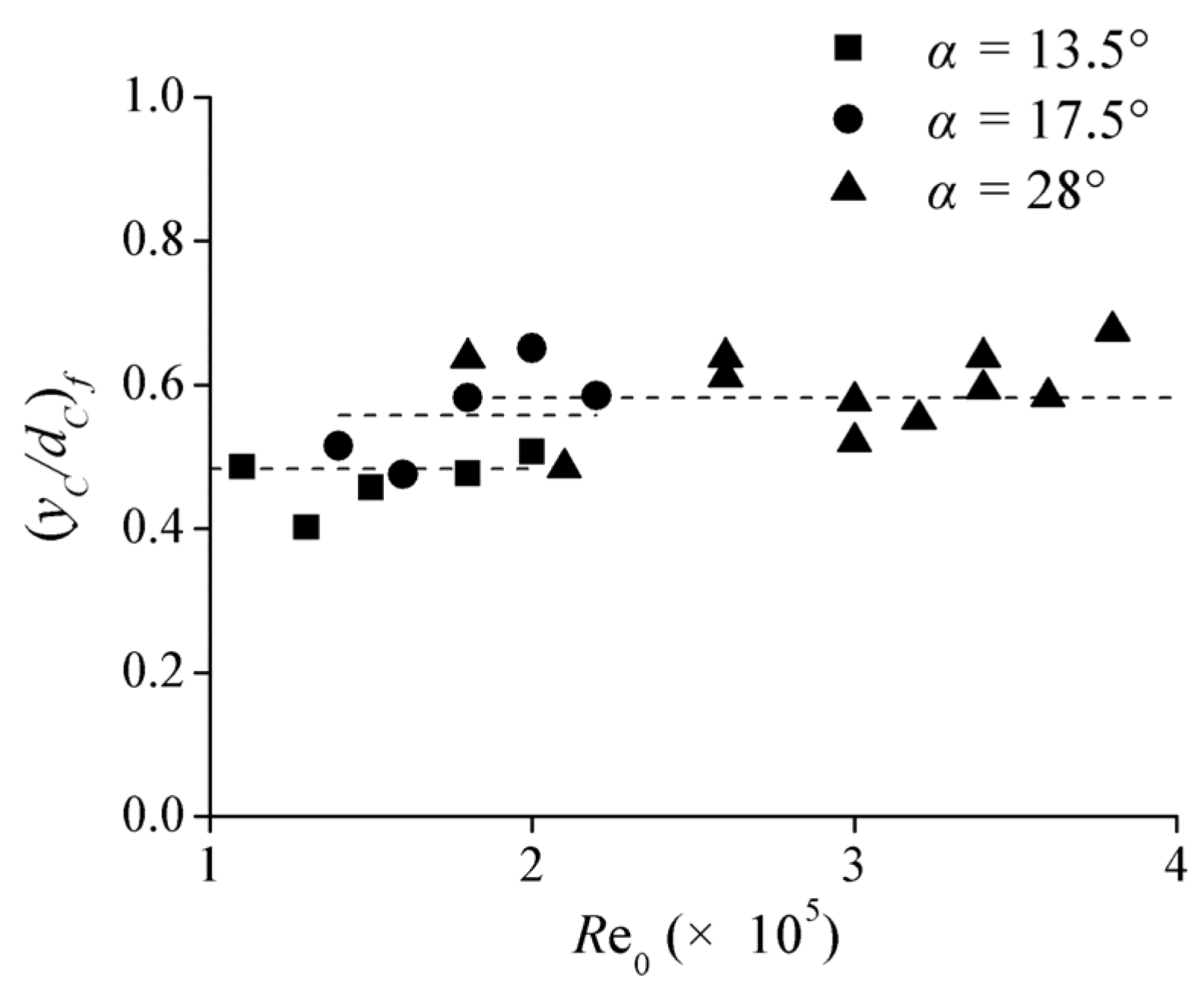
3.2. Air–Water Transfer Frequency in Aeration Regions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Halbronn, G.; Durand, R.; Cohen de Lara, G. Air entrainment in steeply sloping flumes. In Proceeding of 5th IAHR Congress; IAHR-ASCE: Minneapolis, MI, USA, 1953. [Google Scholar]
- Straub, L.G.; Anderson, A.G. Experiments on Self-aerated flow in open channels. J. Hydraul. Div. ASCE 1958, 84, 1–35. [Google Scholar] [CrossRef]
- Thandaveswara, B.S. Self-Aerated Flow Characteristics in Developing Zones and in Hydraulic Jumps. Ph.D. Thesis, Deptement of Civil Engrg India, Institute of Science Bangalore, Bangalore, India, 1974. [Google Scholar]
- Valero, D.; Bung, D.B. Reformulating self-aeration in hydraulic structures: Turbulent growth of free surface perturbations leading to air entrainment. Int. J. Multiph. Flow 2018, 84, 127–142. [Google Scholar] [CrossRef]
- Chen, X.P.; Xi, R.Z.; Shao, D.C. New concept of air entrainment effect on mitigating cavitation damage. J. Hydraul. Eng. 2003, 34, 70–74. (In Chinese) [Google Scholar]
- Wilhelms, S.C. Self-Aerated Spillway Flow. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 1997. [Google Scholar]
- Chanson, H. Self-aerated flows on chutes and spillways. J. Hydraul. Eng. 1993, 119, 220–243. [Google Scholar] [CrossRef]
- Hager, W.H. Uniform aerated chute flow. J. Hydraul. Eng. 1991, 118, 528–533. [Google Scholar] [CrossRef]
- Wood, I.R. Uniform region of self-aerated flow. J. Hydraul. Eng. 1983, 109, 447–461. [Google Scholar] [CrossRef]
- Cain, P.; Wood, I.R. Instrumentation for aerated flow on spillways. J. Hydraul. Div. 1981, 107, 1407–1424. [Google Scholar] [CrossRef]
- Cain, P.; Wood, I.R. Measurements of self-aerated flow on a spillway. J. Hydraul. Div. 1981, 107, 1425–1444. [Google Scholar] [CrossRef]
- Chanson, H.; Carosi, G. Turbulent time and length scale measurements in high-velocity open channel flows. Exp. Fluids 2007, 42, 385–401. [Google Scholar] [CrossRef]
- Sene, K.J.; Hunt, J.C.R.; Thomas, N.H. The role of coherent structures in bubble transport by turbulent shear flows. J. Fluid. Mech. 1994, 259, 219–240. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, H.; Chanson, H. Turbulence and aeration in hydraulic jumps: Free-surface fluctuation and integral turbulent scale measurements. Environ. Fluid Mech. 2013, 13, 189–204. [Google Scholar] [CrossRef]
- Gulliver, J.S.; Thene, J.R.; Rindels, A.J. Indexing gas transfer in self-aerated flows. J. Environ. Eng. 1990, 116, 503–522. [Google Scholar] [CrossRef]
- Chanson, H. Air bubble entrainment in open channels. Flow structure and bubble size distributions. Int. J. Multiph. Flow 1997, 23, 193–203. [Google Scholar] [CrossRef]
- Toombes, L.; Chanson, H. Surface waves and roughness in self-aerated supercritical Flow. Environ. Fluid Mech. 2007, 7, 259–270. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Triple decomposition technique in air–water flows: Application to instationary flows on a stepped spillway. Int. J. Multiph. Flow 2014, 58, 139–153. [Google Scholar] [CrossRef]
- Guenther, P.; Felder, S.; Chanson, H. Flow aeration, cavity processes and energy dissipation on flat and pooled stepped spillways for embankments. Environ. Fluid Mech. 2013, 13, 503–525. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H. Self-entrainment of air on stepped spillways. Int. J. Multiph. Flow 2011, 37, 99–107. [Google Scholar] [CrossRef]
- Pagliara, S. Self-aeration and friction over rock chutes in uniform flow conditions. J. Hydraul. Eng. 2010, 136, 447–461. [Google Scholar] [CrossRef]
- Pagliara, S.; Carnacina, I.; Roshni, T. Inception point and air entrainment on flows under macroroughness condition. J. Environ. Eng. 2011, 137, 629–638. [Google Scholar] [CrossRef]
- Robinson, K.M.; Rice, C.E.; Kadavy, K.C. Design of rock chutes. Am. Soc. Agric. Eng. Trans. 1988, 41, 621–626. [Google Scholar] [CrossRef]
- Toombes, L. Experimental Study of Air-Water Flow Properties on Low-Gradient Stepped Cascades. Ph.D. Thesis, University of Queensland, Brisbane, Australia, 2002. [Google Scholar]
- Kramer, M. Turbulent free-surface in self-aerated flows: Superposition of entrapped and entrained air. J. Fluid Mech. 2024, 980, A25. [Google Scholar] [CrossRef]
- Wilhelms, S.C.; Gulliver, J.S. Bubbles and waves description of self-aerated spillway flow. J. Hydraul. Res. 2005, 43, 522–531. [Google Scholar] [CrossRef]
- Wei, W.; Deng, J. Free surface aeration and devel opment dependence in chute flows. Sci. Rep. 2022, 12, 1477. [Google Scholar]
- Felder, S.; Chanson, H. Energy dissipation, flow resistance and gas-liquid interfacial area in skimming flows on moderate-slope stepped spillways. Environ. Fluid Mech. 2009, 9, 427–441. [Google Scholar] [CrossRef]
- Kramer, M.; Valero, D. Linking turbulent waves and bubble diffusion in self-aerated open-channel flows: Two state air concentration. J. Fluid Mech. 2023, 966, A37. [Google Scholar] [CrossRef]
- Deane, G.B.; Stokes, M.D. Scale dependence of bubble creation mechanisms in breaking waves. Nature 2002, 418, 834–844. [Google Scholar] [CrossRef]
- Vela-Martín, A.; Avila, M. Memoryless drop breakup in turbulence. Sci. Adv. 2022, 8, eabp9561. [Google Scholar] [CrossRef]
- Wei, W.; Xu, W.; Deng, J.; Tian, Z.; Zhang, F. Bubble formation and scale dependence in free-surface air entrainment. Sci. Rep. 2019, 9, 11008. [Google Scholar] [CrossRef]
- Wei, W.; Xu, W.; Deng, J.; Guo, Y. Self-aeration development and fully cross-sectional air diffusion in high-speed open channel flows. J. Hydraul. Res. 2022, 60, 445–459. [Google Scholar] [CrossRef]
- Hsiao, F.; Lamb, O.P.; Pilch, M. Report on the High Velocity Flow of Water in a Small Rectangular Channel; Project Report Advanced Hydraulic Laboratory Nos. CE 194 and CE 195 the University of Minnesota: Minneapolis, MN, USA, 1947. [Google Scholar]
- Chen, X.P.; Shao, D.C. Measuring bubbles sizes in aerated flow. In Proceedings of the Conference of Global Chinese Scholars on Hydrodynamics, Shanghai, China, 16 August 2006; pp. 470–474. [Google Scholar]
- Deng, J.; Wei, W.R.; Xu, W.L.; Tian, Z.; Zhang, F.X. Experimental study on air-phase frequency in self-aerated flow. Water Manag.-ICE 2015, 168, 153–161. [Google Scholar] [CrossRef]
- Anwar, H.O. Discussion on “Self-aerated flows on chutes and spillways”. J. Hydraul. Eng. 1994, 120, 778–779. [Google Scholar] [CrossRef]
- Wei, W.; Xu, W.; Deng, J.; Tian, Z.; Zhang, F. Experimental study of air-water interface properties in self-aerated flows. J. Hydrodyn. 2019, 31, 940–948. [Google Scholar] [CrossRef]



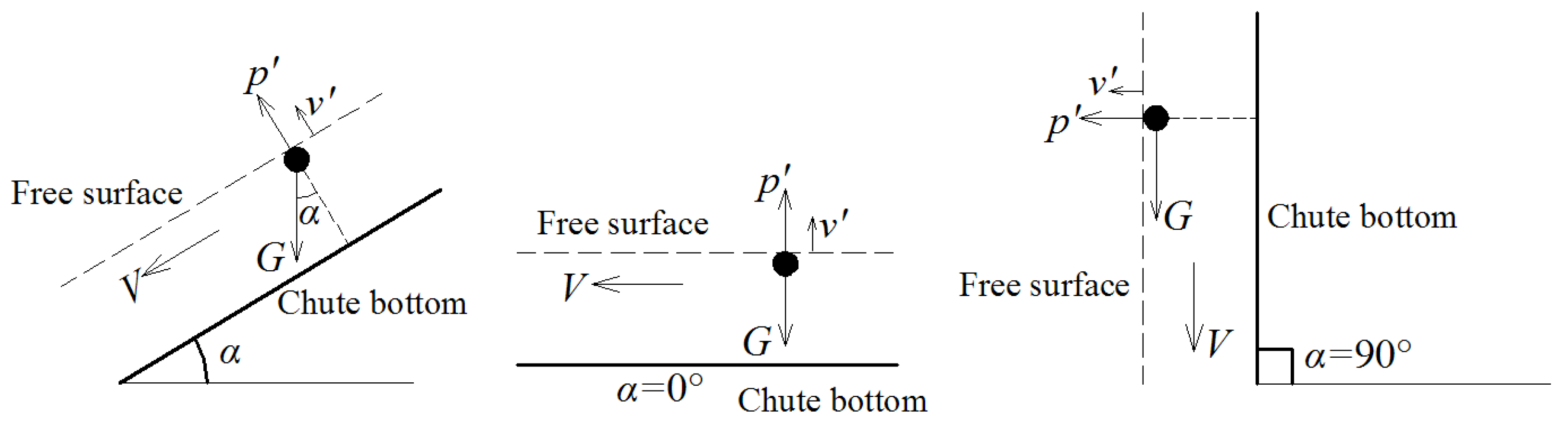
| α (°) | d0 (m) | V0 (m/s) | Re0 (×105) |
|---|---|---|---|
| 13.5 | 0.05 | 3.5 | 1.1 |
| 4.3 | 1.3 | ||
| 5.0 | 1.5 | ||
| 5.8 | 1.8 | ||
| 6.4 | 2.0 | ||
| 17.5 | 0.05 | 4.5 | 1.4 |
| 5.2 | 1.6 | ||
| 6.0 | 1.8 | ||
| 7.0 | 2.1 | ||
| 7.8 | 2.4 | ||
| 28.0 | 0.05 | 6.2 | 1.8 |
| 7.5 | 2.1 | ||
| 9.0 | 2.6 | ||
| 0.08 | 6.6 | 2.6 | |
| 7.5 | 3.0 | ||
| 8.5 | 3.4 | ||
| 0.10 | 6.5 | 3.0 | |
| 7.5 | 3.4 | ||
| 8.4 | 3.8 | ||
| 0.12 | 6.2 | 3.2 | |
| 7.0 | 3.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Wei, W. Microscopic Air–Water Properties in Non-Uniform Self-Aerated Flows. Water 2025, 17, 1587. https://doi.org/10.3390/w17111587
Yang C, Wei W. Microscopic Air–Water Properties in Non-Uniform Self-Aerated Flows. Water. 2025; 17(11):1587. https://doi.org/10.3390/w17111587
Chicago/Turabian StyleYang, Caiyong, and Wangru Wei. 2025. "Microscopic Air–Water Properties in Non-Uniform Self-Aerated Flows" Water 17, no. 11: 1587. https://doi.org/10.3390/w17111587
APA StyleYang, C., & Wei, W. (2025). Microscopic Air–Water Properties in Non-Uniform Self-Aerated Flows. Water, 17(11), 1587. https://doi.org/10.3390/w17111587






