A New Methodology to Estimate the Level of Water Stress (SDG 6.4.2) by Season and by Sub-Basin Avoiding the Double Counting of Water Resources
Abstract
1. Introduction
State of the Art and Bottlenecks
2. Methodology
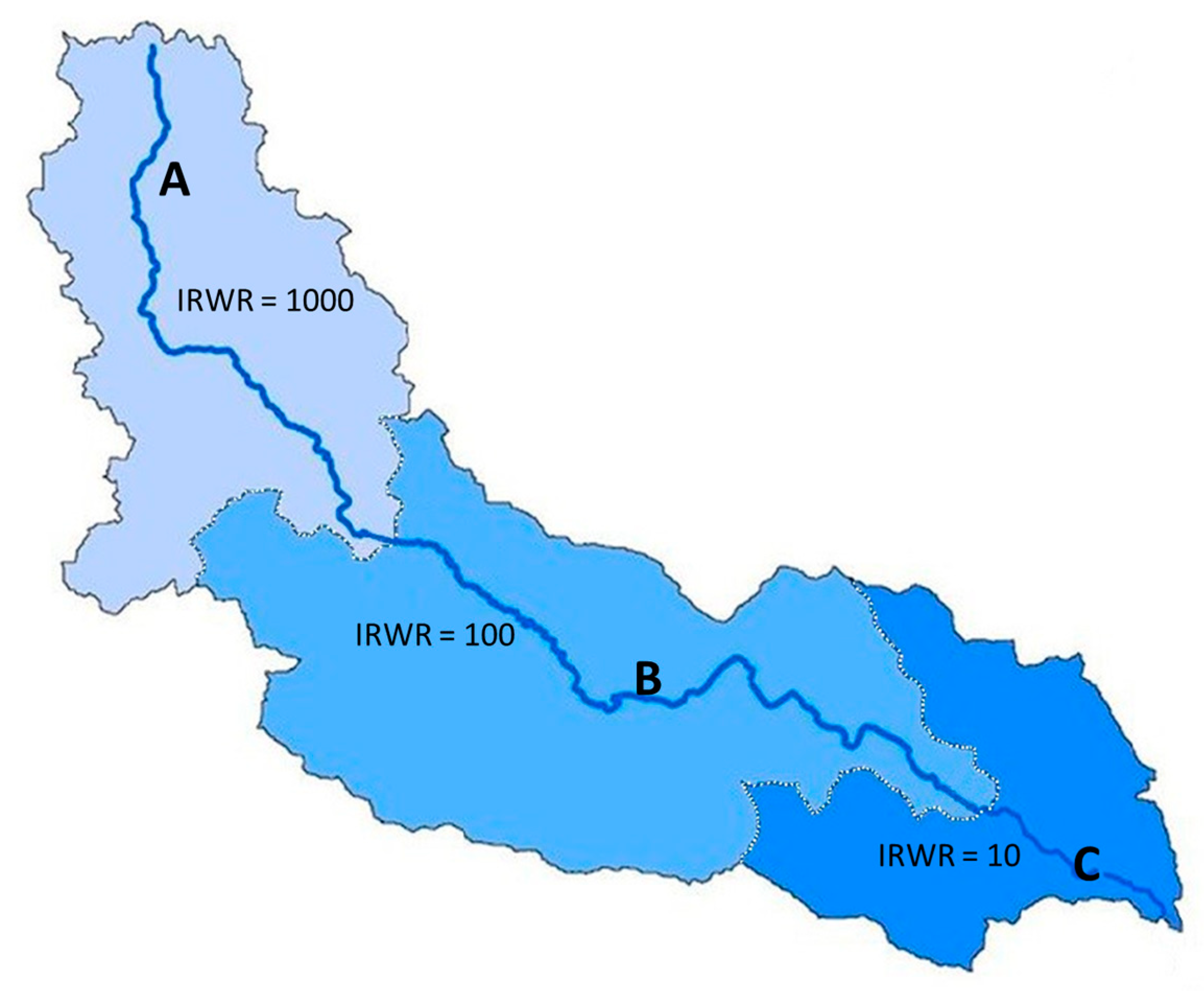
2.1. Internal Renewable Freshwater Resources
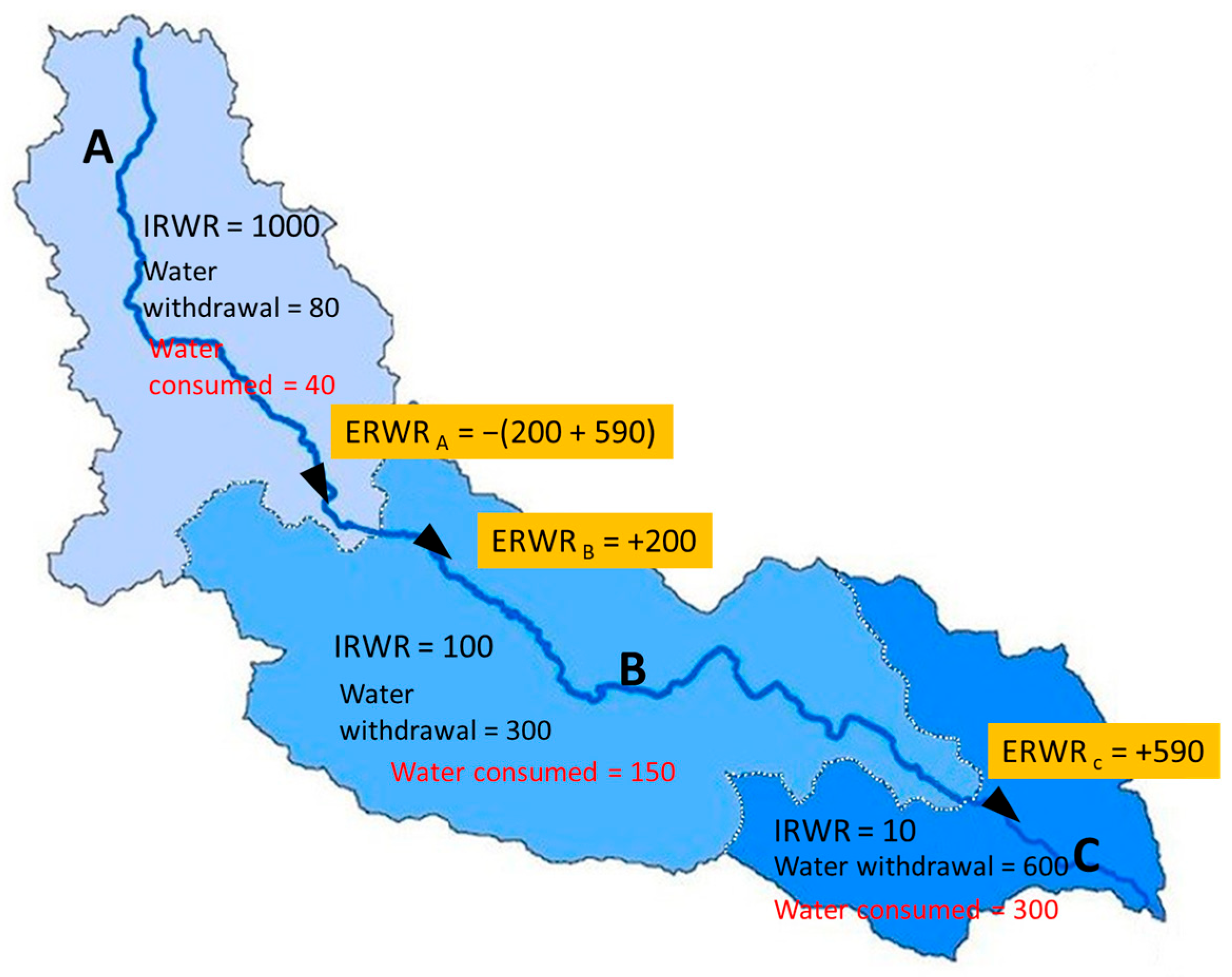
2.2. External Renewable Freshwater Resources
2.3. Total Renewable Freshwater Resources
2.3.1. Use of Unconventional Water Resources and Water Transferred Artificially
2.3.2. The Temporal Disaggregation
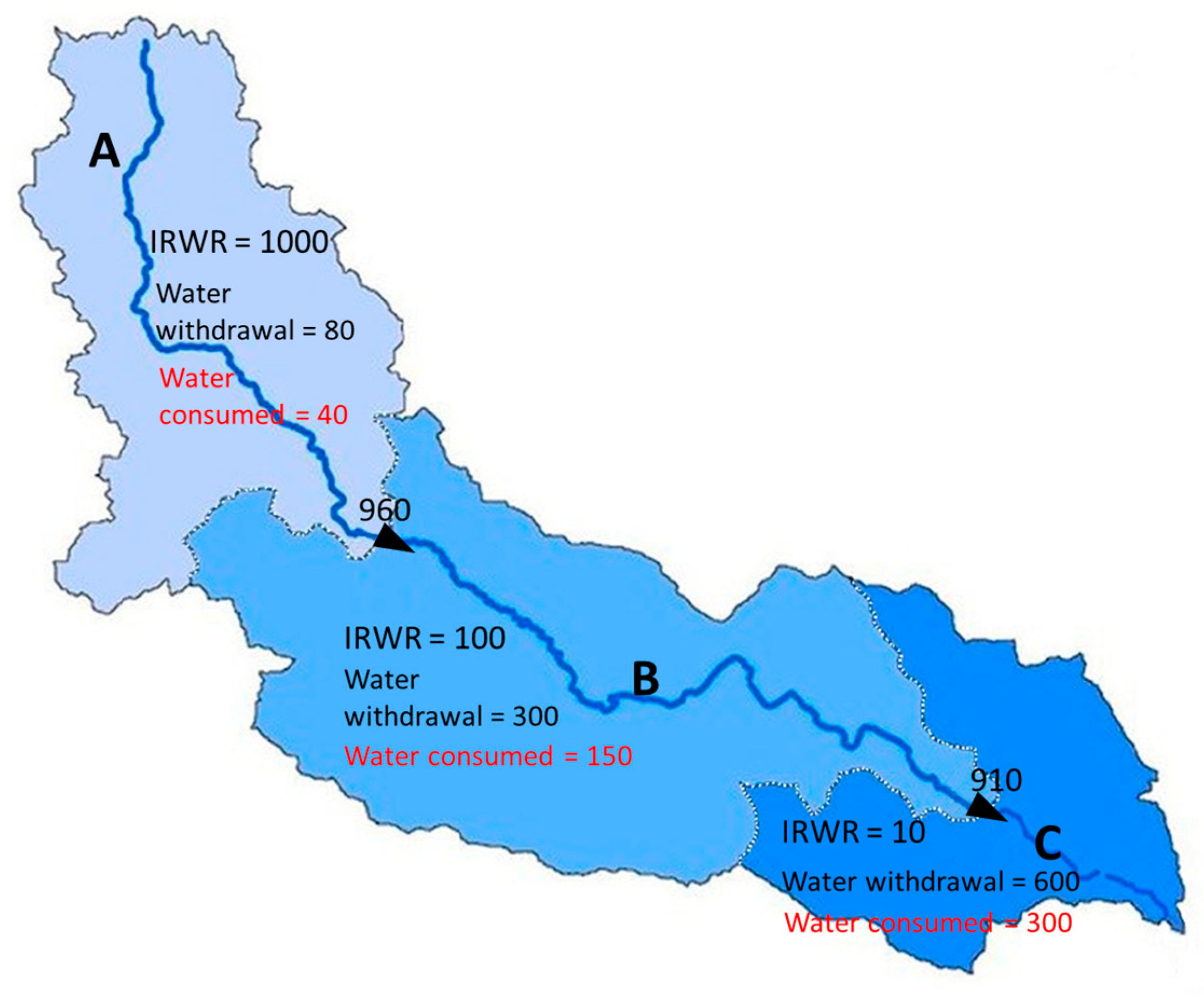
2.4. Total Freshwater Withdrawals
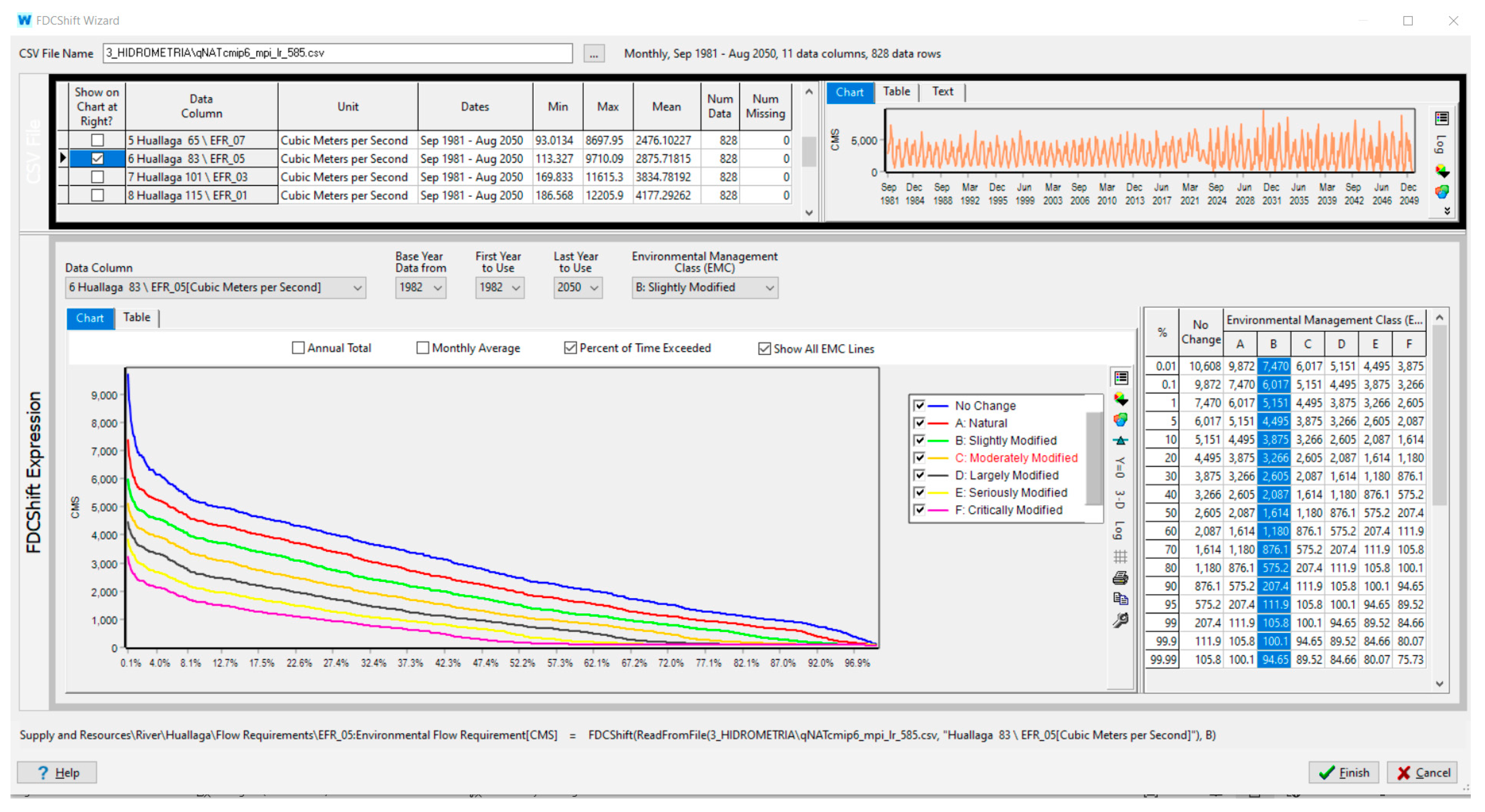
2.5. The Environmental Flow Requirements
3. The WEAP Water Stress Plugin
3.1. SDG 6.4.2—Level of Water Stress in the Senegal River Basin
3.1.1. Presentation of the Study Area
3.1.2. Scenario Development
3.1.3. Schematisation of the WEAP Model
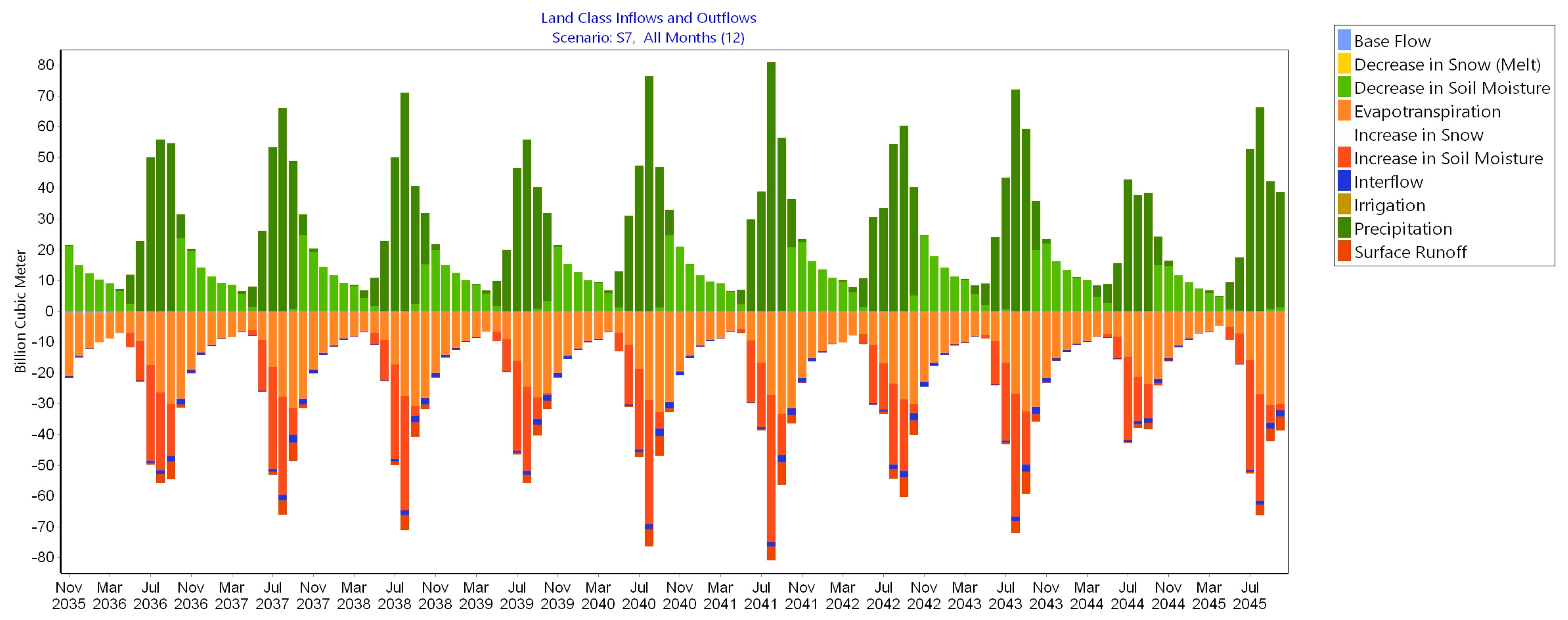
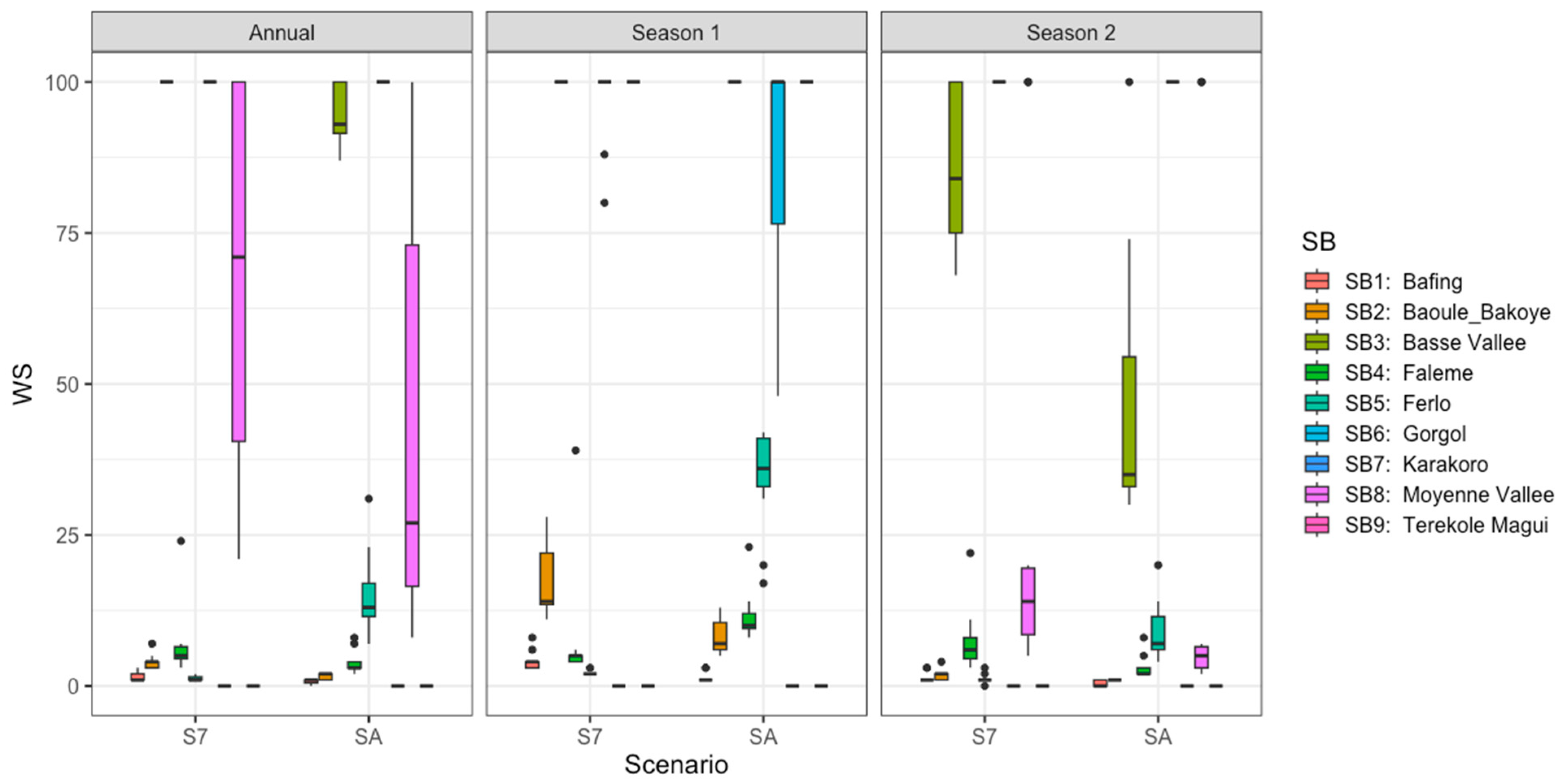
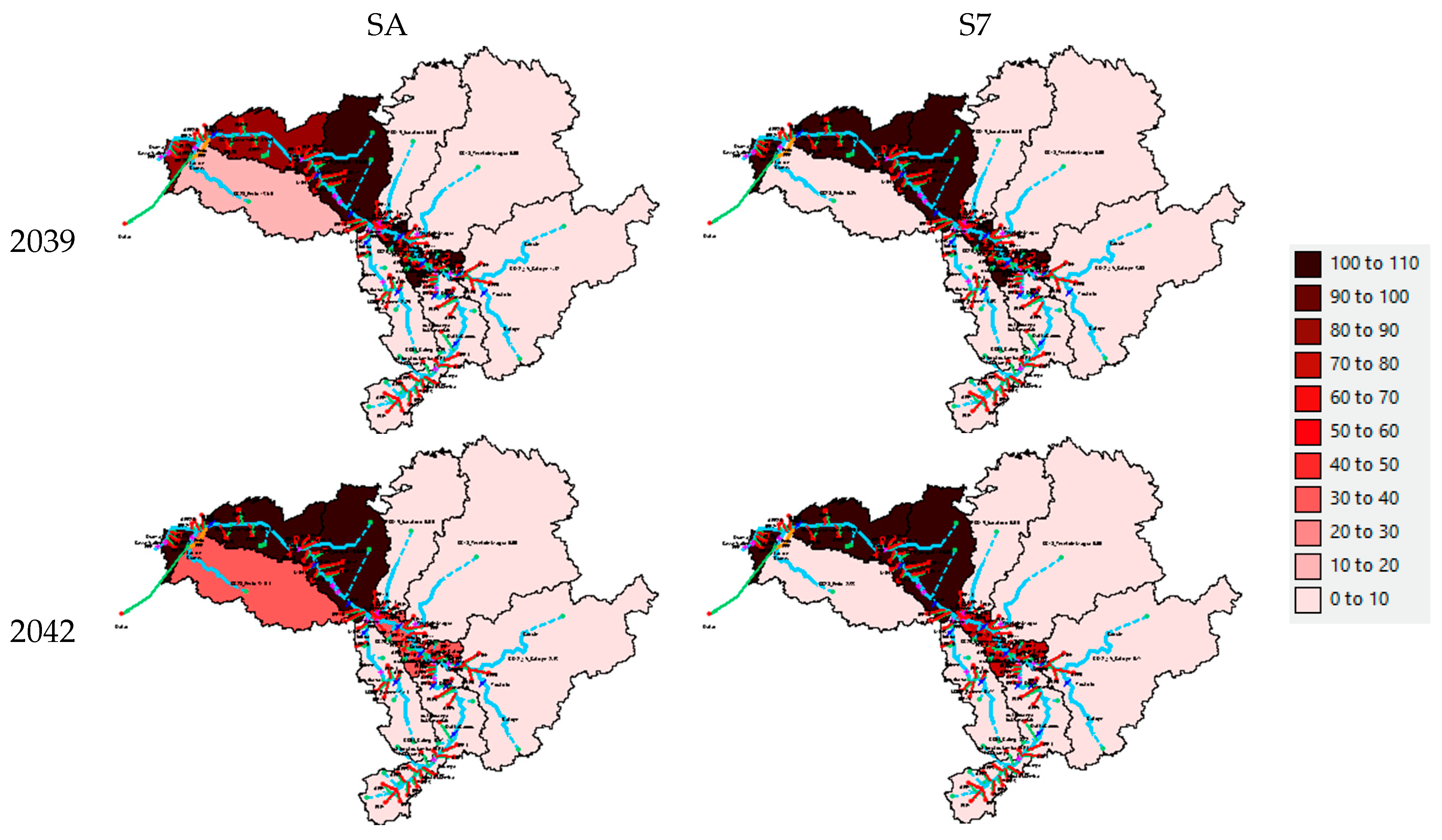
3.1.4. Analysis of the Results of Modelling
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Jury, W.A.; Vaux, H.J., Jr. The emerging global water crisis: Managing scarcity and conflict between water users. Adv. Agron. 2007, 95, 1–76. [Google Scholar]
- Mishra, R.K. Fresh water availability and its global challenge. Br. J. Multidiscip. Adv. Stud. 2023, 4, 1–78. [Google Scholar] [CrossRef]
- FAO. The Future of Food and Agriculture—Trends and Challenges; Food and Agriculture Organization of the United Nations: Rome, Italy, 2017; Available online: http://www.fao.org/3/a-i6583e.pdf (accessed on 5 December 2024).
- FAO. Coping with Water Scarcity. An Action Framework for Agriculture and Food Security. 2012. Available online: http://www.fao.org/3/a-i3015e.pdf (accessed on 5 December 2024).
- Ahopelto, L.; Veijalainen, N.; Guillaume, J.H.A.; Marko Keskinen, M.; Marttunen, M.; Varis, O. Can There be Water Scarcity with Abundance of Water? Analyzing Water Stress during a Severe Drought in Finland. Sustainability 2019, 11, 1548. [Google Scholar] [CrossRef]
- United Nations General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development. 2015. Available online: https://sdgs.un.org/2030agenda (accessed on 5 December 2024).
- FAO. Integrated Monitoring Initiative for SDG 6 Step-by-Step Monitoring Methodology for Indicator 6.4.2. Version: 4. 2019. Available online: https://openknowledge.fao.org/server/api/core/bitstreams/43ceaf5d-0837-40e6-82d4-98935a75752a/content (accessed on 5 December 2024).
- Biancalani, R.; Marinelli, M. Assessing SDG indicator 6.4.2 ‘level of water stress’ at major basins level. UCL Open Environ. 2021, 3. [Google Scholar] [CrossRef] [PubMed]
- FAO and UN-Water. Progress on the Level of Water Stress—Mid-Term Status of SDG Indicator 6.4.2 and Acceleration Needs, with Special Focus on Food Security; Food and Agriculture Organization of the United Nations: Rome, Italy, 2024. [Google Scholar] [CrossRef]
- Vanham, D.; Hoekstra, A.Y.; Wada, Y.; Bouraoui, F.; de Roo, A.; Mekonnen, M.M.; van de Bund, W.J.; Batelaan, O.; Pavelic, P.; Bastiaanssen, W.G.M.; et al. Physical water scarcity metrics for monitoring progress towards SDG target 6.4: An evaluation of indicator 6.4.2 “Level of water stress”. Sci. Total Environ. 2018, 613–614, 218–232. [Google Scholar] [CrossRef] [PubMed]
- Hoekstra, A.Y.; Mekonnen, M.M.; Chapagain, A.K.; Mathews, R.E.; Richter, B.D. Global Monthly Water Scarcity: Blue Water Footprints versus Blue WaterAvailability. PLoS ONE 2012, 7, e32688. [Google Scholar] [CrossRef] [PubMed]
- FAO. AQUASTAT: FAO’s Global Information System on Water and Agriculture. 2021. Available online: http://www.fao.org/aquastat/en/ (accessed on 23 February 2021).
- FAO. Hydrological Basins Derived from Hydroshed. 2011. Available online: https://data.apps.fao.org/map/catalog/srv/eng/catalog.search#/metadata/7707086d-af3c-41cc-8aa5-323d8609b2d1 (accessed on 1 March 2020).
- Karimi, P.; Bastiaanssen, W.G.M.; Molden, D. Water Accounting Plus (WA+)—A water accounting procedure for complex river basins based on satellite measurements. Hydrol. Earth Syst. Sci. Discuss. 2013, 9, 12879–12919. [Google Scholar] [CrossRef]
- Batchelor, C.; Hoogeveen, J.; Faurès, J.M.; Peiser, L. Water Accounting and Auditing: A Sourcebook; FAO Water Reports No. 43; Food and Agriculture Organization of the United Nations: Rome, Italy, 2016. [Google Scholar]
- OECD. Water Resources Allocation: Sharing Risks and Opportunities; OECD Studies on Water; OECD Publishing: Paris, UK, 2015. [Google Scholar] [CrossRef]
- Zhu, Z.; Giordano, M.; Cai, X.; Molden, D. The Yellow River Basin: Water Accounting, Water Accounts, and Current Issues. Water Int. 2004, 29, 2–10. [Google Scholar] [CrossRef]
- Viessman, W.; Lewis, G.L. Introduction to Hydrology; HarperCollins College Publishers: HarperCollins, NY, USA, 1996. [Google Scholar]
- FAO. Water Stress Plugin for Water Evaluation and Planning System (WEAP). Using the Water Evaluation and Planning Tool for the Calculation of Sustainable Development Goal Indicator 6.4.2; Food and Agriculture Organization of the United Nations: Rome, Italy, 2024. [Google Scholar] [CrossRef]
- UNSD. Metadata of Indicator 6.4.2. 2024. Available online: https://unstats.un.org/sdgs/metadata/files/metadata-06-04-02.pdf (accessed on 5 December 2024).
- Balk, D.L.; Deichmann, U.; Yetman, G.; Pozzi, F.; Hay, S.I.; Nelson, A. Determining Global Population Distribution: Methods, Applications and Data. Global Mapping of Infectious Diseases: Methods, Examples and Emerging Applications. Adv. Parasitol. 2006, 62, 119–156. [Google Scholar] [CrossRef] [PubMed]
- CIESIN. Global Rural-Urban Mapping Project. 2020. Available online: https://sedac.ciesin.columbia.edu/data/collection/grump-v1 (accessed on 1 March 2020).
- CIESIN. Gridded Population of the World, Version 4 (GPWv4); Population Density Adjusted to Match 2015 Revision of UN WPP Country Totals, Revision 10. NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2017. Available online: https://sedac.ciesin.columbia.edu/data/collection/gpw-v4 (accessed on 1 March 2020).
- Landscan Global. Oak Ridge National Laboratory. 2019. Available online: https://landscan.ornl.gov/ (accessed on 1 March 2020).
- WorldPop. Open Spatial Demographic Data and Research. 2020. Available online: https://www.worldpop.org/ (accessed on 1 March 2020).
- GHS Population Grid. European Commission, Joint Research Center. 2020. Available online: https://ghslsys.jrc.ec.europa.eu/ghs_pop.php (accessed on 1 March 2020).
- Arthington, A.H.; Bhaduri, A.; Bunn, S.E.; Jackson, S.; Tharme, R.E.; Tickner, D.; Young, W.; Acreman, M.; Natalie Baker, N.; Capon, S.; et al. The Brisbane Declaration and Action Agenda on Environmental Flows. Front. Environ. Sci. 2018, 6, 45. [Google Scholar] [CrossRef]
- FAO. Incorporating Environmental Flows into “Water Stress” Indicator 6.4.2—Guidelines for a Minimum Standard Method for Global Reporting; Food and Agriculture Organization of the United Nations: Rome, Italy, 2019; 32p. [Google Scholar]
- Smakhtin, V.; Anputhas, M. An Assessment of Environmental Flow Requirements of Indian River Basins; IWMI Research Report 107; International Water Management Institute (IWMI): Colombo, Sri Lanka, 2006; 42p. [Google Scholar]
- Smakhtin, V.U.; Eriyagama, N. Developing a software package for global desktop assessment of environmental flows. Environ. Model. Softw. 2008, 23, 1396–1406. [Google Scholar] [CrossRef]
- Sood, A.; Smakhtin, V.; Eriyagama, N.; Villholth, K.G.; Liyanage, N.; Wada, Y.; Ebrahim, G.; Dickens, C. Global Environmental Flow Information for the Sustainable Development Goals; IWMI Research Report 168; International Water Management Institute (IWMI): Colombo, Sri Lanka, 2017; 37p. [Google Scholar] [CrossRef]
- Eriyagama, N.; Messager, M.L.; Dickens, C.; Tharme, R.; Stassen, R. Towards the Harmonization of Global Environmental Flow Estimates: Comparing the Global Environmental Flow Information System (GEFIS) with Country Data; IWMI Research Report 186; International Water Management Institute (IWMI): Colombo, Sri Lanka, 2024; 53p. [Google Scholar] [CrossRef]
- Shaeri Karimi, S.; Yasi, M.; Eslamian, S. Use of hydrological methods for assessment of environmental flow in a river reach. Int. J. Environ. Sci. Technol. 2012, 9, 549–558. [Google Scholar] [CrossRef]
- Perry, C.J.; Bucknall, J. Water resource assessment in the Arab world: New analytical tools for new challenges. In Water in the Arab World: Management Perspective and Innovations; Jagannathan, N.J., Mohamed, A.S., Kremer, A., Eds.; The World Bank: Washington, DC, USA, 2009. [Google Scholar]
- Al-Mukhtar, M.; Mutar, G. Modelling of Future Water Use Scenarios Using WEAP Model: A Case Study in Baghdad City, Iraq. Eng. Technol. J. 2021, 39, 488–503. [Google Scholar] [CrossRef]
- RaziSadath, P.V.; RinishaKartheeshwari, M.; Elango, L. WEAP Model Based Evaluation of Future Scenarios and Strategies for Sustainable Water Management in the Chennai Basin, India. AQUA-Water Infrastruct. Ecosyst. Soc. 2023, 72, 2062–2080. [Google Scholar] [CrossRef]
- Yang, L.; Bai, X.; Khanna, N.; Yi, S.; Hu, Y.; Deng, J.; Gao, H.; Tuo, L.; Xiang, S.; Zhou, N. Water evaluation and planning (WEAP) model application for exploring the water deficit at catchment level in Beijing. Desalin. Water Treat. 2018, 118, 12–25. [Google Scholar] [CrossRef]
- Stockholm Environment Institute (SEI) Website. Available online: https://www.sei.org/tools/weap/ (accessed on 5 December 2024).

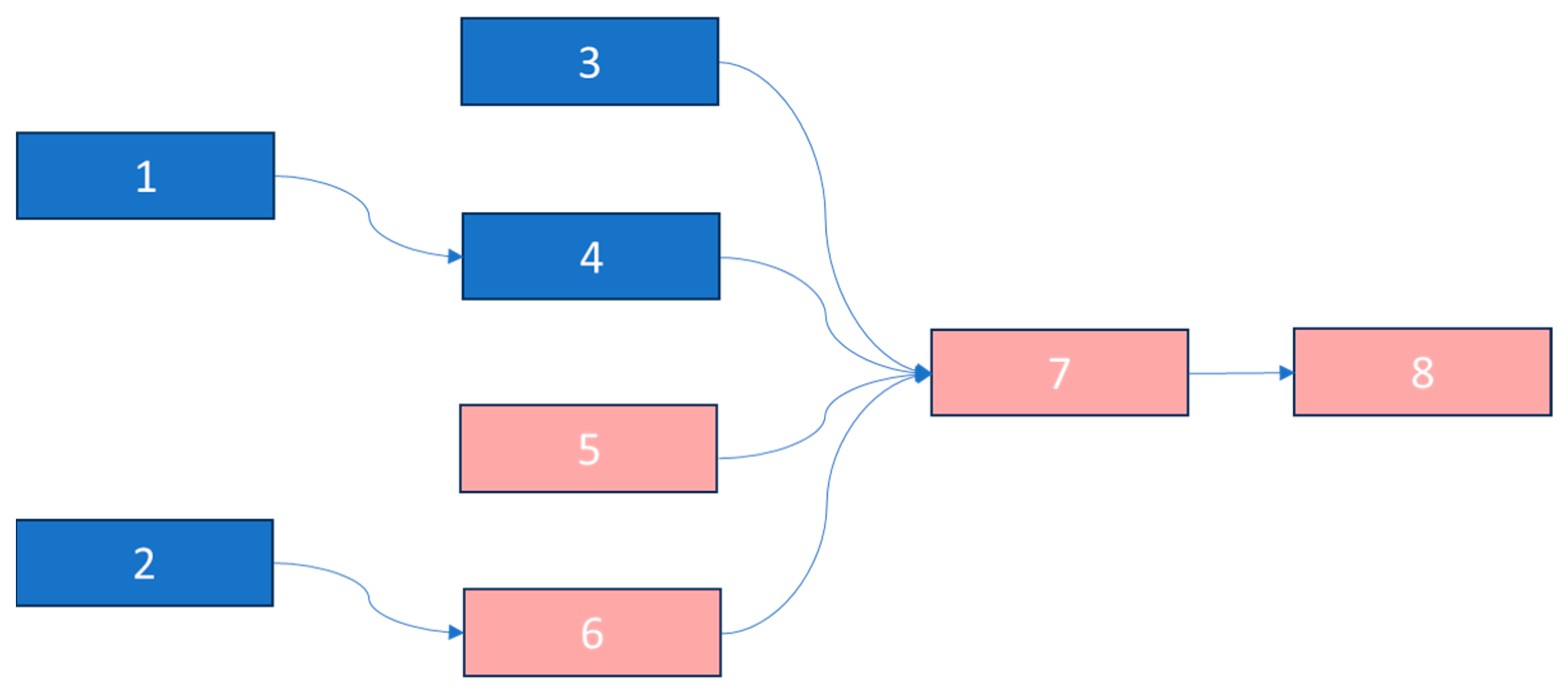
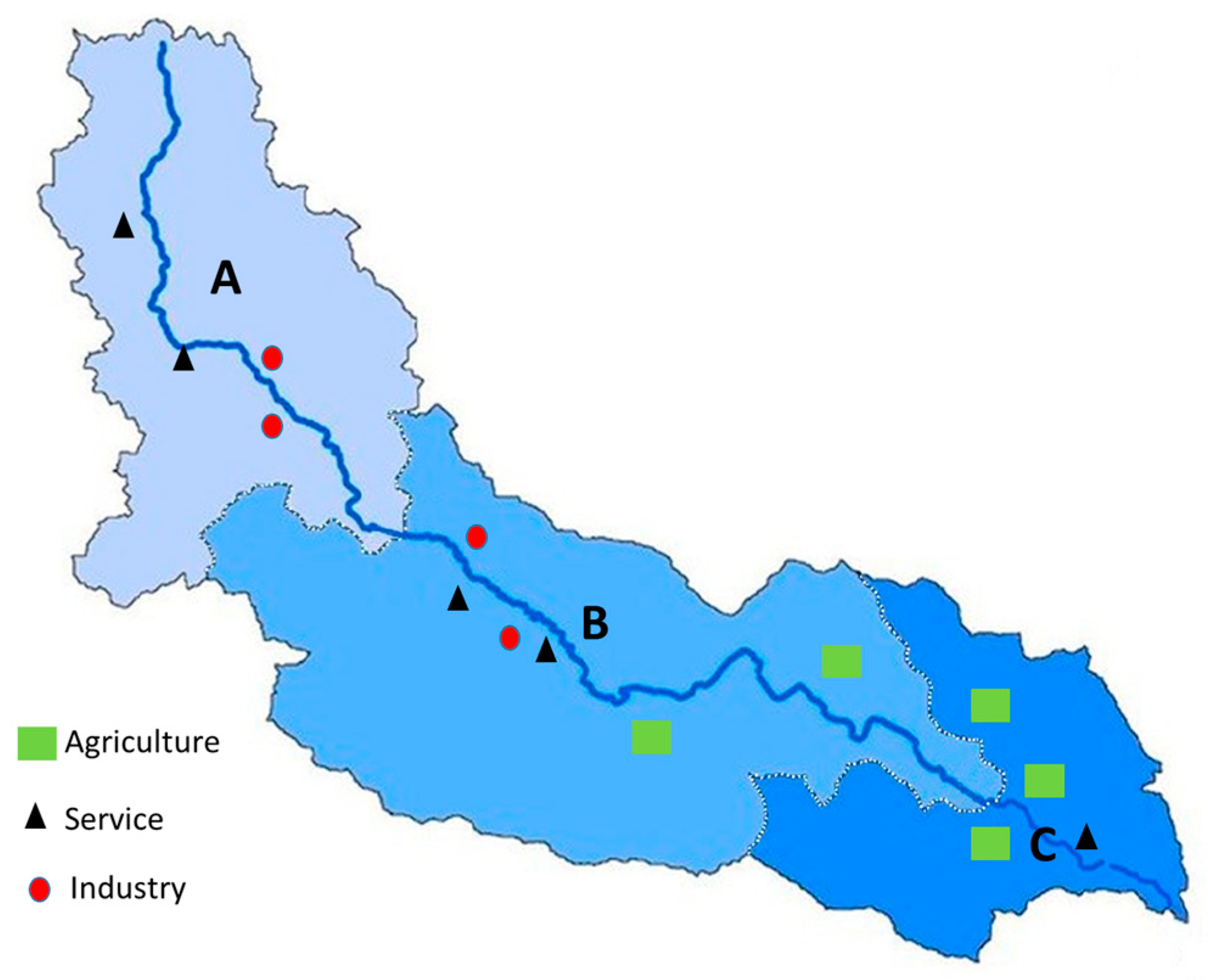
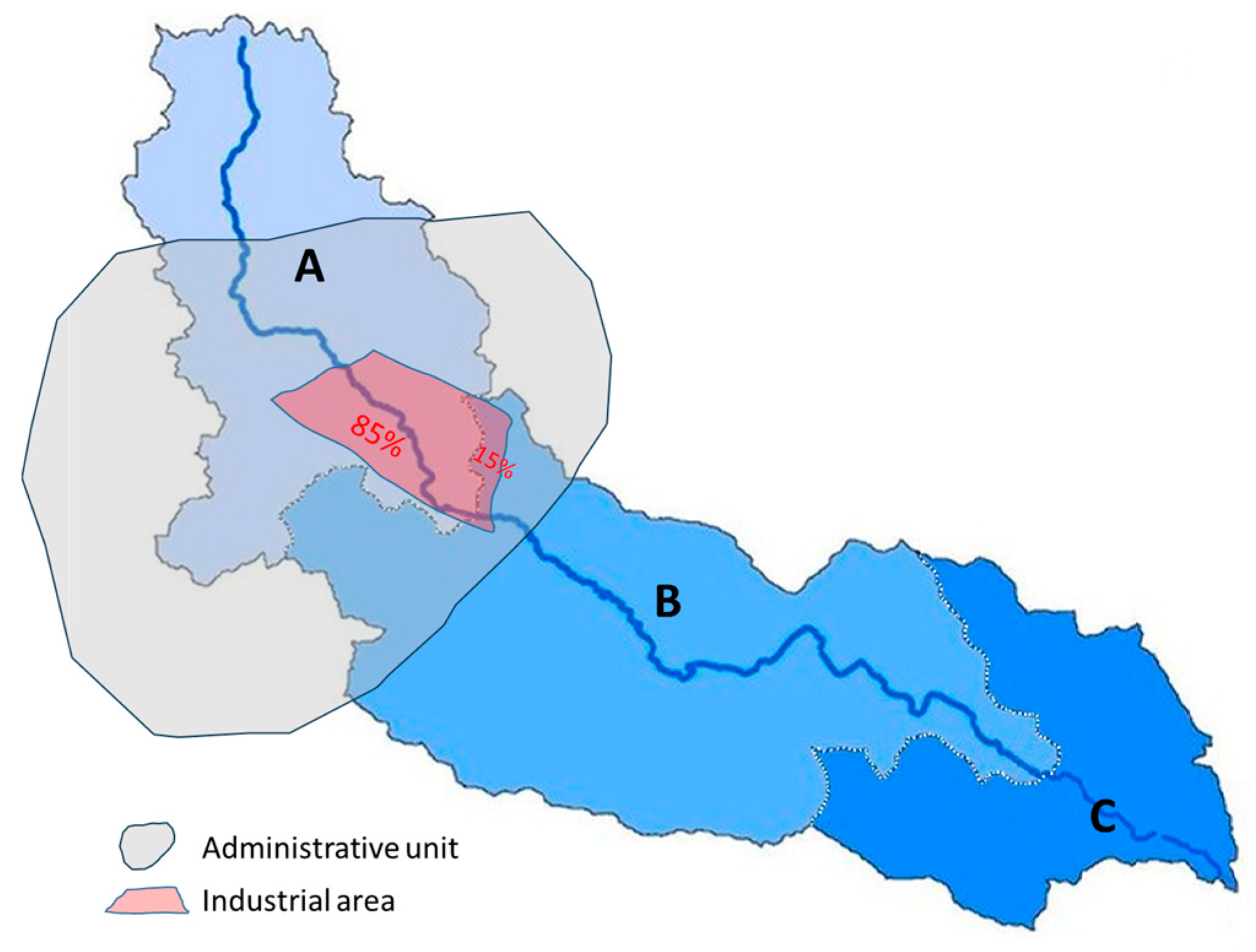
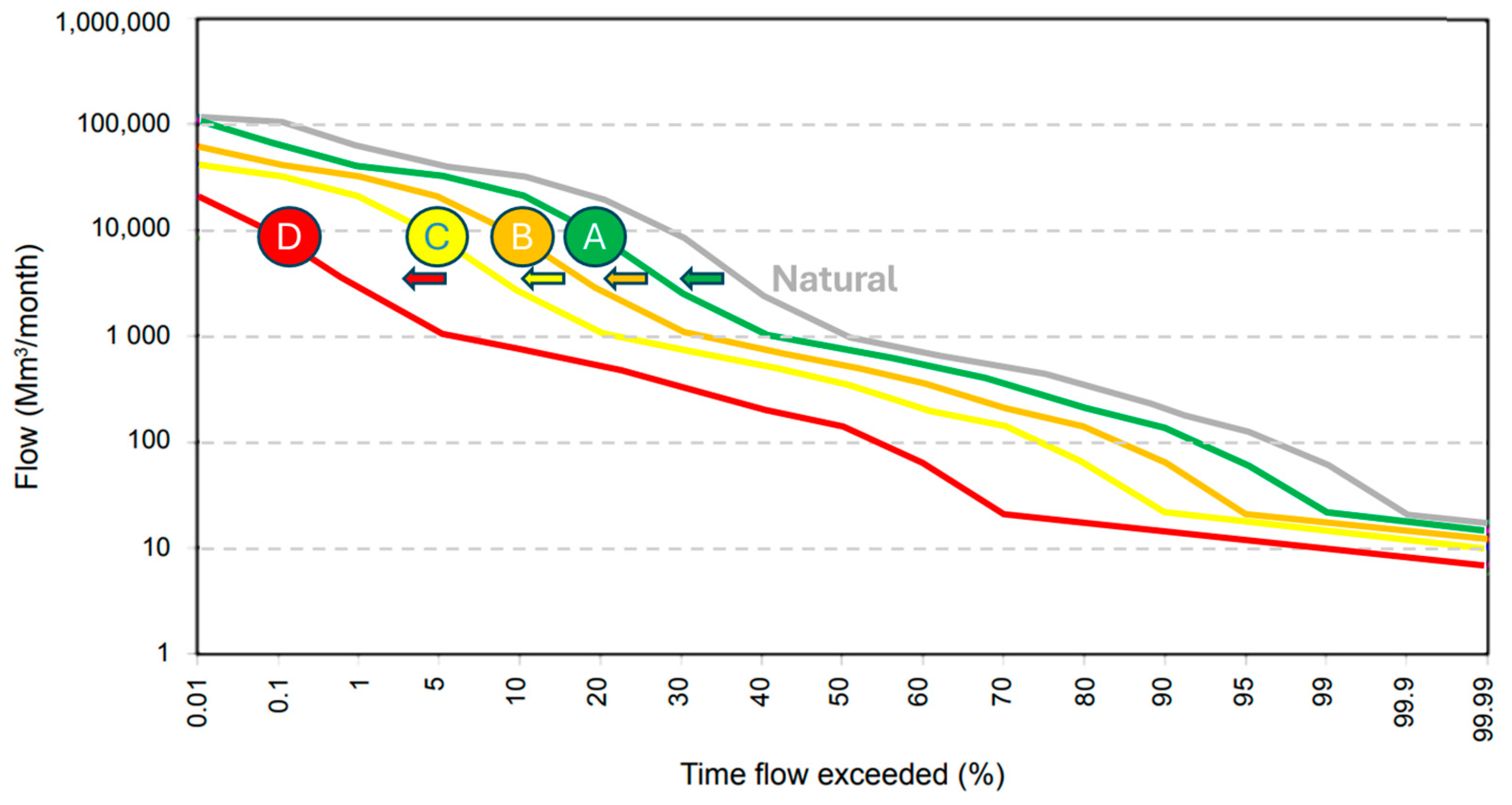
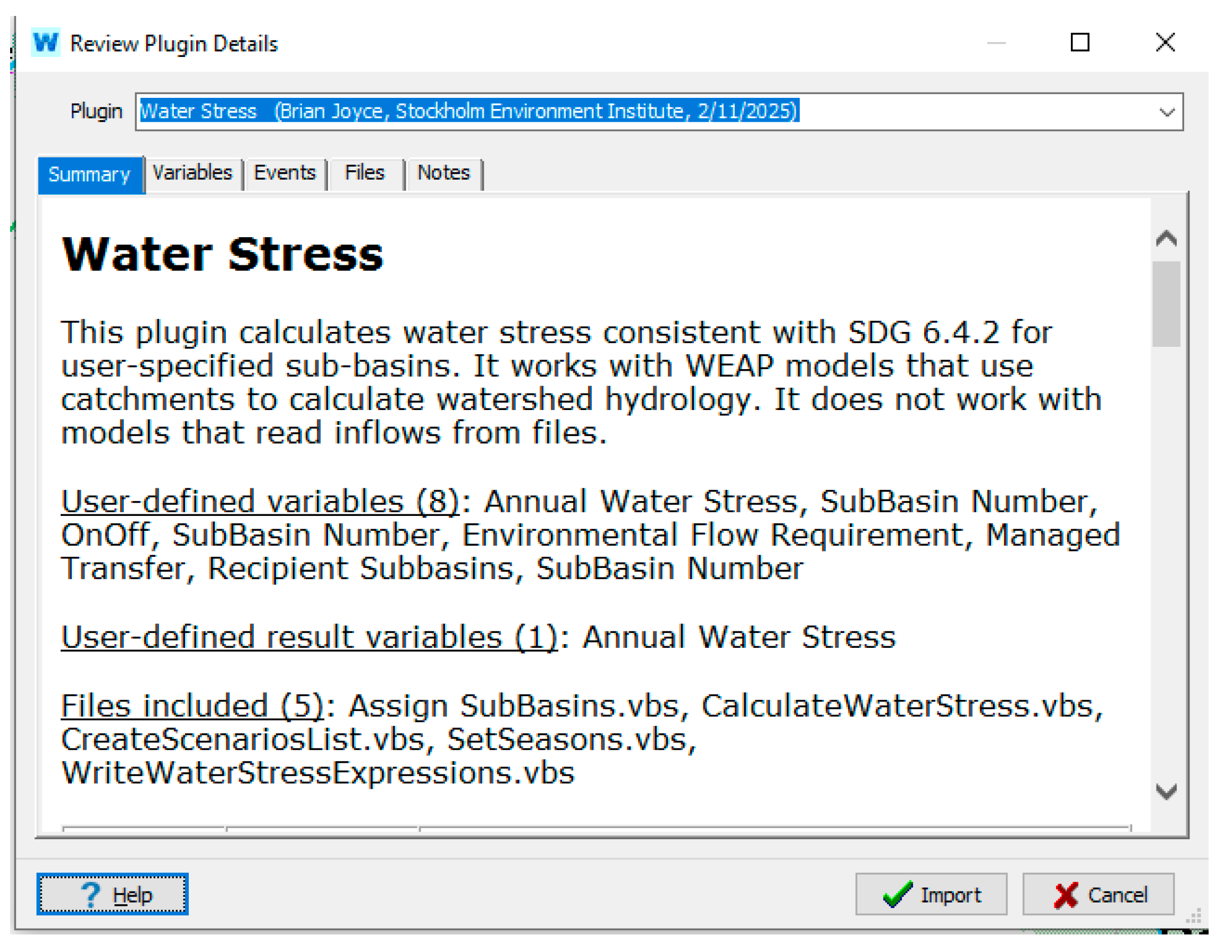


| SB1 | SB2 | SB3 | SB4 | SB5 | SB6 | SB7 | SB8 | Number of SBs Immediately Downstream | |
|---|---|---|---|---|---|---|---|---|---|
| SB1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| SB2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| SB3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| SB4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| SB5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| SB6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| SB7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| SB8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Number of SBs Immediately Upstream | 0 | 0 | 0 | 1 | 0 | 1 | 4 | 1 |
| SB1 | SB2 | SB3 | SB4 | SB5 | SB6 | SB7 | SB8 | Total Number of SBs Downstream | |
|---|---|---|---|---|---|---|---|---|---|
| SB1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 3 |
| SB2 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 3 |
| SB3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| SB4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| SB5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| SB6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| SB7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| SB8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Total Number of SBs Upstream | 0 | 0 | 0 | 1 | 0 | 1 | 6 | 7 |
| SB1 | SB2 | SB3 | SB4 | SB5 | SB6 | SB7 | SB8 | Total Number of SBs Downstream to Reserve Water for (Downstream Reserve) | |
|---|---|---|---|---|---|---|---|---|---|
| SB1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| SB2 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 3 |
| SB3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| SB4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| SB5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SB6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SB7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SB8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Total number of SBs upstream to request water from | 0 | 0 | 0 | 0 | 0 | 1 | 4 | 4 |
| SA | S7 | ||
|---|---|---|---|
| Drinking water supply (Mm3) | Directly inside the SRB | 116.9 | 312.3 |
| Transferred outside the SRB | 178 | 196.2 | |
| Livestock (Mm3) | 119.7 | 190.5 | |
| Mining (Mm3) | 241.1 | 582.7 | |
| Irrigation (Mm3) | 3558.4 | 5918.9 | |
| Hydroelectricity | Total storage capacity (Mm3) | 11,300 | 17,000 |
| Environment | Target low-water flow at Bakel (m3/s) | 52 | 52 |
| Target peak flood flow at Bakel (m3/s) | -- | 2200 | |
| Shipping | Bakel flow between July and January (m3/s) | -- | 300 |
| Diama flow between July and January (m3/s) | -- | 200 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marinelli, M.; Biancalani, R.; Joyce, B.; Djihouessi, M.B. A New Methodology to Estimate the Level of Water Stress (SDG 6.4.2) by Season and by Sub-Basin Avoiding the Double Counting of Water Resources. Water 2025, 17, 1543. https://doi.org/10.3390/w17101543
Marinelli M, Biancalani R, Joyce B, Djihouessi MB. A New Methodology to Estimate the Level of Water Stress (SDG 6.4.2) by Season and by Sub-Basin Avoiding the Double Counting of Water Resources. Water. 2025; 17(10):1543. https://doi.org/10.3390/w17101543
Chicago/Turabian StyleMarinelli, Michela, Riccardo Biancalani, Brian Joyce, and Metogbe Belfrid Djihouessi. 2025. "A New Methodology to Estimate the Level of Water Stress (SDG 6.4.2) by Season and by Sub-Basin Avoiding the Double Counting of Water Resources" Water 17, no. 10: 1543. https://doi.org/10.3390/w17101543
APA StyleMarinelli, M., Biancalani, R., Joyce, B., & Djihouessi, M. B. (2025). A New Methodology to Estimate the Level of Water Stress (SDG 6.4.2) by Season and by Sub-Basin Avoiding the Double Counting of Water Resources. Water, 17(10), 1543. https://doi.org/10.3390/w17101543









