Spatial–Temporal Evolution of Agricultural Water Use Efficiency Based on DEA Approach and Spatial Autocorrelation
Abstract
1. Introduction
2. Study Area
3. Materials and Methods
3.1. Data Sources and Literature Review
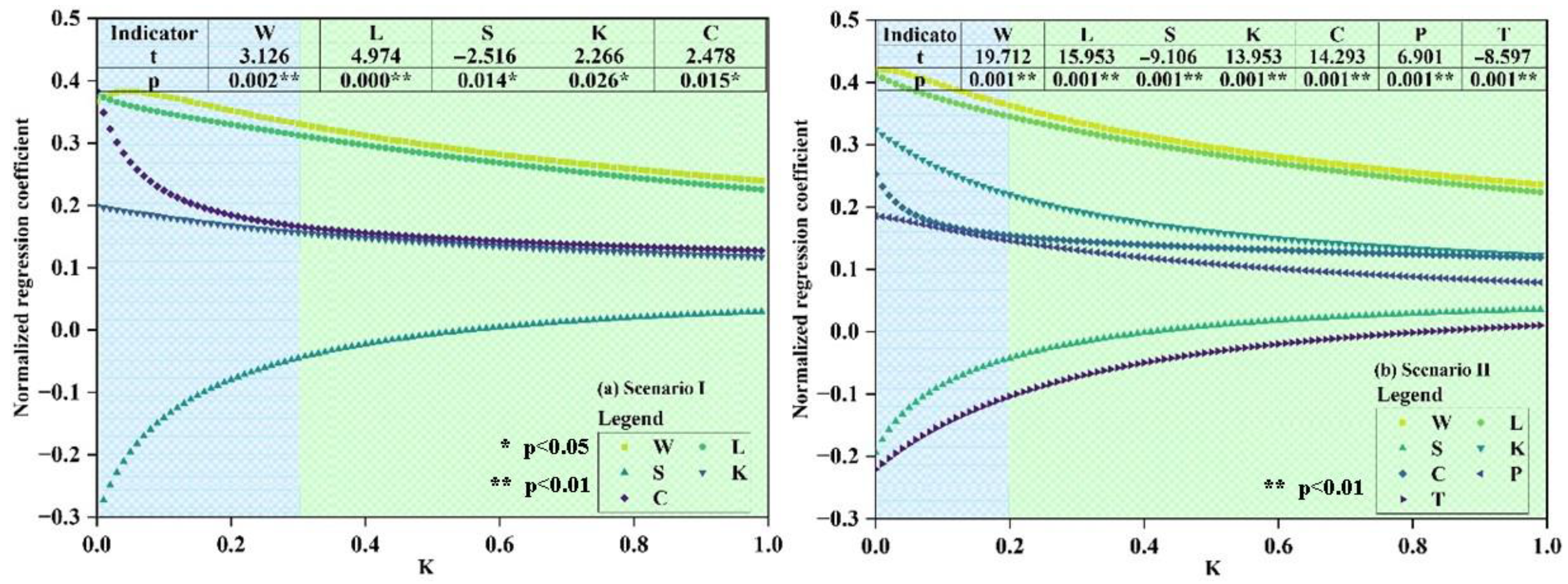
3.2. The Lasso Regression Model
3.3. Data Envelopment Analysis Model
3.4. Spatial Autocorrelation Analysis Based on GMI and GOGI
3.4.1. Global Spatial Autocorrelation
3.4.2. Local Spatial Autocorrelation
4. Results and Discussion
4.1. Descriptive Statistics and Correlation Analysis of Input–Output Indicators
4.2. Determined the Indicators of AWUE Based on the Lasso Model
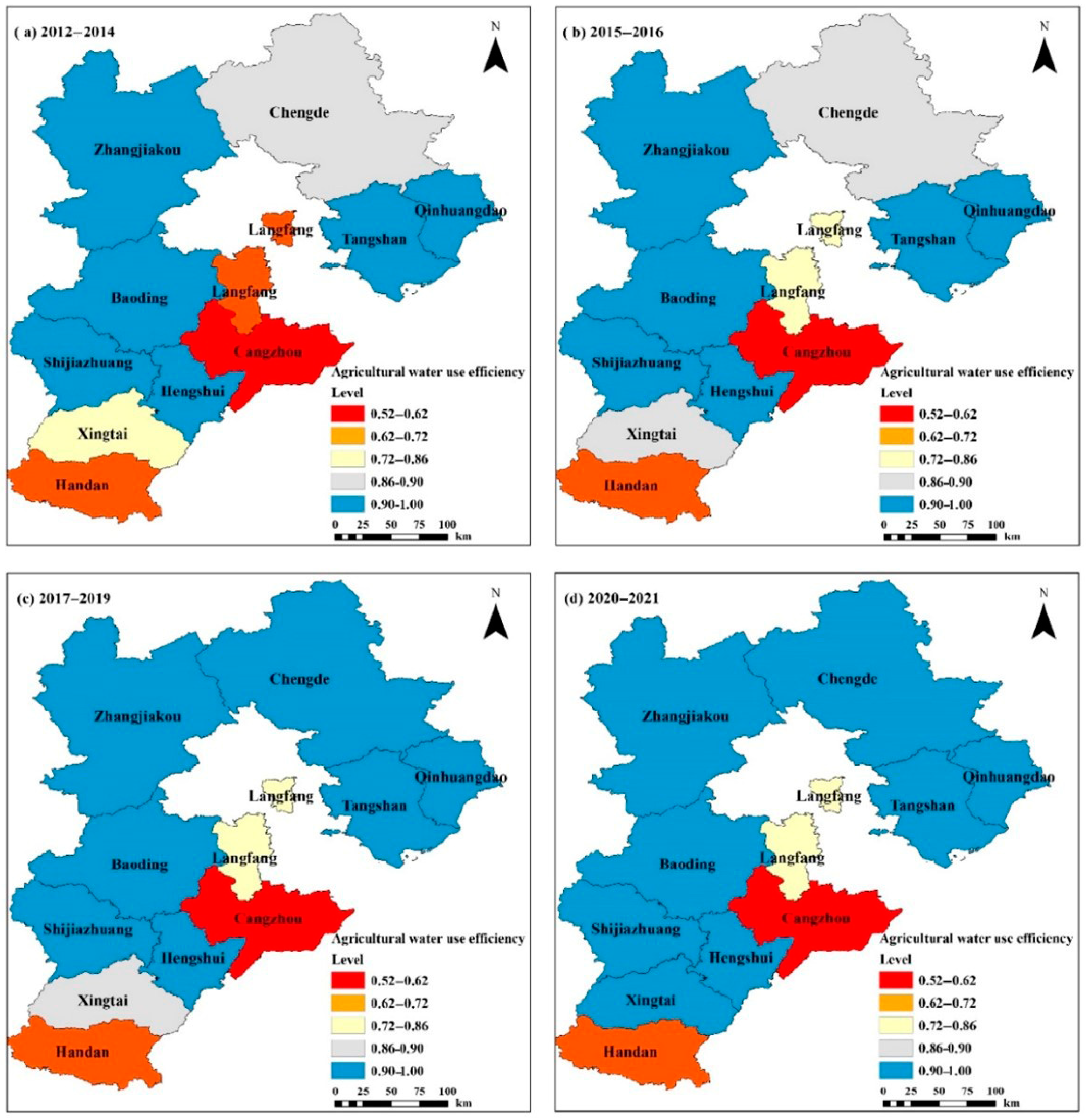
4.3. AWUE Evaluation Analysis Based on DAE from the Time Scale
4.4. AWUE Autocorrelation Analysis Based on GMI and GOGI from the Spatial Scale
4.4.1. Global Spatial Autocorrelation Analysis of AWUE
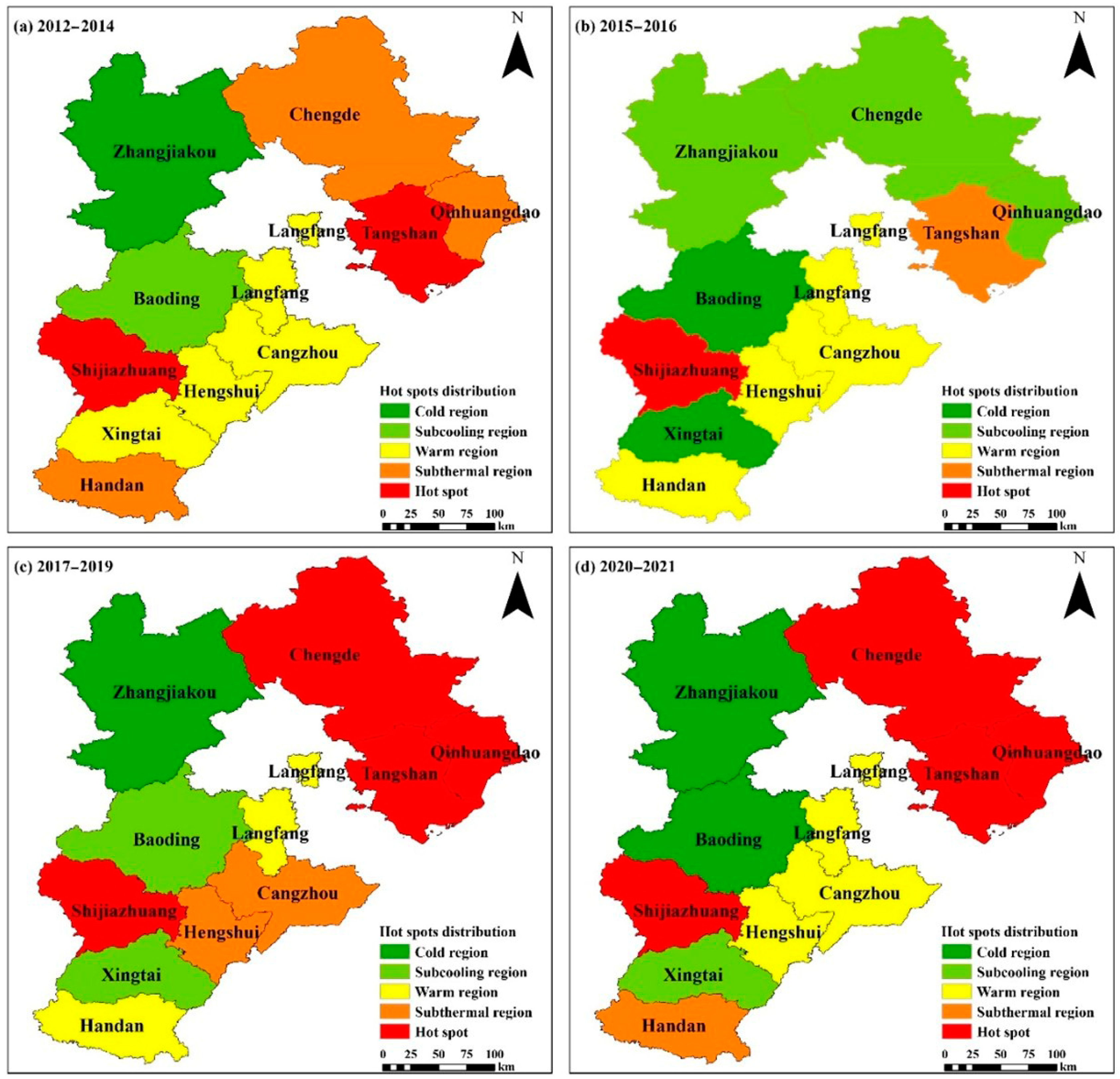
4.4.2. Local Spatial Autocorrelation Analysis of AWUE
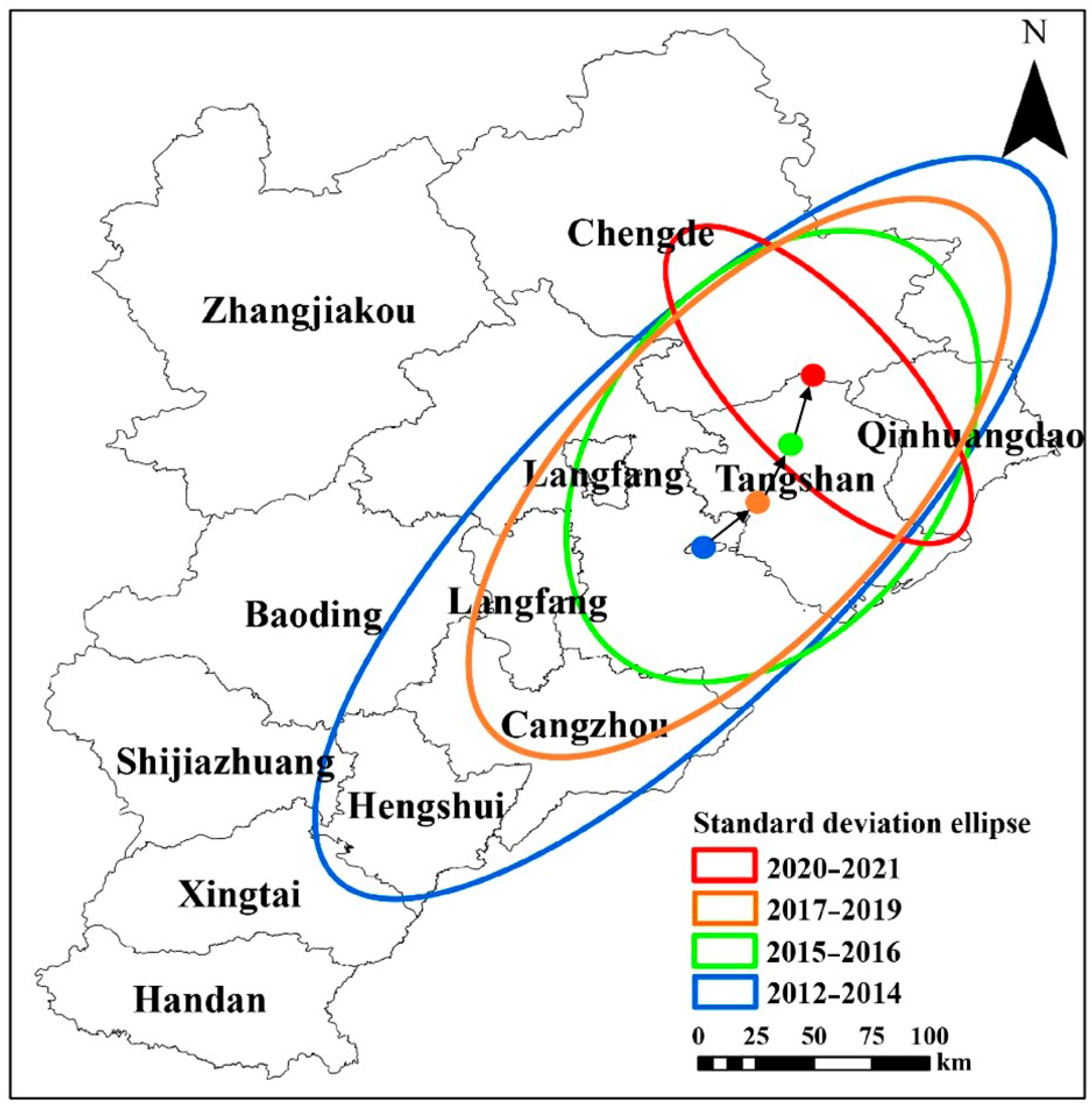
4.5. Evolution Trend and Direction Analysis of AWUE
5. Conclusions
- (1)
- On the whole, under the changing environment from 2012 to 2021, the AWUE of the Hebei Province did not reach DEA effectiveness, and the average overall efficiency was 0.828, indicating that the AWUE still has potential and room for improvement. Among them, the annual average of AWUE in the southwest region is lower than 0.8, which are invalid DEA cities that need to be improved. The average AWUE of the northeast region is between 0.77 and 0.91, which is a strong EDA efficiency.
- (2)
- From the dynamic trend, the average value of each region of AWUE in the Hebei Province shows a fluctuating development trend of first rising, then falling, and then rising with time under the changing environment during the study period. AWUE reached the maximum in the window period 2014–2016.
- (3)
- The distribution of AWUE shows a directional pattern from southwest to northeast. The AWUE in the southwest region has always been low, while the efficiency of agricultural water use in the northeast region has always been a high-value area, with the center of gravity gradually shifting towards the northeast from 2012 to 2021. The results of the hotspot centroid and standard deviation ellipse further indicate that attention should be paid to improving AWUE in the southwest region.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qi, H.; Dong, Z.L.; You, X.S.; Li, Y.; Zhao, Y.R.; Sun, X.T. Extended exergy accounting for assessing the sustainability of agriculture: A case study of Hebei Province, China. Ecol. Indic. 2023, 150, 110240. [Google Scholar] [CrossRef]
- Liu, S.Y.; Wu, X.D.; Han, M.Y.; Zhang, J.J.; Chen, B.; Wu, X.F.; Wei, W.D.; Li, Z. A three-scale input-output analysis of water use in a regional economy: Hebei province in China. J. Clean. Prod. 2017, 156, 962–974. [Google Scholar] [CrossRef]
- Liu, T.X.; Zhang, D.S.; Shi, Y.F.; Li, Y.; Sun, J.C.; Zhang, X.P. The Influence of the South-to-North Water-Diversion Project on Terrestrial Water-Storage Changes in Hebei Province. Water 2023, 15, 3112. [Google Scholar] [CrossRef]
- Li, S.L.; Yan, J.J.; Pei, Q.M.; Sha, J.H.; Liu, F. Dynamic Relationship Between Water Resources and New Urbanization Based on a Vector Autoregressive Model: A Case Study of Hebei Province, China. Front. Environ. Sci. 2022, 10, 941726. [Google Scholar] [CrossRef]
- Li, Y.G.; Sun, M.H.; Yuan, G.H.; Liu, Y.J. Evaluation methods of water environment safety and their application to the three northeast provinces of China. Sustainability 2019, 11, 5135. [Google Scholar] [CrossRef]
- Yang, G.S.; Xie, Q.H. Study on spatial and temporal differentiation of green water resource efficiency in the YREB. Resour. Environ. Yangtze Basin 2019, 28, 349–358. [Google Scholar]
- Zhang, X.D.; Zhu, S. Spatial differences and influencing factors of regional agricultural water resource utilization efficiency in Heilongjiang Province China. Water Supply 2019, 19, 545–552. [Google Scholar]
- Song, J.F.; Chen, X.N. Eco-efficiency of grain production in China based on water footprints: A stochastic frontier approach. J. Clean. Prod. 2019, 236, 117685. [Google Scholar] [CrossRef]
- Zhou, Y.W. Utilization efficiency and influencing factors of agricultural water resource in Hubei province. Desalination Water Treat. 2019, 168, 201–206. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, Z. Evaluation of water resource utilization efficiency in provincial areas of China based on the unexpected output SBM model. J. Environ. Public Health 2022, 2022, 9554730. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S. The impact of environmental regulation on water resources utilization efficiency. Front. Environ. Sci. 2022, 10, 1022929. [Google Scholar] [CrossRef]
- Jo, J.; Kim, S. Assessing shoring strategies based on efficiency. Expert Syst. Appl. 2022, 207, 118032. [Google Scholar] [CrossRef]
- Yao, T.; Liu, S. Comparison of the variation characteristics of water resource use efficiency indicators in the Beijing-Tianjin-Hebei region. Adv. Earth Sci. 2021, 36, 1195–1207. [Google Scholar] [CrossRef]
- Shi, C.F.; Li, L.J.; Chiu, Y.H.; Pang, Q.H.; Zeng, X.Y. Spatial differentiation of agricultural water resource utilization 508 efficiency in the Yangtze River Economic Belt under changing environment. J. Clean. Prod. 2022, 346, 131200. [Google Scholar] [CrossRef]
- Chang, M.; Chen, S.B.; Ma, B.R.; Liu, Y. Analysis of grain water resources utilization efficiency and influencing factors: An empirical study based on China’s provincial panel data. J. Ecol. Rural Environ. 2020, 36, 145–151. [Google Scholar]
- Deng, M.H.; Zhang, T.S. Spatial-temporal evolution of water resources utilization efficiency in Jiangsu province. Water Supply 2023, 23, 2539–2552. [Google Scholar] [CrossRef]
- Charnes, A.; Clark, C.T.; Cooper, W.W. A developmental study of data envelopment analysis in measuring the efficiency of maintenance units in the U.S. Air forces. Ann. Oper. Ann. Oper. Res. 1983, 2, 95–112. [Google Scholar] [CrossRef]
- Zhu, D.; Tang, L.; Xie, Q.W.; Ma, M.; Rao, K.F. Efficiency assessment of water resource utilization cities based on data envelopment analysis. Acta Ecol. Sin. 2020, 40, 1956–1966. [Google Scholar]
- Shao, L.G.; Yu, X.; Feng, C. Evaluating the eco-efficiency of China’s industrial sectors: A two-stage network data envelopment analysis. J. Environ. Manag. 2019, 247, 551–560. [Google Scholar] [CrossRef]
- Cho, I.; Heo, E.; Park, J. Water resource R&D efficiency in Korea-toward sustainable integrated water resource management. Water Policy 2021, 23, 581–598. [Google Scholar]
- Wang, X.X.; Cui, B.L.; Chen, Y.N.; Feng, T.; Li, Z.; Fang, G.H. Dynamic changes in water resources and comprehensive assessment of water resource utilization efficiency in the Aral Sea basin, Central Asia. J. Environ. Manag. 2024, 351, 120198. [Google Scholar] [CrossRef] [PubMed]
- Ji, L.; Tao, S.G.; Liu, J.W.; Sun, Y.N.; Chiu, Y.H. Assessing the Efficiency of Industrial Water Use and Wastewater Treatment Across Provinces in China After Considering the Impact of Precipitation. Water Econ. Policy 2025. [Google Scholar] [CrossRef]
- Zhou, Z.X.; Li, M.Y.; Xu, X.Z.; Wu, H.Q. Integrating spatial relationships in the DEA approach for ecological efficiency evaluation: A case study of the Chaohu watershed. Ecol. Indic. 2024, 169, 112868. [Google Scholar] [CrossRef]
- Quan, Z.M.; Zuo, Q.T.; Zang, C.; Wu, Q.S. A multi-index comprehensive evaluation method for assessing the water use balance between economic society and ecology considering efficiency-development-health-harmony. Sci. Rep. 2024, 14, 25924. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, C.; Liu, Q.C.; Xu, C.X.; Song, M. Spatiotemporal evolution and optimization analysis of investment efficiency in China’s agricultural water conservancy infrastructure based on a two-stage DEA model. Front. Earth Sci. 2024, 12, 145535. [Google Scholar] [CrossRef]
- Yin, C.J.; See, K.F.; Hsiao, B. Assessing the performance of water supply operations in Chinese water companies: A union dynamic multi-activity network data envelopment analysis. J. Clean. Prod. 2024, 482, 143750. [Google Scholar] [CrossRef]
- Zhou, C. COVID-19: Challenges to GIS with big data. Geogr. Sustain. 2020, 1, 77–87. [Google Scholar] [CrossRef]
- Yang, W.P.; Zhang, Z.Y.; Luo, P.P.; Wang, Y.J. Temporal and spatial evolution and influencing factors of urban ecological total factor productivity in the Yellow River basin under strong sustainable development. Sci. Prog. 2023, 106, 8504. [Google Scholar] [CrossRef]
- Wu, Y.P.; Du, B.H.; Xu, C.Y.; Wei, S.B.; Yang, J.H.; Zhao, Y.P. Research on the Temporal and Spatial Distribution of Marginal Abatement Costs of Carbon Emissions in the Logistics Industry and Its Influencing Factors. Sustainability 2025, 17, 2839. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Wang, M.X. Spatio-temporal evolution characteristics and influencing factors of environmental welfare performance in Chinese cities. Front. Public Health 2025, 13, 1543745. [Google Scholar] [CrossRef]
- Lv, T.G.; Li, Z.Y.; Zhang, X.M.; Geng, C.; Hu, H.; Xiao, J. Spatial-Temporal Differences and Influencing Factors of Agricultural Water Use Efficiency in the Main Grain-Producing Areas of the Middle Reaches of the Yangtze River. Pol. J. Environ. Stud. 2024, 33, 753–765. [Google Scholar] [CrossRef] [PubMed]
- Han, S.X.; Fu, D.; Xu, T.X.; Li, Q.; Othman, M.H.D.; Kurniawan, T.A. Water resource utilization efficiency and driving factors in northern Anhui (China) based on the DEA Malmquist model. Water Supply 2023, 23, 4539–4553. [Google Scholar] [CrossRef]
- Tian, Y.; Shi, X.Y. Analysis of Dynamic Evolution and Driving Factors of Low-Carbon Utilization Efficiency of Cultivated Land in China. Agriculture 2024, 14, 526. [Google Scholar] [CrossRef]
- Wan, D.J.; Liu, J.P.; Ma, H.X. Temporal-spatial variation characteristics of utilization efficiency of water resources in Changbai Mountain area. Desalination Water Treat. 2022, 276, 1–12. [Google Scholar] [CrossRef]
- Zeng, L.G.; Li, P.L.; Yu, Z.; Nie, Y.; Li, S.Z.; Gao, G.Y.; Huang, D. Spatiotemporal Characteristics and Influencing Factors of Water Resources’ Green Utilization Efficiency in China: Based on the EBM Model with Undesirable Outputs and SDM Model. Water 2022, 14, 2908. [Google Scholar] [CrossRef]
- Zhang, T.M.; Huang, J.; Xu, Y.J. Evaluation of the Utilization Efficiency of Water Resources in China Based on ZSG-DEA: A Perspective of Water-Energy-Food Nexus. Int. J. Comput. Intell. Syst. 2022, 15, 56. [Google Scholar] [CrossRef]
- Wang, H.K.; Chen, H.; Tran, T.T.; Qin, S. An Analysis of the Spatiotemporal Characteristics and Diversity of Grain Production Resource Utilization Efficiency under the Constraint of Carbon Emissions: Evidence from Major Grain-Producing Areas in China. Int. J. Environ. Res. Public Health 2022, 19, 7746. [Google Scholar] [CrossRef]
- Li, D.L.; Zuo, Q.T.; Zhang, Z.Z. A new assessment method of sustainable water resources utilization considering fairness-efficiency-security: A case study of 31 provinces and cities in China. Sustain. Cities Soc. 2022, 81, 103839. [Google Scholar] [CrossRef]
- Xie, Q.W.; Ma, H.W.; Zheng, X.L.; Wang, X.; Wang, F.Y. Evaluation and Spatial-Temporal Difference Analysis of Urban Water Resource Utilization Efficiency Based on Two-Stage DEA Model. IEEE Trans. Comput. Soc. Syst. 2022, 9, 1282–1296. [Google Scholar] [CrossRef]
- Ming, X.X.; Wang, Q.; Luo, K.; Zhang, L.J.; Fan, J.R. An integrated economic, energy, and environmental analysis to optimize evaluation of carbon reduction strategies at the regional level: A case study in Zhejiang, China. J. Environ. Manag. 2024, 351, 119742. [Google Scholar] [CrossRef]
- Yang, Y. Evaluation of China’s water-resource utilization efficiency based on a DEA-Tobit two-stage model. Water Supply 2021, 21, 1764–1777. [Google Scholar] [CrossRef]
- Wang, X.B.; Wang, Z.L. Research on the impact of environmental regulation on water resources utilization efficiency in China based on SYS-GMM model. Water Supply 2021, 21, 3643–3656. [Google Scholar] [CrossRef]
- Lu, W.N.; Liu, W.X.; Hou, M.Y.; Deng, Y.J.; Deng, Y.; Zhou, B.Y.; Zhao, K. Spatial-Temporal Evolution Characteristics and Influencing Factors of Agricultural Water Use Efficiency in Northwest China-Based on a Super-DEA Model and a Spatial Panel Econometric Model. Water 2021, 13, 632. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Siampour, L.; Vahdatpour, S.; Jahangiri, M.; Mostafaeipour, A.; Atabani, A. Techno-enviro assessment and ranking of Turkey for use of home-scale solar water heaters. Sustain. Energy Technol. Assess. 2021, 43, 100948. [Google Scholar] [CrossRef]
- Battese, G.; Coelli, T. A model for technical inefficiency effects in a stochastic frontier production function for panel data. Empir. Econ. 1995, 20, 325–332. [Google Scholar] [CrossRef]
- Brockett, P.; Charnes, A.; Cooper, W.; Huang, Z.; Sun, D. Data transformations in DEA cone ratio envelopment approaches for monitoring bank performances. Eur. J. Oper. Res. 1997, 98, 250–268. [Google Scholar] [CrossRef]





| Indicator | Symbol | Proxy Variables | Unit |
|---|---|---|---|
| Output indicators | Y | Gross agricultural output value | RMB |
| Land input | S | Total sown area | Hectares |
| Labor input | L | Agricultural labor force | People |
| Capital investment | K | Total power of agricultural machinery | Kilowatt |
| Material input | C | Consumption of chemical fertilizer | Tonnes |
| Agricultural water consumption input | W | Agricultural water consumption | Cubic meters |
| Precipitation input | P | Precipitation | mm |
| Temperature input | T | Temperature | °C |
| Year | Variables | Mean | Standard | Coefficient | Min | 10th | 25th | 50th | 75th | 90th | Max |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Deviation | Variation | ||||||||||
| 2017–2012 | Y | 5,179,588 | 1,841,388 | 0.36 | 2,574,006 | 3,134,141 | 3,633,196 | 4,546,801 | 6,594,927 | 7,604,342 | 9,220,393 |
| S | 760,201 | 307,479 | 0.40 | 190,086 | 366,188 | 455,617 | 790,095 | 1,001,133 | 1,108,306 | 1,207,825 | |
| L | 1,189,088 | 559,409 | 0.47 | 626,584 | 668,225 | 779,174 | 1,024,230 | 1,357,500 | 1,700,738 | 2,725,340 | |
| K | 6,919,309 | 5,194,505 | 0.75 | 290 | 1047 | 2,613,891 | 7,404,278 | 9,839,985 | 12,864,047 | 20,360,714 | |
| C | 286,365 | 136,692 | 0.48 | 100,283 | 108,290 | 140,110 | 291,890 | 429,412 | 472,825 | 487,732 | |
| W | 12 | 5 | 0.41 | 5 | 6 | 7 | 12 | 16 | 18 | 20 | |
| P | 550.61 | 90.24 | 0.16 | 391.91 | 426.24 | 488.53 | 552.04 | 612.48 | 680.11 | 742.35 | |
| T | 12.15 | 2.67 | 0.22 | 6.32 | 7.13 | 10.97 | 13.34 | 14.13 | 14.41 | 14.63 | |
| 2021–2018 | Y | 3,613,351 | 2,751,687 | 0.76 | 91 | 500 | 221,881 | 3,988,795 | 5,695,937 | 6,996,701 | 9,764,508 |
| S | 320,565 | 394,552 | 1.23 | 110 | 197 | 722 | 1053 | 686,247 | 954,173 | 1,095,623 | |
| L | 1,676,139 | 1,096,828 | 0.65 | 94,453 | 567,031 | 916,396 | 1,341,842 | 2,499,099 | 3,492,980 | 3,928,995 | |
| K | 3,052,876 | 4,046,765 | 1.33 | 104 | 176 | 806 | 1311 | 7,410,765 | 9,728,382 | 12,833,239 | |
| C | 120,381 | 151,987 | 1.26 | 6 | 10 | 25 | 41 | 283,681 | 347,252 | 438,829 | |
| W | 9 | 4 | 0.49 | 2 | 2 | 5 | 9 | 12 | 14 | 17 | |
| P | 528.89 | 102.33 | 354.31 | 0.19 | 406.58 | 456.69 | 508.07 | 582.06 | 679.62 | 783.68 | |
| T | 11.77 | 2.68 | 5.13 | 0.23 | 6.99 | 10.65 | 12.90 | 13.81 | 14.14 | 14.65 |
| Value | 2012–2014 | 2015–2016 | 2017–2019 | 2020–2021 |
|---|---|---|---|---|
| Global Moran’ I | 0.841 | 0.832 | 0.826 | 0.813 |
| Z-Score | 9.350 | 9.260 | 9.188 | 9.032 |
| P | 0.030 | 0.045 | 0.045 | 0.060 |
| Year | Type | Longitude (°) | Latitude (°) | Rotation Angle (°) | Displacement (km) |
|---|---|---|---|---|---|
| 2012–2014 | Efficiency value | 117.521 | 39.494 | 44.92 | - |
| 2015–2016 | Efficiency value | 117.201 | 39.634 | 20.51 | 49.85 |
| 2017–2019 | Efficiency value | 118.071 | 39.944 | 37.74 | 26.34 |
| 2020–2021 | Efficiency value | 118.356 | 40.392 | 136.46 | 35.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, L.; Jia, R.; Wei, S.; Chen, M.; Ma, Q.; Jia, T.; Sun, J.; Han, Z. Spatial–Temporal Evolution of Agricultural Water Use Efficiency Based on DEA Approach and Spatial Autocorrelation. Water 2025, 17, 1456. https://doi.org/10.3390/w17101456
Huo L, Jia R, Wei S, Chen M, Ma Q, Jia T, Sun J, Han Z. Spatial–Temporal Evolution of Agricultural Water Use Efficiency Based on DEA Approach and Spatial Autocorrelation. Water. 2025; 17(10):1456. https://doi.org/10.3390/w17101456
Chicago/Turabian StyleHuo, Litao, Ruitao Jia, Sa Wei, Meijing Chen, Qingqing Ma, Tengfei Jia, Jiawei Sun, and Zonglin Han. 2025. "Spatial–Temporal Evolution of Agricultural Water Use Efficiency Based on DEA Approach and Spatial Autocorrelation" Water 17, no. 10: 1456. https://doi.org/10.3390/w17101456
APA StyleHuo, L., Jia, R., Wei, S., Chen, M., Ma, Q., Jia, T., Sun, J., & Han, Z. (2025). Spatial–Temporal Evolution of Agricultural Water Use Efficiency Based on DEA Approach and Spatial Autocorrelation. Water, 17(10), 1456. https://doi.org/10.3390/w17101456





