Characterization of a Contaminated Site Using Hydro-Geophysical Methods: From Large-Scale ERT Surface Investigations to Detailed ERT and GPR Cross-Hole Monitoring
Abstract
1. Introduction
2. Site Description
2.1. Geological Framework
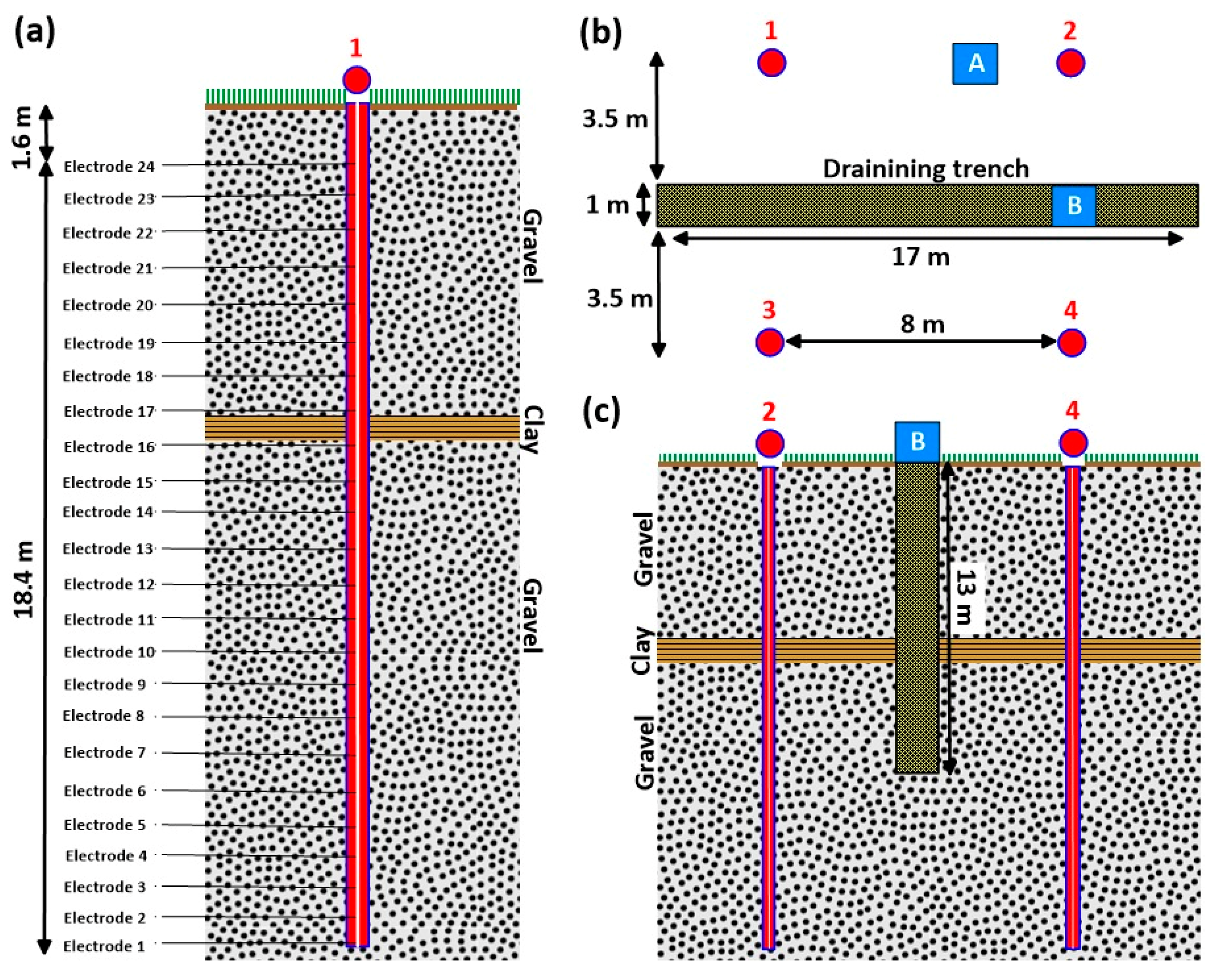
2.2. Experimental Area
3. Methods
3.1. Electrical Resistivity Tomography (ERT)
3.1.1. ERT Forward Modelling
3.1.2. ERT Inverse Modelling
3.1.3. ERT Time-Lapse Survey
3.1.4. ERT Data Acquisition
3.2. Ground-Penetrating Radar (GPR)
4. Results
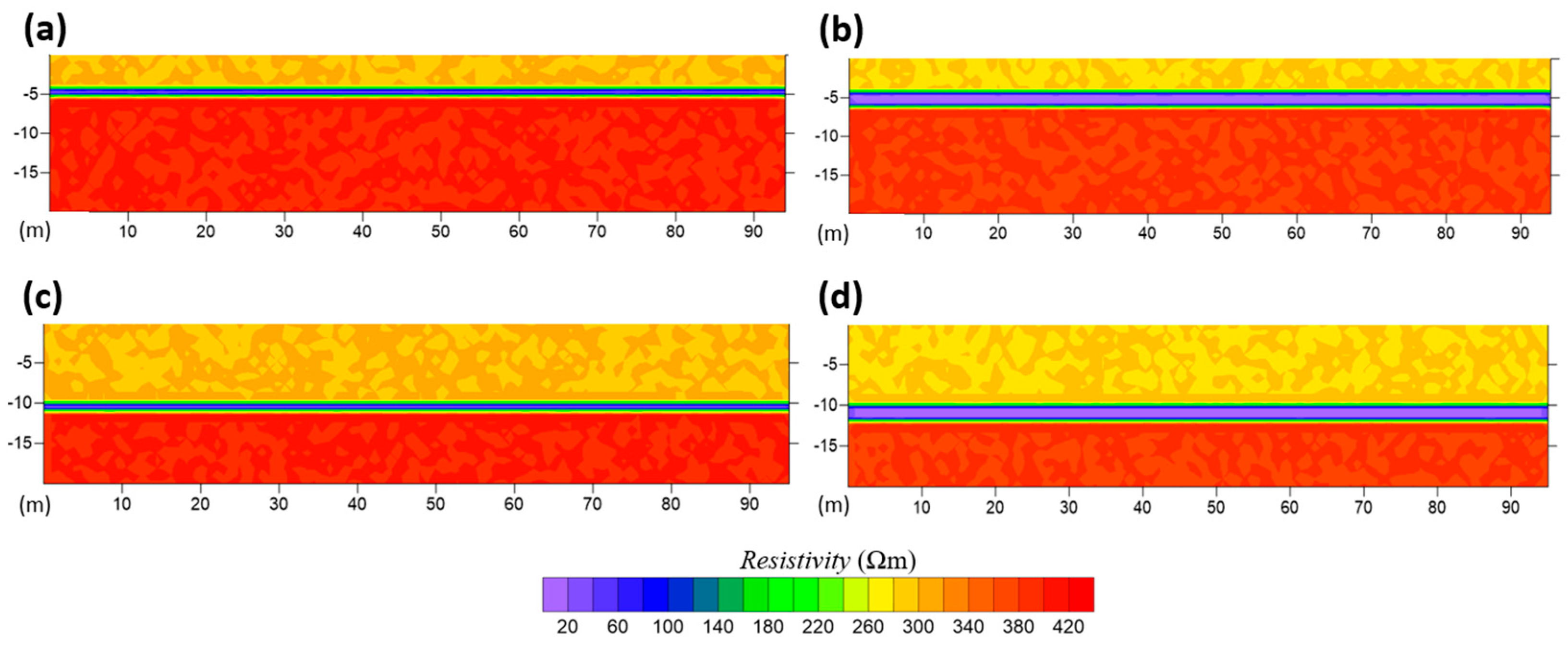
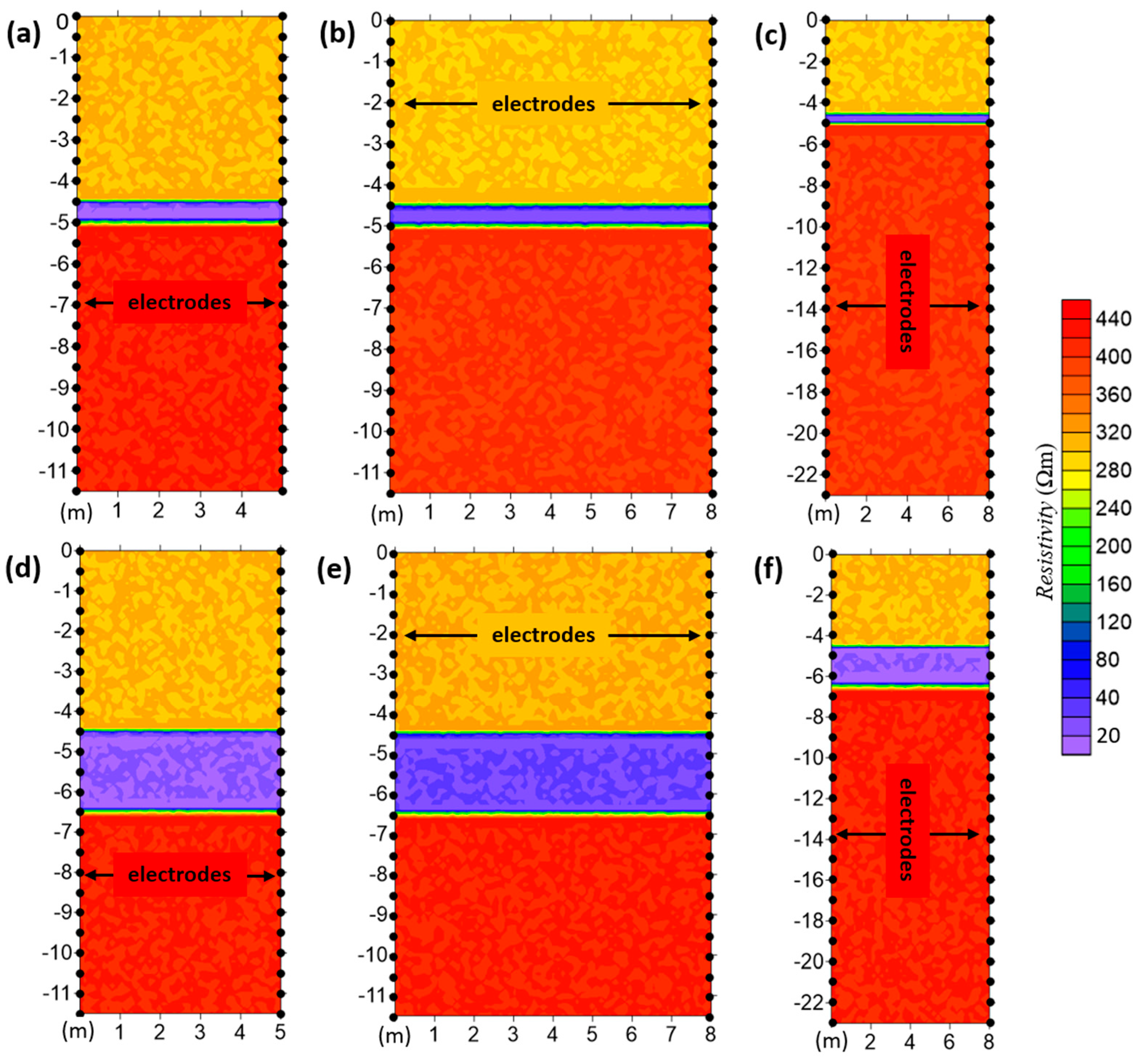
4.1. ERT Forward Modelling Results
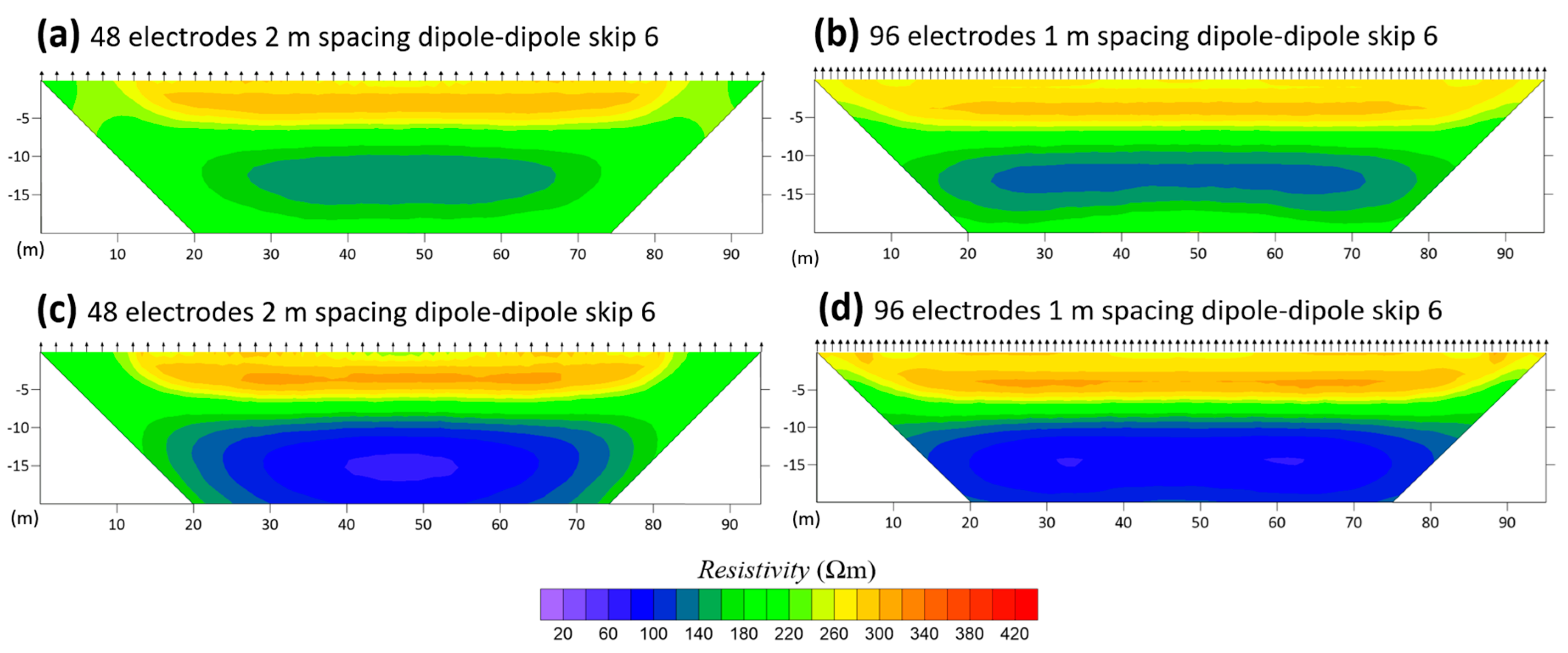
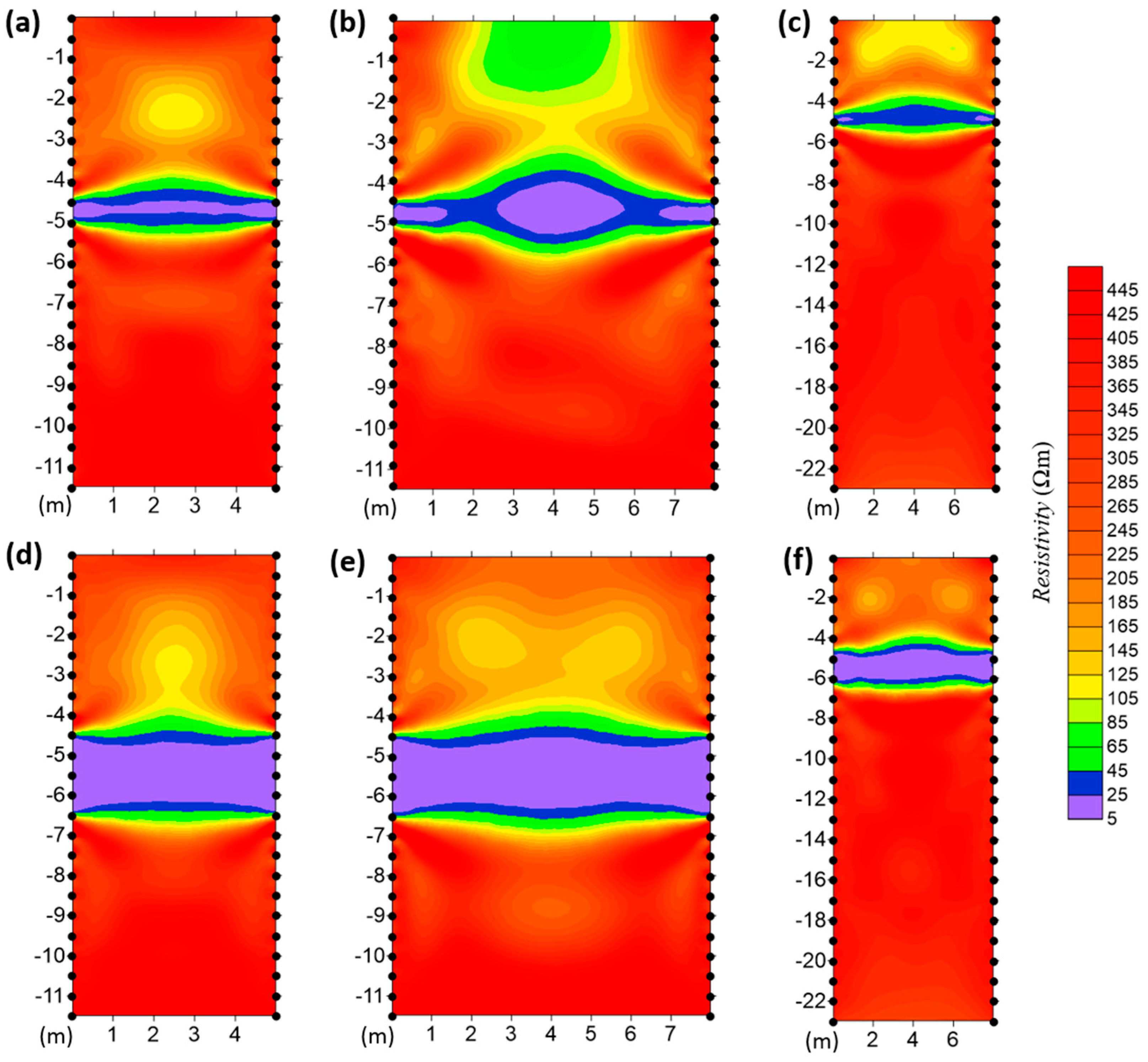
4.2. ERT Field Data Inversion
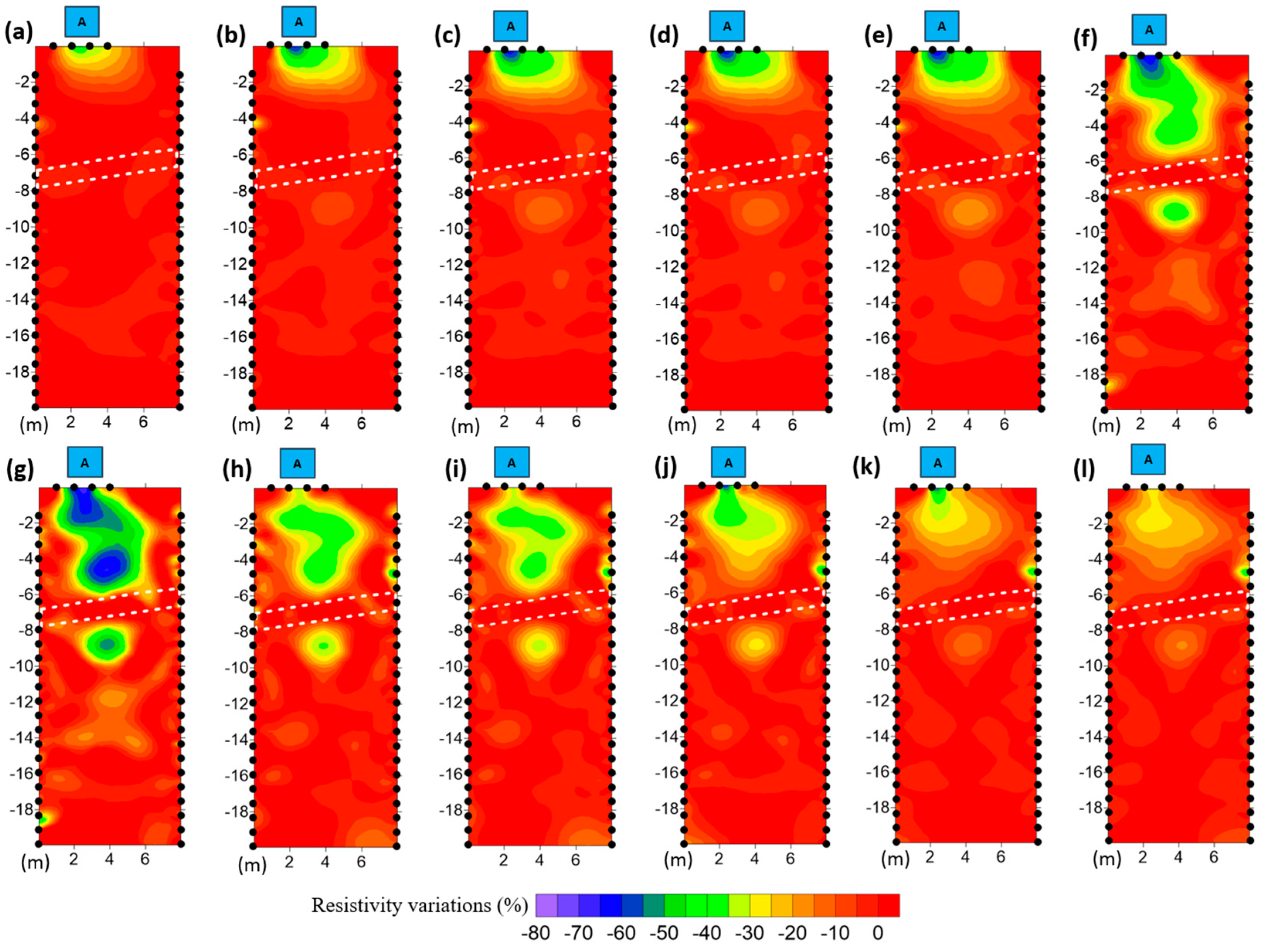
4.3. ERT Time-Lapse Inversions during Water Infiltration Experiments
4.4. GPR Monitoring during Water Infiltration Experiments
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cassiani, G.; Binley, A.; Kemna, A.; Wehrer, M.; Orozco, A.F.; Deiana, R.; Boaga, J.; Rossi, M.; Dietrich, P.; Werban, U.; et al. Noninvasive Characterization of the Trecate (Italy) Crude-Oil Contaminated Site: Links between Contamination and Geophysical Signals. Environ. Sci. Pollut. Res. 2014, 21, 8914–8931. [Google Scholar] [CrossRef] [PubMed]
- Binley, A.; Hubbard, S.S.; Huisman, J.A.; Revil, A.; Robinson, D.A.; Singha, K.; Slater, L.D. The Emergence of Hydrogeophysics for Improved Understanding of Subsurface Processes over Multiple Scales. Water Resour. Res. 2015, 51, 3837–3866. [Google Scholar] [CrossRef]
- Wang, T.P.; Chen, C.C.; Tong, L.T.; Chang, P.Y.; Chen, Y.C.; Dong, T.H.; Cheng, S.N. Applying FDEM, ERT and GPR at a site with soil contamination: A case study. J. Appl. Geophys. 2015, 121, 21–30. [Google Scholar] [CrossRef]
- Godio, A.; Arato, A.; Stocco, S. Geophysical Characterization of a Nonaqueous-Phase Liquid–Contaminated Site. Environ. Geosci. 2010, 17, 141–161. [Google Scholar] [CrossRef]
- Binley, A. Tools and Techniques: Electrical Methods. In Treatise on Geophysics; Elsevier: Amsterdam, The Netherlands, 2015; pp. 233–259. [Google Scholar]
- Doetsch, J.; Linde, N.; Pessognelli, M.; Green, A.G.; Günther, T. Constraining 3-D Electrical Resistance Tomography with GPR Reflection Data for Improved Aquifer Characterization. J. Appl. Geophys. 2012, 78, 68–76. [Google Scholar] [CrossRef]
- Santi, P.M.; McCray, J.E.; Martens, J.L. Investigating Cross-Contamination of Aquifers. Hydrogeol. J. 2006, 14, 51–68. [Google Scholar] [CrossRef]
- Doetsch, J.; Linde, N.; Binley, A. Structural Joint Inversion of Time-lapse Crosshole ERT and GPR Traveltime Data. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Deiana, R.; Cassiani, G.; Kemna, A.; Villa, A.; Bruno, V.; Bagliani, A. An Experiment of Non-invasive Characterization of the Vadose Zone via Water Injection and Cross-hole Time-lapse Geophysical Monitoring. Near Surf. Geophys. 2007, 5, 183–194. [Google Scholar] [CrossRef]
- Steelman, C.M.; Klazinga, D.R.; Cahill, A.G.; Endres, A.L.; Parker, B.L. Monitoring the evolution and migration of a methane gas plume in an unconfined sandy aquifer using time-lapse GPR and ERT. J. Contam. Hydrol. 2017, 205, 12–24. [Google Scholar] [CrossRef]
- Fontana, A.; Mozzi, P.; Marchetti, M. Alluvial Fans and Megafans along the Southern Side of the Alps. Sediment. Geol. 2014, 301, 150–171. [Google Scholar] [CrossRef]
- Fontana, A.; Mozzi, P.; Bondesan, A. Alluvial Megafans in the Venetian–Friulian Plain (North-Eastern Italy): Evidence of Sedimentary and Erosive Phases during Late Pleistocene and Holocene. Quat. Int. 2008, 189, 71–90. [Google Scholar] [CrossRef]
- Hippe, K.; Fontana, A.; Hajdas, I.; Ivy-Ochs, S. A High-Resolution 14 C Chronology Tracks Pulses of Aggradation of Glaciofluvial Sediment on the Cormor Megafan between 45 and 20 Ka BP. Radiocarbon 2018, 60, 857–874. [Google Scholar] [CrossRef]
- Fontana, A.; Rossato, S.; Poli, M.E.; Furlani, S.; Stefani, C. Carta delle Unità Geologiche della Pianura del Friuli Venezia Giulia: Scala 1:150.000; Università degli Studi di Trieste: Trieste, Italy, 2019; ISBN 9788894039429. [Google Scholar]
- Binley, A.; Kemna, A. DC Resistivity and Induced Polarization Methods. In Hydrogeophysics; Rubin, Y., Hubbard, S.S., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 129–156. [Google Scholar]
- Blanchy, G.; Saneiyan, S.; Boyd, J.; McLachlan, P.; Binley, A. ResIPy, an Intuitive Open Source Software for Complex Geoelectrical Inversion/Modeling. Comput. Geosci. 2020, 137, 104423. [Google Scholar] [CrossRef]
- Wagner, F.M.; Uhlemann, S. An Overview of Multimethod Imaging Approaches in Environmental Geophysics. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1–72. [Google Scholar]
- Constable, S.C.; Parker, R.L.; Constable, C.G. Occam’s Inversion: A Practical Algorithm for Generating Smooth Models from Electromagnetic Sounding Data. Geophysics 1987, 52, 289–300. [Google Scholar] [CrossRef]
- Slater, L.; Binley, A. Synthetic and Field-Based Electrical Imaging of a Zerovalent Iron Barrier: Implications for Monitoring Long-Term Barrier Performance. Geophysics 2006, 71, B129–B137. [Google Scholar] [CrossRef]
- Pavoni, M.; Carrera, A.; Boaga, J. Improving the Galvanic Contact Resistance for Geoelectrical Measurements in Debris Areas: A Case Study. Near Surf. Geophys. 2022, 20, 178–191. [Google Scholar] [CrossRef]
- Pavoni, M.; Boaga, J.; Carrera, A.; Zuecco, G.; Carturan, L.; Zumiani, M. Brief Communication: Mountain Permafrost Acts as an Aquitard during an Infiltration Experiment Monitored with Electrical Resistivity Tomography Time-Lapse Measurements. Cryosphere 2023, 17, 1601–1607. [Google Scholar] [CrossRef]
- Pavoni, M.; Boaga, J.; Wagner, F.M.; Bast, A.; Phillips, M. Characterization of Rock Glaciers Environments Combining Structurally-Coupled and Petrophysically-Coupled Joint Inversions of Electrical Resistivity and Seismic Refraction Datasets. J. Appl. Geophys. 2023, 215, 105097. [Google Scholar] [CrossRef]
- Nielson, T.; Bradford, J.; Pierce, J.; Seyfried, M. Soil Structure and Soil Moisture Dynamics Inferred from Time-Lapse Electrical Resistivity Tomography. Catena 2021, 207, 105553. [Google Scholar] [CrossRef]
- Lapenna, V.; Perrone, A. Time-Lapse Electrical Resistivity Tomography (TL-ERT) for Landslide Monitoring: Recent Advances and Future Directions. Appl. Sci. 2022, 12, 1425. [Google Scholar] [CrossRef]
- Doetsch, J.; Linde, N.; Vogt, T.; Binley, A.; Green, A.G. Imaging and quantifying salt-tracer transport in a riparian groundwater system by means of 3D ERT monitoring. Geophysics 2012, 77, B207–B218. [Google Scholar] [CrossRef]
- Daily, W.; Ramirez, A.; LaBrecque, D.; Nitao, J. Electrical Resistivity Tomography of Vadose Water Movement. Water Resour. Res. 1992, 28, 1429–1442. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L. Measurement of Soil Water Content Using Time-domain Reflectrometry (TDR): A Field Evaluation. Soil Sci. Soc. Am. J. 1985, 49, 19–24. [Google Scholar] [CrossRef]
- Roth, K.; Schulin, R.; Flühler, H.; Attinger, W. Calibration of Time Domain Reflectometry for Water Content Measurement Using a Composite Dielectric Approach. Water Resour. Res. 1990, 26, 2267–2273. [Google Scholar] [CrossRef]
- van Overmeeren, R.A.; Sariowan, S.V.; Gehrels, J.C. Ground Penetrating Radar for Determining Volumetric Soil Water Content; Results of Comparative Measurements at Two Test Sites. J. Hydrol. 1997, 197, 316–338. [Google Scholar] [CrossRef]
- Robinson, D.A.; Friedman, S.P. A Method for Measuring the Solid Particle Permittivity or Electrical Conductivity of Rocks, Sediments, and Granular Materials. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Rossi, M.; Cassiani, G.; Binley, A. A Stochastic Analysis of Cross-Hole Ground-Penetrating Radar Zero-Offset Profiles for Subsurface Characterization. Vadose Zone J. 2012, 11, vzj2011-0078. [Google Scholar] [CrossRef]
- Parkin, G.; Redman, D.; Von Bertoldi, P.; Zhang, Z. Measurement of soil water content below a wastewater trench using ground-penetrating radar. Water Resour. Res. 2000, 36, 2147–2154. [Google Scholar] [CrossRef]
- Deiana, R.; Cassiani, G.; Villa, A.; Bagliani, A.; Bruno, V. Calibration of a Vadose Zone Model Using Water Injection Monitored by GPR and Electrical Resistance Tomography. Vadose Zone J. 2008, 7, 215–226. [Google Scholar] [CrossRef]
- Pringle, J.K.; Westerman, A.R.; Clark, J.D.; Guest, J.A.; Ferguson, R.J.; Gardiner, A.R. The use of vertical radar profiling (VRP) in GPR surveys of ancient sedimentary strata. In Ground Penetrating Radar in Sediments; Geological Society: London, UK, 2003; Volume 211, pp. 225–246. [Google Scholar] [CrossRef]
- Doetsch, J.A.; Coscia, I.; Greenhalgh, S.; Linde, N.; Green, A.; Günther, T. The Borehole-Fluid Effect in Electrical Resistivity Imaging. Geophysics 2010, 75, F107–F114. [Google Scholar] [CrossRef]
- LaBrecque, D.; Alumbaugh, D.L.; Yang, X.; Paprocki, L.; Brainard, J. Chapter 15 Three-Dimensional Monitoring of Vadose Zone Infiltration Using Electrical Resistivity Tomography and Cross-Borehole Ground-Penetrating Radar. In Methods in Geochemistry and Geophysics; Elsevier: Amsterdam, The Netherlands, 2002; pp. 259–272. [Google Scholar]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic Determination of Soil Water Content: Measurements in Coaxial Transmission Lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]







| Time | ERT Time Step | Water Released |
|---|---|---|
| 11.00 | t0 | - |
| 12:00 | - | Start |
| 12:35 | t1 | 1000 L |
| 13:08 | t2 | 2000 L |
| 13:45 | t3 | 3000 L |
| 14:20 | t4 | 4000 L |
| 14:55 | t5 | 5000 L |
| 15:30 | t6 | 6000 L |
| 16:00 | t7 | 7000 L |
| 21:30 | - | 16,600 L (End) |
| 07:50 (+1 day) | t8 | - |
| 10:00 (+1 day) | t9 | - |
| 12:00 (+1 day) | t10 | - |
| 14:00 (+1 day) | t11 | - |
| 16:00 (+1 day) | t12 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavoni, M.; Boaga, J.; Peruzzo, L.; Barone, I.; Mary, B.; Cassiani, G. Characterization of a Contaminated Site Using Hydro-Geophysical Methods: From Large-Scale ERT Surface Investigations to Detailed ERT and GPR Cross-Hole Monitoring. Water 2024, 16, 1280. https://doi.org/10.3390/w16091280
Pavoni M, Boaga J, Peruzzo L, Barone I, Mary B, Cassiani G. Characterization of a Contaminated Site Using Hydro-Geophysical Methods: From Large-Scale ERT Surface Investigations to Detailed ERT and GPR Cross-Hole Monitoring. Water. 2024; 16(9):1280. https://doi.org/10.3390/w16091280
Chicago/Turabian StylePavoni, Mirko, Jacopo Boaga, Luca Peruzzo, Ilaria Barone, Benjamin Mary, and Giorgio Cassiani. 2024. "Characterization of a Contaminated Site Using Hydro-Geophysical Methods: From Large-Scale ERT Surface Investigations to Detailed ERT and GPR Cross-Hole Monitoring" Water 16, no. 9: 1280. https://doi.org/10.3390/w16091280
APA StylePavoni, M., Boaga, J., Peruzzo, L., Barone, I., Mary, B., & Cassiani, G. (2024). Characterization of a Contaminated Site Using Hydro-Geophysical Methods: From Large-Scale ERT Surface Investigations to Detailed ERT and GPR Cross-Hole Monitoring. Water, 16(9), 1280. https://doi.org/10.3390/w16091280








