Abstract
Regularly, large parts of the agricultural areas of the Great Hungarian Plain are inundated due to excessive rainfall and insufficient evaporation and infiltration. Climate change is expected to lead to increasingly extreme weather conditions, which may even increase the frequency and extent of these inundations. Shallow “floods”, also defined as inland excess water, are phenomena that occur due to a complex set of interrelated factors. Our research presents a workflow based on active and passive satellite data from Sentinel-1 and -2, combined with a large auxiliary data set to detect and predict these floods. The workflow uses convolutional neural networks to classify water bodies based on Sentinel-1 and Sentinel-2 satellite data. The inundation data were complimented with meteorological, soil, land use, and GIS data to form 24 features that were used to train an XGBoost model and a deep neural network to predict future inundations, with a daily interval. The best prediction was reached with the XGBoost model, with an overall accuracy of 86%, a Kappa value of 0.71, and an F1 score of 0.86. The SHAP explainable AI method showed that the most important input features were the amount of water detected in the satellite imagery during the week before the forecast and during the period two weeks earlier, the number of water pixels in the surroundings on the day before the forecast, and the potential evapotranspiration on the day of the forecast. The resulting inland excess water inundation time series can be used for operational action, planning, and prevention.
1. Introduction
Since the introduction of the river regulations at the end of the 19th century in Hungary, shallow floods, also described as inland excess water (IEW), became increasingly problematic in large parts of the cultivated areas of the country. Prior to the regulations, the rivers featured expansive floodplains, which were subject to regular inundation. Farmers cultivated these periodically flooded regions by adjusting to the conditions. The notion of IEW was unfamiliar to them. However, with the construction of the flood embankments, the IEW generated in the protected areas could no longer flow back into the natural watercourses, causing prolonged inundations. The term IEW was first used when the former flood plains, mainly low-lying areas without drainage, were inundated [1]. In winter and early spring, as a result of low temperatures, ground frost prevents infiltration into the ground, saturated air prevents evaporation, and cultivated plants can utilize less water; therefore, the large quantities of accumulated, usually solid, precipitation suddenly melts as the temperature rises and causes water coverage on the surface. In spring and summer, high intensity or prolonged precipitation can cause water cover to appear on the surface. From a topographical point of view, accumulated water is not able to infiltrate into the soil in the local surface depressions. The phenomenon, which is unfavorable from a water management perspective, was described as early as the mid-19th century, but the concept of IEW itself was not used until years later [2]. A significant part of Hungary’s arable land (7.3 million hectares) is agricultural land (5.3 million hectares), of which about 1.9 million hectares can be considered at potential risk of IEW inundation [3,4]. On average, 100–150 thousand hectares are inundated every 2–3 years, due to extreme hydrological conditions. Mainly the Great Hungarian Plain, the Little Plain, and some scattered areas (e.g., the Dráva valley and around the southern shore of Lake Balaton) are affected. The natural/environmental factors that determine the formation of IEW can be divided into two parts, based on their temporal variability [5]. Permanent factors like topography, soil composition and structure, shallow geology, and abandoned riverbeds form the conditions required for IEW formation, while the phenomenon is generated by factors that vary over time, like meteorology, hydrology, and groundwater flow. In addition to these natural factors, anthropogenic influences, like poor farming practices (disc and plough pan), the state of the drainage network, land use patterns, etc., also play a significant role in the formation and persistence of IEW. The former shows that the IEW phenomenon is a complex hydrological extreme, of which the precise definition is still difficult today. There are several definitions, which Pálfai [2] has attempted to summarize, as follows: “IEW is a temporary but chronic phenomenon in flat areas, caused by natural hydrometeorological events; it is not only open water cover but also the excessively wet state of the soil”.
The latest climate change projections predict that extreme weather could increase the likelihood of high-intensity precipitation [6]. According to model simulations, the variability and extreme nature of the precipitation distribution is increasing, which is likely to be more pronounced in the Carpathian Basin [7]. According to the study of Bartholy et al. [8], the total annual precipitation will not change significantly, but winter precipitation is expected to increase by about 20%, while summer precipitation is expected to decrease by 20%.
IEW is not specific to Hungary, but also affects other countries around the world (e.g., China, India, Germany, Netherlands, Poland, Romania, and Russia) [9,10]. Governments have invested substantial financial and human resources to effectively address the damage, through comprehensive protection and prevention measures. Initially, IEW mapping was studied based on field surveys and then hydrological models emerged from various technical and engineering sides (e.g., [11,12,13]). Such models require the collection of many high-resolution input parameters that are often not available or are costly to acquire using surveys. Their applicability is, therefore, restricted to limited scales, like catchment areas, water management districts, and pilot areas.
Various studies on the vulnerability of flat areas to IEW at a national scale have been carried out; first by Pálfai [4] and later by Pálfai et al. [14], Pásztor et al. [15], and Laborczi et al. [16]. Recent research on IEW mapping and monitoring is often based on remote sensing data [17,18,19]. Unmanned aerial vehicles, aerial surveys, and active and passive data from satellites provide sufficient spatial and temporal resolution for these studies. Various methods (index-based slicing, classification, traditional machine learning, and deep neural networks) have been applied to delineate IEW. In recent years, neural networks, especially deep neural networks (DNNs) such as the convolutional neural network (CNN) [20], have gained increasing popularity in earth science applications [21,22,23,24]. In our previous study, eight methods were used to detect IEW, of which CNNs proved to be the most accurate on the Sentinel-2 high-resolution multispectral satellite images [25].
So far, the prediction of IEW has been performed using hydrological modeling on small areas [11,12,13]. The prediction of the inundation using a data-driven approach has not been attempted. In this research, a methodology is presented that uses a large remote sensing-based data set, complemented with meteorological, soil, geomorphological, and land use data, to predict the development of IEW several days in the future. For this purpose, a deep neural network (DNN) and an Extreme Gradient Boosting (XGBoost) model have been evaluated. The DNN has been applied to determine the non-linear relationship between dependent and independent features in many earth science fields [26,27,28]. Currently, one of the most successful data-driven methods in machine learning is the XGBoost method. This is an ensemble version of the decision tree method [29]. It has been found to provide good results for the exploration of nonlinear relationships in many fields. Li et al. [30], for example, used the method to predict soybean yield, based on a combination of spatial data including satellite images, climate, meteorological, and soil data. Urban flooding susceptibility, based on hydrometeorological and building data, and surface morphological parameters was modeled by Wang et al. [31]. They also presented an analysis of the input data using SHapley Additive exPlanations (SHAP) [32], an explainable Artificial Intelligence method (xAI). xAI methods have been developed to increase the interpretability of advanced machine learning methods, which are often considered as black boxes.
The aim of our research is to develop a spatial information model that allows the generation of daily flood maps over large areas, using static and dynamic data and active and passive satellite imagery, as well as the possibility to make short-term forecasts. The proposed workflow is based on a combination of machine learning algorithms that are fully data-driven. The methodology can help to identify water management priorities in real time and to mitigate damage by creating a time series of water coverage maps and predicting inundations several days ahead. The study of the inundations over a one-year period from 1 June 2020 to 31 May 2021 helps to understand the development and disappearance of the phenomenon. A specific problem of the use of optical satellite imagery in IEW studies is the unavailability of useful data during cloudy weather. In the present study, we sought to address this problem by complementing Sentinel-2 multispectral images with the Radar Vegetation Index (RVI) and Gray Level Co-Occurrence Matrix (GLCM) textures, derived from the Sentinel-1 radar images [33,34,35].
2. Materials and Methods
2.1. Study Area
The study area of 1600 km2 is located in the center of the Great Hungarian Plain (Figure 1). Its surface is uniformly flat, with distinct microrelief. The climate is moderately warm and dry, with an annual average precipitation ranging between 450 and 550 mm. The depressions of abandoned riverbeds and oxbows in the landscape are filled with muddy–silty sediments and loess mud. Due to poor water management in the soil, as well as the meteorological conditions, the area is affected not only by IEW, but also by frequent droughts [36].
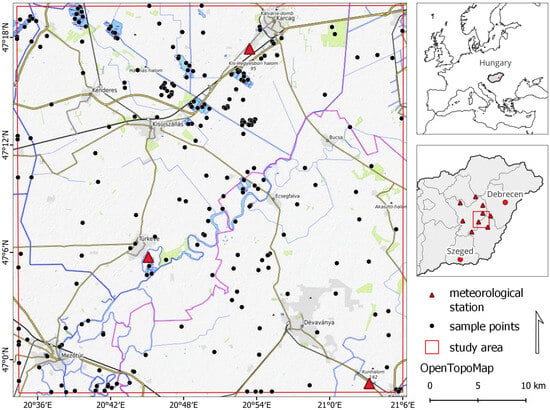
Figure 1.
Study area with meteorological stations and sample points.
2.2. Data
Our analysis was based on the Sentinel-1 radar and Sentinel-2 multispectral images, combined with continuous data for the period 1 January 2020–31 May 2021. The delineation of the water surfaces was achieved by applying two different models for the two types of satellite imagery. The continuous data consisted of meteorological, land cover, soil, elevation, and distance maps. The prediction of the inundations is based on the derived water surfaces, as well as dynamic and static data.
Sentinel-1 is a constellation of two satellites orbiting in a sun-synchronous orbit. The satellites are equipped with identical radar instruments that acquire images of the Earth’s surface, with a swath width of 250 km. Since the decommissioning of Sentinel-1B in December 2021, only Sentinel-1A data have been available. The satellite collects images regardless of the time of day, weather, and atmospheric conditions, with a return time of about three days for Hungary. Its imaging instrument is a C-band synthetic aperture radar with a central frequency of 5.405 GHz. The instrument is capable of transmitting and receiving radar signals in vertical–vertical (VV—vertical–vertical) and vertical–horizontal (VH—vertical–horizontal) polarization modes. For this study, we used Sentinel-1 Ground Range Detected (GRD) data in interferometric Wide-Swath (IW) mode with a spatial resolution of 5 × 20 m.
Sentinel-2A and Sentinel-2B are multispectral imaging satellites, providing optical data, with a revisit time of 3–4 days for Hungary. The images consist of 13 spectral bands covering the spectrum from visible to near infrared and shortwave infrared. The data have spatial resolutions of 10, 20, and 60 m.
The National Meteorological Service’s (OMSZ) meteorological data repository [37] provides daily meteorological data. Per meteorological station, the station ID, geographic coordinates, precipitation (mm), global radiation (J/m2), relative humidity (%), average minimum and maximum temperature (°C), and average wind speed (m/s) at 10 m altitude were extracted. From these data, the potential evapotranspiration was calculated. In our model, precipitation is regarded as a source for the inundations, while potential evapotranspiration and wind speed are regarded as factors that reduce them.
The Ecosystem Map of Hungary, with a spatial resolution of 20 × 20 m (NÖSZTÉP, [38]), was used to determine the land use/cover. The map from 2020 shows the actual distribution, extent, and frequency of the ecosystems at a national level. It was used to determine which land use categories are vulnerable to IEW.
The multilayered European Soil Hydraulic Database (EU Soil Grids) was derived with European pedotransfer functions [39], based on the soil information of 250 m grids. It incorporates soil taxonomical, physical, and chemical data at seven soil depths. The following soil properties were used to calculate the soil hydraulic properties: clay, silt, and sand content (mass %); organic carbon content (g kg−1); bulk density (kg m−3); pH in water; and depth to bedrock (cm) at 0, 5, 15, 30, 60, 100, and 200 cm depth. Saturated water content (THS), water content at field capacity and wilting point (FC), and saturated hydraulic conductivity (KS) were used in the prediction model to relate soil water management parameters to IEW.
Slope, profile, and plan curvature were derived from the national digital elevation model [40], with a spatial resolution of five meters. Profile curvature is the curvature intersecting the plane defined by the Z axis and the direction of the maximum gradient. Positive values describe the convex profile curvature, while negative values describe the concave profile curvature. The plan curvature describes the horizontal curvature intersecting the XY plane. Slope, profile, and plane curvature are geomorphological characteristics that influence where inundations may occur.
The input data set includes maps based on distances to the closest road, canal, or settlement. The base data for these maps was collected from OpenStreetMap. Distances to anthropogenic features may impact on the frequency of occurrence of IEW. The produced maps have a spatial resolution of 10 × 10 m and the distances were expressed in meters.
2.3. Methodology
The training of the inundation prediction model requires a large data set, consisting of satellite-based inundation maps, as well as dynamic and static data. Each data set went through a complex set of preprocessing steps to be able to use it for training and, later, for prediction (Figure 2).
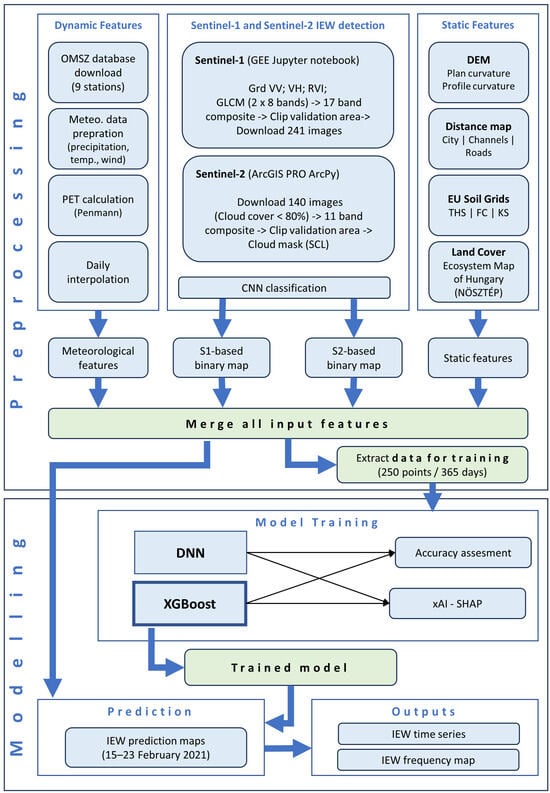
Figure 2.
Preprocessing and modeling workflow.
2.3.1. Data Preparation
The input data for the models consisted of static and dynamic data. The satellite data-based water maps and the meteorological data form the dynamic maps, while the static data consists of the soil and distance maps.
- Sentinel-1 data preparation
The Sentinel-1 images were collected and processed using Google Earth Engine (GEE). GEE is a cloud-based platform for scientific analysis and the visualization of spatial data sets [41]. It stores satellite imagery in a public data repository and provides the ability to analyze large data sets. During the study period, there were a total of 241 image acquisitions that covered our study area. From these images, those that did not cover at least 40% of the area were filtered out, resulting in a total of 182 processed images. The images were subjected to a preprocessing process where thermal noise removal and radiometric calibration, as well as topographic correction, were applied to create 10 × 10 m resolution sigma0 backscatter images [42].
Radar Vegetation Indexes (RVIs) are used for monitoring vegetation growth levels in time series data analysis and are used as an alternative to the Normalized Difference Vegetation Index (NDVI) method applied in optical image processing studies. An RVI is a normalized index, with limits ideally varying between zero and one. For smooth, unvegetated surfaces, the value is close to zero, increasing in proportion to the increase in vegetation density. In our approach, low RVI values are expected to represent areas without vegetation.
To calculate the RVI, the following formula was used [43,44]:
where VH is the vertical–horizontal band and VV is the vertical–vertical band of Sentinel-1.
The Gray Level Co-occurrence Matrix (GLCM) method was first introduced by Haralick et al. [33]. It is a mathematical method used in digital image processing to analyze image texture [35,45]. It shows the frequency of occurrence of pairs of pixel values at a certain distance and angle in a grayscale image. The covariance matrix of grayscale levels represents a more regular spatial arrangement and texture of the same surfaces (in our case, water surfaces). The Google Earth Engine’s glcmTexture function was applied to calculate the 14 GLCM textures proposed by Haralick et al. [33], as well as four additional textures proposed by Conners et al. [34]. The 18 texture maps were analyzed and it was concluded that eight textures provided the following water-related characteristics: contrast, overall average, difference variance, difference, inertia, cluster shadow, cluster salience, and inverse difference moment. Speckle noise in Sentinel-1 images often interfered with the extraction of GLCM textures and frequently resulted in the misclassification of water bodies; therefore, a RefineLee single image speckle filter was applied during the preprocessing of the radar images [46]. Data downloading, preprocessing, and RVI and GLCM calculation happened in a Jupiter Notebook using the Google Earth Engine, Python API, and ArcPy. The raw VV and VH bands, the RVI, and 2 × 8 GLCM textures were combined to 19-band composite images.
- Sentinel-2 data preparation
The Sentinel-2A and Sentinel-2B satellite images were processed in an ArcGIS Pro ArcPy environment. For the period under study, 140 satellite images were available in the ESA Copernicus database. Images with a cloud cover larger than 80% were excluded, resulting in 63 remaining multispectral images. Ten bands from thirteen spectral bands of the raw imagery were processed. The red edge bands 5, 6, 7, and 8A, as well as shortwave infrared band 11, with a spatial resolution of 20 m, were resampled to reach a uniform resolution of 10 × 10 m for all bands. The masking of atmospheric disturbances (clouds and cloud shadows) was performed based on the Scene Classification Layer (SCL) provided by ESA. From the 11 SLC classes, the areas delimited by the classes identified as clouds and cloud shadows were removed (classes 3, 8, 9, and 10). In the study by Kajári et al. [25], a detailed description on the preprocessing of the Sentinel-1 data is provided. After preprocessing, all images were cropped to the study area and stored as 10-band composites.
- Meteorological data
Minimum, maximum, and mean temperature; window speed; relative humidity; global radiation; elevation; and latitude information at each measurement station were downloaded from the OMSZ database. Nine meteorological stations were identified within a 40 km buffer around our research area (Figure 1). The number of stations beyond the study area needed to be extended, because only three stations fall within the original study area, which proved insufficient for the generation of continuous maps of meteorological data. Furthermore, the extension accommodated the continuous nature of interpolation calculations. Potential evapotranspiration (PET) values were calculated using the Penman method implemented in the pyet Python package [47]. The Penman method is a combination method, in which the total evaporation rate is calculated by weighing the evaporation rate due to net radiation and the evaporation rate due to mass transfer [48]. The meteorological data from the nine stations were interpolated using the Inverse Distance Weighted method. Mean temperature, precipitation, PET, and wind speed maps were generated with a spatial resolution of 10 × 10 m.
- Static data
The following three anthropogenic static factors were included in the model: the influence of (1) settlements, (2) roads, and (3) canals on the development of IEW. These layers were extracted from OpenStreetMap. Euclidean distance maps were created from each layer, with a spatial resolution of 10 × 10 m. Three data sets were selected from the European Soil Hydraulic database to incorporate the influence of the soil in the development of IEW, as follows: (1) saturated water content (THS), (2) water content at field capacity and wilting point (FC), and (3) saturated hydraulic conductivity (KS) at seven depths (0, 5, 15, 30, 60, 100, and 200 cm). The data from the top 30 cm and from 30 to 60 cm were averaged, resulting in two maps for each of the three data sets. Each map had a spatial resolution of 10 × 10 m.
2.3.2. Water Classification Using Convolutional Neural Network Satellite Data
Sentinel-1 and -2 satellite data were not available for classification on every examined day during the study period. Due to the orbit of the Sentinel-1 satellites, data were available every 2–3 days, resulting in a total of 241 images, of which 60 were discarded because they did not cover at least 40% of the study area. Usable Sentinel-2 data were available for 140 days. In total, 76 images were excluded, due to too-high cloud coverage (>80%), but many of the remaining Sentinel-2 images were also partly cloudy. On 31 days, both Sentinel-1 and -2 data were available.
The Sentinel-1 classification algorithm is described in detail by Kajári et al. [49]. The algorithm uses a convolutional neural network (CNN) as a classification model. The input features consisted of the original VV and VH bands, radar vegetation index, and GLCM texture layers. The F1 score of the model was 0.84. The Sentinel-2 images were also classified using a CNN model. This model used 10 input features, consisting of visual, near infrared, and shortwave infrared bands. Its overall accuracy was 0.98 and its Kappa score was 0.61. More details can be found in Kajári et al. [50]. Each available satellite image was classified to a binary water map. Its values were 1 for water, 0 for no water, and No Data if the CNN model could not determine if there was water or not.
2.3.3. Water Time Series and Generation of IEW Inundation History
An iterative method was developed to create a time series of water coverage maps based on the satellite-derived binary water cover maps that were described in Section 2.3.2. First, all available maps were stacked according to their date. If a classified water map was available from both Sentinel-1 and -2 for the same date, the intersection between the maps was taken. This resulted in a slight underestimation of the total amount of water in the time series, but prevented the incorporation of cloud shadow pixels in Sentinel-2 images that were misclassified as water.
Figure 3 presents our methodology to create a continuous time series from the Sentinel-1- and -2-based water maps. If, on a certain date, no classified water map was available, an empty map was created at its place in the stack. During the next step, the algorithm evaluated the first map in the stack for pixels without data. If a pixel without data was found, the data of one day before (at t−1) and one day after (at t+1) were considered. If Xt−1 and Xt+1 were available, then Xt0 = [(Xt+1 + Xt−1) /2], where X is the value 0 (“no water”) or 1 (“water”) of the pixel, and Xt0 were rounded up to the closest integer. This means that, if there was water in the pixel before or after the date under consideration, the pixel was designated as “water”. If Xt−1 or Xt+1 were missing, Xt−2 and Xt+2 were considered. If data were still unavailable, another day earlier and/or later was considered, up until Xt−4 and /or Xt+4. If there was still no data available, the earlier and later water information were regarded as unreliable and the pixel was assigned as “no water”. After all no data pixels in the map were filled with either 0 or 1, the next date in the stack was considered, and so on, until all no data pixels in each daily water cover map were filled. Finally, a frequency map was created based on the complete time series. For each pixel, it was determined how many times water occurred and a relative frequency was calculated.
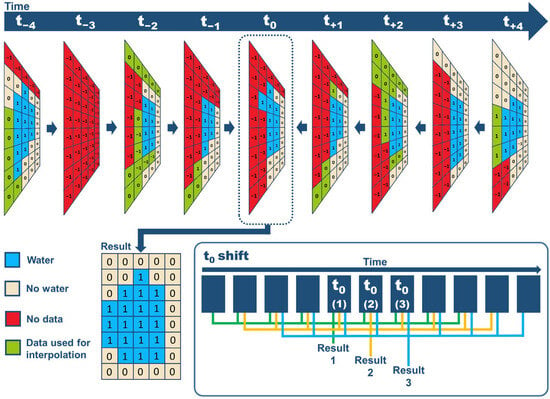
Figure 3.
Scheme for temporal interpolation of water cover.
2.3.4. Training of Prediction Models
Based on the binary water classification of the Sentinel-2 image of 23 February 2021, 250 sample points were randomly selected, of which 50% were designated as a water pixel and 50% as a no water pixel. For each sample point and each date, features were extracted from the separate data sets resulting in 91,250 samples. All samples that had missing data for one or more features were deleted. Areas that were always classified as water or always dry, according to the frequency map, during the 365 days of the test period were excluded from the data set. The final number of samples was 50,315. The features and statistics of the samples are shown in Table 1.

Table 1.
Water (light blue), meteorological (purple), and static (light orange) input features.
All samples were split into the following two data sets: one with water occurrences and one without. From each set, 3000 samples were randomly extracted. The two sets of 3000 samples were then randomly split into 70% (4200) training and 30% (1800) test samples. Finally, all training water and no water samples, as well as all test water and no water samples, were combined. The training and test set were split into dependent and independent features. The NÖSZTÉP land use feature is categorical data and was converted into binary features using one-hot-encoding, resulting in 56 new features, one for each land use class. All features were then scaled using the standard scaler of sklearn [51].
Two models were trained to predict the future occurrence of water in a pixel. The first model was a deep neural network (DNN), with four densely connected layers with 32, 16, 12, and 1 neurons. Other architectures were tested, but deeper models resulted in overfitting. The first three layers had an ReLU activation function, while the last layer was activated using the Sigmoid function. The model was trained with the Adam training algorithm. A binary cross-entropy loss function was applied and the accuracy metric was used to evaluate the training results. The DNN classifier was implemented using the Keras library [52].
The second algorithm was the XGBoost (Extreme Gradient Boosting) algorithm, developed by Chen and Guestrin [29]. It is a sequential machine learning algorithm, published as an open-source library that combines several weak learners, to provide more robust learning [31]. This tree-based ensemble method is faster than most other algorithms, reduces overfitting, and improves computational efficiency. It is one of the most successful machine learning libraries [29]. The optimal hyper parameters for the models such as learning rate and decay, batch size, and number of epochs were selected using the Keras Grid Search with 3-fold cross-validation [52].
For the training of the models, at first, we used the scaled 24 input parameters and 56 one-hot-encoded land use classes, as presented in Table 1. The dependent variable was “Occurrence of water”, which is a binary feature. The training was evaluated with the following metrics:
where TP is true positive, TN is true negative, FP is false positive, and FN is false negative.
To understand the role of the input features during training, we used the SHAP xAI method [32]. The algorithm is designed to evaluate the contribution of each input feature to the prediction. The variance inflation factor (VIF) was calculated to identify multicollinearity among the independent variables [53]. Exclusion of multicollinearity between independent values increased the interpretability of the XGBoost model using SHAP [31].
2.4. Prediction and Forecast with the Trained Model
Prediction on new data was performed using the XGBoost model, because it had a slightly better accuracy and a much better performance than the DNN. Based on the results of the xAI analysis, it was decided to remove the features with very low importance (Table 1, features: 9; 18; 19; 21; 22; 23; and 24). For each of the remaining 17 input features, continuous raster maps were generated (Table 2). The static feature maps do not change in time and need to be generated only once. The surrounding water map was dynamically generated for t−1, the day before the day of the prediction. The water history maps were stored as the water time series (see Section 2.3.3). For the forecast of t0, water maps from t−1 to t−7 (“one week ago”) and t−8 to t−15 (“two weeks ago”) were used. Similarly, the precipitation, evapotranspiration, and wind maps were generated for one week and two weeks before t0. All data were stacked to each other and split into batches of 250 × 250 pixels, to reduce the computational load. The separate batches were scaled using the same scaler as the training data and were fed to the model. The prediction results were merged to the original geometry of the input files, to obtain the final prediction result.

Table 2.
Input features for prediction on tn. The x indicates which data sets are used.
Forecasting follows the same procedure as prediction, but is performed iteratively. To forecast the water cover on day tn, we predict the water on consecutive days t0, t+1, t+2, etc., until tn, while each time using the predictions of the preceding day(s).
3. Results
The presented algorithms provide three types of results. First, the frequency of inundations shows how vulnerable the area is to IEW. Second, the assessment of the training of the machine learning models shows their applicability to map water, and, finally, the prediction algorithm gives the water cover for several days in the future.
3.1. IEW Inundation Time Series
For each pixel in the study area, the frequency of inundation can be evaluated (Figure 4). The daily water maps show where and for how long the area was covered by water. Pixels with water coverage of >0.4 were designated as “Permanent water”, pixels with a frequency between 0.23 and 0.40 were classified as “high”, pixels with a frequency between 0.18 and 0.23 were classified as “middle”, and pixels less than 0.13 were designated as “low”. The permanent water surfaces are a good reflection of lakes, ponds, rivers, and canals with wider cross-sections in the study area. Areas of high inundation include poorly managed runoff areas such as former riverbeds. Rice paddies (square and rectangular shapes) also fall into this category, as they are covered by water for most of the year. Medium and low frequency areas are negligible. They usually mark the shallowest water sources or the edges of larger patches, which dry out or become re-covered with water over time.
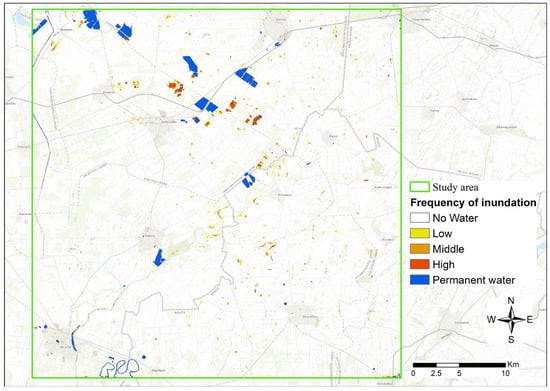
Figure 4.
IEW inundation frequency map of the total study area.
Figure 5 shows two examples of areas with a high frequency of IEW inundation. The shapes of the flooded rice fields are clearly visible in the upper map (A). There may be small patches classified as “Permanent water”, because these areas were under continuous water cover for most of the year. Another example is the accumulation of water in an old, buried, undrained riverbed (B). The deeper areas have a high frequency of water coverage, while the shallower areas are IEW areas with middle-to-low frequency.
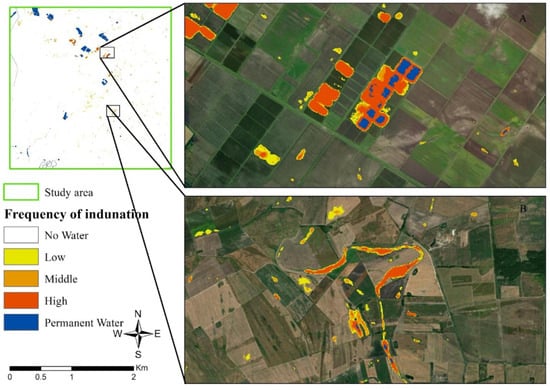
Figure 5.
IEW inundation frequency for flooded rice fields (A) and an old riverbed (B).
The relationship between daily water maps and precipitation during the studied period of one year is illustrated on a selected parcel in Figure 6. It is clearly visible that no inundations (blue line) occur during the high precipitation (orange line) in the summer months, due to high temperatures, high potential evapotranspiration, and the high water absorption capacity of the crops. In autumn and winter though, rainfall is lower, but plant activity and temperatures are also lower, so evapotranspiration is also lower. When runoff, evapotranspiration, and infiltration are low enough, water remains on the surface (from 1 January to early April).
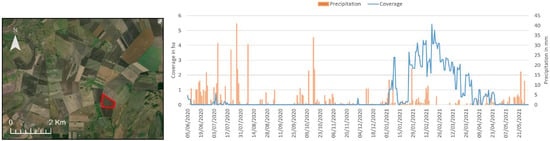
Figure 6.
Development of IEW and precipitation during the study period for a selected parcel of 64 ha.
3.2. Training of Prediction Model
The DNN training was optimized with a learning rate of 0.001 and a decay of 0.0001. The best training result was reached with a batch size of 10 and 100 epochs. The overall accuracy was 0.84, Cohen’s Kappa was 0.68, and F1 was 0.84 (Table 3). XGBoost ran with a learning rate of 0.02, 350 estimators, a maximum depth of six, a minimum child weight of three, and a gamma value of zero. It gave a slightly better overall accuracy, of 0.852, than the DNN. The Kappa and F1 scores were also better, with values of 0.703 and 0.854. The XGBoost model runs about five times faster (18 s vs. 102 s) than the deep learning model.

Table 3.
Accuracy analysis of the DNN and XGBoost training, based on 1800 independent test samples.
The calculation of the multicollinearity of the input features using VIF resulted in the exclusion of the PETSUMtmin1 and FC_0_30 variables, which had a VIF higher than 10 [54]. All other variables had a VIF value lower than four. Moreover, the SHAP analysis resulted in the exclusion of input features that had minimal impact on the training (Figure 7). The importance values show that, for both models, the surrounding water coverage (WATER) and the IEW inundation occurrences of the last week (IEWSUMweek1) and of two weeks (IEWSUMweek2) earlier are of decisive importance. The final models were trained with 17 input features.
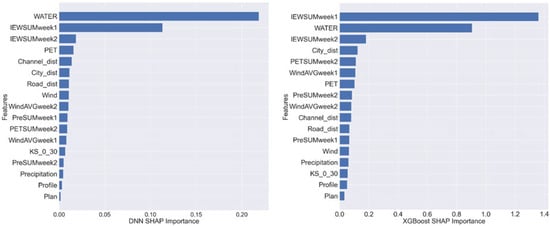
Figure 7.
Input features sorted according to their SHAP importance for the DNN (left) and XGBoost (right) models.
3.3. Results of the Inundation Prediction
The XGBoost model outperformed the DNN in terms of both accuracy and performance. Consequently, it was employed to predict water coverage during a 9-day inundation period in the study area in 2021 (15–23 February 2021) (Figure 8). The prediction for the 15th of February was based on the water time series data that were derived from the satellite data. The consecutive days used the model predictions from the preceding days. A validation analysis was conducted between the predictions and used the separately calculated CNN-based water coverage maps as reference. The overall accuracy (15 February 2021: 0.97; 23 February 2021: 0.98), Cohen’s Kappa (15 February 2021: 0.55; 23 February 2021: 0.69), and F1 scores (15 February 2021: 0.56; 23 February 2021: 0.71) were calculated for the statistical evaluation of the water classifications. The confusion matrix prepared for the whole 1600 km2 study area is presented in Table 4.
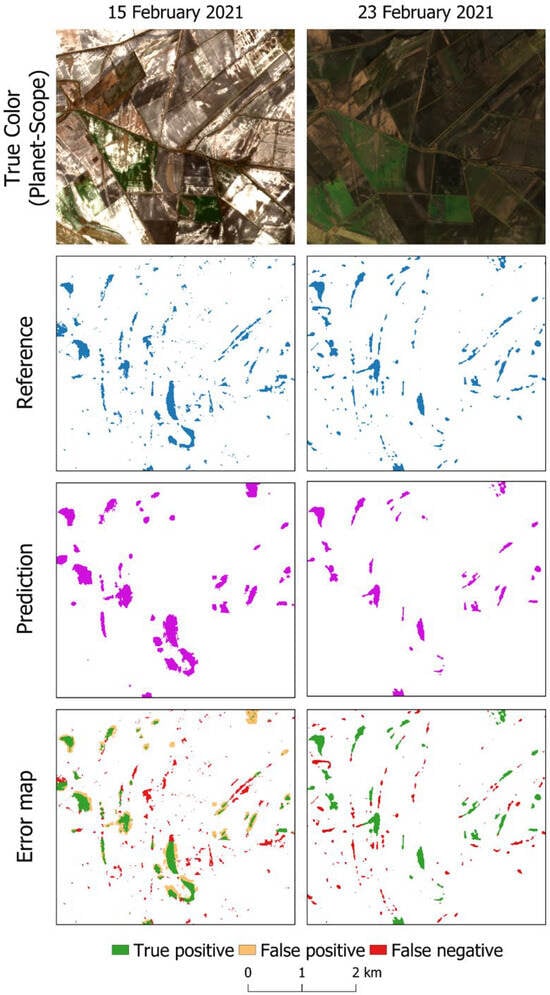
Figure 8.
Reference and prediction water map differences in a subset of the study area.

Table 4.
Accuracy assessment based on water coverage and prediction maps. Background colors indicate the type of pixels: green: true positive, orange: false positive and red: false negative.
Figure 8 shows the difference between the reference and predicted water coverage in a selected area for 15 and 23 February 2021. The figure shows the periodic accumulation of water in the runoff areas, which collected in the former riverbeds. The water maps retrieved from satellite imagery were used to validate the prediction maps. They were not used in the calculation of the predictions. The error map shows the difference between the maps generated using the two models. This is a useful tool for understanding how the prediction models behave, how well they perform, and where they might make mistakes. The reference data are the water maps, against which the prediction maps were compared. The true positive (green) pixels indicate where the prediction model correctly predicts the positive (water) class. False positive (orange) results are when the prediction model incorrectly predicted the positive (water) class. These mistakes are clearly visible in the map from 15 February 2021. They appear at the edges of the larger water patches, indicating shallow intermittent drying water surfaces and saturated soil. It is likely that the model is sensitive to moistened soils. False negative (red) values are cases where the model did not predict water, although it should have. These are mainly small or narrow water patches. It is possible that these patches were not part of the training set. The 23 February 2021 error map shows a better forecast. On this date, the overestimation at the edges of the larger inundations did not happen, but many small or narrow undetected patches remained. Overall, the two models identified IEW patches well, with F1 scores of 0.56 and 0.71.
4. Discussion
The DNN and XGBoost models with the same 24 input parameters gave almost identical results, but the training and prediction with XGBoost are much faster. Therefore, this model was used for prediction.
To the best of our knowledge, no study has yet been carried out to forecast IEW using data-driven, machine learning-based methods. The XGBoost model can predict water surfaces for one or two weeks ahead, which is similar to the soybean crop forecasting model of Li et al. [30] and the daily precipitation forecasting system developed by Dong et al. [54]. XGBoost has also been successfully used for flash flood forecasting [55], hazard mapping with similar input data (precipitation, topography, anthropogenic factors, and flash flood events). Another study by Abedi et al. [56] similarly investigated flash flood susceptibility within a watershed, where input parameters like land cover (LULC), hydrological soil groups, lithology, slope, and profile curvature were used in XGBoost, Random Forest, and boosted regression tree models, where the models investigated performed similarly well in flood susceptibility mapping. Our approach differs from earlier studies, because it predicts inundations that are very shallow and discontinuous in nature. The methodology is also new because it uses data from two weeks ahead of the prediction date.
The XGBoost model can predict a few days ahead but does not include knowledge of past IEW behavior. On the contrary, long short-term memory (LSTM) models do incorporate this knowledge [57]. The LSTM, which is widely recognized as one of the best deep learning algorithms for forecasting problems, has the ability to identify trends and provide better forecasts and would, therefore, be a suitable candidate for future research on the prediction of IEW inundations.
As shown in our earlier research [25], CNNs provide the best results for producing inundation maps. Another advantage of the CNN model compared to other methods is that it is robust and can be reused on data sets of other dates, which is required for time series studies. With other classification algorithms, such as index-based slicing, a different threshold must be set for each date, due to differences in spectral reflectance. In traditional machine learning (e.g., Support Vector Machine, Random Forest, and Maximum Likelihood), classes must be constructed repeatedly [58].
During the SHAP analysis, the relative importance of the first three factors in the model was found to be highest for the “surrounding water map” and the “one and two weeks before water maps”. Following these were evapotranspiration and anthropogenic factors (roads, cities, and canals). A sensitivity analysis could provide additional insight into the role of the input features, but the current research did not cover this aspect. This might be a direction for future development.
Despite the model performing well, there are still limiting factors related to the input data, preprocessing, and modeling. For the input data, the meteorological stations could be more densely distributed, leading to more accurate interpolated maps. The resolution of land cover, elevation, and soil maps could also be better. The meteorological data were interpolated with the relatively simple IDW algorithm. More sophisticated interpolation algorithms may provide better results, especially for larger areas. The water classification maps based on the CNN models are the basis of the predictions. The accuracy of these water maps has a high F1 score [50], but strongly depends on the available Sentinel-1 and/or Sentinel-2 data. Missing satellite data results in limitations in the accuracy of the water forecast. More satellite data reduces the need for temporal interpolation.
Since satellite images were not available for every day, due to cloud cover and limitations of the return time of the platform, missing data had to be corrected using the temporal interpolation algorithm. The stack of daily water maps provided an intermediate of this research—the frequency map. It was possible to investigate where temporarily inundated inland areas are located next to permanent water surfaces. The IEW frequency map can also be used to determine the area’s vulnerability, like the IEW hazard maps published in earlier research [4,14,15,16]. The advantage of our method compared to the common static vulnerability maps is that it can update the IEW frequency map dynamically when new data becomes available.
Daily predictions enable water resource managers to adjust water allocation schedules in alignment with potential IEW events, facilitating the removal of IEW from agricultural fields while preventing over-drainage. These forecasts support the implementation of strategic measures to manage and divert surplus water, thus safeguarding agricultural lands, irrigation infrastructure, and other water management systems. IEW events can occur during the summer season, necessitating daily forecasts to optimize irrigation schedules and maintain adequate soil moisture levels, without causing oversaturation in affected areas. Predictions are integral for the precise application of fertilizers and pesticides in agricultural production, as they can mitigate the risk of agrochemical runoff into water sources during IEW events. Daily forecasts enhance coordination among water resource authorities, farmers, and other relevant stakeholders, promoting a unified approach to IEW prevention and management. Proactive agricultural water management based on daily predictions can lead to cost savings, by reducing the expenses associated with emergency interventions, damage compensation, and losses in agricultural productivity.
Optical satellite imagery inherently suffers from disturbances due to clouds and cloud shadows. This problem is reduced in four ways in the proposed workflow. First, only images that had less than 80% cloud cover were considered in the analysis. Second, based on Sentinel-2’s SCL layer, clouds and cloud shadows were excluded. Third, Sentinel-1 active radar data, that is more or less weather independent was incorporated in the algorithms. Fourth, the excluded cloud and cloud shadow pixels were replaced by pixels with water/no water information from a maximum of 4 days before or ahead of the day with missing data. During the analysis, it became clear that the SCL layer does not always provide good cloud or cloud shadow masks, therefore other algorithms like F-mask will be considered to refine our model in the future.
The presented methodology is suitable for the short-term forecasting of IEW inundations and, thus, to mitigate economic damage. The inclusion of other factors like shallow geology, groundwater regime, land use changes, actual agricultural practices, irrigation, drainage system, amelioration, etc., may improve the forecasting. The incorporation of water maps based on complementing satellite data with higher temporal or spatial resolution (e.g., Landsat or PlanetScope) can reduce the need for interpolation of missing data or provide a higher spatial resolution, which improves the training data set for the forecast.
The methodology was implemented and tested on a study area on the Great Hungarian Plain but can be applied at other locations with similar geographic characteristics. The models are implemented using open-source libraries and the Sentinel satellite data are freely available for large parts of the world. The other data sets on land cover, meteorology, soil, elevation, and anthropogenic factors (distance from built environment, roads, cities, and canals) are available for most places in the world.
In our current research, we investigated a period of one year with moderate IEW. A longer time series based on Sentinel or other satellite data sets from drier and wetter years may make the prediction model more robust.
5. Conclusions
The aim of this study was to develop a methodology for the detection and prediction of IEW inundations. The phenomenon was investigated for one year (1 June 2020–31 May 2021) in a 1600 km2 study area. Prediction models were constructed using water maps from active and passive imagery from Sentinel satellites, with static and dynamic natural factors as input data. The most accurate results were obtained with an XGBoost model. The short-term predictions provide an opportunity for IEW prevention, damage mitigation, and, indirectly, the sustainable use of water in agriculture (i.e., supplemental irrigation and water retention), as well as water management (i.e., water storage, groundwater recharge, and wetland restoration). The Carpathian Basin region is susceptible to IEW due to its complex topography and climatic conditions. Enhanced IEW prediction in the region can yield notable economic and social outcomes. Economically, precise IEW forecasting can alleviate the adverse financial impacts of IEW inundations, by enabling the implementation of timely preventive measures. This diminishes damage to agricultural fields, infrastructure, and real estate. Accurate prediction can result in reduced insurance and damage mitigation expenses, as risks can be lowered according to the region’s specific attributes, thereby minimizing potential harm. Consequently, predictive insights allow businesses to better anticipate IEW, enabling punctual agricultural operations and operational continuity, which, in turn, minimizes economic losses. A decrease in the risk of unexpected damage in agricultural areas, due to predictions, can enhance the region’s appeal to investors, by ensuring production stability. From a social standpoint, it is essential to advocate for the interpretation of IEW predictions within communities through educational forums and training sessions. This fosters agricultural communities equipped with knowledge that enhances their resilience to the adverse effects of IEW and facilitates the adoption of coordinated strategies. Within a well-informed and prepared agricultural environment, infrastructure enhancements such as upgrading drainage systems become feasible, thereby providing opportunities for the adoption of more sophisticated agricultural technologies, compared to prior capabilities. In the future, the presented methodology can be extended to a regional or national level.
Author Contributions
Conceptualization, B.K., Z.T. and B.V.L.; Methodology, B.K. and B.V.L.; Software, B.V.L.; Validation, B.K. and Z.T.; Formal analysis, B.V.L.; Investigation, B.K., Z.T. and B.V.L.; Resources, B.K. and B.V.L.; Data curation, B.K.; Writing—original draft, B.K., Z.T., N.T., C.B. and B.V.L.; Writing—review and editing, B.K., Z.T., N.T. and B.V.L.; Visualization, B.K. and Z.T.; Supervision, B.V.L.; Project administration, B.V.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the project RRF-2.3.1-21-2022-00008, “National Laboratory for Water Science and Water Safety”; the “Agricultural water management (irrigation development, excess water management, land use rationalization)” research program at the Research Center for Irrigation and Water Management of the Institute of Environmental Sciences of the Hungarian University of Agricultural and Life Sciences; and “The ÚNKP-23-3 New National Excellence Program of the Ministry for Culture and Innovation from the source of the National Research, Development and Innovation Fund.
Data Availability Statement
Sentinel-1 and -2 remote sensing data are available in publicly accessible repositories. Other data presented in this study are available on request from the corresponding author.
Conflicts of Interest
Author Boudewijn van Leeuwen was employed by the company Bay Zoltán Nonprofit Ltd. for Applied Research. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflicts of interest.
References
- Dunka, S.; Fejér, L.; Vágás, I. A Verítékes Honfoglalás: A Tisza-Szabályozás Története [The Sweaty Conquest: The History of the Tisza Regulation]; MKVM: Budapest, Hungary, 1996; p. 12. (In Hungarian) [Google Scholar]
- Pálfai, I. A belvíz definíciói [Definitions of inland excess water]. Vízügyi Közlemények 2001, 83, 376–392. (In Hungarian) [Google Scholar]
- Hungarian Central Statistical Office. Available online: https://www.ksh.hu/stadat_files/mez/hu/mez0008.html (accessed on 3 March 2024).
- Pálfai, I. Az Alföld belvíz-veszélyeztetettségi térképe [Excess water risk and dought sensitivity of the Great Plain]. Vízügyi közlemények 1994, 76, 278–290. (In Hungarian) [Google Scholar]
- Bozán, C.; Takács, K.; Körösparti, J.; Laborczi, A.; Túri, N.; Pásztor, L. Integrated spatial assessment of inland excess water hazard on the Great Hungarian Plain. Land Degrad. Dev. 2018, 29, 4373–4386. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023; pp. 35–115. [Google Scholar] [CrossRef]
- Mezősi, G.; Meyer, B.C.; Loibl, W.; Aubrecht, C.; Csorba, P.; Bata, T. Assessment of regional climate change impacts on Hungarian landscapes. Reg. Environ. Change 2013, 13, 797–811. [Google Scholar] [CrossRef]
- Bartholy, J.; Pongrácz, R.; Pieczka, I.; Torma, C.S. Dynamical downscaling of projected 21st century climate for the Carpathian Basin. In Climate Change—Research and Technology for Adaptation and Mitigation; Blanco, J.A., Kheradmand, H., Eds.; Intech: Rijeka, Croatia, 2011; pp. 3–22. ISBN 978-953-307-621-8. [Google Scholar] [CrossRef]
- Kuti, L.; Kerék, B.; Vatai, J. Problem and prognosis of excess water inundation based on agrogeological factors. Carpth. J. Earth Environ. Sci. 2006, 1, 5–18. [Google Scholar]
- Jong, P.; Hobma, F. Rights and responsibilities in Dutch land-use planning aimed at flood protection and prevention of waterlogging. In Proceedings of the 6th International Conference of the International Academic Association on Planning, Law and Property Rights, Belfast, UK, 7–10 February 2012. [Google Scholar]
- Bíró, T. Amikor sok víz van a területen–Belvíz [When there is a lot of water in the area—Inland excess water]. Magy. Tudomány 2017, 178, 1216–1227. (In Hungarian) [Google Scholar] [CrossRef]
- Thyll, S.; Bíró, T. A belvíz-veszélyeztetettség térképezése. Hidrológiai Közlemények 1999, 81, 709–717. [Google Scholar]
- Kozma, Z.; Jolánkai, Z.; Kardos, M.K.; Muzelák, B.; Koncsos, L. Adaptive water management-land use practice for improving ecosystem services—A Hungarian Modelling Case Study. Period. Polytech. Civ. Eng. 2022, 66, 256–268. [Google Scholar] [CrossRef]
- Pálfai, I. Belvizek és aszályok Magyarországon: Hidrológiai tanulmányok [Excess water and drought in Hungary: Hydrological studies]; Közlekedési Dokumentációs Kft: Budapest, Hungary, 2004; 99p, ISBN 963-552-382-3. (In Hungarian) [Google Scholar]
- Pásztor, L.; Körösparti, J.; Bozán, C.; Laborczi, A.; Takács, K. Spatial risk assessment of hydrological extremities: Inland excess water hazard, Szabolcs-Szatmár-Bereg County, Hungary. J. Maps 2015, 11, 636–644. [Google Scholar] [CrossRef]
- Laborczi, A.; Bozan, C.; Körösparti, J.; Szatmari, G.; Kajari, B.; Turi, N.; Kerezsi, G.; Pasztor, L. Application of hybrid prediction methods in spatial assessment of inland excess water hazard. ISPRS Int. J. Geo-Inf. 2020, 9, 268. [Google Scholar] [CrossRef]
- Tobak, Z.; Szatmári, J.; Van Leeuwen, B. Small Format Aerial Photography—Remote Sensing Data Acquisition for Environmental Analysis. J. Environ. Geogr. 2008, 3, 21–26. [Google Scholar] [CrossRef]
- Balázs, B. Belvizes területek felmérése geoinformatikai módszerekkel [Survey of Inland Excess Water using geoinformatics methods]. In Geoinformatika és Domborzatmodellezés: A HunDEM 2009 és a GeoInfo 2009 Konferencia és Kerekasztal Válogatott Tanulmányai; Hegedűs, A., Ed.; Miskolci Egyetem: Miskolc, Hungary, 2010; pp. 1–10. (In Hungarian) [Google Scholar]
- Bangira, T.; Iannini, L.; Menenti, M.; Van Niekerk, A.; Vekerdy, Z. Flood extent mapping in the Caprivi floodplain using sentinel-1 time series. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5667–5683. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, S.J.; Henderson, D.; Howard, E.R.; Hubbard, W.; Jackel, D.L. Handwritten Digit Recognition with a Back-Propagation Network. In Advances in Neural Information Processing Systems 2 (NIPS 1989); Touretzky, D., Ed.; Morgan Kaufmann: Denver, CO, USA, 1990; Volume 2, pp. 396–403. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Giulia, C.; De Fioravante, P.; Dichicco, P.; Congedo, L.; Marchetti, M.; Munafò, M. Land Cover Mapping with Convolutional Neural Networks Using Sentinel-2 Images: Case Study of Rome. Land 2023, 12, 879. [Google Scholar] [CrossRef]
- Yichen, L.; James, T.; Schillaci, C.; Lipani, A. Snow Detection in Alpine Regions with Convolutional Neural Networks: Discriminating Snow from Cold Clouds and Water Body. GIScience Remote Sens. 2022, 59, 1321–1343. [Google Scholar] [CrossRef]
- Simón Sánchez, A.-M.; González-Piqueras, J.; de la Ossa, L.; Calera, A. Convolutional Neural Networks for Agricultural Land Use Classification from Sentinel-2 Image Time Series. Remote Sens. 2022, 14, 5373. [Google Scholar] [CrossRef]
- Kajári, B.; Bozán, C.; Van Leeuwen, B. Monitoring of Inland Excess Water Inundations Using Machine Learning Algorithms. Land 2023, 12, 36. [Google Scholar] [CrossRef]
- Jiang, W.; He, G.; Long, T.; Ni, Y.; Liu, H.; Peng, Y.; Lv, K.; Wang, G. Multilayer Perceptron Neural Network for Surface Water Extraction in Landsat 8 OLI Satellite Images. Remote Sens. 2018, 10, 755. [Google Scholar] [CrossRef]
- Devi, M.S.; Chib, S. Classification of Satellite Images Using Perceptron Neural Network. Int. J. Comput. Intell. Res. 2019, 15, 1–10. [Google Scholar]
- Bravo-López, E.; Fernández Del Castillo, T.; Sellers, C.; Delgado-García, J. Landslide Susceptibility Mapping of Landslides with Artificial Neural Networks: Multi-Approach Analysis of Backpropagation Algorithm Applying the Neuralnet Package in Cuenca, Ecuador. Remote Sens. 2022, 14, 3495. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Li, Y.; Zeng, H.; Zhang, M.; Wu, B.; Zhao, Y.; Yao, X.; Cheng, T.; Qin, X.; Wu, F. A county-level soybean yield prediction framework coupled with XGBoost and multidimensional feature engineering. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103269. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y.; Yuan, H.; Zhou, S.; Wang, Y.; Ikram, R.M.A.; Li, J. An XGBoost-SHAP approach to quantifying morphological impact on urban flooding susceptibility. Ecol. Indic. 2023, 156, 111137. [Google Scholar] [CrossRef]
- Lundberg, M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Conners, R.W.; Trivedi, M.M.; Harlow, C.A. Segmentation of a high-resolution urban scene using texture operators. Comput. Vis. Graph. Image Process. 1984, 25, 273–310. [Google Scholar] [CrossRef]
- Allagwail, S.; Gedik, O.S.; Rahebi, J. Face Recognition with Symmetrical Face Training Samples Based on Local Binary Patterns and the Gabor Filter. Symmetry 2019, 11, 157. [Google Scholar] [CrossRef]
- Csorba, P. Magyarország Kistájai; Meridián Táj-és Környezetföldrajzi Alapítvány: Debrecen, Hungary, 2021; ISBN 978-963-89712-4-1. [Google Scholar]
- Bihari, Z.; Babolcsai, G.; Bartholy, J.; Ferenczi, Z.; Gerhátné Kerényi, J.; Haszpra, L.; Homokiné Ujváry, K.; Kovács, T.; Lakatos, M.; Németh, Á.; et al. Éghajlat. In Magyarország Nemzeti Atlasza: Természeti Környezet; Kocsis, K., Ed.; Magyar Tudományos Akadémia, Csillagászati és Földtudományi Kutatóközpont, Földrajztudományi Intézet: Budapest, Hungary, 2018; pp. 58–69. ISBN 978-963-9545-56-4. [Google Scholar]
- Vári, Á.; Tanács, E.; Tormáné Kovács, E.; Kalóczkai, Á.; Arany, I.; Czúcz, B.; Bereczki, K.; Belényesi, M.; Csákvári, E.; Kiss, M.; et al. National Ecosystem Services Assessment in Hungary: Framework, Process and Conceptual Questions. Sustainability 2022, 14, 12847. [Google Scholar] [CrossRef]
- Tóth, B.; Weynants, M.; Pásztor, L.; Hengl, T. 3D soil hydraulic database of Europe at 250 m resolution. Hydrol. Process. 2017, 31, 2662–2666. [Google Scholar] [CrossRef]
- Lechner Knowledge Center. Available online: https://lechnerkozpont.hu/oldal/domborzatmodell (accessed on 3 March 2024).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- van Leeuwen, B.; Tobak, Z.; Kovács, F. Sentinel-1 and -2 Based near Real Time Inland Excess Water Mapping for Optimized Water Management. Sustainability 2020, 12, 2854. [Google Scholar] [CrossRef]
- Szigarski, C.; Jagdhuber, T.; Baur, M.; Thiel, C.; Parrens, M.; Wigneron, J.-P.; Piles, M.; Entekhabi, D. Analysis of the Radar Vegetation Index and Potential Improvements. Remote Sens. 2018, 10, 1776. [Google Scholar] [CrossRef]
- Nasirzadehdizaji, R.; Balik Sanli, F.; Abdikan, S.; Cakir, Z.; Sekertekin, A.; Ustuner, M. Sensitivity Analysis of Multi-Temporal Sentinel-1 SAR Parameters to Crop Height and Canopy Coverage. Appl. Sci. 2019, 9, 655. [Google Scholar] [CrossRef]
- Kupidura, P. The Comparison of Different Methods of Texture Analysis for Their Efficacy for Land Use Classification in Satellite Imagery. Remote Sens. 2019, 11, 1233. [Google Scholar] [CrossRef]
- Mullissa, A.; Vollrath, A.; Odongo-Braun, C.; Slagter, B.; Balling, J.; Gou, Y.; Gorelick, N.; Reiche, J. Sentinel-1 SAR Backscatter Analysis Ready Data Preparation in Google Earth Engine. Remote Sens. 2021, 13, 1954. [Google Scholar] [CrossRef]
- Vremec, M.; Collenteur, R. PyEt—A Python package to estimate potential and reference evapotranspiration. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021; p. EGU21-15008. [Google Scholar] [CrossRef]
- Ponce, V.M. Engineering Hydrology: Principles and Practices; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; Volume 640, Available online: http://ponce.sdsu.edu/330textbook_hydrology_chapters.html (accessed on 29 June 2022).
- Kajári, B.; Van Leeuwen, B. Sentinel-1 és Sentinel-2 felvételek belvízveszélyeztetettségi idősoros elemzése konvolúciós neurális hálózatokkal [Sentinel-1 and Sentinel-2 based time series analysis of inland excess water hazard using convolutional neural networks]. Geodézia És Kartográfia 2024. Available online: https://edit.elte.hu/xmlui/static/pdf-viewer-master/external/pdfjs-2.1.266-dist/web/viewer.html?file=https://edit.elte.hu/xmlui/bitstream/handle/10831/107835/GK.76.2024.1.2-DOI.pdf?sequence=1&isAllowed=y (accessed on 25 April 2024). [CrossRef]
- Kajári, B.; Bozán, C.; van Leeuwen, B. Belvízelöntés Detektálása Sentinel-1-es Műhold Felvételeken GLCM Textúrák és Konvolúciós Neurális Hálózat Segítségével [Inland Excess Water Detection Based on Sentinel-1 Satellite Images Using GLCM Textures and Convolutional Neural Network]; Abriha-Molnár, V.É., Ed.; Az Elmélet és Gyakorlat Találkozása a Térinformatikában XIV: Theory Meets Practice in GIS Debrecen; Debreceni Egyetemi Kiadó: Debrecen, Hungary, 2023; pp. 93–101. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://github.com/fchollet/keras (accessed on 1 December 2023).
- O’Brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. Int. J. Methodol. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Dong, J.; Zeng, W.; Wu, L.; Huang, J.; Gaiser, T.; Srivastava, A.K. Enhancing short-term forecasting of daily precipitation using numerical weather prediction bias correcting with XGBoost in different regions of China. Eng. Appl. Artif. Intell. 2023, 117, 105579. [Google Scholar] [CrossRef]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-based method for flash flood risk assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Abedi, R.; Costache, R.; Shafizadeh-Moghadam, H.; Pham, Q.B. Flash-flood susceptibility mapping based on XGBoost, random forest and boosted regression trees. Geocarto Int. 2021, 37, 5479–5496. [Google Scholar] [CrossRef]
- van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Abdi, A.M. Land cover and land use classification performance of machine learning algorithms in a boreal landscape using Sentinel-2 data. GIScience Remote. Sens. 2019, 57, 1–20. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).