Figure 1.
A roadside meteorological station in Qatar that measures temperature, humidity, visibility, precipitation, wind speed, and wind direction. Solar panels partly obstruct rainfall measurements from the north, and the pole creates turbulence around the gauge.
Figure 1.
A roadside meteorological station in Qatar that measures temperature, humidity, visibility, precipitation, wind speed, and wind direction. Solar panels partly obstruct rainfall measurements from the north, and the pole creates turbulence around the gauge.
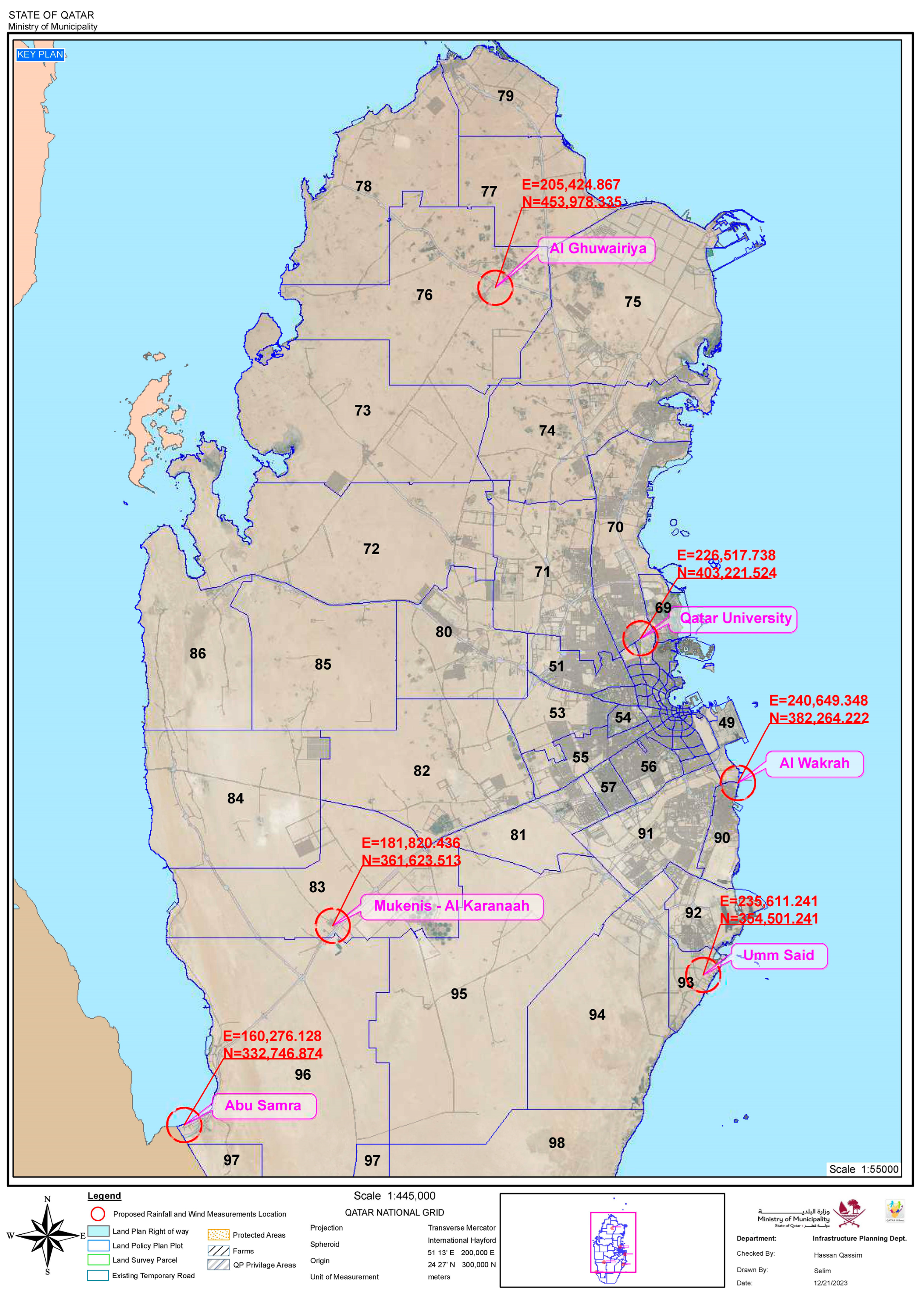
Figure 2.
Location of stations with long-duration wind speed, wind direction, and rainfall intensity measurements fulfilling the requirements of 14 years of measurements. The numbers indicate zones used by the Ministry in their planning.
Figure 2.
Location of stations with long-duration wind speed, wind direction, and rainfall intensity measurements fulfilling the requirements of 14 years of measurements. The numbers indicate zones used by the Ministry in their planning.
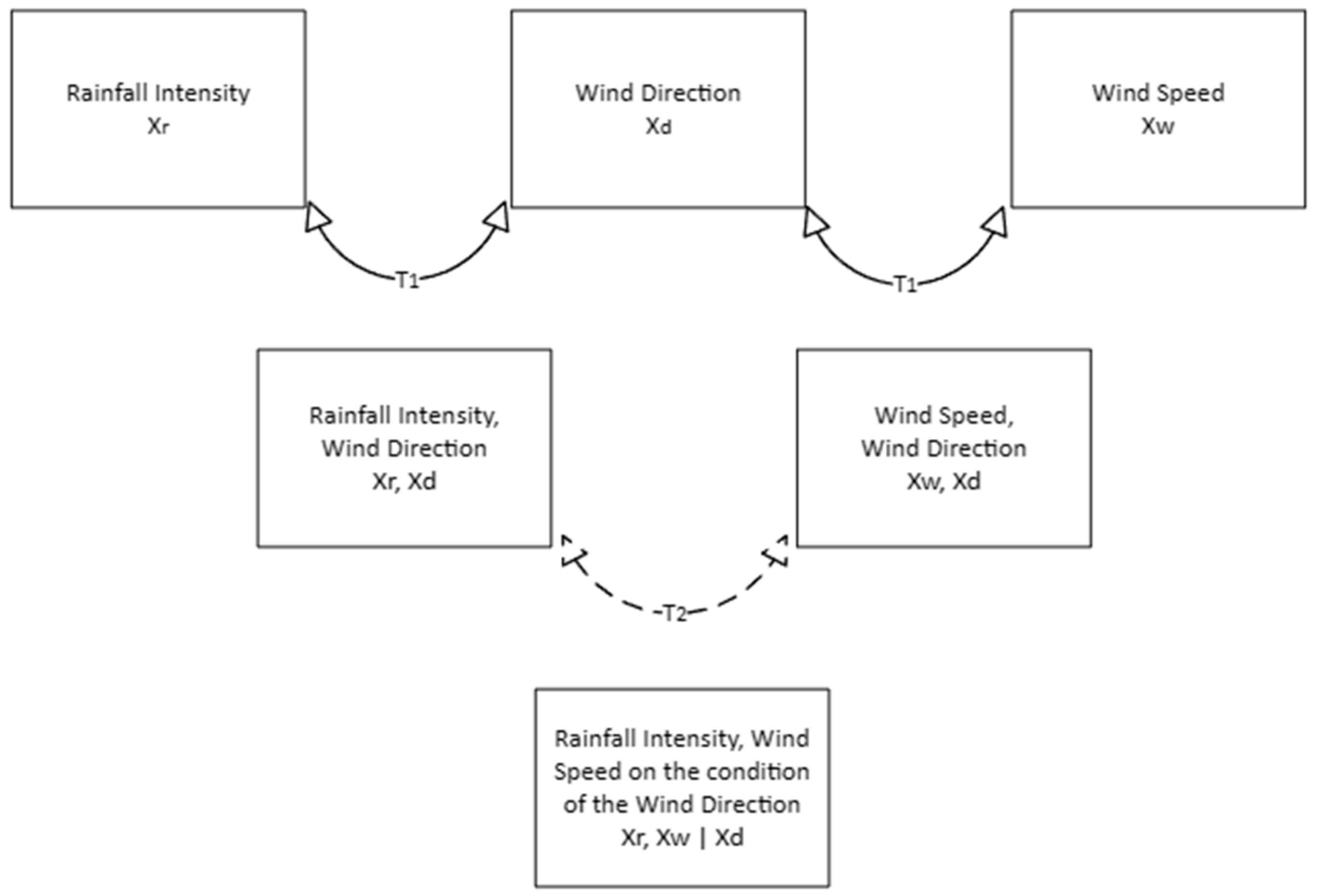
Figure 3.
The D-vine dependence structure is applied to construct the multivariate distribution between rainfall intensity, wind speed, and wind direction. T1 symbolises the first tree, and T2 the second.
Figure 3.
The D-vine dependence structure is applied to construct the multivariate distribution between rainfall intensity, wind speed, and wind direction. T1 symbolises the first tree, and T2 the second.
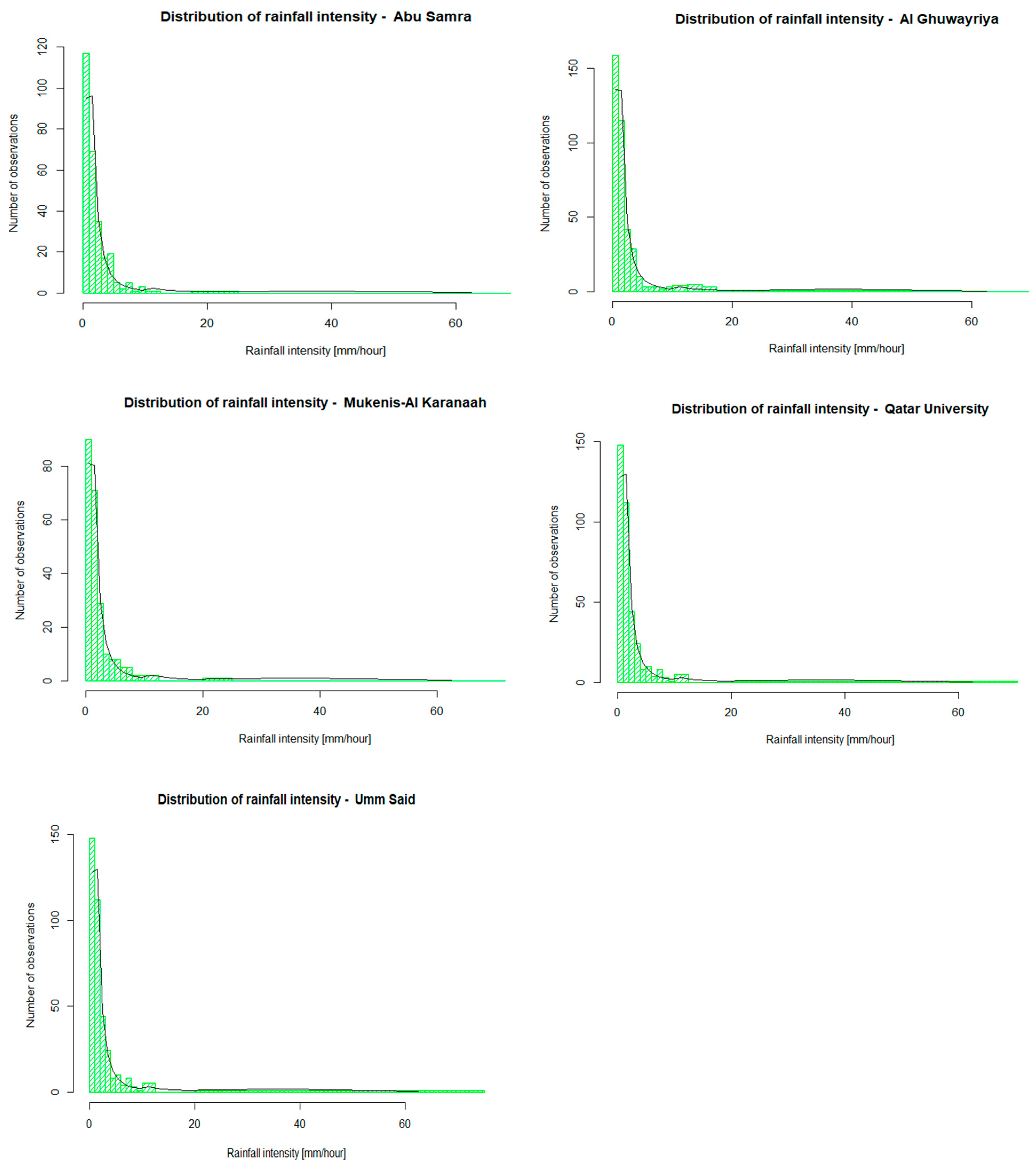
Figure 4.
Marginal distribution of the rainfall intensity for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left). The green curve indicates the observed values as a histogram, and the black line is the theoretically derived marginal distribution.
Figure 4.
Marginal distribution of the rainfall intensity for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left). The green curve indicates the observed values as a histogram, and the black line is the theoretically derived marginal distribution.
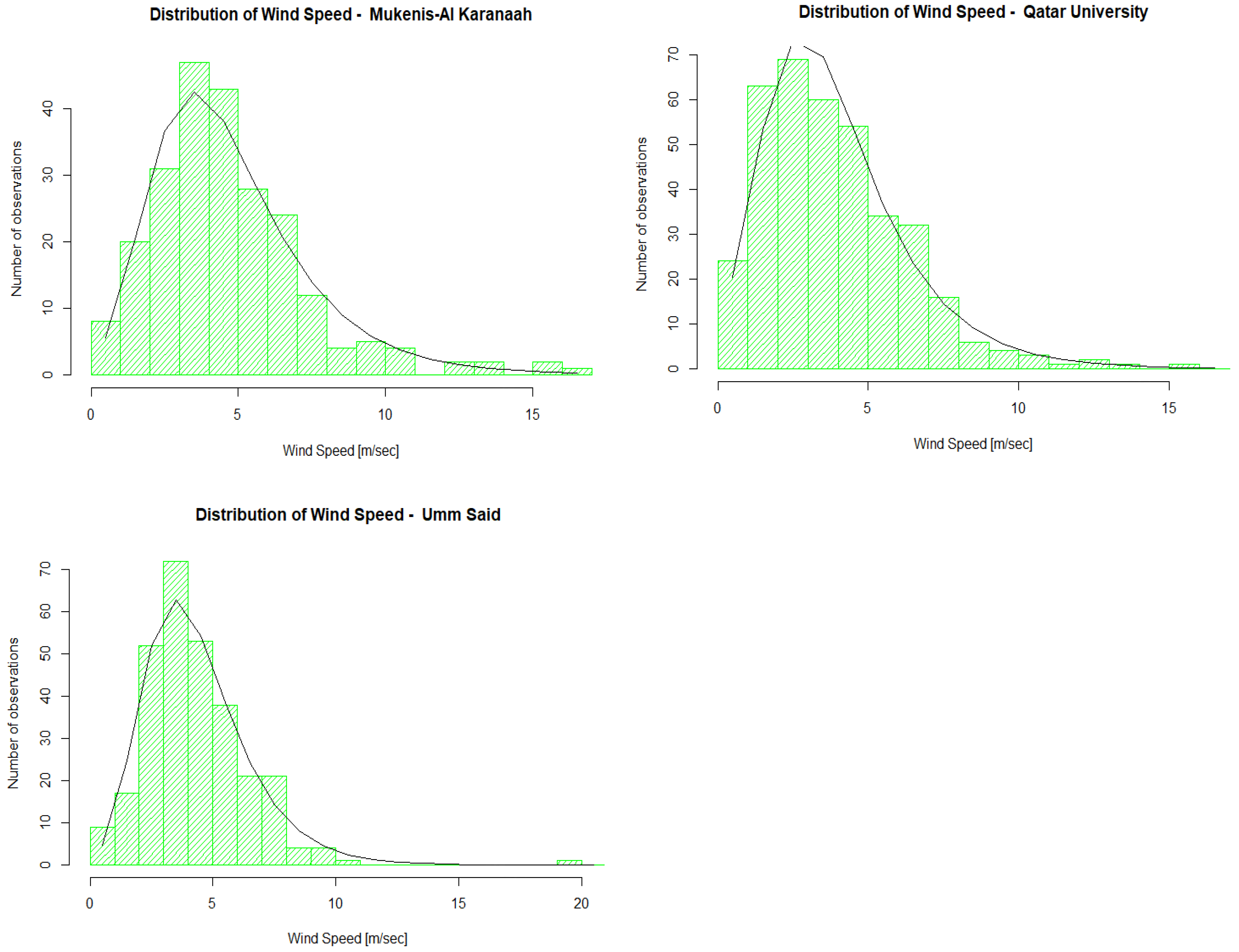
Figure 5.
Marginal distribution of the wind speed for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left). The green curve indicates the observed values as a histogram, and the black line is the theoretically derived marginal distribution.
Figure 5.
Marginal distribution of the wind speed for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left). The green curve indicates the observed values as a histogram, and the black line is the theoretically derived marginal distribution.
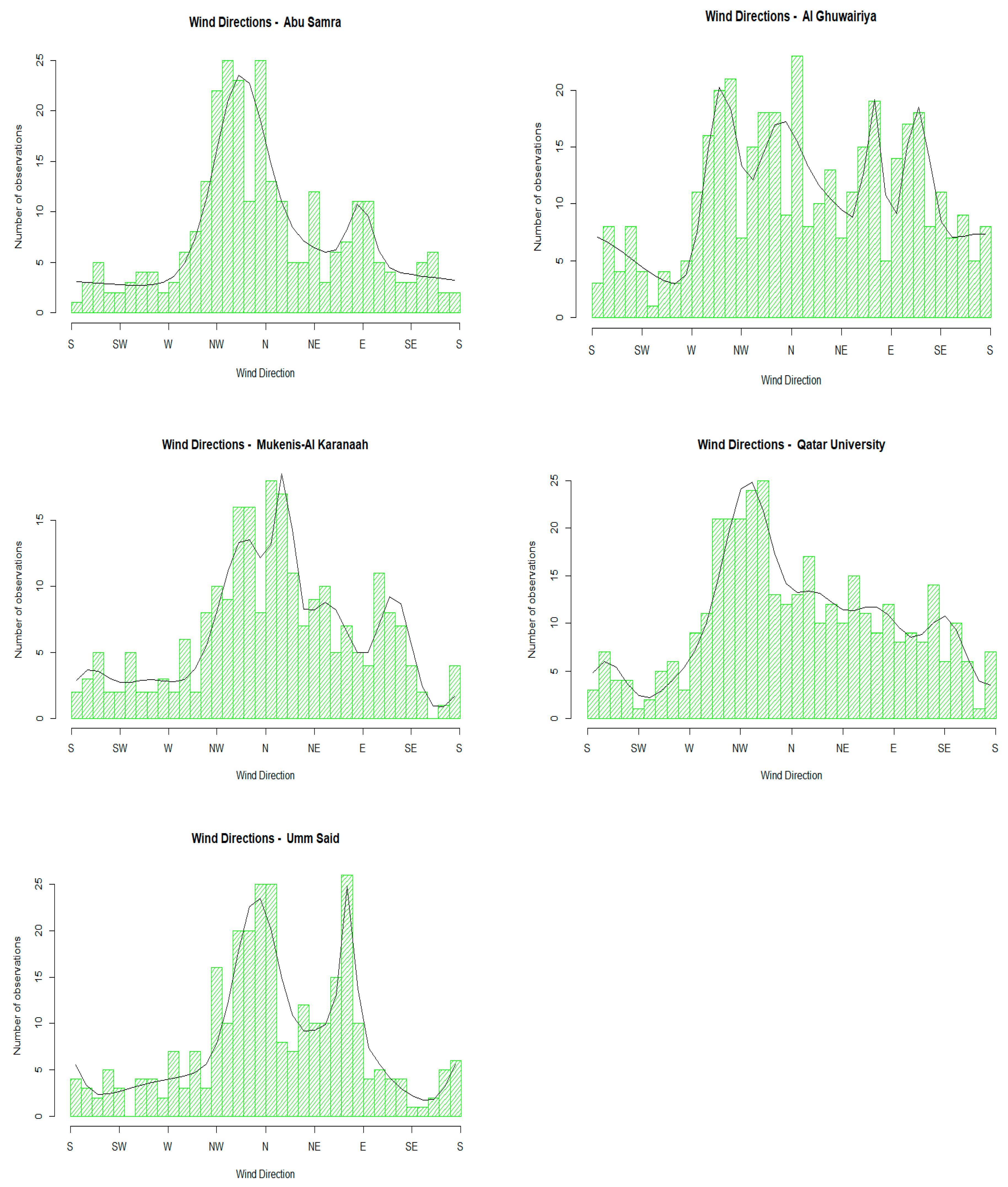
Figure 6.
Marginal distribution of the wind direction for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left). The green curve indicates the observed values as a histogram, and the black line is the theoretically derived marginal distribution.
Figure 6.
Marginal distribution of the wind direction for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left). The green curve indicates the observed values as a histogram, and the black line is the theoretically derived marginal distribution.
Figure 7.
Bivariate density function of the wind speed and wind direction based on Bernstein Copula functions shown as 3D-plots for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left).
Figure 7.
Bivariate density function of the wind speed and wind direction based on Bernstein Copula functions shown as 3D-plots for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left).
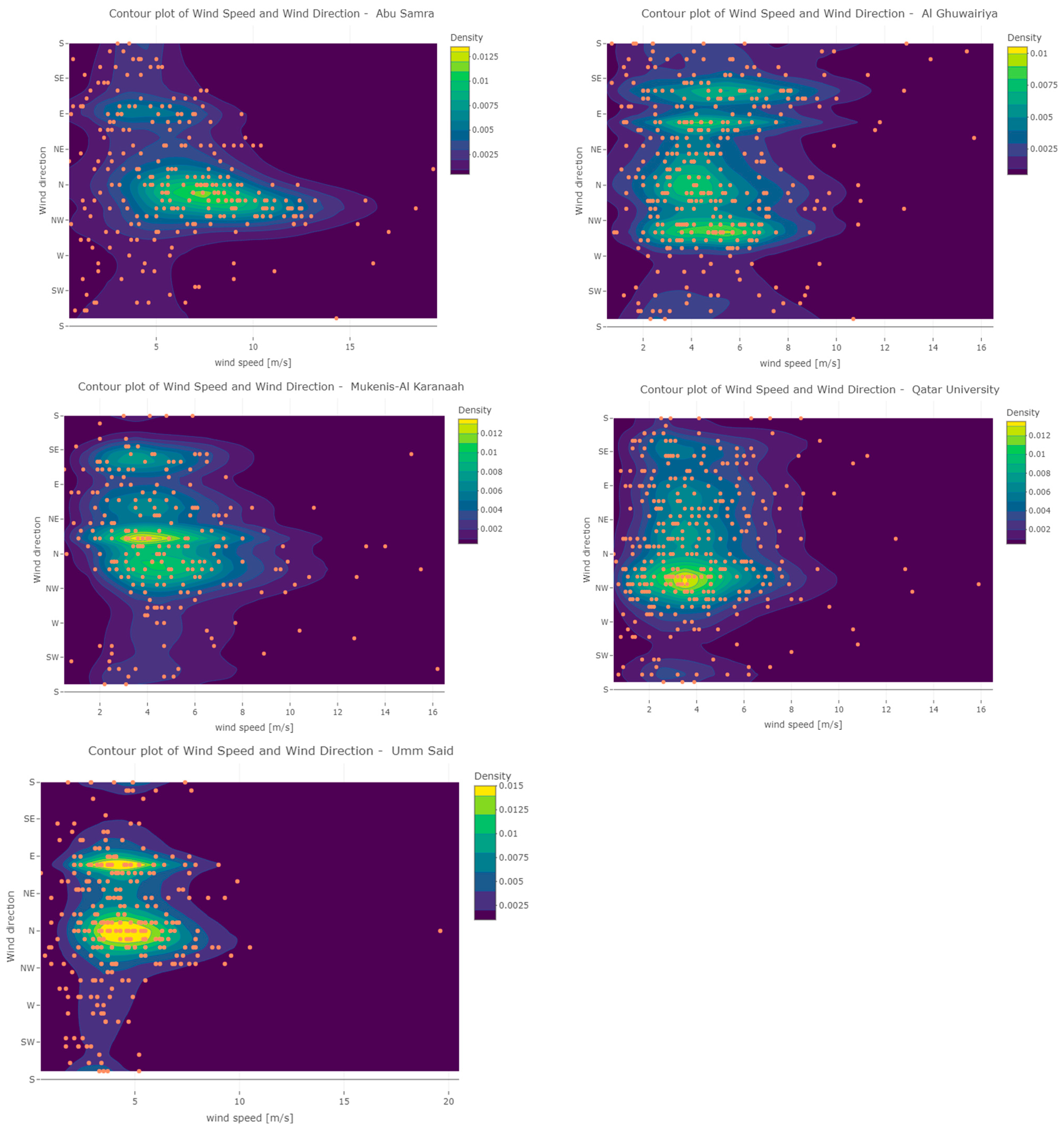
Figure 8.
Bivariate density function based on Bernstein Copula functions of the wind speed and wind direction, shown as contour plots for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left). The orange points are individual observations of wind speed and wind direction. The orange dots are the observations.
Figure 8.
Bivariate density function based on Bernstein Copula functions of the wind speed and wind direction, shown as contour plots for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left). The orange points are individual observations of wind speed and wind direction. The orange dots are the observations.
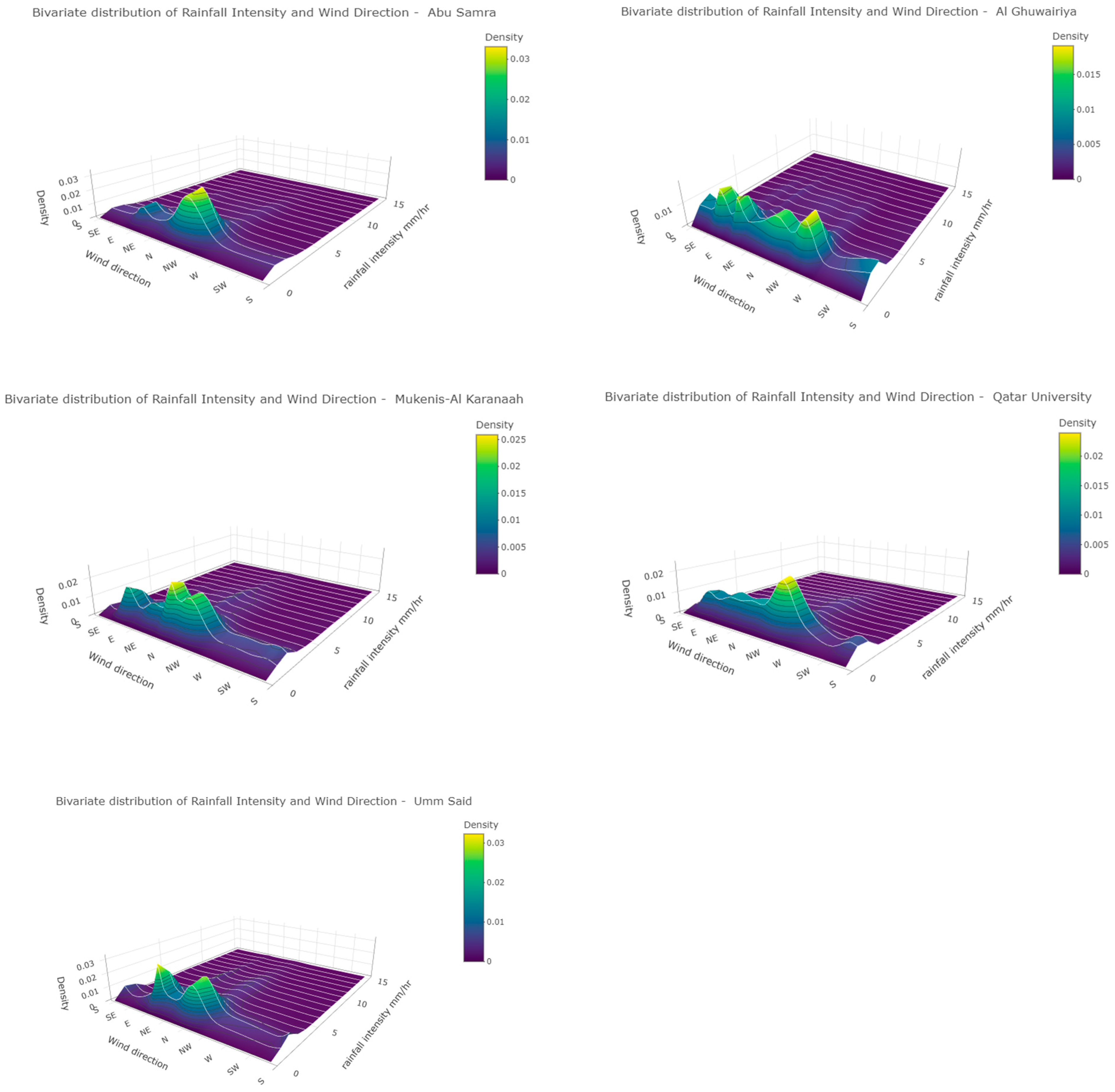
Figure 9.
Bivariate density functions of the rainfall intensity and wind direction based on Bernstein Copula functions shown as 3D plots for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left).
Figure 9.
Bivariate density functions of the rainfall intensity and wind direction based on Bernstein Copula functions shown as 3D plots for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left).
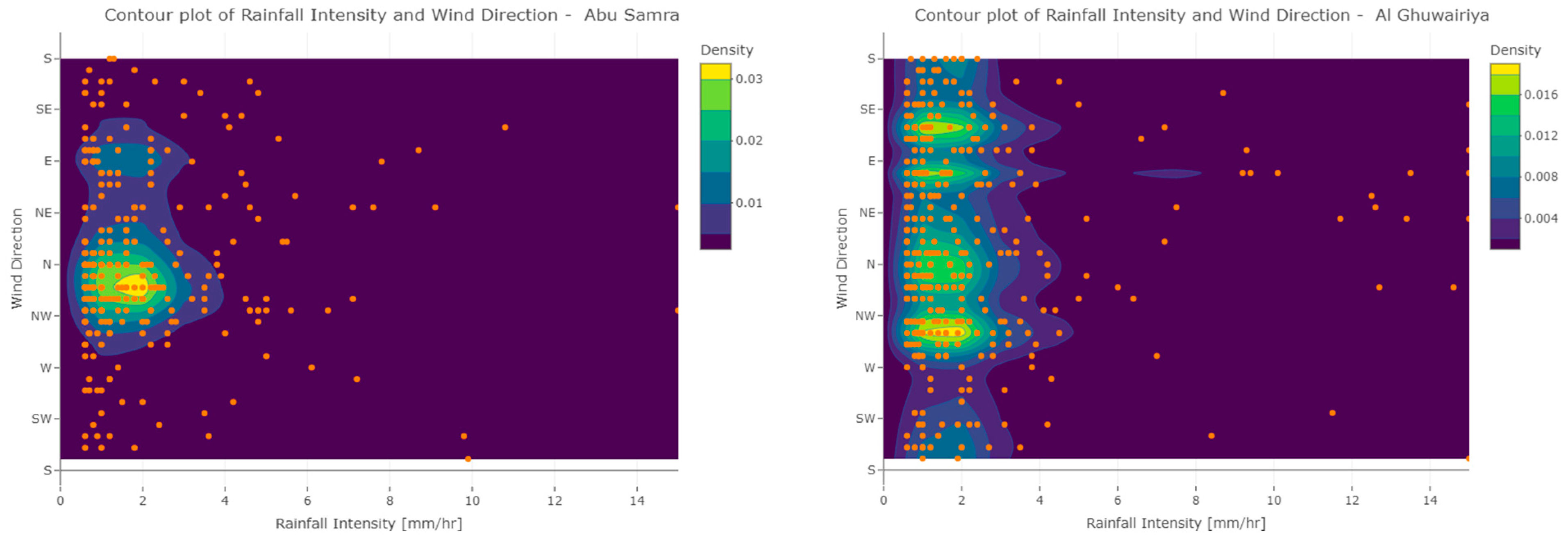
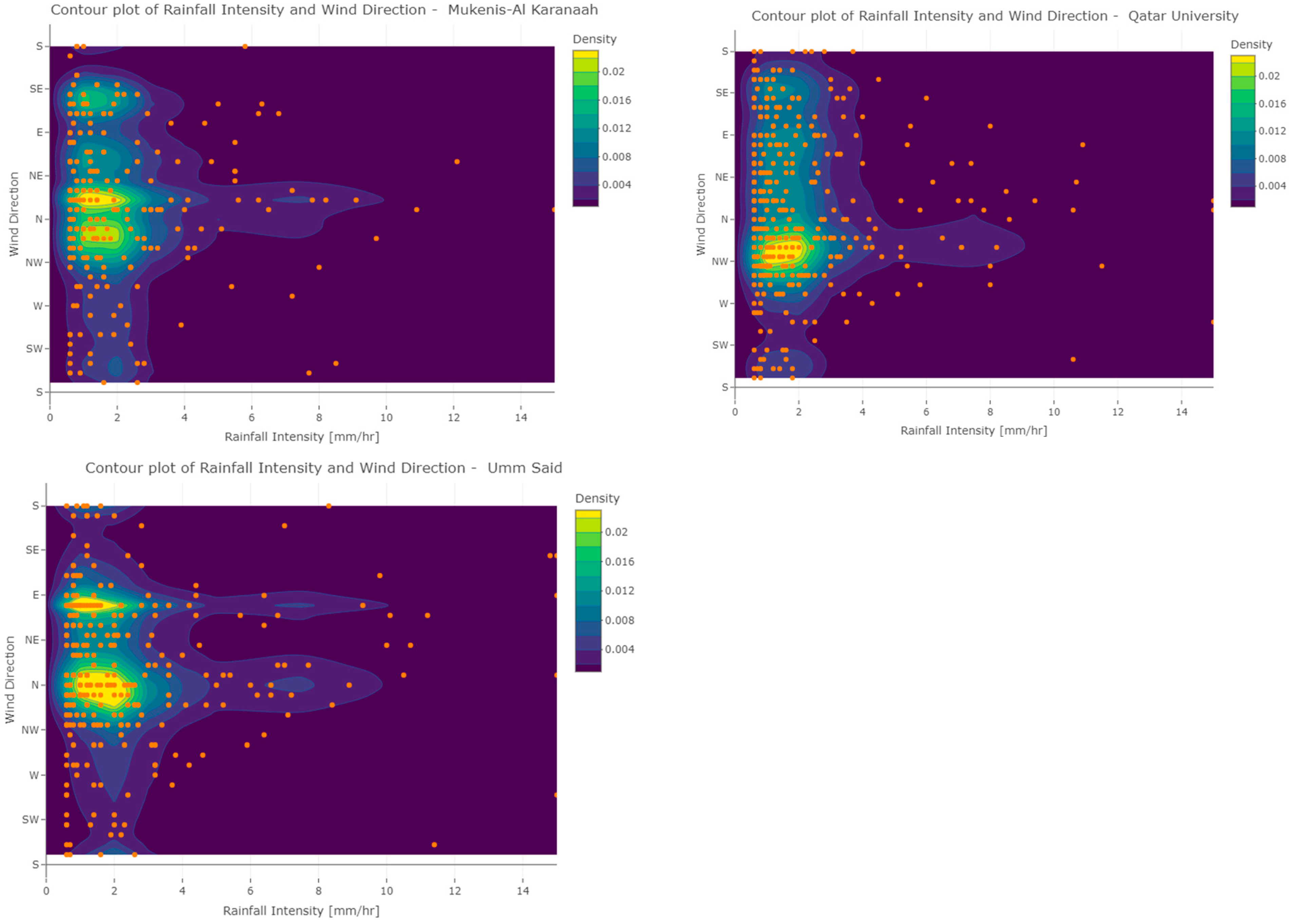
Figure 10.
Bivariate density function based on Bernstein Copula functions of the rainfall intensity and wind direction, shown as contour plots for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left). The orange points are individual observations of wind speed and wind direction. The orange dots are observations.
Figure 10.
Bivariate density function based on Bernstein Copula functions of the rainfall intensity and wind direction, shown as contour plots for the five stations: Abu Samra (upper left), Al Ghuwayriya (upper right), Mukenis-Al Karanaah (mid left), Qatar University (mid right), and Umm Said (bottom left). The orange points are individual observations of wind speed and wind direction. The orange dots are observations.
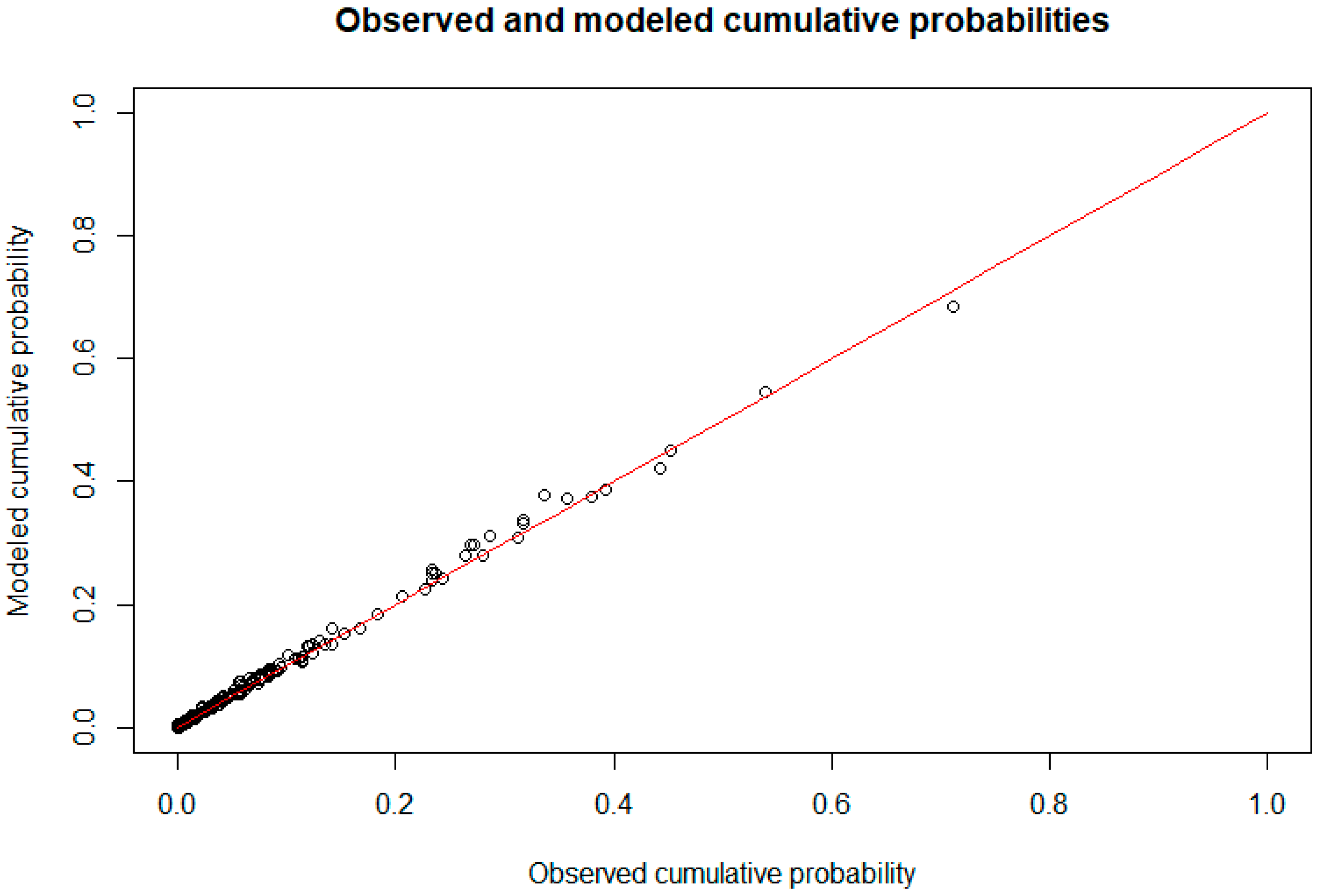
Figure 11.
Plot of the modeled and observed cumulative probabilities (circles) of ranked normalized observations of the trivariate distribution between rainfall intensity, wind speed, and wind direction. The line indicates where observed values are equal modeled values.
Figure 11.
Plot of the modeled and observed cumulative probabilities (circles) of ranked normalized observations of the trivariate distribution between rainfall intensity, wind speed, and wind direction. The line indicates where observed values are equal modeled values.
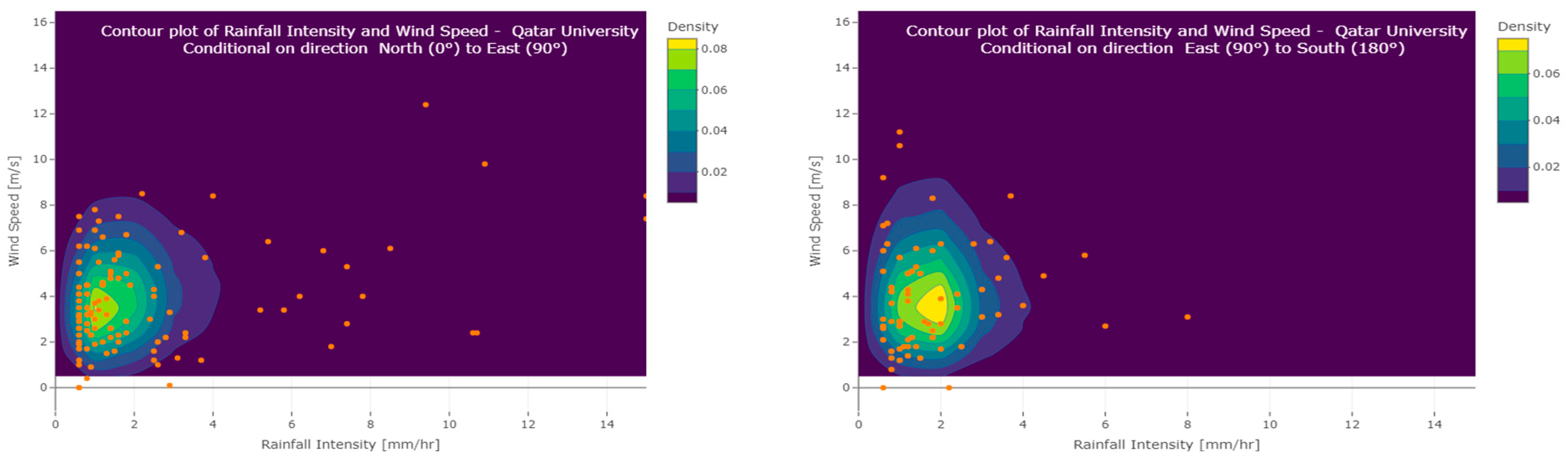
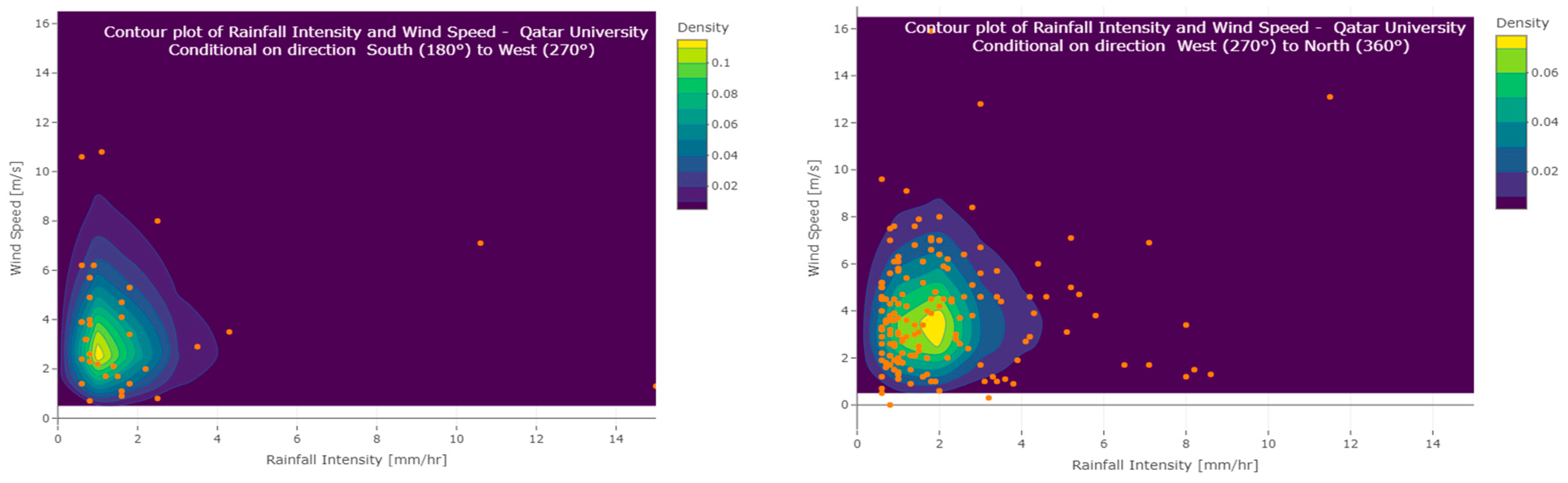
Figure 12.
Contour plot of the rainfall intensity and wind speed under the condition of a wind direction (upper left) from north (0 degrees) to east (90 degrees), (upper right) from east (90 degrees) to south (180 degrees), (lower left) from south (180 degrees) to west (270 degrees), and (lower right) from west (270 degrees) to north (360 degrees). The orange dots are observations.
Figure 12.
Contour plot of the rainfall intensity and wind speed under the condition of a wind direction (upper left) from north (0 degrees) to east (90 degrees), (upper right) from east (90 degrees) to south (180 degrees), (lower left) from south (180 degrees) to west (270 degrees), and (lower right) from west (270 degrees) to north (360 degrees). The orange dots are observations.
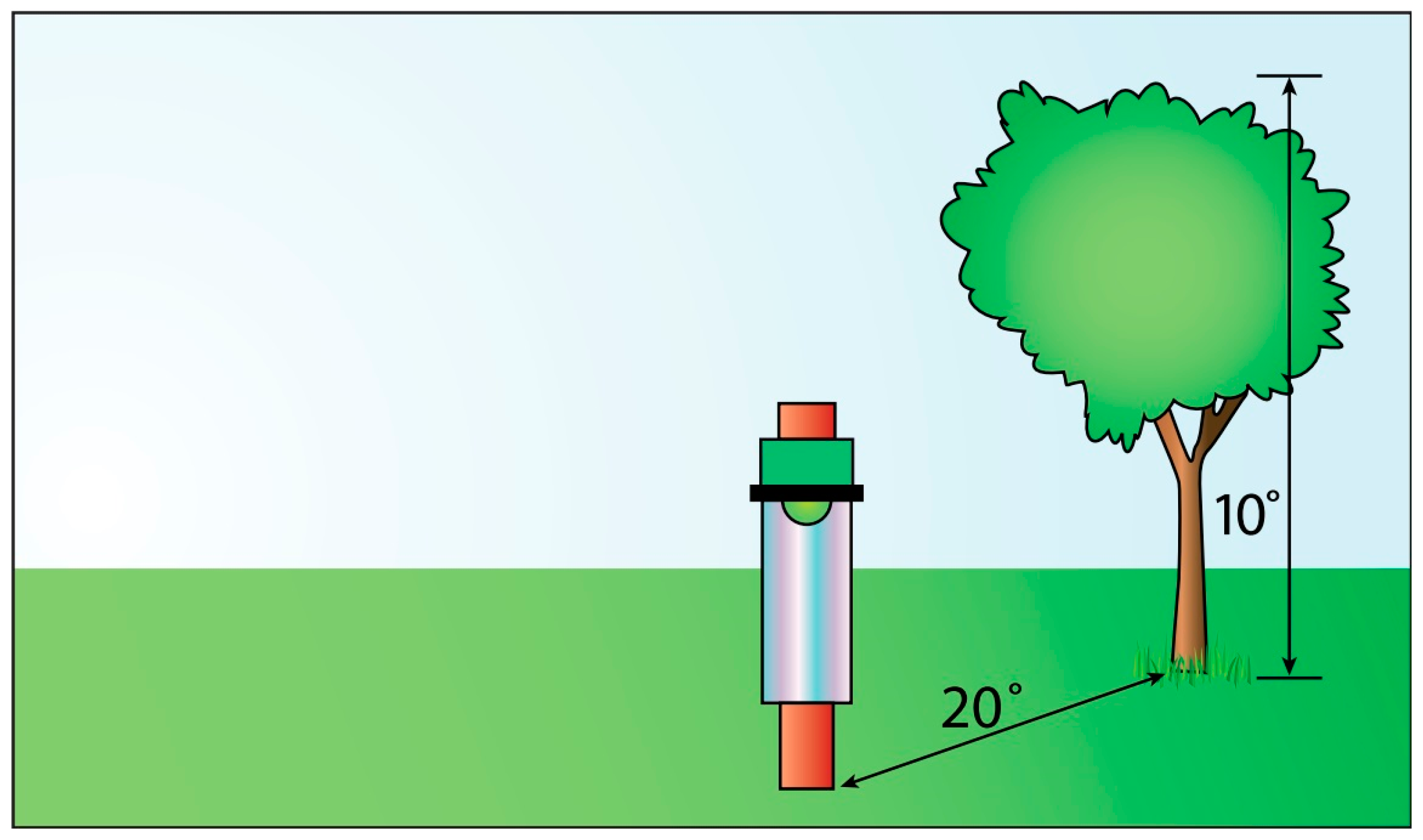
Figure 13.
Positioning of a rain gauge in relation to surrounding objects (WMO [
61]).
Figure 13.
Positioning of a rain gauge in relation to surrounding objects (WMO [
61]).
Table 1.
Overview of the individual stations used by the study.
Table 1.
Overview of the individual stations used by the study.
| Station Name | Lat (N) | Lon I | Start Date | End Date | Period [Years] | QA-Test |
|---|
| Abu Samra | 24°44′44.78″ N | 50°49′23.45″ E | 1 March 2007 | 31 March 2023 | 16.08 | Passed |
| Al Ghuwairiya | 25°50′26.47″ N | 51°16′12.22″ E | 1 January 2009 | 31 March 2023 | 14.24 | Passed |
| Al Wakrah | 25°11′34.02″ N | 51°37′8.95″ E | 1 January 2009 | 31 March 2023 | 14.24 | Failed |
| Mukenis-Al Karanaah | 25°6′13.41″ N | 51°10′25.46″ E | 1 January 2009 | 31 March 2023 | 14.24 | Passed |
| Qatar University | 25°22′56.34″ N | 51°28′45.90″ E | 31 March 2007 | 31 March 2023 | 16.08 | Passed |
| Umm Said | 24°56′32.34″ N | 51°34′6.51″ E | 1 December 2007 | 31 March 2023 | 15.33 | Passed |
Table 2.
Overview of the number of observations at the meteorological stations: The first column also includes dry periods, the second column contains all observations with rainfall, and the third column contains all observations where the rainfall exceeds the threshold of 0.5 mm/h.
Table 2.
Overview of the number of observations at the meteorological stations: The first column also includes dry periods, the second column contains all observations with rainfall, and the third column contains all observations where the rainfall exceeds the threshold of 0.5 mm/h.
| Station Name | Number of All Observations | Number of Observations with Rainfall | Number of Observations with Rainfall Intensity Exceeding the Threshold 0.5 mm/h |
|---|
| Abu Samra | 141,000 | 524 | 276 |
| Al Ghuwairiya | 124,872 | 759 | 234 |
| Mukenis-Al Karanaah | 124,872 | 759 | 233 |
| Qatar University | 141,000 | 1037 | 370 |
| Umm Said | 134,400 | 749 | 293 |
Table 3.
Estimated Log Pearson Type III (LP3) density parameters and corresponding p-values and χ2 sums for fitting rainfall intensity distribution.
Table 3.
Estimated Log Pearson Type III (LP3) density parameters and corresponding p-values and χ2 sums for fitting rainfall intensity distribution.
| Station Name | α | β | γ | p-Value | Χ2 | Χ2 Critical (α = 0.05) |
|---|
| Abu Samra | 2.795 | 0.4766 | −0.9084 | 0.2821 | 9.76 | 15.51 |
| Al Ghuwairiya | 2.302 | 0.5219 | −0.7851 | 0.0610 | 14.91 | 15.51 |
| Mukenis Al Karanaa | 3.194 | 0.4526 | −1.023 | 0.0589 | 13.59 | 15.51 |
| Qatar University | 2.798 | 0.4766 | −0.9083 | 0.2402 | 10.37 | 15.51 |
| Umm Said | 3.490 | 0.4551 | −1.069 | 0.0694 | 14.51 | 15.51 |
| Average | | | | 0.1432 | 12.63 | 15.51 |
Table 4.
Estimated GEV density parameters and corresponding p-values and χ2 sums in fitting the wind speed data.
Table 4.
Estimated GEV density parameters and corresponding p-values and χ2 sums in fitting the wind speed data.
| Station Name | ξ (Location) | α (Scale) | k (Shape) | p-Value | Χ2 | Χ2 Critical (α = 0.05) |
|---|
| Abu Samra | 4.6690 | 3.1204 | −0.0801 | 0.9215 | 3.20 | 15.51 |
| Al Ghuwairiya | 3.6053 | 2.2580 | −0.0688 | 0.8267 | 4.32 | 15.51 |
| Mukenis Al Karanaa | 3.5319 | 1.9980 | 0.0352 | 0.7740 | 4.05 | 15.51 |
| Qatar University | 2.8214 | 1.8082 | 0.0288 | 0.4524 | 7.81 | 15.51 |
| Umm Said | 3.4199 | 1.6947 | −0.0217 | 0.2828 | 9.75 | 15.51 |
| Average | | | | 0.6515 | 5.83 | |
Table 5.
Chi-square and p-values for the Mixed von Misses distribution with divisions into 3, 4, 5, and 6 segments to fit wind directional data with 12 bins.
Table 5.
Chi-square and p-values for the Mixed von Misses distribution with divisions into 3, 4, 5, and 6 segments to fit wind directional data with 12 bins.
| Station Name | MvM-3 | MvM-4 | MvM-5 | MvM-6 | |
|---|
| | p-Value | Χ2 | p-Value | Χ2 | p-Value | Χ2 | p-Value | Χ2 | Χ2 Critical (α = 0.05) |
|---|
| Abu Samra | 0.708 | 6.32 | 0.685 | 6.54 | 0.687 | 6.52 | 0.863 | 4.65 | 16.92 |
| Al Ghuwairiya | 0.722 | 6.16 | 0.909 | 4.02 | 0.828 | 5.07 | 0.914 | 3.96 | 16.92 |
| Mukenis Al Karanaa | 0.972 | 2.78 | 0.966 | 2.93 | 0.973 | 2.77 | 0.979 | 2.56 | 16.92 |
| Qatar University | 0.553 | 7.81 | 0.611 | 7.24 | 0.584 | 7.50 | 0.892 | 4.28 | 16.92 |
| Umm Said | 0.424 | 9.14 | 0.424 | 9.14 | 0.806 | 5.30 | 0.836 | 4.97 | 16.92 |
| Average | 0.676 | 6.44 | 0.719 | 5.97 | 0.776 | 5.43 | 0.897 | 4.08 | |
Table 6.
Overview of the estimated MvM-6 distribution parameters at the different stations.
Table 6.
Overview of the estimated MvM-6 distribution parameters at the different stations.
| Segment | Abu Samra | Al Ghuwairiyah | Mukeynis Al Karanaah | Qatar University | Umm Said |
|---|
| | μ | κ | w | μ | κ | w | μ | κ | w | μ | κ | w | μ | κ | w |
|---|
| 1 | −0.4132 | 6.0448 | 0.4251 | −1.1131 | 18.6038 | 0.1557 | −2.8757 | 13.1470 | 0.0488 | −2.8459 | 13.2362 | 0.0628 | −1.1938 | 0.7405 | 0.2802 |
| 2 | 0.5412 | 1.4308 | 0.1568 | −0.2385 | 8.6024 | 0.1353 | −1.8918 | 2.6354 | 0.1169 | −1.4947 | 4.1703 | 0.0912 | −0.1431 | 8.4372 | 0.3506 |
| 3 | 1.4743 | 0.1904 | 0.0889 | 0.4395 | 1.8221 | 0.2865 | −0.3289 | 5.7281 | 0.3557 | −0.6628 | 7.1227 | 0.3494 | 1.0123 | 4.0224 | 0.1331 |
| 4 | 1.5361 | 30.8243 | 0.0590 | 1.3006 | 77.8444 | 0.0588 | 0.3043 | 53.8937 | 0.1077 | 0.3154 | 7.1536 | 0.1593 | 1.3267 | 122.0460 | 0.0778 |
| 5 | 1.6481 | 0.1102 | 0.1371 | 1.9794 | 27.8985 | 0.0968 | 0.9901 | 6.1351 | 0.2202 | 1.3113 | 4.2433 | 0.2198 | 1.3967 | 3.6699 | 0.1188 |
| 6 | 2.3210 | 0.2815 | 0.1330 | 2.9926 | 1.2796 | 0.2671 | 2.0826 | 14.4063 | 0.1507 | 2.3898 | 10.1177 | 0.1176 | 3.1315 | 33.0517 | 0.0395 |
Table 7.
Overview of Spearman’s rho correlation, Kendall’s Tau, and Blomqvist’s Beta of the observed wind speed and direction data.
Table 7.
Overview of Spearman’s rho correlation, Kendall’s Tau, and Blomqvist’s Beta of the observed wind speed and direction data.
| Station Name | Abu Samra | Al Ghuwairiya | Mukenis-Al Karanaah | Qatar University | Umm Said |
|---|
| Dep. Structure parameter | | | | | |
|---|
| Sampled Spearman Rho (ρ) | −0.23 | 0.05 | −0.19 | 0.06 | 0.06 |
| Sampled Kendall’s Tau (τ) | −0.17 | 0.04 | −0.13 | 0.04 | 0.03 |
| Blomqvist Beta (β) | −0.22 | 0.01 | −0.20 | −0.02 | 0.04 |
Table 8.
The Spearman Rho, Kendall’s Tau, and Blomqvist Beta for the Bernstein Copula for wind speed and wind direction.
Table 8.
The Spearman Rho, Kendall’s Tau, and Blomqvist Beta for the Bernstein Copula for wind speed and wind direction.
| Station Name | Abu Samra | Al Ghuwairiya | Mukenis-Al Karanaah | Qatar University | Umm Said |
|---|
| Dep. Structure parameter | | | | | |
|---|
| BC Spearman Rho (ρ) | −0.21 | 0.04 | −0.16 | 0.05 | 0.05 |
| BC Kendall’s Tau (τ) | −0.15 | 0.02 | −0.12 | 0.02 | 0.03 |
| BC Blomqvist Beta (β) | −0.19 | 0.02 | −0.13 | 0.03 | 0.03 |
Table 9.
Overview of Spearman’s rho correlation, Kendall’s Tau, and Blomqvist’s Beta of the observed rainfall intensity and wind direction data.
Table 9.
Overview of Spearman’s rho correlation, Kendall’s Tau, and Blomqvist’s Beta of the observed rainfall intensity and wind direction data.
| Station Name | Abu Samra | Al Ghuwairiya | Mukenis-Al Karanaah | Qatar University | Umm Said |
|---|
| Dep. Structure parameter | | | | | |
|---|
| Sampled Spearman Rho (ρ) | 0.00 | −0.02 | −0.06 | 0.02 | 0.02 |
| Sampled Kendall’s Tau (τ) | 0.00 | −0.02 | −0.04 | 0.01 | 0.01 |
| Blomqvist Beta (β) | −0.02 | −0.03 | −0.06 | −0.03 | −0.02 |
Table 10.
The Spearman Rho, Kendall’s Tau, and the Blomqvist Beta for the Bernstein Copula for rainfall intensity and wind direction data.
Table 10.
The Spearman Rho, Kendall’s Tau, and the Blomqvist Beta for the Bernstein Copula for rainfall intensity and wind direction data.
| Station Name | Abu Samra | Al Ghuwairiya | Mukenis-Al Karanaah | Qatar University | Umm Said |
|---|
| Dep. Structure parameter | | | | | |
|---|
| BC Spearman Rho (ρ) | 0.02 | −0.03 | −0.05 | 0.01 | 0.01 |
| BC Kendall’s Tau (τ) | 0.00 | −0.03 | −0.05 | 0.00 | 0.01 |
| BC Blomqvist Beta (β) | 0.01 | −0.02 | −0.05 | 0.00 | −0.02 |
Table 11.
The marginal LP3 distribution of the rainfall intensity under the condition of the wind direction for the Qatar University station. The column NEvents indicates how many events are observed for each wind direction shown in the first column.
Table 11.
The marginal LP3 distribution of the rainfall intensity under the condition of the wind direction for the Qatar University station. The column NEvents indicates how many events are observed for each wind direction shown in the first column.
Direction
(Bearing Degrees) | α | β | γ | NEvents |
|---|
| N-E (0–90 degrees) | 1.872 | 0.690 | −0.826 | 109 |
| E-S (90–180 degrees) | 5.617 | 0.278 | −1.209 | 69 |
| S-W (180–270 degrees) | 0.902 | 0.960 | −0.552 | 35 |
| W-N (270–360 degrees) | 5.476 | 0.314 | −1.271 | 157 |
Table 12.
The marginal GEV distribution of the rainfall intensity under the condition of the wind direction for the Qatar University station. The column NEvents indicates how many events are observed for each wind direction shown in the first column.
Table 12.
The marginal GEV distribution of the rainfall intensity under the condition of the wind direction for the Qatar University station. The column NEvents indicates how many events are observed for each wind direction shown in the first column.
Direction
(Bearing Degrees) | ξ (Location) | α (Scale) | k (Shape) | NEvents |
|---|
| N-E (0–90 degrees) | 2.938 | 1.850 | −0.045 | 109 |
| E-S (90–180 degrees) | 2.963 | 1.873 | −0.020 | 69 |
| S-W (180–270 degrees) | 2.418 | 1.570 | 0.226 | 35 |
| W-N (270–360 degrees) | 2.764 | 1.774 | 0.069 | 157 |
Table 13.
The Joe Copula functions for the bivariate distribution between rainfall intensity and wind speed for a given wind direction.
Table 13.
The Joe Copula functions for the bivariate distribution between rainfall intensity and wind speed for a given wind direction.
Direction
(Bearing Degrees) | Preferred Copula | Copula Parameter θ | Blomqvist β | Kendall’s τ | NEvents |
|---|
| N-E (0–90 degrees) | Joe Copula | 1.294 | 0.14 | 0.14 | 109 |
| E-S (90–180 degrees) | Independent | 1.000 | 0.00 | 0.00 | 69 |
| S-W (180–270 degrees) | Independent | 1.000 | 0.00 | 0.00 | 35 |
| W-N (270–360 degrees) | Joe Copula | 1.083 | 0.04 | 0.05 | 157 |