Flexural-Gravity Waves in a Channel with a Compressed Ice Cover
Abstract
1. Introduction
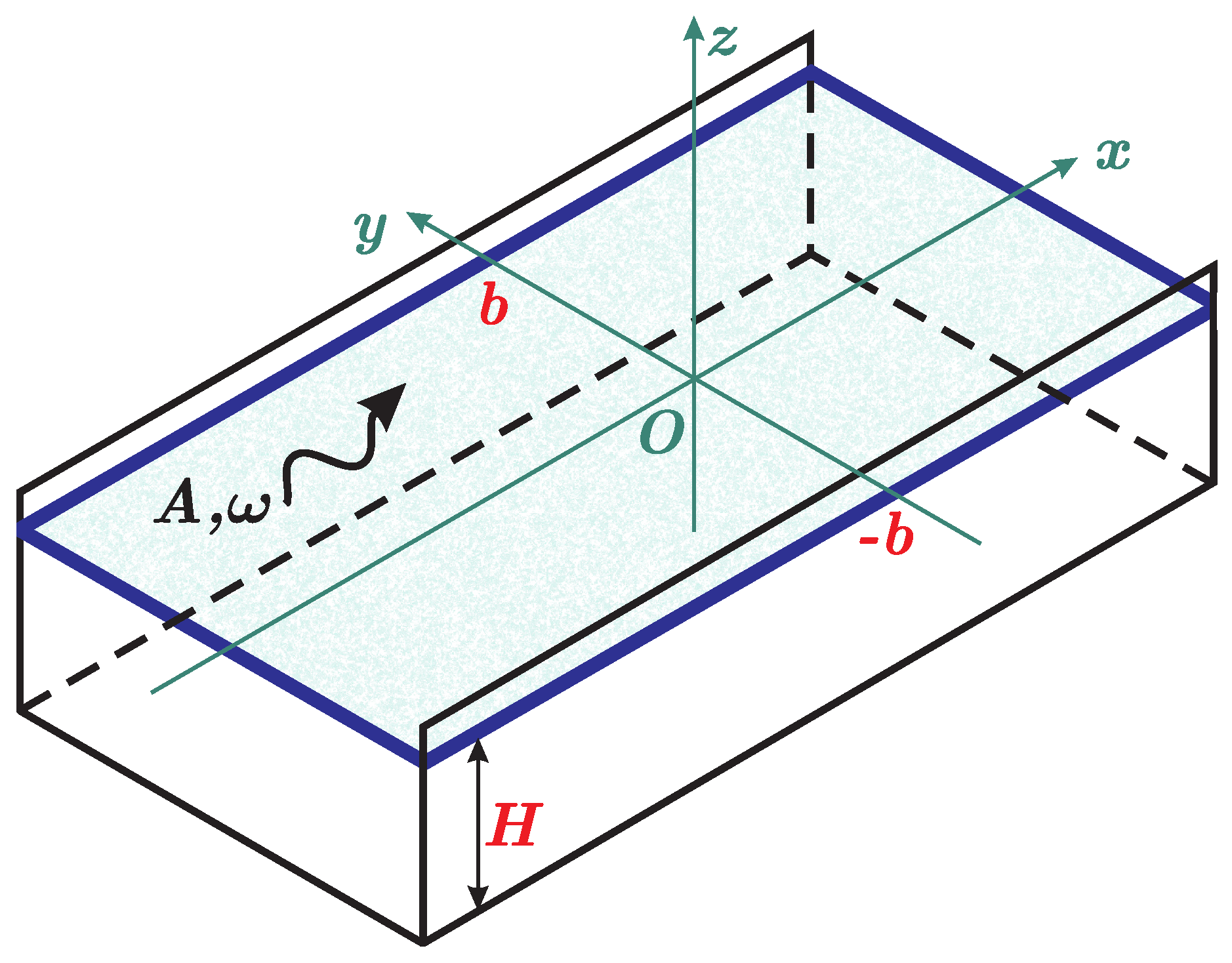
2. Formulation of the Problem
3. Solution to the Problem by Normal Modes Method
Strains in the Ice Cover
4. Numerical Results
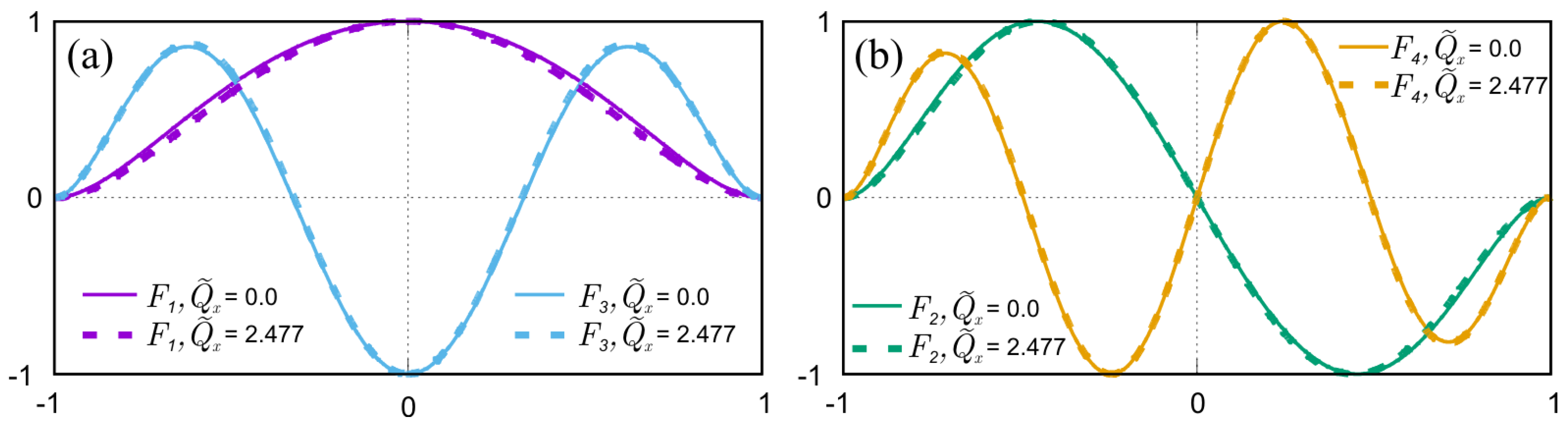
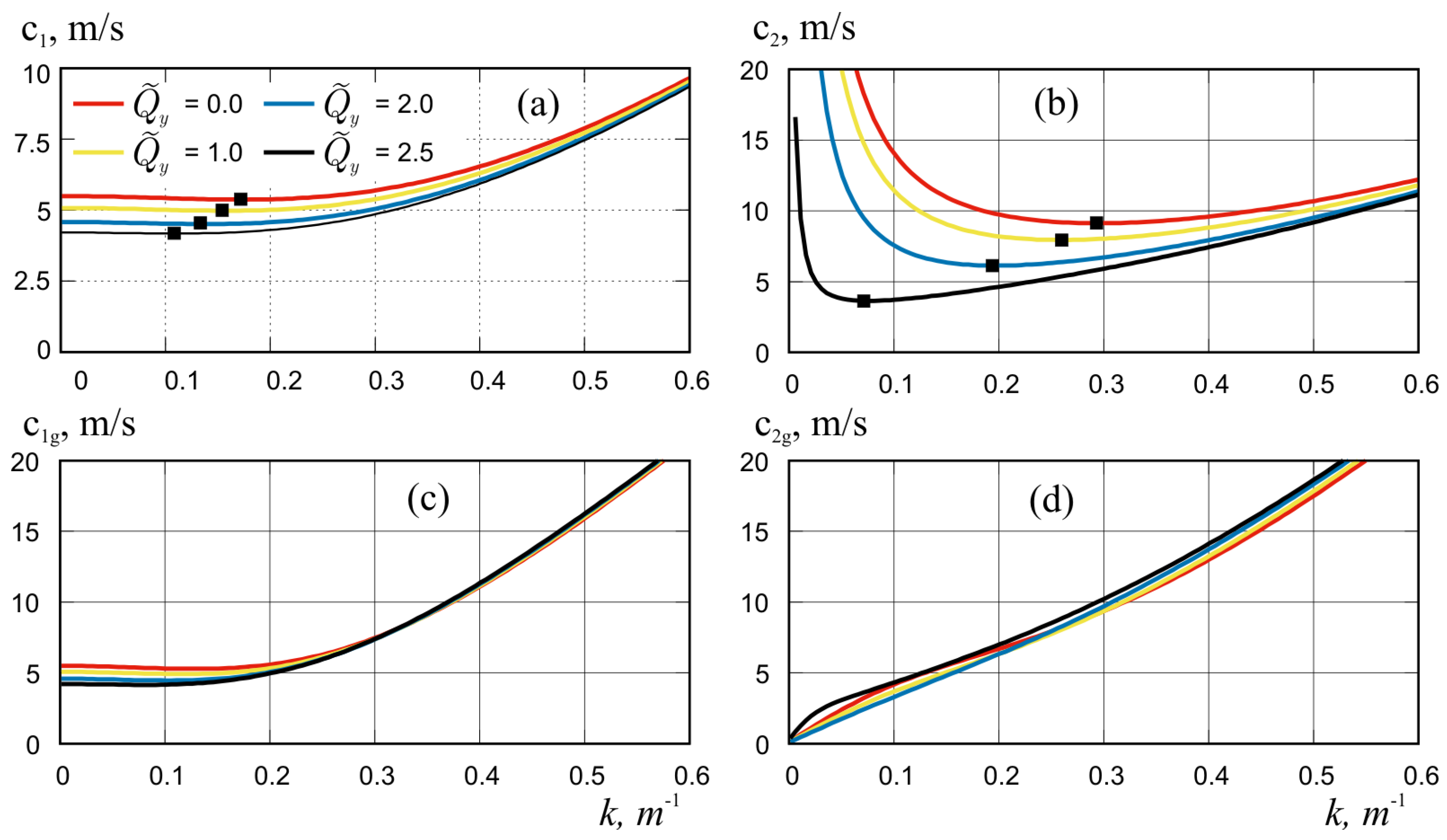
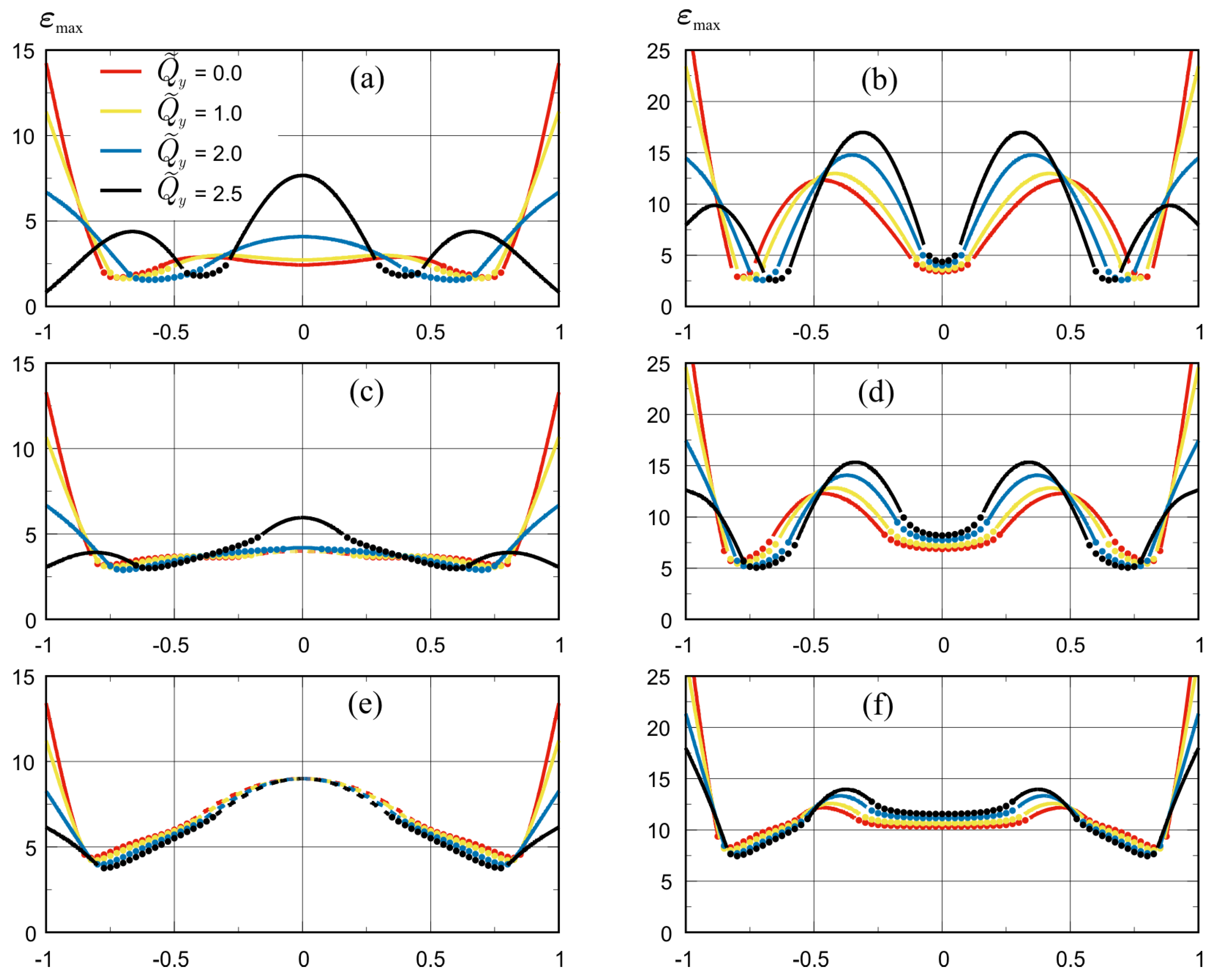
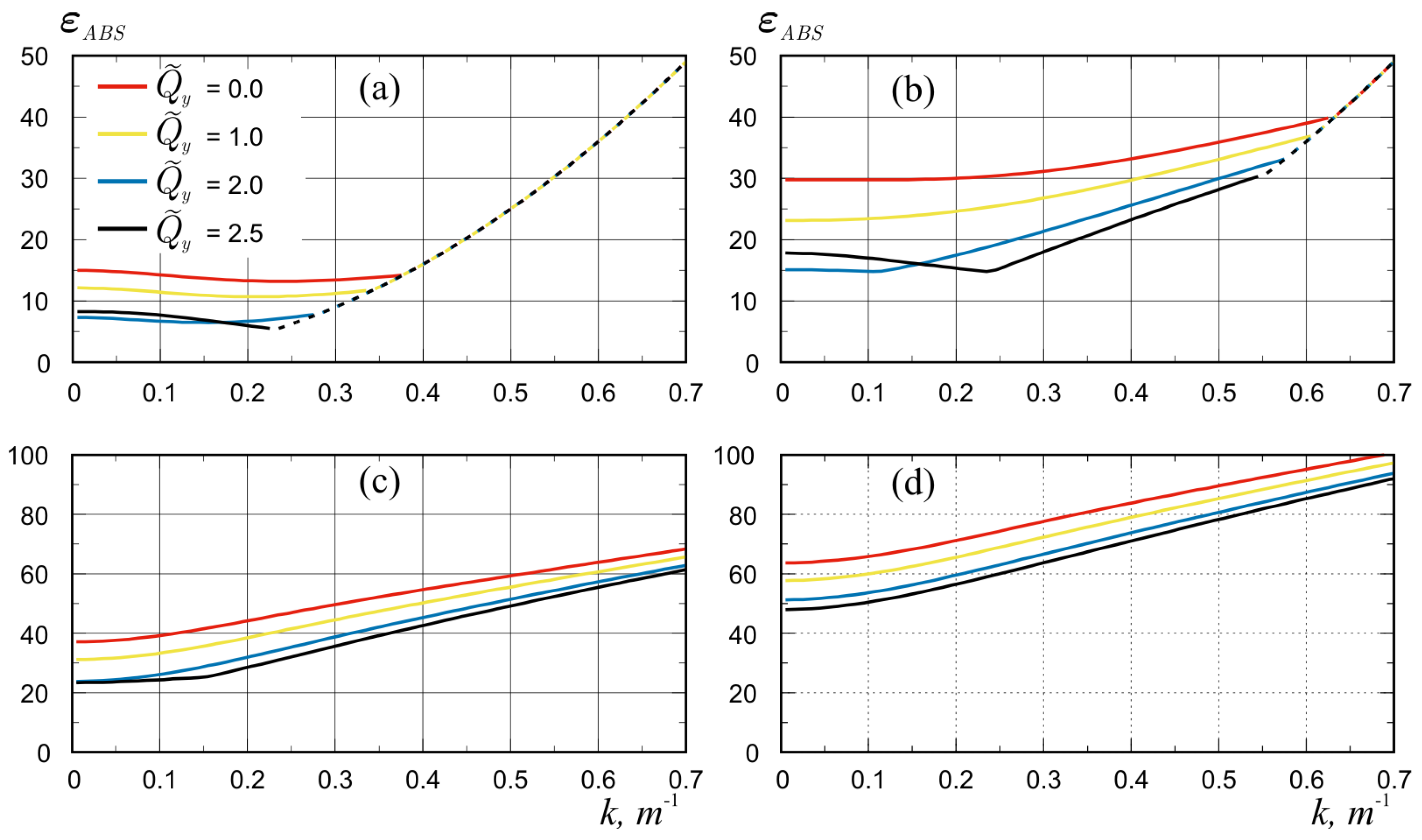
4.1. Compression along the Channel (Longitudinal Compression)
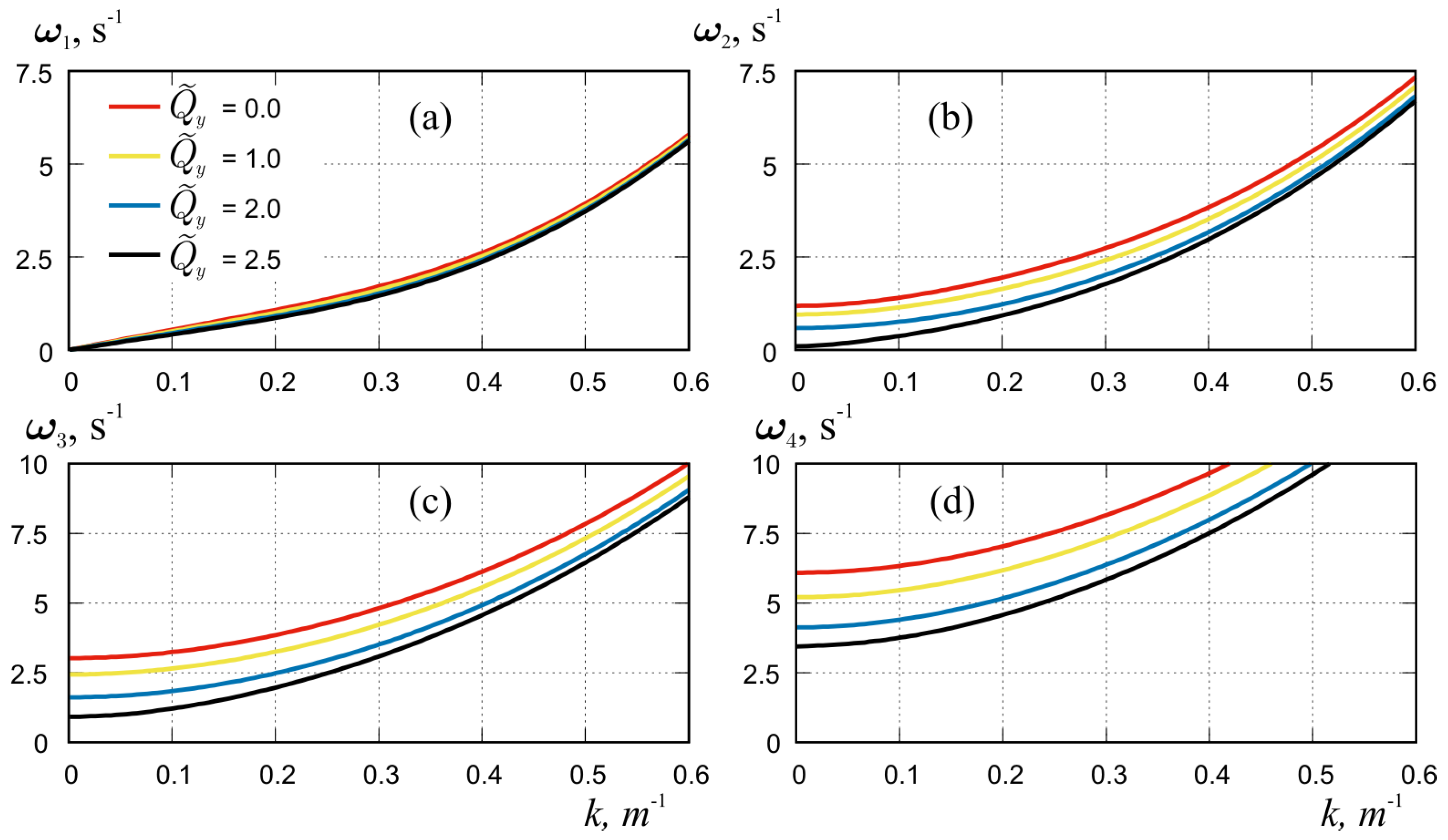
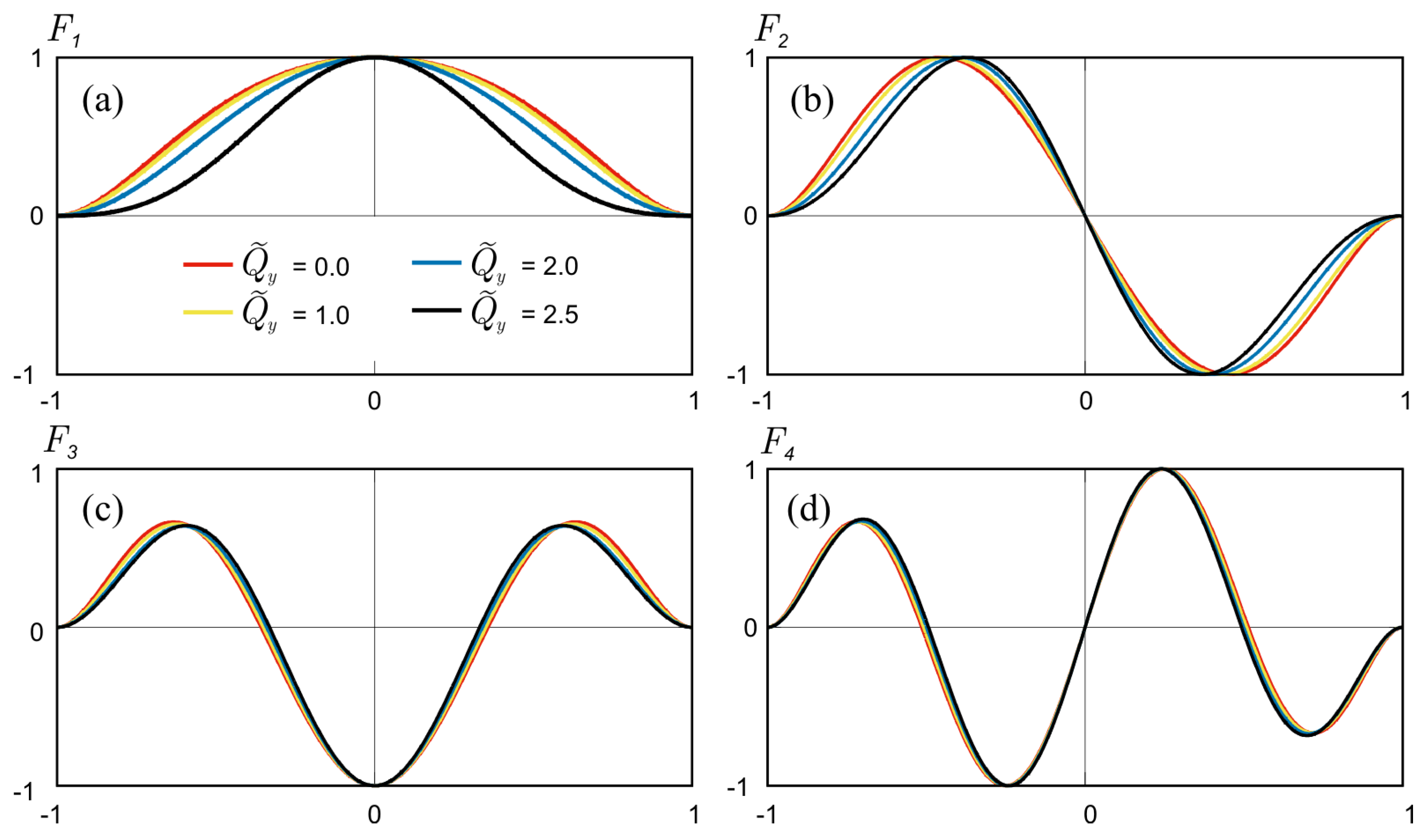
4.2. Compression across the Channel (Transverse Compression)
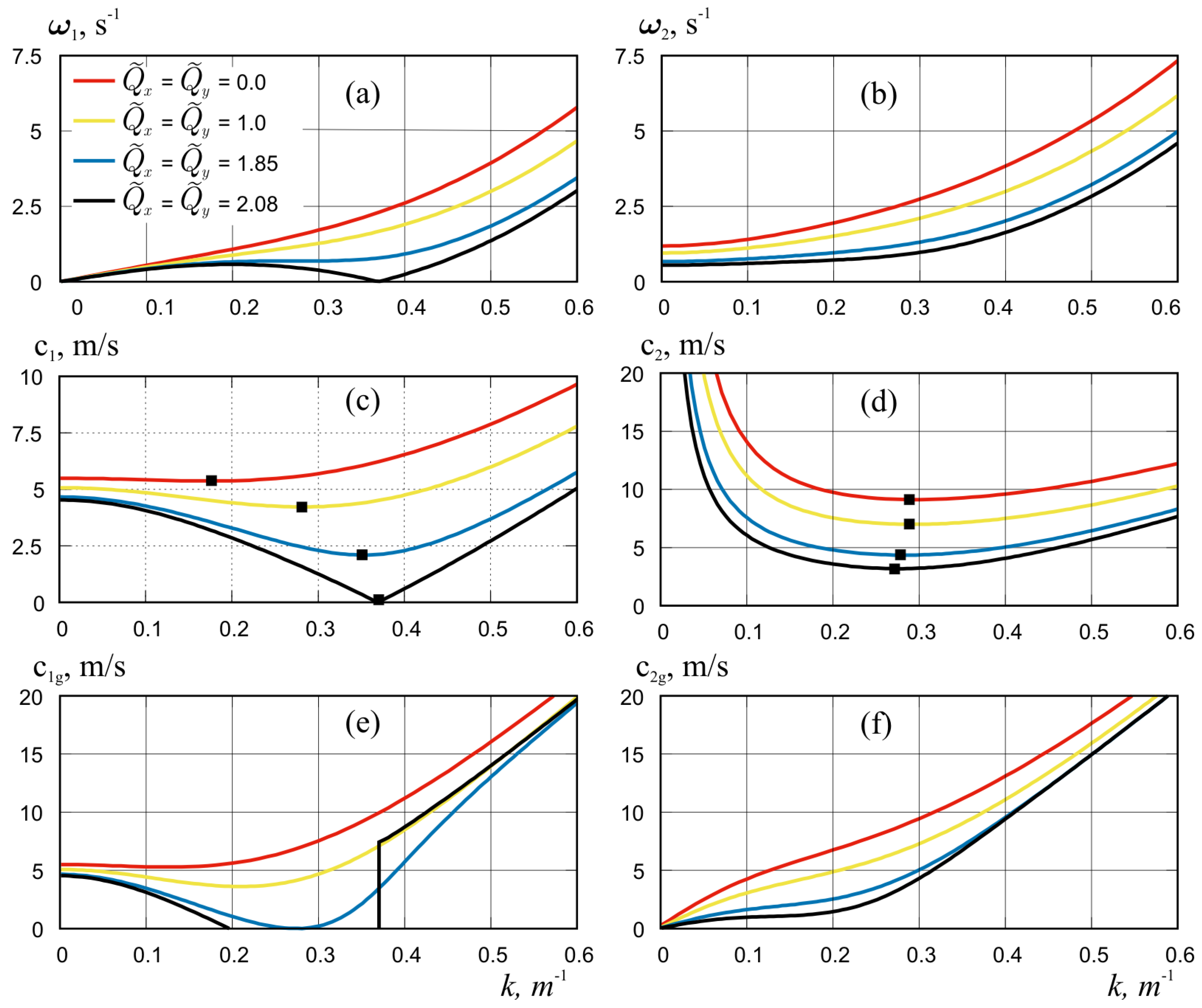
4.3. Compression with Longitudinal and Transverse Components
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aksenov, Y.; Popova, E.E.; Yool, A.; Nurser, A.J.G.; Williams, T.D.; Bertino, L.; Bergh, J. On the future navigability of Arctic sea routes: High-resolution projections of the Arctic Ocean and sea ice. Mar. Policy 2017, 75, 300–317. [Google Scholar] [CrossRef]
- Greenhill, A.G. Wave motion in hydrodynamics. Am. J. Math. 1886, 9, 62–96. [Google Scholar] [CrossRef]
- Kheysin, D.Y. Moving load on an elastic plate which floats on the surface of an ideal fluid. Izv. Akad. Nauk SSSR Otd. Tekh. Nauk Mekh. i Mashinostr. 1963, 1, 178–180. (In Russian) [Google Scholar]
- Kheysin, D.Y. Dinamika ledyanogo pokrova (Dynamics of Floating Ice Covers). In Leningrad: Gidrometeorologicheskoe Izdatel’stvo; Technical Translation FSTC-HT-23-485-69; US Army Foreign Science and Technology Center: Charlottesville, VA, USA, 1967. [Google Scholar]
- Nevel, D.E. Moving Loads on a Floating Ice Sheet; No. CRREL-RR-261; US Army Cold Regions Research and Engineering Lab.: Hanover, NH, USA, 1970. [Google Scholar]
- Squire, V.A.; Hosking, R.; Kerr, A.; Langhorne, P.J. Moving Loads on Ice Plates; Kluwer: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Schulkes, R.M.S.M.; Hosking, R.J.; Sneyd, A.D. Waves due to a steadily moving source on a floating ice plate. Part 2. J. Fluid Mech. 1987, 180, 297–318. [Google Scholar] [CrossRef]
- Hosking, R.J.; Sneyd, A.D.; Waugh, D.W. Viscoelastic response of a floating ice plate to a steadily moving load. J. Fluid Mech. 1988, 196, 409–430. [Google Scholar] [CrossRef]
- Squire, V.A.; Robinson, W.H.; Langhorne, P.J.; Haskell, T.G. Vehicles and aircraft on floating ice. Nature 1988, 333, 159–161. [Google Scholar] [CrossRef]
- Hinchey, M.; Colbourne, B. Research on low and high speed hovercraft icebreaking. Can. J. Civ. Eng. 1995, 22, 32–42. [Google Scholar] [CrossRef]
- Zhestkaya, V.D. Numerical solution of the problem of an ice sheet under a moving load. J. Appl. Mech. Tech. Phys. 1999, 40, 770–775. [Google Scholar] [CrossRef]
- Yeung, R.W.; Kim, J.W. Effects of a translating load on a floating plate—Structural drag and plate deformation. Fluids Struct. 2000, 14, 993–1011. [Google Scholar] [CrossRef]
- Kashiwagi, M. Transient responses of a VLFS during landing and take-off of an airplane. J. Mar. Sci. Technol. 2004, 9, 14–23. [Google Scholar] [CrossRef]
- Pogorelova, A.V. Wave Resistance of an Air-Cushion Vehicle in Unsteady Motion over an Ice Sheet. J. Appl. Mech. Tech. Phys. 2008, 49, 71–79. [Google Scholar] [CrossRef]
- Meylan, M.H.; Sturova, I.V. Time-dependent motion of a two-dimensional floating elastic plate. J. Fluids Struct. 2009, 25, 445–460. [Google Scholar] [CrossRef]
- Pogorelova, A.V.; Kozin, V.M.; Matyushina, A.A. Stress-strain state of ice cover during aircraft takeoff and landing. J. Appl. Mech. Tech. Phys. 2015, 56, 920–926. [Google Scholar] [CrossRef]
- Tkacheva, L.A. Behavior of a semi-infinite ice cover under a uniformly moving load. J. Appl. Mech. Tech. Phys. 2018, 59, 258–272. [Google Scholar] [CrossRef]
- Johnsen, K.; Kalisch, H.; Părău, E.I. Ship wave patterns on floating ice sheets. Sci. Rep. 2022, 12, 18931. [Google Scholar] [CrossRef]
- Brocklehurst, P.; Korobkin, A.A.; Pǎrǎu, E.I. Interaction of hydro-elastic waves with a vertical wall. J. Eng. Math. 2010, 68, 215–231. [Google Scholar] [CrossRef]
- Brocklehurst, P.; Korobkin, A.; Pǎrǎu, E.I. Hydroelastic Wave Diffraction by a Vertical Cylinder. Philos. Trans. R. Soc. A 2011, 369, 2832–2851. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, J.; Guedes Soares, C. Flexural Gravity Wave over a Floating Ice Sheet near a Vertical Wall. J. Eng. Math. 2012, 75, 29–48. [Google Scholar] [CrossRef]
- Korobkin, A.A.; Malenica, S.; Khabakhpasheva, T. Interaction of Flexural-Gravity Waves in Ice Cover with Vertical Walls. Philos. Trans. R. Soc. A. 2018, 376, 20170347. [Google Scholar] [CrossRef]
- Ren, K.; Wu, G.X.; Ji, C.Y. Diffraction of Hydroelastic Waves by Multiple Vertical Circular Cylinders. J. Eng. Math. 2018, 113, 45–64. [Google Scholar] [CrossRef]
- Tkacheva, L.A. Oscillations of a Cylinder beneath an Ice Cover in the Neighborhood of a Vertical Wall. Fluid Dyn. 2020, 55, 300–313. [Google Scholar] [CrossRef]
- Disibuyuk, N.B.; Yilmaz, O.; Korobkin, A.A.; Khabakhpasheva, T.I. An Iterative Method for Interaction of Hydro-Elastic Waves with Several Vertical Cylinders of Circular Cross-Sections. J. Mar. Sci. Eng. 2022, 10, 723. [Google Scholar] [CrossRef]
- Evans, D.V.; Porter, R. Wave scattering by narrow cracks in ice sheets floating on water of finite depth. J. Fluid Mech. 2003, 484, 143165. [Google Scholar] [CrossRef]
- Porter, D.; Evans, D. Diffraction of flexural waves by finite straight cracks in an elastic sheet over water. J. Fluids Struct. 2007, 23, 309–327. [Google Scholar] [CrossRef]
- Tkacheva, L.A. Wave motion in an ice sheet with crack under uniformly moving Load. Fluid Dyn. 2019, 54, 14–32. [Google Scholar] [CrossRef]
- Barman, S.C.; Das, S.; Sahoo, T.; Meylan, M.H. Scattering of flexural-gravity waves by a crack in a floating ice sheet due to mode conversion during blocking. J. Fluid Mech. 2021, 916, A11. [Google Scholar] [CrossRef]
- Wang, R.; Shen, H.H. Gravity waves propagating into an ice-covered ocean: A viscoelastic model. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Meylan, M.; Bennetts, L.; Peter, M. Water-wave scattering and energy dissipation by a floating porous elastic plate in three dimensions. Wave Motion 2017, 70, 240–250. [Google Scholar] [CrossRef]
- Chen, H.; Gilbert, R.P.; Guyenne, P. Dispersion and attenuation in a porous viscoelastic model for gravity waves on an ice-covered ocean. Eur. J. Mech.-B/Fluids 2019, 78, 88–105. [Google Scholar] [CrossRef]
- Zavyalova, K.N.; Shishmarev, K.A.; Korobkin, A.A. The response of a poroelastic ice plate to an external pressure. J. Sib. Fed. Univ. Math. Phys. 2021, 14, 87–97. [Google Scholar] [CrossRef]
- Wu, Q.Y.; Khabakhpasheva, T.I.; Ni, B.Y.; Korobkin, A.A. Small-amplitude waves in a floating poroelastic plate forcing by vertical pitching plate. Phys. Fluids 2023, 35, 117127. [Google Scholar] [CrossRef]
- Pǎrǎu, E.I.; Dias, F. Nonlinear effects in the response of a floating ice plate to a moving load. J. Fluid Mech. 2002, 460, 281–305. [Google Scholar] [CrossRef]
- Marchenko, A. Nonlinear Phenomena in Resonant Excitation of Flexural–Gravity Waves. J. Ship Ocean Technol. Soc. Nav. Archit. Korea 2003, 7, 1–12. [Google Scholar]
- Plotnikov, P.I.; Toland, J.F. Modelling nonlinear hydroelastic waves. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2011, 369, 2942–2956. [Google Scholar] [CrossRef] [PubMed]
- Dinvay, E.; Kalisch, H.; Părău, E.I. Fully dispersive models for moving loads on ice sheets. J. Fluid Mech. 2019, 876, 122–149. [Google Scholar] [CrossRef]
- Ni, B.Y.; Khabakhpasheva, T.I.; Semenov, Y.A. Nonlinear gravity waves in the channel covered by broken ice. Phys. Fluids 2023, 35, 102118. [Google Scholar] [CrossRef]
- Van der Sanden, J.J.; Short, N.H. Radar satellites measure ice cover displacements induced by moving vehicles. Cold Reg. Sci. Technol. 2017, 133, 56–62. [Google Scholar] [CrossRef]
- Kozin, V.M.; Pogorelova, A.V. Wave resistance of amphibian aircushion vehicles during motion on ice fields. J. Appl. Mech. Tech. Phys. 2003, 44, 193–197. [Google Scholar] [CrossRef]
- Zhestkaya, V.D.; Kozin, V.M. Ice Breaking with Air-Cushion Vessels Using a Resonant Method; Dal’nauka: Vladivostok, Russia, 2003; 160p. (In Russian) [Google Scholar]
- Kozin, V.M. The Resonant Method of Ice Breaking: Inventions and Experiments; Academy of Natural Sciences: Moscow, Russia, 2007. (In Russian) [Google Scholar]
- Korobkin, A.A.; Khabakhpasheva, T.I.; Papin, A.A. Waves propagating along a channel with ice cover. Eur. J. Mech.-B/Fluids 2014, 47, 166–175. [Google Scholar] [CrossRef]
- Batyaev, E.A.; Khabakhpasheva, T.I. Hydroelastic waves in a channel covered with a free ice sheet. Fluid Dyn. 2015, 50, 775–788. [Google Scholar] [CrossRef]
- Ren, K.; Wu, G.X.; Li, Z.F. Hydroelastic waves propagating in an ice-covered channel. J. Fluid Mech. 2020, 886, A18. [Google Scholar] [CrossRef]
- Shishmarev, K.; Zavyalova, K.; Batyaev, E.; Khabakhpasheva, T. Hydroelastic waves in a frozen channel with non-uniform thickness of ice. Water 2022, 14, 281. [Google Scholar] [CrossRef]
- Shishmarev, K.A.; Khabakhpasheva, T.I.; Korobkin, A.A. The response of ice cover to a load moving along a frozen channel. Appl. Ocean Res. 2016, 59, 313–326. [Google Scholar] [CrossRef]
- Shishmarev, K.A.; Khabakhpasheva, T.I.; Korobkin, A.A. Ice response to an underwater body moving in a frozen channel. Appl. Ocean Res. 2019, 91, 101877. [Google Scholar] [CrossRef]
- Zeng, L.D.; Korobkin, A.A.; Ni, B.Y.; Xue, Y.Z. Moving load in an ice channel with a crack. Appl. Ocean Res. 2022, 121, 103086. [Google Scholar] [CrossRef]
- Khabakhpasheva, T.I.; Shishmarev, K.A.; Korobkin, A.A. Large-time response of ice cover to a load moving along a frozen channel. Appl. Ocean Res. 2019, 86, 154–165. [Google Scholar] [CrossRef]
- Kerr, D. The critical velocities of a load moving on a floating ice plate that is subjected to in-plane forces. Cold Reg. Sci. Technol. 1983, 6, 267–274. [Google Scholar] [CrossRef]
- Bukatov, A.E. Influence of a longitudinally compressed elastic plate on the non-stationary wave motion of a homogeneous liquid. Fluid Dyn. 1980, 15, 687–693. [Google Scholar] [CrossRef]
- Bukatov, A.E.; Zharkov, V.V.; Zav’yalov, D.D. Three-dimensional bent-gravity waves with non-uniform compression. J. Appl. Mech. Tech. Phys. 1991, 32, 867–872. [Google Scholar] [CrossRef]
- Eyov, E.; Klar, A.; Kadri, U.; Stiassnie, M. Progressive waves in a compressible-ocean with an elastic bottom. Wave Motion 2013, 50, 929–939. [Google Scholar] [CrossRef]
- Il’ichev, A.T. Solitary wave packets beneath a compressed ice cover. Fluid Dyn. 2016, 51, 327–337. [Google Scholar] [CrossRef]
- Stepanyants, Y.; Sturova, I. Waves on a compressed floating ice plate caused by motion of a dipole in water. J. Fluid Mech. 2021, 907, A7. [Google Scholar] [CrossRef]
- Stepanyants, Y.; Sturova, I. Hydrodynamic Forces Exerting on an Oscillating Cylinder under Translational Motion in Water Covered by Compressed Ice. Water 2021, 13, 822. [Google Scholar] [CrossRef]
- Sturova, I.V. Motion of a load over an ice sheet with non-uniform compression. Fluid Dyn. 2021, 56, 503–512. [Google Scholar] [CrossRef]
- Das, S.; Sahoo, T.; Meylan, M.H. Dynamics of flexural gravity waves: From sea ice to Hawking radiation and analogue gravity. Proc. R. Soc. A 2018, 474, 20170223. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batyaev, E.; Khabakhpasheva, T. Flexural-Gravity Waves in a Channel with a Compressed Ice Cover. Water 2024, 16, 1255. https://doi.org/10.3390/w16091255
Batyaev E, Khabakhpasheva T. Flexural-Gravity Waves in a Channel with a Compressed Ice Cover. Water. 2024; 16(9):1255. https://doi.org/10.3390/w16091255
Chicago/Turabian StyleBatyaev, Evgeniy, and Tatiana Khabakhpasheva. 2024. "Flexural-Gravity Waves in a Channel with a Compressed Ice Cover" Water 16, no. 9: 1255. https://doi.org/10.3390/w16091255
APA StyleBatyaev, E., & Khabakhpasheva, T. (2024). Flexural-Gravity Waves in a Channel with a Compressed Ice Cover. Water, 16(9), 1255. https://doi.org/10.3390/w16091255






