Parameter Optimization of Frazil Ice Evolution Model Based on NSGA-II Genetic Algorithm
Abstract
1. Introduction
2. Model Formulation
2.1. Heat Exchanges and Water Temperature
2.2. Initial Seeding
2.3. Ice Particle Growth
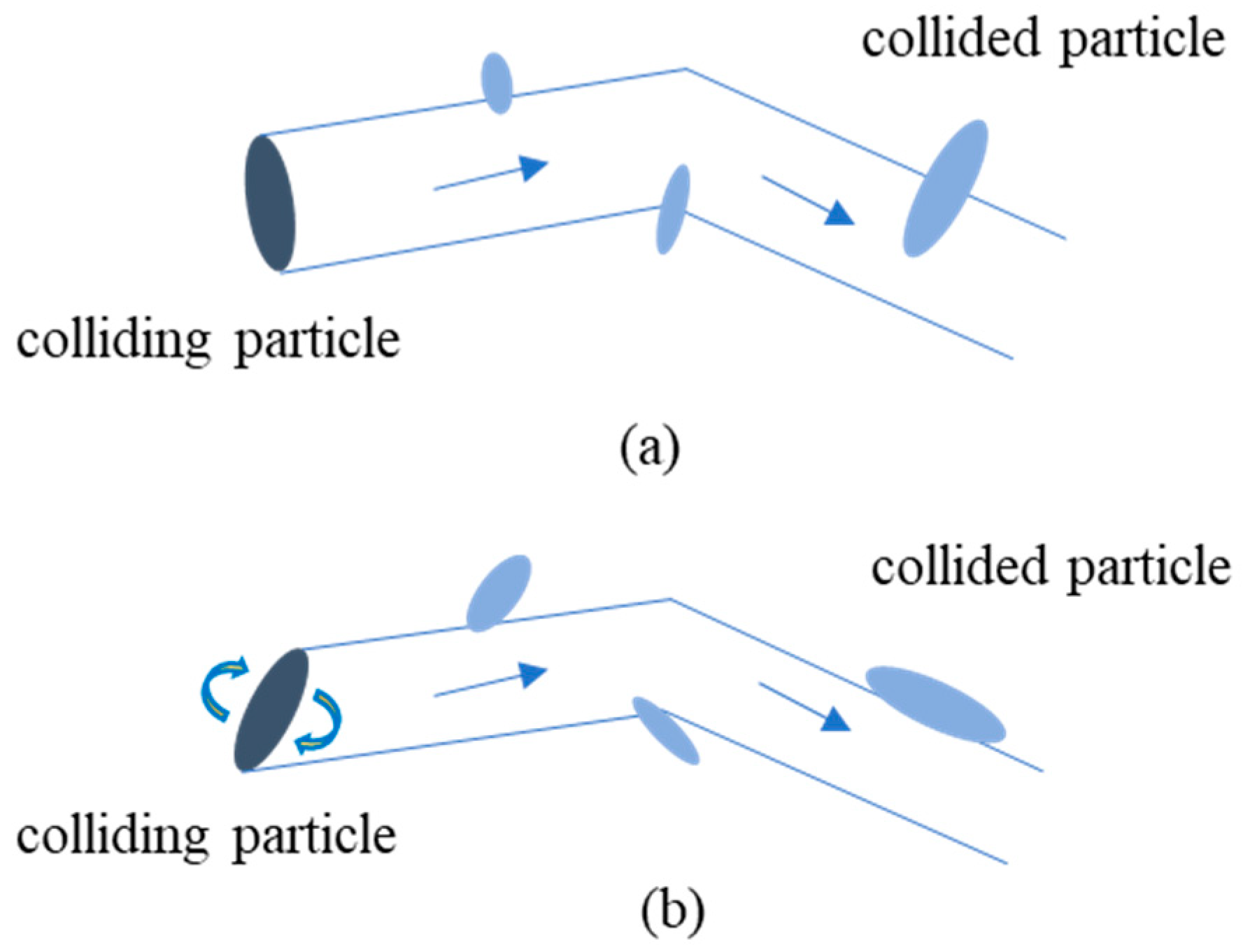
2.4. Ice Particle Collision Frequency
2.5. Flocculation/Breakup
2.6. Gravitational Removal
3. NSGA-II Non-Dominated Sorting Genetic Algorithm
3.1. Optimization Parameters and Objective Function Equation
3.2. A Fast Non-Dominated Sorting Approach
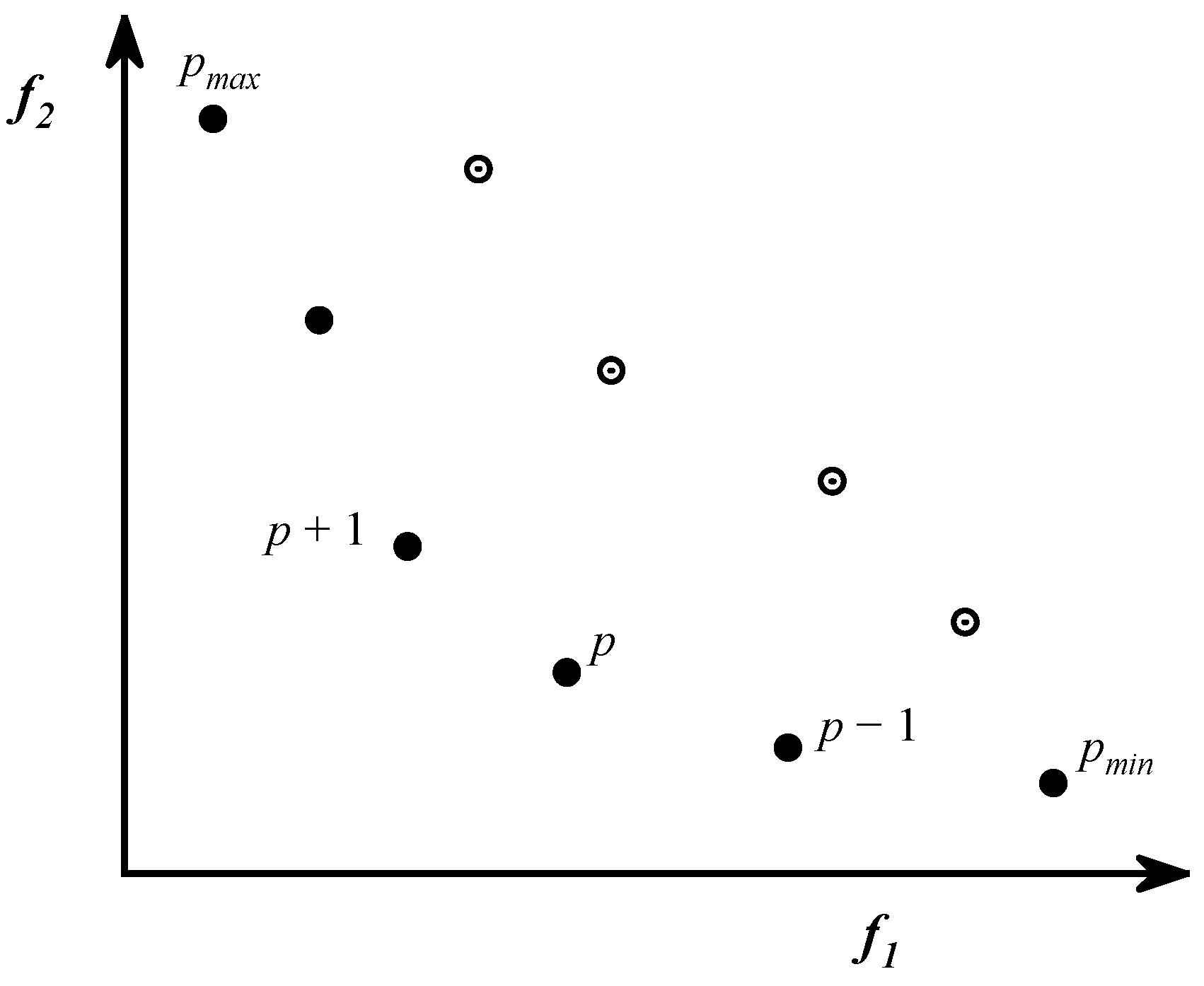
3.3. Density Estimation
3.4. Crowded Comparison Operator
3.5. Selection, Crossover, and Mutation
- (1)
- Selection
- (2)
- Crossover
- (3)
- Mutation
3.6. Elite Strategy
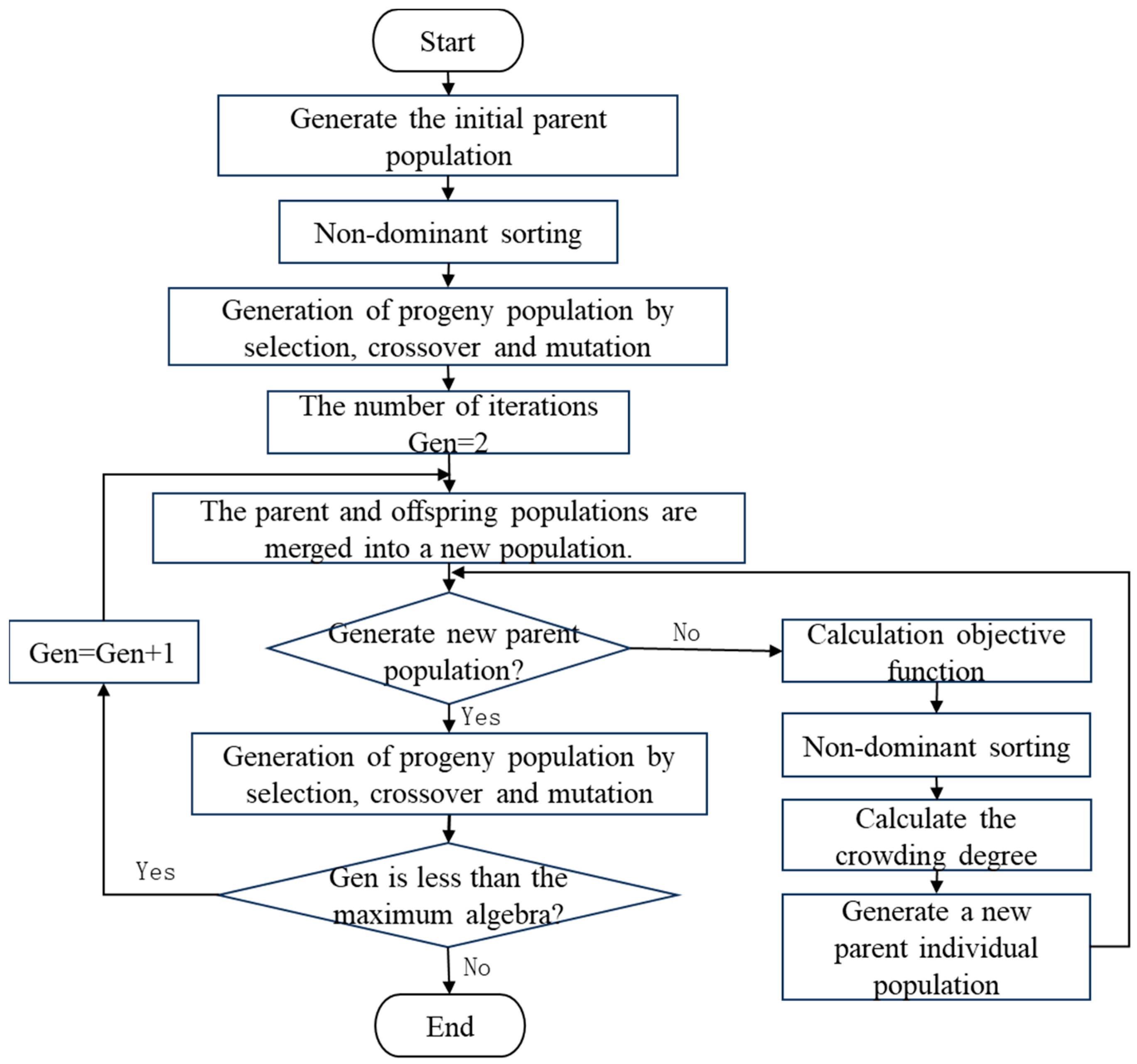
3.7. Algorithm Implementation Steps
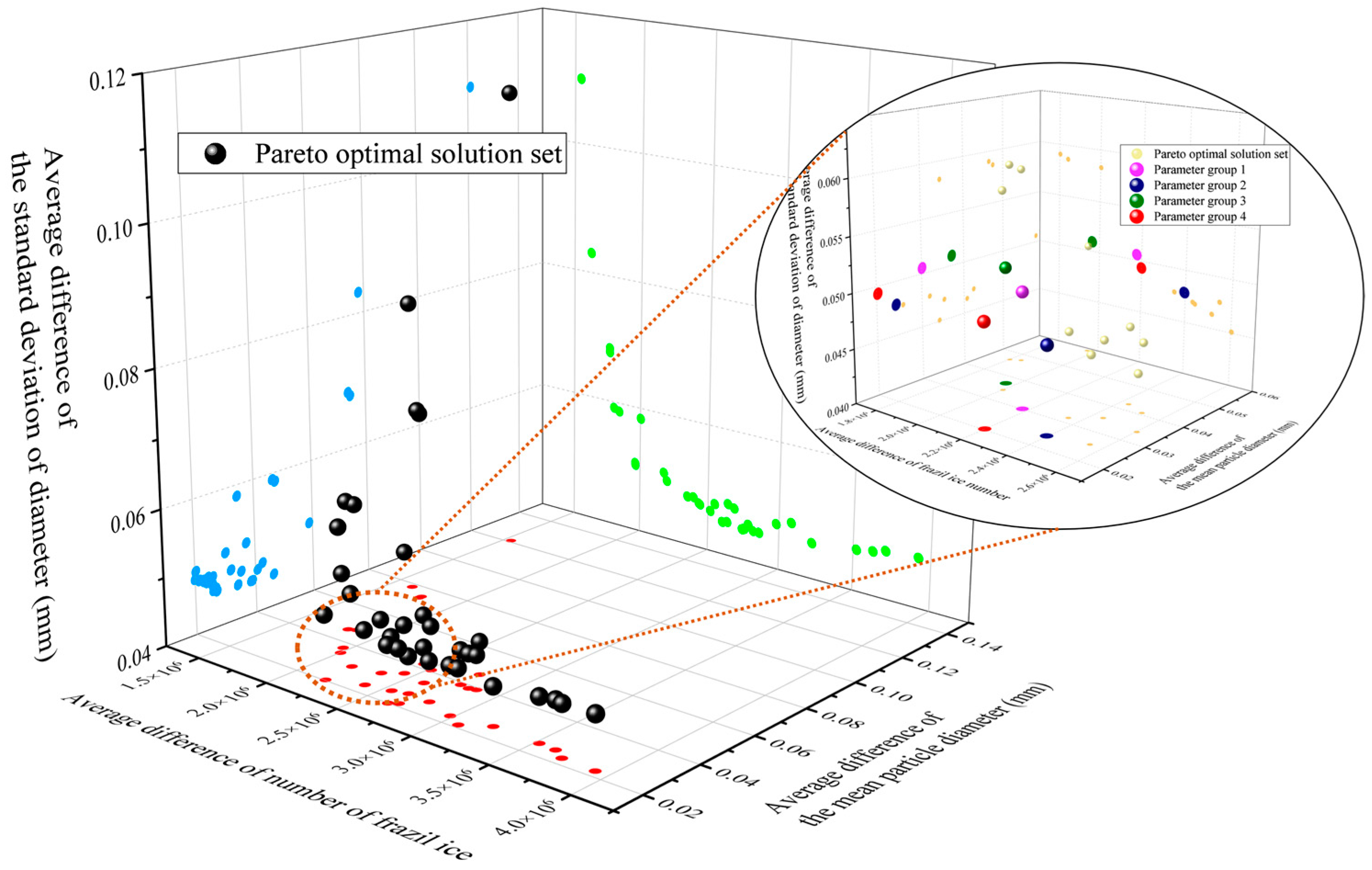
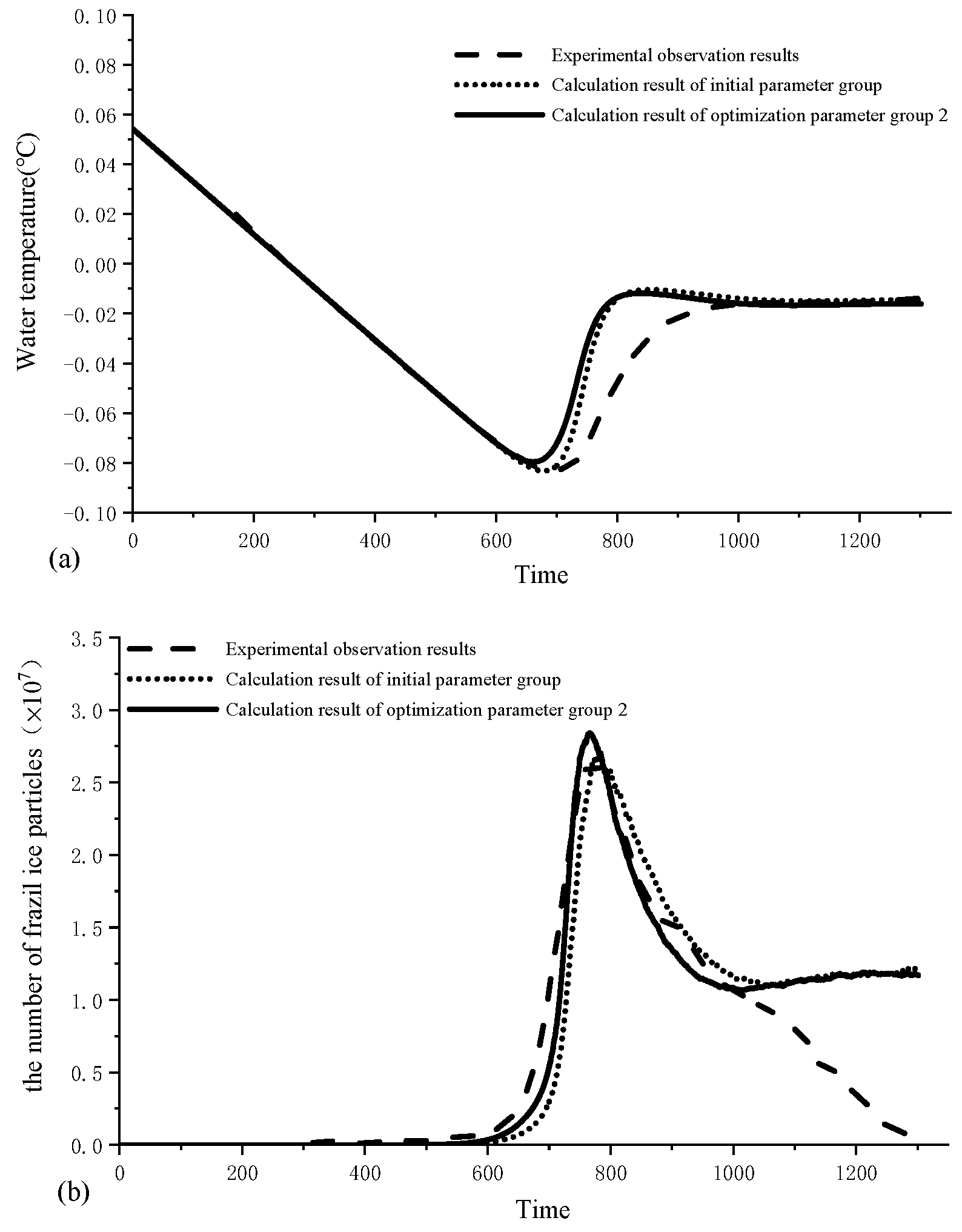
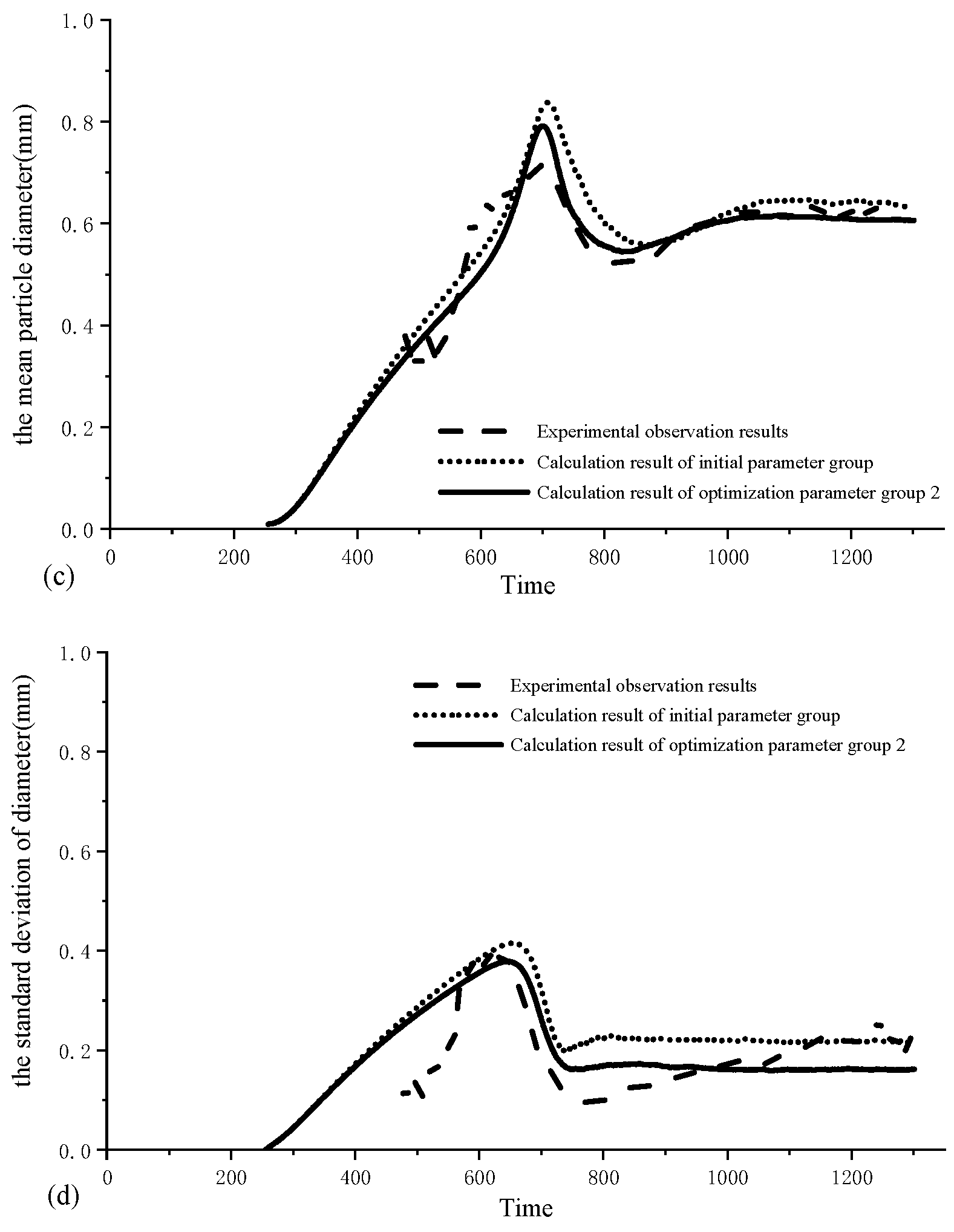
4. Optimization of Calculation Results
5. Discussion
5.1. The Improvement of the Frazil Ice Evolution Model
- (1)
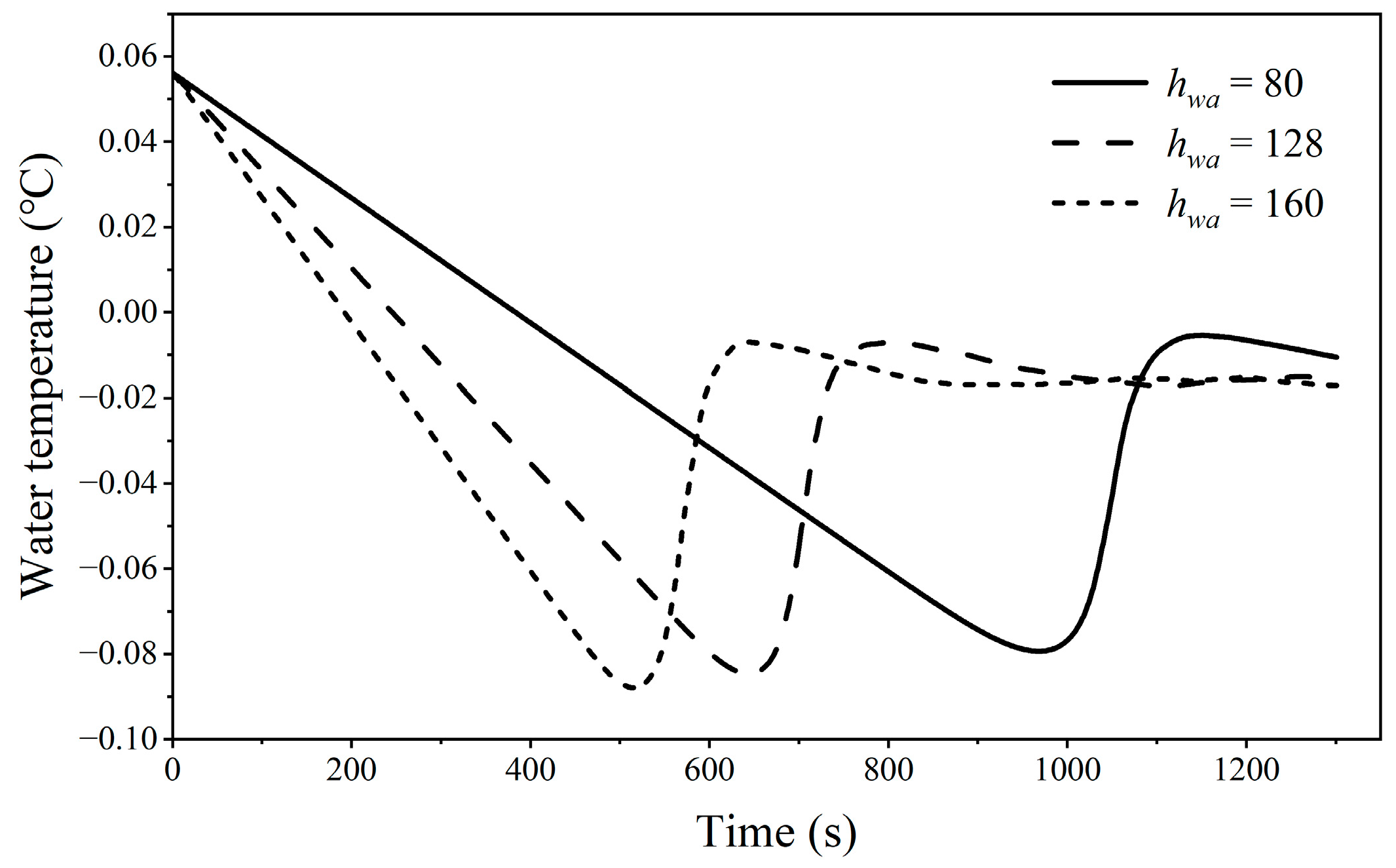
- Initial Seeding
- (2)
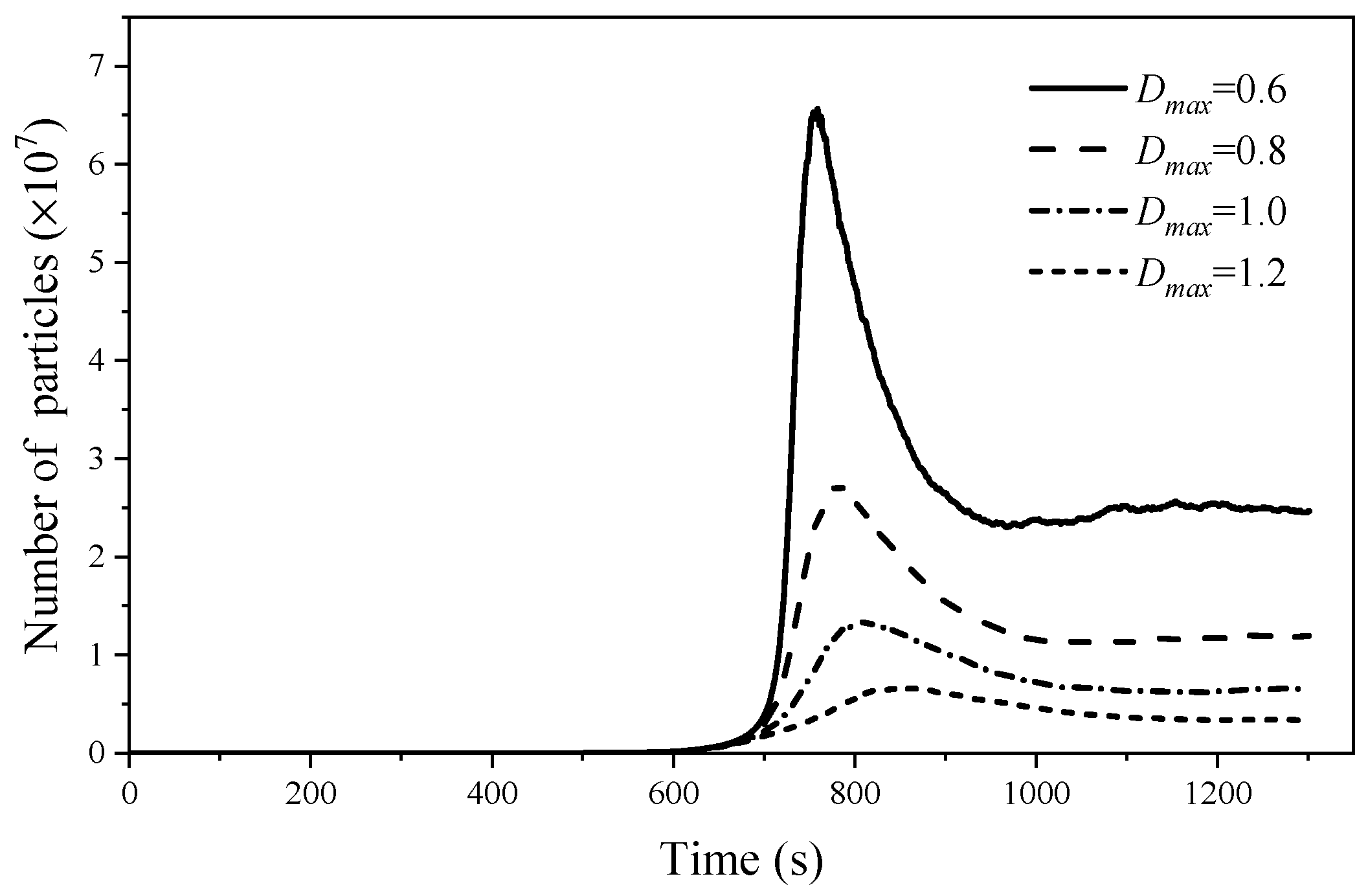
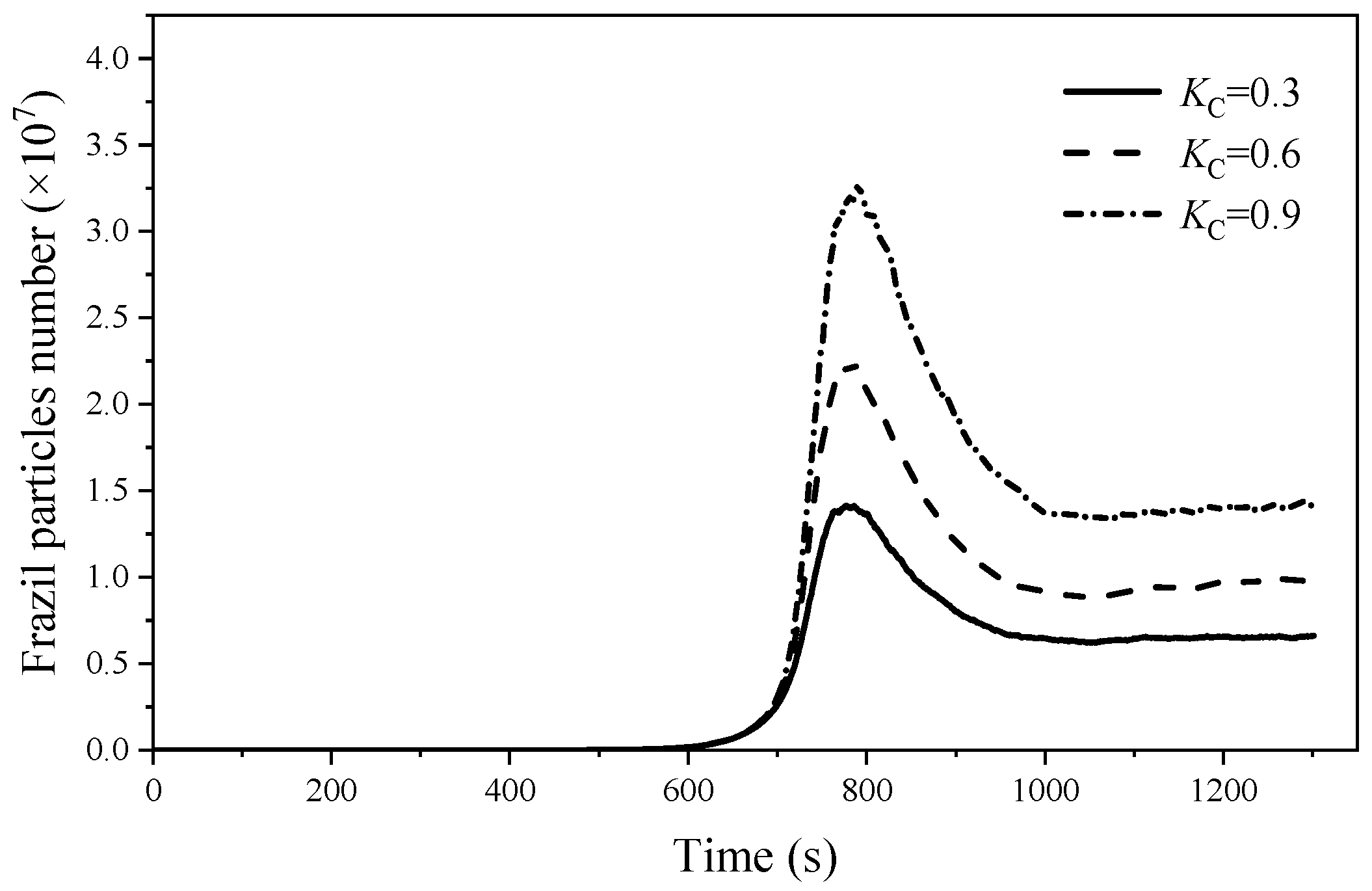
- Ice Particles Collision Frequency and Flocculation/Breakup
5.2. Selection of Optimization Parameters and Objective Functions
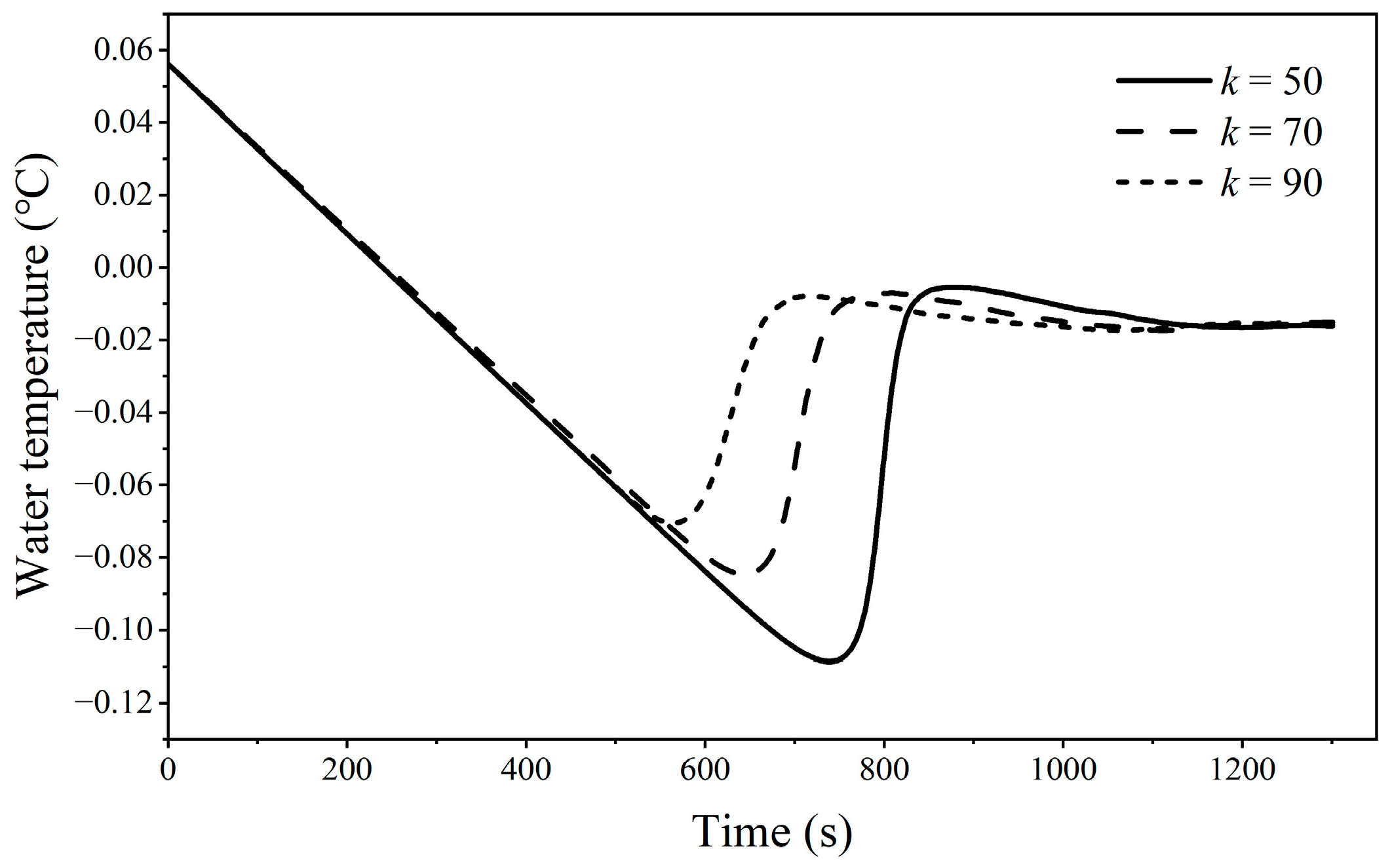
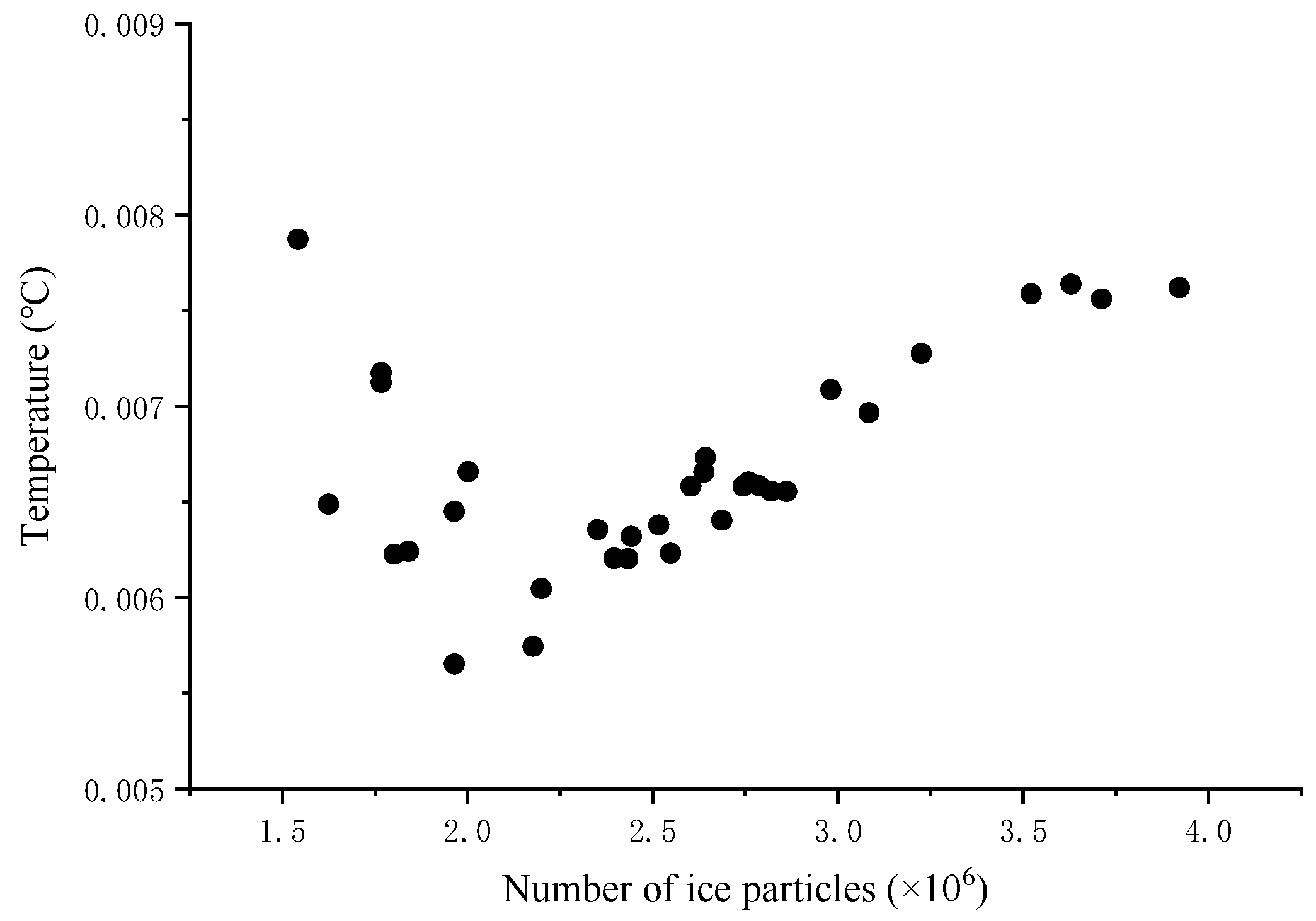
5.3. The Water Temperature Difference of Each Optimization Parameter Group on the Pareto Front
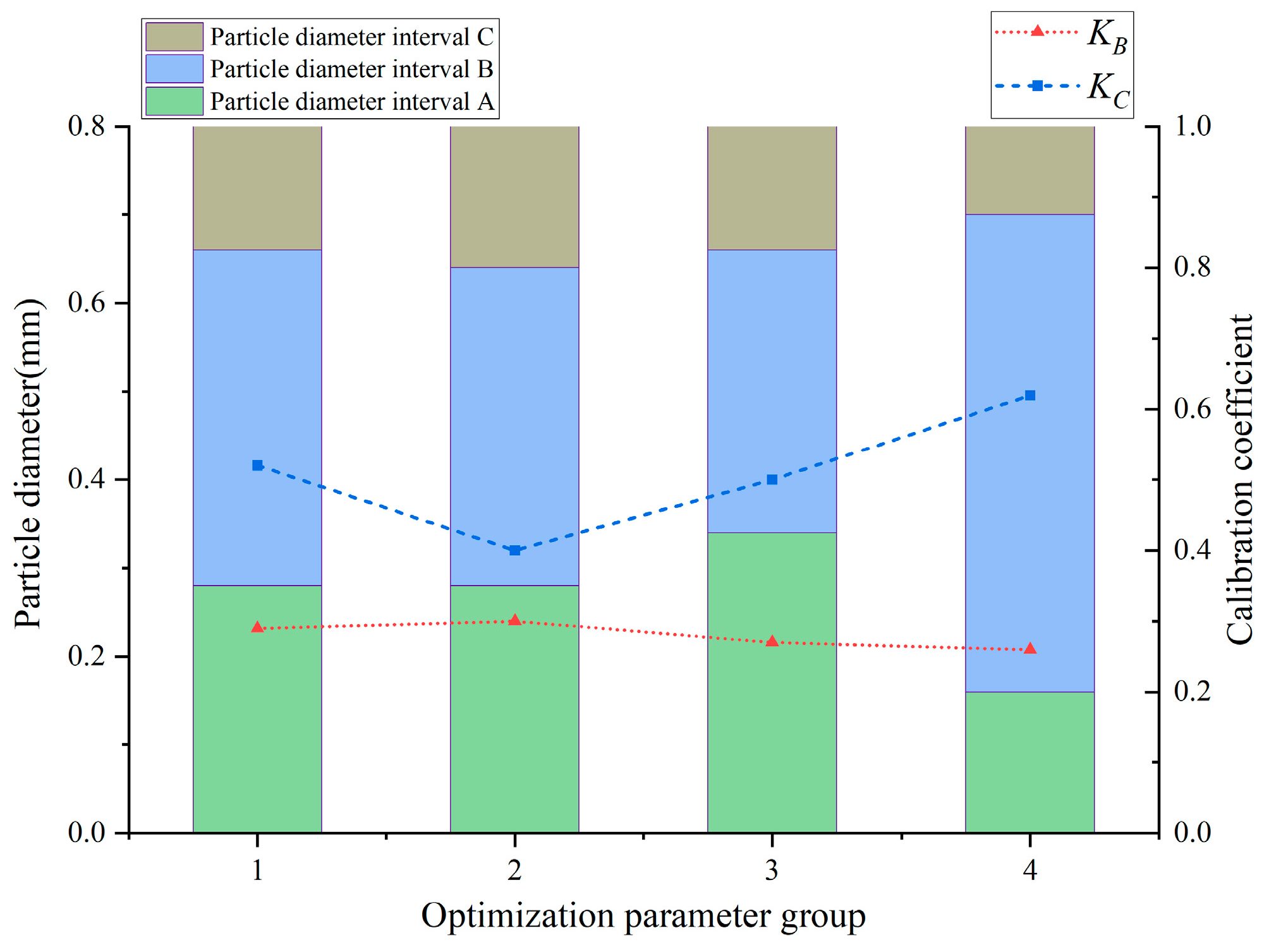
5.4. Discussion of the Optimal Parameters Obtained from the Optimization Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Lian, J.; Zhao, X.; Guo, Q.; Yang, D. Advances in Frazil Ice Evolution Mechanisms and Numerical Modelling in Rivers and Channels in Cold Regions. Water 2023, 15, 2582. [Google Scholar] [CrossRef]
- Omstedt, A.; Svensson, U. Modeling supercooling and ice formation in a turbulent Ekman layer. J. Geophys. Res. 1984, 89, 735–744. [Google Scholar] [CrossRef]
- Osterkamp, T.E.; Gosink, J.P. Frazil ice formation and ice cover development in interior Alaska streams. Cold Reg. Sci. Technol. 1983, 8, 43–56. [Google Scholar] [CrossRef]
- Svensson, U.; Omstedt, A. Simulation of supercooling and size distribution in frazil ice dynamics. Cold Reg. Sci. Technol. 1994, 22, 221–233. [Google Scholar] [CrossRef]
- Wang, S.M.; Doering, J.C. Numerical simulation of supercooling process and frazil ice evolution. J. Hydraul. Eng.-ASCE 2005, 131, 889–897. [Google Scholar] [CrossRef]
- Hammar, L.; Shen, H.T. Frazil evolution in channels. J. Hydraul. Res. 1995, 33, 291–306. [Google Scholar] [CrossRef]
- Ye, S.Q.; Doering, J. Simulation of the supercooling process and frazil evolution in turbulent flows. Can. J. Civ. Eng. 2004, 31, 915–926. [Google Scholar] [CrossRef]
- Wang, S.M.; Doering, J.C. Development of a mathematical model of frazil ice evolution based on laboratory tests using a counter-rotating flume. Can. J. Civ. Eng. 2007, 34, 210–218. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Spaceborne GNSS-R Sea Ice Detection Using Delay-Doppler Maps: First Results from the U.K. TechDemoSat-1 Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4795–4801. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Moloney, C. Neural Networks Based Sea Ice Detection and Concentration Retrieval from GNSS-R Delay-Doppler Maps. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3789–3798. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Sea ice sensing from GNSS-R data using convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1510–1514. [Google Scholar] [CrossRef]
- Naali, F.; Alipour-Fard, T.; Arefi, H. Spatial reslution sensitivity analysis of classifciation of sentinel-2 images by pre-trained deep models from big earth net database. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, XLIII-B3-2021, 87–92. [Google Scholar] [CrossRef]
- Ghiasi, Y.; Duguay, C.R.; Murfitt, J.; Asgarimehr, M.; Wu, Y. Potential of GNSS-R for the Monitoring of Lake Ice Phenology. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 660–673. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Multiobjective Function Optimization Using Nondominated Sorting Genetic Algorithms. Evol. Comput. 1994, 2, 1301–1308. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. Lect. Notes Comput. Sci. 2000, 1917, 849–858. [Google Scholar] [CrossRef]
- Kurek, W.; Ostfeld, A. Multi-objective optimization of water quality, pumps operation, and storage sizing of water distribution systems. J. Environ. Manag. 2013, 115, 189–197. [Google Scholar] [CrossRef]
- Wang, H.; Du, L.; Ma, S. Multi-objective open location-routing model with split delivery for optimized relief distribution in post-earthquake. Transp. Res. Part E Logist. Transp. Rev. 2014, 69, 160–179. [Google Scholar] [CrossRef]
- Hussain, I.; Parveen, A.; Ahmad, A.; Qadri, M.Y.; Qadri, N.N.; Ahmed, J. NSGA-II-based design space exploration for energy and throughput aware multicore architectures. Cybern. Syst. 2017, 48, 536–550. [Google Scholar] [CrossRef]
- Che, Z.H.; Chiang, T.A.; Lin, T.T. A multi-objective genetic algorithm for assembly planning and supplier selection with capacity constraints. Appl. Soft Comput. 2021, 101, 107030. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, J.; Xu, Y.P.; Guo, Y.; Wang, Y. Scenario-based multi-objective optimization of reservoirs in silt-laden rivers: A case study in the Lower Yellow River. Sci. Total Environ. 2022, 829, 154565. [Google Scholar] [CrossRef]
- Khare, V.; Yao, X.; Deb, K. Performance scaling of multi-objective evolutionary algorithms. In Proceedings of the Evolutionary Multi-Criterion Optimization (EMO 2003), Faro, Portugal, 8–11 April 2003; Springer: Berlin, Germany, 2003; pp. 376–390. [Google Scholar]
- Purshouse, R.C.; Fleming, P.J. Evolutionary many-objective optimisation: An exploratory analysis. In Proceedings of the Congress on Evolutionary Computation (CEC 2003), Canberra, ACT, Australia, 8–12 December 2003; pp. 2066–2073. [Google Scholar]
- Wagner, T.; Beume, N.; Naujoks, B. Pareto-, aggregation-, and indicator-based methods in many-objective optimization. In Proceedings of the Conference on Evolutionary Multi-Criterion Optimization (EMO 2007), Matsushima, Japan, 5–8 March 2007; Springer: Berlin, Germany, 2007; pp. 742–756. [Google Scholar]
- Brockhoff, D.; Zitzler, E. Objective reduction in evolutionary multiobjective optimization: Theory and applications. Evol. Comput. 2009, 17, 135–166. [Google Scholar] [CrossRef]
- Von Lücken, C.; Barán, B.; Brizuela, C. A survey on multi-objective evolutionary algorithms for many-objective problems. Comput. Optim. Appl. 2014, 58, 707–756. [Google Scholar] [CrossRef]
- Li, B.; Li, J.; Tang, K.; Yao, X. Many-objective evolutionary algorithms: A survey. ACM Comput. Surv. 2015, 48, 1–35. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Imada, R.; Setoguchi, Y.; Nojima, Y. Performance comparison of NSGA-II and NSGA-III on various many-objective test problems. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation, CEC 2016, Vancouver, BC, Canada, 24–29 July 2016; pp. 3045–3052. [Google Scholar]
- McFarlane, V.; Loewen, M.; Hicks, F. Measurements of the evolution of frazil ice particle size distributions. Cold Reg. Sci. Technol. 2015, 120, 45–55. [Google Scholar] [CrossRef]
- Holland, P.R.; Feltham, D.L.; Daly, S.F. On the Nusselt number for frazil ice growth—A correction to “Frazil evolution in channels” by Lars Hammar and Hung-Tao Shen. J. Hydraul. Res. 2007, 45, 421–424. [Google Scholar] [CrossRef]
- Daly, S.F. Frazil Ice Dynamics; US Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1984. [Google Scholar]
- Osterkamp, T. Frazil Ice Formation: A Review. J. Hydraul. Div. 1978, 104, 1239–1255. [Google Scholar] [CrossRef]
- Osterkamp, T.E.; Gosink, J.P. An Investigation of Frazil and Anchor Ice: Formation, Properties, Evolution and Dynamics; Alaska University: Fairbanks, AK, USA, 1985; pp. 1–18. [Google Scholar]
- Chow, R.; Mettin, R.; Lindinger, B.; Kurz, T.; Lauterborn, W. The importance of acoustic cavitation in the sonocrystallisation of ice—High speed observations of a single acoustic bubble. In Proceedings of the 2003 IEEE Ultrasonics Symposium, Honolulu, HI, USA, 5–8 October 2003; pp. 1447–1450. [Google Scholar]
- Clark, S.; Doering, J. Laboratory Experiments on Frazil-Size Characteristics in a Counterrotating Flume. J. Hydraul. Eng. 2006, 132, 94–101. [Google Scholar] [CrossRef]
- Clark, S.; Doering, J. Experimenta0l investigation of the effects of turbulence intensity on frazil ice characteristics. Can. J. Civ. Eng. 2008, 35, 67–79. [Google Scholar] [CrossRef]
- Matoušek, V. Frazil and skim ice formation in rivers. In Proceedings of the 11th International Symposium on Ice, Banff, AB, Canada, 15–19 June 1992; pp. 1–22. [Google Scholar]



| Parameter Range | k | Lower Limit Value of Stable Particle Size Range DB-min | Upper Limit Value of Stable Particle Size Range DB-max | Thickness-to-Width Ratio Std | Initial Value of Collision Frequency Calibration Coefficient Sequences M1 | Collision Fragmentation Calibration Coefficient KB | Collision Fragmentation Calibration Coefficient KC |
|---|---|---|---|---|---|---|---|
| Minimum value xi-min | 50 | 0.1 | 0.6 | 0.1 | 0.1 | 0 | 0.3 |
| Maximum values xi-max | 60 | 0.6 | 1.2 | 0.01 | 1 | 0.3 | 1 |
| Group | k | DB-min | DB-max | Std | M1 | KB | KC |
|---|---|---|---|---|---|---|---|
| Initial group | 53 | 0.4 | 0.8 | 0.1 | 0.9 | 0.32 | 0.7 |
| Optimization group 1 | 58 | 0.28 | 0.66 | 0.1 | 0.68 | 0.29 | 0.52 |
| Optimization group 2 | 60 | 0.28 | 0.64 | 0.1 | 0.66 | 0.3 | 0.4 |
| Optimization group 3 | 58 | 0.34 | 0.66 | 0.1 | 0.6 | 0.27 | 0.5 |
| Optimization group 4 | 58 | 0.16 | 0.7 | 0.1 | 0.86 | 0.26 | 0.62 |
| Water Temperature | Number of Frazil Ice Particles | Mean Particle Diameter | Standard Deviation of Diameter | |||||
|---|---|---|---|---|---|---|---|---|
| Average Difference Rate (%) | Average Difference Rate for 600–1000 s (%) | Average Difference Rate (%) | Average Difference Rate for 600–1000 s (%) | Average Difference Rate (%) | Average Difference Rate for 600–1000 s (%) | Average Difference Rate (%) | Average Difference Rate for 600–1000 s (%) | |
| Initial parameter group | 14.68 | 35.10 | 140.06 | 29.29 | 7.64 | 8.46 | 44.94 | 61.01 |
| Optimization group 1 | 15.49 | 33.64 | 127.83 | 19.74 | 5.53 | 6.16 | 33.75 | 37.90 |
| Optimization range (%) | −5.52 | 4.16 | 8.73 | 32.60 | 27.62 | 27.19 | 24.90 | 37.88 |
| Optimization group 2 | 16.69 | 33.08 | 126.62 | 17.83 | 4.37 | 4.43 | 30.39 | 26.33 |
| Optimization range (%) | −13.69 | 5.75 | 9.60 | 39.13 | 42.80 | 47.64 | 32.38 | 56.84 |
| Optimization group 3 | 15.12 | 34.50 | 128.81 | 18.93 | 6.54 | 7.60 | 33.68 | 37.63 |
| Optimization range (%) | −3.00 | 1.71 | 8.03 | 35.37 | 14.40 | 10.17 | 25.06 | 38.32 |
| Optimization group 4 | 15.05 | 35.54 | 138.89 | 17.88 | 3.87 | 3.48 | 33.45 | 38.41 |
| Optimization range (%) | −2.52 | −1.25 | 0.84 | 38.96 | 49.35 | 58.87 | 25.57 | 37.04 |
| Optimization Parameter Group | Average Difference Rate of Water Temperature (%) | Average Difference in Water Temperature (°C) | Maximum Difference Value of Water Temperature (°C) |
|---|---|---|---|
| 1 | 15.49 | 0.0057 | 0.044 |
| 2 | 16.69 | 0.0062 | 0.042 |
| 3 | 15.12 | 0.0057 | 0.043 |
| 4 | 15.05 | 0.0060 | 0.048 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Lian, J.; Zhao, X.; Yang, D. Parameter Optimization of Frazil Ice Evolution Model Based on NSGA-II Genetic Algorithm. Water 2024, 16, 1232. https://doi.org/10.3390/w16091232
Chen Y, Lian J, Zhao X, Yang D. Parameter Optimization of Frazil Ice Evolution Model Based on NSGA-II Genetic Algorithm. Water. 2024; 16(9):1232. https://doi.org/10.3390/w16091232
Chicago/Turabian StyleChen, Yunfei, Jijian Lian, Xin Zhao, and Deming Yang. 2024. "Parameter Optimization of Frazil Ice Evolution Model Based on NSGA-II Genetic Algorithm" Water 16, no. 9: 1232. https://doi.org/10.3390/w16091232
APA StyleChen, Y., Lian, J., Zhao, X., & Yang, D. (2024). Parameter Optimization of Frazil Ice Evolution Model Based on NSGA-II Genetic Algorithm. Water, 16(9), 1232. https://doi.org/10.3390/w16091232






