A Research on Multi-Index Intelligent Integrated Prediction Model of Catchment Pollutant Load under Data Scarcity
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
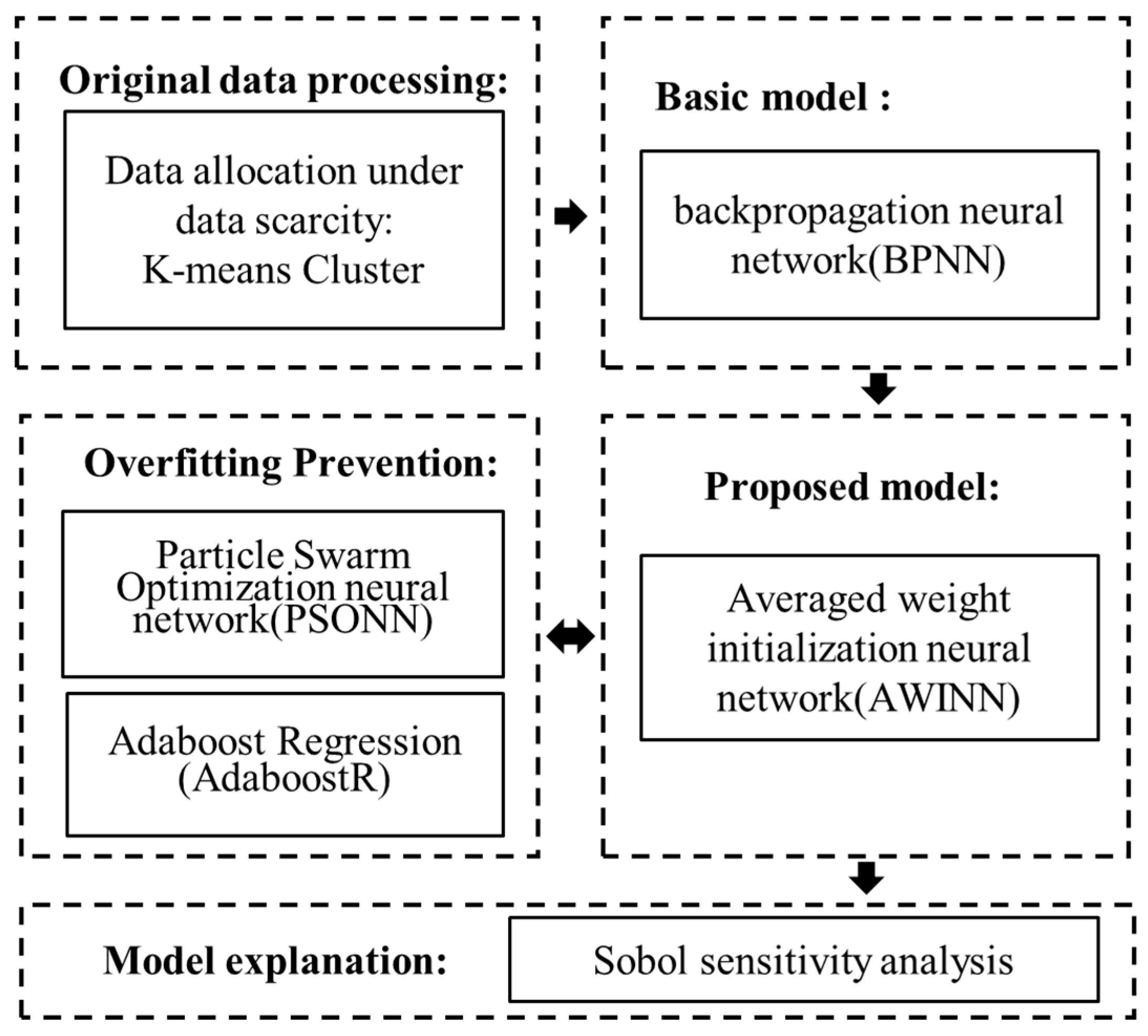
2.3. Methodology
2.3.1. Settings of BPNN Model
| Number of Hidden Layers | Structure | Setting Scheme 1 | Setting Scheme 2 |
|---|---|---|---|
| One | 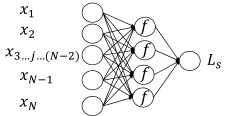 | {29,50,1} | {29,14,1} |
| Two | 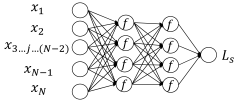 | {29,50,35,1} | {29,14,10,1} |
| Three | 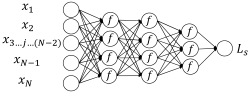 | {29,50,25,10,1} | {29,14,10,6,1} |
2.3.2. K-Means Clustering Algorithm and Division of Training–Validation–Test (TVT) Set

2.3.3. Fitting Precision
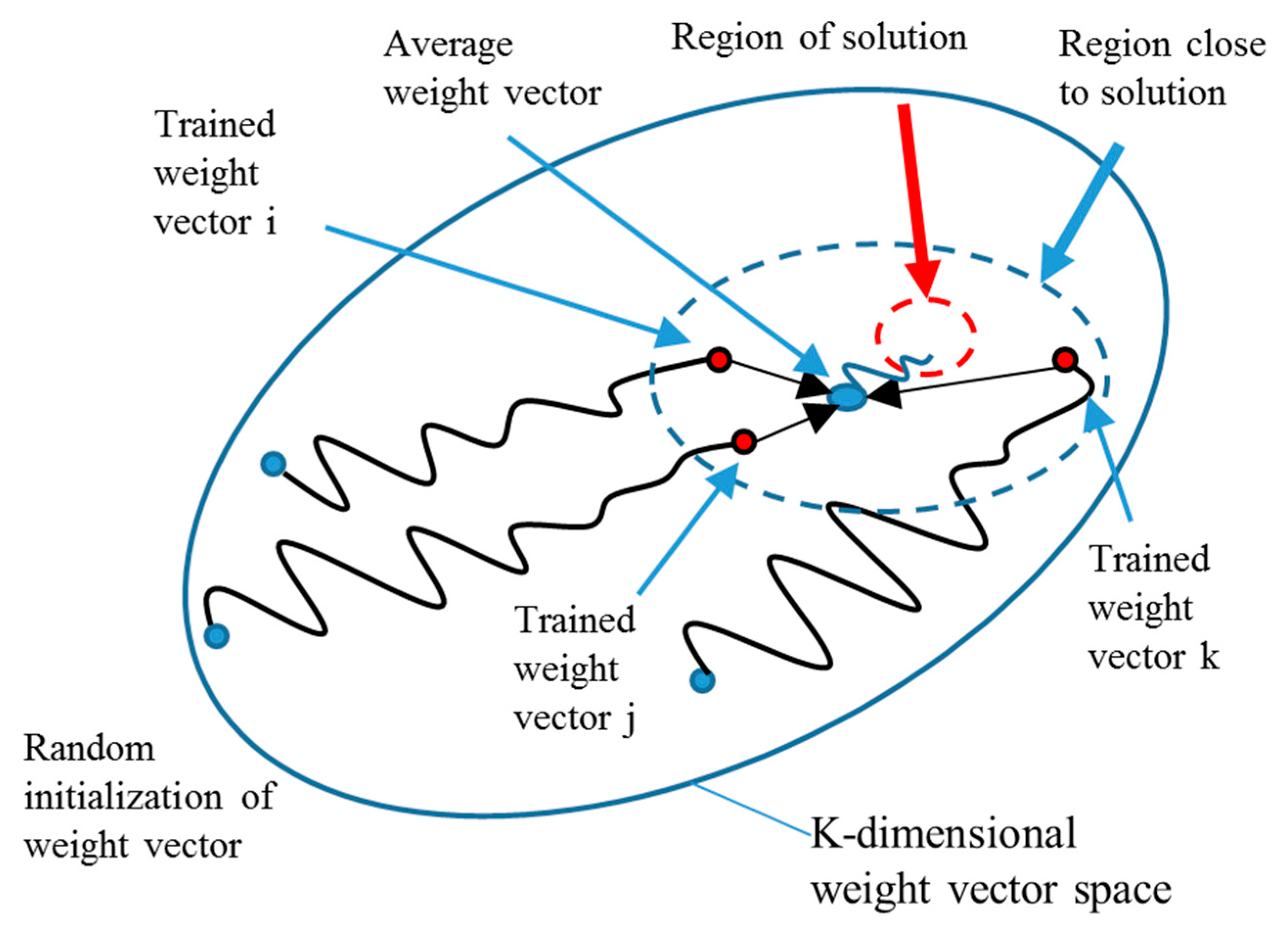
2.3.4. Average Weight Initialization Neural Network
- Implement the K-means algorithm in the existing dataset and divide the dataset into K categories. The TVT set is divided in the proportion of 70%:15%:15%. The number of groups of the TVT sets is .
- Train the training sets on the TVT sets. When the accuracy of the training–validation sets is up to standard, subtract the weight of the trained BPNN model as follows:
- 3.
- Average the weights of the trained models:
- 4.
- Divide the existing dataset into k TVT sets. The average weight in step (3) is applied as the initial weight to train and validate the NN models by the k TVT sets. The k-fold cross-validation method is used to assess the performance of the average weight initialization algorithm. The process stops when the accuracy in the test set reaches the standard of accuracy.
- 5.
- The average of the k models’ outputs can be used as the total output of the AWINN model.
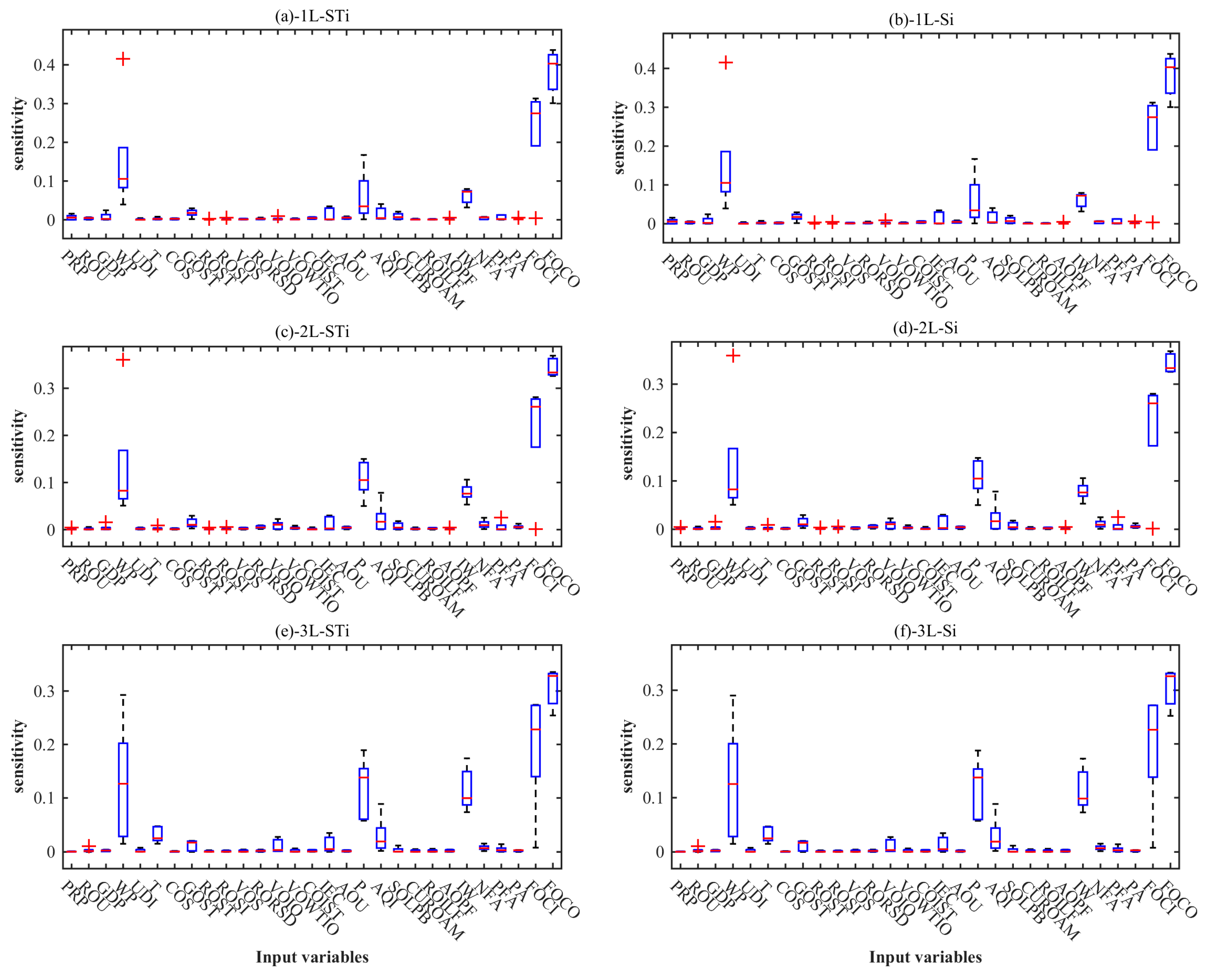
2.3.5. Sobol Sensitivity Analysis
- First-order sensitivity coefficient : standing for the sole influence of a single input parameter :
- Second-order sensitivity coefficient : standing for the joint influence of two input parameters and :
- Total sensitivity coefficient : standing for all of the influences, including a single input parameter :
2.3.6. Methods of Overfitting Prevention
3. Results
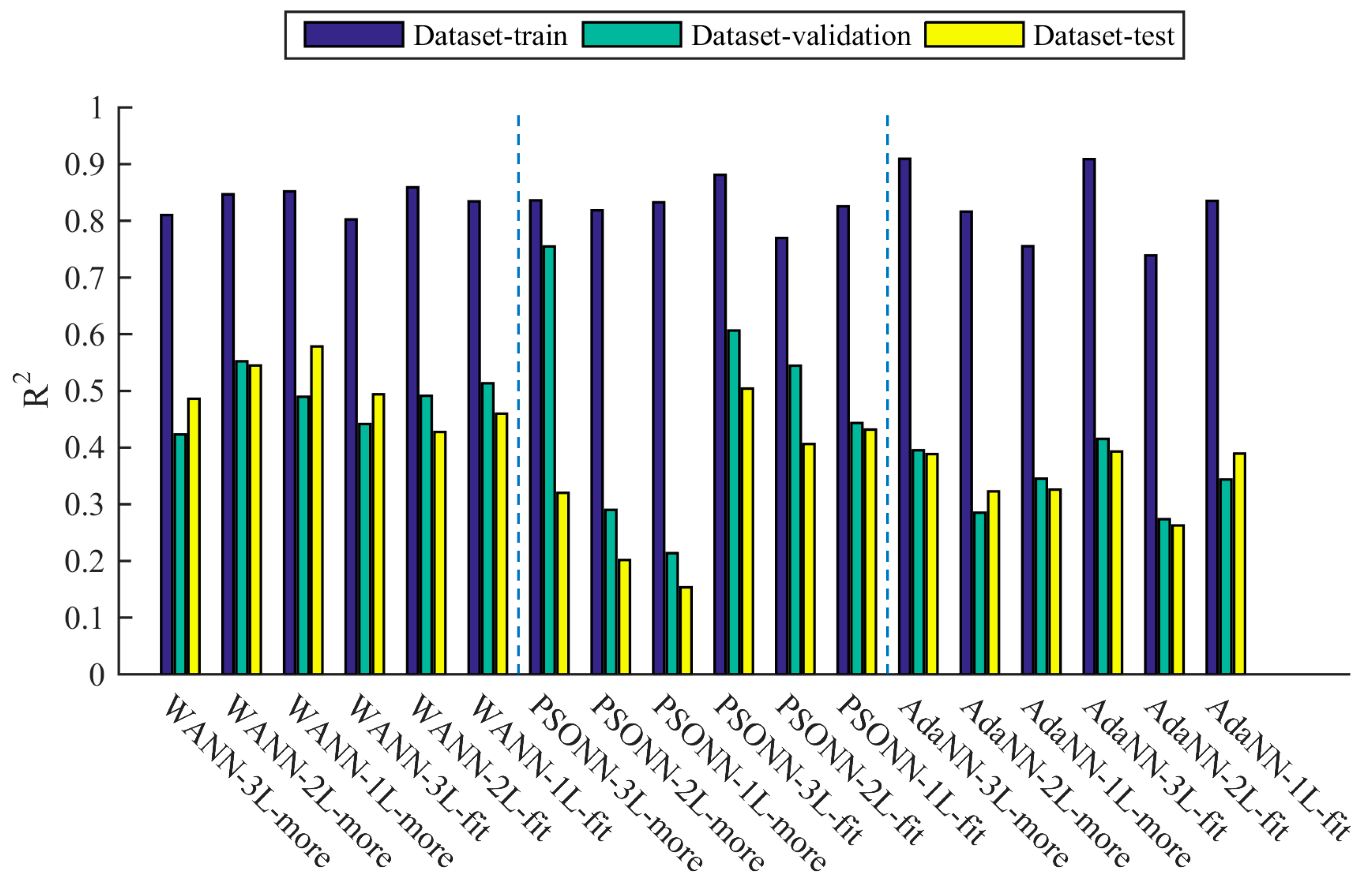
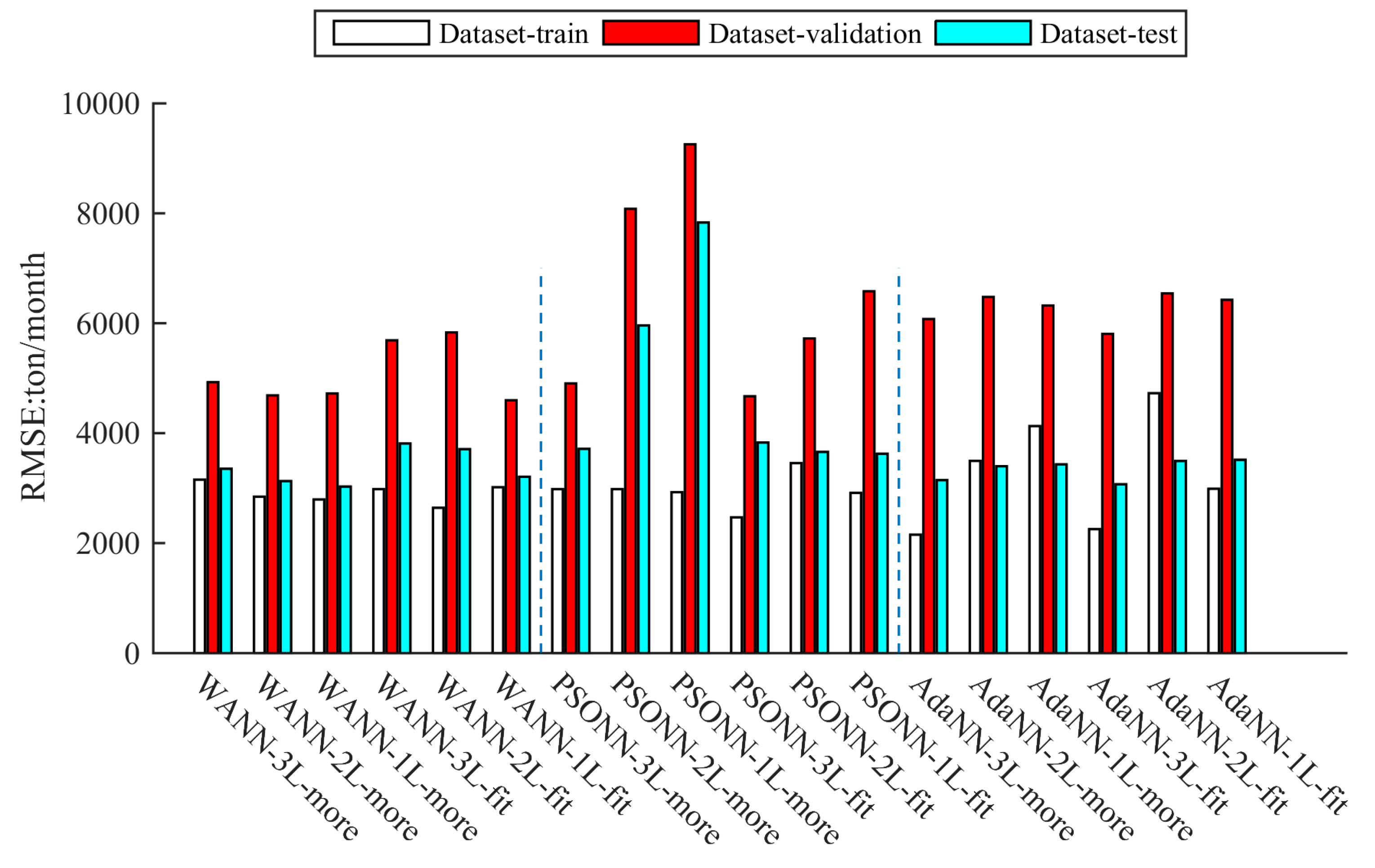
3.1. Comparison of Different Algorithms’ Fitting Accuracy
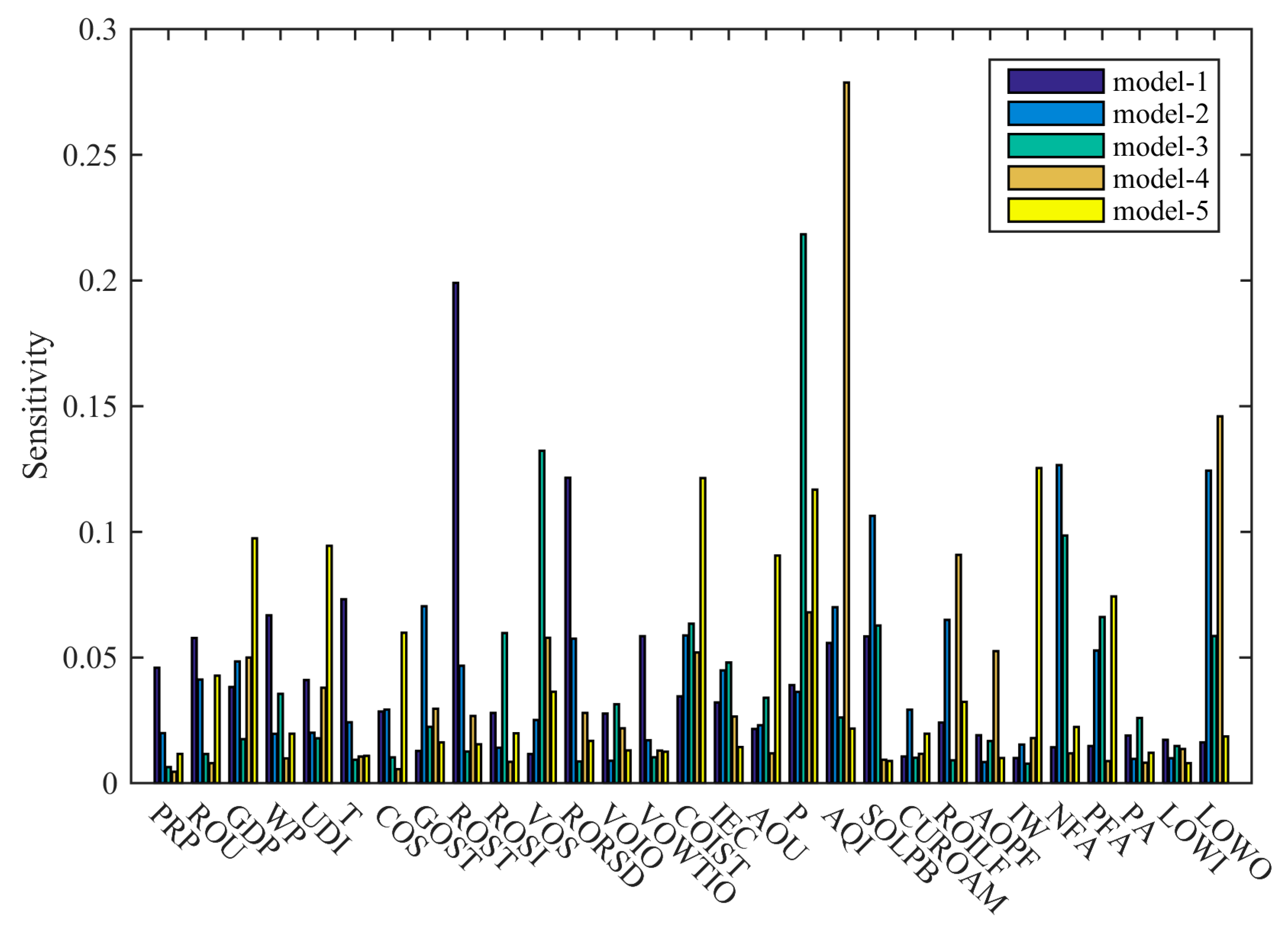
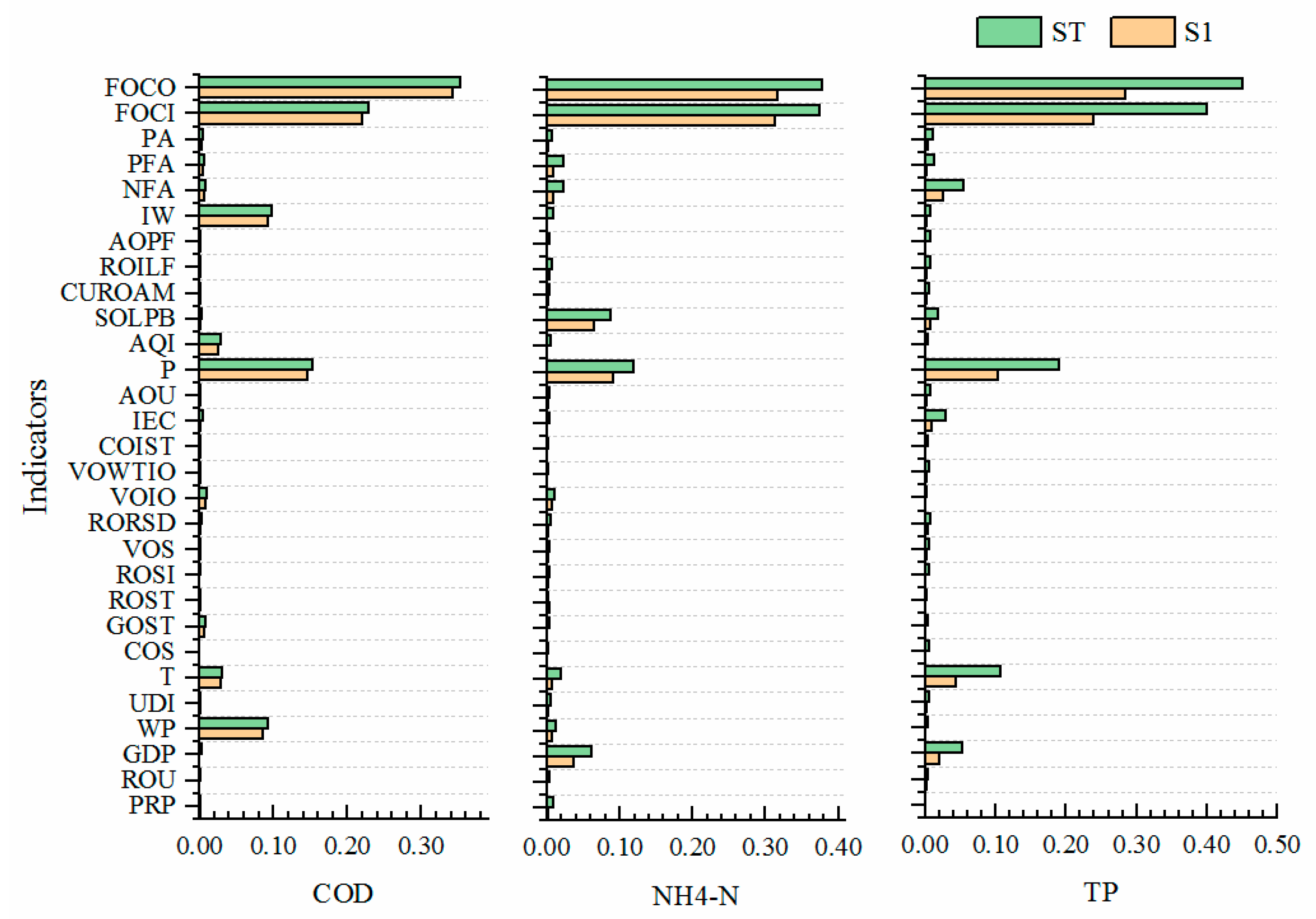
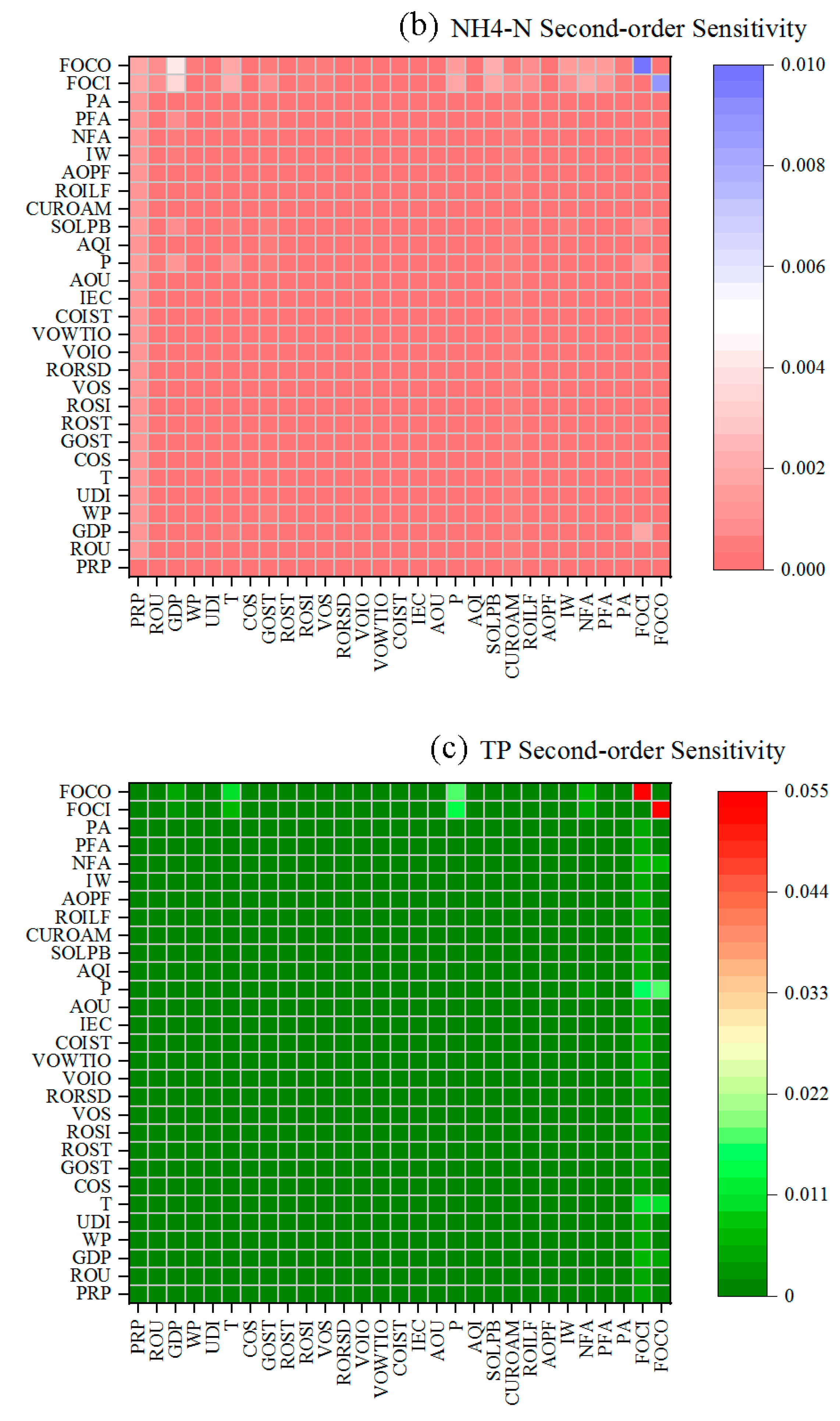
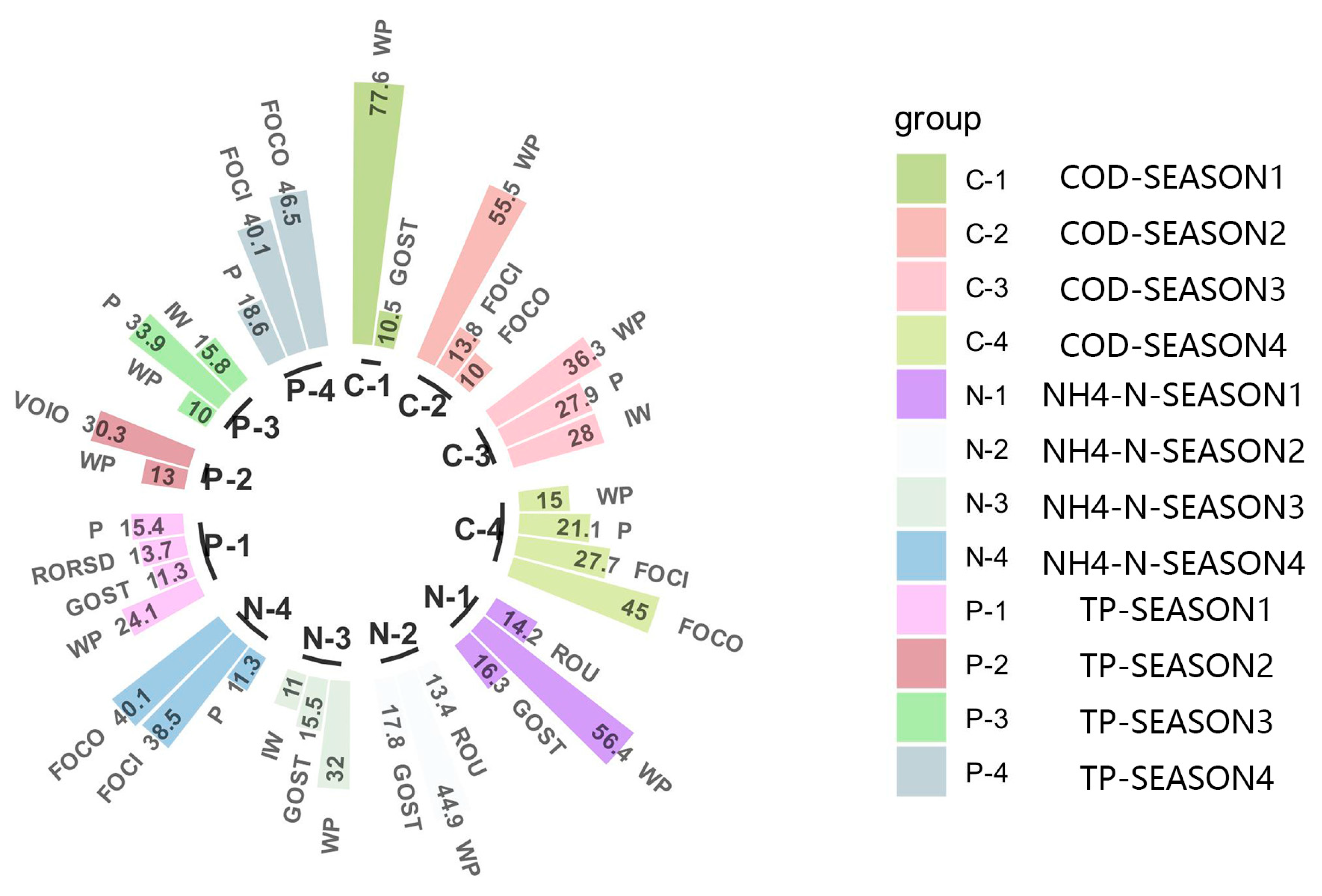
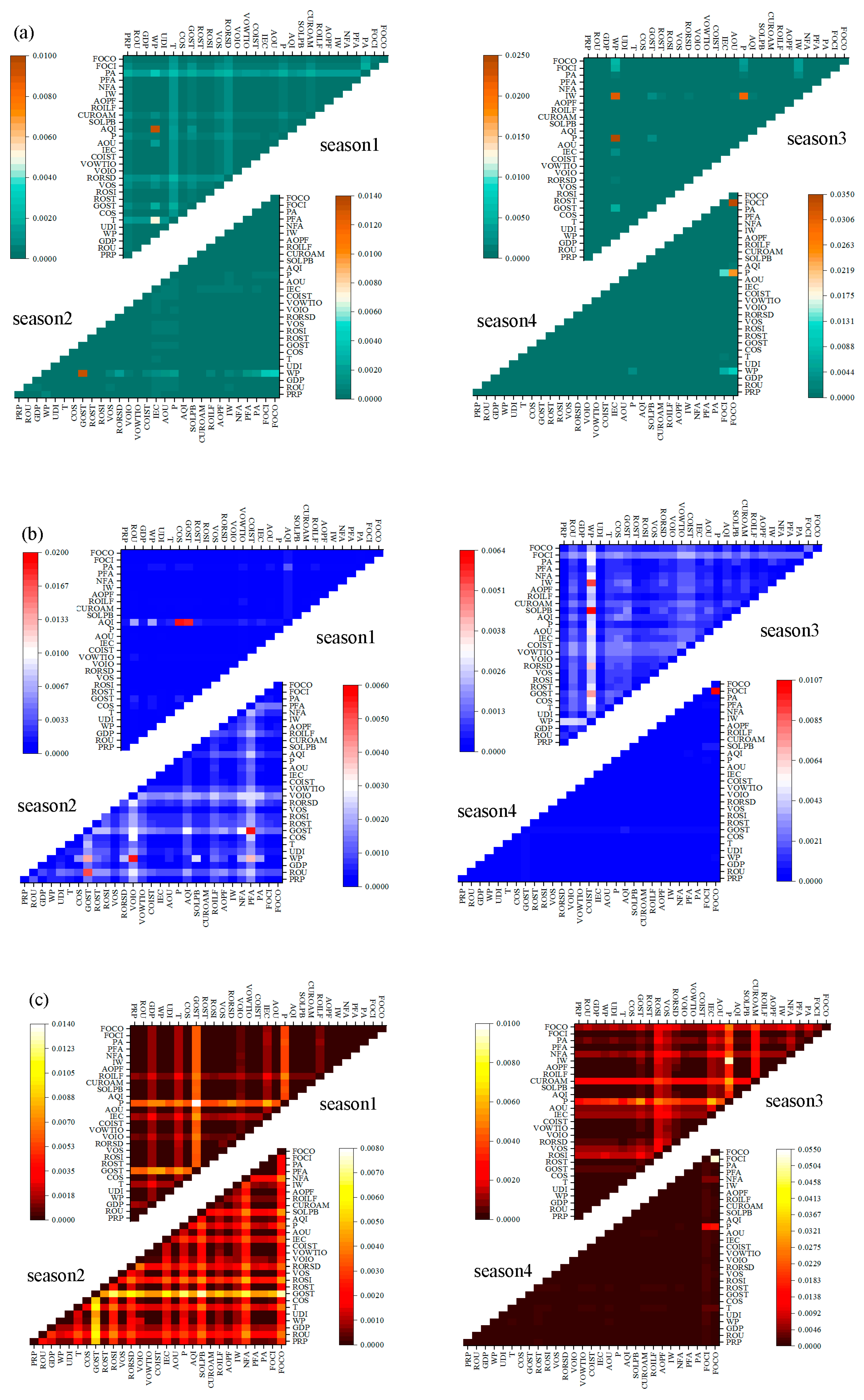
3.2. Results of Sensitivity Analysis
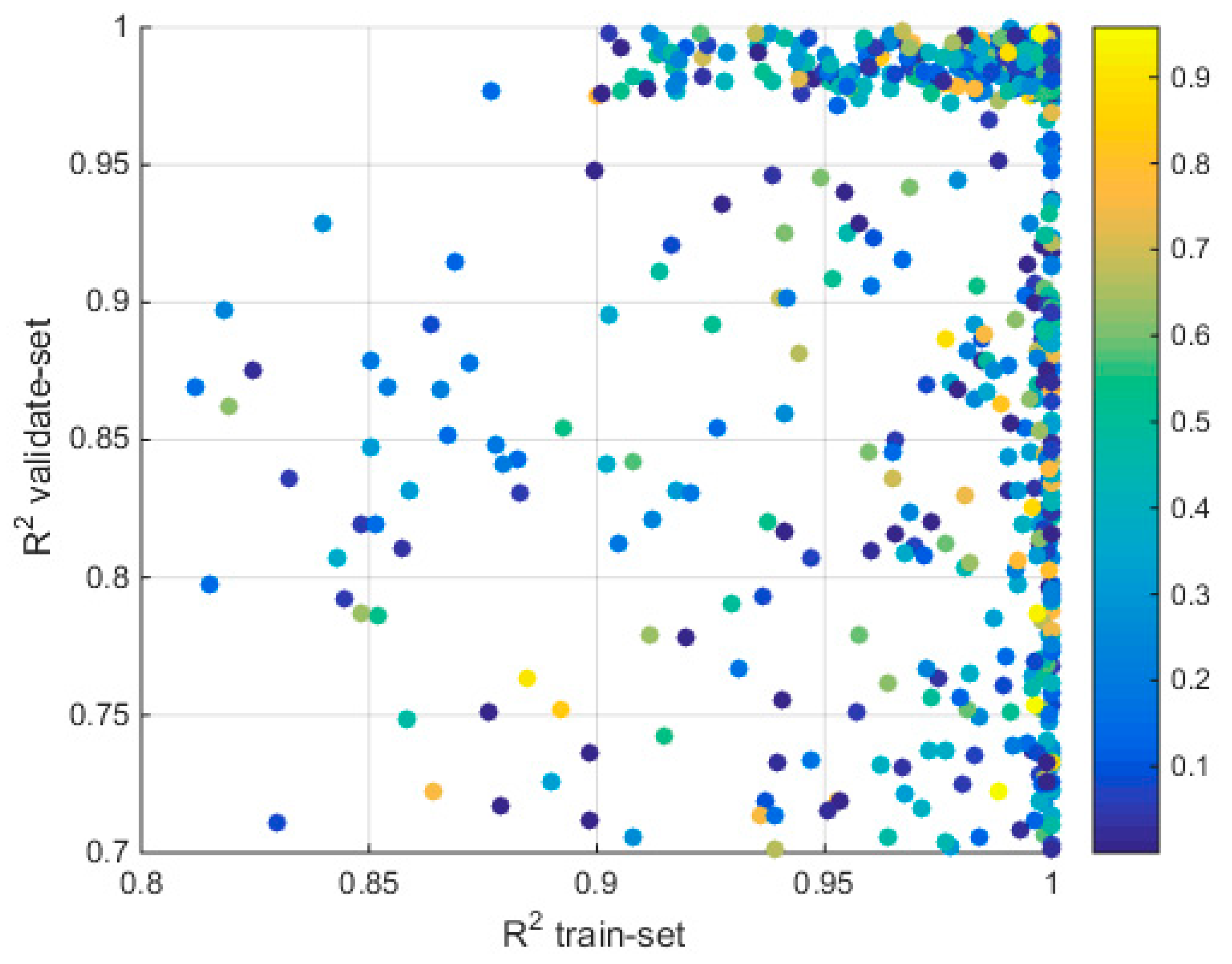
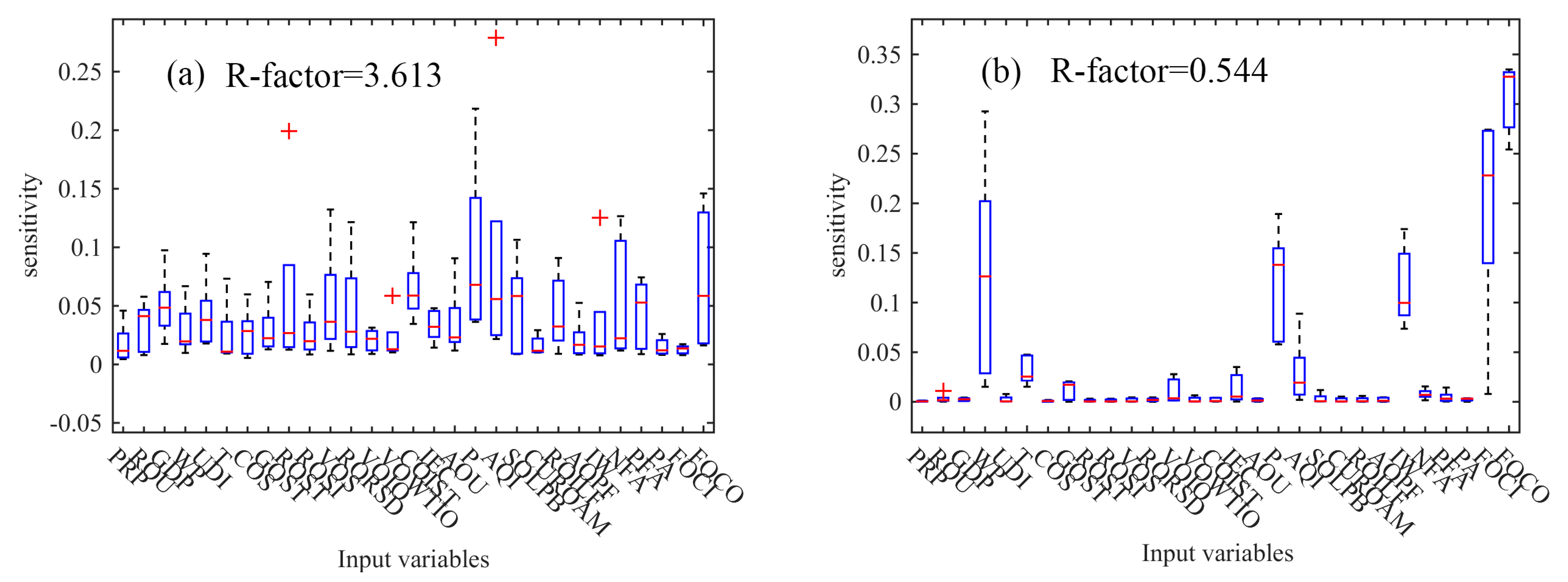
3.3. Results of Model Stability
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Monthly Data Collection and Data Processing of Input Factors
Appendix B. Details of Output Data
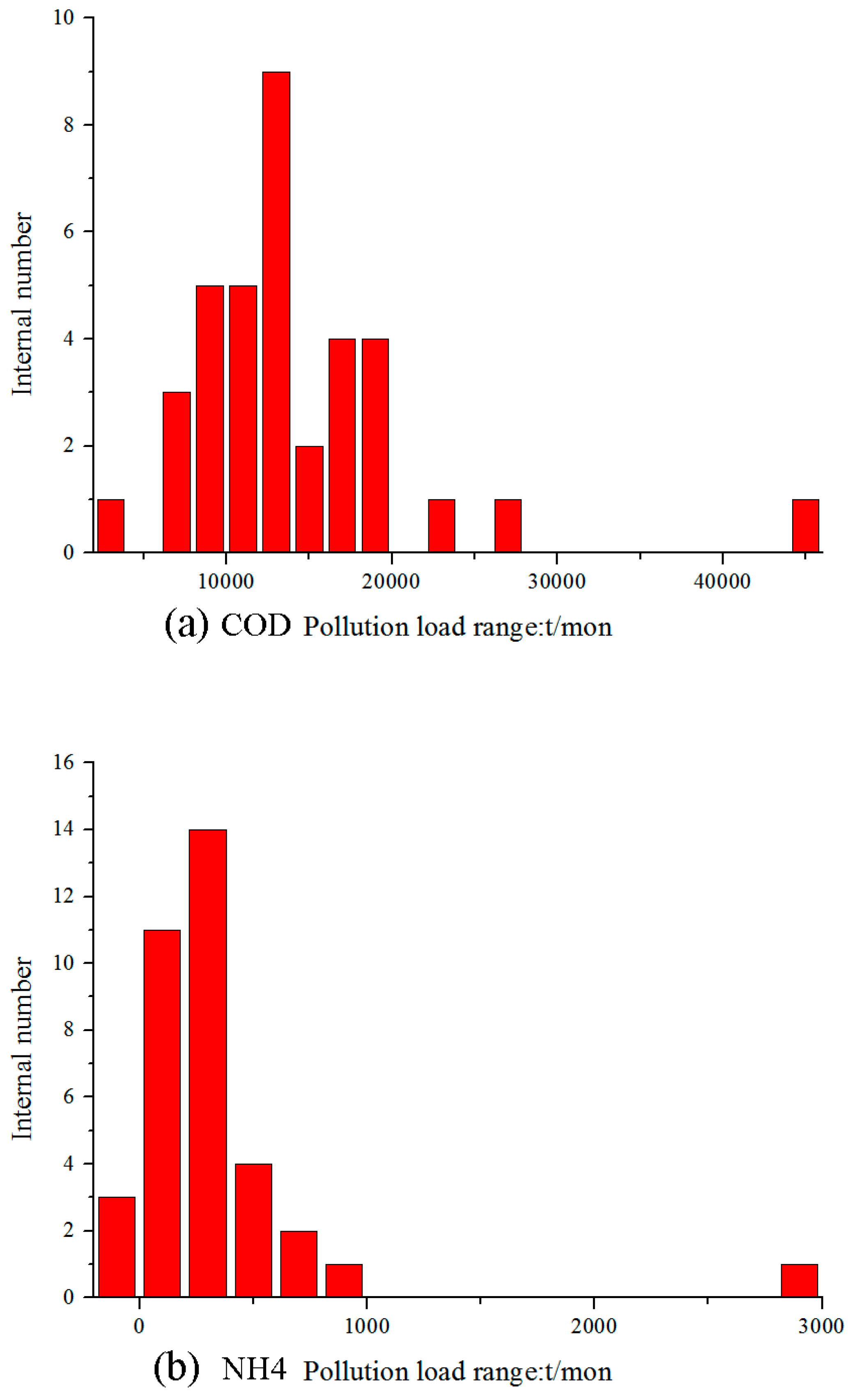
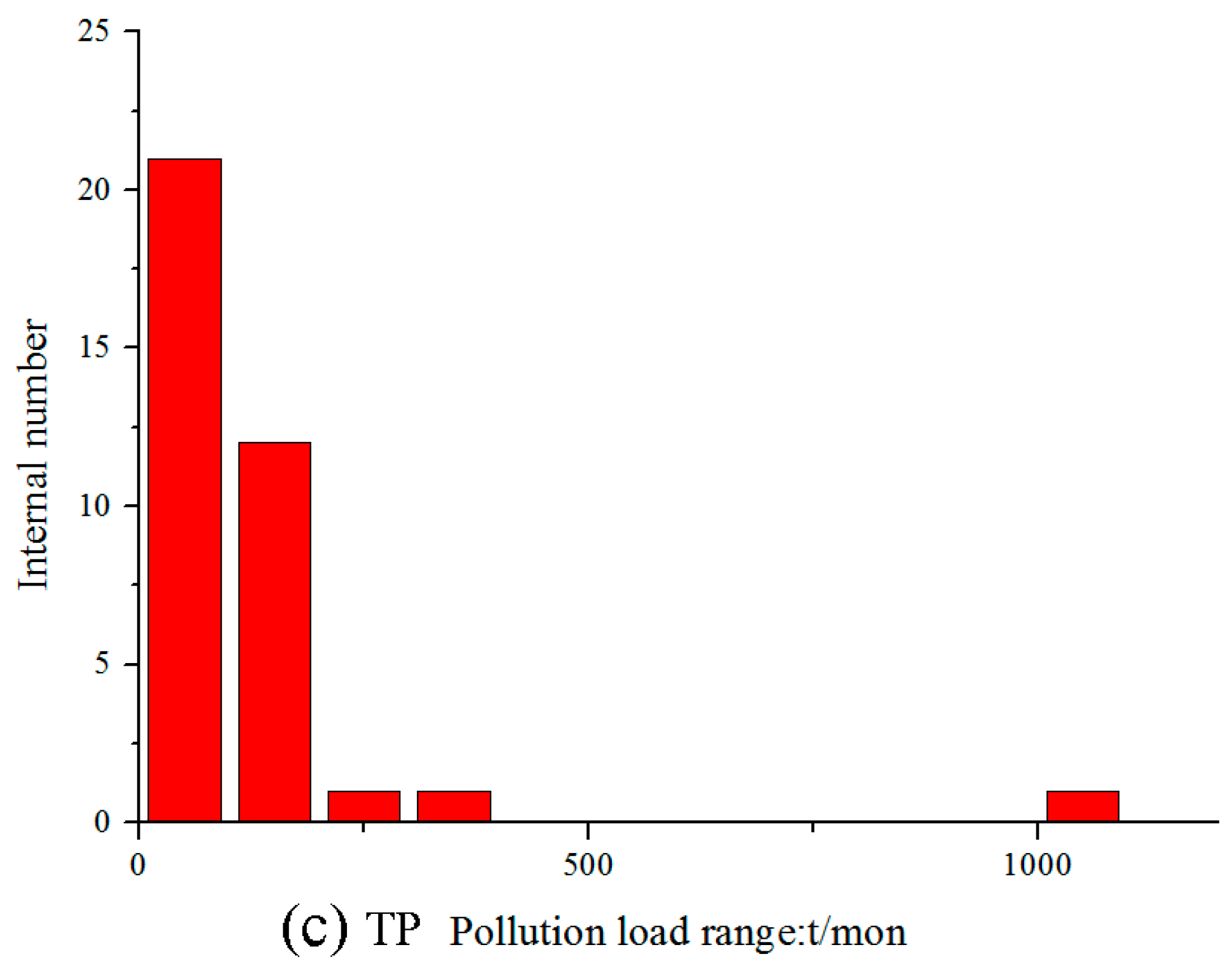
Appendix C. Overfitting and Instability of the Random Weight Initialization BP Algorithm
References
- Deletic, A.; Wang, H. Water Pollution Control for Sustainable Development. Engineering 2019, 5, 839–840. [Google Scholar] [CrossRef]
- Bowes, B.D.; Wang, C.; Ercan, M.B.; Culver, T.B.; Beling, P.A.; Goodall, J.L. Reinforcement learning-based real-time control of coastal urban stormwater systems to mitigate flooding and improve water quality. Environ. Sci. Water Res. Technol. 2022, 8, 2065–2086. [Google Scholar] [CrossRef]
- Najah Ahmed, A.; Binti Othman, F.; Abdulmohsin Afan, H.; Khaleel Ibrahim, R.; Ming Fai, C.; Shabbir Hossain, M.; Ehteram, M.; Elshafie, A. Machine learning methods for better water quality prediction. J. Hydrol. 2019, 578. [Google Scholar] [CrossRef]
- Liu, J.; Dietz, T.; Carpenter, S.R.; Alberti, M.; Folke, C.; Moran, E.; Pell, A.N.; Deadman, P.; Kratz, T.; Lubchenco, J.; et al. Complexity of coupled human and natural systems. Science 2007, 317, 1513–1516. [Google Scholar] [CrossRef] [PubMed]
- Larsen, T.A.; Hoffmann, S.; Lüthi, C.; Truffer, B.; Maurer, M. Emerging solutions to the water challenges of an urbanizing world. Science 2016, 352, 928–933. [Google Scholar] [CrossRef] [PubMed]
- Johnes, P.J. Evaluation and management of the impact of land use change on the nitrogen and phosphorus load delivered to surface waters: The export coefficient modelling approach. J. Hydrol. 1996, 183, 323–349. [Google Scholar] [CrossRef]
- Cheng, X.; Chen, L.; Sun, R.; Jing, Y. An improved export coefficient model to estimate non-point source phosphorus pollution risks under complex precipitation and terrain conditions. Environ. Sci. Pollut. Res. Int. 2018, 25, 20946–20955. [Google Scholar] [CrossRef] [PubMed]
- Poor, C.J.; Ullman, J.L. Using regression tree analysis to improve predictions of low-flow nitrate and chloride in Willamette River Basin watersheds. Environ. Manag. 2010, 46, 771–780. [Google Scholar] [CrossRef] [PubMed]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.; Van Griensven, A.; Van Liew, M.W. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, L.; Zhang, Y.; Hong, H.; Deng, H. Validation of an agricultural non-point source (AGNPS) pollution model for a catchment in the Jiulong River watershed, China. J. Environ. Sci. 2008, 20, 599–606. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Chen, H.; Zhou, C.; Huang, Y.; Qi, X.; Shen, R.; Liu, F.; Zuo, M.; Zou, X.; Wang, J.; et al. Comparative analysis of surface water quality prediction performance and identification of key water parameters using different machine learning models based on big data. Water Res. 2020, 171, 115454. [Google Scholar] [CrossRef] [PubMed]
- Heddam, S.; Kisi, O. Extreme learning machines: A new approach for modeling dissolved oxygen (DO) concentration with and without water quality variables as predictors. Environ. Sci. Pollut. Res. Int. 2017, 24, 16702–16724. [Google Scholar] [CrossRef] [PubMed]
- Kurniawan, I.; Hayder, G.; Mustafa, H. Predicting Water Quality Parameters in a Complex River System. J. Ecol. Eng. 2021, 22, 250–257. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Jiang, P.; Xu, H.; Lin, G.; Guo, D.; Wu, H. Water quality prediction based on recurrent neural network and improved evidence theory: A case study of Qiantang River, China. Environ. Sci. Pollut. Res. Int. 2019, 26, 19879–19896. [Google Scholar] [CrossRef] [PubMed]
- Ye, Q.; Yang, X.; Chen, C.; Wang, J. River Water Quality Parameters Prediction Method based on LSTM-RNN Model. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3 June 2019; pp. 3024–3028. [Google Scholar]
- Yu, J.W.; Kim, J.S.; Li, X.; Jong, Y.C.; Kim, K.H.; Ryang, G.I. Water quality forecasting based on data decomposition, fuzzy clustering and deep learning neural network. Environ. Pollut. 2022, 303, 119136. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-F.; Fitch, P.; Thorburn, P.J. Predicting the Trend of Dissolved Oxygen Based on the kPCA-RNN Model. Water 2020, 12, 585. [Google Scholar] [CrossRef]
- Guo, H.; Huang, J.J.; Zhu, X.; Wang, B.; Tian, S.; Xu, W.; Mai, Y. A generalized machine learning approach for dissolved oxygen estimation at multiple spatiotemporal scales using remote sensing. Environ. Pollut. 2021, 288, 117734. [Google Scholar] [CrossRef]
- Hu, W.; Liu, J.; Wang, H.; Miao, D.; Shao, D.; Gu, W. Retrieval of TP Concentration from UAV Multispectral Images Using IOA-ML Models in Small Inland Waterbodies. Remote Sens. 2023, 15, 1250. [Google Scholar] [CrossRef]
- Golden, H.E.; Lane, C.R.; Prues, A.G.; D’Amico, E. Boosted Regression Tree Models to Explain Watershed Nutrient Concentrations and Biological Condition. JAWRA J. Am. Water Resour. Assoc. 2016, 52, 1251–1274. [Google Scholar] [CrossRef]
- Granata, F.; Papirio, S.; Esposito, G.; Gargano, R.; De Marinis, G. Machine Learning Algorithms for the Forecasting of Wastewater Quality Indicators. Water 2017, 9, 105. [Google Scholar] [CrossRef]
- Lek, S.; Guiresse, M.; Giraudel, J.-L. Predicting stream nitrogen concentration from watershed features using neural networks. Water Res. 1999, 33, 3469–3478. [Google Scholar] [CrossRef]
- Li, S.; Cai, X.; Emaminejad, S.A.; Juneja, A.; Niroula, S.; Oh, S.; Wallington, K.; Cusick, R.D.; Gramig, B.M.; John, S.; et al. Developing an integrated technology-environment-economics model to simulate food-energy-water systems in Corn Belt watersheds. Environ. Model. Softw. 2021, 143, 105083. [Google Scholar] [CrossRef]
- Liu, M.; Lu, J. Support vector machine-an alternative to artificial neuron network for water quality forecasting in an agricultural nonpoint source polluted river? Environ. Sci. Pollut. Res. Int. 2014, 21, 11036–11053. [Google Scholar] [CrossRef] [PubMed]
- Bejani, M.M.; Ghatee, M. A systematic review on overfitting control in shallow and deep neural networks. Artif. Intell. Rev. 2021, 54, 6391–6438. [Google Scholar] [CrossRef]
- Ying, X. An Overview of Overfitting and Its Solutions. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; p. 022022. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Solomatine, D.P.; Shrestha, D.L. AdaBoost. RT: A Boosting Algorithm for Regression Problems. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; pp. 1163–1168. [Google Scholar]
- Bartoletti, N.; Casagli, F.; Marsili-Libelli, S.; Nardi, A.; Palandri, L. Data-driven rainfall/runoff modelling based on a neuro-fuzzy inference system. Environ. Model. Softw. 2018, 106, 35–47. [Google Scholar] [CrossRef]
- Jia, W.; Zhao, D.; Zheng, Y.; Hou, S. A novel optimized GA–Elman neural network algorithm. Neural Comput. Appl. 2017, 31, 449–459. [Google Scholar] [CrossRef]
- Rohmat, F.I.W.; Gates, T.K.; Labadie, J.W. Enabling improved water and environmental management in an irrigated river basin using multi-agent optimization of reservoir operations. Environ. Model. Softw. 2021, 135, 104909. [Google Scholar] [CrossRef]
- Shao, D.; Nong, X.; Tan, X.; Chen, S.; Xu, B.; Hu, N. Daily Water Quality Forecast of the South-To-North Water Diversion Project of China Based on the Cuckoo Search-Back Propagation Neural Network. Water 2018, 10, 1471. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A Cooperative Approach to Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 225–239. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-term water quality variable prediction using a hybrid CNN–LSTM deep learning model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Chen, H.; Chen, A.; Xu, L.; Xie, H.; Qiao, H.; Lin, Q.; Cai, K. A deep learning CNN architecture applied in smart near-infrared analysis of water pollution for agricultural irrigation resources. Agric. Water Manag. 2020, 240, 106303. [Google Scholar] [CrossRef]
- Nouraki, A.; Alavi, M.; Golabi, M.; Albaji, M. Prediction of water quality parameters using machine learning models: A case study of the Karun River, Iran. Environ. Sci. Pollut. Res. Int. 2021, 28, 57060–57072. [Google Scholar] [CrossRef] [PubMed]
- Bousquet, O.; Elisseeff, A. Stability and generalization. J. Mach. Learn. Res. 2002, 2, 499–526. [Google Scholar]
- Narkhede, M.V.; Bartakke, P.P.; Sutaone, M.S. A review on weight initialization strategies for neural networks. Artif. Intell. Rev. 2021, 55, 291–322. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Nguyen, D.; Widrow, B. Improving the Learning Speed of 2-layer Neural Networks by Choosing Initial Values of the Adaptive Weights. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; pp. 21–26. [Google Scholar]
- Go, J.; Lee, C. Analyzing Weight Distribution of Neural Networks. In Proceedings of the IJCNN’99. International Joint Conference on Neural Networks. Proceedings (Cat. No. 99CH36339), Washington, DC, USA, 10–16 July 1999; pp. 1154–1157. [Google Scholar]
- Go, J.; Baek, B.; Lee, C. Analyzing Weight Distribution of Feedforward Neural Networks and Efficient Weight Initialization. In Proceedings of the Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR), Lisbon, Portugal, 18–20 August 2004; pp. 840–849. [Google Scholar]
- Akhtar, N.; Syakir Ishak, M.I.; Bhawani, S.A.; Umar, K. Various Natural and Anthropogenic Factors Responsible for Water Quality Degradation: A Review. Water 2021, 13, 2660. [Google Scholar] [CrossRef]
- Pastres, R.; Franco, D.; Pecenik, G.; Solidoro, C.; Dejak, C. Local sensitivity analysis of a distributed parameters water quality model. Reliab. Eng. Syst. Saf. 1997, 57, 21–30. [Google Scholar] [CrossRef]
- Wang, R.; Kim, J.H.; Li, M.H. Predicting stream water quality under different urban development pattern scenarios with an interpretable machine learning approach. Sci. Total Environ. 2021, 761, 144057. [Google Scholar] [CrossRef] [PubMed]
- Razavi, S.; Jakeman, A.; Saltelli, A.; Prieur, C.; Iooss, B.; Borgonovo, E.; Plischke, E.; Lo Piano, S.; Iwanaga, T.; Becker, W.; et al. The Future of Sensitivity Analysis: An essential discipline for systems modeling and policy support. Environ. Model. Softw. 2021, 137, 104954. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Moré, J.J. The Levenberg-Marquardt Algorithm: Implementation and Theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Schoner, W. Reaching the generalisation maximum of backpropagation networks. In Artificial Neural Networks; Aleksandr, I., Taylor, J., Eds.; Elsevier: Amsterdam, The Netherlands, 1992; Volume 2, pp. 91–94. [Google Scholar]
- Wang, Y.; Zhang, W.; Zhao, Y.; Peng, H.; Shi, Y. Modelling water quality and quantity with the influence of inter-basin water diversion projects and cascade reservoirs in the Middle-lower Hanjiang River. J. Hydrol. 2016, 541, 1348–1362. [Google Scholar] [CrossRef]
- Cheng, B.-F.; Zhang, Y.; Xia, R.; Zhang, N.; Zhang, X.-F. Temporal and spatial variations in water quality of Hanjiang river and its influencing factors in recent years. Huan Jing Ke Xue = Huanjing Kexue 2021, 42, 4211–4221. [Google Scholar] [PubMed]
- Runkel, R.L.; Crawford, C.G.; Cohn, T.A. Load Estimator (LOADEST): A FORTRAN Program for Estimating Constituent Loads in Streams and Rivers; U.S. Publications Warehouse: Reston, VA, USA, 2004; pp. 2328–7055. Available online: https://pubs.usgs.gov/publication/tm4A5 (accessed on 24 March 2024).



| Category | Related Factor |
|---|---|
| Point source of urban life | Permanent resident population (PRP), gross national product * (GDP), rate of urbanization (ROU), water price * (WP), urban disposable income * (UDI), temperature * (T), capacity of sewage treatment plant * (COS), grade of sewage treatment * (GOST), rate of sewage treatment (ROST), rate of sewage interception * (ROSI) |
| Point source of industry | Value of industrial output * (VOIO), volume of water by CNY 10,000 industrial output (VOWTIO), capacity of industrial sewage treatment (COIST), industrial electricity consumption * (IEC), value of service industry output * (VOS) |
| Non-point source of urban life | Area of urban (AOU), precipitation * (P), ratio of rainwater and sewage diversion * (RORSD), air-quality index * (AQI) |
| Non-point source of rural life | Rural population (RP), volume of rural life water utilization (VORLWU), precipitation * (P) |
| Non-point source of planting | Area of paddy field (AOPF), irrigation water (IW), nitrogen fertilizer application (NFA), phosphate fertilizer application (PFA), pesticide application (PA), precipitation * (P) |
| Non-point source of the breeding industry | Stock of livestock and poultry breeding (SOLPB), rate of intensive livestock farm (ROILF), comprehensive utilization rate of aquaculture manure (CUROAM), precipitation * (P) |
| Pollutant reaction in channel | Flow of catchment inlet * (FOCI), flow of catchment outlet * (FOCO) |
| Related Factor | Source |
|---|---|
| PRP, ROU, WP, COS, GOST, ROST, ROSI, COIST, AOU, RORSD | Statistical Yearbook of Xiangyang City 1980–2020 |
| AOPF, NFA, PFA, PA, SOLPB, ROILF | Rural Yearbook of Hubei Province 2015–2020 |
| GDP, UDI, VOIO, IEC | Xiangyang City statistics monthly report January 2015–December 2017 |
| AQI | PM2.5 historical data website https://www.aqistudy.cn/historydata/ (accessed on 1 January 2015) |
| T, P | China meteorological data website http://data.cma.cn/ (accessed on 1 January 2015) |
| FOCI, FOCO | Official website of Hubei Water Conservancy Department https://slt.hubei.gov.cn/ (accessed on 1 January 2015) |
| Water quality (WQ) | Water Resources Department of Hubei Province |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, D.; Gu, W.; Li, W.; Liu, J.; Hu, W.; Feng, J.; Shao, D. A Research on Multi-Index Intelligent Integrated Prediction Model of Catchment Pollutant Load under Data Scarcity. Water 2024, 16, 1132. https://doi.org/10.3390/w16081132
Miao D, Gu W, Li W, Liu J, Hu W, Feng J, Shao D. A Research on Multi-Index Intelligent Integrated Prediction Model of Catchment Pollutant Load under Data Scarcity. Water. 2024; 16(8):1132. https://doi.org/10.3390/w16081132
Chicago/Turabian StyleMiao, Donghao, Wenquan Gu, Wenhui Li, Jie Liu, Wentong Hu, Jinping Feng, and Dongguo Shao. 2024. "A Research on Multi-Index Intelligent Integrated Prediction Model of Catchment Pollutant Load under Data Scarcity" Water 16, no. 8: 1132. https://doi.org/10.3390/w16081132
APA StyleMiao, D., Gu, W., Li, W., Liu, J., Hu, W., Feng, J., & Shao, D. (2024). A Research on Multi-Index Intelligent Integrated Prediction Model of Catchment Pollutant Load under Data Scarcity. Water, 16(8), 1132. https://doi.org/10.3390/w16081132





