Abstract
Due to the long duration and high cost of traditional pumping tests, the response of well water levels to seismic waves, earth tides, and barometric pressure provides a feasible method for determining continuous changes in aquifer hydraulic parameters. Aimed at the problem that the response phase shift of well BB water levels to tide M2 is greater than that of tide O1, this paper preferentially calculated the time series changes in S, Be, n, and BKu based on the response mechanism of well water levels to barometric pressure and earth tides with the help of the smooth moving method. Then, by using the mixed flow model, the variation in the transmissivity and leakage coefficient over time was simultaneously obtained, and the evolution process and characteristics of aquifer parameters near well BB caused by the Wenchuan earthquake are ultimately discussed. The calculation results are basically consistent with the previous pumping test, and have been verified and compared by using other scholars’ methods. This solving process avoids problems such as excessive dependence on initial values, multiple solutions, and unstable tide O1, which has a promoting effect on the study of the impact of seismic activity on aquifer systems.
1. Introduction
As the main hydrodynamic parameters of an aquifer, the transmissivity (T) and leakage coefficient (σ) represent the horizontal and vertical water exchange capacity of the aquifer, respectively, which directly determine the characteristics of groundwater movement and the law of solute transport [1]. The accurate calculation of aquifer hydraulic parameters and their continuous changes play an important role in guiding the rational development and utilization of groundwater resources, and also provide a theoretical basis for the stability analysis of underground space, the safe burial of nuclear waste, and the migration of groundwater pollutants [2].
Groundwater-level dynamics is an important observation reflecting the crustal activity, which is often affected by many factors, such as barometric pressure [3,4,5], earth tides [6,7], seismic wave propagation [8,9,10], and fault activity [11,12], so the response of well water levels to these factors provides a feasible method for determining aquifer hydraulic parameters. Cooper et al. [8] established a model for the response of well water levels to periodic loading, and proposed that the response amplitude of well water levels to pore pressure mainly depends on the dimensions of the well and the transmissivity and storage coefficient (S) of the aquifer. Hsieh et al. [7] and Rojstaczer [13] estimated the hydraulic parameters of an aquifer by using the response models of well water levels to barometric pressure and earth tides. Following Roeloffs [14], Doan and Brodsky [15] developed a tutorial to estimate the poroelastic parameters and the permeability of the reservoir by analyzing the amplitude and phase of the tidal response. Wang et al. [16,17] established a mixed flow model for the tidal response of groundwater in an aquifer; the model gave the expressions of the T and σ, and they provided an important supplement to the previous tidal analysis model. Based on the analysis of changes in groundwater responses to earth tides and barometric pressure, Wang and Manga [18] reviewed the latest research progress on the effects of earthquakes on aquifer parameters, and stressed the importance of real-time and continuous monitoring of groundwater. The above models have been widely used in the study of co-seismic well water level response mechanisms [19,20,21], the response of well–aquifer systems to different frequency waves [22,23], and changes in aquifer permeability caused by earthquakes [24,25,26,27,28,29,30]. For example, Shi et al. [20] identified five types of co-seismic groundwater level responses and two types of post-earthquake responses by recording the response of a large number of well water levels to earthquakes. Sun et al. [22] compared the sensitivity of two wells to different cyclic loads in the same area. Wang et al. [26] analyzed the causes and frequency of increases in the vertical permeability of an aquifer caused by large earthquakes.
Previous studies could only calculate the permeability (T) or leakage coefficient (σ) of an aquifer using the horizontal flow model or the vertical flow model separately [7,26], which cannot reflect the horizontal and vertical water exchange capacity of the aquifer simultaneously. Sun et al. [31] calculated the aquifer parameters using a graphical method, where only one set of T and σ values can be obtained at a time. Yang et al. [30,32,33] used tide M2 and O1 responses in a least squares inversion of the unknown parameters in the leaky aquifer model, with three inputs used to obtain three parameters (S, T, and σ) simultaneously, which reflect the water storage capacity and the horizontal and vertical water exchange capacity of the aquifer. This method is suitable for situations where the phase shift of tide O1 is greater than that of tide M2. For the situation that the phase shift of tide M2 is larger than that of tide O1 in well BB, the time series and correct solution cannot be obtained by using Yang et al.’s method. And there will be multiple solutions in the calculation results using this method. Here, taking well BB near the Huayingshan fault as an example, this paper attempts to explore the way of obtaining the time series changes in aquifer hydraulic parameters in this case by synthesizing the barometric pressure and earth tide effect on the well water level, and discusses the accuracy, applicability, and advantages and disadvantages of the solution process, so as to achieve the purpose of explaining the changes in aquifer hydraulic characteristics caused by seismic activities.
2. Observation Background and Data
The Huayingshan fault is located in southwest China and is a type of dextral strike slip reverse fault that is about 460 km long. It is a boundary fault between the block-type fold belt in eastern Sichuan and the gentle structure of central Sichuan. Well BB is located within 10 km of the Huayingshan fault zone (Figure 1a) (Table S1), which is a typical “red bed” area in Sichuan basin; that is to say, the main exposed strata in this area are interbeds of purplish-red mudstone and gray–white arkose. The underground aquifer is mainly composed of feldspathic sandstone with a thickness of about 10~50 m. The upper and lower water-bearing sandstones are sandwiched by relatively impermeable mudstones. This type of aquifer is widespread and has numerous hydraulic connections. The confined water in this area’s red bed is recharged primarily by precipitation in the outcrop area, followed by vertical infiltration of the surface water and partial leakage of adjacent aquifers. The precipitation and surface water infiltrate the aquifer through the exposed crack near the surface, and runoff or vertical leakage occurs along the river bed or along the sandstone fissure. When the aquifer is depleted, groundwater is discharged into the surface water or spring, and it can also be discharged through the adjacent aquifers.
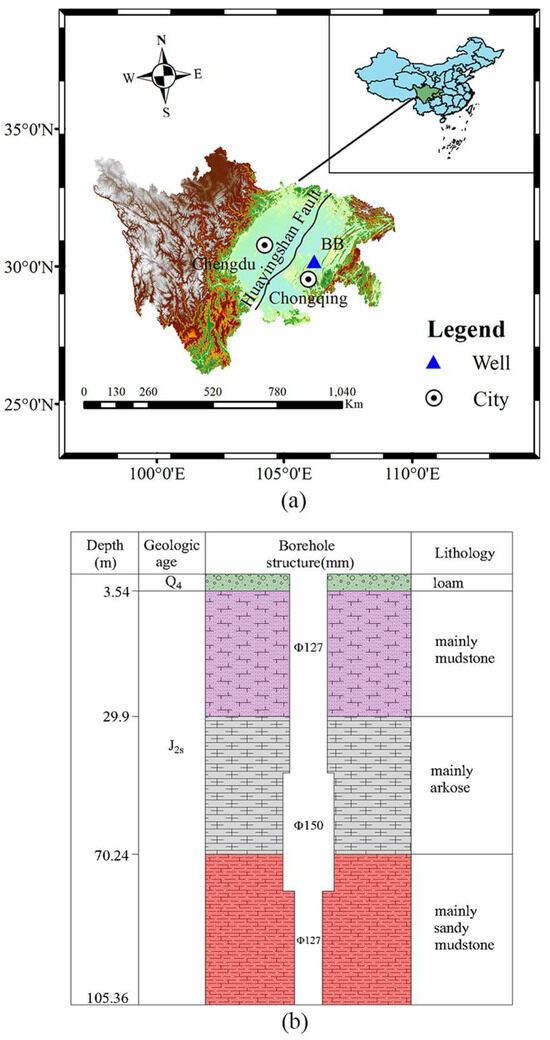
Figure 1.
(a) The locations of Sichuan and Chongqing in southwest China. The basemap was downloaded from Natural Earth at http://www.naturalearthdata.com/ (accessed on 5 August 2023). Well BB is subordinate to Chongqing. (b) The stratigraphy of well BB.
The lithology of borehole BB is shown in Figure 1b. The depth of well BB is 105.36 m, the diameter of the 127 mm casing is lowered to 42.1 m, and the casing is sealed with cement. Purple mudstone is found at 3.54~29.90 m. The main aquifer is located at 29.90~70.24 m, and the borehole lithology is light grayish-white medium–coarse-grained thick-bedded arkose of the middle Jurassic. The level of 70.24~105.36 m is mainly purplish-red sandy mudstone with purplish-gray siltstone bands. The well water level is observed in static water with an LN-3A digital piezometer, with a sampling interval of 1 min, an accuracy of 1 cm, and a resolution of 1 mm (Table S2).
As shown in Figure 2, the daily dynamic fluctuations in the groundwater level in well BB are stable, with a typical change amplitude of about 6 cm. And it has clear tidal variation characteristics of two peaks and two valleys, which are negatively correlated with the barometric pressure. A spectrum analysis of the groundwater level, barometric pressure, and earth tide data was performed using the calculation package Matlab® (Mathworks Inc., Natick, MI, USA), with spectrum analysis power plotted according to period (days/period) (Figure 3). According to the spectrum analysis results of well BB, the main tidal components of well water level are tides O1, K1, M2, and S2 (M2 and O1 are half-diurnal and diurnal tides caused by the moon, respectively; K1 is the diurnal tide caused by the sun and moon; S2 is the half-diurnal tide caused by the sun), and is affected by both barometric pressure and earth tide. Considering that tides S2 and K1 are affected by barometric pressure and have small signal-to-noise ratios, tides O1 and M2 are mainly used in well water level tidal analysis to reduce calculation errors. Among them, the tide M2 groundwater level data typically have a significant amplitude and a modest amount of errors.
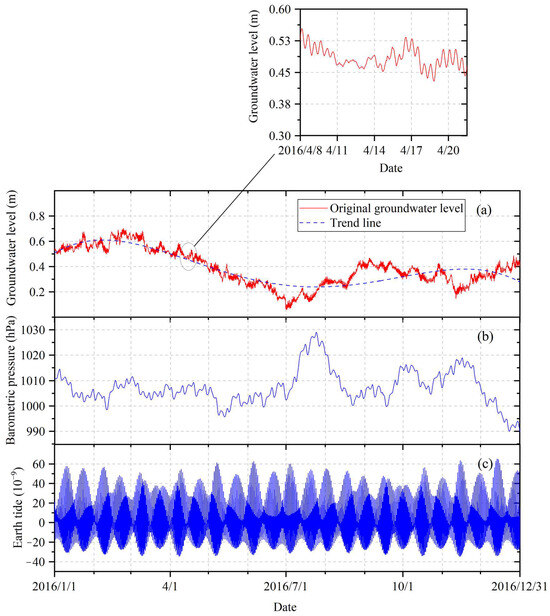
Figure 2.
(a) Groundwater level, (b) barometric pressure, and (c) theoretical tidal volumetric strain of well BB in 2016. The data of groundwater level and barometric pressure were obtained from the China Earthquake Precursor Monitoring Network; the theoretical tidal volumetric strain was obtained using the program EIS2000.
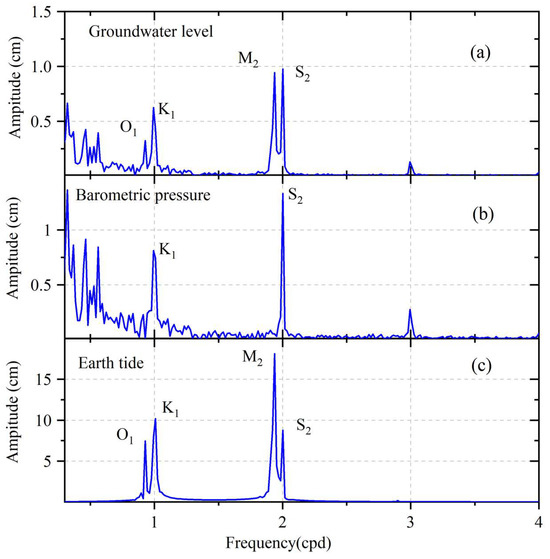
Figure 3.
Results of spectrum analysis of well BB’s hourly values of (a) groundwater level, (b) barometric pressure, and (c) earth tide in 2016.
3. Methods
To solve the unknown parameters in the mixed flow model proposed by Wang et al. [16], a tidal analysis of the well water level should be performed first. Through the tidal analysis of well BB’s hourly values of the groundwater level in 2016 (Figure 4), it can be found that the M2 phase shift (the average is 26.435°) is greater than the O1 phase shift (the average is 14.92°), which does not match the standards of the literature [30]. And due to the unstable phase shift of tide O1, it is challenging for us to obtain time series and correct solutions using Yang et al.’s method for calculations, while tide M2 has the advantages of having sufficient amplitude, being easily extracted, and not being affected by barometric pressure [34,35]. Therefore, here, only the response of the well water level to tide M2 was used to estimate the T and σ of the aquifer near well BB. Based on the mixed flow model of aquifers proposed by Wang et al. [16], there are four unknowns (S, T, σ, and BKu) in the analytical expressions of the tidal factor () and the phase shift (η) ( is the ratio of the measured amplitude of the tide to the theoretical amplitude of the earth tide; η represents the lag of the well water level relative to the pressure head). S and BKu were determined beforehand based on the barometric influence and tidal effect of the well water level; then, the numerical solutions of T and σ were solved simultaneously using the least square method.
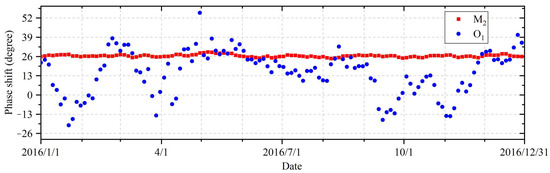
Figure 4.
Phase shift of tides M2 and O1 obtained through tidal analysis using the Baytap08 program [36], with the time window of 30 days and the running step of 3 days.
3.1. Determination of Storage Coefficient
The specific storativity (Ss) is a parameter that describes the water release capacity of an aquifer [L−1]. Assuming that the change in the aquifer porosity is equal to the change in the aquifer volume, the Ss of a confined aquifer can be expressed as [37,38]
where refers to the density of water [L−3M], n refers to the porosity of the entire aquifer, is tidal factor [L], M refers to the aquifer thickness [L], and K and Kw refer to the bulk modulus of the aquifer and water [LM−1T−2], respectively.
To obtain the in the aquifer, the tidal analysis data of the Baytap08 program were used [36]; the program uses Akaike’s Bayesian information criterion. The following sections are presumptively possible for a time series [15,36,39]:
The tidal component is the first term on the right-hand side: and are theoretically computed values for the mth group of tidal elements, and and are the tidal response constants to be established in the statistical model. The barometric response element is established as , where is the observed barometric pressure and is the response coefficient, is the long-term trend, and is the noise. The Akaike Bayesian information criterion is established from Equation (3), and this program features a Bayesian inversion procedure that enables the parameters and to be calculated and subsequently evaluated. The result of the Baytap08 analysis provides the and η for each tide group [40].
3.2. Determination of BKu
BKu represents the elasticity of the rock (B is the Skempton coefficient; Ku is the undrained bulk modulus [41]), which is related to the bulk modulus of porous media (K), the bulk modulus of solids (Ks), the bulk modulus of fluids (Kw), and the porosity (n) of porous media. The calculation equations for Ku are shown in Table 1 [42,43,44].

Table 1.
Calculation equations of BKu and related physical quantities.
In this calculation, the aquifer porosity is determined by the response of the well water level to barometric pressure [45]:
where Kw = 2.065 × 103 MPa; ρg = 9.8 × 10−3 MPa/m. Be is the barometric efficiency (dimensionless); it is a key index to directly reflect the barometric effect of the well water level. Here, in order to eliminate the influence of earth tide, the daily series values of the groundwater level and barometric pressure were selected to obtain Be. The well water level () is mainly composed of a trend term (), the response to barometric pressure (), and rainfall ():
The first-order difference is calculated using Equation (5) to eliminate the influence of the trend term, so that the value of Be is calculated:
where is the change value of the well water level; represents the water column height corresponding to the change values of the barometric pressure. The barometric efficiency obtained by the first-order difference method can eliminate the influence of trend change factors on the groundwater level. It is worth noting that the signs of and are both positive or negative at the same time, and ; all of these can avoid the interference of rainfall () on the well water level.
3.3. Calculation Theory of Horizontal Transmissivity and Leakage Coefficient
According to the borehole structure of well BB (Figure 1b), it is considered that 3.54~29.90 m is the aquitard, and 29.90~70.24 m is the aquifer. It meets the requirements of the mixed flow model of Wang et al. [16]; that is, the thickness and leakage of the aquifer should not be too small. Based on the mixed flow model proposed by Wang et al., the analytical expressions of and η are as follows:
where and η can be obtained through tidal analysis using the Baytap08 program [36]; A is the amplitude ratio (amplitude ratio of well water level to pressure head fluctuation); ω is the tidal wave frequency; Kn is the second kind of modified Bessel function (BesselK function) with order n and aquifer leakage coefficient ( and represent the permeability coefficient and thickness of the aquitard in the vertical direction, respectively); and rw and rc represent the well radius and the case radius. When S, BKu, , and η are known, Equation (7) can be used to simultaneously obtain T and σ.
4. Results
Considering that there were no major earthquakes in Sichuan–Chongqing area in 2016, and that the characteristics of the well water level are not interfered with by human factors, information on the well water level of well BB in 2016 was collected for research. A tidal analysis was performed on the hourly groundwater levels of well BB with a time window of 30 days and a running step of 3 days (Figure 5a,b); then, the dynamic change in S (Figure 5c) was obtained according to (Equations (1) and (2)). Based on the first-order difference method to solve Be, the time series change in Be was obtained by taking 30 days as a group and sliding for 3 days at a time (Figure 5d). And then the aquifer n was obtained according to the corresponding equation (Equation (4)), and finally, the BKu values of the aquifer were obtained (Table 1; Figure 5e). The mean values of S and BKu are 6.88 × 10−5 and 7.22 GPa, respectively.
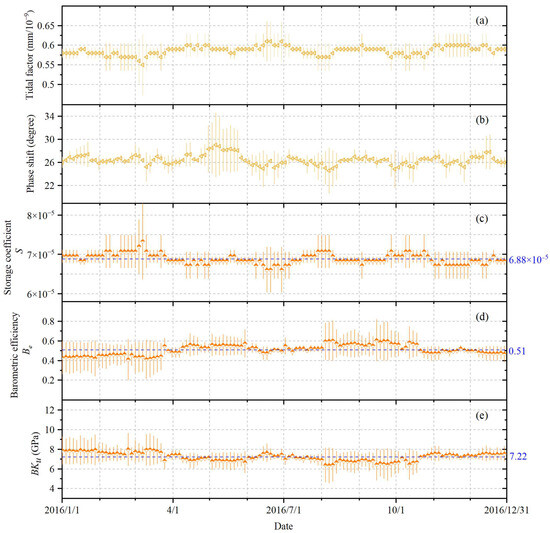
Figure 5.
The change characteristics of (a) tidal factor, (b) phase shift, (c) storage coefficient, (d) Barometric efficiency, and (e) BKu in 2016. Here, the error bars are three times the standard deviation; the blue lines represent the mean of the data set.
According to Equation (7), when the values of S and BKu are determined, Equation (7) has two equations with two unknowns (T and σ). Based on the least square method to solve the equations, if we input the corresponding parameters (S, BKu, , and η) in the Matlab program, the time series changes in the aquifer hydraulic parameters near well BB (Figure 6) can be obtained. The mean values of T and σ are 3.7 × 10−6 m2/s and 1.35 × 10−8 s−1, respectively. The hydraulic parameters are relatively stable as a whole because the aquifer near well BB was not disturbed significantly in 2016.

Figure 6.
The changes in aquifer parameters near well BB in 2016, including (a) transmissivity and (b) leakage coefficient. The blue lines represent the mean of the data set.
5. Discussion
5.1. Verification of Results
Since there are always inconsistencies between the assumed conditions established by the theoretical equations and the actual site conditions, certain errors will inevitably occur in the process of solving. In this calculation, the variation of aquifer n near well BB ranges from 15.6% to 22% (Figure S1). The main lithology of well BB’s aquifer is sandstone; according to Zhou et al.’s survey and laboratory test of the sandstone reservoir in the area where well BB is located [46,47,48,49], the n of the sandstone reservoir in this area ranges from 5% to 30%.
The previous pumping test showed that the T of the aquifer in the observed section of the well was 6.94 × 10−6 m2/s, which is close to the current calculation (Figure 6a). In order to further verify the calculation results of the aquifer parameters of well BB, the methods of Sun et al. [31] and Yang et al. [30] were cited and calculated based on the tidal analysis results. Based on the method of Sun et al. [31], the relationship between the hydraulic parameters of the aquifer (T and σ) and the tidal parameters (A and η) of well BB was calculated and is established in Figure 7. When A and η were 0.831 and 26.435° (point data, the mean of tidal analysis results of well BB in 2016), the variation curves of T and σ could be obtained and cross-solved to establish them as 3.76 × 10−6 m2/s and 1.38 × 10−8 s−1. Although Yang et al.’s method [30] is challenging to obtain time series changes in parameters of the aquifer near well BB, it can be used to obtain point values to validate the results of this paper. All results of the above methods are shown in Table 2, which indicates that the calculation results of the aquifer parameters near well BB in this paper are reliable.

Figure 7.
In the calculation, when S = 6.88 × 10−5, rc = 63.5 mm, rw = 75 mm, and τ = 12.42 hr, the relationship between the hydraulic parameters of aquifer (T and σ) and the tidal parameters (A (a) and η (b)) of well BB are determined. The red lines represent the mean tidal parameters for well BB in 2016; the T and σ can be obtained when they intersect.

Table 2.
Comparison of hydraulic parameters calculated by various methods.
The graphical method proposed by Sun et al. [31] can guarantee the accuracy of the results, but only one set of T and σ can be calculated and obtained at a time, making it challenging to calculate the time series changes in aquifer parameters. Yang et al.’s method [30] can simultaneously obtain the S, T, and σ of the aquifer. The outcomes of the calculations using the least square optimal fitting method, however, also depend on the initial values of the parameters to a certain extent, and there will be various solutions. Considering that when it is applied to an aquifer such as well BB (the phase shift of tide M2 is greater than tide O1), it is difficult to obtain a correct solution even if a reasonable initial value is set. Here, firstly, the barometric pressure and earth tide effects of the well water level were introduced to solve the S and BKu, and then only the relatively stable tide M2 was considered to solve Equation (7). By reducing the number of unknown parameters in the equations compared with the method of Yang et al., the dependence of the results on the initial values is greatly reduced. In addition, when substituting the calculated values of the horizontal transmissivity and leakage coefficient into Equation (7), the error of each equation was less than 1 × 10−5.
5.2. The Effects of Earthquakes
Based on the above solving process, the effects of the Ms8.0 Wenchuan earthquake on the aquifer parameters near well BB is discussed. The values of S and BKu of the aquifer before and after (4/12–6/12) the Wenchuan earthquake were firstly calculated (Figure 8a,b). The mean value of S caused by the earthquake increased from 6.32 × 10−5 before the earthquake to 1.27 × 10−4 after the earthquake, and the mean value of BKu decreased from 7.21 GPa before the earthquake to 4.36 GPa after the earthquake. The results showed that the T increased from 3.59 × 10−6 m2/s (mean value) to 1.03 × 10−5 m2/s (the maximum value after the earthquake) (Figure 8c), and the σ increased from 1.71 × 10−8 s−1 (mean value) to 4.16 × 10−8 s−1 (the maximum value after the earthquake) (Figure 8d). It can be inferred that the Wenchuan earthquake led to an increase in the aquifer’s permeability. According to the changes in the co-seismic pore volumetric strain proposed by Shi et al. [50] and Lai et al. [51] during the Wenchuan earthquake, well BB was located in an expanding area and the aquifer permeability was enhanced accordingly.
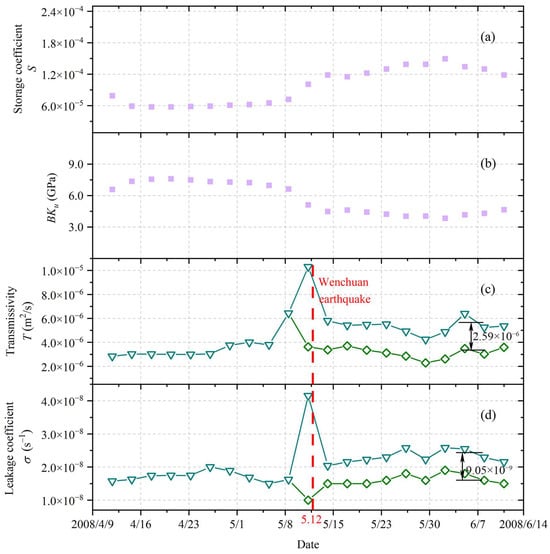
Figure 8.
The time series changes in (a) S, (b) BKu, and hydraulic parameters ((c) T and (d) σ) of the aquifer before and after the Wenchuan earthquake. The green lines (–◇–) represent the changes in hydraulic parameters after the earthquake using the mean values of S and BKu one month before the earthquake as the input parameters.
Some scholars believe that even if S changes by one order of magnitude, the change in the value of T is very small [22]. If the mean values of S and BKu (S = 6.32 × 10−5, BKu = 7.21 GPa) before the earthquake were used as input parameters to solve the aquifer after the earthquake (the tidal parameters were still post-earthquake), although it did not make a big difference to the outcomes (the error of T is about 2.59 × 10−6 m2/s, and the error of σ is 9.05 × 10−9 s−1), the variation interval of aquifer parameters (–◇–) will be the same as that before the earthquake. And the impact of the earthquake on the aquifer characteristics cannot be accurately reflected. Therefore, it is necessary to obtain the dynamic changes in S and BKu, especially when the stratum is seriously disturbed.
6. Conclusions
Based on the response of well water levels to barometric pressure and earth tides, the aquifer parameters near well BB are estimated in this paper with the help of a mixed flow model. The evolution process and characteristics of the aquifer parameters near well BB caused by the Wenchuan earthquake are also obtained. The calculation results are unique and continuous, and have little dependence on the initial values in the least square method and do not utilize the unstable tide O1. The results have reference significance for the estimation of aquifer parameters near other wells. Due to the simplification and assumption of the mathematical model, there may be errors between the calculation results and the actual situation. And the process of solving aquifer parameters in this paper is a little complicated; the more accurate determination of S and BKu values can improve the accuracy of aquifer parameter estimation.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/w16081119/s1: Table S1. Longitude and latitude of well BB. Table S2. Groundwater level of well BB. Figure S1. Dynamic change in aquifer n near well BB in 2016.
Author Contributions
Conceptualization, P.Q.; methodology, P.Q. resources, S.L.; data curation, H.G.; writing—original draft preparation, P.Q. and S.L.; writing—review and editing, P.Q., S.L. and H.G.; supervision, Z.M.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Beijing Natural Science Foundation of China (8222003) and the National Natural Science Foundation of China (41807180).
Data Availability Statement
Data is contained within the article (and supplementary materials).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Manga, M. Origin of postseismic streamflow changes inferred from baseflow recession and magnitude-distance relations. Geophys. Res. Lett. 2001, 28, 2133–2136. [Google Scholar] [CrossRef]
- Carrigan, C.R.; King, G.C.P.; Barr, G.E.; Bixler, N.E. Potential for water-table excursions induced by seismic events at yucca mountain, nevada. Geology 1991, 19, 1157–1160. [Google Scholar] [CrossRef]
- Weeks, E.P. Barometric fluctuations in wells tapping deep unconfined aquifers. Water Resour. Res. 1979, 15, 1167–1176. [Google Scholar] [CrossRef]
- Van der Kamp, G.; Gale, J. Theory of earth tide and barometric effects in porous formations with compressible grains. Water Resour. Res. 1983, 19, 538–544. [Google Scholar] [CrossRef]
- Rojstaczer, S.; Riley, F.S. Response of the water level in a well to earth tides and atmospheric loading under unconfined conditions. Water Resour. Res. 1990, 26, 1803–1817. [Google Scholar] [CrossRef]
- Bredehoeft, J.D. Response of well-aquifer systems to Earth tides. J. Geophys. Res. 1967, 72, 3075–3087. [Google Scholar] [CrossRef]
- Hsieh, P.A.; Bredehoeft, J.D.; Farr, J.M. Determination of aquifer transmissivity from Earth tide analysis. Water Resour. Res. 1987, 23, 1824–1832. [Google Scholar] [CrossRef]
- Cooper, H.H., Jr.; Bredehoeft, J.D.; Papadopulos, I.S. Response of a finite-diameter well to an instantaneous charge of water. Water Resour. Res. 1967, 3, 263–269. [Google Scholar] [CrossRef]
- Liu, L.B.; Roeloffs, E.; Zheng, X.Y. Seismically induced water level fluctuations in the Wali well, Beijing, China. J. Geophys. Res.-Solid Earth 1989, 94, 9453–9462. [Google Scholar] [CrossRef]
- Brodsky, E.E.; Roeloffs, E.; Woodcock, D.; Gall, I.; Manga, M. A mechanism for sustained groundwater pressure changes induced by distant earthquakes. J. Geophys. Res.-Solid Earth 2003, 108, 2390. [Google Scholar] [CrossRef]
- Wakita, H. Water wells as possible indicators of tectonic strain. Science 1975, 189, 553–555. [Google Scholar] [CrossRef] [PubMed]
- Roeloffs, E.; Quilty, E.; Scholtz, C. Case 21 water level and strain changes preceding and following the August 4, 1985 Kettleman Hills, California, earthquake. Pure Appl. Geophys. 1997, 149, 21–60. [Google Scholar] [CrossRef]
- Rojstaczer, S. Determination of fluid flow properties from the response of water levels in wells to atmospheric loading. Water Resour. Res. 1988, 24, 1927–1938. [Google Scholar] [CrossRef]
- Roeloffs, E. Poroelastic techniques in the study of earthquake-related hydrologic phenomena. Adv. Geophys. 1996, 37, 135–195. [Google Scholar]
- Doan, M.-L.; Brodsky, E.E.; Prioul, R.; Signer, C. Tidal Analysis of Borehole Pressure—A Tutorial; University of California, Santa Cruz: Santa Cruz, CA, USA, 2006; Volume 25, p. 27. [Google Scholar]
- Wang, C.Y.; Doan, M.L.; Xue, L.; Barbour, A.J. Tidal response of groundwater in a leaky aquifer—Application to Oklahoma. Water Resour. Res. 2018, 54, 8019–8033. [Google Scholar] [CrossRef]
- Liang, X.; Wang, C.Y.; Ma, E.; Zhang, Y.K. Effects of unsaturated flow on hydraulic head response to Earth tides—An analytical model. Water Resour. Res. 2022, 58, e2021WR030337. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Manga, M. Changes in Tidal and Barometric Response of Groundwater during Earthquakes—A Review with Recommendations for Better Management of Groundwater Resources. Water 2023, 15, 1327. [Google Scholar] [CrossRef]
- Elkhoury, J.E.; Niemeijer, A.; Brodsky, E.E.; Marone, C. Laboratory observations of permeability enhancement by fluid pressure oscillation of in situ fractured rock. J. Geophys. Res.-Solid Earth 2011, 116, B02311. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, G.; Manga, M.; Wang, C.-Y. Mechanism of co-seismic water level change following four great earthquakes–insights from co-seismic responses throughout the Chinese mainland. Earth Planet. Sci. Lett. 2015, 430, 66–74. [Google Scholar] [CrossRef]
- Sun, X.; Wang, G.; Yang, X. Coseismic response of water level in Changping well, China, to the Mw 9.0 Tohoku earthquake. J. Hydrol. 2015, 531, 1028–1039. [Google Scholar] [CrossRef]
- Sun, X.; Xiang, Y.; Shi, Z.; Hu, X.; Zhang, H. Sensitivity of the response of well-aquifer systems to different periodic loadings: A comparison of two wells in Huize, China. J. Hydrol. 2019, 572, 121–130. [Google Scholar] [CrossRef]
- Yan, R.; Wang, G.; Shi, Z. Sensitivity of hydraulic properties to dynamic strain within a fault damage zone. J. Hydrol. 2016, 543, 721–728. [Google Scholar] [CrossRef]
- Liao, X.; Wang, C.Y.; Liu, C.P. Disruption of groundwater systems by earthquakes. Geophys. Res. Lett. 2015, 42, 9758–9763. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, S.; Yan, R.; Wang, G. Fault zone permeability decrease following large earthquakes in a hydrothermal system. Geophys. Res. Lett. 2018, 45, 1387–1394. [Google Scholar] [CrossRef]
- Wang, C.Y.; Liao, X.; Wang, L.P.; Wang, C.H.; Manga, M. Large earthquakes create vertical permeability by breaching aquitards. Water Resour. Res. 2016, 52, 5923–5937. [Google Scholar] [CrossRef]
- Elkhoury, J.E.; Brodsky, E.E.; Agnew, D.C. Seismic waves increase permeability. Nature 2006, 441, 1135–1138. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, G. Aquifers switched from confined to semiconfined by earthquakes. Geophys. Res. Lett. 2016, 43, 11166–11172. [Google Scholar] [CrossRef]
- Shi, Y.; Liao, X.; Zhang, D.; Liu, C. Seismic waves could decrease the permeability of the shallow crust. Geophys. Res. Lett. 2019, 46, 6371–6377. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, Y.; Fu, L.-Y.; Ma, Y.; Hu, J. Vertical leakage occurred after an earthquake: Suggestions for utilizing the mixed flow model. Lithosphere 2021, 2021, 8281428. [Google Scholar] [CrossRef]
- Sun, X.; Shi, Z.; Xiang, Y. Frequency dependence of in situ transmissivity estimation of well-aquifer systems from periodic loadings. Water Resour. Res. 2020, 56, e2020WR027536. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.Y.; Fu, L.Y.; Yang, Q.Y. Are deep aquifers really confined? Insights from deep groundwater tidal responses in the North China Platform. Water Resour. Res. 2021, 57, e2021WR030195. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, X.; Huang, T.; Qi, S.; Fu, L.-Y.; Yang, Q.-Y.; Hu, J.; Zheng, B.; Zhang, W. Possible continuous vertical water leakage of deep aquifer: Records from a deep well in Tianjin province, North China. Geofluids 2022, 2022, 4419310. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, Z.; Wang, G.; Sun, X.; Yan, R.; Liu, C. Large earthquake reshapes the groundwater flow system: Insight from the water-level response to earth tides and atmospheric pressure in a deep well. Water Resour. Res. 2019, 55, 4207–4219. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, C.-Y.; Yan, R. Frequency-dependent groundwater response to earthquakes in carbonate aquifer. J. Hydrol. 2021, 603, 127153. [Google Scholar] [CrossRef]
- Tamura, Y.; Sato, T.; Ooe, M.; Ishiguro, M. A procedure for tidal analysis with a Bayesian information criterion. Geophys. J. Int. 1991, 104, 507–516. [Google Scholar] [CrossRef]
- Cutillo, P.A.; Bredehoeft, J.D. Estimating aquifer properties from the water level response to earth tides. Groundwater 2011, 49, 600–610. [Google Scholar] [CrossRef] [PubMed]
- Merritt, M.L. Estimating Hydraulic Properties of the Floridan Aquifer System by Analysis of Earth-Tide, Ocean-Tide, and Barometric Effects, Collier and Hendry Counties, Florida; US Department of the Interior: Washington, DC, USA; US Geological Survey: Reston, VA, USA, 2004. [Google Scholar]
- Tamura, Y.; Agnew, D. Baytap08 User’s Manual; Scripps Institution of Oceanography: San Diego, CA, USA, 2008. [Google Scholar]
- Burbey, T.J. Fracture characterization using Earth tide analysis. J. Hydrol. 2010, 380, 237–246. [Google Scholar] [CrossRef]
- Wang, H. Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology; Princeton University Press: Princeton, NJ, USA, 2000; Volume 2. [Google Scholar]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Hamiel, Y.; Lyakhovsky, V.; Agnon, A. Rock dilation, nonlinear deformation, and pore pressure change under shear. Earth Planet. Sci. Lett. 2005, 237, 577–589. [Google Scholar] [CrossRef]
- Jacob, C.E. On the flow of water in an elastic artesian aquifer. Trans. Am. Geophys. Union 1940, 21, 574–586. [Google Scholar]
- Zhou, X.-P.; Xiao, N. A novel 3D geometrical reconstruction model for porous rocks. Eng. Geol. 2017, 228, 371–384. [Google Scholar] [CrossRef]
- Liu, X.; Lu, W.; Li, M.; Zeng, N.; Li, T. The thermal effect on the physical properties and corresponding permeability evolution of the heat-treated sandstones. Geofluids 2020, 2020, 8838325. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G.; Ran, Y.; Zhou, Z. Predictive distribution of high-quality reservoirs of tight gas sandstones by linking diagenesis to depositional facies: Evidence from Xu-2 sandstones in the Penglai area of the central Sichuan basin, China. J. Nat. Gas. Sci. Eng. 2015, 23, 97–111. [Google Scholar] [CrossRef]
- Wang, B.; Chen, X.; Chen, J.; Yao, J.; Tan, K. Elastic characteristics and petrophysical modeling of the Jurassic tight sandstone in Sichuan Basin. Chin. J. Geophys. 2020, 63, 4528–4539. [Google Scholar]
- Shi, Z.; Wang, G.; Liu, C. Co-seismic groundwater level changes induced by the May 12, 2008 Wenchuan earthquake in the near field. Pure Appl. Geophys. 2013, 170, 1773–1783. [Google Scholar] [CrossRef]
- Lai, G.; Ge, H.; Xue, L.; Brodsky, E.E.; Huang, F.; Wang, W. Tidal response variation and recovery following the Wenchuan earthquake from water level data of multiple wells in the nearfield. Tectonophysics 2014, 619, 115–122. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).