Predicting Epipelic Algae Transport in Open Channels: A Flume Study to Quantify Transport Capacity and Guide Flow Management
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Physical Figure of Suspension of Epipelic Algae Group
3.2. Establishment of a Critical Theoretical Formula for the Suspension of the Epipelic Algae Group
3.2.1. Analysis of Transport Capacity of Epipelic Algae Group
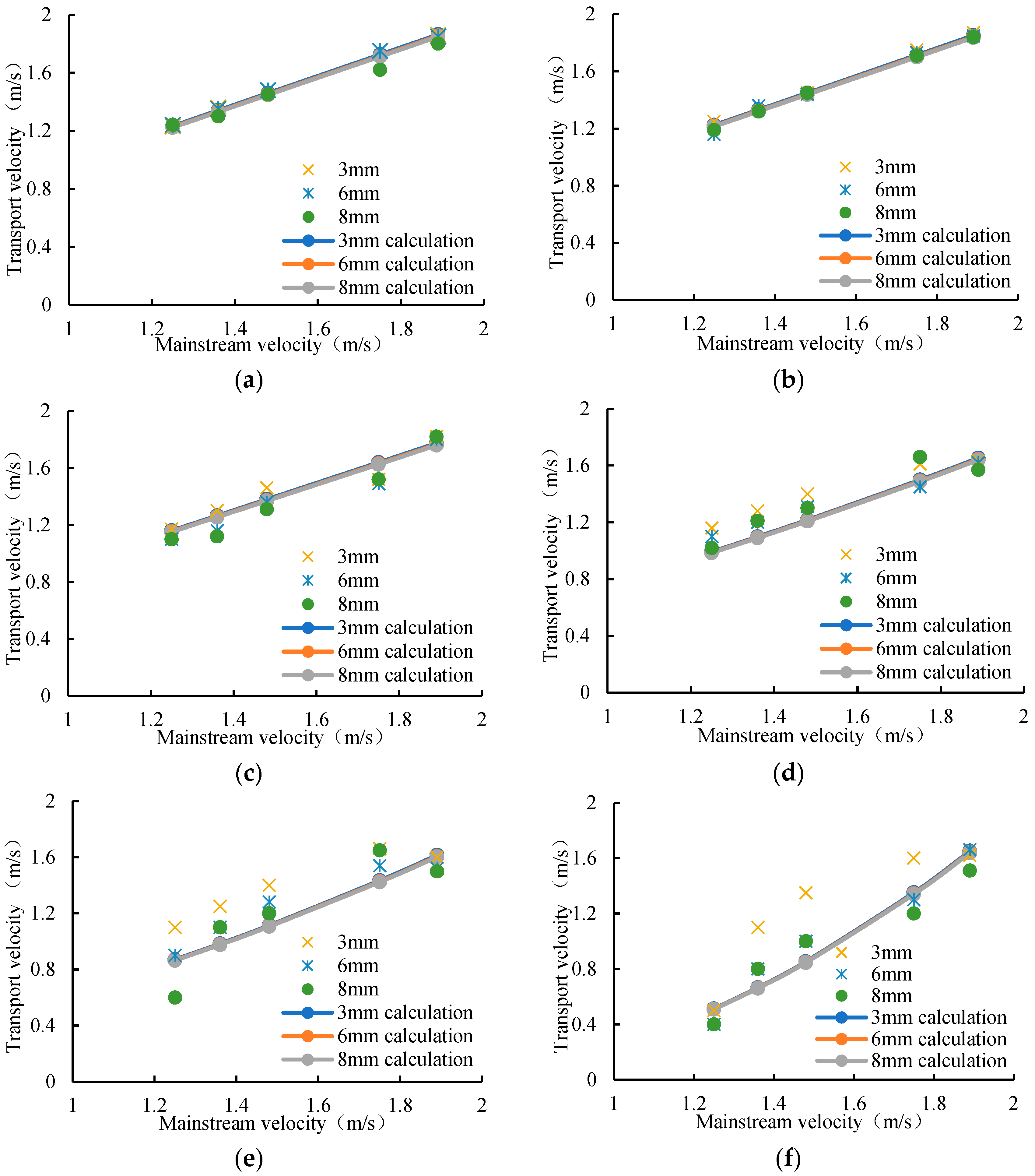
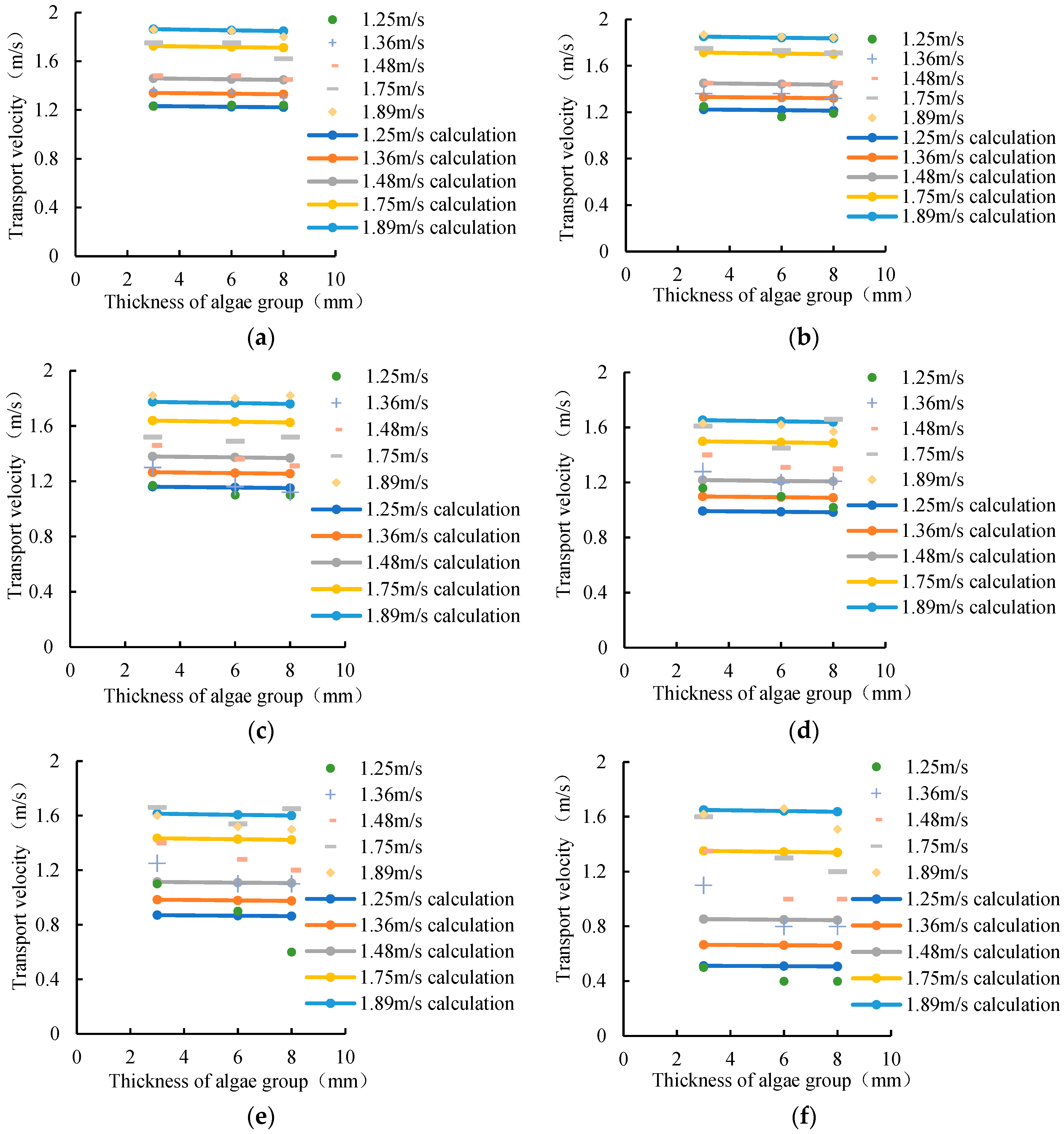
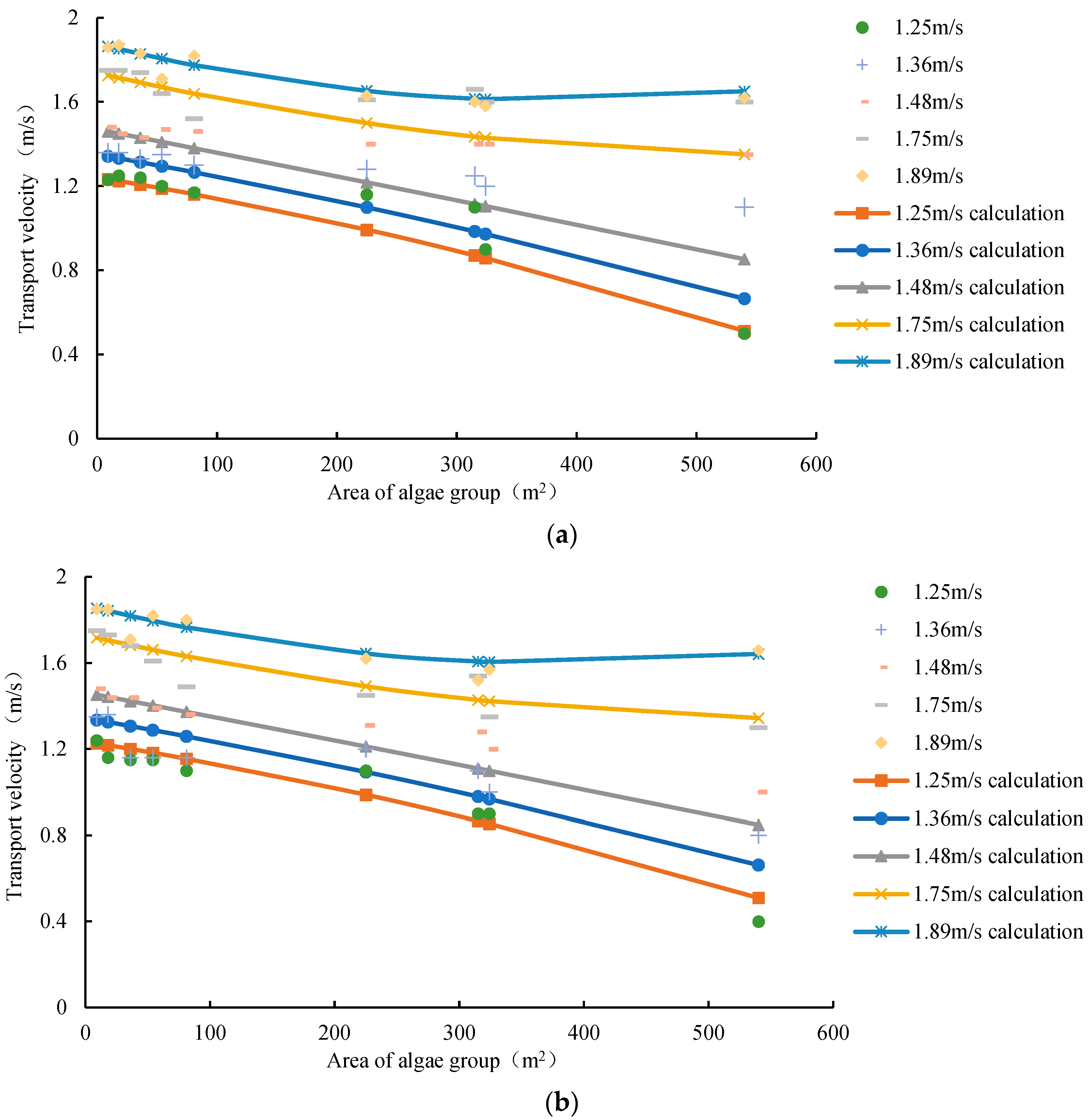
3.2.2. Analysis of Influencing Factors on the Transport Velocity of Epipelic Algae Groups and Verification of Model Test
- (1)
- The effect of the average flow velocity of the main stream on the transport velocity of epipelic algae groups.
- (2)
- The effect of algae thickness on the transport velocity of epipelic algae group.
- (3)
- The effect of algae area on the transport velocity of epipelic algae groups.
4. Discussion
4.1. Research Results of Longitudinal Transport Velocity along the Sidewall
4.2. Study on the Influence of Wind on Transport
4.3. Study on the Influence of Water Flow Characteristics on Transport
4.4. Research Results of Gathering Place Prediction
5. Conclusions
- (1)
- Epipelic algae have many forms, including flip suspension, no-flip suspension, aggregation transport, and settlement transport, and its suspension state is directly related to the main flow velocity and flow rate of the channel.
- (2)
- When the velocity V of the algae group reaches more than 95% of the main flow velocity V0, it can be considered that the algae group has all moved forward with the water flow without relative lag, that is, it is suspended on the water surface. If it reaches 95~85% of the main flow velocity, it is considered that the algae group is lagging behind, that is, it is transported with the water flow below the water surface. If it reaches 85~80% of the main flow velocity, it is first settled and then transported with the water flow. If it is lower than 80% of the main flow rate, with the increase in time, the epipelic algae group is likely to stop moving after a certain distance.
- (3)
- The hydrodynamic formula of an epipelic algae suspension was established, and the formula was verified using experimental data. The results showed that the formula calculation and the data were in good agreement.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shang, X.; Lou, A.; Sun, X.; Sun, Y. Numerical simulation of petroleum hydrocarbons transport in Bohai Sea and the influences on water quality. Mar. Environ. Sci. 2015, 31, 58–65. [Google Scholar]
- He, L.; Wang, Z.; Hu, Q.; Jiang, J.; Cai, Q. On the oil leakage and diffusion regularity for the underground buried oil pipelines. J. Saf. Environ. 2019, 19, 1232–1239. [Google Scholar]
- Huang, H.; Wang, Z. Numerical analysis of suspended sediment diffusion caused by underwater excavation. Port Waterw. Eng. 2015, 505, 25–35. [Google Scholar]
- Mi, T.; Yao, J. Simulation of Pollutant Diffusion in Y-type River Confluence. Environ. Sci. Technol. 2020, 43, 9–16. [Google Scholar]
- Li, Y.; Wu, J.; Cheng, H. Simulation of Pollutant Diffusion in Tanghe Reservoir Based on EFDC Model. J. Shenyang Jianzhu Univ. (Nat. Sci.) 2022, 38, 945–952. [Google Scholar]
- Shi, B.; Hou, J.; Wang, J.; Kang, Y.; Sun, Y.; Guo, M.; Zhang, Z. Simulation of pollutant transport in sudden water pollution accident based on GAST model. Eng. J. Wuhan Univ. 2022, 55, 1112–1119. [Google Scholar]
- Tao, Y.; Lei, K.; Xia, J. Main hydrodynamic factors identification for pollutant transport in sudden water pollution accident in Shenzhen Bay. Adv. Water Sci. 2017, 28, 888–897. [Google Scholar]
- Grifoll, M.; Jordà, G.; Espino, M.; Romo, J.; García-Sotillo, M. A management system for accidental water pollution risk in a harbor: The Barcelona case study. J. Mar. Syst. 2011, 88, 60–73. [Google Scholar] [CrossRef]
- Li, H.; Sun, S. Experimental study on the transport characteristics of pollutants on the underlying surface covered by plants. Yellow River 2023, 45, 79–81. [Google Scholar]
- Fang, H.; Yang, Z. Effects of submerged vegetation and bed absorption boundary on pollutant transport in wetland. Adv. Water Sci. 2023, 34, 126–133. [Google Scholar]
- Pan, L.; Zhao, L.; Zhang, M.; Lai, Z. Experimental Study of the Hydrodynamics of an Open Channel with Algae Attached to the Side Wall. Water 2023, 15, 2921. [Google Scholar] [CrossRef]
- Xiong, H.; Sun, Z.; Chen, L.; Liu, C. Analysis of the Effects of Varying Density in Wharf Groups on River Hydrodynamics and Pollutant Transport: A Case Study in Wuhan Reach. Resour. Environ. Yangtze Basin 2021, 30, 2205–2216. [Google Scholar]
- Yu, C.; Ren, C. An experimental study on horizontal two-dimensional transport and diffusivity of dye under irregular waves in surf zone. Mar. Environ. Sci. 2021, 40, 34–40. [Google Scholar]
- Shu, Y.; Gao, C. Numerical simulation of wind-driven current and pollutant transport and diffusion in Taihu Lake. Water Resour. Prot. 2021, 37, 120–127. [Google Scholar]
- Wang, H.; Li, S.; Zhu, Z.; Huai, W. Analyzing solute transport in modeled wetland flows under surface wind and bed absorption conditions. Int. J. Heat Mass Transf. 2020, 30, 119319. [Google Scholar] [CrossRef]
- Zhao, G.; Gao, X. Influence of Turbulent Disturbance on Algae in the Large Shallow Lake. Ph.D. Thesis, Tianjin University, Tianjin, China, 2020; pp. 1–161. [Google Scholar]
- Zhu, J.; Liu, X.; Deng, J.; Peng, J.; Zhang, H. Pollutant transport rates in the rivers around western Lake Taihu. J. Lake Sci. 2018, 30, 1509–1517. [Google Scholar]
- Zhang, Y.; Lai, X.; Zhang, L.; Yao, X.; Deng, H. Influence of aquatic vegetation on flow structure under wind-driven waves: A case study in Lake Taihu (China) with two typical submerged vegetations. Adv. Water Sci. 2020, 31, 441–449. [Google Scholar]
- Ji, D.; Li, G.; Yang, Z.; Ma, J.; Huang, Y.; Liu, D. Water Transport Capacity for Algal Bloom in Tributaries of Three Gorges Resevoir. Water Resour. Power 2013, 31, 75–77. [Google Scholar]
- Musielak, M.M.; Karp-Boss, L.; Jumars, P.A.; Fauci, L.J. Nutrient transport and acquisition by diatom chains in a moving fluid. J. Fluid Mech. 2009, 638, 401–421. [Google Scholar] [CrossRef]
- Galabov, V.; Kavortche, A.; Marinski, J. Simulation of tanker accidents in the bay of Burgas, using hydrodynamic model. In Proceedings of the International Multidisciplinary Scientific GeoConference Surveying, Geology and Mining, Ecology and Management, Albena, Bulgaria, 16–22 June 2012; Volume 3, p. 993. [Google Scholar]

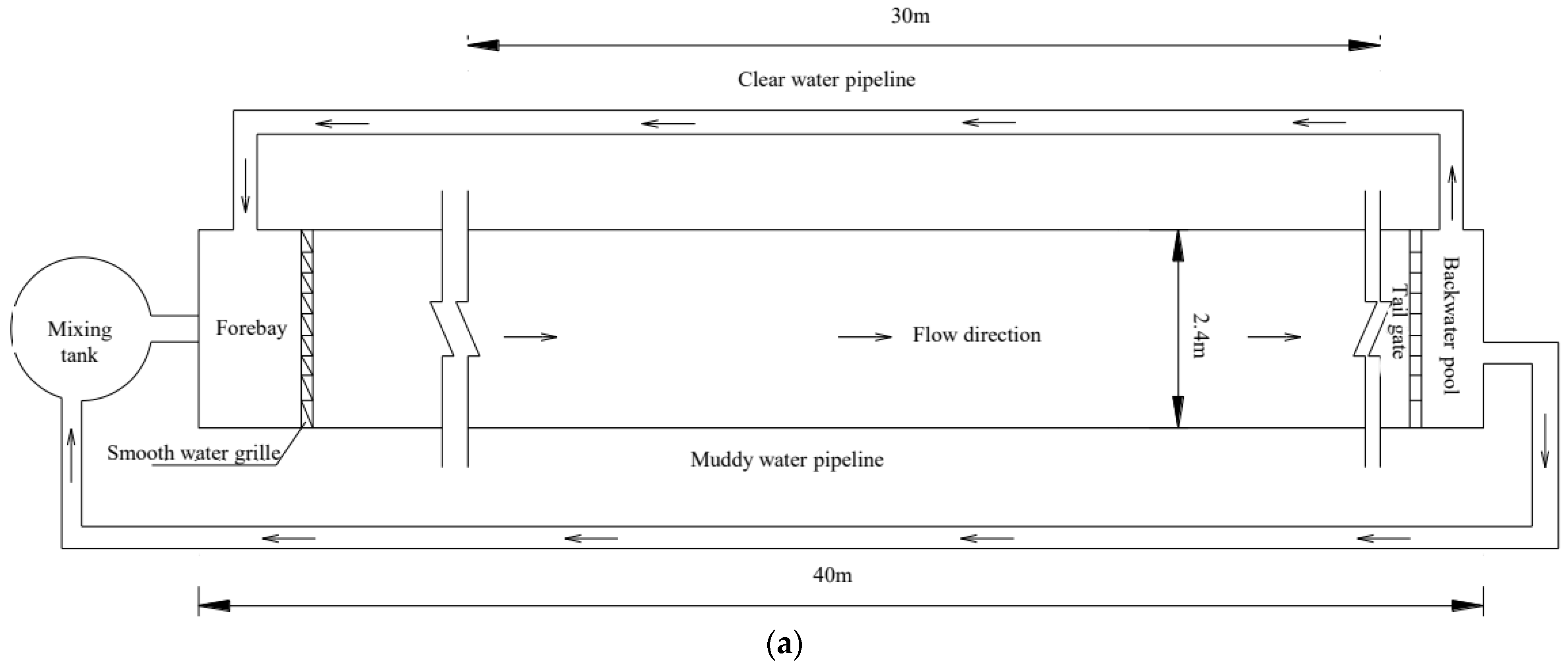
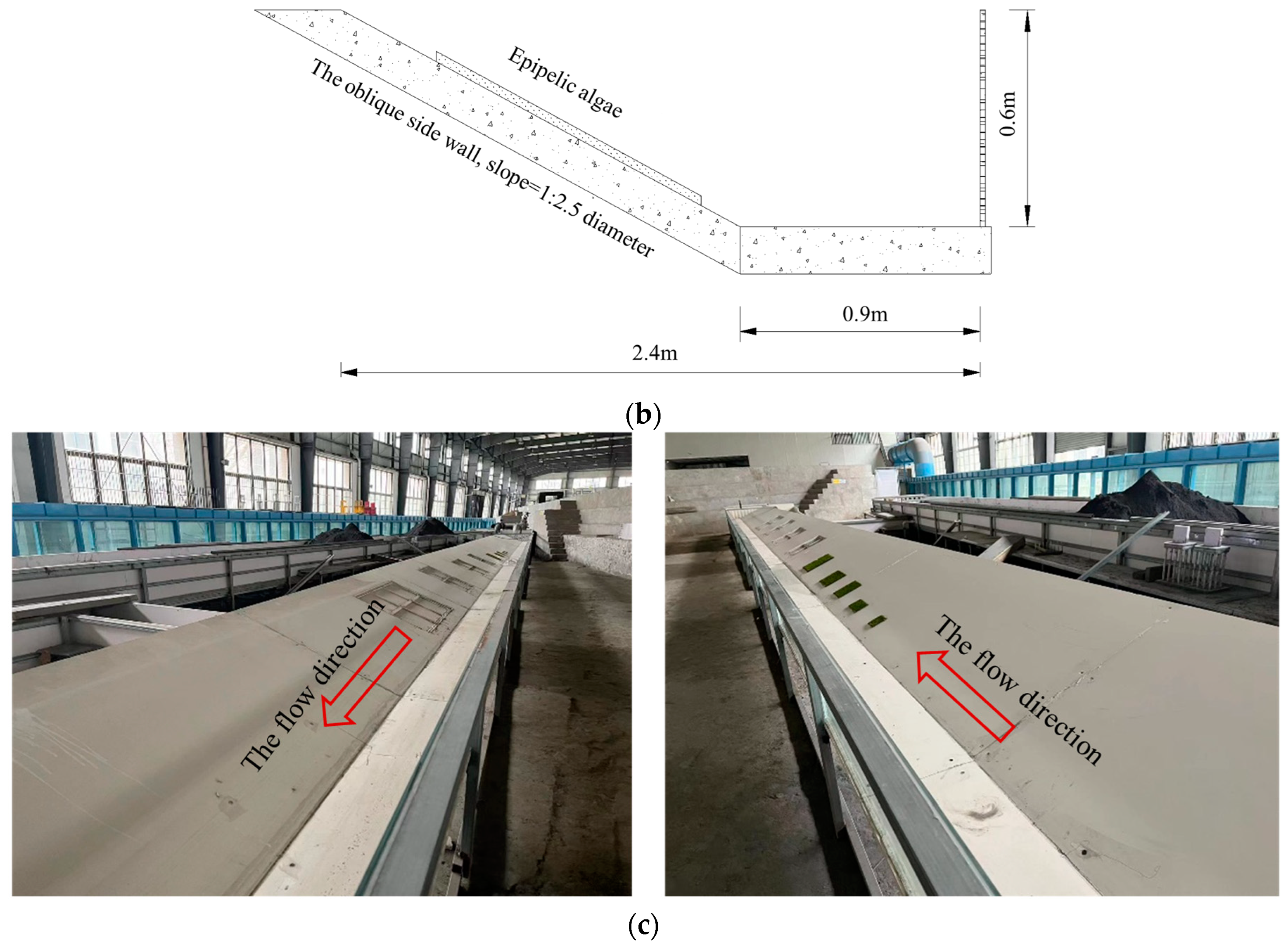



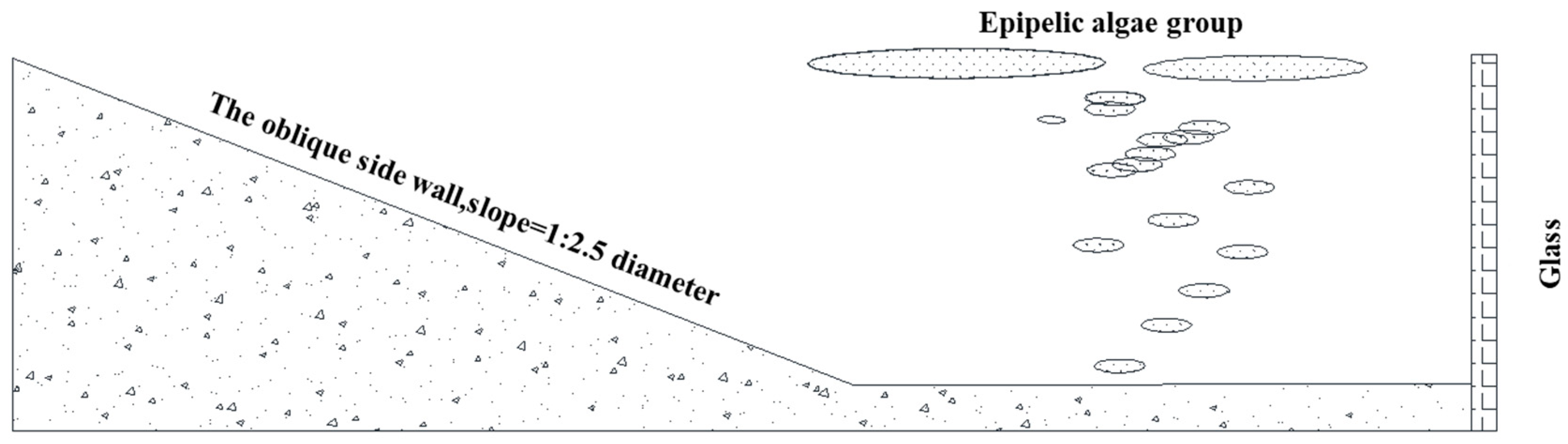
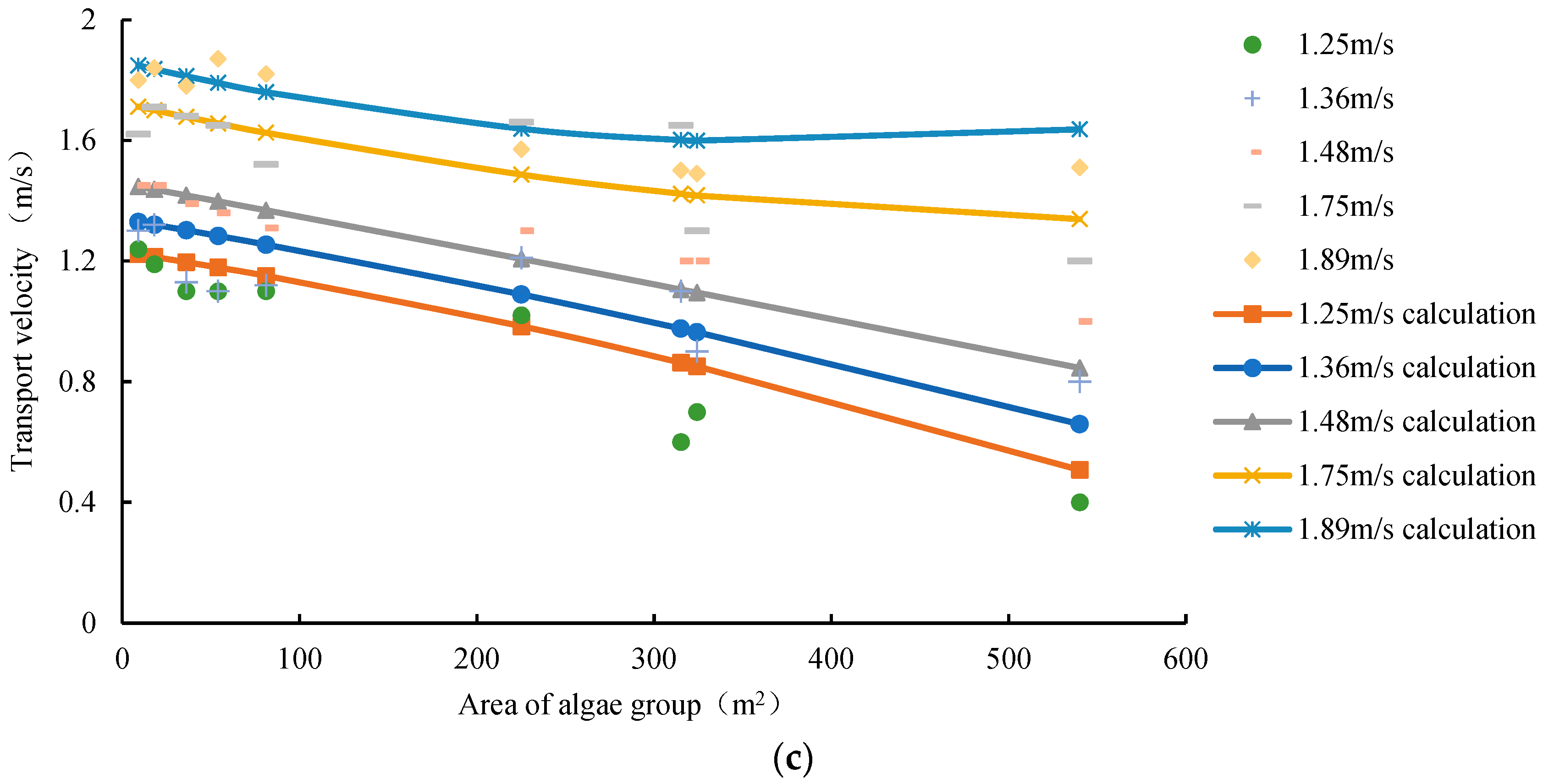
| Flow rate (m3/s) | 36.53 | 68.03 | 102.04 | 220.84 | 301.69 | |
| The mainstream velocity (m/s) | 1.25 | 1.36 | 1.48 | 1.75 | 1.89 | |
| Length × width of algae group | Thickness of algae group | The percentage of the transport velocity of the epipelic algae group to the mainstream velocity (%) | ||||
| 3 m × 3 m | 3 mm | 98.25 | 99.89 | 100.00 | 100.00 | 98.24 |
| 6 mm | 99.44 | 99.39 | 100.02 | 100.00 | 98.13 | |
| 8 mm | 99.51 | 96.01 | 97.97 | 92.42 | 95.12 | |
| 6 m × 3 m | 3 mm | 100.35 | 100.12 | 97.82 | 100.10 | 98.94 |
| 6 mm | 92.97 | 100.12 | 97.13 | 98.73 | 97.80 | |
| 8 mm | 95.05 | 97.18 | 97.97 | 97.71 | 97.36 | |
| 6 m × 6 m | 3 mm | 99.20 | 97.63 | 96.54 | 99.26 | 96.71 |
| 6 mm | 92.00 | 85.13 | 97.39 | 96.20 | 90.56 | |
| 8 mm | 88.00 | 83.31 | 94.17 | 95.91 | 94.30 | |
| 9 m × 6 m | 3 mm | 96.00 | 99.39 | 99.32 | 93.80 | 90.66 |
| 6 mm | 92.00 | 85.40 | 94.01 | 91.78 | 96.39 | |
| 8 mm | 88.00 | 80.98 | 92.06 | 94.56 | 98.68 | |
| 9 m × 9 m | 3 mm | 93.60 | 95.70 | 98.86 | 86.94 | 96.28 |
| 6 mm | 88.00 | 85.40 | 92.21 | 85.20 | 95.24 | |
| 8 mm | 88.00 | 82.45 | 88.51 | 86.78 | 96.49 | |
| 15 m × 15 m | 3 mm | 92.80 | 94.23 | 94.59 | 92.24 | 86.51 |
| 6 mm | 88.00 | 88.34 | 88.51 | 82.65 | 85.66 | |
| 8 mm | 81.60 | 89.08 | 87.84 | 95.13 | 83.28 | |
| 21 m × 15 m | 3 mm | 88.00 | 92.02 | 94.59 | 94.75 | 84.66 |
| 6 mm | 72.00 | 80.98 | 86.49 | 87.92 | 80.43 | |
| 8 mm | 48.00 | 80.98 | 81.08 | 94.27 | 79.37 | |
| 18 m × 18 m | 3 mm | 72.00 | 88.34 | 94.59 | 91.43 | 83.60 |
| 6 mm | 72.00 | 73.62 | 81.08 | 77.14 | 82.96 | |
| 8 mm | 56.00 | 66.26 | 81.08 | 74.29 | 78.89 | |
| 30 m × 18 m | 3 mm | 40.00 | 80.98 | 91.22 | 91.43 | 85.82 |
| 6 mm | 32.00 | 58.89 | 67.57 | 74.29 | 87.91 | |
| 8 mm | 32.00 | 58.89 | 67.57 | 68.57 | 80.06 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, L.; Wu, G.; Zhang, M.; Zhang, Y.; Wang, Z.; Lai, Z. Predicting Epipelic Algae Transport in Open Channels: A Flume Study to Quantify Transport Capacity and Guide Flow Management. Water 2024, 16, 983. https://doi.org/10.3390/w16070983
Pan L, Wu G, Zhang M, Zhang Y, Wang Z, Lai Z. Predicting Epipelic Algae Transport in Open Channels: A Flume Study to Quantify Transport Capacity and Guide Flow Management. Water. 2024; 16(7):983. https://doi.org/10.3390/w16070983
Chicago/Turabian StylePan, Li, Guoying Wu, Mingwu Zhang, Yuan Zhang, Zhongmei Wang, and Zhiqiang Lai. 2024. "Predicting Epipelic Algae Transport in Open Channels: A Flume Study to Quantify Transport Capacity and Guide Flow Management" Water 16, no. 7: 983. https://doi.org/10.3390/w16070983
APA StylePan, L., Wu, G., Zhang, M., Zhang, Y., Wang, Z., & Lai, Z. (2024). Predicting Epipelic Algae Transport in Open Channels: A Flume Study to Quantify Transport Capacity and Guide Flow Management. Water, 16(7), 983. https://doi.org/10.3390/w16070983





