1. Introduction
Water in soil exists in various forms, including structural water, bound water, free water, solid-state water, and gaseous water. Investigating the quantity of water in soil is of paramount importance [
1,
2]. The amount of water in soil is typically expressed as moisture content, which fundamentally represents the ratio of water, excluding structural water, to the mass or volume of the solid or soil body. This can be expressed in two primary methods: mass moisture content and volumetric moisture content. Buckingham and Gardner conducted initial research on the amount of water with respect to the energy level with which water is held in the soil, and the relationship is known as the soil water characteristic curve (SWCC) [
3,
4]. SWCC is a relationship between the moisture content in the soil and soil suction (soil moisture potential), and it is unique for each soil type. SWCC is used to predict soil moisture storage and field capacity and to understand the drying and wetting characteristics of the soil and its pore structure [
5,
6]. The water movement equation in unsaturated soil is a mathematical model describing the process of water movement within soil, which holds significant importance in understanding soil moisture distribution, hydrological cycles, and agricultural irrigation practices. Water movement in soil is typically influenced by soil properties, initial moisture conditions, boundary conditions, and environmental factors. In the early 20th century, Richards proposed the renowned Richards equation, which has been widely employed to describe water movement in unsaturated soil. This equation, grounded on Darcy’s law and the principle of mass conservation, incorporates factors such as soil moisture, soil water potential, and hydraulic conductivity, and it has been extensively utilized to investigate various scenarios of soil water movement [
7]. As research progressed, scholars recognized limitations in the Richards equation when describing certain situations, such as nonlinearity and a lack of physical interpretability. Consequently, to address these issues, several improved models have been proposed, including the Brooks–Corey model, the Van Genuchten model, and others [
8,
9]. These models take into account factors such as soil pore structure and capillary pressure curves, providing a more accurate description of the soil moisture movement process. In determining soil engineering properties, controlling the quality of compacted soil construction, monitoring and forecasting geological hazards, managing agricultural production with precision, and preserving cultural relics, it is essential to conduct the testing and monitoring of soil moisture conditions [
10,
11]. Therefore, achieving the real-time monitoring of deep soil moisture holds significant importance.
Surface soil moisture can be retrieved through GNSS-R signals, meeting the demand for all-weather autonomous monitoring. GNSS, which stands for Global Navigation Satellite System, primarily includes the United States GPS system, China’s BDS system, Russia’s GLONASS system, and the European Union’s GALILEO system [
12]. These navigation satellites not only provide navigation positioning and timing information to users in real-time but also offer L-band microwave signals suitable for remote sensing detection characterized by global coverage, strong penetration, and a high temporal resolution [
13]. Retrieving soil moisture data from GNSS-R signals involves capturing both direct and reflected satellite signals, analyzing the time delay or power changes of the surface-reflected signals, and deducing relevant parameters reflecting surface features based on the geometric relationships among GNSS satellites, ground receivers, reflection points, and the variations in reflection signal characteristics and surface soil properties. The technology for retrieving surface soil moisture data through GNSS-R signals has become relatively mature. In 2002, the University of Colorado and others, under the leadership of NASA, conducted a series of soil moisture retrieval experiments, and experimental data validated the accuracy of the monitoring results [
14]. The Starlab Institute in Spain has designed a soil moisture detection device based on L-band GNSS signal observations. This device analyzes the GNSS signals after interference to obtain relevant information about soil moisture [
15]. Utilizing the Advanced Integrated Equation Model (AIEM), a method for soil moisture monitoring was derived, and the accuracy of the GNSS-R soil moisture monitoring model was validated based on existing experimental data [
16].
Current soil monitoring methods face challenges in achieving the large-scale, real-time monitoring of deep soil moisture. Various methods are available for soil moisture monitoring, including the drying–weighing method, Time Domain Reflectometry (TDR), Ground Penetrating Radar (GPR), the soil resistance method, and the capacitance method for single-point or small-scale soil moisture monitoring. Remote sensing technology is commonly used for spatial and temporal distribution and changes in soil moisture over large areas [
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41]. However, several issues persist in real-time soil moisture monitoring. For instance, the applicability and accuracy of testing methods are often influenced and constrained due to soil characteristics. Furthermore, instruments and sensors commonly suffer from issues such as a large size, high energy consumption, and a high cost, resulting in high real-time monitoring expenses [
17,
18,
19]. The L-band signals carried by Global Navigation Satellite Systems (GNSSs) are highly sensitive to soil moisture, making them particularly suitable for monitoring soil moisture variations [
42]. By utilizing signal power or delay as attributes and actual soil moisture values as labels, inversion models based on navigation signals can be established through the combination of empirical dielectric constant models, Support Vector Machines (SVMs), Random Forest algorithms, and neural network methods such as BP and Deep Belief Networks [
43,
44,
45]. Therefore, the introduction of soil moisture data retrieved from GNSS-R signals largely overcomes the limitations of traditional soil moisture measurement methods in terms of small effective measurement area and a lack of representativeness, meeting the demand for all-weather autonomous monitoring. However, the penetration depth of GNSSs’ L-band signals is limited to only 10 cm. As a result, soil moisture data within 10 cm depth can be retrieved through GNSS-R signal inversion, and soil moisture data within 5 cm depth can be more accurately inverted through GNSS-R signals. In summary, current soil monitoring methods face challenges in achieving the large-scale, real-time monitoring of deep soil moisture. However, deep soil moisture data are crucial in agriculture, geological hazard monitoring, engineering construction, and site preservation.
Therefore, by integrating soil–water characteristics and soil moisture at a depth of 1 m with surface soil moisture data retrieved from GNSS-R signal inversion, deep soil moisture prediction models can be developed. These models enable the prediction of soil moisture values in the 0–1 m depth range, facilitating the large-scale, real-time dynamic monitoring of deep soil moisture.
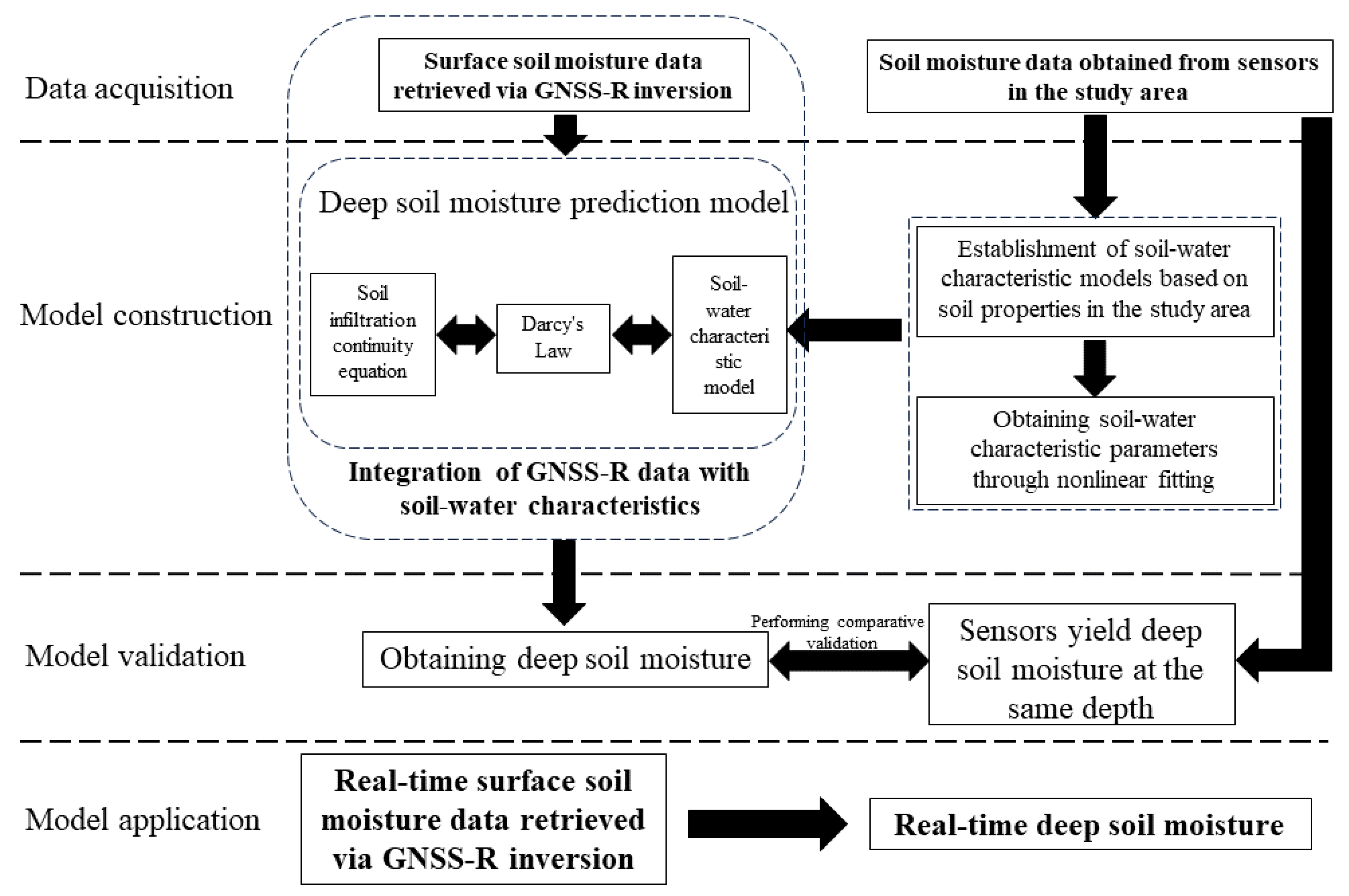
This paper addresses the current challenge of the inability of existing soil moisture monitoring methods to achieve the large-scale, real-time dynamic monitoring of deep soil moisture. It innovatively proposes a real-time prediction approach to deep soil moisture combining GNSS-R data and water movement model in unsaturated soil. This approach, relying on soil moisture data retrieved from GNSS-R signal inversion, largely overcomes the limitations of traditional soil moisture measurement methods, such as small effective measurement areas and a lack of representativeness, thereby meeting the demand for all-weather autonomous monitoring. By integrating soil–water characteristics and soil moisture values at a depth of 1 m with surface soil moisture data retrieved from GNSS-R signal inversion, the approach can predict soil moisture values in the 0–1 m depth range. This approach overcomes the limitation of GNSS-R signal inversion, which is restricted to the soil surface. The proposed method realizes the large-scale, real-time dynamic monitoring of deep soil moisture and is expected to play a crucial role in agriculture, geological hazard monitoring, engineering construction, and site preservation.
3. Results
Firstly, soil moisture data at the surface and depths of 0.1 m, 0.2 m, 0.5 m, and 1 m at monitoring points A and B were obtained from the International Soil Moisture Network for 20 October, 25 October, 30 October, 4 November, 9 November, 14 November, and 19 November 2023. The soil moisture data from 25 October, 30 October, 4 November, 9 November, 14 November, and 19 November 2023 at monitoring points A and B were primarily used to compare with the results obtained from the real-time prediction approach for deep soil moisture proposed in this paper. The soil moisture data from 20 October 2023 at monitoring points A and B were mainly used to establish the soil–water characteristic model and the deep soil moisture prediction model for the study area.
Next, using the soil moisture data from monitoring points A and B at the surface and depths of 0.1 m, 0.2 m, 0.5 m, and 1 m on 20 October 2023, we performed the nonlinear fitting of Equation (
13) to establish the soil–water characteristic model and the deep soil moisture prediction model for the study area. Subsequently, utilizing the surface soil moisture data from monitoring points A and B on 25 October, 30 October, 4 November, 9 November, 14 November, and 19 November 2023, we obtained the predicted values of soil moisture at depths from 0 to 1 m using the deep soil moisture prediction model.
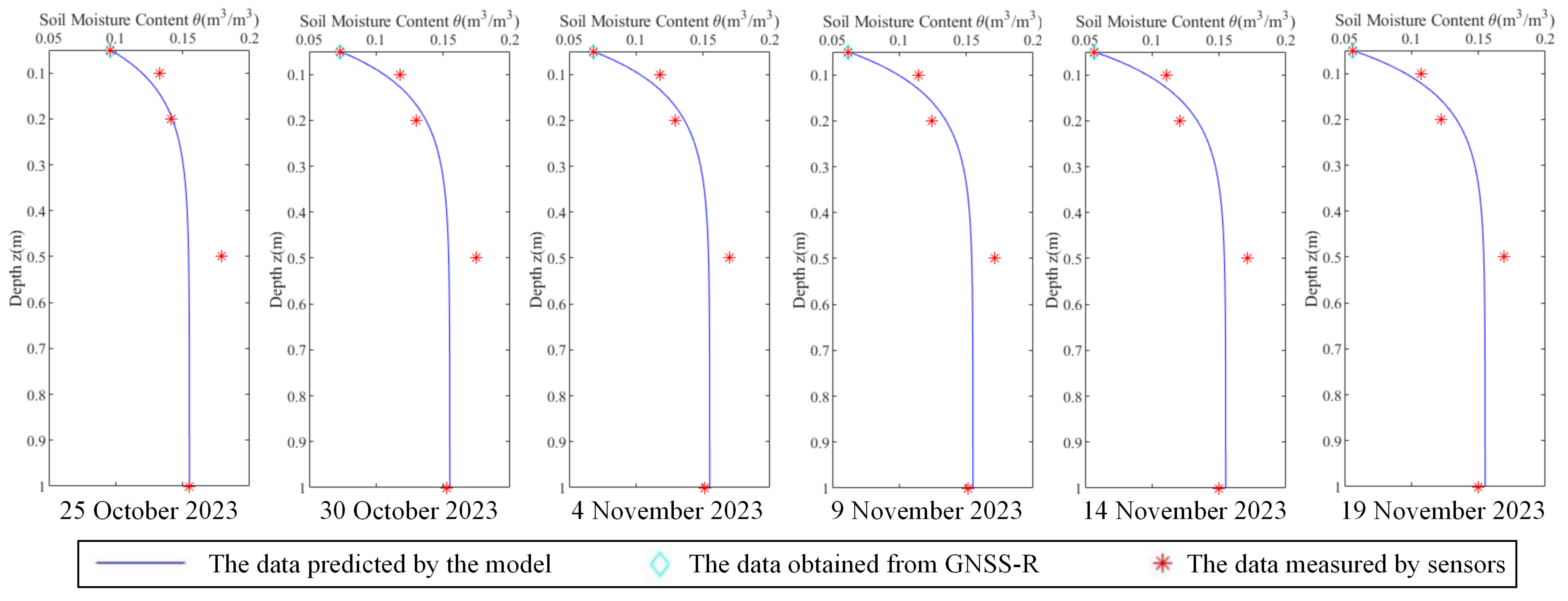
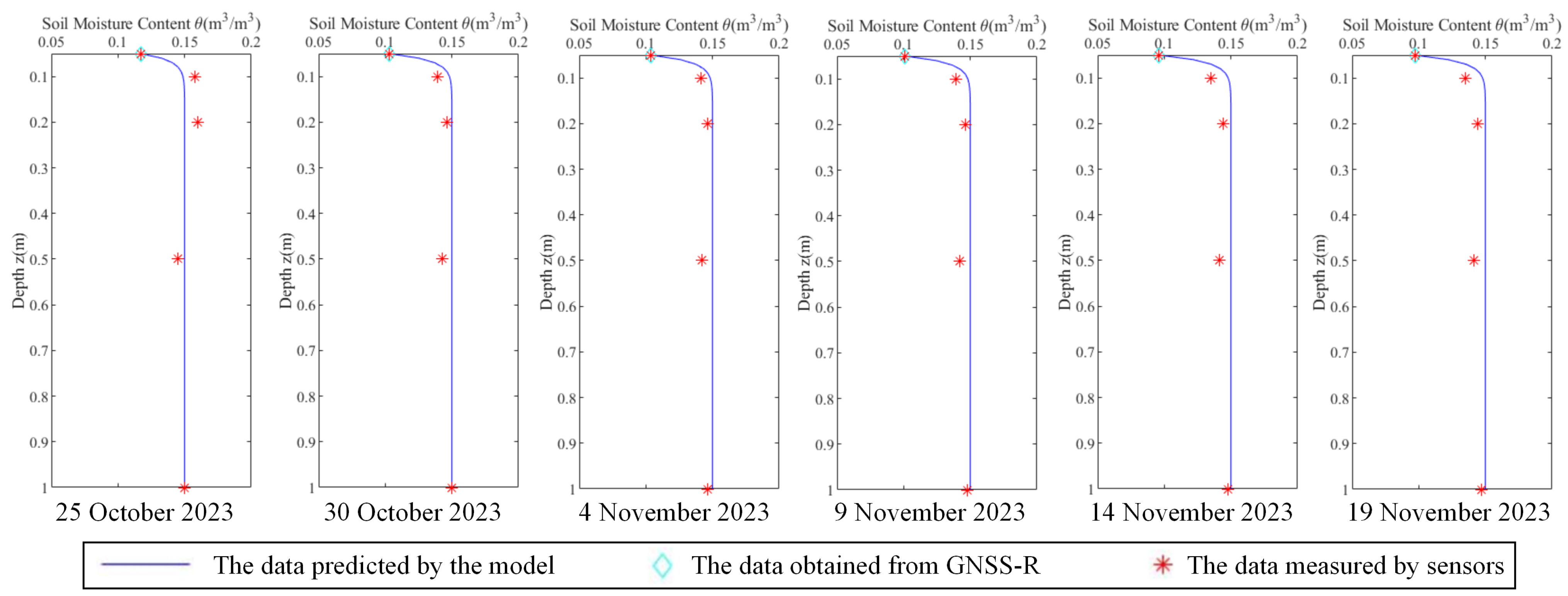
Finally, the predicted values and true values of soil moisture at the surface and depths of 0.1 m, 0.2 m, 0.5 m, and 1 m for monitoring points A and B on the six dates were compared. The results are shown in
Figure 3 and
Figure 4. From the figures, it can be qualitatively observed that the predicted values of soil moisture at the monitoring points correspond well with the true values.
3.1. Assessment of Predicted Values
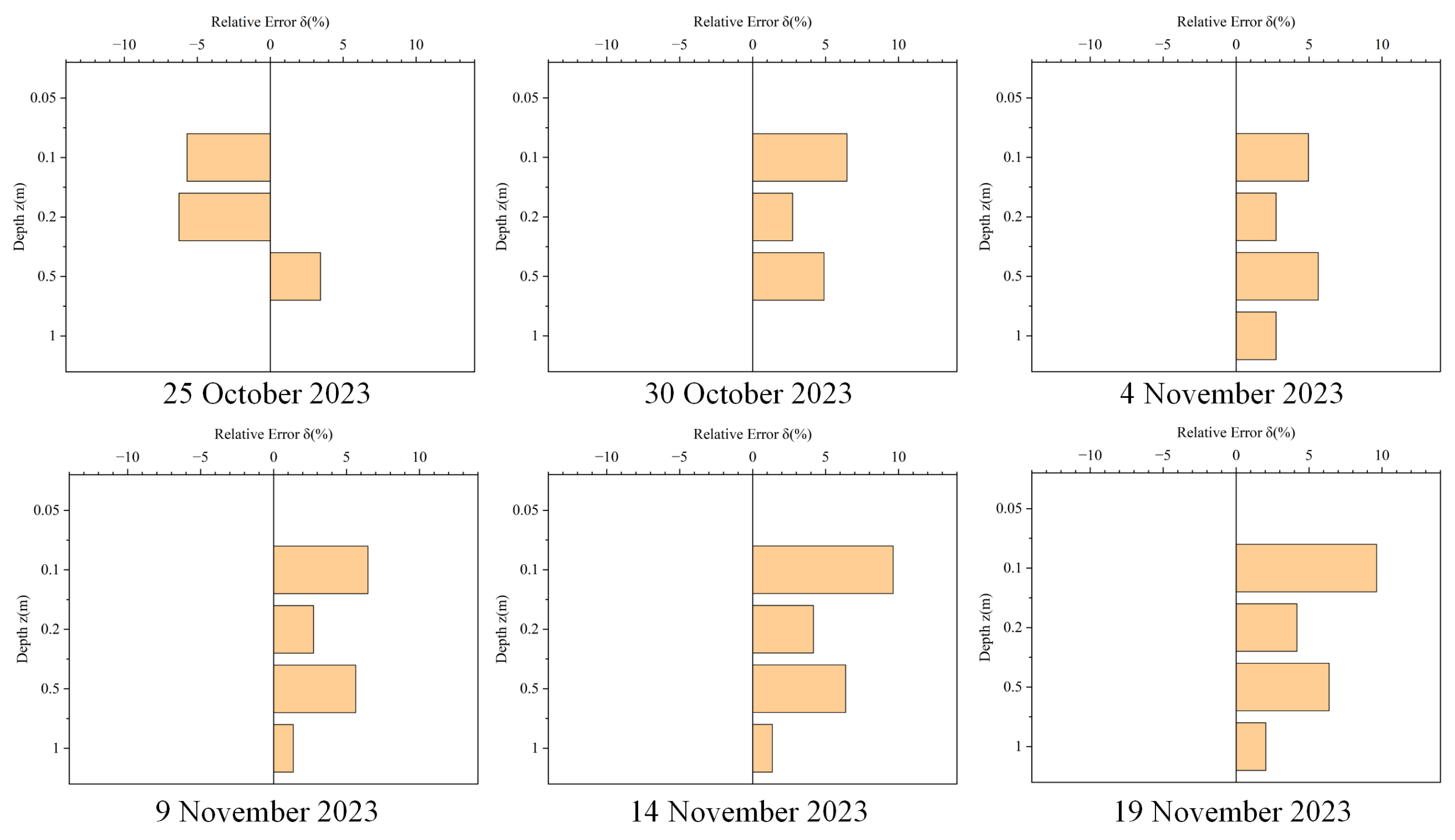
3.1.1. Relative Error of the Predicted Values
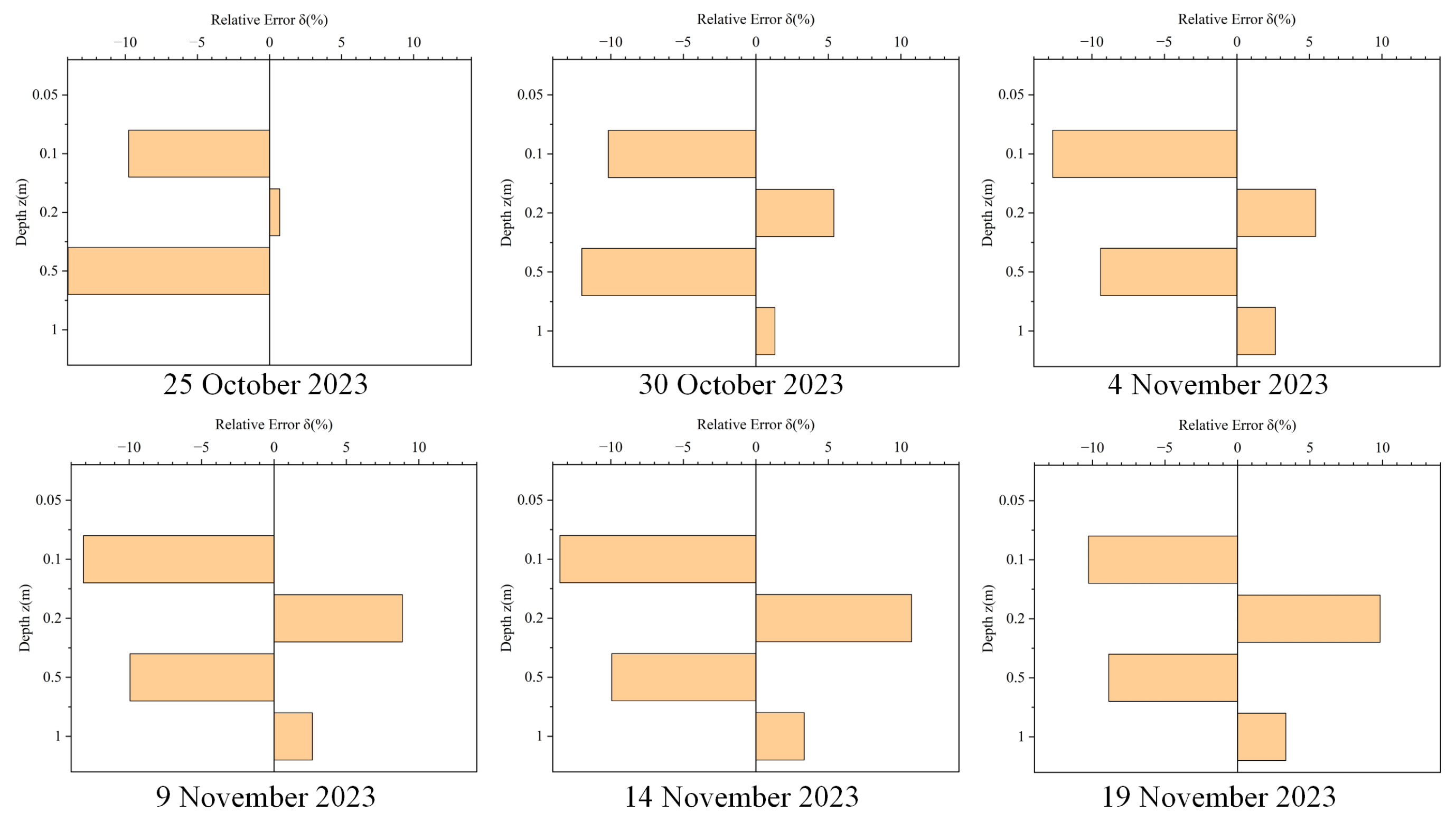
Subsequently, the relative error (
) between the predicted and true soil moisture values at different depths for monitoring points A and B over the six days was utilized to quantitatively evaluate the accuracy of the model predictions, as depicted in
Figure 5 and
Figure 6. On 25 October 2023, the relative error (
) of the predicted soil moisture values at different depths for monitoring point A ranged from −13.97% to 0.71%, while for monitoring point B, it ranged from −6.25% to 3.45%. Similarly, on 30 October 2023, the relative error (
) for monitoring point A varied from −12.00% to 5.38%, and for monitoring point B, it ranged from 2.74% to 6.47%. On 4 November 2023, the relative error (
) for monitoring point A ranged from −12.71% to 5.43%, while for monitoring point B, it ranged from −2.74% to 5.63%. On 9 November 2023, the relative error (
) for monitoring point A ranged from −13.16% to 8.87%, and for monitoring point B, it ranged from 1.35% to 6.47%. On 14 November 2023, the relative error (
) for monitoring point A varied from −13.51% to 10.74%, and for monitoring point B, it ranged from 1.35% to 9.63%. Finally, on 19 November 2023, the relative error (
) for monitoring point A ranged from −10.28% to 9.84%, while for monitoring point B, it ranged from 2.04% to 9.63%. The relative errors (
) of soil moisture predictions relative to true values at different depths for monitoring points A and B over the six days were all within a small range, indicating minimal deviation between predicted and true soil moisture values. Therefore, this validates the feasibility of the real-time prediction approach to deep soil moisture combining GNSS-R data and a water movement model in unsaturated soil.
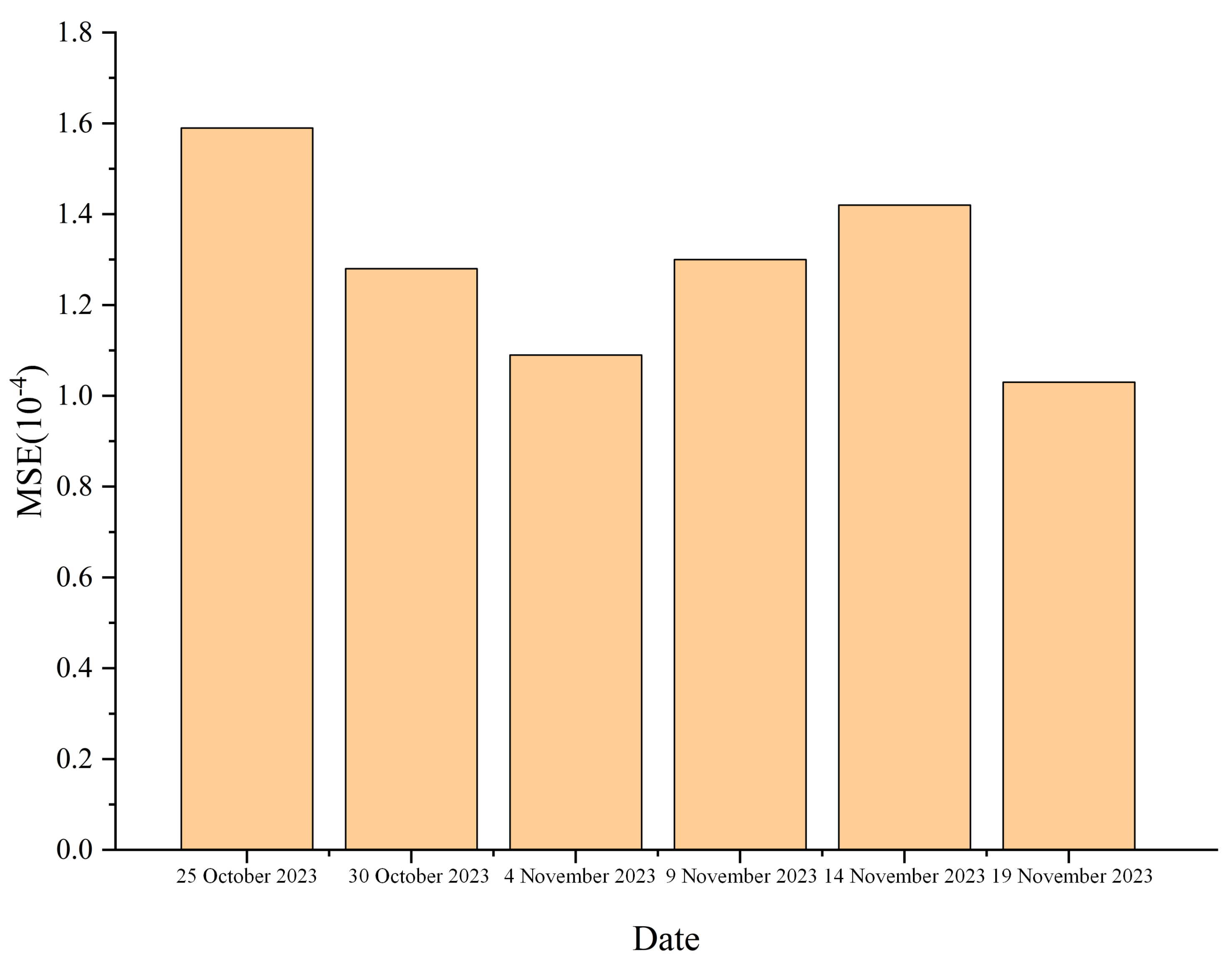
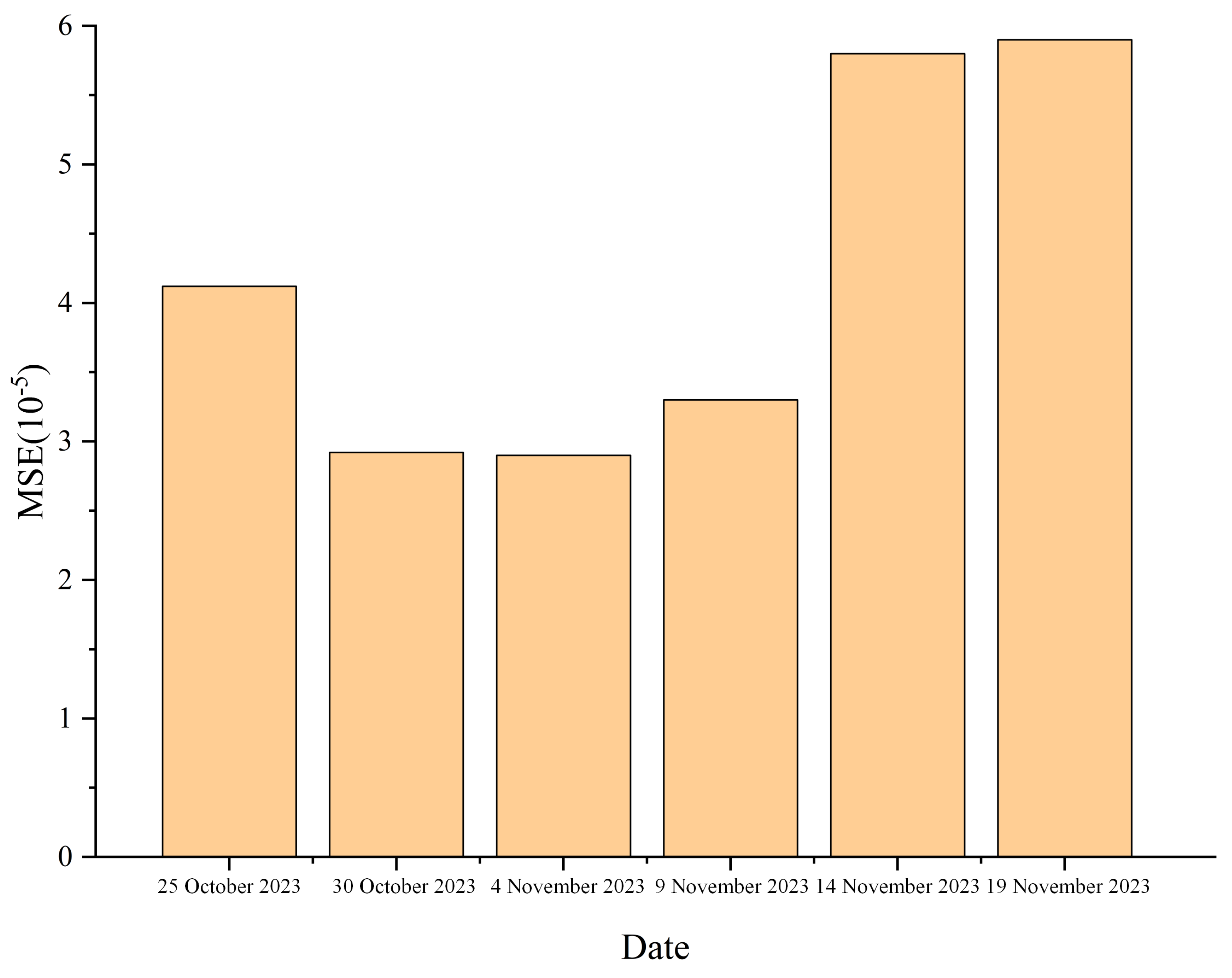
3.1.2. MSE and of the Predicted Values
Based on the mean square error (MSE) and the coefficient of determination () relative to the true values of soil moisture predictions over the six days, a more in-depth quantitative analysis of the model’s prediction accuracy could be conducted.
According to computations, the mean square error (MSE) of soil moisture predictions for monitoring point A on 25 October 2023 was 1.59 ×
, while for monitoring point B, it was 4.12 ×
. On 30 October 2023, the MSE for monitoring point A was 1.28 ×
, and for monitoring point B, it was 2.92 ×
. For 4 November 2023, the MSE for monitoring point A was 1.09 ×
, and for monitoring point B, it was 2.90 ×
. On 9 November 2023, the MSE for monitoring point A was 1.30 ×
, and for monitoring point B, it was 3.30 ×
. For 14 November 2023, the MSE for monitoring point A was 1.42 ×
, and for monitoring point B, it was 5.80 ×
. Finally, on 19 November 2023, the MSE for monitoring point A was 1.03 ×
, and for monitoring point B, it was 5.90 ×
, as shown in
Figure 7 and
Figure 8. It is evident that the prediction accuracy from the surface to the deep soil moisture prediction models shows a high degree of fit with the true values. Therefore, it validates the feasibility of the real-time prediction approach to deep soil moisture combining GNSS-R data and a water movement model in unsaturated soil.
Through calculations, it was determined that the coefficient of determination
for the soil moisture predictions at monitoring point A on 25 October 2023 was 78.68%, while at monitoring point B, it was 82.80%. On 30 October 2023, the coefficient of determination
for soil moisture predictions at monitoring point A was 89.27%, and at monitoring point B, it was 89.88%. By 4 November 2023, the coefficient of determination
for soil moisture predictions at monitoring point A increased to 90.89%, whereas at monitoring point B, it decreased slightly to 88.71%. On 9 November 2023, the coefficient of determination
for soil moisture predictions at monitoring point A was 90.54%, and at monitoring point B, it was 89.08%. By 14 November 2023, the coefficient of determination
for soil moisture predictions at monitoring point A was 90.60%, and at monitoring point B, it was 83.73%. Finally, on 19 November 2023, the coefficient of determination
for soil moisture predictions at monitoring point A was 93.19%, while at monitoring point B, it was 82.45%, as illustrated in
Figure 9 and
Figure 10. It is evident that the predictive models for soil moisture content from the surface to deep layers exhibit a high degree of conformity between predicted and actual values. Therefore, the feasibility of the real-time prediction approach to deep soil moisture content, which integrates GNSS-R detection data and soil moisture characteristics, can be validated.
When combining the mean square errors (MSEs) and coefficients of determination () relative to the true values for soil moisture predictions at monitoring points A and B at depths from the surface of 0.1 m, 0.2 m, 0.5 m, and 1 m on 25 October, 30 October, 4 November, 9 November, 14 November, and 19 November 2023, it is evident that the deep soil moisture prediction model achieves a high degree of fit between predicted and actual values. Thus, it validates the feasibility of the real-time prediction approach to deep soil moisture combining GNSS-R data and water movement model in unsaturated soil.
3.2. Effects of Soil–Water Characteristic Model on Predicted Values
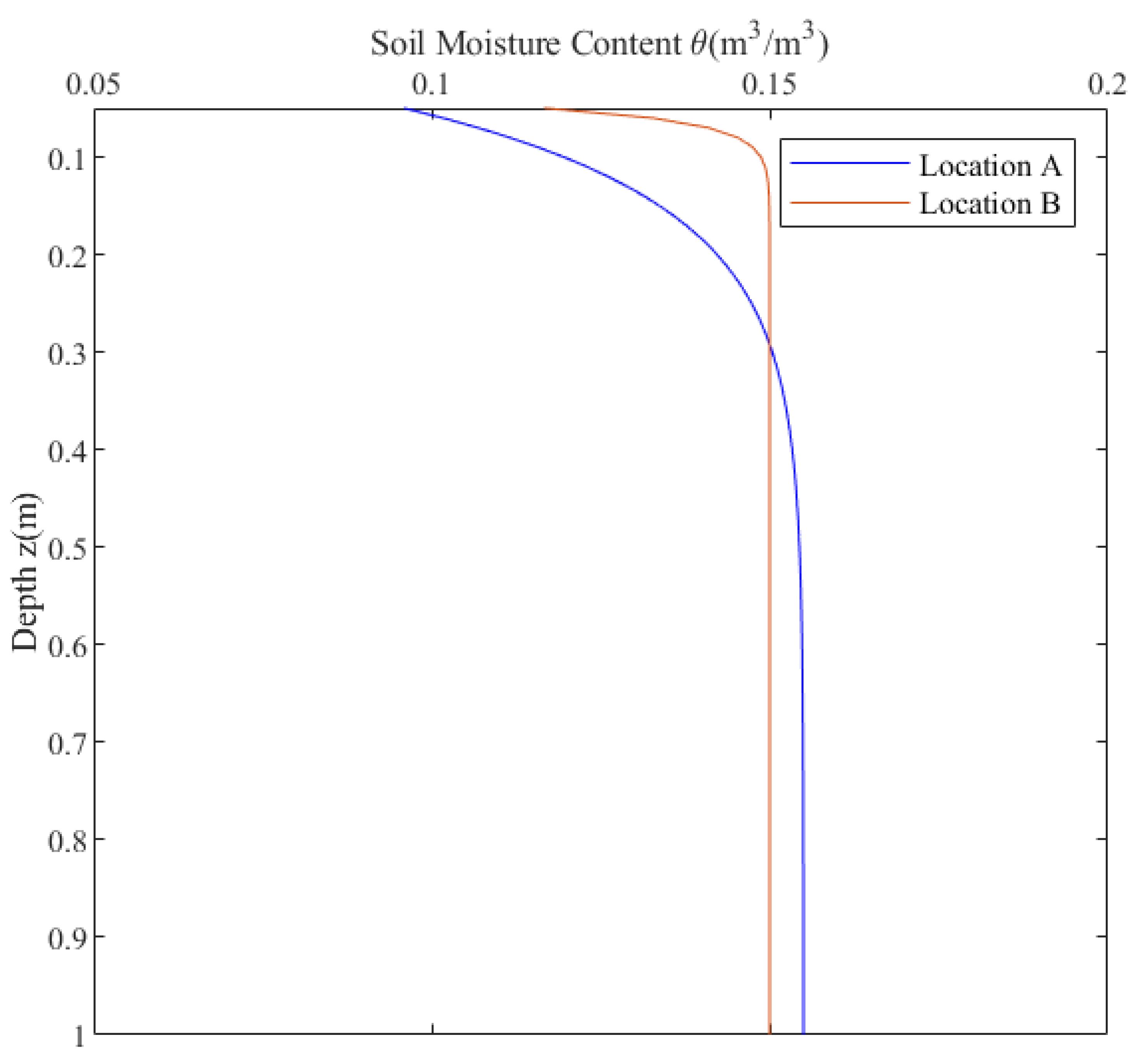
Using the real-time prediction approach to deep soil moisture combining GNSS-R data and a water movement model in unsaturated soil, soil moisture predictions for monitoring points A and B on 25 October 2023 were obtained, revealing significant discrepancies in the predicted values, as shown in
Figure 11. The deep soil moisture prediction model used for monitoring both points, A and B, is consistent, with the only variable being the soil–water characteristic parameters
,
n, and
m in the deep soil moisture prediction model. However, these parameters,
,
n, and
m, are related to the soil properties at monitoring points A and B. Therefore, a comparison of the soil–water characteristic models between monitoring points A and B was warranted.
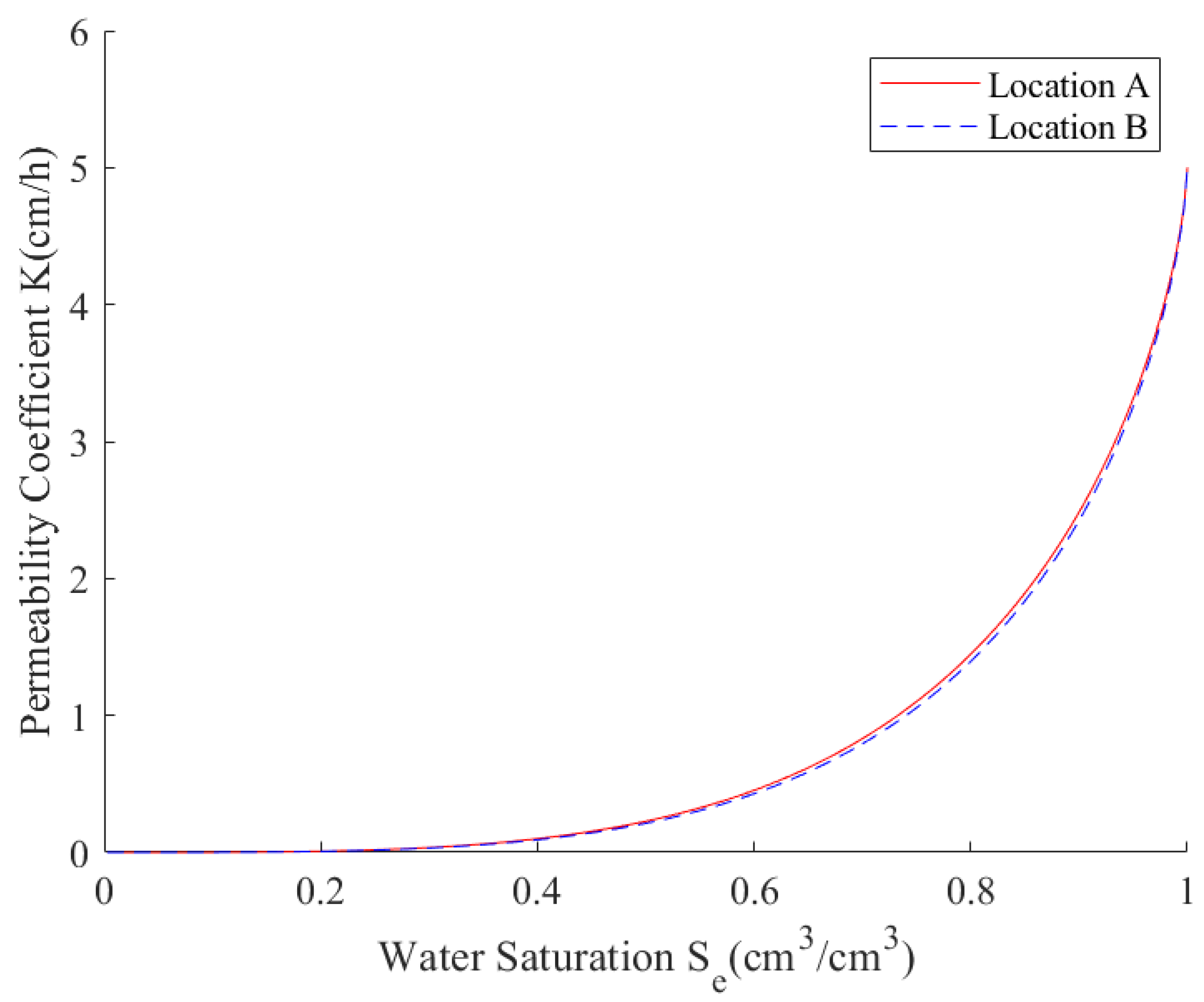
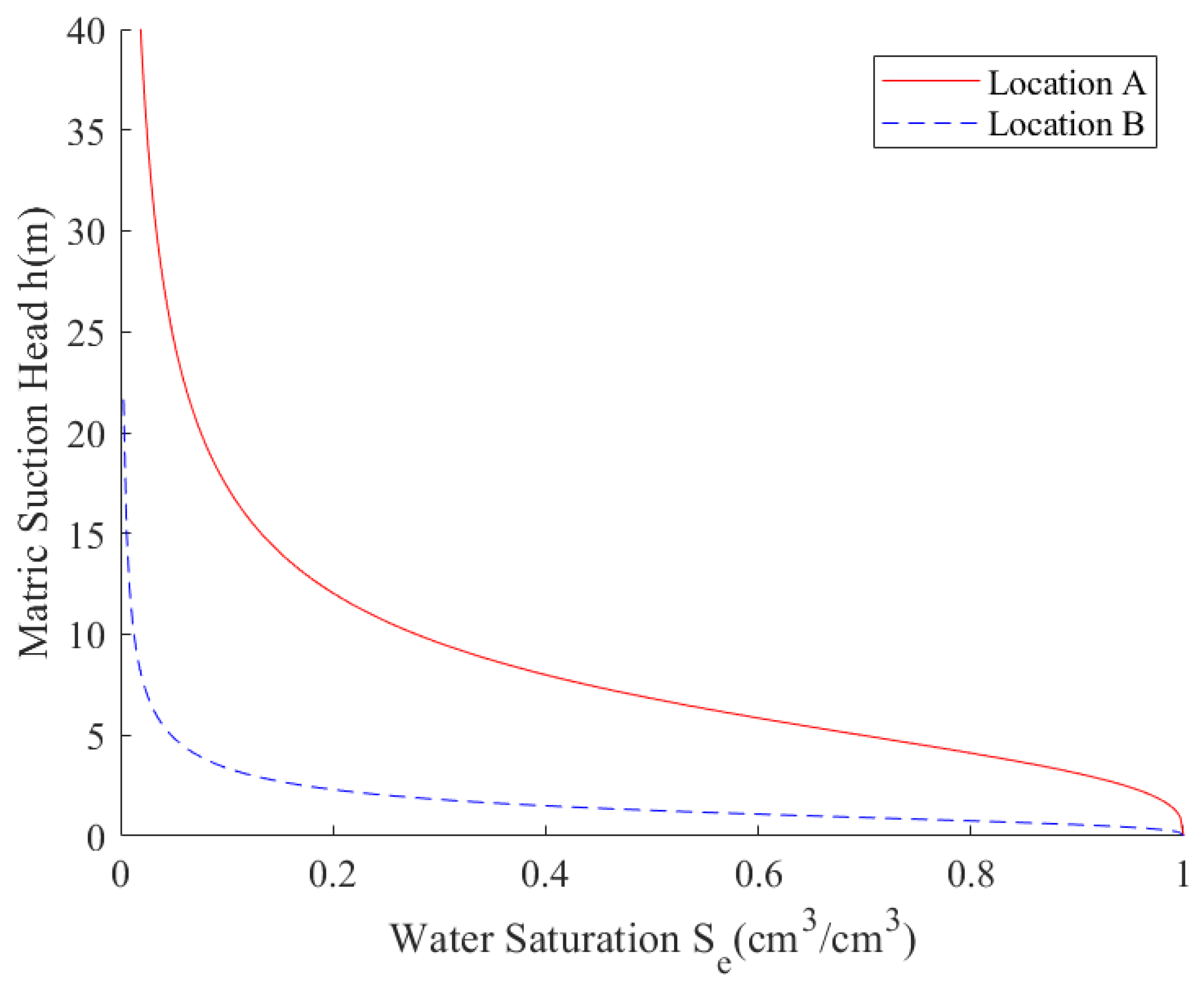
Figure 12 illustrates the permeability coefficient characteristic curves of monitoring points A and B, while
Figure 13 depicts the matric suction head characteristic curves of monitoring points A and B. It can be observed that the infiltration coefficient characteristic curves of monitoring points A and B are relatively similar, whereas the matric suction head characteristic curves of monitoring points A and B exhibit significant differences. This discrepancy contributes to the considerable disparity in the predicted soil moisture between monitoring points A and B.
3.3. Effects of Model Lower Boundary Depth on Predicted Values
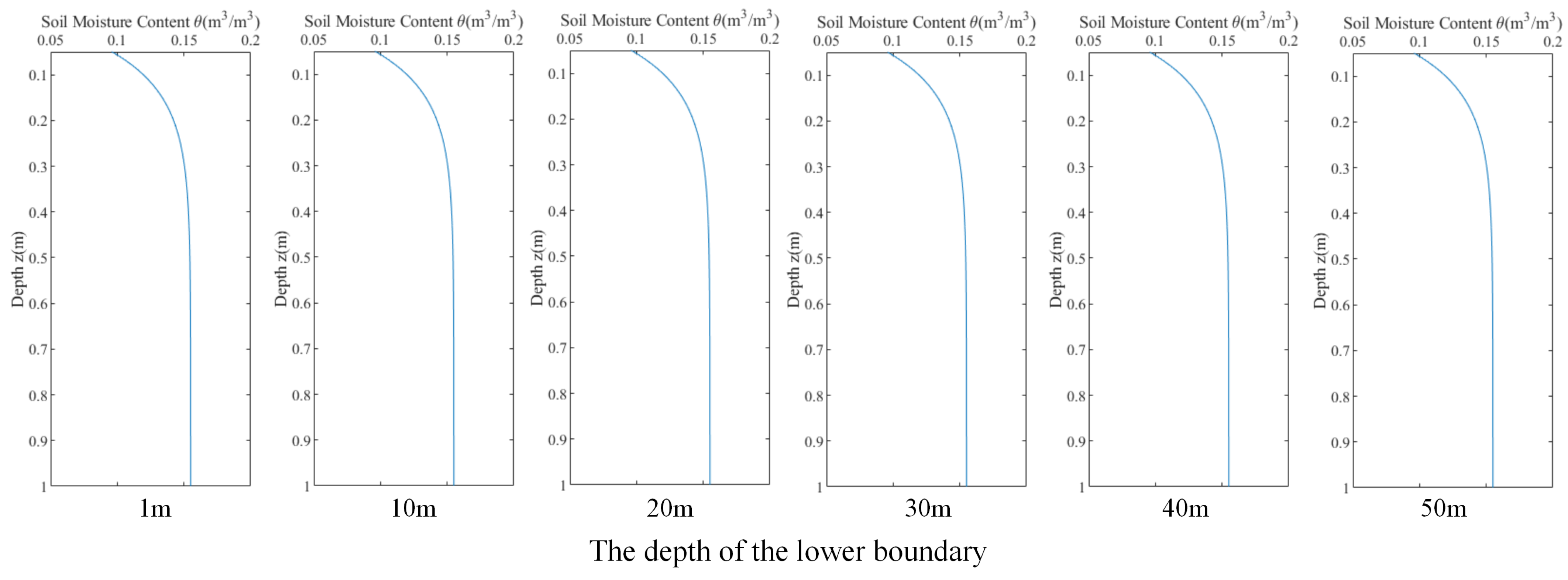
The real-time prediction approach to deep soil moisture combining GNSS-R data and a water movement model in unsaturated soil proposed in this paper sets the depth of the lower boundary of the moisture movement control equation in unsaturated soil to 1 m. To investigate the influence of the lower boundary depth setting on soil moisture prediction, this paper sets the lower boundary depth to 1 m, 10 m, 20 m, 30 m, 40 m, and 50 m, obtaining the corresponding predicted values for monitoring point A on 25 October 2023 and comparing them, as shown in
Figure 14.
From the graph, it can be observed that the lower boundary depth of the unsaturated soil moisture movement control equation has no effect on soil moisture prediction values when it exceeds 1 m. Therefore, choosing 1 m as the lower boundary depth of the unsaturated soil moisture movement control equation is reasonable.
4. Discussion
Due to the close correlation between soil moisture and variables such as soil properties and climatic conditions, the deep soil moisture prediction model proposed in this paper incorporates variables such as soil properties and climatic conditions during the construction process, aiming to achieve applicability under different soil properties and climatic conditions. As our model integrates the soil–water characteristic model, the deep soil moisture prediction model we obtained is parameterized. Through the initial data fitting process, the parameters in the model are solved, reflecting the characteristics of soil types. Since the soil composition in many regions within the depth range of 0–1 m is relatively homogeneous, resembling a homogeneous porous medium, our model is applicable in regions where the soil composition is uniform.
In cases of heterogeneous soil, it is possible to conduct stratified research on the soil in the study area. By combining the corresponding soil–water characteristic parameters of each soil layer, our model can be applied to conduct research effectively. Due to the close correlation between surface soil moisture data and climatic conditions, incorporating GNSS-R-retrieved surface soil moisture data into the process of predicting deep soil moisture through modeling implies that the model takes climate condition variables into consideration. In summary, the real-time prediction approach to deep soil moisture combining GNSS-R data and a water movement model in unsaturated soil proposed in this paper exhibits strong applicability and holds potential for future deployment in various regions. However, further optimization is necessary to enhance the method’s universality.
5. Conclusions
The real-time monitoring of deep soil moisture has significant implications for controlling the quality of compacted soil construction, geological disaster monitoring and forecasting, the precise management of agricultural production, and other areas. However, traditional methods of soil moisture monitoring suffer from inefficiency and high costs when applied to large-scale areas. Additionally, methods that rely on GNSS-R signal inversion to obtain soil moisture data are limited due to their shallow monitoring depth. To address the limitations of current soil moisture monitoring methods, particularly their inability to dynamically monitor deep soil moisture over large areas in real time, this study innovatively proposed a real-time prediction approach to deep soil moisture combining GNSS-R data and a water movement model in unsaturated soil. This approach utilizes surface soil moisture data obtained through GNSS-R signal inversion and integrates it with soil–water characteristics and soil moisture data at a depth of 1 m. By employing a deep soil moisture prediction model, it is possible to obtain predicted soil moisture values for depths ranging from 0 to 1 m, enabling the large-scale, real-time monitoring of deep soil moisture. The proposed method was validated using data provided by the International Soil Moisture Network, focusing on a field in Goodwell, Texas County, OK, USA, as the study area.
By calculating the relative error of the predicted soil moisture values relative to the true values at monitoring points A and B in the study area at the surface and depths of 0.1 m, 0.2 m, 0.5 m, and 1 m on six days (25 October, 30 October, 4 November, 9 November, 14 November, and 19 November 2023), it was found that the relative error remained within a relatively low range. The relative error at monitoring point A was controlled within ±14%, while at monitoring point B, it was controlled within ±10%. Therefore, it is evident that the deep soil moisture prediction model fits the true values quite well. Furthermore, by computing the mean square error (MSE) and coefficient of determination () of the soil moisture predictions relative to the true values at monitoring points A and B in the study area at the surface and depths of 0.1 m, 0.2 m, 0.5 m, and 1 m on the same six days, it was observed that the MSE at monitoring point A ranged from 1.03 × to 1.59 × , and at monitoring point B, it ranged from 2.90 × to 5.90 × , indicating a relatively low overall control level. The at monitoring point A ranged from 78.68% to 93.19%, while at monitoring point B, it ranged from 82.45% to 89.88%, indicating a relatively high overall control level. Therefore, it can be concluded that the deep soil moisture prediction model achieves a high level of fitting with the true values. Consequently, the soil moisture data predicted using this method align well with actual soil moisture data, validating the feasibility of the real-time prediction approach to deep soil moisture combining GNSS-R data and a water movement model in unsaturated soil. The soil–water characteristic model influences soil moisture prediction values, rendering the method applicable across different geographic features. Moreover, the depth of the lower boundary in the unsaturated soil moisture transport control equation does not affect soil moisture prediction values when it exceeds 1 m, justifying the selection of 1 m as a reasonable depth for the lower boundary in the unsaturated soil moisture transport control equation.
The real-time prediction approach to deep soil moisture combining GNSS-R data and a water movement model in unsaturated soil achieves the real-time and dynamic monitoring of deep soil moisture over a wide range, which can play a significant role in various fields, such as agricultural production, geological disaster management, engineering construction, and heritage preservation.