Measurements and Simulations of the Flow Distribution in a Down-Scaled Multiple Outlet Spillway with Complex Channel
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Numerical Setup
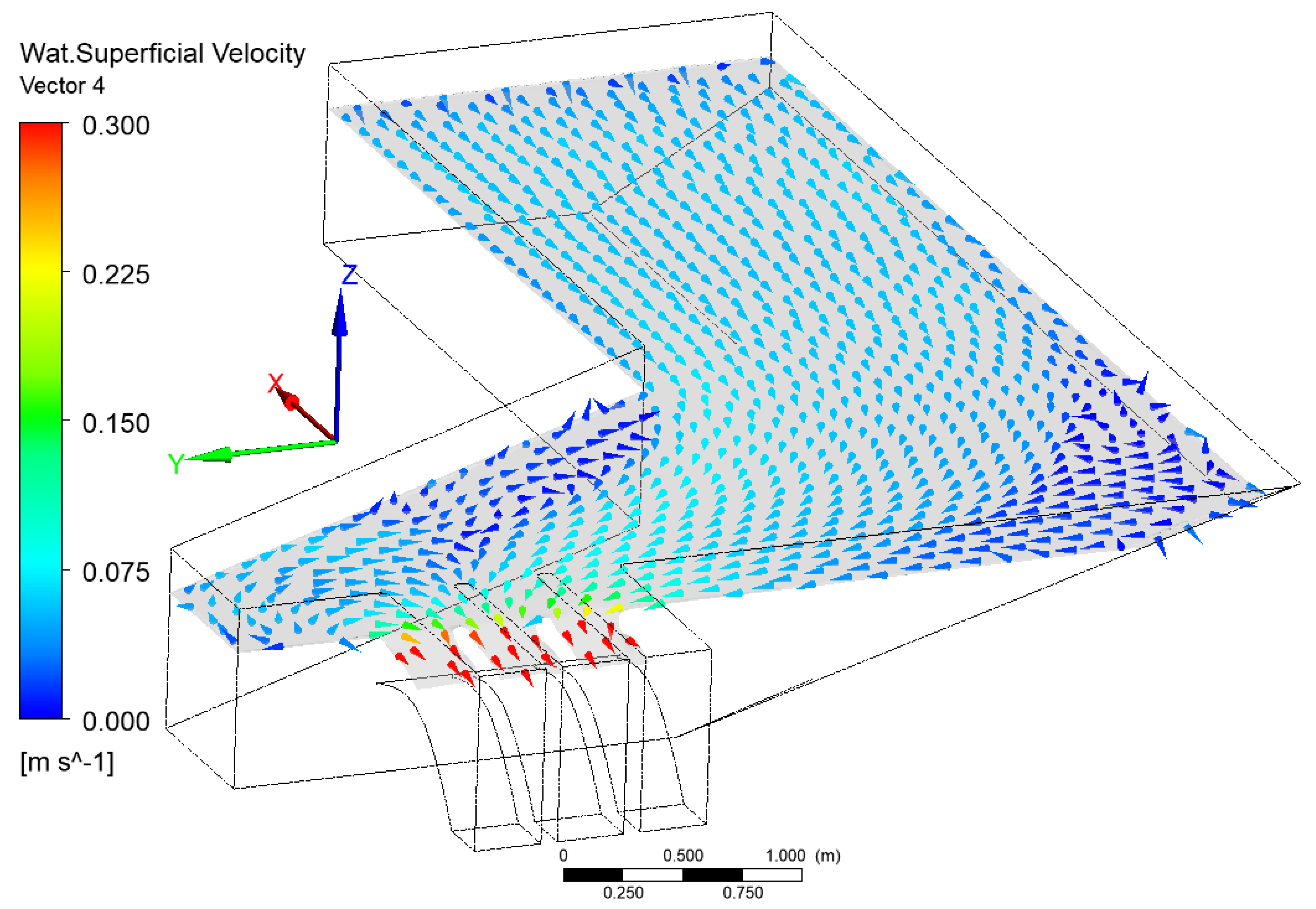
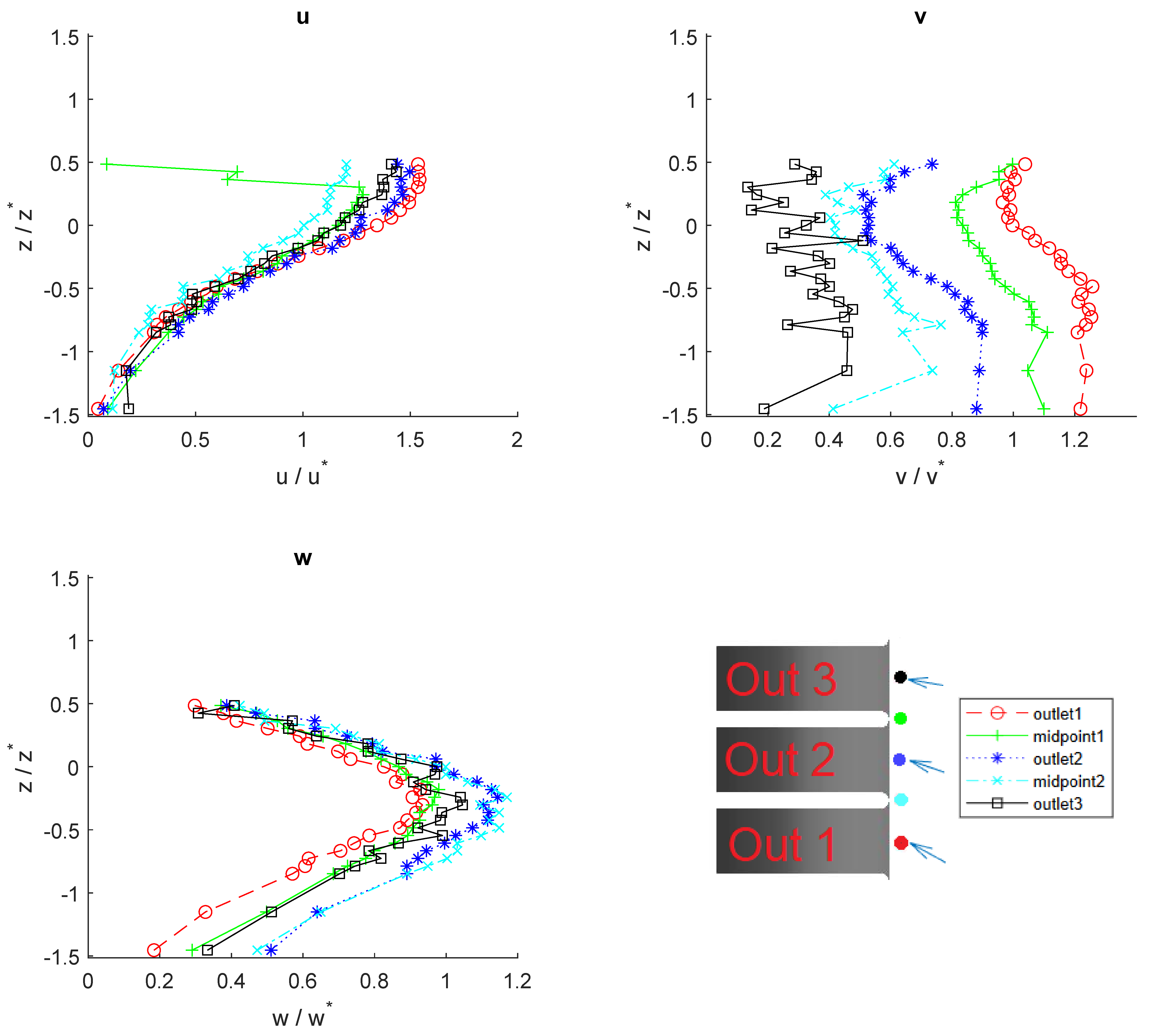
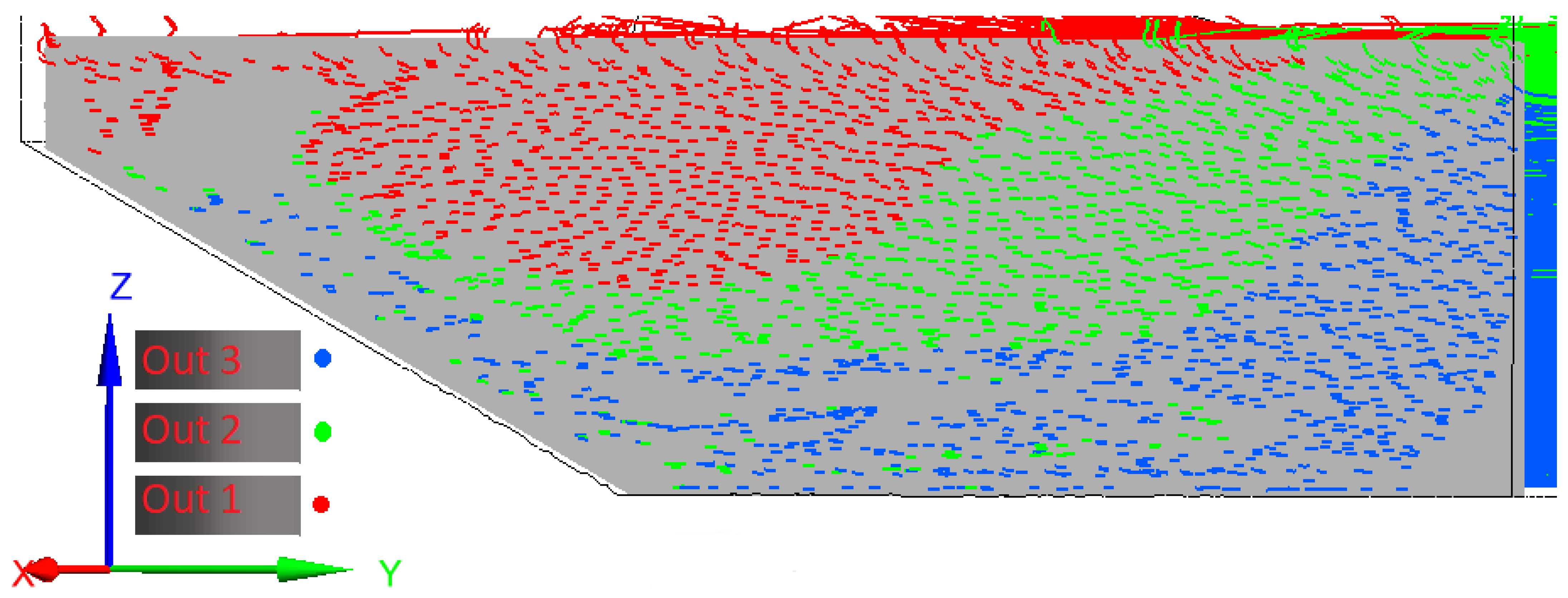
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hellgren, R.; Bartsch, M. Book on Dams the Swedish Experience. Available online: https://www.svk.se/siteassets/3.sakerhet-och-beredskap/dammsakerhet/vagledningar-och-stod/book_on_dams.pdf (accessed on 15 March 2024).
- Yang, J.; Patrik, P.; Teng, P.; Xie, Q. The Past and Present of Discharge Capacity Modeling for Spillways—A Swedish Perspective. Fluids 2019, 4, 10. [Google Scholar] [CrossRef]
- Peltier, Y.; Dewals, B.; Archambeau, P.; Pirotton, M.; Erpicum, S. Pressure and velocity on an ogee spillway crest operating at high head ratio: Experimental measurements and validation. J. Hydro-Environ. Res. 2018, 19, 128–136. [Google Scholar] [CrossRef]
- Solheim, N.; Hedberg, P.A.M.; Lunde, H.; Pummer, E.; Lia, L. Modified Guide Walls for Incremental Increase of Spillway Capacity. In Proceedings of the 40th IAHR World Congress, Vienna, Austria, 21–25 August 2023; pp. 1978–1983. [Google Scholar]
- Stilmant, F.; Erpicum, S.; Peltier, Y.; Archambeau, P.; Dewals, B.; Pirotton, M. Flow at an Ogee Crest Axis for a Wide Range of Head Ratios: Theoretical Model. Water 2022, 14, 2337. [Google Scholar] [CrossRef]
- Mozaffari, S.; Amini, E.; Mehdipour, H.; Neshat, M. Flow Discharge Prediction Study Using a CFD-Based Numerical Model and Gene Expression Programming. Water 2022, 14, 650. [Google Scholar] [CrossRef]
- Kocaer, Ö.; Yarar, A. Experimental and Numerical Investigation of Flow Over Ogee Spillway. Water Resour. Manag. 2020, 13, 3949–3965. [Google Scholar] [CrossRef]
- Savage, B.; Johnson, M. Flow over ogee spillway: Physical and numerical model case study. J. Hydraul. Eng. 2001, 8, 640–649. [Google Scholar] [CrossRef]
- Johnson, M.; Savage, B. Physical and Numerical Comparison of Flow over Ogee Spillway in the Presence of Tailwater. J. Hydraul. Eng. 2006, 12, 640–649. [Google Scholar] [CrossRef]
- Andersson, A.G.; Andreasson, P.; Lundström, T.S. CFD-Modelling and Validation of Free Surface Flow During Spilling of Reservoir in Down-Scale Model. Eng. Appl. Comput. Fluid Mech. 2013, 7, 159–167. [Google Scholar] [CrossRef]
- Lee, J.H.; Julien, P.Y.; Thornton, C.I. Interference of Dual Spillways Operations. J. Hydraul. Eng. 2019, 10, 142–149. [Google Scholar] [CrossRef]
- Li, L.; Xu, W.; Tan, Y.; Yang, Y.; Yang, J.; Tan, D. Fluid-induced vibration evolution mechanism of multiphase free sink vortex and the multi-source vibration sensing method. Mech. Syst. Signal Process. 2023, 189, 110058. [Google Scholar] [CrossRef]
- Li, L.; Li, Q.; Ni, Y.; Wang, C.; Tan, Y.; Tan, D. Critical penetrating vibration evolution behaviors of the gas-liquid coupled vortex flow. Energy 2024, 292, 130236. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; He, X. Modeling transient flow dynamics around a bluff body using deep learning techniques. Ocean Eng. 2024, 295, 116880. [Google Scholar] [CrossRef]
- Kadia, S.; Lia, L.; Albayrak, I.; Pummer, E. The effect of cross-sectional geometry on the high-speed narrow open channel flows: An updated Reynolds stress model study. Comput. Fluids 2024, 271, 106184. [Google Scholar] [CrossRef]
- Li, S.; Cain, S.; Wosnik, M.; Miller, C.; Kocahan, H.; Wyckoff, R. Numerical Modeling of Probable Maximum Flood Flowing through a System of Spillways. J. Hydraul. Eng. 2011, 137, 66–74. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, L.; Ansar, M.; Damisse, E.; González-Castro, J.A. Applications of Computational Fluid Dynamics to Flow Ratings at Prototype Spillways and Weirs. I: Data Generation and Validation. J. Irrig. Drain. Eng. 2017, 143, 04016072. [Google Scholar] [CrossRef]
- Yildiz, A.; Yarar, A.; Kumcu, S.Y.; Marti, A.I. Numerical and ANFIS modeling of flow over an ogee-crested spillway. Appl. Water Sci. 2020, 10, 90. [Google Scholar] [CrossRef]
- De Morais, V.H.P.; Gireli, T.Z.; Vatavuk, P. Numerical and experimental models applied to an ogee crest spillway and roller bucket stilling basin. Braz. J. Water Resour. 2020, 25, e18. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, Y.; Kim, D.; Kang, S. Flume Experiments for Flow around Debris Accumulation at a Bridge. KSCE J. Civ. Eng. 2024, 28, 1049–1061. [Google Scholar] [CrossRef]
- Pandey, M.; Sharma, P.K.; Ahmad, Z.; Singh, U.K.; Karna, N. Three-dimensional velocity measurements around bridge piers in gravel bed. Mar. Georesources Geotechnol. 2018, 36, 663–676. [Google Scholar] [CrossRef]
- Mikael, H.; Gunnar, H.; Nils, S. Experimental and Computational Evaluation of Fish Passageway with Porous Media Boundary. In Proceedings of the 40th IAHR World Congress, Vienna, Austria, 21–25 August 2023; pp. 2422–2428. [Google Scholar]
- Singh, U.K.; Ahmad, Z.; Kumar, A. Turbulence characteristics of flow over the degraded cohesive bed of clay–silt–sand mixture. ISH J. Hydraul. Eng. 2017, 3, 308–318. [Google Scholar] [CrossRef]
- Ömer, K. Distribution of turbulence statistics in open-channel flow. Int. J. Phys. Sci. 2011, 6, 3426–3436. [Google Scholar]
- Hedberg, M.; Hellström, G.; Andreasson, P.; Andersson, A.G.; Angele, K.; Andersson, R. Numerical modelling of flow in parallel spillways. In Proceedings of the 8th IAHR International Symposium on Hydraulic Structures ISHS2020, Santiago, Chile, 12–15 May 2020; Volume 1. [Google Scholar]
- Nortek, A.S. The Comprehensive Manual for Velocimeters; Nortek AS: Rud, Norway, 2018; Available online: https://www.nortekgroup.com/assets/software/N3015-030-Comprehensive-Manual-Velocimeters_1118.pdf (accessed on 15 March 2024).
- Erpicum, S.; Tullis, B.P.; Lodomez, M.; Archambeau, P.; Dewals, B.J.; Pirotton, M. Scale effects in physical piano key weirs models. J. Hydraul. Res. 2016, 6, 692–698. [Google Scholar] [CrossRef]
- USACE. Hydraulic Design of Spillways; U.S. Army Corps of Engineers: Washington, DC, USA, 1990. [Google Scholar]




| Inflow | Out1 | Ratio1 % | Out2 | Ratio2 % | Out3 | Ratio3 % | W, H (mm) | SumRatio % |
|---|---|---|---|---|---|---|---|---|
| 61.86 | 20.48 | 33.11 | 20.20 | 32.68 | 20.55 | 33.19 | 148.07 | 98.98 |
| 61.81 | 20.20 | 32.67 | 20.25 | 32.82 | 20.72 | 33.48 | 147.99 | 98.97 |
| 61.79 | 20.71 | 33.57 | 20.37 | 32.97 | 20.70 | 33.45 | 148.04 | 99.99 |
| 61.92 | 20.82 | 33.55 | 20.49 | 33.10 | 20.57 | 33.29 | 148.15 | 99.94 |
| Inflow | Out1 | Ratio1 % | Out2 | Ratio2 % | Out3 | Ratio3 % | ΣRatio % |
|---|---|---|---|---|---|---|---|
| 90.50 | 30.31 | 33.52 | 30.01 | 33.11 | 30.36 | 33.56 | 100.19 |
| 90.55 | 30.47 | 33.67 | 30.24 | 33.40 | 30.64 | 33.82 | 100.89 |
| 90.43 | 30.31 | 33.49 | 29.94 | 33.14 | 29.88 | 33.03 | 99.66 |
| 90.49 | 30.32 | 33.53 | 30.06 | 33.22 | 30.22 | 33.37 | 100.12 |
| 90.33 | 30.38 | 33.68 | 30.08 | 33.30 | 30.26 | 33.46 | 100.44 |
| 90.30 | 30.34 | 33.64 | 30.13 | 33.34 | 30.30 | 33.53 | 100.51 |
| 90.35 | 30.28 | 33.49 | 29.94 | 33.15 | 30.07 | 33.30 | 99.94 |
| 90.41 | 30.14 | 33.34 | 30.05 | 33.25 | 30.08 | 33.25 | 99.84 |
| 90.34 | 29.95 | 33.15 | 30.08 | 33.30 | 30.10 | 33.31 | 99.76 |
| 99.27 | 33.14 | 33.41 | 32.97 | 33.17 | 33.06 | 33.32 | 99.90 |
| 98.80 | 32.73 | 33.32 | 32.68 | 33.08 | 33.03 | 33.25 | 99.65 |
| 99.12 | 33.32 | 33.60 | 33.05 | 33.34 | 33.37 | 33.68 | 100.62 |
| 100.02 | 33.67 | 33.62 | 33.28 | 33.31 | 33.21 | 33.21 | 100.14 |
| 100.17 | 33.41 | 33.45 | 33.33 | 33.23 | 33.51 | 33.39 | 100.07 |
| 100.77 | 33.78 | 33.68 | 33.62 | 33.20 | 33.83 | 33.56 | 100.44 |
| 99.55 | 33.52 | 33.65 | 33.24 | 33.31 | 33.09 | 33.34 | 100.30 |
| 99.53 | 32.84 | 32.98 | 32.94 | 33.16 | 32.99 | 33.10 | 99.24 |
| 99.68 | 33.44 | 33.55 | 33.08 | 33.17 | 33.00 | 33.12 | 99.84 |
| 109.64 | 36.72 | 33.41 | 36.86 | 33.66 | 36.32 | 33.16 | 100.23 |
| 109.78 | 36.80 | 33.51 | 36.39 | 33.12 | 36.50 | 33.29 | 99.92 |
| 109.59 | 36.57 | 33.39 | 36.41 | 33.23 | 36.53 | 33.30 | 99.92 |
| 109.49 | 36.97 | 33.71 | 36.09 | 33.06 | 36.49 | 33.27 | 100.04 |
| 109.46 | 36.76 | 33.61 | 36.50 | 33.27 | 36.35 | 33.25 | 100.13 |
| 109.26 | 36.59 | 33.43 | 36.37 | 33.28 | 36.41 | 33.40 | 100.11 |
| 109.83 | 36.84 | 33.57 | 36.39 | 33.11 | 36.54 | 33.27 | 99.95 |
| 109.78 | 36.51 | 33.24 | 36.33 | 33.12 | 36.36 | 33.10 | 99.46 |
| 109.80 | 36.57 | 33.30 | 36.22 | 33.00 | 36.52 | 33.23 | 99.53 |
| 200.46 | 66.05 | 32.99 | 67.31 | 33.53 | 67.59 | 33.71 | 100.23 |
| 200.33 | 64.70 | 32.25 | 66.54 | 33.25 | 67.15 | 33.53 | 99.03 |
| 199.93 | 65.71 | 32.90 | 67.19 | 33.53 | 66.97 | 33.53 | 99.96 |
| 199.46 | 65.89 | 33.04 | 67.05 | 33.58 | 66.94 | 33.59 | 100.21 |
| 199.39 | 67.03 | 33.53 | 66.71 | 33.54 | 65.65 | 32.92 | 99.99 |
| Mean Inflow | Mean Out1 | Mean Ratio1 | Mean Out2 | Mean Ratio2 | Mean Out3 | Mean Ratio3 | ΣRatios |
|---|---|---|---|---|---|---|---|
| 90.41 | 30.27 | 33.50 | 30.05 | 33.24 | 30.21 | 33.40 | 100.14 |
| 99.65 | 33.31 | 33.47 | 33.13 | 33.21 | 33.23 | 33.33 | 100.01 |
| 109.62 | 36.70 | 33.46 | 36.39 | 33.20 | 36.44 | 33.25 | 99.91 |
| 110 (sim) | 37.06 | 33.69 | 37.07 | 33.70 | 35.72 | 32.47 | 99.86 |
| 199.91 | 65.87 | 32.94 | 66.96 | 33.48 | 66.86 | 33.45 | 99.87 |
| 200 (sim) | 66.45 | 33.22 | 67.66 | 33.83 | 65.89 | 32.94 | 99.99 |
| Average Flow (L/s) | Height Point 1 (mm) | Height Point 2 (mm) | Height Point 3 (mm) |
|---|---|---|---|
| 90.42 | 181.78 | 181.74 | 182.34 |
| 99.66 | 191.91 | 191.72 | 192.43 |
| 109.63 | 202.59 | 202.35 | 203.21 |
| 110 (sim) | 205.82 | 205.49 | 206.01 |
| 199.91 | 284.64 | 283.8 | 285.5 |
| 200 (sim) | 286.86 | 286.01 | 287.6 |
| Difference % | |||
| 0.34 | 1.58 | 1.54 | 1.37 |
| 0.05 | 0.78 | 0.78 | 0.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hedberg, P.A.M.; Hellström, J.G.I.; Andersson, A.G.; Andreasson, P.; Andersson, R.L. Measurements and Simulations of the Flow Distribution in a Down-Scaled Multiple Outlet Spillway with Complex Channel. Water 2024, 16, 871. https://doi.org/10.3390/w16060871
Hedberg PAM, Hellström JGI, Andersson AG, Andreasson P, Andersson RL. Measurements and Simulations of the Flow Distribution in a Down-Scaled Multiple Outlet Spillway with Complex Channel. Water. 2024; 16(6):871. https://doi.org/10.3390/w16060871
Chicago/Turabian StyleHedberg, P. A. Mikael, J. Gunnar I. Hellström, Anders G. Andersson, Patrik Andreasson, and Robin L. Andersson. 2024. "Measurements and Simulations of the Flow Distribution in a Down-Scaled Multiple Outlet Spillway with Complex Channel" Water 16, no. 6: 871. https://doi.org/10.3390/w16060871
APA StyleHedberg, P. A. M., Hellström, J. G. I., Andersson, A. G., Andreasson, P., & Andersson, R. L. (2024). Measurements and Simulations of the Flow Distribution in a Down-Scaled Multiple Outlet Spillway with Complex Channel. Water, 16(6), 871. https://doi.org/10.3390/w16060871






