Analyzing the Effect of Sewer Network Size on Optimization Algorithms’ Performance in Sewer System Optimization

Abstract

Sewer systems are a component of city infrastructure that requires large investment in construction and operation. Metaheuristic optimization methods have been used to solve sewer optimization problems. The aim of this study is to investigate the effects of network size on metaheuristic optimization algorithms. Cuckoo Search (CS) and four versions of Grey Wolf Optimization (GWO) were utilized for the hydraulic optimization of sewer networks. The purpose of using different algorithms is to investigate whether the results obtained differ depending on the algorithm. In addition, to eliminate the parameter effect, the relevant algorithms were run with different parameters, such as population size. These algorithms were performed on three different-sized networks, namely small-sized, medium-sized, and large-sized networks. Friedman and Wilcoxon tests were utilized to statistically analyze the results. The results were also evaluated in terms of the optimality gap criterion. According to the results based on the optimality gap, the performance of each algorithm decreases as the network size increases.

1. Introduction

Sewer systems are a component of city infrastructure that requires large investment in construction and operation. The construction cost includes the costs of sewer networks, pumping stations, and treatment plants, while the operation cost includes energy, maintenance, and rehabilitation costs [1,2,3]. Therefore, the aim is often to plan the system with the lowest cost while ensuring it performs its function. To minimize the construction cost in the planning phase, first, the layout of the sewer network is established and then the hydraulic calculations are made. Efforts to reduce the cost of the system are generally carried out by experts through a trial-and-error approach. The path followed is subjective and highly dependent on an experts’ experience. At this point, researchers are trying to overcome this trial-and-error approach and reach the optimum solution by using different optimization methods [4,5].

In a sewer system optimization problem, the aim is to obtain the lowest cost value by determining the network layout, pipe diameters, and slopes or cover depths. There are three different approaches in the literature. The first approach in research is obtaining all the variables simultaneously [6,7,8,9,10]. The second approach is performing the hydraulic optimization to determine the pipe diameters and slopes or cover depths with a predefined layout [11,12,13,14,15,16,17,18,19,20]. The last approach is layout optimization only [21,22,23,24,25].

There are many optimization methods in the literature [26]. One of these is metaheuristic optimization methods, which are used in solving sewer optimization problems as well as in different problems. The no-free-lunch theorem [27] suggests that an optimization method may not perform well in solving all problems due to the unique structure of problems. For this reason, different optimization algorithms are used to solve optimization problems, and their performances are compared.

In the related literature, many metaheuristic algorithms, namely, the genetic algorithm [5,12,13,18,28], cellular automata [20,29,30,31], ant colony algorithm [15,32,33,34], and particle swarm optimization algorithm [7,35], are utilized to solve sewer optimization problems.

In this study, two optimization algorithms, the Grey Wolf Optimization Algorithm (GWO) and Cuckoo Search Algorithm (CS), are used. There are studies on the solving of different optimization problems with both algorithms. GWO is employed to solve many problems in the field of water resources and hydraulics, such as water resources optimization [36,37], water resources management [38], forecasting of reservoir water availability [39], and open-channel optimization [40]. Masoumi et al. [41] have used GWO and a hybrid version of GWO (shuffled GWO) in sewer optimization and studied the performance of their algorithms in different scales of sewer networks. Their results showed that GWO and hybrid GWO are suitable to use in sewer optimization. In addition, CS is also employed to solve similar problems, such as reservoir operations [42,43,44,45], optimum design of water distribution systems [46,47,48], water quality forecast [49], and drought forecast [50]. Cetin and Turan [51] have observed that CS was suitable to use in sewer optimization.

In optimization algorithms, besides the performance of the algorithm in solving the problem, the factors affecting the performance are also investigated in the literature. One of these factors is the population size. Mora-Melià et al. [52] studied population size in a pipe-sizing problem of water network optimization in different-sized networks with the Pseudo-Genetic Algorithm, the Harmony Search Optimization Algorithm, the modified Particle Swarm Algorithm, and the modified Shuffled Frog Leaping Algorithm. They showed that using a small population size is more efficient out of all the sizes of networks [52]. Gao and Chen [53] studied the prediction of service life for tunnel structures in carbonation environments and the effects of population size and sample size with genetic programming. They showed that when the population size increases, the computing error decreases, and the decreasing extent reduces [53]. Xuea et al. [54] studied the design of environments with improved thermal comfort level, air quality, and reduced energy consumption of the heating, ventilating, and air-conditioning systems with a genetic algorithm. They tested the effect of the population size on this problem as well as other parameters that were used. They showed that they obtained better results when the population size increased [54]. Palod et al. [55] used Jayanet for water distribution network optimization and studied the effect of population size on this problem with this new algorithm. They showed that the number of function evaluations were found to increase with population size for all networks, that the increase is greater for large networks, and that the rate of convergence is seen to be dependent on the size of the network [55]. Piotrowski et al. [56] studied the performance of eight PSO variants with different population sizes on different benchmark and real-world problems. They found different results on different problems, and said that in metaheuristics any control parameter setting is inevitably problem-dependent and cannot possibly be assumed to be universal [56]. As demonstrated by the findings of the preceding investigations, the effect of optimization algorithms and changes in algorithm parameters on the performance of various tasks differs.

In this study, the effects of sewer network size on the performance of optimization algorithms were examined. The CS algorithm and four versions of the GWO algorithm were used to investigate the effect of the algorithm on the results. These algorithms were implemented on three different network sizes: small, medium, and large. Different population sizes were used in all the algorithms to investigate the effect of population size on the results. To make fair comparisons, the number of fitness evaluations was fixed. To find the best values for each network size, results were summarized in tables and box plots and analyzed statistically with the Friedman and Wilcoxon tests. The results were also assessed using the optimality gap criterion. Finally, by using the best values, the effects of network size were revealed according to the optimality gap criterion. From this perspective, the effects of network size on the performance of an algorithm, which has not been addressed before, is investigated for the first time.

2. Materials and Methods

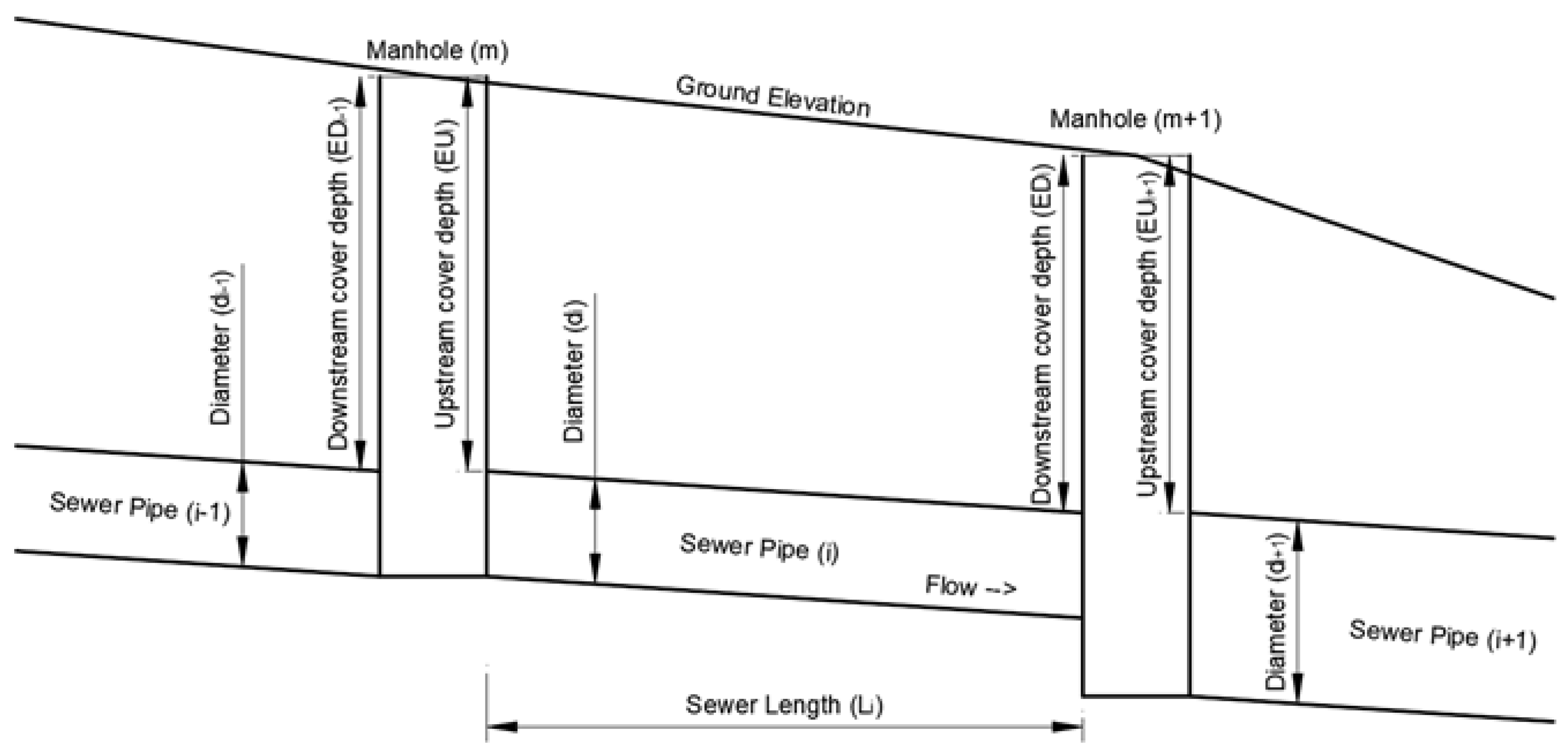
2.1. Sewer Network Hydraulic Optimization

The aim of sewer network optimization is minimizing the cost of a sewer network. In general, the cost of a sewer system for hydraulic optimization includes pipe, manhole, excavation, and pump costs. The objective function of the optimization of the problem can be defined as in Equation (1).

$$MinC=\sum _{i=1}^N{L}_i{C}_{p_i}+\sum _{j=1}^M{C}_{m_j}+\sum _{k=1}^P{C}_{{pump}_k}$$

(1)

where C is the cost of the sewer system for a predefined layout, N is the total number of sewer pipes, i is the considered pipe, $C_{p_i}$ is the unit cost of the sewer pipe construction defined as a function of its diameter d_i, L_i is the length of pipe i, M is the total number of manholes, j is the considered manhole, $C_{m_j}$ is the cost of the manhole construction defined as a function of manhole height $h_m$, P is the total number of pumps, k is the considered pump, and $C_{{pump}_k}$ is the cost of pumps. These variables are illustrated in Figure 1.

The sewer network optimization problem has constraints for hydraulic, operational, and availability reasons. The constraints of the problem can be defined by Equations (2)−(10).

Subject to the following:

$$d_i\in D,({\forall }_i=1,...,N)$$

(2)

$$d_i\ge D^{\prime },({\forall }_i=1,...,N)$$

(3)

$$V_i\ge V_{min},\left({\forall }_i=1,...,N\right)$$

(4)

$$V_i\le V_{max},({\forall }_i=1,...,N)$$

(5)

$${\beta }_i\ge {\beta }_{min},\left({\forall }_i=1,...,N\right)$$

(6)

$${\beta }_i\le {\beta }_{max},\left({\forall }_i=1,...,N\right)$$

(7)

$$S_i\ge S_{min},\left({\forall }_i=1,...,N\right)$$

(8)

$$E\ge E_{min},\left({\forall }_i=1,...,N,{\forall }_m=1,...,M\right)$$

(9)

$$E\le E_{max},\left({\forall }_i=1,...,N,{\forall }_m=1,...,M\right)$$

(10)

where $d_i$ is the diameter of the sewer pipe, $D$ is the discrete set of available commercial sewer pipe diameters, $D^{\prime }$ is the set of upstream pipe diameters of pipe, $V_i$ is the velocity of the considered pipe, $V_{min}$ and $V_{max}$ are the allowable minimum and maximum velocities, ${\beta }_i$ is the relative flow depth in the considered pipe, ${\beta }_{min}$ and ${\beta }_{max}$ are the allowable minimum and maximum relative flow depth values, $S_i$ is the slope of the considered pipe, $S_{min}$ is the allowable minimum slope value, $E$ is the set of upstream pipe cover depth values of manholes, and $E_{min}$ and $E_{max}$ are the allowable minimum and maximum cover depth values.

Manning’s equation, as in Equation (11), is used for the hydraulic calculations in this study.

$$Q_i=\frac{1}{n}{A}_i{R}_i^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{S}_i^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},({\forall }_i=1,...,N)$$

(11)

$$R_i=\frac{A_i}{P_i},({\forall }_i=1,...,N)$$

(12)

where $Q_i$ is the discharge, n is the Manning coefficient, $A_i$ is the wetted cross section area, $R_i$ is the hydraulic radius, $S_i$ is the sewer pipe slope, and $P_i$ is the wetted perimeter.

2.2. Grey Wolf Optimization Algorithm (GWO)

GWO was proposed by Mirjalili et al. [57] and is a swarm-based algorithm. GWO was developed with inspiration from the social and hunting behavior of grey wolves. A grey wolf pack has social hierarchy. The highest level consists of alphas (the best solution) that are leading the pack, the second level consists of betas (the second-best solution) that are subordinate wolves that help alphas in decision making or other activities, the third level consists of deltas (other solutions) that obey alphas and betas, and the lowest level consists of omegas wolves [57].

The hunting mechanism has been expressed by searching for prey (exploration), encircling the prey, hunting, and attacking the prey (exploitation). The hunting mechanism of a grey wolf pack mathematically is modelled as

$$X_i^{t+1}=\overrightarrow{X_p}\left(t\right)-\overrightarrow{A}·\overrightarrow{D}$$

(13)

$$D⃗=|C⃗·(X\_p)⃗(t)-X⃗(t\left)\right|$$

(14)

where t is the current iteration, $\overrightarrow{A}$ and $C$ are coefficient vectors, and $\overrightarrow{X_p}$ and $\overrightarrow{X}$ are position vectors of the prey and a grey wolf, respectively [57].

$$\overrightarrow{A}=2a·\overrightarrow{r_1}-a$$

(15)

$$\overrightarrow{C}=2·\overrightarrow{r_2}$$

(16)

$$a=2-t\frac{2}{T}$$

(17)

where T is the total number of iterations and $\overrightarrow{r_1},\overrightarrow{r_2}$ are random vectors in [0, 1]. $\overrightarrow{A}$ is a vector that is linearly decreased from 2 to 0. Updating of wolves’ positions is as follows [57]:

$$\overrightarrow{X_1}=\overrightarrow{X_a}-\overrightarrow{A_1}·\overrightarrow{D_a}$$

(18)

$$\overrightarrow{X_2}=\overrightarrow{X_{\beta }}-\overrightarrow{A_2}·\overrightarrow{D_{\beta }}$$

(19)

$$\overrightarrow{X_3}=\overrightarrow{X_{\delta }}-\overrightarrow{A_3}·\overrightarrow{D_{\delta }}$$

(20)

$$\overrightarrow{D_{\alpha }}=\left|\overrightarrow{C_1}·\overrightarrow{X_a}-\overrightarrow{X}\right|$$

(21)

$$\overrightarrow{D_{\beta }}=\left|\overrightarrow{C_2}·\overrightarrow{X_{\beta }}-\overrightarrow{X}\right|$$

(22)

$$\overrightarrow{D_{\beta }}=\left|\overrightarrow{C_2}·\overrightarrow{X_{\beta }}-\overrightarrow{X}\right|$$

(23)

where $\overrightarrow{X_a}$, $\overrightarrow{X_{\beta }}$, $\overrightarrow{X_{\delta }}$ are the first three best solutions in iteration t. Positions are updated by Equation (24) [57].

$$\overrightarrow{X}\left(t+1\right)=\frac{\overrightarrow{X_1}+\overrightarrow{X_2}+\overrightarrow{X_3}}{3}$$

(24)

A and C are the control parameters of GWO. These parameters allow GWO to transition between exploration and exploitation, which are the divisions of the search process into two phases. The exploration phase is about the process of investigating the promising area of the search space, while the exploitation phase refers to the local search capability around the regions obtained in the exploration phase [57]. Exploration is promoted with the value of A > 1 or A < −1, whereas there is emphasis on exploitation with the value of A between −1 and 1 [58].

Mirjalili et al. [57] also indicated that GWO is prone to stagnation in local solutions with these operators. To overcome this stagnation, three main approaches are studied in the literature. The first approach is changing the formulation of the adjustable parameters of GWO (a and/or C). Some researchers attempt to change parameter a by replacing Equation (17) [59,60,61], while other researchers attempt to change parameter C by replacing Equation (16) [62]. The second approach is changing the main updating equation of Equation (24) [63,64,65,66,67]. The third approach is using the first and the second approaches together or using combinations of GWO and other optimization algorithms [58,68,69,70,71,72,73].

In this study, in addition to use of the original version of a, three different GWO versions with modified a parameters were also used. In the first version of GWO called GWO_V1, a is calculated as in the original GWO shown in Equation (17).

Mirjalili et al. [61] replaced Equation (17) with Equation (25) and suggested using 0.5, 1, 1.5, 2, 2.5, 3, 3.5, and 4 as a_ini.

$$a=a_{ini}-t\frac{a_{ini}}{T}$$

(25)

Mirjalili et al. [61] have said that when a_ini is equal to 0.5, 1, and 1.5 which are less than 2, the value in the original GWO, the convergence curves of GWO have faster convergence rates. Therefore, a_ini is preferred to be 0.5 in the second version of GWO called GWO_V2.

In the third version of GWO called GWO_V3, a parameter recommended by Singh and Bansal [73] given in Equation (26) is used.

$$a=2e^{\left(-\frac{t^2}{{\left(0.3·T\right)}^2}\right)}$$

(26)

Finally, in the fourth version of GWO called GWO_V4, Equation (27), inspired by Khodadadi et al. [74], is used.

$$a=2\left(1-\sqrt{\frac{t}{T}}\right)$$

(27)

2.3. Cuckoo Search Algorithm (CS) via Lévy Flight

CS is an optimization algorithm developed by Yang and Deb [75] inspired by the aggressive breeding strategies of cuckoos. Cuckoos lay their own eggs in other birds’ nests and aim for the other bird to incubate their own eggs. To increase the chance of their own eggs hatching, they may discard the eggs of host bird in the nest [75].

CS has three general rules [75]:

• Cuckoos produce one egg per egg laying and lay their eggs in a randomly selected nest;
• The characteristics of the best nests with high quality eggs are passed on to the next generation;
• The number of existing host nests where the egg is laid is fixed. The host bird of the nest may notice the egg laid by the cuckoo with probability p ∈ [0, 1]. In this case, the host bird can throw the egg out of the nest or can leave the nest and build a new one.

In CS, each egg in the nest corresponds to a solution.

Lévy flight is applied to the i^th solution while generating the new solution $x_i^{(t+1)}$:

$$x_i^{(t+1)}=x_i^{\left(t\right)}+\alpha \oplus \mathrm{L}\mathrm{é}\mathrm{v}\mathrm{y}\left(\lambda \right)$$

(28)

where $x_i^{\left(t\right)}$ is i^th solution of the i^th iteration and α that is a positive value is the step size, which is usually taken as 1. Equation (28) is a stochastic equation used for random walking. This random walk is a Markov chain wherein the next location depends on the current location ($x_i^{\left(t\right)}$) and the transition probability ($\alpha \oplus \mathrm{L}\mathrm{é}\mathrm{v}\mathrm{y}\left(\lambda \right)$). The product is entry-wise multiplications [75].

The Lévy flight essentially provides a random walk while the random step length is drawn from a Lévy distribution:

$$\mathrm{L}\mathrm{é}\mathrm{v}\mathrm{y}\left(\lambda \right)=t^{-\mathrm{l}},(1<\lambda \le 3)$$

(29)

CS becomes more functional with the use of the Lévy flight operator. So, the mean and variance of the flight step can approach infinity. Approaching infinity is more suitable for large-scale optimization problems [76]. Another reason is that larger steps drawn from time to time from the Lévy distribution make it easier to escape from the local optimum [75].

A complete Lévy flight operator is formulated with the current best solution of t^th generation as follows:

$${x_i^{(t+1)}=x}_i^{\left(t\right)}+\alpha \frac{u}{{\left|v\right|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.}}\left(x_i^{\left(t\right)}-x_{best}^{\left(t\right)}\right),(1<\beta \le 2)$$

(30)

where β is (λ − 1) and the default value of β is equal to 1.5, and u and ν are random values from normal distribution as N(0, ${\sigma }_u^2$) and N(0, ${\sigma }_v^2$), respectively [42].

$$x_i^{(t+1)}=x_i^{\left(t\right)}+\alpha \frac{u}{{\left|v\right|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.}}\left(x_i^{\left(t\right)}-x_{best}^{\left(t\right)}\right),(1<\beta \le 2)$$

(31)

$${\sigma }_v^2=1$$

(32)

2.4. Application

In this study, the effect of network size on the performance of optimization algorithms was investigated. For this purpose, three predefined sewer networks that have different sizes as devised by Moeini and Afshar [77] were chosen. These networks were created as base networks to be used in layout optimization without specifying flow directions [77]. In this study, the versions with flow directions specified by Moeini and Afshar [8] and their associated cost values were used.

The networks are named Network1, Network2, and Network3 according to their size, respectively. The number of lines in the networks used was 12 lines in Network1, which is a small-sized network; 40 lines in Network2, which is a medium-sized network; and 144 lines in Network3, which is a large-sized network. The lengths of all the lines in networks are 100 m. The ground elevation levels of the starting manholes of each network are given as 1000 m. The elevation levels of each manhole are calculated by the elevation level of the starting point of each network, pipe lengths, and the slope value of 2% [8]. The design parameters are the same for all three networks and are summarized in

Table 1. Design parameters.

Pipe lengths L (m)	100
Minimum velocity $V_{min}$ (m/s)	0.75
Maximum velocity $V_{max}$ (m/s)	6
Minimum allowable relative flow ${\beta }_{min}$	0.10
Maximum allowable relative flow ${\beta }_{max}$	0.83
Minimum slope $S_{min}$	0.0005
Minimum cover depth $E_{min}$ (m)	2.5
Maximum cover depth $E_{max}$ (m)	10
Manning coefficient n	0.013

. These design parameters were taken from Moeini and Afshar [8] to compare results.

Moeini and Afshar [8] have mentioned that the manning coefficient value n was taken as 0.015 in their study. However, when the given results were reviewed, it was determined that the flow depth and flow velocity values could be calculated only with n = 0.013. For the results to be comparable, n = 0.013 was used in this study.

The sets of available commercial sewer pipe (D) diameters for the hydraulic calculations are given in

Table 2. Sets of commercial pipe diameters (mm).

100	150	200	250	300	350	400	450	500	550	600	650
700	750	800	850	900	950	1000	1100	1200	1300	1400	1500

.

The cost function given by Moeini and Afshar [8] was used and is presented in Equations (33)–(35).

$$K_p=10.93e^{3.43d_i}+0.012{\overline{E}}_i^{1.53}+0.437{\overline{E}}_i^{1.47}{d}_i$$

(33)

$$K_m=41.46h_m$$

(34)

$$K_{Total\_Cost}=K_p+K_m$$

(35)

where $i$ is the considered pipe, $K_p$ is the unit cost of sewer pipe construction, $d_i$ is the diameter of the sewer pipe, $\overline{E_i}$ is the average cover depth of the sewer pipe, $K_m$ is the cost of manhole construction, and h_m is the height of the manhole.

Once the values about the networks were determined, there were assumptions to be clarified for the optimization phase. Pipe diameter, cover depth at upstream manhole, and cover depth at downstream manhole were selected as decision variables for each sewer network pipe. In other words, three decision variables were considered for each network pipe. Consequently, the total number of decision variables was 36 for Network1, 120 for Network2, and 432 for Network3. The solution vector instance representation is given in

Table 3. Solution vector instance.

d1

EU1

ED1

…

…

…

$d_l$

EUl

EDl

and l is the number of lines in each network.

Values of 50, 100, 200, and 500 were chosen as the population sizes for each algorithm. Thus, considering all the networks, algorithms, and population sizes, a total of 60 cases were obtained. Trial combinations of all networks and population sizes were run with 30 different starting values, and a total of 1800 trials were performed. At the same time, the number of function evaluations (FE) was kept the same for all the cases to compare the results fairly. FEs was chosen as a fixed value of 500 × 10⁶. Finally, each trial was run 30 times to statistically evaluate the results.

3. Results

The results obtained at the end of the trials were summarized in tables and box plots and analyzed statistically. The cases are named with the algorithm version and the population size, such as GWO_V1-100 or CS-500.

The box plots are based on the best cost value of 30 results in each case. According to the box plots, when the box length of one case is shorter than the box lengths of other cases, it means that the results of the case with shorter box lengths are more consistent.

The box plots of Network1 are shown in Figure 2. It can be seen from Figure 2 that the minimum result and the most consistent case of GWO_V1 was obtained from GWO_V1-100 with a value of 22,924.4. The trials of GWO_V2 have similar results and the minimum result and the most consistent case of GWO_V2 was achieved in GWO_V2-100, with a value of 23,001.7. The minimum result and the most consistent case of GWO_V3 was delivered from GWO_V3-100, with a value of 22,925.0. The most consistent case of GWO_V4 was GWO_V4-500. On the other hand, the minimum result of GWO_V4 was obtained from GWO_V4-50, with a value of 22,924.1. The minimum result and the most consistent case of CS were achieved in CS-500, with a value of 23,001.7. This minimum value was also obtained from CS with other population sizes.

The boxplots of Network2 are shown in Figure 3. It can be seen from Figure 3 that the most consistent case of GWO_V1 was GWO_V1-200. In addition, the minimum value of GWO_V1 was obtained from GWO_V1-50, with a value of 85,018.2. Similarly, according to Figure 3, the most consistent case of GWO_V2 was GWO_V2-50, while the minimum value of GWO_V2 was obtained from GWO_V2-100, with a value of 85,006.6. The minimum result and the most consistent case of GWO_V3 were achieved in GWO_V3-50, with a value of 84,730.3. Figure 3 shows that the most consistent case of GWO_V4 was GWO_V4-50. The minimum result of GWO_V4 was obtained from GWO_V4-200, with a value of 85,014.3. Figure 3 indicates that the most consistent case of CS was CS-100. The minimum result of CS was obtained from CS-500, with a value of 87,460.4.

The boxplots of Network3 are shown in Figure 4. It can be seen from Figure 4 that the most consistent case of GWO_V1 was GWO_V1-50. The minimum result of GWO_V1 was obtained from GWO_V1-100, with a value of 389,323.5. According to Figure 4, the minimum result and the most consistent case of GWO_V2 were achieved in GWO_V2-50, with a value of 374,692.6. The most consistent case of GWO_V3 was GWO_V3-200, while the minimum value of GWO_V3 was obtained from GWO_V3-50, with a value of 376,703.0. Figure 4 shows that the most consistent case of GWO_V4 was GWO_V4-50, while the minimum value was with GWO_V4-100, with a value of 379,903.2. Figure 4 indicates that the minimum result and the most consistent case of CS were obtained from CS-50, with a value of 371,082.5.

The Friedman test and Wilcoxon signed-rank test were used to statistically analyze the results further. The results of the statistical tests are given in

Table 4. Friedman and Wilcoxon signed-rank test results on Network1.

Average Rankings Achieved by Friedman Test		Wilcoxon Signed-Rank Test
Algorithm	Sum of Ranks	CS-500 vs.	p-Value
GWO_V1-50	9.966667 (10)	GWO_V1-50	0.003609
GWO_V1-100	9.600000 (8)	GWO_V1-100	0.008730
GWO_V1-200	7.666667 (3)	GWO_V1-200	0.298944
GWO_V1-500	8.466667 (6)	GWO_V1-500	0.245190
GWO_V2-50	14.400000 (17)	GWO_V2-50	0.000002
GWO_V2-100	14.733333 (19)	GWO_V2-100	0.000002
GWO_V2-200	14.633333 (18)	GWO_V2-200	0.000002
GWO_V2-500	14.933333 (20)	GWO_V2-500	0.000002
GWO_V3-50	11.766667 (14)	GWO_V3-50	0.000014
GWO_V3-100	10.333333 (11)	GWO_V3-100	0.000125
GWO_V3-200	11.500000 (12)	GWO_V3-200	0.000002
GWO_V3-500	12.800000 (16)	GWO_V3-500	0.000031
GWO_V4-50	8.366667 (5)	GWO_V4-50	0.110926
GWO_V4-100	11.600000 (13)	GWO_V4-100	0.000241
GWO_V4-200	9.666667 (9)	GWO_V4-200	0.000831
GWO_V4-500	9.400000 (7)	GWO_V4-500	0.012453
CS-50	11.933333 (15)	CS-50	0.000023
CS-100	8.050000 (4)	CS-100	0.001953
CS-200	5.850000 (2)	CS-200	0.125000
CS-500	4.333333 (1)

,

Table 5. Friedman and Wilcoxon signed-rank test results on Network2.

Average Rankings Achieved by Friedman Test		Wilcoxon Signed-Rank Test
Algorithm	Sum of Ranks	GWO_V2-50 vs.	p-Value
GWO_V1-50	8.933333 (11)	GWO_V1-50	0.071903
GWO_V1-100	10.366667 (16)	GWO_V1-100	0.015658
GWO_V1-200	9.466667 (14)	GWO_V1-200	0.013194
GWO_V1-500	7.866667 (4)	GWO_V1-500	0.614315
GWO_V2-50	6.300000 (1)	GWO_V2-100	0.360039
GWO_V2-100	7.200000 (2)	GWO_V2-200	0.040702
GWO_V2-200	8.900000 (10)	GWO_V2-500	0.328571
GWO_V2-500	7.500000 (3)	GWO_V3-50	0.130592
GWO_V3-50	8.633333 (9)	GWO_V3-100	0.097772
GWO_V3-100	8.200000 (5)	GWO_V3-200	0.012453
GWO_V3-200	9.600000 (15)	GWO_V3-500	0.152861
GWO_V3-500	8.500000(8)	GWO_V4-50	0.082206
GWO_V4-50	8.433333 (7)	GWO_V4-100	0.035009
GWO_V4-100	9.033333 (12)	GWO_V4-200	0.047162
GWO_V4-200	8.233333 (6)	GWO_V4-500	0.047162
GWO_V4-500	9.033333 (13)	CS-50	0.000002
CS-50	18.783333 (19)	CS-100	0.000002
CS-100	19.300000 (20)	CS-200	0.000002
CS-200	18.366667 (18)	CS-500	0.000002
CS-500	17.350000 (17)

, and

Table 6. Friedman and Wilcoxon signed-rank test results on Network3.

Average Rankings Achieved by Friedman Test		Wilcoxon Signed-Rank Test
Algorithm	Sum of Ranks	CS-50 vs.	p-Value
GWO_V1-50	16.000000 (17)	GWO_V1-50	0.000002
GWO_V1-100	16.800000 (18)	GWO_V1-100	0.000002
GWO_V1-200	18.066667 (19)	GWO_V1-200	0.000002
GWO_V1-500	19.333333 (20)	GWO_V1-500	0.000002
GWO_V2-50	4.566667 (2)	GWO_V2-50	0.000332
GWO_V2-100	5.633333 (3)	GWO_V2-100	0.000028
GWO_V2-200	6.066667 (4)	GWO_V2-200	0.000016
GWO_V2-500	8.266667 (9)	GWO_V2-500	0.000003
GWO_V3-50	6.266667 (5)	GWO_V3-50	0.000005
GWO_V3-100	7.533333 (7)	GWO_V3-100	0.000007
GWO_V3-200	7.633333 (8)	GWO_V3-200	0.000006
GWO_V3-500	11.566667 (13)	GWO_V3-500	0.000002
GWO_V4-50	10.233333 (10)	GWO_V4-50	0.000002
GWO_V4-100	11.166667 (11)	GWO_V4-100	0.000002
GWO_V4-200	11.800000 (14)	GWO_V4-200	0.000002
GWO_V4-500	14.933333 (16)	GWO_V4-500	0.000002
CS-50	1.900000 (1)	CS-100	0.000012
CS-100	6.433333 (6)	CS-200	0.000003
CS-200	11.166667 (12)	CS-500	0.000002
CS-500	14.633333 (15)

for Network1, Network2, and Network3, respectively.

The minimum results and the most consistent cases of each algorithm for the three network problems are close to the minimum of all cost values. Therefore, the minimum results of the most consistent cases were chosen as the best result. These best results were used to compare the performance of the algorithms.

The results of Moeni and Afshar [8] are accepted as the benchmark to finding the answer of the effect of sewer network size on the performance of optimization algorithms. The decision criterion is the optimality gap criterion. The formulation of the optimality gap is given in Equation (36).

$$Opt.Gap=\frac{{Cost}_{ThisSt}-{Cost}_{Lit}}{{Cost}_{Lit}}\times 100$$

(36)

where ${Cost}_{ThisSt}$ is the best cost value obtained in this study, and ${Cost}_{Lit}$ is the best cost value obtained for the same networks by Moeini and Afshar [8]. Optimality gap values, the best cost values from both this study, and those from Moeini and Afshar [8] are shown in

Table 7. Comparison of costs.

	Model	Cost	Optimality Gap (%)
Network1 Small-sized Network	CABACOATGA3 (Moeini and Afshar [8])	23,467.8
	GWO_V1	22,924.4	−2.32
	GWO_V2	23,001.7	−1.99
	GWO_V3	22,925.0	−2.31
	GWO_V4	22,925.4	−2.31
	CS	23,001.7	−1.99
Network2 Medium-sized Network	CABACOATGA3 (Moeini and Afshar [8])	85,957.6
	GWO_V1	85,033.4	−1.08
	GWO_V2	85,023.0	−1.09
	GWO_V3	84,730.3	−1.43
	GWO_V4	85,024.1	−1.09
	CS	88,041.1	2.42
Network3 Large-sized Network	CABACOATGA2 (Moeini and Afshar [8])	361,919.0
	GWO_V1	389,667.5	7.67
	GWO_V2	374,692.6	3.53
	GWO_V3	379,684.0	4.91
	GWO_V4	381,227.8	5.34
	CS	371,082.5	2.53

. The optimality gap values according to the algorithms for each network are also shown in Figure 5.

The input data of the networks and results of the optimized hydraulic design are given in the Supplementary Material. Input data of Network1 and results of the optimized hydraulic design by GWO_V1, input data of Network2 and results the optimized hydraulic design by GWO_V3, input data of Network3 and results of the optimized hydraulic design by CS are shown in Table S1, Table S2, and Table S3, respectively.

4. Discussion

The effect of sewer network size on the optimization algorithms’ performances in sewer system optimization was analyzed. Optimization algorithms, including a CS algorithm and four versions of the GWO algorithm, were applied to three different network sizes: small, medium, and large. The results are first discussed in terms of the best values and consistency obtained on a network basis, population size, and by algorithm. Then, according to the purpose of this study, the effect of network size on the performance of the algorithms is investigated.

According to the results presented in Figure 2, the best cost values of all cases differ minimally. When this difference is evaluated according to the change in population size, the best cost values for Network1 do not change according to the population size. In other words, there is no relation between the decrease or the increase in the population size and the results and consistency in Network1. When the results are considered in terms of consistency, unlike GWO, CS performs more consistently as the population size increases. In contrast to the effect of changing population size on the best results, it influenced the consistency of the CS. Table 4 shows that CS-500 performs the best among others in Network1 according to the Friedman test. Moreover, according to the Wilcoxon signed-rank test, the differences between CS-500 and GWO_V1-200, CS-500 and GWO_V1-500, CS-500 and GWO_V4-50, and CS-500 and CS-200 were found to be negligible as p > 0.05. In other words, there is no statistical difference between the performance of CS-500 and the performances of GWO_V1-200, GWO_V1-500, and GWO_V4-50, CS-200. On the other hand, CS-500 performs slightly better than GWO_V1-50, GWO_V1-100, GWO_V2-50, GWO_V2-100, GWO_V2-200, GWO_V2-500, GWO_V3-50, GWO_V3-100, GWO_V3-200, GWO_V3-500, GWO_V4-100, GWO_V4-200, GWO_V4-500, CS-50, and CS-100, as the p-value < 0.05.

According to the results shown in Figure 3, CS has the worst results compared to the GWO cases. There is no relation between the decrease or the increase in the population size and the results and consistency in Network2 as in Network1. Table 5 indicates that GWO_V2-50 performs the best in Network2. According to the Wilcoxon signed rank test results, the performance of GWO_V2-50, GWO_V1-50, GWO_V1-500, GWO_V2-100, GWO_V2-500, GWO_V3-50, GWO_V3-500, and GWO_V4-50 are statistically indifferent as p > 0.05. Additionally, GWO_V2-50 performs slightly better than GWO_V1-100, GWO_V1-200, GWO_V2-200, GWO_V3-200, GWO_V4-100, GWO_V4-200, GWO_V4-500, CS-50, CS-100, CS-200, and CS-500, as p < 0.05.

According to the results depicted in Figure 4, there is no relation between the decrease or the increase in the population size and the results and consistency in Network3 for the GWO cases. In CS, the algorithm performance degrades as the population size increases in Network3. Table 6 shows that CS-50 performs the best among the other cases. In addition, the Wilcoxon signed rank test results proves that CS-50’s performance is statistically different than the others, as p < 0.05 in all cases.

The algorithms were analyzed with optimality gap values according to both Table 7 and Figure 5. In the instance of a small-sized network, all the algorithms have similar optimality gap values and all of them are better than the benchmark. In the instance of a medium-sized network, the GWO versions have similar optimality gap values and all of them are better than the benchmark; on the contrary, CS is worse than the benchmark. In the instance of a large-sized network, all the algorithms are worse than the benchmark. As the network size grows, optimality gap values become worse for all the versions of GWO. However, the decrease in CS performance begins to be seen in the medium-sized network. The GWO versions have different optimality gap values for the large-sized network. According to all the results based on the optimality gap, it can be stated that the performance of all the algorithms decreases as the network size increases.

According to the results, larger or smaller population sizes in GWO and CS do not guarantee promising results in all network sizes. This interpretation of the effect of population size is in accordance with that mentioned by Piotrowski et al. [56].

The best result in the small-sized network was obtained with CS, the best result in the medium-sized network was obtained with GWO_V2, while the best result in the large-sized was obtained with CS. Each network size can be accepted as a different problem. Therefore, as stated in the no-free-lunch theorem [27], algorithms may show different performances in different problems due to their unique structures.

5. Conclusions

In this study, the effects of the sewer network size on the performance of CS and four different versions of GWO are investigated. From this perspective, the effects of network size on the different algorithms’ performance are explored for the first time in this research.

The results are interpreted by using box plots, statistical tests, and optimality gap values.

According to all the results based on the performances compared to the benchmark, it can be stated that the performance of all the algorithms decreases as the network size increases. However, as the network size increases, the performance decreases for the GWO versions become faster, whereas the performance decrease for CS becomes slower.

In the future work, this study might be reproduced with alternative metaheuristic optimization algorithms and sewer networks.