Abstract
Multi-objective reservoir operation of reservoir flood control involves numerous factors and complex model solving, and exploring effective methods for solving the operation models has always been a hot topic in reservoir optimization operation research. The Multi-Objective Ant Lion Algorithm (MOALO) is an emerging heuristic intelligent optimization algorithm, but it has not yet been applied in reservoir optimization operation. Testing the effectiveness of this method on multi-objective reservoir scheduling and further improving the optimization performance of this method is of great significance for enhancing the overall benefits of reservoir operation. In this study, MOALO is applied to the optimal scheduling of reservoir flood control. To increase the search efficiency of MOLAO, the advanced MOALO method (AMOLAO) is proposed by reconstructing the search distribution in MOALO using a power function. Taking the Songshu Reservoir and Dongfeng Reservoir in the Fuzhou River Basin in Dalian City as an example, MOALO, AMOLAO, and other two traditional methods are applied for solving the multi-objective reservoir operation problem. Results show that the AMOALO method has high search efficiency, strong optimization ability, and good stability. AMOALO performs better than MOALO and the two traditional methods. The study provides an efficient method for solving the problems in multi-objective reservoir operation.
1. Introduction
Typically, there are multiple flood protection objectives in a multi-reservoir system. It not only requires considering the flood safety of the reservoir itself, but also handles various complex issues, such as compensatory scheduling between the reservoir and downstream protection points and coordinating flood control conflicts among reservoirs [1,2]. This problem falls into the category of multi-objective optimization problems. Deriving optimal operational policies for the reservoir systems is very complicated due to the large dimension of the problem, the conflicts among the different objectives, and the stochastic nature of the effective parameters. Such complexity has created a tendency among researchers toward developing efficient methods for optimization of multi-reservoir operation [3].
The classical optimization methods for reservoir operation mainly include linear programming, non-linear programming, and dynamic programming. These algorithms can solve small-scale optimization problems quickly and have been widely applied in the past [4,5]. However, classical optimization methods, such as dynamic programming, linear programming, and non-linear programming, are not appropriate for multi-objective optimization. Firstly, when dynamic programming is applied to a multi-reservoir system, it involves a major problem in regard to the curse of dimensionality with the increase in the number of state variables. Techniques like linear programming and non-linear programming have essential approximation problems in dealing with discontinuous, non-differentiable, non-convex multi-objective functions [6]. Secondly, the classical optimization methods, such as dynamic programming, linear programming, and non-linear programming, use a point-by-point search approach, the outcome of which is a single optimal solution [6]. Thirdly, most of the classical optimization methods consider multiple objective functions, using a weighted approach or constrained approach, without considering all the objectives simultaneously [7,8]. Furthermore, traditional optimization techniques are trapped in local optimal solutions and prove difficult to solve in regard to multi-objective, non-distinctive, non-convex and discontinuous functionalities [9].
In contrast, the meta-heuristic methods, because of their many proven advantages, have become very popular in solving complex optimization problems [10]. They have many respective merits, such as ease of use, high accuracy, gradient-free mechanisms, broad applicability, local optima avoidance, and satisfying results [11]. Accordingly, in recent years, meta-heuristics have been acknowledged as promising tools for supporting decision-making in various hydrology and water resources engineering problems [12]. The meta-heuristic methods include artificial neural networks [13], the genetic algorithm [14], particle swarm optimization [15], ant colony optimization [16], honey bee mating optimization [17], and so on. Meta-heuristic methods can be divided into two main categories: Single solution-based methods and population-based methods [18]. In single solution-based methods, algorithms conduct searches using individual search agents, whereas population-based methods utilize a group of search agents [19]. In population-based methods, each solution adjusts its position based on both individual and social information [20]. This integration of information reduces the risk of getting trapped in local optima [19]. Additionally, with multiple solutions exploring a wide range of the search space, population-based methods are more likely to yield superior final results compared to single solution-based methods [21,22,23,24].
In recent years, multi-objective evolutionary algorithms have been successfully applied to the multi-objective optimization problem to obtain a set of Pareto optimal solutions in a single run, which are the best tradeoff solutions among different objectives [25,26,27]. Currently, multi-objective optimization evolutionary algorithms can be classified into three main categories [4]. The first category consists of Pareto-dominance-based algorithms, such as the non-dominated sorting genetic algorithm II (NSGA-II) [28] and the Multi-Objective Ant Lion Optimizer (MOALO) [29]. The second category includes the Strength Pareto evolutionary algorithm II (SPEA2) [30] and indicator-based algorithms like the Indicator-Based Evolutionary Algorithm [31]. Lastly, the third category comprises decomposition-based algorithms, such as the multi-objective evolutionary algorithm based on decomposition [32]. The MOALO is a novel bio-inspired swarm intelligence algorithm proposed by Mirjalili et al. [29]. It is a global optimization algorithm developed by simulating the hunting mechanism of antlion larvae in nature. MOALO has the characteristics of a few adjustable parameters, high convergence accuracy, and good robust performance; however, research on this algorithm in the field of reservoir operation is scarce.
According to the No Free Lunch theorem, no single algorithm can deal with all optimization problems. In other words, the optimization performance of an algorithm may perform well in one set of problems and poorly in another. Therefore, the No Free Lunch theorem encourages finding and developing more optimizers with satisfactory performance [20]. The objective of this paper is to further improve the MOALO method and explore its applicability in the field of reservoir flood control scheduling. Thus, the traditional Ant Lion Optimization (ALO), MOALO and advanced MOALO (AMOLO) are shown in Section 2.1. The optimization operation model and evaluation indexes are shown in Section 2.2 and Section 2.3, respectively. A case study of the Songshu Reservoir and Dongfeng Reservoir in Northeast China is introduced in Section 3, while the methodology is illustrated via this case in Section 4. Lastly, conclusions are provided in Section 5.
2. Methods
2.1. Improved Multi-Objective Ant Lion Algorithm
2.1.1. Ant Lion Algorithm
The Ant Lion Optimization (ALO) algorithm simulates the behavior of antlions hunting ants in nature to optimize problem-solving [33]. Before hunting, antlions create a funnel-shaped trap on sandy ground and hide themselves beneath the sand at the bottom of the funnel. They use their large mandibles to flick sand outwards, making the surroundings of the funnel smooth and steep. When ants or small insects crawl into the trap, the loose sand causes them to slide down, and the antlion continuously flicks sand outward, pushing the prey towards the center of the quicksand. The antlion then captures and feeds on its prey. The steps of the ALO algorithm are as follows:
- Initialization
In the space (taking one-dimensional space as an example, the handling method for multi-dimensional space is similar), there are a total of ants and an equal number of antlions. First, initialize the populations of ants and antlions:
In Equations (1) and (2), and are the initial positions (generation 0) of the -th ant and the -th antlion, respectively. Additionally, and are the lower and upper bounds of the problem-solving space, respectively. is a random number between 0 and 1.
- Random walk of ants
The original random walk utilized in the ALO algorithm to simulate the random walk of ants is as follows:
where t shows the step (iteration) of random walk, is the maximum number of iteration, is an array calculating the cumulative sum function and is a random stochastic function.
To ensure that the ant’s random walk stays within the feasible domain, the following, Equation (5), is used to normalize the ant’s position:
In Equation (5), represents the position of the -th ant after it has walked around the antlion that captures it (each ant can only be captured by one antlion) in the -th generation. and are equal to and , respectively. Additionally, and represent the minimum and maximum values allowed for the -th ant to walk in the -th generation, determined by Equations (6) and (7).
In the equation, represents the position of the j-th antlion that captures the i-th ant in the previous generation, determined by Equations (8) and (9).
In Equations (8) and (9), T is the maximum number of iterations. From Equations (5)–(9), it can be observed that, as the number of iterations increases, the space in which the ants walk around the antlions rapidly shrinks. This mimics the process in nature where ants slide towards antlions in traps.
- Updating antlion positions
When the fitness value of an ant after random walking is higher than the fitness value of the antlion that captures it, the position of that antlion is updated to the position of the ant. Therefore, the position of the j-th antlion that captures the i-th ant is updated according to the following equation:
- Updating ant positions
The algorithm saves the elite individuals in each generation and influences the walking of all ants during the iteration process. The position update of the i-th ant in the t-th generation is as follows:
In the equation, represents the position of the i-th ant after random walking around the j-th antlion that captures it, and represents the position of the i-th ant after random walking around the elite antlion from the previous generation.
2.1.2. Multi-Objective Ant Lion Algorithm
There are various approaches available to identify the Pareto solution set for heuristic algorithms. MOALO, in particular, emulates the Multi-Objective Particle Swarm Optimization algorithm by utilizing an external archive to store the set of Pareto optimal solutions. To assess the quality of the solution set stored in the external archive, the algorithm incorporates a niching technique. Initially, it identifies the non-dominated solutions within the antlion population. Subsequently, the algorithm computes the crowding distance for each antlion in the non-dominated solutions. A smaller crowding distance corresponds to a higher likelihood of being chosen for inclusion in the external archive. As the external archive reaches its capacity, antlions with larger crowding distances are eliminated. The crowding distance is determined using Equation (12).
In the equation, is a constant greater than 1, and represents the number of solutions within a fixed range around the i-th solution.
Additionally, Equation (10) needs to be modified as follows:
In the equation, represents that for a given multi-objective optimization problem, while dominates .
Furthermore, in Equation (10), the antlion capturing the ant and the elite antlion are selected from the external archive using a roulette wheel selection method.
2.1.3. Improved Multi-Objective Ant Lion Algorithm
The ant-lion algorithm imitates the process of an ant-lion preying on ants by rapidly narrowing down the search range. However, as the search range continues to shrink, positions close to the antlion may be repeatedly searched, while positions far from the antlion are searched fewer times and eventually abandoned. This is not conducive to the efficiency and diversity of the solution. Therefore, after the original algorithm standardizes the ants, namely Equation (5), this paper uses a power function to reconstruct the distribution to improve the search method. The constructed reconstruction formula and schematic diagram are shown in Equation (14).
In Equation (14), represents the position of the -th ant after it has walked around the antlion that captures it in the -th generation by the improved method. Notably, is the parameter of the reconstruction function, and . The larger the value of , the more uniform the speed at which the ant slides towards the antlion. Through experiments in this paper, was chosen as 0.18. When equals , it is the same as the original algorithm. The parameter m is calculated by Equation (15).
From Figure 1, it can be seen that the positions of the ants before improvement are on the horizontal axis, while the corresponding positions of the ants after improvement are on the vertical axis. On the vertical axis, the distribution density is higher at positions further away from the center and lower at positions closer to the center ().
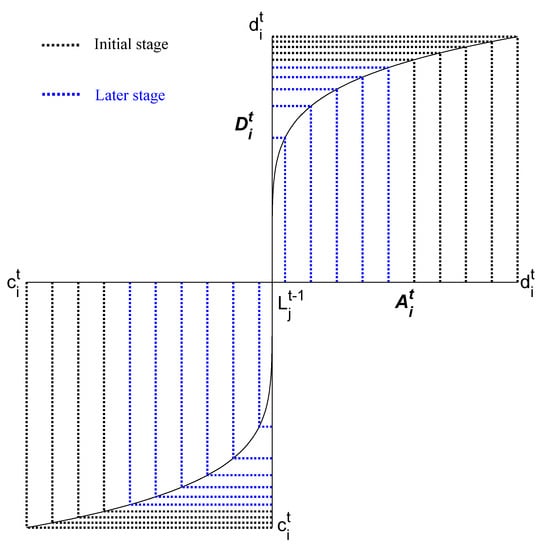
Figure 1.
Schematic diagram of the posterior distribution of rain in the forecast of the two products.
By reconstructing the distribution of the search range, the improved method AMOLO has two advantages over the traditional method MOLO. On one hand, for the improved method, in the initial stage of searching for the optimal solution, it increases the diversity of solutions by slowing down the convergence speed, thus avoiding quickly falling into local optima. In the later stage of the search, it accelerates the convergence speed, improving the efficiency of the algorithm. Therefore, the improved method can enhance the solution accuracy without significantly reducing the computational speed. On the other hand, when ants first fall into a trap (corresponding to the initial stage of the algorithm search), their struggle slows down the speed at which they slide towards the antlion. As ants approach the antlion (corresponding to the later stage of the algorithm search), their struggle becomes almost ineffective, leading to an acceleration in the speed at which they slide towards the antlion. Therefore, the improved method can better simulate the process of antlions capturing ants compared to the traditional method.
2.2. Reservoir Flood Control Optimization Operation Model
2.2.1. Objective Function
The main purpose of flood control operation is to protect the person and property in the basin and the safety of water engineering. The following three indicators are selected as objective functions: The maximum occupancy of flood control storage during flood dispatching (mainly considering dam safety and the extent of inundation), the occupancy of flood control storage at the end of dispatching (considering the connection between two flood dispatches), and the maximum outflow of the reservoir (mainly considering downstream flood control safety). The objective function combination is set as follows :
2.2.2. Constraint Conditions
- Water balance constraint
In the equation, and represent the initial and final water demands of the i-th reservoir at time t and t + 1, respectively. and represent the average inflow and outflow of the i-th reservoir at time t, respectively. Additionally, is the duration of each period.
- 2.
- Water level constraint
In the equation, represents the water level of the i-th reservoir at time t; and are the lower and upper limits of the water level of the i-th reservoir at time , respectively; and are the minimum and maximum values of the water level of the reservoir during the flood.
- 3.
- Reservoir outflow constraint
In the equation, represents the maximum outflow capacity of the i-th reservoir at the time t (corresponding to water level ).
The above constraints can be simplified as a combination of equality and inequality constraints:
2.2.3. Penalty Function
When Equation (17) is not satisfied, the paper constructs a penalty function in the following form:
In Equation (20), M is calculated by Equation (21).
2.3. Evaluation Indexes for Multi-Objective Algorithm
- 4.
- Efficiency
If the algorithm finds a set of solutions in one run, and if this set satisfies all the constraint conditions and the number of feasible solutions is greater than one, then this search is considered successful. The efficiency of the algorithm, denoted as P, is calculated as follows:
represents the total number of iterations for the algorithm, which is 50 in this paper; represents the number of groups of valid solution sets obtained.
- 5.
- Uniformity of distribution
In Equation (23), represents the number of non-dominated solutions found by the algorithm; represents the Euclidean distance between the -th solution in the non-dominated set found by the algorithm and its nearest neighbor solution; represents the average of all .
- 6.
- Convergence
represents the C-index of A with respect to B, which measures the proportion of solutions in B that are dominated by solutions in A. If , it indicates that the convergence of solution set A is superior to B and vice versa.
- 7.
- Distribution range of each objective function
This paper selects three objective functions. If the Pareto set of a certain algorithm has a smaller minimum value in one of the objective functions, it indicates that the algorithm performs better in terms of searching results for this objective function. Therefore, the distribution range of the Pareto solution sets of each algorithm can be used to determine the quality of their search performance.
3. Study Area
The Fuzhou River is located in the eastern region of China, in Dalian City, Liaoning Province. It is the second largest river in Dalian City. The Fuzhou River Basin has a terrain that is higher in the northeast and lower in the southwest, forming various landforms, such as low mountains, hills, plains, depressions, and coastal salt fields. The basin has a complex topography, with a total area of 1647.7 km2, of which mountainous areas account for 44%, hills account for 42%, and plains account for 14%. In the upper reaches of the Fuzhou River basin, low hills and ridges dominate, while the middle reaches belong to a flat and fertile plain with a mix of hills, making it a major grain-producing area. It is also prone to frequent flooding. The lower reaches are in a coastal area with thick soil layers and high salinity. Due to tidal influences, the convergence of floodwaters and tides can lead to riverbank overflow, causing flooding of farmland and aquaculture facilities on both sides of the river. The topography is shown in Figure 2.
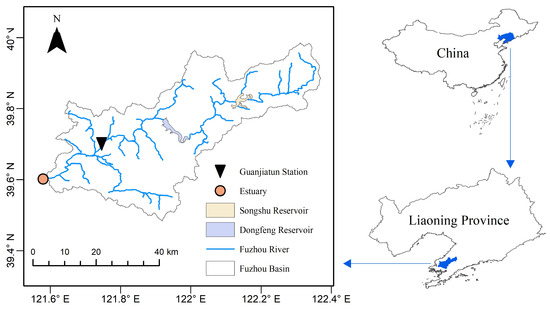
Figure 2.
Schematic of the Fuzhou Basin.
The Fuzhou River basin is located in a warm temperate semi-humid continental monsoon climate zone with an average annual precipitation of 675.4 mm. There are significant differences in precipitation throughout the year, with approximately 83.3% of the annual precipitation occurring from June to September. Due to the concentration of rainfall in the summer, it is highly susceptible to flooding disasters.
Based on the hydrological observation data and design data of Guanjiatun Hydrological Station over the years, it is required that the downstream discharge flow of the Dongfeng Reservoir should not exceed 1500 m3/s during a flood with a return period of 20 years. However, the flood control standards of the embankments in the Fuzhou River Basin under current conditions are not high, and many sections of the embankments do not meet the 20-year flood control standard. There is a risk of flooding or even breaching of the embankments when the reservoir discharge flow is large or the reservoir water level is high. Therefore, this study selected the design flood with a return period of 20 years for flood regulation and analyzed the results of different algorithms. The objective function is denoted as the maximum value of the sum of the occupied flood storage capacity of the Dongfeng Reservoir and the Songshu Reservoir during the flood regulation process. The objective function is denoted as the sum of the occupied flood storage capacity of the two reservoirs at the end of the flood regulation. The objective function is denoted as the maximum discharge flow of the Dongfeng Reservoir during the flood regulation process, respectively.
4. Results and Discussion
To verify the performance of MOALO and AMOALO, this study selected the classical NSGA-II and SPEA-II algorithms for comparative analysis in multi-objective optimization problems. The evaluation was conducted using the following three kinds of indicators.
4.1. Parameters of the Multi-Objective Algorithms
Due to the significant impact of parameters on the computational results of intelligent algorithms, to ensure the comparability of the results of each algorithm, their common parameters should be consistent, as shown in Table 1.

Table 1.
Each forecast product parameter.
4.2. Results
For each algorithm, independent calculations were performed 50 times to obtain 50 sets of solution sets. The effective efficiency was calculated based on Equation (22), as shown in Table 2. From the effective solution set, 30 sets were randomly selected, and these 30 sets of solution sets were merged to extract the non-dominated solutions as the merged Pareto solution set, denoted as . The and metrics were calculated separately. The results of the three metrics are shown in Table 2 and Table 3.

Table 2.
The metrics P and SP for each algorithm.

Table 3.
The metric
for each algorithm.
In Table 2, the efficiency of the Ant Lion Algorithm and the Improved Ant Lion Algorithm both reached 100%, while the efficiency of NSGA-II and SPEA-II was 42% and 60%, respectively. The SPEA-II has the best indicator, followed by the AMOALO, and the MOALO performs better than NSGA-II.
From Table 3, it can be found that the indicator of the AMOALO is 0, indicating that none of its solutions are dominated by the solution sets of other algorithms, indicating the best convergence. For the other three algorithms, based on the comparison formula of the indicator, it can be determined that the MOALO performs better than SPEA-II, while NSGA-II performs the worst.
Based on the solutions , a scatter plot is generated, as shown in Figure 3. The four subfigures in Figure 3 respectively show the distribution of the Pareto solution sets calculated by four algorithms. From Figure 3, it can also be observed that the solution set of SPEA-II is the most evenly distributed, followed by AMOALO and MOALO. Although the solution set of NSGA-II does not have any outliers, its dispersion leads to a higher value. The solution set of the NSGA-II algorithm is further away from the origin compared to other algorithms, indicating that many solutions in this algorithm are not true Pareto solutions. Therefore, the quality of the solution set generated by the NSGA-II algorithm is relatively poor, consistent with the conclusion in Table 3.
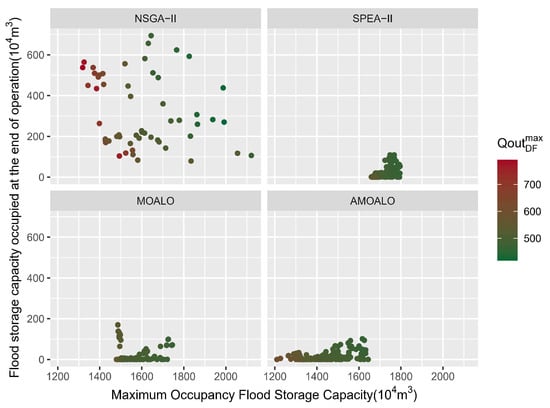
Figure 3.
Pareto solution sets of each algorithm .
In the solutions , the ranges of the three objective functions and the regular operation results are shown in Table 4.

Table 4.
The range of objective functions in
and conventional scheduling results.
From Table 4, it can be seen that the values of and for all four algorithms are better than the results of the conventional scheduling. With the exception of NSGA-II, the other three algorithms and the conventional scheduling have a value of (the final occupied flood storage capacity) being equal to 0. The AMOALO and NSGA-II have the best minimum values for and , respectively.
To further compare the results of different algorithms, each algorithm is merged again (i.e., merging all the scatter points in Figure 3), and the non-dominated solutions are extracted as the new Pareto solution set, denoted as . The distribution of is shown in Figure 4.
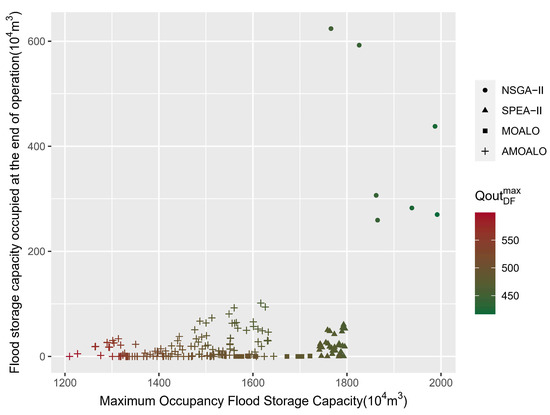
Figure 4.
Combining pareto solution sets from different algorithms.
From Figure 4, it can also be observed that AMOALO has a larger number of points, indicating that, after merging the Pareto solution sets of the four algorithms, fewer points are eliminated from its solution set, validating its better convergence. NSGA-II has the fewest number of points, confirming its worst convergence. In addition, we can also observe the main distribution areas of the solution sets generated by different methods. The solution set of the AMOALO algorithm is mainly distributed in the lower left area, while the MOALO and SPEA-II solutions are mainly distributed in the lower right area, and the NSGA-II solutions are mainly distributed in the upper right area. This indicates that the AMOALO algorithm focuses on the flood safety of the reservoir itself, NSGA-II focuses on downstream flood safety, while the MOALO and SPEA-II lie between the two. Decision-makers can integrate multiple algorithms and ultimately choose the decision solution that best suits their needs. It should be noted that these are only analysis results for the Fuzhou River basin, and different conclusions may exist for various optimization methods in other river basins.
Through comprehensive comparison, it can be concluded that both the MOALO and the AMOALO exhibit good efficiency and convergence. SPEA-II has the best uniformity in its Pareto solution set, while the results of NSGA-II are not satisfactory in the first three indicators. The AMOALO shows improvements in both the uniformity and convergence of its Pareto solution set compared to MOALO. The Pareto solution sets of all four intelligent algorithms have significantly improved the minimum values of the three objective functions compared to conventional scheduling.
5. Conclusions
Reservoir flood control operation involves many factors, and the model-solving process is complex. Exploring new solving methods for operation models has always been a hot topic in reservoir optimization research. The MOALO is an emerging multi-objective intelligent optimization algorithm. In order to further improve the performance of the algorithm, this paper reconstructs the distribution of the ant search range in the algorithm using power functions. The application example in the Fuzhou River Basin shows the following conclusions:
(1) Among the four intelligent algorithms, the AMOALO has good efficiency, uniformity and convergence with the Pareto solution set, and optimization ability in finding the minimum value of the objective function.
(2) Compared with the original algorithm, the MOALO, the uniformity and convergence of the Pareto solution set of the AMOALO have been significantly improved.
(3) Different optimization methods may focus on different operation objectives. Therefore, integrating different optimization algorithms and combining them with decision-maker preferences can help formulate decisions that are more optimal for decision-makers.
The AMOALO algorithm performs well in multi-objective optimization scheduling in the Fuzhou River basin. However, the Fuzhou River basin is relatively small. For large-scale basins with more reservoirs, multi-objective optimization scheduling becomes more complex and challenging. Therefore, further research is needed to investigate the flood optimization effectiveness of this algorithm in large-scale basins.
Author Contributions
Conceptualization, Y.N.; Methodology, Y.N., M.R., G.L., B.H. and R.T.; Resources, M.R., S.G., G.L., B.H. and X.L.; Writing—review & editing, Y.N. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the National Key Research and Development Program of China (Grant No. 2022YFC3006400; 2022YFC3006403), the Scientific Research Project Fund of China Three Gorges Corporation (Grant No. 0704203) and the National Natural Science Foundation of China (Grant No. 51779030).
Data Availability Statement
The data presented in this study are available on request from the corresponding authors. The data are not publicly available due to requirements of the reservoir management agency.
Conflicts of Interest
Authors Shuai Guo and Xiaoyang Liu were employed by the China Three Gorges Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wei, G.; Liang, G.; Ding, W.; He, B.; Wu, J.; Ren, M.; Zhou, H. Deriving Optimal Operating Rules for Flood Control Considering Pre-Release Based on Forecast Information. J. Hydrol. 2022, 615, 128665. [Google Scholar] [CrossRef]
- Ning, Y.; Ding, W.; Liang, G.; He, B.; Zhou, H. An Analytical Risk Analysis Method for Reservoir Flood Control Operation Considering Forecast Information. Water Resour. Manag. 2021, 35, 2079–2099. [Google Scholar] [CrossRef]
- Sharifi, M.R.; Akbarifard, S.; Madadi, M.R.; Akbarifard, H.; Qaderi, K. Comprehensive Assessment of 20 State-of-the-Art Multi-Objective Meta-Heuristic Algorithms for Multi-Reservoir System Operation. J. Hydrol. 2022, 613, 128469. [Google Scholar] [CrossRef]
- Sun, X.; Luo, J.; Xie, J. Multi-Objective Optimization for Reservoir Operation Considering Water Diversion and Power Generation Objectives. Water 2018, 10, 1540. [Google Scholar] [CrossRef]
- Yeh, W.W.-G. Reservoir Management and Operations Models: A State-of-the-Art Review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Reddy, M.J.; Kumar, D.N. Optimal Reservoir Operation Using Multi-Objective Evolutionary Algorithm. Water Resour. Manag. 2006, 20, 861–878. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, C.; Cai, X.; Li, Y.; Zhou, H. Multiobjective Hedging Rules for Flood Water Conservation: Hedging for Flood Water Conservation. Water Resour. Res. 2017, 53, 1963–1981. [Google Scholar] [CrossRef]
- Feng, M.; Liu, P.; Guo, S.; Yu, D.J.; Cheng, L.; Yang, G.; Xie, A. Adapting Reservoir Operations to the Nexus across Water Supply, Power Generation, and Environment Systems: An Explanatory Tool for Policy Makers. J. Hydrol. 2019, 574, 257–275. [Google Scholar] [CrossRef]
- Kumar, V.; Yadav, S.M. Multi-Objective Reservoir Operation of the Ukai Reservoir System Using an Improved Jaya Algorithm. Water Supply 2022, 22, 2287–2310. [Google Scholar] [CrossRef]
- Yıldız, B.S.; Kumar, S.; Pholdee, N.; Bureerat, S.; Sait, S.M.; Yildiz, A.R. A New Chaotic Lévy Flight Distribution Optimization Algorithm for Solving Constrained Engineering Problems. Expert Syst. 2022, 39, e12992. [Google Scholar] [CrossRef]
- Yıldız, B.S.; Pholdee, N.; Bureerat, S.; Erdaş, M.U.; Yıldız, A.R.; Sait, S.M. Comparision of the Political Optimization Algorithm, the Archimedes Optimization Algorithm and the Levy Flight Algorithm for Design Optimization in Industry. Mater. Test. 2021, 63, 356–359. [Google Scholar] [CrossRef]
- Akbarifard, S.; Sharifi, M.R.; Qaderi, K.; Madadi, M.R. Optimal Operation of Multi-Reservoir Systems: Comparative Study of Three Robust Metaheuristic Algorithms. Water Supply 2021, 21, 941–958. [Google Scholar] [CrossRef]
- Chaves, P.; Chang, F.-J. Intelligent Reservoir Operation System Based on Evolving Artificial Neural Networks. Adv. Water Resour. 2008, 31, 926–936. [Google Scholar] [CrossRef]
- Chang, L.-C.; Chang, F.-J.; Wang, K.-W.; Dai, S.-Y. Constrained Genetic Algorithms for Optimizing Multi-Use Reservoir Operation. J. Hydrol. 2010, 390, 66–74. [Google Scholar] [CrossRef]
- Marković, I.; Jurić-Kavelj, S.; Petrović, I. Partial Mutual Information Based Input Variable Selection for Supervised Learning Approaches to Voice Activity Detection. Appl. Soft Comput. 2013, 13, 4383–4391. [Google Scholar] [CrossRef]
- Jalali, M.R.; Afshar, A.; Mariño, M.A. Multi-Colony Ant Algorithm for Continuous Multi-Reservoir Operation Optimization Problem. Water Resour. Manag. 2007, 21, 1429–1447. [Google Scholar] [CrossRef]
- Haddad, O.B.; Afshar, A.; Mariño, M.A. Multireservoir Optimisation in Discrete and Continuous Domains. Proc. Inst. Civ. Eng.-Water Manag. 2011, 164, 57–72. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Nematollahi, A.F.; Rahiminejad, A.; Vahidi, B. A Novel Meta-Heuristic Optimization Method Based on Golden Ratio in Nature. Soft Comput. 2020, 24, 1117–1151. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung Beetle Optimizer: A New Meta-Heuristic Algorithm for Global Optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Roni, M.H.K.; Rana, M.S.; Pota, H.R.; Hasan, M.M.; Hussain, M.S. Recent Trends in Bio-Inspired Meta-Heuristic Optimization Techniques in Control Applications for Electrical Systems: A Review. Int. J. Dyn. Control. 2022, 10, 999–1011. [Google Scholar] [CrossRef]
- Mahajan, S.; Abualigah, L.; Pandit, A.K.; Al Nasar, M.R.; Alkhazaleh, H.A.; Altalhi, M. Fusion of Modern Meta-Heuristic Optimization Methods Using Arithmetic Optimization Algorithm for Global Optimization Tasks. Soft Comput. 2022, 26, 6749–6763. [Google Scholar] [CrossRef]
- Chen, D.; Ge, Y.; Wan, Y.; Deng, Y.; Chen, Y.; Zou, F. Poplar Optimization Algorithm: A New Meta-Heuristic Optimization Technique for Numerical Optimization and Image Segmentation. Expert Syst. Appl. 2022, 200, 117118. [Google Scholar] [CrossRef]
- Verma, P.; Alam, A.; Sarwar, A.; Tariq, M.; Vahedi, H.; Gupta, D.; Ahmad, S.; Shah Noor Mohamed, A. Meta-Heuristic Optimization Techniques Used for Maximum Power Point Tracking in Solar PV System. Electronics 2021, 10, 2419. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimisation Using Evolutionary Algorithms: An Introduction. In Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Wang, L., Ng, A.H.C., Deb, K., Eds.; Springer: London, UK, 2011; pp. 3–34. ISBN 978-0-85729-652-8. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Li, K.; Deb, K.; Yao, X. R-Metric: Evaluating the Performance of Preference-Based Evolutionary Multiobjective Optimization Using Reference Points. IEEE Trans. Evol. Comput. 2018, 22, 821–835. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jangir, P.; Saremi, S. Multi-Objective Ant Lion Optimizer: A Multi-Objective Optimization Algorithm for Solving Engineering Problems. Appl. Intell. 2017, 46, 79–95. [Google Scholar] [CrossRef]
- Dariane, A.B.; Sabokdast, M.M.; Karami, F.; Asadi, R.; Ponnambalam, K.; Mousavi, S.J. Integrated Operation of Multi-Reservoir and Many-Objective System Using Fuzzified Hedging Rule and Strength Pareto Evolutionary Optimization Algorithm (SPEA2). Water 2021, 13, 1995. [Google Scholar] [CrossRef]
- Chouikha, I.; Bree, A.; Moulin-Schouleur, M.; Gilot, P.; Germon, P. Differential Expression of iutA and ibeA in the Early Stages of Infection by Extra-Intestinal Pathogenic E. coli. Microbes Infect. 2008, 10, 432–438. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).