Abstract
In China, the water network project plays a pivotal role in optimizing water resources allocation, enhancing regional water resources carrying capacity, and bolstering high-quality economic development. This study is grounded in the spatial interconnection of water resources, serving as the foundation for constructing a spatial measurement model. Leveraging data from 558 panel samples encompassing 31 provinces (including municipalities and districts) in China between 2003 and 2020, this research unveils the inherent correlation between the establishment of the water network and economic as well as social development. The findings indicate the following: (1) Considering inputs, outputs, and nonconsensual outputs, regional disparities in the SBM (slacks-based measure) value of the water network exist, demonstrating an overall increasing trend annually. In 2020, the nationwide average benefit level of input–output in water network construction reached 0.603. (2) Moran’s I test, predicated on the weight matrix of spatial water transfer information, reveals a spatial positive autocorrelation. All tests pass the significance threshold of 5%, affirming the presence of spatial agglomeration due to project construction, operation, and the interconnectedness of water resources. (3) SDM (spatial Durbin model) regression analysis elucidates that per capita GDP, resource endowment, technological innovation level, consumption index, and average wage significantly influence the growth of water network efficiency. Specifically, per capita GDP and the consumption index exert negative influences. Moreover, aspects such as regional resource endowment, technological innovation level, industrial and agricultural water demand, average wage, and other spatial dependencies exhibit a notable positive spatial spillover effect. (4) The SDM model suggests that per capita GDP growth fails to yield a significant spatial spillover effect on neighboring regions. Instead, it highlights a substantial indirect effect and spatial dependence of government attention among regions. These analyses are instrumental in optimizing the water resources allocation network system and enhancing investment efficacy.
1. Introduction
Water stands as the fundamental cornerstone of survival and the bedrock of civilization. During the symposium on the high-quality development of the South-to-North Water Diversion Follow-up Project on 14 May 2021, China’s General Secretary, Xi Jinping, underscored the imperative of expediting the construction of a national water network. This network is envisioned to provide a robust guarantee of water security, crucial for the comprehensive establishment of a modernized socialist country. Subsequently, in December 2021, the Ministry of Water Resources issued the ‘Guidelines on the Implementation of Major National Water Network Projects’, which explicitly advocates for the acceleration of constructing a national water network characterized by being systematic, comprehensive, safe, reliable, intensive, efficient, environmentally sustainable, and intelligent; facilitating smooth circulation; and maintaining orderly regulation. Additionally, it outlined the ‘14th Five-Year Plan’ for executing significant national water network projects. Over the years, China has integrated endeavors such as water disaster prevention and control, conservation of water resources, restoration and protection of water ecology, and management of the water environment. This integration has led to the implementation of several pivotal cross-basin and cross-regional water diversion and transfer projects. Noteworthy among these are the South-to-North Water Diversion East and Central Route Project, the Hubei-Hebei Regional Water Resources Allocation Project, Yunnan Water Diversion, Shaanxi Hanjiang-to-Weihe Water Transfer Project, and Shanxi Central Yellow Water Diversion, among others. These projects have consistently elevated China’s efficiency in utilizing water resources, leading to the realization of sustainable water resource management. The water resources allocation project stands as a critical engineering endeavor aimed at addressing temporal and spatial disparities in water resource distribution and promoting a more intensive and economical utilization of water resources within China. The National Water Resources Development Statistics Bulletin primarily encompasses statistical data related to cross-regional water diversion and transfer projects, large-scale irrigation initiatives, and water system connection projects. According to the Bulletin’s data, investment in China’s water resources allocation projects has displayed a consistent year-on-year increase since 2007, as illustrated in Table 1.

Table 1.
Statistics on investment and construction of national water allocation projects, 2007–2020.
Recognized as a scarce yet crucial strategic economic resource vital for national economic development and societal welfare, the prudent development, production, and utilization of water resources with a focus on achieving optimal output efficiency constitute the customary trajectory of economic activities. Embedded within natural river and lake systems, the continual enhancement of the engineering framework for the optimal allocation of water resources stands as a pivotal and fundamental element in establishing the national water network. For the sake of subsequent discussion, this study collectively addresses various forms of water resources optimization and allocation engineering, referring to them as components constituting the construction of a water network. The establishment of this network, to a considerable extent, shapes the economic and social development blueprint of a country or region. It fosters a closely interconnected ecological and economic framework along water bodies and exerts influence by stimulating the development of neighboring regions [1]. Considering this, the focus turns to evaluating the efficacy level of water network construction in optimizing the pattern of water resources allocation in China. Is there room for further enhancement, and does a spatial interaction effect impact economic development? Subsequently, this paper employs spatial measurement methodologies, constructs a weight matrix for water transfer information, and conducts a quantitative analysis to ascertain the value contribution of water network construction to regional economic growth.
The spatial econometrics theory, pioneered by Anselin [2] in 1988, posits that a particular economic or geographical phenomenon or attribute within a given spatial unit exhibits a relationship with the corresponding phenomenon or attribute in neighboring regions. Spatial econometric analysis methods have been employed to measure the spatial correlations between economic, environment, infrastructure construction, energy, and water resources utilization. Within economic and environment research, R. Hanna [3] measured the response of US-based multinationals to the Clean Air Act Amendments and estimated the effect of regulation on a multinational’s foreign production decisions. Liu [4] showed that there exist significant differences in both these disaggregate and aggregate drags for the province groups. Within infrastructure research, Chu et al. [5] investigated the bidirectional mutual feedback and spatial interactions between urban municipal infrastructure investment and economic development using sample data from 241 cities. Wang and Fu [6] highlighted the impact of alterations in grid topology on regional energy intensity, revealing the influence of regional infrastructure connectivity on spatial correlation and its underlying mechanisms. Pan et al. [7] measured energy efficiency across 30 Chinese provinces and cities from 1997 to 2009 using the data envelopment method, employing a spatial econometric model to explore the spatial spillover effect of energy efficiency. Additionally, Yi et al. [8] utilized complex network analysis to construct China’s high-speed rail network and, based on panel data from 336 cities, established a spatial Durbin model to evaluate the spatial spillover effects of high-speed rail. Lv et al. [9] explored the driving factors and spatial influence of transportation networks on the three-dimensional ecological footprint model in the urban agglomerations in the middle reaches of the Yangtze River, China. Regarding water resources utilization, Sun et al. [10] assessed the technical efficiency of water resources and the environment across 31 Chinese provinces from 1997 to 2010 using the radial DEA method incorporating ‘non-expected output’. Another study utilized the SBM model to compute the green efficiency of water resources in the Yangtze River Economic Zone from 2004 to 2018 [11]. The study analyzed its spatial autocorrelation and spatial spillover effects through the spatial Durbin model. Qin et al. [12,13] identified constrained water resource characteristics in most areas of the Yangtze River Economic Belt, illustrating a decrease of 0.6% in China’s urbanization rate within the belt due to hindrances in interregional water resource development. Furthermore, they delved into dynamic interactive effects and spatial relationships of interprovincial water resource efficiency in China and concluded that economic development level, technological innovation, openness, and informatization significantly influence the evolution of the spatial correlation network of water resource efficiency. Ding et al. [14] estimated water resource utilization efficiency of provinces and cities from 2003 to 2015 using the non-expected output SE-SBM model. They further explored driving factors influencing water resource utilization efficiency using the Tobit model. Within water consumption and water conversation policies, areas with high urbanization levels have a lower water consumption drag effect and they can avoid the ‘resource curse’ of water resource constraints [15]. Ward F.A. [16] analyzed a series of water conservation policies, emphasizing that genuine water savings necessitate precise institutional, technical, and accounting measures that accurately monitor and economically reward reduced water depletions. Research is increasingly focusing on the spatial pattern characteristics of carbon emissions in these years, such as green technology innovation and agricultural carbon emissions [17,18,19].
Presently, there is a wealth of research focusing on agricultural water use efficiency, interprovincial water use efficiency, and the green efficiency of water resources within the Yangtze River Economic Zone, examining their spatial and temporal characteristics. However, there exists a paucity of scholarly attention dedicated to evaluating the efficacy of China’s sustained investment in engineering and construction aimed at optimizing the pattern of water resource allocation. In addition, the selection of the indicator system often fails to sufficiently capture the evolving landscape of water resource allocation patterns, and comprehensive systematic analyses of spatial effects on water resources remain lacking. This study is grounded in China’s longstanding commitment to achieving optimal interregional water resource allocation and understanding the intricate interaction of water resources within interregional circulation. To address this gap, this study employs the SBM (slacks-based measure) model to assess the input–output efficiency of the water network. Furthermore, it compiles information on interbasin and interregional water transfers to construct a weight matrix for water transfer information. Subsequently, this study investigates the spatial correlation of the water network and its spatial effects on water resources, employing a bidirectional fixed-effect spatial Durbin model (SDM). Leveraging panel data encompassing 31 provinces (municipalities, districts) from 2003 to 2020 (excluding Hong Kong, Macao, and Taiwan), this paper aims to elucidate the mechanism underlying the transmission of the spillover effect of the water network. By exploring these aspects, this study endeavors to unveil the influence of transmission mechanisms of the water network’s spillover effect. Ultimately, it aims to offer insights and recommendations pertinent to China’s national water network construction.
2. Research Variables and Data Sources
2.1. Input–Output Measurement Indicators
According to the growth model created by Solow [20], economic growth is determined by three crucial factors: technological progress, capital formation, and labor inputs. Informed by the indicator selection practices observed in prior studies, this study proposes a framework for measuring the input–output benefits of water network construction. It involves the selection of specific input elements and output indicators. In measuring the input elements’ efficacy in water network construction, the selected inputs encompass resource, capital, and labor inputs. These inputs include the total water resources (in billion m3) and the annual interbasin and interregional water transfer (in billion m3) to gauge their impact on regional economic growth. Additionally, investment in fixed assets allocated for water conservancy construction (in CNY 100 million), the length of urban water supply pipelines supported by diversion and transfer projects (in kilometers), and local scientific and technological expenditures (in CNY 100 million) contribute as capital inputs influencing regional economic growth. Labor inputs, represented by the employment rate of urban residents (%) and the average level of education, are characterized by per capita education expenditure (in CNY). In terms of output indicators, the ratio of regional GDP to total water resources signifies the correlation between regional economic development and water resources and serves as the consensual output indicator. Furthermore, acknowledging that efficient water resource utilization may still necessitate additional cost inputs for water recycling, the total volume of discharged wastewater (in 10,000 metric tons) is included as a nonconsensual output indicator. Refer to Table 2 for a comprehensive overview of the input–output benefit measurement index system for water network construction.

Table 2.
Input–output benefit measurement index system for water network construction.
2.2. Spatial Measurement Indicator Variables
Tobler [21] posited that geographical proximity between regions fosters closer economic connections. Zhang [22] and Wu [23] explored the spillover effects of transportation infrastructure, such as highways and railroads, on economic growth by introducing four spatial weight matrices: geographic connectivity, economic connectivity, industrial connectivity, and technological connectivity. Similarly, other scholars, including Chu et al. [5], empirically demonstrated spatial correlations between the construction of high-voltage power grids, urban municipalities, and other infrastructures and economic growth through panel data analysis. Their findings highlight that per capita GDP, resource endowment, regional industrial structure, consumption level, and other economic indicators significantly influence the extent of spatial spillover effects. Moreover, Li et al. [24] employed the physical–factual–humane system methodology, selecting factors such as the degree of economic development; innovation and economic inputs; industrial structure; government support level; and population education to analyze the spatial and temporal efficiency characteristics of green innovation in the manufacturing industry. Elhorst [25,26,27,28] underscored the importance of considering spatial correlation in economic indicators during spatial econometric analysis to prevent biased regression results. Drawing on prior studies, our analysis of the potential spatial spillover effects of water network construction and its underlying mechanisms aims to select elemental indicators affecting water network construction patterns, water allocation, and water resource utilization. These indicators, not within the control of the sample, encompass eight dimensions: regional economic development, resource endowment, social progress (education, science, and technology), governmental attention, water usage structure, water demand, residents’ consumption level, and residents’ income. We selected eight explanatory variables from various dimensions to capture these aspects, as detailed in Table 3, which includes symbols, definitions, and data representations for the variables.

Table 3.
Meaning of variables and data representations.
2.3. Data Sources
The data utilized for this study, encompassing nine input–output indicators and explanatory variables for measuring spatial spillover effects, were sourced from several reputable publications and databases. These include the China Statistical Yearbook, China Water Resources Bulletin, National Water Resources Development Statistics Bulletin, Water Resources Bulletins of Provinces (Municipalities, Districts), and information available on the National Bureau of Statistics (NBS) website. The data cover the period from 2003 to 2020.
3. Theoretical Model
3.1. SBM Model Considering Nonconsensual Outputs
Tone [29,30] introduced the SBM (slacks-based measure) model, followed by an SBM model incorporating non-expected outputs. Both models serve as evaluative tools for assessing effectiveness or efficiency levels. Additionally, in cases where efficiency values of decision units are identical, Andersen and Petersen [31] proposed the superefficiency (superefficiency model) ranking method to further distinguish efficiency levels. The primary objective of this research is twofold: firstly, to gauge the input–output efficiency of water network construction across 31 provinces (municipalities, districts) in China from 2003 to 2020; and secondly, to analyze its spatio-temporal dynamic developmental patterns. The model for this research is structured as follows:
where U, M, and I are the number of inputs, consensual outputs, and nonconsensual outputs; here, U = 7, M = 1, I = 1. T denotes the study period. K denotes the total provinces. (,,) are the input and output values; the double summations of three constraint equations with t as the first index are to calculate the input and output values, which are decided by the DMUs. Each DMU means the data of inputs, consensual output, and nonconsensual output in one province at t period. ,, and are the relaxation vector of inputs and outputs, and refers to the linear combination coefficients of the decision-making units. Y represents the level of input–output benefits derived from water network construction for each DMU; if we see all the DMUs’ efficiency value, we can see Y as a . Also, the objective function Y exhibits a strict monotonic decrease concerning the relaxation vectors, and. when Y = 1, it is considered that the decision-making unit is completely effective, there is no loss of efficiency, and no further superefficiency ranking is carried out in this study. Conversely, when Y < 1, it indicates a loss of efficiency in the decision-making unit, signifying potential optimization and enhancement opportunities for the inputs and outputs associated with water network construction. Furthermore, for this model to possess validity and significance, a fundamental prerequisite is the necessity of interbasin and interregional water transfers due to their crucial role in meeting the region’s essential needs. This necessity stems from its direct impact on the livelihoods of the population, the environment, and the broader economic and social development.
3.2. Spatial Spillover Effects Measurement Model
3.2.1. Spatial Water Transfer Information Weight Matrix
The traditional spatial weight matrix typically allocates values based on the geographic relationship between the objects under study, and Lee and Yu [32] pointed out that the matrix must be a constant term. Denote as the distance weight matrix that is based on the geographic location relationship, while the element of row i and column j in can be represented as . If the distance between region i and region j is denoted as , the spatial weight of the two regions can be defined as
Using geographical maps containing information from 31 provinces (municipalities, districts), we utilized Stata15. 1 software to acquire positional coordinates for each province (city, district) and computed the distance matrix for central region distances. It is important to note that in our study, we utilized a planar coordinate system, resulting in a Euclidean distance matrix. Subsequently, according to Equation (2), we were able to derive . To facilitate subsequent calculations, row standardization can be performed. This process can also be implemented using Geoda1.14 software. While considering the research object of this paper, the cross-basin interregional water transfer information matrix on the time series of each region is introduced; when the element of E is denoted as, then the following occurs:
- (I)
- When, , in which refers to interbasin and interregional water transfer volume in area i in the t year; these data can be obtained through Water Resources Bulletins directly. refers to the starting year of this study period, i.e., 2003, and refers to the ending year of the period. refers to the average volume of water transferred in 2003–2020.
- (II)
- When, . Eventually, a spatial water transfer information weight matrix is introduced, drawing on the approach of Lin et al. [33]:where and E are constant and nonnegative matrices, each of size 31 31, and Equation (3) involves element-wise multiplication (Hadamard product) as a standard inner product of the improved Euclidean space. This spatial water transfer information weight matrix helps to fit the construction and scheduling of the water network in each province (municipality and district).
3.2.2. Spatial Autocorrelation Test
We should first examine whether there is spatial autocorrelation between regions before we measure the spatial spillover effect of water network construction. In this paper, we choose the commonly used index for measuring spatial autocorrelation, global Moran’s I [34], with the following expression:
where is the variance of the sample, is the spatial water transfer information weight matrix calculated by Equation (3), and = 0 when i = j. and denote the values of the X variable in regions i and j, respectively. is the average value, and n represents the total number of spatial units. The correspondence are shown in Table 4.

Table 4.
Correspondence between I and spatial autocorrelation.
Chen [35] highlighted the dependence of the Moran index I on the spatial weight matrix. Selecting an appropriate spatial matrix or employing diverse spatial matrices plays a crucial role in scrutinizing the robustness of results. Hence, the construction of the Section 3.2.1 spatial weight matrix is grounded in this critical consideration.
3.2.3. Spatial Measurement Model
The spatial spillover effect is commonly evaluated through spatial measurement models such as the spatial autoregressive model (SAR), spatial error model (SEM), and spatial Durbin model (SDM). The SDM model, encompassing spatial lag terms of explanatory variables and spatial error terms, accounts for both the spatial interactions among explanatory variables and the spatial effects of error terms [36,37]. Employing the SDM model allows for the assessment of the impact level of water network construction and operation on a region, as well as the spillover effects observed in neighboring provinces (municipalities, districts). The equation expression for the SDM model is provided below:
where Y is the explained variable, which is the result of Equation (1); X is the explanatory variable, and when there are H explanatory variables, X is an N × H matrix; is the spatial autoregressive lag coefficient, which characterizes the spillover effect of the water network construction in the surrounding regions on the region; is the spatial water transfer information weight matrix, Y is the spatial lag value of the explained variable; X is the spatial lag value of the explanatory variable;and are coefficient vectors of the explanatory variable X, which characterizes the regional spatial dependence; andis the residual term. In this study, we denote the r-th explanatory variable (n × 1 column vector) , and we denoteand ; therefore, Equation (5) can be expanded as
where the t in Equation (6) denotes the year; the derivation of the equations gives
Equation (7) indicates that the variablein the region j under a certain year may have effects on the explained variable in any region. Particularly, when , is the direct effect of the variable to , similarly, the average of the sum of the main diagonal elements of matrix is the average direct effect of the variable. The average of all the elements of the matrix is the average total effect of the variable. The difference between the average total effect and the direct effect is the average indirect effect, and the equations are shown in (10) and (11).
where ADE presents the average direct effect, and ATE presents the average total effect.
In order to eliminate the effects of the explanatory variables’ magnitude and heteroskedasticity, both sides of Equation (5) are taken logarithmically, and GS2SLS [38,39] estimation is carried out. Equation (5) can be expressed as
This study utilizes a comprehensive dataset encompassing 558 panels spanning 18 years across 31 provinces (municipalities, districts). The organization of this dataset plays a pivotal role in shaping the conclusions drawn from the regression analysis. Therefore, undertaking equation transformation and rewriting is essential to enhance the clarity and accuracy of illustrating the relationship between the model and the data. By ensuring a robust transformation process, we aim to provide a more nuanced understanding of the intricate dynamics between variables and their impact on the outcomes of our analysis. This meticulous approach is crucial for deriving reliable insights and making informed decisions based on the findings of our study.
4. Empirical Results and Analysis
4.1. Input–Output Benefits Level of Water Network Construction
Based on the panel data of 31 provinces (municipalities, districts) from 2003 to 2020, this study quantified the SBM (slacks-based measure) value pertaining to water network construction, factoring in nonconsensual outputs. This value serves as an indicator reflecting the level of input–output benefits derived from water network construction. Table 5 presents the results of the SBM input–output benefit level measurements for selected years only, and the mean values represent the arithmetic average for 2003–2020.

Table 5.
Each province’s SBM value of water network construction, 2003–2020.
The SBM model calculations indicate that in 2003, Ningxia exhibited the lowest input–output benefits concerning water network construction. Conversely, Sichuan, Hubei, Anhui, and Jiangxi demonstrated the most favorable benefits, showcasing regions where water resource development and utilization are harmonized with economic and social development. Over the time series, most provinces exhibited an increasing trend in input–output benefits derived from water network construction. However, Jiangxi and Anhui did not show significant improvements and even appeared to constrain economic and social development. Analyzing the changing trends and statistical data of indicators, regions such as Beijing, Hebei, Shanxi, Henan, and Shandong showed the most conspicuous enhancements. Spatially, northeastern areas including Liaoning, Jilin, and Heilongjiang; northwestern regions such as Xinjiang, Inner Mongolia, Qinghai, Gansu, and Ningxia; and coastal areas in South China like Guangxi and Hainan displayed incremental improvements annually but still maintained an overall lower level. The statistical data and analysis reveal a spatial clustering effect in the input–output benefits associated with water network construction. By 2020, the nationwide average input–output benefits level of water network construction reached 0.603, yet more than half of the provinces, municipalities, and districts still registered lower levels. This analysis suggests considerable room for improvement, underscoring the necessity of the national water network construction project.
4.2. Spatial Spillover Effect of the Water Network
4.2.1. Spatial Autocorrelation Test
(I) Global spatial correlation: using Equation (4), a global spatial autocorrelation test was carried out by using Stata15.1, and the results and the signifiance test (p-value *) are shown in Table 6, with the trend of the Moran’s I index change shown in Figure 1. In 2003–2020, all 31 provinces exhibited positive values of the Moran’s I index, indicating spatial positive autocorrelation. Furthermore, all values surpassed the significance test at a 5% level, signifying significant spatial correlation in water network construction. These findings suggest a notable spatial correlation attributed to the construction, operation of the project, and interconnection of water resources, thereby indicating the presence of spatial agglomeration. Table 6 presents the results of autocorrelation tests for selected years only, with preliminary evidence of the existence of spatial effects.

Table 6.
The results of global Moran’s I test.
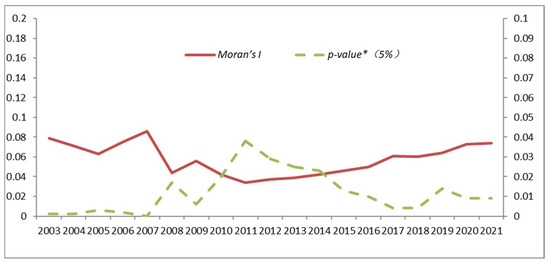
Figure 1.
Global Moran’s I index in 31 provinces in China, 2003–2020.
(II) Local spatial correlation: the years 2006 and 2017 were selected, and the local Moran’s I index was calculated to test the local spatial correlation and to plot the scatterplots, shown as Figure 2 and Figure 3.
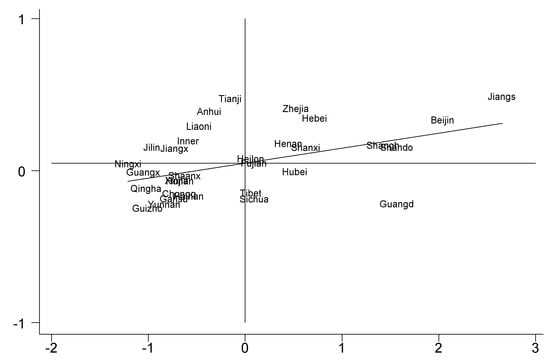
Figure 2.
The scatterplot (year 2006).
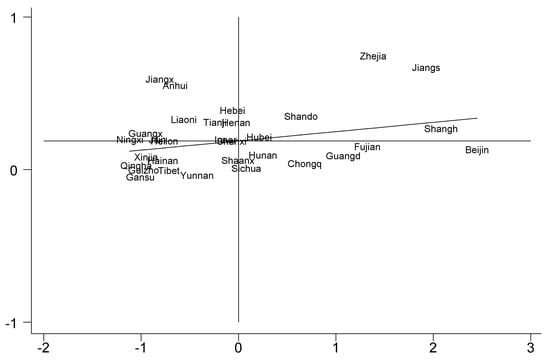
Figure 3.
The scatterplot (year 2017).
In 2006, the water network construction exhibited spatial homogeneity characteristics, with Heilongjiang, Fujian, and Ningxia presenting Moran indices close to 0, indicating the presence of an ‘island’ effect. By 2017, the overall trend still depicted spatial homogeneity, with only Shaanxi Province showcasing a Moran index close to 0. Conversely, Henan and Hebei exhibited noticeable spatial heterogeneity characteristics, depicting a ‘high–low’ aggregation effect. This effect suggests an evolving pattern in regional water resource distribution due to water network construction interventions. The positive slope observed in the Moran scatterplot regression line signifies that the water network construction continues to exhibit spatial homogeneity in space, indicating significant spatial autocorrelation.
4.2.2. Measurement and Analysis of the Water Network Spatial Spillover Effect
The spatial panel regression analysis was conducted using Stata15.1 software, employing the spatial weight matrix W and incorporating panel data comprising eight spatial spillover effect measurement indicators as explanatory variables. In performing data regression analysis, a spatial lag model (SLM), a spatial error model (SEM), and a spatial Durbin model (SDM) were constructed and are presented in Table 7. The findings from Table 7 indicate the following: (I) Both the SLM and SEM models confirm the presence of spatial autocorrelation within the models. (II) Results of Hausman’s test suggest the preference for selecting the spatial fixed-effects model across all models. (III) Considering the transformed relationship between the SEM and SDM, the SDM model’s nondegradation was confirmed through the Wald test and LR test [40,41]. Consequently, the two-way fixed-effects SDM model was supported as the final estimation model. The estimation outcomes of the SDM model, alongside the direct effect, indirect effect, and total effect of each influencing factor, are presented in Table 7.

Table 7.
Results of SDM regression analysis.
(I) Per capita GDP (PGDP): The SDM estimation reveals the significance of the PGDP at the 5% level. It suggests that with every 1% increase in the PGDP, there is a corresponding decrease of 0.165% in water network benefits. The model highlights that although economic development may instigate water network construction projects, unresolved regional water constraints and an imperfect water resources allocation system, among other factors, hinder China’s ability to harness economic growth and direct investment to fully capitalize on the benefits of water network construction. The SDM estimates show a direct effect of −0.1617, significant at the 5% level, consistent with the regression coefficient. Conversely, the indirect effect of −0.016, deemed insignificant, indicates that PGDP growth in interconnected water resource provinces might impede water resource output benefits in the region. However, its spatial dependence lacks significance. The cumulative effect, after combining the direct and indirect effects, stands at −0.1777, which is also statistically insignificant. This suggests that when considering the spatial spillover effect, the influence of the PGDP should not be overly emphasized.
(II) Per capita water resources (PWR): The SDM estimation underscores the significance of PWR at the 5% level, indicating that with every 1% increase in PWR, there is a corresponding 0.041% increase in water network benefits. This reveals a positive influence of water resources endowment on water network construction, suggesting that regions with ample water resources facilitate a virtuous cycle. The SDM estimates a direct effect of 0.0432, significant at the 1% level, in line with the model’s regression coefficient. Conversely, the indirect effect of 0.1948, significant at the 10% level, signifies that a 1% enhancement in PWR in other interconnected regions leads to a 0.195% increase in this region. This elucidates a clear positive spillover relationship. Notably, the total effect derived from the SDM surpasses the outcomes of the SLM and SEM, indicating the importance of considering spatial spillover effects when evaluating water resources endowment. Moreover, the indirect effect outweighs the direct effect, suggesting that water network construction acts as a channel for regulating regional disparities, endorsing China’s efforts to bolster regionally significant water resources allocation projects. With a total effect of 0.2380, significant at the 5% level, it emphasizes the significance of accounting for other interconnected regions’ water resources endowment.
(III) Technological innovation level (TI): According to the SDM estimation, the level of technological innovation holds significance at the 1% level, signifying that a 1% increase in research and experimental inputs yields a 0.039% increase in water network benefits. This highlights the positive impact of R&D investment on water network benefits, suggesting that greater regional investment in research and development might lead to reduced investment in water network construction. Consequently, technological innovation has the potential to stimulate economic output. The SDM estimates a direct effect of 0.0418, significant at the 1% level, aligning closely with the model’s regression coefficient of 0.0392. Conversely, the indirect effect is calculated at 0.2955, significant at the 5% level, indicating that a 1% improvement in other interconnected regions’ TI leads to a 0.296% increase in this region. This signifies a pronounced positive spillover relationship. The total effect, recorded as 0.3374 and significant at the 5% level, underscores that investment in regional synergistic technological innovation does not diminish the investment in water network construction but rather forms a mutually reinforcing driving force among regions.
(IV) Government attention (GA): The SDM estimates an elasticity coefficient for government attention at −0.5551, which is statistically insignificant. This indicates that limited government financial investment fails to distinctly foster noticeable benefit growth. This underscores the government’s primary focus on catering to the region’s life production and economic development. The SDM estimates a nonsignificant direct effect of 0.0815, showcasing a considerable variance from the model’s regression coefficient. Specifically, when examining solely within this region, government emphasis exhibits a positive contribution to water network construction. Conversely, the SDM-derived indirect effect registers at −1.4312, significant at the 1% level, while the total effect stands at −1.3527, also significant at the 1% level. This implies that a 1% increase in financial expenditures in other interconnected regions leads to a 1.3527% augmentation in the benefits of the water network within this region. The observable positive spillover relationship, along with the negative sign, indicates that the extent of government investment manifests through financial expenditure. The estimation outcomes underscore a discernible indirect impact of government financial investment support on water network construction, emphasizing a robust spatial dependence and significant spatial spillover effect between regions. This highlights the need for collaborative regional planning and the establishment of synergies in water network development.
By incorporating both technological innovation input and the level of government attention, we can observe a positive correlation with the promotion of spillover effects in water network construction. When local governments in China embark on water network construction initiatives, it is imperative that they prioritize technological innovation input that serves as a driving force for local development. Moreover, given the constraints of limited government funds, they must actively explore strategies to attract social capital and pioneer innovative investment and financing mechanisms for water network construction. This may involve reforms in water network pricing mechanisms to ensure that regions engaged in water source transfer and receiving areas collaborate effectively to support the construction and operation of water networks. Furthermore, establishing interregional dialogue and negotiation mechanisms among regional governments is essential. This ensures the coordination and optimization of regional interests, facilitating progress in regional development through water network construction initiatives.
(V) Industrial water demand (IWD): The SDM estimates an elasticity coefficient for industrial water demand at 0.0178, which is statistically insignificant. This suggests that industrial water demand marginally stimulates the growth of water network input–output benefits. This growth might emanate from two perspectives. Firstly, the escalation in industrial water demand might necessitate corresponding water network construction. Secondly, the decrease in water consumption per CNY ten thousand of industrial added value might foster a relative growth in water network benefits. The SDM estimates a nonsignificant direct effect of 0.0268, alongside a significant indirect effect of 0.8126 at the 5% level. The total effect of the two stands at 0.8394, also significant at the 5% level. This implies that industrial water demand exhibits spatial interdependence and radiative influence. However, there is a need for vigilance in controlling the water consumption growth rates within high-water-consuming industrial enterprises and ensuring compliance with wastewater discharge standards among industrial firms.
(VI) Agricultural water demand (AWD): The SDM estimates the elasticity coefficient of agricultural water demand at 0.0294, which lacks statistical significance. It suggests that agricultural water demand marginally affects the efficiency of the water network. The model yields a nonsignificant direct effect of 0.05. However, the indirect effect is notable, measuring 1.9514 and significant at the 1% level, resulting in a total effect of 2.0014, also significant at the 1% level. Studies focusing on agricultural water use efficiency across China’s provinces, as noted in the works by Chen [42] and Liu [43], affirm that the efficiency of agricultural water use in neighboring provinces influences the efficiency of agricultural water use in the examined region, demonstrating the existence of spatial spillover effects. Overall, the impact of agricultural water demand on water network efficiency and spatial spillover mirrors the explanatory factor of industrial water demand (IWD). However, the spatial spillover effect of agricultural water demand is more pronounced. These model-derived conclusions endorse the scientific rationale behind China’s ongoing major water network projects, particularly those aimed at renovating and reconstructing large and medium-sized irrigation districts.
(VII) Consumer index (CI): According to the SDM estimation, the elasticity coefficient of the consumer index stands at −3.9349, signifying significance at the 1% level. This result implies that a 1% rise in the consumer price index leads to a consequential 3.9365% reduction in the construction benefits of the water network. This outcome underscores that heightened prices necessitate increased input for the water network, consequently resulting in decreased unit benefits. It is worth noting that excessively high or low consumer price indices may indicate economic growth instability, suggesting that the assumption of increased input–output benefits for water network construction during a decrease in the consumer price index is not viable. In practice, when consumer demand contracts, investment in water conservancy projects, as a component of a nation’s infrastructure development, can assist in stabilizing and elevating the economy. The SDM estimates a direct effect of −3.9365, significant at the 1% level. Additionally, it computes an indirect effect of −4.2246, with a total effect of −8.1611. However, both the indirect and total effects lack significance, indicating an absence of spatial dependence concerning regional price fluctuations. Consequently, a significant spatial spillover effect is not evident.
(VIII) Average wage (AW): The SDM estimation reveals that the average wage maintains significance at the 1% level, indicating that a 1% increase in the average wage corresponds to a 0.1115% rise in the input–output benefits of water network construction. This outcome implies that an elevation in residents’ income levels correlates with increased project benefits. This escalation might stem from amplified project benefits due to heightened water consumption accompanying income level increases. Alternatively, the synchronized economic growth spurred by income rise might drive the benefits upward. The SDM estimates a direct effect of 0.1352, maintaining significance at the 1% level, which closely aligns with the model’s regression coefficient of 0.115. The indirect effect stands at 1.3294, also significant at the 1% level, indicating that a 1% increase in residents’ income in interconnected water resource provinces triggers a 1.3294% rise in water network benefits in this region, displaying a clear positive spillover relationship. The total effect reaches 1.4647, maintaining significance at the 1% level, signifying substantial spatial dependence and spatial spillover effect on residents’ income levels. This suggests that the implementation and functioning of the water network can foster job opportunities in neighboring areas, consequently contributing to further growth in per capita income.
5. Conclusions
The water network significantly influences the economic and social development patterns of countries or regions [1]. Water network projects play an indispensable role in optimizing water resource allocation, enhancing regional water resource capacity, and fostering high-quality economic development. Xie et al. [44] substantiated that the South-to-North Water Diversion Project alone effectively raised economic development levels by 6.1% in recipient counties and alleviated water resource constraints in those areas. This study utilizes medium- and long-term panel data, employing a spatial econometric model to quantify the input–output benefits of water network construction. The research delves into revealing the transmission mechanism of the spatial spillover effect of the water network. The primary conclusions derived are as follows:
(I) Examining resource inputs, capital inputs, and consensual and nonconsensual outputs from 2003 to 2020, Beijing, Hebei, Shanxi, Henan, and Shandong exhibit the most pronounced improvements in the input–output benefits of water network construction. Meanwhile, the northeast regions (Liaoning, Jilin, Heilongjiang), northwest regions (Xinjiang, Inner Mongolia, Qinghai, Gansu, Ningxia), and coastal areas of South China (Guangxi, Hainan) display incremental improvements annually. By 2020, the average input–output benefits level of China’s water network construction reached 0.629. To sustain this upward trajectory and alleviate water resource constraints, continued investment in and enhancement of water network projects are imperative.
(II) The implementation of water network projects has reshaped regional physical–spatial relationships. In this study, a spatial water transfer information weight matrix was constructed to illustrate these changes. Initial conclusions drawn from spatial autocorrelation tests on panel data indicate a significant spatial correlation within the water network, manifesting spatial agglomeration. Notably, the spatial and temporal complementarity observed in the Hanjiang-to-Weihe water transfer project [45] contributes to mitigating the ‘island effect’ in Shaanxi Province. However, this study did not establish a control group for the matrix, warranting further exploration of its dynamic changes and influence on measuring spatial spillover effects in subsequent studies.
(III) Two-way fixed-effects SDM regression analysis identifies several significant factors influencing water network efficiency growth. Per capita GDP, resource endowment, technological innovation level, consumption index, and average wage demonstrate notable impacts. Specifically, the per capita GDP and consumption index act as negative influencing variables. Moreover, the analysis of current spatial spillover effects affecting the water network underscores the significance of resource endowment, technological innovation level, governmental emphasis, industrial and agricultural water demand, and average wage, all displaying evident spatial dependence and spillover effects.
Among these factors, an increase in per capita GDP marginally diminishes water network efficiency without triggering a conspicuous spatial spillover effect in surrounding regions. This underscores the necessity to develop and utilize water resources with a focus on high efficiency and intensification. Prolonged, unchecked exploitation of water resources ceases to be conducive to regional development. The SDM model findings also reveal that while limited government financial input fails to directly bolster water network efficiency, it does generate observable indirect effects and spatial interdependencies among regions. The enhancement and advancement of regional water network projects’ layout and urban agglomerations’ water resource allocation hinge upon fostering synergy and coordinated development among local governments.
(IV) As the national water network project unfolds, the spatial water transfer information weight matrix can undergo dynamic updates and adjustments, facilitating the dynamic measurement of spatial spillover effects from transregional water resource allocation projects. Recent developments in Henan and Hebei reflect a gradual alleviation of water scarcity stemming from resource-based deficits, illustrated in the Moran scatter plot depicting a ‘high–low’ agglomeration effect in these areas, thereby stimulating neighboring water-scarce regions. Nonetheless, transregional water resource allocation endeavors do not aim to create an abundance of water resources. Economic development must consistently prioritize water conservation and reinforce stringent constraints on water resource management.
(V) The national water network has become an integral part of constructing a modern water infrastructure system, and its existence with spatial spillover effects is conducive to maximizing overall social welfare. Existing studies on infrastructure construction, such as electricity grids, high-speed railways, and urban infrastructure, and their spatial spillover effects indicate that strengthening infrastructure construction can reduce resource intensity. In other words, a scientifically designed water network spatially is likely to reduce the overall water consumption in society. Unlike other areas of infrastructure construction, water network construction heavily relies on sustainably extractable water resources. Therefore, it is imperative to adhere to river ethics and strengthen water resource protection.
Author Contributions
Conceptualization, J.G. and X.N.; methodology, F.C.; software, X.D.; validation, J.G.; formal analysis, F.C.; investigation, X.D.; data curation, X.N.; writing—original draft preparation, J.G. and F.C.; writing—review and editing, X.N. and X.D.; funding acquisition, X.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Major Science and Technology Programs of the Ministry of Water Resources (MWR) (SKS-2022142) and North China University of Water Resources and Electric Power Doctoral Student Innovation Fund Project (NCWUBC202223).
Data Availability Statement
The study data can be requested from the corresponding author. The data are not publicly available due to confidentiality requirements in Fund grants.
Conflicts of Interest
Author F.C. was employed by the company Yellow River Engineering Consulting Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zhao, Y.; Wang, H.; Ma, H.; He, G.H.; He, F. Conception of China’s “Double T”-shaped water network economic pattern construction. J. Hydraul. Eng. 2022, 53, 1271–1279. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models; Kluwer: Dordrecht, The Netherlands, 1988. [Google Scholar] [CrossRef]
- Hanna, R. US Environmental Regulation and FDI: Evidence from a Panel of US-based Multinational Firms. Am. Econ. J. Appl. Econ. 2010, 2, 158–189. [Google Scholar] [CrossRef]
- Liu, Y. Resource drag in an endogenous growth context: A panel data-based estimation with cross-sectional dependences and structural breaks. Appl. Econ. 2014, 46, 1586–1598. [Google Scholar] [CrossRef]
- Chu, J.; Liu, Y.M.; Lin, X.B.; De, T. Spatial Mutual Effects between Municipal Infrastructure Investment and Economic Development. Beijing Da Xue Xue Bao 2021, 57, 291–298. [Google Scholar] [CrossRef]
- Wang, B.; Fu, Q. Analysis on the spatial spillover mechanism change induced by infrastructure construction. Eng. Manag. 2020, 34, 127–134. [Google Scholar] [CrossRef]
- Pan, X.F.; Yang, Y.; Zhang, W.W. The Spatial Spillover Effect of China’s Regional Energy Efficiency. Eng. Manag. 2014, 28, 132–136. [Google Scholar] [CrossRef]
- Yi, Q.G.; Ma, C.; Ding, R. Analysis of the spatial spillover effect of high-speed rail on regional economic development. Stat. Decis. 2021, 583, 129–133. [Google Scholar] [CrossRef]
- Lv, T.Y.; Zeng, C.; Lindsay, C.S. The spatial spillover effect of transportation networks on ecological footprint. Ecol. Indic. 2021, 132, 108309. [Google Scholar] [CrossRef]
- Sun, C.Z.; Zhao, L.S.; Zou, W. Water Resource Utilization Efficiency and Spatial Spillover Effects in China. Acta Geogr. Sin. 2014, 24, 771–788. [Google Scholar] [CrossRef]
- Song, M.; Du, S.X. Dynamic changes and spatial overflow of water resources green efficiency: A case study on Yangtze River Economic Zone. Resour. Ind. 2021, 583, 129–133. [Google Scholar] [CrossRef]
- Qin, T.; Zhang, H.Q.; Tong, J.P. Water resource constraint on urbanization in Yangtze River Economic Belt. China Popul. Resour. Environ. 2018, 28, 39–45. [Google Scholar] [CrossRef]
- Qin, T.; Tong, J.; Zhang, H. Construction and evolutionary factors of spatial correlation network of China’s provincial water resource efficiency under environmental constraints. China Popul. Resour. Environ. 2020, 30, 84–94. [Google Scholar] [CrossRef]
- Ding, X.H.; He, J.H.; Wang, L.Y. Inter-provincial water resources utilization efficiency and its driving factors considering undesirable outputs. China Popul. Resour. Environ. 2018, 28, 157–164. [Google Scholar] [CrossRef]
- An, M.; Butsic, V.; He, W.J.; Zhang, Z.F.; Qin, T.; Huang, Z.W.; Yuan, L. Drag Effect of Water Consumption on Urbanization—A Case Study of the Yangtze River Economic Belt from 2000 to 2015. Water 2018, 10, 1115. [Google Scholar] [CrossRef]
- Ward, F.A.; Pulido-Velazquez, M. Water conservation in irrigation can increase water use. Proc. Natl. Acad. Sci. USA 2008, 105, 18215–18220. [Google Scholar] [CrossRef]
- Adewale, C.; Reganold, J.P.; Higgins, S.; Evans, R.D. Improving carbon footprinting of agricultural systems: Boundaries, tiers, and organic farming. Environ. Impact Assess. Rev. 2018, 71, 41–48. [Google Scholar] [CrossRef]
- Rong, J.; Hong, J.; Guo, Q.; Fang, Z.; Chen, S.K. Path mechanism and spatial spillover effect of green technology innovation on agricultural CO2 emission intensity: A case study in Jiangsu Province, China. Ecol. Indic. 2023, 157, 111147. [Google Scholar] [CrossRef]
- Chen, H.Y.; Yi, J.Z.; Chen, A.B.; Peng, D.X.; Yang, J.Q. Green technology innovation and CO2 emission in China: Evidence from a spatial-temporal analysis and a nonlinear spatial durbin model. Energy Policy 2023, 172, 113338. [Google Scholar] [CrossRef]
- Solow. Science and Ideology in Economics. In Contemporary Issues in Economics; Grandall, E., Ed.; Little Brown Inc.: Boston, MA, USA, 1972. [Google Scholar]
- Tobler, W.R. Cellular Geography. Theory Decis. Libr. 1979, 20, 379–386. [Google Scholar]
- Zhang, X.L. Has Transport Infrastructure Promoted Regional Economic Growth?—With an Analysis of the Spatial Spillover Effects of Transport Infrastructure. China Soc. Sci. 2013, 34, 24–47. [Google Scholar]
- Wu, Y.J.; Zhang, M.Q. An Empirical Analysis of the Relationship between Transport Infrastructure, Spatial Spillover and Economic Growth. Stat. Decis. 2017, 116–120. [Google Scholar] [CrossRef]
- Li, G.; Zhang, X.S.; Tian, A.R.; Zhou, Y. Spatial and Temporal Differentiation of Green Innovation Efficiency in Manufacturing Industry Based on Super-SBM-ESDA and Tobit Model: Taking the Yangtze River Economic Belt as an Example. Ecol. Econ. 2023, 11. Available online: https://link.cnki.net/urlid/53.1193.F.20231102.1132.002 (accessed on 2 November 2023).
- Elhorst, J.P. Spatial Econometrics from Cross-Sectional Data to Spatial Panels; Briefs in Regional Science; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Elhorst, J.P. Specification and estimation of spatial panel data models. Int. Reg. Sci. Rev. 2003, 26, 244–268. [Google Scholar] [CrossRef]
- Elhorst, J.P. Spatial Panel Data Models; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Elhorst, J.P. Matlab Software for Spatial Panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef]
- Tone, K.A. Slacks-based Measure Efficiency in Data Envelopment Analysis. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Tone, K.A. Strange Case of the Cost and Allocative Efficiencies in DEA. Oper. Res. Soc. 2002, 53, 1225–1231. [Google Scholar] [CrossRef]
- Andersen, P.; Petersen, N.C. A Procedure for Ranking Efficient Units in Data Envelopment Analysis. Manag. Sci. 1993, 39, 1179–1297. [Google Scholar] [CrossRef]
- Lee, L.; Yu, J. Some recent developments in spatial panel data models. Reg. Sci. Urban Econ. 2010, 40, 255–271. [Google Scholar] [CrossRef]
- Lin, G.P.; Long, Z.H.; Wu, M. A Spatial investigation of σ-convergence in China. J. Quant. Technol. Econ. 2006, 4, 14–21. [Google Scholar]
- Moran, P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q. Spatial Econometrics; Higher Education Press: Beijing, China, 2014. [Google Scholar]
- Lee, L.F.; Yu, J. A spatial dynamic panel data model with both time and individual fixed effects. Econom. Theory 2010, 26, 564–597. [Google Scholar] [CrossRef]
- Xie, R.; Chen, Y.; Han, F.; Fang, J.Y. Research on Influence and Time-space Effect of New-type Urbanization on Urban Eco-environmental Quality. Manag. Rev. 2018, 30, 230–241. [Google Scholar]
- LeSage, J.; Pace, R.K. Introduction to Spatial Economics; Chapman and Hall/CRC: New York, NY, USA, 2009. [Google Scholar]
- Arraiz, I.; Drukker, D.M.; Kelejian, H.H.; Prucha, I.R. A Spatial Cliff-Ord-type Model with Heteroskedastic Innovations: Small and Large Samples Results. J. Region. Sci. 2010, 50, 592–614. [Google Scholar] [CrossRef]
- Yang, Z.L. A robust LM test for spatial error components. Reg. Sci. Urban Econ. 2010, 40, 299–310. [Google Scholar] [CrossRef]
- Xu, X.B.; Lee, L.F. Theoretical foundations for spatial econometric research. Reg. Sci. Urban Econ. 2019, 76, 2–12. [Google Scholar] [CrossRef]
- Chen, H.B. Provincial agricultural water use efficiency evaluation and spatial spillover effect in China. J. Arid Resour. Environ. 2017, 31, 85–90. [Google Scholar] [CrossRef]
- Liu, D.D.; Zhu, X.Y.; Wang, Y.F. China’s agricultural green total factor productivity based on carbon emission: An analysis of evolution trend and influencing factors. J. Clean. Prod. 2021, 278, 123692. [Google Scholar] [CrossRef]
- Xie, Z.; Jing, Z.; Yang, M. Water Constraint Mitigation and Regional Economic Growth: Evidence from the South-to-north Water Diversion Project. J. Quant. Technol. Econ. 2023, 9, 93–115. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, H.; Deng, M.J.; He, G.H.; He, F.; Wang, Y. Jiziwan water network in the Yellow River Basin: Conceptualizing the east extension project of the west route of the South-to-Nouth Water Diversion. J. Hydraul. Eng. 2023, 54, 1015–1024. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).