Dynamic Response of PCCP under the Rockfall Impact Based on the Continuous–Discontinuous Method: A Case Study
Abstract
1. Introduction
2. Principle of the Continuous–Discontinuous Coupling Method
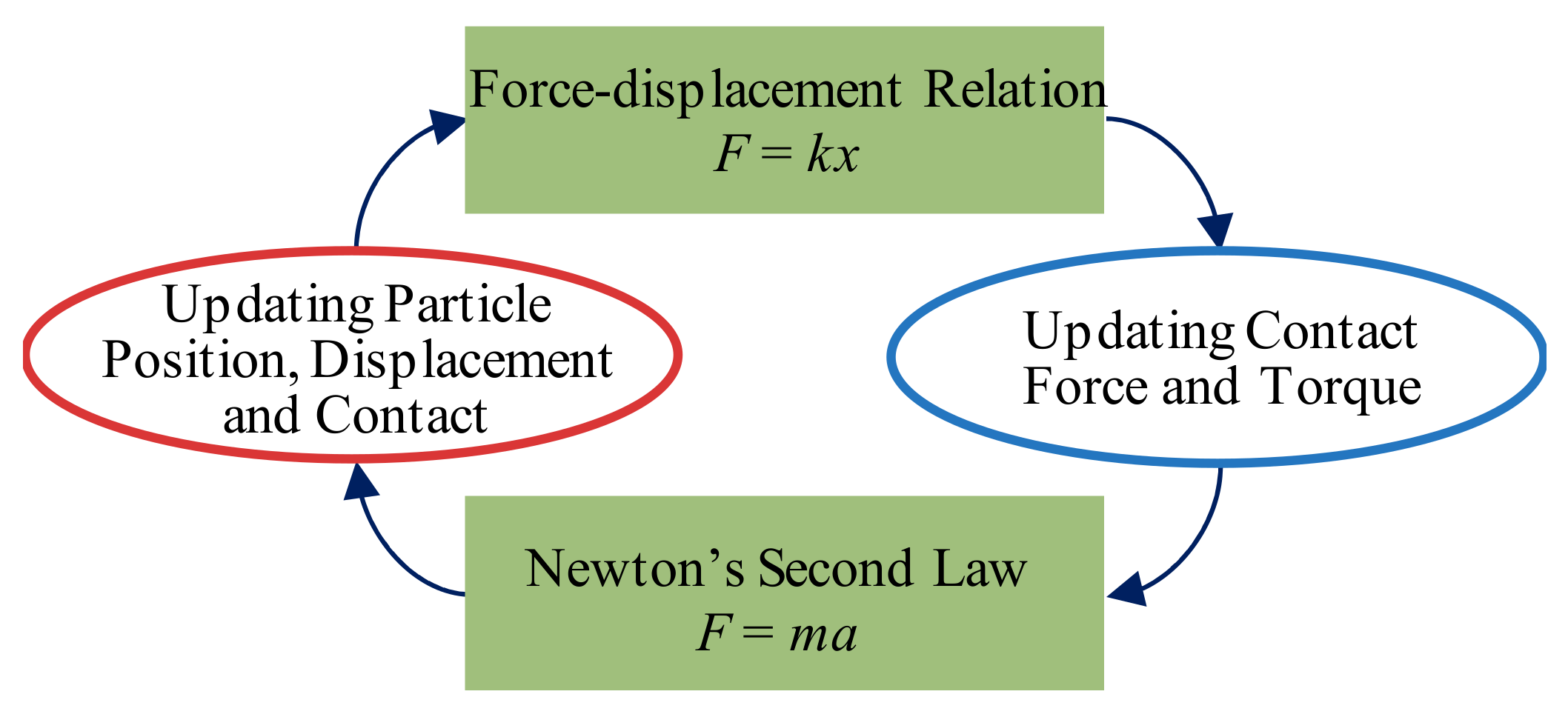
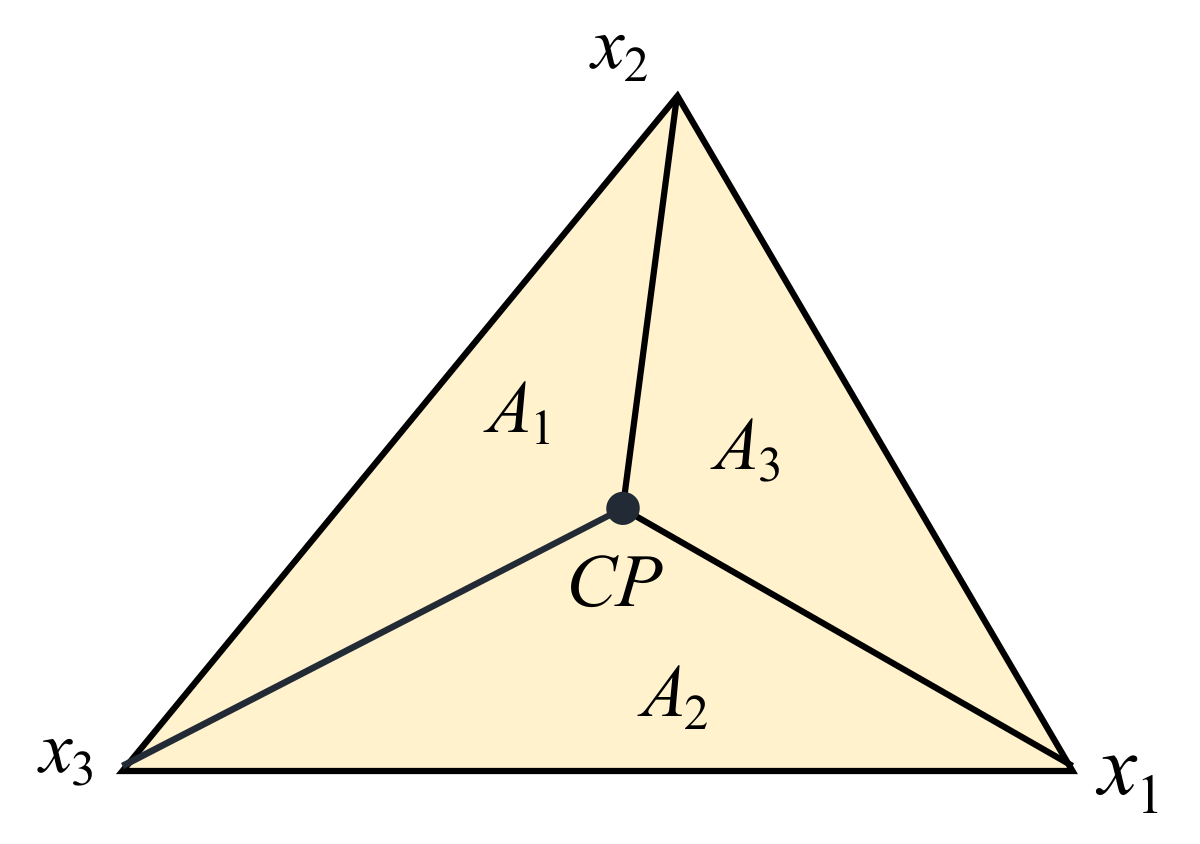
2.1. Principles of Discrete Element Method (DEM) and the Contact Model
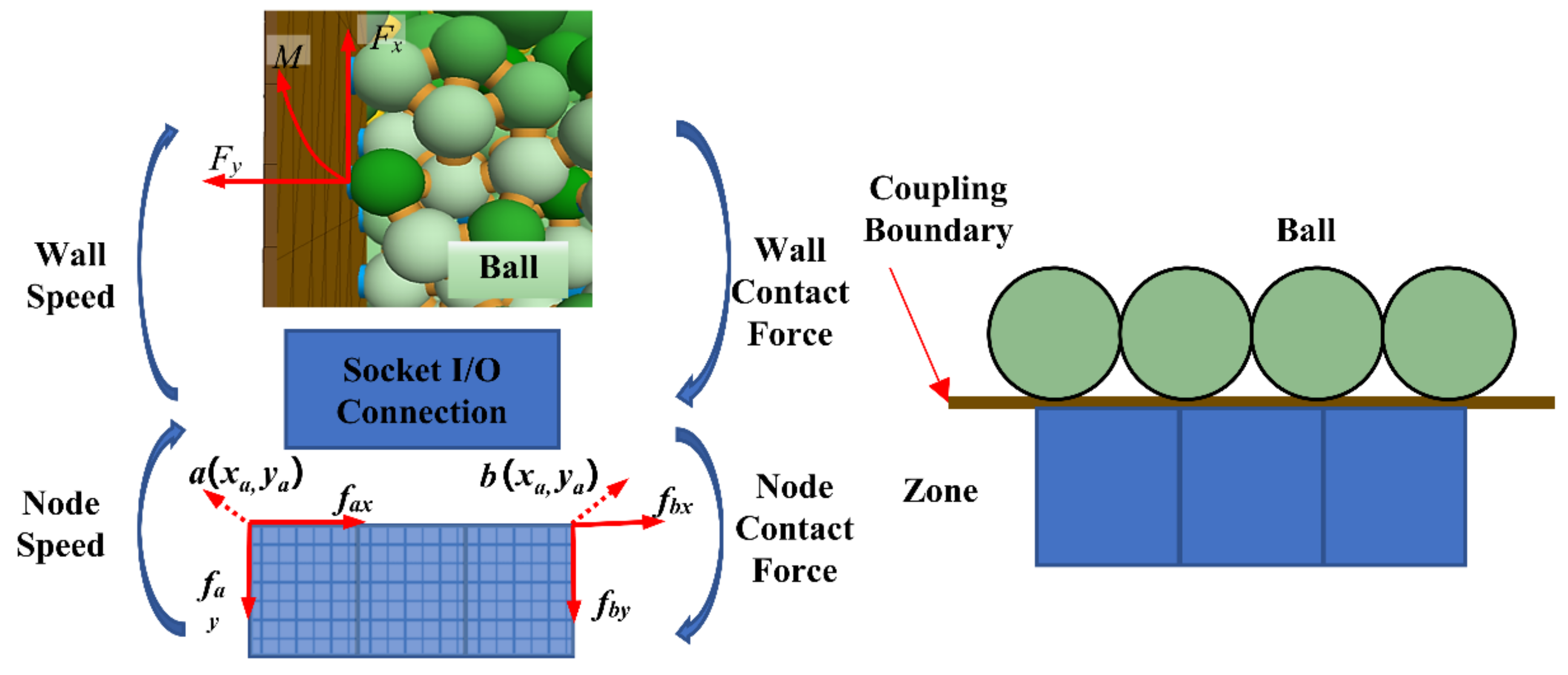
2.2. Principle of the Continuous–Discontinuous Coupling Method
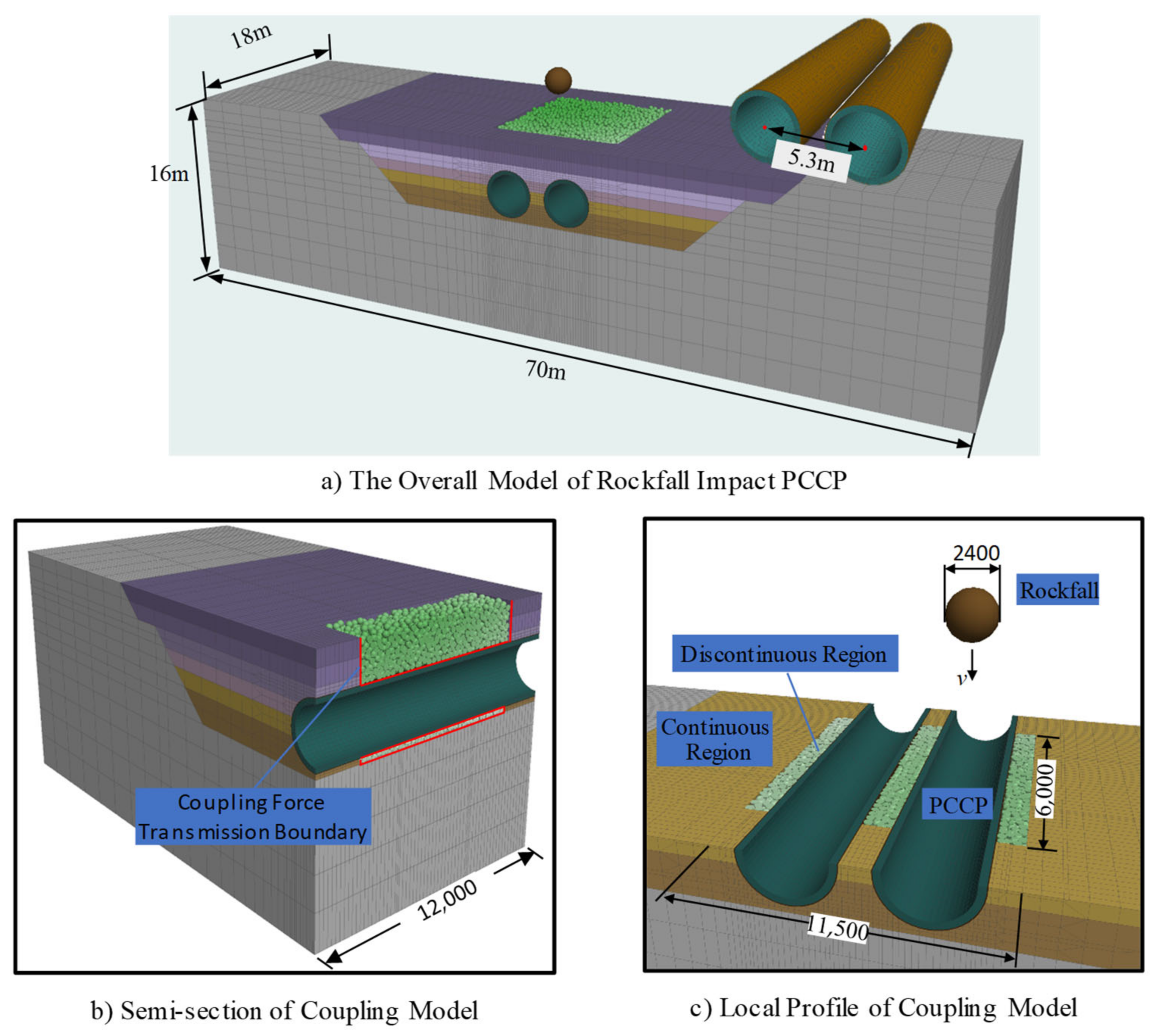
3. Construction of the “Pipe-Soil-Rock” Continuous–Discontinuous Model
3.1. Construction of the Continuous–Discontinuous Model of the Soil
3.2. Construction of the PCCP Continuous Model
3.3. Construction of the Discontinuous Model of Rockfall and Setting of Calculation Conditions
4. Analysis of the Spatial–Temporal Evolution of a PCCP under an Impact Load
4.1. The Simulation Results of the Rockfall Impact Process
4.2. Analysis of a PCCP under an Impact Load
5. Effects of Rockfall Parameters on the Response of a PCCP
5.1. Impact of Rockfall Radius on PCCP Response
5.2. Impact of Rockfall Height on PCCP Response
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- AWWA C304-92; AWWA Standard for Design of Prestressed Concrete Cylinder Pipe. AWWA: Denver, CO, USA, 1993.
- Zarghamee, M.S.; Moharrami, M. Experimental Study and Numerical Simulation of Three-Edge Bearing Test of Large Diameter Prestressed Concrete Cylinder Pipes. In Proceedings of the Pipelines 2018 American Society of Civil Engineers, Toronto, ON, Canada, 12 July 2018; pp. 776–787. [Google Scholar]
- Zhang, Y.; Yan, Z.; Zhu, H.; Ju, J.W. Experimental Study on the Structural Behaviors of Jacking Prestressed Concrete Cylinder Pipe. Tunn. Undergr. Space Technol. 2018, 73, 60–70. [Google Scholar] [CrossRef]
- Ge, S.; Sinha, S. Failure Analysis, Condition Assessment Technologies, and Performance Prediction of Prestressed-Concrete Cylinder Pipe: State-of-the-Art Literature Review. J. Perform. Constr. Facil. 2014, 28, 618–628. [Google Scholar] [CrossRef]
- Hu, S. Study on structural safety evaluating technique for pre-stressed concrete cylinder pipe (PCCP) in the South-to-North Water Diversion Project. Hydro-Sci. Eng. 2009, 4, 74–82. [Google Scholar] [CrossRef]
- Yu, L.; Zhao, X.; Hu, S.; Lu, J.; Lu, W. Finite element analysis study on pipeline pressure of PCCP in service based on ABAQUS. Concrete 2015, 135–138. [Google Scholar] [CrossRef]
- Xiong, H.; Li, P.; Li, Q. FE Model for Simulating Wire-Wrapping during Prestressing of an Embedded Prestressed Concrete Cylinder Pipe. Simul. Model. Pract. Theory 2010, 18, 624–636. [Google Scholar] [CrossRef]
- Gomez, H.; Garrido, A.; Arrondo, J.I.; Falcinelli, S. Fracturas Laterales de Cadera. 100 Primeros Casos Utilizando Sistema de Estabilización PCCP. Rev. Asoc. Arg. Ort. Traumatol. 2016, 81, 206. [Google Scholar] [CrossRef]
- Hajali, M.; Alavinasab, A.; Abi Shdid, C. Structural Performance of Buried Prestressed Concrete Cylinder Pipes with Harnessed Joints Interaction Using Numerical Modeling. Tunn. Undergr. Space Technol. 2016, 51, 11–19. [Google Scholar] [CrossRef]
- Ge, S.; Sinha, S. Effect of Mortar Coating’s Bond Quality on the Structural Integrity of Prestressed Concrete Cylinder Pipe with Broken Wires. JMSR 2015, 4, 59. [Google Scholar] [CrossRef]
- Mao, H.; Chen, L.; Yang, J.; Ma, C.; Yuan, X. Stress-strain response of buried PCCP under rockfall impact load. J. Yangtze River Sci. Res. Inst. 2022, 39, 113–119. [Google Scholar]
- Khosrozadeh, A.; Hashemnia, K.; Vatankhah, R. Investigating Impact-Induced Vibrations of Fluid-Conveying Elastic Pipes Considering Hertz Theory. Mech. Res. Commun. 2021, 116, 103762. [Google Scholar] [CrossRef]
- Thornton, C.; Ning, Z. A Theoretical Model for the Stick/Bounce Behaviour of Adhesive, Elastic-Plastic Spheres. Powder Technol. 1998, 99, 154–162. [Google Scholar] [CrossRef]
- Muleski, G.E.; Ariman, T.; Aumen, C.P. A Shell Model of a Buried Pipe in a Seismic Environment. J. Press. Vessel. Technol. 1979, 101, 44–50. [Google Scholar] [CrossRef]
- Wang, S. Evaluation of Underground Pipe-Structure Interface for Surface Impact Load. Nucl. Eng. Des. 2017, 317, 59–68. [Google Scholar] [CrossRef]
- Tian, J.; Zhang, J.; Dong, F.; Du, G. Dynamic Response of Buried Pipeline Subject to Impact Loads Using Piezoceramic Transducers. Int. J. Press. Vessel. Pip. 2019, 177, 103984. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, Z.; Han, C.; Zhang, H. Buckling Behaviour Analysis of a Buried Steel Pipeline in Rock Stratum Impacted by a Rockfall. Eng. Fail. Anal. 2015, 58, 281–294. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, Z.; Feng, D.; Zhang, C.; Xia, C.; Tu, Y. Response of the Buried Steel Pipeline Caused by Perilous Rock Impact: Parametric Study. J. Loss Prev. Process Ind. 2016, 43, 385–396. [Google Scholar] [CrossRef]
- Xiong, J.; Deng, Q.; Zhang, H.; Pang, W. Safety Assessment on the Response of Buried Pipeline Caused by Rockfall Impact Load. Saf. Environ. Eng. 2013, 20, 108–114. [Google Scholar]
- Tavakoli Mehrjardi, G.; Karimi, M. Numerical Modeling of Buried Steel Pipe Subjected to Impact Load. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021048. [Google Scholar] [CrossRef]
- Leine, R.I.; Schweizer, A.; Christen, M.; Glover, J.; Bartelt, P.; Gerber, W. Simulation of Rockfall Trajectories with Consideration of Rock Shape. Multibody Syst. Dyn. 2014, 32, 241–271. [Google Scholar] [CrossRef]
- Liu, M.; Yang, M. Modeling the Behavior of Natural Gas Pipeline Impacted by Falling Objects. Eng. Fail. Anal. 2014, 42, 45–59. [Google Scholar] [CrossRef]
- Deng, X.; Xue, S.; Tong, X. Numerical simulation on response of buried pipeline induced by rock-fall transverse impaction. J. China Univ. Pet. (Ed. Nat. Sci.) 2009, 33, 111–115+120. [Google Scholar]
- Huang, W. Study on Rockfall Motion Characteristics and Dynamic Response of Shed Cave-Wall Based on Coupling of PFC~ (3D) and FLAC~ (3D). Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2022. [Google Scholar]
- Wang, D.; Liu, H.; Pe, X.; Sun, X.; Zhou, L.; Liu, Y. Study on dynamic response of cushion layer of rolling stone impact tunnel based on discrete element-finite difference coupling. Vib. Shock. 2021, 40, 246–253. [Google Scholar]
- Hou, C.; Cheng, Y.; Li, Y.; Sun, Z.; Jiang, X. Simulation and analysis of load loading process of buried pipeline based on discrete-continuous coupling method. J. Hefei Univ. Technol. (Nat. Sci. Ed.) 2023, 46, 96–103. [Google Scholar]
- Huang, K.; Sun, Y.; Chen, X.; Deng, X.; Liu, R.; Wu, Q. Study on three-dimensional displacement characteristics of earth mass before shield excavation based on FDM-DEM coupling. China Highw. J. 2023, 36, 190–206. [Google Scholar] [CrossRef]
- Tu, Y.; Chen, X.; Wang, X.; Chai, H.; Zhang, L.; Zhang, R. Slope stability analysis based on continuous-discrete coupling strength reduction method. Eng. Mech. 2023, 40, 1–12. [Google Scholar]
- Cheng, B.; Dou, T.; Xia, S.; Zhao, L.; Yang, J.; Zhang, Q. Experimental Study on Mechanical Properties of Prestressed Concrete Cylinder Pipes (PCCPs) under External Load. Int. J. Press. Vessel. Pip. 2021, 191, 104365. [Google Scholar] [CrossRef]
- Cheng, B.; Dou, T.; Xia, S.; Zhao, L.; Yang, J.; Zhang, Q. Mechanical Properties and Loading Response of Prestressed Concrete Cylinder Pipes under Internal Water Pressure. Eng. Struct. 2020, 216, 110674. [Google Scholar] [CrossRef]
- Plassiard, J.-P.; Donze, F. Rockfall Impact Parameters on Embankments: A Discrete Element Method Analysis. Struct. Eng. Int. 2009, 19, 333–341. [Google Scholar] [CrossRef]
- Zheng, L.; Wu, Y.; Wu, W.; Zhang, H.; Peng, X.; Zhang, X.; Wu, X. Efficient Investigation of Rock Crack Propagation and Fracture Behaviors during Impact Fragmentation in Rockfalls Using Parallel DDA. Adv. Civ. Eng. 2021, 2021, 5901561. [Google Scholar] [CrossRef]
- Bertrand, D.; Trad, A.; Limam, A.; Silvani, C. Full-Scale Dynamic Analysis of an Innovative Rockfall Fence Under Impact Using the Discrete Element Method: From the Local Scale to the Structure Scale. Rock Mech. Rock Eng. 2012, 45, 885–900. [Google Scholar] [CrossRef]
- Cheng, Y.P.; Nakata, Y.; Bolton, M.D. Discrete Element Simulation of Crushable Soil. Géotechnique 2003, 53, 633–641. [Google Scholar] [CrossRef]
- Shiu, W.-J.; Lee, C.-F.; Chiu, C.-C.; Weng, M.-C.; Yang, C.-M.; Chao, W.-A.; Liu, C.-Y.; Lin, C.-H.; Huang, W.-K. GeoPORT Working Group Analyzing Landslide-Induced Debris Flow and Flow-Bridge Interaction by Using a Hybrid Model of Depth-Averaged Model and Discrete Element Method. Landslides 2022, 20, 331–349. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A Discrete Numerical Model for Granular Assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, L.; Zhu, H.; Zhang, Q. Effect of Model Scale and Particle Size Distribution on PFC3D Simulation Results. Rock Mech. Rock Eng. 2014, 47, 2139–2156. [Google Scholar] [CrossRef]
- Naito, N.; Maeda, K.; Konno, H.; Ushiwatari, Y.; Kawase, R. Rockfall Impacts on Sand Cushions with Different Soil Mechanical Characteristics Using Discrete Element Method. Soils Found 2020, 60, 384–397. [Google Scholar] [CrossRef]
- Yuan, S.; Zhao, P.; Li, L.; Wang, X.; Liu, J.; Zhang, B. A Discrete Numerical Study of the Effect of the Thickness and the Porosity of the Sand Cushion on the Impact Response Due to the Rockfall. CMES-Comp. Model. Eng. Sci. 2022, 130, 1683–1698. [Google Scholar] [CrossRef]
- Guzev, M.A. Non-Classical Solutions of a Continuum Model for Rock Descriptions. J. Rock Mech. Geotech. Eng. 2014, 6, 180–185. [Google Scholar] [CrossRef]
- Madhavi Latha, G.; Garaga, A. Elasto-Plastic Analysis of Jointed Rocks Using Discrete Continuum and Equivalent Continuum Approaches. Int. J. Rock Mech. Min. Sci. 2012, 53, 56–63. [Google Scholar] [CrossRef]
- Breugnot, A.; Lambert, S.; Villard, P.; Gotteland, P. A Discrete/Continuous Coupled Approach for Modeling Impacts on Cellular Geostructures. Rock Mech. Rock Eng. 2016, 49, 1831–1848. [Google Scholar] [CrossRef]
- Wang, Y.S.; Zhang, K.Y.; Tang, J.H.; Liang, D. Model Test Research of the Influences of Rock-Fall Impaction on Accelerations of the Cut-and-Cover Tunnel Structure. AMM 2011, 117–119, 206–211. [Google Scholar] [CrossRef]
- Cao, W.; Li, X.; Tao, M.; Zhou, Z. Vibrations Induced by High Initial Stress Release during Underground Excavations. Tunn. Undergr. Space Technol. 2016, 53, 78–95. [Google Scholar] [CrossRef]
- Su, Y.; Cui, Y.; Ng, C.; Choi, C.E.; Kwan, J. Effects of Particle Size and Cushioning Thickness on the Performance of Rock-Filled Gabions Used in Protection against Boulder Impact. Can. Geotech. J. 2019, 56, 198–207. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Morioka, H.; Minami, M.; Maejima, T.; Tasaka, Y.; Kurose, H. FLAC/PFC Coupled Numerical Simulation of AE in Large-Scale Underground Excavations. Int. J. Rock Mech. Min. Sci. 2007, 44, 550–564. [Google Scholar] [CrossRef]
- Wei, C.; Apel, D.; Katsaga, T. Coupled Finite-Difference and Discrete-Element Method for Modelling Direct Shear Tests on Combined Rock-Cemented Rockfill Specimens. Min. Metall. Explor. 2022, 39, 89–109. [Google Scholar] [CrossRef]
- Kawahara, S.; Muro, T. Effects of Dry Density and Thickness of Sandy Soil on Impact Response Due to Rockfall. J. Terramechan 2006, 43, 329–340. [Google Scholar] [CrossRef]
- Liu, F.; Tang, C.; Zhang, Y.; Ma, T. Rockburst and Microseismicity Characteristics in the Qinling Water Conveyance Tunnel of the Hanjiang-to-Weihe River Diversion Project. Int. J. Rock Mech. Min. Sci 2021, 148, 104973. [Google Scholar] [CrossRef]
- Indraratna, B.; Ngo, N.T.; Rujikiatkamjorn, C.; Sloan, S.W. Coupled Discrete Element–Finite Difference Method for Analysing the Load-Deformation Behaviour of a Single Stone Column in Soft Soil. Comput. Geotech. 2015, 63, 267–278. [Google Scholar] [CrossRef]
- Jia, M.; Yang, Y.; Liu, B.; Wu, S. PFC/FLAC Coupled Simulation of Dynamic Compaction in Granular Soils. Granul. Matter 2018, 20, 76. [Google Scholar] [CrossRef]
- Liu, G.; Li, J. A Three-Dimensional Discontinuous Deformation Analysis Method for Investigating the Effect of Slope Geometrical Characteristics on Rockfall Behaviors. Int. J. Comput. Methods 2019, 16, 1850122. [Google Scholar] [CrossRef]
- Thoeni, K.; Giacomini, A.; Lambert, C. A 3D Discrete Element Modelling Approach for Rockfall Analysis with Drapery Systems. Int. J. Rock Mech. Min. Sci. 2014, 68, 107–119. [Google Scholar] [CrossRef]
- Ma, C.; Chen, L.; Yang, K.; Yang, J.; Tu, Y.; Cheng, L. Intelligent Calibration Method for Microscopic Parameters of Soil–rock Mixtures Based on Measured Landslide Accumulation Morphology. Comput. Methods Appl. Mech. Eng. 2024, 422, 116835. [Google Scholar] [CrossRef]
- Zhan, R.; Chen, Z.; Zeng, G.; Cheng, X. Development characteristics and prevention suggestions of geological disasters in Danjiangkou Reservoir area. Water Resour. Hydropower Express 2020, 41, 31–36. [Google Scholar] [CrossRef]
- Liang, Y.; Niu, F.; Xie, W. Development and distribution law of geological hazards along the Jiwei project in Yanhan, Shaanxi Province. Shaanxi Geol. 2021, 39, 96–102. [Google Scholar]


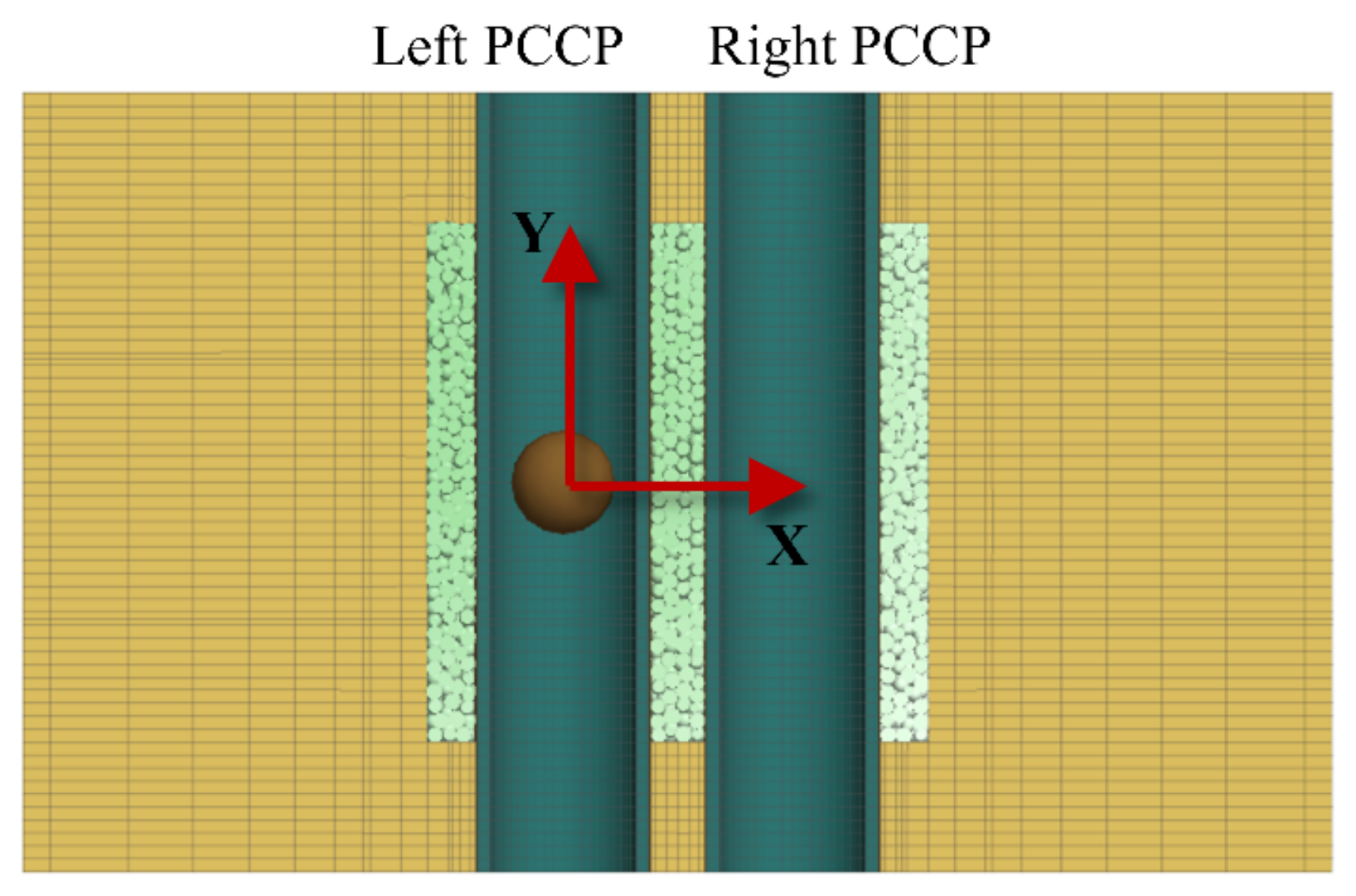
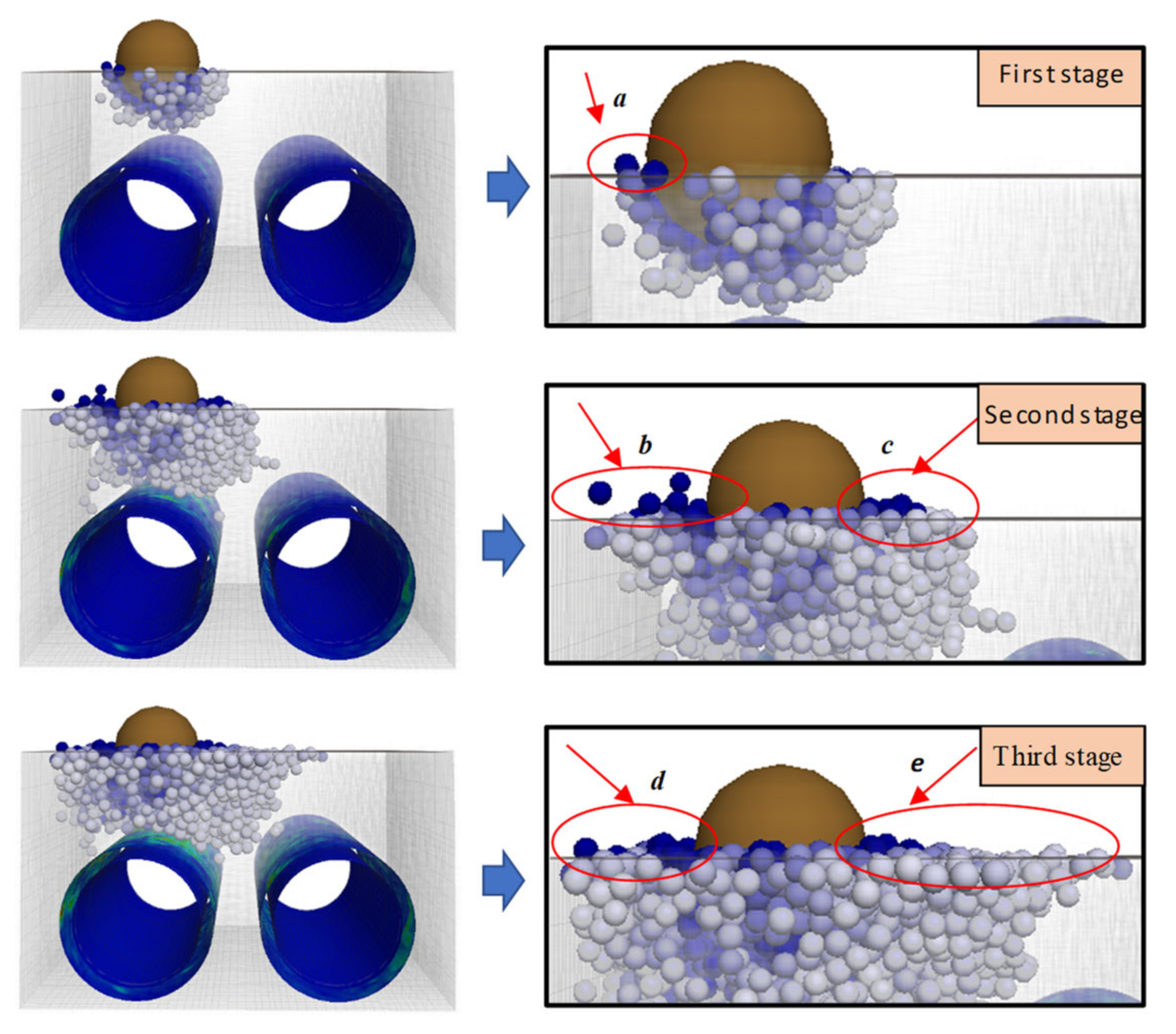
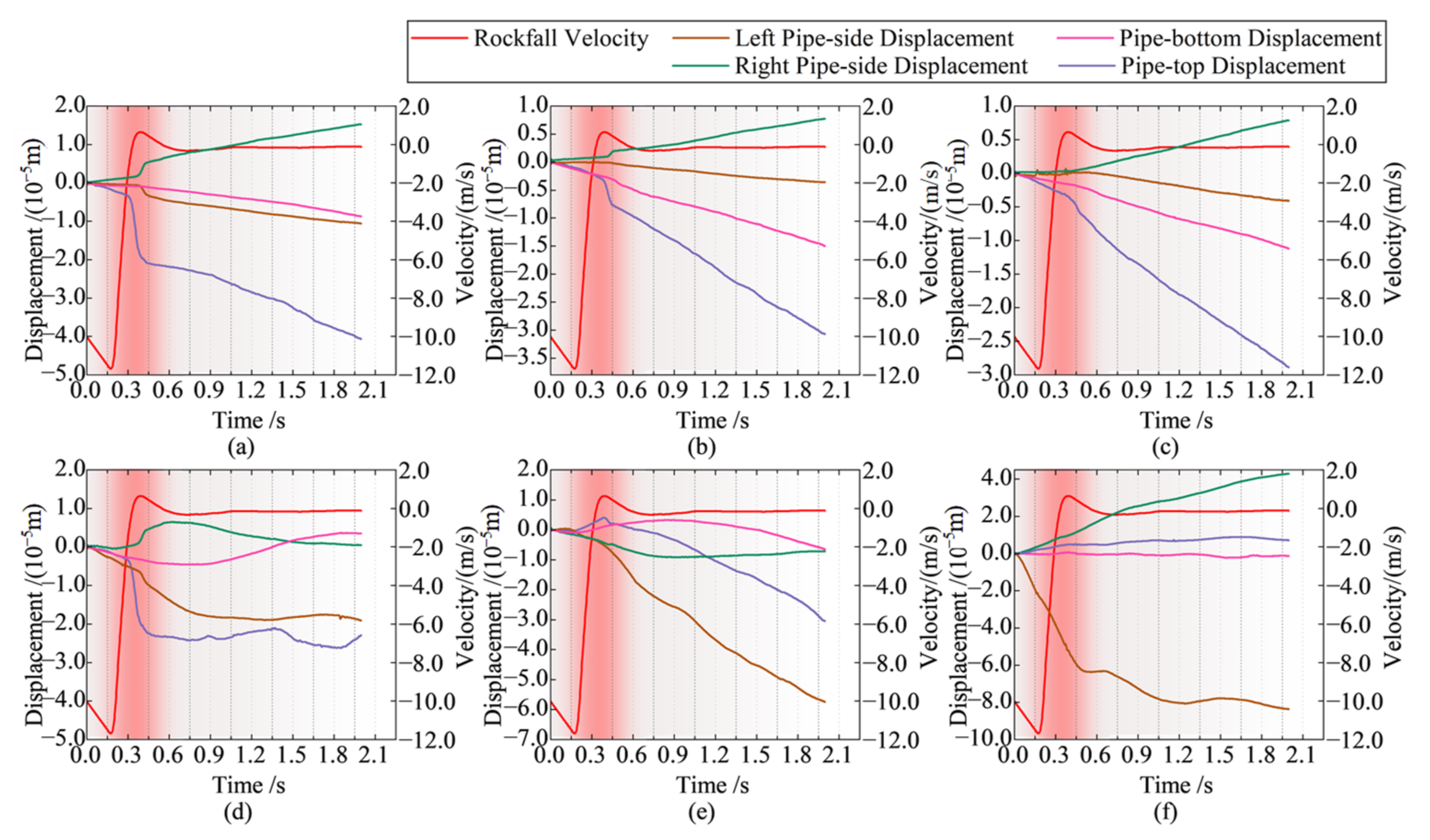
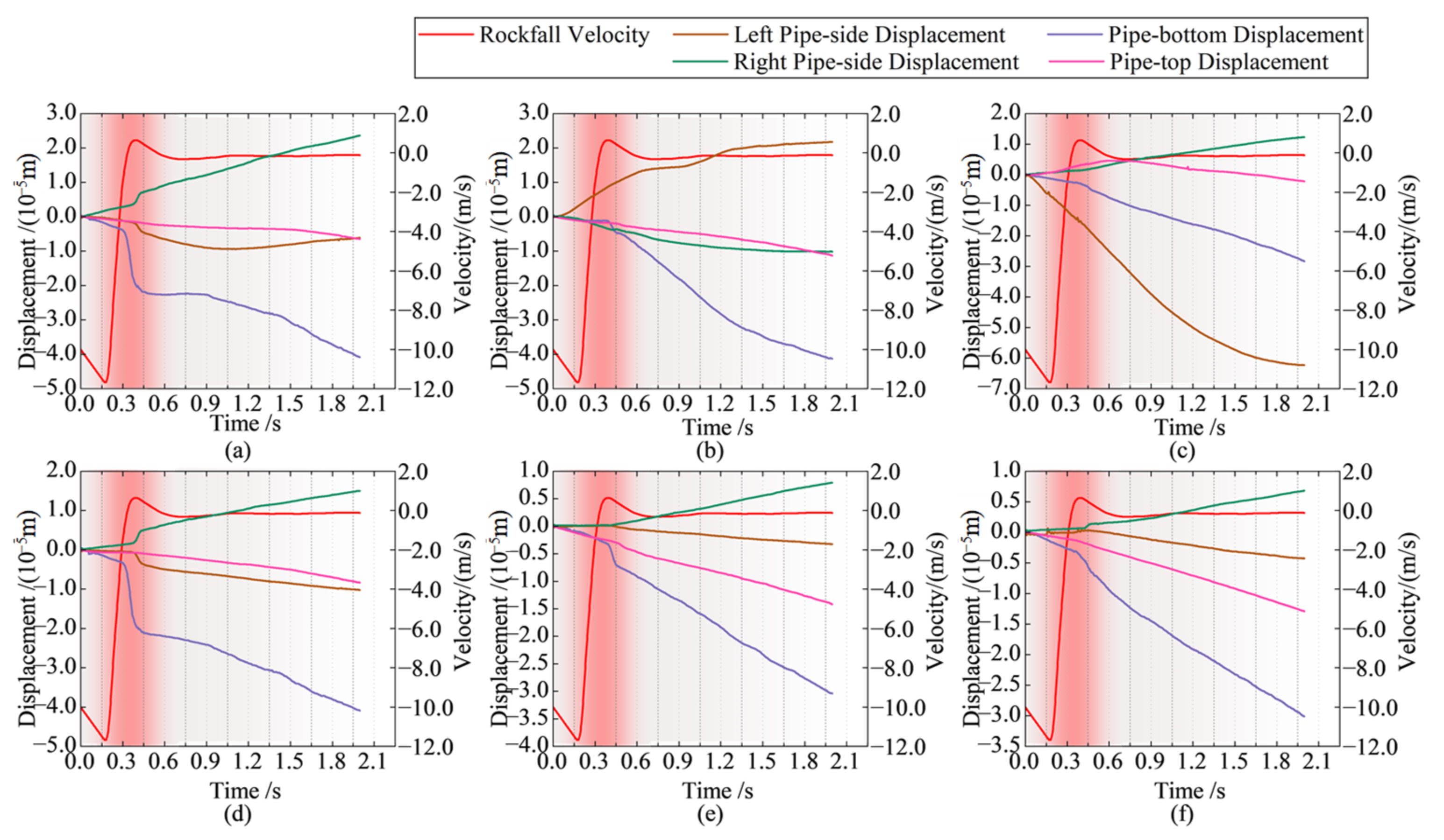
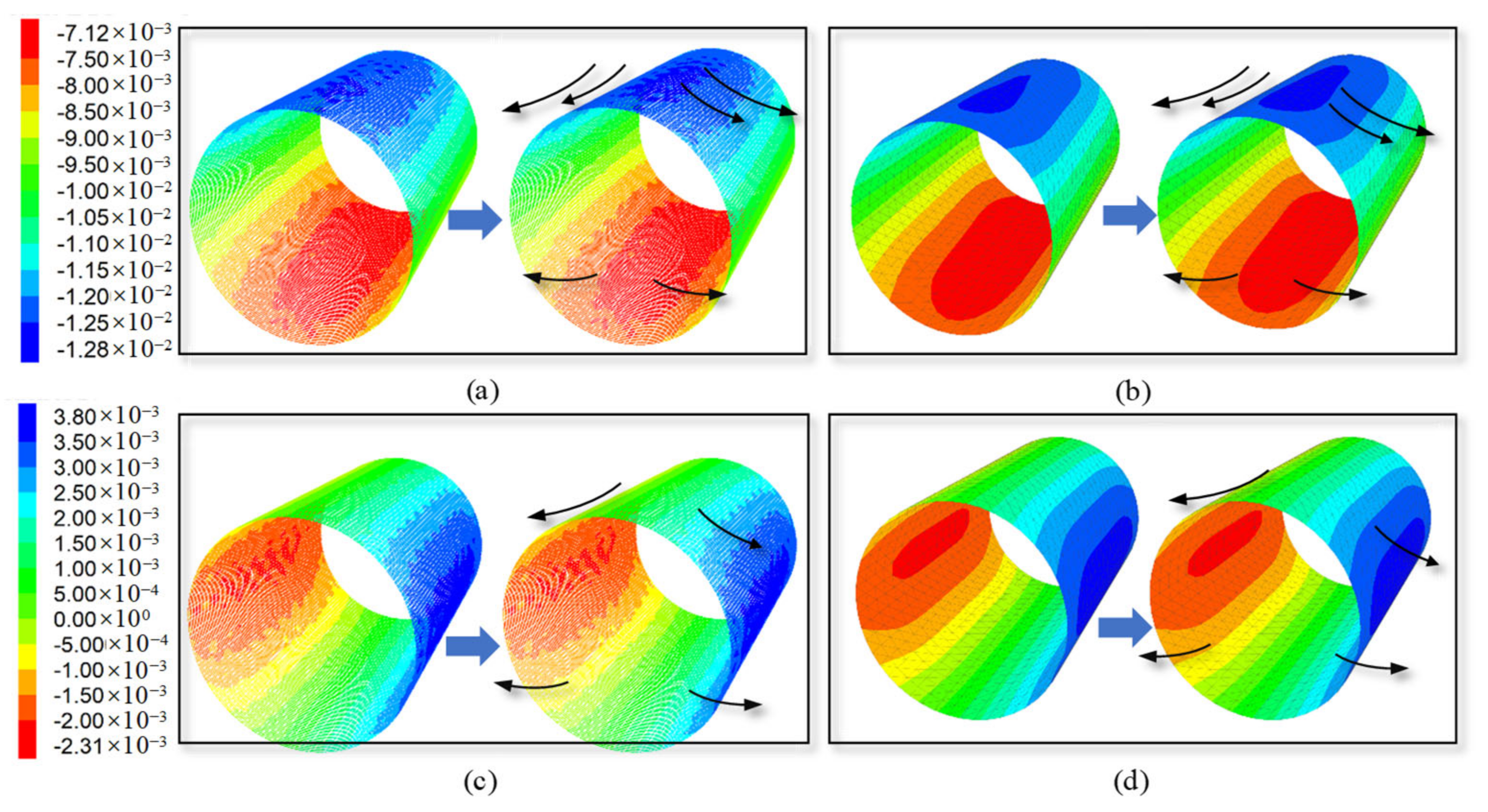
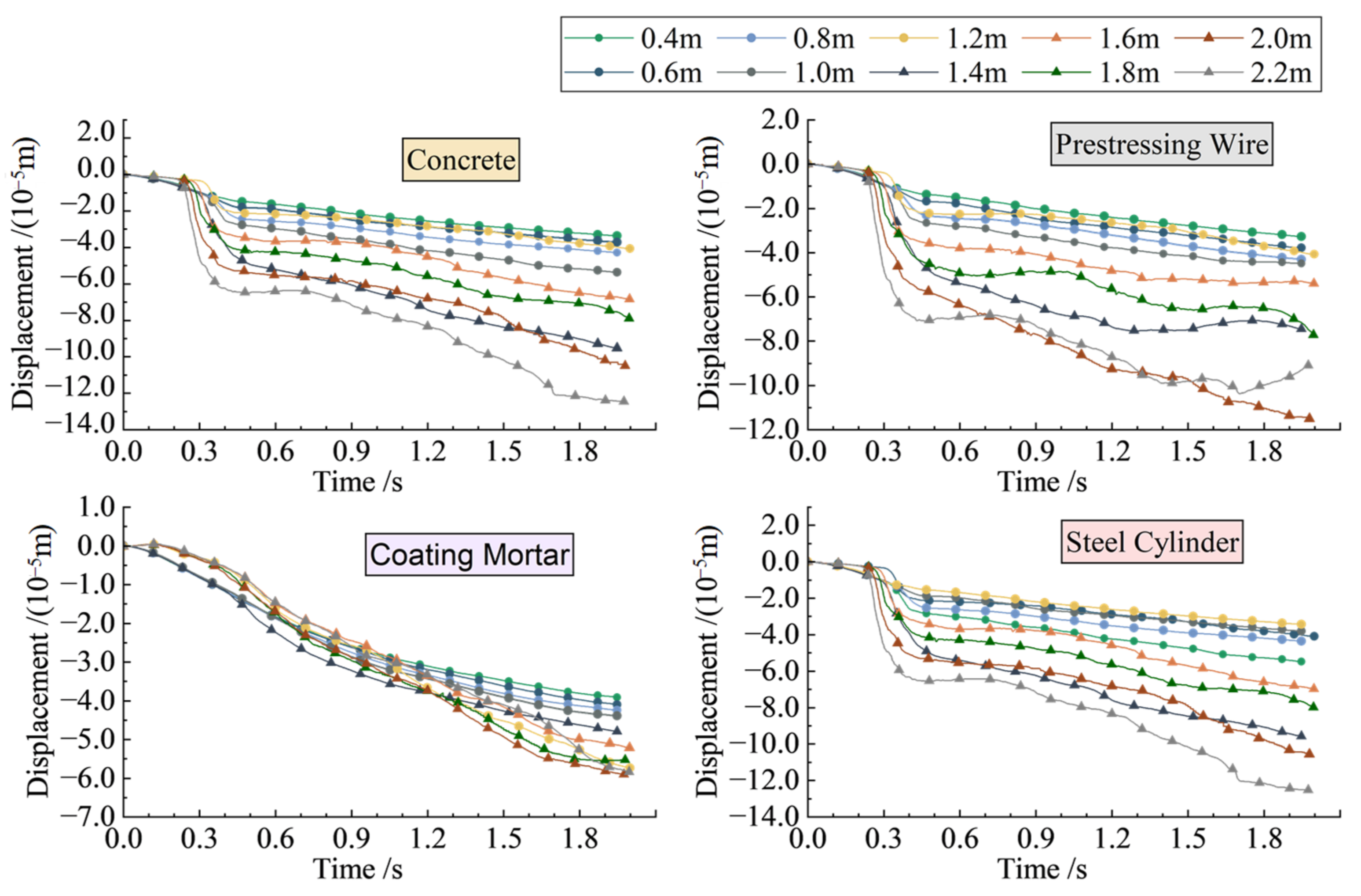


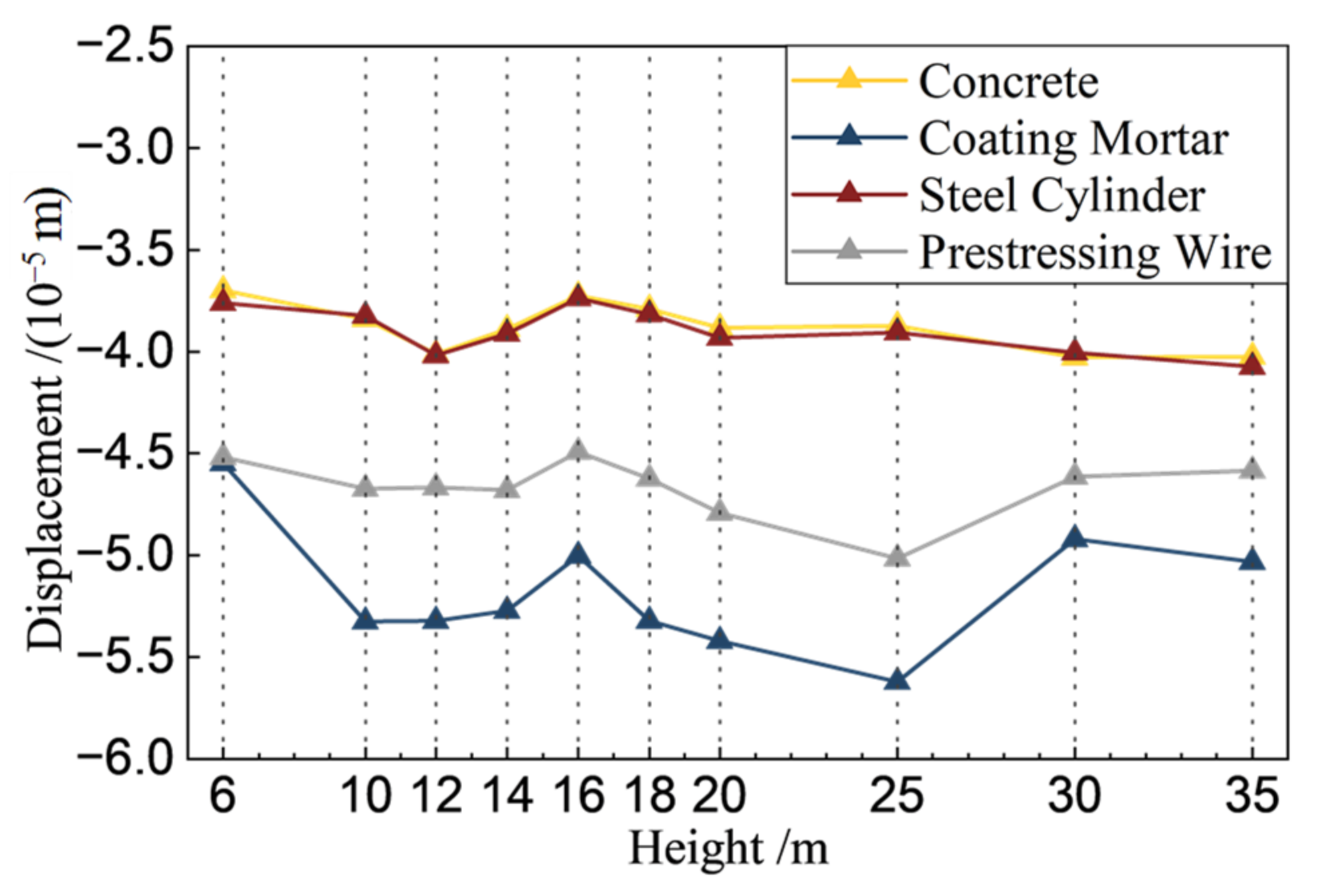
| Part | Density (kg/m3) | Elastic Modulus (Pa) | Poisson’s Ratio |
|---|---|---|---|
| Foundation | 1770 | 4 × 107 | 0.3 |
| Cushion | 1770 | 4 × 107 | 0.3 |
| Backfill | 2000 | 1.055 × 107 | 0.3 |
| Materials | Poisson’s Ratio | Radius (m) | Damp |
|---|---|---|---|
| Cushion | 0.3 | 0.12~0.15 | 0.7 |
| Backfill | 0.3 | 0.18~0.20 | 0.7 |
| Project | Contact Model | Emod (Pa) | Kratio | pb_ten (Pa) | pb_coh (Pa) |
|---|---|---|---|---|---|
| Rockfall–backfill | Linear contact model | 1.055 × 107 | 1.0 | \ | \ |
| Cushion–cushion | Linear contact model | 4 × 106 | 1.0 | \ | \ |
| Backfill–backfill | Linear contact model | 1.055 × 107 | 1.0 | \ | \ |
| Cushion–wall | Parallel contact model | 4 × 107 | 1.0 | 1 × 10100 | 1 × 10100 |
| Backfill–wall | Parallel contact model | 1.055 × 108 | 1.0 | 1 × 10100 | 1 × 10100 |
| Materials | Elasticity Modulus (MPa) | Strength of Extension (MPa) | Compressive Strength (MPa) | Density (kg/m3) | Thickness (mm) |
|---|---|---|---|---|---|
| Prestressing wire | 205,000 | 1570 | 1570 | 7833 | 10.39 (diameter) |
| Steel cylinder | 206,000 | 235 | 235 | 7833 | 1.5 |
| Concrete core | 35,500 | 35.5 | 2.74 | 2500 | 300 |
| Mortar coating | 24,165 | 45 | 3.49 | 2200 | 40 |
| Spigot steel ring | 206,000 | 235 | 235 | 7833 | 20 |
| Socket steel ring | 206,000 | 235 | 235 | 7833 | 10 |
| Condition | Radius (m) | Height (m) | Condition | Radius (m) | Height (m) |
|---|---|---|---|---|---|
| 1 | 0.4 | 8.0 | 11 | 1.2 | 6 |
| 2 | 0.6 | 8.0 | 12 | 1.2 | 10 |
| 3 | 0.8 | 8.0 | 13 | 1.2 | 12 |
| 4 | 1.0 | 8.0 | 14 | 1.2 | 14 |
| 5 | 1.2 | 8.0 | 15 | 1.2 | 16 |
| 6 | 1.4 | 8.0 | 16 | 1.2 | 18 |
| 7 | 1.6 | 8.0 | 17 | 1.2 | 20 |
| 8 | 1.8 | 8.0 | 18 | 1.2 | 25 |
| 9 | 2 | 8.0 | 19 | 1.2 | 30 |
| 10 | 2.2 | 8.0 | 20 | 1.2 | 35 |
| Section Position | Left Pipe-Side | Right Pipe-Side | Pipe-Top | Pipe-Bottom | |
|---|---|---|---|---|---|
| Material Location | |||||
| Concrete | Midspan | 0.06669 | 0.17284 | 1.60132 | 0.01144 |
| Spigot joint | 0.00356 | 0.01771 | 0.17210 | 0.05368 | |
| Socket joint | 0.05310 | 0.00685 | 1.24774 | 0.03417 | |
| Coating mortar | Midspan | 0.18973 | 0.20350 | 1.69477 | 0.05670 |
| Spigot joint | 0.24315 | 0.16059 | 0.19237 | 0.13048 | |
| Socket joint | 1.46315 | 0.21760 | 0.08769 | 0.12013 | |
| Prestressing wire | Midspan | 0.10703 | 0.17874 | 1.61942 | 0.03652 |
| Spigot joint | 0.25720 | 0.12501 | 0.02563 | 0.01008 | |
| Socket joint | 0.36339 | 0.02568 | 0.06576 | 0.12159 | |
| Steel cylinder | Midspan | 0.02897 | 0.01274 | 0.13522 | 0.05012 |
| Spigot joint | 0.00058 | 0.00239 | 0.12804 | 0.04947 | |
| Socket joint | 0.09584 | 0.12652 | 1.61959 | 0.00708 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Tu, Y.; Zhou, Y.; Yang, J.; Cheng, L. Dynamic Response of PCCP under the Rockfall Impact Based on the Continuous–Discontinuous Method: A Case Study. Water 2024, 16, 801. https://doi.org/10.3390/w16060801
Ma C, Tu Y, Zhou Y, Yang J, Cheng L. Dynamic Response of PCCP under the Rockfall Impact Based on the Continuous–Discontinuous Method: A Case Study. Water. 2024; 16(6):801. https://doi.org/10.3390/w16060801
Chicago/Turabian StyleMa, Chunhui, Ying Tu, Yonglin Zhou, Jie Yang, and Lin Cheng. 2024. "Dynamic Response of PCCP under the Rockfall Impact Based on the Continuous–Discontinuous Method: A Case Study" Water 16, no. 6: 801. https://doi.org/10.3390/w16060801
APA StyleMa, C., Tu, Y., Zhou, Y., Yang, J., & Cheng, L. (2024). Dynamic Response of PCCP under the Rockfall Impact Based on the Continuous–Discontinuous Method: A Case Study. Water, 16(6), 801. https://doi.org/10.3390/w16060801









