Development and Application of a New Exponential Model for Hydraulic Conductivity with Depth of Rock Mass
Abstract
1. Introduction
2. Methodology
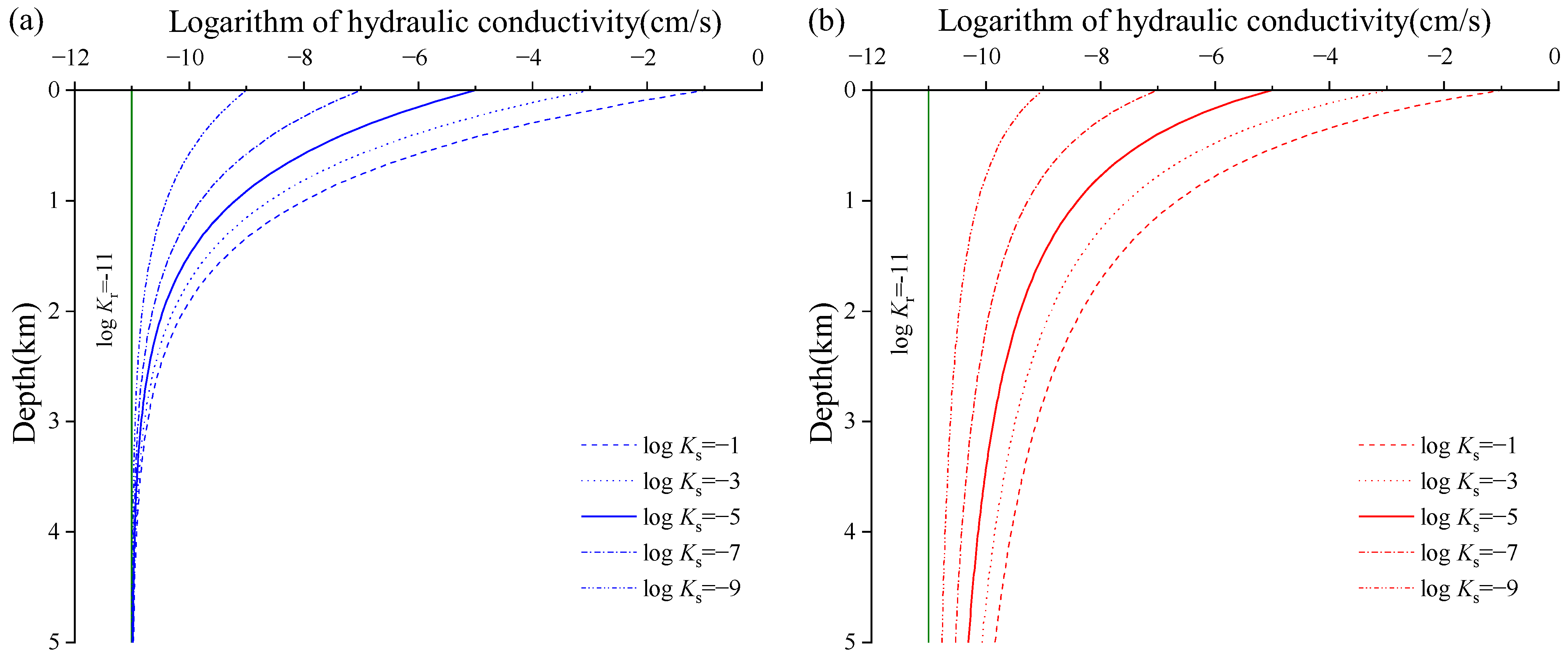
2.1. Model Analysis
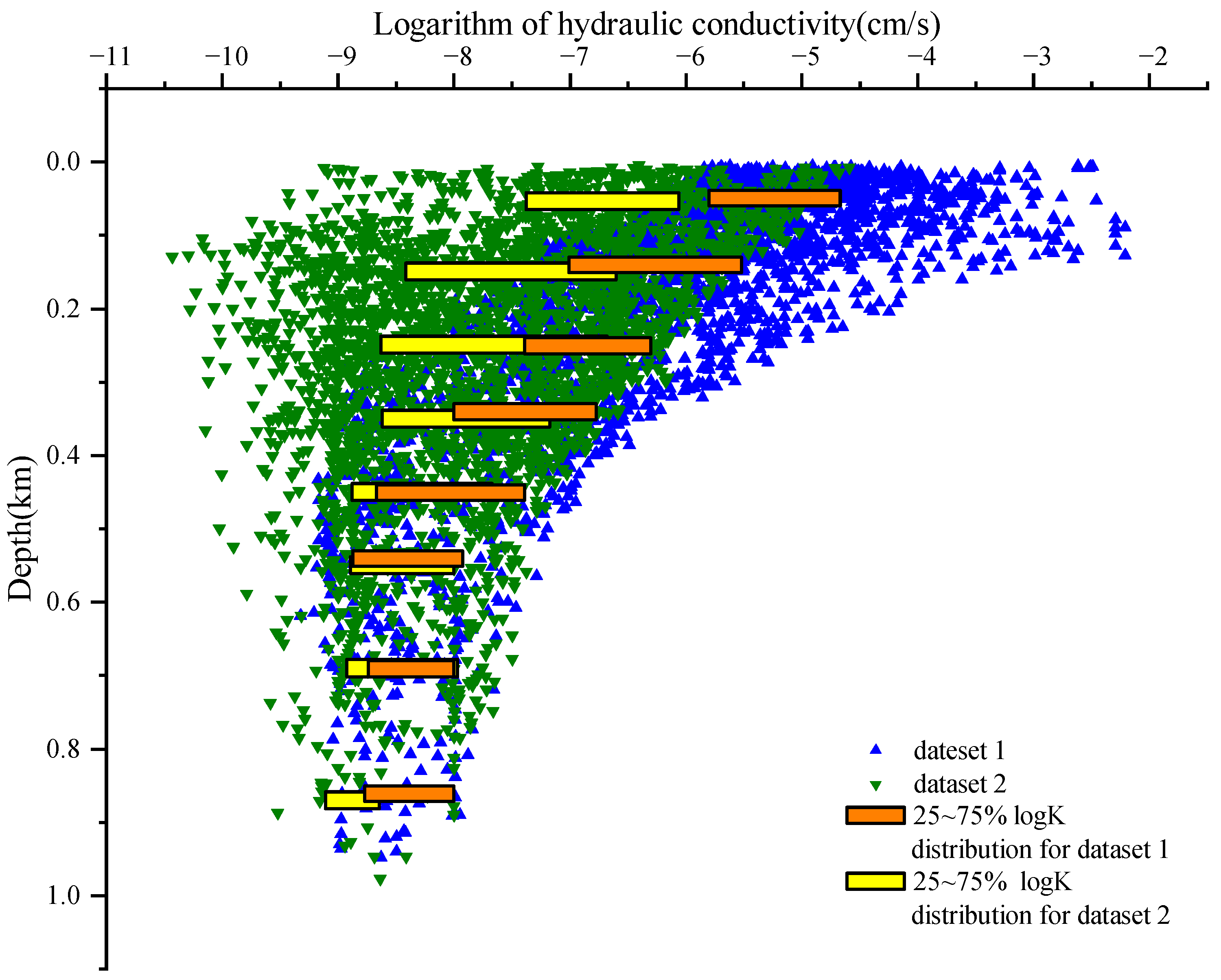
2.2. Source and Classification of Database
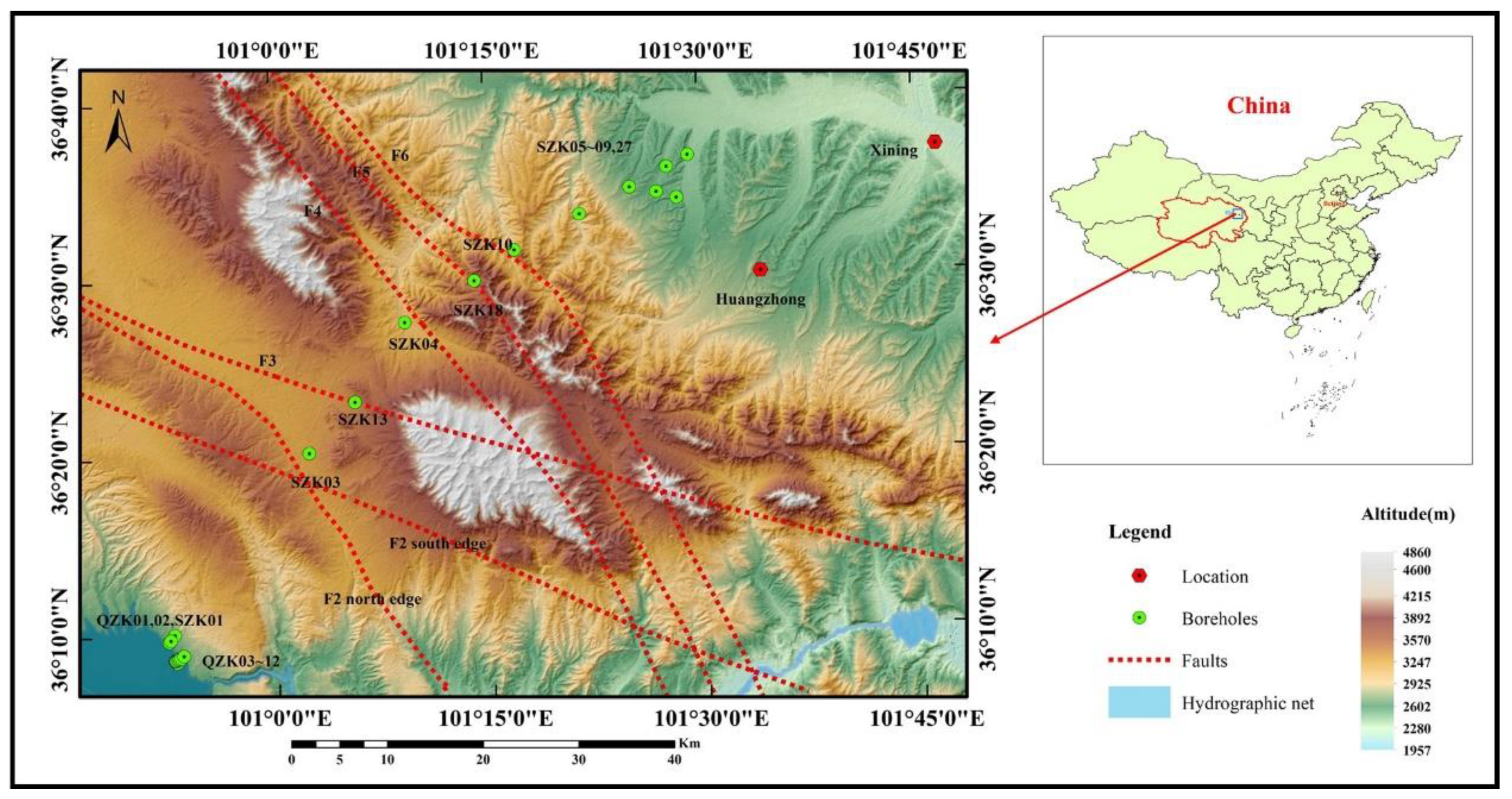
2.3. Geological Setting of Qinghai Engineering Project
3. Results and Discussions
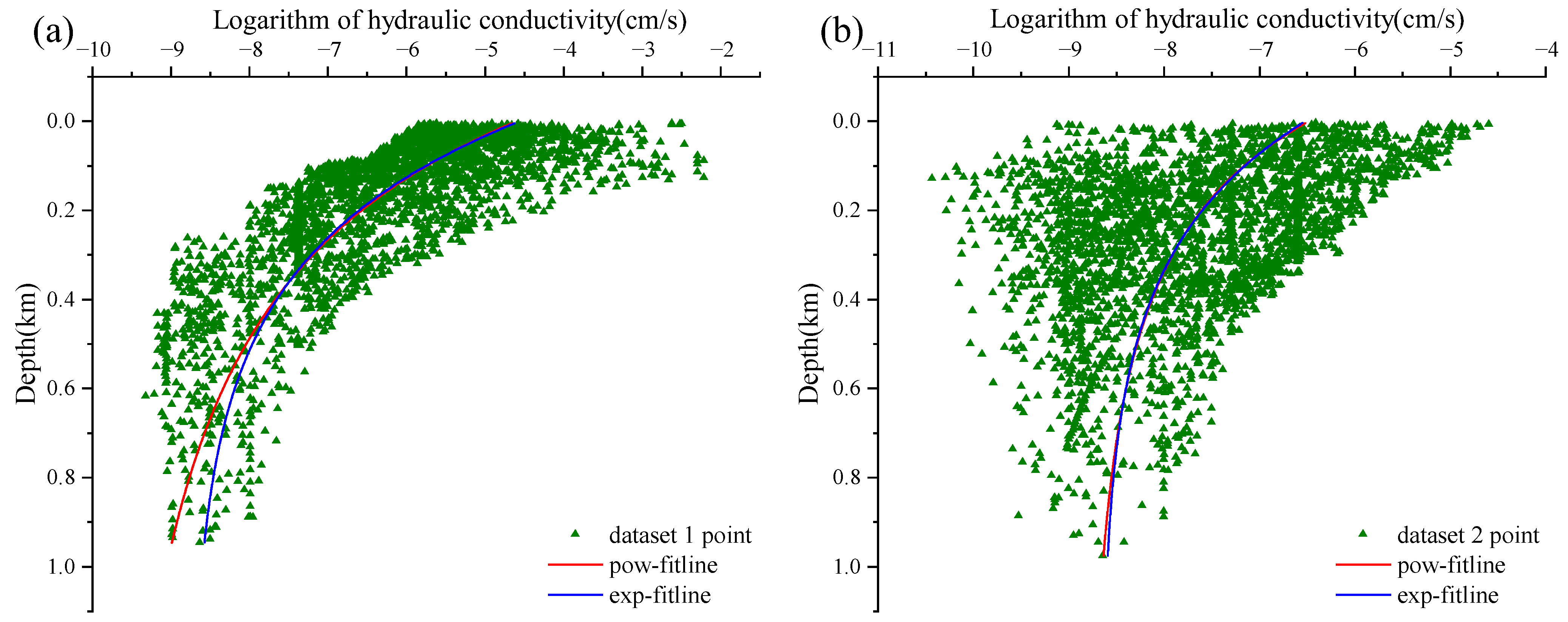
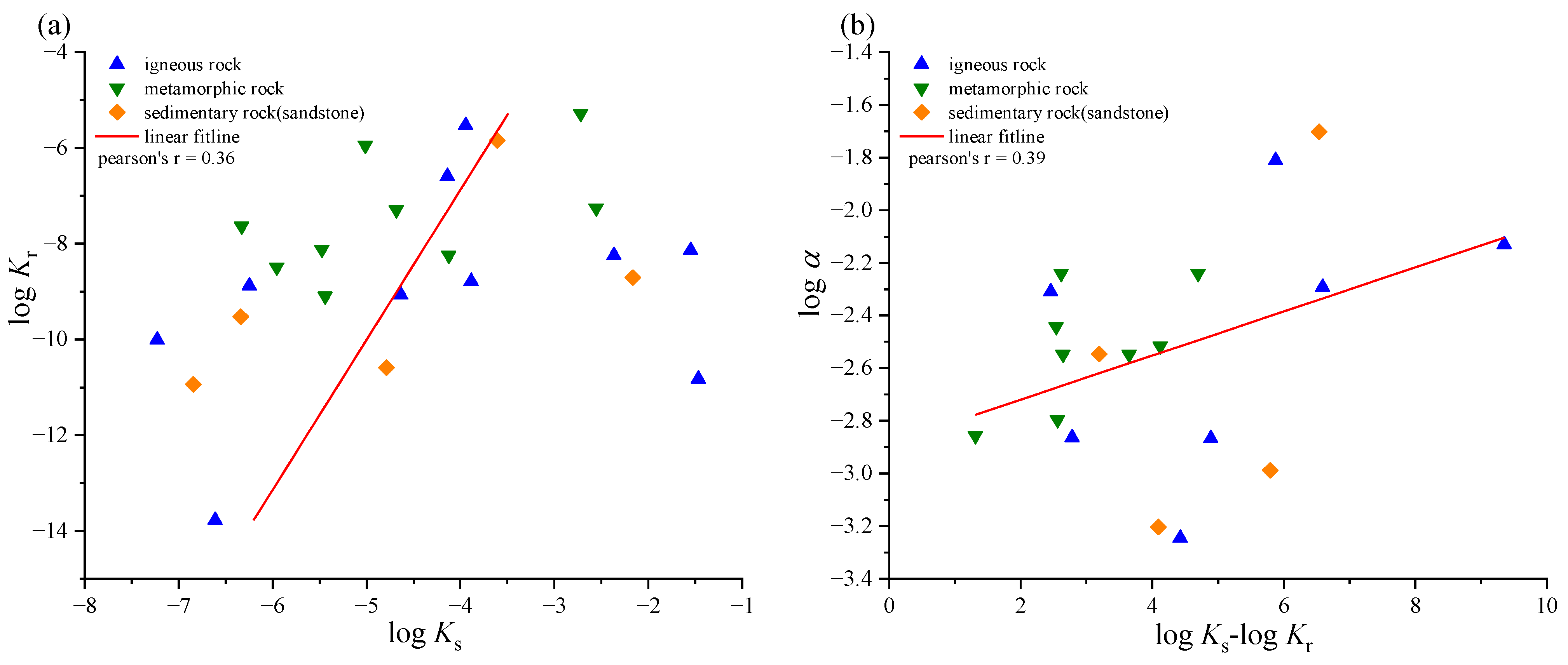
3.1. Performance of the Two Models
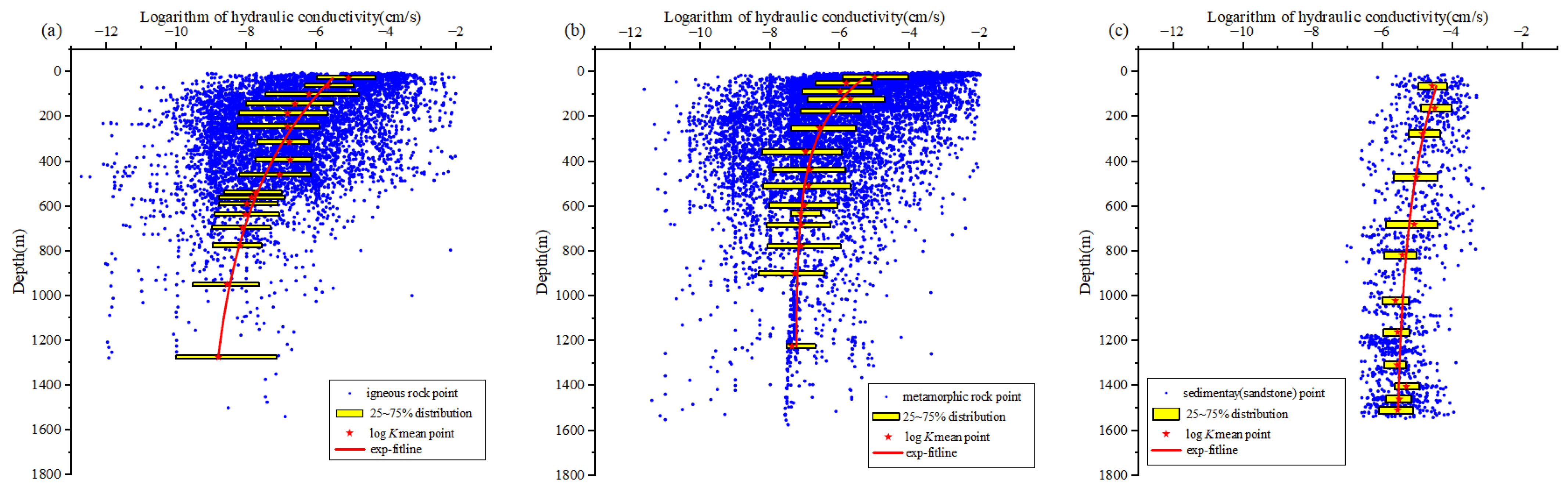
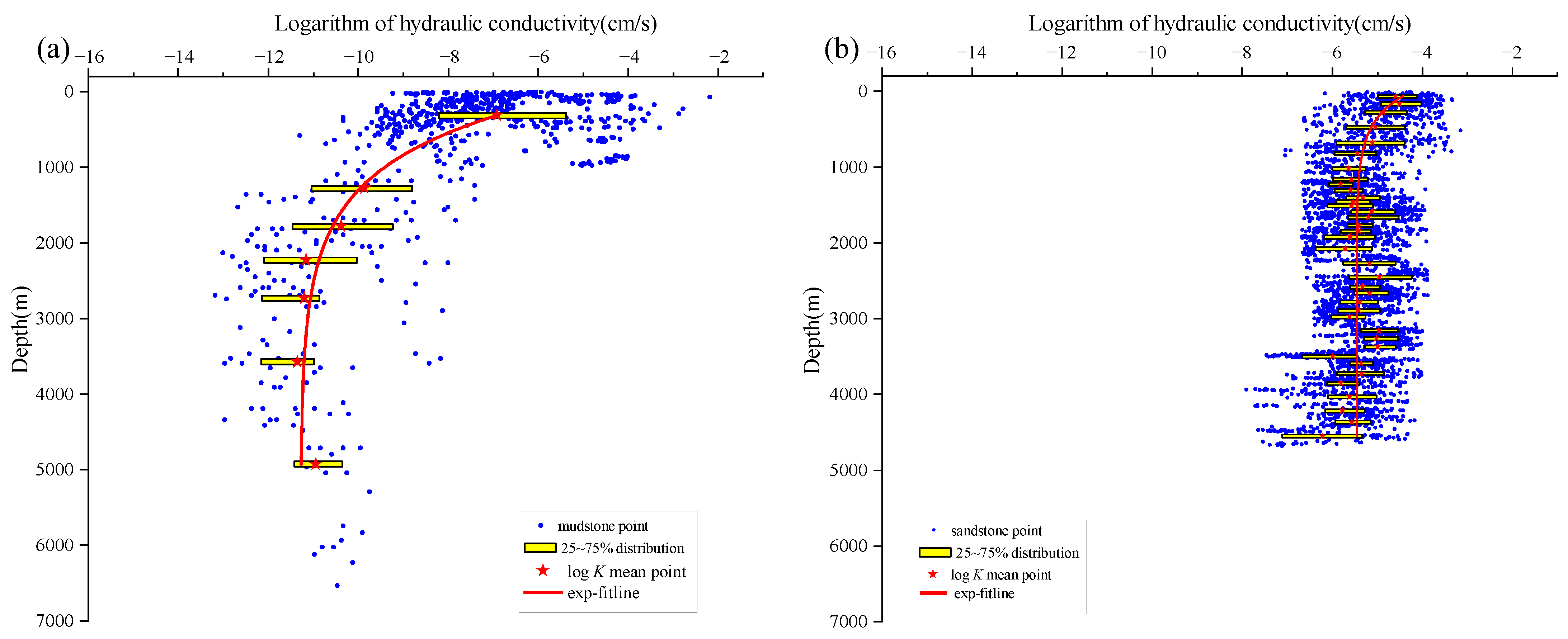
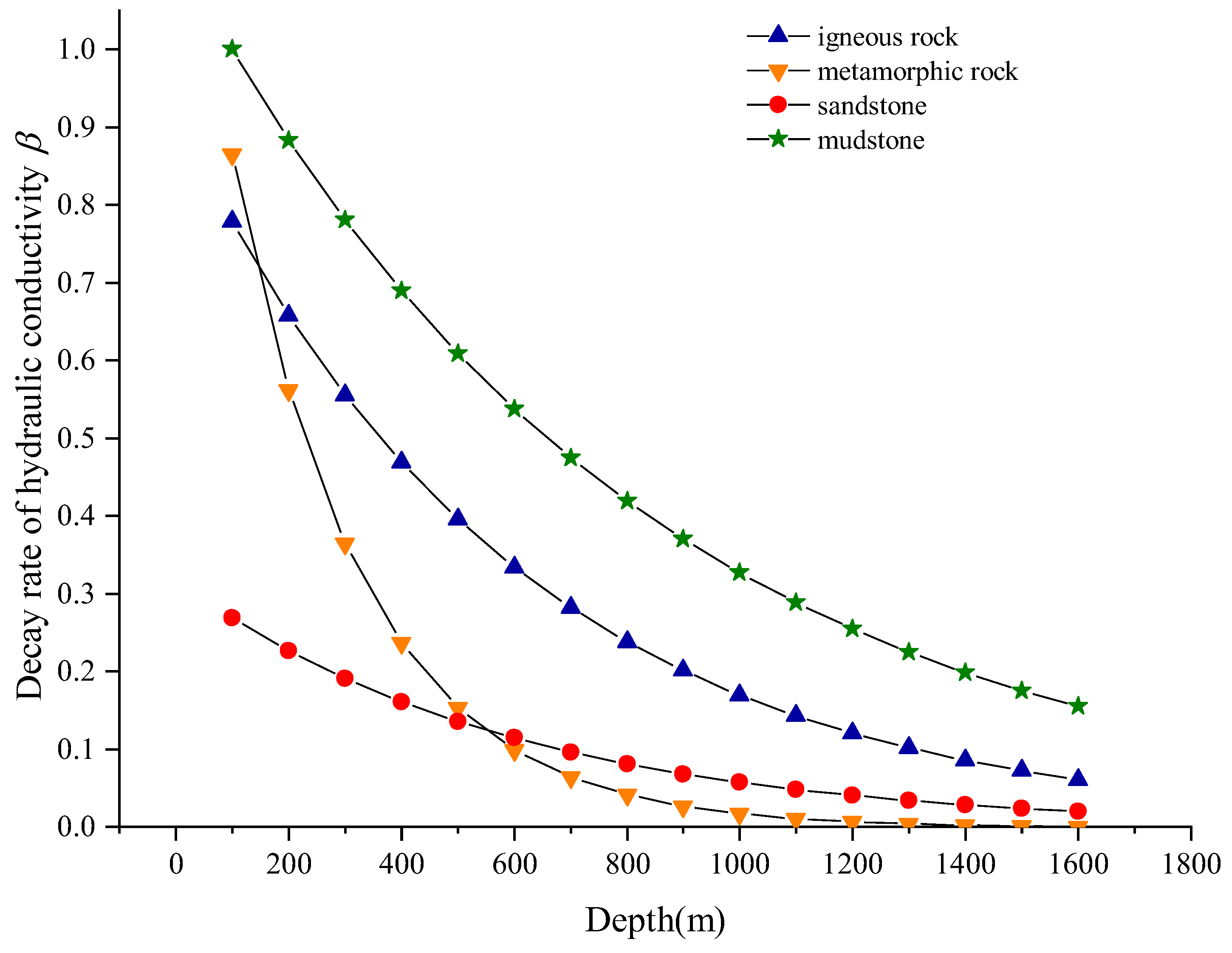
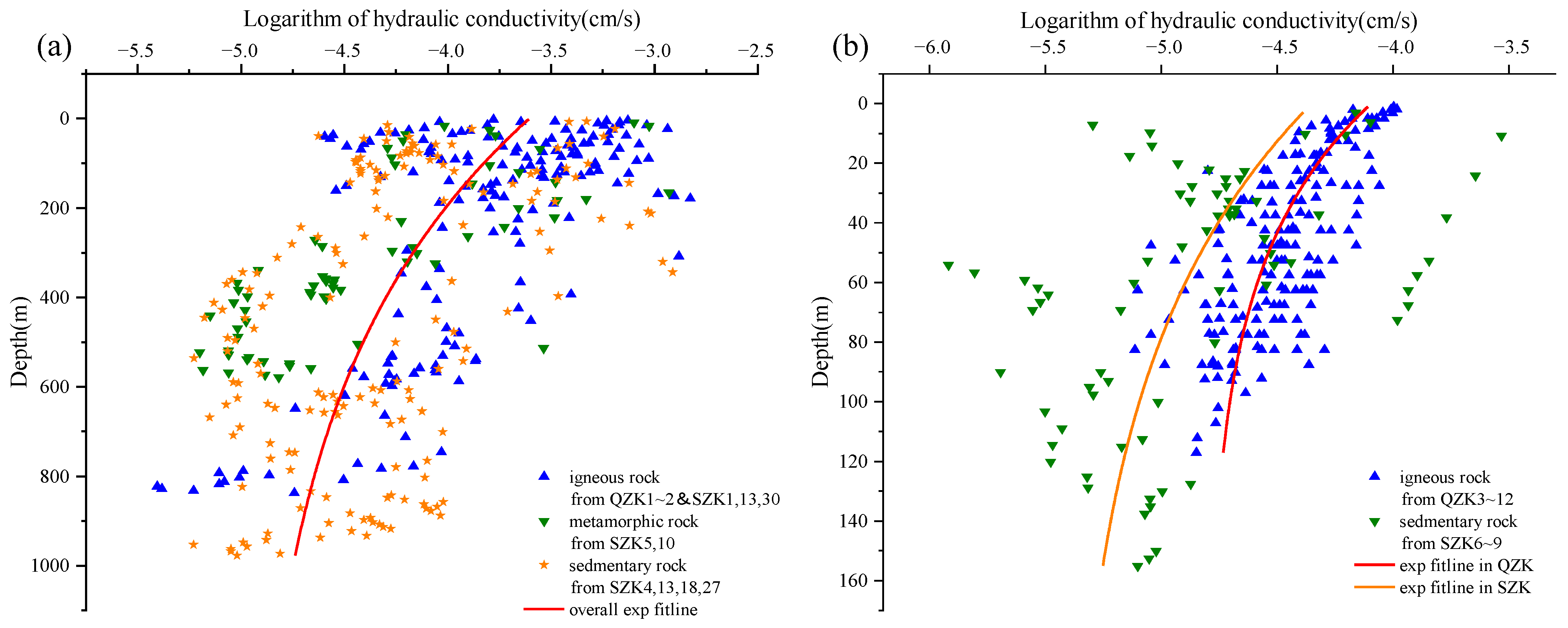
3.2. Lithology Influence on the Hydraulic Conductivity with the Exponential Model
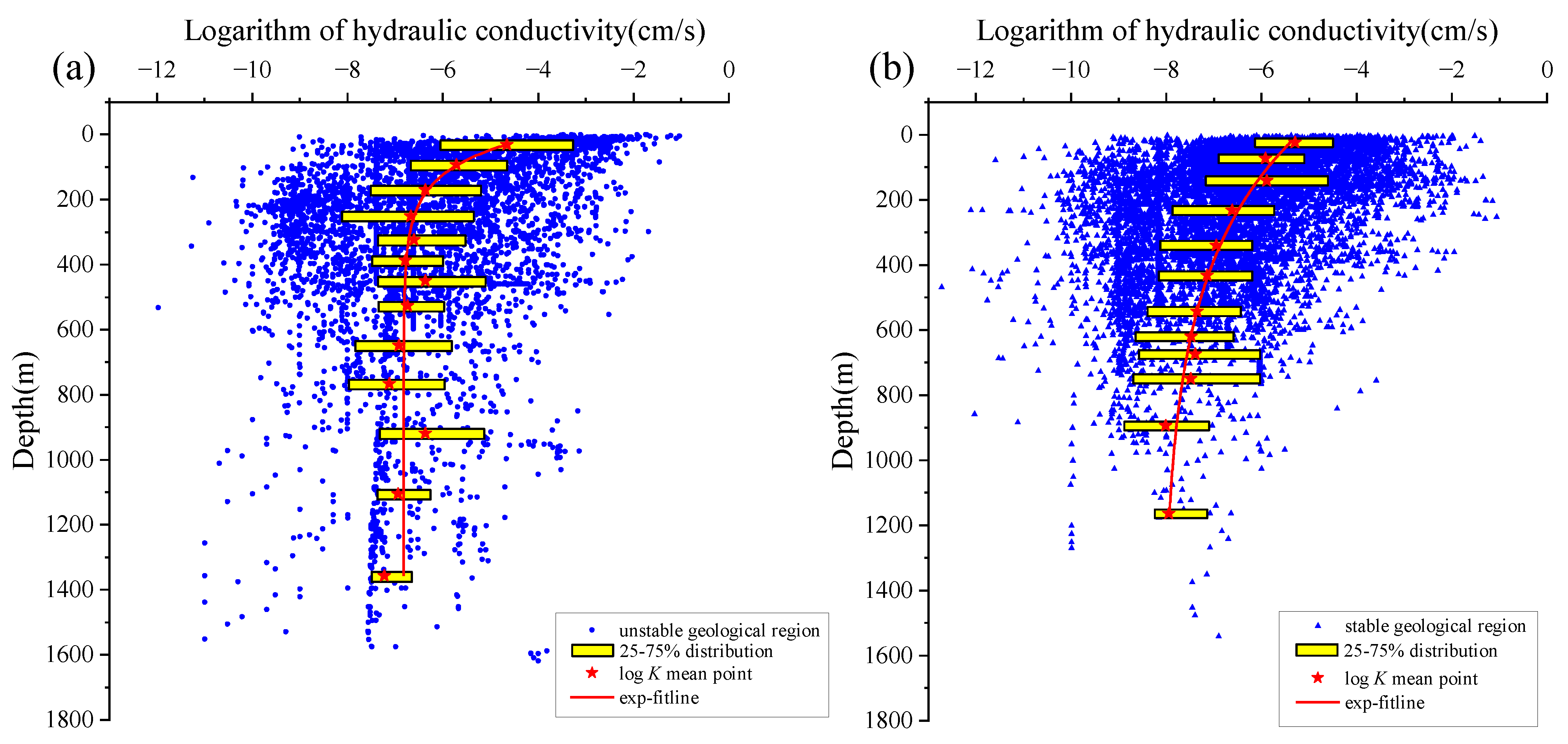
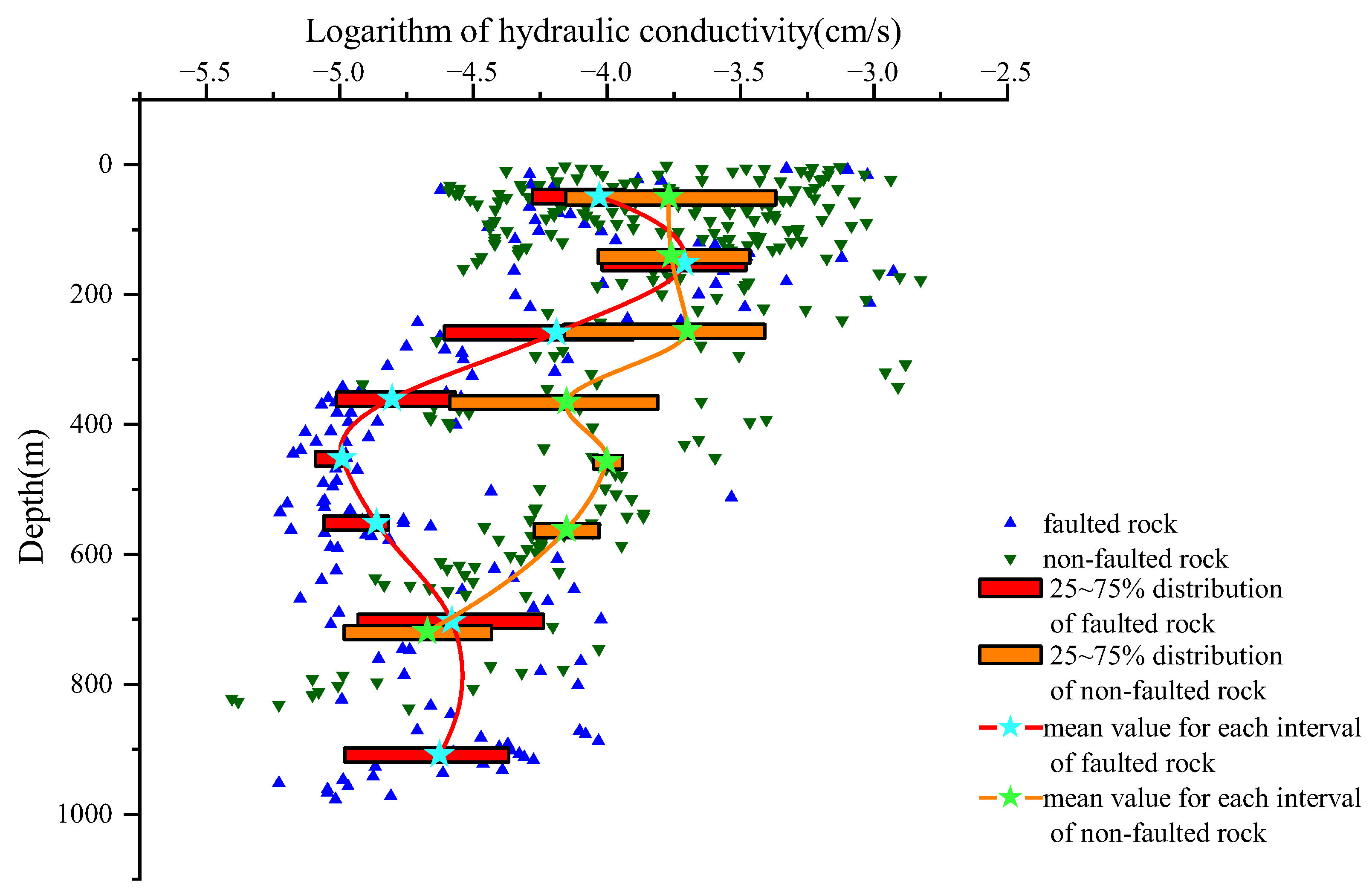
3.3. Geological Region’s Stableness, Faults’ Influence on the Hydraulic Conductivity with the Exponential Model
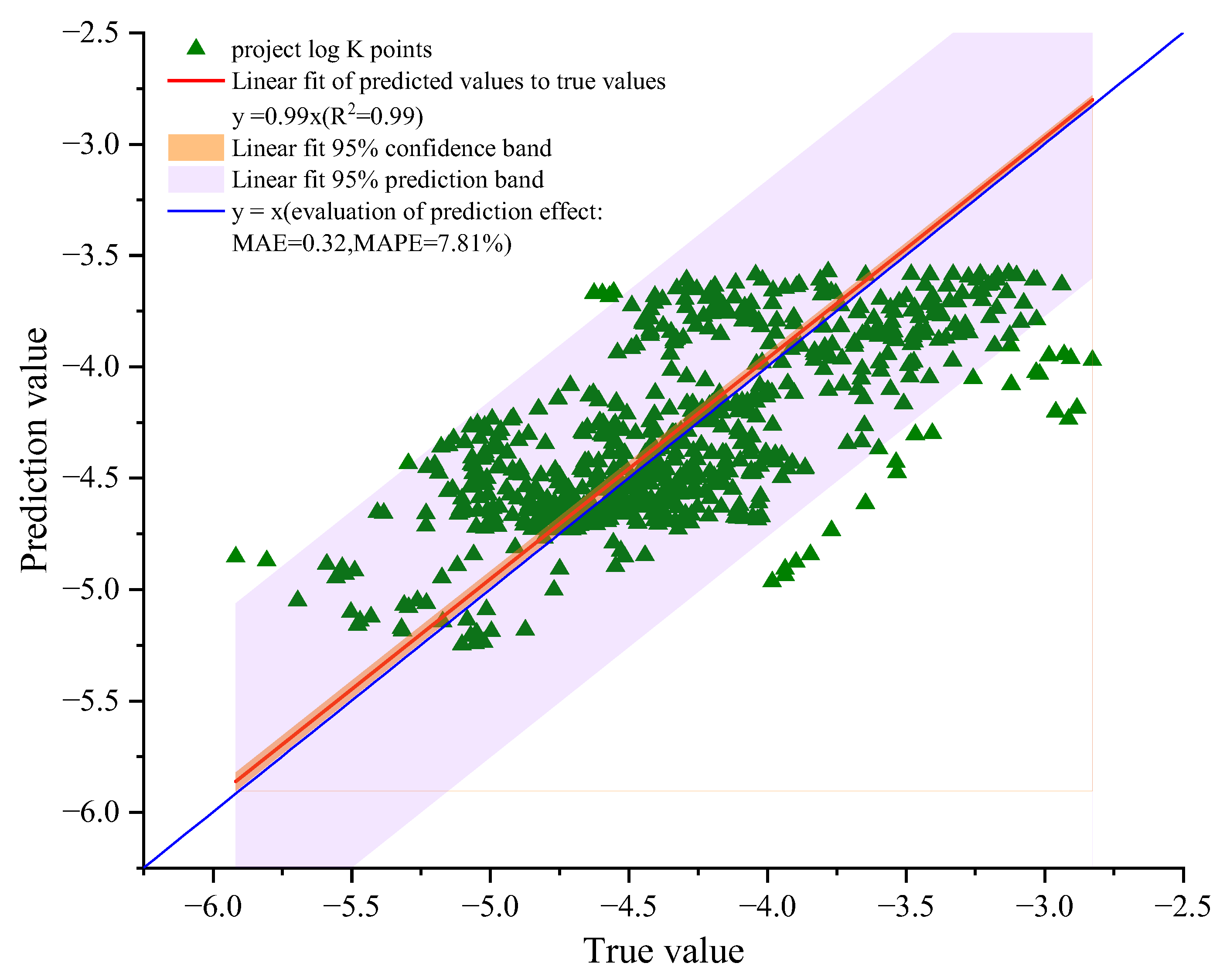
3.4. Exponential Model Application in Qinghai Engineering Project
4. Conclusions
- The proposed exponential model overcame the two main limitations of the power-like model: First, it can effectively represent residual hydraulic conductivity in specific engineering conditions. Second, it captured the fast stabilization effects of the datasets well.
- Igneous rocks, metamorphic rocks, and mudstones have a similar distribution range for Log K within a range of (−13 to −2), while the sandstone is (−7 to −3). In addition, the hydraulic conductivity decays to stability from fast to slow in the order of metamorphic rocks, sandstones, igneous rocks, and mudstones.
- Hydraulic conductivity in stable regions is approximately one-tenth of unstable regions. Faults can limit and promote seepage, with hydraulic conductivity declining through fault cores and increasing through fault damage zones.
- In the application of the exponential model to the Qinghai engineering project, the model provides an accurate prediction of hydraulic conductivities in engineering projects.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brady, B.H.G.; Brown, E.T. Rock Mass Structure. In Rock Mechanics: For Underground Mining; Springer: Dordrecht, The Netherlands, 1985; pp. 48–85. [Google Scholar]
- Hsu, S.M.; Hsu, J.P.; Ke, C.C.; Lin, Y.T.; Huang, C.C. Rock mass permeability classification schemes to facilitate groundwater availability assessment in mountainous areas: A case study in Jhuoshuei river basin of Taiwan. Geosci. J. 2020, 24, 209–224. [Google Scholar] [CrossRef]
- MacDonald, A.; Davies, J.; Dochartaigh, B.Ó. Simple methods for assessing groundwater resources in low permeability areas of Africa. Br. Geol. Surv. 2001, 168, CR/01. [Google Scholar]
- Hamill, L.; Bell, F.G. Groundwater Resource Development; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Dobson, P.F.; Kneafsey, T.J.; Hulen, J.; Simmons, A. Porosity, permeability, and fluid flow in the Yellowstone geothermal system, Wyoming. J. Volcanol. Geotherm. Res. 2003, 123, 313–324. [Google Scholar] [CrossRef]
- Murphy, H.D.; Tester, J.W.; Grigsby, C.O.; Potter, R.M. Energy extraction from fractured geothermal reservoirs in low-permeability crystalline rock. J. Geophys. Res. Solid Earth 1981, 86, 7145–7158. [Google Scholar] [CrossRef]
- Panja, P.; McLennan, J.; Green, S. Influence of permeability anisotropy and layering on geothermal battery energy storage. Geothermics 2021, 90, 101998. [Google Scholar] [CrossRef]
- Honarpour, M.M. Relative Permeability of Petroleum Reservoirs; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Subasi, A.; El-Amin, M.F.; Darwich, T.; Dossary, M. Permeability prediction of petroleum reservoirs using stochastic gradient boosting regression. J. Ambient. Intell. Humaniz. Comput. 2020, 13, 3555–3564. [Google Scholar] [CrossRef]
- You, X.; Liu, S.; Dai, C.; Guo, Y.; Zhong, G.; Duan, Y. Contaminant occurrence and migration between high-and low-permeability zones in groundwater systems: A review. Sci. Total Environ. 2020, 743, 140703. [Google Scholar] [CrossRef] [PubMed]
- Hadley, P.W.; Newell, C. The new potential for understanding groundwater contaminant transport. Groundwater 2014, 52, 174–186. [Google Scholar] [CrossRef] [PubMed]
- Nobaharan, K.; Bagheri Novair, S.; Asgari Lajayer, B.; van Hullebusch, E.D. Phosphorus Removal from Wastewater: The Potential Use of Biochar and the Key Controlling Factors. Water 2021, 13, 517. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, J.; Feng, S.J. The era of low-permeability sites remediation and corresponding technologies: A review. Chemosphere 2023, 313, 137264. [Google Scholar] [CrossRef] [PubMed]
- Armitage, P.; Worden, R.H.; Faulkner, D.R.; Butcher, A.R.; Espie, A.A. Permeability of the Mercia Mudstone: Suitability as caprock to carbon capture and storage sites. Geofluids 2016, 16, 26–42. [Google Scholar] [CrossRef]
- Cinar, Y.; Bukhteeva, O.; Neal, P.R.; Allinson, W.G.; Paterson, L. CO2 storage in low permeability formations. In SPE Improved Oil Recovery Conference? SPE: Kuala Lumpur, Malaysia, 2008. [Google Scholar]
- Tan, Y.; Nookuea, W.; Li, H.; Thorin, E.; Yan, J. Property impacts on Carbon Capture and Storage (CCS) processes: A review. Energy Convers. Manag. 2016, 118, 204–222. [Google Scholar] [CrossRef]
- Farhadi, H.; Najafzadeh, M. Flood Risk Mapping by Remote Sensing Data and Random Forest Technique. Water 2021, 13, 3115. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X.; Li, X.; Li, Z.; Sun, C. A New Quantitative Evaluation Index System for Disaster-Causing Factors of Mud Inrush Disasters in Water-Rich Fault Fracture Zone. Appl. Sci. 2023, 13, 6199. [Google Scholar] [CrossRef]
- Zhang, L. Engineering Properties of Rocks; Butterworth-Heinemann: Oxford, UK, 2016. [Google Scholar]
- Bryant, S.; Cade, C.; Mellor, D. Permeability prediction from geologic models. AAPG Bull. 1993, 77, 1338–1350. [Google Scholar]
- Louis, C. Introduction a l’hydraulique des roches [Introduction to rock hydraulics]. Bur. Rech. Géol. Min. 1974, III, 283–356. [Google Scholar]
- Piscopo, V.; Baiocchi, A.; Lotti, F.; Ayan, E.A.; Biler, A.R.; Ceyhan, A.H.; Cüylan, M.; Dişli, E.; Kahraman, S.; Taşkın, M. Estimation of rock mass permeability using variation in hydraulic conductivity with depth: Experiences in hard rocks of western Turkey. Bull. Eng. Geol. Environ. 2018, 77, 1663–1671. [Google Scholar] [CrossRef]
- Wan, L.; Jiang, X.; Wang, X. A Common Regularity of Aquifers: The Decay in Hydraulic Conductivity with Depth. Geol. J. China Univ. 2010, 16, 7–12. [Google Scholar]
- Ahlbom, K.; Albino, B.; Carlsson, L.; Danielsson, J.; Nilsson, G.; Olsson, O.; Stenberg, L. Evaluation of the Geological, Geophysical and Hydrogeological Conditions at Kamlunge; Swedish Nuclear Fuel Supply Co.: Stockholm, Sweden, 1983. [Google Scholar]
- Manning, C.E.; Ingebritsen, S.E. Permeability of the continental crust: Implications of geothermal data and metamorphic systems. Rev. Geophys. 1999, 37, 127–150. [Google Scholar] [CrossRef]
- Achtziger-Zupančič, P.; Loew, S.; Mariéthoz, G. A new global database to improve predictions of permeability distribution in crystalline rocks at site scale. J. Geophys. Res. Solid Earth 2017, 122, 3513–3539. [Google Scholar] [CrossRef]
- Chen, Y.F.; Hu, S.H.; Hu, R.; Zhou, C.B. Estimating hydraulic conductivity of fractured rocks from high-pressure packer tests with an Izbash’s law-based empirical model. Water Resour. Res. 2015, 51, 2096–2118. [Google Scholar] [CrossRef]
- Chen, Y.-F.; Ling, X.-M.; Liu, M.-M.; Hu, R.; Yang, Z. Statistical distribution of hydraulic conductivity of rocks in deep-incised valleys, Southwest China. J. Hydrol. 2018, 566, 216–226. [Google Scholar] [CrossRef]
- Stober, I.; Bucher, K. Hydraulic properties of the crystalline basement. Hydrogeol. J. 2007, 15, 213–224. [Google Scholar] [CrossRef]
- Zhang, L. Aspects of rock permeability. Front. Struct. Civ. Eng. 2013, 7, 102–116. [Google Scholar] [CrossRef]
- Wei, Z.; Hudson, J. Permeability of jointed rock masses. In ISRM International Symposium; ISRM: Lisbon, Portugal, 1988. [Google Scholar]
- Wei, Z.; Egger, P.; Descoeudres, F. Permeability predictions for jointed rock masses. In International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Kuang, X.; Jiao, J.J. An integrated permeability-depth model for Earth’s crust. Geophys. Res. Lett. 2014, 41, 7539–7545. [Google Scholar] [CrossRef]
- Asem, P.; Gardoni, P. A probabilistic, empirical model for permeability of mudstone. Probabilistic Eng. Mech. 2022, 69, 103262. [Google Scholar] [CrossRef]
- Geoprovider; Bormann, P. Porosity, Permeability, Rock Type Data from 1240 Norwegian Exploration, Appraisal and Development Wells. Core Data (2.0) [Data set]. Zenodo 2021. [Google Scholar] [CrossRef]
- Great Artesian Basin Porosity and Permeability; Geoscience Australia: Canberra, Australia, 2013. Available online: https://ecat.ga.gov.au/geonetwork/srv/eng/catalog.search#/metadata/76562 (accessed on 15 January 2024).
- Snowdon, A.P.; Normani, S.D.; Sykes, J.F. Analysis of crystalline rock permeability versus depth in a Canadian Precambrian rock setting. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020998. [Google Scholar] [CrossRef]
- Snow, D.T. Packer Injection Test Data from Sites on Fractured Rock; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 1979. [Google Scholar]
- Stevenson, D.R.; Brown, A.; Davison, C.C.; Gascoyne, M.; McGregor, R.G.; Ophori, D.U.; Tomsons, D.K. A Revised Conceptual Hydrogeologic Model of a Crystalline Rock Environment, Whiteshell Research Area, Southeastern Manitoba, Canada (No. AECL-11331); Atomic Energy of Canada Ltd.: Chalk River, ON, Canada, 1996. [Google Scholar]
- Johnson, R.L.; Glassborow, B.; Scott, M.P.; Pallikathekathil, Z.J.; Datey, A.; Meyer, J.J. Utilizing current technologies to understand permeability, stress azimuths and magnitudes and their impact on hydraulic fracturing success in a coal seam gas reservoir. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, QC, Australia, 18–20 October 2010; OnePetro: Richardson, TX, USA, 2010. [Google Scholar]
- Burger, U.; Perello, P.; Reinhardt, S.; Torri, R. Verification and Validation of Hydraulic Packer Test Results in a Deep Lying Tunnel Project. In Engineering Geology for Society and Territory-Volume 6: Applied Geology for Major Engineering Projects; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Fulton, P.M.; Harris, R.N.; Saffer, D.M.; Brodsky, E.E. Does hydrologic circulation mask frictional heat on faults after large earthquakes? J. Geophys. Res. 2010, 115, B09402. [Google Scholar] [CrossRef]
- Fisher, A.T.; Zwart, G. 15. Packer Experiments along the Décollement of the Barbados Accretionary Complex: Measurements of In Situ Permeability1. Proc. Ocean Drill. Prog. Sci. Res. 1997, 156, 199–218. [Google Scholar]
- Milnes, A.G.; Aaltonen, I.; Kemppainen, K.; Mattila, J.; Wikström, L.; Kärki, A.; Ahokas, T. Geological Data Acquisition for Site Characterisation at Olkiluoto: A Framework for the Phase of Underground Investigations; Posiva Oy: Eurajoki, Finland, 2007. [Google Scholar]
- Gale, J.E. The effects of fracture type (induced versus natural) on the stress-fracture closure-fracture permeability relationships. In ARMA US Rock Mechanics/Geomechanics Symposium; ARMA: Berkeley, CA, USA, 1982. [Google Scholar]
- Pfister, M.; Rybach, L. High-resolution digital temperature logging in areas with significant convective heat transfer. Geothermics 1995, 24, 95–100. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, H.; Ma, F.; Li, K.; Zhao, C. Investigating the permeability of fractured rock masses and the origin of water in a mine tunnel in Shandong Province, China. Water Sci. Technol. 2015, 72, 2006–2017. [Google Scholar] [CrossRef] [PubMed]
- Achtziger-Zupančič, P.; Loew, S.; Hiller, A.; Mariethoz, G. 3D fluid flow in fault zones of crystalline basement rocks (Poehla-Tellerhaeuser Ore Field, Ore Mountains, Germany). Geofluids 2016, 16, 688–710. [Google Scholar] [CrossRef]
- Ikari, M.J.; Saffer, D.M.; Marone, C. Frictional and hydrologic properties of clay-rich fault gouge. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Winkler, G.; Reichl, P. Scale dependent hydraulic investigations of faulted crystalline rocks–examples from the Eastern Alps, Austria. Fract. Rock Hydrogeol. 2014, 20, 181–196. [Google Scholar]
- MacDonald, A.M.; Taylor, R.G.; Bonsor, H.C. Groundwater in Africa: Is there sufficient water to support the intensification of agriculture from ‘land grabs’? In Handbook of Land and Water Grabs in Africa; Routledge: Abingdon, UK, 2012; pp. 376–383. [Google Scholar]
- Vandenberg, J.; Herrell, M.; Faithful, J.W.; Snow, A.M.; Lacrampe, J.; Bieber, C.; Dayyani, S.; Chisholm, V. Multiple modeling approach for the aquatic effects assessment of a proposed northern diamond mine development. Mine Water Environ. 2015, 35, 350–368. [Google Scholar] [CrossRef][Green Version]
- Achtziger-Zupančič, P.; Loew, S.; Hiller, A. Factors controlling the permeability distribution in fault vein zones surrounding granitic intrusions (Ore Mountains/Germany). J. Geophys. Res. Solid Earth 2017, 122, 1876–1899. [Google Scholar] [CrossRef]
- Wibberley, C.A.J.; Yielding, G.; Di Toro, G. Recent advances in the understanding of fault zone internal structure: A review. Geol. Soc. Lond. Spec. Publ. 2022, 299, 5–33. [Google Scholar] [CrossRef]
- Scibek, J. Global Compilation and Analysis of Fault Zone Permeability. In Department of Earth and Planetary Sciences; McGill University: Montréal, QC, USA, 2019. [Google Scholar]
- He, M.; Zhang, Z.; Zhu, J.; Li, N.; Li, G.; Chen, Y. Correlation between the rockburst proneness and friction characteristics of rock materials and a new method for rockburst proneness prediction: Field demonstration. J. Pet. Sci. Eng. 2021, 205, 108997. [Google Scholar] [CrossRef]
- He, M.; Ding, M.; Yuan, Z.; Zhao, J.; Luo, B.; Ma, X. Numerical simulation of rock bursts triggered by blasting disturbance for deep-buried tunnels in jointed rock masses. Comput. Geotech. 2023, 161, 105609. [Google Scholar] [CrossRef]
- Wu, K.; He, M.; Yuan, Z.; Liu, X.; Luo, B.; Ma, X.; Ma, C. Characterizing rock transverse anisotropic spatial variations using digital drilling. Geoenergy Sci. Eng. 2024, 232, 212451. [Google Scholar] [CrossRef]

| Model Name | Model Formula | Parameter Significance |
|---|---|---|
| The linear model [21,22,23,24] | Ks refers to the hydraulic conductivity at the depth of 0 (refer to surface hydraulic conductivity), α is the decay coefficient, and z is the depth. | |
| The logarithmic model [26,27,28,29,30] | Ks refers to the hydraulic conductivity at a depth of 1 km (refer to surface hydraulic conductivity), α is the decay coefficient, and z is the depth. | |
| The power-like model [33] | Ks refers to the hydraulic conductivity at the depth of 0 (referring to surface hydraulic conductivity), Kr is the residual hydraulic conductivity at depths exceeding the study area, α is the decay coefficient, and z is the depth. | |
| Other models [31,32] | Ks is the surface hydraulic conductivity and z is the depth. The remaining parameters do not have physical meaning that can be directly correlated to hydrological properties. |
| Groups | Sub-Dataset | Description | Source | |
|---|---|---|---|---|
| Lithology | 1. Igneous | Granite, granodiorite, and diorite Location: Europe, Asia, North America Z (0, 1600 m) | Snow [38]; Stevenson [39] Li Wan [23]; Yi Feng Chen [28]; Achtziger [26] | |
| 2. Metamorphic | Quartzite, marble, gneiss, and amphibolite Location: Europe, Asia, North America Z (0, 1600 m) | P. Snowdon [37]; Burger [41]; Achtziger [26] | ||
| Sedimentary | 3. Sandstone | Location: Norway, Australia, China Z (0, 5000 m) | Pouyan [34]; Geoprovider [35]; Geoscience Australia [36] | |
| 4. Mudstone | Location: Alpine Basin, China, Japan Z (0, 7000 m) | Saffer [49]; Fisher [43]; Pouyan [34] | ||
| Geological | 1. Stable | Cratons, Shields, located in Europe, Asia, North America Z (0, 1600 m) | Gale [45]; Macdonald [51]; Achtziger [26,48] | |
| 2. Unstable | Volcanic arcs, Rift Valleys, Ophiolite mafic belts, located in Europe, Asia, North America Z (0, 1600 m) | Pfister [46]; Zhao [47]; Achtziger [26,53] | ||
| Fault Presence | 1. Faulted | A fault passes through or near a rock mass, located in Europe, Asia, North America Z (0, 1200 m) | Winkler [50]; Zhao [47]; Achtziger [26,53] | |
| 2. Non-Faulted | A complete rock mass that has not been crossed by a fault, located in Europe, Asia, North America Z (0, 1400 m) | Macdonald [51]; Vandenberg [52]; Achtziger [26] | ||
| Dataset | True Log Kr | Log Kre | Log Krp | Ie | Ip |
|---|---|---|---|---|---|
| 1 | −8.51 | −8.60 | −9.05 | 0.09 | 0.54 |
| 2 | −8.73 | −8.66 | −8.85 | 0.07 | 0.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, Z.; Huang, X.; Wan, W.; Zeng, F.; Wang, C. Development and Application of a New Exponential Model for Hydraulic Conductivity with Depth of Rock Mass. Water 2024, 16, 778. https://doi.org/10.3390/w16050778
Dou Z, Huang X, Wan W, Zeng F, Wang C. Development and Application of a New Exponential Model for Hydraulic Conductivity with Depth of Rock Mass. Water. 2024; 16(5):778. https://doi.org/10.3390/w16050778
Chicago/Turabian StyleDou, Zhi, Xin Huang, Weifeng Wan, Feng Zeng, and Chaoqi Wang. 2024. "Development and Application of a New Exponential Model for Hydraulic Conductivity with Depth of Rock Mass" Water 16, no. 5: 778. https://doi.org/10.3390/w16050778
APA StyleDou, Z., Huang, X., Wan, W., Zeng, F., & Wang, C. (2024). Development and Application of a New Exponential Model for Hydraulic Conductivity with Depth of Rock Mass. Water, 16(5), 778. https://doi.org/10.3390/w16050778






