An Improved One-Line Evolution Formulation for the Dynamic Shoreline Planforms of Embayed Beaches
Abstract
1. Introduction
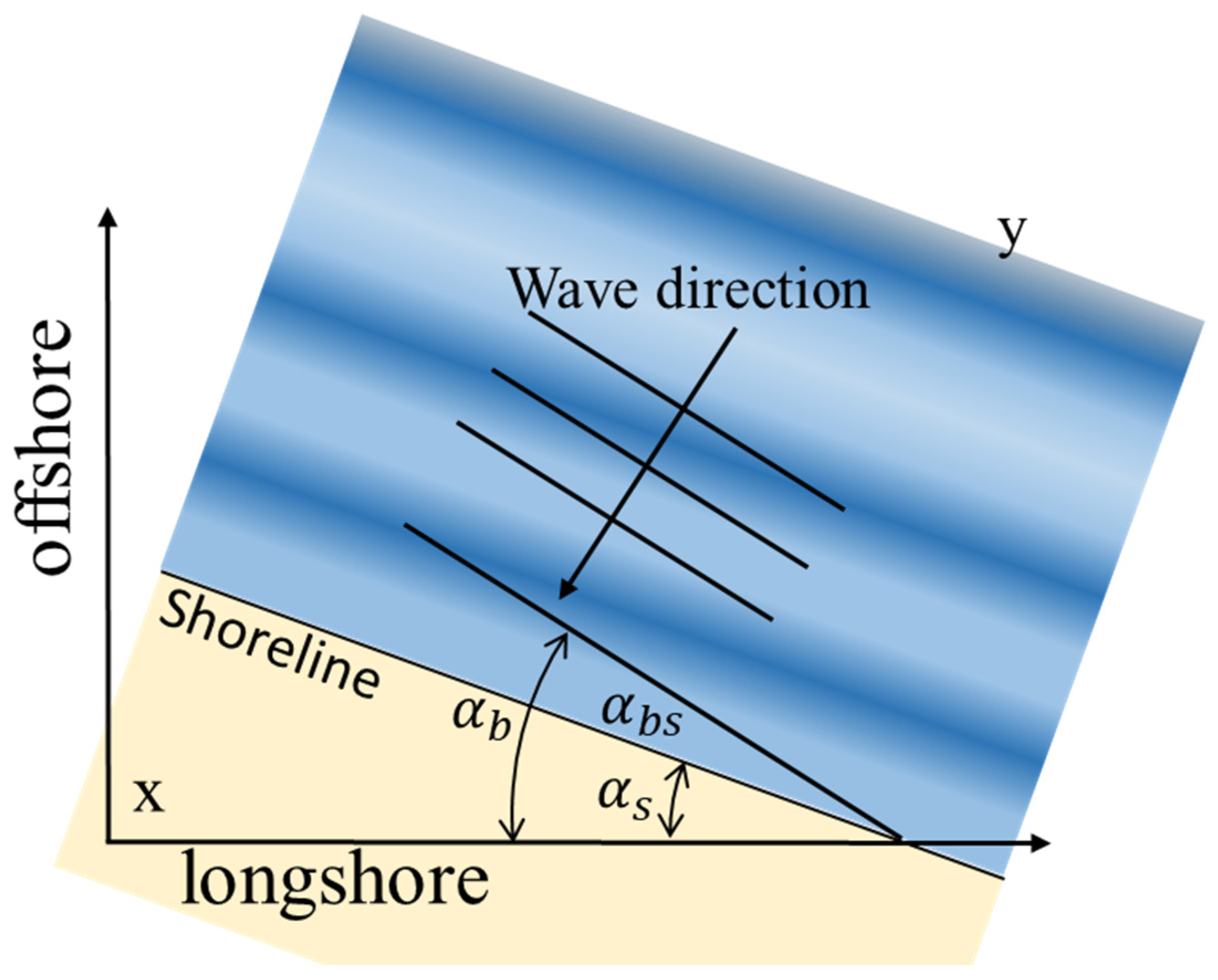
2. Shoreline Model for Dynamic Planforms
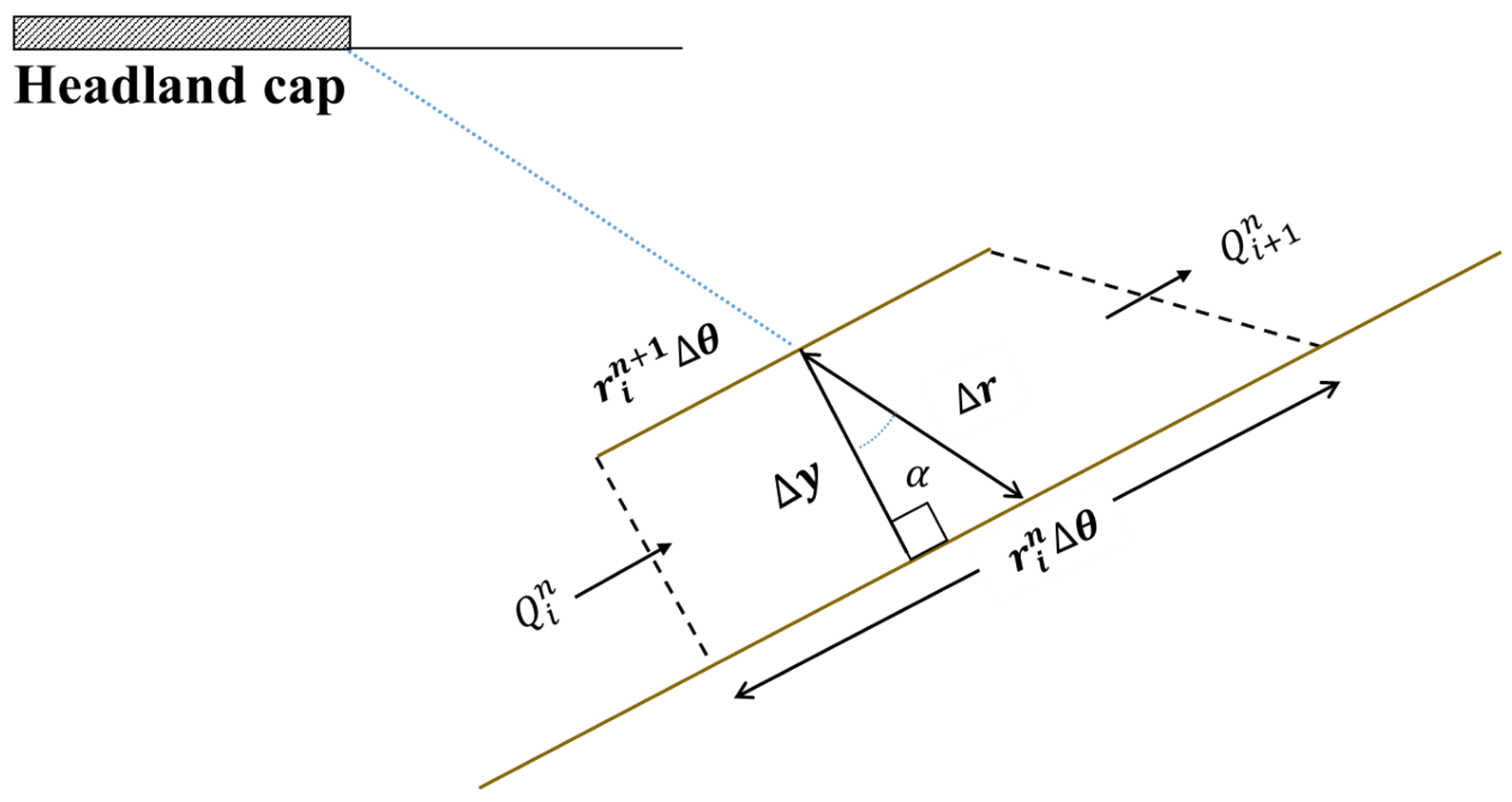
2.1. The Proposed Improved Evolution Formulation
- The shape of the beach profile remains constant.
- The shoreward and seaward depth limits of the profile are constant; meanwhile, sand is transported alongshore via the action of breaking waves.
- The detailed structure of nearshore circulation is ignored.
- There is a long-term trend in shoreline evolution.
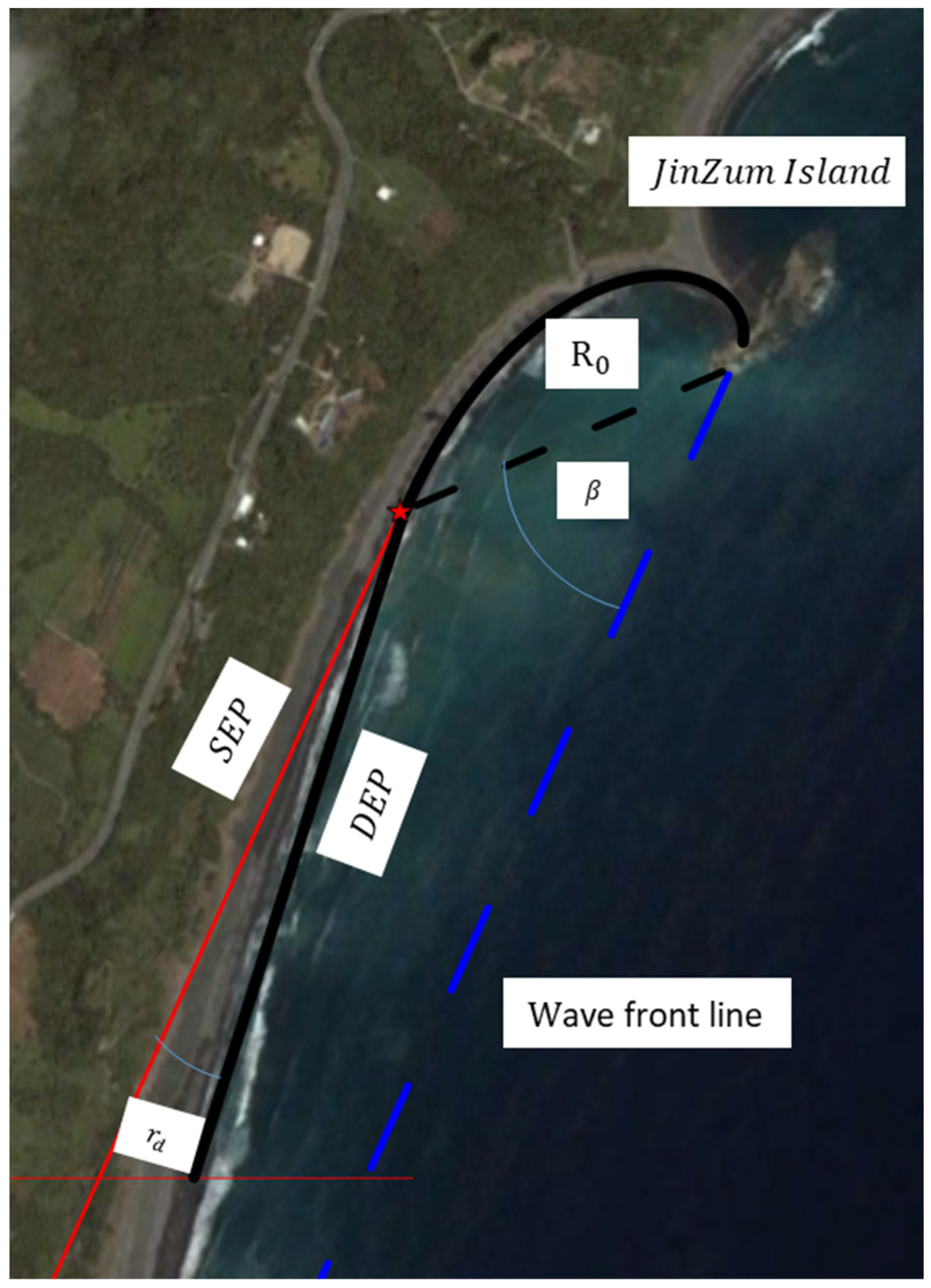
2.2. Dynamic Equilibrium Planform (DEP)
2.3. GenCade [23]
3. Verification of the Proposed Improved Model
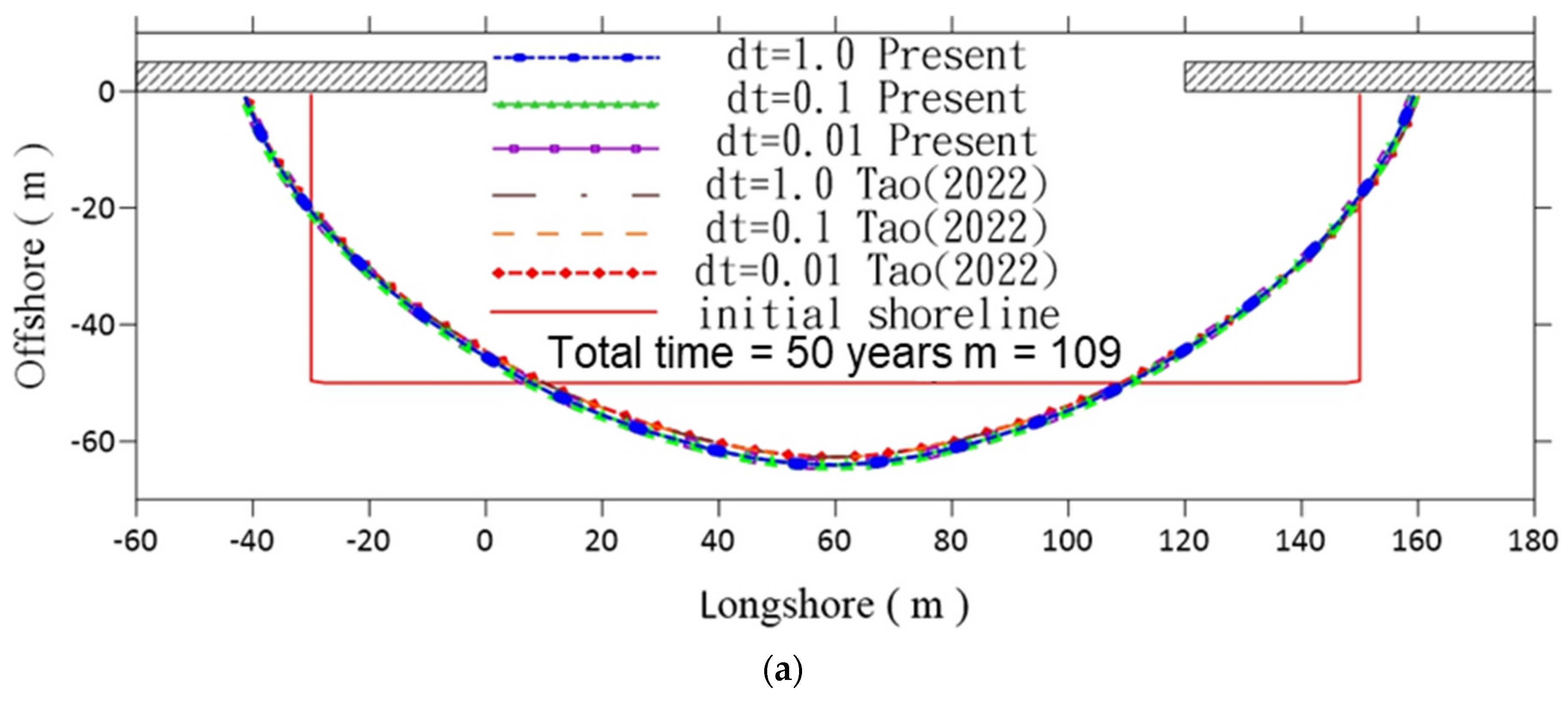
3.1. Example 1: Stability and Consistency
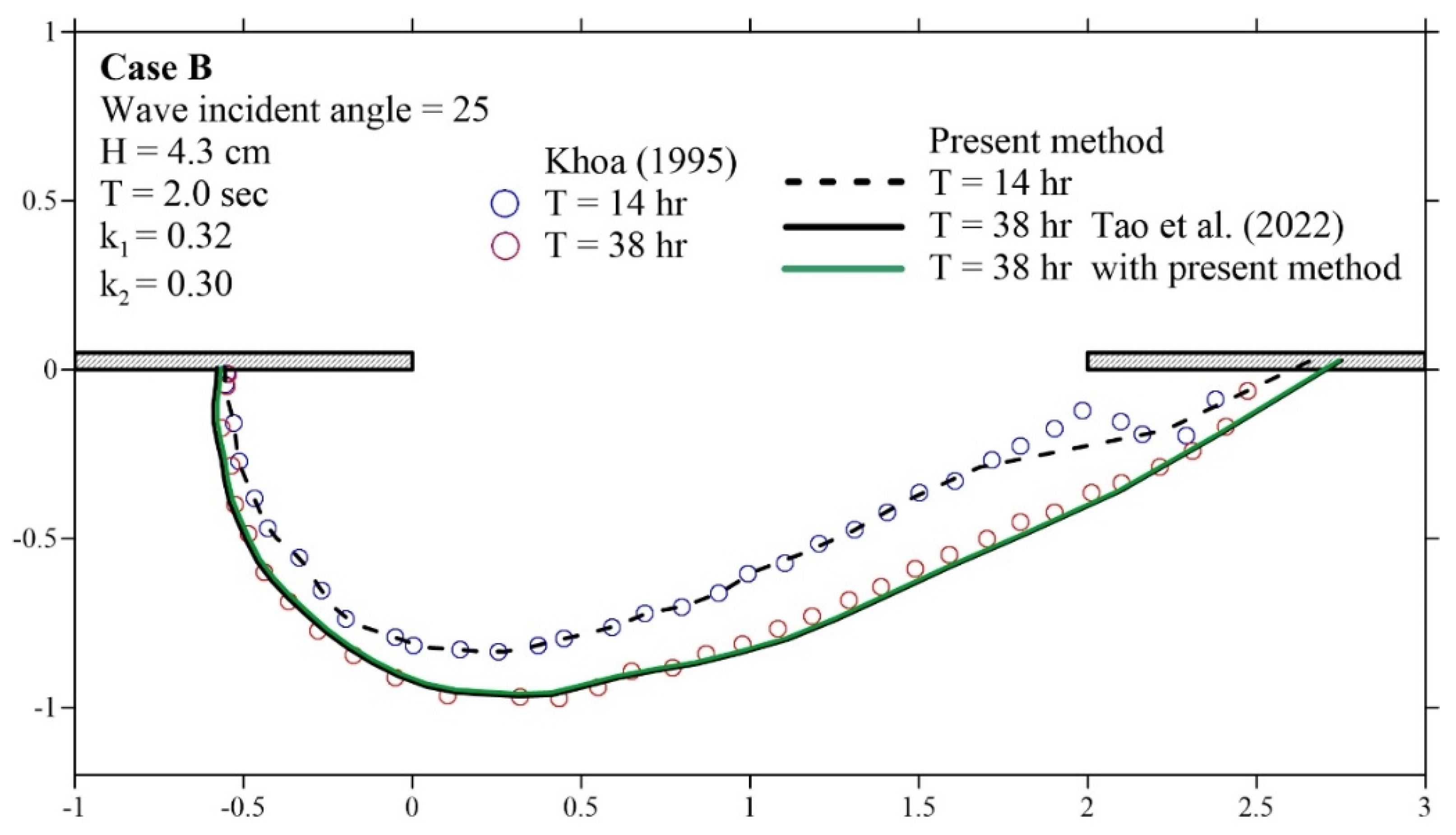
3.2. Example 2: Verification with Experimental Data
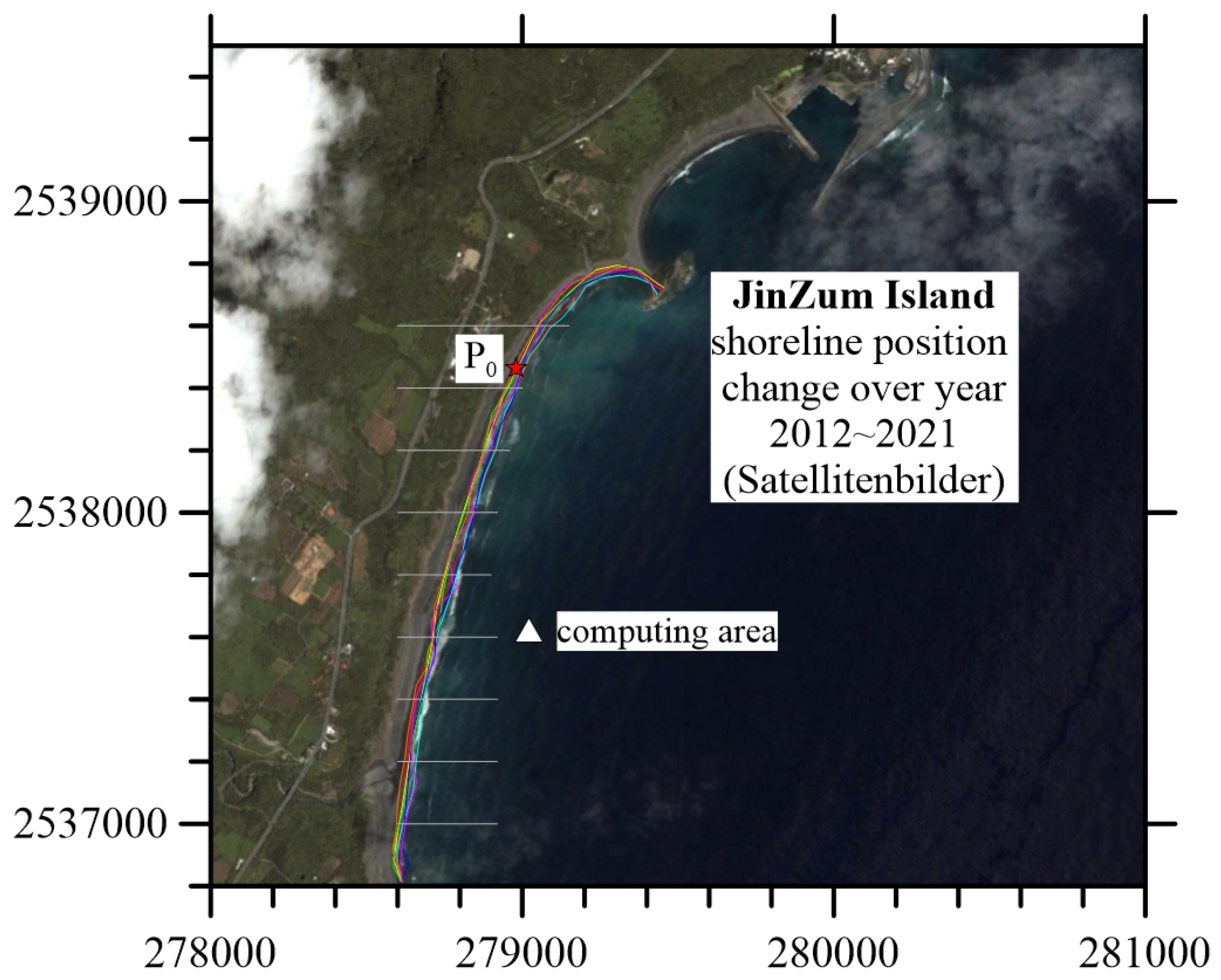
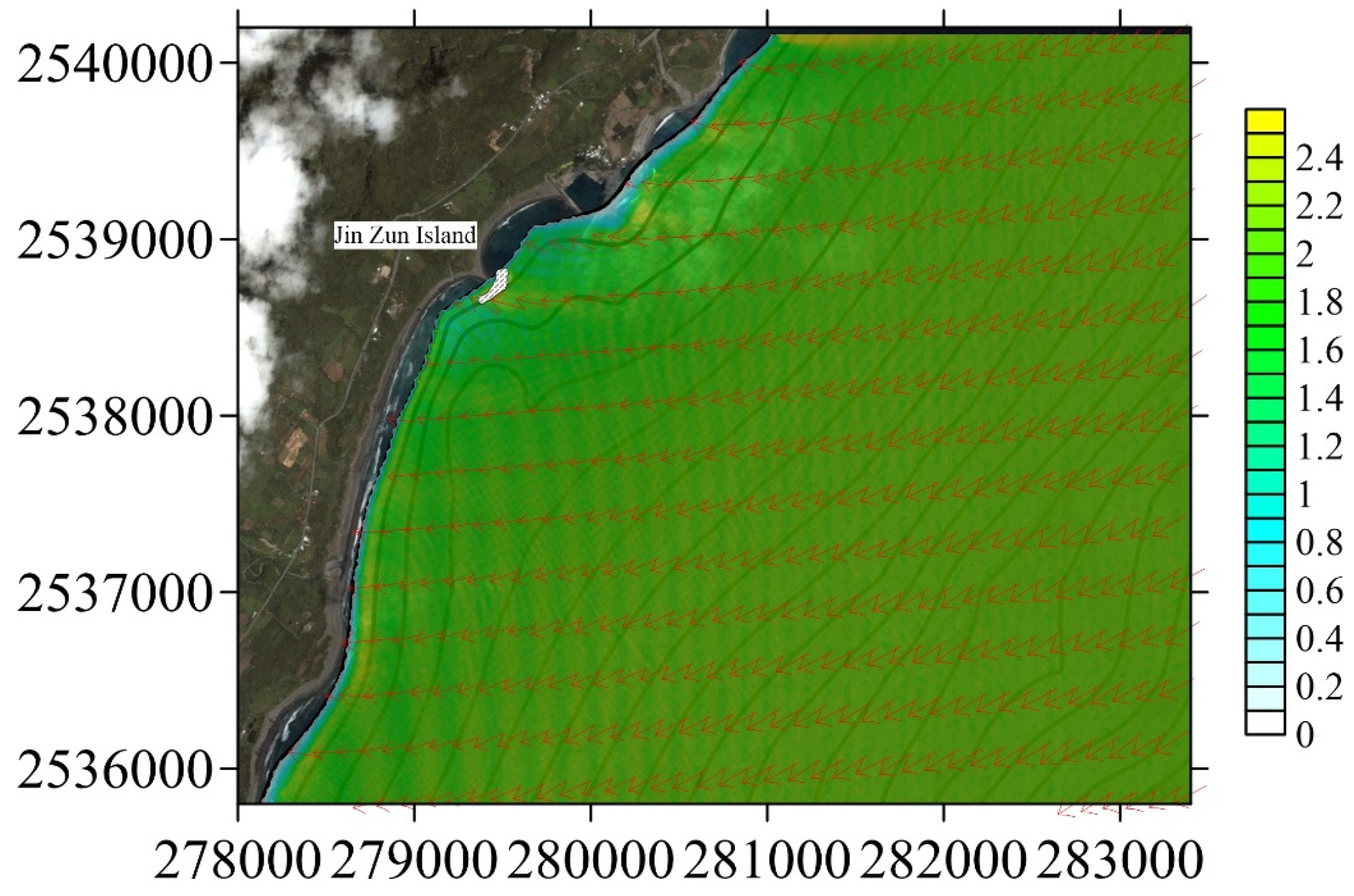
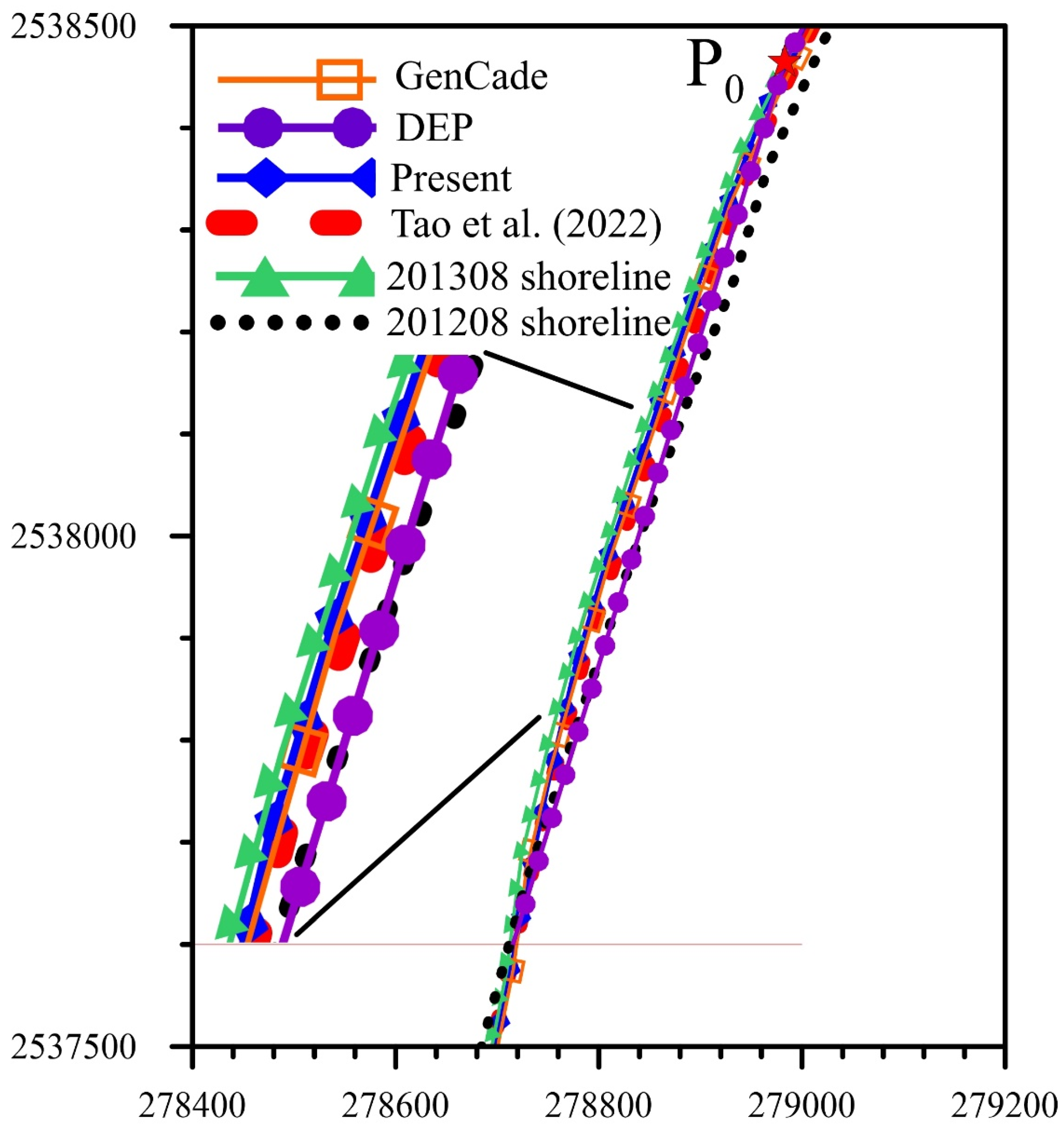
4. Engineering Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Safari, M.D. A short review of submerged breakwaters. In Proceedings of the MATEC Web of Conferences, Malang, Indonesia, 30–31 August 2018; p. 01005. [Google Scholar]
- Skaggs, L.L.; McDonald, F.L. National Economic Development Procedures Manual. Coastal Storm Damage and Erosion; Army Engineer Inst for Water Resources Alexandria Va (USA): Alexandria, VA, USA, 1991. [Google Scholar]
- Lin, T.; Van Onselen, V.; Vo, L. Coastal erosion in Vietnam: Case studies and implication for integrated coastal zone management in the Vietnamese south-central coastline. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Surakarta, Indonesia, 24–25 August 2021; p. 012009. [Google Scholar]
- Özölçer, İ.H.; Kömürcü, M.İ.; Birben, A.R.; Yüksek, Ö.; Karasu, S. Effects of T-shape groin parameters on beach accretion. Ocean Eng. 2006, 33, 382–403. [Google Scholar] [CrossRef]
- Liang, T.-Y.; Chang, C.-H.; Hsiao, S.-C.; Huang, W.-P.; Chang, T.-Y.; Guo, W.-D.; Liu, C.-H.; Ho, J.-Y.; Chen, W.-B. On-Site Investigations of Coastal Erosion and Accretion for the Northeast of Taiwan. J. Mar. Sci. Eng. 2022, 10, 282. [Google Scholar] [CrossRef]
- Putro, A.H.S.; Lee, J.L. Analysis of longshore drift patterns on the littoral system of nusa dua beach in bali, indonesia. J. Mar. Sci. Eng. 2020, 8, 749. [Google Scholar] [CrossRef]
- Hsu, J.R.C.; Evans, C. Parabolic Bay Shapes and Applications. Proc. Inst. Civ. Eng. 1989, 87, 557–570. [Google Scholar] [CrossRef]
- Yasso, W.E. Plan geometry of headland-bay beaches. J. Geol. 1965, 73, 702–714. [Google Scholar] [CrossRef]
- Hsu, J.R.; Silvester, R.; Xia, Y.-M. Applications of headland control. J. Waterw. Port Coast. Ocean Eng. 1989, 115, 299–310. [Google Scholar] [CrossRef]
- Pelnard-Considère, R. Essai de theorie de l’evolution des formes de rivage en plages de sable et de galets. Journ. Hydraul. 1957, 4, 289–298. [Google Scholar]
- Francone, A.; Simmonds, D.J. Assessing the Reliability of a New One-Line Model for Predicting Shoreline Evolution with Impoundment Field Experiment Data. J. Mar. Sci. Eng. 2023, 11, 1037. [Google Scholar] [CrossRef]
- Hanson, H. GENESIS: A generalized shoreline change numerical model. J. Coast. Res. 1989, 5, 1–27. [Google Scholar]
- Weesakul, S.; Tasaduak, S. Experimental investigation on dynamic equilibrium bay shape. Coast. Eng. 2012, 2, 1–13. [Google Scholar] [CrossRef]
- Tao, H.-C.; Hsu, T.-W.; Fan, C.-M. Developments of Dynamic Shoreline Planform of Crenulate-Shaped Bay by a Novel Evolution Formulation. Water 2022, 14, 3504. [Google Scholar] [CrossRef]
- Ozasa, H.; Brampton, A. Mathematical modelling of beaches backed by seawalls. Coast. Eng. 1980, 4, 47–63. [Google Scholar] [CrossRef]
- Kraus, N.C.; Harikai, S. Numerical model of the shoreline change at Oarai Beach. Coast. Eng. 1983, 7, 1–28. [Google Scholar] [CrossRef]
- Weesakul, S.; Rasmeemasmuang, T.; Tasaduak, S.; Thaicharoen, C. Numerical modeling of crenulate bay shapes. Coast. Eng. 2010, 57, 184–193. [Google Scholar] [CrossRef]
- Tan, S.-K.; Chiew, Y.-M. Analysis of bayed beaches in static equilibrium. J. Waterw. Port Coast. Ocean Eng. 1994, 120, 145–153. [Google Scholar] [CrossRef]
- Tan, S.; Chiew, Y. Bayed beaches in dynamic equilibrium. Adv. Hydro-Sci. Eng. I 1993, 1737–1742. [Google Scholar]
- Elshinnawy, A.I.; Medina, R.; González, M. Dynamic equilibrium planform of embayed beaches: Part 1. A new model and its verification. Coast. Eng. 2018, 135, 112–122. [Google Scholar] [CrossRef]
- Elshinnawy, A.I.; Medina, R.; González, M. Dynamic equilibrium planform of embayed beaches: Part 2. Design procedure and engineering applications. Coast. Eng. 2018, 135, 123–137. [Google Scholar] [CrossRef]
- Frey, A.E.; Connell, K.J.; Hanson, H.; Larson, M.; Thomas, R.C.; Munger, S.; Zundel, A. GenCade Version 1 Model Theory and User’s Guide; U.S. Army Engineer Research and Development Center, Coastal and Hydraulics Laboratory: Vicksburg, MS, USA, 2012. [Google Scholar]
- Hsu, T.-W.; Wen, C.-C. A parabolic equation extended to account for rapidly varying topography. Ocean Eng. 2001, 28, 1479–1498. [Google Scholar] [CrossRef]
- Hsu, T.-W.; Wen, C.-C. On radiation boundary conditions and wave transformation across the surf zone. China Ocean Eng. 2001, 15, 395–406. [Google Scholar]
- Khoa, V. Experimentation on Bayed Beaches between Headlands for Small Wave Angle. Master’s Thesis, Asian Institute of Technology, Bangkok, Thailand, 1995. Volume 10. 90p. [Google Scholar]








| Parameters | Case B [25] |
|---|---|
| Incident wave angle (degree) | 25 |
| Wave height (cm) | 4.3 |
| Wave period (s) | 2.0 |
| Water depth at generator (cm) | 20 |
| Median grain size, (mm) | 0.3 |
| Initial beach slope | 1.4 |
| Running time (h) | 24 |
| Cross-Section | 2,538,600 | 2,538,400 | 2,538,200 | 2,538,000 | 2,537,800 | 2,537,600 | 2,537,400 | 2,537,200 | |
|---|---|---|---|---|---|---|---|---|---|
| Date | |||||||||
| Aug-12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Jun-13 | −15.32 | −25.45 | −21.62 | −13.74 | −15.96 | −6.79 | 1.85 | −8.59 | |
| Aug-13 | −33.53 | −31.52 | −36.50 | −30.07 | −22.88 | 1.11 | 14.79 | 6.66 | |
| Dec-13 | −11.92 | −12.17 | −36.00 | −36.27 | −4.36 | −4.75 | 2.15 | 12.08 | |
| Jul-14 | −13.74 | −28.94 | −36.24 | −26.78 | −16.24 | 3.72 | 18.26 | 14.09 | |
| Jul-16 | 11.76 | 0.31 | 0.43 | 3.98 | 16.12 | 14.76 | 24.61 | 29.54 | |
| Jun-17 | −16.59 | −2.87 | −12.42 | 5.24 | 9.83 | 9.58 | 16.21 | 10.02 | |
| Jan-18 | −32.12 | −7.04 | −17.19 | 5.75 | 0.99 | −1.46 | −3.16 | 15.67 | |
| Dec-18 | −49.04 | −21.25 | −34.72 | −8.87 | −1.09 | 1.54 | 4.42 | 13.25 | |
| Apr-21 | −56.51 | −62.86 | −72.43 | −40.74 | −28.78 | −16.10 | 3.70 | −14.04 | |
| Jul-21 | −37.63 | −37.48 | −39.46 | −14.68 | −25.85 | 4.16 | −8.15 | −8.93 | |
| Shoreline change rate (m/year) | −4.02 | −2.45 | −3.03 | −0.03 | −0.71 | −0.025 | −0.70 | −0.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, H.-C.; Hsu, T.-W.; Fan, C.-M. An Improved One-Line Evolution Formulation for the Dynamic Shoreline Planforms of Embayed Beaches. Water 2024, 16, 774. https://doi.org/10.3390/w16050774
Tao H-C, Hsu T-W, Fan C-M. An Improved One-Line Evolution Formulation for the Dynamic Shoreline Planforms of Embayed Beaches. Water. 2024; 16(5):774. https://doi.org/10.3390/w16050774
Chicago/Turabian StyleTao, Hung-Cheng, Tai-Wen Hsu, and Chia-Ming Fan. 2024. "An Improved One-Line Evolution Formulation for the Dynamic Shoreline Planforms of Embayed Beaches" Water 16, no. 5: 774. https://doi.org/10.3390/w16050774
APA StyleTao, H.-C., Hsu, T.-W., & Fan, C.-M. (2024). An Improved One-Line Evolution Formulation for the Dynamic Shoreline Planforms of Embayed Beaches. Water, 16(5), 774. https://doi.org/10.3390/w16050774