Collapse Susceptibility Assessment in Taihe Town Based on Convolutional Neural Network and Information Value Method
Abstract
1. Introduction
- (1)
- Referring to the existing literature and expert experience, we sort previous studies in the study area; collect distance from water system, distance from the road, land cover type, normalized difference vegetation index, planform curvature, profile curvature, slope, aspect, and geological data; and conduct data pre-treatment.
- (2)
- Conduct correlation analysis on the data and eliminate the data with strong correlation. The data are classified, and the information quantity carried by each classification factor is calculated. Based on the information value of each factor, the collapse susceptibility partition map is made by superposition.
- (3)
- Standardize the data and make the data set; Construct the CNN and use data sets for training and validation. The CNN was tested after training. The tested CNN was used to predict the susceptibility of the study area to collapse.
- (4)
- The susceptibility zoning maps based on the two methods were compared using ROC curves.
2. Materials and Methods
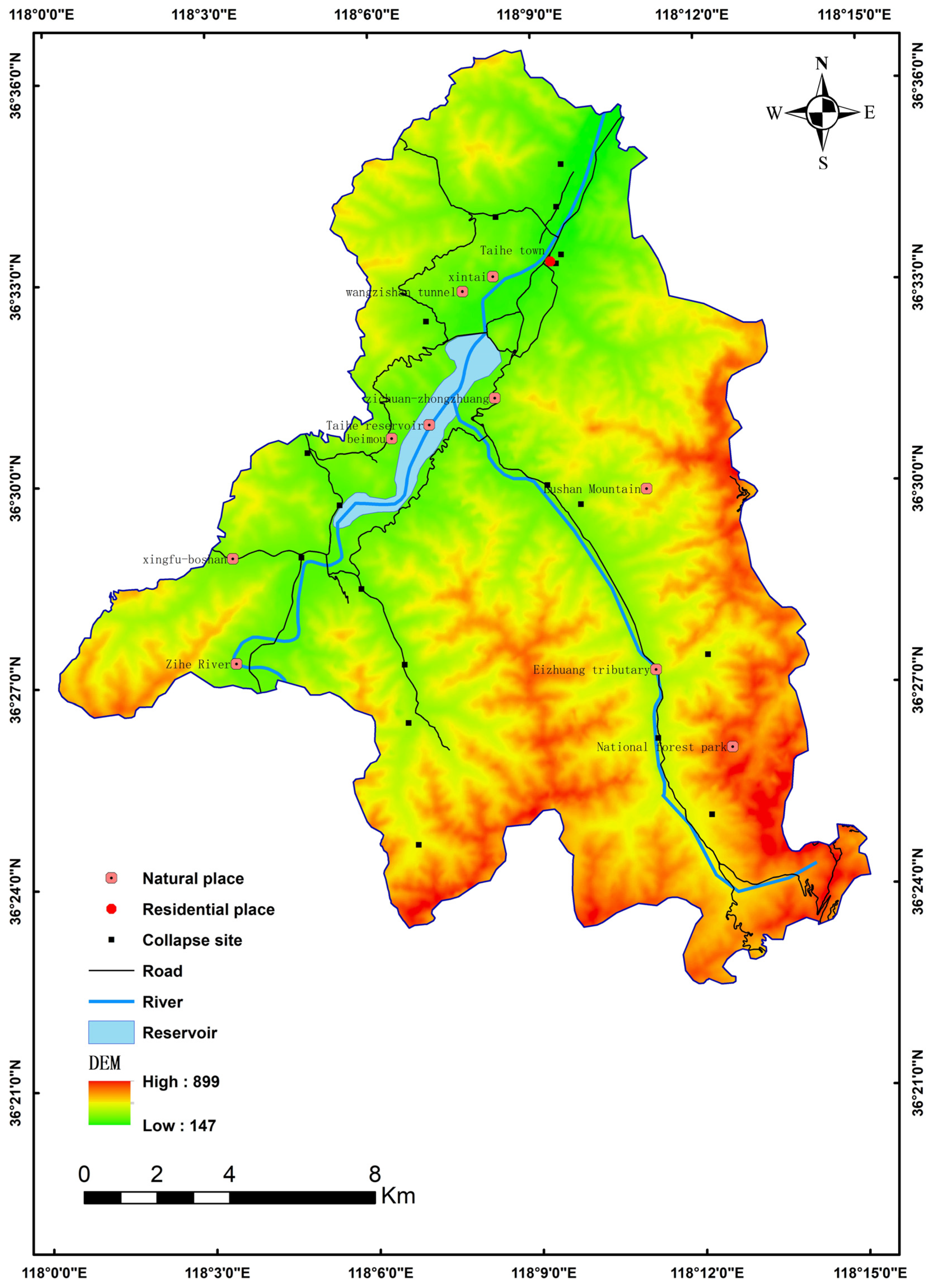
2.1. Overview of the Study Area
2.2. Multi-Source Data
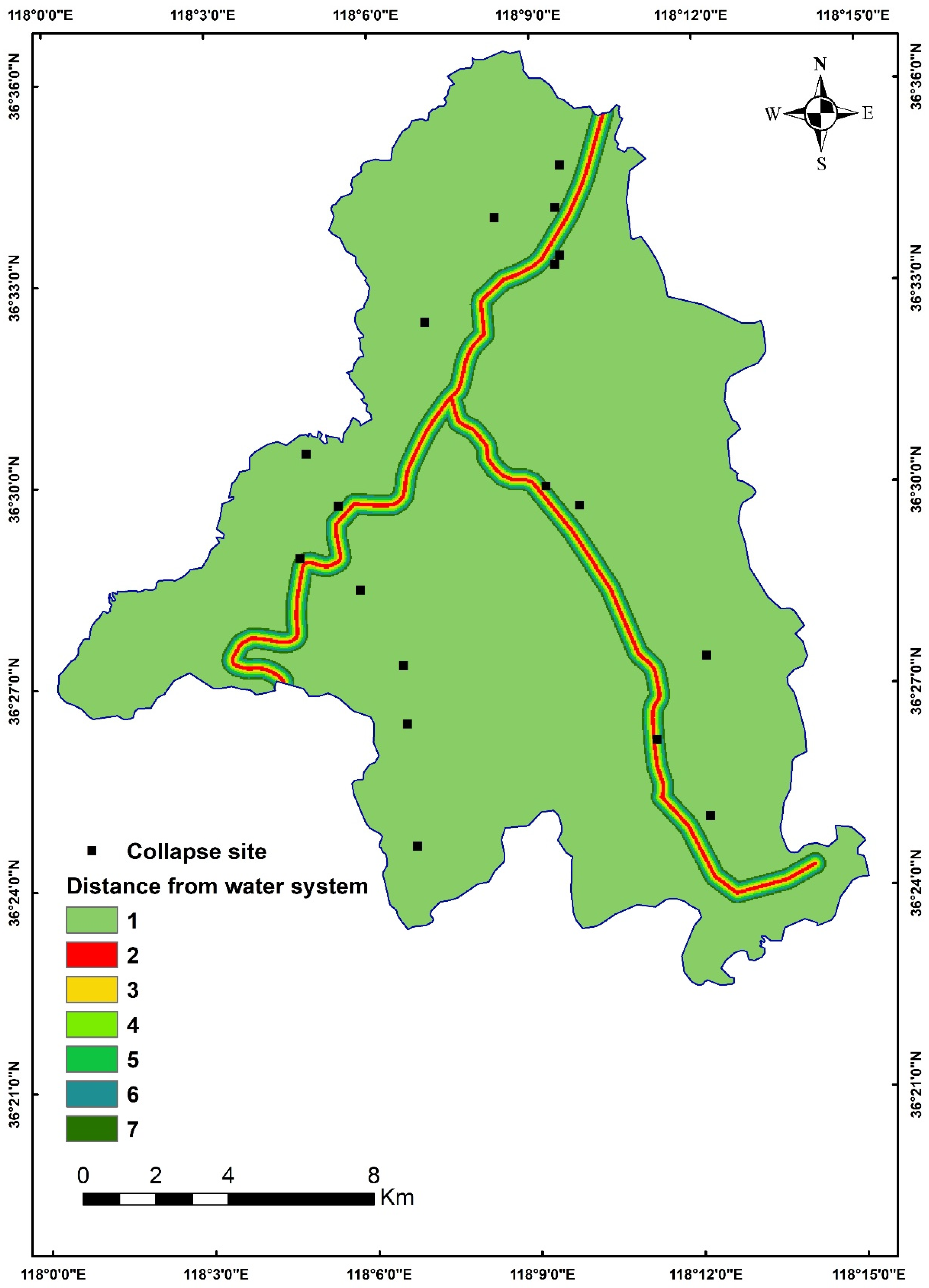
2.2.1. Distance from Water System
2.2.2. Distance from Road
2.2.3. Land Cover Type
2.2.4. Normalized Difference Vegetation Index (NDVI) Data
2.2.5. Planform Curvature
2.2.6. Profile Curvature
2.2.7. Slope
2.2.8. Aspect
2.2.9. Geological Data
2.3. Methods
2.3.1. Information Value Method
2.3.2. Convolutional Neural Network
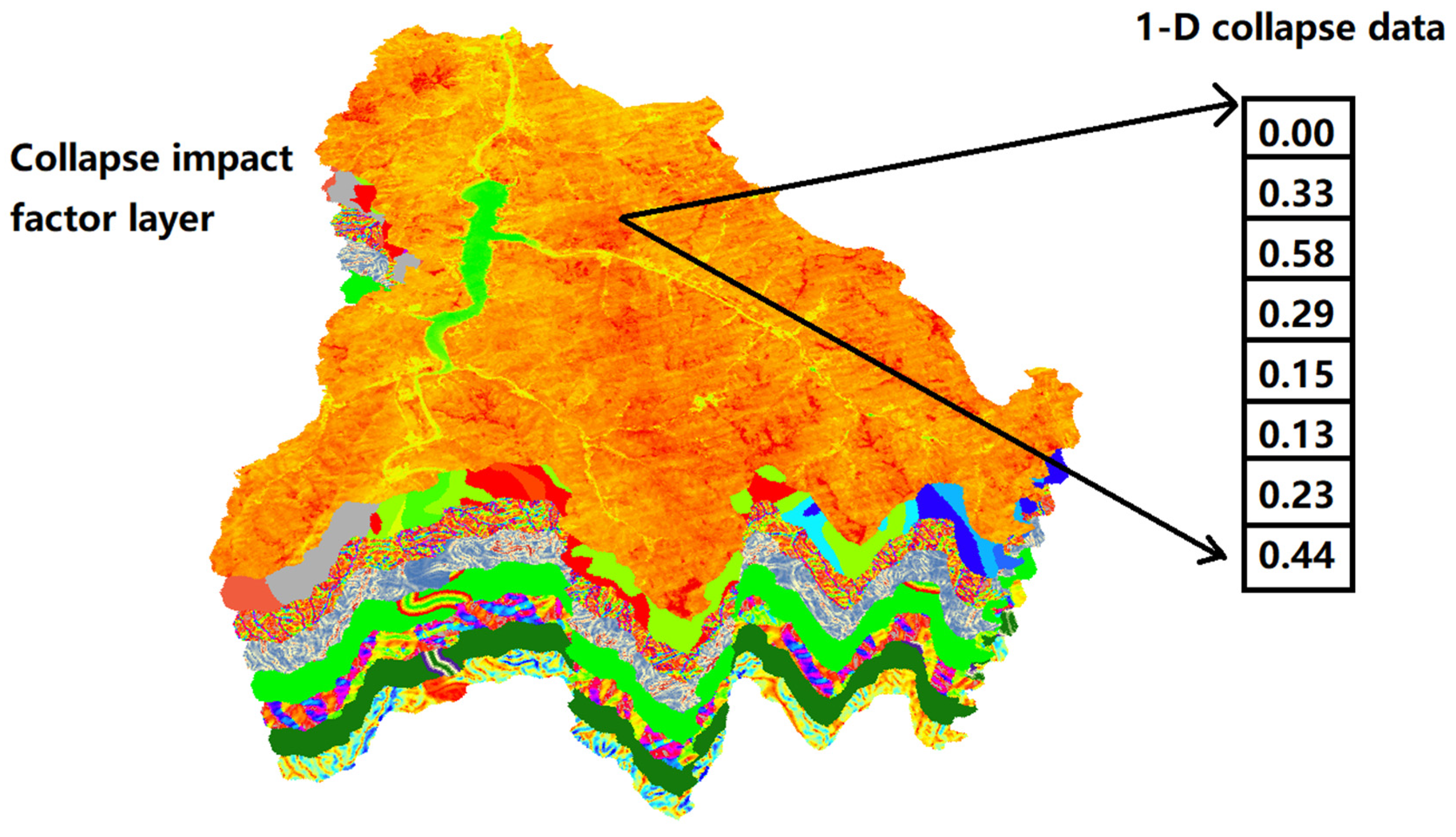
2.3.3. Data Set Construction
2.3.4. CNN Construction
2.3.5. The CNN Training and Verification
3. Results
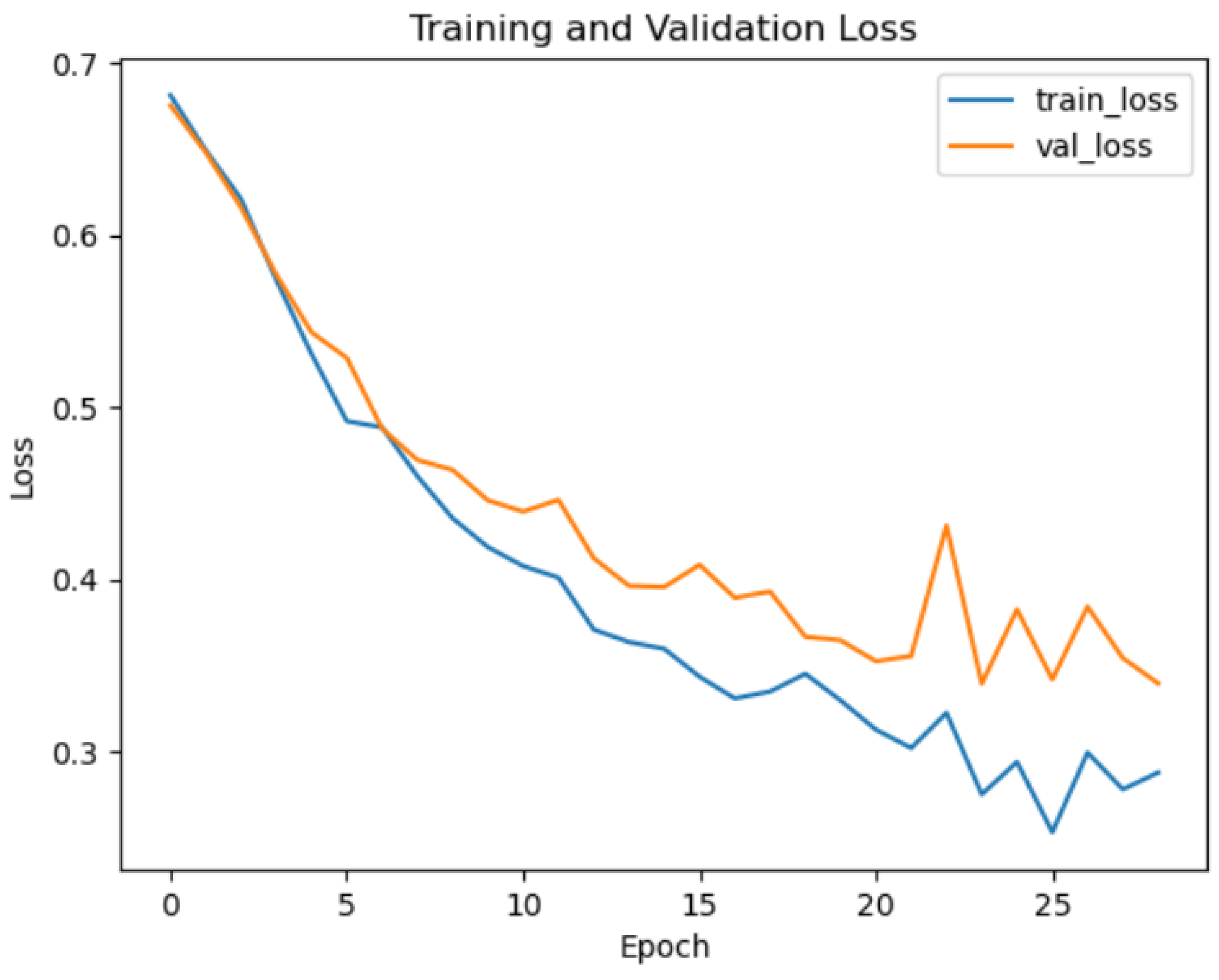
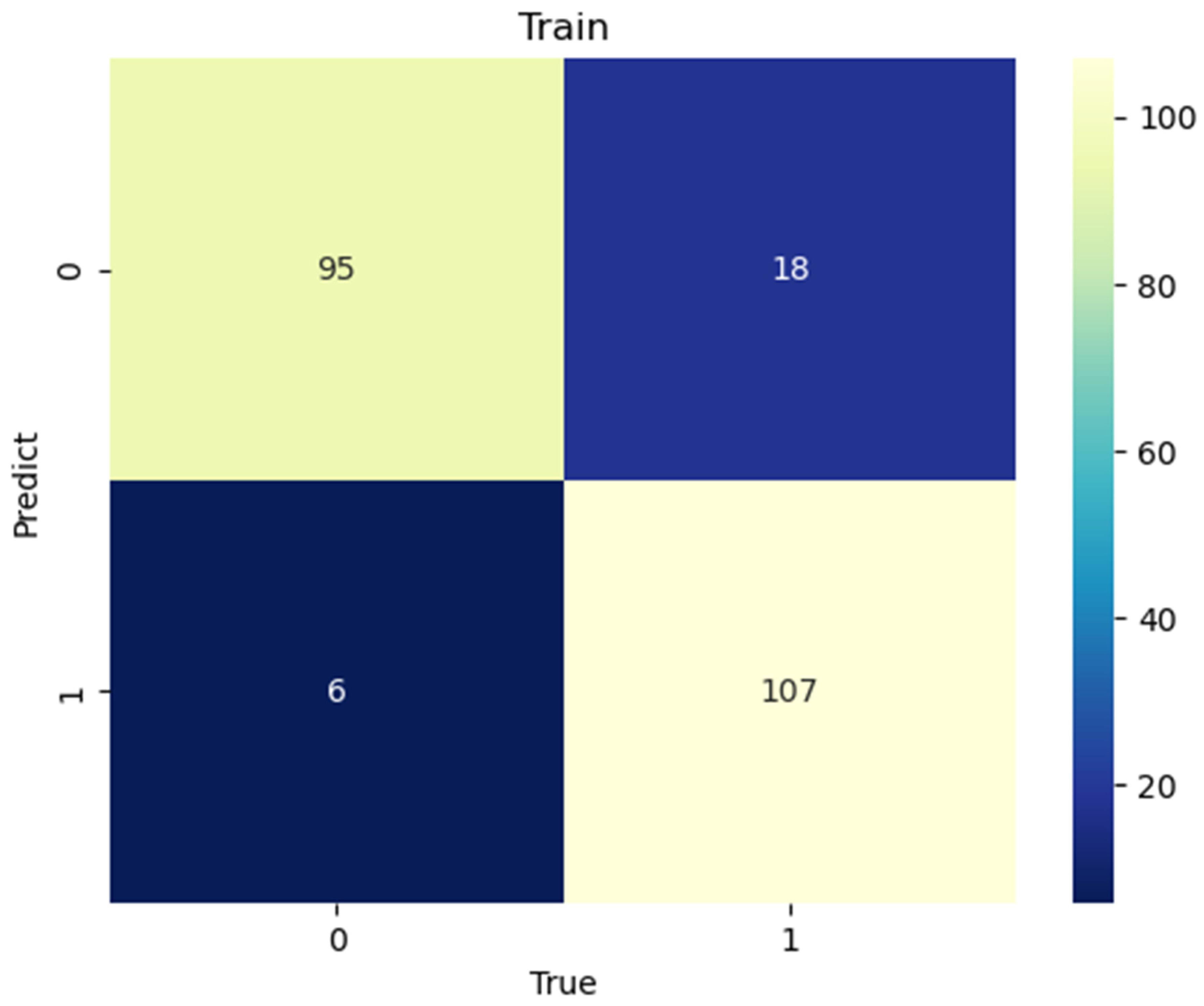
3.1. CNN Calibration and Verification
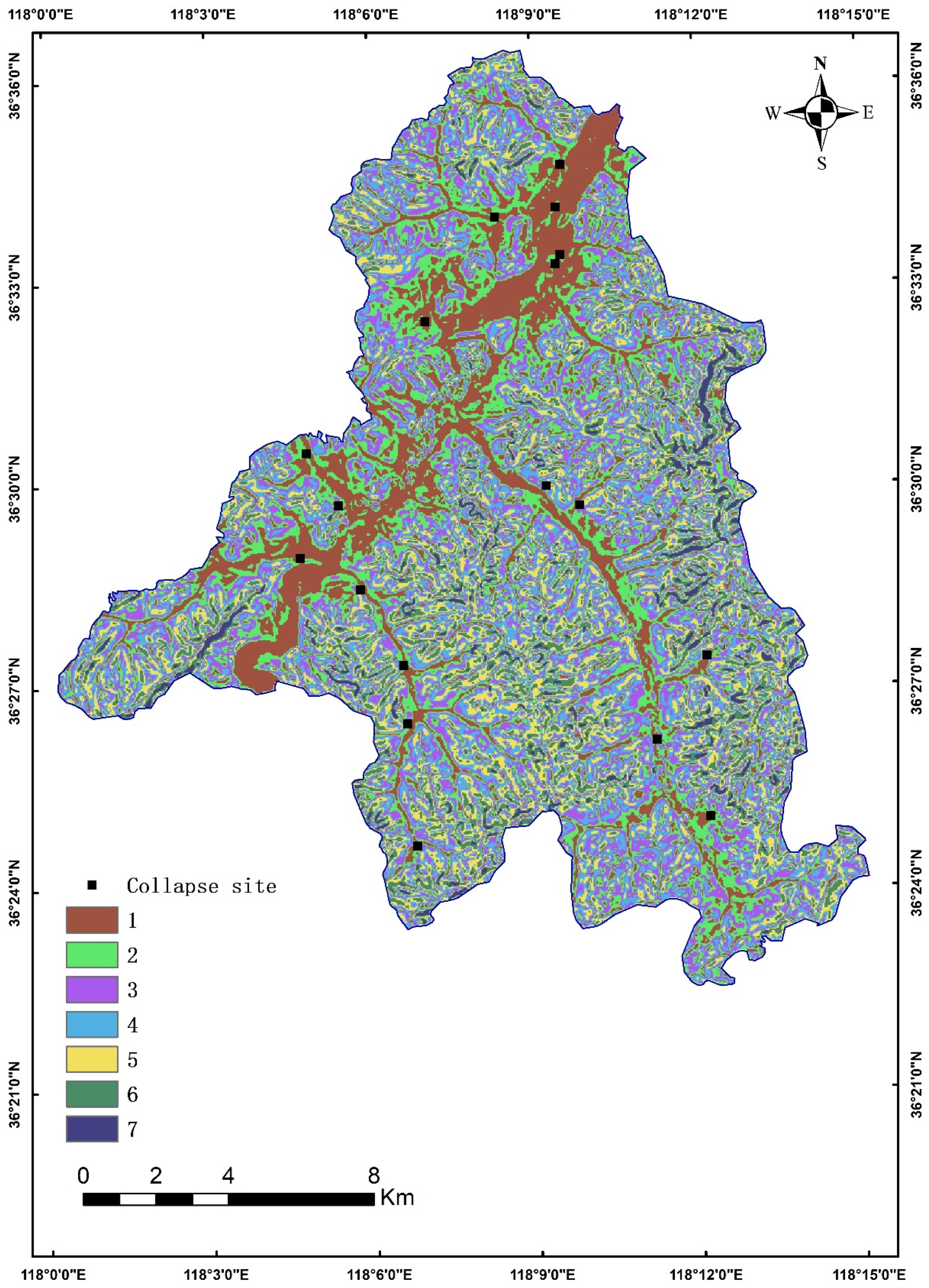
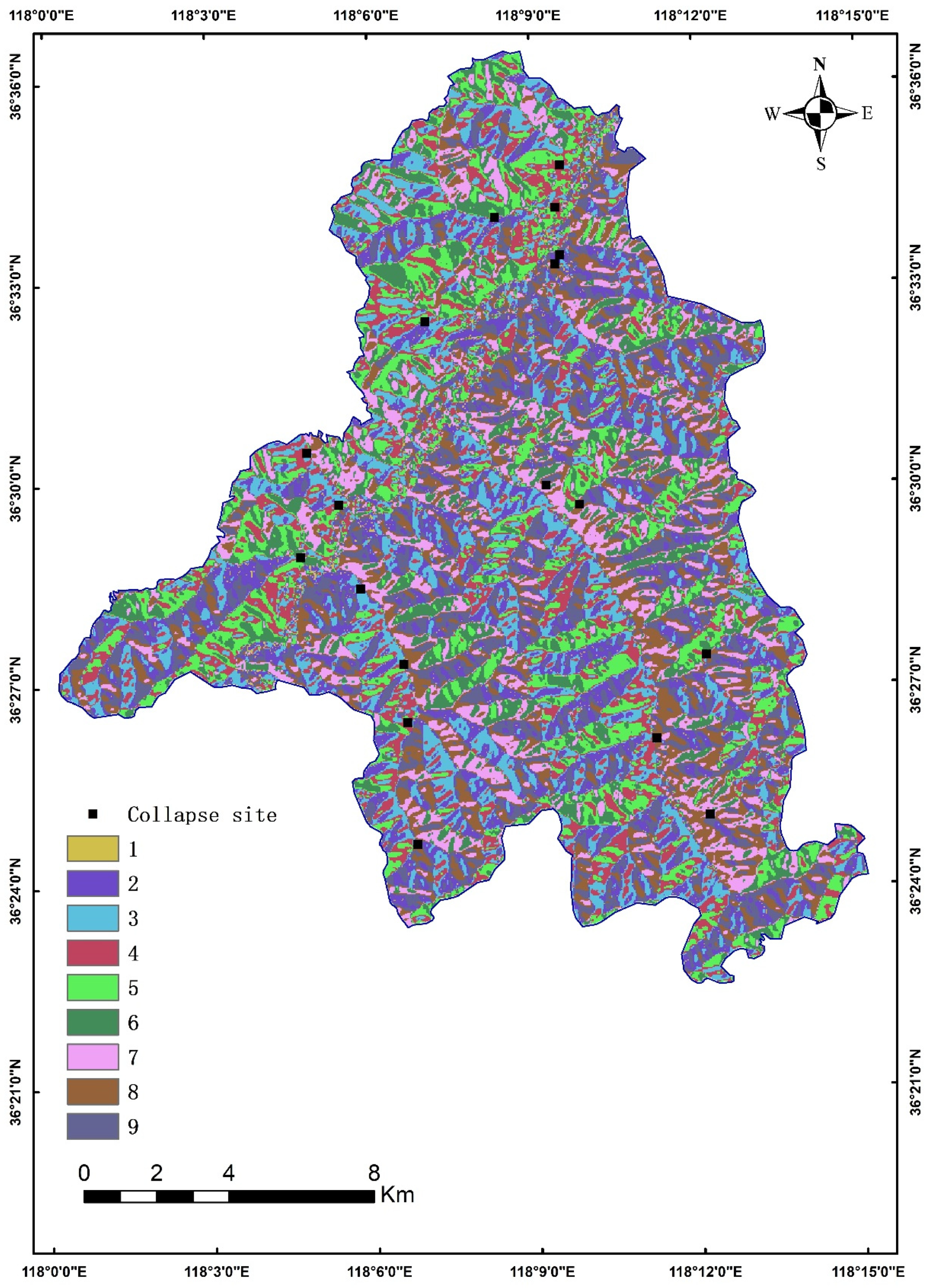
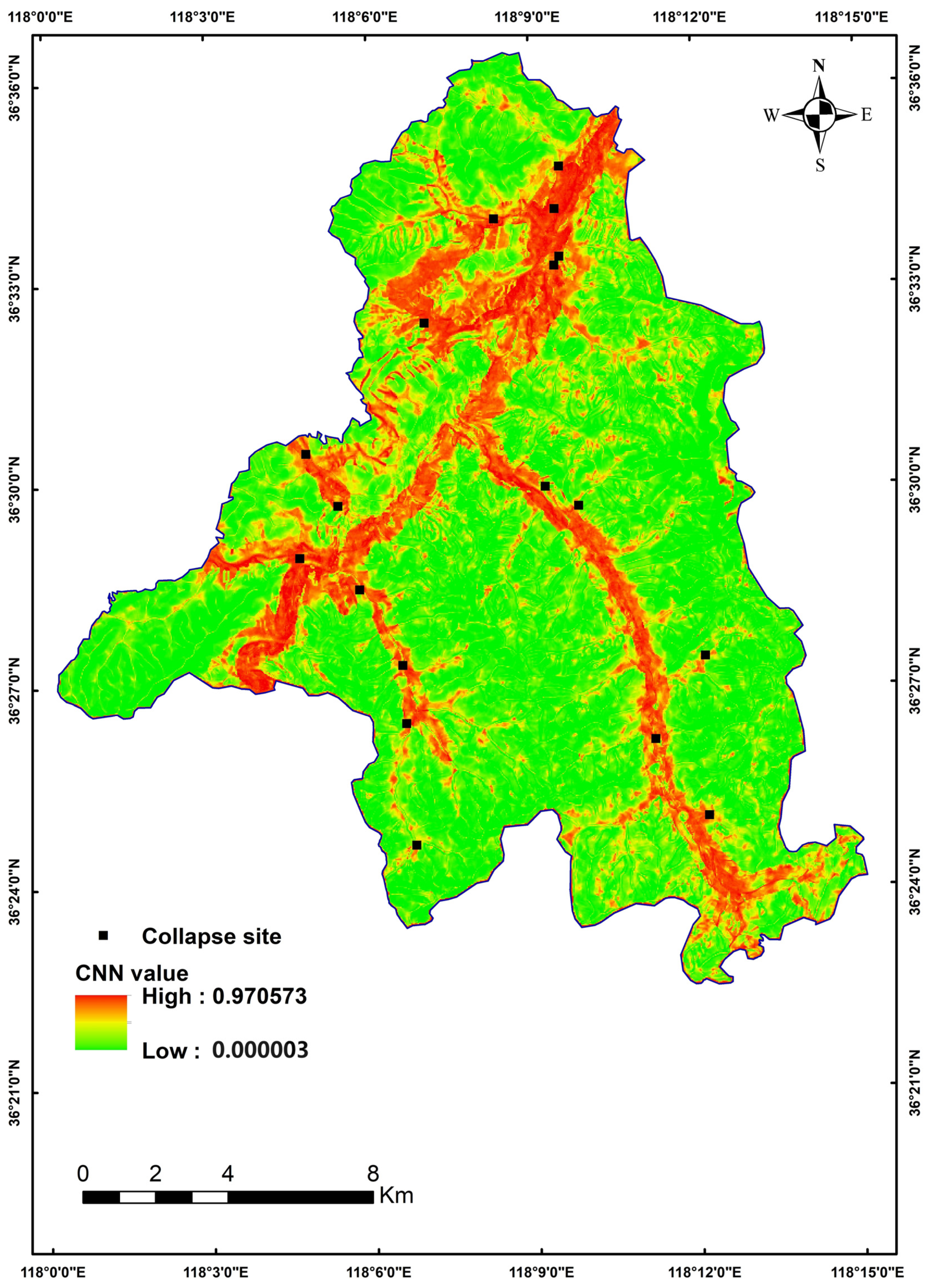
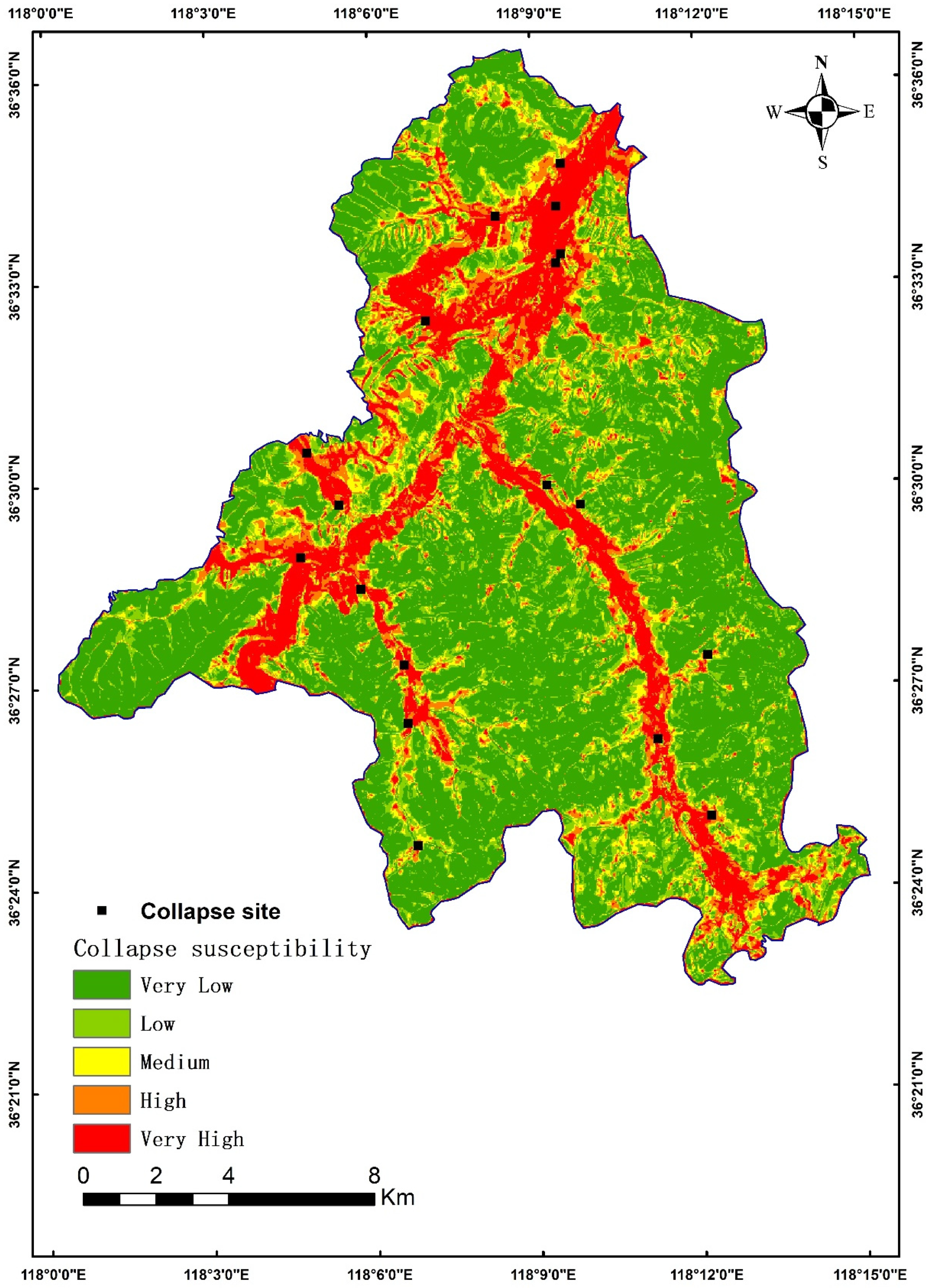
3.2. Collapse Zoning Map Based on the CNN and IV Method
4. Discussion
5. Conclusions
- (1)
- The results of collapse susceptibility assessment based on both the IV and CNN methods can effectively characterize the susceptibility of collapse in the study area, with a large number of collapse points falling in the high susceptibility zones. The accuracy of the CNN-based results was higher than that of the IV method by approximately 1.5% to 2.8%, indicating that the CNN-based results are more accurate and reliable than those obtained using the information value method.
- (2)
- The 1D-CNN structure based on one-dimensional data achieved reliable prediction results in collapse susceptibility assessment, with an accuracy of 87.9% and 87.4%. The one-dimensional data structure can effectively present the relationship between collapse and influencing factors.
- (3)
- This study demonstrated the feasibility of using incremental data in dataset construction (Section 2.3.3). If non-disaster points can be accurately selected or sufficient data is available when expanding the non-disaster points, the accuracy of the results may be further improved.
- (4)
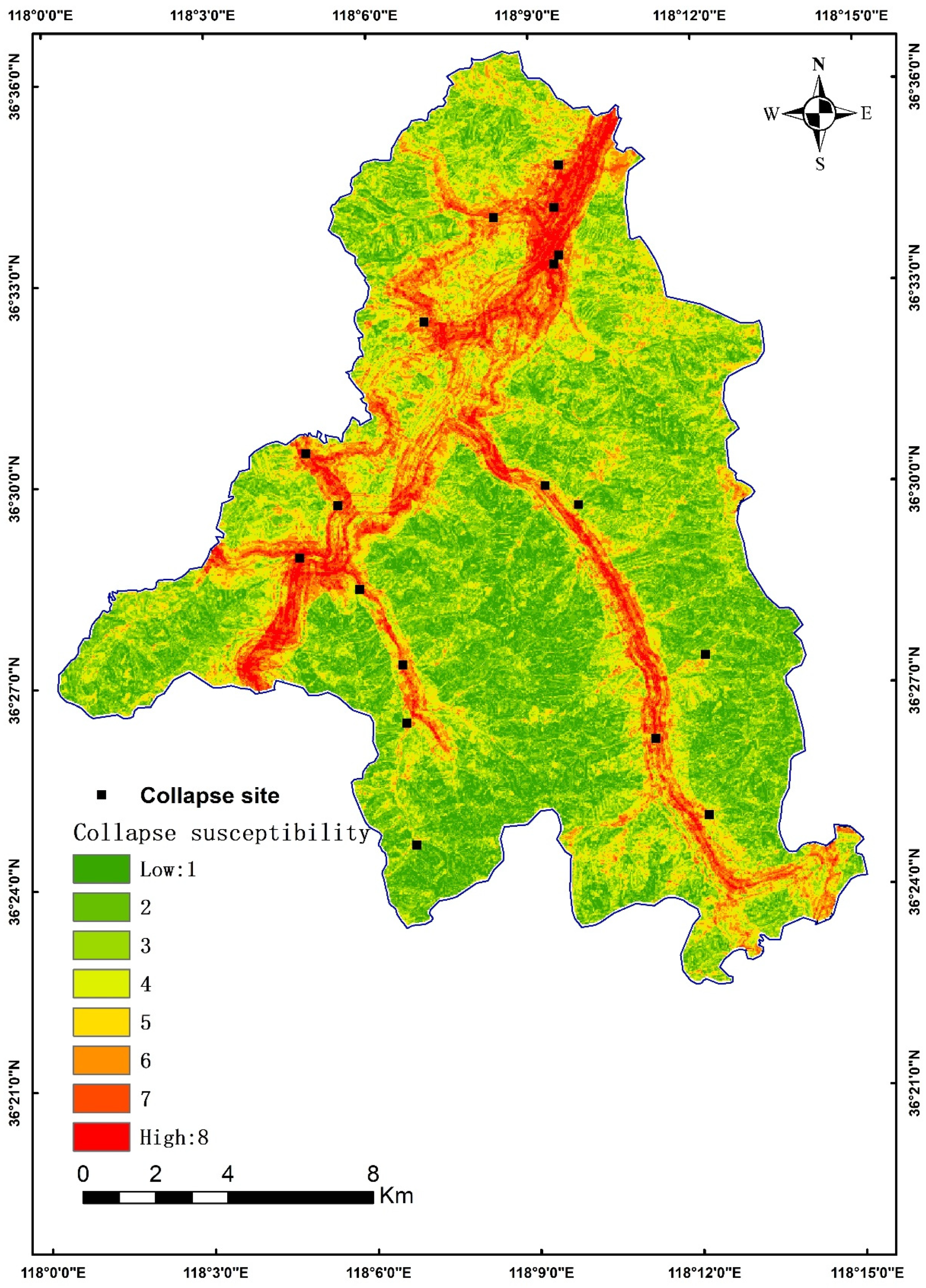
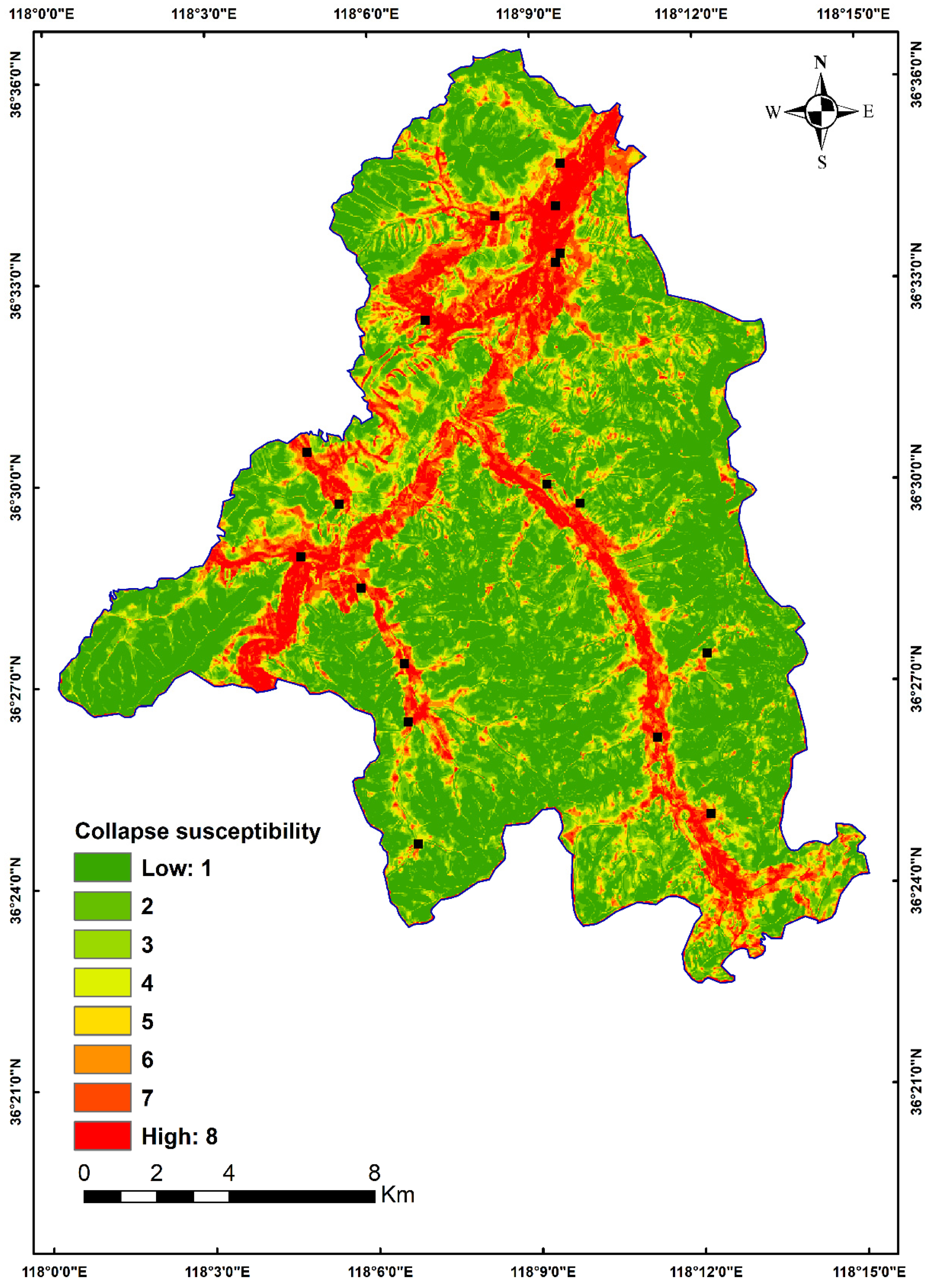
- When the zoning map was reclassified into five or eight classes, the AUC values did not show the same or decreasing trend, indicating that increasing the number of classification data does not necessarily improve the growth rate.
- (5)
- The CNN constructed in this study is not the optimal neural network structure, and if all structures can be exhaustively searched, it may be possible to find model parameters and hyperparameters with higher accuracy.
- (6)
- In this study, the effectiveness of the two methods was compared using ROC curves, and the comparison was not based on the differences in the zoning maps. The next step could be to use new methods to quantitatively characterize the degree of difference between the two susceptibility zoning maps.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, L.; Liang, H.; He, S.; Liu, W.; Zhang, Q.; Li, G. Failure mechanism and dynamic processes of rock avalanche occurrence in Chengkun railway, China, on August 14, 2019. Landslides 2020, 17, 943–957. [Google Scholar] [CrossRef]
- Liu, C.; Xiao, R. Mechanism analysis on Yanchihe avalanche disaster in Yuan’an, Hubei. J. Catastrophology 2021, 36, 130–133+150. [Google Scholar]
- Kubwimana, D.; Brahim, L.A.; Bousta, M.; Dewitte, O.; Abdelouafi, A.; Bahaj, T. Landslides susceptibility assessment using AHP method in Kanyosha watershed (Bujumbura-Burundi): Urbanisation and management impacts. MATEC Web Conf. 2018, 149, 02071. [Google Scholar]
- Shirzadi, A.; Chapi, K.; Shahabi, H.; Solaimani, K.; Kavian, A.; Ahmad, B.B. Rock fall susceptibility assessment along a mountainous road: An evaluation of bivariate statistic, analytical hierarchy process and frequency ratio. Environ. Earth Sci. 2017, 76, 152. [Google Scholar] [CrossRef]
- Abdeldjalil, G.; Mostefa, G.; Said, G.M. GIS-Based Multi-Criteria Decision Analysis Approach (GIS-MCDA) for investigating mass movements’ hazard susceptibility along the first section of the Algerian North-South Highway. Arab. J. Geosci. 2021, 14, 850. [Google Scholar]
- Masanori, K.; Yuki, H. Landslide Susceptibility Assessment in the Japanese Archipelago Based on a Landslide Distribution Map. ISPRS Int. J. Geo-Inf. 2023, 12, 37. [Google Scholar]
- Majeed, M.; Lu, L.; Anwar, M.M.; Tariq, A.; Qin, S.; El-Hefnawy, M.E.; El-Sharnouby, M.; Li, Q.; Alasmari, A. Prediction of flash flood susceptibility using integrating analytic hierarchy process (AHP) and frequency ratio (FR) algorithms. Front. Environ. Sci. 2023, 10, 1037547. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, C.; Nie, R.; Yang, Z.; Li, W.; Dai, X.; Cheng, J.; Zhang, J.; Ma, L.; Fu, X.; et al. A Comparative Analysis of Certainty Factor-Based Machine Learning Methods for Collapse and Landslide Susceptibility Mapping in Wenchuan County, China. Remote Sens. 2022, 14, 3259. [Google Scholar] [CrossRef]
- Li, Y.; Sheng, Y.; Chai, B.; Zhang, W.; Zhang, T.; Wang, J. Collapse susceptibility assessment using a support vector machine compared with back-propagation and radial basis function neural networks. Geomat. Nat. Hazards Risk 2020, 11, 510–534. [Google Scholar] [CrossRef]
- Ma, J.; Wang, X.; Yuan, G. Evaluation of Geological Hazard Susceptibility Based on the Regional Division Information Value Method. ISPRS Int. J. Geo-Inf. 2023, 12, 17. [Google Scholar] [CrossRef]
- Zhong, R.H.; He, D.M.; Hu, J.M.; Duan, X.W.; Huang, J.C.; Cheng, X.P. Distribution and Susceptibility Assessment of Collapses and Landslides in the Riparian Zone of the Xiaowan Reservoir. Chin. Geogr. Sci. 2019, 29, 70–85. [Google Scholar] [CrossRef]
- Lei, C.; Liu, C.; Zhang, Y.; Cheng, J.; Zhao, R. Evaluation of collapse susceptibility in Guangdong Province based on comprehensive intelligent analysis. Chin. J. Rock Mech. Eng. 2023, 42, 4248–4260. [Google Scholar]
- Li, P.; Huang, J. Study on geological hazard prone zoning and prevention measures in Xin’an County. Soil Water Conserv. China 2023, 10, 55–59. [Google Scholar]
- Chen, L.; Guo, H.; Gong, P.; Yang, Y.; Zuo, Z.; Gu, M. Landslide susceptibility assessment using weights-of-evidence model and cluster analysis along the highways in the Hubei section of the Three Gorges Reservoir Area. Comput. Geosci. 2021, 156, 104899. [Google Scholar] [CrossRef]
- Losasso, L.; Sdao, F. The artificial neural network for the rockfall susceptibility assessment. A case study in Basilicata (Southern Italy). Geomat. Nat. Hazards Risk 2018, 9, 737–759. [Google Scholar] [CrossRef]
- Yilmaz, I.; Marschalko, M.; Bednarik, M. An assessment on the use of bivariate, multivariate and soft computing techniques for collapse susceptibility in GIS environ. J. Earth Syst. Sci. 2013, 122, 371–388. [Google Scholar] [CrossRef][Green Version]
- Abhik, S.; Kumar, V.V.G.; Ashutosh, B. Development and Assessment of GIS-Based Landslide Susceptibility Mapping Models Using ANN, Fuzzy-AHP, and MCDA in Darjeeling Himalayas, West Bengal, India. Land 2022, 11, 1711. [Google Scholar]
- Guo, F.; Wu, D.; Wang, X.; Dai, Q.; Lai, P.; Chen, Y.; Xia, D. Susceptibility Assessment of Benggang Based on Random Forests Model and Geodetector in Xingguo County of South Jiangxi. J. China Three Gorges Univ. Nat. Sci. 2023, 45, 44–50. [Google Scholar]
- Yang, D.; Zhu, J.; Liu, S.; Ma, B.; Dai, X. Comparative analyses of susceptibility assessment for landslide disasters based on information value, weighted information value and logistic regression coupled model in Luoping County, Yunnan Province. Chin. J. Geol. Hazard Control 2023, 34, 43–53. [Google Scholar]
- Li, W.B.; Fan, X.M.; Huang, F.M.; Chen, W.; Hong, H.Y.; Huang, J.S.; Guo, Z.Z. Uncertainties Analysis of Collapse Susceptibility Prediction Based on Remote Sensing and GIS: Influences of Different Data-Based Models and Connections between Collapses and Environmental Factors. Remote Sens. 2020, 12, 4134. [Google Scholar] [CrossRef]
- Chen, B.; Wei, N.; Qu, T.Q.; Zhang, L.Z.; Li, Y.Y.; Long, X.; Lin, Y.X. Research on weighting method of geological hazard susceptibility evaluation index based on apriori Algorithm. Front. Earth Sci. 2023, 11, 12. [Google Scholar] [CrossRef]
- Liu, S.; Zhu, J.Y.; Yang, D.H.; Ma, B. Comparative Study of Geological Hazard Evaluation Systems Using Grid Units and Slope Units under Different Rainfall Conditions. Sustainability 2022, 14, 16153. [Google Scholar] [CrossRef]
- Wang, Y.; Kentaro, I.; Takuya, M.; Keisuke, A.; Narumi, T.; Kenji, S. Coastal tsunami prediction in Tohoku region, Japan, based on S-net observations using artificial neural network. Earth Planets Space 2023, 75, 154. [Google Scholar] [CrossRef]
- Mulia, I.E.; Gusman, A.R.; Satake, K. Applying a Deep Learning Algorithm to Tsunami Inundation Database of Megathrust Earthquakes. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019690. [Google Scholar] [CrossRef]
- Parisa, K.; Mohammadreza, K.; Ehsan, J.; Amin, R. A CNN-BiLSTM model with attention mechanism for earthquake prediction. J. Supercomput. 2023, 79, 19194–19226. [Google Scholar]
- Dost, M.; Iftikhar, A.; Imran, K.M.; Wajeeha, K.; Ovais, A.M. A Generalized Deep Learning Approach to Seismic Activity Prediction. Appl. Sci. 2023, 13, 1598. [Google Scholar]
- Wang, J.; Sun, P.; Chen, L.; Yang, J.; Liu, Z.; Lian, H. Recent Advances of Deep Learning in Geological Hazard Forecasting. Comput. Model. Eng. Sci. 2023, 137, 1381–1418. [Google Scholar] [CrossRef]
- Yohei, Y.; Ahyi, K.; Takao, O. Reappraisal of volcanic seismicity at the Kirishima volcano using machine learning. Earth Planets Space 2023, 75, 183. [Google Scholar]
- Ding, Q.; Shao, Z.; Huang, X.; Orhan, A.; Zhuang, Q.; Hu, B. Monitoring, analyzing and predicting urban surface subsidence: A case study of Wuhan City, China. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102422. [Google Scholar] [CrossRef]
- Habumugisha, J.M.; Chen, N.S.; Rahman, M.; Islam, M.M.; Ahmad, H.; Elbeltagi, A.; Sharma, G.; Liza, S.N.; Dewan, A. Landslide Susceptibility Mapping with Deep Learning Algorithms. Sustainability 2022, 14, 1734. [Google Scholar] [CrossRef]
- Abaker, M.; Dafaalla, H.; Eisa, T.A.E.; Abdelgader, H.; Mohammed, A.; Burhanur, M.; Hasabelrsoul, A.; Alfakey, M.I.; Morsi, M.A. Deep Learning- and IoT-Based Framework for Rock-Fall Early Warning. Appl. Sci. 2023, 13, 9978. [Google Scholar] [CrossRef]
- Tian, Y.; Luo, L.; Yu, Z.; Xu, H.; Ni, F. Noncontact vision-based impact force reconstruction and spatial-temporal deflection tracking of a flexible barrier system under rockfall impact. Comput. Geotech. 2023, 153, 105070. [Google Scholar] [CrossRef]
- Ge, Y.F.; Liu, G.; Tang, H.M.; Zhao, B.B.; Xiong, C.R. Comparative analysis of five convolutional neural networks for landslide susceptibility assessment. Bull. Eng. Geol. Environ. 2023, 82, 26. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Niu, R.; Peng, L. Landslide Susceptibility Analysis based on Deep Learning. J. Geo-Inf. Sci. 2021, 23, 2244–2260. [Google Scholar]
- Yue, L.; Qu, J.; Zhou, S.; Qu, B.; Zhang, Y.; Xu, Q. Seismic event classification based on a two-step convolutional neural network. J. Seismol. 2023, 27, 527–535. [Google Scholar] [CrossRef]
- Song, J.; Ren, X.L.; Cha, S.H.; Zhao, X. Study on Ecological Water System Planning of Ezhuang Tributary in Taihe Town, Zibo City. Des. Water Resour. Hydroelectr. 2020, 39, 34–37+56. [Google Scholar]
- Zhang, B.; Cheng, W. Analysis on the effect of mountain closure and forest cultivation in Zichuan District. Agric. Technol. 2020, 40, 70–72. [Google Scholar]
- Kanwarpreet, S.; Virender, K. Hazard assessment of landslide disaster using information value method and analytical hierarchy process in highly tectonic Chamba region in bosom of Himalaya. J. Mt. Sci. 2018, 15, 808–824. [Google Scholar]
- Zhou, G.; Zhuang, W.; Chen, Y.; Xi, B.; Jia, W.; Zhou, Y.; Yu, G. RS/GIS-based regional evaluation of landslide hazard risk: A case study of Guangchang County, Jiangxi Province. J. Nat. Disasters 2008, 17, 68–72. [Google Scholar]
- Guo, C.; Tang, J.; Wu, R.; Ren, S. Landslide Susceptibility Assessment Based on WOE Model along Jiacha—Langxian County Section of Sichuan—Tibet Railway, China. Mt. Res. 2019, 37, 240–251. [Google Scholar]
- Wang, S.; Zhang, C.; Liu, H.; Ding, M. New progress of Quaternary geology in Shandong Province. Shandong Land Resour. 1999, 2, 3–10. [Google Scholar]
- Liu, Z.; Gao, X.; Jia, X.; Xue, B.; Fu, S.; Li, K.; Huang, X.; Huang, Z. Correlation-based feature partition regression method for unsupervised anomaly detection. Appl. Intell. 2022, 52, 15074–15090. [Google Scholar] [CrossRef]
- Jiao, W.; Zhang, M.; Xie, X.; Li, C.; Liu, T.; Pang, H. Susceptibility Evaluation of Urban Geological Disaster Based on GlS and Weighted Information Value Model—A Case Study of Daxin Town. Saf. Environ. Eng. 2022, 29, 119–128. [Google Scholar]
- Qin, H.; Wang, J.; Mao, X.; Zhao, Z.A.; Gao, X.; Lu, W. An Improved Faster R-CNN Method for Landslide Detection in Remote Sensing Images. J. Geovis. Spat. Anal. 2023, 8, 1. [Google Scholar] [CrossRef]
- Kang, J.; Guan, H.; Ma, L.; Wang, L.; Xu, Z.; Li, J. WaterFormer: A coupled transformer and CNN network for waterbody detection in optical remotely-sensed imagery. ISPRS J. Photogramm. Remote Sens. 2023, 206, 222–241. [Google Scholar] [CrossRef]
- Xu, L.; Shi, S.; Liu, Y.; Zhang, H.; Wang, D.; Zhang, L.; Liang, W.; Chen, H. A large-scale remote sensing scene dataset construction for semantic segmentation. Int. J. Image Data Fusion 2023, 14, 299–323. [Google Scholar] [CrossRef]
- Han, Z.; Chao, Y.; Shaoping, W.; Bing, G. Landslide susceptibility mapping based on landslide classification and improved convolutional neural networks. Nat. Hazards 2022, 116, 1931–1971. [Google Scholar]
- Diego, R.; Adriana, C.E.; Estibaliz, M.; Sarah, W.S. CNN-Based Model for Landslide Susceptibility Assessment from Multispectral Data. Appl. Sci. 2022, 12, 8483. [Google Scholar]
- Youssef, A.M.; Pradhan, B.; Dikshit, A.; Al-Katheri, M.M.; Matar, S.S.; Mahdi, A.M. Landslide susceptibility mapping using CNN-1D and 2D deep learning algorithms: Comparison of their performance at Asir Region, KSA. Bull. Eng. Geol. Environ. 2022, 81, 165. [Google Scholar] [CrossRef]
- Bopche, L.; Rege, P.P. Landslide Susceptibility Mapping: An Integrated Approach using Geographic Information Value, Remote Sensing, and Weight of Evidence Method. Geotech. Geol. Eng. 2022, 40, 2935–2947. [Google Scholar] [CrossRef]
- Achour, Y.; Boumezbeur, A.; Hadji, R.; Chouabbi, A.; Cavaleiro, V.; Bendaoud, E.A. Landslide susceptibility mapping using analytic hierarchy process and information value methods along a highway road section in Constantine, Algeria. Arab. J. Geosci. 2017, 10, 194. [Google Scholar] [CrossRef]
- Can, Y.; Lei-Lei, L.; Faming, H.; Lei, H.; Xiao-Mi, W. Machine learning-based landslide susceptibility assessment with optimized ratio of landslide to non-landslide samples. Gondwana Res. 2023, 123, 198–216. [Google Scholar]
- Shi, J. Comparative Study of Landslide susceptibilities Using the Machine Learning MaxEnt Model on Different Sampling Strategies. J. Catastrophology 2023, 38, 50–55. [Google Scholar]
- An, K.; Niu, R. Landslide Susceptibility Assessment Using Support Vector Machine Based on Weighted-information Model. J. Chang. River Sci. Res. Inst. 2016, 33, 47–51+58. [Google Scholar]
- Wang, Z.; Xu, S.; Liu, J.; Wang, Y.; Ma, X.; Jiang, T.; He, X.; Han, Z. A Combination of Deep Autoencoder and Multi-Scale Residual Network for Landslide Susceptibility Evaluation. Remote Sens. 2023, 15, 653. [Google Scholar] [CrossRef]








| Layer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.000 | 0.240 | 0.224 | −0.290 | 0.024 | −0.129 | −0.205 | −0.017 | 0.005 |
| 2 | 0.240 | 1.000 | 0.178 | −0.154 | −0.016 | −0.206 | −0.271 | −0.021 | 0.033 |
| 3 | 0.224 | 0.178 | 1.000 | −0.566 | −0.012 | −0.120 | −0.288 | −0.056 | 0.085 |
| 4 | −0.290 | −0.154 | −0.566 | 1.000 | −0.038 | 0.113 | 0.262 | 0.014 | −0.065 |
| 5 | 0.024 | −0.016 | −0.012 | −0.038 | 1.000 | 0.110 | −0.384 | −0.007 | −0.045 |
| 6 | −0.129 | −0.206 | −0.120 | 0.113 | 0.110 | 1.000 | 0.302 | 0.033 | −0.053 |
| 7 | −0.205 | −0.271 | −0.288 | 0.262 | −0.384 | 0.302 | 1.000 | 0.047 | −0.054 |
| 8 | −0.017 | −0.021 | −0.056 | 0.014 | −0.007 | 0.033 | 0.047 | 1.000 | −0.063 |
| 9 | 0.005 | 0.033 | 0.085 | −0.065 | −0.045 | −0.053 | −0.054 | −0.063 | 1.000 |
| Layers/ | Value | j | |||||
|---|---|---|---|---|---|---|---|
| Distance from water system | 1 | >300 | 272,871 | 14 | 0.778 | 0.908 | −0.155 |
| 2 | 0 ≤ 50 | 4638 | 0 | 0.000 | 0.015 | 0.000 | |
| 3 | 50 ≤ 100 | 4581 | 1 | 0.056 | 0.015 | 1.293 | |
| 4 | 100 ≤ 150 | 4610 | 0 | 0.000 | 0.015 | 0.000 | |
| 5 | 150 ≤ 200 | 4630 | 0 | 0.000 | 0.015 | 0.000 | |
| 6 | 200 ≤ 250 | 4561 | 2 | 0.111 | 0.015 | 1.991 | |
| 7 | 250 ≤ 300 | 4587 | 1 | 0.056 | 0.015 | 1.292 | |
| Distance from road | 1 | >300 | 243,257 | 6 | 0.333 | 0.810 | −0.887 |
| 2 | 0 ≤ 50 | 11,362 | 6 | 0.333 | 0.038 | 2.176 | |
| 3 | 50 ≤ 100 | 10,125 | 2 | 0.111 | 0.034 | 1.193 | |
| 4 | 100 ≤ 150 | 9651 | 1 | 0.056 | 0.032 | 0.548 | |
| 5 | 150 ≤ 200 | 9187 | 0 | 0.000 | 0.031 | 0.000 | |
| 6 | 200 ≤ 250 | 8631 | 1 | 0.056 | 0.029 | 0.660 | |
| 7 | 250 ≤ 300 | 8265 | 2 | 0.111 | 0.028 | 1.396 | |
| NDVI | 1 | −0.2 ≤ 0.012 | 5943 | 0 | 0.000 | 0.020 | 0.000 |
| 2 | ≤0.228 | 7082 | 1 | 0.056 | 0.024 | 0.857 | |
| 3 | ≤0.313 | 28,487 | 8 | 0.444 | 0.095 | 1.545 | |
| 4 | ≤0.369 | 79,830 | 4 | 0.222 | 0.266 | −0.179 | |
| 5 | ≤0.421 | 95,414 | 3 | 0.167 | 0.318 | −0.645 | |
| 6 | ≤0.492 | 65,680 | 1 | 0.056 | 0.219 | −1.370 | |
| 7 | ≤0.713 | 18,023 | 1 | 0.056 | 0.060 | −0.077 | |
| Planform curvature | 1 | ≤11.546 | 56,136 | 5 | 0.278 | 0.191 | 0.375 |
| 2 | ≤20.847 | 64,660 | 5 | 0.278 | 0.220 | 0.234 | |
| 3 | ≤30.790 | 49,622 | 3 | 0.167 | 0.169 | −0.012 | |
| 4 | ≤42.015 | 36,046 | 3 | 0.167 | 0.123 | 0.307 | |
| 5 | ≤54.524 | 26,866 | 0 | 0.000 | 0.091 | 0.000 | |
| 6 | ≤68.636 | 23,884 | 0 | 0.000 | 0.081 | 0.000 | |
| 7 | ≤82.106 | 36,891 | 2 | 0.111 | 0.125 | −0.121 | |
| Profile curvature | 1 | ≤2.849 | 78,882 | 10 | 0.556 | 0.268 | 0.728 |
| 2 | ≤5.249 | 80,357 | 4 | 0.222 | 0.273 | −0.207 | |
| 3 | ≤7.948 | 62,218 | 3 | 0.167 | 0.212 | −0.238 | |
| 4 | ≤10.947 | 38,825 | 1 | 0.056 | 0.132 | −0.865 | |
| 5 | ≤14.546 | 21,662 | 0 | 0.000 | 0.074 | 0.000 | |
| 6 | ≤19.795 | 9640 | 0 | 0.000 | 0.033 | 0.000 | |
| 7 | ≤38.390 | 2521 | 0 | 0.000 | 0.009 | 0.000 | |
| Slope | 1 | ≤6.516 | 50,050 | 7 | 0.389 | 0.168 | 0.837 |
| 2 | ≤11.869 | 63,884 | 7 | 0.389 | 0.215 | 0.593 | |
| 3 | ≤16.989 | 62,680 | 3 | 0.167 | 0.211 | −0.235 | |
| 4 | ≤21.877 | 53,944 | 0 | 0.000 | 0.181 | 0.000 | |
| 5 | ≤27.229 | 39,417 | 0 | 0.000 | 0.133 | 0.000 | |
| 6 | ≤34.211 | 21,192 | 1 | 0.056 | 0.071 | −0.249 | |
| 7 | ≤59.346 | 6093 | 0 | 0.000 | 0.020 | 0.000 | |
| Aspect | 1 | flat | 1864 | 0 | 0.000 | 0.006 | 0.000 |
| 2 | north | 39,613 | 2 | 0.111 | 0.133 | −0.182 | |
| 3 | northeast | 38,874 | 1 | 0.056 | 0.131 | −0.856 | |
| 4 | east | 34,563 | 6 | 0.333 | 0.116 | 1.053 | |
| 5 | southeast | 34,731 | 2 | 0.111 | 0.117 | −0.050 | |
| 6 | South | 32,863 | 0 | 0.000 | 0.111 | 0.000 | |
| 7 | southwest | 33,422 | 5 | 0.278 | 0.112 | 0.904 | |
| 8 | west | 37,812 | 0 | 0.000 | 0.127 | 0.000 | |
| 9 | northwest | 43,518 | 2 | 0.111 | 0.146 | −0.276 | |
| Geological data | 1 | νδfK↓1↑1 | 13,415 | 0 | 0.000 | 0.045 | 0.000 |
| 2 | χCK↓1↑4 | 468 | 0 | 0.000 | 0.002 | 0.000 | |
| 3 | ∈↓4→O↓1→J∠s | 54,927 | 2 | 0.111 | 0.183 | −0.498 | |
| 4 | s | 4788 | 0 | 0.000 | 0.016 | 0.000 | |
| 5 | νδfK↓1↑1 | 1406 | 0 | 0.000 | 0.005 | 0.000 | |
| 6 | ∈↓3→J∠z^ | 10,006 | 0 | 0.000 | 0.033 | 0.000 | |
| 7 | ∈↓2→C^∠z^ | 914 | 0 | 0.000 | 0.003 | 0.000 | |
| 8 | ∈↓2–3→C^∠m | 4341 | 0 | 0.000 | 0.014 | 0.000 | |
| 9 | ∈↓3–4→J∠g | 24,371 | 4 | 0.222 | 0.081 | 1.008 | |
| 10 | ∈↓4→O↓1→J∠c^ | 80,778 | 3 | 0.167 | 0.269 | −0.478 | |
| 11 | Qh∠y | 25,527 | 8 | 0.444 | 0.085 | 1.655 | |
| 12 | O↓2→Mw | 12,826 | 0 | 0.000 | 0.043 | 0.000 | |
| 13 | O↓2→Mt | 3189 | 0 | 0.000 | 0.011 | 0.000 | |
| 14 | O↓2→Mt-w | 801 | 0 | 0.000 | 0.003 | 0.000 | |
| 15 | O↓2→Md | 9367 | 0 | 0.000 | 0.031 | 0.000 | |
| 16 | O↓2→Md-b | 19,719 | 0 | 0.000 | 0.066 | 0.000 | |
| 17 | O↓2→Mb | 12,154 | 0 | 0.000 | 0.040 | 0.000 | |
| 18 | O↓2→Mb-w | 1315 | 0 | 0.000 | 0.004 | 0.000 | |
| 19 | O↓1→J∠s⊥↑a-b | 20,166 | 1 | 0.056 | 0.067 | −0.189 |
| Layer (Type) | Output Shape | Param # |
|---|---|---|
| conv1d (Conv1d) | (None, 6, 32) | 128 |
| conv1d_1 (Conv1d) | (None, 6, 32) | 6208 |
| max_pooling1d (MaxPooling1D) | (None, 2, 64) | 0 |
| flatten (Flatten) | (None, 128) | 0 |
| dense (Dense) | (None, 128) | 8256 |
| dropout (Dropout) | (None, 128) | 0 |
| dense_1 (Dense) | (None, 128) | 65 |
| Total params: 14,657 Trainable params: 14,657 Non-trainable params: 0 | ||
| Confusion | Predicted Value | ||
|---|---|---|---|
| Positive Example | Negative Example | ||
| True value | Positive example | TP | FN |
| Negative example | FP | TN | |
| Precision | Recall | F1-Score | |
|---|---|---|---|
| Train dataset Report | |||
| 0.0 | 0.94 | 0.84 | 0.89 |
| 1.0 | 0.86 | 0.95 | 0.90 |
| Test dataset Report | |||
| 0.0 | 0.88 | 0.86 | 0.84 |
| 1.0 | 0.86 | 0.88 | 0.87 |
| Name | Susceptibility | Grid Number | Collapse Number | Grid Ratio | Disaster Proportion | AUC |
|---|---|---|---|---|---|---|
| CNN TO 5 TYPE | 1 | 150,537 | 0 | 0.501 | 0.000 | 0.879 |
| 2 | 48,033 | 1 | 0.160 | 0.056 | ||
| 3 | 29,542 | 0 | 0.098 | 0.000 | ||
| 4 | 27,408 | 4 | 0.091 | 0.222 | ||
| 5 | 44,958 | 13 | 0.150 | 0.722 | ||
| IV TO 5 TYPE | 1 | 73,360 | 1 | 0.249 | 0.056 | 0.851 |
| 2 | 100,329 | 1 | 0.341 | 0.056 | ||
| 3 | 63,802 | 2 | 0.217 | 0.111 | ||
| 4 | 38,535 | 2 | 0.131 | 0.111 | ||
| 5 | 18,079 | 12 | 0.061 | 0.667 | ||
| CNN TO 8 TYPE | 1 | 127,531 | 0 | 0.424427 | 0.000 | 0.874 |
| 2 | 45,276 | 1 | 0.15068 | 0.056 | ||
| 3 | 26,382 | 0 | 0.0878 | 0.000 | ||
| 4 | 19,515 | 0 | 0.064947 | 0.000 | ||
| 5 | 16,765 | 1 | 0.055794 | 0.056 | ||
| 6 | 16,810 | 1 | 0.055944 | 0.056 | ||
| 7 | 20,138 | 8 | 0.06702 | 0.444 | ||
| 8 | 28,061 | 7 | 0.093388 | 0.389 | ||
| IV TO 8 TYPE | 1 | 36,302 | 0 | 0.123432 | 0.000 | 0.859 |
| 2 | 63,830 | 1 | 0.217031 | 0.056 | ||
| 3 | 61,603 | 1 | 0.209459 | 0.056 | ||
| 4 | 47,636 | 0 | 0.161969 | 0.000 | ||
| 5 | 34,070 | 2 | 0.115843 | 0.111 | ||
| 6 | 24,755 | 2 | 0.084171 | 0.111 | ||
| 7 | 17,358 | 5 | 0.05902 | 0.278 | ||
| 8 | 8551 | 7 | 0.029075 | 0.389 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Hu, B.X.; Lin, B.; Zhu, S.; Meng, F.; Li, Y. Collapse Susceptibility Assessment in Taihe Town Based on Convolutional Neural Network and Information Value Method. Water 2024, 16, 709. https://doi.org/10.3390/w16050709
Li H, Hu BX, Lin B, Zhu S, Meng F, Li Y. Collapse Susceptibility Assessment in Taihe Town Based on Convolutional Neural Network and Information Value Method. Water. 2024; 16(5):709. https://doi.org/10.3390/w16050709
Chicago/Turabian StyleLi, Houlu, Bill X. Hu, Bo Lin, Sihong Zhu, Fanqi Meng, and Yufei Li. 2024. "Collapse Susceptibility Assessment in Taihe Town Based on Convolutional Neural Network and Information Value Method" Water 16, no. 5: 709. https://doi.org/10.3390/w16050709
APA StyleLi, H., Hu, B. X., Lin, B., Zhu, S., Meng, F., & Li, Y. (2024). Collapse Susceptibility Assessment in Taihe Town Based on Convolutional Neural Network and Information Value Method. Water, 16(5), 709. https://doi.org/10.3390/w16050709





