Hydrological Simulation Study in Gansu Province of China Based on Flash Flood Analysis
Abstract
1. Introduction
2. Research Area and Methods
2.1. Research Area
2.2. Data Sources and Processing
2.3. CNFF Hydrology Model Principles and Methods
2.3.1. Runoff Module
2.3.2. Convergence Module
2.3.3. River Routing
2.4. Evaluation Criteria
3. Results and Analysis
3.1. Hydrological Model Construction
3.2. Sensitivity Analysis
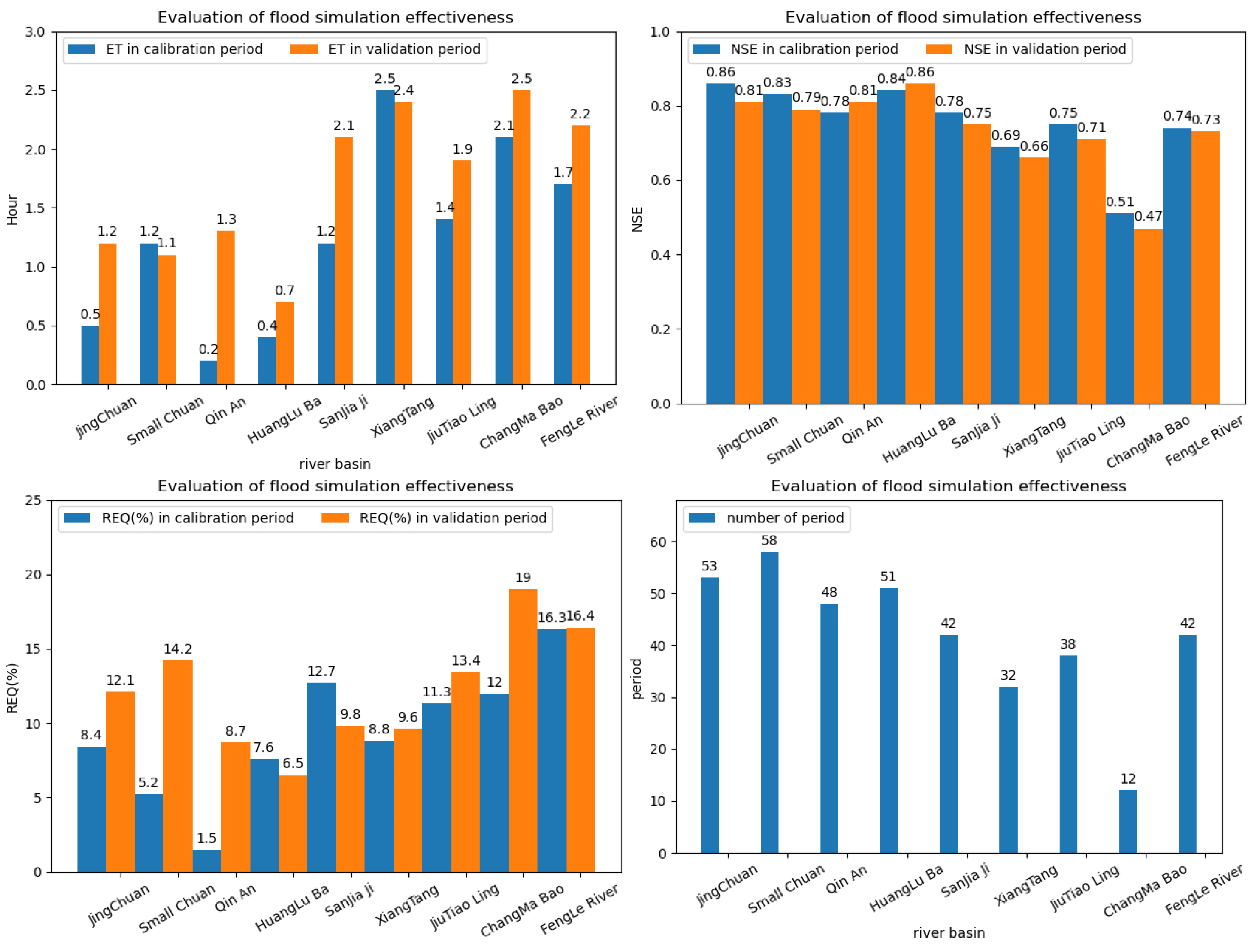
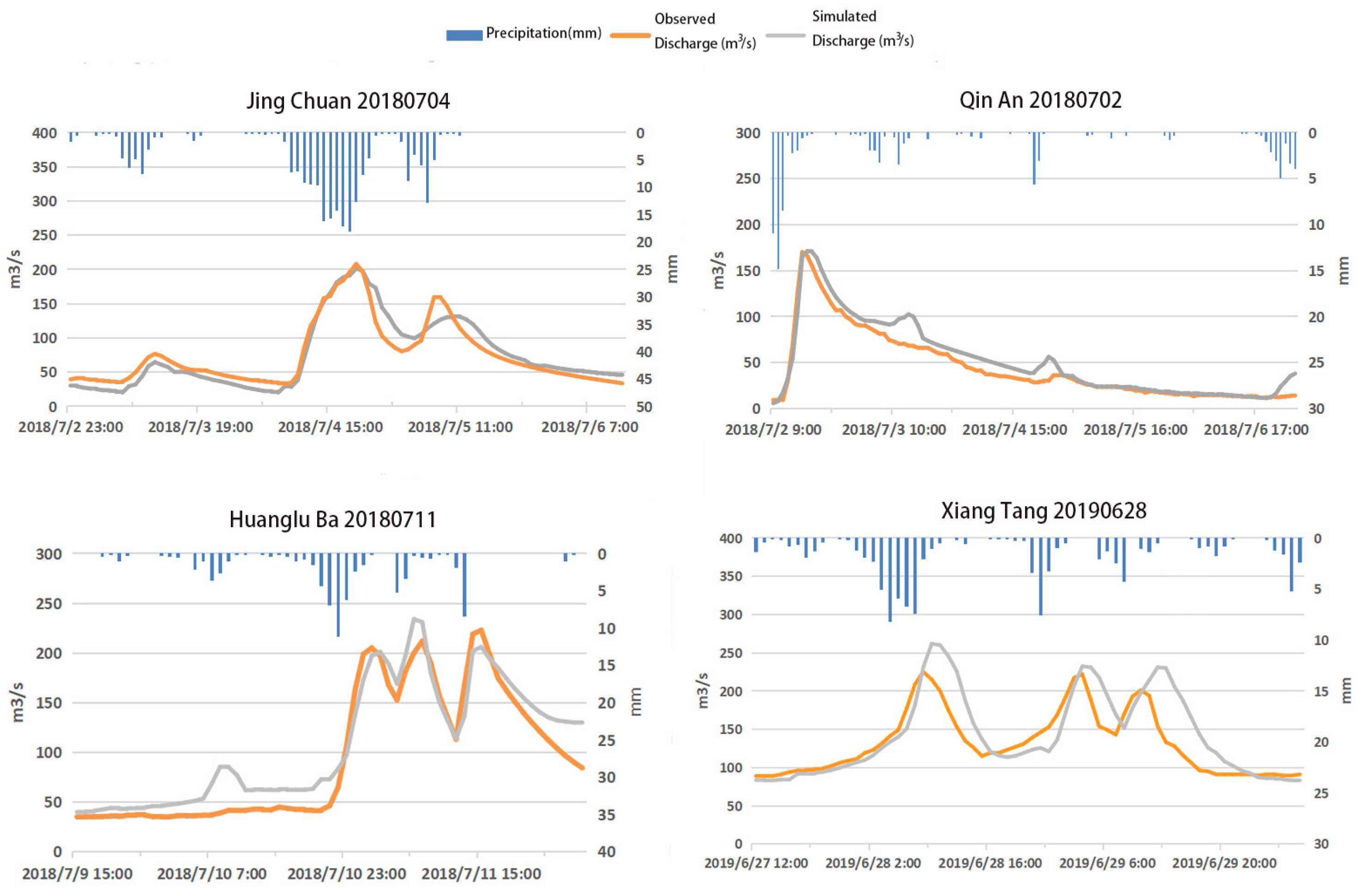
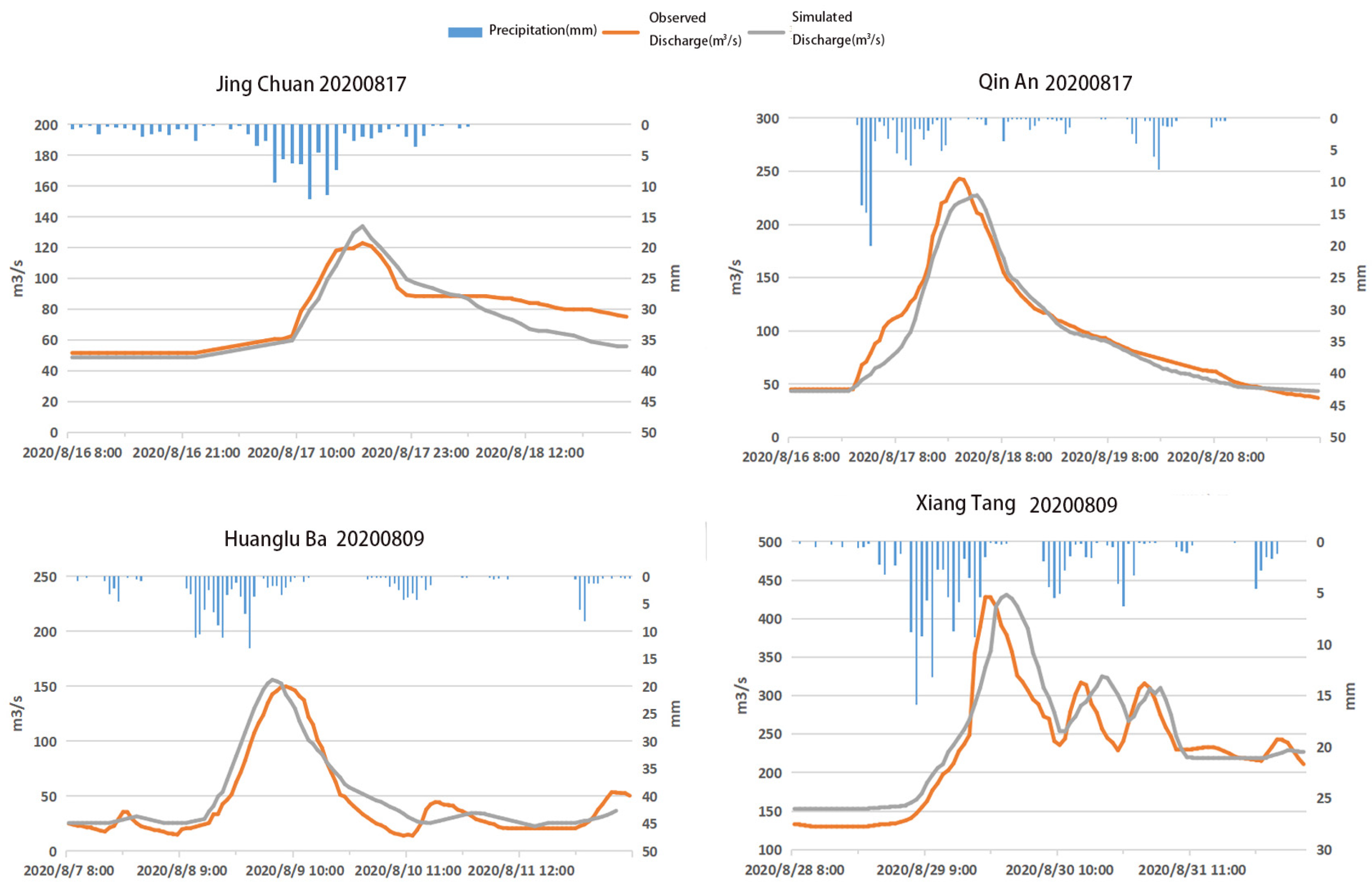
3.3. Model Calibration
3.4. Model Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, Z.; He, B.; Tian, J.; Lu, J.; Liu, R. The theoretical framework for digitalized mountain flood control and its implementation path. China Water Resour. 2022, 8, 41–46. [Google Scholar]
- Trigo, R.M.; Ramos, C.; Pereira, S.S.; Ramos, A.M.; Zêzere, J.L.; Liberato, M.L.R. The deadliest storm of the 20th century striking Portugal: Flood impacts and atmosphere circulation. J. Hydrol. 2016, 541, 597–610. [Google Scholar] [CrossRef]
- He, B.; Huang, X.; Guo, L. Mountain flood disaster prevention routes and core construction contents in China. Flood Prev. Drought Relief China 2012, 22, 19–22. [Google Scholar]
- Sun, D.; Liu, C.; He, B. Research progress on theory and technology of mountain flood disaster prevention and control. Flood Prev. Drought Relief China 2022, 32, 24–33. [Google Scholar]
- Singh, V.P. Hydrologic modeling: Progress and future directions. Geosci. Lett. 2018, 5, 15. [Google Scholar] [CrossRef]
- Jia, P.; Liu, R.; Ma, M.; Liu, Q.; Wang, Y.; Zhai, X.; Xu, S.; Wang, D. Flash Flood Simulation for Ungauged Catchments Based on the Distributed Hydrological Model. Water 2019, 11, 76. [Google Scholar] [CrossRef]
- Hydrologic Engineering Center. HEC-1 Food Hydrograph Package: User’s Manual; Army Corps of Engineers: Davis, CA, USA, 1968. [Google Scholar]
- Metcalf and Eddy, Inc.; University of Florida and Water Resources Engineers, Inc. Storm Water Management Model, Vol 1-Fnal Report; EPA Report No. 11024DOV07/71 (NITS PB-203289); Environmental Protection Agency: Washington, DC, USA, 1971. [Google Scholar]
- Burnash, R.J.C.; Ferral, R.L.; McGuire, R.A. A Generalized Streamflow Simulation System-Conceptual Modeling for Digital Computers Report; U.S. National Weather Service, Silver Spring, Maryland, and Department of Water Resources, State of California: Sacramento, CA, USA, 1973. [Google Scholar]
- Leavesley, G.H.; Lichty, R.W.; Troutman, B.M.; Saindon, L.G. Precipitation Run of Modeling System-User’s Manual; U. S. Geological Survey Water Resources Investigations Report 83-4238; USGS: Denver, CO, USA, 1983. [Google Scholar]
- Beven, K. TOPMODEL: A critique. Hydrol. Process. 1997, 11, 1069–1085. [Google Scholar] [CrossRef]
- Singh, V.P.; Frevert, D.K. (Eds.) Watershed Models; CRC Press: Boca Raton, FL, USA; Taylor and Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- El-Nasr, A.A.; Arnold, J.G.; Feyen, J.; Berlamont, J. Modelling the hydrology of a catchment using a distributed and a semi-distributed model. Hydrol. Process. 2005, 19, 573–587. [Google Scholar] [CrossRef]
- Zoccatelli, D.; Borga, M.; Viglione, A.; Chirico, G.B.; Schl, G.B. Spatial moments of catchment rainfall: Rainfall spatial organisation, Catchment morphology, and flood response. Hydrol. Earth Syst. Sci. Discuss. 2011, 8, 5811–5847. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, R.; Guo, L.; Tian, J.; Zhang, X.; Ding, L.; Wang, C.; Shang, Y. Forecasting and Providing Warnings of Flash Floods for Ungauged Mountainous Areas Based on a Distributed Hydrological Model. Water 2017, 9, 776. [Google Scholar] [CrossRef]
- Barthold, F.E.; Workoff, T.E.; Cosgrove, B.A.; Gourley, J.J.; Novak, D.R.; Mahoney, K.M. Improving Flash Flood Forecasts: The HMT-WPC Flash Flood and Intense Rainfall Experiment. Bull. Am. Meteorol. Soc. 2015, 96, 1859–1866. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Wang, Q.J.; Pagano, T.C. A review of advances in flash flood forecasting. Hydrol. Process. 2011, 25, 2771–2784. [Google Scholar] [CrossRef]
- Wagner, W.; Scipal, K.; Pathe, C.; Gerten, D.; Lucht, W.; Rudolf, B. Evaluation of the agreement between the first global remotely sensed soil moisture data with model and precipitation data. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modeling: The Primer; John Wiley & Sons: Chichester, UK, 2012; pp. 84–96. [Google Scholar]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydro logical System, ‘SHE’, 1: History and philosophy of a physically-based, distributed modeling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydro logical System, ‘SHE’, 2: Structure of a physically-based, distributed modeling system. J. Hydrol. 1986, 87, 61–77. [Google Scholar] [CrossRef]
- Kuriqi, A.; Ardiclioglu, M.; Muceku, Y. Investigation of seepage effect on river dike’s stability under steady state and transient conditions. Pollack Period. 2016, 11, 87–104. [Google Scholar] [CrossRef]
- National Geomatics Center of China. National Geomatics Database. 2019. Available online: https://ngcc.cn/ngcc/ (accessed on 1 January 2023).
- Wang, X.; Zhai, X.; Zhang, Y.; Guo, L. Evaluating flash flood simulation capability with respect to rainfall temporal variability in a small mountainous catchment. J. Geogr. Sci. 2023, 33, 2530–2548. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Binger, R.L.; Harmel, R.D.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Green, W.; Ampt, G. Studies of soil physics-the flow of air and water through soils. J. Agric. Sci. 1911, 4, 11–24. [Google Scholar]
- Huo, W.; Li, Z.; Zhang, K.; Wang, J.; Yao, C. GA-PIC: An improved Green-Ampt rainfall-runoff model with a physically based infiltration distribution curve for semi-arid basins. J. Hydrol. 2020, 586, 124900. [Google Scholar] [CrossRef]
- Liu, R.; Guo, L.; Wang, Y.; Zhang, X.; Liu, Q.; Shang, Y.; Zhai, X.; Tian, J.; Huang, X. A Parallel Flood Forecasting and Warning Platform Based on HPC Clusters. EPiC Ser. Eng. 2018, 3, 1232–1239. [Google Scholar]
- Song, X.; Kong, F.; Zhu, Z. Application of Muskingum routing method with variable parameters in ungauged basin. Water Sci. Eng. 2011, 4, 1–12. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Kavetski, D.; Kuczera, G.; Franks, S.W. Bayesian Analysis of Input Uncertainty in Hydrological Modeling: Application. Water Resour. Res. 2006, 42, W03407. [Google Scholar] [CrossRef]
- Stewart, R.D. A dynamic multidomain Green-Ampt infiltration model. Water Resour. Res. 2018, 54, 6844–6859. [Google Scholar] [CrossRef]
- Wu, S.J.; Hsu, C.T.; Lien, H.C.; Chang, C.H. Modeling the effect of uncertainties in rainfall characteristics on flash flood warning based on rainfall thresholds. Nat. Hazards 2015, 75, 1677–1711. [Google Scholar] [CrossRef]
- Spear, R.C.; Hornberger, G.M. Eutrophication in Peel Inlet, II, Identification of critical uncertainties via generalized sensitivity analysis. Water Res. 1980, 14, 43–49. [Google Scholar] [CrossRef]
- Xu, S.; He, G.; Fang, H.; Bai, S.; Wu, X. Parameter uncertainty and sensitivity analysis of the three Gorges Reservoir and Xiangxi River EFDC model. J. Hydrol. 2022, 610, 127881. [Google Scholar] [CrossRef]
- Li, C. Research of Distributed Hydrologic Modeling in a Typical Large Scale Watershed in Longxi Loess Plateau of China. Ph.D. Thesis, Lanzhou University, Lanzhou, China, 2006. [Google Scholar]
- Shang, L. Estimate Runoffs Based on HIMS model of Xiying River Basin. Ph.D. Thesis, Gansu Agriculture University, Lanzhou, China, 2013. [Google Scholar]
- Sun, B. Research on Distributed Hydrological Simulation and Impact Assessment of Climate Change in Arid and Semi-Arid Regions of Northwest China. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2014. [Google Scholar]
- Wen, L.; Yu, Z.; Zhang, K.; Ragettli, S.; Zhou, M.; Gao, Y.; Ju, Q.; Liu, C. Factors influencing calibration of a semi-distributed mixed runoff hydrological model: A study on nine small mountain catchments in China. J. Hydrol. Reg. Stud. 2023, 47, 101418. [Google Scholar] [CrossRef]

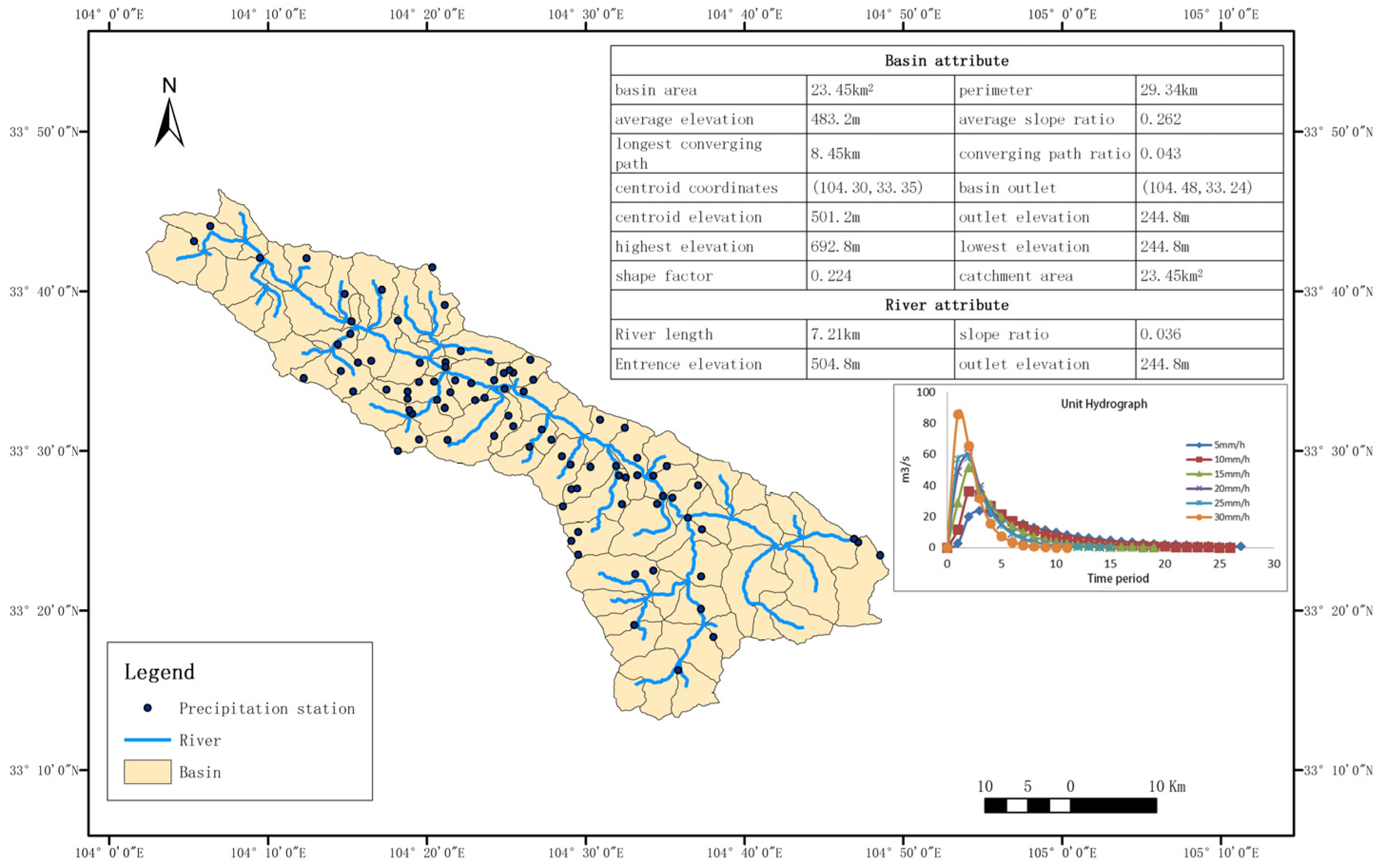
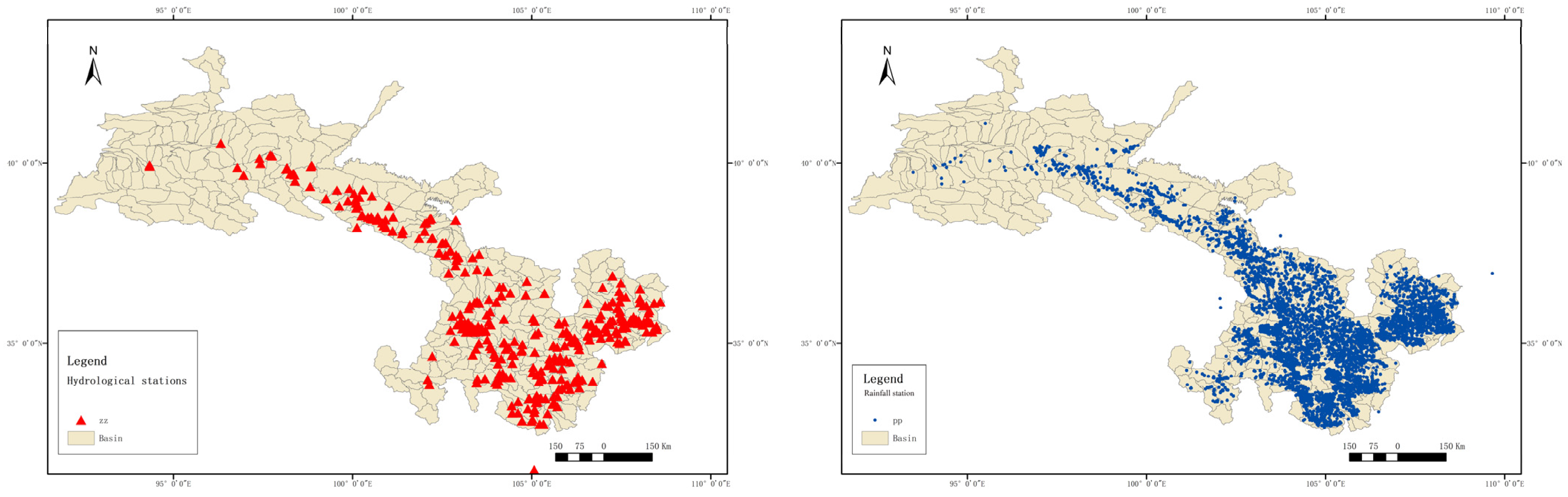
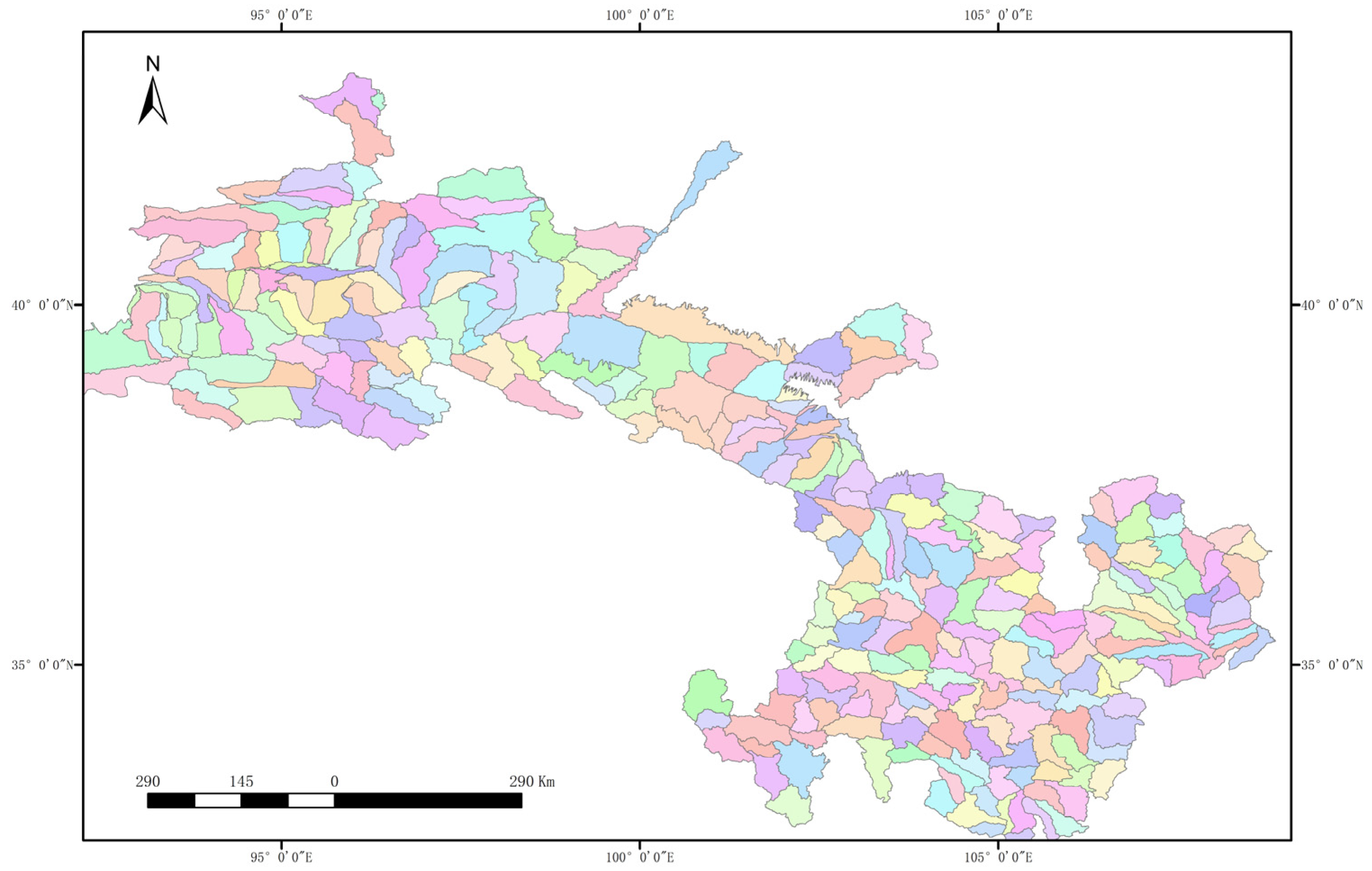

| Water System | Length |
|---|---|
| Shule River | 336.45 km |
| Sugan Lake | 245.7 km |
| Black River | 306.05 km |
| Shiyang River | 146.89 km |
| Huang River | 154.84 km |
| Tao River | 268.04 km |
| Yellow River | 215.54 Km |
| Wei River | 221.43 km |
| Jialing River | 321.84 km |
| Jing River | 254.51 km |
| Beiluo River | 90.80 km |
| Response Unit | Description | Deeper Classification | Runoff Generation Method | Infiltration Rate | Soil Saturation Rate, κ0/(cm/h) | Average Slope, J/° | Soil Depth, h/cm |
|---|---|---|---|---|---|---|---|
| Fast response | Runoff generation is fast, and it is easily influenced by rainfall | fast | Infiltration-excess runoff | μ ≤ 0.25 | κ0 ≤ 0.1 | J > 0.1 | h ≤ 20 |
| middle | Mixed Saturation-excess runoff | 0.25 ≤ μ ≤ 0.6 | 0.1 ≤ κ0 ≤ 0.6 | 20 < J ≤ 25 | |||
| slow | Saturation-excess interflow | 0.6 ≤ μ ≤ 1 | 0.6 ≤ κ0 ≤ 1 | 15 < J ≤ 20 | |||
| Slow response | Runoff generation is slow, and it starts to generate when rainfall reaches a certain amount | Fast | Infiltration-excess runoff Mixed Saturation-excess runoff | 1 ≤ μ ≤ 1.5 | 1 ≤ κ0 ≤ 5 | J ≤ 15 | 20 < h ≤ 50 |
| meddle | Infiltration-excess runoff Mixed Saturation-excess runoff | 5 ≤ κ0 ≤ 15 | |||||
| slow | interflow | 15 ≤ κ0 ≤ 30 | |||||
| Delay response | Hardly influenced by rainfall | Infiltration | μ ≤ 1.5 | κ0 > 30 | J ≤ 15 | 50 < h ≤ 80 |
| Model Cluster | Sub-Basin | Hydrological Model | Area (km2) |
|---|---|---|---|
| Beiluo River basin | 349 | 3 | 4830 |
| Black River basin | 5706 | 30 | 81,231 |
| Yellow River basin | 4633 | 39 | 66,296 |
| Huangshui River basin | 678 | 6 | 10,469 |
| Jialing River basin | 3454 | 34 | 52,645 |
| Jing River basin | 2789 | 31 | 41,627 |
| Shiyang River basin | 4094 | 33 | 62,965 |
| ShuLe River basin | 7180 | 59 | 111,159 |
| Sugan River basin | 1735 | 9 | 27,977 |
| Tao River basin | 2062 | 22 | 31,690 |
| Wei River basin | 2216 | 23 | 32,490 |
| Parameters | Objective Function | Combined Objective Function | ||
|---|---|---|---|---|
| NSE | REQ | ET | C | |
| Rmax | ** | * | * | * |
| Cnonliner | * | ** | ** | |
| Expnonliner | * | * | * | |
| Satv | *** | ** | ** | *** |
| RsoilMax | * | * | * | |
| SoilMax | * | ** | ||
| SoilGMax | * | |||
| SGExp | * | ** | ||
| Cfast_sq | * | * | * | |
| Cslowsq | * | |||
| CG | ||||
| CGSink | ||||
| Parameters | Jing River | Wei River | Jialing River | Tao River | Yellow River | Huang River | Shiyang River | Black River | ShuLe River |
|---|---|---|---|---|---|---|---|---|---|
| Rmax | 0.8 | 0.7 | 0.9 | 0.8 | 0.5 | 0.5 | 0.4 | 0.5 | 0.5 |
| Cnonliner | 0.08 | 0.05 | 0.05 | 0.04 | 0.03 | 0.03 | 0.028 | 0.01 | 0.01 |
| Expnonliner | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| Satv | 75 | 70 | 80 | 75 | 70 | 70 | 70 | 70 | 60 |
| RsoilMax | 15 | 15 | 20 | 15 | 13 | 13 | 13 | 13 | 11 |
| SoilGMax | 0.1 | 0.1 | 0.1 | 0.1 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| Soilmax | 55 | 40 | 60 | 50 | 50 | 50 | 50 | 40 | 40 |
| SGExp | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Cfast_sq | 0.08 | 0.05 | 0.05 | 0.04 | 0.04 | 0.04 | 0.04 | 0.05 | 0.04 |
| Cslowsq | 0.05 | 0.03 | 0.03 | 0.02 | 0.02 | 0.02 | 0.03 | 0.02 | 0.03 |
| CG | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| CGSink | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| Ssnow | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Wei, Y.; Liu, R.; Tian, S.; Wei, K. Hydrological Simulation Study in Gansu Province of China Based on Flash Flood Analysis. Water 2024, 16, 488. https://doi.org/10.3390/w16030488
Zhang B, Wei Y, Liu R, Tian S, Wei K. Hydrological Simulation Study in Gansu Province of China Based on Flash Flood Analysis. Water. 2024; 16(3):488. https://doi.org/10.3390/w16030488
Chicago/Turabian StyleZhang, Bingyu, Yingtang Wei, Ronghua Liu, Shunzhen Tian, and Kai Wei. 2024. "Hydrological Simulation Study in Gansu Province of China Based on Flash Flood Analysis" Water 16, no. 3: 488. https://doi.org/10.3390/w16030488
APA StyleZhang, B., Wei, Y., Liu, R., Tian, S., & Wei, K. (2024). Hydrological Simulation Study in Gansu Province of China Based on Flash Flood Analysis. Water, 16(3), 488. https://doi.org/10.3390/w16030488





