Optimization of Chlorine Injection Schedule in Water Distribution Networks Using Water Age and Breadth-First Search Algorithm

Abstract

Chlorine decay over time and distance travelled poses challenges in maintaining consistent chlorine levels from treatment plants to demand nodes in water distribution networks (WDNs). Many studies have focused on optimizing chlorine booster systems and addressing dosage and location. This study proposes a chlorine injection optimization model for maintaining spatial and temporal chlorine residuals within an acceptable range. First, the approach involves identifying potential pathways from the source to demand nodes using a breadth-first search (BFS) algorithm. Subsequently, the required chlorine injection to maintain a 0.2 mg/L residual chlorine level at demand nodes is estimated based on water age. Finally, a single-objective genetic algorithm optimizes the chlorine injection schedule at the source. The results demonstrated that chlorine estimation based on water age exhibited promising results with an average error below 10%. In addition, the four-interval injection scheme performed well in adapting to changing demand patterns, making the method robust to varying demand patterns. Moreover, the model could accommodate fluctuating water temperature conditions according to operating seasons. This study provides valuable insights into effectively managing chlorine levels and operations of WDNs, and paves the way for using water age for chlorine estimation.

1. Introduction

Water distribution networks (WDNs) play a crucial role in securing human health by delivering sanitized and clean water to prevent waterborne diseases. Chlorine is a widely used disinfectant owing to its cost-effectiveness and efficiency [1]. However, it decays as it travels through pipes, resulting in lower chlorine residuals at distant demand nodes [2]. The World Health Organization (WHO) [3] recommends maintaining residual chlorine levels between 0.2 mg/L and 5.0 mg/L for normal domestic use. This reduces odor complaints and minimizes potential hazards associated with toxic disinfection byproducts [4]. Therefore, ensuring water supply to all demand nodes while maintaining acceptable residual chlorine levels is imperative.

Several studies have optimized chlorine injection in WDNs, primarily focusing on booster chlorination [5,6]. These studies examined various aspects, such as optimizing booster injection schedules [4,7,8,9,10] and booster location [5]. Some studies explored combinations of booster scheduling and location [11,12,13,14]. In addition, chlorine injection schedule optimization was extended to include hydraulic controls as decision variables, such as pump scheduling [15,16] and valve operations [17].

In addition to chlorine, water age is a crucial factor in water quality evaluation, serving as a surrogate measure [18]. The combination of the water age and chlorine concentration in WDNs has gained substantial attention. Xin et al. [19] introduced the concept of chlorine age, a metric derived from water age, to overcome the challenges associated with acquiring the chlorine calculation parameters necessary for optimizing chlorine boosters. This concept enables determining optimal booster locations, reducing chlorine dosages, and uncertainty analysis of residual chlorine. Furthermore, Monteiro et al. [20] evaluated water age performance by incorporating chlorine concentration, and exploring the correlation between water age and free-chlorine concentration, demonstrating that water age is a valuable tool for assessing water quality through WDN behavior. In a related context, Geng et al. [21] examined the relationship between water age and chlorine to control the maximum water age based on total chlorine decay in the secondary water supply system, highlighting the practical application of water age in enhancing water quality, particularly in older communities, and improving the taste of tap water.

Previous studies have presented effective methods for maintaining residual chlorine levels and reducing mass disinfection at the water source. This study emphasizes the significance of optimizing the initial chlorine injection at the source and reducing computational difficulties in WDN water quality simulations. Computational difficulties primarily refer to the challenges posed by dealing with many variables when multiple chlorine boosters are employed, each requiring optimization to work effectively with the dynamic behavior of the WDN. This study focuses on a single variable—chlorine injection at the source—by considering water age as a factor. Research on the combined use of water age and chlorine level in water quality simulations is increasing. However, the incorporation of water age in estimating the initial chlorine at the source has not been considered despite its substantial potential for enhancing water quality assessment in WDNs.

This study focuses on methodologies for estimating the initial chlorine injection at the source as part of chlorine injection scheduling using water age. The objectives of this study are as follows: (1) to assess water age performance in estimating the initial chlorine injection and (2) to develop an optimal schedule for chlorine injection at the source to maintain chlorine levels of 0.2–1.0 mg/L at demand nodes. This approach estimates the initial chlorine injection based on water age while considering the first-order decay equation. Furthermore, the individual wall decay for each pipe is calculated using the breadth-first search (BFS) algorithm by tracing the possible water delivery pathways from the source to each demand node. Subsequently, the optimal chlorine injection schedule is determined using a genetic algorithm (GA). This study introduces a new approach for optimizing chlorine injection, and enhancing the efficiency and practicality of WDNs.

The remainder of this paper is structured as follows: Section 2 outlines the materials and methods used for chlorine injection estimation and optimization. Section 3 presents and discusses the results. Finally, Section 4 provides concluding remarks and summarizes the findings and suggestions for future studies.

2. Materials and Methods

In this study, a single-objective optimal chlorine scheduling scheme was developed by employing water age and the BFS algorithm. The first step involved the identification of water delivery pathways, aiming to determine all potential routes from the source to the demand nodes. Subsequently, the study moved on to chlorine injection estimation, where the required chlorine injection at the source was calculated to maintain residual chlorine levels within the range of 0.2–1.0 mg/L at the various demand nodes. Finally, the optimization phase focused on refining the chlorine injection schedule at the source, utilizing the BFS algorithm to enhance the efficiency and effectiveness of the overall chlorine distribution system. This multi-step approach contributes to the development of an optimized and reliable chlorine scheduling scheme at the source. 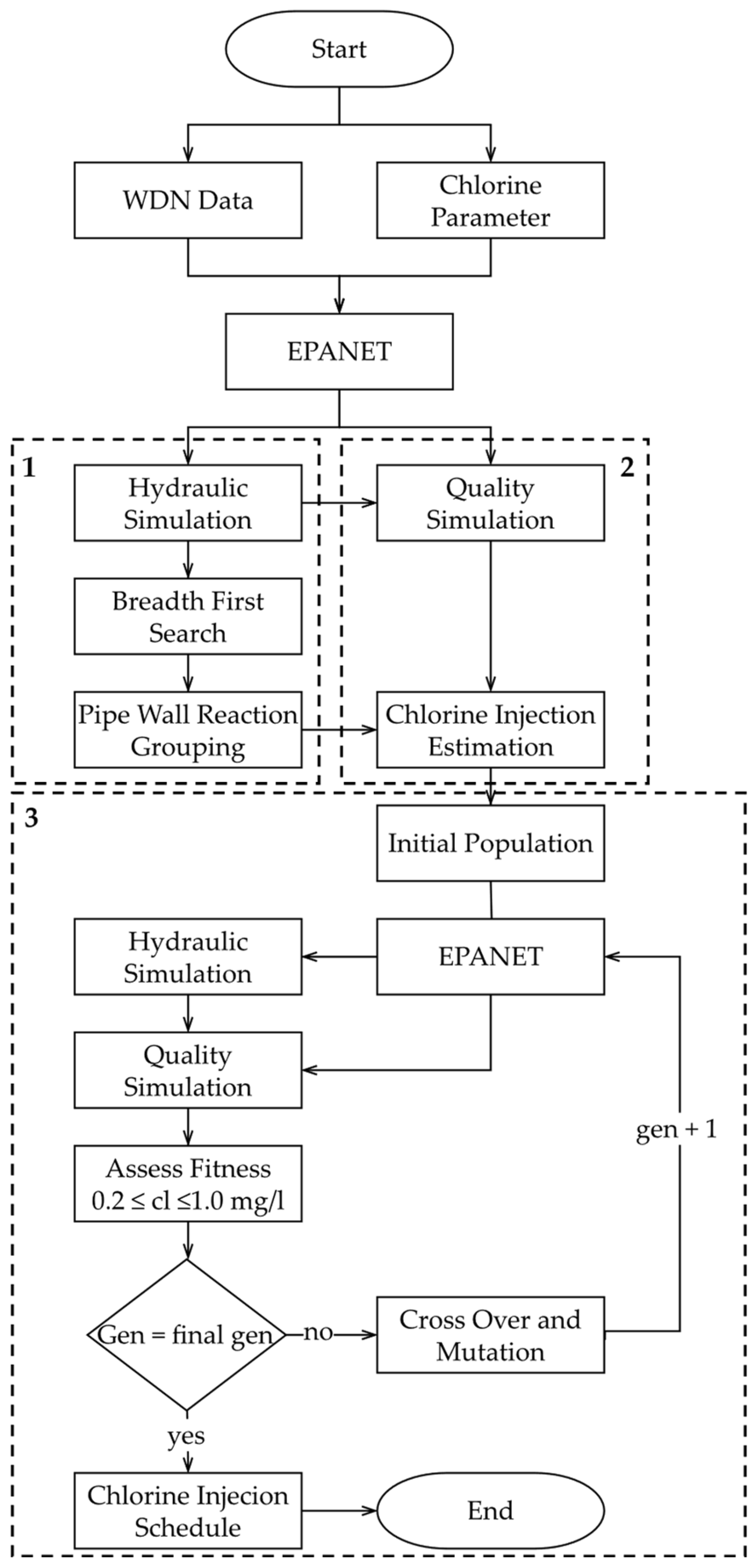Figure 1 illustrates the proposed method.

2.1. Chlorine Decay

The model in this study adopts first-order chlorine decay kinetics [22], expressed as

$$C\left(t\right)=C_0 e^{-kt}$$

(1)

where $C\left(t\right)$ represents the chlorine concentration (mg/L) at time $t$, $C_0$ is the initial chlorine concentration (mg/L), $t$ is the residence time within the network (day), and $k$ is the chlorine decay constant (day⁻¹). The decay constant, $k$, is determined by the sum of two components: the bulk reaction constant ($kb$) and pipe wall reaction constant ($kwall$), representing reactions within the bulk fluid and with the pipe wall material, respectively. Mathematically, $k$ can be expressed as

$$k=kb+kwall$$

(2)

$kb$ is typically determined through bottle testing, involving sample collection for analysis [23]. By contrast, $kwall$ is influenced by several parameters, including mass transfer kinetics [24]. The following equation defines mass transfer kinetics:

$$kf=Sh\frac{Dm}{D}$$

(3)

where $kf$ is the mass transfer coefficient (m/day), $Sh$ is the Sherwood number, $Dm$ is the molecular diffusivity responsible for the spreading component owing to molecular motion (m²/day), and $D$ is the pipe diameter (m). The value of $Sh$ varies with the type of fluid flow. In a laminar flow, $Sh$ is calculated as follows:

$$Sh=3.65+\frac{0.0668 \left(\frac{D}{L}\right) Re Sc}{1+0.04 {\left[\left(\frac{D}{L}\right)Re Sc\right]}^{\frac{2}{3}}}$$

(4)

where $Re$ represents the Reynolds number, $Sc$ represents the Schmidt number ($\nu /Dm$), characterizing the kinematic viscosity of water divided by the molecular diffusivity, and $L$ denotes the pipe length (m). For a turbulent flow, the expression for $Sh$ becomes

$$Sh=0.0149 R{e}^{0.88}S{c}^{\frac{1}{3}}$$

(5)

The overall $kwall$ is determined as

$$kwall=\frac{2 kw kf}{R\left(\right|kw|+kf)}$$

(6)

where $kw$ denotes the wall reaction rate (m/day) and $R$ represents the pipe radius (m).

2.2. Study Area

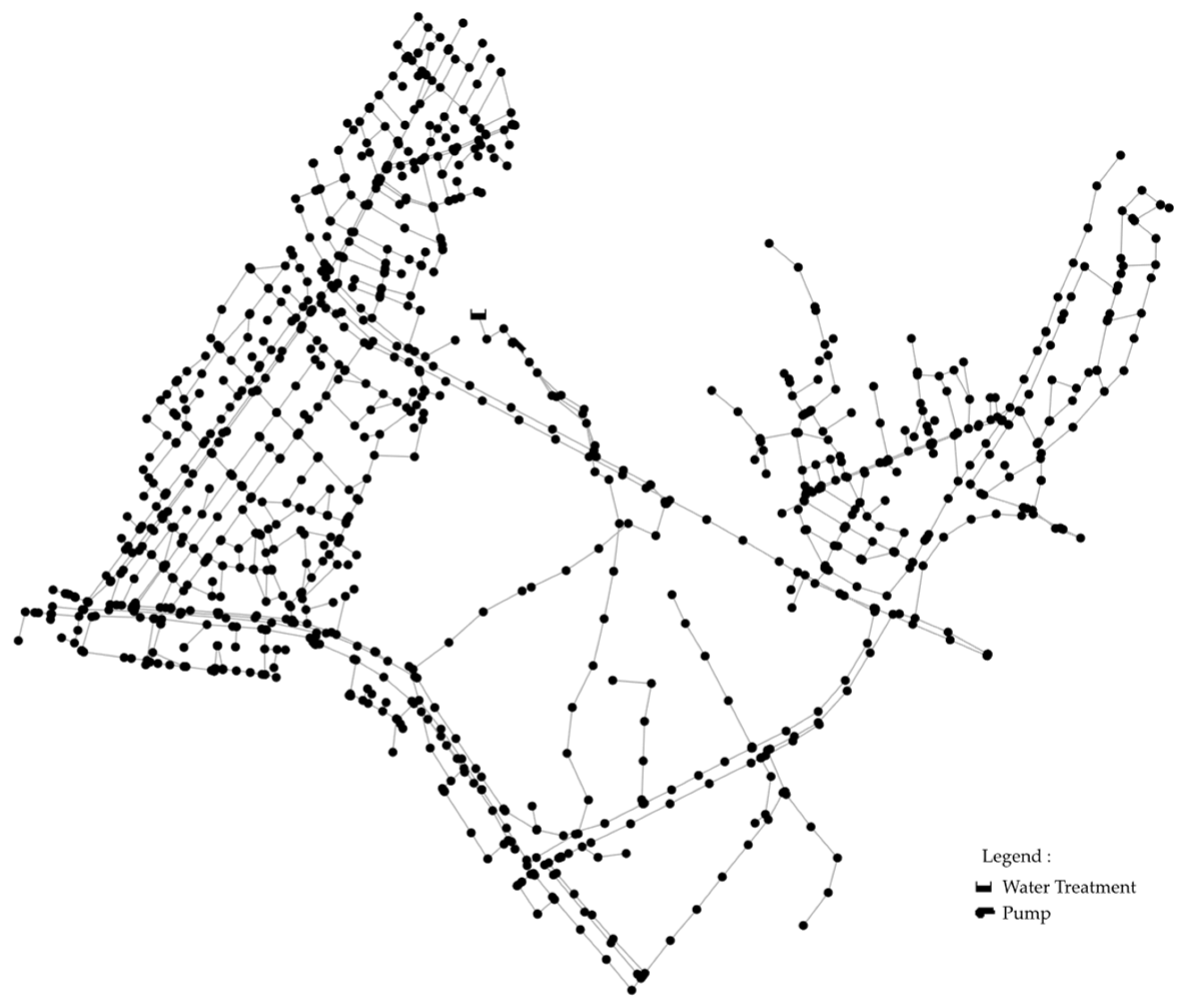
The proposed model was implemented on an actual operational WDN in South Korea, as shown in Figure 2. Several modifications were made for demonstration purposes. The network comprised 1032 demand nodes, one source, one pump, and 1159 pipes. In this study, chlorine parameters were sourced from previous studies. The bulk reaction constant ($kb$), measured in day⁻¹, was estimated by Lee [25] in the domestic P-city in South Korea as 0.576 (25 °C), 0.1872 (18 °C), and 0.1056 (4.5 °C) day⁻¹, corresponding to typical water temperatures in summer, spring/fall, and winter, respectively.

The wall reaction rate ($kw$) expressed in m/day, was set to 0.01 m/day based on a range reported by K-water [26] of 0.001 m/day to 0.05 m/day, aligning with values found in the previous study. The kinematic viscosity ($\nu$) and molecular diffusivity ($Dm$), measured in m²/s, contribute to the temperature-dependent variability of $kw$. The values for these parameters, specifically kinematic viscosity [27] and molecular diffusivity [28], were obtained from the literature. Subsequently, data from these sources were interpolated and extrapolated to yield relevant results. It should be noted that these steps were undertaken for research purposes.

Table 1. Chlorine parameter data.

Temp (°C)	$\mathit{k}\mathit{b}$ (day−1)	$\mathit{\nu }$ (m2/s)	$\mathit{D}\mathit{m}$ (m2/s)
4.5	0.1056	1.55 × 10−6	6.74 × 10−10
18.0	0.1872	1.06 × 10−6	1.14 × 10−9
25.0	0.576	9.03 × 10−7	1.38 × 10−9

presents the summarized data.

This study primarily aimed to formulate a schedule for the initial chlorine injection at the source. Accordingly, two operational scenarios were considered, as detailed in

Table 2. Chlorine injection scenarios.

Scenario	Operation Method	Number of Decision Variable	Interval Time Step (hour)
1	Single Injection	1	24
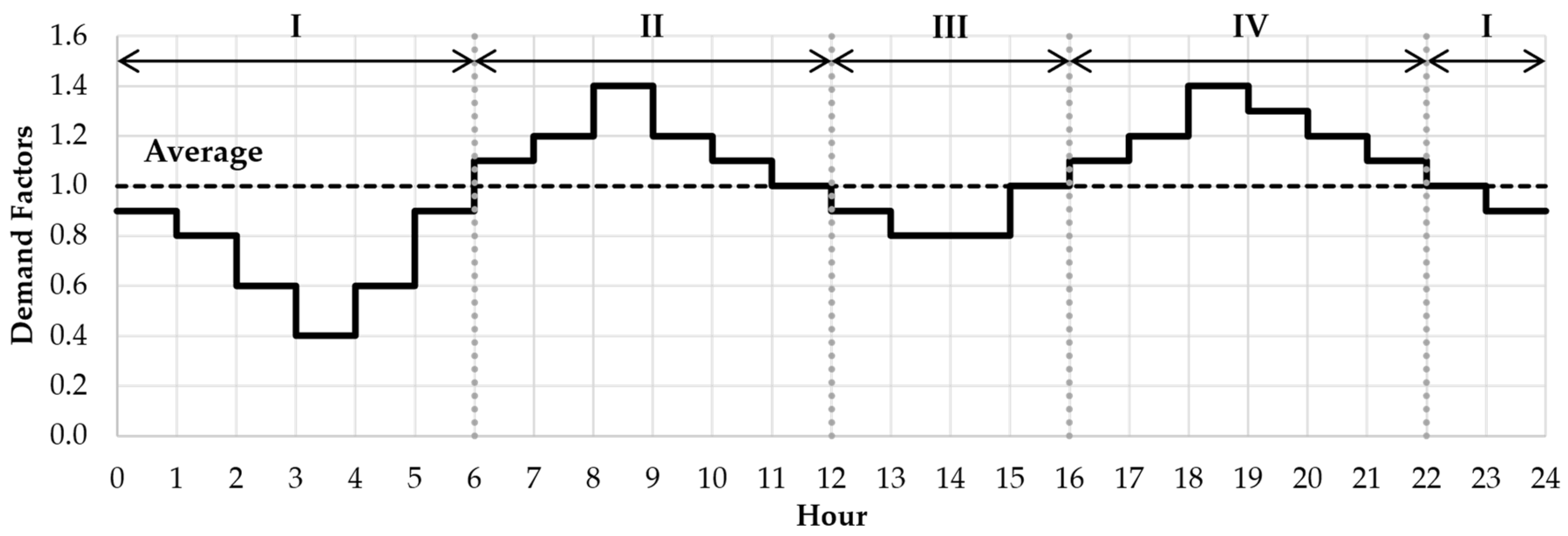
2	4-Interval Injection	4	8–6–4–6

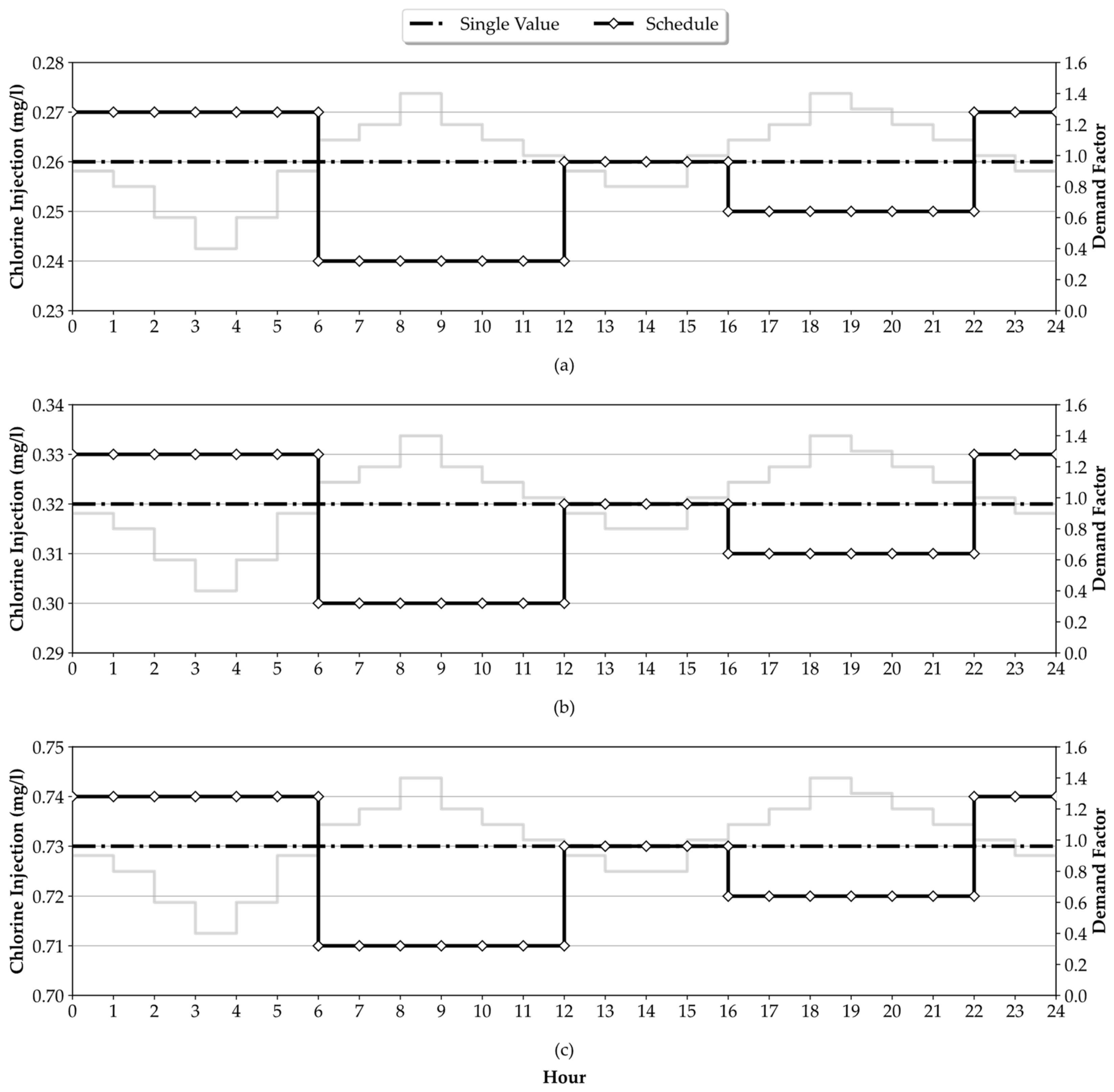
. These scenarios were investigated to assess the uniformity of residual chlorine concentration at the demand nodes. Scenario 1 represents a conventional operation involving single-value chlorine injection, serving as a reference for comparison. Scenario 2 considers the demand pattern of the WDN, as illustrated in Figure 3. In this scenario, chlorine injection is divided into four intervals, each aligned with variations in demand levels, encompassing high- and low-demand groups.

2.3. Hydraulic and Water Quality Simulation

This study developed the hydraulic and water quality model using EPANET 2.2 [29] and WNTR [30], a Python [31] package designed for EPANET. The hydraulic simulation results assisted in calculating $kwall$ for each pipe in the WDN, whereas the water quality simulation determined the water age and residual chlorine concentration. Water quality simulation specifically extracts water age, representing the time required for water to travel from the source to a demand node. Several network attributes, such as the demand quantity, tank design and operation, and network layout, influence water age [32]. In EPANET, water entering the network is considered to be of age zero, with its age increasing over time owing to a zeroth-order growth reaction at a reaction rate of one [29]. The pipe volumes and flow rates for various paths from the source to the demand node determine the water age [19]. The simulation time was set to seven days, and the final 24 h was allocated for data collection. This extended simulation duration is essential for ensuring a stable water age output. Consequently, each demand node in the network had 24 distinct water ages.

2.4. Water Delivery Pathway Identification

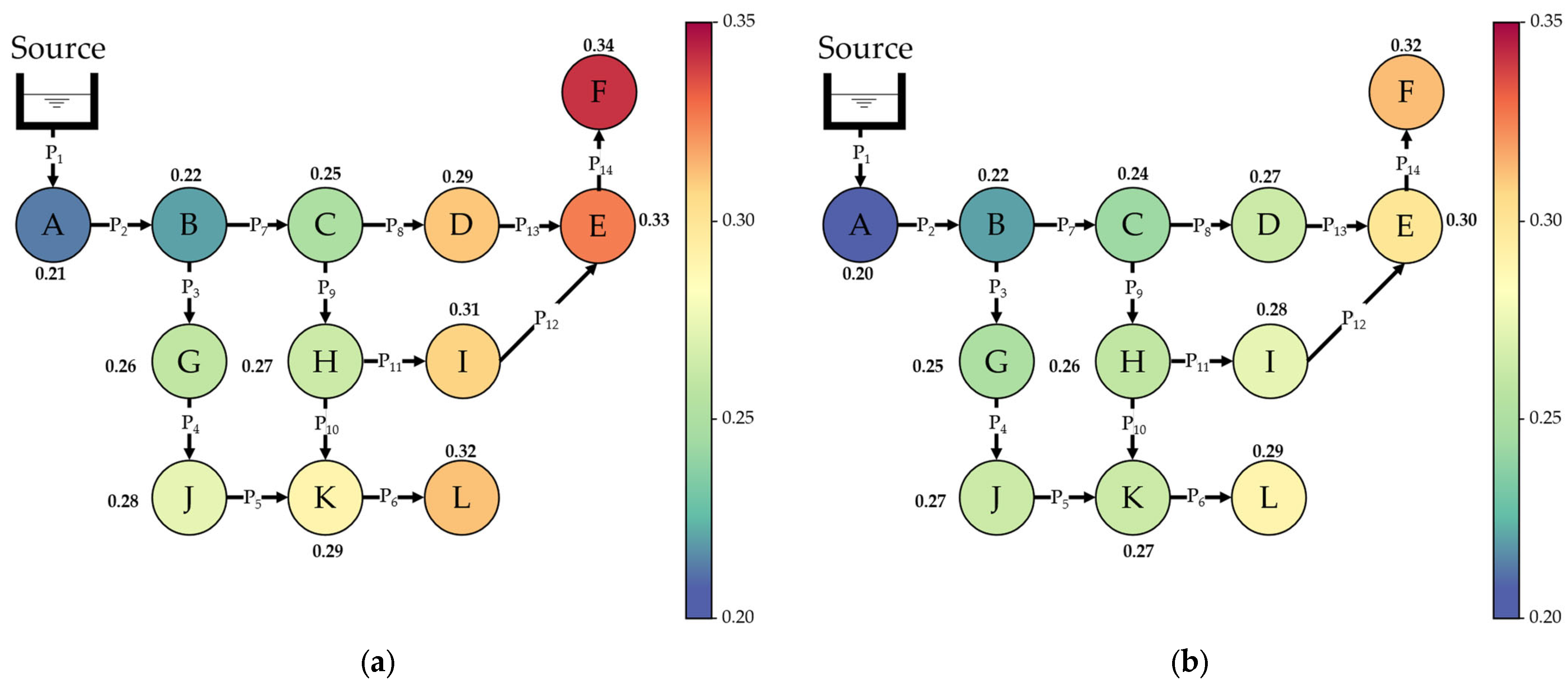
In a WDN, each pipe has a unique $kwall$ value owing to its individual properties, as referenced in Equation (6). Since water from a source follows specific paths to different demand nodes, employing a global average pipe $kwall$ may lead to inaccuracies due to variations in $kwall$ values. To address this, BFS algorithm is utilized to group $kwall$ values for each pipe based on the water delivery paths from the source to each demand node. BFS is known for its systematic exploration of all network nodes. 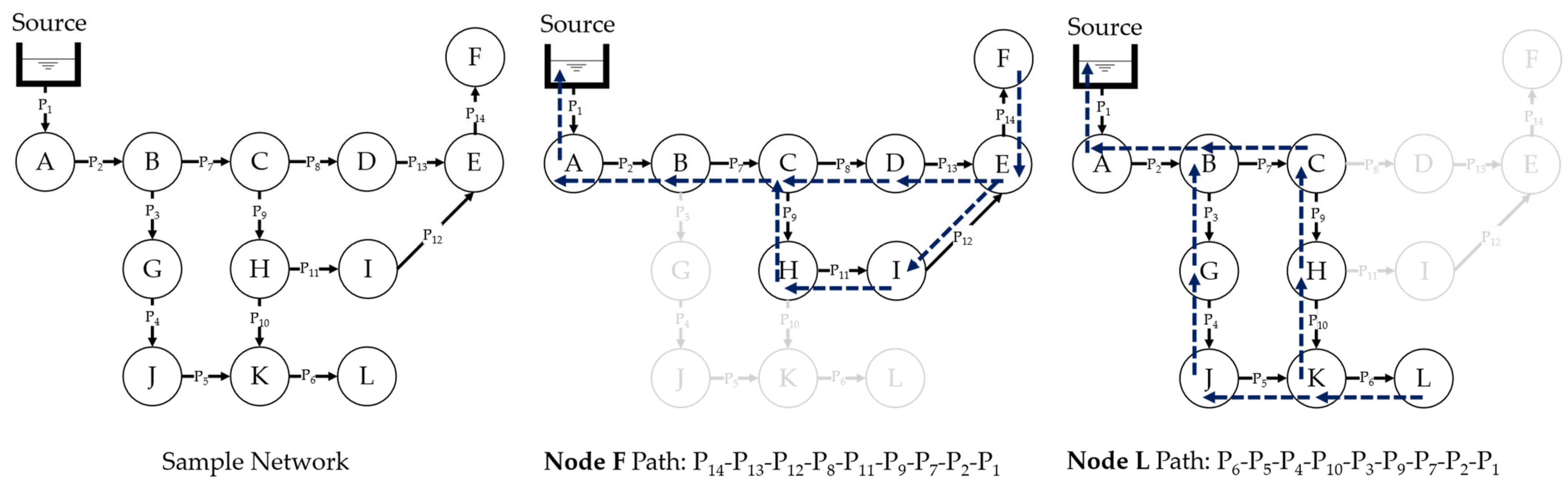Employing the first-in-first-out queue method [33], BFS enables identifying all possible pathways from the source to each demand node, as shown in Figure 4.

Figure 4 shows a sample network in which the BFS is applied to determine the paths from demand nodes F and L to the source. The BFS efficiently revealed all possible routes. For example, for node F, the pipe path was P₁₄-P₁₃-P₁₂-P₈-P₁₁-P₉-P₇-P₂-P₁. Each path for every demand node was stored to compute the average $kwall$ value of each node using a weighted average approach, with the flow rate as the weighting factor, defined as follows:

$$\overline{{kwall}_n}=\frac{\sum _{i=1}^{Npipe}{w}_i {kwall}_i}{\sum _{i=1}^{Npipe}{w}_i }$$

(7)

where $\overline{kwal{l}_n}$ represents the $kwall$ value for node $n$, ${kwall}_i$ is the $kwall$ value of pipe $i$ obtained using Equation (6), $w_i$ is the flow rate at pipe $i$, and $Npipe$ is the number of pipes in the flow path from the source to node $n$.

2.5. Chlorine Injection Estimation

With the decay constant $k$ (= $kb$ + $kwall$) obtained for each node, the required chlorine injection at the source can be estimated for each node using Equation (8), modified from Equation (1) as follows:

$$C_0\left(t\right)=C e^{k·{WA}_t}$$

(8)

While the variables remained the same as in Equation (1), $C_0\left(t\right)$ and $C$ were redefined in this study. $C_0\left(t\right)$ represents the required chlorine concentration to be injected at the source at time $t$ to maintain the target chlorine level $C$ at the demand node. In this study, the target chlorine residue at the node was set to 0.2 mg/L, whereas the maximum chlorine level was limited to 1.0 mg/L. In Equation (8), ${WA}_t$ is the water age of the target node at time $t$.

Figure 5 illustrates the required chlorine injection. The value of each node indicates the chlorine concentration required at the source to ensure that the target level of 0.2 mg/L is met at each node during specific hours in the sample network. The chlorine requirements vary uniquely for each node, fluctuating at various times throughout the 24-h period. The demonstration focused on hours 4 (the lowest demand time) and 19 (one of the peak demand periods) following the demand pattern presented in Figure 3.

For example, in Figure 5a, the value at each node represents the amount of chlorine to be injected at the source to achieve the target chlorine level of 0.2 mg/L for every node at hour 4. Validation is crucial after determining the required source-injection chlorine concentration. This involves inputting the calculated source-injection chlorine value into the EPANET simulation, which calculates the residual chlorine of each demand node. The obtained values are then compared with the target value of 0.2 mg/L for assessment. This process ensures the validity of Equation (8) for estimating the source-injection chlorine concentration using the water age.

Notably, each node has distinct hourly requirements and applying all requirements at the source is unfeasible. To optimize the chlorine injection schedule at the source, the maximum required chlorine for each hour was collected from all demand nodes, resulting in 24 specific values. The minimum (i.e., 0.2 mg/L) and maximum values were then set as boundaries for the chlorine injection optimization process described in the next section.

2.6. Chlorine Injection Optimization

A single-objective GA was employed to optimize the chlorine injection schedule. The objective was to determine the optimal chlorine injection concentration at the source to ensure a uniform spatiotemporal residual chlorine distribution across the network. This optimization process uses the mean absolute percentage error (MAPE) as the objective function, defined as follows:

$$minimize f=\frac{1}{T}{\displaystyle \sum _{t=1}^T}\frac{1}{Nnode}\sum _{n=1}^{Nnode}\frac{{|c{l}^{*}-cl}_n^t|}{c{l}^{*}},$$

(9)

subject to

$$0.2\le {cl}_n^t\le 1.0$$

(10)

where $Nnode$ represents the number of nodes in the network, $c{l}_n^t$ denotes the residual chlorine concentration at node $n$ at time $t$, and $c{l}^{*}$ denotes the target chlorine concentration (0.2 mg/L). A smaller MAPE value indicates a more uniform chlorine distribution within the WDN, with zero being the ideal value. The GA was executed with a population size of 100 and run for 1000 generations with the assistance of the Pymoo library [34].

3. Results and Discussion

Chlorine injection was used to assess the water age approach. Two scenarios were presented, each with three different $kb$ values, to reflect the water treatment plant operation and account for seasonal temperature changes. The chlorine injection was optimized to obtain the optimal schedule.

3.1. Required Chlorine Injection Estimation

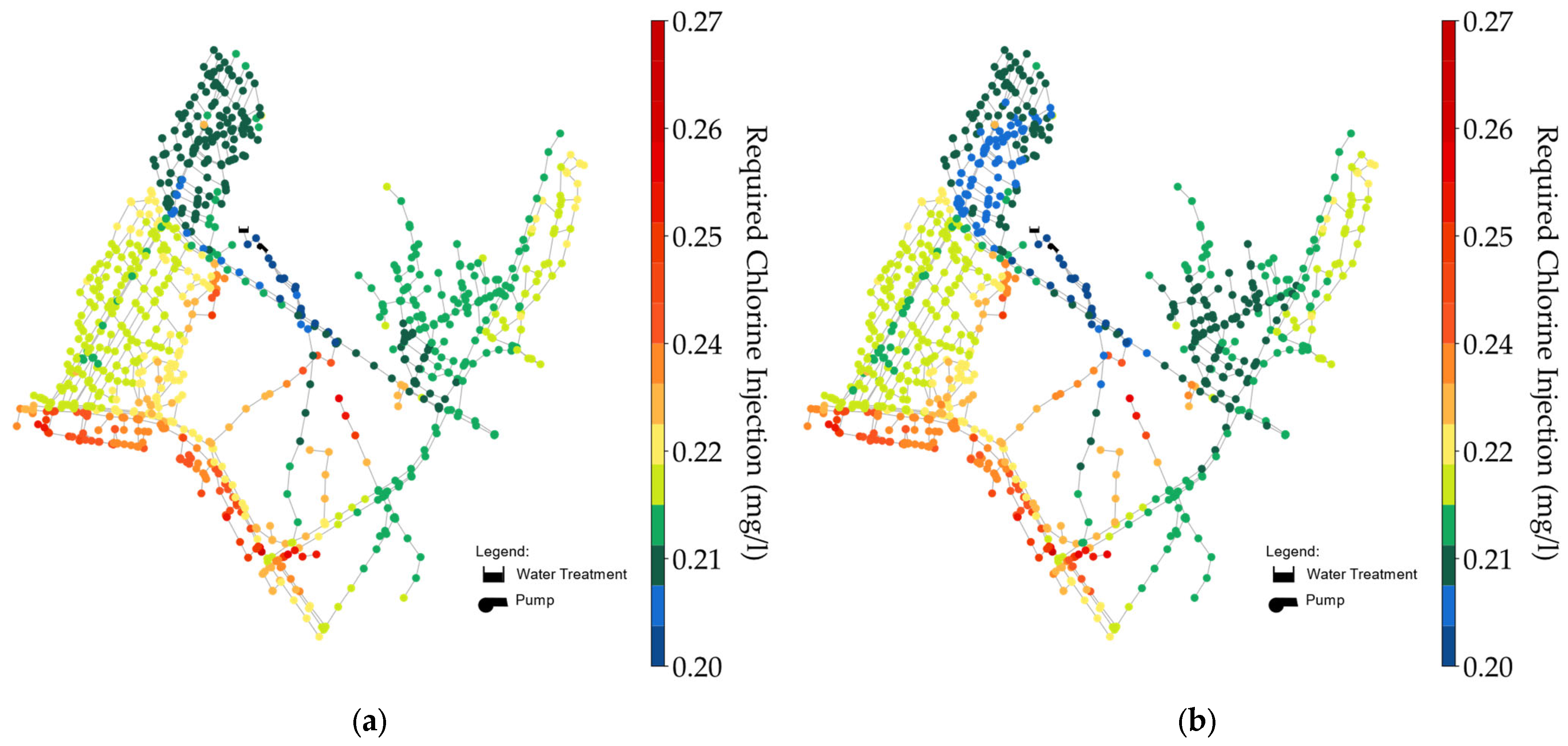
Following the flow pathway determined by the BFS and Equation (8), the required chlorine injection at the source was calculated and visualized for each node, as shown in Figure 6. The figure illustrates the required source-injection chlorine concentration for $kb$= 0.1056 day⁻¹ (winter season) at hours 4 and 19, representing the lowest and highest demand times, respectively. Figure 6 shows the distribution dynamics of the required chlorine injection at the source for each node to achieve the target chlorine residual value of 0.2 mg/L within the WDN. The water age and required source-injection chlorine concentration increased with the distance from the source. The required chlorine injection differed at both times; the graph shows that hour 4 had higher injections than hour 19. This was because of the longer residence time of water in the network during low-demand periods, leading to higher chlorine decay. By contrast, water moved faster during high-demand periods, reducing travel time; thus, a relatively lower chlorine injection was acceptable to meet the target nodal chlorine. This highlights the impact of chlorine decay over time and the distance traveled within the network.

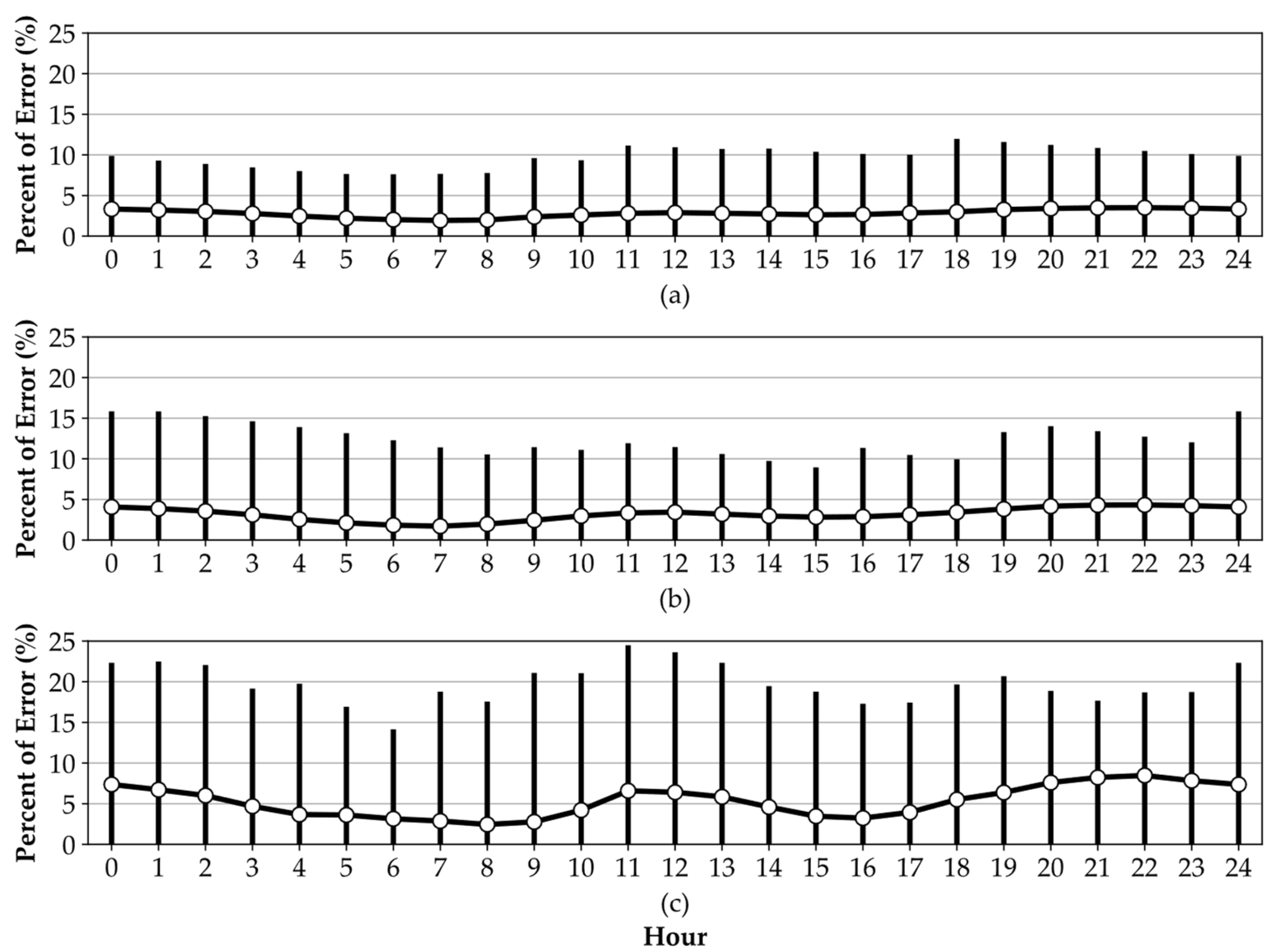
The estimated source-injection chlorine amount was assessed through water quality simulation using EPANET and compared with the target value (0.2 mg/L). Figure 7 shows the percentage error for the three $kb$ conditions. The circle denotes the average percentage error over all nodes at each hour. The upper and lower edges of the bar represent the maximum and minimum percentage errors, respectively, for each hour. The figure reveals that the highest percentage of error remained below 25%, indicating a small margin of error in the source chlorine injection estimates using the water age. The average error percentage consistently remained under 10%, highlighting the overall accuracy of the suggested approach using the water age. For example, at a $kb$ of 0.1056 day⁻¹, only three demand nodes exceeded a 10% error rate. Furthermore, increased $kb$ values of 0.1872 and 0.576 day⁻¹ increased the numbers of nodes with errors exceeding 10% to 14 and 21, respectively. These three error rates collectively accounted for 0.3, 1.4, and 2.0% of all nodes, respectively. Notably, the errors are primarily attributed to the estimation of the average $kwall$ value using a weighted average approach in Equation (7) and the usage of water age rather than the actual decay time to each node in Equation (8).

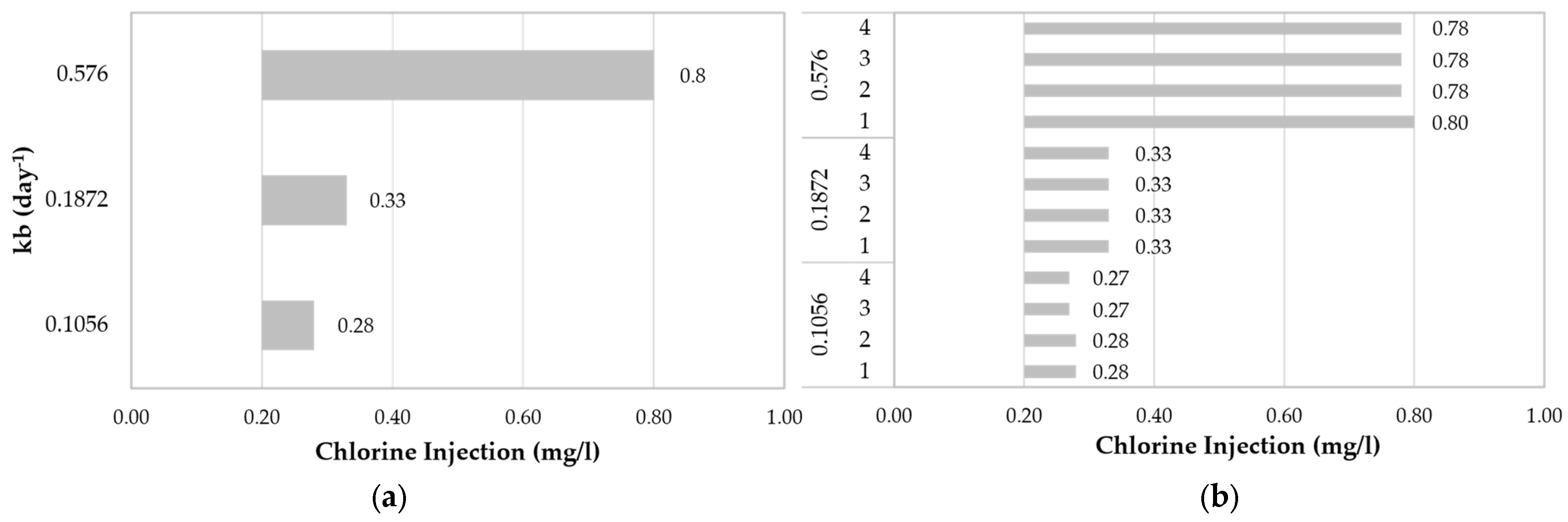
3.2. Potential Source-Injection Chlorine Range

The range of the source-injection chlorine concentration was determined based on the required injection values obtained in the previous section. Two operational scenarios, single injection and four-interval injection, were tested, as listed in Table 2. Figure 8 shows the obtained ranges for both scenarios, demonstrating a direct correlation between the $kb$ and chlorine injection ranges; that is, a higher $kb$ resulted in a broader range for potential chlorine injection. This approach reduces the search space in the optimization process (described in the next section) by predefining the acceptable chlorine injection ranges, reducing the extensive computational effort of water quality simulations using EPANET.

3.3. Chlorine Injection Optimization

Figure 9 shows the optimization results obtained using the GA. These results represent values derived from various chlorine injection schedules yielding the lowest MAPE from the target residual chlorine (0.2 mg/L) without violating the constraint of chlorine levels within the range of 0.2–1.0 mg/L for each $kb$. The figure shows the chlorine injection schedule at the source for each $kb$ value in the two injection-scheduling scenarios, demonstrating that the injection pattern of the four-interval schedule aligned with the demand pattern and exhibited an inverse-proportional relationship. Specifically, low-demand periods required higher injection concentrations and vice versa. As mentioned previously, a lower demand requires a higher injection rate owing to a longer residence time. However, during high-demand periods, characterized by faster water movement, a lower chlorine injection rate is sufficient. Notably, the three $kb$ values shared a similar injection pattern, offering practical insights into managing dynamically fluctuating demands.

Table 3. Statistics of optimal results for two scenarios.

Statistics	kb = 0.1056		kb = 0.1872		kb = 0.576
	Sce.1	Sce.2	Sce.1	Sce.2	Sce.1	Sce.2
Mean Concentration (mg/L)	0.243	0.237	0.279	0.285	0.521	0.516
Standard Deviation Concentration (mg/L) *	0.044	0.038	0.086	0.081	0.332	0.328
Minimum Concentration (mg/L)	0.206	0.200	0.204	0.200	0.200	0.200
Maximum Concentration (mg/L)	0.260	0.270	0.320	0.330	0.730	0.740
Dosage Input (kg/day) [A]	92.7	90.5	114.1	111.9	260.3	258.1
Dosage Output (kg/day) [B]	87.0	84.8	102.0	99.9	188.4	186.7
Dosage Decay (kg/day) [A-B-C]	8.0	7.9	14.8	14.6	77.2	76.6
Dosage Storage Change (kg/day) [C]	−2.26	−2.21	−2.68	−2.63	−5.20	−5.15

* Standard deviation was calculated using the target residual chlorine value (0.2 mg/L).

summarizes the various statistics for a 24-h simulation period. The standard deviation, calculated from the target chlorine value of 0.2 mg/L, reflects the variability in chlorine concentrations. In Scenario 2, the standard deviation was consistently lower than in Scenario 1, indicating a more controlled chlorine distribution. This is consistent with the reduced mean concentrations, demonstrating the effectiveness of the four-interval schedule in maintaining chlorine levels close to the target value. Scenario 2 exhibited a slight reduction in chlorine usage and user consumption, resulting in 2.3, 1.9, and 0.8% savings for the three $kb$ values, attributed to the enhanced injection flexibility. In the table, “Dosage Input” corresponds to the total obtained by multiplying the chlorine injection concentration by the flow discharged from the water treatment plant. Conversely, “Dosage Output” denotes the supplied residual chlorine multiplied by the demand at the consumer node. The “Storage Change” represents the sum of the remaining chlorine within the pipes. Note that the network did not have a storage tank. “Dosage Decay” signifies the chlorine decay in the WDN and is calculated as [Dosage Input–Dosage Output–Storage Change].

3.4. Spatiotemporal Chlorine Residuals

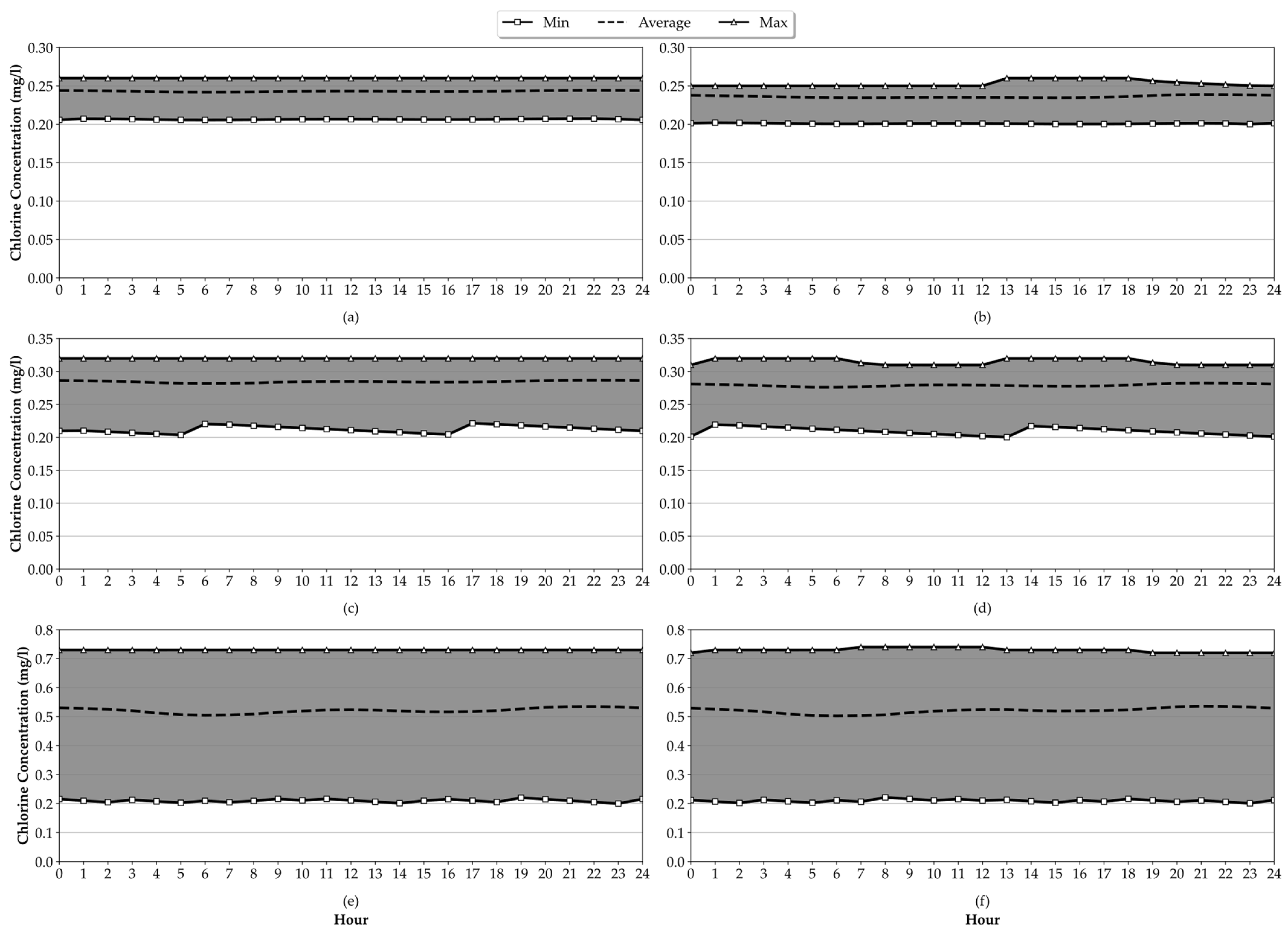
Figure 10 illustrates the temporal variability in chlorine residuals, showing the minimum and maximum chlorine residual values at each hour for both scenarios. Notably, a larger $kb$ value resulted in a broader gap between the maximum and minimum residual chlorine values. Although both scenarios shared similar seasonal average residual chlorine values, Scenario 2 exhibited more temporal variability in the spread between the maximum and minimum values.

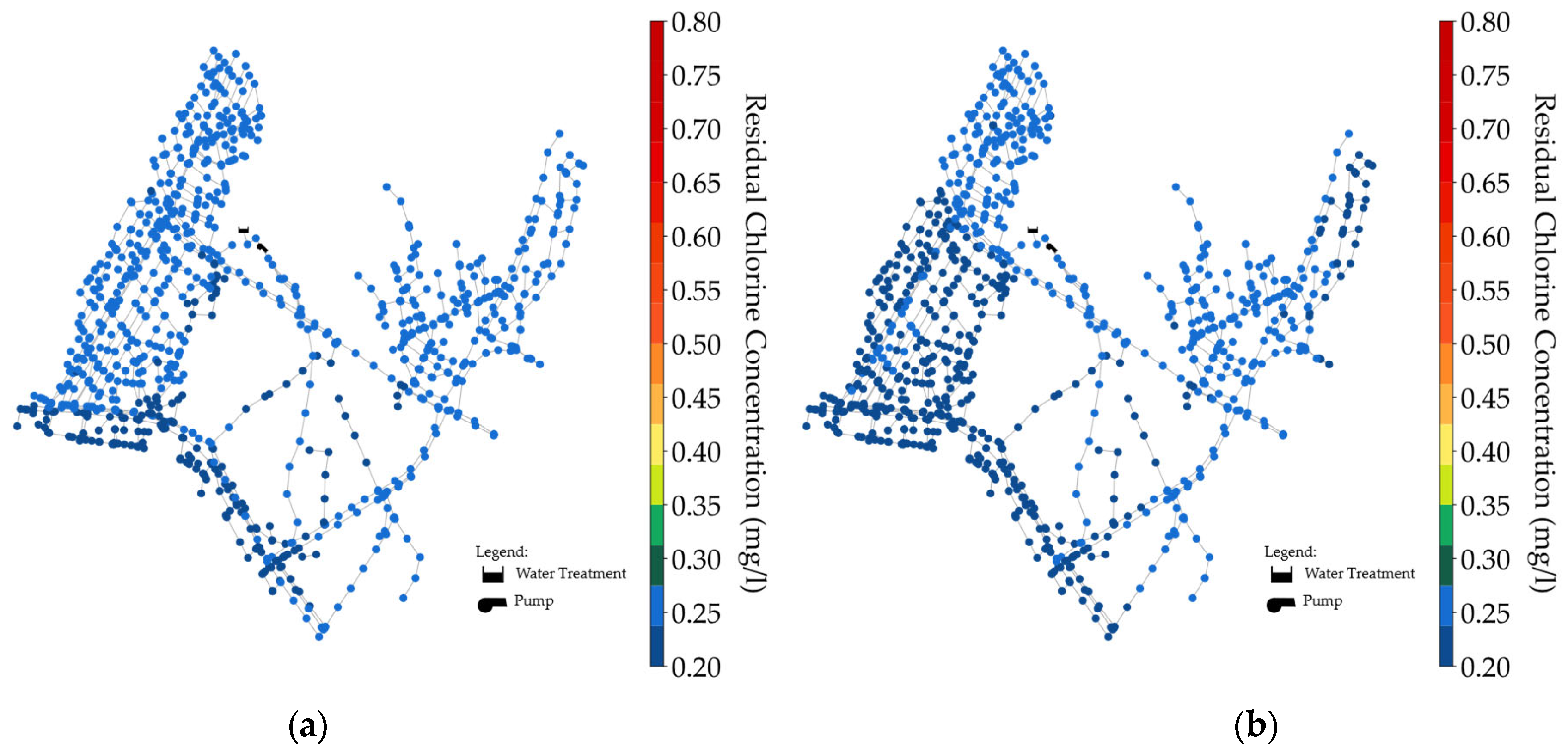
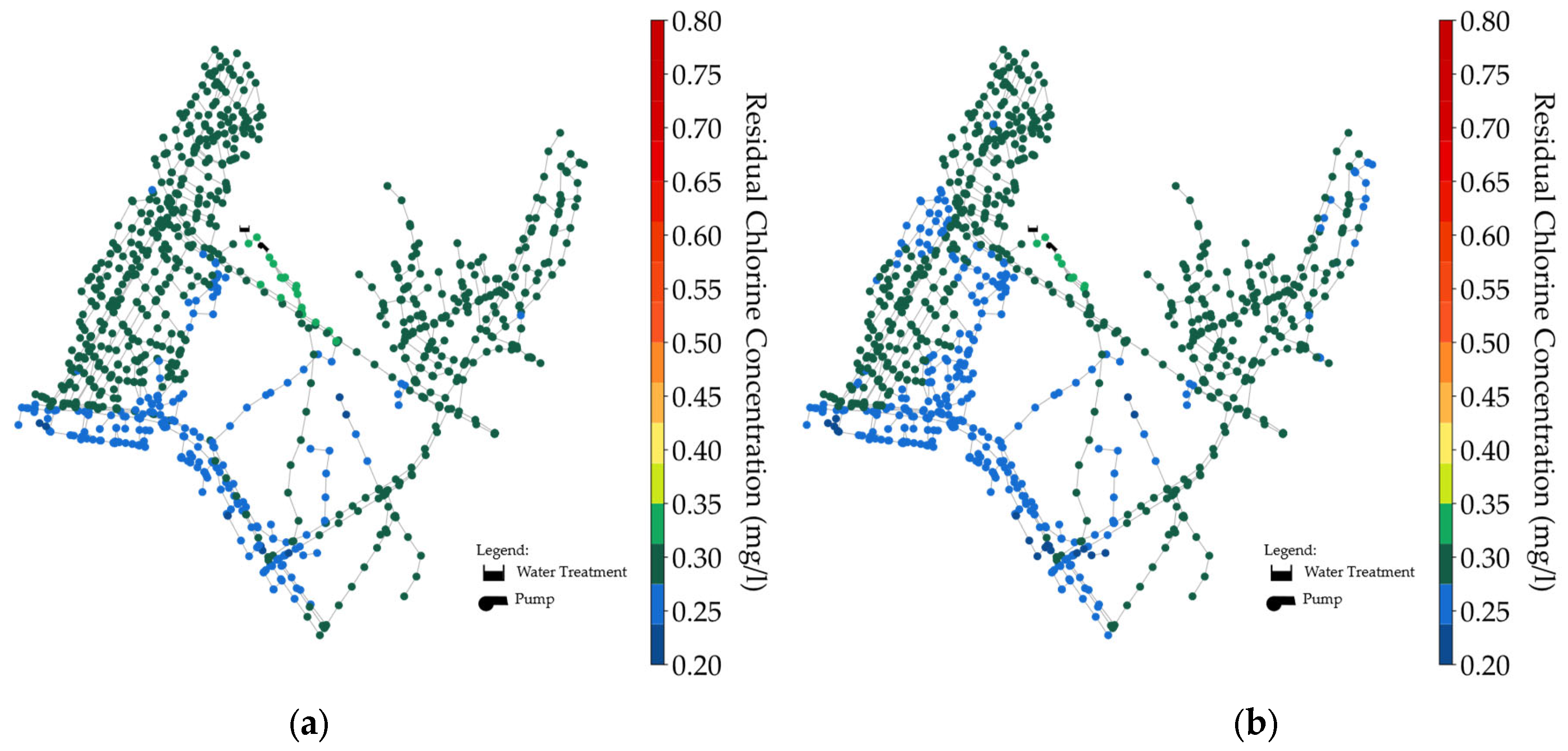
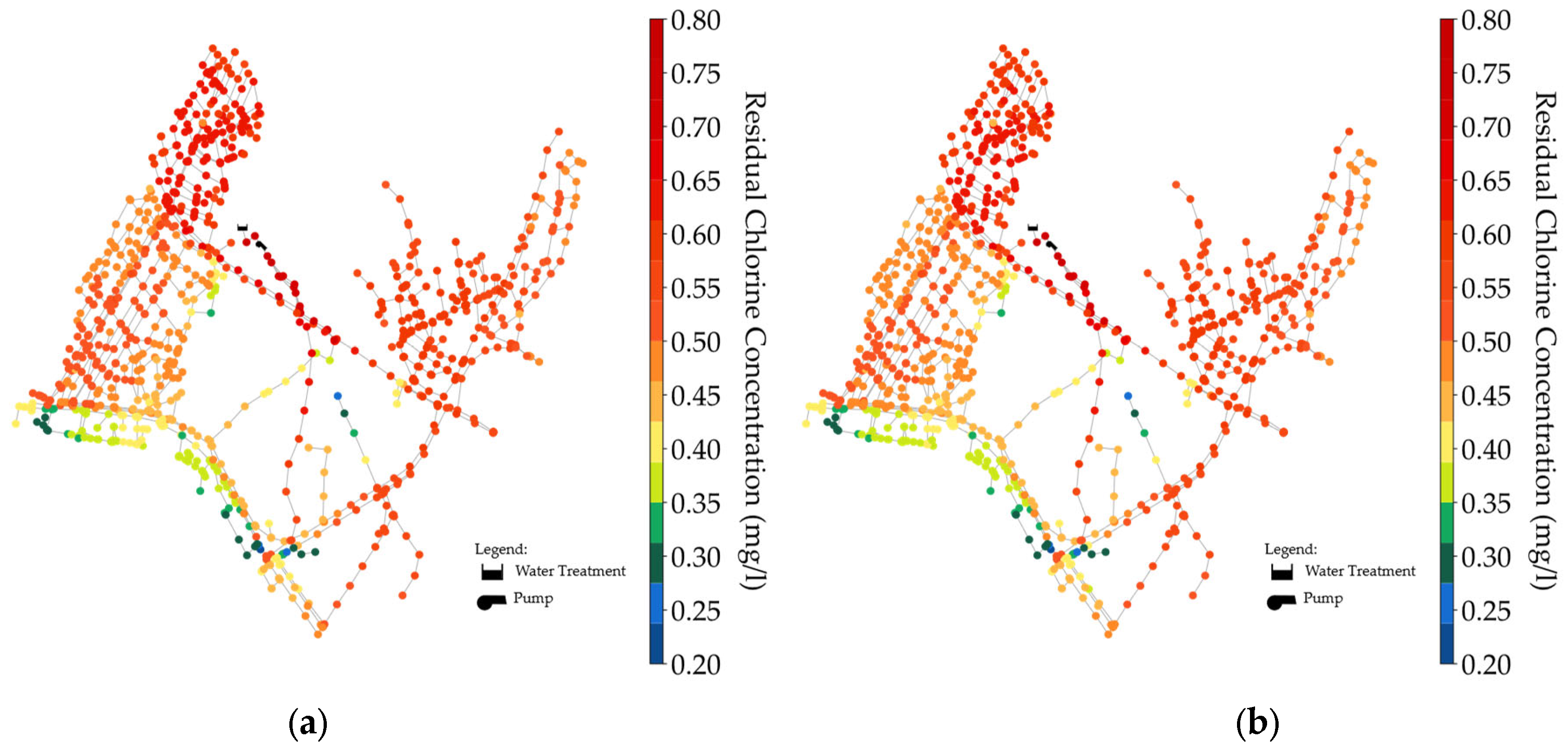
To investigate the spatial variability, the average residual chlorine concentrations over 24 h are presented in Figure 11, Figure 12 and Figure 13. The maximum average residual chlorine values were 0.260, 0.320, and 0.730 mg/L for Scenario 1, and 0.256, 0.316, and 0.726 mg/L for Scenario 2, corresponding to $kb$ values of 0.1056, 0.1872, and 0.576 day⁻¹, respectively. Notably, the nodes near the source exhibited elevated chlorine concentrations. Overall, the chlorine residual distribution across the network was acceptable for $kb$ values of 0.1056 day⁻¹ (winter season) and 0.1872 day⁻¹ (spring/fall season), with corresponding MAPE values (apart from the 0.2 mg/L) of 18 and 39%, respectively. The MAPE value increased to 158% for $kb$ = 0.576 day⁻¹ (summer). This increase is attributed to the substantial residual chlorine produced by the higher source-injection chlorine concentration. The elevated MAPE values suggest the need for possibly booster chlorination in the study network. Nonetheless, the spatiotemporal residual chlorine data highlighted in the figures provide valuable insights and a foundation for future improvements.

4. Conclusions

This study established a chlorine injection optimization model for maintaining uniform residual chlorine concentrations and reducing mass injection. By incorporating water age in estimating the required chlorine injection concentration, this method offers a more efficient approach for determining the optimal chlorine injection schedule by predetermining the potential required source-injection chlorine rate. The performance of this method was assessed based on percentage errors, yielding promising results, with an average error of less than 10% observed across all demand nodes.

The chlorine schedule was optimized using the GA under two operational scenarios: single and four-interval injection. The results demonstrated that the chlorine injection concentration and demand pattern were inversely correlated, demonstrating that chlorine injection should be increased during low-demand periods owing to long water retention times in the pipe. The four-interval injection slightly outperformed the single-injection scenario owing to its flexibility in injection decisions. This study focused on the flexibility of the method to accommodate fluctuating demands, offering an efficient, simple, and fast method for estimating chlorine injection for water treatment operations.

Analysis of residual chlorine concentrations across the network revealed spatial variability, with elevated levels at nodes close to the source. The distribution was generally acceptable for lower $kb$ values (0.1056 and 0.1872 day⁻¹ for winter and spring/fall seasons, respectively), with MAPE values of 18 and 39% from the targeted value (0.2 mg/L), respectively. A substantial increase in the error at 158% was observed for $kb$ = 0.576 day⁻¹ (operation in summer). Nevertheless, the results demonstrated that the proposed method could effectively manage chlorine injection under fluctuating seasonal temperature conditions.

The findings of this study provide valuable insights into effectively managing chlorine levels and operations of WDNs. Using spatiotemporal uniformity facilitated by water age is a promising strategy for enhancing network performance and chlorine distribution. This research paves the way for utilizing water age in chlorine estimation, with the potential for further refinement and application for water quality management in WDNs. For future research, a significant improvement direction will involve expanding the scope to include multiple sources and storage tanks. Additionally, introducing more objectives in the optimization approach aims to enhance the comprehensiveness of the model’s results. Another essential aspect is assessing the model by comparing it with existing approaches, providing a substantial justification for the model’s benefits, and identifying areas for improvement based on other methodologies. These endeavors can offer valuable insights and pave the way for potential avenues in future research.