Abstract
Reclamation of treated sewage is an important way to alleviate urban water scarcity and optimize ecological layout, especially in irrigating urban turfgrass. Nevertheless, the irrational use of reclaimed sewage could result in risk of excessive nitrogen (N) pollution, which requires a scientific understanding and assessment. This study examined the water-N transport process of the turfgrass system with a HYDRUS-2D model that was accurately calibrated and validated using a set of field experimental data in North China. By integrating 15 scenarios with different irrigation levels and N applications into the model, the turfgrass water flow and N fate characteristics were estimated. The results showed that the adjusted HYDRUS-2D model effectively simulated the volumetric soil water content, drainage water, N leaching, and soil N residual. The temporal variation in turfgrass water loss and N leaching consistently followed that of precipitation and irrigation, with more than 60% of the total drainage water occurring from June to August. The N leaching was at its peak during April and August, and total ammonium-N and nitrate-N leaching was 2.86 and 2.02 kg/hm2, respectively. In simulated scenarios, the turfgrass drainage water was significantly reduced by 26.82% under I60%S1/3-I60%S3 scenarios (I was 100%, 80%, or 60% of total irrigation and S was 1/3, 1/2, 1, 2, or 3 times the experimental sewage concentration), while root water uptake only decreased by 0.85%. Meanwhile, N leaching and soil N residual were significantly reduced by 3.94% and 26.56% under I60%S1/2, respectively. Furthermore, by the TOPSIS entropy weight method, I60%S1/2 was identified as an optimal turfgrass irrigation strategy for the semi-arid region of North China. These results provide a guiding basis for sewage green treatment and urban sustainable irrigation on turfgrass.
1. Introduction
Water is a crucial strategic resource for supporting social and ecological development, but ensuring its sustainability presents huge challenges. Due to the highly uneven distribution of global freshwater resources, combined with rapid population growth and accelerated urbanization, some countries and regions have already experienced varying degrees of water scarcity. It is predicted that at least 5 billion people will face water insecurity by 2050 worldwide [1]. Although China’s total water resources (2876.12 billion m3) are relatively abundant, accounting for approximately 5.1% of the world’s total water resources, per capita water resources are only one-quarter of the global average [2]. Meanwhile, China’s sewage discharges have been increasing year by year, with urban sewage annual discharge rising sharply from 46.27 billion tons in 2012 to 63.93 billion tons in 2022 [3].
Urban turfgrass is an essential component of urban green land, playing important roles in regulating water balance, improving microclimate conditions, and preventing soil erosion [4]. In recent years, the rapid development of urbanization has led to the continuous expansion of urban turfgrass space. Currently, the area of turfgrass in the United States is between 1640 and 2020 hm2, more than three times the area of any irrigated crop [5]. In 2022, China’s urban green land coverage rate achieved 42.69%, but the establishment and maintenance of turfgrass lacked matching water resources. Rational reclamation of treated sewage (also known as reclaimed sewage) for irrigating turfgrass has become a major strategy to ensure the sustainable development of water-shortage cities. For instance, the state of Florida in the United States is a major consumer of reclaimed sewage, with more than 50% of reclaimed sewage used for irrigation purposes in golf courses, parks, sports fields, and other recreational landscapes [6]. Australia uses 300 million m3 of reclaimed sewage annually, of which about 76% is allocated for landscape environment and agricultural irrigation [7]. China has achieved the treated sewage reuse of 6 billion m3 annually, with approximately 25% of urban green land adopting reclaimed sewage for irrigation in Beijing City [8]. Recycling of treated sewage provides an effective approach to address global water scarcity.
Due to the advantages of stable supply, abundant quantity, and easy accessibility, reclaimed sewage has become an important water source for turfgrass irrigation in arid and semi-arid regions [9]. On the one hand, large amounts of nitrogen (N) in sewage provide important nutrients for crop growth and development, thereby reducing fertilizer application [10]. On the other hand, excessive N input into the plant–soil–groundwater system poses threats to environmental safety and human health [11]. Determining the optimal concentration of N in reclaimed sewage to meet the basic requirements of plants while preventing groundwater contamination and excessive N accumulation in the soil poses a major challenge [12]. Some studies on irrigating turfgrass with reclaimed sewage have primarily focused on the effects on soil physicochemical properties (e.g., soil water, salt, and nutrient status) [13,14], turfgrass growth and quality [15,16], microbial community characteristics [17], and environmental pollution risks [18,19,20]. However, there is very limited knowledge of combining different reclaimed sewage irrigation strategies to evaluate the turfgrass water and N dynamics.
For measuring water flow and N transport processes in turfgrass, the complexity and uncertainty of the various influences within the soil environment render field investigations expensive and time- and labor-consuming. The HYDRUS-2D model developed by the U.S. Salinity Laboratory can address these limitations and effectively assess the impact of different approaches to field management on the two-dimensional movement of water and solutes in the variably saturated zone [21]. This model has been successfully used to simulate water flow and N leaching of turfgrass [22,23,24], demonstrating that HYDRUS-2D is an effective tool for conducting such studies and the simulation results are convincing. Despite some relevant studies, there have been no investigations into developing an optimal reclaimed sewage irrigation strategy for turfgrass using HYDRUS-2D.
Therefore, this study aimed to address the following objectives based on turfgrass field experiments and the application of the HYDRUS-2D model: (1) to calibrate and validate the processes of soil water, ammonium-N (NH4+-N), and nitrate-N (NO3−-N) transport, (2) to clarify the dynamic response of turfgrass water flow and N leaching under reclaimed sewage irrigation, and (3) to assess the impact of different irrigation strategies on soil water and N fate.
2. Materials and Methods
2.1. Field Experiments
2.1.1. Site Description
The field study was carried out during the 2020 growing season of turfgrass at the Hebei University of Architecture in Zhangjiakou, China. The site is located at 40°45′ N latitude, 114°53′ E longitude, located in an arid and semi-arid region, with an average altitude of 724.2 m above sea level. Weather conditions during the experimental period (5 April to 5 November) (Figure 1) showed that the daily maximum temperature ranged from 6.48 °C to 37.56 °C, the daily minimum temperature ranged from −4.26 °C to 24.44 °C, with a total precipitation of 305.21 mm, which occurred mostly from June to August. The soil profile at the experimental field was 120 cm with the texture of sandy loam, a pH of 8.51, organic matter of 7.8 g/kg, and conductivity of 0.13 ms/cm [2]. The initial soil N concentrations were 0.49 g/kg (total N), 38.28 mg/kg (alkali-hydrolyzable N), 3.45 mg/L (NH4+-N), and 1.59 mg/L (NO3−-N).
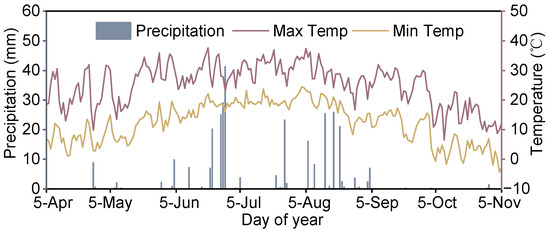
Figure 1.
Daily maximum and minimum temperature and precipitation during the simulation period in 2022.
2.1.2. Experimental Design
The turfgrass species selected for the experiment was Poa annua L., which was planted in June 2019. The experimental device was 80 cm × 80 cm × 120 cm with a filter layer of 10 cm gravel at the bottom, drainage hole was installed to collect regularly the leachate of free drainage using a plastic container (Figure 2). The irrigated water experienced primary and secondary treatment by the campus sewage treatment station, in which the average concentrations of total N, NH4+-N, and NO3−-N were 29.62, 23.09, and 4.65 mg/L, respectively. The irrigation amount per time and irrigation frequency of the turfgrass were formulated according to the reference evapotranspiration (ET0) subtracted from precipitation (P) in this month of the previous year, where ET0 was determined by the FAO Penman–Monteith equation [25]. Irrigation was performed thirty times in total during the experimental period, with the irrigation amount per time ranging from 9.38 to 15.63 mm. Turfgrass was mowed every half month at a height of 5 cm, while weeds were pulled in the experimental field.
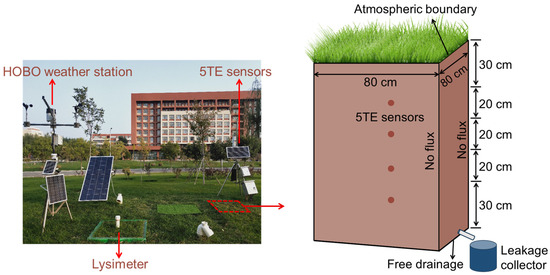
Figure 2.
Structural geometry and boundary conditions of the experimental plot.
2.1.3. Field Measurements and Analysis
In order to obtain experimental data for model calibration and validation, the volumetric soil water content (VSWC, cm3/cm3) of the turfgrass was constantly monitored every thirty minutes using soil moisture monitoring sensors (5TE) at soil depths of 30, 50, 70, and 90 cm in 2022. At the same time, the amount of drainage water (mm) from the bottom of the soil (120 cm) at the experimental plot was observed using a rain gauge from 21 June to 6 August 2022. After each irrigation and precipitation event, the volume of collected drainage water was measured and stored immediately in a refrigerator at 4 °C. After the water samples were filtered through a 0.45 µm filter membrane using the vacuum pump, NH4+-N and NO3−-N concentrations of the water samples were determined in less than 24 h by Nassler’s reagent spectrophotometry and ultraviolet spectrophotometry with national standards [26,27], respectively. On the last day of the experimental period (5 November), soil samples were collected by layer at the depths of 0–30, 30–50, 50–70, 70–90, and 90–120 cm with an auger, soil NH4+-N and NO3−-N contents were determined by a UV–visible spectrophotometer. Basic data such as temperature, precipitation, relative humidity, wind speed, and sunshine hours were constantly monitored relying on the HOBO-U30 weather station. The turfgrass evapotranspiration (ET) was calculated and corrected based on the ET0 and the water balance method with a large-scale weighing lysimeter.
2.2. Modeling Approach
2.2.1. Model Description
The HYDRUS-2D model is based on a numerical approach to calculate two-dimensional finite elements of water flow and solute transport processes in variably saturated porous media [28]. Neglecting the effects of gas phase and temperature in soil water flow movement, the isothermal Darcy two-dimensional flow control equation is obtained by solving the Richards equation:
where θ is the volumetric soil water content (cm3/cm3); t is time (d); h is the pressure head (cm); K(h) is the unsaturated hydraulic conductivity function (cm/d); Kij and Kiz are components of dimensionless anisotropic tensor; xi and xj are the spatial coordinates (cm); S is the sink for water uptake by crop roots (cm/d), which is defined by Faddes et al. [29] as
where α(h) is the water stress response function, which ranges from 0 to 1; Sp is the potential root water uptake rate (d−1). The two-dimensional spatial distribution function of the potential root water uptake is implemented in HYDRUS-2D [30,31,32] by the following equation:
where Zm and Xm are the maximum rooting lengths in the spatial coordinate directions (cm); z* and x* are the depths or radius of maximum intensity (cm); pz and pr are the empirical parameters. The unsaturated soil hydraulic properties parameters were expressed using the Van Genuchten model [33] as follows:
where θs and θr are saturated and residual water content (cm3/cm3), respectively; α is the inverse of the air entry value; n is the pore size distribution index, m = 1 − 1/n (n > 1); l is the pore connectivity parameter; Se is the effective saturation. Transformations and reactions of soil solute are described using convection–dispersion equations:
where c is the solute concentration in the liquid phase (mg/cm3); k is the number of reaction chains; Dij is the dispersion coefficient tensor (cm2/d); qi is the volumetric flux density (cm/d); µ is the first-order reaction rate constant (d−1); µ’ is the similar first-order reaction rate constant (d−1); γ is the zero-order reaction rate constant (d−1); cr is the concentration of the sink term (mg/cm3).
2.2.2. Domain Initial and Boundary Conditions
Measured soil water and N content at five depths (0–30 cm, 30–50 cm, 50–70 cm, 70–90 cm, and 90–120 cm) before the experiment was used as the initial conditions, and missing data were supplemented by linear interpolation, while observation points were set up at the corresponding locations in the profile of the study area. To simplify the transformation process of soil N, due to the organic N concentration in the irrigation water used for the turfgrass being small, the solute reactions were only considered for the adsorption, volatilization, and nitrification of NH4+-N and denitrification of NO3−-N. The upper boundary of the domain was set as the atmospheric boundary, the lower boundary as free drainage, and the left and right boundaries as no flux (Figure 2). At the same time, the flux boundary condition (third type) was selected as the upper and lower boundaries for solute transport. The measured ET in the experimental field was divided into E and T as follows:
where k is the extinction coefficient, which is 0.463 [34]; LAI is the leaf area index, which is 4.11 [35].
2.2.3. Input Parameters
The initial values of soil hydraulic parameters were obtained using neural network predictions (Rosetta) in the HYDRUS-2D model and optimized by continuous inverse solution results (Table 1), in which the l value was set to 0.5. Initial values of solute transport parameters were determined based on previous studies [36,37,38,39] and calibrated by inverse analysis (Table 2). The longitudinal dispersivity (DL) was considered to be one-tenth of the soil profile depth (1.2 cm) and transverse dispersivity (DT) was set to one-tenth of the DL (0.12 cm) [37]. Molecular diffusion in the soil air (Da) was neglected [38] and the molecular diffusion coefficient in free water (Dw) for NH4+-N and NO3−-N was 1.52 and 1.64 cm2/d, respectively [39]. Root water uptake was described using water stress parameter values (model defaults) proposed for turfgrass by Feddes et al. [29]. The root solutes were considered as passive uptake by setting the Cmax to 10 mg/L [23], which represented allowing N uptake to occur without limitation.

Table 1.
Soil hydraulic parameters of the water flow model.

Table 2.
Soil solute parameters of N transport model.
2.2.4. Evaluation of the Model
In this study, measured water and N data from 5 April to 5 November 2022 were used to optimize the parameters of HYDRUS-2D. For the hydraulic parameters, the time step was set to 2 days with odd days selected for the calibration period (total 108 days) and even days selected for the validation period (total 107 days). For solute parameters, the N leaching concentrations during the experimental period (5 April to 5 November) were used for the calibration period and the soil N residual on the last day (5 November) was used for the validation period. The root mean square error (RMSE) and index of agreement (d) were calculated to assess the simulation results by
where Pi is the simulated values; Oi is the measured values; n is the amount of data; Oavg is the average of the measured values. Close to zero value of RMSE and to one value of d indicate a better efficiency of the model.
2.3. Optimization of Irrigation Strategies
2.3.1. Setup of Irrigation Scenarios
After calibration and validation of the HYDRUS-2D model, it was used to simulate water and N dynamics under different irrigation scenarios. The two factors (the amount of irrigation water and the concentration of N application) were considered in the scenario setting. Based on the cumulative reference evapotranspiration (ET0) and cumulative precipitation (P) of the turfgrass from April to October, three different levels of irrigation water were set as 100% (ET0-P) (full irrigation), 80% (ET0-P) (mild deficit irrigation), and 60% (ET0-P) (moderate deficit irrigation). The amount of water for each irrigation was set at 15.63 mm and the frequency of irrigation was equally distributed according to the precipitation situation of the month. Five concentration levels of N application (1/3, 1/2, 1, 2, and 3 times) were set based on the NH4+-N and NO3−-N concentrations of reclaimed sewage in the experiment. Fifteen irrigation scenarios were obtained for each combination of irrigation levels and N concentration levels (Table 3), enabling the comparison of simulated changes in water and N leaching, root water and N uptake, and soil N distribution (30, 50, 70, 90, 120 cm depths).

Table 3.
Scenario setting for irrigating turfgrass with reclaimed sewage.
2.3.2. Evaluation of Irrigation Scenarios: TOPSIS Entropy Weight Method
Currently, commonly used comprehensive indicator methods are mainly the analytic hierarchy process (AHP) and fuzzy comprehensive evaluation (FCE). However, the subjective factors to be considered are numerous and complex, which do not apply to the assessment of irrigation scenarios in this study. The TOPSIS entropy weight method, an integration of TOPSIS (technique for order of preference by similarity to ideal solution) and entropy, calculates the objective weights for each indicator and evaluates the advantages and disadvantages of the alternatives based on weighted distances close to the ideal solution [40]. This methodology not only alleviates the shortcomings of conventional subjective weighting but also enables a comprehensive evaluation of the original data across multiple levels, making results more objective and reliable. Consequently, the TOPSIS entropy weight method was selected to evaluate the effects of different irrigation scenarios on turfgrass water and N dynamics. The specific calculation steps are as follows:
(1) Use the entropy method to determine evaluation index weight
The initial matrix is X = {xij}m×n, where m and n are the number of programs and the number of indicators, respectively. Construction of normalized decision matrix:
Calculation of the information entropy:
Calculation of index weight:
(2) Use the TOPSIS model to evaluate the scheme
Construction of weight decision matrix:
Determination of the positive and negative ideal solution:
Calculation of distance to the positive and negative ideal solution:
Calculation of closeness coefficient:
3. Results and Discussion
3.1. Model Calibration and Validation
3.1.1. Simulation of Water Flow
The simulation efficiency of N transport is closely related to the water flow simulation. The hydraulic parameters of HYDRUS-2D were tested with the measured VSWC at depths of 30, 50, 70, and 90 cm and deep drainage water at a depth of 120 cm in the experimental field. Figure 3 and Figure 4 illustrate the difference between the measured and simulated values of turfgrass water flow movement during the calibration (odd days in experimental period) and validation (even days in experimental period) periods. The results indicated that HYDRUS-2D was capable of effectively simulating the variations in VSWC, with the RMSE ranging from 0.004 to 0.005 cm3/cm3 and the d ranging from 0.60 to 0.75 (Figure 3). During the 90 to 110 days, the measured values showed a significant fluctuating downward trend. Due to the peak growth period for turfgrass, which had a large demand for water. However, the precipitation and irrigation were not sufficient. Additionally, the high temperature resulted in rapid depletion of soil moisture and upward movement of water in deep soil, which reduced the VSWC to an unsaturated state. The simulated values of VSWC were overall lower than the measured values at 90 cm soil depth in the later phases of the experiment, which may be attributed to the model’s inability to incorporate the influence of excessive precipitation and irrigation on the water retention properties of heavily textured soil.
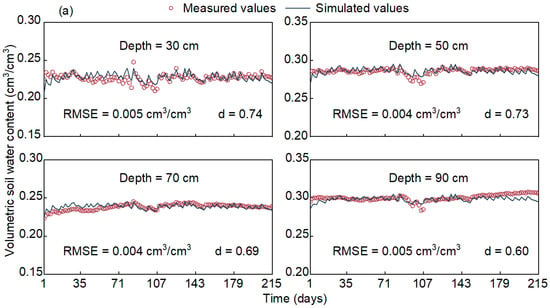
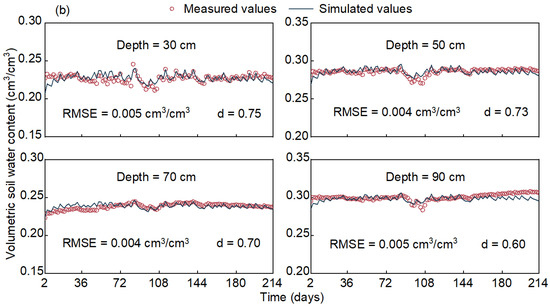
Figure 3.
Measured and simulated volumetric soil water content (VSWC) at different depths (0, 30, 50, and 70 cm) during the (a) calibration and (b) validation periods.
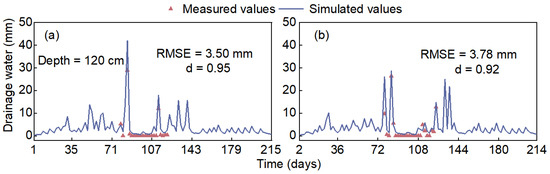
Figure 4.
Measured and simulated drainage water at 120 cm soil depth during the (a) calibration and (b) validation periods.
Regarding the simulation results for drainage water during the calibration and validation periods, the RMSE was 3.50 and 3.78, respectively, and d was 0.95 and 0.92 during the calibration and validation periods (Figure 4). Although the measured values of drainage water were slightly lower than the simulated values due to measurement errors of the experimental equipment, there were the same variations with the simulated and measured drainage water. In summary, the HYDRUS-2D model had a reasonable agreement on simulating turfgrass water flow under the reclaimed sewage irrigation based on the selected evaluation indicators (RMSE and d).
3.1.2. Simulation of N Transport
Using the optimized soil hydraulic parameters, the solute transport parameters of HYDRUS-2D were further tested based on the N field data (N leaching and N residual in different soil layers) that were collected during the turfgrass growing season in 2020. Figure 5 shows the turfgrass NH4+-N and NO3−-N leaching from 120 cm soil depth during the calibration period. The RMSE and d between the simulated and measured NH4+-N leaching were 1.49 mg/m2 and 0.87, while the RMSE and d of NO3−-N leaching were 0.99 mg/cm2 and 0.92, respectively, which indicated that the simulated N leaching had a good agreement with the measured values. Although the overall trends of N leaching were the same, there were still differences between the simulated and measured values. The main reason was that the model failed to consider that the high salt concentration in the reclaimed sewage may lead to a decrease in soil porosity [41], which affected soil hydraulic conductivity and resulted in a deviation between the measured N leaching and the simulated values.
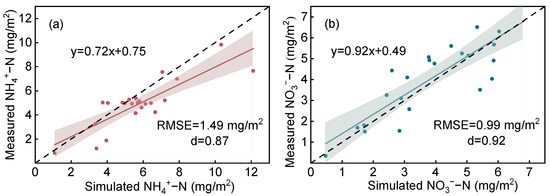
Figure 5.
Measured and simulated (a) NH4+-N and (b) NO3−-N leaching from the entire soil during the calibration period.
Figure 6 shows differences between simulated and measured N residual at varying soil depths during the validation period. The results showed that the RMSE and d for soil NH4+-N residual were 0.17 mg/kg and 0.75, and for NO3−-N residual, they were 0.40 mg/kg and 0.73, respectively. The evaluation indicators remained within a reasonable range, indicating a satisfactory performance of the model. However, there was still acceptable deviation in the spatial trend between the simulated and measured values for N residual, probably because the model did not consider more complex soil N transformation processes (e.g., organic N mineralization and ammonium immobilization). Additionally, long-term irrigation and precipitation may cause non-linear solute concentration gradients in the soil, whereas the model assumed a homogeneous soil environment [42]. Generally, the optimized set of solute transport parameters in the model was reasonable and suitable for simulating the migration and transformation of N in the turfgrass of the study area.
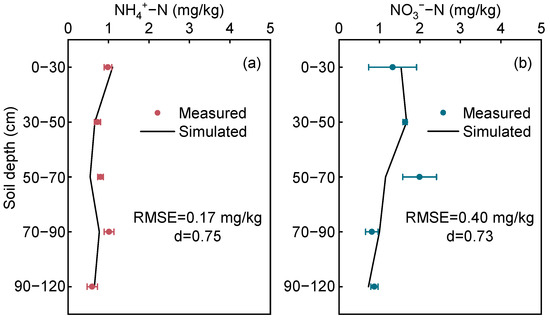
Figure 6.
Measured and simulated different soil depth residual of (a) NH4+-N and (b) NO3−-N during the validation period.
3.2. Characterization of Water and N Dynamics
3.2.1. Volumetric Water Content and Deep Seepage
Based on the VSWC measured in the field and the deep drainage water simulated by HYDRUS-2D, the temporal dynamic variations in turfgrass water flow were analyzed during the experimental period in 2022 (Figure 7). For the entire soil profile (0–120 cm), the VSWC of turfgrass ranged from 0.209 to 0.308 cm3/cm3 with a similar temporal trend. The VSWC at different depths decreased in the order of 90, 50, 70, and 30 cm, in which the VSWC at 30 cm depth was affected by surface evaporation and plant uptake, resulting in a strong response to precipitation and irrigation infiltration with the greatest fluctuation. The average VSWC at 50 cm depth was 0.286 cm3/cm3, which was 20.09% higher than the VSWC at 70 cm soil depth. This difference may be attributed to the fact that the 50–70 cm soil layer was the root tip meristematic zone of the turfgrass [43], where a significant amount of soil water and inorganic salts could be absorbed, and thus, the VSWC at 70 cm depth was relatively lower. The trend of VSWC at 90 cm depth fluctuated steadily, with an average value of 0.301 cm3/cm3.
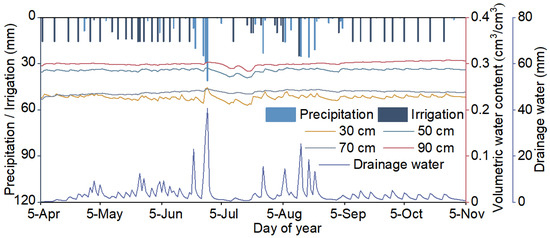
Figure 7.
Changes in measured volumetric soil water content (VSWC) and simulated drainage water at different depths during the experimental period in 2022.
Deep soil drainage is the primary pathway for turfgrass water loss. Similar to the distribution characteristics of VSWC, there was a significant positive correlation between drainage water and precipitation as well as irrigation, with a cumulative drainage water of 719.79 mm in the turfgrass growing season. The drainage water showed an uneven seasonal distribution predominantly concentrated in June and August, which accounted for 27.60% and 20.96% of the cumulative drainage water with daily average drainage water of 7.19 and 5.43 mm in these months, respectively. A heavy precipitation event occurred from 26 to 28 June with a cumulative precipitation of 95.2 mm, resulting in the maximum drainage water of 41.95 mm on 28 June in the turfgrass system.
3.2.2. N Leaching
N leaching is the main pathway for soil N loss from a turfgrass system, and its variations are determined by N application, precipitation, irrigation management, and plant uptake [44]. Figure 8 illustrates the daily changes in simulated N leaching at 120 cm soil depth during the experimental period. The results showed that NH4+-N and NO3−-N leaching varied significantly with the fluctuations in precipitation and irrigation, which was consistent with the transport process of soil water flow. The cumulative NH4+-N leaching was 2.86 kg/hm2, slightly higher than the cumulative NO3−-N leaching (2.02 kg/hm2). The N leaching dynamics were consistent with the turfgrass water flow characteristics, and the NH4+-N and NO3−-N leaching accounted for 49.36% and 49.48% of the cumulative leaching in June and August, respectively. Influenced by the heavy precipitation, the NH4+-N and NO3−-N leaching reached the maximum values of 0.15 and 0.10 kg/hm2 on 28 June, respectively. Therefore, precipitation played an important role in increasing N loss from turfgrass fields, which was consistent with the findings of Mehrabi et al. [45] on winter wheat fields.
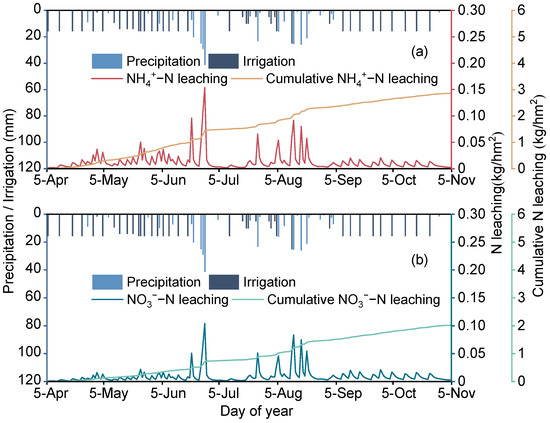
Figure 8.
Changes in simulated (a) NH4+-N and (b) NO3−-N leaching and cumulative N leaching during the experimental period in 2022.
There were seasonal differences in N leaching variations during the turfgrass growth period. The NH4+-N and NO3−-N leaching accounted for 81.38% and 73.12% of the cumulative N leaching from 5 April to 31 August, respectively, which indicated that turfgrass N leaching mainly occurred in spring and summer. In the autumn (1 September to 5 November), the cumulative NO3−-N leaching (0.54 kg/hm2) was 1.95% higher than the cumulative NH4+-N leaching, indicating that NO3−-N leaching was dominant during the period. The main reason for this was that the soil NH4+-N initial concentration in turfgrass was relatively high, and using reclaimed sewage irrigation may promote increased soil organic matter, which affected the nitrification reaction rate, resulting in a gradual increase in soil NO3−-N content [46]. Under long-term precipitation and irrigation, NO3−-N is prone to leaching deeper soil layers and into groundwater. Therefore, it is important to adopt appropriate irrigation management to enhance the efficient utilization of N and reduce the background concentrations of soil N.
3.3. Assessing Different Irrigation Scenarios
3.3.1. Cumulative Drainage Water and Root Water Uptake
Variations in irrigation amount and frequency will affect soil water loss through the pathways of deep drainage water and root water uptake (RWU). The turfgrass cumulative drainage water and cumulative RWU were simulated under three irrigation scenarios (I100%, I80%, and I60%) using the HYDRUS-2D model (Figure 9). The results revealed significant decreases in both drainage water and RWU with decreases in irrigation amount. Under the premise of maintaining proper turfgrass growth, the cumulative drainage water of the I80% and I60% scenarios decreased by 12.01% and 26.82% in comparison to that of the I100% scenario (587.46 mm), respectively, which indicated that the soil water loss was significantly lower in the I60% scenario than in the I80% and I100% scenarios. However, the cumulative RWU varied slightly among the three irrigation scenarios. Specifically, the cumulative RWU in the I80% and I60% scenarios only exhibited reductions of 0.43% and 0.85% in comparison to the I100% scenario (553.67 mm), respectively. Similar results were reported by Karandish et al. [47] on the positive effects of reducing irrigation levels in maintaining ETa (actual crop evapotranspiration). In summary, the I60% scenario exhibited significantly reduced drainage water while maintaining a favorable level of RWU, indicating that the soil water use efficiency of the turfgrass was highest.
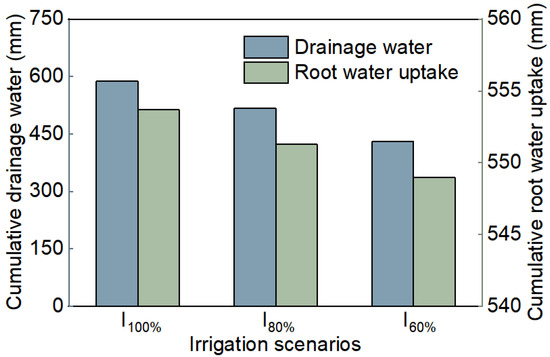
Figure 9.
Predicted cumulative drainage water and cumulative root water uptake (RWU) under different irrigation scenarios during the turfgrass growing season from April to October 2022.
3.3.2. Cumulative Root N Uptake and N Leaching
Figure 10 displays the cumulative root N uptake and cumulative deep soil (120 cm) N leaching under different reclaimed sewage irrigation scenarios. The results indicated that when the N application was fixed, a decrease in irrigation amount (from I100% to I60%) would lead to a slight reduction in root N uptake by 1.22% to 7.60%, which was attributed to the potential negative impact on root N uptake due to a decrease in RUW. However, the N leaching significantly decreased by 12.55% to 25.86%, suggesting that the negative impact on root N uptake was overshadowed by the positive effect of N leaching. Therefore, considering the previous water movement results (Figure 9), adopting the I60% irrigation scenario was effective in reducing turfgrass water loss and N leaching.
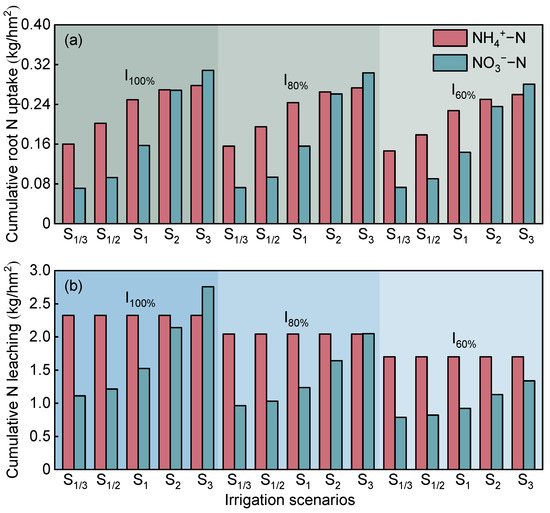
Figure 10.
Predicted cumulative (a) root N uptake and (b) N leaching under different irrigation scenarios during the turfgrass growing season from April to October 2022.
In the I60% irrigation scenario, the root N uptake increased significantly with increasing N application concentration (from S1/3 to S3) by 11.24% to 37.67%. However, NH4+-N leaching (1.70 kg/hm2) remained unchanged, and excess NH4+-N was retained in the soils. The increase in N application concentration resulted in an obvious upward trend in NO3−-N leaching, rising by 4.38% to 22.40%, which was consistent with the results of Groenveld et al. [48], with the N emission being higher as the N application increased. This demonstrated that high levels of N application concentration may result in NO3−-N leaching into deeper soil layers, potentially reducing the efficiency of root NO3−-N uptake [49].
3.3.3. Soil N Residual
The soil N residual in the turfgrass was analyzed for different irrigation scenarios on the last day of the simulation period (31 October, Figure 11). When the N application was fixed, the NH4+-N residual at 0–30 cm soil depth under the I80% and I60% irrigation scenarios was reduced by 11.75% to 16.80% and 16.47% to 25.44%, respectively, compared to the I100% scenario (0.74 to 5.37 mg/kg). For the 30–120 cm soil depth, the NH4+-N residual under the I80% and I60% scenarios were decreased by 1.46% to 4.54% and 1.80% to 8.15%, respectively, compared to the I100% scenario (0.64 to 0.75 mg/kg). This indicated that the response of the NH4+-N residual for the 0–30 cm soil depth was significantly greater than for the 30–120 cm, which was attributed to the fact that NH4+-N was easily adsorbed by negatively charged soil colloids, making it difficult to leach downward with water transport, thus mainly aggregating in the surface soil. However, it was easily leached into deeper soil along with water movement for NO3−-N, resulting in the NO3−-N residual at different soil depths all responding significantly to irrigation amount variations. Under the I80% and I60% scenarios, the NO3−-N residual at the 0–120 cm soil depth was reduced by 1.04% to 10.28% and 2.79% to 23.75%, respectively, compared to the I100% scenario (0.40 to 2.23 mg/kg). Overall, the N residual showed a decreasing trend with a decrease in irrigation amount, which indicated that moderate water deficit irrigation (I60%) was beneficial for promoting turfgrass root N uptake and reducing N loss.
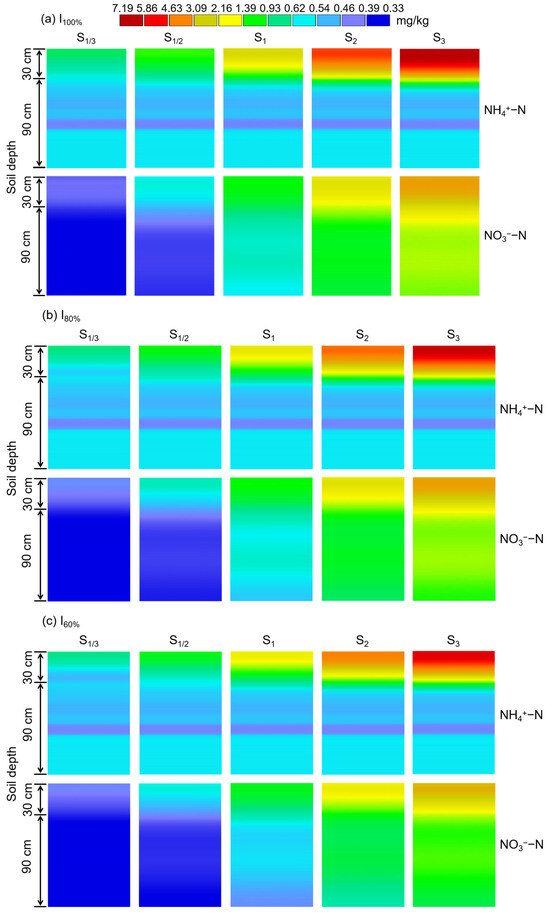
Figure 11.
Predicted NH4+-N and NO3−-N residual profiles under the (a) I100%, (b) I80%, and (c) I60% irrigation scenarios on the last day (31 October 2022) of simulation.
Under the I60% irrigation scenario, the rise in N application concentration caused a significant increase in NH4+-N residual at the topsoil (0–30 cm) by 34.11% to 46.45%, whereas NH4+-N residual at the 30–120 cm soil depth only increased by 0.56% to 3.22%. As for the NO3−-N residual, the entire soil profile (0–120 cm) showed a significant increase of 21.26% to 40.92% with the rise in N application. The excessive N that was not absorbed by crops accumulated in the soil during the winter posed a potential pollution risk as it was susceptible to leaching into water bodies by precipitation and irrigation during spring and summer.
3.3.4. TOPSIS Entropy Weight Method
According to integrating five evaluation indicators (drainage water, RWU, root N uptake, N leaching, and soil N residual), the TOPSIS entropy weight method was utilized to identify the optimal reclaimed sewage irrigation scenarios (Table 4). The calculation results for fifteen irrigation scenarios indicated that I60%S1/2 achieved the minimum value (0.058) in the distance to the positive ideal solution (d+) and a relatively large value (1.259) in the distance to the negative ideal solution (d−). Additionally, the closeness coefficient (C, 0.956) was very close to 1. Compared to the I60%S1 scenario, although cumulative root N uptake decreased by 27.36%, the cumulative N leaching and soil N residual (0–120 cm) of the I60%S1/2 scenario decreased by 3.94% and 26.56%, respectively. Therefore, I60%S1/2 is selected as the optimal reclaimed sewage irrigation strategy for turfgrass in the study area.

Table 4.
Comprehensive evaluation and ranking of irrigation scenarios.
4. Conclusions
In order to evaluate the effects of different reclaimed sewage irrigation strategies on water and N dynamics in urban turfgrass system, this study conducted field soil column leaching experiments. After calibration and validation, the HYDRUS-2D model demonstrated a good agreement on simulated values and measured values of variations in volumetric soil water content, drainage water, N leaching, and N residual. By analyzing the temporal variations in water and N during the turfgrass growing period in 2022 using the simulated values, the volumetric water contents at different depths were ranked as 90 cm > 50 cm > 70 cm > 30 cm, ranging from 0.209 to 0.308 cm3/cm3. The drainage water mainly occurred from June to August, which accounted for 62.53% of the cumulative drainage water (719.79 mm). For the soil NH4+-N and NO3−-N, leaching was mainly concentrated in spring and summer (April to August), accounting for 81.38% and 73.12% of the cumulative NH4+-N (2.86 kg/hm2) and cumulative NO3−-N (2.02 kg/hm2) leaching, respectively. Furthermore, the N leaching was primarily dominated by NO3−-N in autumn (September to October). The evaluation of the irrigation scenarios (I100%S1/4-I60%S4) indicated that I60%S1/2 (irrigation amount of 248.57 mm, and NH4+-N and NO3−-N application concentrations of 11.54 and 2.33 mg/L, respectively) was the optimal irrigation strategy with the highest water use efficiency and the minimum pollution risk. In conclusion, the application of these simulation results will help formulate appropriate water and N management decisions for the study area, enabling more environmentally friendly turfgrass irrigation practices.
Author Contributions
Conceptualization, Y.L. and H.P.; methodology, H.P.; software, Y.L.; validation, Y.L., H.P., and H.Z.; formal analysis, Y.L.; investigation, M.L. and H.Z.; resources, H.P.; data curation, Y.L.; writing—original draft preparation, Y.L.; writing—review and editing, H.P.; visualization, Y.L.; supervision, Y.L.; project administration, Y.L.; funding acquisition, H.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Hebei Provincial Key R&D Programme (No. 22377001D), Natural Science Foundation of China (No. 41701017), and Science Foundation of Hebei Education Department (No. ZD2022015).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Scanlon, B.R.; Fakhreddine, S.; Rateb, A.; de Graaf, I.; Famiglietti, J.; Gleeson, T.; Grafton, R.Q.; Jobbagy, E.; Kebede, S.; Kolusu, S.R.; et al. Global water resources and the role of groundwater in a resilient water future. Nat. Rev. Earth. Envion. 2023, 4, 87–101. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Liu, M.; Shen, Y.; Pei, H. Water Budget of Urban Turf Field and Optimal Irrigation Schedule Simulation in an Ecotone between Semi-Humid and Semi-Arid Regions, Northern China. Agronomy 2023, 13, 273. [Google Scholar] [CrossRef]
- NBSC (National Bureau of Statistics of China). China Statistical Yearbook 2022; National Bureau of Statistics Press: Beijing, China, 2022.
- Sevostianova, E.; Leinauer, B. Subsurface-Applied Tailored Water: Combining Nutrient Benefits with Efficient Turfgrass Irrigation. Crop Sci. 2014, 54, 1926–1938. [Google Scholar] [CrossRef]
- Leinauer, B.; Devitt, D.A. Irrigation Science and Technology. In Agronomy Monograph 56; Horgan, B.P., Stier, J.C., Bonos, S.A., Eds.; ASA, CSSA, and SSSA: Madison, WI, USA, 2013; pp. 1075–1133. [Google Scholar] [CrossRef]
- Fan, J.; Hochmuth, G.; Kruse, J.; Sartain, J. Effects of Reclaimed Water Irrigation on Growth and Nitrogen Uptake of Turfgrass. HortTechnology 2014, 24, 565–574. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Xu, A.; Lu, Y.; Wu, Y.; Hao, S.; Hu, H. Situation analysis and inspirations of water reuse in Australia. Environ. Eng. 2022, 40, 1–7+26. [Google Scholar] [CrossRef]
- Zhu, Z.; Dou, J. Current status of reclaimed water in China: An overview. J. Water Reuse Desalination 2018, 8, 293–307. [Google Scholar] [CrossRef]
- Vo, P.T.; Ngo, H.H.; Guo, W.S.; Zhou, J.L.; Nguyen, P.D.; Listowski, A.; Wang, X.C. A mini-review on the impacts of climate change on wastewater reclamation and reuse. Sci. Total Environ. 2014, 494, 9–17. [Google Scholar] [CrossRef]
- Nogueira, S.F.; Pereira, B.F.F.; Gomes, T.M.; de Paula, A.M.; dos Santos, J.A.; Montes, C.R. Treated sewage effluent: Agronomical and economical aspects on bermudagrass production. Agric. Water Manag. 2013, 116, 151–159. [Google Scholar] [CrossRef]
- Lyu, S.; Chen, W.; Wen, X.; Chang, A.C. Integration of HYDRUS-1D and MODFLOW for evaluating the dynamics of salts and nitrogen in groundwater under long-term reclaimed water irrigation. Irrig. Sci. 2019, 37, 35–47. [Google Scholar] [CrossRef]
- Leinauer, B.; Sevostianova, E.; Velasco-Cruz, C.; Sallenave, R.; Serena, M.; Horvath, I.; Skerker, J. Establishing three warm-season turfgrasses with tailored water: II. Root development, nitrate accumulation in plant tissue and soil, and relationship with leaching. J. Environ. Qual. 2022, 51, 238–249. [Google Scholar] [CrossRef]
- Semiz, G.D.; Suarez, D.L.; Lesch, S.M. Electromagnetic sensing and infiltration measurements to evaluate turfgrass salinity and reclamation. Sci. Rep. 2022, 12, 5115. [Google Scholar] [CrossRef]
- Devitt, D.A.; Wright, L.; Young, M.H. Water and Salt Status of Bare Soil and Turfgrass Systems Irrigated with Recycled Water. Agron. J. 2013, 105, 1051–1060. [Google Scholar] [CrossRef]
- Yerli, C.; Senol, N.D.; Yaganoglu, E. The changes in yield, quality, and soil properties of turfgrass grown by applying varying levels of hazelnut husk compost and irrigating with wastewater in soils with different textures, and their effects on carbon dioxide emissions from the soil. Water Air Soil Pollut. 2023, 234, 311. [Google Scholar] [CrossRef]
- Zalacáin, D.; Martínez-Pérez, S.; Bienes, R.; García-Díaz, A.; Sastre-Merlín, A. Turfgrass biomass production and nutrient balance of an urban park irrigated with reclaimed water. Chemosphere 2019, 237, 124481. [Google Scholar] [CrossRef]
- Bihadassen, B.; Hassi, M.; Hamadi, F.; Aitalla, A.; Bourouache, M.; El Boulani, A.; Mimouni, R. Irrigation of a golf course with UV-treated wastewater: Effects on soil and turfgrass bacteriological quality. Appl. Water Sci. 2020, 10, 7. [Google Scholar] [CrossRef]
- Toor, G.S.; Occhipinti, M.L.; Yang, Y.-Y.; Majcherek, T.; Haver, D.; Oki, L. Managing urban runoff in residential neighborhoods: Nitrogen and phosphorus in lawn irrigation driven runoff. PLoS ONE 2017, 12, e0179151. [Google Scholar] [CrossRef]
- Sidhu, H.S.; Wilson, P.C.; O’Connor, G.A. Endocrine-Disrupting Compounds in Reclaimed Water and Residential Ponds and Exposure Potential for Dislodgeable Residues in Turf Irrigated with Reclaimed Water. Arch. Environ. Contam. Toxicol. 2015, 69, 81–88. [Google Scholar] [CrossRef]
- Chen, W.; Xu, J.; Lu, S.; Jiao, W.; Wu, L.S.; Chang, A.C. Fates and transport of PPCPs in soil receiving reclaimed water irrigation. Chemosphere 2013, 93, 2621–2630. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef]
- Mccoy, E.L.; Mccoy, K.R. Simulation of putting-green soil water dynamics: Implications for turfgrass water use. Agric. Water Manag. 2009, 96, 405–414. [Google Scholar] [CrossRef]
- Geza, M.; Deb, S.K.; Leinauer, B.; Stanek, S.; Sevostianova, E.; Serena, M. Modeling NO3−-N leaching during establishment of turfgrasses irrigated with tailored reclaimed water. Vadose Zone J. 2021, 20, e20112. [Google Scholar] [CrossRef]
- del Campo, M.M.A.; Esteller, M.V.; Morell, I.; Expósito, J.L.; Bandenay, G.L.; Morales-Casique, E. Effect of organic matter and hydrogel application on nitrate leaching in a turfgrass crop: A simulation study using HYDRUS. J. Soils Sediments 2021, 21, 1190–1205. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- HJ535-2009; Water Quality-Determination of Ammonia Nitrogen-Nessler’s Reagent Spectrophotometry. Ministry of Ecology and Environment of People’s Republic of China: Beijing, China, 2009. (In Chinese)
- HJ/T346-2007; Water Quality-Determination of Nitrate-Nitrogen-Ultraviolet Spectrophotometry. Ministry of Ecology and Environment of People’s Republic of China: Beijing, China, 2007. (In Chinese)
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15, 1–25. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield (Simulation Monographs); Pudoc: Wageningen, The Netherlands, 1978. [Google Scholar]
- Vrugt, J.A.; Bouten, W. Validity of first-order approximations to describe parameter uncertainty in soil hydrologic models. Soil Sci. Soc. Am. J. 2002, 66, 1740–1751. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Hopmans, J.W.; Šimůnek, J. Calibration of a two-dimensional root water uptake model. Soil Sci. Soc. Am. J. 2001, 65, 1027–1037. [Google Scholar] [CrossRef]
- Vrugt, J.A.; van Wijk, M.T.; Hopmans, J.W.; Šimůnek, J. One-, two-, and three-dimensional root water uptake functions for transient modeling. Water Resour. Res. 2001, 37, 2457–2470. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Chen, M.; Willgoose, G.R.; Saco, P.M. Spatial prediction of temporal soil moisture dynamics using HYDRUS-1D. Hydrol. Process. 2014, 28, 171–185. [Google Scholar] [CrossRef]
- Yu, L.; Su, D.; Liu, Y. Characters of leaf water absorption for three turfgrass. J. Beijing For. Univ. 2013, 35, 97–101. [Google Scholar]
- Filipović, V.; Toor, G.S.; Ondrašek, G.; Kodešová, R. Modeling water flow and nitrate-nitrogen transport on golf course under turfgrass. J. Soils Sediments 2015, 15, 1847–1859. [Google Scholar] [CrossRef]
- Shafeeq, P.M.; Aggarwal, P.; Krishnan, P.; Rai, V.; Pramanik, P.; Das, T.K. Modeling the temporal distribution of water, ammonium-N, and nitrate-N in the root zone of wheat using HYDRUS-2D under conservation agriculture. Environ. Sci. Pollut. Res. Int. 2020, 27, 2197–2216. [Google Scholar] [CrossRef]
- Mokari, E.; Shukla, M.K.; Šimůnek, J.; Fernandez, O.L. Numerical Modeling of Nitrate in a Flood-Irrigated Pecan Orchard. Soil Sci. Soc. Am. J. 2019, 83, 555–564. [Google Scholar] [CrossRef]
- Shahrokhnia, M.H.; Sepaskhah, A.R. Water and nitrate dynamics in safflower field lysimeters under different irrigation strategies, planting methods, and nitrogen fertilization and application of HYDRUS-1D model. Environ. Sci. Pollut Res. 2018, 25, 8563–8580. [Google Scholar] [CrossRef]
- Li, Z.; Luo, Z.; Wang, Y.; Fan, G.; Zhang, J. Suitability evaluation system for the shallow geothermal energy implementation in region by Entropy Weight Method and TOPSIS method. Renew. Energy 2022, 184, 564–576. [Google Scholar] [CrossRef]
- García-Orenes, F.; Caravaca, F.; Morugán-Coronado, A.; Roldán, A. Prolonged irrigation with municipal wastewater promotes a persistent and active soil microbial community in a semiarid agroecosystem. Agric. Water Manag. 2015, 149, 115–122. [Google Scholar] [CrossRef]
- Mguidiche, A.; Provenzano, G.; Douh, B.; Khila, S.; Rallo, G.; Boujelben, A. Assessing HYDRUS-2D to simulate soil water content (SWC) and salt accumulation under an SDI system: Application to a potato crop in a semi-arid area of central Tunisia. Irrig. Drain. 2015, 64, 263–274. [Google Scholar] [CrossRef]
- Yuan, Y.; Bai, X.; Zhu, Y.; Zhang, Y.; Yan, Y.; Zhang, C.; Li, Y. Correlation between the rhizome expansion ability and endogenous hormones contents of wild Poa pratensis in Gansu Province. Chin. J. Eco-Agric. 2021, 29, 1359–1369. [Google Scholar] [CrossRef]
- Perego, A.; Basile, A.; Bonfante, A.; De Mascellis, R.; Terribile, F.; Brenna, S.; Acutis, M. Nitrate leaching under maize cropping systems in Po Valley (Italy). Agric. Ecosyst. Environ. 2012, 147, 57–65. [Google Scholar] [CrossRef]
- Mehrabi, F.; Sepaskhah, A.R. Soil drainage water and nutrient leaching in winter wheat field lysimeters under different management practices. Int. J. Plant Prod. 2021, 15, 13–28. [Google Scholar] [CrossRef]
- Jeong, H.; Jang, T.; Seong, C.; Park, S. Assessing nitrogen fertilizer rates and split applications using the DSSAT model for rice irrigated with urban wastewater. Agric. Water Manag. 2014, 141, 1–9. [Google Scholar] [CrossRef]
- Karandish, F.; Šimůnek, J. Two-dimensional modeling of nitrogen and water dynamics for various N-managed water-saving irrigation strategies using HYDRUS. Agric. Water Manag. 2017, 193, 174–190. [Google Scholar] [CrossRef]
- Groenveld, T.; Argaman, A.; Šimůnek, J.; Lazarovitch, N. Numerical modeling to optimize nitrogen fertigation with consideration of transient drought and nitrogen stress. Agric. Water Manag. 2021, 254, 106971. [Google Scholar] [CrossRef]
- Jia, X.; Shao, L.; Liu, P.; Zhao, B.; Gu, L.; Dong, S.; Bing, S.H.; Zhang, J.; Zhao, B. Effect of different nitrogen and irrigation treatments on yield and nitrate leaching of summer maize (Zea mays L.) under lysimeter conditions. Agric. Water Manag. 2014, 137, 92–103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).