Impact of CO2 Viscosity and Capillary Pressure on Water Production in Homogeneous and Heterogeneous Media
Abstract
1. Introduction
2. Numerical Simulation Results
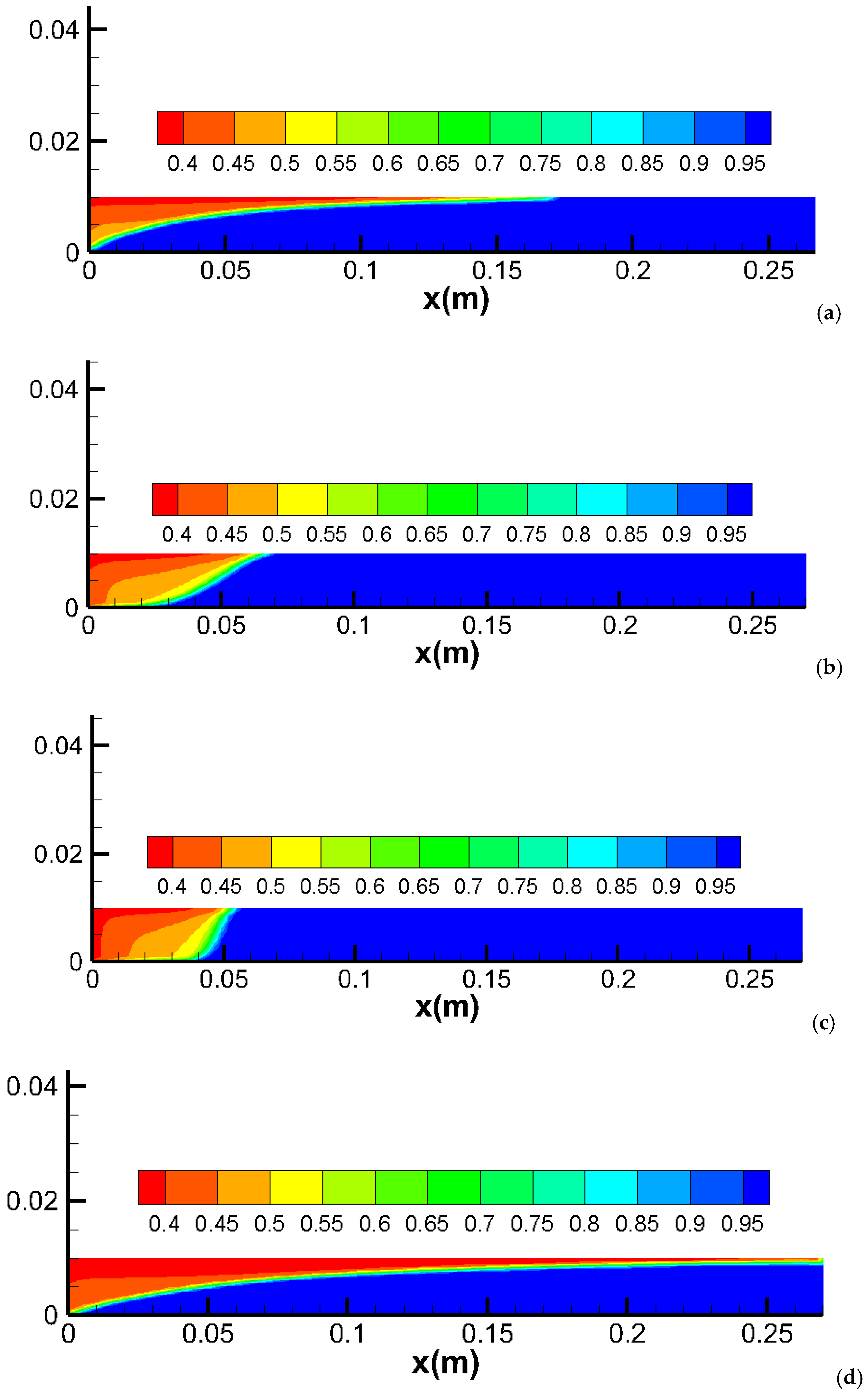
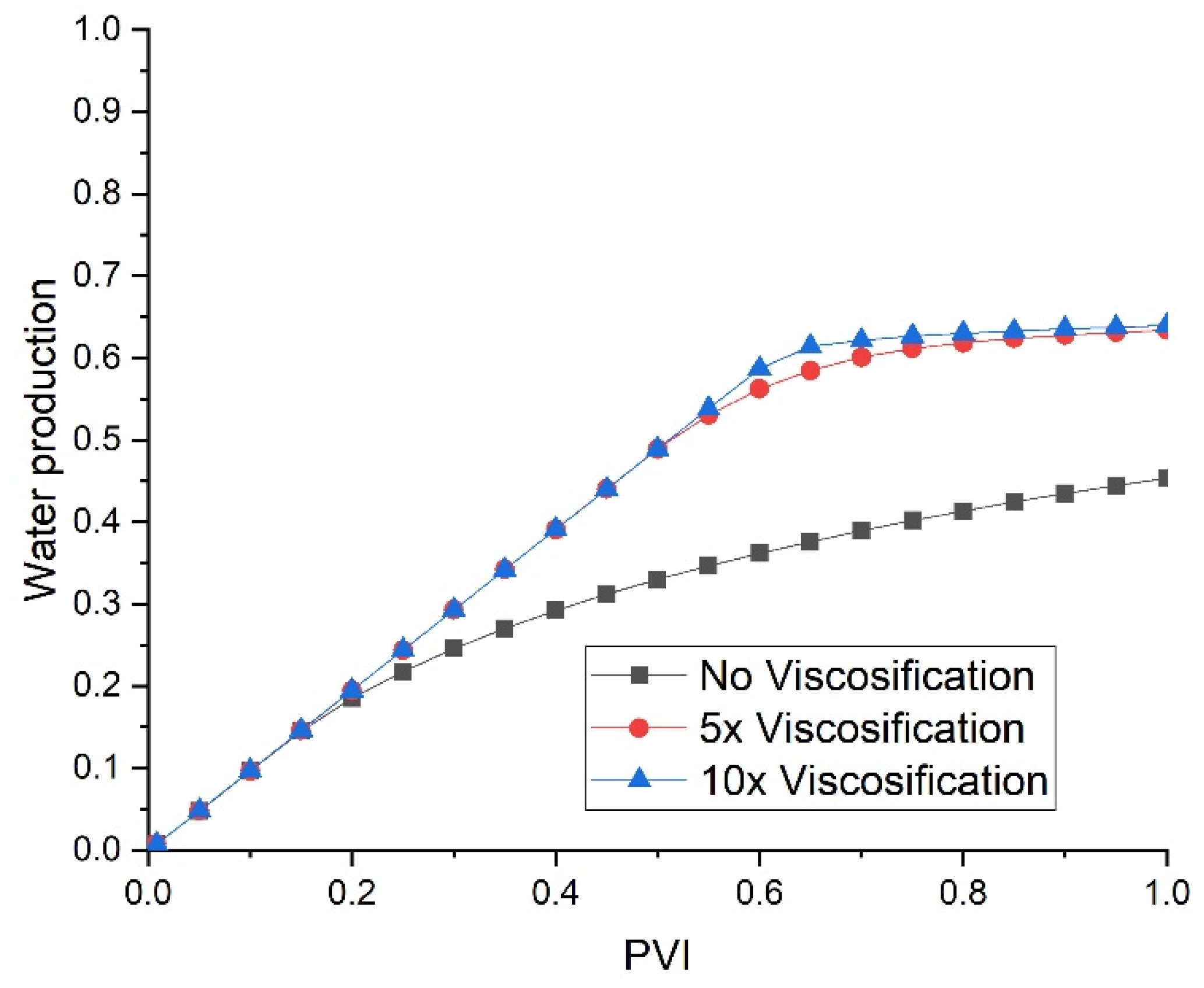
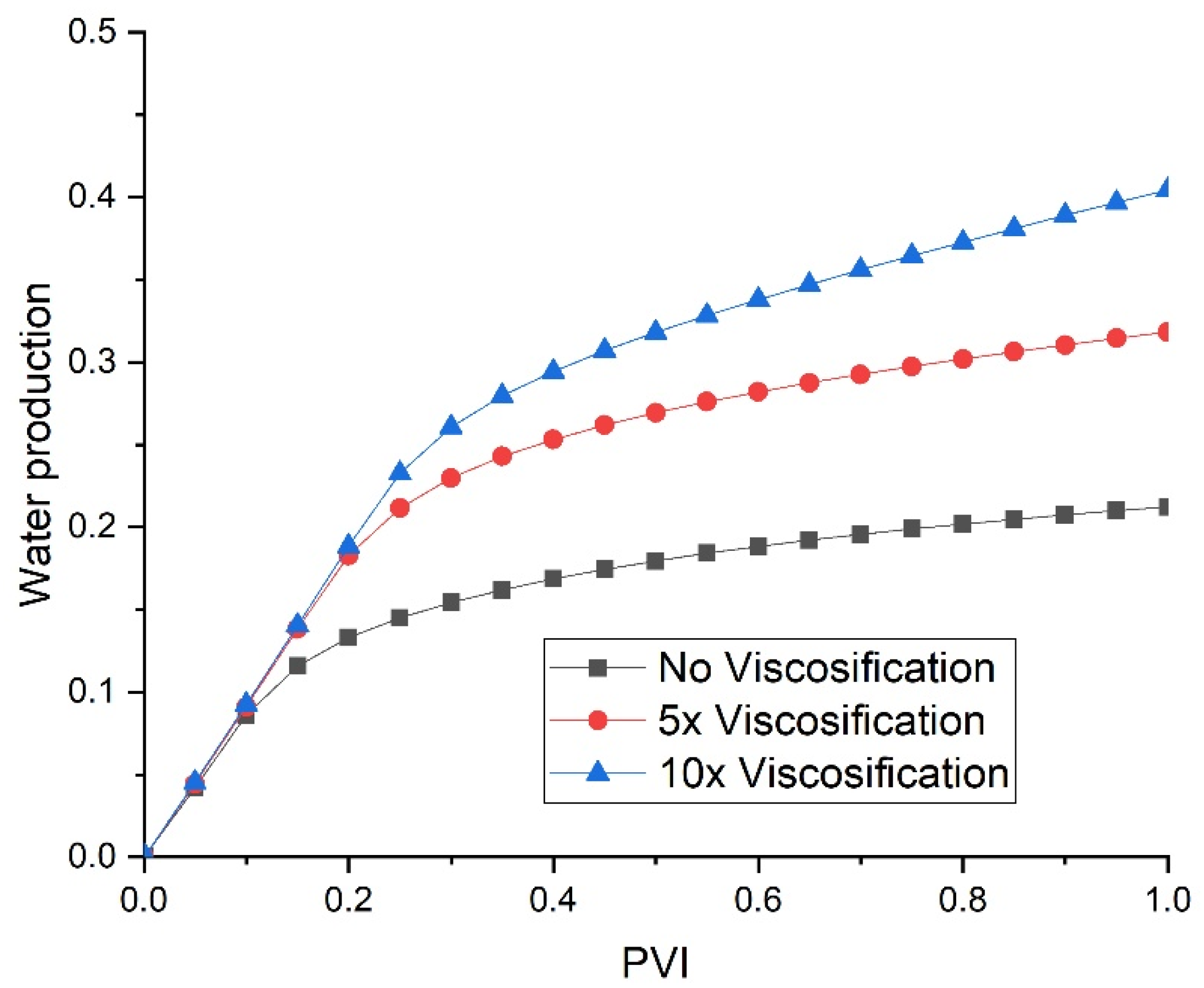
2.1. Simulation in a Homogeneous Domain
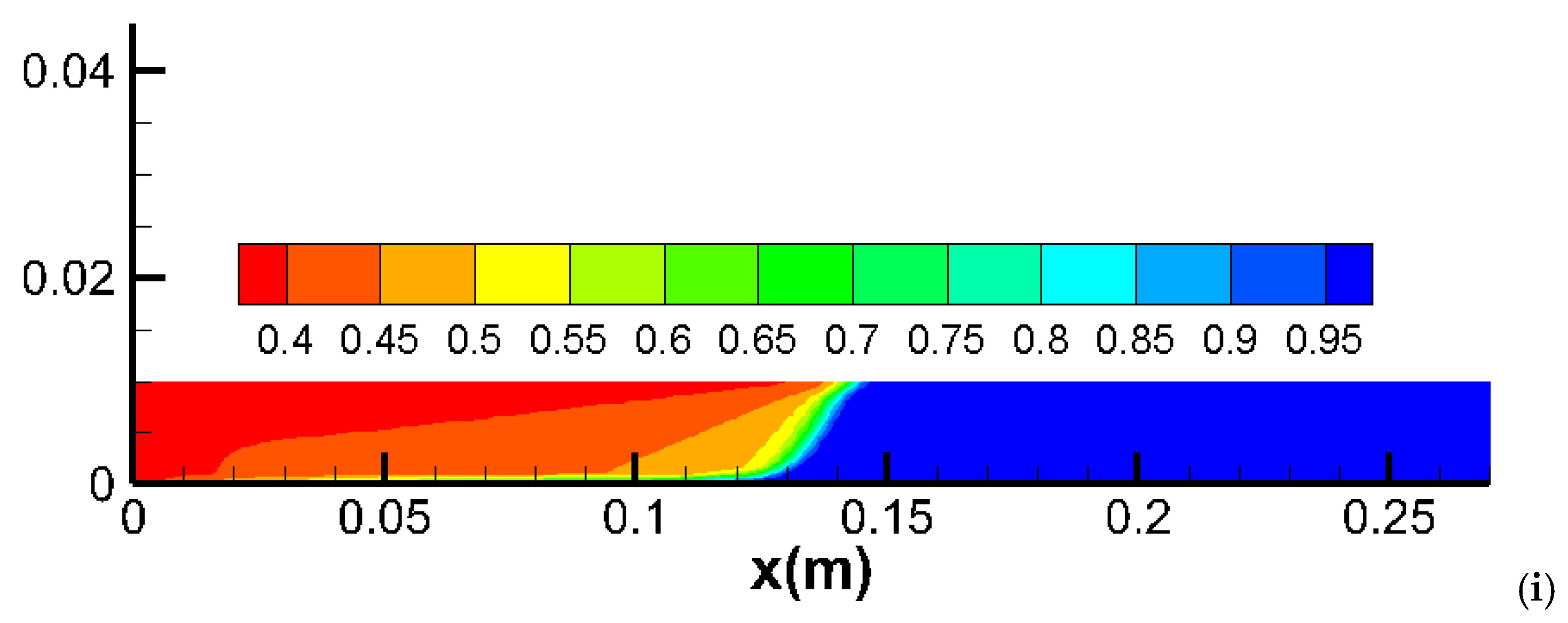
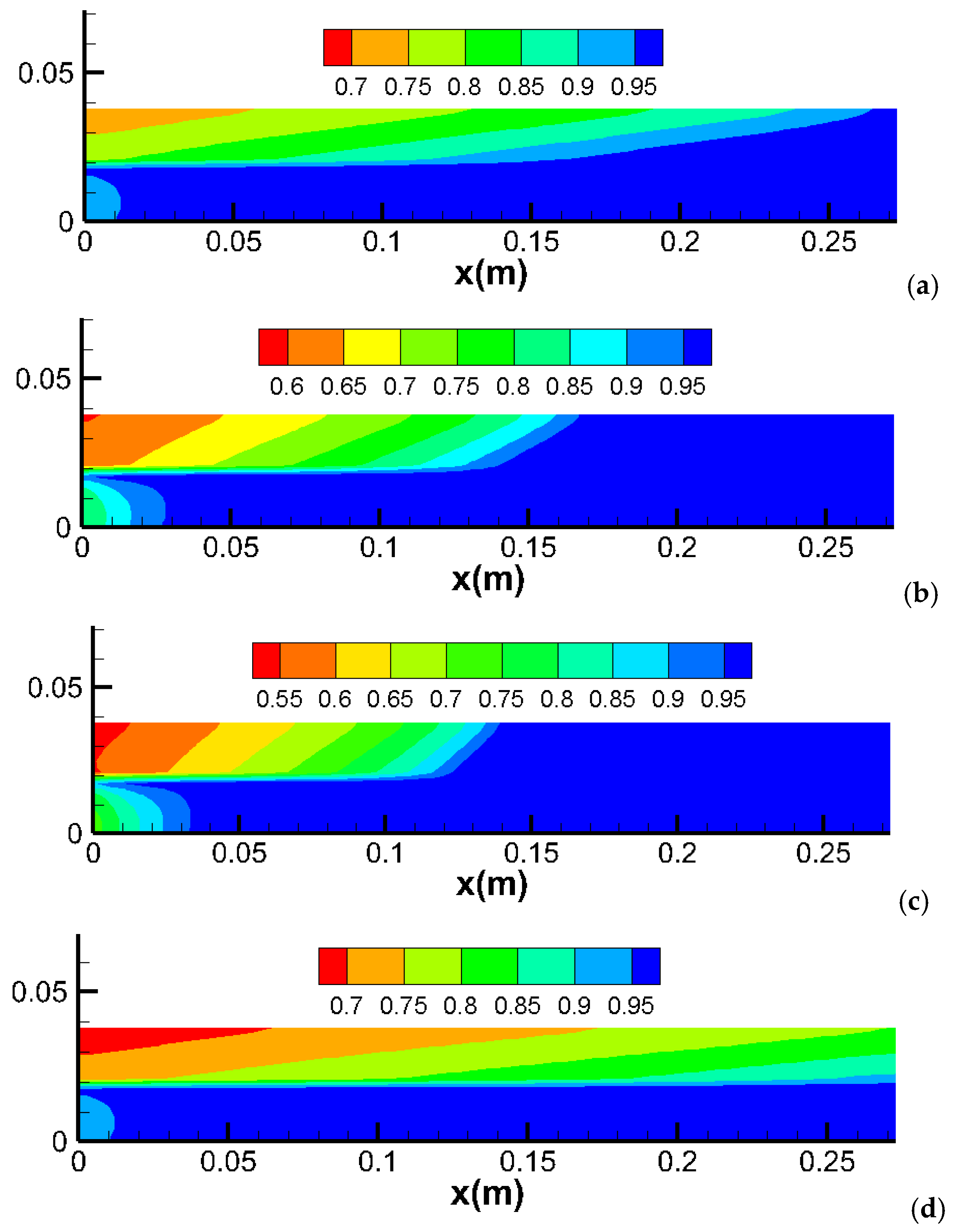
2.2. Simulation in a Slim Core
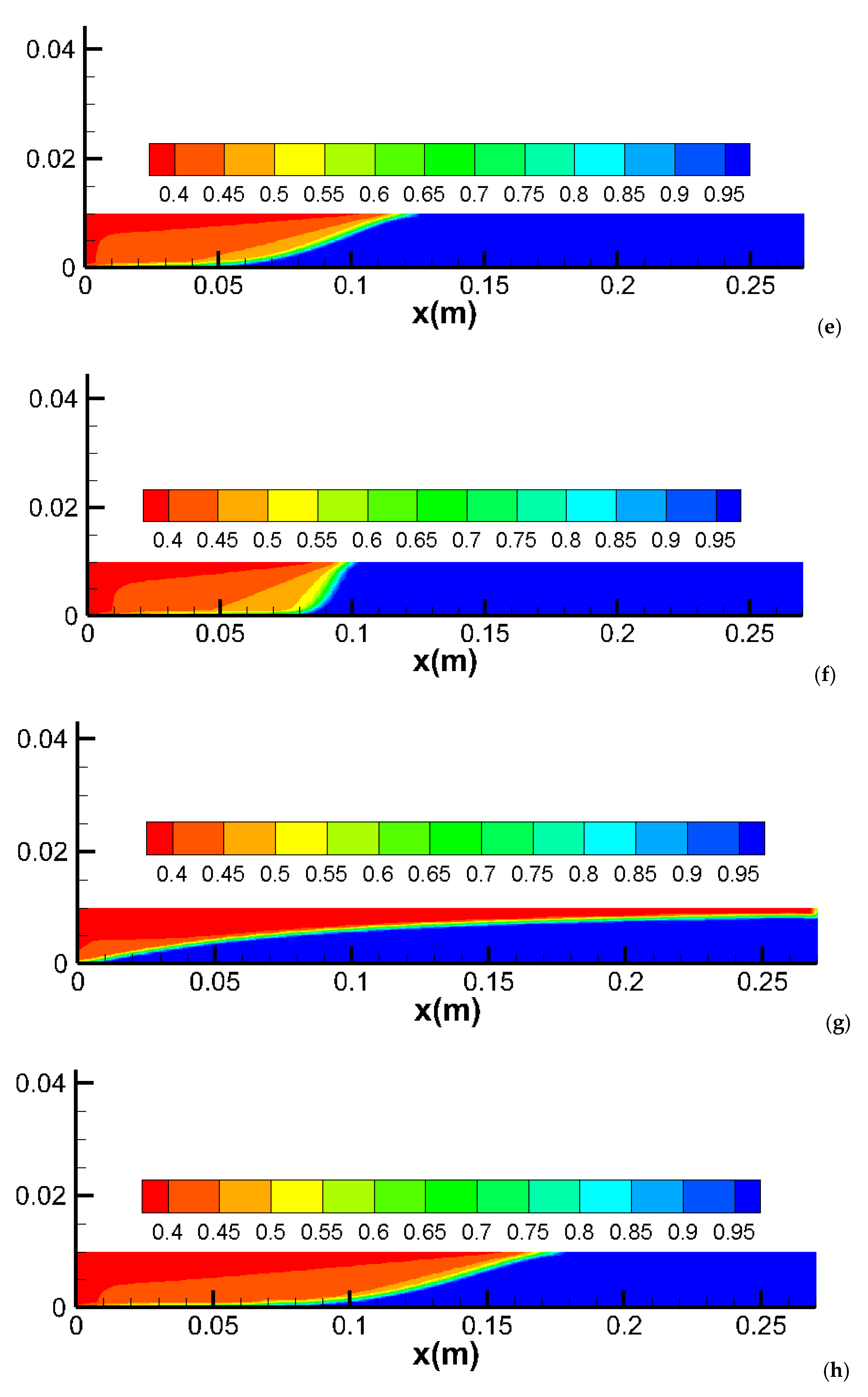
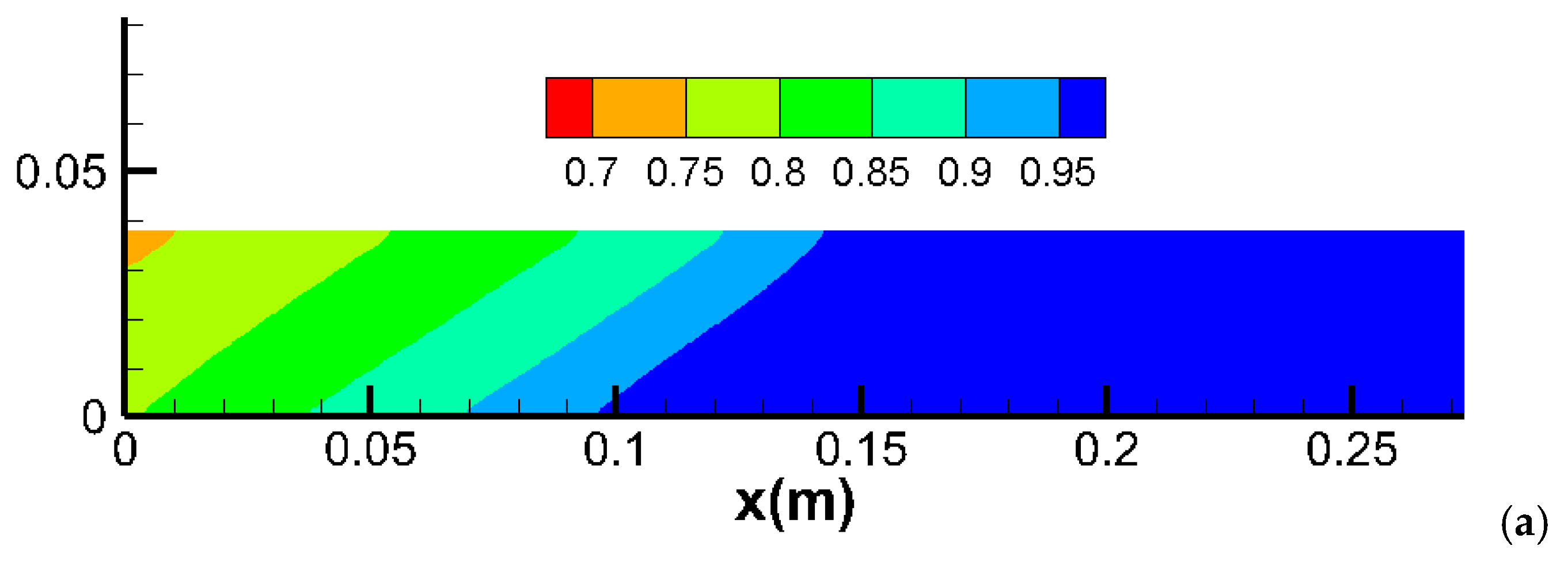
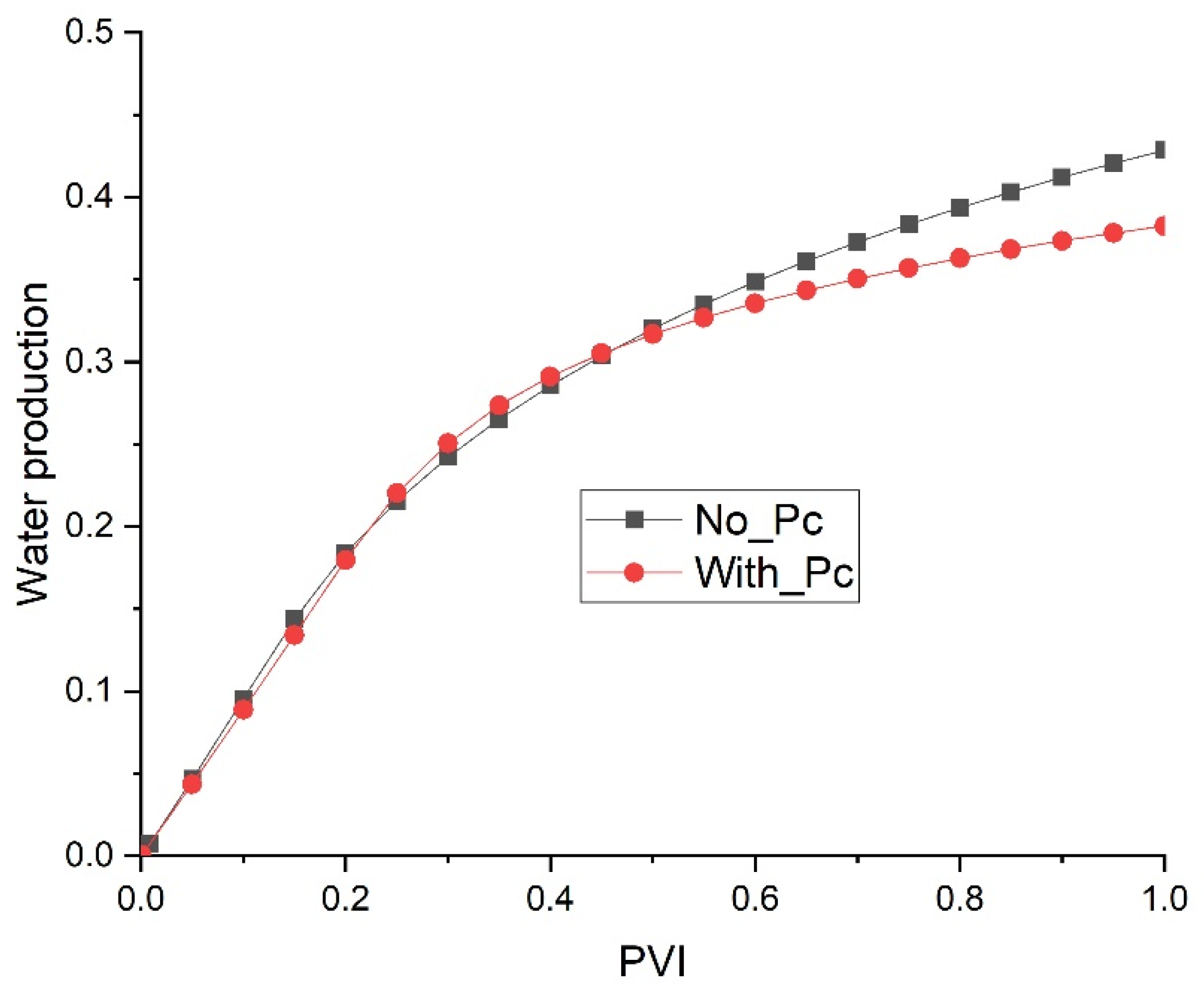
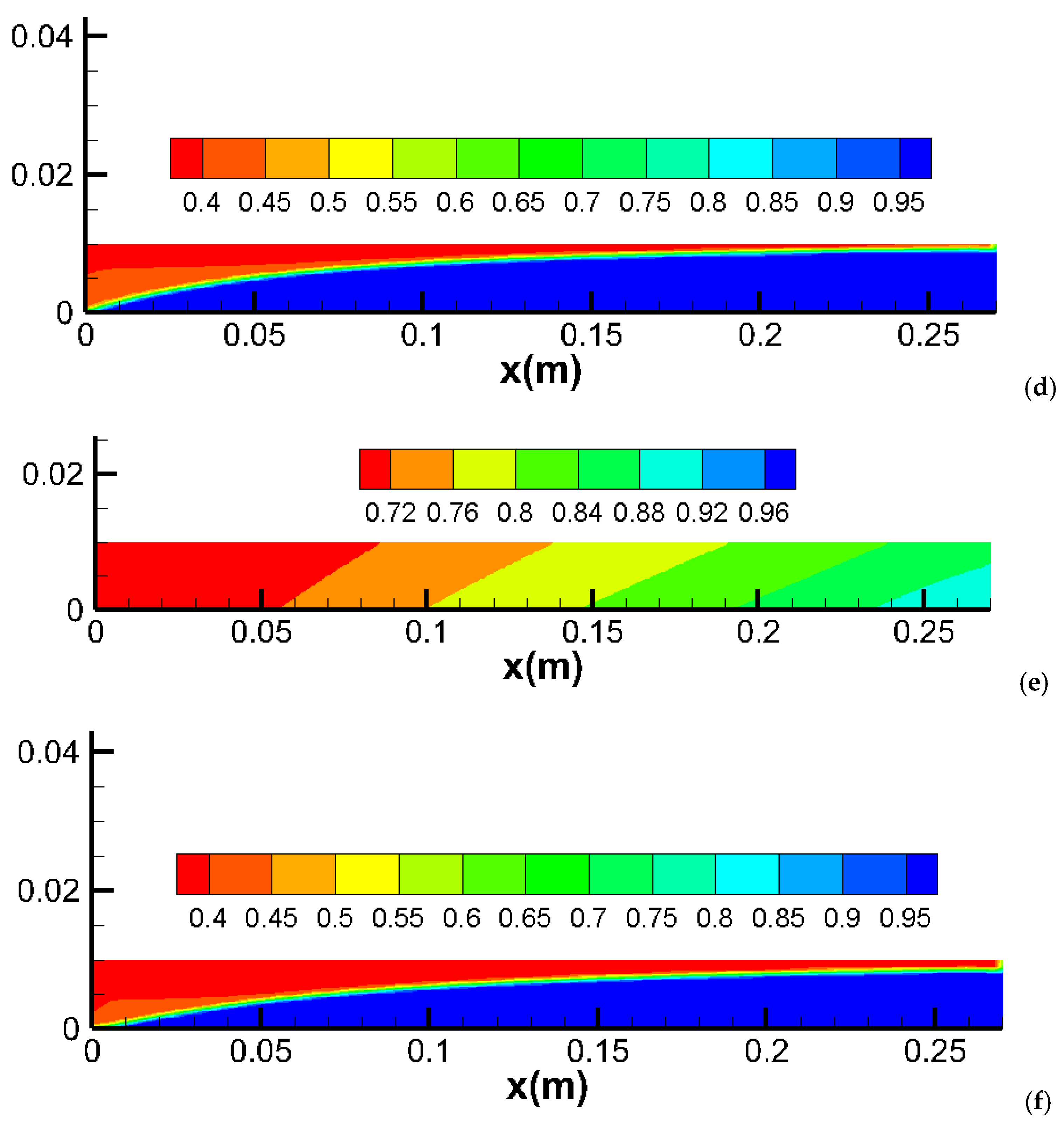
2.3. Effect of Capillary Pressure
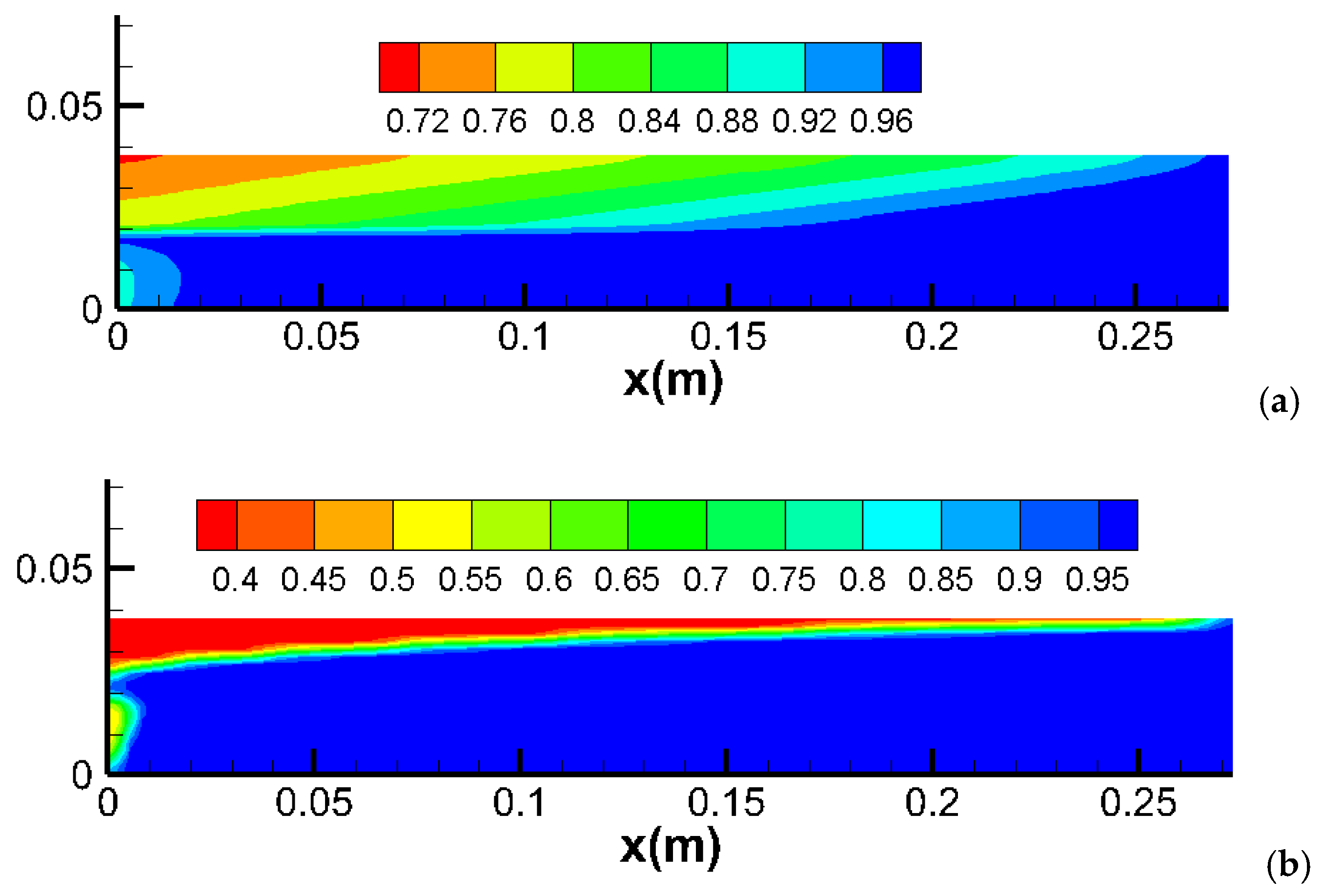
2.4. Capillary Pressure in a Heterogeneous Core
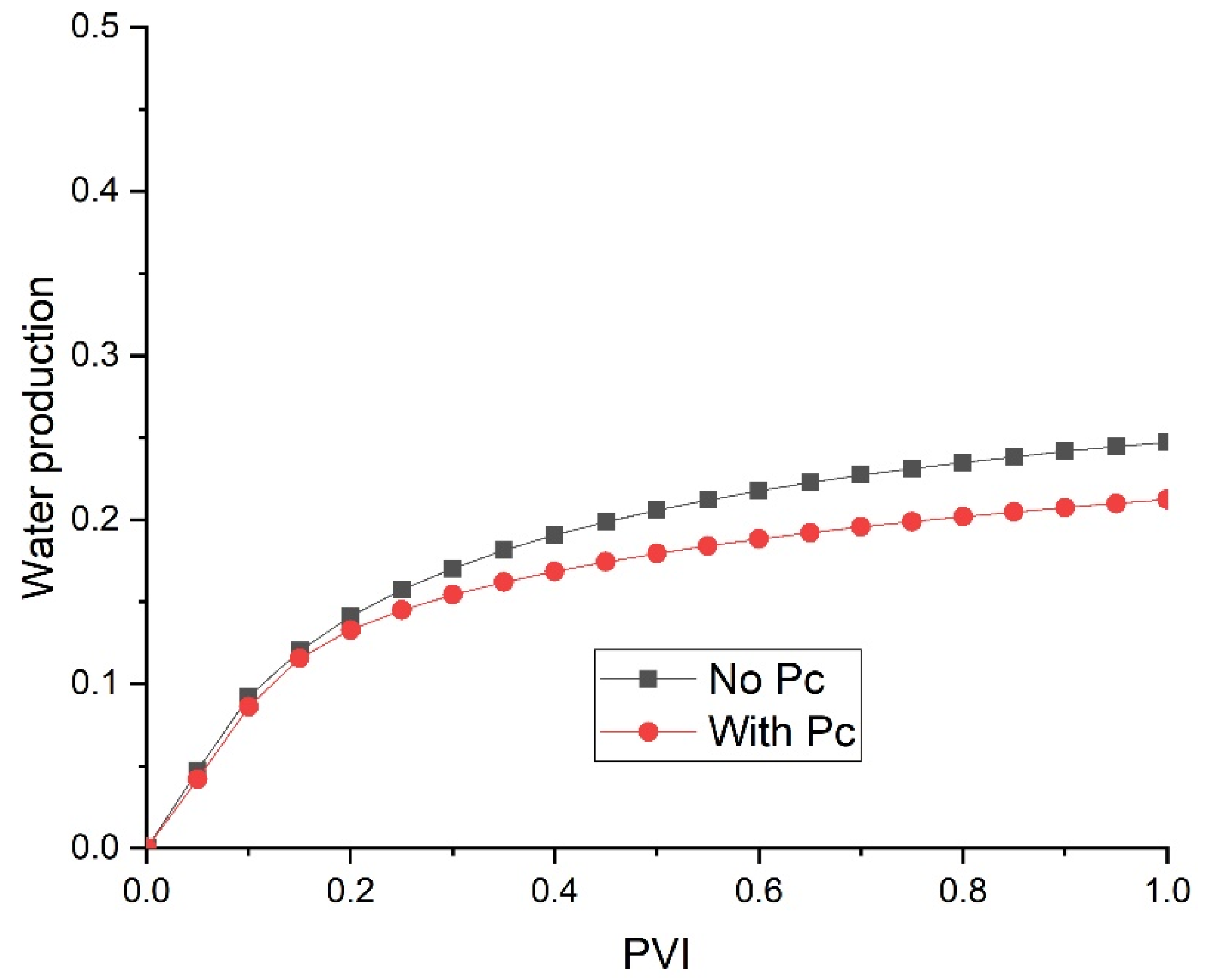
2.5. Capillary Pressure in a Slim Core
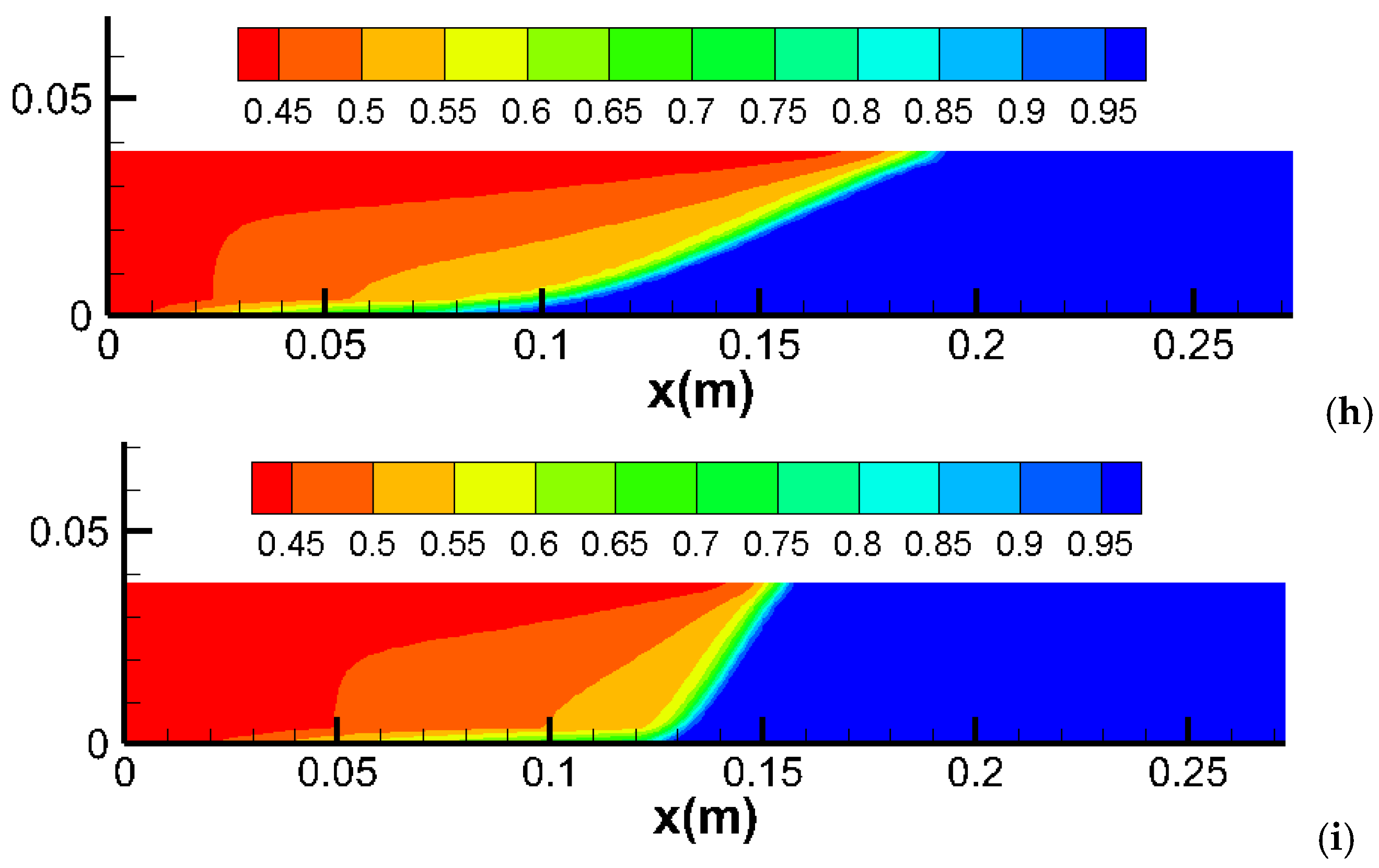
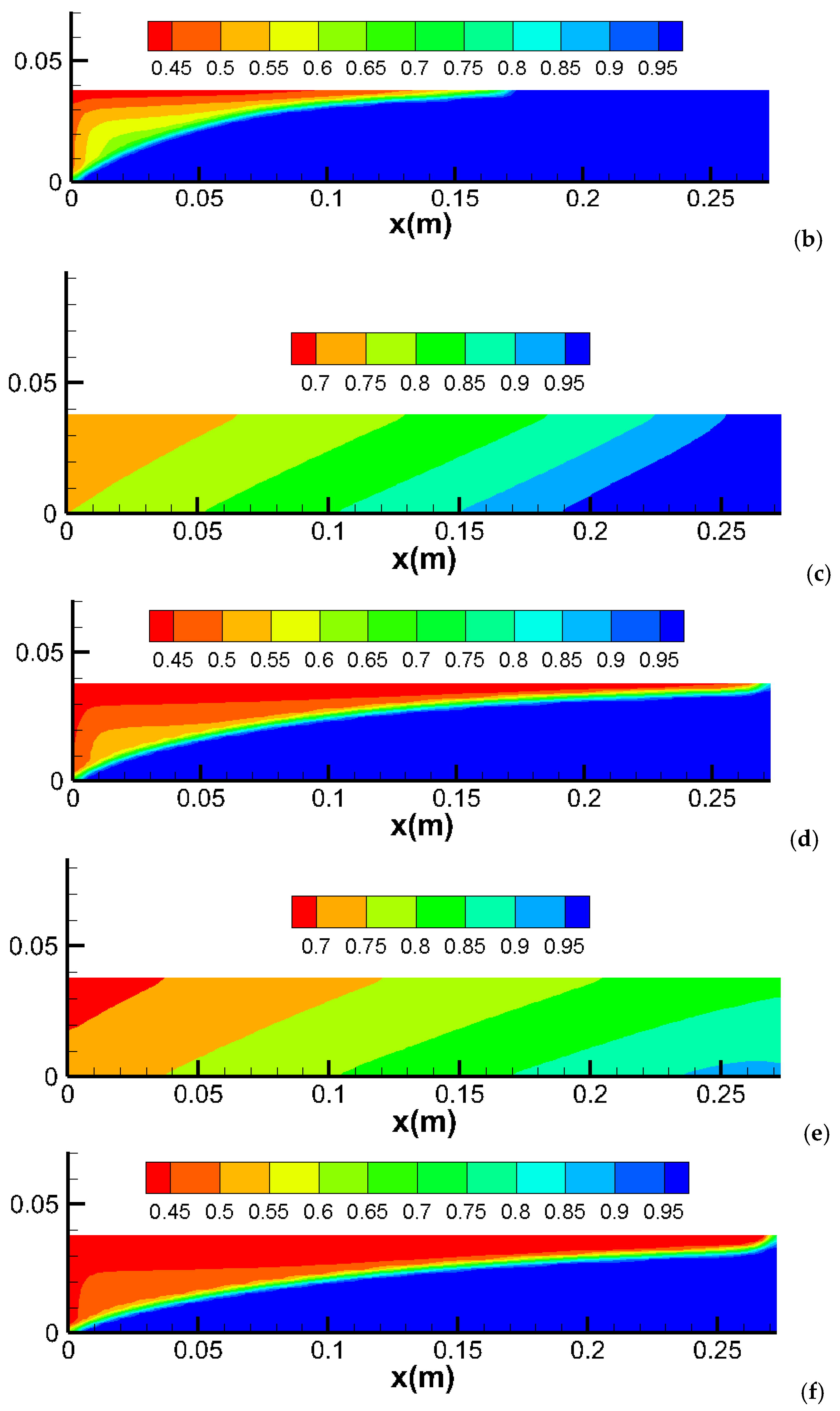
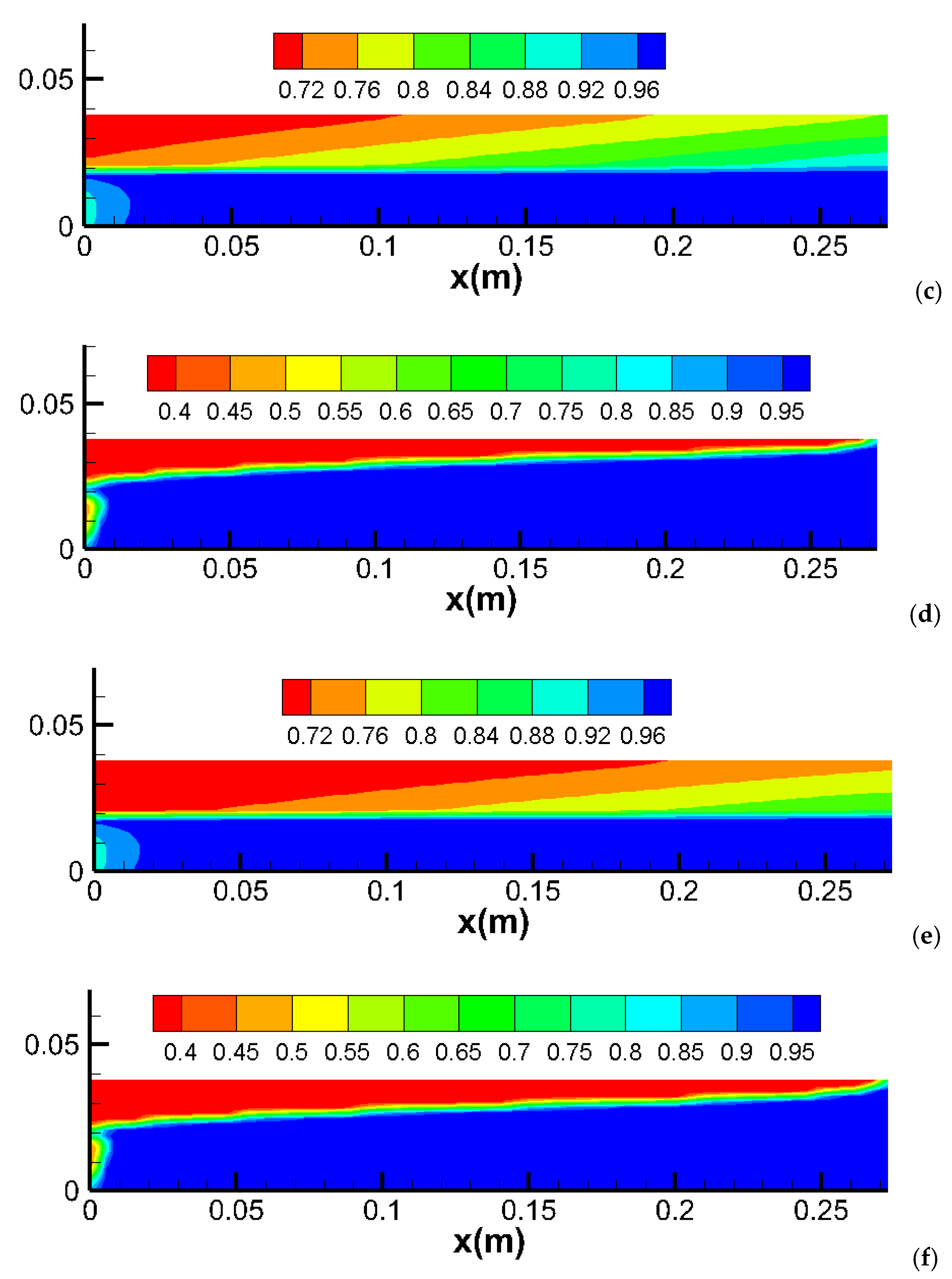
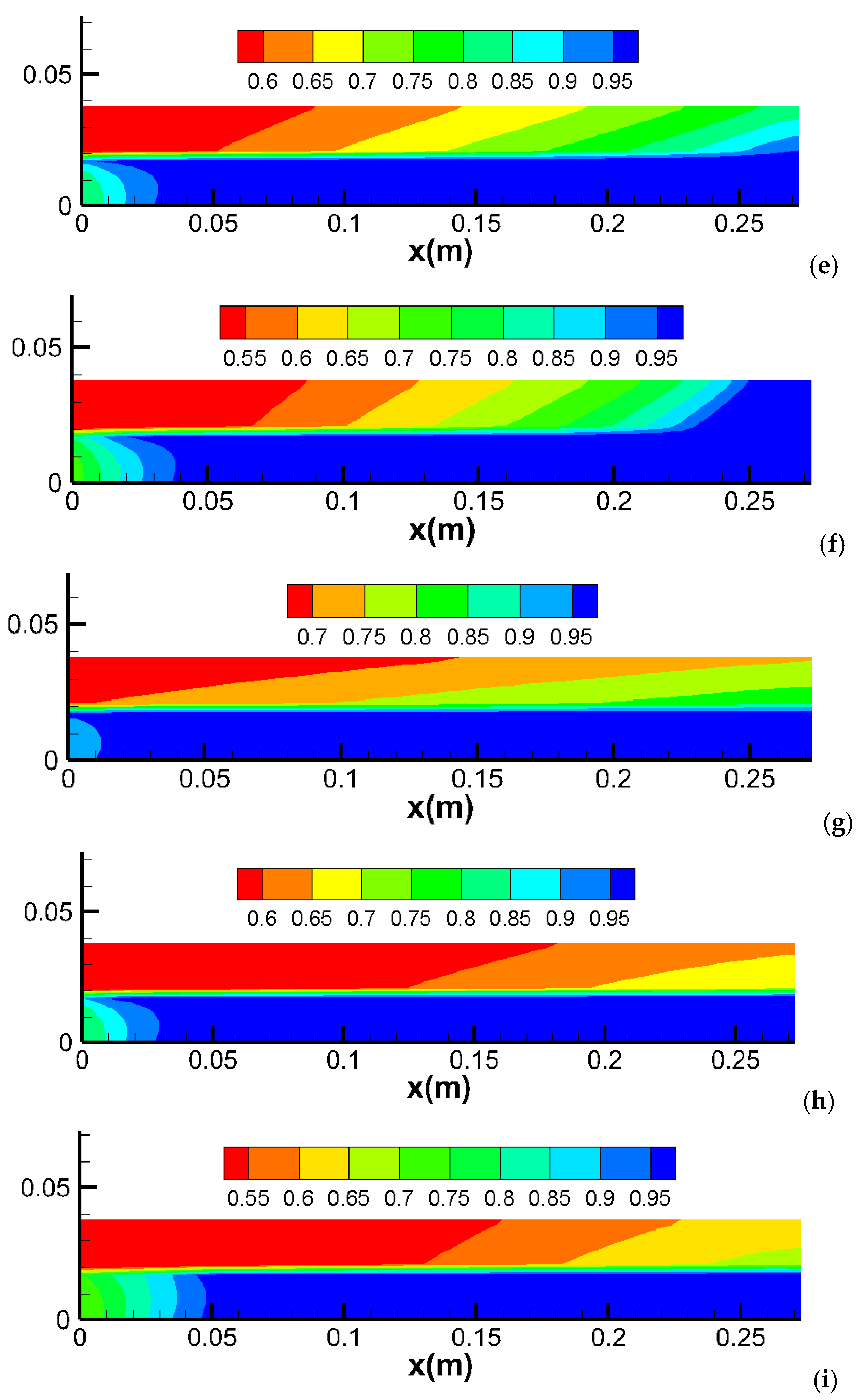
2.6. Viscosification in a Layered Core with Capillary Pressure
3. Discussion
- o
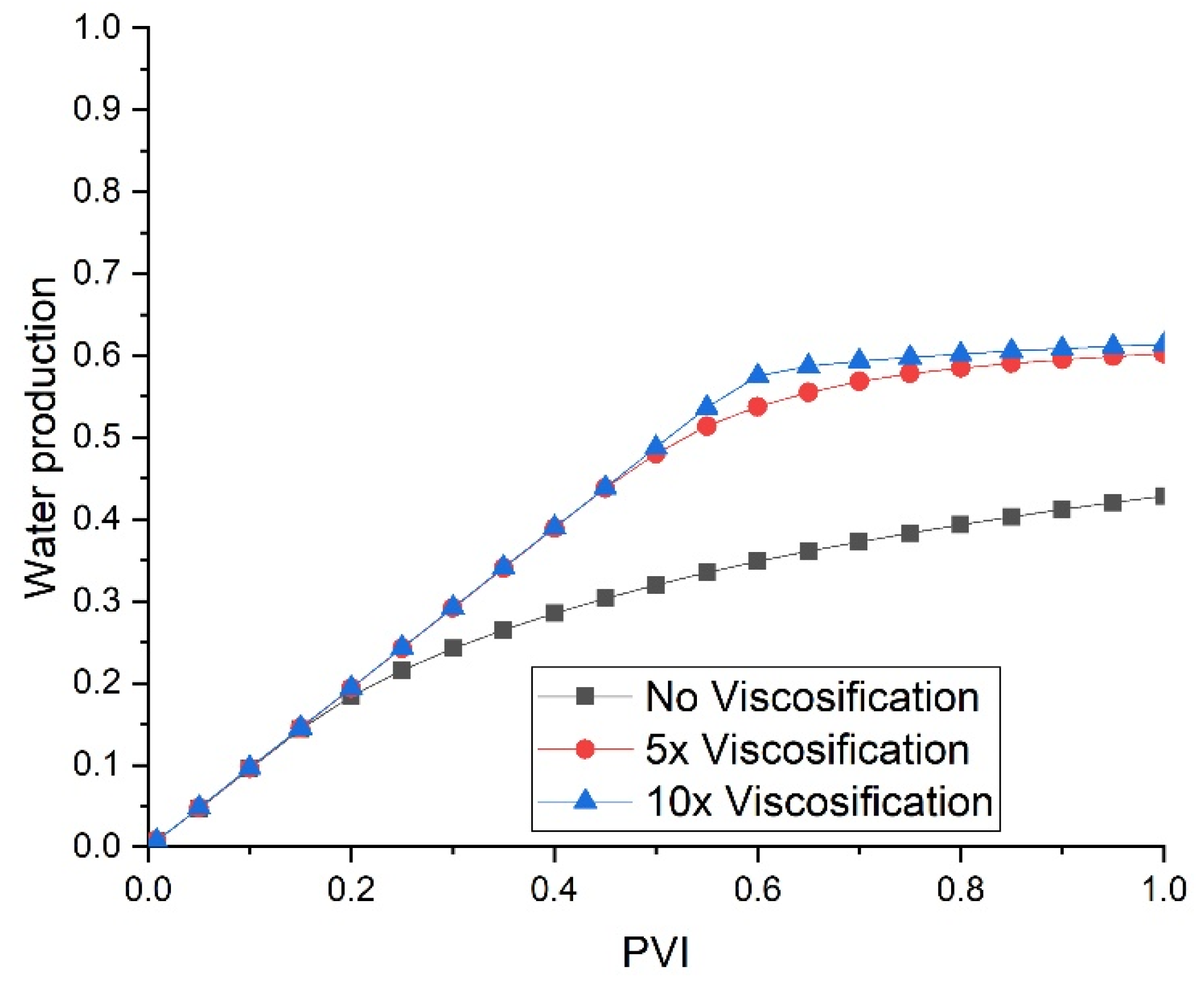
- Mechanism: Increasing the viscosity of CO2 enhances its ability to displace water by reducing the mobility ratio between the injected CO2 and the resident water. This leads to a more stable displacement front and improved sweep efficiency;
- o
- Simulation Results: The simulations show that increasing CO2 viscosity by a factor of 5 significantly enhances water production. However, further increasing the viscosity from 5 to 10 has minimal additional impact. This is consistent with the concept of diminishing returns, where beyond a certain point, further increases in viscosity do not proportionally improve displacement efficiency;
- o
- Alignment with Observations: These findings align with the experimental studies that have demonstrated improved sweep efficiency with increased CO2 viscosity, up to an optimal point beyond which the benefits plateau.
- o
- Mechanism: The effect of CO2 viscosification is expected to be consistent across different core sizes due to the uniform impact of viscosity on fluid flow dynamics;
- o
- Simulation Results: The effect of CO2 viscosification is consistent in both slim (1 cm) and thick (3.8 cm) cores. This indicates that the benefits of increased CO2 viscosity are not significantly influenced by the core thickness;
- o
- Alignment with Observations: This consistency is supported by theoretical predictions and experimental observations, which suggest that viscosity effects are largely independent of core size, provided the flow regime remains similar.
- o
- Mechanism: Capillary pressure influences the distribution and movement of fluids within the porous medium. High capillary pressure can delay the breakthrough of the injected phase and reduce overall sweep efficiency by trapping more of the resident phase;
- o
- Simulation Results: Introducing capillary pressure in a homogeneous core delays breakthrough and reduces CO2 sweeping efficiency, resulting in lower production. This effect is more pronounced in slim cores compared to thick cores, as capillary forces are more significant in smaller pore spaces;
- o
- Alignment with Observations: These results are consistent with theoretical predictions and experimental observations that highlight the role of capillary pressure in fluid displacement processes. Studies have shown that capillary pressure can significantly affect the efficiency of CO2 injection, particularly in fine-grained media.
- o
- Mechanism: In heterogeneous layered cores, capillary pressure affects fluid distribution differently due to variations in permeability and porosity. High permeability layers tend to dominate fluid flow, reducing the overall impact of capillary pressure;
- o
- Simulation Results: Capillary pressure has a similar effect in heterogeneous layered cores as in homogeneous cores. However, the difference in water production between the base case (no capillary pressure) and with capillary pressure is less significant in layered domains. This is because the high permeability layer predominantly produces the recovered water in both scenarios;
- o
- Alignment with Observations: These findings align with experimental and field studies that demonstrate the impact of reservoir heterogeneity on fluid flow and displacement efficiency. In layered systems, high permeability zones often control the flow dynamics, mitigating the effects of capillary pressure.
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Mixed Finite Element Discretization
Appendix A.2. Discontinuous Galekrin Discretization
Appendix A.3. Model Verification
| Parameter | Value |
|---|---|
| Length, width, and Height of the domain | 300 m, 1 m, 1 m |
| Porosity | 20% |
| Permeability | 1 mD |
| Viscosity ratio between the phases | 1 |
| Density ratio between the phases | 1 |
| Residual water saturation | 0 |
| Residual oil saturation | 20% |
| Injection rate | 5 × 10−4 PoreVolume/Day. |

References
- Hadlow, R.E. Update of Industry Experience with CO2 Injection. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992. [Google Scholar] [CrossRef]
- Alam, M.M.M.; Hassan, A.; Mahmoud, M.; Sibaweihi, N.; Patil, S. Dual Benefits of Enhanced Oil Recovery and CO2 Sequestration: The Impact of CO2 Injection Approach on Oil Recovery. Front. Energy Res. 2022, 10, 877212. [Google Scholar] [CrossRef]
- Ampomah, W.; Balch, R.S.; Grigg, R.B.; Cather, M.; Will, R.A.; Lee, S.Y. Optimization of CO2-EOR Process in Partially Depleted Oil Reservoirs. In Proceedings of the SPE Western Regional Meeting, Anchorage, AK, USA, 23–26 May 2016. [Google Scholar]
- Dai, Z.; Viswanathan, H.; Xiao, T.; Middleton, R.; Pan, F.; Ampomah, W.; Yang, C.; Zhou, Y.; Jia, W.; Lee, S.-Y.; et al. CO2 Sequestration and Enhanced Oil Recovery at Depleted Oil/Gas Reservoirs. Energ. Proced. 2017, 114, 6957–6967. [Google Scholar] [CrossRef]
- Khosrokhavar, R.; Elsinga, G.; Farajzadeh, R.; Bruining, H. Visualization and investigation of natural convection flow of CO2 in aqueous and oleic systems. J. Pet. Sci. Eng. 2014, 122, 230–239. [Google Scholar] [CrossRef]
- Both, J.; Gasda, S.; Aavatsmark, I.; Kaufmann, R. Gravity-driven convective mixing of CO2 in oil. In Proceedings of the Third Sustainable Earth Sciences Conference and Exhibition, Celle, Germany, 13–15 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Wu, Z.; Huiqing, L.; Wang, X.; Zhang, Z. Emulsification and improved oil recovery with viscosity reducer during steam injection process for heavy oil. J. Ind. Eng. Chem. 2017, 61, 348–355. [Google Scholar] [CrossRef]
- Green, D.W.; Willhite, G.P. Enhanced Oil Recovery: Society of Petroleum Engineers Textbook; Series, V.6; SPE: Richardson, TX, USA, 1998. [Google Scholar]
- Torabi, F.; Jamaloei, B.Y.; Zarivnyy, O.; Paquin, B.A.; Rumpel, N.J.; Wilton, R.R. Effect of Oil Viscosity Permeability and Injection Rate on Performance of Waterflooding, CO2 Flooding and WAG Processes on Recovery of Heavy Oils. In Proceedings of the Canadian Unconventional Resources and International Petroleum Conference, Calgary, AB, Canada, 19–21 October 2010. [Google Scholar]
- Bond, D.C.; Holbrook, O.C. Gas Drive Oil Recovery Process. U.S. Patent 2,866,507, 30 December 1958. [Google Scholar]
- Fried, A.N. The Foam Drive Process for Increasing the Recovery of Oil; re. inv 5866; US Bureau of Mines: Washington, DC, USA, 1961. [Google Scholar]
- Yang, S.H.; Reed, R.L. Mobility Control Using CO2 Forms. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–11 October 1989. [Google Scholar]
- Khulman, M.I. Visualizing the Effect of Light Oil on CO2 Foams. J. Pet. Technol. 1990, 42, 902–908. [Google Scholar] [CrossRef]
- Manlowe, D.J.; Radke, C.J. A Pore-Level Investigation of Foam/Oil Interactions in Porous Media. Soc. Pet. Eng. 1990, 5, 495–502. [Google Scholar] [CrossRef]
- Nikolov, A.D.; Wasan, D.T.; Huang, D.W.; Edwards, D.A. The Effect of Oil on Foam Stability: Mechanisms and Implications for Oil Displacement by Foam in Porous media. In Proceedings of the 61st ATCE of SPE, New Orleans, LA, USA, 5 October 1986. [Google Scholar]
- Bernard, G.G.; Holm, L. Effect of Foam on Permeability of Porous Media to Gas. Soc. Pet. Eng. J. 1965, 4, 267. [Google Scholar] [CrossRef]
- Gallo, G.; Erdmann, E. Simulation of Viscosity Enhanced CO2 Nanofluid Alternating Gas in Light Oil Reservoirs. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, 17–19 May 2017. [Google Scholar]
- Bae, J.H.; Irani, C.A. A Laboratory Investigation of Viscosified CO2. Process. Soc. Pet. Eng. 1993, 1, 166–171. [Google Scholar]
- Xu, J.; Enick, R.M. Thickening Carbon Dioxide with the Fluoroacrylate-Styrene Copolymer. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–3 October 2001. [Google Scholar]
- Huang, Z.; Xu, S.J.; Kilic, R.M. Enhancement of Viscosity of Carbon Dioxide Using Styrene/Fluoroacrylate Copolymers. Macromolecules 2000, 33, 5437–5442. [Google Scholar] [CrossRef]
- Zaberi, H.A.; Lee, J.J.; Enick, R.M.; Beckman, E.J.; Cummings, S.D.; Dailey, C.; Vasilache, M. An experimental feasibility study on the use of CO2-soluble polyfluoroacrylates for CO2 mobility and conformance control applications. J. Pet. Sci. Eng. 2020, 184, 106556. [Google Scholar] [CrossRef]
- Lemaire, P.C.; Alenzi, A.; Lee, J.J.; Beckman, E.J.; Enick, R.M. Thickening CO2 with Direct Thickeners, CO2-in-Oil Emulsions, or Nanoparticle Dispersions: Literature Review and Experimental Validation. Energy Fuels 2021, 35, 8510–8540. [Google Scholar] [CrossRef]
- Kilic, S.; Enick, R.M.; Beckman, E.J. Fluoroacrylate-Aromatic Acrylate Copolymers for Viscosity Enhancement of Carbon Dioxide. J. Supercrit. Fluids 2019, 146, 38–46. [Google Scholar] [CrossRef]
- CMG Software Package. Available online: https://www.cmgl.ca/solutions/software/builder/ (accessed on 29 October 2024).
- Younes, A.; Fahs, M.; Zidane, A.; Huggenberger, P.; Zechner, E. A new benchmark with high accurate solution for hot–cold fluids mixing. Heat Mass Transf. 2015, 51, 1321–1336. [Google Scholar] [CrossRef]
- Zidane, A. CO2 Viscosification for Mobility Alteration in Improved Oil Recovery and CO2 Sequestration. Water 2023, 15, 1730. [Google Scholar] [CrossRef]
- Al-Menhali, A.; Niu, B.; Krevor, S. Capillarity and wetting of carbon dioxide and brine during drainage in Berea sandstone at reservoir conditions. Water Resour. Res. 2015, 51, 7895–7914. [Google Scholar] [CrossRef]
- Brezzi, F.; Fortin, M. Mixed and Hybrid Finite Element Methods, Environmental Engineering; Springer: New York, NY, USA, 1991. [Google Scholar]
- Chavent, G.; Salzano, A. A finite-element method for the 1-D water flooding problem with gravity. J. Comput. Phys. 1982, 45, 307–344. [Google Scholar] [CrossRef]
- Chavent, G.; Cockburn, B. The local projection p0p1-discontinuous Galerkin finite element method for scalar conservation laws. ESAIM Math. Model. Numer. Anal. 1989, 23, 565–592. [Google Scholar] [CrossRef]
- van Leer, B. Towards the ultimate conservative scheme: II. J. Comput. Phys. 1974, 14, 361–376. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservative laws II: General frame-work. Math. Comp. 1989, 52, 411–435. [Google Scholar]
- Cockburn, B.; Shu, C. The local discontinuous Galerkin finite element method for convection–diffusion systems. SIAM J. Numer. Anal. 1998, 35, 2440–2463. [Google Scholar] [CrossRef]
- Buckley, S.; Leverett, M. Mechanism of fluid displacement in sands. Trans. AIME 1942, 146, 187–196. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zidane, A. Impact of CO2 Viscosity and Capillary Pressure on Water Production in Homogeneous and Heterogeneous Media. Water 2024, 16, 3566. https://doi.org/10.3390/w16243566
Zidane A. Impact of CO2 Viscosity and Capillary Pressure on Water Production in Homogeneous and Heterogeneous Media. Water. 2024; 16(24):3566. https://doi.org/10.3390/w16243566
Chicago/Turabian StyleZidane, Ali. 2024. "Impact of CO2 Viscosity and Capillary Pressure on Water Production in Homogeneous and Heterogeneous Media" Water 16, no. 24: 3566. https://doi.org/10.3390/w16243566
APA StyleZidane, A. (2024). Impact of CO2 Viscosity and Capillary Pressure on Water Production in Homogeneous and Heterogeneous Media. Water, 16(24), 3566. https://doi.org/10.3390/w16243566






