Towards Accurate Flood Predictions: A Deep Learning Approach Using Wupper River Data
Abstract
1. Introduction
- We compile a unique dataset spanning 19 years, including rainfall measurements and water level data from the Wupper river in Germany [9].
- We conduct a thorough assessment of state-of-the-art deep learning models specifically tailored for time-series analysis. Nine state-of-the-art deep learning models (such as Pyraformer, Informer and TimesNet) are compared on a classification task to issue warning forecasts in case of flood events in the near future. This benchmarking on real-world flood events offers crucial insights into model suitability and performance in issuing timely warning forecasts, a vital step toward reliable flood early warning systems.
- We study the effect of strongly reduced sensor numbers on the model performance, offering a novel estimate of the minimum sensor count necessary for reliable flood forecasting.
2. Related Work
2.1. Traditional Flood Forecasting Models
- Conceptual models aim to represent the hydrological process using simplified components. Even though they use parameters that are partially based on physical understanding, they are generally calibrated with observed data. An example for a conceptual model is the Hydrologiska Byråns Vattenbalansavdelning (HBV) [13], which balances simplicity and physical realism, making it efficient for flood prediction, even with limited data.
- Empirical models are data driven, relying on statistical correlations between rainfall and runoff without the detailed consideration of physical processes. It is said they are best suited for areas with extensive historical data but limited environmental detail. Developed by Cronshey [14], the Soil Conservation Service Curve Number (SCS-CN) estimates runoff based on land use, soil type, and rainfall.
- Physical models, also known as deterministic models, use mathematical equations to simulate the physicals processes affecting runoff, such as infiltration and evaporation. The Soil and Water Assessment Tool (SWAT) [15] simulates the impact of land management practices on water, sediment, and nutrient yields in large watersheds, providing a framework to assess water resource changes.
2.2. Deep Learning Models
- Flood forecasting using RNN and LSTM networks for time-series prediction of rainfall, river flow, and flood occurrence;
- Flood susceptibility mapping and flood extent detection with CNN for spatial data analysis, such as satellite and remote sensing imagery;
- Synthetic data generation with Generative Adversarial Networks (GANs) to supplement datasets in regions with scarce real data;
- Feature extraction through autoencoders and Self-Organizing Maps (SOMs) for the dimensionality reduction and identification of critical flood-related features.
2.3. Deep Learning for Time Series
3. Materials and Method
3.1. Dataset
- Water level sensor;
- Discharge sensor;
- Precipitation sensor.
- Different measurement frequencies for different sensors;
- Missing data points.
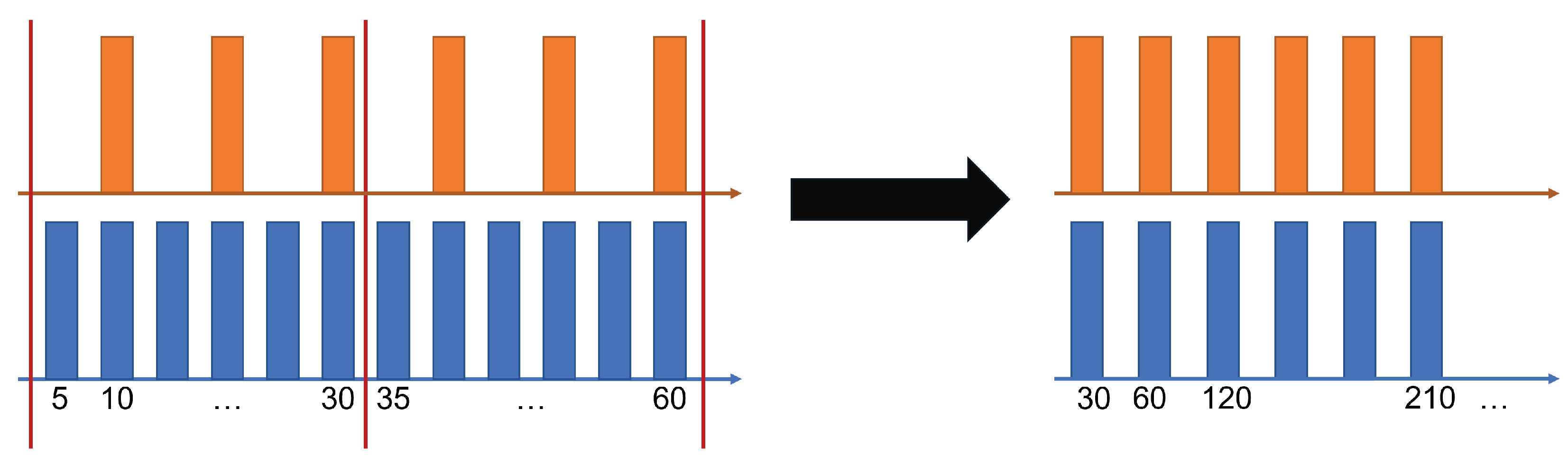
3.1.1. Different Frequencies
3.1.2. Data Imputation
3.1.3. Sensor Distances
3.2. Methodology
3.2.1. Experimental Design
3.2.2. K-Fold Cross Validation
3.2.3. Hyperparameter Search
- We performed a random search ([54]) on hyperparameters, such as learning rate, training epochs, and model-specific parameters.
- Training the model on a reduced subset of train data from the first fold.
- Evaluating the models’ performance (in regards to the F1-score), using the validation dataset from the first fold.
3.2.4. Training
4. Experiments
4.1. Flood Warning Event Forecasting
4.2. Case Study Extreme Events
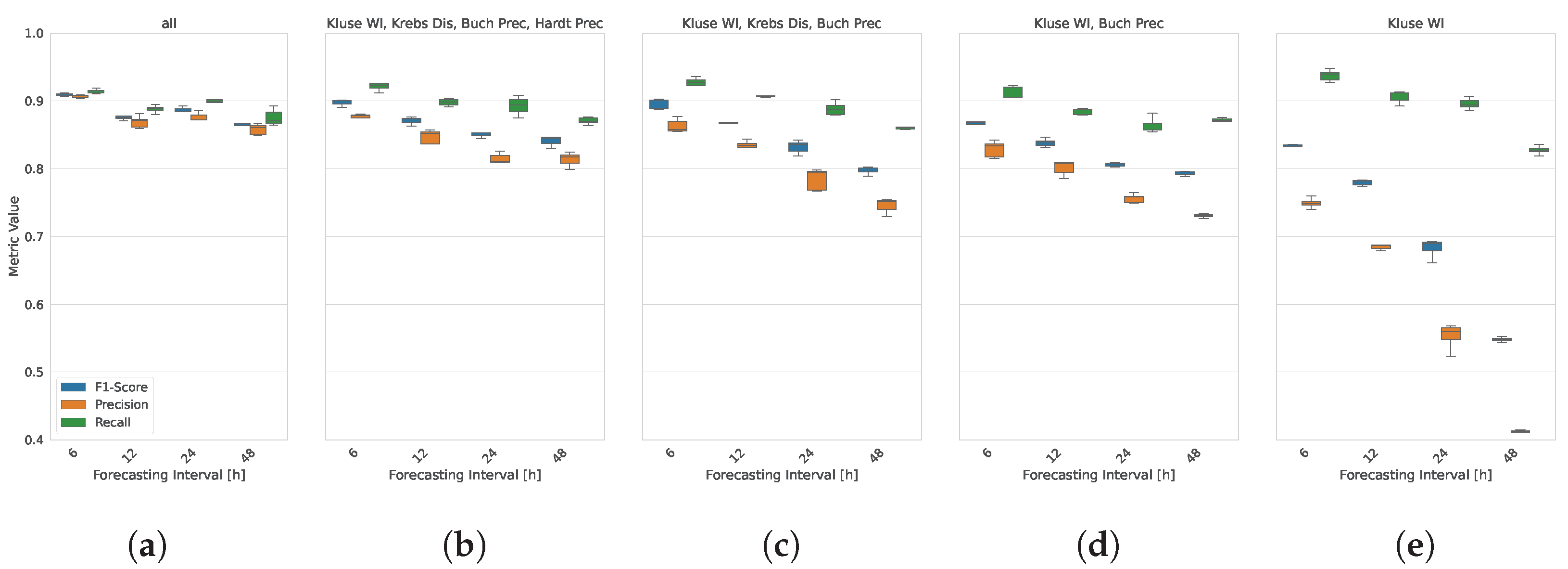
4.3. Minimum Viable Sensor Count
5. Conclusions
- We present a unique, publicly available dataset comprising several years of data from three types of sensors—water level, discharge, and precipitation—strategically positioned throughout Wuppertal and its surrounding areas. This dataset serves as a valuable resource for flood forecasting research and model benchmarking.
- We evaluate the performance of multiple deep learning models, demonstrating their ability to issue reliable flood warnings with high accuracy. Our top-performing algorithm, the SegRNN model, successfully issued warnings in approximately 91% of flood occurrences, underscoring the effectiveness of deep learning for flood forecasting.
- Our results indicate a false warning rate of approximately 10%, highlighting the importance of balancing sensitivity and specificity in flood prediction applications. This finding offers valuable insights into model performance trade-offs and suggests potential areas for enhancing flood warning accuracy.
Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Myhre, G.; Alterskjær, K.; Stjern, C.W.; Hodnebrog, Ø.; Marelle, L.; Samset, B.H.; Sillmann, J.; Schaller, N.; Fischer, E.; Schulz, M.; et al. Frequency of extreme precipitation increases extensively with event rareness under global warming. Sci. Rep. 2019, 9, 16063. [Google Scholar] [CrossRef] [PubMed]
- Unisdr, C. The Human Cost of Natural Disasters: A Global Perspective. 2015. Available online: https://climate-adapt.eea.europa.eu/en/metadata/publications/the-human-cost-of-natural-disasters-2015-a-global-perspective (accessed on 20 November 2024).
- Biswas, A.K. History of Hydrology; North-Holland Publishing: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Hakim, D.K.; Gernowo, R.; Nirwansyah, A.W. Flood prediction with time series data mining: Systematic review. Nat. Hazards Res. 2024, 4, 194–220. [Google Scholar] [CrossRef]
- Ahmed, M.I.; Stadnyk, T.; Pietroniro, A.; Awoye, H.; Bajracharya, A.; Mai, J.; Tolson, B.A.; Shen, H.; Craig, J.R.; Gervais, M.; et al. Learning from hydrological models’ challenges: A case study from the Nelson basin model intercomparison project. J. Hydrol. 2023, 623, 129820. [Google Scholar] [CrossRef]
- Souffront Alcantara, M.A.; Nelson, E.J.; Shakya, K.; Edwards, C.; Roberts, W.; Krewson, C.; Ames, D.P.; Jones, N.L.; Gutierrez, A. Hydrologic Modeling as a Service (HMaaS): A New Approach to Address Hydroinformatic Challenges in Developing Countries. Front. Environ. Sci. 2019, 7, 158. [Google Scholar] [CrossRef]
- Kumar, V.; Azamathulla, H.M.; Sharma, K.V.; Mehta, D.J.; Maharaj, K.T. The State of the Art in Deep Learning Applications, Challenges, and Future Prospects: A Comprehensive Review of Flood Forecasting and Management. Sustainability 2023, 15, 10543. [Google Scholar] [CrossRef]
- Bentivoglio, R.; Isufi, E.; Jonkman, S.N.; Taormina, R. Deep learning methods for flood mapping: A review of existing applications and future research directions. Hydrol. Earth Syst. Sci. 2022, 26, 4345–4378. [Google Scholar] [CrossRef]
- Wönkhaus, M.; Hahn, Y.; Kienitz, P.; Meyes, R.; Meisen, T. Flood Classification Dataset from the River Wupper in Germany. Zenodo 2024. [Google Scholar] [CrossRef]
- Jain, S.K.; Mani, P.; Jain, S.K.; Prakash, P.; Singh, V.P.; Tullos, D.; Kumar, S.; Agarwal, S.P.; Dimri, A.P. A Brief review of flood forecasting techniques and their applications. Int. J. River Basin Manag. 2018, 16, 329–344. [Google Scholar] [CrossRef]
- Kauffeldt, A.; Wetterhall, F.; Pappenberger, F.; Salamon, P.; Thielen, J. Technical review of large-scale hydrological models for implementation in operational flood forecasting schemes on continental level. Environ. Model. Softw. 2016, 75, 68–76. [Google Scholar] [CrossRef]
- Jehanzaib, M.; Ajmal, M.; Achite, M.; Kim, T.W. Comprehensive Review: Advancements in Rainfall-Runoff Modelling for Flood Mitigation. Climate 2022, 10, 147. [Google Scholar] [CrossRef]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- Cronshey, R. Urban Hydrology for Small Watersheds; Number 55; US Department of Agriculture, Soil Conservation Service, Engineering Division: Washington, DC, USA, 1986. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Norbiato, D.; Borga, M.; Dinale, R. Flash flood warning in ungauged basins by use of the flash flood guidance and model-based runoff thresholds. Meteorol. Appl. 2009, 16, 65–75. [Google Scholar] [CrossRef]
- Cannon, S.H.; Gartner, J.E.; Wilson, R.C.; Bowers, J.C.; Laber, J.L. Storm rainfall conditions for floods and debris flows from recently burned areas in southwestern Colorado and southern California. Geomorphology 2008, 96, 250–269. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Wang, Q.J.; Pagano, T.C. A review of advances in flash flood forecasting. Hydrol. Processes 2011, 25, 2771–2784. [Google Scholar] [CrossRef]
- Giannaros, C.; Dafis, S.; Stefanidis, S.; Giannaros, T.M.; Koletsis, I.; Oikonomou, C. Hydrometeorological analysis of a flash flood event in an ungauged Mediterranean watershed under an operational forecasting and monitoring context. Meteorol. Appl. 2022, 29, e2079. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, H.; Bai, M.; Xu, Y.; Dong, S.; Rao, H.; Ming, W. A Comprehensive Review of Methods for Hydrological Forecasting Based on Deep Learning. Water 2024, 16, 1407. [Google Scholar] [CrossRef]
- Gude, V.; Corns, S.; Long, S. Flood Prediction and Uncertainty Estimation Using Deep Learning. Water 2020, 12, 884. [Google Scholar] [CrossRef]
- Luppichini, M.; Barsanti, M.; Giannecchini, R.; Bini, M. Deep learning models to predict flood events in fast-flowing watersheds. Sci. Total Environ. 2022, 813, 151885. [Google Scholar] [CrossRef]
- Widiasari, I.R.; Nugroho, L.E.; Widyawan. Deep learning multilayer perceptron (MLP) for flood prediction model using wireless sensor network based hydrology time series data mining. In Proceedings of the 2017 International Conference on Innovative and Creative Information Technology (ICITech), Salatiga, Indonesia, 2–4 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, J.; Liao, Z.; Zhou, Y.; Wang, H.; Pei, Q. A short-term flood prediction based on spatial deep learning network: A case study for Xi County, China. J. Hydrol. 2022, 607, 127535. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, Y.; Wang, H.; Jiang, Z. Depth prediction of urban flood under different rainfall return periods based on deep learning and data warehouse. Sci. Total Environ. 2020, 716, 137077. [Google Scholar] [CrossRef] [PubMed]
- Kimura, N.; Yoshinaga, I.; Sekijima, K.; Azechi, I.; Baba, D. Convolutional Neural Network Coupled with a Transfer-Learning Approach for Time-Series Flood Predictions. Water 2019, 12, 96. [Google Scholar] [CrossRef]
- Sankaranarayanan, S.; Prabhakar, M.; Satish, S.; Jain, P.; Ramprasad, A.; Krishnan, A. Flood prediction based on weather parameters using deep learning. J. Water Clim. Chang. 2020, 11, 1766–1783. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, R.; Yang, M.; Tu, T.; Ma, M.; Hong, Y.; Wang, X. Large-scale flash flood warning in China using deep learning. J. Hydrol. 2022, 604, 127222. [Google Scholar] [CrossRef]
- Panahi, M.; Jaafari, A.; Shirzadi, A.; Shahabi, H.; Rahmati, O.; Omidvar, E.; Lee, S.; Bui, D.T. Deep learning neural networks for spatially explicit prediction of flash flood probability. Geosci. Front. 2021, 12, 101076. [Google Scholar] [CrossRef]
- Lin, S.; Lin, W.; Wu, W.; Zhao, F.; Mo, R.; Zhang, H. SegRNN: Segment Recurrent Neural Network for Long-Term Time Series Forecasting. arXiv 2023, arXiv:2308.11200. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in Time Series: A Survey. arXiv 2023, arXiv:2202.07125. [Google Scholar]
- Lim, B.; Arık, S.O.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Nie, Y.; Nguyen, N.H.; Sinthong, P.; Kalagnanam, J. A Time Series is Worth 64 Words: Long-term Forecasting with Transformers. arXiv 2023, arXiv:2211.14730. [Google Scholar]
- Liu, Y.; Wu, H.; Wang, J.; Long, M. Non-stationary Transformers: Exploring the Stationarity in Time Series Forecasting. arXiv 2022, arXiv:2205.14415. [Google Scholar] [CrossRef]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. Timesnet: Temporal 2d-variation modeling for general time series analysis. In Proceedings of the Eleventh International Conference on Learning Representations, Virtual Event, 25–29 April 2022. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. arXiv 2024, arXiv:2310.06625. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Bandara, K.; Bergmeir, C.; Smyl, S. Forecasting across time series databases using recurrent neural networks on groups of similar series: A clustering approach. Expert Syst. Appl. 2020, 140, 112896. [Google Scholar] [CrossRef]
- Wen, Q.; Yang, F.; Song, X.; Gao, Y.; Zhao, P.; Deng, H. A robust decomposition approach to forecasting in the presence of anomalies: A case study on web traffic. IEEE Trans. Knowl. Data Eng. 2020, 32, 2398–2409. [Google Scholar]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting. In Proceedings of the 39th International Conference on Machine Learning, Proceedings of Machine Learning Research, Baltimore, MD, USA, 17–23 July 2022; Chaudhuri, K., Jegelka, S., Song, L., Szepesvari, C., Niu, G., Sabato, S., Eds.; PMLR 162. pp. 27268–27286. [Google Scholar]
- Liu, S.; Yu, H.; Liao, C.; Li, J.; Lin, W.; Liu, A.X.; Dustdar, S. Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting. In Proceedings of the International Conference on Learning Representations, Virtual, 25 April 2022. [Google Scholar]
- Noor, N.M.; Al Bakri Abdullah, M.M.; Yahaya, A.S.; Ramli, N.A. Comparison of Linear Interpolation Method and Mean Method to Replace the Missing Values in Environmental Data Set. Mater. Sci. Forum 2014, 803, 278–281. [Google Scholar] [CrossRef]
- Wolbers, M.; Noci, A.; Delmar, P.; Gower-Page, C.; Yiu, S.; Bartlett, J.W. Standard and reference-based conditional mean imputation. Pharm. Stat. 2022, 21, 1246–1257. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An imperative style, high-performance deep learning library. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA, 2019. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Reback, J.; McKinney, W.; Jbrockmendel; Van den Bossche, J.; Augspurger, T.; Cloud, P.; Hawkins, S.; Gfyoung; Sinhrks; Petersen, T.; et al. pandas-dev/pandas: Pandas; Zenodo: Geneva, Switzerland, 2020. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11121–11128. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]

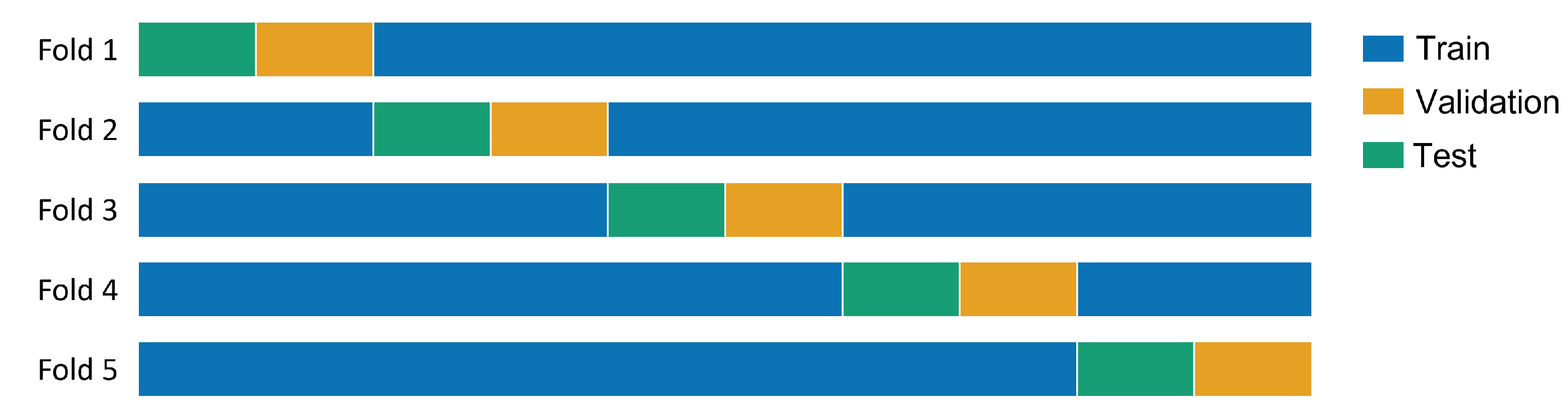


| Prec BWV | Prec BUC | Prec HAR | Prec SCH | Prec WAL | Prec ZDD | Prec RO | Prec ROT | WL KLU | WL KRE | |
|---|---|---|---|---|---|---|---|---|---|---|
| Prec BWV | 0.0 | 8.11 | 3.02 | 1.78 | 10.25 | 3.53 | 5.44 | 5.45 | 3.4 | 9.88 |
| Prec BUC | 0.0 | 5.47 | 8.26 | 2.89 | 11.63 | 6.99 | 5.41 | 4.86 | 13.72 | |
| Prec HAR | 0.0 | 2.79 | 7.31 | 6.41 | 5.82 | 4.99 | 0.67 | 11.77 | ||
| Prec SCH | 0.0 | 9.98 | 3.99 | 7.0 | 6.74 | 3.41 | 11.65 | |||
| Prec WAL | 0.0 | 13.72 | 9.86 | 8.29 | 6.85 | 16.6 | ||||
| Prec ZDD | 0.0 | 7.89 | 8.42 | 6.88 | 9.96 | |||||
| Prec RO | 0.0 | 1.58 | 5.43 | 6.76 | ||||||
| Prec ROT | 0.0 | 4.47 | 8.32 | |||||||
| WL KLU | 0.0 | 11.6 | ||||||||
| WL KRE | 0.0 |
| Model | Reference | Architecture | Main Focus |
|---|---|---|---|
| DLinear | Zeng et al. [52] | Linear Layers | Efficient linear trend analysis for long-term time series |
| SegRNN | Lin et al. [30] | RNN | Long-term forecasting with segment-wise input iterations and parallel forecasting |
| TimesNet | Wu et al. [37] | CNN | Multiperiodicity modeling for enhanced feature representation in time series |
| Transformer | Vaswani et al. [32] | Transformer | Capturing temporal dependencies in general-purpose time-series data |
| PatchTST | Nie et al. [35] | Transformer | Patching mechanism for local feature extraction in temporal sequences |
| Informer | Zhou et al. [39] | Transformer | Sparse attention for scalable long-sequence forecasting |
| Non-stationary Transformer | Liu et al. [36] | Transformer | Adaptive handling of non-stationary series without stationarization |
| iTransformer | Liu et al. [38] | Transformer | Enhanced interpretability with focus on capturing long-range dependencies |
| Pyraformer | Liu et al. [45] | Transformer | Hierarchical pyramidal attention for efficient processing of long sequences |
| Model | Accuracytest | F1-Scoretest | Precisiontest | Recalltest |
|---|---|---|---|---|
| Transformer | 0.762 ± 0.241 | 0.212 ± 0.101 | 0.131 ± 0.071 | 0.902 ± 0.140 |
| Pyraformer | 0.981 ± 0.005 | 0.630 ± 0.060 | 0.476 ± 0.071 | 0.954 ± 0.021 |
| DLinear | 0.987 ± 0.001 | 0.709 ± 0.020 | 0.567 ± 0.025 | 0.946 ± 0.015 |
| iTransformer | 0.993 ± 0.001 | 0.819 ± 0.021 | 0.736 ± 0.025 | 0.923 ± 0.022 |
| PatchTST | 0.994 ± 0.001 | 0.831 ± 0.020 | 0.762 ± 0.031 | 0.914 ± 0.025 |
| Informer | 0.995 ± 0.001 | 0.867 ± 0.013 | 0.809 ± 0.022 | 0.936 ± 0.018 |
| Non-stationary Transformer | 0.996 ± 0.000 | 0.889 ± 0.011 | 0.857 ± 0.023 | 0.926 ± 0.021 |
| TimesNet | 0.997 ± 0.001 | 0.896 ± 0.014 | 0.876 ± 0.033 | 0.918 ± 0.017 |
| SegRNN | 0.997 ± 0.000 | 0.910 ± 0.011 | 0.906 ± 0.021 | 0.914 ± 0.019 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hahn, Y.; Kienitz, P.; Wönkhaus, M.; Meyes, R.; Meisen, T. Towards Accurate Flood Predictions: A Deep Learning Approach Using Wupper River Data. Water 2024, 16, 3368. https://doi.org/10.3390/w16233368
Hahn Y, Kienitz P, Wönkhaus M, Meyes R, Meisen T. Towards Accurate Flood Predictions: A Deep Learning Approach Using Wupper River Data. Water. 2024; 16(23):3368. https://doi.org/10.3390/w16233368
Chicago/Turabian StyleHahn, Yannik, Philip Kienitz, Mark Wönkhaus, Richard Meyes, and Tobias Meisen. 2024. "Towards Accurate Flood Predictions: A Deep Learning Approach Using Wupper River Data" Water 16, no. 23: 3368. https://doi.org/10.3390/w16233368
APA StyleHahn, Y., Kienitz, P., Wönkhaus, M., Meyes, R., & Meisen, T. (2024). Towards Accurate Flood Predictions: A Deep Learning Approach Using Wupper River Data. Water, 16(23), 3368. https://doi.org/10.3390/w16233368









