Seasonal WaveNet-LSTM: A Deep Learning Framework for Precipitation Forecasting with Integrated Large Scale Climate Drivers
Abstract
1. Introduction
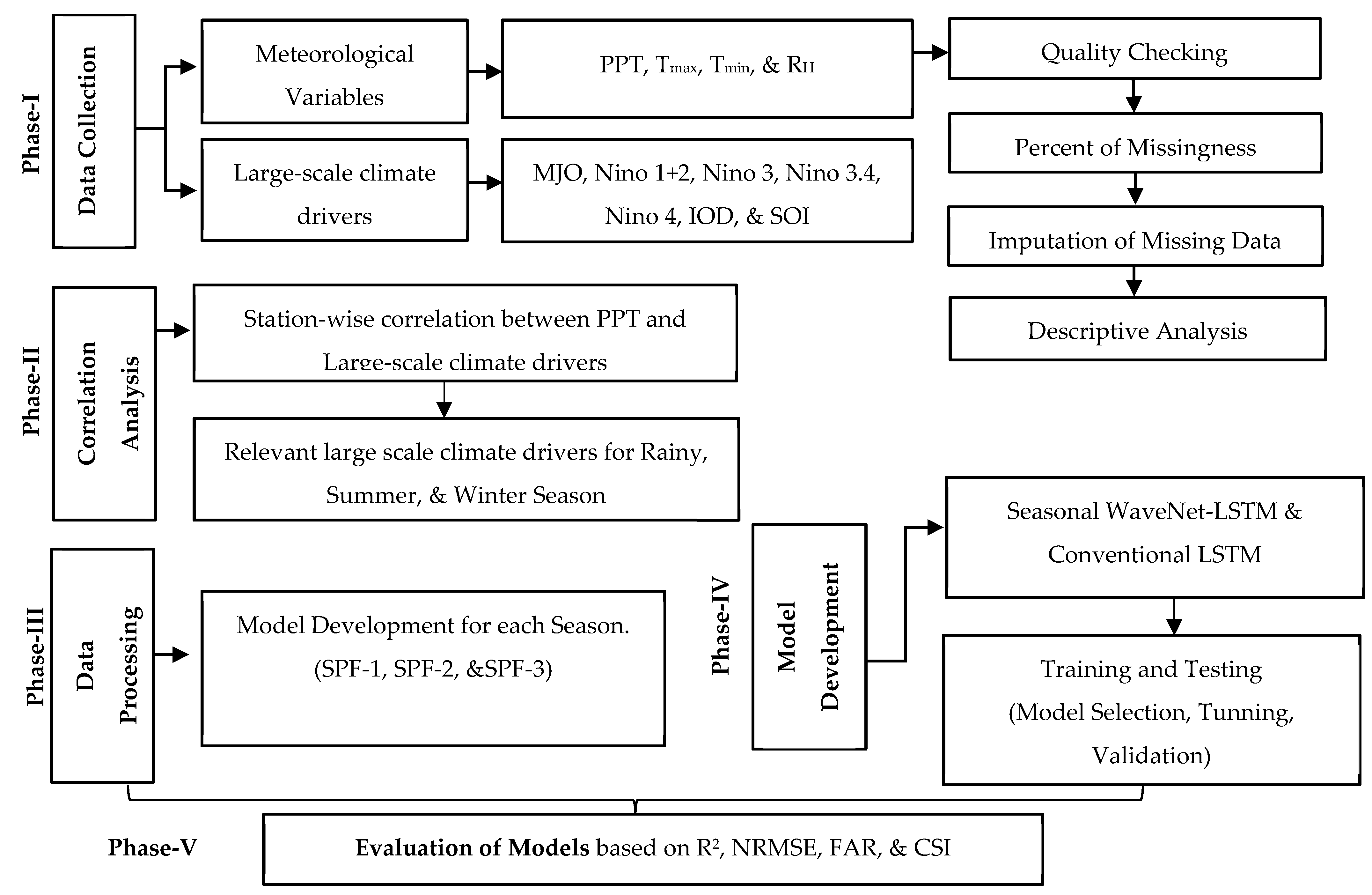
2. Materials and Methods
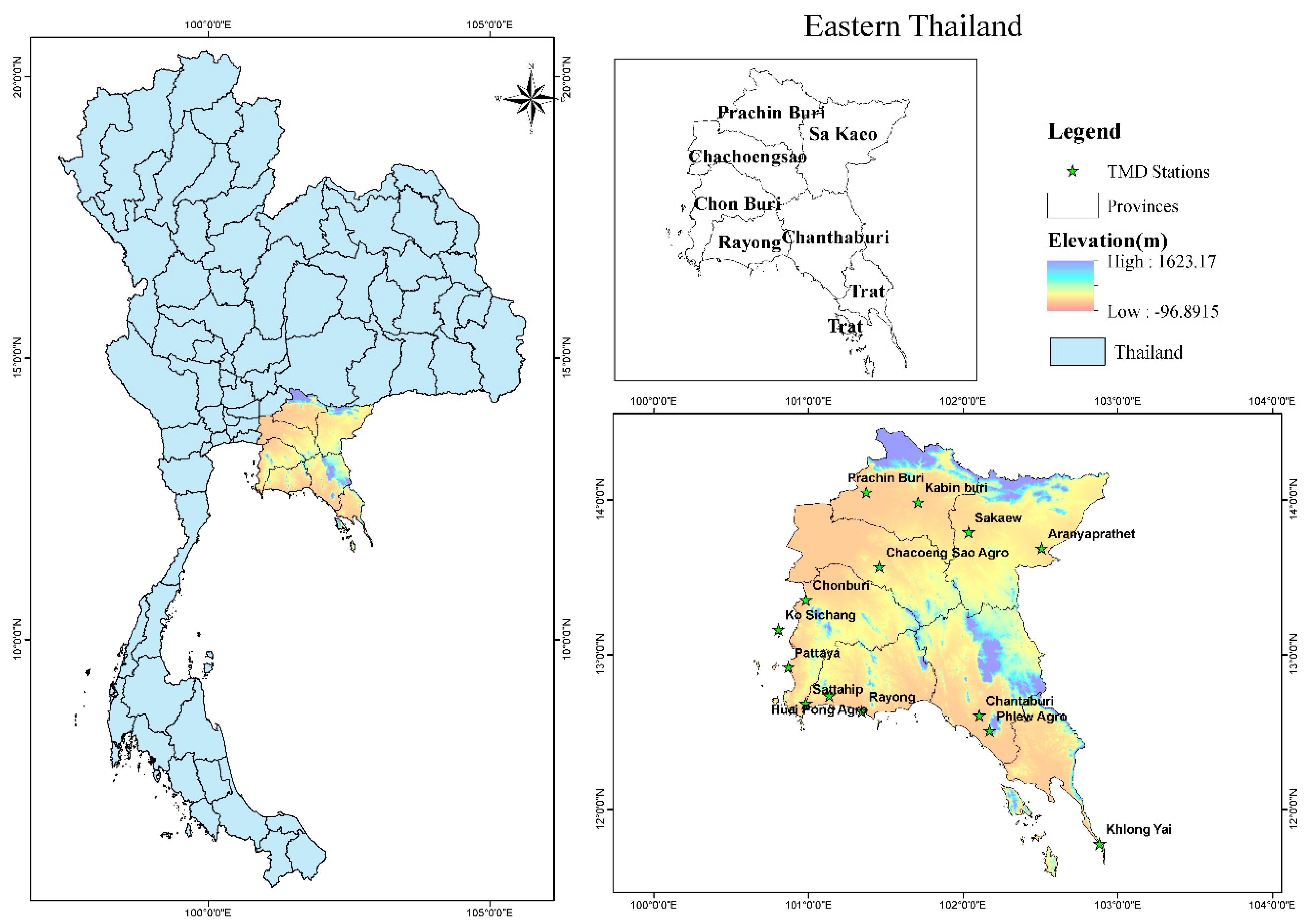
2.1. Study Area
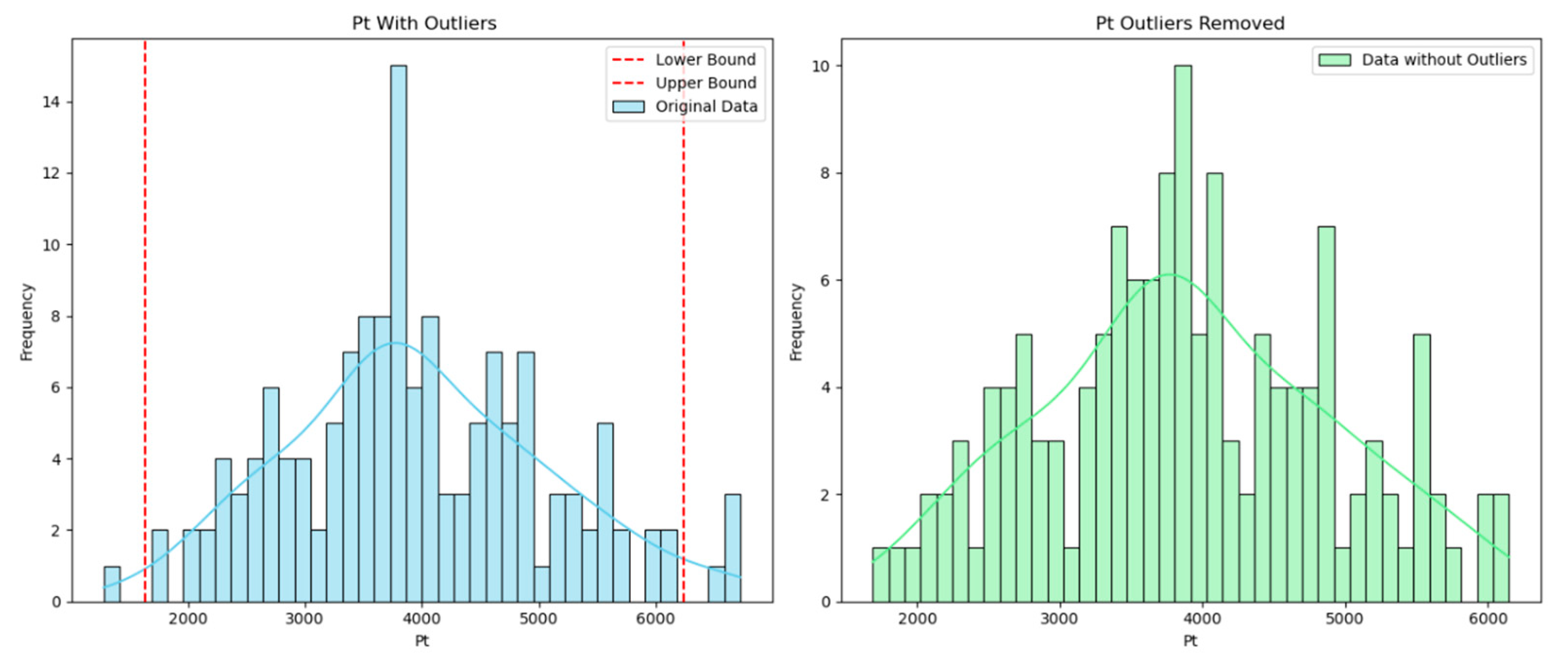
2.2. Data Collection and Quality Checking
2.3. Correlation Analysis Between Seasonal Precipitation and Large-Scale Climate Drivers
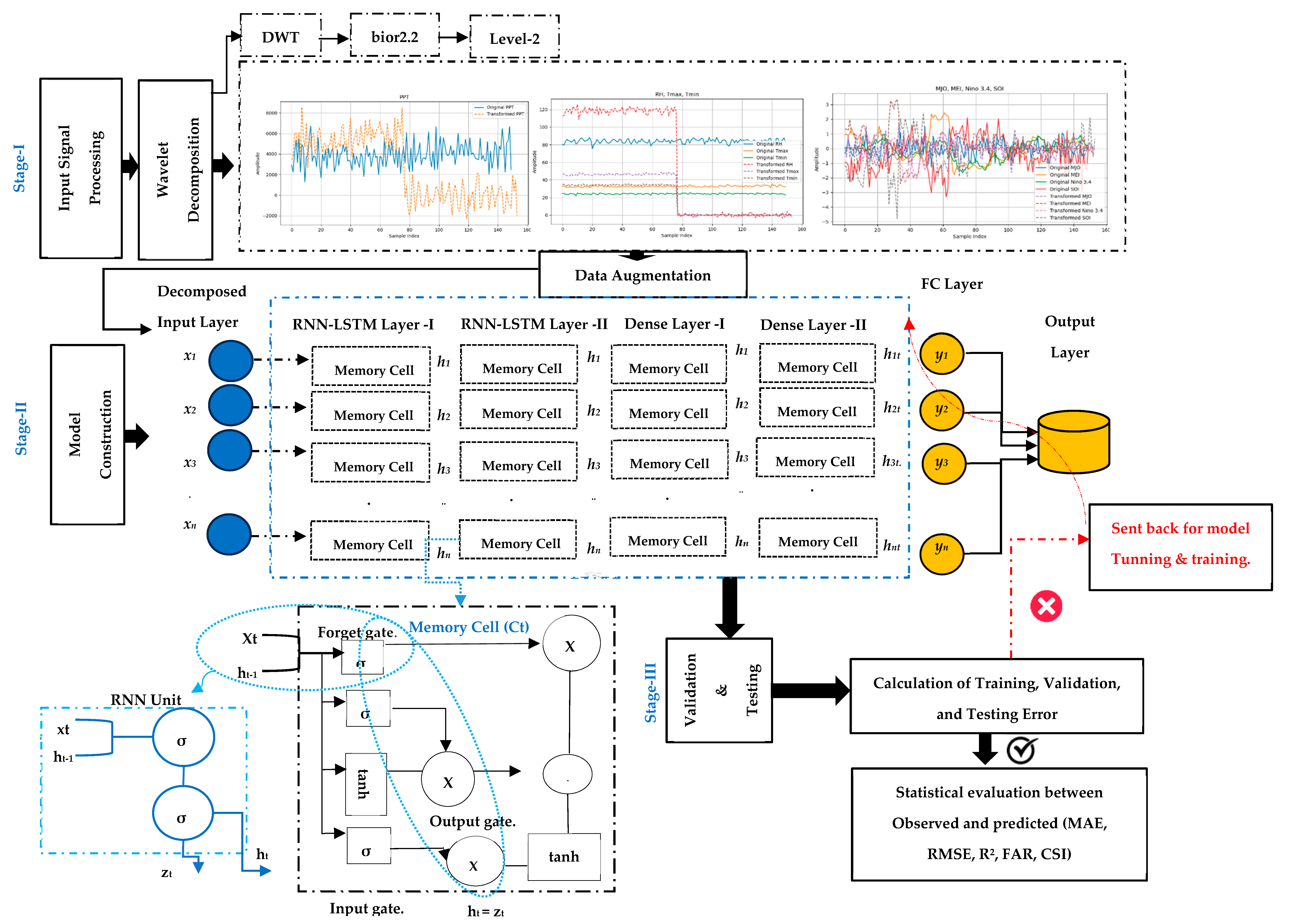
2.4. Model Development
2.5. Seasonal WaveNet-LSTM
Limitations of Seasonal WaveNet-LSTM
2.6. Evaluation Criteria
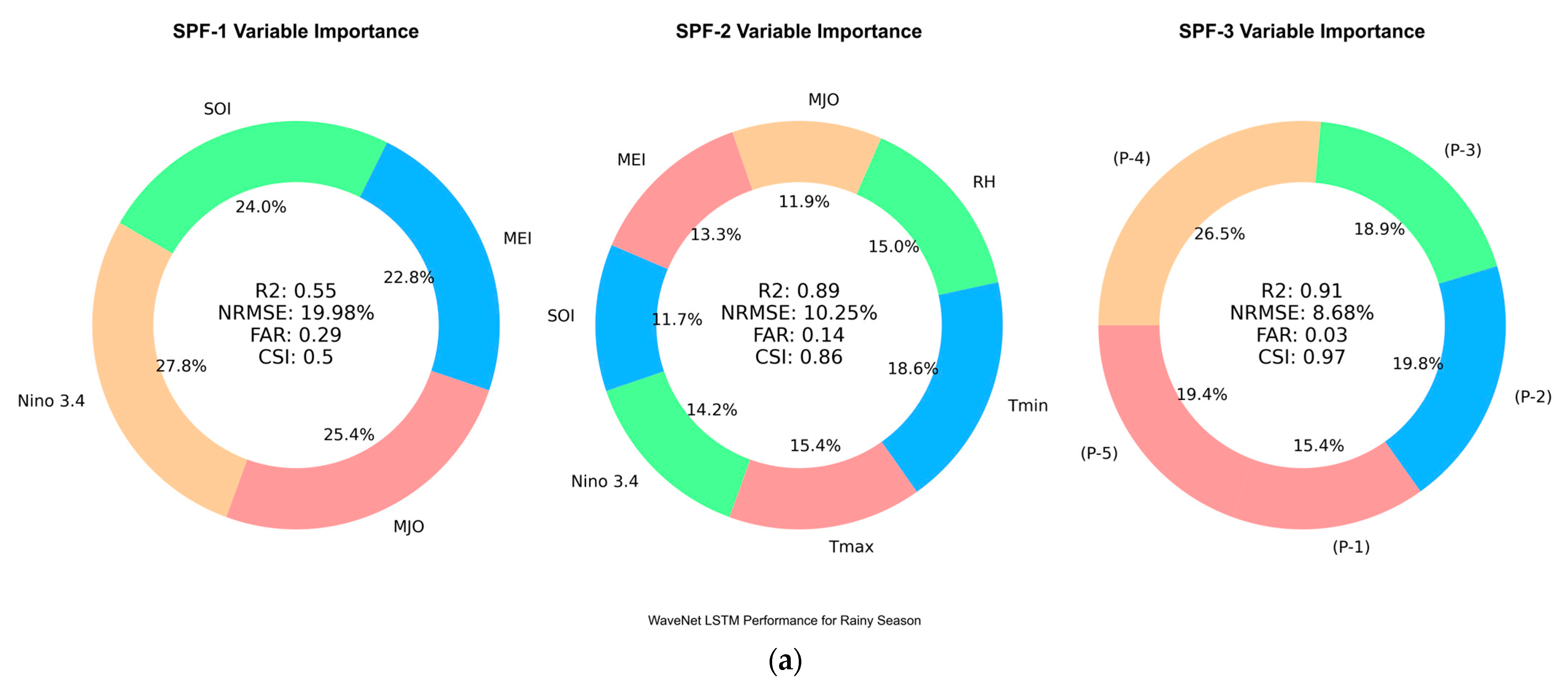
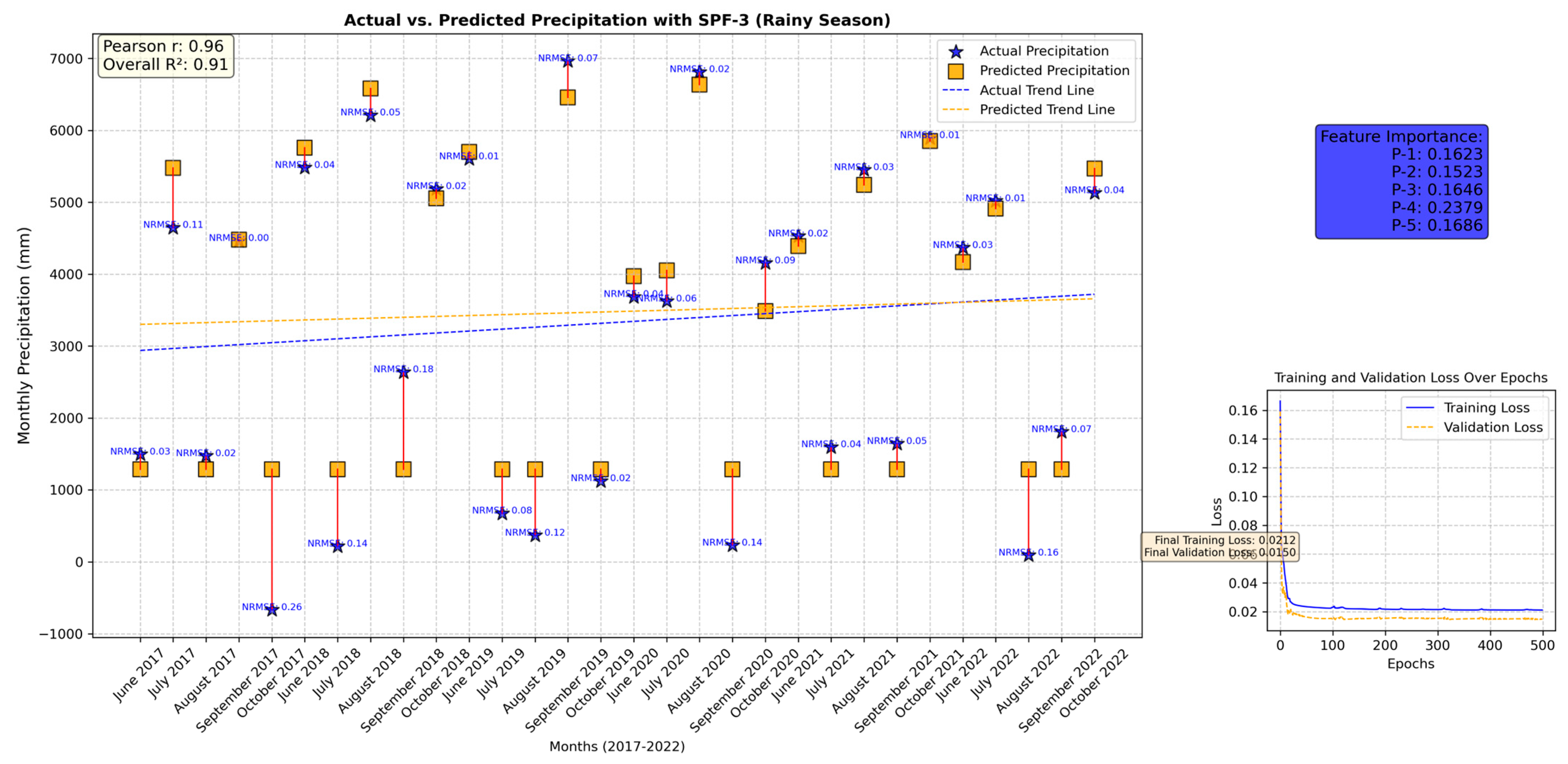
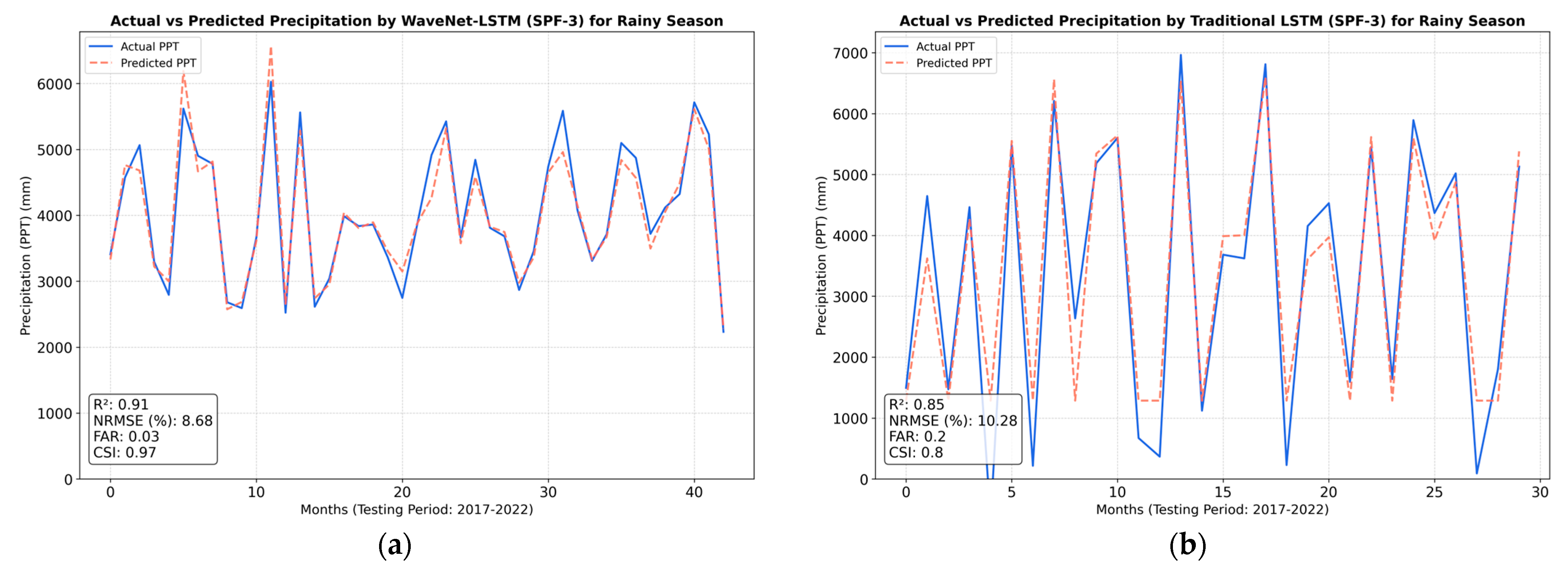
3. Results
3.1. Comparative Analysis and Role of Climate Drivers in Prediction
3.2. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SPF | Seasonal Precipitation Forecasting |
| LSTM | Long Short-Term Memory |
| RNNs | Recurrent Neural Networks |
| WT | Wavelet Transform |
| IOD | Indian Ocean Dipole |
| ENSO | El Niño–Southern Oscillation |
| SOI | Southern Oscillation Index |
| MJO | Madden–Julian Oscillation |
| MEI | Multivariate Enso Index |
| NRMSE | Normalized Root Mean Square Error |
| FAR | False Alarm Ratio |
| CSI | Critical Success Index |
| SOI | Southern Oscillation Index |
| AITs | Artificial Intelligence Techniques |
| ML | Machine Learning |
| DL | Deep Learning |
| ANNs | Artificial Neural Networks |
| RNN | Recurrent Neural Networks |
| GNN | Graph Neural Networks |
| CNN | Conventional Neural Networks |
| TNN | Transformer Neural Network |
| DTs | Decision Trees |
| WANN | Wavelet Artificial Neural Networks |
| TMD | Thai Meteorological Department |
| LSTM-RNN | Long Short-Term Memory Recurrent Neural Network |
| SD | Standard Deviation |
| r | Pearson’s Correlation |
| FA | False Alarm |
| OLR | Outgoing Longwave Radiation |
| POD | Probability of Detection |
| MSE | Mean Squared Error |
| R2 | Coefficient of Determination |
| MAE | Mean Absolute Error |
| DWT | Discrete wavelet transforms |
| CWT | Continuous wavelet transforms |
References
- Lu, S.; Zhu, G.; Meng, G.; Lin, X.; Liu, Y.; Qiu, D.; Xu, Y.; Wang, Q.; Chen, L.; Li, R. Influence of atmospheric circulation on the stable isotope of precipitation in the monsoon margin region. Atmos. Res. 2024, 298, 107131. [Google Scholar] [CrossRef]
- Portele, T.C.; Lorenz, C.; Dibrani, B.; Laux, P.; Bliefernicht, J.; Kunstmann, H. Seasonal forecasts offer economic benefit for hydrological decision making in semi-arid regions. Sci. Rep. 2021, 11, 10581. [Google Scholar]
- Li, Q.; Wang, T.; Wang, F.; Liang, X.Z.; Zhao, C.; Dong, L.; Zhao, C.; Xie, B. Dynamical downscaling simulation of the East Asian summer monsoon in a regional Climate-Weather Research and Forecasting Model. Int. J. Climatol. 2021, 41, E1700–E1716. [Google Scholar] [CrossRef]
- Muangsong, C.; Cai, B.; Pumijumnong, N.; Hu, C.; Cheng, H. An annually laminated stalagmite record of the changes in Thailand monsoon rainfall over the past 387 years and its relationship to IOD and ENSO. Quat. Int. 2014, 349, 90–97. [Google Scholar] [CrossRef]
- Konapala, G.; Mishra, A.K.; Wada, Y.; Mann, M.E. Climate change will affect global water availability through compounding changes in seasonal precipitation and evaporation. Nat. Commun. 2020, 11, 3044. [Google Scholar] [CrossRef]
- Huang, X.; Ding, A. Aerosol as a critical factor causing forecast biases of air temperature in global numerical weather prediction models. Sci. Bull. 2021, 66, 1917–1924. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Chen, N.; Chen, Z.; Zhang, C.; Yu, H. Spatiotemporal forecasting in earth system science: Methods, uncertainties, predictability and future directions. Earth-Sci. Rev. 2021, 222, 103828. [Google Scholar] [CrossRef]
- Hossain, I.; Rasel, H.; Imteaz, M.A.; Mekanik, F. Long-term seasonal rainfall forecasting using linear and non-linear modelling approaches: A case study for Western Australia. Meteorol. Atmos. Phys. 2020, 132, 131–141. [Google Scholar] [CrossRef]
- Boonwichai, S.; Shrestha, S.; Babel, M.S.; Weesakul, S.; Datta, A. Climate change impacts on irrigation water requirement, crop water productivity and rice yield in the Songkhram River Basin, Thailand. J. Clean. Prod. 2018, 198, 1157–1164. [Google Scholar] [CrossRef]
- Limsakul, A.; Singhruck, P. Long-term trends and variability of total and extreme precipitation in Thailand. Atmos. Res. 2016, 169, 301–317. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W.; Wangwongchai, A.; Dechpichai, P.; Zarin, R.; Hlaing, P.T. Incorporating novel input variable selection method for in the different water basins of Thailand. Alex. Eng. J. 2024, 86, 557–576. [Google Scholar] [CrossRef]
- Xoplaki, E.; González-Rouco, J.; Luterbacher, J.; Wanner, H. Wet season Mediterranean precipitation variability: Influence of large-scale dynamics and trends. Clim. Dyn. 2004, 23, 63–78. [Google Scholar] [CrossRef]
- Yang, S.; Li, Z.; Yu, J.-Y.; Hu, X.; Dong, W.; He, S. El Niño–Southern Oscillation and its impact in the changing climate. Natl. Sci. Rev. 2018, 5, 840–857. [Google Scholar] [CrossRef]
- Wang, C.; Deser, C.; Yu, J.-Y.; DiNezio, P.; Clement, A. El Niño and southern oscillation (ENSO): A review. In Coral Reefs of the Eastern Tropical Pacific: Persistence and Loss in a Dynamic Environment; Springer: Dordrecht, The Netherlands, 2017; pp. 85–106. [Google Scholar]
- Trakolkul, C.; Charoenphon, C.; Satirapod, C. Impact of El Niño--Southern Oscillation (ENSO) on the Precipitable Water Vapor in Thailand from Long Term GPS Observation. Int. J. Geoinform. 2022, 18, 13–20. [Google Scholar]
- Mukherjee, S.; Pal, J.; Manna, S.; Saha, A.; Das, D. El-Niño Southern Oscillation and its effects. In Visualization Techniques for Climate Change with Machine Learning and Artificial Intelligence; Elsevier: Amsterdam, The Netherlands, 2023; pp. 207–228. [Google Scholar]
- Generoso, R.; Couharde, C.; Damette, O.; Mohaddes, K. The growth effects of El Nino and La Nina: Local weather conditions matter. Ann. Econ. Stat. 2020, 140, 83–126. [Google Scholar] [CrossRef]
- Howard, E.; Thomas, S.; Frame, T.H.; Gonzalez, P.L.; Methven, J.; Martínez-Alvarado, O.; Woolnough, S.J. Weather patterns in Southeast Asia: Relationship with tropical variability and heavy precipitation. Q. J. R. Meteorol. Soc. 2022, 148, 747–769. [Google Scholar] [CrossRef]
- Räsänen, T.A.; Kummu, M. Spatiotemporal influences of ENSO on precipitation and flood pulse in the Mekong River Basin. J. Hydrol. 2013, 476, 154–168. [Google Scholar] [CrossRef]
- Singhrattna, N.; Rajagopalan, B.; Kumar, K.K.; Clark, M. Interannual and interdecadal variability of Thailand summer monsoon season. J. Clim. 2005, 18, 1697–1708. [Google Scholar] [CrossRef]
- Buckley, B.M.; Palakit, K.; Duangsathaporn, K.; Sanguantham, P.; Prasomsin, P. Decadal scale droughts over northwestern Thailand over the past 448 years: Links to the tropical Pacific and Indian Ocean sectors. Clim. Dyn. 2007, 29, 63–71. [Google Scholar] [CrossRef]
- Prasanna, K.; Chowdary, J.S.; Naidu, C.; Gnanaseelan, C.; Parekh, A. Diversity in ENSO remote connection to northeast monsoon rainfall in observations and CMIP5 models. Theor. Appl. Climatol. 2020, 141, 827–839. [Google Scholar] [CrossRef]
- Shimizu, M.H.; Ambrizzi, T.; Liebmann, B. Extreme precipitation events and their relationship with ENSO and MJO phases over northern South America. Int. J. Climatol. 2017, 37, 2977–2989. [Google Scholar] [CrossRef]
- Loo, Y.Y.; Billa, L.; Singh, A. Effect of climate change on seasonal monsoon in Asia and its impact on the variability of monsoon rainfall in Southeast Asia. Geosci. Front. 2015, 6, 817–823. [Google Scholar] [CrossRef]
- Nakburee, A.; Shrestha, S.; Mohanasundaram, S.; Loc, H.H.; Maharjan, M. Influences of teleconnections on climate variables in northern and northeastern Thailand. J. Water Clim. Chang. 2023, 14, 3460–3483. [Google Scholar] [CrossRef]
- Bridhikitti, A. Multi-decadal trends and oscillations of Southeast Asian monsoon rainfall in northern Thailand. Songklanakarin J. Sci. Technol. 2019, 41, 74–80. [Google Scholar]
- Limsakul, A. Trends in Thailand’s extreme temperature indices during 1955–2018 and their relationship with global mean temperature change. Appl. Environ. Res. 2020, 42, 94–107. [Google Scholar] [CrossRef]
- Taweesin, K.; Seeboonruang, U. The relationship between the climatic indices and the rainfall fluctuation in the lower central plain of Thailand. Int. J. Innov. Comput. Inf. Control 2019, 15, 107–127. [Google Scholar]
- Jin, W.; Luo, Y.; Wu, T.; Huang, X.; Xue, W.; Yu, C. Deep learning for seasonal precipitation prediction over China. J. Meteorol. Res. 2022, 36, 271–281. [Google Scholar] [CrossRef]
- Lavers, D.A. Seasonal Hydrological Prediction in Great Britain—An Assessment; University of Birmingham: Birmingham, UK, 2011. [Google Scholar]
- Bierkens, M.; Van Beek, L. Seasonal predictability of European discharge: NAO and hydrological response time. J. Hydrometeorol. 2009, 10, 953–968. [Google Scholar] [CrossRef]
- Tang, J.; Zheng, L.; Han, C.; Yin, W.; Zhang, Y.; Zou, Y.; Huang, H. Statistical and machine-learning methods for clearance time prediction of road incidents: A methodology review. Anal. Methods Accid. Res. 2020, 27, 100123. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W.; Wangwongchai, A.; Dechpichai, P.; Ahmad, S. Potential of Artificial Intelligence-Based Techniques for Rainfall Forecasting in Thailand: A Comprehensive Review. Water 2023, 15, 2979. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Deng, Q.; Lu, P.; Zhao, S.; Yuan, N. U-Net: A deep-learning method for improving summer precipitation forecasts in China. Atmos. Ocean. Sci. Lett. 2023, 16, 100322. [Google Scholar] [CrossRef]
- Basha, C.Z.; Bhavana, N.; Bhavya, P.; Sowmya, V. Rainfall prediction using machine learning & deep learning techniques. In Proceedings of the 2020 International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 2–4 July 2020; pp. 92–97. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems 28, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Ghosh, A. Spectrum Usage Analysis and Prediction Using Lstm Networks. Master’s Thesis, University of Utah, Salt Lake City, UT, USA, 2020. [Google Scholar]
- Alan, A.R.; Bayındır, C.; Ozaydin, F.; Altintas, A.A. The Predictability of the 30 October 2020 İzmir-Samos Tsunami Hydrodynamics and Enhancement of Its Early Warning Time by LSTM Deep Learning Network. Water 2023, 15, 4195. [Google Scholar] [CrossRef]
- Chase, R.J.; Harrison, D.R.; Lackmann, G.M.; McGovern, A. A machine learning tutorial for operational meteorology. Part II: Neural networks and deep learning. Weather Forecast. 2023, 38, 1271–1293. [Google Scholar] [CrossRef]
- Barnes, A.P.; McCullen, N.; Kjeldsen, T.R. Forecasting seasonal to sub-seasonal rainfall in Great Britain using convolutional-neural networks. Theor. Appl. Climatol. 2023, 151, 421–432. [Google Scholar] [CrossRef]
- Civitarese, D.S.; Szwarcman, D.; Zadrozny, B.; Watson, C. Extreme precipitation seasonal forecast using a transformer neural network. arXiv 2021, arXiv:2107.06846. [Google Scholar]
- Waqas, M.; Shoaib, M.; Saifullah, M.; Naseem, A.; Hashim, S.; Ehsan, F.; Ali, I.; Khan, A. Assessment of advanced artificial intelligence techniques for streamflow forecasting in Jhelum River Basin. Pak. J. Agric. Res. 2021, 34, 580. [Google Scholar] [CrossRef]
- Ghamariadyan, M.; Imteaz, M.A. Prediction of seasonal rainfall with one-year lead time using climate indices: A wavelet neural network scheme. Water Resour. Manag. 2021, 35, 5347–5365. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W.; Hliang, P.T.; Wangwongchai, A.; Dechpichai, P. Advancements in Daily Precipitation Forecasting: A Deep Dive into Daily Precipitation Forecasting Hybrid Methods in the Tropical Climate of Thailand. MethodsX 2024, 12, 102757. [Google Scholar] [CrossRef]
- Sharghi, E.; Nourani, V.; Najafi, H.; Molajou, A. Emotional ANN (EANN) and wavelet-ANN (WANN) approaches for Markovian and seasonal based modeling of rainfall-runoff process. Water Resour. Manag. 2018, 32, 3441–3456. [Google Scholar] [CrossRef]
- Chong, K.L.; Lai, S.H.; Yao, Y.; Ahmed, A.N.; Jaafar, W.Z.W.; El-Shafie, A. Performance enhancement model for rainfall forecasting utilizing integrated wavelet-convolutional neural network. Water Resour. Manag. 2020, 34, 2371–2387. [Google Scholar] [CrossRef]
- Nounmusig, W. Analysis of rainfall in the eastern Thailand. GEOMATE J. 2018, 14, 150–155. [Google Scholar] [CrossRef]
- Khedari, J.; Sangprajak, A.; Hirunlabh, J. Thailand climatic zones. Renew. Energy 2002, 25, 267–280. [Google Scholar] [CrossRef]
- Bordalo, A.; Nilsumranchit, W.; Chalermwat, K. Water quality and uses of the Bangpakong River (Eastern Thailand). Water Res. 2001, 35, 3635–3642. [Google Scholar] [CrossRef]
- Chansawang, B.; Zarin, R.; Wongwises, P.; Waqas, M.; Wangwongchai, A. Efficient and consistent adaptive mesh generation for geophysical models: A case study over the Gulf of Thailand. AIP Adv. 2024, 14, 055135. [Google Scholar] [CrossRef]
- Chitradon, R. Risk Management of Water Resources in Thailand in the Face of Climate Change. 2010. Available online: https://tiwrm.hii.or.th/web/index.php/knowledge/128-hydro-and-weather/295-riskmanagementclimate.html (accessed on 8 August 2024).
- Zhang, Y.; Li, T.; Wang, B.; Wu, G. Onset of the summer monsoon over the Indochina Peninsula: Climatology and interannual variations. J. Clim. 2002, 15, 3206–3221. [Google Scholar] [CrossRef]
- Wangwongchai, A.; Waqas, M.; Dechpichai, P.; Hlaing, P.T.; Ahmad, S.; Humphries, U.W. Imputation of missing daily rainfall data; A comparison between artificial intelligence and statistical techniques. MethodsX 2023, 11, 102459. [Google Scholar] [CrossRef] [PubMed]
- Costa, V.; Fernandes, W.; Naghettini, M. A Bayesian model for stochastic generation of daily precipitation using an upper-bounded distribution function. Stoch. Environ. Res. Risk Assess. 2015, 29, 563–576. [Google Scholar] [CrossRef]
- Grubbs, F.E.; Beck, G. Extension of sample sizes and percentage points for significance tests of outlying observations. Technometrics 1972, 14, 847–854. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci. 1971, 28, 702–708. [Google Scholar] [CrossRef]
- Goodwin, L.D.; Leech, N.L. Understanding correlation: Factors that affect the size of r. J. Exp. Educ. 2006, 74, 249–266. [Google Scholar] [CrossRef]
- Song, L.; Chen, S.; Chen, W.; Chen, X. Distinct impacts of two types of La Niña events on Australian summer rainfall. Int. J. Climatol. 2017, 37, 2532–2544. [Google Scholar] [CrossRef]
- Meyers, G.; McIntosh, P.; Pigot, L.; Pook, M. The years of El Niño, La Niña, and interactions with the tropical Indian Ocean. J. Clim. 2007, 20, 2872–2880. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W. A critical review of RNN and LSTM variants in hydrological time series predictions. MethodsX 2024, 13, 102946. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Halidou, A.; Mohamadou, Y.; Ari, A.A.A.; Zacko, E.J.G. Review of wavelet denoising algorithms. Multimed. Tools Appl. 2023, 82, 41539–41569. [Google Scholar] [CrossRef]
- Rhif, M.; Ben Abbes, A.; Farah, I.R.; Martínez, B.; Sang, Y. Wavelet transform application for/in non-stationary time-series analysis: A review. Appl. Sci. 2019, 9, 1345. [Google Scholar] [CrossRef]
- Hurley, C. Wavelet: Analysis and Methods; Scientific e-Resources: New Delhi, India, 2018. [Google Scholar]
- Scolaro, G.; Azevedo, F.; Boos, C. Evaluation of different wavelet functions applied in the development of digital filters to attenuate the background activity in EEG signals. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Beijing, China, 26–31 May 2012; pp. 340–343. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Lee, J.-H.; Na, S.-H. Predictor-estimator using multilevel task learning with stack propagation for neural quality estimation. In Proceedings of the Second Conference on Machine Translation, Copenhagen, Denmark, 7–8 September 2017; pp. 562–568. [Google Scholar]
- Shoaib, M.; Shamseldin, A.Y.; Khan, S.; Khan, M.M.; Khan, Z.M.; Sultan, T.; Melville, B.W. A comparative study of various hybrid wavelet feedforward neural network models for runoff forecasting. Water Resour. Manag. 2017, 32, 83–103. [Google Scholar] [CrossRef]
- Shcherbakov, M.V.; Brebels, A.; Shcherbakova, N.L.; Tyukov, A.P.; Janovsky, T.A.; Kamaev, V.A. A survey of forecast error measures. World Appl. Sci. J. 2013, 24, 171–176. [Google Scholar]
- Nayak, M.A.; Ghosh, S. Prediction of extreme rainfall event using weather pattern recognition and support vector machine classifier. Theor. Appl. Climatol. 2013, 114, 583–603. [Google Scholar] [CrossRef]
- Gerapetritis, H.; Pelissier, J.M. On the BEHAVIOR of the Critical Success Index. 2004. Available online: https://repository.library.noaa.gov/view/noaa/6657 (accessed on 15 August 2024).
- Srivastava, K. Significant Improvement in Rainfall Forecast over Delhi: Annual and Seasonal Verification. J. Atmos. Sci. Res. 2022, 5, 10–25. [Google Scholar] [CrossRef]
- Mekonnen, K.; Melesse, A.M.; Woldesenbet, T.A. Spatial evaluation of satellite-retrieved extreme rainfall rates in the Upper Awash River Basin, Ethiopia. Atmos. Res. 2021, 249, 105297. [Google Scholar] [CrossRef]
- Pour, S.H.; Abd Wahab, A.K.; Shahid, S. Physical-empirical models for prediction of seasonal rainfall extremes of Peninsular Malaysia. Atmos. Res. 2020, 233, 104720. [Google Scholar] [CrossRef]
- Ashok, K.; Behera, S.K.; Rao, S.A.; Weng, H.; Yamagata, T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. Ocean. 2007, 112, C11007. [Google Scholar] [CrossRef]
- Wang, G.; Sun, Y.; Wang, J. Automatic image-based plant disease severity estimation using deep learning. Comput. Intell. Neurosci. 2017, 2017, 1–8. [Google Scholar] [CrossRef]
- Li, S.; Hou, W.; Feng, G. Atmospheric circulation patterns over East Asia and their connection with summer precipitation and surface air temperature in Eastern China during 1961–2013. J. Meteorol. Res. 2018, 32, 203–218. [Google Scholar] [CrossRef]
- Wood, A.W.; Kumar, A.; Lettenmaier, D.P. A retrospective assessment of National Centers for Environmental Prediction climate model–based ensemble hydrologic forecasting in the western United States. J. Geophys. Res. Atmos. 2005, 110, D0410. [Google Scholar] [CrossRef]
- Kumar, B.; Abhishek, N.; Chattopadhyay, R.; George, S.; Singh, B.B.; Samanta, A.; Patnaik, B.; Gill, S.S.; Nanjundiah, R.S.; Singh, M. Deep learning based short-range forecasting of Indian summer monsoon rainfall using earth observation and ground station datasets. Geocarto Int. 2022, 37, 17994–18021. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, L.; Chen, L.; Wang, D.; Dai, M.; Xu, W.; Yan, T. Water compensation and its implication of the Three Gorges Reservoir for the river-lake system in the middle Yangtze River, China. Water 2018, 10, 1011. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Maloney, E.D.; Kiehl, J.T. MJO-related SST variations over the tropical eastern Pacific during Northern Hemisphere summer. J. Clim. 2002, 15, 675–689. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Regional climate models for hydrological impact studies at the catchment scale: A review of recent modeling strategies. Geogr. Compass 2010, 4, 834–860. [Google Scholar] [CrossRef]





| Stations | Summer (Mid-Feb to Mid-May) | Rainy (Mid-May to Mid-Oct) | Winter (Mid-Oct to Mid-Feb) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Min | Max | SD | CV | Skew | Mean | Min | Max | SD | CV | Skew | Mean | Min | Max | SD | CV | Skew | |
| Chacoeng Sao Agro | 3.80 | 0 | 101.60 | 9.55 | 2.52 | 4.11 | 6.33 | 0 | 130.50 | 11.96 | 1.89 | 3.40 | 1.16 | 0 | 88.90 | 4.64 | 3.99 | 10.06 |
| Chonburi | 2.84 | 0 | 105.40 | 8.76 | 3.08 | 5.21 | 6.16 | 0 | 163.40 | 13.14 | 2.13 | 3.95 | 0.99 | 0 | 74.00 | 4.00 | 4.02 | 7.48 |
| Ko Sichang | 2.40 | 0 | 105.20 | 8.06 | 3.36 | 5.51 | 5.57 | 0 | 184.00 | 12.50 | 2.25 | 4.25 | 1.03 | 0 | 95.70 | 5.10 | 4.94 | 9.83 |
| Pattaya | 2.26 | 0 | 113.30 | 7.73 | 3.42 | 5.37 | 5.20 | 0 | 194.20 | 12.75 | 2.45 | 5.07 | 1.14 | 0 | 64.50 | 4.91 | 4.32 | 7.12 |
| Sattahip | 3.16 | 0 | 156.20 | 10.33 | 3.27 | 6.11 | 6.23 | 0 | 244.40 | 14.54 | 2.33 | 5.61 | 1.57 | 0 | 80.10 | 5.60 | 3.57 | 6.53 |
| Rayong | 3.35 | 0 | 128.40 | 10.70 | 3.19 | 5.20 | 6.50 | 0 | 193.00 | 14.80 | 2.28 | 4.27 | 1.27 | 0 | 147.50 | 5.76 | 4.52 | 11.36 |
| Huai Pong Agro | 3.91 | 0 | 123.00 | 10.98 | 2.81 | 5.01 | 7.05 | 0 | 183.90 | 14.19 | 2.01 | 3.85 | 1.74 | 0 | 111.30 | 6.29 | 3.63 | 7.15 |
| Chantaburi | 5.92 | 0 | 135.00 | 13.81 | 2.33 | 3.80 | 15.23 | 0 | 394.90 | 25.21 | 1.65 | 3.83 | 1.94 | 0 | 113.80 | 6.13 | 3.16 | 6.68 |
| Phlew Agro | 6.86 | 0 | 204.80 | 15.34 | 2.23 | 4.48 | 16.98 | 0 | 409.50 | 27.37 | 1.61 | 3.44 | 2.25 | 0 | 96.30 | 6.79 | 3.02 | 5.42 |
| Khlong Yai | 7.98 | 0 | 164.40 | 15.77 | 1.98 | 3.43 | 25.95 | 0 | 445.30 | 40.32 | 1.55 | 3.26 | 3.16 | 0 | 102.40 | 8.23 | 2.60 | 4.33 |
| Laem Chabang Port | 2.18 | 0 | 100.20 | 7.15 | 3.29 | 5.55 | 5.27 | 0 | 126.00 | 11.75 | 2.23 | 3.94 | 0.99 | 0 | 176.50 | 5.06 | 5.14 | 17.97 |
| Prachin Buri | 3.10 | 0 | 189.00 | 10.67 | 3.45 | 6.25 | 8.95 | 0 | 194.90 | 16.90 | 1.89 | 3.44 | 0.44 | 0 | 72.90 | 3.39 | 7.73 | 13.96 |
| Kabin Buri | 2.97 | 0 | 125.40 | 9.54 | 3.21 | 5.48 | 7.75 | 0 | 159.90 | 14.21 | 1.83 | 3.14 | 0.58 | 0 | 99.70 | 4.23 | 7.24 | 14.12 |
| Sakaew | 2.06 | 0 | 119.90 | 7.17 | 3.49 | 5.99 | 5.41 | 0 | 181.50 | 12.13 | 2.24 | 4.54 | 0.49 | 0 | 70.40 | 3.17 | 6.45 | 13.02 |
| Large-Scale Climate Drivers | Spatial Domain | Technical Description | Data Source |
|---|---|---|---|
| NIÑO3.4 | (5 S–5 N,170 W–120 W) | The ENSO phenomenon is recognized via two leading indicators: (a) the SOI, which measures anomalies in sea level pressure between Darwin and Tahiti, and (b) SST anomalies, assessed using the Niño indices: Niño3, Niño4, and Niño3.4 in the equatorial Pacific Ocean [8]. | https://www.cpc.ncep.noaa.gov/data/indices/sstoi.indices (accessed on 12 February 2024) |
| NIÑO3 | (5 N–5 S, 150 W–90 W) | ||
| NIÑO4 | (5 N–5 S, 160 E–150 W) | ||
| NIÑO1+2 | (0–10 S, 90 W–80 W) | ||
| IOD | (50° E–70° E and 10° S–10° N) (90° E–110° E and 10° S–0° S) | The IOD is measured using the DMI, which represents the difference in average sea surface temperature anomalies between the tropical western Indian Ocean (50° E–70° E, 10° S–10° N) and the tropical Eastern Indian Ocean (90° E–110° E, 10° S–0° S). | https://psl.noaa.gov/gcos_wgsp/Timeseries/Data/dmi.had.long.data (accessed on 12 February 2024) |
| SOI | --- | The SOI reflects anomalies in sea level pressures between Darwin and Tahiti [8]. | https://climexp.knmi.nl (accessed on 12 February 2024) |
| MJO | --- | The MJO is an eastward-moving cloud and rainfall pattern that takes 30 to 60 days to return to its starting point. Unlike ENSO, the MJO’s characteristics vary weekly, offering intra-seasonal tropical climate variability. Multiple MJO events can occur in a single season [57]. | https://iridl.ldeo.columbia.edu/SOURCES/.BoM/.MJO/.RMM/.RMM1/ (accessed on 12 February 2024) |
| MEI | (30° S–30° N, 100° E–70° W) | The MEI is a time series from an EOF analysis of sea level pressure, sea surface temperature, wind components, and OLR in the tropical Pacific. It accounts for ENSO seasonality across overlapping two-month periods to minimize intra-seasonal variability. | https://psl.noaa.gov/enso/mei/ (accessed on 12 February 2024) |
| Model/ Target | Features | ||
|---|---|---|---|
| Summer | Rainy | Winter | |
| SPF-1/PPT | Niño 1+2FMAM, MJOFMAM, MEIFMAM, SOIFMAM | MJOMJJASO, MEIMJJASO, Niño 3.4MJJASO, SOIMJJASO | Niño 3ONDJF, Niño 3.4ONDJF, Niño 4ONDJF, SOIONDJF |
| SPF-2/PPT | TminFMAM, TmaxFMAM, RHFMAM, Niño 1+2FMAM, MEIFMAM, MJOFMAM, SOIFMAM | TminMJJASO, TmaxMJJASO, RHMJJASO, MJOMJJASO, MEIMJJASO, Niño 3.4MJJASO, SOIMJJASO | TminONDJF, TmaxONDJF, RHONDJF, Niño 3ONDJF, Niño 3.4ONDJF, Niño 4ONDJF, SOIONDJF |
| SPF-3/PPT | P(t − 1) FMAM, P(t − 2) FMAM, P(t − 3) FMAM, P(t − 4) FMAM and P(t − 5) FMAM | P(t − 1) MJJASO, P(t − 2) MJJASO, P(t − 3) MJJASO, P(t − 4) MJJASO and P(t − 5) MJJASO | P(t − 1) ONDJF, P(t − 2) ONDJF, P(t − 3) ONDJF, P(t − 4) ONDJF and P(t − 5) ONDJF |
| Feature Name | Optimal Configuration | Mathematical Description |
|---|---|---|
| Features | Large-scale climate drivers, Tmax, Tmin, RH, and Lagged PPT | (2) (3) (4) (5) (6) (7) The weight matrices and bias for the input, forget, cell candidate, and output gates are denoted by “W” and “b”, respectively. “Xt” represents the memory cell’s input, “ht−1” represents the hidden state at the previous time step “t − 1”, and “Ct−1” and “Ct” represent the cell states at the previous time step “t − 1” and the current time step “t”, respectively. |
| Responses | Precipitation in mm | |
| No. of hidden nodes | 50 in each LSTM layer | |
| Optimizer | Adam | |
| Learning rate | 0.001 | |
| Epoch | 500 | |
| Wavelet decomposition | bior2.2 at level 2 | |
| LSTM Layer Configuration 1 | LSTM (50, activation = ‘tanh’, return sequences = True) | |
| LSTM Layer Configuration 2 | LSTM (50, activation = ‘tanh’) | |
| Dense Layer Configuration 1 | Dense (20, activation = ‘tanh’) | |
| Dense Layer Configuration 2 | Dense (20, activation = ‘sigmoid’) | |
| Output Layer | Dense (1, activation = ‘sigmoid’) | |
| Bias Initialization | Unit-forget-gate bias initialization | |
| Function (gates) | Sigmoid activation function | |
| Function (input weights) | Orthogonal initialization for input weights | |
| Function (recurrent weights) | Bi-orthogonal initialization for recurrent weights | |
| Performance metrics | R2, NRMSE, FAR, CSI |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waqas, M.; Humphries, U.W.; Hlaing, P.T.; Ahmad, S. Seasonal WaveNet-LSTM: A Deep Learning Framework for Precipitation Forecasting with Integrated Large Scale Climate Drivers. Water 2024, 16, 3194. https://doi.org/10.3390/w16223194
Waqas M, Humphries UW, Hlaing PT, Ahmad S. Seasonal WaveNet-LSTM: A Deep Learning Framework for Precipitation Forecasting with Integrated Large Scale Climate Drivers. Water. 2024; 16(22):3194. https://doi.org/10.3390/w16223194
Chicago/Turabian StyleWaqas, Muhammad, Usa Wannasingha Humphries, Phyo Thandar Hlaing, and Shakeel Ahmad. 2024. "Seasonal WaveNet-LSTM: A Deep Learning Framework for Precipitation Forecasting with Integrated Large Scale Climate Drivers" Water 16, no. 22: 3194. https://doi.org/10.3390/w16223194
APA StyleWaqas, M., Humphries, U. W., Hlaing, P. T., & Ahmad, S. (2024). Seasonal WaveNet-LSTM: A Deep Learning Framework for Precipitation Forecasting with Integrated Large Scale Climate Drivers. Water, 16(22), 3194. https://doi.org/10.3390/w16223194









